Micromechanics of elastic lamellae: unravelling the role of structural inhomogeneity in multi-scale arterial mechanics

Abstract

Microstructural deformation of elastic lamellae plays important roles in maintaining arterial tissue homeostasis and regulating vascular smooth muscle cell fate. Our study unravels the underlying microstructural origin that enables elastic lamellar layers to evenly distribute the stresses through the arterial wall caused by intraluminal distending pressure, a fundamental requirement for tissue and cellular function. A new experimental approach was developed to quantify the spatial organization and unfolding of elastic lamellar layers under pressurization in mouse carotid arteries by coupling physiological extension–inflation and multiphoton imaging. Tissue-level circumferential stretch was obtained from analysis of the deformation of a thick-walled cylinder. Our results show that the unfolding and extension of lamellar layers contribute simultaneously to tissue-level deformation. The inner lamellar layers are wavier and unfold more than the outer layers. This waviness gradient compensates the larger tissue circumferential stretch experienced at the inner surface, thus equalizing lamellar layer extension through the arterial wall. Discoveries from this study reveal the importance of structural inhomogeneity in maintaining tissue homeostasis through the arterial wall, and may have profound implications on vascular remodelling in aging and diseases, as well as in tissue engineering of functional blood vessels.

1. Introduction

Elastic fibre is an extracellular matrix (ECM) constituent that endows many connective tissues of vertebrates with unique mechanical and biological functionality [1]. In arteries, elastic fibres form concentric layers of elastic lamella that are subjected to billions of stretch cycles during a lifetime. Alternating layers of smooth muscle cells anchor on either side to the adjacent lamellar layers through elastin extensions that forms a contractile–elastic lamellar unit [2,3]. It has been well documented that organized elastic lamellar units are crucial for vascular smooth muscle cells (VSMCs) to maintain their quiescent and contractile states [4–16]. Disruption of elastic fibres leads VSMCs to dedifferentiate, migrate, proliferate and occlude arteries [17].

The lamellar units support and evenly distribute the stresses in the arterial wall caused by intraluminal distending pressure and plays an important role in maintaining tissue homeostasis [1]. Wall stress distribution can alter the local permeability and pressure gradient, which governs many important physiological events [18]. Early studies found that the number of aortic lamellae layers is linearly proportional to the artery diameter, with a few layers for mouse while more than 50 layers for human [19]. According to the law of Laplace, the tangential wall tension is the product of artery diameter and distending pressure. Considering that the species variation in mean blood pressure is quite small compared with the range of wall diameters, the average tension in each lamellae layer was suggested to be about same regardless of species [19]. These earlier insightful findings pointed out the important role of elastic lamella as a fundamental functional unit in biology, however it is still unclear as to how the highly ordered concentric lamellar layers in the arterial wall are able to evenly distribute the stress radially through the arterial wall. Stress analysis of a homogeneous thick cylindrical wall subjected to intraluminal pressure showed that the inner luminal surface experiences higher wall stress/strain than the outer surface of the arterial wall [20]. Findings in the 1960s suggest the existence of residual stress in an artery even when there is no distending pressure [21], although the origin of residual stress is still not well understood. Since then, residual stress has been considered in numerous computational models by including a stress-free configuration, which induces a negative stress gradient in the arterial wall with negative stress at the lumen surface [18]. With such phenomenological compensation, a more evenly distributed wall stress can be achieved, however to date, there is no understanding on whether there are any structurally build-in mechanisms to enable the elastic lamellar layers in the arteries to accommodate the pulsatile blood flow and evenly distribute the wall stress transmurally.

The role of the ECM in maintaining vascular homeostasis cannot be overstated. Waviness of elastic lamellae was noticed in transverse histological section of arterial tissue in early studies [1]. Several previous studies on the structure of elastic lamellae relying on histological analysis of biological tissue found that the elastic lamellar layers uncoil when subjected to deformation [22,23]. However, tissue fixation, histological preparation, and tissue retraction upon removal of mechanical loading may alter the structure of the ECM [22,24,25]. Moreover, the three-dimensional architecture of elastic lamellae cannot be captured by single histological slices. The micromechanics of elastic lamellae at physiological loading are not fully understood [26] and to date the local deformation at the lamellar level has not been measured directly.

Here, we studied the micromechanics of elastic lamellae layers through integrated three-dimensional multiphoton imaging, tissue-level mechanical characterization and constitutive modelling. Multiphoton microscopy was used to visualize the microstructural deformation of elastic lamellae in mouse carotid arteries under physiological pressurization and axial stretching. The three-dimensional structure of the elastic lamellae was reconstructed in order to analyse its spatial distribution and unfolding under biaxial mechanical loading. Combined with a structurally motivated constitutive model that considers thick-walled cylindrical deformation, our study investigates the structural basis underlying the micromechanics of elastic lamellae and its relationship with tissue-level vascular mechanics. By combining the deformation of elastic lamellae and constitutive modelling, we developed a new approach to quantify the local deformation of elastic lamellae and discovered the importance of structural inhomogeneity in multiscale tissue mechanics.

2. Methods

2.1. Sample preparation

All animal experimental procedures were approved by the institutional animal care and use committee (IACUC) at Boston University Medical Campus. Carotid arteries were gently isolated from eight-week-old C57BL/6 J mice and dissected free of fat and connective tissue. Arteries were maintained at 4°C in 1× phosphate-buffered saline (PBS) and were imaged and tested within 24 h of harvesting. Nine 5 mm carotid segments were sectioned from the arteries. Four segments were used for imaging and five samples were used for mechanical testing.

2.2. Multiphoton microscopy

A mode-locked Ti:sapphire laser (Maitai-HP, excitation wavelength 800 nm, Spectra-Physics, Santa Clara, CA) was used to generate second-harmonic generation from collagen at 400 nm (417/80 nm) and two-photon-excited fluorescence from elastin (525/45 nm), as we previously described [27]. The laser power was set to 80 mW to image as deep as possible without causing saturation of the two-photon-excited fluorescence from elastin at the external elastic lamella.

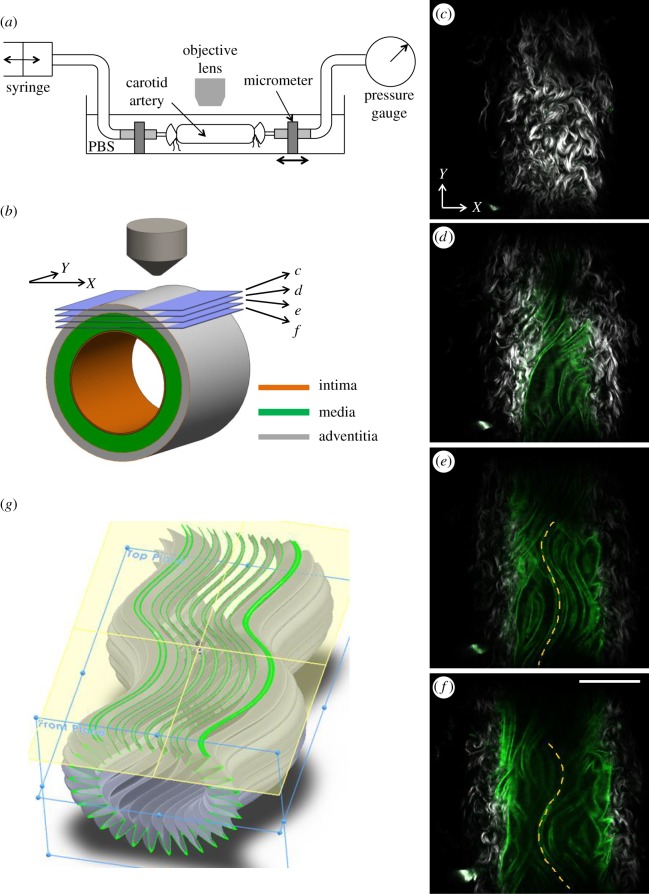
A custom-made tissue stretching–inflation chamber was made that allows biaxial stretching–pressurization deformation while the artery was being imaged (figure 1a,b). Briefly, each arterial segment was cannulated and secured on stainless steel cannulas with 6-O suture and immersed in PBS solution bath at room temperature during imaging. The arterial segment was pressurized with PBS through the inlet tube. The pressure in the artery was measured with a pressure gauge that was connected to the outlet of the cannula. A longitudinal stretch was applied to the segment through a micrometer that was connected to the cannula. Samples were imaged under intraluminal pressure from 0 to 120 mmHg (0, 15, 30, 45, 60, 90 and 120 mmHg) at axial stretching from 1 to 1.8 (1.0, 1.3, 1.4, 1.6 and 1.8). Each sample was imaged with a field of view of 360 µm × 360 µm to a depth of about 50 µm with 2 µm spacing from the outer surface of the arterial wall using a water immersion objective (60×, NA 1.0 W, LUMPlanN, Olympus). The acquired images were stored in Z-stacks (figure 1c–f) and used for subsequent image analysis.

Figure 1.

Multiphoton imaging while the artery undergoes mechanical loading. (a) Schematic of the experimental set-up. A multiphoton microscope was used to image the elastic lamellar layers in a mouse carotid artery while the artery underwent biaxial extension–inflation. (b) Schematic of a carotid artery with intima, media and adventitia layers. Horizontal slices represent the multiphoton imaging planes shown in (c–f). (c–f) Representative multiphoton images of a carotid artery. Grey, SHG from collage; green, fluorescence from elastin; scale bar: 100 µm. (c) Wavy collagen fibres in the adventitial layer. (d–f) Both adventitial collagen and medial elastin are visible. The longitudinally undulated elastic lamella is highlighted in (e,f). (g) Schematic of an elastic lamella that is wavy in both circumferential and longitudinal directions. The green wavy lines in (g) represent slices of elastic lamella appearing in the multiphoton images.

2.3. Three-dimensional reconstruction of elastic lamellae and imaging analysis

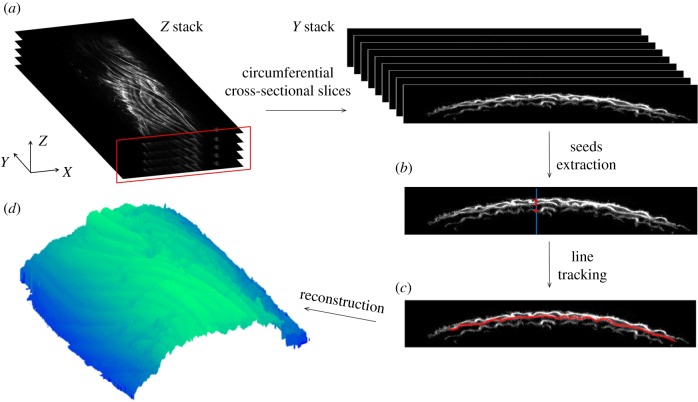
To quantify lamellar unfolding during mechanical deformation, a custom image processing procedure was developed using the MATLAB Image Processing Toolbox (version R2013b, The MathWorks, Inc., Natick, MA). To generate a transverse cross-sectional view of the elastic lamella, first the acquired Z-stack images along the radial direction were reorganized into a Y-stack along the longitudinal direction in MATLAB (figure 2a). In each of the Y-stack images, an intensity threshold value (5 on 8-bit scale) was chosen to eliminate the background. Object connectivity analysis was then performed using the bwconncomp function to identify the connected components and remove isolated signals with less than 8 pixels [28].

Figure 2.

Three-dimensional reconstruction of elastic lamellae and imaging analysis. (a) The original Z-stack multiphoton images were resliced along the longitudinal direction (y-axis) to show the transverse cross-sectional view of the elastic lamellae. An image processing algorithm was performed to reconstruct the lamellar layers and consisted primarily of (b) extraction of seed points and (c) line tracking from the seed points to identify the three layers. (d) Representative image of a reconstructed elastic lamella.

Three to four layers of elastic lamellae were observed in intact mouse carotid arteries. The first three layers of elastic lamellae were used for three-dimensional reconstruction and analysis. The fourth layer could not systematically be visualized and its reconstruction was not reliable due to the low signal-to-noise ratio. No analysis of this layer was therefore conducted. As the elastic lamellae layers have decreasing light intensity through the arterial wall, a simple thresholding segmentation method is not enough to separate out the elastic lamellae. Considering the lamellar layers have a continuous structure and are very thin (approx. 2 µm), a line-tracking method was used to reconstruct the three-dimensional elastic lamellae [29]. From the fluorescence intensity profile along the Z-direction, peaks corresponding to the first three lamellar layers were identified (figure 2b). The corresponding pixels were extracted as seed points for line tracking. Then one of the eight adjacent pixels with maximum light intensity value were selected as the next seed point. Pixels that were already extracted were excluded from the search. The line-tracking algorithm terminates when all the eight adjacent pixels reached a value of zero (figure 2c). Using this method, the centreline of an individual elastic lamella was tracked in each Y-stack image and was used to reconstruct the three-dimensional lamellar layer (figure 2d).

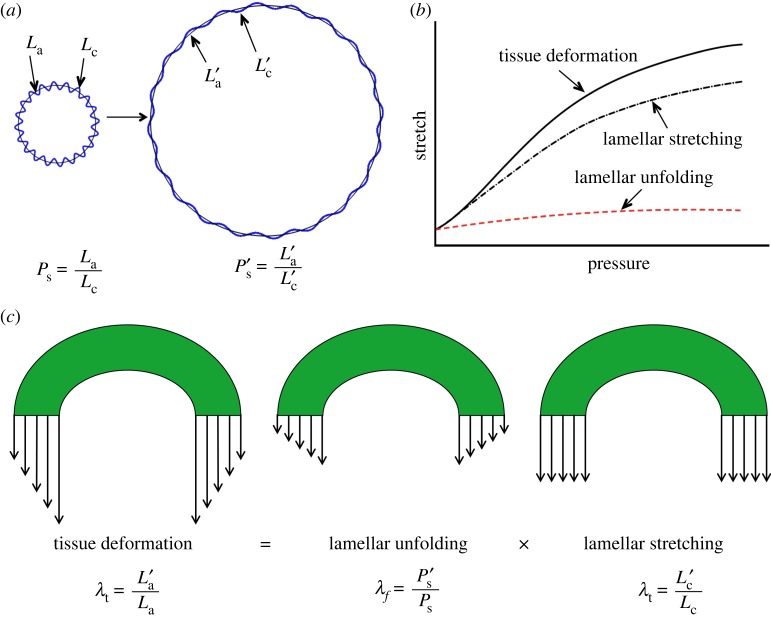
Structural analysis was performed on the three-dimensional reconstructed elastic lamella. Based on the extracted centre lines of the lamellar layers (L1, L2 and L3), corresponding concentric arcs along the arterial wall were computed based on a least-squares fit [30]. The straightness parameter, defined as the ratio between the length of fitted arcs L_a and the contour length of the lamella L_c, was calculated and denoted as P_s (figure 3b).

2.1

Figure 3.

Microstructural quantification of elastic lamellae during tissue deformation. (a) Reconstructed transverse cross-sectional images revealing elastic lamellar layers L1, L2 and L3 (with L1 being the outermost layer) in the arterial wall at 0, 15, 30, 45, 60, 90 and 120 mmHg. The axial stretch was 1.6. Scale bar: 50 µm. (b) Schematic of the three elastic lamellar layers in the arterial wall. The inter-lamellar distance and the straightness parameter P_s, which is the ratio of arc length L_a to contour length L_c, are also defined. (c) Straightness parameter as a function of pressure for the three lamellar layers. (d) Unfolding of elastic lamellar layers in a mouse carotid artery when pressure increases from 0 to 120 mmHg at an axial stretch of 1.6. (Online version in colour.)

Interlamellae distance can be evaluated by calculating the difference between the radii of the fitted arcs (figure 3b). In each sample, the straightness parameter and inter-lamellar distance was computed in 200 Y-stack images and averaged over the imaged longitudinal length. Results from a total of four samples were further averaged and presented in this study. The straightness parameter, lamellar unfolding, lamellar stretching and inter-lamellar distance was presented as mean ± standard error of the mean (SEM).

2.4. Mechanical testing

To characterize the pressure–diameter response of mouse carotid arteries, 5 mm carotid arterial segments (n = 5) were tested on a pressure myograph (DMT, 110P), which allows the intraluminal pressure and axial force to be measured during the testing. Samples were carefully cannulated and kept in PBS bath at room temperature during mechanical testing. The arteries were pre-stretched to 1.6× of ex vivo length in the longitudinal direction, which closely resembles the in vivo axial stretch [31]. The samples were preconditioned via three cycles of pressurization from 0 to 140 mmHg while maintained at 1.6× followed by three cycles of axial stretching from 1× to 1.6× while maintained at 50 mmHg intraluminal pressure [32]. After preconditioning, mechanical testing was performed by increasing intraluminal pressure from 0 to 120 mmHg with 10 mmHg increments. The change in outer diameter was monitored using a CCD camera mounted on a microscope. Since the custom-made tissue stretching bath-chamber was not equipped with load cells, multiphoton imaging and mechanical testing were not performed sequentially on age-matched samples.

2.5. Kinematics and equilibrium equations

Transmural distribution in stress and stretch was calculated considering the deformation of a thick-walled circular cylinder [20]. Briefly, the deformation gradient from a load-free reference configuration (R, Θ, Z) to current loading configuration (r, θ, z) in cylindrical coordinates is given by the deformation gradient:

2.2

where λ_Z is the (constant) axial stretch. With incompressibility assumption, we have detF = 1, so that

2.3

Integrating equation (2.3) gives

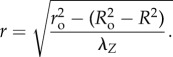2.4

The radial position r in the deformed arterial wall can be mapped into load-free configuration through equation (2.4). From equilibrium equation in the radial direction, transmural pressure can be calculated as [20]:

2.5

Where p_i, p_o represents the inner and outer pressures, respectively. t_θθ and t_rr are circumferential and radial stresses, respectively. From equilibrium equation in the longitudinal direction, the axial force, F, can be determined from [20]:

2.6

where t_ZZ is the longitudinal stress. Equations (2.5) and (2.6) were evaluated numerically by using Gaussian integration scheme [20].

2.6. Constitutive relation

The Cauchy stress tensor can be obtained as

2.7

where p is the Lagrange multiplier, I is the identity tensor, Ψ is the strain-energy function and 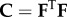is the right Cauchy–Green deformation tensor.

A structurally motivated strain–energy function considering four families of collagen fibres was used for the analysis of mechanical behaviour of the arterial wall [33].

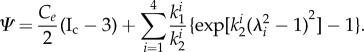2.8

In equation (2.8) C_e is a stress-like material parameter associated with elastin, 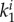and 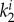are material parameters associated with the kth fibre family. In this model, one circumferential, one axial and two symmetrically diagonal fibre families were considered. I_c is the first invariant of the right Cauchy–Green tensor C, λ_i is the stretch in the direction of the ith fibre family, determined by

2.9

where β is the angle of the ith family with respect to the circumferential directional of the artery in load-free configuration.

2.7. Parameter estimation

Eight unknown material parameters (C_e, 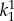, , 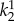, , 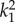, , 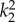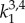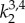β) were estimated by minimizing the difference between experimentally measured and calculated values of pressure and axial force based on equations (2.5) and (2.6), in the form of following objective function [34]:

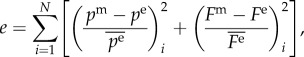2.10

where N = 15 is the number of data points and p^m, F^m are pressure and axial force from the model, p^e, F^e are experimentally measured pressure and axial force. The objective function is minimized using the Nelder–Mead direct search method implemented in the fminsearch function in MATLAB. The material parameters from five samples were then averaged and used to calculate the circumferential stretch at each lamellar position.

3. Results

3.1. Three-dimensional imaging and reconstruction of elastic lamellae

Elastic lamellar layers in an intact mouse carotid artery were imaged using a multiphoton microscope while the artery underwent biaxial extension–inflation (figure 1a,b, see Methods). The multiphoton images in figure 1c–f show wavy collagen fibres in the adventitial layer of a mouse carotid artery at various imaging depths. In the medial layer, no visible collagen signal was observed. The signal from elastin appeared as long, wavy lines. Elastic fibres in the media of the mouse carotid arteries aggregate to form a series of concentric lamellae, and cannot be individually resolved with our microscope. The long, wavy lines shown in figure 1c–f are therefore the cross-section through the folded elastic lamellae, as highlighted in green in figure 1g. The quality of the elastin image was sufficient to produce transverse cross-sectional views of the elastic lamella (figure 2a–c, see Methods), which were used for quantitative structural analysis. Figure 2d shows the reconstructed full three-dimensional architecture of an elastic lamella.

3.2. Structure inhomogeneity and lamellar unfolding

Three lamellar layers were successfully reconstructed, and used for structural quantification. Figure 3a shows the transverse section view of the three lamellar layers in a mouse carotid artery when pressure increases from 0 to 120 mmHg at a physiological axial stretch ratio of 1.6. At low pressure, elastic lamellae appeared as continuous concentric wavy arcs. As the pressure increased, the elastic lamellae appeared to straighten. Structural analysis was performed to quantify the relation of circumferential waviness of the elastic lamellae to pressure through the use of the straightness parameter (figure 3b, see Methods). Lamellar layers that are closer to the inner wall have a lower straightness parameter, thus are more undulated than lamellar layers closer to the outer wall (figure 3c). As the pressure increases, the straightness parameter of all layers increased and gradually approached the value of 1. Unfolding of the elastic lamellar layers, λ_f, which represents the straightening of the elastic lamellae, was calculated by normalizing the straightness parameters at each pressure level, P_s′, by the straightness parameter at zero pressure P_s, i.e. 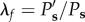. It can be seen from figure 3d that the lamellar layers all unfolded with pressure, however the inner lamellar layers unfolded more than the outer layers. Also, unfolding is more prominent at lower pressures and tends to plateau when pressure is higher than 60 mmHg.

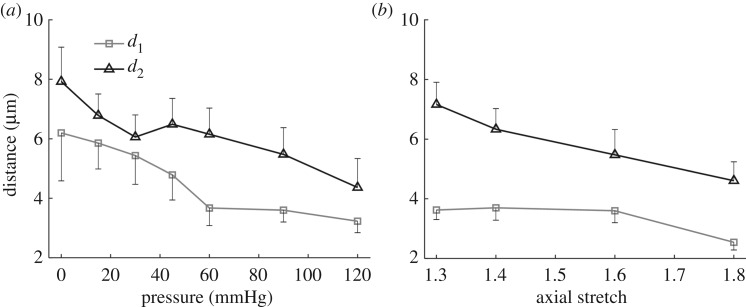
During pressurization, the elastic lamellae unfolded and the distance between lamellae layers decreased (figure 4a). The inter-lamellar distance between L1 and L2 and between L2 and L3 at the unloaded state was 6.2 ± 1.4 and 7.9 ± 1.4 µm, respectively. This distance decreased by about 50%, to 3.2 ± 0.4 and 4.4 ± 1.1 µm, respectively, at 120 mmHg (figure 4a). The inter-lamellar distance also decreased with axial stretching from 3.6 ± 0.3 and 7.2 ± 0.7 µm to 2.5 ± 0.3 and 4.6 ± 0.6 µm when axial stretch increases from 1.3 to 1.8 at a transluminal pressure of 120 mmHg (figure 4b). The carotid artery buckled at 90 mmHg when the axial stretch is below 1.3.

Figure 4.

Inter-lamellar distance during mechanical loading. Inter-lamellar distance as a function of (a) pressure when carotid arteries were subjected to an axial stretch of 1.6, and (b) axial stretch when the pressure was maintained at 90 mmHg. d₁ and d₂ are the distances between layer L1 and L2, and layer L2 and L3, respectively.

3.3. Tissue-level deformation

The tissue-level circumferential stretch as a function of transmural position was obtained from modelling the arterial wall as a thick-walled cylinder [20]. Average model parameters (electronic supplementary material, table S1) were obtained based on fitting the pressure-diameter testing data of five carotid arteries (electronic supplementary material, figure S1). It can be seen from figure 5a that the circumferential stretch, λ_t, decreases from the inner to the outer surface of the arterial wall, i.e. the lamellar layer closer to inner wall underwent more tissue-level deformation than those closer to the outer wall. To compare the tissue circumferential stretch with lamellar unfolding, λ_t was obtained at the radial position of lamellar layers L1, L2 and L3. To do so, the position of L1 at the unloaded state was assumed to be located at two-thirds of the wall thickness from the lumen surface [20]. The position of L2 and L3 can thus be determined by subtracting the inter-lamellar distances d₁ and (d₁ + d₂) from L1, respectively. The tissue circumferential stretch, λ_t, was then plotted as a function of pressure at the position of lamellar layers L1, L2 and L3 (figure 5b). We can see that the tissue circumferential stretch increased with pressure. However, the increasing trend gradually slowed down at pressures greater than 60 mmHg. The lamellar layers closer to the lumen surface consistently underwent higher tissue-level deformation.

Figure 5.

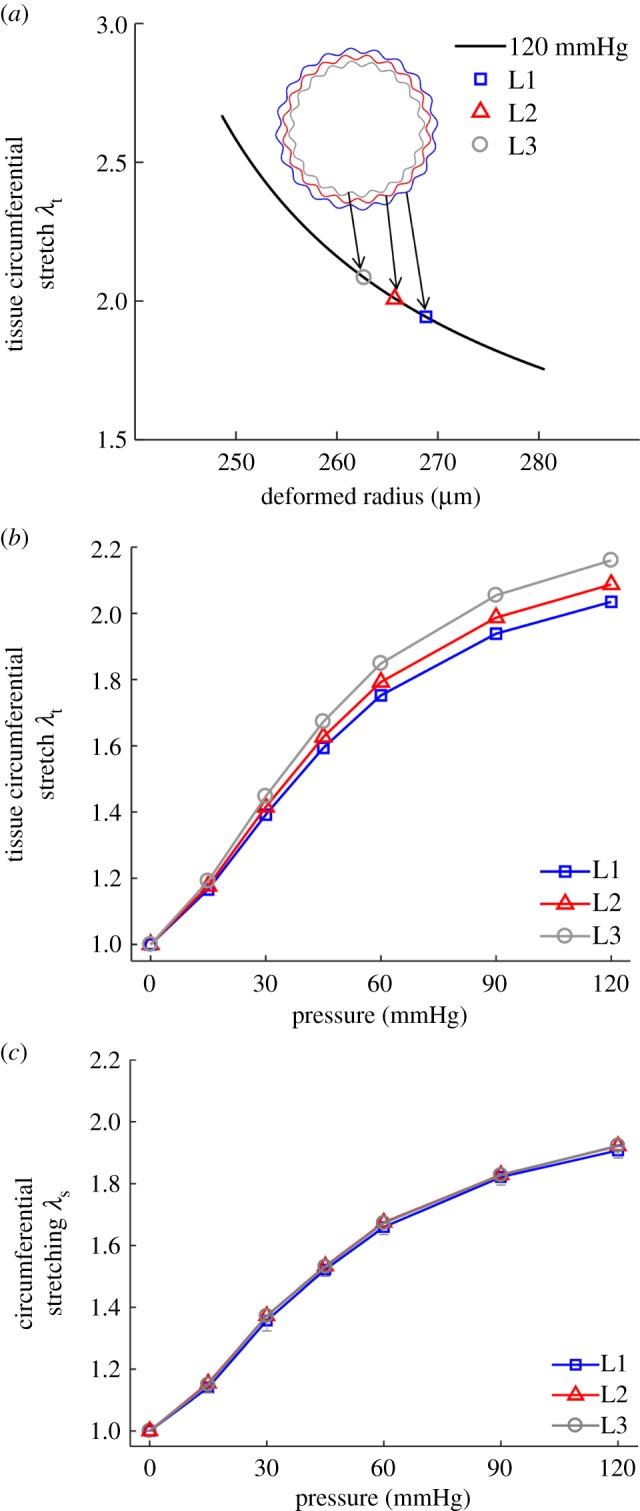
Tissue-level deformation and its relation to micromechanics. (a) Transmural circumferential stretch distribution in the arterial wall from modelling at 1.6 axial stretch and 120 mmHg pressure. Markers show the tissue circumferential stretch at the position of lamellar layers L1, L2 and L3. (b) Tissue circumferential stretch as a function of pressure at the position of lamellar layers L1, L2 and L3. (c) Lamellar stretching as a function of pressure, determined from the tissue-level deformation (b) and lamellar unfolding (figure 3d), was equivalent in all layers. (Online version in colour.)

3.4. Relationship among tissue deformation, lamellar unfolding and lamellar stretching

Tissue circumferential stretch (figure 5b) and lamellar unfolding (figure 3d) both followed similar increasing trends with pressure and position dependence on lamellar position, however, lamellar unfolding was much smaller than tissue circumferential stretch, indicating that during mechanical deformation, the elastic lamellae layers were not only subjected to unfolding, but also stretching, or elongation. We thus propose a new model that describes the deformation of an elastic lamellar layer. When the artery is pressurized, the tissue circumferential stretch at a specific lamellar position, λ_t, can be represented by the ratio of the arc length of elastic lamella in the deformed configuration, 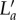, to the arc length in the initial configuration, L_a, as shown in equation (3.1). We can see that λ_t can be decomposed into the product of lamellar unfolding, λ_f, and lamellar stretching, λ_s:

3.1

where 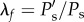, λ_s is the ratio of contour length of elastic lamella in the deformed configuration, 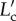, to the contour length in the initial configuration, L_c. λ_s characterizes the changes in the contour length of the elastic lamella due to stretching/elongation, which cannot be measured. Knowing both λ_t and λ_f, λ_s can be obtained. We can see from figure 5c that stretching for lamellar layers, λ_s, are similar in all three lamellar layers at each pressure level.

4. Discussion

The present study leads to several new insights on the micromechanics of elastic lamellae and its relation to tissue-level mechanics in the arterial wall. A new method was developed to reconstruct the three-dimensional architecture of elastic lamellae in mouse carotid arteries and was used to quantify the unfolding of elastic lamellae during biaxial extension–inflation loading. Our study shows that unfolding and extension of elastic lamellar layers contributed simultaneously to tissue-level deformation (figure 6a,b). Moreover, the higher lamellae unfolding in the inner lamellae layer compensates the larger strain experienced at the inner surface of the arterial wall, thus maintaining a more evenly distributed circumferential extension/stress in the lamellar layers through the arterial wall (figure 6c). Our study establishes, for the first time, that microstructural inhomogeneity plays an important role in maintaining tissue homeostasis and achieving mechanical homogeneity.

Figure 6.

The role of micromechanics of elastic lamellae in arterial tissue mechanics. (a) Schematic of an elastin lamella undergoing unfolding and stretching when the arterial wall is pressurized. The multiphoton imaging data allowed us to quantify the lamellar unfolding λ_f, however stretching of the elastic lamella λ_s cannot be measured and was calculated using equation (3.1). (b) Stretching of the lamellae occurs at the onset of pressurization and is a main contributor to the overall tissue deformation. (c) The primary role of lamellar unfolding is to make uniform the stretching of elastic lamellae through the arterial wall, while tissue deformation is not uniform. (Online version in colour.)

Multiphoton microscopy [27,35–37] has been employed to study the ECM organization in blood vessels. Multiphoton microscopy has the ability to image the ECM architecture of biological tissues with minimal sample preparation [26], and has been employed to examine the structure of collagen and elastic fibres in various types of biological tissues such as skin, tendon, ligament and blood vessels [38–41]. In previous studies, orientation distribution and recruitment of ECM fibres were studied based on two-dimensional images from maximum intensity projection of stack images [27,42,43]. However, such an analysis method is not appropriate for studying the spatial structure of tubular-shaped elastic lamellae in mouse arteries. The orientation of elastic fibres in larger animals are quite distinct [27,44–47], however, it is not possible to obtain the orientation of elastic fibres from mice carotid arteries. The reason for this structural difference between large and small animals remains to be understood. To understand the micromechanics of elastic lamellae, there is a need to quantify the three-dimensional architectures of elastic lamellae under mechanical loading. Three-dimensional reconstruction shows that elastic lamellae in a mouse carotid artery are wavy in both circumferential and longitudinal directions, which is important for an artery to accommodate multi-axial deformation (figure 2d). Waviness of elastic lamellae was noticed in transverse histological section of arterial tissue in early studies [1]. It is important to note that the wavy lines that appear in multiphoton images (figure 1d–f) are not elastic fibres, as mentioned in earlier studies [48,49], but actually slices of the wavy concentric sheets of elastic lamellae (figure 1g). The complex structure of elastic lamellae and the natural cylindrical shape of an artery call for three-dimensional reconstruction to reveal the lamellar architecture before performing structural analysis.

The waviness of elastic lamellar layers decreases as intraluminal pressure increases. This is in line with earlier histological observations [1,22,23]. The waviness and spatial distribution of elastic lamellae vary transmurally with wavier elastic lamella towards the inner surface of the arterial wall (figure 3c). Lamellar layers closer to the inner wall are more undulated than lamellar layers closer to the outer wall. When the artery is pressurized, the more undulated inner lamellar layer also undergoes larger unfolding (figure 3d). At the tissue-level, the circumferential stretch decreases from the inner to outer wall (figure 5a). However, we found that the tissue-level circumferential stretch (figure 5b) is much greater than the unfolding stretch (figure 3d). Indeed, the autofluorescence from elastin enabled quantifying the unfolding of the elastic lamellae, but not the lamellar stretching. This is unlike the SHG signal from collagen which can inform on the stretch level through the average molecular orientation [50].

Our study demonstrates that lamellar unfolding and stretching occurs simultaneously and both contribute to tissue-level circumferential stretch (figure 6b). Arteries experience larger strain at the inner surface of the arterial wall. The higher lamellae unfolding in the inner lamellae layer compensates the tissue circumferential stretch gradient, and thus plays an important role in maintaining a more evenly distributed stretching in the lamellar layers through the arterial wall (figure 6c). This is important as lamellar stretching/elongation is directly related to stress development in the lamellar layers. This strongly supports the suggestion of Dobrin [23] that the artery wall behaves mechanically as a homogeneous material, despite its histologic heterogeneity. Elastin in the arterial wall is organized into concentric lamellar layers of approximately the same thickness throughout the arterial wall [1]. The lamellar unit is designed to support and evenly distribute the mechanical load in the arterial wall. Our study sheds light on the importance of structural inhomogeneity in maintaining tissue homeostasis. Our bodies have built-in mechanisms to more evenly distribute stress through vessels.

Previous studies based on histological images suggested the deformation of elastic lamellae as a two-step process: from zero to diastolic pressure, the lamellae unfold; then at pressures above the diastolic pressure, the lamellae were stretched [1,22,23]. Our study, however, quantitatively shows that unfolding/straightening of elastic lamellae, λ_f, only contributes to a small fraction of the circumferential tissue deformation, λ_t, even at low pressure (figures 5b and 3d). The fact that λ_s increases from 0 mmHg pressure indicates elastic lamellae were stretched at the onset of artery extension, not after lamellar layers were fully unfolded. Stretching and unfolding of elastic lamellae, occurs simultaneously with deformation, and both contribute to tissue-level deformation λ_t, from the onset (figure 5c). These findings unravel the important role of the radial waviness gradient in equalizing local circumferential stresses and preparing the elastic lamellae for physiological tissue circumferential stretching, during which lamellar stretching is the main contributor, and is directly related to local stress development in the lamellar layers and thus, the microenvironment for cells. It is important to consider elastic lamella and elastic fibres as two structural hierarchies in the arterial wall. While the elastic lamellae appear to be wavy in the circumferential cross-sectional view, there is plenty of evidence to suggest that elastic fibres within the elastic lamellae are under tension due to somatic growth, even at zero load condition [51–53]. Thus the elastic fibres within the elastic lamellae can be stretched while the elastic lamellae appear wavy. Our study thus suggests that when studying arterial wall mechanics, it is important to distinguish the deformation of individual structural hierarchies, and the structural and mechanical correspondence should be made carefully.

Waviness and inter-lamellar distance are two main features of elastic lamellae organization. Apart from straightening and decrease in inter-lamellar distance with increase of intraluminal pressure, we also observed decrease in inter-lamellar distance under axial stretching at specific pressure. The inter-lamellar distances d₁ and d₂ measured at 90 mmHg with axial stretch of 1.6 in mouse carotid artery are 3.6 and 5.5 µm (figure 4) which is comparable to the value of 0.006 mm at 100 mmHg reported by Wolinsky and Glagov in mouse aorta [19] without axial stretch. Thinning of the arterial wall was due mainly to the decrease of inter-lamellar distance. This is in line with the histological observations by Wolinsky & Glagov [1] of aorta fixed at in vivo extension with and without distension. Sokolis et al. [22] reported no change in spatial distribution from axial stretching. This discrepancy is possibly related to the uniaxial tensile test used by Sokolis et al. [22]. Several studies have pointed out that biaxial tensile tests can better mimic the state of deformation encountered in the body and is thus a preferred method [54,32].

As local stress state is an important parameter that governs tissue growth and remodelling [55], numerous studies have been carried out with a focus on stress analysis of the arterial wall. Such studies are often based on a specific form of strain-energy function, in which the medial layer of the arterial wall is usually assumed to be a homogeneous material. Predicted stress distribution based on such assumption results in a prominent stress gradient in the arterial wall, especially in the medial layer that contains layers of elastic lamella [56–60]. To reduce the stress gradient, a residual stress was introduced into the model, in which a deformation state was introduced so that when the artery is intact the residual stress adds a circumferential compressive stress to the inner wall and a circumferential tensile stress to the outer wall. In many cases, such phenomenological treatment has been shown to be insufficient to balance the stress gradient [20,55]. Our study reports new observations that the elastic lamellae have a radial waviness gradient. This structural inhomogeneity compensates the inhomogeneous tissue-level deformation, thus equalizing the local circumferential stresses through the arterial wall. It is thus necessary to develop microstructure-inspired models and to incorporate such structural information at the lamellar level in the existing theories on growth and remodelling in future studies.

4.1. Limitations

In this study, different samples were used for imaging and mechanical testing. Thus the model parameters were averaged to calculate the circumferential stretch at each lamellar position. This is in accordance with previous studies [61,62], in which the mean estimated material parameters were used to predict the behaviour of the group of the samples. In an ideal situation imaging and mechanical testing should be performed on the same artery, and thus to have a sample-specific structure and function. However this is often difficult to achieve, especially in small arteries like mice carotid arteries because the samples are very fragile and usually won't survive multiple cannulation processes. Although visible in histological images, multi-photon imaging cannot pick up the signal from the loosely arranged fine medial collagen fibres in mice carotid arteries [43,63]. It is possible that the SHG signal is too weak to be detected. More importantly, our study characterized medial elastin, independently of medial and adventitial collagen.

5. Conclusion

Micromechanics of elastic lamellar layer were investigated by combining multiphoton imaging, mechanical testing and constitutive modelling. A new approach was developed to quantify the three-dimensional microstructure of elastic lamellar layers under physiological biaxial extension–inflation mechanical loading. Our study demonstrates that stretching and unfolding of elastic lamellae occurs simultaneously during deformation and that both contribute to tissue-level circumferential stretch. While the lamellar stretching dominates the tissue deformation, the radial waviness gradient of elastic lamellar layers plays a critical role in equalizing the local circumferential stresses throughout the arterial wall. By looking at the micromechanics of the elastic lamellar layer, we discovered the importance of structural inhomogeneity in maintaining tissue homeostasis. Our study uncovered the underlying structural origin that enables elastic lamellar layers to evenly distribute the stresses through the arterial wall, a fundamental requirement for tissue and cellular function. Our study also emphasized the importance of adopting a multiscale and multimodal perspective when dissecting the role of ECM components in tissue mechanics. Using the mouse carotid artery as a model allowed us to access the lamellar layers using multiphoton microscopy while keeping the artery intact. Extension of the findings from this study to large arteries is likely promising, as based on the Law of Laplace, the average tension per lamellar unit of an aortic media is constant regardless of species [19]. Discoveries from this study will likely inspire the development of tissue-engineered blood vessels that consider structural inhomogeneity, and the creation of new microstructure-inspired models of arteries for better understanding of tissue growth and remodelling. Ageing and diseases could have profound impacts on the composition and structure of the arterial wall. Our imaging and analysis method can be applied to study the structural and mechanical alterations in elastic lamellae, and to understand the role of structural inhomogeneity in maintaining tissue homeostasis in arterial remodelling.

Authors' contributions

X.Y., R.T. and Y.Z. designed the study. X.Y. and R.T. conducted the multiphoton imaging and developed the imaging analysis method. X.Y. performed the modelling and mechanical testing experiments. F.S. contributed to sample preparation. Y.Z. supervised the entire study. X.Y., Y.Z. and R.T. wrote the manuscript. All authors discussed the results and commented on the manuscript.

Competing interests

The authors have no competing interests.

Funding

This work was supported by National Institute of Health (R01HL098028 to Y.Z., R01HL136311 to F.S.) and National Science Foundation (CMMI 1463390 and CAREER 0954825 to Y.Z.).