Biodiversity, functional redundancy and system stability: subtle connections

Abstract

The relationship between biodiversity and functional redundancy has remained ambiguous for over a half-century, likely due to an inability to distinguish between positivist and apophatic (that which is missing) properties of ecosystems. Apophases are best addressed by mathematics that is predicated upon absence, such as information theory. More than 40 years ago, the conditional entropy of a flow network was proposed as a formulaic way to quantify trophic functional redundancy, an advance that has remained relatively unappreciated. When applied to a collection of 25 fully quantified trophic networks, this authoritative index correlates only poorly and transitively with conventional Hill numbers used to represent biodiversity. Despite such a weak connection, the underlying biomass distribution remains useful in conjunction with the qualitative diets of system components for providing a quick and satisfactory emulation of a system's functional redundancy. Furthermore, an information-theoretic cognate of the Wigner Semicircle Rule can be formulated using network conditional entropy to provide clues to the relative stability of any ecosystem under study. The necessity for a balance between positivist and apophatic attributes pertains to the functioning of a host of other living ensemble systems.

1. Background

The intuitive relationship between biodiversity and ecosystem stability or persistence has remained an unresolved theme of ecosystems science for almost seven decades now. The widely shared consensus is that a positive relationship does exist between the two attributes, and significant resources are being devoted globally towards the conservation of biodiversity [1]. Theoretical results that firmly support this hypothesis remain, at best, ambiguous [2–4].

The notion that trophic functional redundancy might contribute to ecosystem persistence harkens back at least to the 1950s when Odum [5] suggested that interruption to any given trophic pathway could be compensated by increased flows along parallel routes—a manifestation of system reliability. That is, if A → M → B is a two-step pathway between autotroph A and carnivore B, and A → N → B is a parallel pathway between the same two endpoints, then any dysfunction in the link A → M might be compensated by an increase in flow over the link A → N and vice-versa. The links A → M and A → N are thus said to be functionally redundant with respect to flows from A to B. MacArthur [6] proposed using the then inchoate field of information theory (IT) to estimate such functional redundancy. In particular, he employed the Shannon–Weaver index of diversity to quantify the variety, D, among the trophic exchanges in an ecosystem:

1.1

where p_i is the relative proportion of total system flow constituted by a particular exchange, i.

It is important to note that both Odum and MacArthur focused upon system processes (exchanges) thereby maintaining the emphasis in ecology upon relationships over objects. For some, however, this focus was problematic, both empirically and philosophically. Measuring exchanges (flows) in the field is far more difficult than is counting numbers of specimens or estimating the biomass of populations. Furthermore, the convention in approaching problems, even in biology, has long been to focus on objects and to investigate how they move according to universal laws, that is, to follow the protocols of physics, which regard flows and processes as secondary and derivative.

Perhaps inevitably then, focus regressed early in the 1960s from processes back towards population numbers and stocks of species, and the quantities p_i came to represent the proportions of population sizes within the system, while D came to be called the system ‘biodiversity’.

Although other measures of diversity were explored (e.g. the Hill numbers [7]), the preoccupation for almost the entire decade of the 1960s became to elucidate a definitive connection between biodiversity and system stability. This ambitious search was brought to a sudden end when a noted physicist employed linear stability analysis to demonstrate that more species actually confer less internal stability to a system [8]. Because IT had played a significant role in the diversity/stability initiative, its reputation among ecologists suffered collateral damage and scant attention was paid to the discipline over the next few decades.

2. Reconsiderations

While a number have questioned the assumptions made in the argument against diversity → stability [9], no analytical demonstration that increased biodiversity contributes to ecosystem persistence has been universally accepted. One is justified in asking why not?

Somewhat surprisingly, it appears that a deficiency in the discipline of physics is to blame. It was remarked in the late 1960s by anthropologist/philosopher Gregory Bateson [10] that physics deals almost exclusively with positivist notions. That is, it treats entities that are palpable and only in very few instances (e.g. the Pauli Exclusion Principle) does physics consider what is missing. That which does not exist is not key to the foundational dynamics of physics and is marginal at best to the formulation of physical models. That which is lacking can, however, make a major difference in ecosystems. (For example, loss of predator or prey species will usually result in significant differences in system dynamics.)

Here that which is absent will be referred to as apophasis (cf. [11]), and in particular, the focus will be upon the lack of constraint (which is key to the concept of entropy). While it may initially sound nonsensical to measure something that does not exist, its magnitude can always be reckoned in relation to that which does [12]. (Consider, for example, a glass that is half empty.) Furthermore, a very propitious tool for quantifying apophasis is the discipline of IT, because the very starting point for IT was Shannon's estimate of the lack of certainty. The intuitive (positivist) concept of information thereby becomes a double negative (i.e. any decrease in uncertainty; ch. 5 in [13]).

That MacArthur applied Shannon's formula to the distribution of flows reveals that he implicitly was regarding the diversity of flows as an apophasis. The same inference carried over into the definition of biodiversity. Little wonder, then, that positivist models were ill-suited for dealing with biodiversity. If one wishes to treat apophases, it is only reasonable to start with tools, such as IT, that incorporate that ontological category into their very constitution.

Fortunately, the sudden decline in interest in diversity/stability studies did not discourage everyone from continuing to apply IT to ecology. For example, a team of electrical engineers from Oklahoma interpreted MacArthur's scenario using subsequent developments in IT [14]. They retained MacArthur's emphasis on ecosystem relationships, and networks of material and energetic exchanges in ecosystems. Their genius was to regard trophic networks not simply as representing the constraints that bind the nodes (as the vast majority of network investigators still do), but also as portraying the (apophatic) indeterminacy inhering in the multiplicity of routes over which material or energy could possibly flow, i.e. trophic functional redundancy. That both constraint and redundancy reside in almost all networks is almost self-evident: If an entity is at a given node (population) in the web, it is very rarely the case that the given node connects with all the other nodes in the structure. It is constrained to interact directly with only a subset of nodes. At the same time, several possibilities usually exist for the next destination and the one that transpires cannot be determined in advance. As Claudia Pahl-Wostl [15] proclaimed, ‘Networks are amalgams of determinism and chaos [apophasis]’.

With this background, we now embark on a quantitative investigation of how well biodiversity serves as an indicator of system functional redundancy. The first task is to establish an unequivocal measure for the apophatic notion of trophic functional redundancy. We then seek data on networks of ecosystem trophic transfers with which to compare biodiversity and the selected measure of functional redundancy within the assembled systems. If these indexes do not correlate well, we then examine other indexes related to the functional redundancy in a search for a reliable surrogate that can estimate functional redundancy as readily as the quick-to-estimate biodiversity. Finally, we seek some threshold among the examined indexes which might provide a clue as to whether a given system is likely to be persistent.

3. Quantifying functional redundancy

Rutledge et al. applied newly formulated measures in IT that employed conditional probabilities to parse out how much of total network activity is constrained along certain pathways and how much remains free to flow in an indeterminate manner.¹ To follow this derivation, one may denote T_ij as the magnitude of a flow from compartment i to compartment j. A dot in the place of an index will signify the sum over all values of that index. Thus, T_i. denotes the partial sum of all flows leaving i, and T._j the aggregate of all flows into compartment j. Finally, T.. will represent the sum of all flows over all origins i and all destinations j, and is commonly referred to as the total systems throughput [17].

One begins by rewriting MacArthur's index of the diversity of flows (1.1) in terms of all origins and destinations as

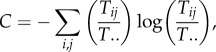3.1

where T_ij/T.. is now the joint probability that a unit of medium (mass or energy) flows from i to j. If one focuses on only the origins of flows, the diversity of their marginal probabilities will be

where it can be proved that C ≥ C_o ≥ 0. One can similarly aggregate all inputs into j and their ensuing diversity as

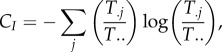where, similarly, C ≥ C_I ≥ 0.

Now, the combined diversities (C_I + C_o) always exceeds (or equals) the joint diversity, C, because the constraints that order how the components are connected (their topology, T_ij) lowers how much indeterminacy is possible without such information. Thus, the difference (C_I + C_o − C) measures the overall constraint in the system topology. Call this difference A, and a little algebra shows that

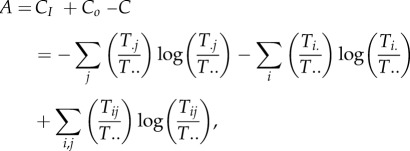Or, collecting terms,

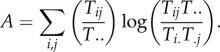3.2

It can be proved that C ≥ A ≥ 0, and A is referred to in IT as the ‘average mutual information’ between inputs and outputs. When A is multiplied by the total system throughput, T.., the product has come to be known as the system's network ascendency—a key measure of system performance [18]. The quotient A/C varies between 0 and 1 and can serve as a convenient index of system organization, or its degree of constraint [19].

Defining A, important as it has since become, was for Rutledge et al. only an intermediate step towards their intended goal, which was to improve upon D as a measure of network functional redundancy. That measure, or the residual freedom, (C − A), has subsequently been termed the system overhead and is denoted by Φ [16]. A little algebra shows it can be written as

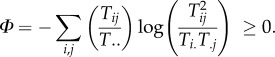3.3

To date, Φ appears to be the most accurate estimate of pathway redundancy possible and provides a reference against which to compare other all other putative assessments of trophic functional redundancy, like D [20]. Φ is related to the logarithmically weighted average number of arcs into and out of a typical node of the network, m, calculated as m = 2^ϕ/2 [19,21].

That (C − A) is known in IT as the ‘conditional entropy’ reveals its nature as an apophasis and a substantial contributor to system indeterminacy, just like D. Because Φ and D share the same ontology, they may be legitimately compared as ‘apples with apples’—in contrast to the futile pursuit of searching for positivist descriptions in terms of species numbers and/or biomasses (apples versus oranges).

4. A short-cut to assessment

Comparison of Φ with D is complicated by two differences: (i) Φ is formulated in terms of process relationships. Although MacArthur used D to describe the variety of flows, its later and more conventional form is reckoned via stocks of mass, energy or some other medium and (ii) the topology of interconnections is woven into Φ, whereas it is completely missing from the conventional formula for D. Furthermore, the data needed to evaluate Φ are precisely of the same high difficulty as it was to assemble MacArthur's original diversity of flows. How, then, to proceed?

Chemical reaction theory holds that reactions rates (processes) between two gases can be assumed proportional to the frequencies of the encounter between molecules of the two types. These collisions in turn are described in mass-action theory as proportional to the product of their respective concentrations (stocks) [22]. This assumption is usually represented as r = k[c_i][c_j], where r is the estimated frequency of collision between molecules of the two types, [c_i] and [c_j] are the concentrations of the two species of interest, i and j, and k is an empirical constant. The constant of proportionality, k, also converts units of (squared) concentrations (which do not bear any dimension of time) into rates of the encounter (as measured on a per-unit-time basis).

Certainly, animals roaming over a habitat bear only loose analogy to a mixture of gases, but the idea that rates of animal encounters might be proportional to the product of their densities has been assumed since the earliest days of ecosystem modelling—the Lotka–Volterra model of encounters between fish populations being perhaps the most famous example [23]. When applied to ecological scenarios, the constant of proportionality will vary according to other factors, such as the probability of capture by the predator and the degree of avoidance on the part of the prey.

In the formula for biodiversity, D, the relative densities of species appear as their biomass frequencies—the p_i. Under the Lotka–Volterra assumptions, the probability of encounter between i and j in the system would be proportional to the product p_ip_j. If one knew nothing more about the nature of the interactions, these products can be arranged as the dyadic product² between the relative distribution vectors p_i and p_j, which for a four-species ensemble looks like table 1.

Table 1.

The dyadic product of the components of the normalized biomass partition vector (p1, p2, p3, p4) along with their column and row sums.

species	1	2	3	4	row sum
1	p1p1	p1p2	p1p3	p1p4	p1
2	p2p1	p2p2	p2p3	p2p4	p2
3	p3p1	p3p2	p3p3	p3p4	p3
4	p4p1	p4p2	p4p3	p4p4	p4
col. sum	p1	p2	p3	p4	1.0

For example, if the four-component system possesses biomasses in the proportions, B₁ = 50, B₂ = 15, B₃ = 30 and B₄ = 5³, then the dyadic product would look like table 2.

Table 2.

The dyadic product of the hypothetical biomass partition (0.50, 0.15, 0.30, 0.05).

species	1	2	3	4	row sum
1	0.25	0.075	0.15	0.025	0.50
2	0.075	0.0225	0.045	0.0075	0.15
3	0.15	0.045	0.09	0.015	0.30
4	0.025	0.0075	0.015	0.0025	0.05
col. sum	0.50	0.15	0.30	0.05	1.0

Now the constants, k_ij, linking each biomass product, p_ip_j with its conjugate flow, T_ij, are usually not known. In addition, the lack of any information about the magnitude of the flows forces one to assume that all k_ij are equal, resulting in a ‘back of the envelope’ estimation of the flows. (This particular estimation technique has resulted in flows that usually pass conventional 5% statistics [24].) Because (3.3) deals entirely with quotients of flows divided by their sums, a uniform constant, k, would cancel from all calculations. Whence, substituting the elements of the dyadic product into (3.3) yields Φ = 3.295 bits (which is exactly twice the value of the biodiversity index D when logarithms are taken to base 2).

Functional redundancies emulated in this manner are almost always overestimates, however, because the network of direct interactions was assumed to be totally connected by equiponderant flows, which is virtually never the case with natural ecosystems.⁴ Rather, many exchanges are simply missing (often greater than 80%). The actual topology of network connection is easy to retrieve, because the diets of most species are usually tabulated and widely available. Knowing the diets of each compartment, allows one to set non-existent transfers to zero.

For example, the dietary exchange network among the four species of the hypothetical system might appear as in figure 1.

Figure 1.

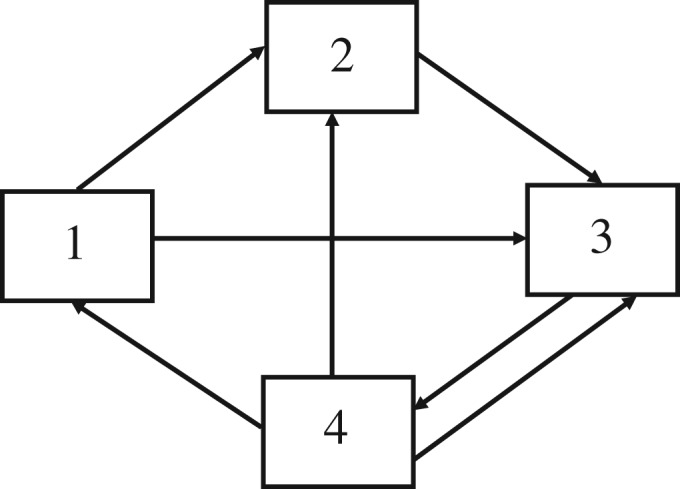
Hypothetical qualitative topology among four components.

In such case, only seven of the possible 16 interactions are realized. The surviving interactions in this case would look like table 3.

Table 3.

Table 2 as revised according to the topology shown in figure 1.

species	1	2	3	4	row sum
1	0.	0.075	0.15	0.	0.225
2	0.	0.	0.045	0.	0.045
3	0.	0.	0.	0.015	0.015
4	0.025	0.0075	0.015	0.	0.0425
col. sum	0.025	0.0825	0.21	0.015	0.3325

Which can be normalized to yield table 4.

Table 4.

Normalized version of table 3.

species	1	2	3	4	row sum
1	0.	0.227	0.450	0.	0.677
2	0.	0.	0.135	0.	0.135
3	0.	0.	0.	0.045	0.045
4	0.075	0.023	0.045	0.	0.143
col.sum	0.075	0.250	0.630	0.045	1.0

When the fractions from table 4 are substituted into equation (3.3), the result will be referred to as the ‘emulated’ functional diversity, Φ_e, where Φ_e = 1.6291 bits.

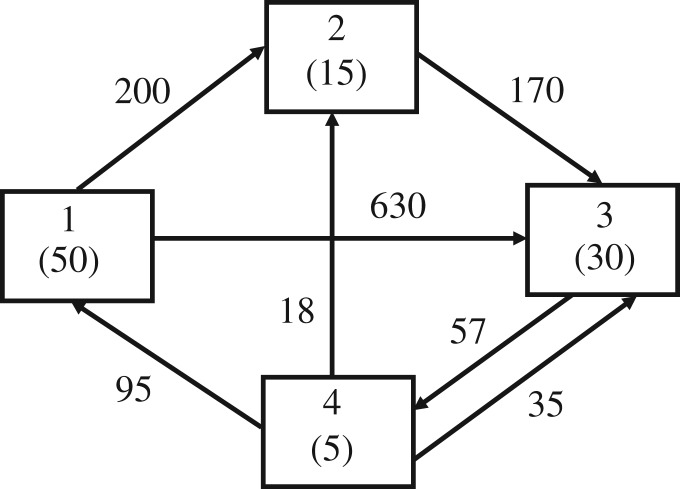
Now, for the sake of demonstration, one supposes that field data reveal that the observed flows per unit time are figure 2.

Figure 2.

Magnitudes of hypothetical flows among the four components in figure 1.

Inserting these values into (3.3) yields an ‘observed’ functional redundancy, call it Φ_o, where Φ_o = 1.45 bits.

Both Φ_e and Φ_o are always less than or equal to the value of Φ when all existing flows are equal in magnitude. Denoting this upper bound by Φ*, the topology in figure 1 yields Φ* = 5.6147. Still further, Φ has a least upper bound when all possible flows are present and equal in magnitude. This value, Φ_max = 2 log(n), where n is the number of nodes.

The various values of Φ are thus ordered as

4.1

That is, the largest possible value of Φ, or Φ_max, is reduced by the amount (Φ_max − Φ*) once one knows the topology of the system (82%). Additional data on the magnitudes of the flows reduce Φ further by the amount (Φ* − Φ), or another 3%. The differences in (4.1) allow one to gauge the relative amounts of information that are gained by ascertaining the topology and by estimating the flow weightings, respectively. The emulated Φ_e and the observed value, Φ_o, bear no fixed analytical relationship to one another.

5. Key questions about the emulation

Given as how Φ_o is the most faithful estimate one can make of trophic functional redundancy, several questions arise:

• —How well does D represent functional redundancy? That is, do D and Φ_o correlate when applied to real, natural systems?
• —To what extent does Φ_e emulate Φ_o? Because Φ_e is far easier to estimate than Φ_o, can the former serve as a better surrogate for functional redundancy than D?
• —What are the relative contributions of system topology versus flow magnitudes towards estimating functional redundancy?
• —What, if anything do any of these indexes reveal about system persistence (the contemporary focus in lieu of ‘stability’)?

6. Description of data

To address these important issues, a suite of 25 quantified trophic flow networks have been assembled from a number of habitats and sources. For each of these systems, all internal trophic exchanges have been estimated as well as the magnitudes of all exogenous inputs and outputs. Only networks with 12 or more components were considered because networks consisting of fewer compartments cannot be trusted to adequately represent ecosystem properties [25].

The 25 systems are summarized in table 5, along with their dimensions and literature citations.

Table 5.

Ecosystem networks, number of components and the literature references.

#	system	n	reference
1	Crystal River Creek (control)	21	Ulanowicz [13]
2	Crystal River Creek (ΔT)	21	Ulanowicz [13]
3	mesohaline Chesapeake Bay	36	Baird & Ulanowicz [26]
4	mesohaline Chesapeake Bay	15	Wulff & Ulanowicz [27]
5	Baltic Sea	15	Wulff & Ulanowicz [27]
6	Florida Bay	125	Ulanowicz et al. [28]
7	gramminoid Everglades	66	Ulanowicz et al. [29]
8	Mondego Estuary	43	Patricio [30]
9	Narragansett Bay	32	Monaco [31]
10	St Marks River	51	Baird et al. [32]
11	polyhaline Chesapeake Bay	34	Hagy [33]
12	southeast Chukchi Sea	51	in preparation [34]
13	northeast Chukchi Sea	51	in preparation [34]
14	Everglades cypress wetlands	68	Ulanowicz et al. [35]
15	Ems Estuary	15	Baird & Ulanowicz [26]
16	Kromme Estuary	16	Baird & Ulanowicz [26]
17	Okefenokee Marsh	24	Patten et al. [36]
18	Swartzkops Estuary	15	Baird & Ulanowicz [26]
19	Ythan Estuary	14	Baird & Ulanowicz [26]
20	Twin Cays fringe mangroves	87	Scharler et al. [37]
21	Twin Cays transition mangroves	74	Scharler et al. [37]
22	Broad Creek	36	Egnotovich [38]
23	N. Benguela Current	24	Heymans & Baird [39]
24	Delaware Bay	34	Monaco [31]
25	Lake Michigan	36	AE Krause & DM Mason (2003, personal communication) see also [40]

Full data on each of the 25 networks are presented in the electronic supplementary material, file <25NETS.CSV>.

7. Results

The values of D, Φ_max, Φ*, Φ_e and Φ_o were calculated for exchanges among the nl living compartments and are compared in table 6. Additionally, internal flows among all compartments (living and non-living) were included in the calculations and thirdly, all endogenous and exogenous flows were accounted in the indexes. The values for these expanded networks can be found in the electronic supplementary material, file <RESULTS.XLS>.

Table 6.

The values of biodiversity (D) and variations of redundancy measures (in bits) corresponding to the 25 sample ecosystems (as calculated using only feeding relationships).

no.	system	nl	D	Ømax	Ø*	Øe	Øo
1	Crystal River Creek (control)	20	0.6325	8.643856	4.2486	2.9381	1.7047
2	Crystal River Creek (ΔT)	20	0.6527	8.643856	3.6831	2.0873	1.4267
3	mesohaline Chesapeake Bay	33	0.2624	10.08879	3.7166	2.2461	1.6214
4	mesohaline Chesapeake Bay	12	0.2219	7.169925	2.6607	1.5866	1.8062
5	Baltic Sea	12	0.0859	7.169925	2.6560	1.5289	1.7770
6	Florida Bay	122	0.7622	13.86147	8.8322	3.9478	3.1524
7	gramminoid Everglades	63	0.4842	11.95456	7.7819	4.225	3.6117
8	Mondego Estuary	42	1.1525	10.78463	6.9377	1.5797	1.5597
9	Narragansett Bay	31	0.5006	9.908392	4.7735	3.8524	2.5843
10	St Marks River	48	0.2526	11.16992	5.5349	3.6705	3.6501
11	polyhaline Chesapeake Bay	31	1.0280	9.908392	3.5408	2.6913	2.4193
12	southeast Chukchi Sea	48	0.8718	11.16992	6.7296	2.8137	2.9091
13	northeast Chukchi Sea	48	0.6063	11.16992	6.5981	2.9224	2.1940
14	Everglades cypress wetlands	65	0.9258	12.04474	7.1215	1.0381	2.0265
15	Ems Estuary	12	0.0143	7.169925	2.8245	2.5431	2.2603
16	Kromme Estuary	13	0.5100	7.400879	2.4747	2.0086	1.1358
17	Okefenokee Marsh	21	0.1774	8.784635	4.4187	2.6368	1.6246
18	Swartzkops Estuary	12	0.6805	7.169925	2.1044	1.4123	1.0838
19	Ythan Estuary	11	0.6652	6.918863	2.2831	1.1329	1.6830
20	Twin Cays fringe mangroves	72	0.6901	12.33985	6.2230	2.0118	1.6940
21	Twin Cays transition mangroves	58	0.7372	11.71596	6.2276	2.3545	2.6064
22	Broad Creek	31	0.4476	9.908392	4.4787	2.4904	2.1427
23	Northern Benguela Current	22	0.5753	8.918863	5.3494	2.7800	1.4480
24	Delaware Bay	33	0.5018	10.08879	5.1920	3.5565	2.6970
25	Lake Michigan	35	2.6230	10.25857	5.1918	3.3972	3.0268

One can immediately compare the columns for D and Φ_o in table 6 to ascertain that biodiversity among feeding species correlate poorly with functional redundancy (R = 0.198, p = 0.342). That is, biodiversity is not a good indicator of trophic functional redundancy among active feeders. The correlation between D and the emulated redundancy, Φ_e, is even worse (R = 0.092, p = 0.663). Significant alone is the correlation between the observed redundancy, Φ_o, and that emulated by the dyadic matrix of biomass densities as supplemented by dietary topology, Φ_e (R = 0.760, p = 0.00001). Because most estimates of biodiversity are reckoned among only living ecosystem compartments, this result suggests that a rough estimate of functional redundancy is possible using only the distribution of biomass and the dietary topology among feeding compartments.

The values for the indexes based on only consumers and producers are presented in table 6. Some maintain that detrital pathways contribute to system stability [41], so that these flows were added to the system and the full ensemble of exchanges among both living and non-living compartments, was examined and results can be found. (See electronic supplementary material, file <RESULTS.XLS>.) One expects that the correlation between Φ_e and Φ_o for all internal flows will be weaker than those reckoned on feeding flows alone, because the dyadic assumption is likely to be less effective when one of the actors is passive and non-living. Indeed, the correlation among indexes incorporating all internal flows is less (R = 0.556, p = 0.004). The correlation between D and Φ_o remains insignificant (R = 0.243, p = 0.313), and that between Φ_e and D improves only marginally (R = 0.384, p = 0.058).

Calculation of the measures using the entire suite of endogenous and exogenous flows becomes problematic in that one must assign values to biomasses associated with the origins and destinations of exogenous flows, and it is not obvious how to accomplish this. One possible assumption is to assign a biomass to the origin of the exogenous inputs that roughly corresponds to the aggregate biomasses of all the primary producers. In order to maintain rough conservation of medium across the system, one can show that the biomass of the destination of all exports and respirations should be roughly the same as that for the origin of all the inputs. Values of all indexes under these assumptions can also be viewed in the electronic supplementary material, file <RESULTS.XLS>.

As with the internal flows, correlations between D and Φ_o and between Φ_e and Φ_o for all flows are marginal (R = 0.118, p = 0.583, and R = 0.055, p = 0.798, respectively). Surprisingly, the correlation between D and Φ_e was borderline significant (R = 0.600, p = 0.002). It remains unknown whether this significant connection is an artefact of the rather arbitrary assumptions made to assign biomasses to the exogenous flows, or whether it constitutes a true natural correlation. The latter remains possible, because if the products in the arguments of the logarithms in (3.3) are expanded as the sum of the logarithms of the factors, the resulting formula resembles an expression that is twice the value of C, and (3.1) in its turn formally resembles expression (1.1) for D.

If this connection happens to be real, then a tentative, transitive relationship has been established between D and Φ_e. That is, D is weakly correlated to Φ_e and Φ_e is marginally correlated to Φ_o, so that D is related to Φ_o in transitive fashion. One still should ask why such a transitive connection was not perceived when dealing with internal flows?

As to the relative contributions of topology versus flow magnitudes of the values of Φ, one observes in table 6 that the drop from the median Φ_max to the median Φ* attributable to the flow topology is 51.8%, while the decrease from Φ_max to Φ_o caused by unequal flow magnitudes resolves another 27.8% of the original ambiguity. When all internal flows enter the calculations, the topology resolves 39.5% and the flow magnitudes eliminate another 40% of the original uncertainty. The respective declines when all flows are used become 42.9% and 31.0%. It seems likely that topology in most instances will account for more information than flow magnitudes, but at times comparable amounts will be resolved by both attributes.

8. Connections with system persistence

It remains to explore what, if anything, these indexes have to do with systems persistence, in light of the fact that none contains any explicit reference to system dynamics? To repeat, considerable effort was invested in developing (mostly dynamical) models in the attempt to associate greater biodiversity with increased systems ‘stability’. The project suffered significantly when linear stability analysis revealed exactly the opposite—that more biodiversity implies less internal stability [8].

It is worth noting that in these attempts stability was taken to mean that the forces causing the system to cohere were on average greater than the tendency for the ensemble to fall apart. In other words, the spotlight was on ‘internal’ cohesion. The goal was to identify a single upper threshold beyond which the system can no longer maintain its dynamical structure. Such is no longer the picture, once attention is broadened from stability to the more general notion of ‘persistence’. Open dynamical systems that are tightly bound tend to be efficient, but ‘brittle’ [42]. Their internal cohesion is high, but with rigid constraint, they become inflexible and less capable of adapting to novel external perturbations. Might a complementary threshold on freedom and flexibility also exist, below which systems become prone to break down under external stress?

Some have suggested these two thresholds coincide and that living systems always reside on the ‘edge of chaos’ [43]. This edge hypothesis was developed, however, using mechanical and algorithmic models that are capable of creating sharp, rigid distinctions, when in fact the very notion of flexibility implies freedom and a degree of indeterminacy. Empirical data on existing trophic networks show that systems tend to cluster within a narrow range of mutual information, demarcating what has been called the ‘window of vitality’ [44]. A collection of 17 trophic networks (including some used here) exhibited normalized (dimensionless) values of ascendency (A/C) that grouped around a value of 0.40 [45].

Presumably, the upper threshold identifies when the system possesses insufficient internal cohesion to maintain itself without spontaneously falling apart. Robert May [8] identified his limit with the Wigner Semicircle Criterion,⁵ which was based on studies of randomly assembled matrices [47]. May deduced that, on average, any network for which α < (nc)^–1/2 will possess local linear stability, where α is the average strength of interaction (cohesion), n is the number of components and c is the topological connectivity (the number of non-zero links divided by the maximum possible).

Ulanowicz developed an information-theoretic analogue to the Wigner Criterion using dimensional reasoning [44]. He noticed that the product nc is the link-density, or the effective number of flows per node, which Ulanowicz & Wolff ([21], appendix A) had shown to be m = 2^Φ/2. As for the effective strength of interaction, Ulanowicz defined it as that constant, a, by which each flow in Φ* must be multiplied in order to yield the same value as Φ. This provided a relationship between Φ and Φ* as

or equivalently, between m and m*,

One can now eliminate a between this latter relationship, and the ersatz Wigner statement, a < (m)^−1/2, to yield the erzatz criterion purely in terms of m and m*,

That is, whenever the observed number of effective links per node is no greater than the expression on the right-hand side, the network is likely to persist.

Using the values of Φ*, Φ_e and Φ_o from table 6, the values of m*, m_e, m_o and the Wigner Criterion (m_max) are displayed in table 7.

Table 7.

Values of the effective link densities (# of links per node) m*, m_e and m_o, as compared with the Wigner Criterion, m_max.

no.	system	nl	m*	me	mo	mmax
1	Crystal River Creek (control)	20	4.359915	2.768395	1.805439	2.879958
2	Crystal River Creek (ΔT)	20	3.583949	2.061436	1.639607	2.749424
3	mesohaline Chesapeake Bay	33	3.625802	2.178070	1.754062	2.75849
4	mesohaline Chesapeake Bay	12	2.514637	1.733034	1.870080	2.392307
5	Baltic Sea	12	2.510544	1.698722	1.851250	2.390319
6	Florida Bay	122	21.34905	3.928286	2.981834	2.701279
7	gramminoid Everglades	63	14.83517	4.324400	3.496351	2.858596
8	Mondego Estuary	42	11.07205	1.728895	1.716952	2.956179
9	Narragansett Bay	31	5.229779	3.800528	2.448927	2.959826
10	St Marks River	48	6.809033	3.568332	3.543193	3.012261
11	polyhaline Chesapeake Bay	31	3.411485	2.541447	2.312815	2.709027
12	southeast Chukchi Sea	48	10.30162	2.651576	2.740711	2.974249
13	northeast Chukchi Sea	48	9.842672	2.753373	2.139094	2.984179
14	Everglades cypress wetlands	65	11.80029	1.433011	2.018453	2.938017
15	Ems Estuary	12	2.661519	2.414208	2.188815	2.459710
16	Kromme Estuary	13	2.357651	2.005970	1.482364	2.311407
17	Okefenokee Marsh	21	4.624669	2.493894	1.756009	2.910053
18	Swartzkops Estuary	12	2.073690	1.631445	1.455889	2.137639
19	Ythan Estuary	11	2.206179	1.480875	1.791912	2.223498
20	Twin Cays fringe mangroves	72	8.642807	2.008196	1.798757	3.005433
21	Twin Cays transition mangroves	58	8.656597	2.261453	2.467756	3.005240
22	Broad Creek	31	4.721843	2.370514	2.101399	2.919689
23	Northern Benguela Current	22	6.385059	2.620787	1.651755	3.005815
24	Delaware Bay	33	6.046080	3.430098	2.546472	2.997271
25	Lake Michigan	35	6.045661	3.245858	2.854820	2.997258

One see from table 7 that the Wigner Criterion, m_max, is exceeded three times by values of m_o and six times by m_e (numbers in italics). Given that m_max is only a dimensional interpretation of the Wigner Criterion and not an analytical mapping, it is not too surprising that some m_o occasionally surpass that estimate. Such violation does not imply that the system in that case is inherently unstable, but it should caution managers to explore it more thoroughly using sensitivity analysis to identify its most vulnerable species and links [48]. Furthermore, because in most instances m_e > m_o, one should expect that m_e > m_max more frequently than m_o > m_max. (This follows from the observation above that Φ_e tends to be higher than Φ_o.) In the large majority of cases, however, the ersatz Wigner Criterion was satisfied by both observation and emulation.

The correlations between all pairs of network indices are given in table 8. With the exception of the correlations between Φ_e and m_e with Φ_o, all other highly significant connections represent functional relationships between definitional formulae. Correlations between D and all the other definitions are uniformly poor. Corresponding correlations pertaining to the internal flows and the full complement of flows are presented in electronic supplementary material, file <RESULTS.XLS>.

Table 8.

Correlations among all pairs of network indices. R-values appear in the upper-right triangular matrix (row < column). Probabilities are given in the lower-left triangle (column c < row). Highly significant correlations (p < 0.1%) are indicated in italics.

		1	2	3	4	5	6	7	8	9
		D	Ømax	Ø*	m*	Øe	me	Øo	mo	mmax
1	D	1	0.301	0.284	0.221	0.0917	0.0929	0.198	0.183	0.282
2	Ømax	0.144	1	0.931	0.864	0.475	0.496	0.61	0.595	0.719
3	Ø*	0.168	<0.00001	1	0.942	0.483	0.514	0.583	0.573	0.720
4	m*	0.289	<0.00001	<0.00001	1	0.431	0.489	0.551	0.553	0.461
5	Øe	0.663	0.0164	0.0144	0.0313	1	0.987	0.760	0.766	0.518
6	me	0.659	0.0117	0.00852	0.0132	<0.00001	1	0.793	0.805	0.473
7	Øo	0.342	0.00121	0.00223	0.00432	<0.001	<0.00001	1	0.992	0.456
8	mo	0.381	0.0017	0.00273	0.00417	<0.00001	<0.00001	<0.00001	1	0.422
9	mmax	0.172	<0.001	<0.001	0.0203	0.008	0.017	0.0218	0.0357	1

As discussed above, the Wigner Criterion is likely only one of two thresholds delimiting persistence. There is almost certainly a minimum m, m_min, above which m_o must remain, lest it become too brittle to persist in a noisy environment. (The smallest value of m_o in all the networks examined was 1.396 links per node.) The conditions that defined m_max were concerned with the homogeneous notion of attraction among compartments, rendering it amenable to analytical considerations. It is likely, however, that the arbitrary and very heterogeneous events associated with the collapse of brittle systems will make it difficult to determine m_min in precise analytical fashion.

9. Macarthur reconsidered

As a postscript, it is interesting to compare how MacArthur's original suggestion (3.1) relates to the Rutledge's authoritative formula for functional diversity (3.3). It happens that (3.1) correlates very well with (3.3) (R = 0.873, p = 0.129 × 10⁻⁷ for the feeding relationships). Such correspondence is not unexpected, because (3.1) serves as a least upper bound on (3.3), i.e. C ≥ Φ, and the ratio of C to A does not vary much. It appears in retrospect that MacArthur's index is more reliable than the later switch to D. Unfortunately, determining C requires exactly the same data as the calculation of Φ, and thus demands far more effort than assessing D. The comparisons just presented suggest, however, that expending the moderate extra work to assemble the dietary topology and calculate Φ_e will yield a far more reliable gauge of functional diversity than is possible with conventional biodiversity. In retrospect, the preoccupation by ecologists with objects and laws has cost the discipline much wasted effort and confusion, so that progress is best resumed by a return to process ecology.

10. Summary and recommendations

Acknowledging and quantifying the role of the apophatic in ecosystem dynamics substantially changes how ecosystem stability and persistence are conceived. No longer is stability simply a matter of cohesion, but becomes instead a balance between the mutually exclusive traits of internal cohesion versus reliability when confronted by novel external disturbances. No longer will a single threshold suffice to characterize system stability, but rather two limits become necessary to demarcate the window of vitality within which ecosystems remain sustainable.

System resilience to external stresses derives principally from the freedom that apophasis allows within the system—mainly in the form of functional redundancy. Such a necessity for parallel pathways constrains the system from channelling excessive resources along its most efficient pathways. Redundancy in trophic networks is accurately characterized by system overhead, Φ, which is expressed and measured using the concept of conditional entropy from IT. Shannon-based IT is eminently suited to quantifying both apophatic freedom and positivist system performance using the same algebraic rubrics.

Rutledge et al. [14] suggested the network conditional entropy as an improvement upon MacArthur's simple entropy of system flows, and because it incorporates trophic topology, it can faithfully capture functional redundancy. Statistical comparison of the Rutledge measure with the later index of biodiversity (based solely on biomass or population distributions) reveals the latter to be a poor index of functional diversity. Biodiversity is considerably easier to measure than system flows, however, and the quantity speaks to the need for a quick evaluation of ecosystem status.

Fortunately, a compromise between realism and ease of evaluation is possible that requires only moderate additional effort to quantify. Data on qualitative dietary items (feeding topology) can be combined with an assessment of biomass distribution to calculate an index that statistically emulates the Rutledge index. It is recommended, therefore, that those lacking the time or resources to quantify all transfers comprising a system undertake the moderate extra effort to compute the ersatz functional redundancy, Φ_e, as a substantial improvement upon conventional indexes for biodiversity.

Precisely what the observed redundancy, Φ_o, and its emulated substitute, Φ_e, tell one about the persistence of a system remains to be fully explored. It is known that an ecosystem requires adequate amounts of mutually exclusive flexibility and performance to persist. Moreover, the balance between emulated performance (A_e) and reliability (Φ_e) can inform a manager whether or not the community is functioning within normal bounds. Further assessment using the ersatz Wigner stability criterion can possibly reveal whether the given system requires additional sensitivity analysis to identify potentially vulnerable compartments and links.

Biodiversity, functional redundancy and system persistence are all entwined, albeit some relationships are more subtle than others. Biodiversity, for example, is only very weakly and transitively related to functional redundancy. The latter, however, is key to maintaining system persistence and can be assessed directly with only moderate additional effort. Both biodiversity and functional redundancy contribute to system persistence—the former only subtly; the latter more significantly. Further accumulation of network data and more inventive use of IT and other quantitative tools for treating apophasis in systems should eventually render these connections more definitive and lead to more effective ecosystem management.

Finally, this emended scenario of ecosystem development should give pause to those theorists who see evolution purely as a variational (min/max) game. Certainly, organisms and systems continue to strive towards greater performance, but achieving greater efficiency can at times seriously jeopardize a system's resilience. The same caution applies to those who study other process-based ensembles, such as those in economics [49], industry [50], society and ontogeny [51]. To continue to ignore the role of the apophatic in natural systems is to pursue science with one eye shut [52].

Data accessibility

All data and tabulated results are available in the electronic supplementary materials created to accompany this article.

Competing interests

I declare I have no competing interests.

Funding

All work on this contribution was performed using the personal resources of the author. No external funding was available.