Passive bristling of mako shark scales in reversing flows

Abstract

Shark skin has been shown to reduce drag in turbulent boundary layer flows, but the flow control mechanisms by which it does so are not well understood. Drag reduction has generally been attributed to static effects of scale surface morphology, but possible drag reduction effects of passive or active scale actuation, or ‘bristling’, have been recognized more recently. Here, we provide the first direct documentation of passive scale bristling due to reversing, turbulent boundary layer flows. We recorded and analysed high-speed videos of flow over the skin of a shortfin mako shark, Isurus oxyrinchus. These videos revealed rapid scale bristling events with mean durations of approximately 2 ms. Passive bristling occurred under flow conditions representative of cruise swimming speeds and was associated with two flow features. The first was a downward backflow that pushed a scale-up from below. The second was a vortex just upstream of the scale that created a negative pressure region, which pulled up a scale without requiring backflow. Both flow conditions initiated bristling at lower velocities than those required for a straight backflow. These results provide further support for the role of shark scale bristling in drag reduction.

1. Introduction

The shortfin mako Isurus oxyrinchus is a coastal and oceanic endothermic shark that attains a maximum total length (TL) of approximately 4 m [1]. It is one of the fastest swimming sharks, using its speed to prey on crustaceans; cephalopods; and teleost fishes, including fast-swimming swordfish (Xiphias gladius) and striped marlin (Tetrapturus audax)—pursuing its prey with rapid bursts of speed. It is also pursued and preyed upon by the fast-swimming white shark (Carcharodon carcharias) [2–5]. The shortfin mako also performs long migrations, typically travelling up to 556 km but sometimes as far as 5500 km [6,7]. Estimating a conservative maximum burst speed of 10 body lengths per second, Motta et al. [8] estimated a speed of 40 m s⁻¹ (144 km h⁻¹) and a Reynolds number (Re) of 1.6 × 10⁸ for a 4 m TL mako shark. Estimated cruise swimming speeds are up to 9.8 m s⁻¹ (35.3 km h⁻¹), corresponding to a cruising Re of 3.9 × 10⁷ for a shark of the same length [7,9–13]. Thus, even at slow cruising speeds, the boundary layer on the vast majority of the body is likely to be in a turbulent state, with transition occurring within several centimetres of any leading edge surface.

Elasmobranch fishes (sharks, skates and rays) are covered with placoid scales (dermal denticles) that encompass a wide range of sizes and shapes, both inter-specifically and intra-specifically. The scales are composed of a crown, a neck and a base. The crown and neck contain a pulp cavity and are composed of dentin, which in the crown is overlaid with an enameloid layer. The bony base is embedded by collagenous Sharpey’s fibres in the superficial layer of the dermis, the stratum laxum (S. spongiosum; figure 1). An epidermis of only a few cell layers lies between the scales but does not cover the crowns [8,11,14–18]. Within the epidermis are mucous producing goblet cells that are more abundant in benthic living elasmobranchs such as skates and rays, and relatively fewer in number in mid-water and pelagic sharks [19,20; PJ Motta 2017, personal observation]. Deep to the stratum laxum is the stratum compactum, a dense layer of type I collagen fibres oriented in cross-helically wound layers. Together, the dermal layers provide a firm and subcutaneously pressurized layer to the denticles [16,17,19,21–24].

Figure 1.

Scanning electron micrograph of mako scales and diagram of engineered riblet surface. (a) Oblique view of the placoid scales of Isurus oxyrinchus from the flank region just posterior to the last gill slit. Note that the anterior to posterior length of the crown is longer than that of the base, allowing the base to pivot by its collagenous attachment to the stratum laxum of the dermis. B, base; C, crown; R, riblets; SL, stratum laxum of the dermis. (b) Engineered riblet surface for comparison.

Shark scales have been shown to reduce drag and improve swimming performance [25–28], in addition to their various other roles, including mechanical and biological protection, abrasion resistance, parasite protection, antifouling and bioluminescence [11,20,29–33]. Biomimetic shark scale models in turbulent boundary layer flows have been found to produce 3–13% lower drag compared to smooth surfaces [27,34–36], and a self-propelled flapping foil covered with shark skin had higher swimming speeds with intact scales than it did with the scales sanded down [28].

Drag reduction effects of shark scales have generally been attributed to static effects of scale morphology [25,26,37–39]. The scale crown may be covered by a series of ridged structures (micro-ridges, ridges and keels) running in an anterior to posterior direction, parallel to the primary flow direction (figure 1a). In fast-swimming sharks such as the shortfin mako I. oxyrinchus the height (approx. 30 μm) and spacing (approx. 40–80 μm) of these structures is quite consistent [11]. Investigators have noted the similarities between these structures and riblets, rows of parallel ridges oriented with their axes along the primary flow direction (figure 1b). Riblets have been shown to reduce turbulent skin friction on engineered surfaces by hindering cross-stream movement of vortices in turbulent boundary layer flows, as reviewed by Walsh [40].

It has also been suggested that passive or active scale actuation, or ‘bristling’, may play a role in drag reduction [27], but the capacity of scales to bristle and possible mechanisms by which bristling might reduce drag have not been investigated until fairly recently [8,41–43]. Morphology and flexibility of the placoid scales differ among shark species and across body regions. In the shortfin mako shark, the scales range from smooth and non-erectable on the leading edges of the fins to ridged and manually erectable to 50^° on the flank, with less flexibility on the pectoral fin trailing edges and tail [8]. The erectable flank scales have long crowns and short bases that are wider than long, the combination of these attributes apparently facilitating the passive pivoting of the scales by increasing the leverage of the crowns [8]. Water tunnel studies with a range of applied adverse pressure gradients, at Re of 1.3 × 10⁵ and 2.5 × 10⁵, showed a reduction in both backflow and the degree of measured flow separation over shark skin as compared with a smooth surface and with shark skin that had been painted over to inhibit bristling [43,44].

Boundary layer separation can be induced in the region of an adverse pressure gradient under both laminar and turbulent conditions. On the body of a shark, this is likely to occur aft of the maximum girth, between the gill slits and the first dorsal fin and on the latter posterior half of the fins. Notably, these are the regions where scale flexibility is highest [8]. Separation of the flow occurs because of viscous effects within the boundary layer. The onset of flow separation involves a patch of low momentum fluid, near the wall and within the boundary layer, which is induced to reverse direction relative to the main flow due to the presence of a negative pressure located upstream. For unsteady flows, flow separation is a process that develops very suddenly (over short timescales) and adjacent to the surface at very small spatial scales [45,46]. Shortfin mako scales are some of the smallest in size, which is inline with their role in drag reduction because higher Re are associated with smaller turbulent structures, such as streamwise vortices and low-speed streaks [47]. By riblet studies [27], it has been shown that the length of a shark scale (approx. 0.2 mm on the shortfin mako) corresponds to about 100 viscous length scales. We hypothesize this is the approximate width of a low-speed streak in the turbulent boundary layer in which reversing flow develops. Furthermore, the corresponding viscous timescale for a fast-swimming mako is calculated to be about 4 μs. A patch of separating fluid expands and thickens while gaining momentum, which in turn leads to global flow separation characterized by an eruptive plume of boundary layer flow ejecting away from the body; the flow detachment results in greater pressure drag [48]. During this process, flow reversal close to the surface can easily exceed 30% of the free stream flow magnitude [43].

In a turbulent boundary layer, three-dimensional patches of reversed flow move upstream and downstream unpredictably within the buffer layer (bottom 1% of the boundary layer) and at various span-wise locations. Thus, in a time-averaged sense, turbulent boundary layer separation is defined as the point where the flow is reversed for 50% or more of a specified time interval [49]. It is this unsteady process of flow reversal adjacent to the shark skin that is believed to initiate scale bristling. It is further hypothesized that bristling inhibits the flow reversal process, preventing more global flow separation that would lead to higher pressure drag on the body of the shark. Bristling may also increase the timescale of the unsteady processes occurring in the boundary layer by inducing mixing, thereby energizing the boundary layer momentarily in the near-surface vicinity and causing a relaxed time for flow reversal in the boundary layer to initiate again due to the adverse pressure gradient.

Detailed kinematic and hydrodynamic measurements of scale bristling have proven difficult to obtain because of the high spatial and temporal resolutions required. For this study, we recorded high-speed, high-resolution videos of passive scale bristling to investigate the hydrodynamics associated with bristling. Based on our analyses, we discuss hydrodynamic mechanisms for scale bristling and possible implications for drag reduction.

2. Material and methods

2.1. Experimental set-up

A piece of flank skin measuring approximately 1 × 5 cm was excised from a shortfin mako shark, I. oxyrinchus, (141.5 cm fork length, 30.4 kg), posterior to the last gill slit and between areas B2 and B5, as defined in fig. 3 in Motta et al. [8]. The skin was cleaned of underlying muscle and glued with cyanoacrylate glue to a steel block, 5.2 × 2.4 × 5.0 cm (length × width × height). The block was centred at the bottom of the working section of a racetrack flume—75.5 × 34.5 × 10 cm (length × width × height), with a 24 cm long ×2.5 cm wide working section—filled to approximately 8 cm depth with water seeded with Nannochloropsis sp. (1.5–2 μm) algae particles (figure 2). Deionized water was used rather than seawater to protect sensitive equipment. With a water temperature of 18^°C, the resulting kinematic viscosity was 1.1 × 10⁻⁶ kg m⁻¹ s⁻¹, approximately 4.3% lower than the kinematic viscosity for a typical seawater salinity of 35.

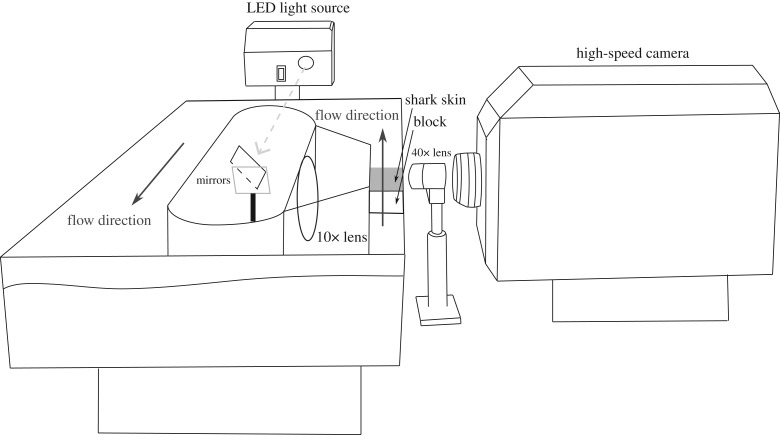
Figure 2.

Diagram of the experimental set-up. Tracing from a photograph of the experimental design showing the PIV tank where videos of the shark skin were recorded. Black solid arrows represent the direction of water flow. The centre part of the tank housed a dry area where an array of mirrors were located to redirect the light (dashed grey arrow) from an LED illuminator over the shark skin. A grey rectangle represents a section of mako shark skin housed in the working section of the tank. A 10× lens was placed between the shark skin and the mirrors to focus the light. Videos were recorded with a high-speed camera, using a 40× microscope objective.

The steel block with attached skin was positioned perpendicular to a high-speed camera (Photron FASTCAM SA-2) with a 40× extra-long working distance Nikon microscope objective lens (approx. 1 cm working distance) placed close to the front wall of the flume, providing a focal plane as far as possible from the wall. The test section was illuminated using a bright-field configuration with the light from an LED light source (Dolan–Jenner Fiber-Lite Mi-LED A2) directed through the back wall of the working section with a pair of mirrors and a lens to produce a bright-field image of the scales. The image area was approximately 1 × 1 mm, with a depth of field of approximately 7.5 μm [50]. We recorded videos of scales exposed to various flow regimes at 50 400 fps with a shutter speed of 1/200 000 s. Flows were generated using a jet of water produced by an aquarium pump (Maxijet 1200) and directed over the surface of the skin through a 3 mm diameter exit. The videos analysed for this paper are available at: doi:10.6084/m9.figshare.6936200.

2.2. Flow types

Recording time was limited due to the high temporal resolution required, so rather than attempting to study time-varying behaviour we analysed individual scale bristling events to determine the flow conditions required to initiate bristling. We extracted scale bristling event sequences from the video to explore possible mechanisms for scale bristling. We define a scale bristling event as consisting of three phases—elevation, during which the scale moves from un-bristled to its maximum bristling angle; peak, after the scale has reached its maximum angle but before it has started to depress; and depression, during which the scales moves from bristled back to un-bristled (figure 3a). We refer to the start of elevation period as ‘initial movement’ and the start of the peak period as ‘maximum angle’ (figure 3a).

Figure 3.

Scale kinematic parameters. (a) Diagram of the sequence of a bristling event. (b,c) Means and SDs of kinematic parameters for all scale bristling events (all; n = 27) and two flow types analysed with particle tracking: forward jet flow over a fence (forward; n = 3) and forward jet flow over a fence with a vortex upstream of the scale (vortex; n = 1). (b) Means of time durations for scale elevation, peak elevation, and depression and SDs for total scale bristling duration. (c) Means and SDs of maximum bristling angle. The forward jet with vortex bristling event had a duration over twice as long as the means for the other flow types, mainly due to a longer time at peak elevation. Bristling angles were similar for all flow types. (Online version in colour.)

We grouped the bristling events into three flow types based on general flow characteristics. The first flow type was a ‘reverse jet’ flow created by directing jet flow posterior to anterior (i.e. in the negative x-direction, or the direction opposite to that produced by normal swimming) with no fence in the flow (figure 4a,d). This flow does not represent a natural flow but provides bounds on maximum scale bristling due to strong flow reversal.

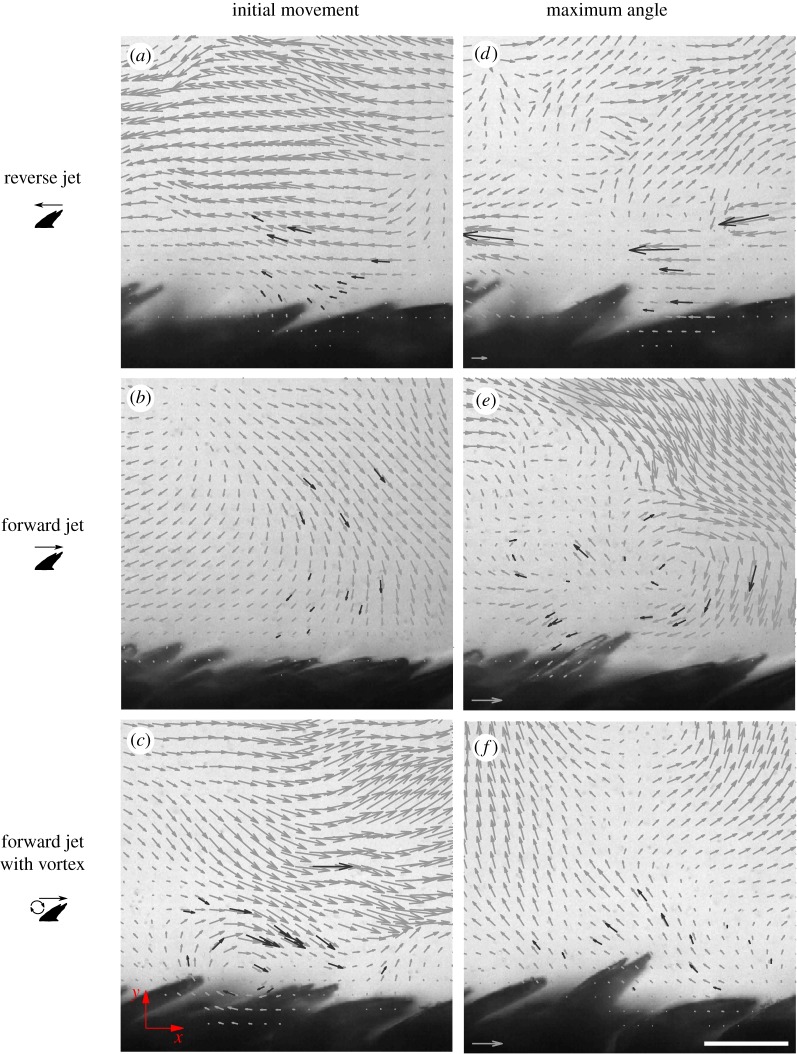
Figure 4.

Representative velocity fields. Velocity fields for three types of flow over shark scales: reverse jet flow, forward jet flow over a fence and forward jet flow over a fence with a vortex upstream of the scale. Frames in (a–c) are close to the time of initial scale movement, and frames in (d–f) are close to the time of maximum scale erection. Black vector arrows represent combine PTV-derived velocity field data, and grey vector arrows represent combined PIV and PTV data. Dark grey vectors indicate PTV tracks. The axes used throughout the study are shown in the bottom left corner. Free stream velocity for forward swimming is from left to right (positive x direction). The scale bar represents a distance of 0.1 mm. Scale arrow represents a flow speed of 1 m s⁻¹. Note that vector arrows are scaled to half the length for the reverse jet compared to the other two cases. (Online version in colour.)

The second flow type was a ‘forward jet’ flow created by directing jet flow in the same direction as that produced by normal swimming (positive x-direction), with a 6.1 mm-diameter cylindrical fence placed in the flow downstream of the jet nozzle and upstream of the scales (figure 4b,e). This flow was designed to simulate the flow created by swimming. We could not produce the complex flow field produced by a swimming shark using our experimental set-up, so the jet and fence were used to generate a flow with turbulent features, including flow reversal, similar to those expected in a boundary layer flow over shark scales [44].

The third flow type was created in the same way as the ‘forward jet’ flow type but was a special case in which a vortex was observed just upstream of the scale of interest near the beginning of the elevation phase. We refer this flow type as the ‘forward jet with vortex’, or simply ‘vortex’, type (figure 4c,f).

2.3. Analysis

We measured kinematic parameters for six scales, with 1–8 bristling events (median 5) analysed for each, to determine kinematic parameters for a total of 27 bristling events (all with a forward jet flow). Kinematic parameters were not calculated for the reverse jet cases because the scales in these cases did not undergo a complete bristling sequence (i.e. they did not depress). We calculated time duration for elevation, peak and depression phases by dividing the number of frames between events by the frame rate (figure 3a). We also measured the maximum angle between the long axis of each scale and the x-axis; we refer to this angle as the maximum bristling angle.

We refer to the events for which we measured kinematic parameters as ‘all’ events to distinguish them from a subset of events for which we characterized the flow fields surrounding each bristling scale. Of this subset of events, three were forward jet cases and one was a forward jet with vortex case. We also characterized flow fields for two reverse jet events, which were not included in the kinematic analyses.

Flow fields were characterized using a combination of particle image velocimetry (PIV), similar to the micro PIV method of Gemmell et al. [50] and particle tracking velocimetry (PTV). Videos were preprocessed for PIV and PTV using the Fiji 2.0 distribution of ImageJ [51] by inverting, adjusting brightness and contrast, and using the ‘find edges’ function. PIV was performed using DaVis 8.3 (LaVision, Göttingen, Germany). The PIV calculations were useful for assessing large-scale flow-field features, but seeding density was generally too low to allow for accurate PIV calculations close to the scales, so PTV was used to quantify flows near the scales.

For PTV, particle positions were tracked manually using the TrackMate package [52] for ImageJ. Velocity components were then calculated for each frame pair by taking mean displacements of particles within a 0.2 × 0.2 mm region centred above the tip of the scale at its maximum bristling angle, using Matlab R2017b (MathWorks, Nattick, MA, USA). In addition to the time series, we calculated flow parameters at two time points, initial scale movement (start of elevation phase) and maximum angle (start of peak phase; figure 3a). For these two time points, we report the mean of the velocity components over three frames, centred on the relevant frame. We also report ranges of maximum velocity magnitude over time across the entire field of view, based on combined PIV and PTV data. These ranges reveal differences between the overall flow fields for the three flow type, but they depend on the field of view and may be affected by PIV error due to high velocities relative to the field of view, so they were not included in further analyses.

For some figures and for pressure calculations, PIV and PTV data were combined in Matlab. First, PTV data were interpolated to the same spatial resolution as PIV data, using Matlab's ‘v4’ implementation of a biharmonic spline interpolation [53]. Then, PIV and PTV data were combined using a weighted mean based on the distance of each grid point from the nearest PTV vector. Pressure fields were calculated from combined PIV and PTV data using the queen 2.0 pressure field calculation package for Matlab, available at http://dabirilab.com/software [54,55].

Scale kinematic parameters are reported as mean plus or minus standard deviation (s.d.). Hydrodynamic parameters are reported as medians and ranges.

3. Results

3.1. Scale kinematics

The mean duration of a complete bristling event; including elevation, peak and depression phases (figure 3a) for all analysed bristling events was 1.7 ± 0.8 ms (figure 3b and table 1). The mean maximum angle was 40 ± 7° (figure 3c and table 1).

Table 1.

Kinematic parameters for bristling events. Means and standard deviations of peak bristling angles and durations of bristling phases for all bristling events (n = 27) and those used in PTV analyses for the forward jet case (n = 3) and the forward jet with vortex case (n = 1).

kinematic parameter	all events	forward jet	vortex
angle	40, 7	42, 4	45
elevation	0.5, 0.3	0.9, 0.5	1.2
peak	0.2, 0.1	0.2, 0.1	2.5
depression	1.0, 0.8	1.0, 0.6	1.0
total	1.7, 0.9	2.1, 0.8	4.6

The forward jet case had a mean maximum angle of 42 ± 4°, similar to the mean for all bristling events. Mean scale bristling elevation, time at peak elevation and depression durations for the forward jet case were similar to those for all bristling events (figure 3c and table 1).

The forward jet flow with upstream vortex case had a maximum angle of 45° (figure 3 and table 1). The total duration for the vortex case was 4.6 ms, over twice the mean for all bristling events (1.7 ± 0.8 ms; figure 3b and table 1). Most of the increase in duration was due to an increase in time at peak erection, which was 2.5 ms, an order of magnitude longer than the mean for all events (0.2 ± 0.1 ms; figure 6b and table 1).

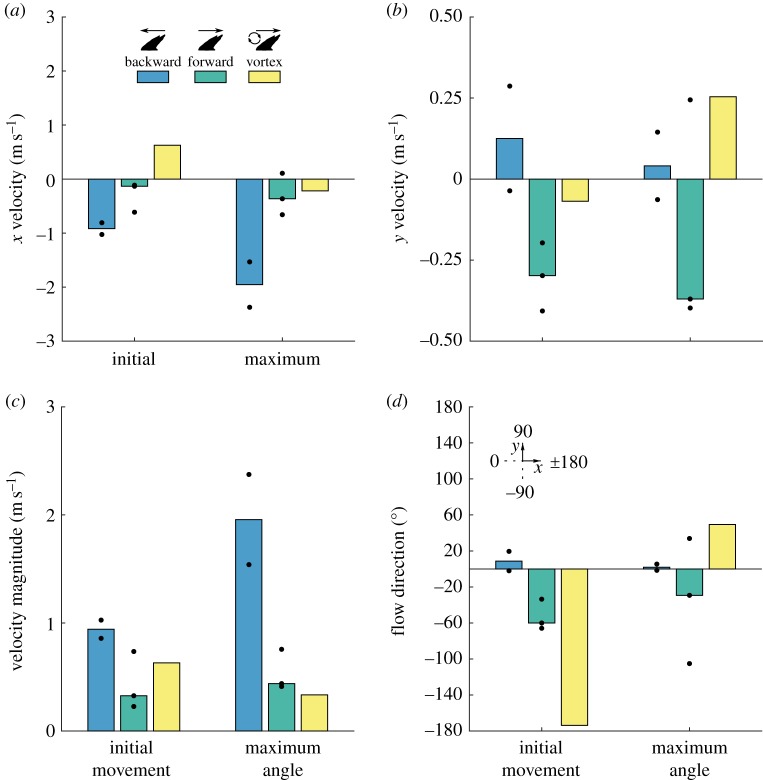
Figure 6.

Velocity components. (a,b) Medians of x and y velocity components, (c) velocity magnitude and (d) flow direction at times of initial scale movement and maximum scale erection for three types of flow past shark scales: reverse jet flow (reverse; n = 2), forward jet flow over a fence (forward; n = 3) and forward jet flow over a fence with a vortex upstream of the scale (vortex; n = 1). Velocities were derived from PTV calculations in a 0.2 × 0.2 mm region above the scale tip. Dots indicate values for individual videos. Velocities were highest for the reverse jet case. In the forward jet case, initial scale bristling occurred without backflow. (Online version in colour.)

3.2. Reverse jet cases

Reverse jet sequences had strong backflows (negative x velocities) and weak vertical (y) velocities (figures 5a, 6 and table 2). Maximum velocity magnitude calculations for the entire field of view ranged from 2.1 to 3.6 m s⁻¹ (not shown), but actually velocities may have been higher because strong particle streaking was observed. At initial scale movement, median x and y velocities near the scale were −0.92 and 0.13 m s⁻¹. Initial scale movement was preceded by an increase in backflow and a slight increase in upward velocity (positive y velocity). Maximum scale bristling occurred after back flow velocity peaked at just over 3 m s⁻¹ (figure 5a).

Figure 5.

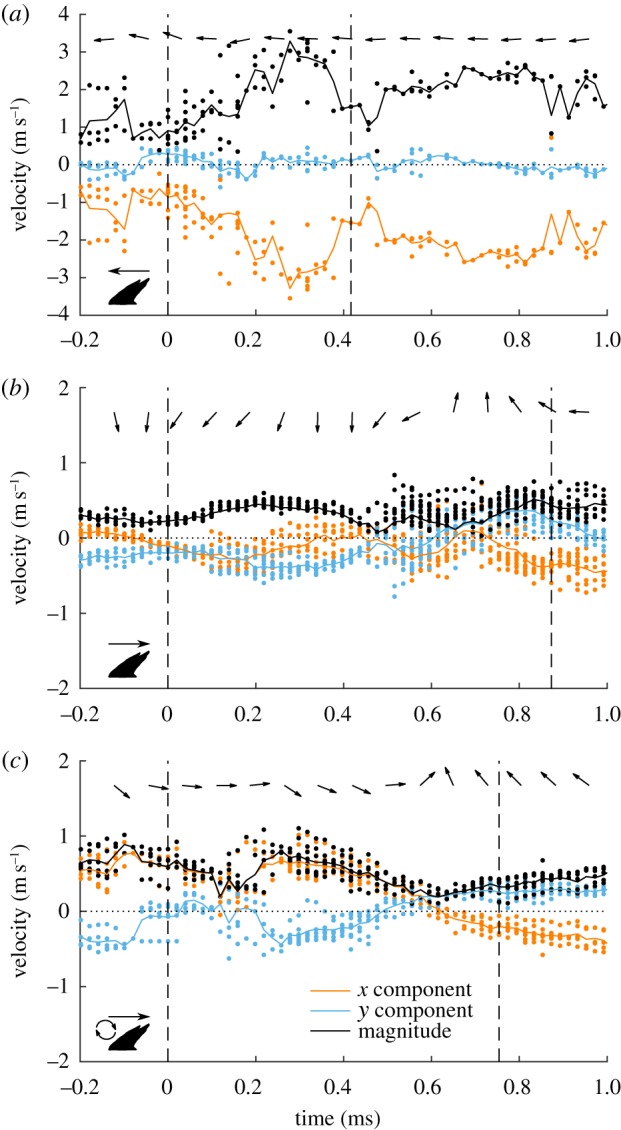
Velocity components time series. Time series of x and y velocity components and velocity magnitude, derived from PTV calculations in a 0.2 × 0.2 mm region above the scale tip. Three flow cases are shown: (a) reverse jet flow, (b) forward jet flow over a fence and (c) forward jet flow over a fence with a vortex upstream of the scale. The flow direction is indicated by arrows at the top of each plot. Dashed vertical lines indicate times during which initial scale movement and maximum scale erection occurred. Note that the y-scale for (a) is compressed compared to (b,c). In the vortex case (c), initial scale bristling occurs in the absence flow reversal.

Table 2.

Velocity parameters for bristling events. PTV-derived velocity parameters at (A) initial scale movement and (B) peak scale bristling. Medians and ranges of mean velocity parameters within a 0.2 × 0.2 mm region centred above the tip of a bristling scale, at peak bristling angle, for three flow cases: a backward jet (n = 2), a forward jet (n = 3) and a forward jet with a vortex upstream of the sale (n = 1).

	backward jet			forward jet			vortex
flow parameter	median	range		median	range		—
A
x velocity (m s−1)	−0.92	−1.03	−0.81	−0.13	−0.61	−0.11	0.63
y velocity (m s−1)	0.13	−0.04	0.29	−0.30	−0.41	−0.20	−0.07
magnitude (m s−1)	0.94	0.86	1.03	0.33	0.23	0.74	0.63
direction (deg.)	8.76	−2.02	19.53	−60.03	−65.88	−33.56	−173.76
B
x velocity (m s−1)	−1.95	−2.37	−1.53	−0.36	−0.66	0.11	−0.22
y velocity (m s−1)	0.04	−0.06	0.14	−0.40	−0.40	0.20	0.25
magnitude (m s−1)	1.96	1.54	2.37	0.44	0.41	0.76	0.33
direction (deg.)	1.93	−1.53	5.40	−29.30	−105.10	33.83	49.32

3.3. Forward jet cases

Forward jet cases had lower velocities overall than did reverse jet flow cases (figure 5b). Maximum velocity magnitudes for the entire field of view ranged from 1.1 to 2.9 m s⁻¹ (not shown). Near the scale, median velocity magnitudes at initial scale movement was 0.33 m s⁻¹, compared to 0.94 m s⁻¹ for reverse jet flows (figures 5b, 6c and table 2). At initial scale movement, forward jet flows had weaker back flow velocities and stronger vertical velocities than did reverse jet flows (figures 3 and 6a, table 2). Forward jet flow velocities had a downward component, compared to a slight upward component for backward jet flows (figure 6b,d and table 2). For the forward jet flow cases, initial scale movement coincided with a change in flow direction from forward and downward to rearward and downward (i.e. a change in sign of x velocity), and maximum scale angle coincided with the strongest rearward flow. Initial movement appears to have been caused by a backflow with a slight downward component, which pushed the tip of the scale up from below.

3.4. Forward jet with vortex case

The forward jet with upstream vortex sequence was a special case of a forward jet flow in which a vortex was found just upstream of the bristling scale. The upstream vortex persisted for approximately 0.4 ms near the initiation of bristling. Maximum velocity magnitudes for the entire field of view ranged from 1.0 to 2.0 m s⁻¹ (not shown). The vortex case had a similar velocity range near the scale to those observed for the forward jet cases (figure 5c) with a slightly higher velocity magnitude than two of the three forward jet flows (0.63 m s⁻¹; figure 6c), but the flow direction for the vortex case was forward and slightly downward at initial scale movement, so backflow was not responsible for the initial scale movement (figure 6a,b,d). Contrasting with the forward jet cases, initial scale movement for the vortex case was not associated with a change in flow direction. For the vortex case, reversal did not occur until just before the scale reached its maximum angle (figures 5c and 6).

We examined the forward jet with upstream case in more detail to determine how scale bristling occurred in the absence of backflow. We took profiles of velocity, vorticity and pressure along a 0.1 mm transect starting at the scale surface and running through the vortex centre for the frame during which the vortex was the strongest (figure 7). Calculations were based on combined PIV and PTV data. Radial (r) and azimuthal (θ) velocity components (with axes centred at the vortex centre) had minimum values of −0.57 and −0.27 m s⁻¹, both at the distal end of the profile, 0.07 mm from the vortex centre (figure 7a,d). Minimum vorticity was −1.3 × 10⁴ s⁻¹ and was located distal 0.03 mm distal to the vortex centre (figure 7c,f). The minimum pressure was −33 Pa, 0.01 mm distal to the vortex centre and 0.04 mm from the scale surface. Pressure adjacent to the scale (profile start) was −24 Pa (figure 7c,f). We also calculated pressure for a transect along the surface of the scale for the same frame (not shown). The mean pressure along the second transect was −13 Pa, and the minimum pressure −24 Pa was located at a position close to the start of the first profile.

Figure 7.

Forward jet with vortex case. Detail of the upstream vortex for forward jet flow over a fence with upstream vortex case. Black vector arrows represent PTV-derived velocity field data, and grey vector arrows represent combined PIV and PTV data. (a) Velocity vector field. (b,c) Velocity vector field with overlaid vorticity and pressure fields. The scale bar in (a) represents a distance of 0.1 mm, and the scale arrow represents a flow speed of 1 m s⁻¹. (d–f) Profiles of polar velocity components, vorticity and pressure along the transect indicated by the dashed lines in (a–c). The transect starts at the scale surface and runs through the vortex centre (yellow circle in (a–c), vertical dashed line in (d–f)). The low-pressure region above the scale (c,f) is likely responsible for the scale bristling in the absence of flow reversal.

4. Discussion

Past studies have demonstrated that shark scales are flexibly connected to the underlying skin and thus are capable of bristling [8] and that preventing scales from bristling increases backflow in a turbulent, reversing flow [43,44], but this study provides the first direct documentation of passive bristling by shark scales in reversing flows.

If scale bristling functions in drag reduction of these high Re swimmers, there would be strong selective pressure for this mechanism to function at cruising speeds. The jet flows used in this study did not have true free-stream velocities as would be the case for boundary-layer flows, but we can estimate the free-stream velocity that would be required to produce similar backflow in a reversing, turbulent boundary layer flow. The reversing velocity components of turbulent boundary layer flows under similar conditions are typically 20–30% of free stream [43]. We calculated back flow velocities of 0.11–0.61 m s⁻¹ at initial scale movement for the forward jet flow case, suggesting that our flows were comparable to boundary layer flows with free-stream velocities of 0.37–3.1 m s⁻¹. These velocities are well within the I. oxyrinchus’s range of cruising speeds, which can be as fast as 9.8 m s⁻¹ [7,9–13], suggesting that passive hydrodynamic scale bristling may be an important drag reduction mechanism, not just during burst swimming events, but for cruise swimming as well. Drag reduction will be especially important at these lower speeds at which I. oxyrinchus swims most of the time, particularly over long migrations, during which I. oxyrinchus typically travel up to 556 km but have been shown to travel far as 5500 km [6,7]. Using a viscous timescale of 4 μs as estimated in the introduction, the mean time at peak 0.2 ms (table 1) corresponds to approximately 50 viscous timescales, which seems appropriate as the viscous sublayer is a similar height in viscous length scales.

The three flow types we examined provide insights into the flow conditions required for scale bristling. For the backward jet case, in which vertical velocities were weaker than horizontal velocities, backflow velocities of 0.81–1.03 m s⁻¹ were required to erect a scale. For the more realistic forward jet case, lower backflow velocities of 0.11–0.61 m s⁻¹ were sufficient to erect the scales, most probably because the flow was directed downward, under the scale tip. The forward jet with upstream vortex case, in contrast to the other two cases, required no backflow to initiate scale bristling. Instead, scale bristling was initiated with a moderate forward velocity component of 0.63 m s⁻¹ and weak horizontal component. The pressure field suggests that scale bristling, in this case, is due to a negative pressure region associated with a vortex just upstream of the scale, with a minimum pressure of −33 Pa. The flow reversal that occurred just before the scale reached peak erection probably held the scale in the bristled position (figure 5c). The long duration of the bristling event for the vortex case, compared to the other cases (figure 3b), may have resulted from the combination of the formation of the upscale vortex and the flow reversal that followed. Our data are insufficient to determine how often such vortices play a role in scale bristling. We identified one other video sequence in which a vortex was located just upstream of a bristling scale, but in this case the vortex formed after initial bristling. We did not include this sequence in our analyses because of our focus on bristling initiation, but pressure calculations revealed a low pressure region near the scale, similar to that from the analysed sequence.

In addition to demonstrating a mechanism for scale bristling, our pressure calculation for the forward jet with upstream vortex case allows us to approximate the force required to lift a scale by multiplying the pressure on the scale at the time of initial scale movement by the area of the scale. Treating the scale as an isosceles triangle with length 200 μm and width 150 μm [8] yields an area of 1.5 × 10⁴ μm². Multiplying this area (in metres) by the mean pressure along the scale, −13 Pa, provides a force estimate of 0.19 μN. This approximation may be useful in predicting other flow conditions that may produce scale bristling when experiments are impractical, for example, to determine how scales on various sections of the body react to local flow conditions.

Motta et al. found that I. oxyrinchus scales from the body region studied here, the flank just behind the gill slits, could be manually erected to a mean of 48° [8]. We observed a mean angle 40° and a maximum 50° for flow driven erection, so realistic boundary layer flows appear capable of bristling scales over their full range of motion. Motta et al. manually erected scales in several regions of the body for I. oxyrinchus [8] and for two other shark species, the blacktip shark Carcharhinus limbatus [8] and the great hammerhead Sphyrna mokarran (PJ Motta, ML Habegger 2012, unpublished data), both of which would be considered fast swimming or large near-shore predators according to Reif’s classification scheme [38]. Of all of the scales in the study, the most flexible found were those of I. oxyrinchus in the flank region studied here; the flexibility of the scales in this region was attributed to a high crown to base length ratio [8]. This is also the region of the body most prone to flow separation [8], so the scale bristling observed in this study may represent the most extreme case, and scales of other sharks and from other regions may experience weaker or no bristling.

This study was designed to document scale bristling rather than show its effect on the flow, but we found some evidence of flow redirection by bristled scales (figure 8). One example of flow redirection is the upstream vortex that formed just upstream of a depressed scale in the forward jet with vortex case (figure 8a). The location of the vortex, in the depression between two scales, suggests that the scales may have played a role in the formation of the vortex. We also identified an example of the flow bifurcating at a scale tip, with part of the flow going over and part going under the scale (figure 8b) and of the start of a vortex under the tip of a scale (figure 8b). These examples show that the flow responds to scale bristling, providing further evidence to support scale bristling as a drag reduction mechanism. Bristled scales may prevent the further development of backflow and lead to mixing, or momentum exchange, within the boundary layer thereby inhibiting the development of flow separation [8,41–43].

Figure 8.

Examples of flow redirection. Example frames from the forward jet with upstream vortex case showing examples of a bristling scale redirecting the flow: an upstream vortex (a), bifurcation of flow at scale tip (b) and a vortex under the scale (c). Grey vector arrows represent combined PIV and PTV data. Particle paths are shown backward from the current frame, coloured by velocity magnitude. The position of the particle at the current frame is indicated by a black dot.

Mako shark scales in most regions of the body, including the flank region studied here, partially overlap, so bristling of one scale often causes adjacent scales posterolateral to the bristling scale to erect [8] (figure 1a). Bristling may therefore occur across small patches. Our depth of field was less than the width of a single scale, however, so we were not able to observe this phenomenon.

Flows over shark scales are complex, varying temporally, spatially across the body, and with swimming speed and kinematics. The interactions of these factors are difficult to parse experimentally, and different scale bristling mechanisms may operate under different conditions. Different regions of the body may also have different flow control requirements, and in some cases scales may be important in increasing thrust as well as reducing drag [28]. For instance, maintaining attached flow over the caudal fin is important at higher Re as the caudal fin generates its thrust mainly by maintaining a large pressure difference on either side of the fin [56]. Computational fluid dynamics (CFD) provides one approach to studying how flow conditions vary under different conditions. Díez et al. [57], for example, used a CFD model of an entire I. oxyrinchus shark, with local roughness values based on scale measurements in different regions along the body to study how lift and drag vary over different parts of the body [57]. Incorporating results from small-scale experimental studies, such as this one, into CFD models of larger portions of the body could provide a more detailed understanding of flows over shark skin and may suggest ways in which these flows can be mimicked to enhance drag reduction for engineered structures.

Data accessibility

The videos analysed for this paper are available at: doi:10.6084/m9.figshare.6936200.

Competing interests

We declare we have no competing interests.

Funding

This material is based upon work supported by, or in part by, the U.S. Army Research Laboratory and the U.S. Army Research Office under contract/grant no. W911NF1510556. This research was also supported in part by the National Science Foundation (UNS-1511996 and IDBR-1455471 to B.J.G.). Additional funding was provided by the Porter Family Foundation.