Human Connectome Project-style resting-state functional MRI at 7 Tesla using radiofrequency parallel transmission

Abstract

We investigate the utility of RF parallel transmission (pTx) for whole-brain resting-state functional MRI (rfMRI) acquisition at 7 Tesla (7T). To this end, Human Connectome Project (HCP)-style data acquisitions were chosen as a showcase example. Five healthy subjects were scanned in pTx and single-channel transmit (1Tx) modes. The pTx data were acquired using a prototype 16-channel transmit system and a commercially available Nova 8-channel transmit 32-channel receive RF head coil. Additionally, pTx single-spoke multiband (MB) pulses were designed to image sagittal slices. HCP-style 7T rfMRI data (1.6-mm isotropic resolution, 5-fold slice and 2-fold inplane acceleration, 3600 volumes and ~ 1-hour scan) were acquired with pTx and the results were compared to those acquired with the original 7T HCP rfMRI protocol. The use of pTx significantly improved flip-angle uniformity across the brain, with coefficient of variation (i.e., std/mean) of whole-brain flip-angle distribution reduced on average by ~39%. This in turn yielded ~17% increase in group temporal SNR (tSNR) as averaged across the entire brain and ~10% increase in group functional contrast-to-noise ratio (fCNR) as averaged across the grayordinate space (including cortical surfaces and subcortical voxels). Furthermore, when placing a seed in either the posterior parietal lobe or putamen estimate seed-based dense connectome, the increase in fCNR was observed to translate into stronger correlation of the seed with the rest of the grayordinate space. We have demonstrated the utility of pTx for slice-accelerated highresolution whole-brain rfMRI at 7T; as compared to current state-of-the-art, the use of pTx improves flip-angle uniformity, increases tSNR, enhances fCNR and strengthens functional connectivity estimation.

Introduction

There has been a growing interest in pushing the spatiotemporal resolutions when using magnetic resonance (MR) neuroimaging to study human brain’s organization and function. Most notably, increasing efforts aimed at generating descriptions of the connections among gray matter locations in the human brain at the millimeter scale are being launched following the approaches used in the Human Connectome Project (HCP) initiative of the National Institutes of Health in the United States. Two MR methods provide the core technologies in the HCP to deduce this connectivity (Glasser et al., 2016a; Uǧurbil et al., 2013). The first is resting-state functional MR imaging (rfMRI), which uses correlations in spontaneous temporal fluctuations in a functional MRI (fMRI) time series to extract ‘functional connectivity’ (Biswal et al., 1995; Essen et al., 2013; Glasser et al., 2016b; Smith et al., 2013a, 2013b; Uǧurbil et al., 2013) the second is diffusion imaging (dMRI), which provides information on ‘structural connectivity’ between gray matter (Aggarwal et al., 2010; Jbabdi and Johansen-Berg, 2011; McNab et al., 2013; Mori and Zhang, 2006; Setsompop et al., 2013; Sotiropoulos et al., 2013).

The original HCP produced a database of high-quality, freely and publicly shared, MRbased neuroimaging data (Glasser et al., 2016b; Uǧurbil et al., 2013; Van Essen et al., 2013) on 1200 subjects at 3 Tesla (3T). In addition, 7 Tesla (7T) data were obtained on 184 of the original 3T subjects. Both the rfMRI and dMRI components of this effort at 7T were obtained with a higher spatial resolution and demonstrated advantages over the 3T data in inferring the brain’s connectivity based on rfMRI (Vu et al., 2017) and dMRI (Sotiropoulos et al., 2016; Vu et al., 2015). However, 7T data were in many ways suboptimal because, at the time, it was only possible to perform such a large scale 7T study with a single-channel radiofrequency (RF) transmit head coil operating in a Circularly Polarized (CP) mode.

It is well recognized that the transmit B₁ (B⁺₁) field generated by a single-channel circumscribing RF head coil suffers from large inhomogeneities across the brain, exhibiting relatively high values in the middle of the brain, but low values in the periphery (Van De Moortele et al., 2005; Vaughan et al., 2001) and lower brain regions such as the cerebellum and inferior temporal lobes (e.g. reviews (Ugurbil, 2014; Uğurbil, 2018) and references therein). Such B₁⁺ inhomogeneities lead to undesirable flip-angle nonuniformity, which in turn results in spatial variations in signal-to-noise ratio (SNR) and image contrast. In the HCP, this B₁⁺ inhomogeneity was only partially mitigated by using passive RF shimming with dielectric padding (Vu et al., 2017, 2015), mainly to increase image signals in lower brain regions.

In addition, whole brain 7T data, like those obtained in the HCP, can suffer limitations in acceleration because of power deposition (i.e. SAR). The HCP relies on accelerated brain coverage using simultaneous multi-slice (SMS) imaging with multiband (MB) RF pulses and EPI-based image acquisition (SMS/MB-EPI) (e.g., (Glasser et al., 2016b; Setsompop et al., 2013; Uǧurbil et al., 2013) and references therein). With this technique, power deposition increases linearly with the slice acceleration factor (i.e. MB factor) when acceleration is employed to acquire MB-fold higher number of volumes (shorter TRs) within a given period of data acquisition time.

The two afore-mentioned transmit limitations significantly disadvantage whole-brain studies at ultrahigh magnetic fields (7T or higher). Following our previous work with dMRI (Wu et al., 2018), we propose that these limitations can be simultaneously tackled with parallel transmission (pTx) techniques (Guérin et al., 2015b; Poser et al., 2014; Ugurbil, 2010; Wu et al., 2013b; Wu et al., 2016; Wu et al., 2018) in order to facilitate rfMRI at 7T. As such, in this paper we demonstrate the utility and advantages of pTx using the 7T HCP-style whole-brain acquisition (i.e., an acquisition similar to that of the HCP 7T rfMRI protocol, covering the whole-brain rapidly using slice-acceleration, 1.6-mm isotropic resolution, 1-sec TR and ~1-hour scan time). We present pTx data using the commercially available Nova 8-channel transmit 32-channel receive (Nova 8Tx32Rx) head coil (Nova Medical, Inc., MA, USA) and compared the results to those of data acquisition using the single-transmit (1Tx) configuration of the same coil (i.e., Nova 1Tx32Rx coil) as employed in the 7T HCP protocol; thus, the receive coils employed in the comparison were identical, facilitating the comparison. Our results demonstrate that pTx can significantly improve flip-angle uniformity across the entire brain, which in turn increases the temporal signal-to-noise ratio (tSNR) and functional contrast-to-noise ratio (fCNR), leading to better estimation of brain’s functional connectivity.

Methods

We conducted human experiments on a 7T MR scanner (Siemens, Erlangen, Germany) equipped with whole-body gradients (70 mT/m maximum amplitude and 200 T/m/s maximum slew rate), which can be operated in 1Tx and pTx modes. In the pTx mode, the MR system can independently drive 16 transmit channels with a 1-kW RF power amplifier each. In the 1Tx mode, the system can drive a 1Tx RF coil with a combined 8-kW RF amplifier. In both modes, the system is capable of receiving MR signals through 32 receive channels.

Human brain images were collected in five healthy subjects (3 males and 2 females, 20–72 years old) who signed a consent form approved by the local Institutional Review Board. Each subject was scanned twice: once in the pTx mode using the Nova 8Tx32Rx head coil and once in the 1Tx mode using the Nova 1Tx32Rx head coil. For pTx acquisition, 8 out of 16 transmit channels were utilized for the 8Tx-only Nova coil. Additionally, to ensure RF safety, the Nova 8Tx32Rx coil was used in the “protected” mode in which total RF power delivery (measured as sum of forward minus reflected power across all of the 8 transmit channels in use) was monitored in real time to be within the power limits specified by the coil manufacturer. In this study, the power limits at the coil plug were set to 11 W for long-term (6 minutes) and 22 W for short-term (10 seconds) RF exposures. For 1Tx acquisition, the Nova 1Tx32Rx coil was used with dielectric padding as in the 7T HCP protocol to improve B₁⁺ in lower brain regions.

Parallel transmit multiband pulse design

In this study, we designed pTx MB pulses with single spokes (corresponding to RF phase and amplitude shimming) for rfMRI acquisition. In particular, these were bandspecific pTx MB pulses which were formed by the sum of single-band pTx pulses, with each single-band pulse having its band-specific phase and amplitude “shim” setting. Because of this, these band-specific pTx MB pulses require fully independent amplitude and phase modulation functions to be played out for each channel during the pulse (Wu et al., 2013b; Wu et al., 2016a).

To increase the time efficiency in B₁⁺ mapping and pulse sequence preparation, we followed the slab-wise design framework (Wu et al., 2016a) and calculated bandspecific RF shim values (i.e. RF amplitude and phase modulations) based on a small number of contiguous, relatively thick B₁⁺ mapping slices (which are defined as B₁⁺ mapping slabs hereafter) instead of on the many relatively thin image slices to be acquired. Furthermore, we designed pTx MB pulses to image sagittal slices in order to capitalize on the coil geometry of azimuthally distributed transmit elements and promote the transmit performance in terms of flip-angle homogenization and SAR reduction (Wu et al., 2016b). Calculation of RF shim sets for pTx pulses was performed in Matlab (The Mathworks Inc., Natick, MA, USA).

Multi-channel B₁⁺ maps covering the entire brain were first obtained at 3-mm isotropic resolution and then manipulated in the slice direction to be compatible with the generalized slab-wise design framework (Wu et al., 2016a) given the targeted MB factor and slice thickness to be used for data acquisition. Specifically, the B₁⁺ maps were acquired within 60 contiguous sagittal slabs (each 3 mm in thickness) spanning 180 mm in the left-right dimension. For each slab, a single set of 8-channel B₁⁺ maps were measured using a hybrid B₁⁺ mapping technique, which has been demonstrated to be capable of providing accurate B₁⁺maps for pTx methods at 7T (Schmitter et al., 2014) and beyond (Wu et al., 2010). Briefly, this method combines a single absolute volumetric B₁⁺ map (obtained in the large-tip-angle regime by transmitting with all channels) together with a series of relative multi-slice B₁⁺ maps obtained in the smalltip-angle regime by transmitting one channel at a time. The single absolute B₁⁺ map was obtained using the actual flip-angle imaging (AFI) (Yarnykh, 2007) with a 3D gradient-recalled-echo (GRE) sequence while the series of relative B₁⁺ maps was acquired using a multi-slice GRE sequence. A CP-like-mode RF phase shimming (Schmitter et al., 2012) was applied on top of the vendor-provided “CP-mode” to increase the B₁⁺ uniformity across the entire brain including the cerebellum. The reconstructed B₁⁺ maps were down-sampled in the slice direction to create another set of B₁⁺ maps with 4.8-mm slice thickness. The central part of this set of B₁⁺ maps, defining 30 contiguous 4.8-mm sagittal slabs and spanning 144 mm in the left-right dimension, was chosen for the subsequent calculation of RF shim values. The choice of 4.8-mm slab thickness and 30 slabs was to match the MB factor of 5 and the resolution of 1.6 mm to be used for image acquisition. Relevant imaging parameters utilized in the acquisitions are reported in the Supporting Materials.

A single set of 8-channel band-specific RF shim values was calculated for each B₁⁺ mapping slab, leading to a total of 30 RF shim sets. All RF shim sets were optimized jointly by solving a regularized magnitude least squares problem based on a two-step procedure for increased robustness (as described in detail in (Wu et al., 2018)).

To improve transmit performance, the calculation of RF shim values considered brainextracted B₁⁺ maps serving as the ROI. To define the ROI, a brain mask was created by acquiring a 0.7-mm, T₁-weighted (T1w) whole-head image with the MPRAGE sequence (Mugler and Brookeman, 1990) (see Supporting Materials for relevant imaging parameters) and by applying the FSL’s brain extraction tool (BET) (Smith, 2002) to extract the entire brain including the cerebrum, midbrain and cerebellum. The impact of B₁⁺ inhomogeneity on inversion pulses of the MPRAGE sequence was minimized by employing adiabatic pulses (Garwood and DelaBarre, 2001; Silver et al., 1984) calculated using the phases obtained from the CP-like-mode RF phase shimming.

pTx-enabled multiband gradient echo EPI pulse sequence

In line with the slab-wise pTx MB pulse design framework ( Wu et al., 2016a), a new 2D gradient-echo echo-planar imaging (2D GRE-EPI) pulse sequence was developed to allow for pTx-enabled, slice-accelerated acquisition of rfMRI data. This new pulse sequence was derived from the 2D GRE-EPI (http://www.cmrr.umn.edu/multiband/index.shtml) pulse sequence that was utilized by the 7T HCP to acquire single-channel-transmit rfMRI data, thereby inheriting all of the preferable and optimized features of this HCP sequence, such as integrated singleband (SB) reference scans, in-plane acceleration and fast online image reconstruction.

More importantly, it can load in band-specific and channel-specific RF shim values from a text file and use them to create pTx SB excitation pulses for SB reference scans and to form pTx MB excitation pulses for image acquisition. When in-plane acceleration is turned on, the new sequence also uses the loaded RF shim values to create pTx excitation pulses for acquisition of auto-calibration signals and allows the autocalibration scans to be performed using an integrative gradient-echo sequence. Note that following the slab-wise framework, the sequence can repeatedly apply a pTx SB (or MB) excitation pulse to excite every image slice residing in the slab (or slabs) that the pulse has been optimized for. We also note that similar sequences have been implemented for MB EPI (Poser and Setsompop, 2018; Tse et al., 2017a) and MB GRE (Tse et al., 2017b) acquisitions.

Resting-state fMRI data acquisition

To demonstrate the utility of pTx for acquiring high-resolution rfMRI data at 7T, we acquired full HCP-style rfMRI data using the pTx MB pulses (defined here as the HCP pTx protocol) and compared the result with that of the protocol utilized in the HCP 7T rfMRI acquisition (defined here as the HCP 1Tx protocol). Our HCP pTx protocol utilized the pTx mode (i.e. using Nova 8Tx32Rx coil in combination with the pTx MB pulse design as described above), whereas the HCP 1Tx protocol employed the singlechannel-transmit mode using the Nova 1Tx32Rx coil and dielectric padding. As in the HCP protocol, a total of five dielectric pads (made of mixture of de-ionized water and calcium titanate) were utilized for data acquisition with the 1Tx mode. Each pad measures 11 cm in width, 11 cm in length and 5 mm in thickness. Following the approach of the HCP protocol, three pads, stitched together side by side to form a bigger rectangular pad of 33 × 11 cm² in size, were placed underneath the head/neck, along with another pad on either side of the head. For all data acquisitions, the subject was instructed to fixate on a black cross displayed at the center of a white screen, in order to keep the subject from falling asleep.

The HCP 1Tx protocol followed the original HCP 7T protocol (exactly) (Vu et al., 2017) for the acquisition of whole-brain rfMRI data. For each subject, data were obtained in four runs. Each run consisted of a timeseries of 900 image volumes, leading to a total of 3600 image volumes. Furthermore, the four runs were acquired with inverted phase encode directions - two runs were acquired with anterior-posterior (AP) phase encodes whereas the other two with PA phase encodes. This is to reduce the impact of susceptibility-induced signal dropout in the final timeseries as created by concatenating the four runs (Smith et al., 2013a). Because the signal dropouts occur in different locations with opposite phase encode directions, the final concatenated timeseries minimizes the number of voxels of signal dropout.

Like the HCP protocol, our HCP pTx protocol also acquired four runs of rfMRI data from each subject with 900 image volumes per run. It also employed most of the imaging parameters of the HCP protocol except that we designed pTx MB excitation pulses to image sagittal slices (instead of oblique-axial slices). This required more slices (90 vs. 85) to be acquired to ensure the whole-brain coverage in the left-right dimension for the subjects scanned in the current study. To keep the same TR of 1 second, pulse length was reduced to 5440 μs (as opposed to 5760 μs for the HCP protocol) and the “fast” gradient mode (increasing the applicable slew rate) was chosen (instead of the “normal” mode for the HCP protocol). The use of “fast” gradient mode also resulted in a small decrease in echo spacing (0.62 vs. 0.64 ms) when keeping other imaging parameters identical to those of the HCP protocol.

For both HCP 1Tx and pTx protocols, we acquired two spin-echo EPI (SE-EPI) datasets with inverted phase encodes for correction of susceptibility-induced EPI distortions: one with AP phase encode and the other with a PA phase encode. Each dataset consisted of three images (for averaging), acquired with the same FOV, spatial resolution and echo train as in the respective rfMRI acquisition. The two SE-EPI datasets were processed by FSL’s “topup” tool (Andersson et al., 2003; Smith et al., 2004) to estimate a field map which was subsequently used for correction of EPI distortion (Smith et al., 2013a). The SE-EPI sequence for the HCP pTx protocol utilized the same RF shim sets as in the pTx rfMRI data acquisition to create the pTx MB excitation and refocusing pulses. Relevant imaging parameters for both rfMRI and SE-EPI acquisitions are reported in Supporting Materials.

Structural T₁w and T₂w image acquisition

To be compatible with the HCP minimal preprocessing pipelines (Glasser et al., 2013) requiring high-resolution structural images, we obtained T₁w and T₂w whole-brain images for each subject at 7T, both with 0.7-mm isotropic resolutions. The T₁w and T₂w brain images were acquired using the Nova 1Tx32Rx coil combined with dielectric padding. The T₁w image was acquired using the MPRAGE sequence, whereas the T₂w image employed the 3D variable-flip-angle turbo-spin-echo sequence (Mugler et al., 2000) with matched FOV, matrix size and spatial resolution. To correct for susceptibilityinduced distortion in the readout dimension and improve the alignment of the two structural images, a field map was acquired using a dual-TE, multi-slice 2D GRE sequence. Relevant imaging parameters for these acquisitions are reported in Supporting Materials.

Data processing and analysis

All data were processed by following the HCP spatial “minimal” (Glasser et al., 2013) and temporal (Smith et al., 2013a) preprocessing pipelines. Briefly, structural T1w and T2w images were first processed to define the subject’s registered standard volume space and standard grayordinate space (consisting of registered standard cortical surfaces and subcortical parcels). The rfMRI data per run were then preprocessed both in space and in time to create an undistorted, detrended and cleaned (Beckmann and Smith, 2004; Salimi-Khorshidi et al., 2014) timeseries in the standard MNI volume space. These volume timeseries were further transformed into the corresponding dense timeseries as defined in the standard grayordinate space.

To demonstrate the usefulness of pTx, tSNR maps were calculated in the MNI standard volume space at subject and group levels. The tSNR map for each subject was obtained by averaging the four per-run tSNR maps, while the group tSNR map by averaging the tSNR maps of individual subjects. In each case, whole-brain tSNR was calculated by averaging across the entire brain. Additionally, region-specific tSNR values at the subject level were quantified for nine brain regions including the cerebellum, as labeled by the MNI152 standard-space structural template image (Grabner et al., 2006).

To correlate flip angles with tSNR at the subject level when comparing the HCP pTx vs. the HCP 1Tx protocols, the flip-angle maps were co-registered to the MNI standard volume space. For this, linear co-registration with 12 degrees of freedom was conducted to align the GRE images of the AFI acquisition to the MNI standard volume space (Supporting Fig. S1), all using FSL’s “flirt” routine (Jenkinson et al., 2002; Jenkinson and Smith, 2001). The difference in flip angles was derived in the MNI standard volume space by subtracting the flip-angle map of the HCP 1Tx protocol from that of the HCP pTx protocol, and likewise the difference in tSNR. The correlation coefficients were then calculated for each subject to quantify the correlation between the flip-angle difference and the tSNR difference across the entire brain.

Additionally, the fCNR was quantified in the standard grayordinate space to further demonstrate the utility of our HCP pTx protocol. For each grayordinate, the fCNR was calculated as the square root of the ratio of BOLD signal variance to unstructured noise variance (Vu et al., 2017). The fCNR map for each subject was derived by averaging the four per-run maps, while the group fCNR map by averaging the fCNR maps across subjects. In each case, the mean fCNR value was also calculated by averaging across the entire grayordinate space.

Dense connectome (or dense connectivity matrix) at the group level was also calculated in order to demonstrate the usefulness of our HCP pTx protocol in estimating functional connectivity. For this, the composite timeseries at each grayordinate was formed by concatenating the demeaned and variance-normalized timeseries across runs and subjects. The dense connectome was then determined by calculating the mutual correlation between the composite timeseries of all grayordinates. The calculation was done using the command-line program “wb_command” and the visualization using the platform “wb_view” from the Connectome Workbench (Marcus et al., 2013).

SAR estimation

In order to confirm that the local SAR in our pTx acquisition was indeed under the safety guideline limit, we calculated the local 10-g SAR by considering all the pulses utilized in the sequence and following the same pulse design procedure and RF specifications and sequence timings as in our experiments, but using the electromagnetic simulation of the Nova 8Tx32Rx coil loaded with a human head model. Our result showed that the maximum local SAR amounted to 0.75 W/kg, which was far under the guideline value of 10 W/kg (as specified for the normal operation mode (IEC, 2008)), corresponding to a safety margin of factor ~13. Given that a safety margin of factor ~3 has been recommended for pTx pulses and utilized in recent 7T studies to image the human brain (Gras et al., 2016, 2017c), the high safety margins in our SAR estimation indicate that indeed we were in compliance with the SAR guidelines.

The SAR for the proposed pTx-enabled rfMRI acquisition had two components: one from the use of pTx MB excitation pulses and the other from the fat saturation employed in the data acquisition to suppress the fat signal. The fat saturation and the pTx MB excitation in the current pTx-enabled rfMRI acquisition were applied with different RF shimming configurations. The fat saturation was applied with the CP-like-mode RF phase shimming, whereas the MB excitation with band-specific RF shimming. As a result, the two spatial distributions of the local SAR due to fat saturation alone and arising from MB excitation alone, were different than each other and not necessarily additive. Indeed, our SAR calculation confirmed this (Supporting Fig. S2) and showed that the maximum local SAR of the final SAR distribution (which was calculated to be 0.75 W/kg) was less than the sum of the two respective maximum local SAR values (which were 0.38 and 0.41 W/kg for MB excitation alone and fat saturation alone, respectively).

Results

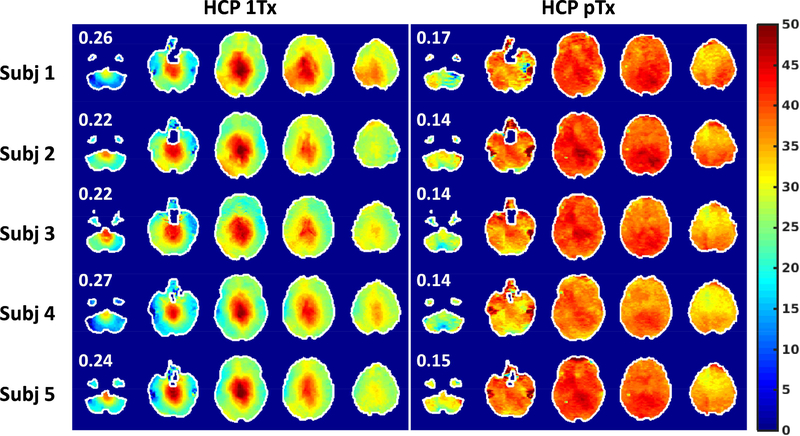
As compared to the 1Tx acquisition, the use of pTx substantially improved RF uniformity across the entire brain (corresponding to improved flip-angle uniformity). This improvement was observed in all of the 5 subjects scanned in the current study (Fig. 1). The coefficient of variation (i.e., standard deviation (std)/mean) of the whole-brain RF distribution was reduced on average by ~39%, with the std/mean on average being ~15% for pTx vs. ~24% for 1Tx.

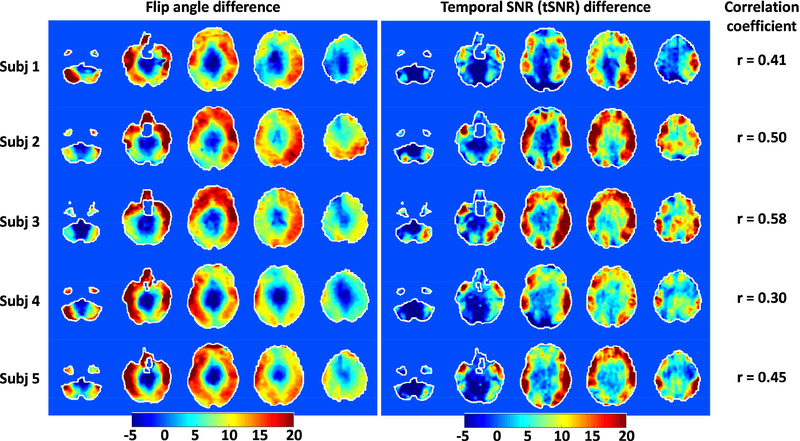
FIG. 1.

Flip angle mapping for HCP 1Tx (left) vs. HCP pTx (right) protocols at the subject level. The HCP 1Tx protocol utilized the Nova single transmit coil and dielectric padding whereas the HCP pTx protocol utilized the Nova 8 transmit coil with pTx multiband pulse design (no dielectric padding). Shown are flip angle maps in degrees in five gapped axial slices, with the number reported being the coefficient of variation (i.e., std/mean) of the flip angles across the whole brain. Flip angle maps were obtained using the actual flip angle imaging method and were co-registered to the MNI standard volume space at 1.6 mm isotropic resolutions. The brain mask resulting from the HCP structural preprocessing pipelines was utilized to mask the flip angle map for each subject. Note that pTx substantially improved flip angle homogeneities across the whole brain, with the coefficient of variation being reduced on average by 39%.

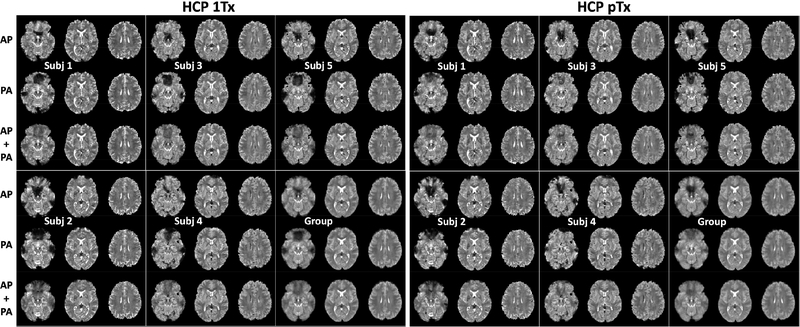
The HCP 1Tx and pTx acquired images from all of the five subjects as well as combined group-level images are displayed in (Fig. 2) as 4D mean images, the average image across the time dimension. These images demonstrate that while the signal dropouts due to susceptibility were observed in either acquisitions with the phase encoding running either in the AP or PA directions, the combination of the two led to little signal dropout. This was observed at both subject and group levels. Furthermore, for each subject, the distortions that are inherent in EPI images were effectively removed by using the HCP preprocessing pipelines.

FIG. 2.

Slice accelerated simultaneous multislice, multiband echo planar imaging (EPI) 4D mean images (i.e., averaged in the time dimension) for the HCP 1Tx and HCP pTx protocols at the subject and group levels. Shown are 4D mean images for Anterior Posterior (AP) phase encode acquisition only, for PA phase encode acquisition only, and for combining both phase encode acquisitions (i.e., AP + PA). For each subject and a given protocol, four runs of resting state fMRI were acquired, each containing 900 image volumes and lasting 16 minutes, leading to a total of 3600 volumes acquired in 64 minutes. All data were acquired with 1.6-mm isotropic resolutions, 5-fold slice acceleration, 2-fold in-plane acceleration, TR/TE=1000/22 ms, but in sagittal and oblique-axial slices for the HCP pTx and 1Tx protocols, respectively. The data underwent the Human-Connectome-Project spatial and temporal preprocessing pipelines including geometric distortion correction, drift removal and denoising. Note that for both HCP 1Tx and pTx protocols, although signal dropout due to susceptibility were observed in both AP and PA acquisitions, the combination of the two resulted in little signal dropout, thereby reducing the effect of off resonances at both subject and group levels.

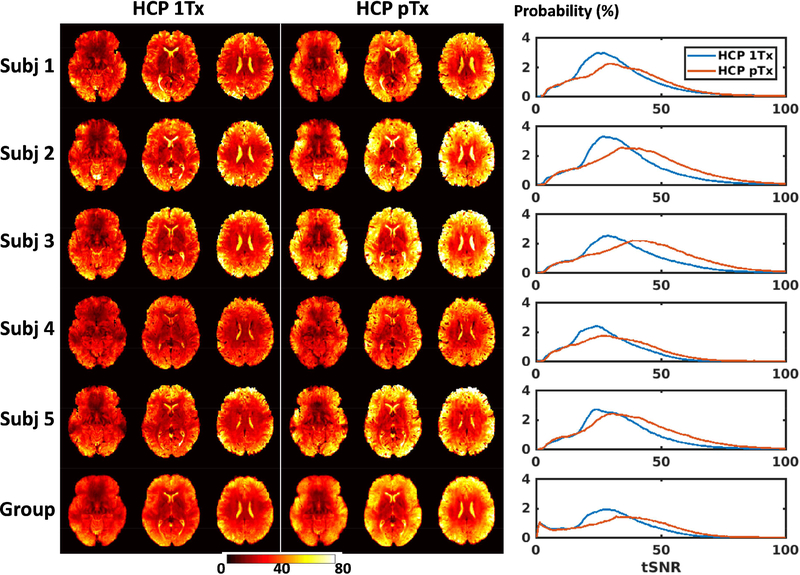
The tSNR was enhanced for the HCP pTx protocol compared to the 1Tx protocol; this is illustrated by comparing the tSNR maps in the MNI standard volume space for three slices (Fig. 3). The tSNR enhancement was observed for all of the 5 subjects, with the improvement mostly identified along the outer edge of the brain. This tSNR improvement was further confirmed by the tSNR histograms (Fig.3 rightmost panel). Quantitatively, the whole-brain tSNR was increased by up to 24% at the subject level and by 17% at the group level for the HCP pTx protocol.

FIG. 3.

Temporal SNR (tSNR) maps for the HCP 1Tx (leftmost panel) vs. HCP pTx (middle panel) protocols at the subject and group levels. For each subject and a given protocol, the four per run tSNR maps were first calculated by considering all of the preprocessed 900 image volumes in each run, and were averaged to form the final tSNR map in the standard MNI volume space at 1.6 mm isotropic resolutions. The group tSNR map was created by averaging tSNR maps of each individual across the 5 subjects. In each case, the tSNR histograms of the two protocols (rightmost panel) were also created for comparison (where the vertical axis is “Probability” defined as the number of observations in bin divided by the total number of observations). The tSNR was enhanced by using the proposed HCP pTx protocol.

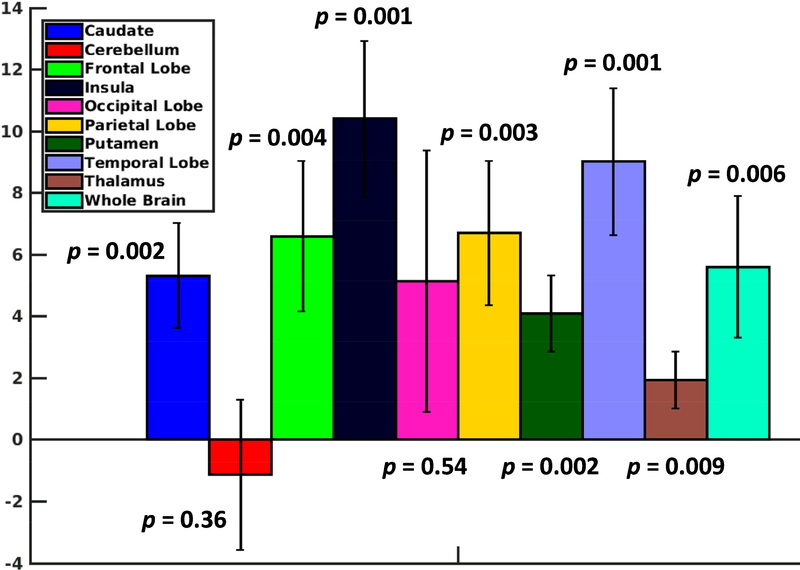
Further, region-specific tSNR comparison showed that the use of the HCP pTx protocol enhanced tSNR across the brain except for the cerebellum (Fig. 4). The tSNR was increased in all of the eight brain regions identified for the cerebrum by the MNI152 standard-space structural atlas, with the increase observed to be significant for all regions (p-value < 0.01, paired t-test with degrees of freedom (dof) = 4) except for the occipital lobe (p-value = 0.054). While the tSNR calculated was slightly decreased on average in the cerebellum, the decrease was not significant (p-value = 0.36, paired ttest with dof = 4). Additionally, the tSNR was higher significantly (p-value = 0.006, paired t-test with dof = 4) when averaged across the entire brain including both cerebrum and cerebellum.

FIG. 4.

Region-specific increase in temporal SNR (tSNR) by using the HCP pTx protocol. For each subject, the increase in tSNR in the MNI standard volume space was first calculated at each voxel by subtracting the tSNR of the HCP 1Tx protocol from that of the HCP pTx protocol, which was then averaged across the brain and in each of the nine brain regions as identified by the MNI152 standard-space structural atlas. The increase in tSNR averaged across the 5 subjects alongside the standard deviation is shown. The numbers shown are the p values obtained from a paired t-test. The use of the HCP pTx protocol enhanced not only the whole brain tSNR but also the regionspecific tSNR in most brain regions.

Spatially, the increase in tSNR for our HCP pTx protocol was largely correlated with the improvement in flip-angle homogeneity (Fig. 5). The flip-angle difference maps as calculated by subtracting the flip-angle map of the HCP 1Tx protocol from that of the HCP pTx protocol resembled tSNR difference in similarly calculated maps. This was observed for each subject, with a high level of similarity identified between the patterns of the two difference maps. This correspondence was further confirmed by examining the correlation coefficients between the two difference maps across the entire brain. The correlation coefficients at the subject level were calculated to range from 0.3 up to 0.58 (Fig. 5), showing a positive correlation between the increase in tSNR and the improvement in flip-angle homogeneity when using our HCP pTx protocol.

FIG. 5.

Correlation between improvements in flip angle and enhancement in tSNR when comparing the HCP pTx vs. the HCP 1Tx protocols. For each subject, the difference in flip angles in degrees (leftmost panel) was derived in the MNI standard volume space by subtracting the flip angle map of the HCP 1Tx protocol from that of the HCP pTx protocol, and likewise the difference in tSNR (middle panel). The correlation coefficients at the subject level (rightmost panel) were also calculated to quantify the correlation between the flip angle difference and the tSNR difference across the entire brain. The high level of similarity observed between the patterns of the two difference maps, which was further confirmed by examining the correlation coefficient, indicates a positive correlation between the two.

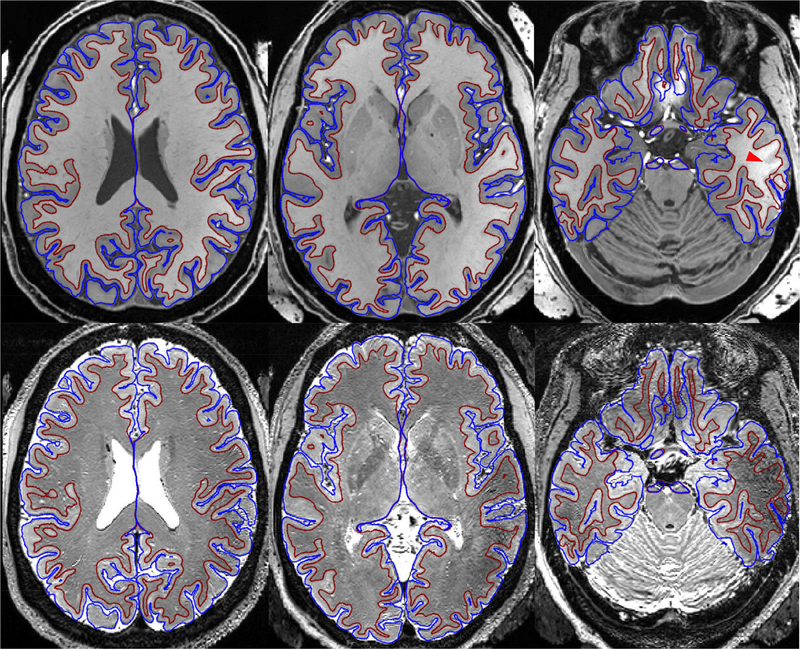
When using the T₁w and T₂w structural images acquired at 7T to delineate the cortical ribbon for surface analysis, good definition of white matter and pial surfaces was achieved nearly across the entire brain (Fig. 6). The white matter and pial surfaces were found to trace the grey and white matter boundary and the outer edge of the gray matter, respectively. In some lower brain regions (such as the inferior temporal lobe), however, the white matter surfaces deviated from the gray and white matter boundary; in the same region, signal dropout was observed in the T₂w image.

FIG. 6.

Output of the HCP structural preprocessing pipelines for a representative subject. Shown are white matter (maroon) and pial (blue) surfaces overlaid on the subject’s T1-weighted (T1w) (top row) and T2w (bottom row) images in the MNI volume space. Both T1w and T2w images were acquired at 0.7 mm resolutions with the Nova 1Tx coil and dielectric padding. The bright objects seen outside the head in the T1w image are dielectric pads. The T1w image was acquired with an MPRAGE sequence with TR/TE/TI=2400/2.68/1300 ms, while the T2w image with a 3D variable-flip-angle turbo-spin-echo sequence with TR/TE=3200/401 ms. To correct readout distortion, gradient echo field mapping was acquired with 2-mm resolution. Good definition of white matter and pial surfaces delineating the cortical ribbon was achieved nearly across the entire brain, only with white matter surfaces deviating from the underlying anatomy in some lower brain regions (e.g., area indicated by the red arrow head) due to low transmit RF field as better seen in the T2w image.

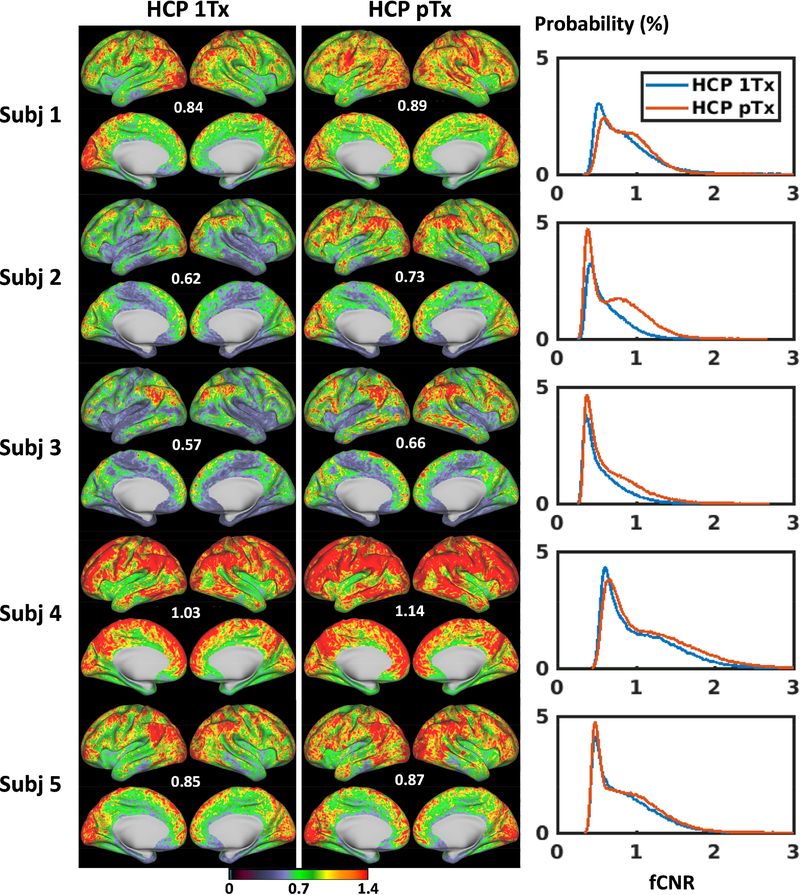
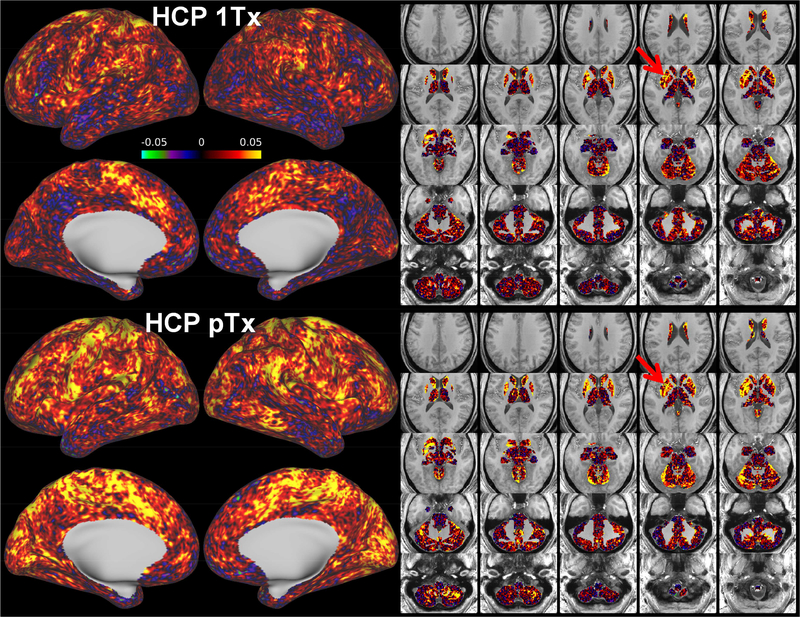
A comparison of fCNR maps in the standard grayordinate space showed that the fCNR was enhanced for the HCP pTx protocol (Fig. 7). The fCNR enhancement was visually identified for all five subjects, with the improvement observed on many cortical surfaces. This fCNR improvement was further confirmed by comparing the fCNR histograms (Fig.7 rightmost panel). Quantitatively, the mean fCNR values at the subject level was calculated to be increased significantly (p-value = 0.006, paired t-test with dof = 4), with the increase being as high as 18%.

FIG 7.

Functional CNR (fCNR) maps for the HCP 1Tx (leftmost panel) vs. HCP pTx (middle panel) protocols at the subject level. For each case, the four per run fCNR maps (which were outputs from the HCP rfMRI preprocessing pipelines) were averaged to form the final fCNR map in the standard grayordinate space. Only cortical fCNR maps are shown here on inflated cortical surfaces, with the number reported being the average fCNR across the entire grayordinate space (including cortical surfaces and subcortical voxels). The fCNR histograms of the two protocols (rightmost panel) across the entire grayordinate space were also created for comparison (where the vertical axis is “Probability” defined as the number of observations in bin divided by the total number of observations). The fCNR was enhanced by using the HCP pTx protocol.

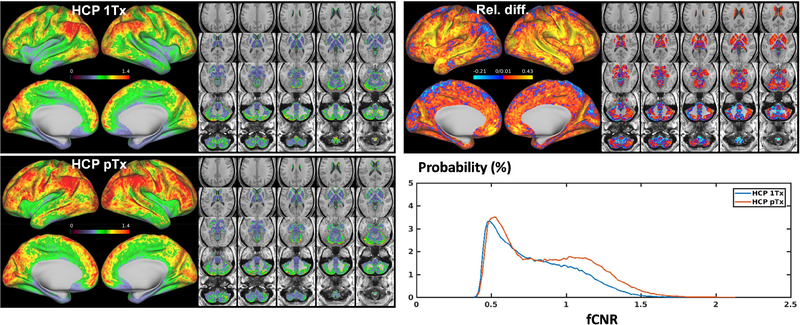
The increase in fCNR with our HCP pTx protocol observed at the subject level was further confirmed by comparing the fCNR maps at the group level (Fig. 8). While both HCP 1Tx and HCP pTx data led to spatially non-uniform fCNR and patches of high fCNR values on the cortical surfaces, the HCP pTx data yielded a group fCNR map that presented more extensive high-value patches and was more homogeneous, with the std/mean of fCNR being reduced by ~5% (0.260 vs. 0.274 for 1Tx). Calculating the relative difference in fCNR between the HCP 1Tx and HCP pTx protocols revealed that the fCNR was improved in most cortical surfaces including those in the frontal, parietal and temporal lobes, with the enhancement in fCNR being as high as ~43%. While a decrease in fCNR of ~21% was noticed in some cortical surfaces and subcortical voxels, the mean fCNR across the entire grayordinate space was calculated to be increased by as high as ~10%. This increase in fCNR was further confirmed by comparing the fCNR histograms of the two protocols.

FIG 8.

Functional CNR (fCNR) maps for the HCP 1Tx vs. HCP pTx protocols at the group level. Shown are group fCNR maps for the HCP 1Tx and HCP pTx protocols, averaged across the same 5 subjects (a total of 20 rfMRI runs) and displayed on inflated cortical surfaces (left panel) and subcortical voxels overlaid on T1 weighed structural images (right panel); also shown is the relative difference map of the two, calculated as (fCNR_ptx – fCNR_1tx)/fCNR_1tx where fCNR_ptx and fCNR_1tx are the fCNR values of the HCP pTx and 1Tx protocols, respectively. In addition, the protocol specific histograms of group fCNR across the entire grayordinate space were also created for comparison (where the vertical axis is “Probability” defined as the number of observations in bin divided by the total number of observations). The HCP pTx protocol resulted in enhanced fCNR in most of the cortical surface and in most subcortical voxels.

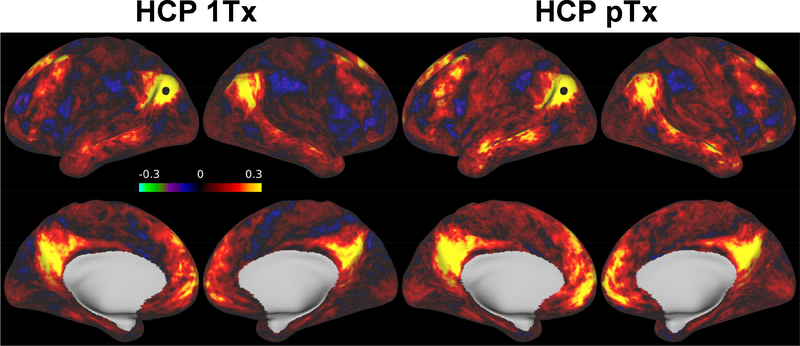
Estimation of seed-based connectivity (Figs. 9 and 10) at the group level by calculating the correlation of a seed with the rest of the brain regions further demonstrated the advantage of the HCP pTx protocol over the HCP 1Tx protocol. For a seed placed at a vertex in posterior parietal cortex (which is known to be part of the default mode network), the HCP pTx data produced stronger correlation values between the seed and the rest of the cortical surfaces (Fig. 9). Likewise, stronger correlation was observed for the HCP pTx protocol when placing a seed in a subcortical gray matter region such as in the putamen (Fig. 10).

FIG. 9.

Performance of HCP 1Tx vs. HCP pTx protocols in seed-based dense connectome. Shown are example connectivity for a seed (as indicated by a black dot) placed in the posterior parietal cortex (part of default mode networks), averaged across the same 5 subjects (a total of 20, 16-min resting state fMRI runs). The 20 runs of fMRI data were preprocessed, demeaned and variance normalized before being concatenated in the time dimension to calculate the correlation of the seed with the rest of the brain. The HCP pTx acquisition yielded stronger correlations as measures of functional connectivity between the seed and the rest of the cortical regions.

FIG. 10.

Another seed-based dense connectome as in Fig. 9, with a seed (as highlighted by a red arrow) placed in the subcortical gray matter putamen. The HCP pTx acquisition led to stronger estimation of the functional connectivity between the seed and the rest of the brain especially the cortical regions.

Discussion

In this study, we demonstrated that the use of parallel transmission can improve HCPstyle whole-brain resting-state fMRI acquisitions at 7 Tesla. Our data obtained using the commercial Nova 8Tx32Rx head RF coil show that the use of pTx can enhance the tSNR and improve BOLD contrast-to-noise ratio (as quantified by fCNR), as compared to the single-transmit configuration using the Nova 1Tx32Rx coil, when acquiring HCPstyle whole-brain rfMRI with 1.6-mm isotropic resolution. Furthermore, the increased BOLD fCNR translates into enhanced functional connectivity calculated as correlations of temporal dynamics between a seed voxel and all other voxels in the brain, a common “functional connectivity” metric employed with resting-state fMRI.

All of the pTx rfMRI data presented here were acquired in the “protected mode” defined by the manufacturer so as to be conservatively consistent with local-SAR limits during pTx use. During each of the ~16-minute rfMRI data acquisitions, we observed that the long-term 6-min total RF power delivery by our pTx MB pulses on average reached up to ~74% of the maximum allowed value (of 11 W as specified by the vendor for the Nova 8Tx32Rx coil). Consequently, we were also always under the manufacturer allowed short-term 10-sec power limit of this “protected mode”, which is higher (22 W).

For HCP 1Tx acquisitions using the Nova 1Tx32Rx coil, three dielectric pads were placed under the head/neck and one pad on each side of the head (five pads in total as in the HCP). The use of these dielectric pads improved not only transmit B1 but also receive B1 in the vicinity of the pads (Yang et al., 2011); the combined effect led to increased image SNR in those areas relative to what was achievable without dielectric pads. Furthermore, this combined effect explains the lack of significant gains in tSNR or fCNR as observed in the cerebellum and the occipital lobe (Figs. 4 and 8) when using pTx to only improve the transmit B1 (not the receive B1). Similarly, the poor correlation seen between flip-angle and tSNR differences (Fig. 5) in the cerebellum and inferior visual cortex were likely caused by the higher receive sensitivity of the 1Tx experiments in that region. When the correlations were calculated only for the superior slices (above a slice between the second and third slices in Fig. 5), they increased to 0.56, 0.54, 0.57, 0.42, and 0.51 for subject 1–5, respectively. Future work will examine how the combination of dielectric pads with pTx can further improve tSNR and fCNR for HCPstyle rfMRI. Following the original 7T HCP rfMRI protocol, the HCP 1Tx acquisition here utilized the phase scrambling scheme to reduce the peak magnitude of the MB5 excitation RF and to minimize the overestimation of SAR arising from hardware imperfection (Vu et al., 2015; Wong, 2012). The HCP pTx acquisition with the pTx pulses, on the other hand, did not encounter such a limitation and consequently did not incorporate any strategy into the pulse design to limit peak RF magnitude. However, whenever there is need to control peak RF magnitude in order to comply with hardware limitations, it can be accomplished by the phase scrambling strategy tailored for pTx MB pulses or directly incorporating explicit peak power constraints into the pulse design (Guérin et al., 2015b; Sharma et al., 2015; Wu et al., 2013c).

One limitation of the current study is that the pTx MB pulses utilized for rfMRI were designed with total-RF-power control and with single spokes (corresponding to RF amplitude and phase shimming for each band). Although these pulses outperform the single-channel-transmit mode, further optimization is possible. For example, pTx MB pulses can be designed with explicit power-related constraints (Guérin et al., 2015b; Hoyos-Idrobo et al., 2014), especially for local SAR, and applied in the “experimental” mode (another mode available on Siemens step-2 pTx systems to enable data acquisition with real-time local SAR supervision). Even after considering a safety margin of ~3 to account for uncertainties in local SAR estimation (Gras et al., 2016, 2017c), this strategy should enable faster rfMRI acquisitions with higher slice accelerations (e.g., MB8 or higher). Further optimization could also utilize pTx multi-spoke pulses (Gras et al., 2017c; Guérin et al., 2014; Setsompop et al., 2008; Thorstensson, 2001; Wu et al., 2013a) that are capable of producing additional improvements in flip-angle uniformity and power deposition for SMS/MB imaging at 7T (Sharma et al., 2015; Wu et al., 2016) and above (Tse et al., 2017b). The pTx fat-saturation pulse design with SAR management targeting uniform flip angles in fat-rich regions could also be incorporated into this design framework.

In this study, the structural T₁w and T₂w images required by the HCP minimal preprocessing pipelines were acquired with the Nova 1Tx32Rx coil in combination with dielectric padding. Although the use of dielectric padding can improve RF uniformity, the resulting RF field distribution across the whole brain still remains quite inhomogeneous (Fig. 1). Consequently, the segmentation of gray and white matter in certain lower brain regions did not always fully conform to the underlying anatomy mostly due to low transmit B1 field, as better seen in the T₂w image (Fig. 6). This suboptimal segmentation, however, is expected to have little impact on the 1Tx vs pTx rfMRI comparison because the way it biased the surface analysis was the same for both 1Tx and pTx datasets and the regions affected were small compared to the whole brain over which the pTx vs. 1Tx comparison was performed. Our future work will be to investigate how segmentation would be improved by acquiring structural T₁w and T₂w images with tailored pTx pulses (Cloos et al., 2012b, 2012a; Eggenschwiler et al., 2014; Malik et al., 2012; Massire et al., 2015; Tse et al., 2016).

We note that the current B₁⁺ mapping strategy was not tailored to the HCP pTx protocol with MB5 and 1.6-mm resolution. Instead, it was created mainly to obtain a set of multichannel volumetric B₁⁺ maps at relatively high resolution that can be downsampled to produce different sets of B₁⁺ maps compatible with other imaging protocols. This was motivated by the fact that sometimes we also acquired in the same pTx session high-resolution diffusion data using different protocols that target MB3 or MB4 and 1.05- or 0.7-mm resolutions. For these cases, we found it helpful to have a flexible B₁⁺ mapping strategy (like the one utilized in this study) that can ease the process of streamlining the entire pTx session. In the case where only a single protocol is considered for SMS/MB imaging, a more tailored B₁⁺ mapping approach optimized to the MB factor and resolution employed (Tse et al., 2017b; Wu et al., 2018) could be sought for improved time efficiency.

In the current HCP pTx protocol, we designed pTx MB pulses to image sagittal slices mainly to leverage the transmit performance (Wu et al., 2016b). It is conceivable that the use of a different slice direction may have contributed to the tSNR gain relative to the HCP 1Tx protocol by changing the performance of the image reconstruction. To investigate this possibility, we acquired additional rfMRI data in two subjects with sagittal vs. oblique-axial slice directions by using the same 1Tx setup (with the Nova 1Tx32Rx coil and dielectric padding). In this comparison, our data showed that using sagittal slices led to a decrease in the tSNR (Supporting Figure S3), with the wholebrain tSNR being reduced on average by ~6%. This observation was consistent with gfactor analysis showing that for this 1Tx32Rx coil and dielectric padding, both mean and maximum g-factors were higher for data acquisition with sagittal slices (Supporting Figure S4); the mean and maximum g-factors, averaged across the two subjects, were elevated by ~4% and ~24%, respectively.

In addition, the impact of acquiring sagittal vs. oblique-axial slices on image distortion and signal dropout was kept small in this study. This was achieved by using the same phase-encode directions and comparable echo train lengths, and more importantly, by employing methods that can reduce the susceptibility-induced off-resonance effects, including applying second-order B0 shimming with matched volumes of interest and combining images acquired with inverted phase encodes. Consequently, the 4D mean of the final concatenated timeseries (Fig. 2) present no difference for upper brain regions and only show subtle difference around air-tissue interfaces between the HCP pTx and 1Tx protocols.

The above comparison of sagittal vs. oblique-axial slice directions also suggests that the choice of acquiring oblique-axial slices in the HCP 1Tx protocol is reasonable when using the Nova 1Tx32Rx coil and dielectric padding because this choice appears to improve the image reconstruction. Furthermore, acquisition of oblique-axial slices requires fewer slices to cover the entire brain (85 vs. 90 for sagittal slices at 1.6-mm resolution), thereby reducing SAR for a constant volume TR. However, when combining the Nova 8Tx32Rx coil with pTx single-spoke MB pulses for rfMRI acquisition (as employed in this study), we recommend that data be acquired in sagittal slices because this would give rise to largely improved flip-angle uniformity that outweighs the potential decrease in image reconstruction performance. To our experience with the Nova 8Tx32Rx coil, designing pTx single-spoke MB pulses to image the whole brain in oblique-axial slices would result in substantial destructive interferences between the RF fields of individual transmit channels, leading to signal dropout in the image. Further analysis based on electromagnetic modeling of the Nova 8Tx32Rx coil and the design method utilized here revealed that designing pulses for imaging oblique-axial slices would not only reduce RF uniformity (with the std/mean of whole-brain RF distribution being increased by ~28%) but increase global SAR (by ~41%) and local SAR (by ~26%) for excitation, as compared to imaging sagittal slices when keeping the maximum flip angle constant. Although better transmit performance may be obtained by designing pTx multi-spoke MB pulses, we expect that such pulses would also benefit from imaging sagittal slices. Investigating how much improvement in data quality would be obtained by designing pTx multi-spoke MB pulses to image sagittal vs. oblique-axial slices for 7T HCP-style rfMRI acquisition would be part of our future work.

A central goal in our work is to push toward higher spatiotemporal resolutions for resting state and task-based fMRI, which is desirable in many human brain applications. To this end, a critical step is to enable higher slice accelerations; this is important for improving SNR per unit time, which can be pushed into suboptimal values with high resolution imaging, and also for achieving higher temporal sampling to properly capture and resolve the dynamics of brain networks (e.g. (Chang and Glover, 2010; Smith et al., 2012)). Higher slice acceleration with an acceptable g-factor noise penalty and interslice signal leakage (Xu et al., 2013) would be feasible by employing improved receive RF coils (e.g., 7T receive arrays with 64- (Auerbach et al., 2017; Moeller et al., 2018) or larger number of channels), possibly in combination with alternative acquisition strategies (e.g. (Bilgic et al., 2015; Chiew et al., 2015) and novel signal processing methods (Sengupta and Mitra, 1999; Veraart et al., 2016). On the transmit side, the performance can also be improved using multi-ring transmit arrays (Adriany et al., 2010; Kozlov and Turner, 2011; Shajan et al., 2014) which have been shown to facilitate flipangle uniformity and SAR reduction (Guérin et al., 2015a; Wu et al., 2015; Wu et al., 2016b). With technical developments on both receive and transmit sides enabling higher acceleration, we fully expect that it would be possible to acquire high-quality whole-brain fMRI data at submillimeter scales (e.g., ≤0.7 mm isotropic) with reasonable temporal resolutions and minimum geometric distortion.

Here we adopted a traditional workflow for pTx pulse design which involved subjectspecific calibration procedures including transmit B1 mapping, brain masking and pulse calculation. Although effective, this workflow takes time. For example, in our case we had to spend over 10 minutes on those calibrations before acquiring the real rfMRI data. This overhead time is undesirable and suboptimal, especially when considering large cohort studies such as the HCP. Fortunately, it is possible to conduct plug-and-play or calibration-free pTx scans using MR fingerprinting (Cloos et al., 2016; Ma et al., 2013) or universal pulses (Gras et al., 2017b). Most notably, the universal pulses have been demonstrated to be effective for image acquisition at 7T with various contrasts including T1w, T2w, and T2*w imaging (Beqiri et al., 2018; Gras et al., 2018, 2017a); therefore, they are likely to play a critical role in enabling pTx in next generation HCP studies at ultrahigh field.

When only single-channel transmission is available, it is also possible to improve the transmit B1 by adjusting the RF voltage on a slice-by-slice basis. Although incapable of improving per-slice flip-angle uniformity, this strategy is expected to homogenize gradient-echo signals across the slices, and most importantly, increase the signal in worst-affected slices where transmit B1 is typically low in magnitude. To evaluate how this strategy would help increase the signal, we ran additional simulations based on the electromagnetic modelling of the Nova 8Tx32Rx coil. A single-channel-transmit mode was mimicked by driving the coil with the CP-like-mode RF phase shimming. The signal was calculated assuming steady-state gradient-echo imaging with complete spoiling (Hargreaves, 2012). When considering oblique axial slices, a 1-sec TR and a 1.9-sec T1 for cortical gray matter (Rooney et al., 2007; Wright et al., 2008), we found that adjusting RF voltage on a slice-by-slice basis to reach a 50-degree maximum flip angle in every slice would increase per-slice SNR by up to ~51% and whole-brain SNR by ~17%. However, these SNR gains would come at the cost of ~2.2-fold increase in SAR, indicating that in practice the effectiveness of this strategy for increasing SNR is likely to be dampened at ultrahigh field due to SAR limits.

Conclusions

We have demonstrated the advantages of RF parallel transmission over a conventional single-transmit configuration when acquiring HCP-type slice-accelerated, highresolution, whole-brain resting state fMRI at 7T. Our data show that parallel transmission can be used to enhance temporal SNR in most brain regions and also improve BOLD contrast-to-noise ratio across most of the cortical surfaces and in many subcortical voxels, yielding stronger correlations when estimating seed-based functional connectivity. These results show that RF parallel transmission will play an important role in rapid acquisitions of high-quality, high-resolution, resting-state fMRI data, which is desirable in many neuroscience and clinical applications.