Towards microstructure fingerprinting: estimation of tissue properties from a dictionary of Monte Carlo diffusion MRI simulations

Abstract

Many closed-form analytical models have been proposed to relate the diffusion-weighted magnetic resonance imaging (DW-MRI) signal to microstructural features of white matter tissues. These models generally make assumptions about the tissue and the diffusion processes which often depart from the biophysical reality, limiting their reliability and interpretability in practice. Monte Carlo simulations of the random walk of water molecules are widely recognized to provide near groundtruth for DW-MRI signals. However, they have mostly been limited to the validation of simpler models rather than used for the estimation of microstructural properties.

This work proposes a general framework which leverages Monte Carlo simulations for the estimation of physically interpretable microstructural parameters, both in single and in crossing fascicles of axons. Monte Carlo simulations of DW-MRI signals, or fingerprints, are pre-computed for a large collection of microstructural configurations. At every voxel, the microstructural parameters are estimated by optimizing a sparse combination of these fingerprints.

Extensive synthetic experiments showed that our approach achieves accurate and robust estimates in the presence of noise and uncertainties over fixed or input parameters. In an in vivo rat model of spinal cord injury, our approach provided microstructural parameters that showed better correspondence with histology than five closed-form models of the diffusion signal: MMWMD, NODDI, DIAMOND, WMTI and MAPL. On whole-brain in vivo data from the human connectome project (HCP), our method exhibited spatial distributions of apparent axonal radius and axonal density indices in keeping with ex vivo studies.

This work paves the way for microstructure fingerprinting with Monte Carlo simulations used directly at the modeling stage and not only as a validation tool.

Introduction

Adequate modeling of the diffusion-weighted magnetic resonance imaging (DW-MRI) signal holds the promise of characterizing white matter tissues at the micrometer level, including information about the principal orientation of axons, their average radius or packing density. Traditionally, a forward signal model is formulated relating the DW-MRI signal measured in a voxel to the externally-applied magnetic field gradient profile and the microstructural properties of the tissue. The estimation stage or inverse problem generally consists in minimizing a cost function incorporating the measured DW-MRI data and the closed-form forward formula.

Estimating microstructural features from closed-form mathematical expressions of the signal poses three major limitations. First, the formulations are generally so complex that simplifying assumptions need to be incorporated to obtain closed-form formulas. For example, representing intra-axonal restriction for molecules trapped inside a simple model of straight cylinders often requires assuming a Gaussian phase distribution (McCall et al., 1963; Vangelderen et al., 1994) or a short gradient pulse (Tanner and Stejskal, 1968; Callaghan, 1995) to obtain analytical formulas. Describing the complex diffusion in the extra-axonal space almost exclusively relies on the basic diffusion tensor (Basser et al., 1994), albeit with possible refinements such as considering a peak-shaped distribution of tensors (Scherrer et al., 2016, 2017) or a dependence on diffusion time (Burcaw et al., 2015; Ning et al., 2017) or gradient frequency (Xu et al., 2014) when more complex DW-MRI sequences are used. Coupling the intra- and extra-axonal models in a physically consistent way is usually addressed by tortuosity models (Whitaker, 1967; Szafer et al., 1995), the accuracy of which has been questioned (Lampinen et al., 2017). Second, generalizing models from the diffusion sequence they were originally designed for, often the pulse-gradient spin-echo (PGSE) (Stejskal and Tanner, 1965), to sequences such as double diffusion encoding (DDE) (Cory et al., 1990; Callaghan and Manz, 1994) or oscillating-gradient spin-echo (OGSE) (Gross and Kosfeld, 1969) generally requires non-trivial modifications (Xu et al., 2014; Lam et al., 2015). Third, the cost function used in the inverse problem is often highly non-linear in the parameters to estimate, leading to the well-known pitfalls of non-linear optimization: convergence to local rather than global minima, multiple equivalent minima (Jelescu et al., 2016; Novikov et al., 2018), long fitting times or sensitivity to the initialization strategy (Harms et al., 2017). These difficulties are usually overcome by making further simplifications to reduce complexity and stabilize the estimation, such as assuming axons with zero radius (Zhang et al., 2012) or neglecting fascicle crossings altogether (Alexander et al., 2010; Zhang et al., 2012). A recent alternative to such simplifications for stabilizing the estimation is to recast the inverse problem into a convex optimization program on a pre-computed dictionary. This was proposed by Daducci et al. (2015) and Sepehrband et al. (2016) for single fascicles and by Auría et al. (2015) for multiple fascicles. It should be noted that some models target the ensemble average propagator (EAP) of water molecules rather than tissue properties directly (Özarslan et al., 2013; Ning et al., 2017). Those frameworks make little to no assumption about the tissue and the signal is linearly decomposed in a chosen functional basis. The estimation of the coefficients of the expansion is done efficiently through convex optimization under positiveness (Özarslan et al., 2013) or sparsity constraints (Merlet et al., 2013) for instance. These models provide indices that must then be interpreted in terms of specific tissue features (Avram et al., 2016; Zucchelli et al., 2016).

Monte Carlo simulations of the random walk of water molecules have the potential to provide near ground-truth forward signals for any type of gradient profile and for any geometry of the cellular environment (Hall and Alexander, 2009; Balls and Frank, 2009). Because they provide numerical results rather than a closed-form formula for the signal, they are not well suited for parameter estimation through traditional continuous optimization. As a consequence, Monte Carlo simulations have been widely used in the validation of simpler closed-form models (Grebenkov, 2007; Fieremans et al., 2008; Nilsson et al., 2009; Hall and Alexander, 2009; Panagiotaki et al., 2010; Fieremans et al., 2010; Nilsson et al., 2010; Drobnjak et al., 2011; Raffelt et al., 2012; Dyrby et al., 2013; Pizzolato et al., 2015; Lam et al., 2015; Clayden et al., 2015; McHugh et al., 2015; Burcaw et al., 2015; Scherrer et al., 2016; Ianuș et al., 2016; Kakkar et al., 2017; Vellmer et al., 2017; Ning et al., 2017; Ginsburger et al., 2018; Mercredi and Martin, 2018). They have also been used to investigate the sensitivity of the DW-MRI signal to complex biophysical features (Hall and Alexander, 2009; Nilsson et al., 2012; Harkins and Does, 2016; Palombo et al., 2017; Rensonnet et al., 2018; Lin et al., 2018). However, their use for the direct estimation of microstructural properties has been scarce and thus far limited to areas containing single fascicles of axons. For instance, in Nilsson et al. (2010), nearest-neighbor matching from a collection of Monte Carlo signals was compared with an analytical model of diffusion considering permeable membranes. In Nedjati-Gilani et al. (2017), a similar analytical model was assessed against a random forest regressor used to learn a mapping between microstructural properties of single fascicles and orientationally-invariant features extracted from their Monte Carlo signals. In the context of MR spectroscopy, Monte Carlo simulations were integrated in a computational model to assess the intracellular diffusion of cell-specific metabolites in rodent and primate brain (Palombo et al., 2016).

The framework proposed in this article aims at exploiting the accuracy and interpretability of Monte Carlo simulations directly in the forward signal model and not solely as a validation tool. Single-fascicle DW-MRI signals or fingerprints are first pre-computed for a large collection of microstructural configurations using Monte Carlo simulations. The final multi-fascicle estimation then consists in selecting the optimal sparse combination of these fingerprints, which is done by solving many small convex sub-problems. The approach is applied to the estimation of an apparent axonal radius index and an axonal density index in single- as well as in crossing-fascicle configurations, using synthetic and in vivo data.

1. Theory

This section first presents our general multi-fascicle signal model incorporating signals from Monte Carlo simulations, the theory of which is reviewed in a second subsection. A third subsection presents mathematical properties that allow large collections of Monte Carlo signals to be obtained at a minimal computational cost. Finally, the inverse problem of estimating microstructural features is formulated as a structured sparse optimization problem in the last subsection.

1.1. Signal model

The DW-MRI signal S at echo time TE under the application of an effective magnetic field gradient profile g(t) (0 ≤ t ≤ TE) in a voxel of white matter is assumed to arise from the independent contributions of K fascicles of axons with principal unit orientation u₁,…,u_K occupying fractions ν₁,…,ν_K of the physical volume of the voxel and of a partial volume ν_csf of cerebrospinal fluid (CSF)

$$\begin{array}{ll}S\hfill & =M_0\cdot \left[\sum _{k=1}^K{\nu }_k{A}_{\text{fasc}}\left({\Omega }_k,T_k,u_k;g\right)+{\nu }_{\text{csf}}{A}_{\text{csf}}\left(D_{\text{csf}},T_{\text{csf}};g\right)\right]\hfill \\ \hfill & =\sum _{k=1}^K{w}_k{A}_k+w_{\text{csf}}{A}_{\text{csf}},\hfill \end{array}$$ (1)

where the scaling factor M₀ captures the net initial transverse magnetization of the voxel detected by the scanner and w_k ≔ M₀ν_k is the NMR-apparent signal weight of the contribution of the k-th fascicle. The normalized DWMRI signal A_k ≔ A_fasc (Ω_k, T_k, u_k; g) of the k-th fascicle is modeled by a Monte Carlo simulation of the random self-diffusion of molecules in an environment characterized by the set of microstructural parameters Ω_k, typically featuring geometrical arrangements of cylinders representing axons. The set of parameters T_k captures NMR relaxation such as T1, T2 and proton density, which is generally assumed to occur independently of diffusion and therefore only affects A_k via a multiplying factor. Water is assumed to diffuse freely and isotropically in the CSF compartment; its normalized DW-MRI contribution A_csf is therefore characterized by a scalar diffusivity D_csf. Since ν₁ + ⋯ +ν_K +ν_csf = 1, the physical volume fractions ν_k have a one-to-one correspondence with the NMR-apparent weights w_k:

$$\begin{array}{ll}{w}_k=M_0{\nu }_k\iff {\nu }_k=\frac{w_k}{{\sum }_{k=1}^{K+1}{w}_k},\hfill & k=1,\dots ,K+1,\hfill \end{array}$$ (2)

where the index k = K + 1 refers to the CSF compartment.

The flexibility of Monte Carlo simulations allows any type of gradient profile g(t) to be used, including PGSE, DDE, OGSE or more general b-tensor encoding (Topgaard, 2017) without the need to mathematically derive a new signal model.

A vector ${\left[A_{\text{fasc}}\left(\Omega ,T,u;g_i\right)\right]}_{i=1}^M$ corresponding to the set of M gradient profiles ${\left\{g_i\left(t\right)\right\}}_{i=1}^M$ making up the acquisition protocol is defined as a fingerprint It uniquely relates to the particular microstructural parameters Ω for given relaxation parameters T and orientation u.

1.2. Monte Carlo simulations

Monte Carlo simulations consist in sampling the distribution of the phase ϕ (g) accumulated at echo time TE by spin-bearing nuclei or spins undergoing random diffusion in a spatial domain Ω when a diffusion-sensitizing gradient profile g(t) (0 ≤ t ≤ TE) is applied. As described in Hall and Alexander (2009), a large set of N_spin Brownian trajectories r_l(t), 1 ≤ l ≤ N_spin, are approximated in the environment Ω by discrete trajectories ${\widehat{r}}_l$ consisting of spatial jumps with random orientation and length

$$L=\sqrt{2nD\delta t}$$ (3)

where the time step δt = TE/N_step is chosen in order to ensure a small bias, D is the local diffusivity and n (1 ≤ n ≤ 3) is the intrinsic spatial dimension of the diffusion process of interest. If Ω consists of parallel straight cylinders for instance, diffusion is unrestricted along the cylinders and Monte Carlo simulations can be limited to the plane perpendicular to the cylinders, implying n = 2. Interactions with boundaries and obstacles in Ω such as cellular membranes are tested for at each spatial jump.

With g_α (t) and r_lα denoting the components of g and r_l(t) along the direction e_α and γ the gyromagnetic ratio of the spin-bearing nuclei, the phase ϕ_l of spin l accumulated at echo time is defined as

$$\begin{array}{ll}{\varphi }_l\left(g\right)\hfill & :=\gamma {\int }_0^{TE}g\left(t\right)\cdot r_l\left(t\right)dt\hfill \\ \hfill & =\sum _{\alpha =1}^n\underset{:={\varphi }_{l\alpha }\left(g_{\alpha }\right)}{\underbrace{\gamma {\int }_0^{TE}{g}_{\alpha }\left(t\right)r_{l\alpha }\left(t\right)dt}}.\hfill \end{array}$$ (4)

It is approximated from the discrete trajectory ${\widehat{r}}_l$ by a numerical quadrature such as a rectangle rule

$$\begin{gathered} {\varphi }_l\left(g\right)\approx {\widehat{\varphi }}_l\left(g\right)=\gamma \delta t\sum _{s=0}^{N_{\text{step}}-1}g\left(s\cdot \delta t\right)\cdot {\widehat{r}}_l\left(s\cdot \delta t\right) \\ =\sum _{\alpha =1}^n\underset{:={\widehat{\varphi }}_{l\alpha }\left(g_{\alpha }\right)}{\underbrace{\gamma \delta t\sum _{s=0}^{N_{\text{step}}-1}{g}_{\alpha }\left(s\cdot \delta t\right){\widehat{r}}_{l\alpha }\left(s\cdot \delta t\right)}} \end{gathered}$$ (5)

where ${\widehat{\varphi }}_{l\alpha }$ is the numerical approximation of the directional phase ϕ_lα due to g_α (t). It should be noted that ϕ (equivalently, $\widehat{\varphi }$) is linear with respect to g(t):

$$\begin{array}{ll}\varphi \left({\beta }_1{g}_1+{\beta }_2{g}_2\right)={\beta }_1\varphi \left(g_1\right)+{\beta }_{2\varphi }\left(g_2\right)\hfill & \left(\forall {\beta }_1,{\beta }_2\in ℝ\right)\hfill \end{array}.$$ (6)

The normalized diffusion attenuation A(g) in Ω associated with the gradient profile g(t) is finally approximated as the empirical mean

$$A\left(g\right)=\langle e^{j\varphi \left(g\right)}\rangle \approx \left|\frac{1}{N_{\text{spin}}}\sum _{l=1}^{N_{\text{spin}}}{e}^{j{\widehat{\varphi }}_l\left(g\right)}\right|,$$ (7)

where j denotes the complex number.

1.3. Data augmentation

1.3.1. Augmenting sequences

This paragraph demonstrates how the generation of directional phases-rather than final DW-MRI signals- can make Monte Carlo simulations reusable for new gradient directions and make the simulation time almost independent of the number of sequences M, at the expense of a moderate increase in storage space.

The M gradient profiles g(t) of a DW-MRI protocol can be expressed as a linear combination of M_χ ≤ M basis temporal profiles χ_m(t)

$$g\left(t\right)=\sum _{m=1}^{M_{\chi }}\sum _{\alpha =1}^n{\beta }_{m\alpha }{\chi }_m\left(t\right)e_{\alpha },$$ (8)

where every β_mα ∈ ℝ. If the n × N_spin × M_χ directional phases ${\widehat{\varphi }}_l\left({\chi }_m{\text{e}}_{\alpha }\right)$ are computed and stored, they can later be used to compute the accumulated phase ${\widehat{\varphi }}_l\left(g\right)$ of spin l arising from the application of any gradient profile g(t)

$$\begin{gathered} {\widehat{\varphi }}_l\left(g\right)={\widehat{\varphi }}_l\left(\sum _{m=1}^{M_{\chi }}\sum _{\alpha =1}^n{\beta }_{m\alpha }{\chi }_m{e}_{\alpha }\right) \\ =\sum _{m=1}^{M_{\chi }}\sum _{\alpha =1}^n{\beta }_{m\alpha }{\widehat{\varphi }}_l\left({\chi }_m{e}_{\alpha }\right) \end{gathered}$$ (9)

based on the linearity of $\widehat{\varphi }$ expressed in Eq. (6). This quantity can then be used to compute the normalized diffusion attenuation A(g) using Eq. (7).

Most current clinical protocols use a small number of temporal profiles, making this strategy particularly useful. For instance, PGSE-based Multi-shell HARDI (Tuch et al., 2002) and CUSP protocols (Scherrer and Warfield, 2012) with gradient duration δ and separation Δ fixed across all shells have an optimal M_χ = 1. Once computed, the n × N_spin × M_χ directional phases are used to simulate every sequence of the protocol. Among others, this approach can efficiently generate signals for patient-specific gradient maps corrected for motion. With a fixed protocol, the stored phases also provide DW-MRI signals for any microstructural orientation by considering an adequately-rotated new set of gradient directions with the same temporal profiles χ_m(t).

Compared with a strategy in which just the final DW-MRI signals are stored, the storage space increases by a factor $\frac{n{N}_{\text{spin}}{M}_{\chi }}{M}$. On the other hand, the computational complexity of the quadrature rule in Eq. (5) is reduced by a factor M/M_χ, e.g., a factor 100 for a protocol with 100 sequences using fixed Δ and δ.

1.3.2. Augmenting configurations

This paragraph demonstrates that many more microstructural configurations Ω can be obtained from a finite set of stored DW-MRI directional phases or signals by leveraging the scaling properties of Brownian diffusion.

Considering spin-bearing particles evolving in an environment with characteristic length scale L and homogeneous diffusivity D under the application of a magnetic gradient profile g(t) with characteristic gradient intensity G and time scale T, dimensional analysis shows that the DW-MRI signal A(L, D; G, T) is entirely characterized by the dimensionless parameters (Grebenkov, 2008)

$$\begin{array}{l}{p}_1=\frac{DT}{L^2},\hfill \\ p_2=\gamma GLT.\hfill \end{array}$$ (10)

The following equivalence

$$A\left(L,D;G,T\right)=A\left(\sqrt{\alpha }L,\alpha D;\frac{G}{\sqrt{\alpha }},T\right)$$ (11)

therefore holds for any real number α > 0, meaning that the same simulated signal can be interpreted as arising from configurations characterized by different spatial dimensions and diffusivity under the application of an adequately scaled magnetic gradient. For instance, the DW-MRI signal arising from an environment with 3 μm-wide axons separated by 1 μm gaps is identical to the signal arising from 6 μm-wide axons separated by 2 μm gaps if the diffusivity is 4 times as large and the gradient magnitude is twice as small.

This property is useful in the context of generating large collections of DW-MRI signals. Instead of running Monte Carlo simulations for all combinations (L_i, D_j) of a biological region of interest [L_min, L_max] × [D_min, D_max] in the space of microstructural parameters Ω, it is sufficient to run simulations for one fixed diffusivity D_sim in [D_min, D_max] and a sampling {L_sim,i}_i spanning a slightly larger region $\left[\sqrt{\frac{D_{\text{sim}}}{D_{\text{max}}}}{L}_{\text{min}},\sqrt{\frac{D_{\text{sim}}}{D_{\text{min}}}}{L}_{\text{max}}\right]$. By setting $\alpha =\frac{D_{\text{sim}}}{D}$ in Eq. (11), a collection of DW-MRI signals corresponding to a new arbitrary D ∈ [D_min, D_max] is then directly obtained as

$$A\left(\sqrt{\frac{D}{D_{\text{sim}}}}{L}_{\text{sim,}i},D;G,T\right)=A\left(L_{\text{sim},i}{D}_{\text{sim}};\sqrt{\frac{D}{D_{\text{sim}}}}G,T\right),$$ (12)

where the left-hand-side corresponds to a sampling ${\left\{\sqrt{\frac{D}{D_{\text{sim}}}}{L}_{\text{sim,}i}\right\}}_i$ covering the region of interest L_min ≤ L ≤ L_max. Appendix A shows that the choice of D_sim does not affect the number of reference simulations N required to achieve sufficient resolution in L for all D ∈ [D_min, D_max].

If the reference simulations with D_sim stored the directional phases as explained in the previous in the previous paragraph, then the right-hand-side of Eq. (12) can be exactly evaluated at $\sqrt{\frac{D}{D_{\text{sim}}}}G$ Otherwise, signal interpolation with respect to G must be performed. In order to avoid extrapolation outside of the range [G_min, G_max] covered by the acquisition protocol, the reference simulations can be run for G spanning the slightly larger interval $\left[\sqrt{\frac{D_{\text{min}}}{D_{\text{sim}}}}{G}_{\text{min}},\sqrt{\frac{D_{\text{max}}}{D_{\text{sim}}}}{G}_{\text{max}}\right]$.

1.4. Inverse problem

Our framework consists in pre-computing a dictionary of Monte Carlo DW-MRI fingerprints, each corresponding to a unique microstructural configuration. At runtime, for every voxel, our method then aims at finding the optimal combination of single-fascicle configurations ${\widehat{\Omega }}_1,\dots ,{\widehat{\Omega }}_K$ and volume fractions ${\widehat{\nu }}_1,\dots ,{\widehat{\nu }}_K$ for a vector y ∈ ℝ^M of M noisy DW-MRIs. More specifically, the process involves five steps: two during the pre-computing stage and three during runtime.

Step 1 (pre-computing) performs a discrete sampling of N points Ω₁,…,Ω_N of the space Ω of microstructural parameters with bounds and granularity justified by tissue biology and the expected resolution of the M diffusion-encoding gradient profiles g₁(t),…,g_M(t) of the protocol $\mathcal{P}={\left\{g_i\left(t\right)\right\}}_{i=1}^M$ at hand.

Step 2 (pre-computing) generates a canonical single-fascicle dictionary F⁰ ∈ ℝ^M×N containing the DW-MRI fingerprints of the N selected microstructural configurations for a single fascicle along a fixed direction u₀

$$F^0=\left[A_1^0,\dots ,A_N^0\right],$$ (13)

where $A_j^0=A_{\text{fasc}}\left({\Omega }_j,T_0,u_0;\mathcal{P}\right)$, 1 ≤ j ≤ N. This the most time-consuming step involving up to N Monte Carlo simulations which, however, need only be performed once and can be done before any data is even acquired.

Step 3 (runtime) requires an external routine to estimate in each voxel the number K of fascicles and their orientations u₁,…, u_K.

Step 4 (runtime) requires an efficient routine for rotating single-fascicle signals in order to obtain the single-fascicle dictionaries F¹,…, F^K ∈ ℝ^M×N from F⁰ along the orientations u₁,…,u_K estimated in Step 3.

Step 5 (runtime) finally consists in solving the following sparse optimization problem

$$\begin{array}{c}\widehat{\text{w}}=\underset{\text{w}\ge 0}{\text{argmin}}{\Vert \mathbf{y}-\left[F^1|\dots |F^K|A_{\text{csf}}\right].\left[\begin{array}{c}{\text{w}}_1\\ ⋮\\ {\text{w}}_K\\ w_{csf}\end{array}\right]\Vert }_2^2\\ \text{subject\hspace{0.17em}to\hspace{0.17em}}{\left|{\mathbf{\text{w}}}_k\right|}_0=1,k=1,\dots ,K,\end{array}$$ (14)

where the sparsity constraints on the sub-vectors w_k guarantee that only one fascicle configuration Ω_jk per single-fascicle dictionary F^k contributes to the measured signal y. Problem (14) is solved exactly by selecting the optimal solution out of N^K independent non-negative least-squares sub-problems of (K + 1) variables

$$\begin{array}{c}\left({\widehat{j}}_1,\dots ,{\widehat{j}}_K\right)=\underset{1\le j_1,\dots ,j_K\le N}{\text{argmin}}\underset{\text{w}\ge 0}{\text{min}}\Vert \mathbf{y}-\left[A_{j_1}^1|\dots |A_{j_K}^K|A_{\text{csf}}\right].\left[\begin{array}{c}{w}_1\\ ⋮\\ w_K\\ w_{csf}\end{array}\right]{\Vert }_2^2\end{array}.$$ (15)

Each sub-problem is convex and is solved exactly by an efficient active-set algorithm (Lawson and Hanson, 1995, chap. 23, p. 161). The optimal microstructural parameters ${\widehat{\Omega }}_k$ are taken as those of the optimal fingerprint ${\widehat{j}}_k$ in each F^k and the volume fractions ${\widehat{\nu }}_k$ are estimated from the corresponding optimal weights ${\widehat{w}}_k$ using Eq. (2). Note that the weights w_k are not required to sum to one since the quantity ${\sum }_{k=1}^{K+1}{\widehat{w}}_k$ should reflect the scale M₀ of the acquired signals y.

2. Materials and Methods

This section presents the synthetic and in vivo experiments performed to validate the general estimation framework described in Section 1.4. The first part is concerned with voxels containing only single fascicles of axons while the second part considers voxels with crossing fascicles. All the synthetic experiments were designed to reproduce the experimental conditions of the in vivo acquisitions as closely as possible.

2.1. Validation on single fascicles

2.1.1. Diffusion protocol

The DW-MRI protocol used for the synthetic and in vivo validation on single-fascicle configurations, referred to as the rodent protocol, consisted of 6 PGSE shells of b-values 300, 700, 1500, 2800, 4500, 6000 s mm⁻² with high gradient intensities G ∈ [140, 628] mT m⁻¹ and short gradient duration δ =4.5 ms and diffusion time Δ = 12 ms, with TE = 23 ms. Each shell contained 36 non-collinear directions computed with the electrostatic repulsion method of Caruyer et al. (2013) and 3 unweighted or b0 images for a total of 234 images.

2.1.2. Implementation details of the dictionary estimation

In Step 1 of the procedure described in Section 1.4, hexagonal packing of straight, impermeable cylinders was selected to represent single fascicles of axons, characterized by a cylinder radius r, interpreted as an apparent axonal radius index, and a cylinder packing density f, interpreted as an axonal density index (Budde and Frank, 2010; Alexander et al., 2010). The space of microstructural parameters Ω = (r, f) was sampled at 34 values for r from 0.4 μm to 7 μm by steps of 0.2 μm and 23 values for f from 0.21 to 0.87 by increments of 0.03. This resulted in a canonical single-fascicle dictionary F⁰ containing the diffusion fingerprints of N = 782 microstructural configurations along a reference orientation. The groundtruth diffusivities of the intra- and extra-axonal or “white matter” space were kept equal and fixed to D_wm = 2.0 × 10⁻⁹ m² s⁻¹ based on the intra-axonal estimate by Dhital et al. (2017). The diffusivity of CSF was set to D_csf = 3.0 × 10⁻⁹ m² s⁻¹ (Xing et al., 1997). Since a PGSE protocol was considered, NMR relaxation consisted of T2 decay of the form exp (−TE/T2), assumed independent of the diffusion process. In order to match our in vivo rat data set acquired at 11.7T, the groundtruth relaxation times were considered to be T2_wm = 30 ms for the intra- and extra-axonal space based on estimates at 11.7T in the rat corpus callosum and cerebellar white matter (de Graaf et al., 2006). For CSF, T2_csf = 120ms was selected in line with rat brain estimates at 7.0T (Crémillieux et al., 1998) and at 11.7T (Pohmann et al., 2011).

The Monte Carlo simulations of Step 2 in our estimation procedure were performed using an in-house software for the extra-axonal signal of the gradient components perpendicular to the cylinders with a number of random walkers N_spins = 150 000 and a time step δt between 1 and 5 μs based on the distance between cylinders (Rensonnet et al., 2015, 2016). Exact intra-axonal signals were obtained using an efficient implementation¹ of the Multiple Correlation Function (MCF) approach (Grebenkov, 2008). As described in Section 1.3.1, one single set of directional phases ϕ_x and ϕ_y per fingerprint needed to be stored in order to compute all 216 diffusion-weighted acquisitions of the rodent protocol.

In Step 3, the number of fascicles in each voxel was limited to K = 1 and the orientations were obtained from a ball-and-sticks model estimated using a maximum a posteriori approach as described in Scherrer et al. (2016), using the CRKIT software² without spatial regularization across voxels.

Since a multi-shell PGSE protocol was considered, the rotation of DWMRI signals required in Step 4 was done by simple linear spline interpolation separately on each shell.

2.1.3. Synthetic experiments

Two synthetic experiments were designed to validate the estimation method in a variety of controlled groundtruth configurations and to investigate the effect of uncertainties on fixed or pre-estimated parameters.

In both experiments, the results of our Monte Carlo based estimations were systematically compared with the output of the minimal model of white matter diffusivity (MMWMD) introduced in Alexander et al. (2010). MMWMD was chosen for comparison as it provides direct indices of the radius and axonal density to which our method can be compared. More specifically, the quantity $\frac{f_{\text{cylinder}}}{f_{\text{cylinder}}+f_{\text{zeppelin}}}$ was used as an axonal density index, where f_cylinder and f_zeppelin are the fractions of signal modeled by the cylinder and the zeppelin-like diffusion tensor, respectively. All MMWMD fitting was performed with the Camino Diffusion MRI Toolkit (Cook et al., 2006) using Markov chain Monte Carlo (MCMC) fitting with 40 samples at intervals of 200 iterations after a burn-in of 2000 iterations as recommended in Alexander et al. (2010).

The signal-to-noise ratio (SNR) was defined as SNR = 0.5M₀/σ, where σ is the standard deviation of the noise in an individual MRI detection coil. The factor 0.5 comes from the mid-point value of the unweighted b0 signal for 0 and 25% of the volume occupied by CSF, using the T2 values described above. The scaling parameter M₀ depends on the sensitivity of the MRI scanner in practice and was fixed to an arbitrary M₀ = 1000 in the groundtruth signals throughout all synthetic experiments.

Experiment 1.A. Single-fascicle groundtruth, effect of fixed diffusivity.

This experiment focused on the estimation of microstructural properties in single fascicles and included no CSF contribution in the synthetic groundtruth and in the fitted models. Consequently Eq. (15) was solved with w_csf = 0 in our Monte Carlo dictionary estimation while the ball and dot compartments were ignored in the MMWMD fitting.

Equation (1) was used to generate reference groundtruth signals for 64 single-fascicle configurations obtained from the combinations of 8 groundtruth radius index values r from 0.6 to 4.8 μm by steps of 0.6 μm and 8 groundtruth density index values f from 0.42 to 0.84 by steps of 0.06. Each signal was corrupted by 10 independent simulations of Rician noise with 10 SNR levels varying from 5 to 150. Estimation was performed for all 4 combinations of groundtruth diffusivity D* = {2.0, 3.0} × 10⁻⁹ m² s⁻¹ and model diffusivity D = {2.0, 3.0} × 10⁻⁹ m² s⁻¹ in order to investigate the effect of fixing D to an under- or overestimated value (with signals generated using data augmentation as explained in Section 1.3.2). This yielded a total of 64 × 10 × 10 × 4 = 25 600 independent synthetic voxels.

Experiment 1.B. CSF partial volumes, effect of fixing T2 values.

In this experiment, partial volumes of CSF were added both to the groundtruth voxels and to the fitted models. The 64 single-fascicle configurations selected in Exp.1.A were considered and isotropic CSF contributions with physical volume fractions ν_csf = {0.0, 0.25, 0.50} were successively added following Eq. (1). The levels of Rician noise corruption and number of repetitions were as in Exp. 1.A and the model diffusivities were set to the groundtruth values. Three configurations of T2 values were examined as detailed in Table 1. The “T2_✓” scenario was the ideal case; in the “T2_✘1” setting the groundtruth values were unchanged but the models assumed uniform T2 at a typical 3T value of 70 ms; the “T2_✘2” case was more challenging as the groundtruth signals were generated with different T2 values in the intra- and extra-axonal space of the single fascicle. MMWMD fitting was performed using the full four-compartment model including a dot compartment.

Table 1:

T2 values of the intra-axonal, extra-axonal and CSF compartments assumed in the groundtruth (GT) and the model in three different scenarios for Exp. 1.B.

	T2✔		T2✘1		T2✘2
	GT	Model	GT	Model	GT	Model
T2in	30	30	30	70	30	70
T2ex	30	30	30	70	45	70
T2csf	120	120	120	70	120	70

2.1.4. In vivo experiment

Animal model of Wallerian degeneration.

Three female Long Evans rats (Janvier Labs, Le Genest-Saint-Isle, France; weight 180 – 200 g) underwent laminectomy of verterbrae L2-L3 to expose the spinal cord. A left unilateral dorsal root axotomy was then performed, inducing Wallerian degeneration in the ipsilateral side of the gracile fasciculus of the spinal cord while leaving the contralateral side untouched. Two similar rats served as the control group and underwent laminectomy at identical vertebral levels without the dorsal root axotomy, leaving the whole spinal cord unaffected. All rats were scanned 51 days after surgery (see next paragraph) and sacrificed immediately after the imaging session. The spinal cords were then extracted, frozen and sliced axially in 20-μm thick sections to perform SMI312 staining, used to expose neurofilaments and indicate the presence of axons. The entire protocol was approved by the local animal care and ethics committee at Université catholique de Louvain (2016/UCL/MD/011).

In vivo DW-MRI.

DW-MRI was performed on all five rats on an 11.7T Bruker BioSpec scanner (Bruker, Billerica, MA) using a 72-mm diameter transmitter volume coil and a 4-channel, 3 × 3 cm surface receiver coil covering the L4-T12 vertebral segments. Rats lay in the dorsal decubitus position on a custom-made bed, anesthetized with an isoflurane-air mixture (2.5% for induction and 1–1.5% for maintenance). Respiration and rectal temperature were continuously monitored and body temperature was kept stable at 37°C using a circulating warm-water pad. Diffusion-weighted images were acquired with the PGSE parameters described in Section 2.1.1 and TR = 3s, using 2-D echo planar imaging (EPI) with in-plane voxel resolution 0.1 × 0.1mm² (128 × 128 matrix) and slice thickness 1 mm for 16 contiguous axial slices, for a total acquisition time of about 2.5 h per rat. Correction for animal motion and Eddy current was achieved by affine registration of each scalar DW-MRI to the b0 images interleaved in the protocol. To this end, images were resampled to a resolution of 0.05 × 0.05 × 0.06mm enabling improved multi-scale pyramidal registration.

Model fitting and statistical analysis.

The gracile fasciculus was manually segmented based on the hypo-intense signal of the anterior spinal vein on the b0 images and the high fractional anisotropy (FA) values of the corticospinal tract obtained from diffusion tensor fitting, while CSF voxels were manually removed at the periphery of the spinal cord.

Estimation was performed in the voxels of the gracile fasciculus of all five rats using our Monte Carlo dictionary approach, yielding estimates of r, f and ν_csf. MMWMD was estimated as described in Exp. 1.B, providing an extra parameter ν_dot. For further comparison, the four closed-form microstructural models DIAMOND (Scherrer et al., 2016), NODDI (Zhang et al., 2012), WMTI (Fieremans et al., 2011) and MAPL (Fick et al., 2016) were also fitted to the data. From DIAMOND, the compartment heterogeneity index cHEI, compartment radial diffusivity cRD, compartment axial diffusivity cAD and isotropic volume fraction ν_iso were examined. From NODDI, the intra-neurite volume fraction f_icvf, orientation dispersion index ODI and isotropic volume fraction ν_iso were estimated using the NODDI Matlab (The MathWorks, Inc, Natick, MA) Toolbox³. From WMTI, the axonal water fraction (AWF), intra-axonal radial diffusivity RD_in, extra-axonal radial diffusivity RD_ex and extra-axonal axial diffusivity AD_ex were estimated using the reconst.dki_micro module from the DIPY software project⁴ (Garyfallidis et al., 2014). From MAPL, the Return-to-Origin Probability RTOP, Return-to-Axis Probability RTAP, Return-to-Plane Probability RTPP and mean squared displacement MSD were estimated using the reconst.mapmri module from DIPY.

After model fitting, the following linear mixed-effect regression was estimated for each of the microstructural parameters described above using Matlab’s fitlme routine

$$y={\beta }_0+{\beta }_{\text{WD}}\times S\times I+{\beta }_{\text{surgery}}\times S+{\beta }_{\text{ipsilateral}}\times I,$$ (16)

where y is the microstructural property of interest, S and I are indicator variables respectively indicating surgery (S = 1) versus controls (S = 0) and ipsilateral (I = 1) versus contralateral (I = 0) sides. A subset of voxels in the gracile fasciculus corresponding to the original DW-MRI resolution were selected for the analysis in order to avoid artificially increasing our sample size and driving p-values to zero. In Eq. (16), the coefficient β_WD captures the effect of Wallerian degeneration. It should only be large for parameters physically impacted by the surgery and not by intrinsic differences between the control and the injured group (β_surgery) or rat-specific differences between the left and right sides of the spinal cord (β_ipsilateral). In this experiment, the quality of a model does not lie in its ability to detect significant group differences but rather in its ability to attribute the signal change to specific microstructural parameters in line with histological observations.

2.2. Validation on crossing fascicles

2.2.1. Diffusion protocol

All synthetic and in vivo experiments on crossing-fascicle configurations were carried out using the MGH-USC Adult Diffusion protocol of the Human Connectome Project (HCP) described in Setsompop et al. (2013). The protocol comprised 4 PGSE HARDI shells containing 64 gradient directions at b = 1000 s mm⁻², 64 at b = 3000 s mm⁻², 128 at b = 5000 s mm⁻², 256 at b = 10 000 s mm⁻² and 40 b0 images interleaved throughout the protocol, for a total of 552 acquisitions. Gradients intensities reached G = 219 mT m⁻¹ with δ/Δ= 12.9/21.8 ms, enabling TE = 57 ms.

2.2.2. Implementation details of the dictionary estimation

In Step 1 of the inverse problem (Section 1.4), the same single-fascicle model as in Section 2.1.2 was selected, along with the same sampling of the microstructural parameter space Ω = (r, f) and identical diffusivities. Groundtruth T2 values were set to typical human brain values at 3T with T2_wm = 70 ms based on Stanisz et al. (2005) and Smith et al. (2008), assumed identical in all fascicles. In CSF, T2_csf = 1000 ms was interpolated from 0.14 T estimates in humans (Condon et al., 1987) as well as rat estimates at 4.7 T (Ting and Bendel, 1992) and 7 T (Crémillieux et al., 1998).

Steps 2, 3, and 4 were performed as in the single-fascicle experiments except that the ball-and-sticks estimation in Step 3 was set to detect up to K = 2 fascicles. In step 5, N² = 611 524 non-negative least squares subproblems were solved in voxels containing two fascicles.

2.2.3. Synthetic experiments

Two synthetic experiments were designed to validate the estimation method in a variety of controlled crossing-fascicle configurations and to investigate the effect of misestimating fixed or estimated parameters.

As with the rodent protocol, the scanner-specific scaling parameter was fixed to M₀ = 1000 and the SNR was computed as SNR = 0.5M₀/σ based on unweighted b0 signals without CSF contamination and with 25% of CSF in the voxel, using the above T2 values.

Experiment 2.A. Independent voxels, effect of orientation misestimation and crossing angle.

This experiment focused on the estimation of microstructural properties in crossing fascicles and included no CSF contribution in the synthetic groundtruth and in the Monte Carlo dictionary estimation, i.e. Eq. (15) was solved with w_csf = 0.

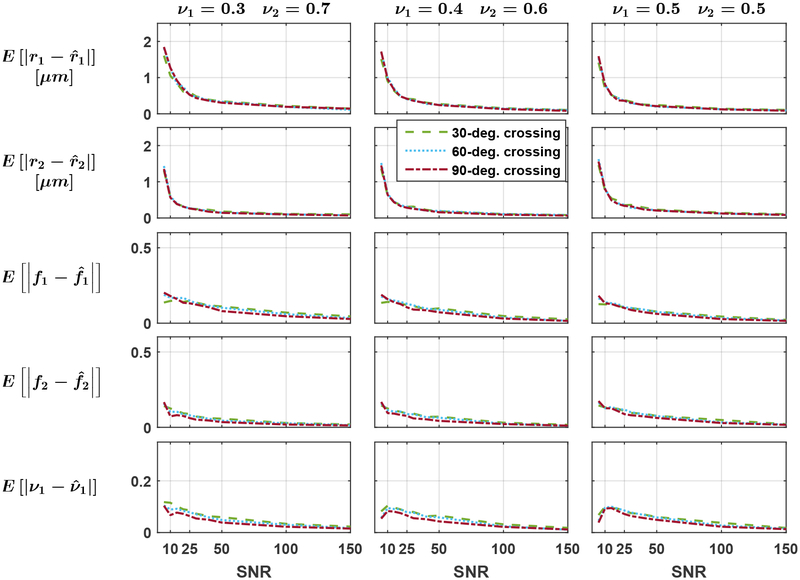
Equation (1) was used to generate reference groundtruth signals for fascicles with identical microstructural properties r = r₁ = r₂ and f = f₁ = f₂ with volume occupied by the first fascicle ν₁ = {0.3, 0.4, 0.5} and ν₂ = 1 − ν₁, for all 32 combinations of 4 radius index values r = {1, 2, 3, 4} μm and 8 density index values f from 0.42 to 0.84 by steps of 0.06. Each signal was corrupted by 10 independent simulations of Rician noise with 10 SNR levels varying from 5 to 150.

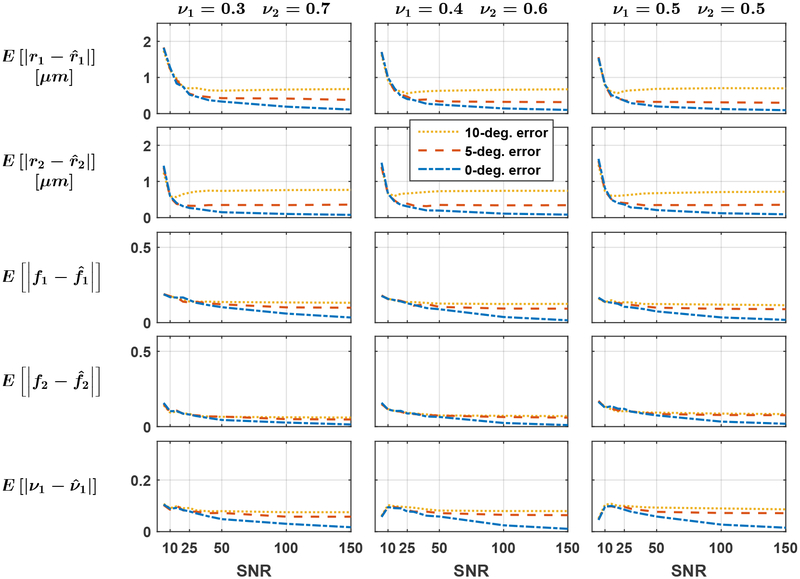
To examine the effect of an incorrect estimation of the fascicle’s orientations in Step 3 of the inverse problem, the estimation was performed by independently selecting u₁ and u₂ randomly on a cone with principal axis along the groundtruth orientations, forcing angular errors of 0°, 5° and 10° successively. Fascicles crossing at angles ∠u₁, u₂ = {30°, 60°, 90°} were considered in order to study the effect of the groundtruth crossing angle, thereby yielding a total of 3 × 32 × 10 × 10 × 3 × 3 = 86 400 independent voxel estimations.

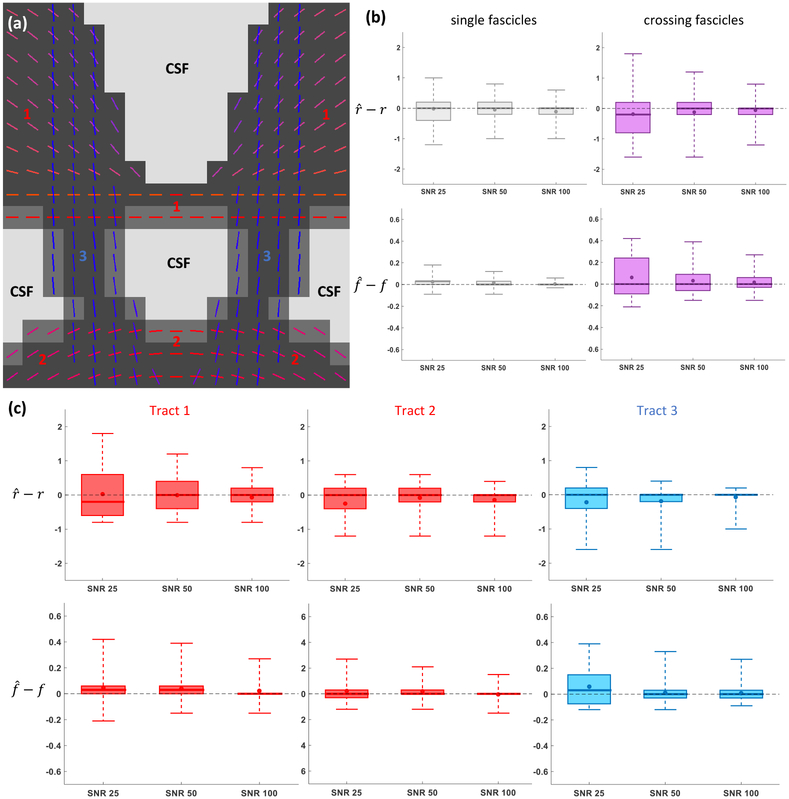
Experiment 2.B. Synthetic 2D phantom, effect of dissimilar fascicles.

A synthetic phantom was designed containing three axonal tracts (see Fig. 7(a)). Each tract had a constant radius index r (respectively 1.2, 1.6 and 2.0 μm) and spatially-smooth variations of the fascicle-specific density index f ranging from 0.45 to 0.81. The complete 2D-slice featured 17 × 17 = 289 voxels including 119 voxels containing one single fascicle of axons, 34 voxels containing a single fascicle with 25% of CSF and 86 voxels containing two fascicles intersecting at angles comprised in [31.4°, 86.0°] with mean 62.7°. The crossing-fascicle configurations were more complex than in Exp. 2.A because the two crossing fascicles had different microstructural properties r₁ ≠ r₂, f₁ ≠ f₂ in general. Estimation was performed at SNR levels of 25, 50 and 100.

Figure 7: (Exp. 2.B) Tract-specific microstructural estimated enabled by Monte Carlo dictionary estimation.

(a) Color-coded direction of all three axonal tracts with the gray-scale background indicating the level of CSF contamination in each voxel. (b) Signed error made on the estimated radius index r and density index f in regions of single (left) and crossing (right) fascicles. (c) Signed errors for the local voxel fascicles of each tract independently. In (b)-(c), the whiskers of the boxplots extend from the minimum to the maximum value of the data.

In the ball-and-sticks estimation of Step 3 of the Monte Carlo dictionary estimation, spatial regularization across voxels was enabled and sticks with directions separated by fewer than 15° were merged. Denoting by β₁ the largest weight attributed to a stick, all secondary sticks were then removed if their weight β verified either β < β₁/2.5 and β < 0.20 or just β < 0.10. The Monte Carlo dictionary estimation of Step 5 set w_csf = 0 when two fascicles were detected in Step 3.

2.2.4. In vivo experiment

In vivo DW-MRI.

One healthy subject was randomly selected from the MGH Adult Diffusion data release⁵ (Setsompop et al., 2013).

Model fitting and statistical analysis.

Voxels containing white matter were identified based on the segmentation obtained with the FAST algorithm (Zhang et al., 2001) from the FMRIB Software Library (FSL)⁶. Monte Carlo dictionary estimation was performed independently in each voxel as described in the synthetic experiments.

Our experiment focused on extracting the distribution of apparent axonal radius index r and density index f of axons passing through the anterior, mid-anterior, central, mid-posterior and posterior sub-regions of the corpus callosum (CC) as identified by the subcortical segmentation tool of the FreeSurfer software (Fischl et al., 2002). As these axons cross other macroscopic tracts such as the corticospinal tract (CST) or the longitudinal fasciculus (LF), each fascicle or peak at the local voxel level had to be assigned to one or more of these macroscopic tracts. In order to do so, probabilistic tractography was first performed with 5 seeds per voxel and streamline segments constrained to follow the orientation of a detected peak in each voxel, using routines from DIPY. The streamlines were clustered into tracts using the white matter query language (Wassermann et al., 2016) and a local voxel fascicle was considered to belong to a macroscopic tract if at least 5% of all streamlines going through the local peak had been assigned to that tract.

3. Results

3.1. Validation on single fascicles

3.1.1. Experiment 1.A. Single-fascicle groundtruth, effect of fixed diffusivity

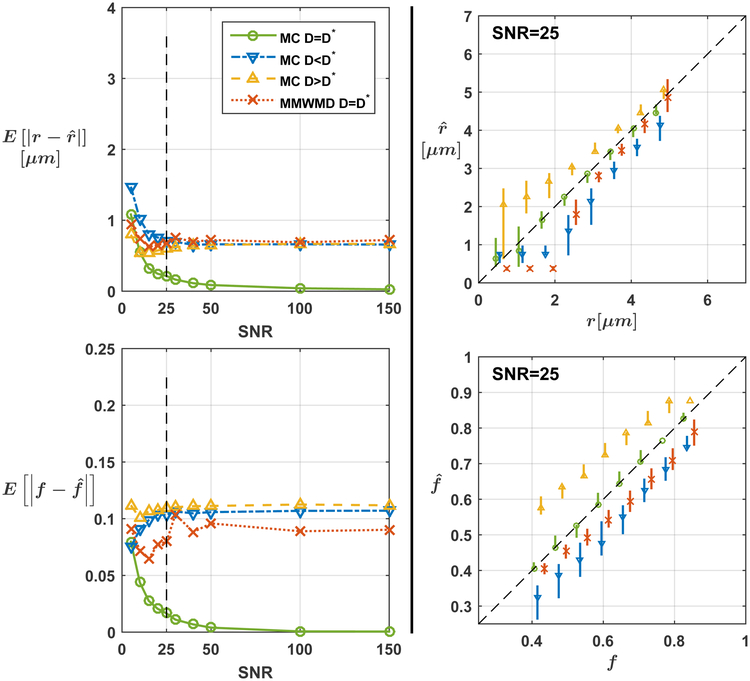
The mean absolute error (MAE) in the estimation of the radius and density index for our approach and for MMWMD are depicted in Fig. 1. When the correct diffusivity D was assumed (green curves), the MAE over all repetitions and over all configurations with our approach converged to zero with increasing SNR. Underestimating (resp. overestimating) D led to a systematic underestimation (resp. overestimation) of r and f as indicated by the blue (resp. yellow) estimate bars at SNR level 25. On the other hand, systematic errors persisted for MMWMD estimates at large SNR values even when the correct value for D was assumed in the model.

Figure 1: (Exp. 1.A) Consistent microstructural estimates in single fascicles with Monte Carlo (MC) dictionary estimation.

The left column displays the mean absolute error on the radius index r (top) and density index f (bottom) as a function of signal-to-noise ratios (SNR). The right column provides a snapshot of estimates at SNR=25, with markers indicating the median over all noise repetitions and groundtruth configurations and bars ranging from the 25th to the 75th percentile of all estimates. Asymptotic errors remained for the minimal model of white matter diffusivity (MMWMD) even though it used the true diffusivity D.

3.1.2. Experiment 1.B. CSF partial volumes, effect of fixing T2 values

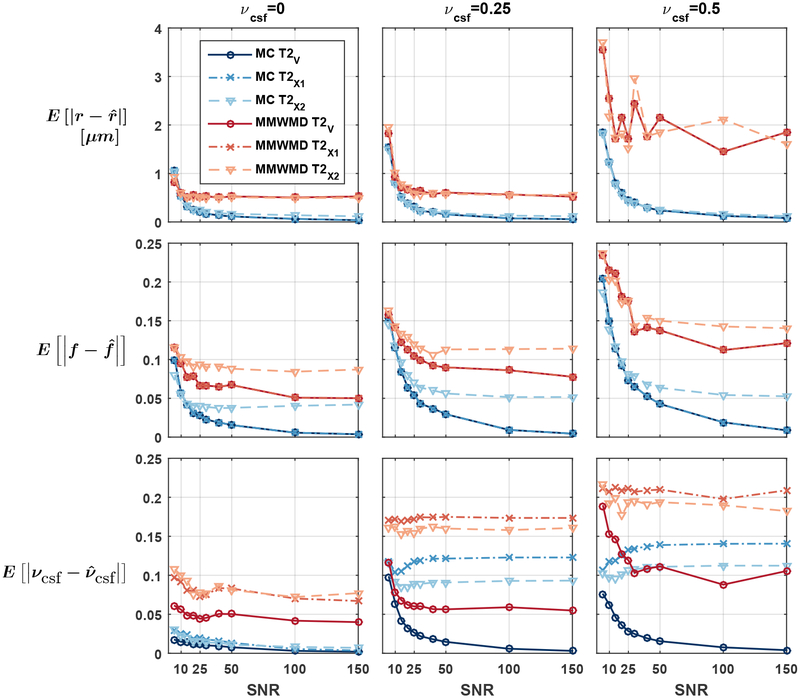
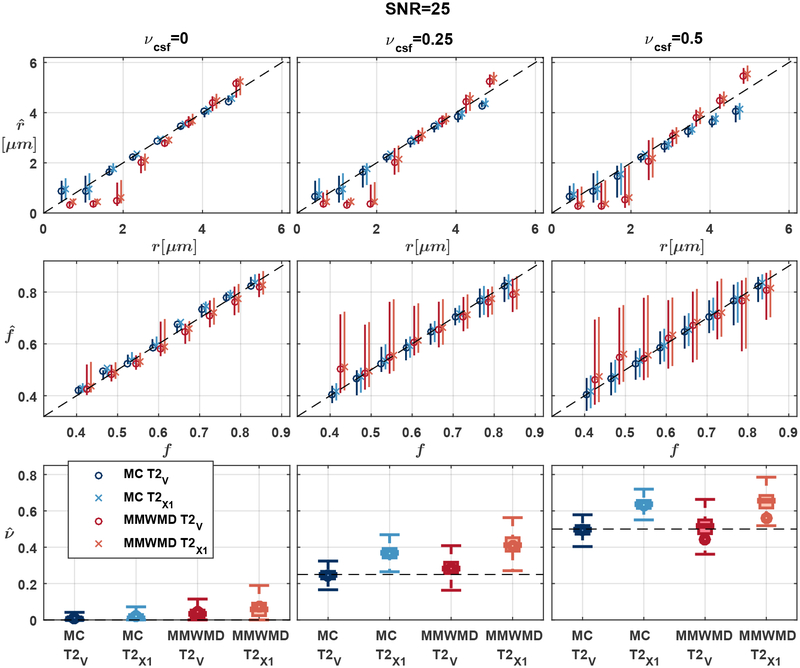
Figure 2 suggests that our approach was able to provide accurate microstructural estimates in the presence of CSF. Errors on r and f exhibited a moderate upward trend as the fraction of CSF increased, likely due to a reduced relative signal (and hence a reduction in apparent SNR) arising from the fascicle of axons. The estimation errors for MMWMD were systematically larger than in Exp. 1.A. The MAE on ν_csf hovered around 0.05 across SNR levels even in the T2_✓ scenario and when there was no CSF in the groundtruth. As shown in Figure 3, the MMWMD estimates exhibited a larger variability than those of our Monte Carlo dictionary approach.

Figure 2: (Exp. 1.B) Consistent microstructural estimates from Monte Carlo dictionary in the presence of CSF contamination.

Mean absolute errors on the radius index r (top), density index f (middle) and cerebrospinal fluid (CSF) volume fraction ν_csf (bottom) as a function of signal-to-noise ratio for various levels of CSF contamination. The MMWMD approach yielded generally larger errors. Assuming incorrect T2 values in the model did not affect the estimation of r and f in the the first two scenarios described in Table 1.

Figure 3: (Exp. 1.B) Consistent microstructural estimates from Monte Carlo dictionary in the presence of CSF contamination.

Snapshot of the estimates of r, f and ν_csf at SNR=25 (see Fig. 2), with markers indicating the median over all noise repetitions and groundtruth configurations and bars ranging from the 25th to the 75th percentile of all estimates. The estimates of the T2_✘2 scenario were left out for clarity. MMWMD had larger variability and more biased estimates.

Notably, the estimates of r and f using the incorrect T2 values of the T2_✘1 scenario (cross markers in Fig. 2) were identical to those obtained with the groundtruth T2 values (circle markers in Fig. 2) for both models. The error in T2 was simply corrected by scaling the fascicle and CSF signals by an adjusted weight w, which then led to a misestimated volume fraction ν_csf. This was no longer the case in the T2_✘2 scenario because the model and the groundtruth signals no longer differed by just a scaling constant.

3.1.3. In vivo experiment

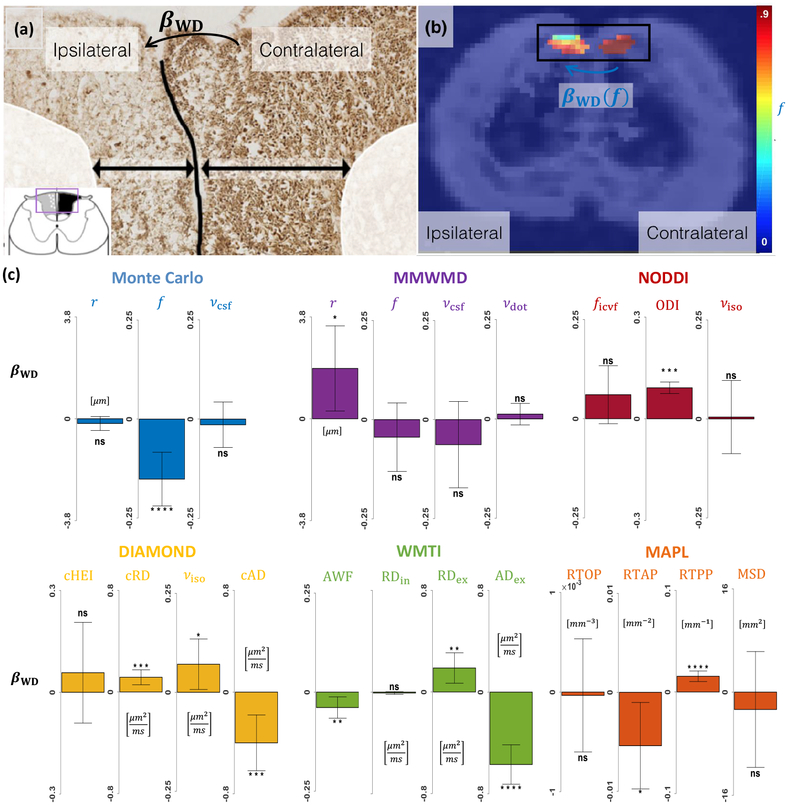
Histological slices of the rats which underwent surgery revealed lighter SMI312 staining on the ipsilateral side, indicating axonal loss induced by Wallerian degeneration (Fig. 4(a)).

Figure 4: Monte Carlo dictionary approach yields physically-interpretable parameters consistent with histology.

(a) Histology of a slice in the spinal cord of a rat which underwent surgery, stained with SMI312 immunohistochemistry. Darker colors indicate more neurofilaments present inside axons. (b) Representative map of axonal density index f obtained with our Monte Carlo dictionary approach, laid atop a fractional anisotropy (FA) map. (c) Effect of Wallerian degeneration (WD) on selected parameters from our approach and from popular closed-form models of the microstructure. Vertical bars indicate the 95% confidence interval on β_WD. Non-significant (ns) corresponds to p > 0.05; * to p ≤ 0.05; ** to p ≤ 0.01; *** to p ≤ 0.001; **** to p ≤ 0.0001.

As depicted in Fig. 4(b–c), our Monte Carlo dictionary approach exhibited an important decrease in axonal density index f (−0.15, p = 1.6 × 10⁻⁵) and statistically non-significant changes in r and ν_csf. In contrast, MMWMD detected no significant change in f and a large increase in r (+1.9 μm, p = 2.1 × 10⁻²) while yielding no statistically-significant changes in ν_csf and ν_dot. NODDI found a non-significant increase in f_icvf, an increase in dispersion (+0.09, p < 2.9 × 10⁻²²) and no significant change in ν_iso. DIAMOND obtained a non-significant change in cHEI, an increase in cRD (+0.12 μm² ms⁻¹, p = 1.4 × 10⁻⁴), a decrease in cAD (−0.40 μm² ms⁻¹, p = 4.2 × 10⁻⁴) and a slight increase in ν_iso (+0.07, p = 3.0 × 10⁻²). WMTI saw a slight decrease in AWF (−0.04, p = 4.8 × 10⁻³), no statistically-significant change in RD_in, an increase in RD_ex (+0.19 μm² ms⁻¹, p = 2.2 10⁻³) and a decrease in AD_ex (−0.57 μm² ms⁻¹, p = 4.4 10⁻¹²). MAPL identified a decrease in RTAP (−5.4 × 10⁻³ μm⁻², p = 1.6 × 10⁻²), an increase in RTPP (+1.5 × 10⁻² μm⁻¹, p = 1.2 × 10⁻⁸) and no statistically-significant changes in RTOP and MSD.

3.2. Validation on crossing fascicles

3.2.1. Experiment 2.A. Independent voxels, effect of orientation misestimation and crossing angle

As suggested by Fig. 5, the crossing angle had a marginal impact on the estimation as all the curves are very close to one another. Figure 6 indicates that the MAE over all noise repetitions and groundtruth configurations converged to zero as the SNR increased when the orientation of each fascicle was perfectly estimated in Step 3 of our estimation procedure (blue curves). Misestimation of the orientation of fascicles introduced systematic errors in the microstructural estimation (red and yellow curves). The estimates were generally slightly better for the dominant groundtruth fascicle: at a crossing angle of 60° with ν₁ = 0.3, the MAE on r₁ exceeded the MAE on r₂ in 25 out of 30 cases with a mean signed difference of 0.23 μm; the MAE on f₁ exceeded the MAE on f₂ in all 30 cases, with a mean difference of 0.060.

Figure 5: (Exp. 2.A) The groundtruth crossing angle has limited impact on the estimation of fascicles’ microstructural properties.

Mean absolute error on each fasicle’s radius index r₁ and r₂, density index f₁ and f₂ and on the physical volume fraction occupied by the first fascicle ν₁. The groundtruth volume fraction of the second fascicle decreases from left to right. The fascicles’ orientations were perfectly estimated.

Figure 6: (Exp. 2.A) Errors in the initial estimation of fascicles’ orientations yield asymptotically-biased estimates.

Mean absolute error on each fasicle’s radius index r₁ and r₂, density index f₁ and f₂ and on the physical volume fraction occupied by the first fascicle ν₁. The groundtruth volume fraction of the second fascicle decreases from left to right and the groundtruth crossing angle was fixed to 60°.

3.2.2. Experiment 2.B. Synthetic 2D phantom, effect of dissimilar fascicles

Figure 7 suggests that the errors on the estimated microstructural properties converged to zero as the SNR increased. At SNR=25, the average absolute error made on the radius index r expressed as a percentage of the groundtruth value was 33.0% in single fascicles, close to its value of 37.4% in voxels of crossing fascicles (Fig. 7(b)). The difference was more pronounced for the density index f with an average 4.94% error in single-fascicle voxels and 29.7% in crossing fascicles. As shown in Fig. 7(c), the fastest convergence with SNR in r occurred for Tract 3, which had the largest groundtruth radius index. Convergence for f was slightly faster in Tracts 1 and 2, which were less exposed to fascicle crossings and CSF contamination. The mean absolute angular error on the fascicles’ orientations by the ball-and-sticks routine at SNR=25 was as low as 0.43° in single-fascicle voxels and 0.85° in crossing-fascicle voxels, suggesting that the impact of Step 3 on the final errors was minimal.

3.2.3. In vivo experiment

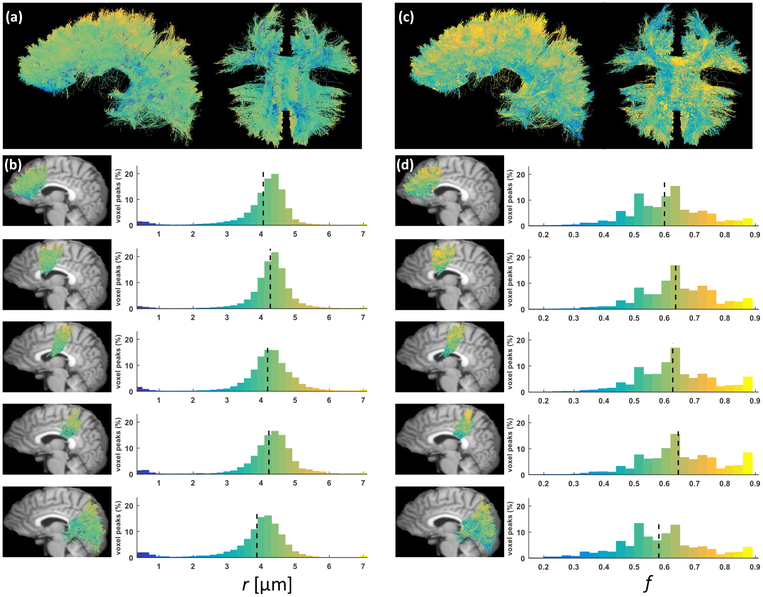
The top row in Fig. 8 suggests that the estimates of both the apparent axonal radius index r and density index f were spatially smooth. The distributions over all voxel-level fascicles (histograms in Fig. 8) were smoother for r than f. As reported in Table 2, both parameters exhibited a low-high-low trend, with lower mean values in axons passing through the anterior and posterior parts of the CC compared to axons of the mid-anterior, central and mid-posterior CC. The standard deviations for the two parameters were very similar across the five considered sub-regions.

Figure 8: Spatially-smooth estimates of apparent radius and density indices obtained with Monte Carlo dictionary estimation.

(a) Left and inferior view of all the axons passing through the corpus callosum (CC), color-coded by the apparent axonal radius index r. (b) Histograms of estimated apparent radius index in the five axonal tracts studied in the experiment, respectively the anterior, mid-anterior, central, mid-posterior and posterior CC tracts. The mid-sagittal maps of color-coded axons are laid atop a referential T1 image warped into the DW-MRI space. (c)-(d) Same as (a) and (b) for the axonal density index f.

Table 2: Low-high-low trend in apparent radius and density index in CC streamlines.

Mean and standard deviation over all local fascicles or peaks assigned to streamlines passing through five sub-regions of the corpus callosum (CC).

	apparent radius index	density index
anterior CC	4.06 ± 0.87	0.599 ± 0.12
mid-anterior CC	4.27 ± 0.73	0.636 ± 0.12
central CC	4.19 ± 0.90	0.627 ± 0.12
mid-posterior CC	4.22 ± 0.93	0.645 ± 0.13
posterior CC	3.87 ± 0.99	0.581 ± 0.14

4. Discussion

Advantages of Monte Carlo modeling

The main strength of Monte Carlo simulations is their ability to provide exact signals for any fixed tissue geometry. This advantage was made apparent throughout the comparison with MMWMD, which captures the same level of tissue complexity as the particular single-fascicle model selected in this study but differs in the way the signal is formulated. MMWMD for instance failed to consistently estimate r and f in Exp. 1.A, which can only be attributed to the formulation of the extra-axonal signal. In Exp. 1.B, a nonzero CSF weight for the full 4-compartment MMWMD persisted although no isotropic compartment was included in the groundtruth, suggesting that some of the extra-axonal signal may be captured by the isotropic compartment. MMWMD relies on a zeppelin-like diffusion tensor with perpendicular diffusivity proportional to the parallel diffusivity and the extra-axonal volume fraction through a tortuosity model. Monte Carlo simulations on the other hand naturally incorporate physical compatibility between the intraand extra-axonal compartment.

Our in vivo rat model of spinal cord injury demonstrated that the parameters provided by Monte Carlo simulations are generally more specific and interpretable than those of closed-form continuous models (Figure 4). Wallerian degeneration is a process with dramatic consequences on the fascicles of the spinal cord which after several weeks is mainly characterized by severe axonal loss (Waller, 1850; George and Griffn, 1994). This was correctly captured by our Monte Carlo dictionary approach but not by MMWMD, which detected an increase in radius index. NODDI attributed all the signal differences to an increase in dispersion and not to a decrease in neurite density. This unexpected result is likely caused by the use of fixed parameters in NODDI which impairs our ability to interpret the remaining free parameters (Scherrer et al., 2016; Jelescu et al., 2016; Hutchinson et al., 2017). The increase in fascicle-specific RD and decrease in fascicle-specific AD detected by DIAMOND were in agreement with a large body of studies correlating diffusion tensor imaging with Wallerian degeneration (Song et al., 2003; Kim et al., 2007; Sun et al., 2008; Zhang et al., 2009; Liu et al., 2013). However no parameter in DIAMOND directly relates to axonal density. The WMTI model predicted a decrease in axonal density similar (although of smaller magnitude) to our Monte Carlo dictionary method as well as changes in extra-axonal RD and AD similar to DIAMOND. Taking the intra-axonal RD as a proxy for axonal radius then the non-significant change agrees with our own findings for r. The good agreement between our approach and WMTI will be investigated in the future. In MAPL, a decrease in RTAP has been shown to represent an increase in mean apparent axonal radius (Fick et al., 2016), similar to what MMWMD detected. Alternatively, considering that Wallerian degeneration causes the number of diffusion barriers to decrease in the extra-axonal space, RTAP could be interpreted as inversely proportional to the extra-axonal RD, which would be in agreement with DIAMOND and WMTI. Similarly, if diffusion is assumed unhindered along the axons, the increase in RTPP can be interpreted as a decrease in AD.

This highlights that signal models such as DIAMOND and MAPL do capture group differences; however these must be carefully interpreted a posteriori. Our approach outperforms geometric models such as MMWMD and NODDI by ascribing the signal difference to the correct variation in microstructural features.

Whole-brain estimation

The whole-brain HCP experiment was intended to showcase the ability of our method to extract microstructural properties in vivo in each voxel locally in areas of crossing fascicles, which is still an open issue in the field. The MIX optimization technique (Farooq et al., 2016) provides a faster and more stable algorithm to fit multi-fascicle extensions of analytical compartment-based models but these models still intrinsically rely on approximate analytical formulas. The multi-fascicle extension of Amico (Daducci et al., 2015) to Amico-X (Auría et al., 2015) uses a simple diffusion tensor for the extra-cellular signal and does not impose the geometrical compatibility between the intra- and extra-axonal signal that is naturally enforced in Monte Carlo simulations. DIAMOND was also formulated as a multi-fascicle model from the onset but its fascicle-specific parameters are tensor-related quantities and are therefore surrogate measurements of tissue properties.

The low-high-low trend in apparent axonal radius r observed in the human CC (Aboitiz et al., 1992) was found to extend to all callosal axons in our experiment. Remarkably, this pattern was obtained by independent estimations of our model at each voxel and was therefore not a consequence of spatial regularization. In Girard et al. (2017), a similar trend for r was observed on most of the 34 HCP subjects, albeit on DW-MRI data upsampled for tractography analysis. In the same work, the streamline-specific estimates of apparent fiber density computed over all 34 subjects were found to be lowest in the anterior CC, intermediate in the mid-anterior and posterior CC and largest in the central and mid-posterior CC. This roughly coincides with the estimates of f obtained in our particular subject. It should be noted that the values of radius index reported in the experiment (≈ 4 μm) are considerably larger than actual measurements of axonal radius in the human brain (≈ 0.5 – 1 μm), as discussed in the next paragraph.

Limitations

In our framework, the tissue geometry selected for the Monte Carlo simulations at the single-fascicle level determines the complexity of the final model. To compare our approach with models of similar tissue complexity such as MMWMD, the simple hexagonal packing geometry was selected in this work. In particular, the use of the single scalar parameter r to characterize the whole intra-axonal signal is known to considerably overestimate actual axonal radii (Alexander et al., 2010; Dyrby et al., 2013) and as such should only be considered as an index of apparent axonal radius.

In order to fully exploit the potential of Monte Carlo simulations, future tissue geometries will need to be more realistic and include randomly-located axons with a distribution of radii (Hall et al., 2017), a myelin sheath around axons (Harkins and Does, 2016), axonal undulation (Nilsson et al., 2012), cells with complex morphology such as glia and neurons (Palombo et al., 2016, 2017) or tissue geometries directly obtained from histological slices (Xu et al., 2014). Incorporating axonal orientation dispersion in synthetic substrates for Monte Carlo simulations requires the careful configuration and location of all axons in order to avoid unrealistic intersections. Axonal oscillations with large periodicity may help achieve apparent orientation dispersion (Nilsson et al., 2012).

It is worth recalling that the only simplifying hypothesis made in our framework is that no water exchange occurs between fascicles during the acquisition, which allowed us to write the fundamental equation (1) as a simple superposition (Rensonnet et al., 2018). This however does not prevent the incorporation of membrane permeability and water exchange within a fascicle.

In theory, the sparsity constraints used in Eq. (14) do not allow mixtures of fingerprints to reconstruct the signal arising from a single fascicle of axons. This could be a limitation for fascicles consisting of several well-delimited sub-regions exhibiting distinct microstructural properties (e.g., one half with a high and one half with a low axonal density). As discussed in Appendix B, with the DW-MRI protocols used in this study, the signals of non-uniform voxels were very similar to the fingerprints of uniform voxels with a density index f precisely corresponding to the average packing density of the non-uniform configuration. If non-uniform configurations were not distinguishable from uniform, “average” configurations, a possible workaround would be to add fingerprints arising from non-uniform configurations to the single-fascicle dictionary (Steps 1 and 2 in Section 1.4).

The traditional PGSE sequence used in our experiments has been shown to have limited sensitivity to microstructural features such as the axonal radius (Dyrby et al., 2013). Improved sensitivity may be obtained using other diffusion-encoding sequences such as OGSE (Drobnjak et al., 2016; Mercredi and Martin, 2018), STEAM-DTI with varying diffusion times (Fieremans et al., 2016) or b-tensor encoding (Topgaard, 2017). One major advantage of the presented framework is precisely its ability to promptly integrate such extensions, which will be considered in future work.

Fixed parameters and external routines

A number of parameters such as the intrinsic diffusivity and the T2 values of the intra-axonal, extra-axonal and CSF compartments were fixed a priori based on literature values rather than estimated from the data in order to simplify the estimation. Our synthetic experiments have shown however that the model is quite resilient to slightly misestimated parameter values, in particular for T2 relaxation which in some situations can be exactly compensated by the free weights w in Eq. (14). As seen in Exp. 1.B, care must be taken in case multiple T2 values should be present within a single fascicle, as has recently been suggested (Veraart et al., 2017).

It was shown in Experiment 2.A (Figure 6) that errors in the orientation of fascicles (estimated with an external routine) could bias the microstructural estimates. To overcome this issue, orientation-estimation methods based on rotationally-invariant dictionary learning (Reisert et al., 2014; Christiaens et al., 2017) could use the estimated fingerprints as their fiber orientation response and retroactively refine the estimated orientations, eventually leading to more accurate microstructural estimates.

Efficiency

The pre-computing stage described as Step 2 of our estimation procedure in Section 1.4 may come with a high computational cost. The two canonical single-fascicle dictionaries used in this study required about 35 days worth of computation time on a standard laptop i5 core. In practice this was reduced to about 1–2 days using computing clusters at Université catholique de Louvain depending on cluster load and availability. Algorithmic improvements such as proposed by Hall et al. (2017), optimized implementation and mathematical properties such as presented in Section 1.3 should further help assuage the burden of massive Monte Carlo simulations in the future.

Runtime efficiency is not an issue in single-fascicle voxels, where Eq. (15) takes less than a second to solve for dictionary sizes N such as used in our experiments. For voxels containing K > 1 fascicles, exactly solving N^K convex problems leads to longer computation times and is likely to become a more important issue with larger dictionaries (resulting from a finer resolution in microstructural parameters for instance). Different techniques can be used to reduce the size of the problem, such as a multi-scale optimization approach starting with a coarse-grained dictionary or initial dictionary pruning using sparsity-enforcing methods (Canales-Rodríguez et al., 2015, 2018).

Conclusion

A framework was proposed for the estimation of microstructural features incorporating Monte Carlo simulations known for their accurate modeling of the DW-MRI signal. The inverse estimation problem was formulated as a sparse optimization problem on a large pre-computed dictionary and decomposed into many independent convex and easy-to-solve sub-problems. Owing to their unique correspondence with a microstructural configuration, the selected diffusion fingerprints provided the microstructural parameters for each fascicle of axons in each voxel.

In single-fascicle voxels, our approach demonstrated more accurate, consistent and interpretable results than popular closed-form microstructural models of the literature in many simulation settings as well as in the analysis of an in vivo dataset of rat spinal cord. When extended to crossing fascicles, our framework achieved consistent estimates of apparent axonal radius and density indices in synthetic experiments and on whole-brain HCP data. Future work will focus on using a more realistic model at the single-fascicle level and generalizing the microstructural trends found in one HCP subject to larger cohorts.

This work paves the way for microstructure fingerprinting in which Monte Carlo simulations are used as the building blocks of a model of the diffusion signal which directly relate to the underlying microstructure. Our framework offers new opportunities for whole-brain quantitative and interpretable microstructure imaging. Such a capability may prove critical for studies exploring the pathogenesis of neurological and psychiatric disorders as well as in the assessment of responses to treatments.

Highlights.

• Diffusion signals are modeled by Monte Carlo simulations rather than analytic formulas

• Measured signals are matched to a large dictionary of simulated signals (fingerprints)

• Microstructural features are more accurately estimated than with conventional models

• Our approach is sensitive and specific to microstructural alterations in axonal loss

• Microstructure fingerprinting separately characterizes crossing fascicles in a voxel

Appendix A. Choice of the reference diffusivity for data augmentation

This appendix discusses the relationship between the number N of reference Monte Carlo simulations required to simulate configurations with different diffusivities and the fixed diffusivity D_sim ∈ [D_min, D_max] used during those simulations, as described in Section 1.3.2. Specifically, we show that N is independent of D_sim and only depends on the desired resolution δ_L in the length scale parameter L, assuming a uniform sampling of L.

Let ${\delta }_L^{\text{sim}}$ be the step size separating consecutive values of L for which reference simulations using a diffusivity D_sim were performed. Given D ≠ D_sim, using Eq. (12) yields a sampling ${\left\{\sqrt{\frac{D}{D_{\text{sim}}}}{L}_{\text{sim,}i}\right\}}_{i=1}^N$ of parameter L. The corresponding step size therefore becomes ${\delta }_L\left(D\right)=\sqrt{\frac{D}{D_{\text{sim}}}}{\delta }_L^{\text{sim}}$, which admits the upper bound ${\delta }_L\left(D\right)\le \sqrt{\frac{D_{\text{max}}}{D_{\text{sim}}}}{\delta }_L^{\text{sim}}$ for all D ∈[D_min, D_max].

Let ${\overline{\delta }}_L$ denote the largest acceptable step size in L for all values of D in [D_min, D_max] (or equivalently, the coarsest acceptable granularity of a dictionary). To ensure that $\begin{array}{ll}{\delta }_L\left(D\right)\le {\overline{\delta }}_L\hfill & \forall D\hfill \end{array}$, it is necessary to guarantee that

$$\sqrt{\frac{D_{\text{max}}}{D_{\text{sim}}}}{\delta }_L^{\text{sim}}\le {\overline{\delta }}_L\iff {\delta }_L^{\text{sim}}\le \sqrt{\frac{D_{\text{max}}}{D_{\text{sim}}}}{\overline{\delta }}_L.$$ (A.1)

Recalling that the sampling of L should cover the interval $\left[\sqrt{\frac{D_{\text{sim}}}{D_{\text{max}}}}{L}_{\text{min}},\sqrt{\frac{D_{\text{sim}}}{D_{\text{min}}}}{L}_{\text{max}}\right]$ during the reference simulations using D_sim, the lower bound on the total number of simulations N becomes

$$\begin{gathered} N-1=\frac{\sqrt{\frac{D_{\text{sim}}}{D_{\text{min}}}}{L}_{\text{max}}-\sqrt{\frac{D_{\text{sim}}}{D_{\text{max}}}}{L}_{\text{min}}}{{\delta }_L^{\text{sim}}} \\ \ge \frac{\sqrt{\frac{D_{\text{sim}}}{D_{\text{min}}}}{L}_{\text{max}}-\sqrt{\frac{D_{\text{sim}}}{D_{\text{max}}}}{L}_{\text{min}}}{\sqrt{\frac{D_{\text{sim}}}{D_{\text{max}}}}{\overline{\delta }}_L}=\frac{L_{\text{max}}/\sqrt{D_{\text{min}}}-L_{\text{min}}/\sqrt{D_{\text{max}}}}{{\overline{\delta }}_L/\sqrt{D_{\text{max}}}}, \end{gathered}$$ (A.2)

where inequality (A.1) was used. Equation (A.2) shows that the minimum number of simulations does not depend on D_sim and is entirely determined by the biophysical constraints of the problem.

Appendix B. Effect of non-uniform voxels on the fitting

The sparsity constraints in Eq. (14) assume that a single fingerprint can explain the signal of a fascicle of axons. With the hexagonal-packing model selected at the single-fascicle level for our experiments, all the fingerprints of our dictionary arise from voxels containing uniform arrangements of axons. In practice however, a voxel may contain sub-regions exhibiting different microstructural properties. The experiment described below examined how the fitted parameters behaved when the groundtruth voxels consisted of axons with spatially heterogeneous packing.

Experiment.

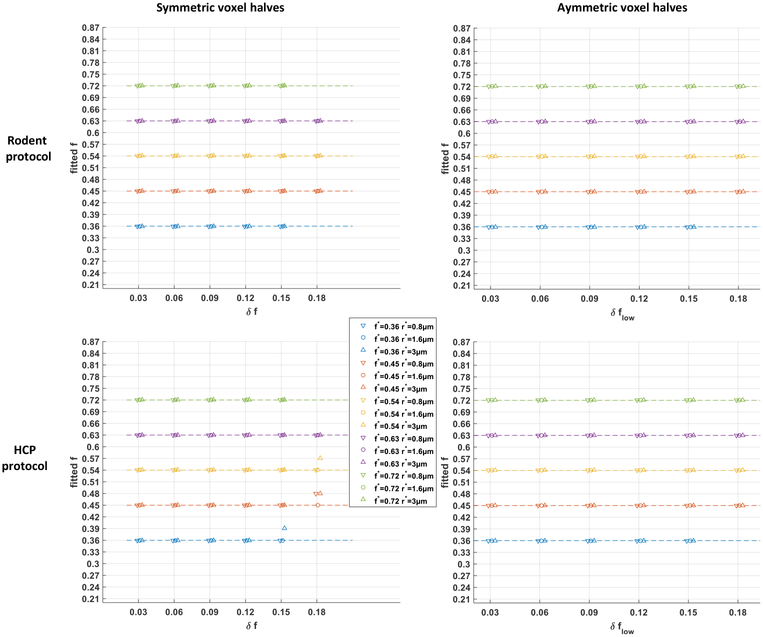
In this experiment, groundtruth voxels were split into two parts with different axonal packing density f. The DW-MRI signal S_mixed for such a non-uniform configuration was obtained as

$$S_{\text{mixed}}\left(\delta f_{\text{low}},\delta f_{\text{high}}\right)={\nu }_{\text{low}}{S}_{\text{unif}}\left(r*,f*-\delta f_{\text{low}}\right)+{\nu }_{\text{high}}{S}_{\text{unif}}\left(r*,f*+\delta f_{\text{high}}\right),$$

where S_unif is the fingerprint of a uniform configuration and where ν_low = δf_high/ (δf_low + δf_high) and ν_high = δf_low/ (δf_low + δf_high) ensure that the average packing density of the non-uniform voxel is f*.

First, non-uniform groundtruth voxels with symmetric halves were considered by setting δf_low = δf_high ≔ δf (leading to ν_low = ν_high = 0.5) and letting δf vary from 0.03 to 0.18 in 6 equal increments. Second, asymmetric halves were studied by setting δf_high = 0.06 and letting δf_low vary from 0.03 to 0.18 in 6 equal increments. In both cases, the fitting procedure of Section 1.4 was performed setting w_csf = 0 for 3 values of reference radius index r* = {0.8, 1.6, 3.0} μm and 5 values of average density index f* equally spaced between 0.36 and 0.72, provided that f* − δf_low > 0.20 and f* + δf_high < 0.90.

Results.

The results are displayed in Figure B.9. In all 168 cases with the rodent protocol, the fitted axonal density index $\widehat{f}$ precisely matched the average density index f* of the non-uniform voxels. This implied that $\left|\widehat{f}-f^{*}\right|\le 0.03$ given the granularity in f of the single-fascicle dictionary used for the estimation (see Section 2.1.2). With the HCP protocol, the bound reached $\left|\widehat{f}-f^{*}\right|\le 0.06$ in only 4 out of 168 cases, systematically for the largest density spread δf. Root-mean-square differences between the normalized groundtruth DW-MRI signals and their best fits were of the order of 1 × 10⁻⁴.

Even though our Monte Carlo fingerprints arise solely from voxels with a uniform packing density, our estimation procedure systematically explained the signal by selecting a packing density corresponding to precisely the average density of the non-uniform voxel.

Figure B.9: Fingerprints assuming uniform microstructural configurations capture the average axonal packing density of non-uniform configurations.

Fitted axonal density index $\widehat{f}$ for groundtruth voxels containing two sub-regions of different axonal packing density, in a symmetric or asymmetric configuration, using the rodent protocol (Section 2.1.1) or the HCP protocol (Section 2.2.1). The missing data points correspond to scenarios in which one of the local density indices fell outside the range ]0.20, 0.90[.