Multiple components in direction learning in smooth pursuit eye movements of monkeys

Abstract

We analyzed behavioral features of smooth pursuit eye movements to characterize the course of acquisition and expression of multiple neural components of motor learning. Monkeys tracked a target that began to move in an initial “pursuit” direction and suddenly, but predictably, changed direction after a fixed interval of 250 ms. As the trial is repeated, monkeys learn to make eye movements that predict the change in target direction. Quantitative analysis of the learned response revealed evidence for multiple, dynamic, parallel processes at work during learning. 1) The overall learning followed at least two trial courses: a fast component grew and saturated rapidly over tens of trials, and a slow component grew steadily over up to 1,000 trials. 2) The temporal specificity of the learned response within each trial was crude during the first 100 trials but then improved gradually over the remaining trials. 3) External influences on the gain of pursuit initiation modulate the expression but probably not the acquisition of learning. The gain of pursuit initiation and the expression of the learned response decreased in parallel, both gradually through a 1,000-trial learning block and immediately between learning trials with different gains in the initiation of pursuit. We conclude that at least two distinct neural mechanisms drive the acquisition of pursuit learning over 100 to 1,000 trials (3 to 30 min). Both mechanisms generate underlying memory traces that are modulated in relation to the gain of pursuit initiation before expression in the final motor output.

NEW & NOTEWORTHY We show that cerebellum-dependent direction learning in smooth pursuit eye movements grows in at least two components over 1,100 behavioral learning repetitions. One component grows over tens of trials and the other over hundreds. Within trials, learned temporal specificity gradually improves over hundreds of trials. The expression of each learning component on a given trial can be modified by external factors that do not affect the underlying memory trace.

INTRODUCTION

The brain receives input from external stimuli and generates an appropriate behavioral response. Because both the environment and individual organism change over time, so too must the motor commands required to generate an appropriate response. Motor learning, spanning a large variety of sensory modalities and motor outputs, depends on the cerebellum (Carey 2011; Christian and Thompson 2003; Gilbert and Thach 1977; Jörntell and Ekerot 2002; Lisberger 1994; Medina and Lisberger 2008; Thompson 2013). Motor learning itself is measured and defined behaviorally, whereas the root mechanisms responsible are changes in neurons and synapses called plasticity (Yang and Lisberger 2014).

The ultimate goal in the study of cerebellar motor learning is to find causal relationships between the relevant neural plasticity processes and the resulting behavioral learning by linking the possible sites and mechanisms of neural learning in the cerebellum to multiple aspects of learning in motor behavior. To do this we are using smooth pursuit eye movements as a model system because it is a particularly well studied and tractable cerebellar motor learning system (Kahlon and Lisberger 2000; Medina and Lisberger 2008, 2009; Yang and Lisberger 2013; 2014). Smooth pursuit behavior allows us to go beyond previous comparisons of behavior before vs. after learning (Boyden et al. 2004; Lisberger 1994; Thompson 2013) and study motor output during the learning process. In the present paper, we use the quantitative analysis of behavior to outline new constraints on how cerebellar learning works, as a prelude to cerebellar recordings to establish neural mechanisms. We use learning blocks with over 1,000 trials to identify two new features of pursuit learning that require elucidation by neural recordings: multiple components with different trial courses of acquisition and modulation of the expression of learning in relation to the strength of pursuit initiation.

Several forms of cerebellar motor learning exhibit multiple components (Boyden et al. 2004; Ethier et al. 2008; Lee and Schweighofer 2009; Raymond and Lisberger 1996; Smith et al. 2006; Yang and Lisberger 2013, 2010, 2014). Force field and saccade adaptation learning rates support a two-state model with a fast learning component and a slow learning component (Ethier et al. 2008; Smith et al. 2006), where the fast component is more labile than the slow component. In classical conditioning of the eyelid response, there is support for the theory that the basic response is learned in the deep cerebellar nuclei, whereas learned timing occurs in the cerebellar cortex (Krupa et al. 1993; Medina et al. 2000; Perrett et al. 1993). In the vestibulo-ocular reflex, there is considerable evidence of different components and mechanisms of plasticity for gain increase vs. decrease learning (Boyden et al. 2004; Voges et al. 2017) and for the suggestion that learning occurs first in the cerebellar cortex and then is at least partly transferred to the deep cerebellar nuclei (Boyden et al. 2004; Lisberger 1994; Miles and Eighmy 1980; Miles and Lisberger 1981). Thus the multiple mechanisms of cerebellar learning (Carey 2011; Gao et al. 2012; Glickstein et al. 2009; Hansel et al. 2001; Lisberger 1994; Thompson 2013) seem to support multiple components of learning (e.g., at least fast and slow learning components).

Cerebellar motor learning can also show an ability of context to modulate learning. In the pursuit system, for example, the size of the reward modulates a monkey’s smooth pursuit eye movements so that the expression of learning is enhanced for larger rewards without any effect on the time course or magnitude of learning acquisition (Joshua and Lisberger 2012). If learning occurs in the cerebellar cortex, then this modulation also must occur in Purkinje cells, or at least within the positive feedback pathway that transmits eye velocity signals to Purkinje cells (Lisberger and Fuchs 1978). In classical conditioning of the eyelid response, running speed modulates both the acquisition and expression of the conditioned eye blink, and the site of the modulation appears to be in the cerebellar cortex (Albergaria et al. 2018). Now, we find effects that may represent an additional example of modulation of the expression of learning.

Our goal is to establish the dynamics of the acquisition and expression of motor learning both across individual movements and within each motor response. We have taken advantage of the smooth pursuit system to increase the number of learning repetitions 5- to 10-fold over prior research in carefully controlled behavioral experiments. We present three major results that both affirm previous cerebellar learning models using the pursuit system and identify novel aspects of cerebellar motor learning. 1) We characterize multiple learning components that evolve over short and long trial courses in smooth pursuit eye movements. 2) We reveal the late emergence of a gradual improvement in the temporal specificity of learning within individual behavioral repetitions. 3) We show that the expression of the learned response on any given trial, but probably not its acquisition, is correlated with the gain of pursuit initiation. Our results place constraints on the timescale, trial course, temporal dynamics, and circuit location of the memory mechanisms that lead to cerebellum-dependent pursuit learning.

METHODS

Two adult male rhesus monkeys (Macaca mulatta; 11–13 kg) served as subjects in these experiments. Animals were cared for in accordance with National Institutes of Health Guide for the Care and Use of Laboratory Animals. The Institutional Animal Care and Use Committee at Duke University approved all experimental procedures. Before experiments, we used sterile procedure with monkeys under general anesthesia to 1) implant a head holder to keep the head stable during experiments and 2) suture an eye coil to the sclera (Ramachandran and Lisberger 2005) to monitor eye position (Robinson and Fuchs 1969). Monkeys were well trained to perform smooth pursuit eye movement tasks and acquired substantial experience with the tasks before data collection began.

Behavioral task.

Visual stimuli were presented at a refresh rate of 85 Hz on a 20-in. cathode ray tube monitor positioned 30 cm from the monkey’s eye. The monitor’s horizontal and vertical spatial resolution was 1,280 × 1,024 pixels subtending a visual field of 59° × 47°. A computer running our laboratory’s “Maestro” software controlled experimental stimuli and task timing. Each trial began with the presentation of a black central fixation spot (0.5° diameter, luminance ~0 cd/m²) on a light gray background (luminance 20.29 cd/m²). Monkeys fixated the spot within a 2° fixation window for a randomly selected interval with a duration between 1,000 and 1,500 ms. After fixation, targets moved according to a step-ramp paradigm (Rashbass 1961) using a 2–4° eccentric step and 20°/s target motion speed. We refer to the direction of initial target motion, immediately after the step, as the “pursuit direction.” During baseline trials, the target spot continued to move along the pursuit direction at 20°/s for 650 ms. The target then jumped an additional 1.5° to prevent backward saccades before target motion stopped and monkeys fixated the spot for an additional 600 ms. Animals were required to track the moving target and then fixate the stationary target within a 4° window to receive a liquid reward.

We used a smooth pursuit directional learning paradigm to induce learned behavior (Medina et al. 2005). During learning trials (Fig. 1), the initial target motion in the pursuit direction was identical to that in baseline trials. Then, 250 ms after target motion onset, an orthogonal 30°/s motion component was added to the target direction. We refer to the added orthogonal motion as the “instruction” and its direction as the “learning direction.” The instruction in the learning direction persisted for 400 ms and was followed by the target jump and final 600-ms fixation interval. On learning trials, target tracking windows were not enforced between target motion onset and the first 300 ms of the instruction interval so that any learned eye movements that deviated from the target were not punished.

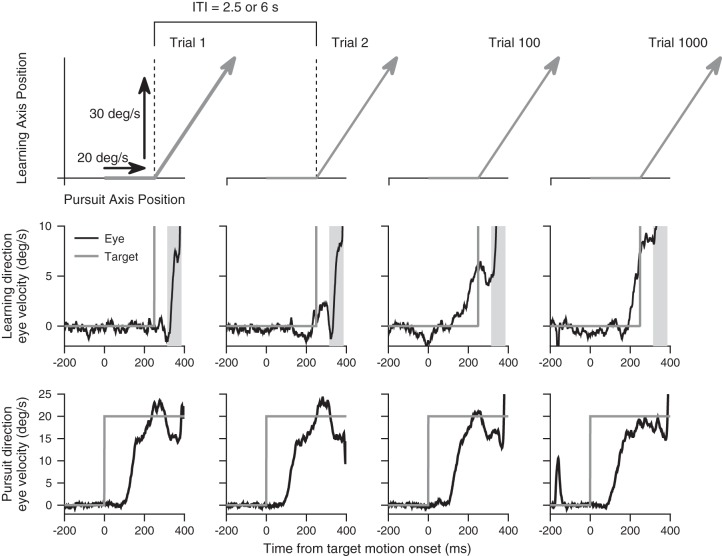
Fig. 1.

The repeated-direction learning paradigm induces learning over 1,000 trials. Top row: schematics illustrate target motion during learning trials. Gray arrows illustrate the trajectory of target position, first along the pursuit axis at 20°/s and then diagonally after a 30°/s motion component is added along the orthogonal learning axis. Dashed vertical lines indicate the time of the instructive change in target direction, 250 ms after the onset of target motion. The time between the dashed vertical lines defines the intertrial interval (ITI). Middle row: black and gray traces show eye and target velocity traces in the learning direction from individual trials at different times during a learning block. The target velocity is 30°/s in the learning direction and therefore goes off scale. Gray shading indicates the time when visual feedback about the direction change is available. Bottom row: same as middle row, but for eye and target velocity in the pursuit direction.

The instruction on one trial caused learning that we probed on subsequent trials, including on the next trial. As part of our experimental design, the time between the learning direction instruction on one trial and the test for the presence of learning on the following trial was a controlled variable. We refer to this duration as the “instruction-test interval” (ITI). The learning trials described in the previous paragraph have a duration of 2,250–2,750 ms, which creates an average ITI of 2.5 s. We created a second type of learning trial that occurred after an average ITI of 6 s by adding 3,500 ms to the duration of the initial fixation, before the onset of target motion in the pursuit direction. An additional drop of liquid reward was given for every 2,500 ms of fixation during 6-s-ITI trials to keep the reward rate comparable to the shorter 2.5-s-ITI trials.

Experimental paradigms.

We began each data collection session by choosing a pursuit axis and an orthogonal learning axis. Direction choices were always along the four cardinal axes and were different for every daily session. At the beginning of each session, we ran a block of 50 baseline trials in the pursuit direction to establish a baseline measure of eye velocity responses before learning began. On some days, we ran multiple learning blocks. When we did so, we alternated the pursuit and learning directions between each block of learning trials, along the axes chosen for the experimental session.

We used two basic block structures for the repeated-direction learning trials. 1) Blocks consisted of 2.5-s-ITI learning trials with 6-s-ITI probe trials inserted every 10th trial. These blocks consisted of 1,100 trials. 2) Blocks consisted of 6-s-ITI learning trials with 2.5-s-ITI probe trials inserted every 10th trial. These blocks consisted of 500 trials. In both cases we refer to trials following the predominate ITI in a block as learning trials and to those following the minority ITI as probe trials.

In a subset of experiments, we used two additional block structures to increase our sampling of learning on probe trials during the rapidly evolving early learning. 1) Blocks consisted of 100 trials with an ITI of 2.5 s, but with 6-s-ITI probe trials inserted every 10th trial beginning after the first 30 trials. 2) Blocks consisted of 1, 2, 3, 5, 7, 10, 15, or 20 trials with an ITI of 2.5 s followed by a single probe trial with an ITI of 6 s. To wash out learning and recheck the baseline responses, we ran a block of 10–20 baseline trials between learning blocks. The same block structures were used to sample early learning during 6-s-ITI trials with 2.5-s-ITI probes.

Finally, we collected data during five sessions of the random learning paradigm. In this paradigm, the pursuit direction is fixed but the learning direction is chosen randomly on each trial from one of the two possible directions along the learning axis (Yang and Lisberger 2014). The purpose of this block structure is to prevent long-term learning while collecting many repetitions of the effects of single-trial learning. The random paradigm was run in sessions of 500–1,200 trials with 2.5- and 6-s ITIs randomly interleaved.

Data acquisition and analysis.

Voltage signals from a magnetic search coil system provided a measure of horizontal and vertical eye position and were differentiated by an analog circuit to create voltages proportional to horizontal and vertical eye velocity. The circuit differentiated frequencies below 25 Hz and filtered out frequencies above 25 Hz (−20 dB per decade). Voltages were sampled at 1 kHz on each channel and stored for offline analysis. Saccades were detected as times when eye acceleration exceeded 1,000°/s² or eye velocity exceeded 30°/s. Times from 20 ms before to 20 ms after data exceeded these criteria were marked as saccades. Except where noted otherwise in the text, trials with saccades that overlapped a window from 50 to 300 ms after target motion onset were removed from all analyses to ensure that saccades were not present on any trials during any of the analysis epochs.

We measured average eye velocity in the learning direction to quantify learning. During the repeated learning paradigm, learned eye velocity was computed in one of two analysis epochs as the average eye velocity during learning trials minus the average eye velocity during the final 10 trials of the preceding baseline block. We adjusted the signs of the data so that positive values of learning indicate eye velocity in the learning direction. We estimated the growth of learning (L) over trials by fitting either a single exponential or a sum of two exponentials to the learned responses:

$$L=A_1\left(1-e^{\frac{T}{{\tau }_1}}\right)$$ (1)

$$L=A_1\left(1-e^{\frac{T}{{\tau }_1}}\right)+A_2\left(1-e^{\frac{T}{{\tau }_2}}\right)$$ (2)

where A_x is the peak magnitude of learning, τ_x is the “trial constant” of learning, and T is the trial number. Exponentials were fitted using maximum likelihood estimation. Fit quality for the single exponential compared with the sum of two exponentials was assessed using a likelihood ratio test. The 95% confidence bounds for parameter estimates and statistical comparisons were calculated from bootstrap distributions of the parameters. To avoid excessively extrapolating the data, we placed an upper bound of 2,000 for values of τ_x.

When we wanted to analyze only changes over trials, rather than quantify learning rates and magnitudes, we used analysis of covariance (ANCOVA). In these analyses the ratio variable was trial number with additional factors of experimental session and ITI. This procedure allows us to statistically assess changes over trials and differences between ITIs while controlling for behavioral differences between experimental sessions. The dependent variable was either pursuit gain (Fig. 3) or learning response for trials after the 150th trial in a learning block (Fig. 5).

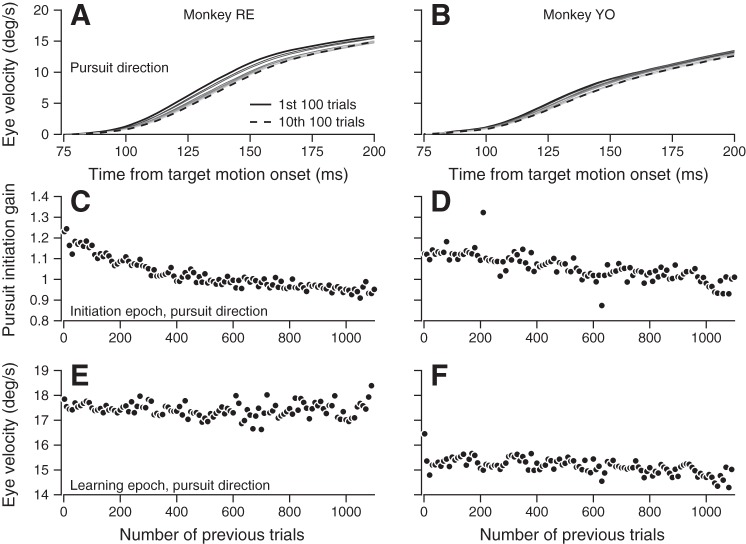
Fig. 3.

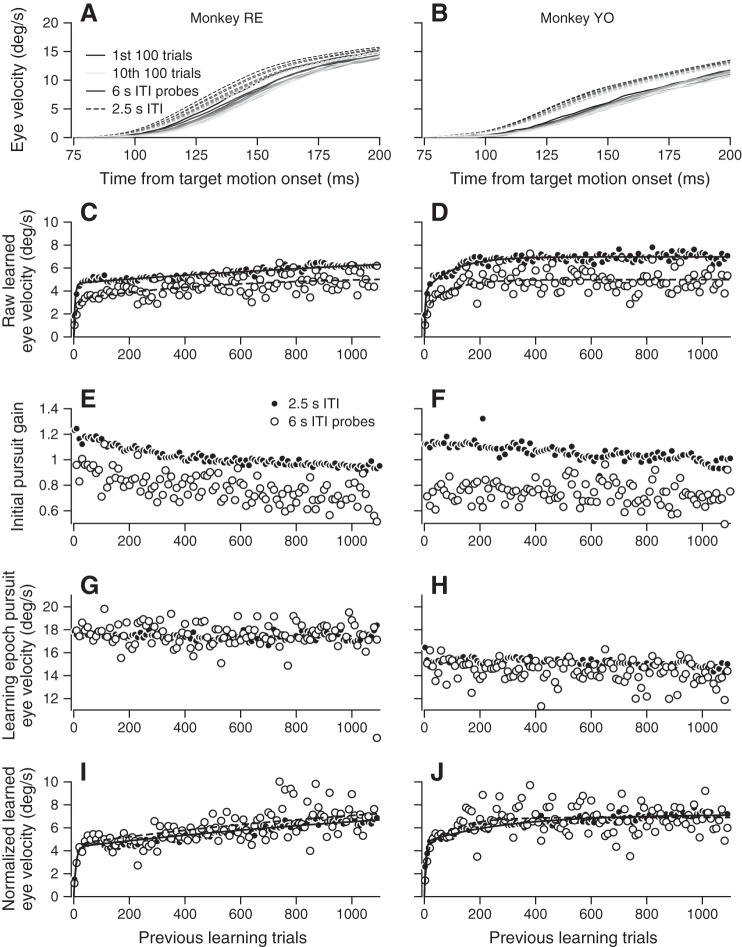
Initial pursuit eye velocity varies systematically over 1,100 learning trials. A and B: pursuit direction eye velocity traces averaged in 100-trial groups across all sessions in each animal. Groups are plotted from the first 100 trials (darkest solid curve) to the last 100 trials (dashed curve), with intermediate trial groups drawn from earliest to latest (darker to lighter). C and D: pursuit initiation gain values calculated from pursuit direction eye velocity traces on each trial are shown as averages in 10-trial bins from across all sessions and trials. E and F: pursuit direction eye velocity during the learning epoch (200–300 ms after target motion onset) averaged in 10-trial bins and across sessions.

Fig. 5.

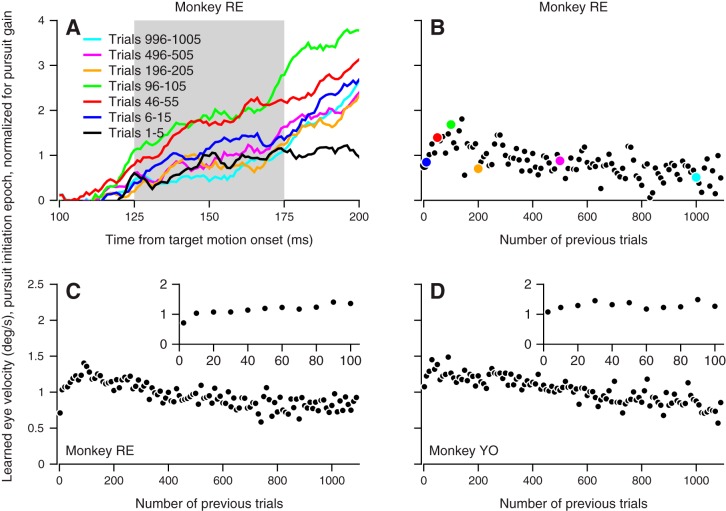
Temporal specificity of the learned response improves over hundreds of trials. A and B: the same single-session example of learning in monkey RE as shown in Fig. 2, A and B. A: average eye velocity in the learning direction is plotted as a function of time for groups of 5 or 10 trials spanning 1,100 trials of the direction learning paradigm. Data are the same as in Fig. 2A, but the time axis has been zoomed to focus on the initiation epoch (gray shading) that immediately follows pursuit onset. B: the trial course of the learned response during the initiation epoch, measured by taking the average of each trace in A (colored circles) during the initiation epoch from 125 to 175 ms after the onset of target motion in the pursuit direction. The average initiation epoch velocities for all other trials (black circles) fill out the remainder of the trial course. Data were averaged in 10-trial bins. C and D: initiation epoch learning trial course for each monkey averaged across all sessions in 10-trial bins. Insets show the same data magnified to reveal early aspects of the trial course.

We measured single-trial learning during the random-direction paradigm similarly to repeated-trial learning with some important differences. We broke the string of trials down into pairs, where the first and second trial in each pair are defined as the “instruction” and “test” trials. Single-trial learning was calculated as the trial-over-trial difference in learning direction eye velocity between the test and instruction trials. The learning direction for each instruction-test pair was defined as the direction of the instructive target motion in the instruction trial. Both trials in the pair were required to be free of saccades in analyses where saccade trials were removed. The learned responses across all trial pairs were rectified so that positive values indicate learning increases in the learning direction before being averaged together over each session separately for 2.5- and 6-s-ITI test trials.

We conducted one analysis on the original data set from Yang and Lisberger (2014), referred to as Y&L 2014. Analyses on this data set were done using session average data from 19 sessions with eye velocity samples collected during saccades treated as missing data (NaN in MATLAB) before averaging over all remaining time points. We performed two additional analyses on a subset of the Y&L 2014 data, referred to as Y&L 1 and Y&L 2. For Y&L 1, learning responses and pursuit gain were calculated for each individual trial separately before being averaged across 12 sessions for statistical analyses. Saccade data were removed by omitting trials with saccades overlapping a window from 50 to 300 ms after target motion onset as done in the rest of our data analysis for the new experiments in this paper. To be included, sessions were required to have at least 15 trials of both 2.5-s ITI (maximum 75) and 6-s ITI (maximum 44). For Y&L 2, learning responses and pursuit gain were again calculated for each individual trial separately before being averaged across 12 sessions for statistical analyses. In this analysis, eye velocity data samples collected during saccades were treated as missing data (NaN in MATLAB) before averaging over all remaining time points, as done in Y&L 2014. To be included, sessions were required to have at least 15 trials of both 2.5-s ITI (maximum 94) and 6-s ITI (maximum 59). Learned eye velocities from Y&L data were calculated as the average in a larger epoch also used by Yang and Lisberger (2014), from 150 to 300 ms after the onset of target motion in the pursuit direction. New single-trial learning data collected in monkey RE were analyzed on individual trials by using saccade trial removal and an average epoch from 200 to 300 ms after target motion onset, as done elsewhere in the present report. Statistical analyses were performed on 715 2.5-s-ITI trials and 572 6-s-ITI pairs of trials pooled across 5 behavioral sessions.

The gain of pursuit initiation was computed separately within each session, and for each trial in that session. First, we averaged eye speed only in the pursuit direction from 50 to 300 ms after target motion onset across all trials in a given session. Next, we found the average pursuit latency as the time at which the average eye speed first exceeded the fixation eye speed by 0.5°/s. We then took a 100-ms segment of the eye speed traces for each trial from 25 ms before to 75 ms after the time chosen as pursuit latency and calculated the average traces in this window over all trials to form an eye speed template. Finally, we computed the gain (G_i) of each individual trial in the pursuit direction from the template speed vector and the individual trial vectors according to the formula:

$$G_i=\frac{ve{l}_i*ve{l}_i}{\overline{vel}*ve{l}_i}$$ (3)

where the $\overline{vel}$ is the average template vector, vel_i is the eye speed vector on the i-th trial, and asterisks indicate the dot product of the two vectors. Placing the dot product of the eye speed vector with itself in the numerator normalizes the gains so that if the speed vector is identical to the template, gain will equal 1. This formula constrains the average gain over all trials within a session to equal 1. Individual trial eye speed vectors that exceed the average template give values of G_i greater than 1, and trial vectors that dip below the template give values of G_i less than 1. Because gain measures were centered on the fixed, trial average behavioral latency, G_i is similarly affected by behavioral latency. Single-trial eye velocity traces that are identical to the average template but shifted later (or earlier) in time will correspondingly give G_i values less than (or greater than) 1. Occasional poor fits produced unusable gain estimates, and these trials were removed from analysis.

We estimated single-trial behavioral pursuit latency by a computation performed on the eye velocity in each individual trial (Lee et al. 2016). For sliding 100-ms windows centered 50 to 150 ms after target motion onset, we used Eq. 3 to calculate the gain relative to the average eye velocity template and then multiplied gain by the eye velocity in the current window. This yielded an eye velocity trace that had been corrected for differences in gain relative to the eye velocity template. We computed the squared error between the average eye velocity template and the gain-corrected eye velocity trace in each window and found the window that yielded the least squared error. The difference between the temporal offset of the window with the least squared error and the average pursuit template latency was taken as the pursuit latency for each trial.

RESULTS

We have used quantitative analysis of behavior to characterize multiple components in the neural mechanisms of direction learning for smooth pursuit eye movements. Unlike previous studies of this learning behavior, which followed learning over sequences of 100–200 trials, we have measured the evolution of learning over 500–1,100 trials, a strategy that revealed multiple components of learning with multiple trial courses. We also have been careful to distinguish the acquisition of learning from the expression of learning by normalizing for one apparent modulator of the expression of learning, namely, the overall gain of pursuit initiation on each trial.

Two trial courses of learning.

The example traces in Fig. 1 show how learning evolves over 1,100 trials. In each trial, the change in target direction is indicated by the step of target velocity in the learning direction (middle row) and by the angle in target position trajectory (top row) at time 250 ms. In trial 1 (first column), the instruction causes an eye velocity in the learning direction that is purely reactive and responds to the instruction with a latency of ~75 ms. We have indicated the interval that contains the visually driven component of the response by shading and repeated the same shading in all 4 trials in Fig. 1. In trial 2 (second column), eye velocity in the learning direction already shows a small transient that precedes the visually driven eye velocity. By trial 100 (third column), the nominal end of most previous studies of this form of behavioral learning, eye velocity in the learning direction shows a fairly strong response that anticipates the change in target direction and reaches a peak of 5°/s at the time of the learning instruction. Finally, in trial 1,000 (fourth column), the learned response that precedes the visually driven response has gotten still larger, reaching a peak of close to 10°/s. It also has become more constrained temporally, as if part of the later component of learning involves tuning an initially broad learned response so that it is more selective for the time of the change in target direction.

The progression of learning appears more clearly when we plot within-trial averages of eye velocity in the learning direction as a function of time for trials at different stages during a learning block (Fig. 2A). Here, we show data only up to 50 ms after the change in target direction so that the entire non-zero eye velocity is due to learning rather than direct visual drive. Traces are averages across 10 consecutive trials (except trials 1–5) so that comparison of the different traces reveals details of the trial course of learning. In the shaded area, defined as the “learning epoch” because it represents a 100-ms interval surrounding the instructive change in target direction, learned eye velocity is present already in the first 5 learning trials and increases steadily throughout 1,100 trials. We also note a learned response in the interval before the learning epoch, from 125 to 175 ms after the onset of pursuit target motion. We call this interval the “pursuit initiation epoch” because it coincides more or less with the initiation of tracking in the pursuit direction defined by the initial target motion. The learned response in the pursuit initiation epoch peaks after ~100 learning trials and then declines throughout the remainder of the learning block.

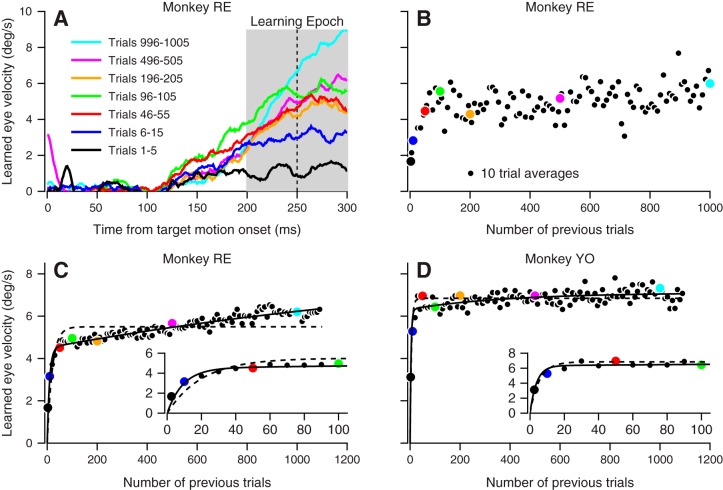
Fig. 2.

Two components of pursuit learning. A: average eye velocity is plotted as a function of time for groups of 5 or 10 trials spanning the 1,000 trials of an example learning block in monkey RE. Vertical dashed line indicates the time of the instructive change in target direction. Gray shading indicates the learning epoch, 200–300 ms after the onset of target motion in the pursuit direction. B: the trial course of learning for the same example learning block. Each symbol is the average eye velocity in the learning direction across the learning epoch. Colored circles refer to the traces in A, and black circles show all other groups of 10 trials. C and D: learning trial course for each monkey averaged across all sessions in 10-trial bins. Color conventions are the same as in A and B. Dashed curves show a single-exponential maximum likelihood fit to the data, and solid curves show the sum of two exponentials fit to the data (see also Table 1). Insets show the same data magnified in time to reveal early features of the trial course.

The trial course of learning implies that learning comprises at least two components that develop over short vs. long trial courses. To quantify how the components of learning evolve and contribute to the learned response over 1,000 trials, we summarized the learned eye velocity in each trial by calculating the mean eye velocity during the learning epoch, from 50 ms before to 50 ms after the instructive change in target direction (Fig. 2A, shading). We then averaged across each set of 10 consecutive trials to plot trial courses for learning (Fig. 2B). The learning curve for a single experiment in monkey RE (Fig. 2B) and the average learning curves over all sessions for both monkeys (Fig. 2, C and D) show that the learned response grows over two distinct trial courses. The first component rises rapidly, whereas the second component continues to grow slowly throughout the entire trial sequence. Fits to the data show that a sum of two exponentials (Eq. 2) is better able to account for the trial course of learning than is a single exponential (Eq. 1). The likelihood-ratio test reveals statistically better fits for the sum of two exponentials in both monkeys (monkeys RE and YO: both P < 0.0001). The early learning component grows over tens of trials and accounts for a majority of the learned response measured even after 1,100 trials. The second component grows over hundreds of trials and contributes less to the learned response over the 1,100-trial experiment (A₁ > A₂ in Table 1). The existence of two exponentials in the trial course of learning implies that there are at least two neural mechanisms for directional pursuit learning but does not demonstrate that either mechanism has an exponential trial course.

Table 1.

Parameter estimates for the two components of learning using 2.5-s-ITI trials for learning acquisition with 6-s-ITI probes

	2.5-s-ITI Trial, Value	2.5-s-ITI Trial, 95% CI	6-s-ITI Probe, Value	6-s-ITI Probe, 95% CI
Monkey RE, raw
A1	4.57	4.51–4.63	3.80	3.58–4.01
τ1	7.60	7.22–8.02	9.91	7.76–12.55
A2	4.17	3.71–4.40	2.99	1.27–3.86
τ2	2,000	1,672–2,000	2,000	572–2,000
Monkey YO, raw
A1	3.99	3.81–4.19	2.57	1.76–3.22
τ1	3.26	2.85–3.72	7.02	3.78–10.29
A2	2.98	2.80–3.16	2.42	1.78–3.23
τ2	105	91.9–122	93.2	61.2–146
Monkey RE, gain normalized
A1	4.28	4.22–4.34	4.56	4.29–4.84
τ1	6.93	6.55–7.33	9.48	7.41–11.9
A2	5.83	5.55–6.09	6.62	5.07–8.03
τ2	2,000		2,000
Monkey YO, gain normalized
A1	4.31	4.09–4.50	4.16	3.10–5.01
τ1	4.18	3.65–4.68	7.60	4.84–10.2
A2	2.67	2.54–2.86	2.75	1.87–3.83
τ2	192	151–249	103	64–181

Parameter estimates were calculated from maximum likelihood estimates according to Eq. 2 using data from all valid trials from all sessions. Confidence bounds were derived from bootstrap distributions of parameters. Estimates are shown for learning curves fit to each monkey and each intertrial interval (ITI) separately. Monkey RE: from 1,100 trial learning blocks, 10 sessions with 6,084 2.5-s-ITI trials and 431 6-s-ITI probes; from 1–100 trial learning blocks, 10 sessions with 2,749 2.5-s-ITI trials and 293 6-s-ITI probes. Monkey YO: from 1,100 trial learning blocks, 9 sessions with 7,038 2.5-s-ITI trials and 565 6-s-ITI probes; from 1–100 trial learning blocks, 14 sessions with 3,351 2.5-s-ITI trials and 658 6-s-ITI probes.

Modulation of the expression of learning.

Analysis of learning over sessions of 1,100 trials raises the question of whether the system is entirely stationary. Over the passage of time across trials, both fatigue and fluctuations in behavioral performance and motivation might alter the expression or acquisition of learning. For example, inspection of our data revealed a consistent trend in the initiation of smooth eye movement in the pursuit direction across a 1,100-trial learning block. Pursuit initiation progressively weakened in both monkeys (Fig. 3). The decrease appears as a reduction in the gain of initial pursuit eye velocity across groups of 100 trials (Fig. 3, A and B; different traces show the eye velocity of pursuit initiation in the first 100 trials in the learning block, in the 10th group of 100 trials, and for successive groups of 100 trials.

The steady decrease in the gain of pursuit initiation appears in plots of the trial course of pursuit initiation gain, based on averages across groups of 10 consecutive trials (Fig. 3, C and D; ANCOVA main effect of trial for monkeys RE and YO: both P < 0.0001). We computed gain using the approach outlined in methods, where eye velocity during the initiation of pursuit in each trial is expressed as gain times the eye velocity averaged across all the trials in the learning block. In contrast to the results for the initiation of pursuit, the average eye velocity in the pursuit direction during the later learning epoch remained relatively stable (Fig. 3, E and F). We attribute the steadiness of the later interval, despite the clear decline in the gain of pursuit initiation, to the closed-loop, feedback configuration of the pursuit system. Negative feedback would use visual motion information to compensate in later analysis intervals for the loss of gain in the first 100 ms of the response and would bring eye speed up to target speed even if the gain of visual-motor mechanisms remained low.

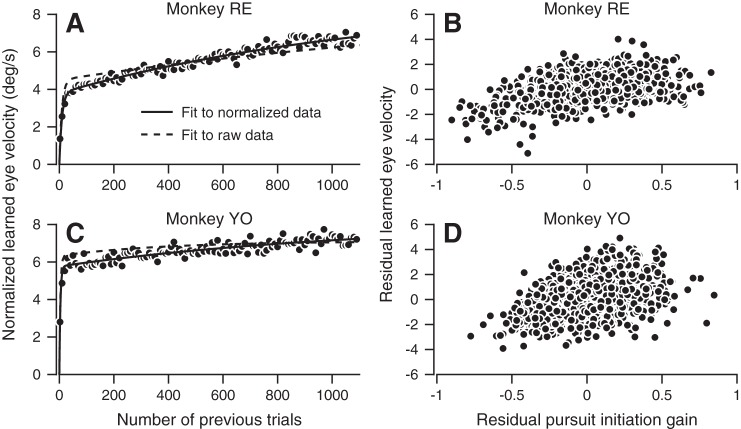
The steady decline in the gain of pursuit initiation across a learning block provoked us to ask whether there might be a relationship between pursuit initiation gain and the expression of learning on each trial. To test for such a relationship, we removed the effect of trial number on both learning and pursuit initiation gain by computing the residuals of the raw learned response relative to the sum of two exponentials fit to the data. We plotted these residuals as a function of the residuals for the gain of pursuit initiation computed relative to an exponential fit to gain as function of trials (as in Fig. 3, C and D). The plots (Fig. 4, B and D) show a clear correlation between the expression of learning and the gain of pursuit initiation (monkey RE: r = 0.41, P < 0.0001; monkey YO: r = 0.38, P < 0.0001). Because the correlation is independent of trial number, we conclude that these two measures are related, meaning that either 1) gain affects the expression of learning or 2) both measures are affected by a common external factor. We conclude that in the rest of the paper, we should account for systematic gain fluctuations to accurately measure learning components.

Fig. 4.

Trial-by-trial relationship between learned eye velocity and initiation gain and its effect on the estimate of early and late learning components. A and C: learned eye velocities normalized by dividing the learned eye velocities on the individual trials by the gain of pursuit initiation on individual trials. Data were averaged in 10-trial bins. Fitted curves show the sum of two exponentials fit to the normalized data (solid curves) and to the raw data (dashed curves) from Fig. 2 for comparison (see also Table 1). B and D: plots of residual learned eye velocity as a function of residual pursuit initiation gain. Each symbol plots data from an individual trial in a single example session. Learned eye velocity residuals were computed as the difference between the learned response on each trial and the sum of two exponentials fit to the data. Pursuit initiation gain residuals were computed as the difference between the gain in each single trial and a decaying exponential fit to all data over trials.

Next, we asked whether the relationship between pursuit initiation gain and the expression of learning could affect our conclusions about the trial course of acquisition of the early and late components of the underlying memory. To quantify the potential effect, we normalized the learned eye velocity for the gain of pursuit initiation on each trial (details in methods) and plotted new trial courses (Fig. 4, A and C). Even after normalization, the trial courses showed multiple learning components and were fitted better with the sum of two exponentials (monkeys RE and YO: both P < 0.0001, likelihood-ratio test). Gain normalization reduced the amplitude of the rapid learning component and increased the amplitude of the slow component (Table 1).

Learning of temporal specificity.

Analysis of the learned eye velocity traces on a finer time base (Fig. 5A) reveals improvement in the temporal specificity of the learned eye velocity response across trials in a learning block. In the first 100 trials, a learned response appears in the pursuit initiation epoch, from 125 to 175 ms after the onset of pursuit target motion (shading in Fig. 5A), and grows quickly to a maximum (traces in Fig. 5A). After 100 trials, learned eye velocity in the pursuit initiation epoch begins to decrease steadily over trials, reaching a minimum after 1,100 trials. Quantitative analysis of learning-direction eye velocity in the pursuit initiation epoch reveals an early increase followed by a steady decline across trials in an example experiment (Fig. 5B) and in averages across sessions in both monkeys (Fig. 5, C and D; ANCOVA main effect of trial from trials 150–1,100 for monkeys RE and YO: both P < 0.0001). The decline contrasts with the steady increase in learned eye velocity over trials in the learning epoch (Fig. 4).

The decay of the learned response in the pursuit initiation epoch was not accounted for by the systematic decrease of pursuit gain over trials. Decay from trials 100–1,100 of eye velocity in the pursuit initiation epoch is seen even though the data in Fig. 5, C and D, have been normalized for pursuit initiation gain, a procedure that will mute, rather than accentuate, the trial course of decline in learned eye velocity in the pursuit initiation epoch. Together, the data in Figs. 4 and 5 show that after ~100 trials, the learned eye velocity in the pursuit initiation epoch decays, whereas the eye velocity during the learning epoch grows. As learning begins, the learned response lacks temporal specificity and is implemented immediately following pursuit onset. Learned temporal specificity develops slowly over hundreds of trials, perhaps as part of the slow component of pursuit learning.

Mechanism of smaller learned responses after an ITI of 6 s.

Based on the demonstration by Yang and Lisberger (2010, 2014) that single-trial pursuit learning is smaller after a 6-s ITI vs. a 2.5-s ITI, we began this project with the hypothesis that the rapid decay of the learned response over 6 s was due to the lability of the underlying memory trace. Furthermore, we expected that probing learning with a 6-s ITI might allow short-term, single-trial learning mechanisms to decay to zero, revealing the properties of long-term learning measured after hundreds of trials. We found that ITI affects the magnitude of the learned response at long trial scales, but the explanation for this effect is completely different from our prediction.

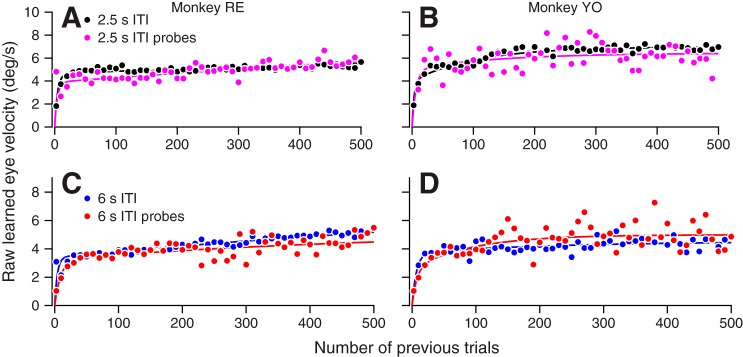
As expected from previous results on single-trial learning, the learned eye velocity in the learning epoch was smaller following a 6-s ITI vs. a 2.5-s ITI (Fig. 6, C and D), but the trial constants of learning appear similar regardless of ITI. These data were obtained by inserting 6-s-ITI probe trials in blocks principally composed of 2.5-s-ITI learning trials (see methods). We then pooled the data from all blocks configured with 2.5-s-ITI learning trials and 6-s-ITI probe trials and plotted the data in 10-trial bins separately for each ITI. We compared the learning curves by fitting a sum of two exponentials to data from each ITI (Table 1). Just like the 2.5-s-ITI learning curves, the fitted learning curves for 6-s ITI probe trials show two components: a rapidly rising component and a slowly growing component (monkeys RE and YO: both P < 0.0001, likelihood-ratio test). The learning components obeyed a similar trial course for the 2.5- and 6-s-ITI trials, yet the magnitude of learned eye velocity for both components is much lower for the 6-s ITI probe trials. These raw learning curves suggest that 6-s-ITI probe trials reduce the learned eye velocity response but do not affect the underlying learning component trial courses.

Fig. 6.

Changes in the gain of pursuit initiation can account for the effect of intertrial interval (ITI) on the expression of pursuit learning. A and B: pursuit direction eye velocity traces as a function of time averaged in 100 trial groups across all sessions in each animal. Solid curves plot pursuit eye velocity for 6-s-ITI probe trials, and dashed curves depict the more frequent 2.5-s-ITI trials. Trial groups are illustrated in progressive shades of gray from darkest to lightest. C and D: measured learning trial courses for each monkey averaged across all sessions in 10-trial bins. Filled circles show data for 2.5-s-ITI trials, and open circles indicate data from 6-s-ITI probe trials. Solid curves display maximum likelihood fits of the sum of two exponentials for the 2.5-s-ITI trials, and dashed curves show the same for 6-s-ITI probe trials. E and F: pursuit initiation gain values calculated from the pursuit direction eye velocity traces averaged in 10-trial bins across all sessions. G and H: average pursuit direction eye velocity during the learning epoch (200–300 ms after target motion onset) for each trial and session averaged in 10-trial bins. I and J: symbols plot the learning trial course in each monkey after normalization for the gain of pursuit initiation and averaged across all sessions in 10-trial bins. Conventions are the same as in C and D.

We also noted that the gain of pursuit initiation varied quite dramatically between the trials that followed ITIs of 2.5 vs. 6 s. To obtain the traces of time-varying eye velocity in Fig. 6, A and B, we combined trials in groups of 100 across each session and plotted the average pursuit direction eye velocity of each group separately for 2.5- and 6-s-ITI trials. The most striking finding is the large difference between the 6-s-ITI probe trials and the 2.5-s-ITI trials: in Fig. 6, A and B, the solid traces lie below the dashed traces for every 100-trial group in both monkeys. Within each ITI, the gain of pursuit initiation decreased from the first group of trials (dark curves) to the last group (light curves). The effects of both trial number during a learning block and ITI appear in the analysis of the trial course of the gain of pursuit initiation in bins of 10 trials (Fig. 6, E and F). Here, we plot the average gain in 10-trial bins over all sessions separately for each ITI. Gain is lower for 6-s-ITI probe trials throughout the trial course of learning and decreases gradually across a session for both ITIs (ANCOVA main effect of ITI and trial for monkeys RE and YO: both P < 0.0001). The effect of a 6-s ITI on pursuit gain is therefore separable from the gain decrease that we documented across trials within a session. In contrast, eye velocity in the pursuit direction reaches comparable levels by the time of the learning epoch for both 2.5-s-ITI trials and 6-s-ITI probe trials (Fig. 6, G and H).

The effect of ITI on the gain of pursuit initiation can account for the parallel effects on the magnitude of the learned eye velocity. For each individual trial, we normalized the learned eye velocity in the learning epoch by dividing by the gain of pursuit initiation on that trial. Normalization eliminated any tangible learning differences between 2.5- and 6-s-ITI trials (Fig. 6, I and J). A model representing the sum of two exponentials gave good fits to the normalized data from each ITI and revealed that the trial constants and amplitudes of the learning curves were not distinguishable for ITIs of 2.5 vs. 6 s (Table 1). This analysis confirms that pursuit initiation gain is sufficient to account for the difference in the expression of learning between 2.5- and 6-s-ITI trials in both monkeys.

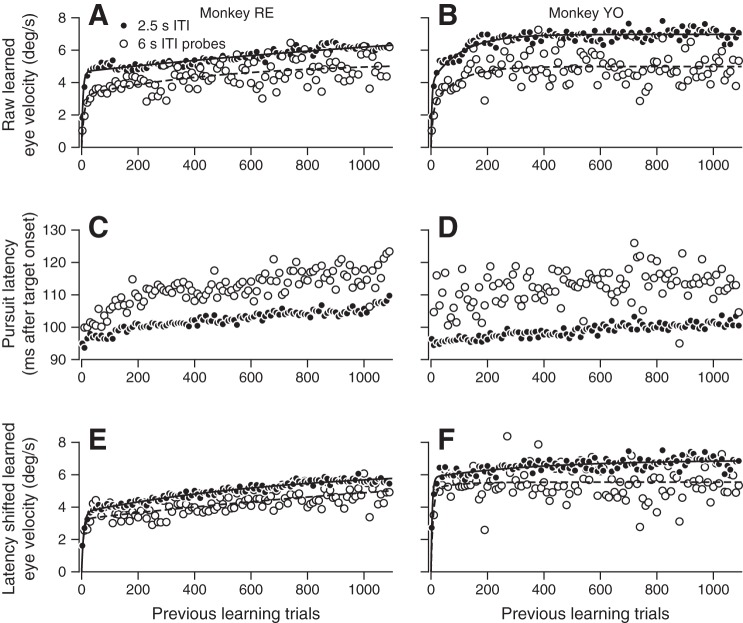
Next, we tested the alternative possibility that systematic shifts in the latency of pursuit initiation and learning expression might account for the differences in learning for ITIs of 2.5 vs. 6 s. Using the same data shown in Fig. 6, we found that pursuit onset latency increases during the trial course of learning and is greater for 6-s-ITI probe trials (Fig. 7, C and D). To test whether these latency discrepancies could account for the observed learning differences, we measured the learned response on each trial from 100 to 200 ms after pursuit onset on that trial, instead of 200–300 ms after target motion onset. This window roughly corresponds to our standard epoch relative to target motion onset.

Fig. 7.

Pursuit latency is insufficient to account for the effect of intertrial interval (ITI) on the expression of pursuit learning. A and B: the same data and graphs as in Fig. 6, C and D. C and D: pursuit onset latency relative to target motion onset averaged in 10-trial bins across all sessions. E and F: plots of the trial course of learning in each monkey averaged across all sessions in 10-trial bins, adjusted by measuring learning in a time window that was fixed relative to pursuit onset latency in each trial.

Plotting the resulting learning curves (Fig. 7, E and F) demonstrates that the effect of latency shifts on our target-aligned learning epoch are small and are unable to account for the learning differences. Our measure of the gain of pursuit initiation, which is scaled by trial-to-trial fluctuations in both gain and latency, does a much better job of accounting for the difference in learning between 2.5- and 6-s-ITI trials (Fig. 6). As a final control, we used an approach similar to that of Lee et al. (2016) to estimate gain and latency separately and obtained results identical to those for the fixed-latency gain measure, but with more parameters and greater complexity. We therefore chose to quantify learned eye velocities during the target motion-aligned learning epoch and normalize on the basis of the single measure of the gain of pursuit initiation, which we regard as a sufficient proxy for the extrinsic factors affecting pursuit learning in our experiments.

Additional evidence that pursuit gain affects learning expression.

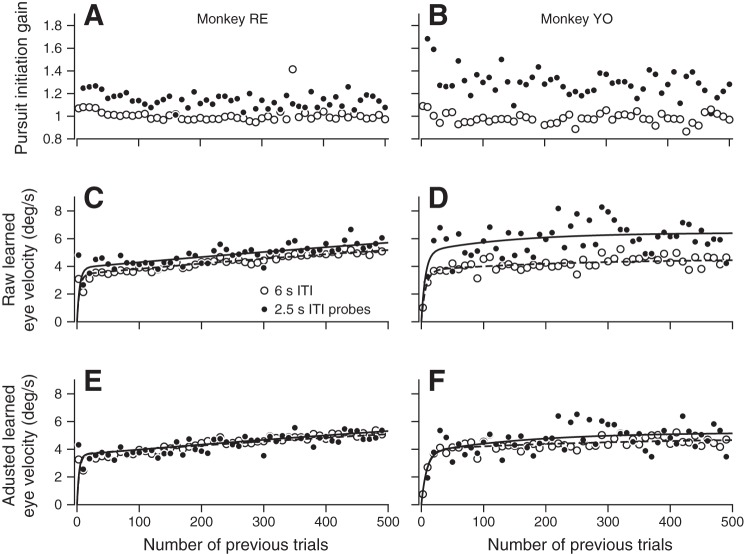
We addressed the relationship between pursuit gain and learning expression further by running learning blocks with an inverted sequence of ITIs. These learning blocks comprised 500 direction learning trials using a 6-s ITI with probe trials after an ITI of 2.5 s inserted every 10th trial. We also sampled early learning in short blocks with more frequent probes. As before, 2.5-s-ITI probe trials exhibited higher pursuit initiation gain than did 6-s-ITI learning trials across the entire trial course of learning (Fig. 8, A and B). Also, the trial courses of learning expression with 6-s-ITI learning and 2.5-s-ITI probe trials matched our previous results (Fig. 8, C and D). Learning curves calculated from both ITIs show at least two components and are fitted best with a fast trial course and a slow trial course progressing across the session (Table 2). As before, the effect of ITI on the magnitude of the learned eye velocity ran in parallel with the gain of pursuit initiation. Learning for 2.5-s-ITI probe trials was consistently greater than learning on 6-s-ITI trials across both learning components, but the trial courses were largely independent of ITI (Table 2). The difference in the measured learned eye velocity between the 2.5-s-ITI probe trials and 6-s-ITI trials disappeared when we normalized for differences in pursuit initiation gain (Fig. 8, E and F, and Table 2).

Fig. 8.

Expression of learning on 2.5-s-intertrial interval (ITI) probes during learning with 6-s-ITI trials. A and B: pursuit initiation gain over the trial course of learning for 500 trials. C and D: measured eye velocity learning trial course of 6-s-ITI trials and 2.5-s-ITI probes. E and F: trial course of normalized eye velocity for 6-s-ITI trials and 2.5-s-ITI probes, normalized by dividing learned eye velocity by the gain of pursuit initiation in each trial. In C–F, dashed and solid curves show the sum of two exponentials fit to the data for 6- and 2.5-s-ITI trials. In A–F, open circles show data for 6-s-ITI learning trials and filled circles show data for 2.5-s-ITI probe trials inserted every 10th trial. Each symbol shows data averaged across all sessions in 10-trial bins.

Table 2.

Parameter estimates for the two components of learning using 6-s-ITI trials for learning acquisition with 2.5-s-ITI probes

	6-s-ITI Trial, Value	6-s ITI Trial, 95% CI	2.5-s-ITI Probe, Value	2.5-s-ITI Probe, 95% CI
Monkey RE, raw
A1	3.41	3.29–3.50	3.90	3.64–4.09
τ1	4.10	3.74–4.44	4.28	3.43–5.07
A2	5.28	2.98–8.32	8.20	2.61–9.57
τ2	1,225	548–2,000	2,000	437–2,000
Monkey YO, raw
A1	3.71	3.05–4.02	5.03	3.88–5.93
τ1	6.81	3.16–10.09	6.52	3.50–10.4
A2	0.83	0.51–2.51	1.40	0.38–2.97
τ2	228	65.7–2,000	144	79.7–1,350
Monkey RE, gain adjusted
A1	3.60	3.52–3.68	3.65	3.44–3.85
τ1	3.26	3.00–3.53	3.89	3.21–4.64
A2	7.76	7.09–8.33	6.51	2.95–7.94
τ2	2,000		2,000	769–2,000
Monkey YO, gain adjusted
A1	3.98	2.96–4.27	3.72	2.78–4.41
τ1	8.87	5.01–12.3	8.38	5.00–12.4
A2	0.87	0.47–3.20	1.49	0.72–2.97
τ2	325	55.7–2,000	165	86.3–1,006

Parameter estimates were calculated from maximum likelihood estimates according to Eq. 2 using data from all valid trials from all sessions. Confidence bounds were derived from bootstrap distributions of parameters. Estimates are shown for learning curves fit to each monkey and each intertrial interval (ITI) separately. Monkey RE: from 500 trial learning blocks, 15 sessions with 4,365 6-s-ITI trials and 536 2.5-s-ITI probes; from 1–100 trial learning blocks, 10 sessions with 1,798 6-s-ITI trials and 260 2.5-s-ITI probes. Monkey YO: from 500 trial learning blocks, 6 sessions with 1,460 6-s-ITI trials and 210 2.5-s-ITI probes; from 1–100 trial learning blocks, 0 sessions and trials.

Pursuit initiation gain affects learning expression rather than acquisition.

The existence of external factors that modify pursuit initiation gain and the expression of learning in parallel raises the question of whether different learning conditions alter the acquisition of learning or only its expression. A hint comes from a comparison of the learned response on identical ITI trials (i.e., matched expression gain) collected during blocks of different ITI trial sequences (i.e., potentially different acquisition gain). Superimposed plots (Fig. 9, A and B) of the raw learning curves for 2.5-s-ITI learning and probe trials show that the magnitude of learning expression is nearly the same whether acquired with a 2.5-s ITI or a 6 s ITI. Comparison of the 95% confidence limits for the fits in Tables 1 and 2 reveals a statistically significant boost in the fast component of learning in monkey RE (0.67°/s, or 13% difference). The same comparison between all 6-s-ITI trials yielded identical results (Fig. 9, C and D). Monkey RE exhibited statistically greater expression of learning (0.39°/s, or 11%) for 6-s-ITI probes vs. 6-s-ITI learning trials for the fast learning component. The rest of the trial courses were largely overlapping and statistically indistinguishable. To draw these conclusions, for example, we compared the fits for the 2.5-s-ITI learning trials in Table 1 with those for the 2.5-s-ITI probe trials in Table 2. The results of this analysis, which compares the expression of learning under uniform test conditions for different acquisition conditions (on different experimental days), conform with expectations if the acquisition of learning is largely independent of ITI.

Fig. 9.

Learning acquisition is largely unrelated to pursuit initiation gain. A and B: black and purple circles show the trial courses of measured raw learned eye velocity for 2.5-s-intertrial interval (ITI) learning trials vs. 2.5-s-ITI probes collected during blocks of 6-s-ITI learning trials. C and D: blue and red circles show the trial courses of measured raw learned eye velocity for 6-s-ITI learning trials vs. 6-s-ITI probes collected during blocks of 2.5-s-ITI learning trials. Each symbol shows data averaged across all sessions in 10-trial bins. Solid curves show the sum of two exponentials fit to the data.

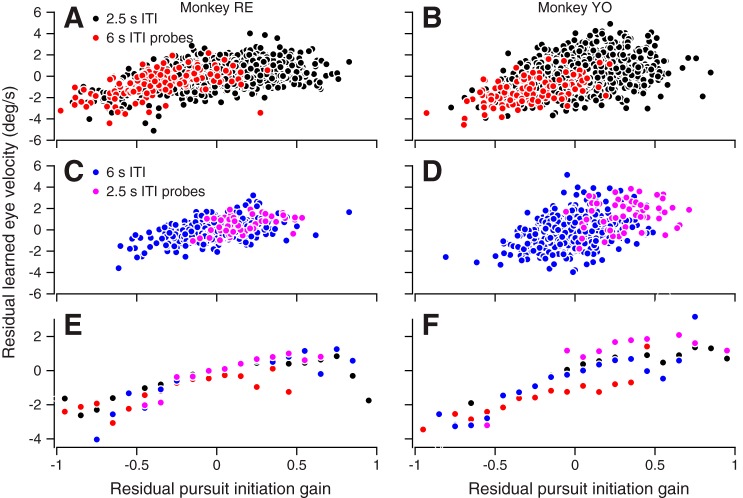
We dug deeper into this issue by isolating the relationship between the gain of pursuit initiation and the learned response from the effect of the trial course of learning. As in Fig. 4, B and D, we fitted separate models of the sums of two exponentials to the raw learned responses for both learning trials and probe trials for each session and computed the residuals of the fit for each trial. We also fitted a single, decaying exponential function to the gain of pursuit initiation as a function of trial number in each session and again computed the residuals of the fit. Plots of the residual learned responses against the residual gain of each trial show the trial-by-trial relationship between the gain of pursuit initiation and the expression of learning independently of trial number (Fig. 10). For the example experiments in Figs. 10, A–D, the expression of learning covaried with the gain of pursuit initiation and followed a single function that appears to be independent of ITI and trial number. Averaged data from all experiments reveal that a single relationship holds across all our data, including those for 2.5-s-ITI learning blocks, 6-s-ITI learning blocks, 2.5-s-ITI probes, and 6-s-ITI probes (Fig. 10, E and F). The learned response varies with the gain of pursuit initiation along lines of the same slope regardless of trial number, ITI, or learning block structure. For monkeys RE and YO, the slope of the relationship was 2.79 and 4.76, respectively, for trials with pursuit initiation gain residuals less than zero and 1.29 and 1.68, respectively, for trials with pursuit initiation gain residuals greater than zero. All slopes were statistically greater than zero (P < 0.05); the slopes for gain residuals below zero were statistically greater than those for gain residuals above zero (P < 0.05).

Fig. 10.

A single relationship between the expression of learning and the gain of pursuit initiation accounts for trial-by-trial variation across all conditions. All plots show the residual learned eye velocity as a function of residual pursuit initiation gain for each monkey, obtained using computations explained in the text. Color conventions are the same as in Fig. 9. A and B: representative example session of single-trial responses with 2.5-s-intertrial interval (ITI) learning trials (black circles) and 6-s-ITI probes (red circles). C and D: same as A and B but for example sessions with 6-s-ITI learning trials (blue circles) and 2.5-s-ITI probes (purple circles). E and F: average data over all sessions. Data were averaged separately for each learning and probe ITI condition with a bin width of 0.1 gain units.

Figure 10 shows that pursuit gain has a uniform relationship with the expression of learning across all stages of acquisition. The strength of this relationship and the range of learning magnitudes that it spans leaves little room for an effect of ITI on learning acquisition. We therefore suggest that the value of ITI has at most a small effect on learning acquisition that is overwhelmed by the relationship between the expression of learning and the gain of pursuit initiation.

Modulation of the expression of learning can explain the effect of ITI in single-trial learning.

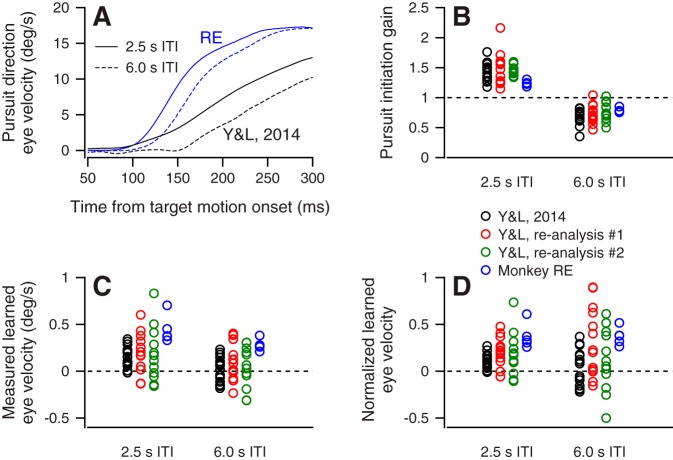
Finally, we place the relationship between the gain of pursuit initiation and learning expression in the context of previous investigations of single-trial learning. We used the random-direction paradigm of Yang and Lisberger (2014), where the direction of the instruction varied randomly along one axis from trial to trial. Using this paradigm, they showed that single-trial learning is much smaller after a 6-s ITI than after a 2.5-s ITI. We reanalyzed data from Yang and Lisberger (2014) and also collected additional data in monkey RE. As they had done, we broke the string of random learning directions into pairs and analyzed the data separately for each of the two possible instruction directions in the first trial of the pair.

Averages of pursuit eye velocity as a function of time after the onset of target motion reveal an effect of ITI on pursuit initiation both in reanalysis of the Y&L 2014 data and in new experiments on monkey RE (Fig. 11A). Pursuit initiation was more vigorous in monkey RE, but pursuit velocity is slower for 6-s-ITI trials in both sets of data. To quantify these effects, we used the approach described in methods to calculate average pursuit initiation gain for each session. For all four analyses (Fig. 11B), pursuit initiation gain was weaker for 6-s than for 2.5-s ITIs (means: Y&L = 1.41, 0.70; Y&L 1 = 1.47, 0.73; Y&L 2 = 1.48, 0.78; monkey RE = 1.21, 0.79; all P < 0.001, 2-sided paired-sample t-test for Y&L, 2-sided 2-sample t-test for monkey RE).

Fig. 11.

Effect of intertrial interval (ITI) on single-trial learning can be accounted for by differences in pursuit initiation gain. A: average pursuit direction eye velocity traces as a function of time across all sessions. Solid traces indicate pursuit velocity after a 2.5-s ITI, and dashed traces indicate 6-s ITI. Black and blue traces show previous data “Y&L 2014” from Yang and Lisberger (2014) and new data from monkey RE. B: each symbol represents the session average pursuit initiation gain of 2.5- and 6-s-ITI trials for each analysis. C: symbols show the average raw learned eye velocity for each session within each ITI group and analysis. D: symbols show the session average adjusted learned eye velocity, calculated by dividing the raw learning responses by their respective pursuit gains. In B–D, data are presented from 4 data sets and analyses: original analysis of Yang and Lisberger (2014) (Y&L 2014; black circles); a subset of data from Y&L 2014, analyzed as in the present report (Y&L 2014, reanalysis 1; red circles); the same subset from Y&L 2014 but analyzed with saccades treated as missing data (Y&L 2014, reanalysis 2; green circles); and new data from monkey RE (blue circles).

The effect of ITI on the gain of pursuit initiation can account for most of the effect of ITI on the learned eye velocity for single-trial learning, just as it did for repeated learning over 1,100 trials. We plotted the session average learned eye velocity separately for each data set and analysis, and again split the trials by ITI (Fig. 11C). The average learned eye velocity was smaller after a 6-s ITI than after a 2.5-s ITI (means: Y&L = 0.34, 0.02, P < 0.001; Y&L 1 = 0.21, 0.12, P = 0.32; Y&L 2 = 0.18, 0.04, P = 0.16; monkey RE = 0.52, 0.30, P < 0.001; 2-sided paired-sample t-test for Y&L, 2-sided 2-sample t-test for monkey RE). The gap between the learned response for 2.5- and 6-s ITIs after single trials was sharply reduced or eliminated by normalization for the gain of pursuit initiation (Fig. 11D; means: Y&L = 0.23, 0.02, P = 0.02; Y&L 1 = 0.19, 0.32, P = 0.26; Y&L 2 = 0.16, 0.11, P = 0.64; monkey RE = 0.45, 0.39, P = 0.33; 2-sided paired-sample t-test for Y&L, 2-sided 2-sample t-test for monkey RE). Only for the original Yang and Lisberger (2014) data set and analysis does a statistically significant difference persist between 2.5- and 6-s-ITI learning after gain normalization. Thus we can attribute learning after a 6-s ITI to either 1) lability of single-trial learning or 2) a relationship between the gain of pursuit initiation and the expression of pursuit learning. We favor the second explanation because it also accounts for the trial-by-trial differences in the expression of learning even when ITI is fixed at 2.5 s (Fig. 4, B and D).

There are some minor differences in how the data were analyzed for the different analyses of the original data of Yang and Lisberger (2014) and our new data on monkey RE, but these do not seem to have had a big impact on the results. We analyzed data in monkey RE using the same learning epoch and saccade removal techniques used throughout the current article. By comparison, Yang and Lisberger (2014) analyzed learned responses using a learning epoch from 150 to 300 ms after target motion onset and treated eye velocity data as missing during saccades. They separated the pairs of trials according to whether or not there was a climbing fiber response on the first trial of each pair, whereas we were not recording from Purkinje cells during the experiments in monkey RE. To take into account the probability of a climbing fiber response and make the reanalysis comparable to the new analyses, we averaged the results from their Fig. 2 with weights of 0.4 and 0.6 for the trials with and without complex spike responses, respectively (Fig. 11). We also reanalyzed a subset of the data from Yang and Lisberger (2014) on a trial-by-trial basis by 1) removing saccade trials from the analysis altogether or 2) treating data as missing during times of saccades (Fig. 11). The results are only subtly different among the original analysis and our two new analyses. Finally, monkey RE (Fig. 11) shows larger learned eye velocities, but the results are otherwise similar to those from the original data.

DISCUSSION

Our behavioral analysis of direction learning in smooth pursuit eye movements over more than 1,000 trials demonstrates three new features of this form of learning. 1) There are at least two separate trial courses of pursuit learning, suggesting that at least two distinct neural mechanisms are responsible for the observed behavioral changes. 2) The temporal specificity of the learned response within individual trials starts out quite broad and begins to tighten after 100 learning trials. 3) The size of the learned response on a given trial is related to the gain of the initiation of pursuit on that trial. Our behavioral data do not resolve whether this is a causal relationship or simply a correlation, whether the gain of the initiation of pursuit has a direct effect on the expression of learning, or if some modulatory mechanism affects the expression of learning and the gain of pursuit initiation in parallel.

Multiple components of learning.

Our finding of at least two trial courses of behavioral learning suggests that the acquisition of direction learning in pursuit is mediated by at least two neural mechanisms. Fitting the trial course of learning with a sum of exponential functions indicates that the faster component of learning accounts for more of the learned response than the slower component. Research in force-field and saccade adaptation also has suggested the existence of two learning systems that operate on timescales of seconds and minutes (Ethier et al. 2008; Kojima et al. 2004; Smith et al. 2006). In these adaptation experiments on human subjects, a two-state model simultaneously captured two critical aspects of the behavior: 1) a strong, rapid learning component and a smaller, slower learning component and 2) the observation that extinction and recovery of learning take place more readily than initial acquisition. In classical conditioning of the eyelid response, different behavioral time and trial courses exist during acquisition, extinction, and recovery of eyelid conditioning. As in the pursuit system, the existence of multiple components of behavioral learning has been taken to imply the existence of multiple neural learning mechanisms (Frey and Ross 1968; Napier et al. 1992; Schneiderman et al. 1962).

Existing knowledge about cerebellar plasticity and learning suggests several plausible neural explanations for the two components of behavioral learning in pursuit. First, learning could begin in the cerebellar cortex and then be transferred to the deep cerebellar nuclei (Kassardjian et al. 2005), in the case of the pursuit system, to floccular target neurons in the vestibular nuclei (Lisberger et al. 1994). Detailed behavioral, physiological, and lesion studies of vestibulo-ocular reflex adaptation and eyelid conditioning have repeatedly implied that both the deep cerebellar nuclei and the cerebellar cortex are important sites of plasticity for motor learning (Boyden et al. 2004; Kimpo et al. 2014; Krupa et al. 1993; Krupa and Thompson 1995; Ohyama et al. 2006). Second, there are multiple sites of plasticity in the cerebellum, and the two components of learning could result from plasticity at different synapses or inside different neurons (Carey 2011; Gao et al. 2012; Hansel et al. 2001; Ke et al. 2009). Our ultimate objective is to pin the behavioral learning components found here to a specific neuronal mechanism. The current behavioral data constrain the neural plasticity mechanisms underlying even the slow component to be implemented well within the 40 min required to run 1,000 learning trials.

Learning temporal specificity of the behavioral response.

Temporal specificity of the learned eye velocity response develops over a fairly long trial course. In the first 100 trials of a learning block, the learned eye velocity grows both during the “pursuit initiation epoch” immediately following movement initiation and the “learning epoch” surrounding the change in target direction. After ~100 trials, the learned response during the pursuit initiation epoch gradually and selectively decreases, whereas the response near the time of the direction change continues to rise. Temporal specificity could emerge from refinement of the memory trace for the late component of learning or might occur simply because a more temporally selective slow and late component of learning supplants a temporally broad fast and early component of learning.

In eyelid conditioning, a popular view is that the deep cerebellar nuclei learn to make a conditioned response, whereas the cerebellar cortex learns the timing of the response (Kalmbach et al. 2010; Perrett et al. 1993). Two features suggest alternative possibilities. First, the existence of multiple sites of plasticity in the cerebellar cortex makes it feasible that temporally broad learning could occur at the parallel fiber to Purkinje cell synapse with learned timing developing later in other synapses (Kalmbach et al. 2011; Medina et al. 2000). Second, learning appears to involve suppression of ill-timed learned responses (Jirenhed et al. 2007). In our system, this could take place through the interaction of depression and potentiation in the inputs to individual Purkinje cells, or it could involve antagonistic learning in Purkinje cells from opposite sides of the cerebellar cortex.

Learning expression vs. acquisition.

Our data imply that the acquisition of a memory trace for motor learning and its expression in a given instance are separable elements. We paid particular attention to factors that affect the expression of a learned response so that we would not mistake reduced or heightened expression of learning for weaker or stronger acquisition of learning per se. We were able to account for most of the trial-by-trial variation in our data, including fairly dramatic effects of changing the ITI, with a single factor: the strength of learning in a given trial was closely related to the gain of the initiation of pursuit in that trial. It is possible to explain the effect of ITI on the size of the learned response as temporal lability that reduces the amplitude of a memory trace during the extra 3.5 s for a 6-s vs. a 2.5-s ITI. However, temporal lability cannot account for our finding that the expression of learning is related to the gain of pursuit initiation within a single ITI, even after we removed the effect of the number of previous learning trials. Furthermore, superposition of the data from all experiments and values of ITI suggests a single relationship between the expression of learning and the gain of pursuit initiation. Therefore, we favor the single explanation of a mechanistic link between learning expression and the gain of pursuit initiation. However, we cannot disprove a dual explanation based on temporal lability of the memory trace to explain the effect of ITI on the size of the learned response, plus a causal link to explain the trial-by-trial variation within a single value of ITI.

Reanalysis of old data plus some new experiments revealed that the previously reported difference in the magnitude of learning for different values of ITI (Yang and Lisberger 2014; Fig. 4B) can be attributed to a relationship between the gain of pursuit initiation and the expression of learning. Our analysis provides a viable alternative to the prior conclusion that lability of the memory trace explains the presence of single-trial learning after a 2.5-s ITI but not after a 6-s ITI (Yang and Lisberger 2014). Thus we can explain a large body of data over many trial courses of learning based on a memory that is only slightly labile over 6 s and a relationship between the expression of learning and the gain of pursuit initiation. Our findings align with the effect of reward size on the expression but not the acquisition of pursuit learning (Joshua and Lisberger 2012). Our conclusion argues that when attempting to ascribe a behavioral response to a neuronal mechanism, it is important to focus not just on the magnitude of measured learning and neural activity, but also their trial course, time course, and susceptibility to external factors.

Our explanation for the effect of ITI on the expression of learning raises a paradox. Yang and Lisberger (2014) presented evidence that climbing fiber inputs onto Purkinje cells cause changes in parallel fiber to Purkinje cell synapses and lead to single-trial pursuit learning where the learned response of floccular Purkinje cells is smaller after an ITI of 6 vs. 2.5 s. In the present report we argue that behavioral learning is smaller after an ITI of 6 s because of a decrease in the expression of the memory trace, and not because of lability of the memory trace itself. If the memory trace itself exists in the parallel fiber synapses onto Purkinje cells, then we might expect the neural expression of learning to remain large after an ITI of 6 s and modulation of the expression of learning to occur downstream from the Purkinje cell. The paradox arises because the recordings of Yang and Lisberger (2014) imply that modulation of the expression of learning occurs upstream from the Purkinje cell, and therefore upstream of the proposed site of the underlying memory.

We suggest three possible mechanisms for how the gain of pursuit initiation could affect the expression of learning while also resolving the paradox raised above. All three will require further physiological recordings to determine their relevance. 1) There may be modulatory inputs to Purkinje cells that alter their input-output gain and thus modify the expression of the memory trace output within the Purkinje cell itself as well as the signals that drive the initiation of pursuit. 2) A site of gain modulation could be downstream from the Purkinje cell in the pathway for the signals that are modified in pursuit learning. The positive feedback of eye movement through the floccular complex (Lisberger and Fuchs 1978; Stone and Lisberger 1990) could amplify the simple spike responses differentially under conditions of modulation, as long as the modulation occurs within the positive feedback pathway. This mechanism also would have a parallel effect on the gain of pursuit initiation and the expression of learning. 3) Higher gains of pursuit initiation, through increased numbers or firing of visual or eye movement mossy fiber inputs, could cause more parallel fiber synapses to contribute to Purkinje cell simple spike firing. This situation might provide more learning substrate, which has been suggested to enhance the expression of learning (Albergaria et al. 2018), and could cause the relationship we have found between the learned eye movement and the gain of pursuit initiation.

GRANTS

This research was supported by National Institute of Neurological Disorders and Stroke (NINDS) Grant R01 NS092623. N. J. Hall received support from NINDS Grant F32 NS103216.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

N.J.H., Y.Y., and S.G.L. conceived and designed research; N.J.H. and Y.Y. performed experiments; N.J.H. and Y.Y. analyzed data; N.J.H. and S.G.L. interpreted results of experiments; N.J.H. and S.G.L. prepared figures; N.J.H. and S.G.L. drafted manuscript; N.J.H. and S.G.L. edited and revised manuscript; N.J.H., Y.Y., and S.G.L. approved final version of manuscript.