Real-time slacking as a default mode of grip force control: implications for force minimization and personal grip force variation

Abstract

During trial-to-trial movement adaptation, the motor system systematically reduces extraneous muscle forces when kinematic errors experienced on previous movements are small, a phenomenon termed “slacking.” There is also growing evidence that the motor system slacks continuously (i.e., in real-time) during arm movement or grip force control, but the initiation of this slacking is not well-characterized, obfuscating its physiological cause. Here, we addressed this issue by asking participants (n = 32) to track discrete force targets presented visually using isometric grip force, then applying a brief, subtle error-clamp to that visual feedback on random trials. Participants reduced their force in an exponential fashion, on these error-clamp trials, except when the target force was <10% maximum voluntary contraction (MVC). This force drift began <250 ms after the onset of the error-clamp, consistent with slacking being an ongoing process unmasked immediately after the motor system finished reacting to the last veridical feedback. Above 10% MVC, the slacking rate increased linearly with grip force magnitude. Grip force variation was approximately 50–100% higher with veridical feedback, largely due to heightened signal power at ~1 Hz, the band of visuomotor feedback control. Finally, the slacking rate measured for each participant during error-clamp trials correlated with their force variation during control trials. That is, participants who slacked more had greater force variation. These results suggest that real-time slacking continuously reduces grip force until visual error prompts correction. Whereas such slacking is suited for force minimization, it may also account for ~30% of the variability in personal grip force variation.

NEW & NOTEWORTHY We provide evidence that a form of slacking continuously conditions real-time grip force production. This slacking is well-suited to promote efficiency but is expected to increase force variation by triggering additional feedback corrections. Moreover, we show that the rate at which a person slacks is substantially correlated with the variation of their grip force. In combination, at the neurophysiological level, our results suggest slacking is caused by one or more relatively smooth neural adaptations.

INTRODUCTION

Motor adaptation is often viewed primarily as a process that relies on sensory motor feedback to adjust motor commands, which originate in and pass through various levels of the hierarchy of the sensorimotor system (reviews by Shadmehr et al. 2010; Wolpert et al. 2011; Wolpert and Flanagan 2016). For example, when adaptation occurs on a trial-to-trial basis, the motor system interprets discrepancies between its sensory prediction and what it actually senses during each trial (Mazzoni and Krakauer 2006). Improved internal models, feedforward and feedback control strategies, and muscle synergies, whether coordinated activation per d’Avella et al. (2006) and Waters-Metenier et al. (2014) or task-specific covariation per Latash (2010), then help the motor system perform the next iteration with greater accuracy and efficiency (Körding and Wolpert 2004; Krakauer and Mazzoni 2011). Although most previous research has investigated how the motor system translates performance measurements into performance improvements, there are indications that the motor system sometimes improves aspects of its performance using mechanisms that do not wait on sensory feedback. For instance, the forward model ascribed to the cerebellum seems to use efferent copy signals to update movements before sensory feedback is available (Pasalar et al. 2006; Shadmehr and Krakauer 2008). Also, the motor system appears to adjust its biomechanical properties (e.g., stiffness; Franklin et al. 2007) to take advantage of various “preflexes” (i.e., corrections made faster than reflexes; Loeb et al. 1999; Raphael et al. 2010). However, still other nonsensory adaptations may help explain high-level features of human motor performance, such as accuracy and efficiency (of energy, fatigue, computation, et cetera).

One likely mode of nonsensory adaptation, and the focus of this study, is the phenomenon of unprompted force drift. The initial study of force drift by Vaillancourt and Russell (2002) investigated the impact of turning off visual feedback during an isometric force tracking task. Isometric force began to decay in an exponential fashion ~1 s later, and the authors speculated the negative drift was caused by the decay of short-lived visuomotor memory. Later studies of cortical activity seemed to corroborate this hypothesis (Poon et al. 2012; Vaillancourt et al. 2003). However, preliminary work by Jo et al. (2016) may cast doubt on this explanation, as drift was observed to occur only while force was produced, not simply as time elapsed. In conjunction with other recent investigations of force drift (Ambike et al. 2016b; Parsa et al. 2016), this suggests that force drift is more likely a form of unguided adaptation than of simple forgetting.

When viewed through the lens of the equilibrium point hypothesis (Feldman 1986), and by extension the referent configuration (RC) hypothesis (Feldman 2011; Latash 2010), the effective cause of force drift would appear to be the realignment of the RC of the body with its actual configuration (AC). This putative “RC back-coupling” (Martin et al. 2009; Zhou et al. 2014) is hypothesized to occur when discrepancies exist between the AC and RC. It operates in the reverse direction of the normal statement of the RC hypothesis, namely that muscle forces and movement are produced when reflexes realign the AC with the centrally controlled RC. This explanation for force drift, developed with experiments involving the upper extremity, has been extrapolated to interpret a number of adaptations observed for both the upper and lower extremities (Parsa et al. 2016) and has been posited as a means of reducing unnecessary exertion that would otherwise fatigue muscles (Ambike et al. 2015). Physiological explanations have been provided for the movement of AC toward RC (via tonic stretch reflex; Feldman 1986) and for the movement of RC itself (by central control of subthreshold potentials across the motoneuron pool; Feldman and Latash 2005). The hypothesized drift of RC back toward AC currently lacks physiological explanation (Zhou et al. 2016) but would be consistent with the notion that the human body, like other physical systems, tends toward states of reduced potential energy (Ambike et al. 2015).

A second lens through which this force drift might be viewed is the phenomenology of slacking. Slacking was first observed in studies of the mechanical interactions between humans and robots. These studies suggest that people automatically reduce their muscle activation from trial to trial when they are achieving a movement goal (i.e., when errors are absent) but are generating forces larger than needed to accomplish that goal (Franklin et al. 2008; Scheidt et al. 2000; Thoroughman and Shadmehr 1999). One effect of such slacking (also termed forgetting) is that it results in a seemingly algorithmic minimization of effort across movement repetitions (Emken et al. 2007). Recent evidence continues to support that slacking, and its tendency to prevent complete adaptation, facilitates important qualities of the motor system, including its conservatism and exploration (van der Kooij et al. 2015; Vaswani et al. 2015). There is also scattered evidence that the motor system seeks to reduce motor output continuously (i.e., “in real time”) throughout the duration of a single movement. When people interact with a robotic device that supplements their force during reaching, they gradually allow the robot to take over unless it permits sufficient reaching errors (Wolbrecht et al. 2008). This finding is consistent with a high-level, phenomenological model of motor control in which the motor system continuously seeks to decrease its force output (Reinkensmeyer et al. 2009). As it was originally framed, this model would predict that force drift is governed centrally, consistent with theories of trial-by-trial adaptation. However, it should be noted that this model does not account for reflexes and other mediating factors between motor command and muscle force, which might either impact force drift or cause it outright (cf. reviews by Heckman and Enoka 2012; Loeb and Tsianos 2015).

A major confounding factor in these various studies of force drift has been the difficulty of observing exact onset and initial characteristics of force drift. In the slacking literature, this onset is obfuscated by the complex human-robot interactions involved. In direct studies of force drift, although simpler visuomotor force tracking tasks were used, the onset was masked by the manner in which drift was triggered, either by overtly discontinuing visual feedback or by applying perturbations. Subjects were instructed not to react to these discontinuities (e.g., “continue doing what you have been doing”; Parsa et al. 2016), but although this approach has been shown to operate moderately consistently (Latash 1994), what systematic effects it has on subjects’ behavior remain unknown. Drift has been shown to begin within the 1st s following the discontinuation of visual feedback (Vaillancourt and Russell 2002), and the inability to characterize this onset has likely hindered the search for physiological explanations of force drift.

Here, we designed an experiment to probe directly the default behavior of the motor system during isometric grip force control, in a way analogous to the “error-clamp” methodology developed for trial-by-trial movement adaptation studies (Scheidt et al. 2000). This allowed us to observe the precise onset of force drift. During a grip force tracking task, we subtly and randomly alternated between providing participants with veridical visual feedback and with nonveridical visual feedback that gave participants the impression they were always producing the target force (i.e., an error-clamp). We hypothesized that if force drift is caused by some ongoing form of adaptation, a sort of “real-time slacking,” then force drift would begin immediately when visual feedback became nonveridical in this manner, after a period of time sufficient for corrections based on prior veridical feedback to end (i.e., a participant’s visuomotor reaction time). We also measured participants’ force variation during both veridical and nonveridical visual feedback to test a second hypothesis that corrections for force drift exacerbate motor noise during force production.

METHODS

Experimental Setup and Maximum Voluntary Contraction Protocol

Grip force was measured using a transducer constructed by fastening acrylic handles to a load cell (SMA Series Miniature S-Type; Interface) and wrapping the assembly in grip tape. Participants held the grip transducer in a power grip in front of their torso (Fig. 1). A total of 32 right-handed participants, 16 women and 16 men with average age of 23.5 yr (SD 2.1), took part in the experiment (Table 1). Performance at the grip force task was measured for both the right and left hands. To minimize order effects, the order of testing of the hands was randomized so that 16 participants (8 women and 8 men) performed the task with their right hand first and 16 with their left hand first. All procedures were approved by the Institutional Review Board of the University of California, Irvine. All participants provided written, informed consent.

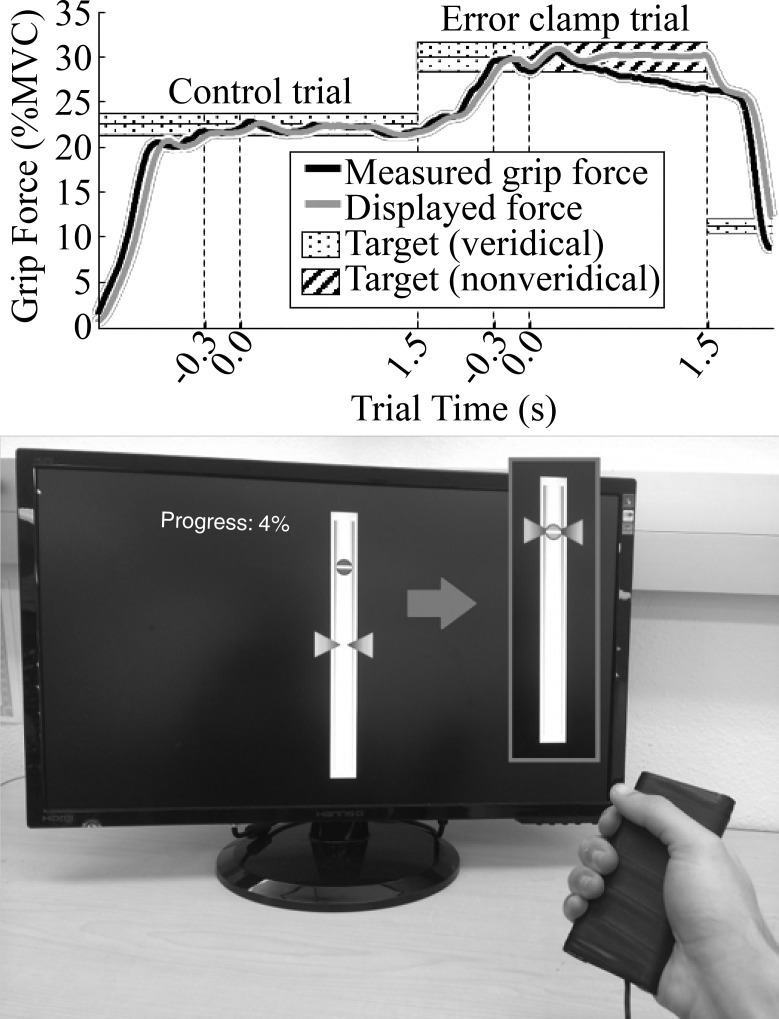
Fig. 1.

Experimental setup. Bottom: participants squeezed a force transducer to move a cursor (triangles) to track a circular target. Vertical positions of the cursor and target on the display were proportional to the participant’s grip force and the target force level, respectively. Target changed colors from red to green whenever the cursor was inside a window around the target (this window was not visible). Top: on each trial, 96 total, the target remained fixed at 1 force level, and the trial waited until the cursor was inside the target window (shaded regions) for a contiguous 0.3 s before a 1.5-s block of grip force data was recorded (the beginning of the block is defined as trial time t = 0 s, the recording continuing even if the cursor left the window). During this block, 1 of 2 feedback conditions was applied. During control trials, the cursor continued to display the participant’s grip force (veridical feedback), although with a short delay due to filtering. During error-clamp trials, however, the average position of the cursor was locked on the target regardless of the participant’s grip force, giving the appearance of 0 error (i.e., nonveridical feedback). After this 1.5-s block, the target moved to a new position and a new trial began. MVC, maximum voluntary contraction.

Table 1.

Participant information

Women			Men
	MVC, N			MVC, N
Age, yr	Right	Left	Age, yr	Right	Left
26	56	57	21	150	99
22	91	109	25	186	184
20	92	61	27	190	174
22	110	104	21	207	203
21	119	121	26	219	246
22	129	97	26	220	155
22	138	119	25	227	196
22	140	123	22	244	212
22	141	113	21	248	248
25	150	131	23	264	253
24	151	135	23	266	185
22	152	132	26	270	216
24	155	158	26	297	247
22	168	175	28	315	270
24	171	167	22	320	254
26	190	162	25	350	324

MVC, maximum voluntary contraction.

The maximum voluntary contraction (MVC) for the grip task was measured for each participant. Participants were asked to squeeze as hard as they could for 4 s without any visual feedback. Participants were given 4 s of rest and then asked to squeeze as hard as they could for another 4 s, but this time visual feedback was provided in the form of a bead on a computer screen that moved higher up a bar the harder they squeezed. The scale of the visual feedback was set such that the average force produced during the first MVC attempt was seen as 50% up the bar during the second attempt. During both MVC attempts, participants were vigorously, verbally encouraged to squeeze harder and harder to ensure that MVC was reached. The peak of the second attempt was taken as the participant’s MVC grip force.

Experimental Grip Force Tracking Task

Participants were then asked to modulate their grip force to track a changing target level. The target level was displayed as a bead (a red circle with a white stripe along its median) that appeared at one of eight different points on a vertical white bar. These eight points corresponded to eight evenly spaced force levels between 4 and 30% MVC. By changing their grip force, participants controlled the position of a cursor up and down the white bar and attempted to match the target level. By moving the cursor within a window (not visible) of the center of the bead, the bead turned from red to green, indicating that the desired grip force had been reached. The bead remained green as long as the cursor was on target, and it reverted to red if the cursor left the window of the target. These windows were chosen based on pilot testing with several participants. They were made large enough so that the participants could remain within each target window with little practice and thus quickly learn to perform the task. This was achieved with window widths that increased quadratically with force: 1.50, 1.51, 1.59, 1.79, 2.08, 2.42, 2.78, and 3.14% MVC for the eight targets in ascending order.

When moving the cursor to new targets, participants were given veridical visual feedback by mapping the vertical position of the cursor to the transducer force signal. That signal was smoothed by a second-order, low-pass Butterworth filter with a 4-Hz cutoff frequency. This filter made the movement of the cursor less noisy and easier to maintain within the target windows. This filter is characterized by a phase shift that corresponds to a maximum delay of 63 ms (for inputs at 3.5 Hz). The visual feedback was updated at the 50-Hz refresh rate of the display (a flat-panel liquid-crystal display monitor), contributing ≤20 ms of delay. A data acquisition system (National Instruments PCI-6221) measured the grip at a sampling rate of 1,000 Hz. Data acquisition and all filtering (including the error-clamp) were performed by a computer running the xPC Target real-time operating system (The MathWorks). The computer program responsible for the visual feedback ran on a separate computer and queried this filtered grip force measurement at a variable frequency faster than the 50-Hz refresh rate. Therefore, data acquisition, filtering, processing, and rendering are expected to have contributed minimal delay beyond those caused by the refresh rate of the display.

Error-Clamp, Control Trials, and Feedback Veracity

Each attempt to move to a target will be referred to as a trial. The experimental task consisted of 12 rounds of 8 trials, 1 trial for each force level in random order. Trials were performed in 2 feedback conditions, control and error-clamp, which were indistinguishable to the participant. For each trial, the experiment waited until the participant managed to stay within the target window for 0.3 s contiguously before recording a 1.5-s block of grip force data (which was not interrupted even if a participant’s force left the target window during it). During this block, the feedback provided to the participants depended on which feedback condition the trial belonged to. For control trials, participants continued to receive veridical visual feedback. For error-clamp trials, however, participants began to receive nonveridical feedback for which the vertical position of the cursor was mapped to only the high-frequency components of the participant’s grip force, whereas the average position of the cursor was locked onto the target bead. This allowed the participant’s actual grip force to drift away from the target force while maintaining the illusion that veridical visual feedback was being provided (since the cursor still moved in response to the higher-frequency components of the participant’s grip force). This high-frequency component was obtained by applying a second-order, high-pass Butterworth filter with a cutoff frequency of 1.5 Hz to the force signal of the transducer (as well as the original 4-Hz low-pass filter, which was applied to both veridical and nonveridical feedback).

The cutoff frequency of 1.5 Hz was chosen based on the finding of Slifkin et al. (2000) that showed that during force tracking, people process visual feedback up to six times per second but only plan corrections about once per second. By causing a participant’s displayed average force error over any 1-s period to approach 0, this nonveridical feedback would be expected to prevent them from making significant corrections for slow drift in their force. People can use feedback of high-frequency force behavior to reduce the high-frequency power of their force variation but not to improve their tracking accuracy (Daneault et al. 2011; Hu and Newell 2010).

After the 1.5-s block of either veridical or nonveridical feedback, the target bead moved instantaneously to the next target force, veridical feedback was returned, and the process was repeated. The 4-Hz low-pass filter helped mask the discontinuity between the mean positions of the nonveridical and veridical feedback during this transition. Participants were also distracted from the discontinuity because it occurred at the same time the target jumped to its next location. The discontinuity at the beginning of the 1.5-s block was much smaller because participants’ force was already inside the target window and was thus imperceptible even without a distraction.

The order of control and error-clamp trials was randomized for each pair of rounds by taking a full set of 8 error-clamp trials and 8 control trials (1 at each force level) and shuffling their order. Each round was made to contain all 8 force levels but in random order and with a random allocation of error-clamp and control trials. Participants were instructed to rest for 6 s between each round, when no target was displayed.

Defining and Measuring Slacking

We define the “drift rate” for a trial as the average rate of change of a person’s force over a temporal window of interest during that trial; drift rate can be positive or negative. We define slacking as drift with a negative drift rate, i.e., a systematic reduction in force manifested when people produce what they perceive as constant levels of force in the absence of feedback-driven corrections. We define “slacking rate” as the instantaneous rate of change in force caused by slacking. Finally, we define the relationship between a participant’s slacking rate for this task and the level of force they produce as their “slacking curve.” This definition for slacking assumes that a participant’s drift rate varies across trials at the same force level because of stochastic elements of force production that are superimposed on the underlying behavior of slacking. It is, therefore, a participant’s drift rate averaged over multiple trials at a given force level that approaches the putative true slacking rate for that force level.

In the present study, we aimed to identify the population mean slacking curve for healthy young participants when they produce isometric force using the power grip. We found that, on average, participants decreased their grip force in an exponential-like fashion during trials for which the error-clamp (nonveridical feedback) was applied (Fig. 3). However, the estimated time constant of this exponential was longer than the trial duration, so rather than applying an exponential fit, the drift rate of each trial was estimated as the slope of the linear fit to the force profile of the trial. Because participants did not begin reducing their force until ~0.25 s after the onset of the error-clamp (see below), the linear fit was performed across a temporal window from 0.25 to 1.5 s for each trial.

Fig. 3.

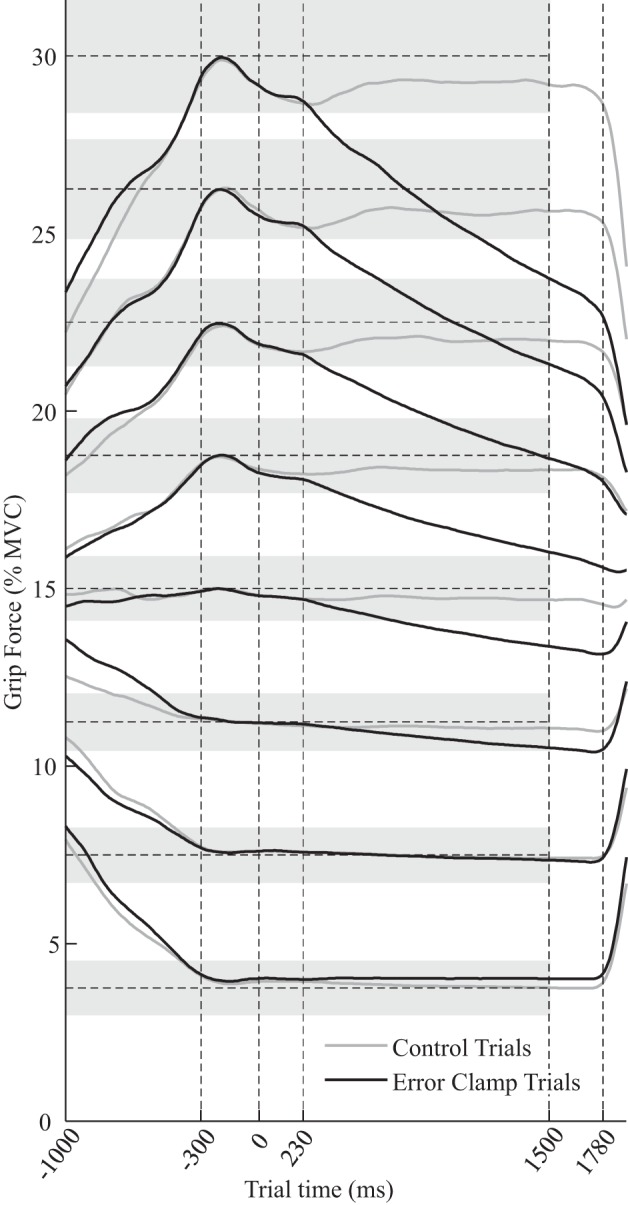
Force profiles and onset of slacking. Mean force profiles were averaged across participants for each target level and feedback condition (right and left hands combined). Shaded regions represent the target windows (see Fig. 1). During error-clamp trials, participants received nonveridical visual feedback from t = 0–1,500 ms. Above 10% maximum voluntary contraction (MVC), participants began to slack 230 ms (SD 52) following the onset of this error-clamp, slightly faster than their reaction to the target level changing at the end of each trial, which took 281 ms (SD 24). These results imply that participants began to slack before they could have reacted to the error-clamp and that slacking is not a response to sensory input but rather the default adaptive mode of force production.

The drift rate of each trial was attributed to an initial force that was itself estimated as the value of the regression line at 0.25 s, the beginning of the temporal window. For each force target, a participant’s slacking rate and associated initial force level were estimated by averaging these drift rates and initial forces across trials with that force target. Grip force was measured in terms of percentage of MVC, and drift rate and slacking rate in terms of change in percentage of MVC per second.

Measuring and Reporting Force Variation

In addition to drift rate, each participant’s force variation for each trial was defined as the coefficient of variation (CV) of their force during the same 1.25-s temporal window. CV was calculated as the standard deviation of all force measurements taken during that 1.25-s window divided by the average magnitude of those force measurements. Because a participant’s grip force was allowed to drift during error-clamp trials, force variation was measured around an estimate of the “trend” in the participant’s grip force during that trial. This trend was acquired for each trial by applying an eighth-order, noncausal, low-pass filter with a cutoff frequency of 0.75 Hz to the force signal. For consistency, this procedure was applied for both error-clamp and control trials. Also, because of the skewed distribution of force variation from trial to trial, the median variation of each participant at each target level was used for analysis.

Measuring the Onset of Slacking and Participant Reaction Time

The timing of the onset of slacking for each participant was estimated by performing a least-squares fit of each participant’s average “drift profile” to the piecewise function:

$$f\left(t\right)=\{\begin{array}{cc}a\left(t-t_0\right)+b,& t\le t_0\\ c\left(1-e^{\frac{t-t_0}{\text{τ}}}\right)+b,& t>t_0\end{array}\mathrm{.}$$ (1)

Each participant’s drift profile was computed over the trial time domain from −0.3 s to 1.5 s (where 0 s indicates the trial time at which the feedback became nonveridical during error-clamp trials). First, an average force profile was calculated for each trial condition (error-clamp or control) pooling data from the five largest force levels (12–30% MVC). Then, the average profile from control trials was subtracted from the average profile from error-clamp trials, yielding the participant’s drift profile. The onset of slacking was then defined as the value of t₀ that arose from the fit. Results are shown in Fig. 2 and indicate a close fit for most participants. However, the two participants with the slowest estimated onset appear to have confounding factors in their force profiles and were excluded from the analysis of onset timing.

Fig. 2.

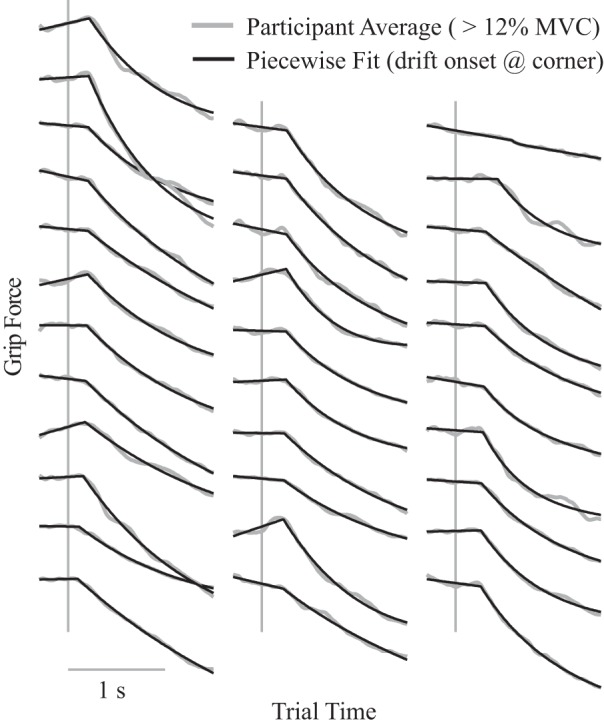
Slacking onset calculation. Each curve represents 1 participant’s difference in average force profile between error-clamp and control trials (averaged across the 5 highest force levels). The piecewise function in Eq. 1 was fit to each participant’s profile, and the onset of slacking was determined as the corner point of the piecewise function (t₀ in Eq. 1). Participants are sorted with fastest onset at the bottom left and progressively slower onsets moving up each column and then proceeding to the right. Vertical lines represent the onset of the error-clamp, and the fit was performed over the range shown from 0.3 s before to 1.5 s after this onset. Data from the 2 participants with the slowest onsets (top right) appear to have confounding features that interfered with this method, and their slacking onsets were likely faster in reality. MVC, maximum voluntary contraction.

This procedure isolated the effect of introducing the nonveridical feedback during error-clamp trials and estimated the onset of the exponential decrease associated with slacking. The linear half of the function was permitted to have a non-0 slope to accommodate possible inconsistency between error-clamp and control trials. For instance, the force level from the previous target would impact the target acquisition behavior fit by that linear portion, and it was not possible to balance error-clamp and control trials by all combinations of previous target levels.

A simpler procedure was used to estimate participants’ reaction time at the end of each trial when they began tracking the target of the next trial, which appeared immediately. These reactions were abrupt compared with the exponential reduction in force during the error-clamp, and a more traditional measure was employed (Wilmut et al. 2006), specifically, identifying reaction time as the first time the derivative of their force exceeded 3% of its maximum value during the transition from one force level to the next. Each participant’s end-of-trial reaction time was determined from the median of these measured times across all target-level transitions. Regression analysis was then performed between the participants’ onset of slacking and their end-of-trial reaction times.

Primary Statistical Analysis

Each participant performed the task at eight force levels in two feedback conditions and with both hands. For each trial, measures of both drift rate and force variation were calculated. Therefore, a three-factor repeated-measures ANOVA was performed to test for significant influences of force level (“Force”), veracity of visual feedback (“Feedback”), and hand dominance (“Hand”) on force drift rate as well as for interaction effects between those factors. For statistical analysis, all of a participant’s trials at each given force level were grouped together despite small variations in initial force between trials in each of these groupings. A second three-factor repeated-measures ANOVA was performed to test for significant influences of the same three factors, and their interactions, on the CV of force. Because two separate ANOVAs were performed, an adjusted α-value of 0.025 was used for claims of significance.

Post Hoc Analysis

In addition to these planned ANOVAs, post hoc t-tests were performed to investigate further the impact of force level and veracity of visual feedback on drift rate and CV. First, the effects of feedback veracity on both drift rate and CV were tested at all eight force levels (eight post hoc tests for each experimental outcome). Next, a test for curvature was applied to the relationship between force level and CV observed for each feedback condition (the algorithm in Table 2 minimize the number of comparisons necessary to test for curvature by moving sequentially through the force levels). Five additional post hoc test were used to test whether 1) slacking onset timing was shorter than end-of-trial reaction time, 2) participants’ slacking onset timing was correlated with their reaction times when switching targets, 3) there was a fatigue effect on drift rate over the course of the experiment, 4) the increase in variation from error-clamp to control trials was accounted for by an increase in power centered at 1 Hz, and 5) participants’ slacking rate was correlated with their personal force variation. A total of 35 post hoc t-tests were performed, and the null hypotheses of these tests were evaluated using Holm-Bonferroni-corrected α-values (Table 3; Holm 1979).

Table 2.

Algorithm for post hoc t-tests

1) Lowest 2 force levels were selected for comparison.

2) Coefficients of variation of the selected force levels were compared by testing for a significant difference between their means.

3) If the comparison from step 2 involved the highest force level, the algorithm stopped. Otherwise, the next highest force level was selected for a new comparison.

4) If the comparison from step 2 yielded a significant difference, the higher of the previously compared force levels was selected for comparison. Otherwise the lower of the compared force levels was selected.

5) Algorithm was repeated, starting at step 2.

Table 3.

Post hoc t-test results with H-B α’s

Hypothesis	df	t	P	α
Drift at 4% MVC	31	2.60	0.013	0.0038
Drift at 8% MVC	31	1.03	0.31	0.0071
Drift at 11% MVC	31	6.79	0.0000	0.0019
Drift at 15% MVC	31	13.8	0.0000	0.0016
Drift at 18% MVC	31	16.0	0.0000	0.0016
Drift at 21% MVC	31	20.3	0.0000	0.0015
Drift at 25% MVC	31	24.0	0.0000	0.0015
Drift at 28% MVC	31	26.7	0.0000	0.0014
CV at 4% MVC	31	4.89	0.0000	0.0023
CV at 8% MVC	31	5.63	0.0000	0.0022
CV at 11% MVC	31	6.14	0.0000	0.0021
CV at 15% MVC	31	6.25	0.0000	0.0020
CV at 18% MVC	31	6.92	0.0000	0.0019
CV at 21% MVC	31	7.66	0.0000	0.0018
CV at 25% MVC	31	9.71	0.0000	0.0017
CV at 28% MVC	31	8.39	0.0000	0.0017
CV clamp 1st = 2nd	31	3.85	0.0003	0.0026
CV clamp 2nd = 3rd	31	3.20	0.0024	0.0033
CV clamp 3rd = 4th	31	1.05	0.30	0.0063
CV clamp 3rd = 5th	31	2.66	0.010	0.0036
CV clamp 3rd = 6th	31	1.18	0.24	0.0056
CV clamp 3rd = 7th	31	0.51	0.61	0.010
CV clamp 3rd = 8th	31	0.25	0.80	0.025
CV control 1st = 2nd	31	3.80	0.0004	0.0028
CV control 2nd = 3rd	31	0.77	0.45	0.0083
CV control 2nd = 4th	31	1.60	0.11	0.0042
CV control 2nd = 5th	31	0.11	0.92	0.050
CV control 2nd = 6th	31	1.37	0.18	0.0045
CV control 2nd = 7th	31	3.48	0.0010	0.0029
CV control 7th = 8th	31	0.50	0.62	0.013
Slacking onset = RT	29	4.48	0.0001	0.0025
Slacking onset ⊥ RT	28	1.31	0.20	0.0050
Drift ⊥ fatigue	31	0.33	0.74	0.017
PSD at 1 Hz = 3 Hz	31	6.79	0.0000	0.0024
Slacking rate ⊥ CV	30	3.37	0.0021	0.0031

Boldface indicates significance per Holm-Bonferroni-corrected α-values (H-B α’s), i.e., if column P < column α. CV, coefficient of variation; MVC, maximum voluntary contraction; PSD, power spectral density; RT, reaction time.

RESULTS

Onset of Slacking

All participants successfully matched the force targets of all 96 trials. During error-clamp trials, participants’ force behavior began to diverge from that observed during control trials starting, on average, 230 ms (SD 52) following the onset of the error-clamp (Fig. 3). After that duration, during error-clamp trials, participants began reducing their force in an exponential-like fashion that became more exaggerated when tracking larger force targets. When tracking the two lowest targets (4 and 8% MVC), this effect became negligible. During control trials, in contrast, participants continued to produce average forces near the target level for the duration of the trial at all levels.

A slightly longer 281-ms (SD 24) delay was observed between the force target changing at the end of each trial and participants beginning to track the new target. For most participants, this was longer than their slacking onset timing (Fig. 4). A post hoc paired t-test confirmed that the participants’ slacking onset timing was significantly shorter than their end-of-trial reaction time (Table 3, “Slacking onset = RT”). In summary, slacking began, on average, 210–250 ms (95% confidence interval) following the onset of the error-clamp, which was 28–74 ms (95% confidence interval) sooner than participants reacted to the target changing at the end of trials. Post hoc analysis did not provide evidence that the participants’ onset of slacking was correlated with their reaction time measured at the end of trials (Table 3, “Slacking onset ⊥ RT”).

Fig. 4.

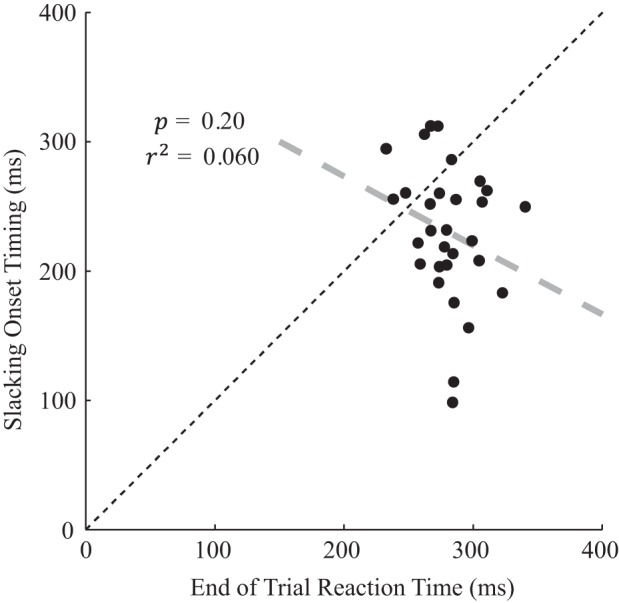
Slacking onset timing. Scatterplot is of estimated slacking onset timing against end-of-trial reaction time for each participant. This end-of-trial reaction was the median time to react to the change in target level following each trial. Excluding the two slowest slacking onsets (see caption for Fig. 2), the average slacking onset occurred 28–74 ms sooner (95% confidence interval) than the end-of-trial reaction time, possibly owing to the predictable direction of slacking. Two participants with especially early slacking onset may suggest the involvement of noncortical reflexes in slacking correction.

Slacking Rate

The average rates of force drift during error-clamp trials (i.e., the slacking rate), depended nonlinearly on the target force (Fig. 5, black lines). At force levels <10% MVC, little to no slacking occurred, but >10% MVC, slacking rates increased (i.e., became more negative) with grip force. For control trials, participants’ success in tracking the target force was reflected by near-zero drift rates across the force levels (Fig. 5, gray lines). Slacking behavior was similar between participants’ dominant, right hands and their left hands (Fig. 5). A three-factor repeated-measures ANOVA (Force × Feedback × Hand), for which results are shown in Table 2, revealed significant effects of Force and Feedback on drift rate as well as a significant Force × Feedback interaction effect. However, there was not a significant impact of Hand or of the remaining interactions. The lack of effect of hand dominance was at odds with a previous finding by Parsa et al. (2016), who found a substantial difference in drift rate between hands.

Fig. 5.

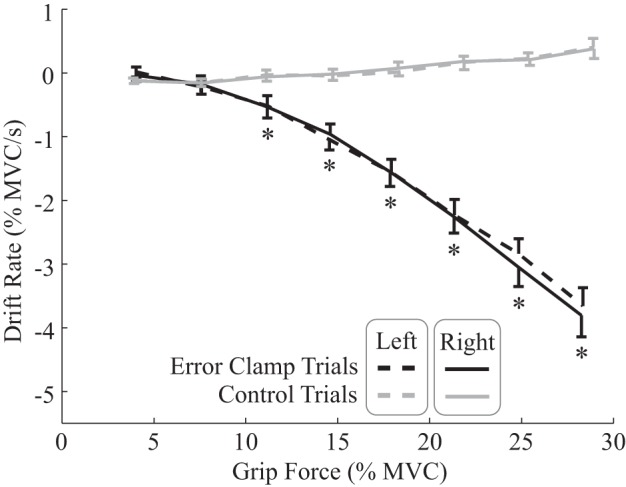
Drift rates during error-clamp and control trials. Mean rates of drift in grip force while participants attempted to maintain different target force levels, averaged across participants for both the right (solid) and left (dashed) hands, are shown. Drift rate and grip force were estimated for each trial using the linear fit to the force profile of the trial from trial time t = 0.25–1.5 s; drift rate was estimated as the slope of this linear fit and grip force as its value at t = 0.25 s. One-sided error bars reflect 95% confidence intervals for the mean with each hand, drawn to avoid overlap. Post hoc analysis revealed significant differences between error-clamp and control trials at all force levels >10% maximum voluntary contraction (MVC; asterisks). Negative drift rates for error-clamp trials depict the mean real-time slacking rates, which increase nonlinearly with grip force.

Post hoc comparisons were then made between the mean drift rates observed for error-clamp and control trials at each force level. Because ANOVA results showed no significant effect of Hand, data from both hands was combined for these tests. Paired t-tests revealed significant differences in mean drift rate between error-clamp and control trials only for the six highest force levels (Table 3, “Drift at x% MVC”). Another post hoc t-test revealed no evidence that participants’ drift rates at the four highest target levels changed from the first to last set of trials (Table 3, “Drift ⊥ fatigue”). Moreover, this change was only −0.032% MVC/s (SD 0.56), which suggests that practice and fatigue had negligible impacts on drift rate over the course of the experiment.

Force Variation during Slacking

Participants’ force variation, expressed in terms of coefficient of variation (CV; i.e., standard deviation of force divided by force level), reached minimum values between 10 and 20% MVC, above which they leveled out during error-clamp trials but increased during control trials (Fig. 6). CVs were higher during control trials than during error-clamp trials. Another three-factor repeated-measures ANOVA (Force × Feedback × Hand), for which results are also shown in Table 4, revealed significant effects of Force, Feedback, and Hand on CV as well as a significant Force × Feedback interaction effect. However, the remaining interactions effects were not significant. Thus participants’ force was slightly more variable with their nondominant hands, but there was no evidence that hand dominance modulated the effects of force level and feedback condition.

Fig. 6.

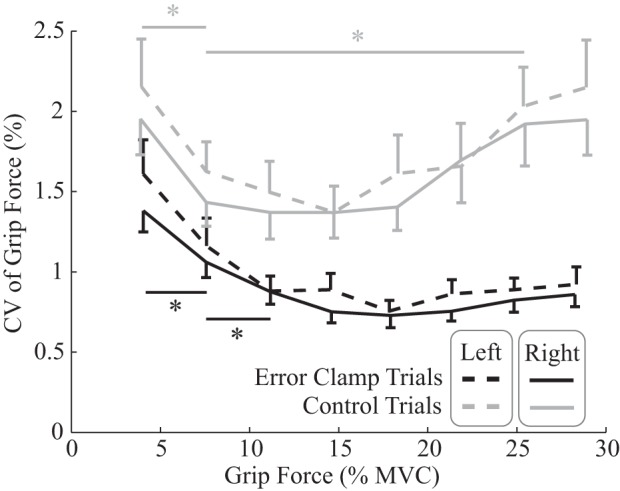
Force variation during error-clamp and control trials. Median coefficients of variation (CV) of detrended grip force (standard deviation of force variance divided by force) while participants attempted to maintain different target force levels, averaged across participants for both the right (solid) and left (dashed) hands, are shown. To control for the difference in drift rate between error-clamp and control trials, CV was calculated around a trend curve obtained by passing each force profile of the trial through a 0.75-Hz low-pass filter. Error bars reflect 95% confidence intervals for these means. Variation was significantly greater for control trials at all force levels. For both feedback conditions, there was a significant decrease in CV up to 15% maximum voluntary contraction (MVC; asterisks), however, only for control trials was there a significant increase in CV >15% MVC (horizontal bars reflect significant difference in CV determined by post hoc t-tests).

Table 4.

ANOVA results: drift rate and variation

	Drift Rate			Force Variation (Coefficient of Variation)
	df	F	P	df	F	P
Force	7, 217	209	0.0000	7, 217	20.3	0.0000
Feedback	1, 217	2,807	0.0000	1, 217	701	0.0000
Hand	1, 217	0.38	0.54	1, 217	10.9	0.0010
Force × Feedback	7, 217	302	0.0000	7, 217	5.20	0.023
Force × Hand	7, 217	0.58	0.77	7, 217	0.33	0.94
Feedback × Hand	1, 217	1.07	0.30	1, 217	1.08	0.30
Force × Feedback × Hand	7, 217	0.91	0.50	7, 217	0.60	0.76

Boldface indicates significance per α = 0.025.

Several post hoc t-tests were then performed to characterize better the effects of Feedback and Force on CV. Because of the small and consistent impact of Hand, data from both hands were combined for these tests. Paired t-tests revealed significant differences between the mean CVs of error-clamp and control trials at all force levels (Table 3, “CV at x% MVC”). Paired t-tests also revealed a significant curvature in the CV-force relationship for each feedback condition (Fig. 6, horizontal bars). For error-clamp trials, CV, on average, decreased as force level increased from 4 to 11% MVC and never significantly changed as force level increased above 11% MVC (Table 3, “CV clamp x = y”). For control trials, CV also, on average, decreased as force level increased from 4 to 8% MVC but then significantly increased as force level increased to 25% MVC (Table 3, “CV control x = y”).

Frequency Content of the Observed Force Variation

We hypothesized that the tendency to slack would require the motor system to make intermittent corrections to its force production to maintain target forces during control trials (Gawthrop et al. 2011). If so, then one would expect heightened signal power around the 0- to 3-Hz range, which is the frequency band that is most influenced by feedback corrections based on visual information (Slifkin et al. 2000; Vaillancourt and Russell 2002). Because the results did show an increase in variation during control trials (Fig. 5), the power spectral densities (PSDs) of the force produced during the two feedback conditions were compared to determine the frequencies over which this increase in power occurred (Fig. 6). The PSD of the detrended force from each trial was computed and normalized relative to target force level. Then, the average of these PSDs across all force levels and both hands was calculated for each participant and feedback condition. Finally, the average PSD across participants was calculated for each feedback condition. Consistent with visually guided feedback correction, a post hoc paired t-test revealed that there was a significantly greater increase in power (vertical distance in Fig. 7) from error-clamp to control trials centered ~1 Hz compared with ~3 Hz (Table 3, “PSD at 1 Hz = 3 Hz”).

Fig. 7.

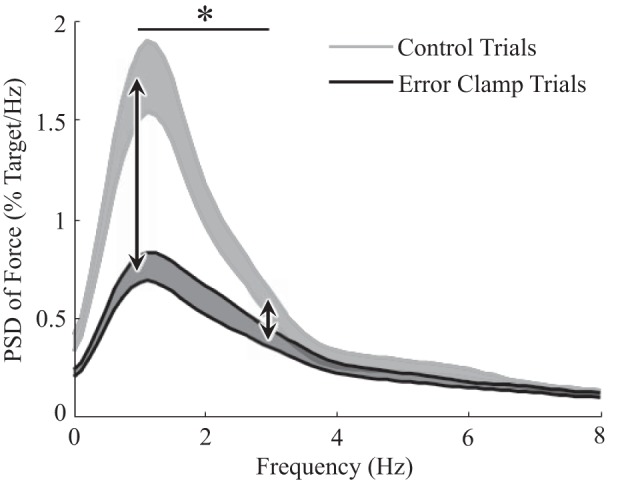
Power spectral density (PSD) of detrended grip force. PSDs were computed for both error-clamp and control trials and used to derive a 95% confidence band of the average PSD across participants (both hands included) for each condition. PSDs were based on detrended force profiles (hence the minimal power at 0 Hz) and normalized relative to target force level. Bands represent 95% confidence intervals of the mean power at each frequency. There was a significantly greater increase in power from error-clamp to control trials at 1 Hz than at 3 Hz (asterisk), implying that the increase in force variation from error-clamp to control trials was caused by heightened visually guided feedback correction.

Relating Participant-Specific Slacking Rates to Force Variation

To follow up on the hypothesis that feedback corrections for slacking accounted for the increase in force variation observed between error-clamp and control trials, linear regression was performed between slacking rate (i.e., negative drift rate measured during error-clamp trials) and CV of force (during control trials) across participants. Each participant’s slacking rate and force variation, averaged across the four highest force levels, represents one point in Fig. 8. There was a significant positive correlation between personal force variation and slacking rate (Table 3, “Slacking rate ⊥ CV”) that explained 29% of the between-participant variability in CV of force during control trials. That is, participants who slacked more exhibited greater force variation during control trials, when apparently they relied on visual feedback to correct for force drift, which was made more dramatic by their faster rates of slacking.

Fig. 8.

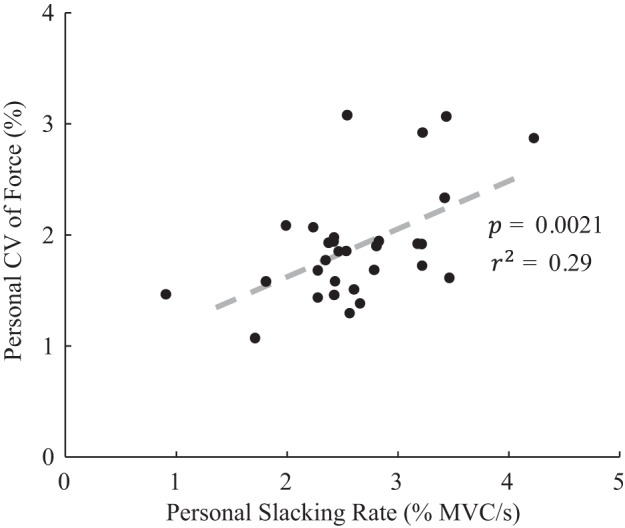
Regression of personal grip force variation against slacking rate. Participants with greater average slacking rates (measured during error-clamp trials) exhibited significantly greater force variation during control trials (both measures were averaged over the 4 highest force levels with both hands included). Between-participant variability in slacking rate explained 29% of the variability in the magnitude of their force variation. This correlation may describe the need for more frequent and dramatic corrections by the participants whose faster slacking rates led to more frequent and dramatic tracking errors. CV, coefficient of variation; MVC, maximum voluntary contraction.

DISCUSSION

Based on these results, we hypothesize that slacking during real-time, visuomotor control of grip force does not occur in response to sensory input but rather as a default, adaptive mode of force production, analogous to its role in trial-to-trial motor adaptation (Emken et al. 2007; Franklin et al. 2008). That is, slacking was operating while participants tracked forces, albeit undetected, even before the error-clamp was applied to the visual feedback they received. The difference in participants’ performance when they received veridical visual feedback, compared with when they received the nonveridical feedback (i.e., the error-clamp), was that veridical feedback enabled them to make regular corrections for slacking to maintained the constant force levels involved in the tracking task. Without these corrections, slacking was manifest as a smooth, exponential reduction in grip force that occurred whenever the error-clamp was applied.

This characterization of slacking during grip force control, along with evidence of its requisite compensation, builds on recent studies by Ambike et al. (2016a) and Parsa et al. (2016) and suggests that unintentional force drift places a key demand on the motor system that has been historically neglected in the motor control literature. We shall discuss 1) how the onset timing of real-time slacking helps elucidate the control mechanisms involved in unintentional force drift, 2) how this characterization of slacking helps account for patterns of force variation in a way that supplements previous models of grip force variation, 3) how this interpretation helps unify several previous findings in the grip force control literature, illustrative of the contribution of slacking to force minimization, and 4) possible physiological explanations for force drift during real-time slacking.

Onset of Slacking

The onset of slacking was observed to occur, on average, 230 ms following the onset of the error-clamp, at which time participants’ force was observed to decay. The immediacy of this observed decay, trailing the error-clamp by roughly one simple reaction time (measured for visuomotor tasks by Carlton and Newell 1987; Carlton et al. 1987; Wilmut et al. 2006), would seem to preclude the possibility that participants adapted to the nonveridical feedback during the error-clamp before beginning to slack. This, in turn, would imply that real-time slacking is a persistent and unprompted behavior that continuously drives force lower unless adequately compensated for. Comparing participants’ slacking onset timing (mean 230 ms, SD 52) with their reaction times measured at the end of each trial (mean 284 ms, SD 24) yields evidence that slacking compensation is a relatively simple dynamic of force production.

The motor system might take advantage of the predicable directionality of slacking (i.e., the tendency of drift to be negative) to simplify and quicken its feedback-mediated compensation. This would explain how slacking onset was so quick. End-of-trial reaction times were comparable with those documented for two-choice, visuomotor control tasks (Carlton et al. 1987). However, it has been shown that two-choice reaction time is shortened whenever it involves selecting the more likely of two unequally likely choices (Smith and Ratcliff 2004). Visually guided slacking compensation, which appears necessary to maintain constant levels of force, might be expected to consist primarily of unidirectional corrections, perhaps increasing force whenever drift below the target is perceived. This likely quickened slacking onset for the majority of participants but seems not enough to explain how some showed even quicker slacking onset.

A physiological explanation for these instances of early slacking onset might instead be found in the literature on reflex-mediated reactions. Recent studies have identified shorter reaction times between 120 and 170 ms for highly reflexive tasks such as reaching to intercept projectiles (Perfiliev et al. 2010) and the case of “stimulus-locked response” (Gu et al. 2016). However, in both cases, these faster reactions only occurred when participants reacted using the limb they selected reflexively. When participants were instructed to use the opposite limb (e.g., blocking a projectile with their contralateral hand), their reactions times slowed to 200–250 ms, more consistent with traditional measures of reaction time. Perfiliev et al. (2010) also discussed how adding abstraction to a task, such as providing feedback via computer monitors, also seemed to inhibit the use of these faster reflex-mediated reactions. Here, depending on the level of abstraction that the experimental task posed to each participant, various barriers might have emerged to prevent purely reflexive compensation.

As such, the relatively wide distribution of slacking onset timing might be explained by variability across participants in their relative involvement of reflexive and cortical feedback when compensating for slacking or in their consistency of prediction that the next error correction would be positive. Of note, the width of this slacking onset distribution does not appear to be attributable to experimental uncertainty, as the average force profiles used to estimate slacking onset followed a tight trend (Fig. 2). Also, the lack of correlation between slacking onset and end-of-trial reaction time (Fig. 4) is consistent with the interpretation above, as the extent to which a participant involves prediction or subcortical reflexes in slacking compensation seems unlikely to be governed by their two-choice reaction time.

Slacking and Grip Force Variation

While participants slacked during nonveridical feedback, their force variation was substantially lower than when they received veridical feedback. During nonveridical feedback (i.e., the error-clamp, when force drift was observed), the CV of their force was relatively constant over most of the range of observed force levels, with a significant inverse relationship with force across the lowest force levels. Both are consistent with previous documentation of signal-dependent noise (Jones et al. 2002; Lindberg et al. 2012). During veridical feedback, the inverse relationship at low force levels switched direction at the larger force levels, resulting in a minima in force variation ~15% MVC. This increasing variation >15% MVC was consistent with the experimental findings of Moritz et al. (2005). These authors employed a model of motor neuron firing rate variability in an attempt to explain the relationship they observed between force amplitude and variation. However, whereas the model explained the inverse relationship below the minima, it did not predict the positive trend above it. We anticipate that this positive trend is instead attributable to the accelerated slacking rates >15% MVC, which we hypothesize prompted feedback corrections to avoid force drift.

Consistent with this hypothesis, power spectral density results indicated that the decrease in force variation observed during nonveridical visual feedback consisted mostly of a reduction in power between 0 and 3 Hz. Reduced power in this band has also been observed when visual feedback was completely removed (Slifkin et al. 2000; Vaillancourt and Russell 2002), suggesting that 0–3 Hz corresponds with visually guided control. The intermittent nature of visual feedback control (Gawthrop et al. 2011), together with participants’ tendency to let their force drift during error-clamps, implies that veridical feedback enabled participants to maintain constant force levels by prompting frequent corrections for this ongoing drift. This would be expected to contribute to force variation, and, as discussed later, the minimal force variation observed during uninterrupted slacking sheds light on the neurophysiology of slacking.

Also of note, although this drift occurred at all force levels, its effect on force variation would be expected to be heightened at larger forces, when participants’ slacking was more pronounced. Thus the parallel increases in both slacking rate and force variation above 10–15% MVC are consistent with an interpretation of slacking that predicts that ongoing feedback corrections are necessary to maintain constant force levels against a persistent tendency toward decay. Moreover, participants who exhibited faster rates of slacking also tended to exhibit greater magnitudes of force variation. Regression analysis revealed that 30% of the between-participant variation in force variation >15% MVC could be explained by between-participant variation in slacking rate. Thus, across force levels and between participants, stronger tendencies to slack seemingly required larger feedback corrections that, in turn, increased force variation. To our knowledge, this is a unique explanation for person-specific variability in grip force variation: some of this variation apparently arises when a person’s motor system is organized in such a way as to increase the rate of their slacking, at least as it pertains to force drift. This would imply a trade-off between grip steadiness (which may contribute to movement accuracy) and grip efficiency (the often posited goal of slacking), echoing the accuracy-energetics trade-off associated with optimal feedback control (Todorov 2004).

Slacking and Force Minimization

By constantly driving force lower, slacking is ideally suited to play a role in force minimization during force production. We here give several examples of this role and how the immediate onset and subsequent rate of force drift may contribute to the broader understanding of motor adaptation that includes significant noncomputational processes.

First, real-time slacking is likely to introduce a persistent bias into motor adaptation during force control tasks, contrary to general expectation that error-based learning removes systematic bias (Wolpert et al. 2011). In the simple case studied here, we demonstrated that negative force drift occurs as soon as a participant begins tracking a force target. If visual feedback prompts corrections for this drift back to the target itself, one would expect the average bias in force production to be below the target. It has been observed, here and elsewhere (Hong et al. 2008; Vaillancourt and Russell 2002), that when participants produce forces large enough to cause slacking, they produce average forces below the target levels, even during visual feedback. Hong et al. (2008) also found that when people track forces with differently scaled visual feedback, smaller visual gains lead to lower average forces. van der Kooij et al. (2015) observed that scaling visual feedback during trial-by-trial slacking has a similar effect. Apparently, smaller visual gains lower the threshold at which error correction and slacking reach equilibrium (per Emken et al. 2007). Finally, when people receive visual feedback intermittently, they produce lower average forces when feedback is updated less frequently (Slifkin et al. 2000), likely because they have longer to slack between feedback updates. This effect is also only seen when people produce forces that are large enough to cause slacking (Sosnoff and Newell 2005). Although many of these interpretations were proposed by Ambike et al. (2016a), the ongoing nature of real-time slacking (here implied by its immediate onset) more directly links force drift to persistent biases during force production.

If we allow that slacking, and the bias it introduces, constitutes more broadly an ability to quickly reduce unnecessary forces, the motor system need not precisely anticipate the optimal forces for tasks for which success depends on a threshold level of force being applied. Instead, the motor system can overestimate the required force and rely on slacking to restore force down to efficient levels. This may expedite the search for “good-enough” movement strategies (Loeb 2012) by removing the need to refine one or more degrees of freedom of the feedforward control signal. For instance, when picking up unfamiliar objects using a pinch grip, people are known initially to produce excessive forces, which they then reduce in an exponential fashion, consistent with slacking, down to regular factors of safety above the slip threshold (Quaney et al. 2005; Westling and Johansson 1984). Likewise, when controlling any number of unstable systems (e.g., using a screwdriver), initiating the task with excessive cocontraction can provide the impedance necessary to prevent a tool from buckling or a load from tipping. Slacking can then quickly reduce cocontraction down to efficient levels, explicative of the observations by Franklin et al. (2008). Moreover, pathways appear to exist to promote the stabilization of task-specific synergies (Reschechtko et al. 2015), such that seemingly unguided force drift can effectively be directed along the uncontrolled manifold of a task (Ambike et al. 2016b). This understanding may position slacking within recent studies of motor adaptation. For instance, Ingram et al. (2013) found evidence that the decay of motor memory was context dependent, similarly to its formation, in a manner conductive to optimizing motor control. As such, decay of motor memory might actually be an updating of motor memory, when the effect of real-time slacking on one movement iteration is remembered for the next. Future work could test this hypothesis by establishing whether real-time slacking operates similarly during movement as it does during isometric force production.

Finally, the characteristic time of force drift measured in this study suggests the moderation of the speed of slacking throughout the evolution of a movement. Here, drift appears to have had a characteristic time of ~4 s (based on the slope of the curve in Fig. 5 between 10 and 30% MVC). Longer characteristic times of ~15 s occurred when isometric force was sustained 4–10 s before visual feedback was withheld (Ambike et al. 2015; Parsa et al. 2016; Vaillancourt and Russell 2002). In our study, forces were sustained for as little as 0.3 s before the error-clamp was applied, implying that real-time slacking slows over the first several seconds that force is sustained. Shorter characteristic times of 1.5 s occurred when hand position was perturbed by external forces (Zhou et al. 2014), for which Parsa et al. (2016) suggested the interpretation that involuntary movement accelerates the mechanism behind force drift. Combined, these modulations match the general progression of grip force during prehension: grip force overshoots and quickly decays to a level that is still well above slip onset, and then grip force decays more slowly until it stabilizes at a consistent threshold above slip onset (Quaney et al. 2005; Westling and Johansson 1984). This stabilized grip may represent the prolonged use of tactile feedback to counteract slacking intermittently. A recent study of grip force control, using a physiologically inspired robotic finger, found that vibrotactile feedback can detect slip up to 50 ms before slip onset (Su et al. 2015), suggesting that ongoing, reflex-mediated drift correction may well explain how prolonged prehension operates at such consistent thresholds above slip onset (Solnik et al. 2014). The persistence of slacking may also explain why objects are occasionally and inadvertently dropped, particularly in aging, which appears to upset the balance between energetic efficiency and reliability (Latash and Anson 1996, 2006).

Neurophysiological Explanations for Force Drift

As discussed in the introduction, new evidence may cast doubt on the original visuomotor memory explanation for force drift (Jo et al. 2016). Ambike et al. (2015) conjectured that isometric force drift, which switches from positive to negative drift above some threshold (e.g., 10% MVC), can be explained via two competing factors: 1) RC back-coupling causing negative drift at larger forces and 2) sensory adaptation of the cutaneous receptors prompting positive drift at small forces. Since physiological explanations for RC back-coupling have not been provided, we will provide a collection of possible physiological explanations for force drift that may be integrated into various hypotheses of motor control.

Attenuation of central command signal.

As originally postulated by Reinkensmeyer et al. (2009), force drift may operate similarly to trial-by-trial slacking and represent an ongoing attenuation of a central command signal governing force production. This would be consistent with the originally posited decay in visuomotor memory (Poon et al. 2012; Vaillancourt et al. 2003). Alternatively, visuomotor memory may offset force drift, even if the physiological cause of real-time slacking lies elsewhere. The contrary evidence by Jo et al. (2016) may then reflect that visuomotor memory decays more quickly during force production, analogous to the context-specific forgetting during reaching movements (Ingram et al. 2013). More definitively, the smooth nature of force drift (i.e., low force variation) necessitates that any central explanation for force drift reflect a continuous process, not one that would involve discrete steps. For instance, this would rule out that real-time slacking involved updating successive motor primitives involved in sustaining isometric force (as might be conjectured per d’Avella et al. 2006).

Adaptation of spindle sensitivity.

Any number of sensory adaptation processes might be expected to lead to the smooth force drift associated with real-time slacking. For instance, the activity of γ-motoneurons might lead the adaptation of muscle spindle sensitivity (reviewed by Loeb 2014). Supposing reflexes are used to maintain a constant level of spindle activity, this could explain force drift in terms of stabilization around a drifting reference point defined by those spindles.

Adaptation of cutaneous receptors.

Leung et al. (2005) reported that cutaneous receptors adapt with a wide range of characteristic times (during vibratory stimulation) with substantial populations of receptors adapting at the time scales reported for force drift (1.5, 4, and 15 s) and with many having even longer characteristic times. The quick decay in the activity of faster time scale receptors may explain why drift grows slower with time. Ambike et al. (2015) expected that such adaptation would lead to positive force drift by reducing the sensation of force produced. However, it seems just as likely that other mechanisms interact with this adaptation in a way that might cause force drift.

Adaptation of proprioceptive receptors.

Originally suggested by Vaillancourt and Russell (2002) as an explanation of force drift, proprioceptive adaptation appears to occur too slowly to explain the pace of force drift observed here. In a study of force sharing with a robot while maintaining hand position, force reduction was quite slow (only 7% in 30 s; Reinkensmeyer et al. 2009), possibly due to the persistence of proprioception. Proprioceptive drift of joint angle has also been found to be minimal, as measured when people are blindfolded (~3° in 30 s; Tsay et al. 2014). This may explain why drift in grip force is not generally coupled with a corresponding drift in hand position. If anything, proprioception may help counteract any impact that real-time slacking would have on joint angles.

Muscle fatigue.

The possibility that muscle fatigue causes force drift is generally dismissed but warrants discussion. Past studies have argued that force levels <30% MVC are unlikely to cause such dramatic fatigue (Ambike et al. 2015; Parsa et al. 2016; Vaillancourt and Russell 2002). On the other hand, fast fatigable (FF) and fast fatigue-resistant (FR) motor units are known to exhibit fatigue within ~250 ms following activation (Burke et al. 1973). Moreover, these units are increasingly recruited as fatigue develops throughout a muscle (Adam and De Luca 2003). Recently, Potvin and Fuglevand (2017) calibrated a motor-unit-based model of muscle fatigue that incorporates the current understanding of motor unit recruitment, firing rate, and fatigue (as well as firing rate adaptation and persistent inward currents; see below). They predicted that during a sustained 20% MVC contraction, fatigue develops over an 8-min period during which force is sustained by increasing a putative “excitation” to all motor units. Were fatigue the primary cause of force drift, this model would be expected to predict an increase in excitation proportional to observed rates of force drift. Instead, excitation increased 0.10%/s initially, which accelerated to 0.35%/s 6 min later (as recruitment increased and fatigue developed throughout the motor pool). This was two orders of magnitude too slow to explain force drift. Even if this discrepancy in rate were explained, these results would still imply a dramatic acceleration of force drift over the time course of this experiment. In contrast, we observed a negligible order effect on drift rate across trials, similar to a finding reported by Ambike et al. (2015). Unless participants fully recovered from fatigue during each 6-s rest period (rests occurred between sets of 8 consecutive trials), participants’ baseline level of fatigue would be expected to increase throughout the experiment, which, according to this model, would substantially moderate the effect of fatigue during each trial. In light of additional studies that fatigue and recovery occur over the course of minutes, not seconds (Enoka and Duchateau 2008; Taylor and Gandevia 2008), we conclude that fatigue was unlikely to have caused the force drift observed here and elsewhere.

Adaptation of motoneurons.

In classic studies of firing rate adaptation (also called “spike frequency adaptation”), motoneuron activity has been found to diminish during injected current stimulation (Bigland-Ritchie et al. 1983; Kernell and Monster 1982). The characteristics of firing rate adaptation are consistent, within an order of magnitude in animal models, with the 10% MVC threshold and characteristic timing of force drift: 1) above a comparable threshold, recruitment begins for FF and slow fatigable (SF) motor units, which are more susceptible to adaptation; and 2) adaptation occurs with at least two time scales, fast and then slow, which may explain the hypothesized deceleration of drift while isometric force is sustained. However, spike frequency adaptation has not been isolated in vivo, either in humans or animals, and it might be obviated in the intact motor system by persistent inward currents and other lesser-understood phenomena (see review by Nordstrom et al. 2007). Based on loose evidence, the model discussed above predicts a slower, fatiguelike interaction between persistent inward currents and firing rate adaptation (Potvin and Fuglevand 2017) rather than the fast drift observed here. Perhaps including the partial recovery of firing rate adaptation between 1-Hz repetitive contractions (as measured in guinea pig models by Llinás and Lopez-Barneo 1988) would replicate the recurring, rapid force drift associated with real-time slacking. Still, experimental verification would likely remain elusive.

Conclusions and Future Work

We applied a brief, subtle error-clamp to the visual feedback presented during an isometric force tracking task and observed two significant consequences of real-time slacking: 1) force drift begins immediately following an error-clamp, implied by a delay of one simple reaction time; and 2) force drift occurs via a discontinuation of visuomotor feedback control, implied by reduced force variation. From these observations, we propose that real-time slacking represents a persistent reduction in muscle force whenever grip force levels exceed ~10% MVC. Similar force drift has been observed for the fingers, but future work would be needed to determine whether real-time slacking is a universal feature of motor control. At least for the hand, we conclude that constant force production requires a person to make ongoing corrections for slacking, a demand that appears to account for a substantial portion of their grip force variation. The predictable directionality of real-time slacking is expected to reduce the cognitive demand of these corrections, leading to relatively quick reaction times. It appears possible that even quicker, noncortical reactions are at play, which may dominate during more naturalistic instances of slacking correction, many of which are likely nonvisual. Regardless of their timing, feedback corrections for slacking appear to contribute to force variation. Future work will investigate whether this relationship between slacking and force variation is causal.

Real-time slacking, as characterized here, appears consistent with the convergence of three evolutionary pressures: 1) a default tendency to reduce muscle force is likely energetically efficient, 2) a predictable tendency to reduce muscle force may broaden the space of good-enough solutions for visuomotor control by quickly mitigating excessive forces in one or more dimensions, and 3) a source of increasing force variation may promote task exploration for these good-enough solutions, which is likely a higher priority than minimizing force variation in most situations (Loeb 2012; Taylor et al. 2014; Wu et al. 2014). This convergence may help explain why slacking occurs only for forces >10% MVC. Above this threshold, energetics would likely be of greater concern and a greater evolutionary benefit would arise from automatically reducing force. Below it, accuracy and precision are likely more important and achievable with minimal energetic consequence. Future work will investigate situations where force variation is detrimental to explore whether slacking is involved in task-related tuning of the motor system (as posited by Loeb and Tsianos 2015). This 10% MVC threshold may also represent a tuning of task exploration that favors more dramatic exploration during intense movements (i.e., to discover these good-enough solutions quickly) but slower exploration during often less-intense precision movements. Future work might test this prediction by investigating the rate of convergence to good-enough solutions for tasks of varying intensity.

The speed of slacking also appears to change based on the dynamics of force production. Based on the results of Ambike et al. (2015) and Parsa et al. (2016), sustaining an isometric force for several seconds appears to slow down real-time slacking. Conversely, the results of Zhou et al. (2014) might be explained by an acceleration of real-time slacking during perturbations that lead to movement. The effects of movement and sustained force on real-time slacking could be tested in follow-up studies that vary the timing of the error-clamp and apply perturbations before measuring drift rate. Finally, it remains to be seen whether real-time slacking, as studied here, occurs more generally across motor control and how this automatic form of motor adaptation might contribute to the apparent optimality of the human sensorimotor system.

GRANTS

The work described was supported by National Institute of Child Health and Human Development Grant R01-HD-062744-01 from the NIH National Center for Medical Rehabilitation Research and by the University of California, Irvine, Institute for Clinical and Translational Science.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

B.W.S., J.B.R., and D.J.R. conceived and designed research; B.W.S. performed experiments; B.W.S. analyzed data; B.W.S. and D.J.R. interpreted results of experiments; B.W.S. prepared figures; B.W.S. drafted manuscript; B.W.S., J.B.R., and D.J.R. edited and revised manuscript; B.W.S., J.B.R., and D.J.R. approved final version of manuscript.