Biophysical basis of subthalamic local field potentials recorded from deep brain stimulation electrodes

Abstract

Clinical deep brain stimulation (DBS) technology is evolving to enable chronic recording of local field potentials (LFPs) that represent electrophysiological biomarkers of the underlying disease state. However, little is known about the biophysical basis of LFPs, or how the patient’s unique brain anatomy and electrode placement impact the recordings. Therefore, we developed a patient-specific computational framework to analyze LFP recordings within a clinical DBS context. We selected a subject with Parkinson’s disease implanted with a Medtronic Activa PC+S DBS system and reconstructed their subthalamic nucleus (STN) and DBS electrode location using medical imaging data. The patient-specific STN volume was populated with 235,280 multicompartment STN neuron models, providing a neuron density consistent with histological measurements. Each neuron received time-varying synaptic inputs and generated transmembrane currents that gave rise to the LFP signal recorded at DBS electrode contacts residing in a finite element volume conductor model. We then used the model to study the role of synchronous beta-band inputs to the STN neurons on the recorded power spectrum. Three bipolar pairs of simultaneous clinical LFP recordings were used in combination with an optimization algorithm to customize the neural activity parameters in the model to the patient. The optimized model predicted a 2.4-mm radius of beta-synchronous neurons located in the dorsolateral STN. These theoretical results enable biophysical dissection of the LFP signal at the cellular level with direct comparison to the clinical recordings, and the model system provides a scientific platform to help guide the design of DBS technology focused on the use of subthalamic beta activity in closed-loop algorithms.

NEW & NOTEWORTHY The analysis of deep brain stimulation of local field potential (LFP) data is rapidly expanding from scientific curiosity to the basis for clinical biomarkers capable of improving the therapeutic efficacy of stimulation. With this growing clinical importance comes a growing need to understand the underlying electrophysiological fundamentals of the signals and the factors contributing to their modulation. Our model reconstructs the clinical LFP from first principles and highlights the importance of patient-specific factors in dictating the signals recorded.

INTRODUCTION

Subthalamic deep brain stimulation (DBS) is an established clinical therapy for advanced Parkinson’s disease (PD). Over the last two decades, subthalamic DBS surgeries have provided unique experimental opportunities to record electrophysiological activity from subthalamic nucleus (STN) neurons in thousands of patients with PD. This wealth of data has provided valuable insights on the pathophysiology of PD and highlighted the possible role of excessive subthalamic nucleus (STN) neural synchrony in the generation of PD symptoms (Oswal et al. 2013). In particular, local field potential (LFP) recordings from DBS macroelectrode contacts represent an established platform for detecting and analyzing neural synchrony in PD.

Chronic LFP recordings from DBS electrodes in the STN are currently the focus of wide-ranging clinical research studies (e.g., Quinn et al. 2015; Swann et al. 2016). The ability to obtain chronic recordings facilitates the possible use of LFPs as clinical biomarkers in closed-loop control systems, which have become a driving force in the development of commercial DBS technology (McIntyre et al. 2015; Stanslaski et al. 2012). Specifically, beta-band (12–30 Hz) activity has received the greatest attention in PD research because of its correlative association with PD symptoms (e.g., Bronte-Stewart et al. 2009; Kühn et al. 2009; Ray et al. 2008). As such, LFP recordings of STN beta activity represent viable control signals for adaptive subthalamic DBS systems in humans (Tinkhauser et al. 2018).

Although the scientific and clinical utility of STN LFPs is already well established, numerous questions on the basic biophysics of these signals remain unanswered. For example, how many STN neurons contribute to the clinical beta signal? What is the degree of synaptic synchrony necessary to create the beta signal? Where are the synchronized neurons located within the STN? Experimentalists have attempted to address some of these questions by coupling microelectrode recordings of single units in the STN with macroelectrode LFP results (Kühn et al. 2005; Marmor et al. 2017; Shimamoto et al. 2013; Yang et al. 2014). Even still, it is currently impossible to individually and simultaneously record from the huge number of neurons responsible for the LFP signal. To address this gap in scientific knowledge, several groups have developed advanced computational modeling methods for simulating LFPs (e.g., Einevoll et al. 2013; Lempka and McIntyre 2013). Modern LFP simulations are capable of explicitly representing thousands of anatomically and electrically realistic neuron models, as well as their individual synaptic inputs. These neural source models are coupled to volume conductor electric field models to then calculate the voltage recorded by the electrode. This computational modeling approach enables detailed dissection of the underlying biophysics of the LFP signal.

First-generation STN LFP models have provided some generalized results on the basic relationships between STN neural synchrony and the spatial extent of the recording volume (Lempka and McIntyre 2013). However, those initial analyses relied on spherical populations of uniformly distributed STN neurons perfectly centered around the DBS electrode. In reality, the STN is a complex three-dimensional (3D) volume (Plantinga et al. 2018), where the density of neurons varies throughout the nucleus (Lévesque and Parent 2005) and the DBS electrodes intersect the nucleus at an oblique angle. As such, each electrode contact is surrounded by a different density and distribution of neurons with different firing characteristics, and these details are likely to play an important role in the recorded signals. Therefore, we developed a patient-specific STN LFP modeling framework and directly compared the simulated LFPs with clinical LFP recordings from the patient. Given multiple simultaneous recording pairs from the DBS electrode, it was possible to define a theoretically optimal location and radius of beta synchrony within the STN LFP model that best matched the clinical recordings. The optimized model predicted the origin of beta synchrony to be in the dorsolateral STN, as numerous previous clinical analyses have also concluded (Chen et al. 2006; Ince et al. 2010; Yoshida et al. 2010; Zaidel et al. 2010). However, the model offers the first quantitative estimate of the spatial extent of that recording volume, the number of neurons responsible, and their synaptic input characteristics. These results enhance our ability to interpret clinical LFP recordings at the cellular level and provide scientific guidance for the design of DBS technology focused on the use of subthalamic beta activity in closed-loop algorithms.

METHODS

The goal of this project was to build an anatomically and electrically accurate model of LFPs recorded from DBS electrodes implanted in the human STN. The computer codes associated with the creation of this model have been uploaded to https://github.com/Nickmaling/STN_LFP_Model and are publicly available under the terms of the Gnu Public License V.3. We created a patient-specific model that was based on a male subject (age = 52 yr) diagnosed with tremor-dominant Parkinson’s disease (disease duration = 4 yr) and implanted with an Activa PC+S DBS system (Medtronic, Minneapolis, MN). The subject was selected from an ongoing clinical investigation at Stanford University (Quinn et al. 2015), and we studied the STN on the right side of his brain. The subject had an excellent response to DBS treatment, with the lateralized Unified Parkinson’s Disease Rating Scale dropping from a preoperative score of 20 to a score of 2 at the 1-yr follow-up. Throughout his first 3 yr of DBS, monopolar stimulation was delivered exclusively from contact 1. Use of the Activa PC+S system enabled us to obtain chronic LFP recordings from the DBS electrodes (Stanslaski et al. 2012). The example clinical LFP data we used were acquired at the 1-mo postoperative follow-up visit. Given that our proof-of-concept analysis was performed at a single time point, it should be noted that the optimized model parameters fit to this patient might not share the same parameters that would be seen in the long-term chronic condition. This project was reviewed and approved by both the Case Western Reserve University and Stanford University institutional review boards. The subject provided informed written consent to participate in the research project.

Anatomical model.

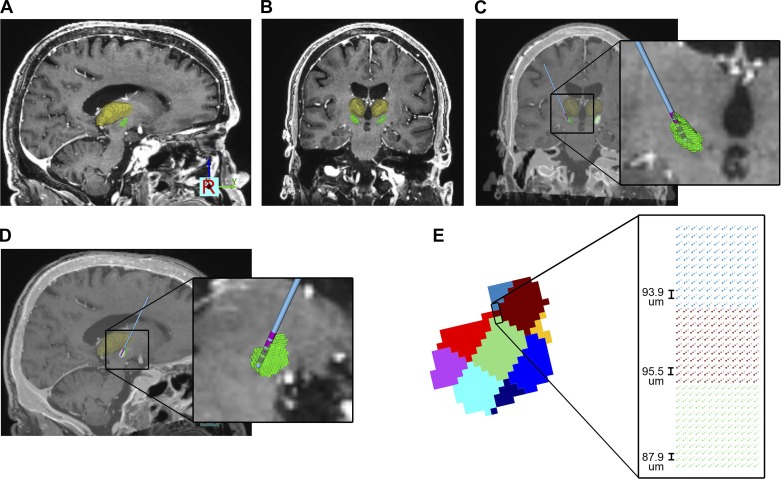
We based our patient-specific anatomical model on CT and MRI data acquired from the patient as part of his standard of care for DBS surgery. A preoperative T1-weighted MRI was used as the anatomical basis for the overall model (Fig. 1). To define the location and position of the STN in our subject, we relied on a 3D volume estimate of the elderly STN (Keuken et al. 2013) placed within MNI152 space. The Harvard-Oxford MNI152 brain atlas (https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/Atlases), consisting of volumetric representation of several basal ganglia nuclei, was then fit to the patient using a 9-degree-of-freedom linear transformation. The subsequently fitted brain atlas provided an STN volume of 163 mm³ that had a centroid located at X = −12.9, Y = −0.2, Z = −2.6 mm relative to the patient’s mid-commissural point (Fig. 1). The postoperative CT was coregistered with the preoperative MRI to determine the DBS lead location. We then defined the location of the four electrodes by placing a virtual 3389 DBS lead within the metal artifacts in the postoperative CT scan (Fig. 1).

Fig. 1.

Anatomical model. A and B: preoperative MRI and 3-dimensional brain atlas fit to the patient [green volume, subthalamic nucleus (STN); yellow volume, thalamus; other nuclei not shown for clarity]. C and D: postoperative CT coregistered to the MRI and used to define the deep brain stimulation (DBS) lead location (blue shaft, pink contacts). E: STN volume divided into 9 segments that represented different regions of neuron cell density. Each voxel in the STN volume was populated with grid of points for the location of the STN neuron cell bodies.

Histological studies of the human STN have documented nonuniform neuronal densities as a function of location within the nucleus (Hardman et al. 2002; Lévesque and Parent 2005). These estimates suggest a neuronal density of ~1,000 neurons/mm³ in the dorsal STN and ~2,000 neurons/mm³ in the ventral STN. Lévesque and Parent (2005) explicitly calculated neuronal densities from nine different regions within the human STN (Table 1), using post mortem evaluations of five men with no known pathology. In turn, we voxelized our patient-specific STN volume to create nine corresponding regions (Fig. 1, D and E). A 3D point cloud was created for each region based on the specified neuronal densities (Table 1). Each point in the STN volume represented a putative location for the cell body of a neuron model. The patient-specific model contained a total of 235,280 STN neurons. These neuron models within the STN volume provided the electrical sources for the LFP simulations (see below). Every neuron was positioned with the longest axis of their dendritic field oriented along the rostrocaudal axis of the STN (Hammond and Yelnik 1983).

Table 1.

Neuronal densities for each sector of the STN

STN Sector	Neuronal Density, neurons/mm3
Anterior dorsal	1,207
Anterior central	1,148
Anterior ventral	1,196
Middle dorsal	1,431
Middle central	1,472
Middle ventral	1,611
Posterior dorsal	1,269
Posterior central	1,626
Posterior ventral	1,872

STN, subthalamic nucleus.

Electrical model.

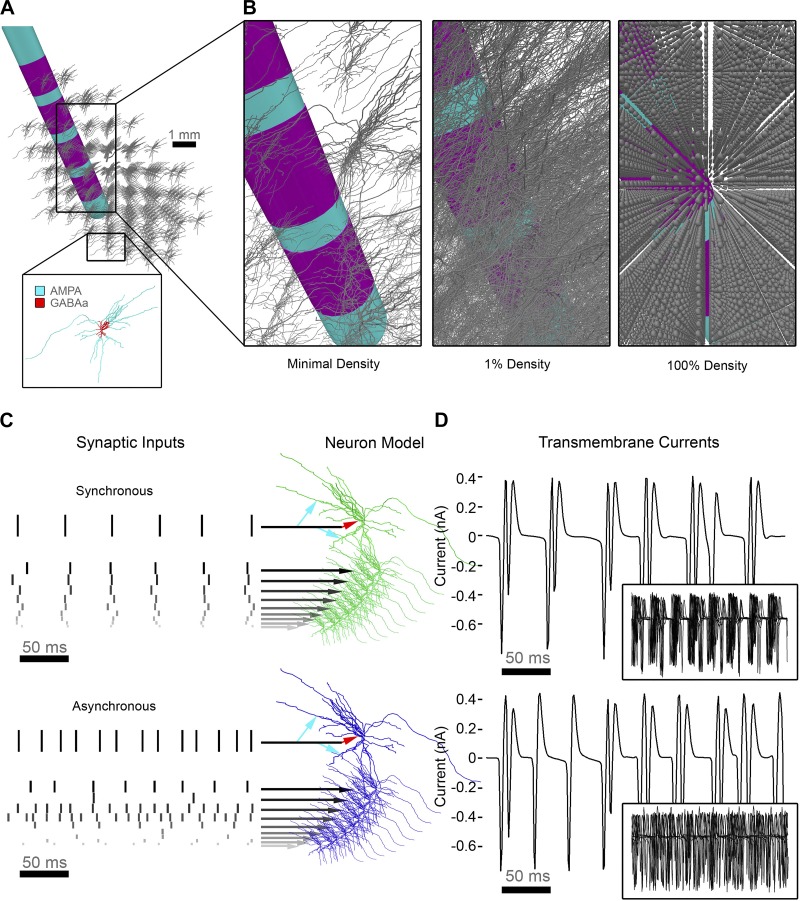
The electrical source component of the overall LFP model system consisted of populations of multicompartment cable models designed to represent STN projection neurons (Fig. 2). The neuron models were based on anatomical reconstructions of the STN neuron morphology (Sato et al. 2000) and the electrical properties of STN neurons (Gillies and Willshaw 2006; Miocinovic et al. 2006). Each STN neuron received 290 different synaptic inputs distributed over its structure for each synaptic input timing trigger (see details below). Each somatic and dendritic compartment received either an excitatory or inhibitory synaptic input, with the inhibitory currents being slightly delayed (Baufreton et al. 2005). Dendritic compartments that were >100 μm from the soma were assigned glutamatergic (excitatory) inputs, and the soma and dendritic compartments that were <100 μm were assigned GABAergic (inhibitory) inputs (Lempka and McIntyre 2013).

Fig. 2.

Neuron source models. A: relative positioning of the deep brain stimulation (DBS) electrode and subthalamic nucleus (STN) neuron models with 1 neuron represented in each voxel of the STN volume. Each neuron received inhibitory (GABA_A) and excitatory (AMPA) synaptic input currents. B: zoomed-in view of the full arborizations of the neuron models displayed at different densities. At the full model density, spheres represent the soma locations. C: each of the 235,280 STN neuron models received a time-varying oscillatory input pattern that triggered their synaptic currents. Inputs were either synchronous (top; green) or asynchronous (bottom; blue), with synchronous inputs designed to represent a 20-Hz beta pattern. D: transmembrane current traces from the soma of a single neuron receiving synchronous (top) or asynchronous (bottom) synaptic inputs. Insets show an overlay of 10 different neurons demonstrating highly correlated output for the synchronous case and no correlation for the asynchronous case.

The synaptic inputs were represented as additional transmembrane currents in the neuron model [I_syn = g_syn (V_m − E_syn)]. We assigned the excitatory AMPA synapses a maximum conductance (g_max) of 0.5 nS and a reversal potential (E_rev) of 0 mV, and the inhibitory GABA_A synapses a g_max of 0.5 nS and E_rev of −80 mV. For a complete description of the synaptic input models and parameters, see Lempka and McIntyre (2013) and Destexhe et al. (1994). To simulate all of the transmembrane currents generated by the neuron models, we used NEURON within the Python programming environment (Hines et al. 2009).

Each STN neuron model was designated to receive either a synchronous beta pattern of synaptic inputs, or randomized uncorrelated synaptic inputs (Fig. 2D; Lempka and McIntyre 2013). For synchronous synaptic activity with a 20-Hz population mean, we added Gaussian noise with a standard deviation of 6.25 ms to the mean synaptic input times for each individual neuron. We also separated the onset times of synaptic inputs to the individual compartments of a particular neuron by randomly selecting from a normal distribution with a standard deviation of √6.25 ms about the mean synaptic input time for that individual neuron. These inputs represented synaptic activation times, which triggered the synaptic current associated with the given compartment to become active. For a complete description of the synaptic input times used to generate beta oscillations, see Lempka and McIntyre (2013).

The asynchronous population of STN neurons were driven by randomized uncorrelated synaptic inputs (Fig. 2D). We constructed the asynchronous inputs from an input frequency, F_i, randomly drawn from an exponential distribution. The exponential distribution had a mean of 20 Hz and was truncated to contain only values between 2 and 200 Hz. We used these means to construct a time-domain input with a time constant of 1/F_i, adding the same Gaussian noise as described above for the synchronous synaptic activity.

Neurons in the synchronous pool receiving the beta pattern of synaptic inputs exhibited highly correlated activity, whereas the neurons in the asynchronous pool receiving the randomized inputs exhibited uncorrelated activity (Fig. 2E). For the LFP simulations (see below), we represented the net current flowing across the membrane of each compartment of each neuron as an independent current source. We calculated the time-dependent transmembrane currents for a period of 1 s.

The volume conductor model consisted of a finite element model (FEM), which included a DBS electrode with the dimensions of the Medtronic 3389 DBS lead (Lempka and McIntyre 2013). We surrounded the DBS electrode by a 0.1-mm interface layer that mimicked tissue encapsulation. We assigned the bulk brain tissue an isotropic conductivity of 0.2 S/m, typical of gray matter (Gabriel et al. 1996), and assigned the interface layer an isotropic conductivity of 0.32 S/m (Howell and McIntyre 2016). The FEM solution was generated in Comsol v5.1 (COMSOL, Burlington, MA).

Integrated STN LFP Model.

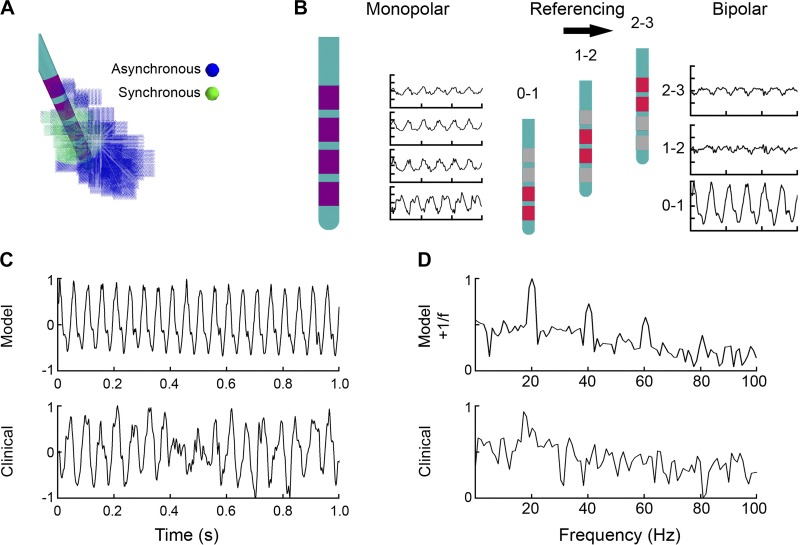
To simulate STN LFP recordings, we coupled the volume conductor model and electrical source models using a reciprocity-based solution (Lempka and McIntyre 2013; Moffitt and McIntyre 2005; Fig. 3). In the coupled FEM-neuron population model, each compartment of each neuron was represented as an independent current source at the appropriate spatial location in the FEM. If any part of a STN neuron model intersected the DBS lead, that neuron was removed from the analysis. The recording voltage was calculated by summing the voltages generated at the electrode by the transmembrane currents of the individual neural compartments. This approach can be formulated mathematically as Φ = K × I, where Φ is a (1 × t) vector containing the voltages recorded at t instances in time on the electrode, K is a (1 × j) vector containing the voltages that would be impressed at the recording electrode for a unit current at the location of each of the j individual neuron compartments, and I is a (j × t) matrix containing the transmembrane currents for the individual neural compartments at each time step. The I matrix was calculated in NEURON, whereas each value in the K vector was derived from the FEM using a reciprocal solution.

Fig. 3.

Integrated subthalamic nucleus (STN) local field potential (LFP) model example. A: each STN neuron received either synchronous (green) or asynchronous (blue) synaptic inputs. This initial example model used a radius of 3 mm, centered on contact 1, to define the synchronous neurons. B: the voltage recorded on each deep brain stimulation (DBS) electrode contact was defined from the sum of all transmembrane currents generated by each compartment of each neuron using a reciprocity-based solution. Bipolar recording pairs were calculated as the difference between the appropriate monopolar recordings. C: comparison of the time-domain simulated LFP with the clinical LFP recorded from the 0–1 contact pair. Normalized amplitudes are expressed in arbitrary units. D: power spectra of the model and clinical LFPs show beta activity in both cases. The initial model example shows high-amplitude narrow peaks not only at 20 Hz but also at its harmonics (40, 60, and 80 Hz).

The reciprocal solution involves placing a unit current source (i.e., 1 A) at the recording electrode and solving for the scalar potentials generated at each node in the FEM. By the theorem of reciprocity, the voltage at a given node in the FEM can be interpreted as the voltage that would be generated at the recording electrode for a unit current. Therefore, the contribution of each neural compartment to the recorded waveform (i.e., individual values in the K vector) can be calculated using interpolation of the voltages from the nearest nodes surrounding each neural compartment.

The Φ value for each DBS electrode contact represents the simulated monopolar LFP. The bipolar LFP was created by subtracting monopolar pairs with the same referencing scheme used for the clinical LFP recordings (Fig. 3B). To coincide with the clinical LFP recordings (Quinn et al. 2015), we low-pass filtered the model LFPs at 100 Hz and downsampled them to 422 Hz. LFP analysis consisted of time-domain amplitude measurements and power spectral density (PSD) measurements. Time-domain amplitude was computed as the root-mean-square (RMS) amplitude of 1 s of the model LFP. PSDs were computed using Welch’s method with a window size of 211, 50% overlap, and a fast Fourier transform length of 844. Beta power was defined as the mean of the PSD in the 15- to 22-Hz band (Blumenfeld et al. 2017). The model lacked a 1/f trend in its power spectra, a feature commonly observed in experimentally recorded LFPs (Milstein et al. 2009). Therefore, a 1/f signal was added to all model LFPs for visual comparison purposes.

We elected to use normalized amplitudes to compare the model and clinical LFPs, which is also common practice in clinical LFP studies. This choice was also made because of uncertainty in the details of proprietary recording hardware and filtering circuitry of the Activa PC+S device. However, it should be noted that the model LFPs underestimated the Activa PC+S recording amplitudes by a factor of ~2 (data not shown).

Model analysis.

We used our model to address three basic questions related to STN LFPs. First, what is the impact of the STN anatomy on the amplitude of the recorded signal? Second, what is the effect of moving a synchronous population of neurons within the STN? Third, what location and radius of synchronous STN neurons best matches the clinical recordings?

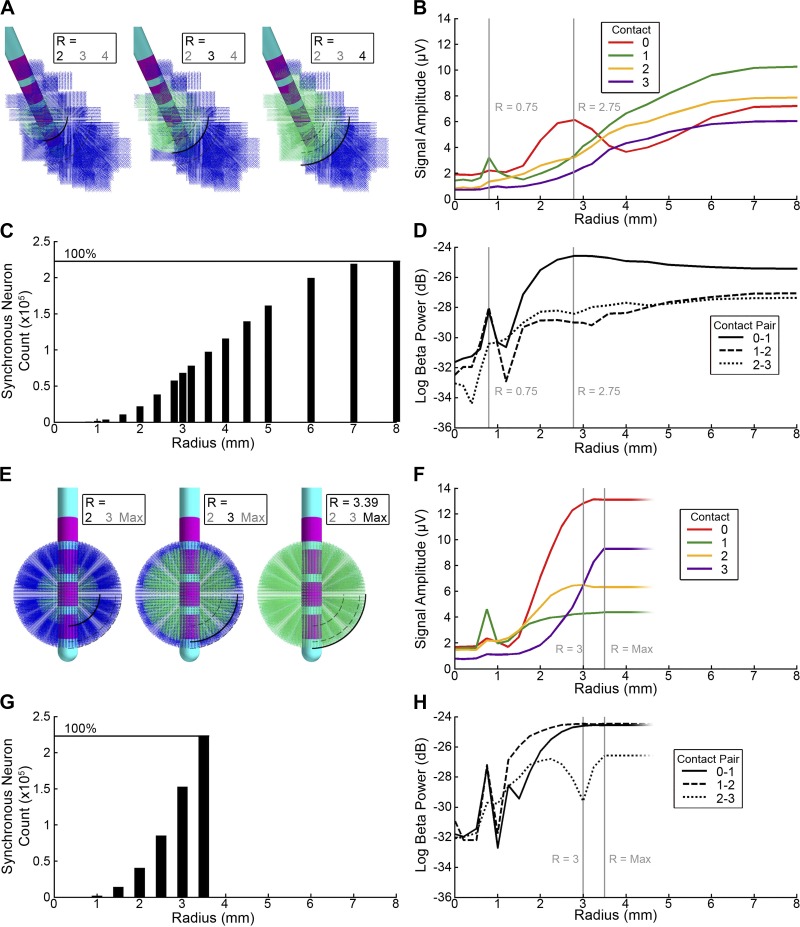
To explore the impact of incorporating a realistic STN anatomical volume into the LFP simulations, we compared the results generated from the patient-specific STN volume with an idealized spherical STN volume (Fig. 4). For the spherical STN, we constructed a uniformly spaced spherical grid that was volume matched to the patient-specific STN volume. We populated each node in the spherical grid with a full multicompartment STN neuron model, and the neurons received the same synaptic inputs as described for the patient-specific STN model. We then positioned contact 1 of the DBS electrode at the geometric center of the spherical volume of STN neurons.

Fig. 4.

Radius of synchronous subthalamic nucleus (STN) neurons. A–D: patient-specific STN local field potential (LFP) model. A: variations in the size of the synchronous neural population centered on contact 1 within the STN volume. B: the root-mean-square (RMS) amplitude of the time-domain LFP recorded on each monopolar contact. Peaks at radius (R) = 0.75 and 2.75 mm reflect the envelope of the sphere of synchronous neurons passing the boundary of contact 1 and 0, respectively. C: the number of neurons in the model receiving synchronous input. D: beta power of the model LFP for each of the bipolar contact pairs showing a maxima on contact pair 0–1 at R = 2.75 mm. E–H: spherical STN LFP model. E: variations in the size of the synchronous neural population centered on contact 1 within a spherical volume. The sphere has a volume matched to the patient-specific STN (163 mm³). F: the RMS amplitude of the time-domain LFP recorded on each monopolar contact. Vertical lines represent R = 3 mm, where the amplitudes on contacts 2 and 3 are nearly identical, and R = 3.38 mm, where the radius of the synchronous population equals that of the volume-matched sphere. G: the number of synchronous neurons in the model increases with the cube of the radius until it fills the sphere. H: beta power for each bipolar contact pair. The case at R = 3 mm, where contacts 2 and 3 have nearly identical amplitude, is represented as an abrupt drop, a consequence of the bipolar referencing scheme subtracting one from the other. In A and E, the bold number below R indicates the radius of synchronous activity.

To explore the effect of changing the radius of the synchronous activity, we first defined an arbitrary point as the center of the population of synchronous neurons. STN model neurons whose cell bodies were within a radius R were then designated as part of the synchronous population. We drew the synaptic input times of these neurons from the pool of synchronous inputs. Synaptic inputs times for STN neurons that were outside of R were drawn from the asynchronous pool. The R values for the patient-specific STN reconstruction varied from 0 (100% asynchronous) to 8 mm (100% synchronous; Fig. 4A). The R values for the spherical comparator model varied from 0 (100% asynchronous) to 3.5 mm (100% synchronous; Fig. 4E).

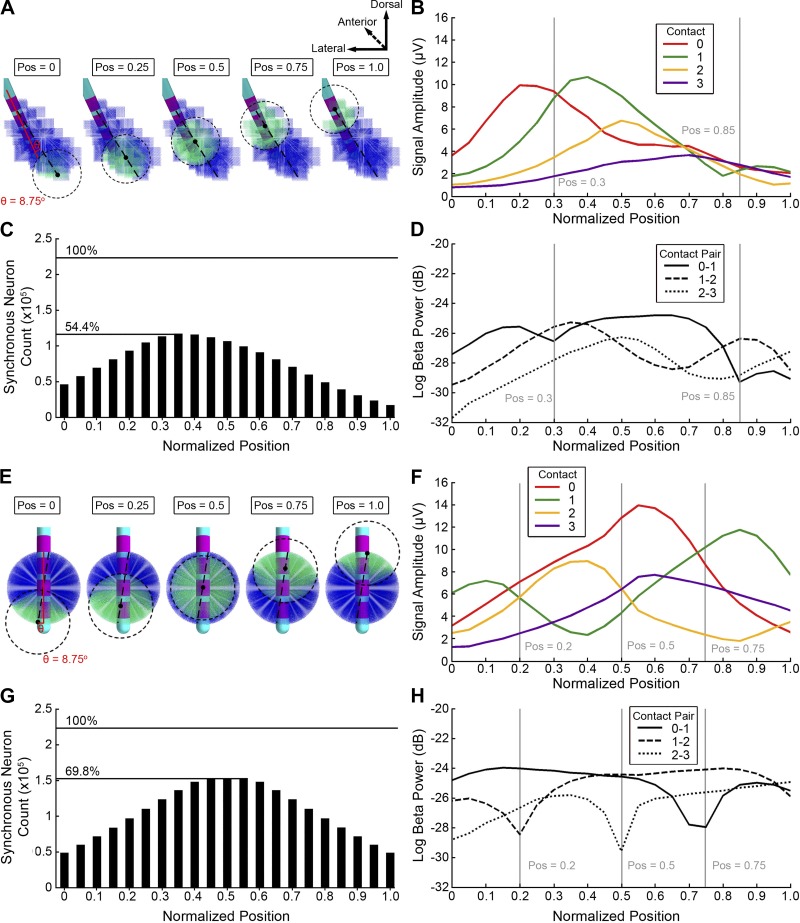
To explore the effect of changing the location of the synchronous pool of neurons within the STN volume, we defined the long axis of the STN and moved the pool along that axis (Fig. 5). The long axis of the STN was defined by determining an anchor point within the volume that was farthest from the center of mass of the STN. The second anchor point was defined as the point farthest from the first point. These two points then formed a vector defining the long axis of the STN volume. The location of the center of the synchronous population of neurons was then centered on a point that moved along the long axis of the STN between either extremes. Distances are expressed as a proportion of the long axis of the STN with a position of 0.0 corresponding to the ventral-medial aspect of the STN and a position of 1.0 corresponding to the dorsal-lateral end.

Fig. 5.

Location of synchronous subthalamic nucleus (STN) neurons. A–D: patient-specific STN local field potential (LFP) model. A: 3-mm radius of synchronous neurons in different positions along the long axis of the STN. B: the root-mean-square (RMS) amplitude of the time-domain model LFP on each of the monopolar contacts. C: the number of STN neurons in the model receiving synchronous input as the synchronous population is moved. D: beta power of the model LFP for each bipolar contact pair showing minima on contact pairs that correspond to positions where the monopolar amplitudes are similar. E–H: spherical STN LFP model. E: 3-mm radius of synchronous STN neurons in different positions within a spherical volume. The trajectory of the synchronous population, relative to the deep brain stimulation lead, had the same angle (θ = 8.75°) as the trajectory used in the patient-specific case. F: the RMS amplitude of the time-domain spherical model LFP on each of the monopolar contacts. G: the number of neurons in the spherical model receiving synchronous input as the synchronous population is moved. H: beta power for each bipolar contact pair in the idealized spherical model. Vertical lines show local minima where the monopolar channels are similar in amplitude. Pos, position.

Model optimization.

To compare the patient-specific model LFP with the clinical LFP, we developed a fitness metric that captured important features of the clinical LFP. For this optimization we considered the shape of the power spectrum (implicitly including the relative magnitude of the peak in the beta band, without inclusion of the 1/f addition to the model) and the distribution of power in the beta band across the electrode array. To capture these features, we used a fitness metric that included two components. The first component was the Pearson’s correlation coefficient between the model power spectra and the experimental power spectrum. The mean of the three coefficients, one for each comparison of the contact pairs, constituted 50% of the fitness metric. We computed the remaining 50% of the fitness metric using an asymmetry ratio. This asymmetry ratio compared the relative normalized narrowband beta power and rewarded the model if a similar proportion of energy was in the beta band. The fitness metric can be expressed as follows:

$$\frac{1}{6}\left[r_{01}+r_{12}+r_{23}+e^{-\ln {\left(\frac{B{m}_{01}}{B{c}_{01}}\right)}^2}+e^{-\ln {\left(\frac{B{m}_{12}}{B{c}_{12}}\right)}^2}+e^{-\ln {\left(\frac{B{m}_{23}}{B{c}_{23}}\right)}^2}\right],$$ (1)

where r is the Pearson’s correlation coefficient between the normalized power spectra of the model LFP and the clinical LFP for each contact pair, and Bm and Bc are the normalized beta power in the model and clinical LFP, respectively. This fitness metric gave a value that varied between 0 and 1, and satisfies the condition that a relative beta power twice as high as expected is penalized with equal severity as a beta power half as high as expected. Importantly, this metric captured similarity across all available contact pairs and utilized the full set of clinically recorded LFPs to match the model LFPs.

RESULTS

Our simulations of STN LFPs were designed to mimic the anatomical and electrical details of a tremor-dominant PD patient implanted with an Activa PC+S DBS system. The model consisted of 235,280 STN neurons positioned around a 3389 DBS electrode. To demonstrate the impact of the STN anatomy, we compared the patient-specific simulations with the results generated, assuming an idealized sphere of STN neurons. To evaluate the role of neuronal synchrony, we drove a population of STN neurons with a beta pattern of synaptic inputs and modulated the location and radius of that synchronous population. We found that explicitly representing the STN anatomy played an important role in the LFP recordings, and modulating the position and radius of neuronal synchrony substantially affected the amplitude and power of beta activity recorded by the DBS electrodes. Finally, we used clinical recordings to optimize the patient-specific LFP model and quantitatively estimate the position and radius of synchronous beta activity within the STN.

Radius of synchrony.

A primary motivation for developing our anatomically and electrically accurate model of STN LFPs is to address the basic biophysical question of how many neurons need to be synchronized to generate the clinical beta signal. We began to explore that question by driving a concentrated group of STN neurons with a highly synchronous beta pattern of activity (Fig. 3). Initially, we arbitrarily set up the model so that neurons within a radius of 3 mm of the center of contact 1 received synchronous input, whereas neurons outside that radius received asynchronous input. The monopolar representation of the LFP on each contact was converted into a bipolar LFP by subtracting each combination of contact pairs (Fig. 3B). This initial patient-specific bipolar LFP model showed high beta activity in accordance with the clinically recorded LFP from the same contact pair (Fig. 3C). However, this initial model LFP contained harmonic peaks absent in the clinical LFP (Fig. 3D).

To evaluate the role of the radius of synchronized activity on the LFP, we incrementally increased the radius from 0 and 8 mm, until every model STN neuron was receiving synchronous input (Fig. 4). The location of the center of the synchronous population remained fixed at the center of contact 1. Increasing the radius of synchronized neurons magnified the mean monopolar amplitude of the LFP in manner that was strongly correlated with the number of synchronous neurons (r = 0.89; Fig. 4, A–D), with exceptions at R = 0.75 and 2.75 mm. The time-domain amplitude was highest on the most distal contact 0 for smaller populations, but fell off for greater radii. The remaining three contacts showed increasing time-domain amplitudes, consistent with their distance from the synchronous neural population. Beta power measurements followed the same trend as time domain amplitude, with the same peaks at R = 0.75 and 2.75 mm (Fig. 4D).

The peaks at R = 0.75 and 2.75 mm can be explained by a phase reversal of the effective dipole of the neurons. When the radius of synchronous neurons expanded past the distal borders of contacts 0 and 1, at R = 0.75 and 2.75 mm, respectively, a phase reversal occurred. A neuron located at the superior aspect of a contact would have a contribution to the LFP equal and opposite to that of a neuron located inferior to the contact, assuming the geometry and orientation of the neurons remained constant. As the radius of synchronous neurons expanded beyond the border of the contact, more current sources were effectively canceled out by equal and opposite neurons in the distal part of the synchronous field. This effect was not observed for contacts 2 and 3, because contact 2 was partially outside the STN and contact 3 was located entirely outside of the STN.

The volume-matched spherical comparison LFP model also showed a correlation between the time domain amplitude and gross number of synchronous neurons (r = 0.76; Fig. 4, E–H). As the radius of synchronous neurons increased, contacts 0 and 2 exhibited the highest recording amplitudes, and contacts 0, 1, and 2 were affected by the phase reversal described above. The idealized sphere was more efficiently filled by the expanding radius of synchronous neurons, reaching maximum synchronicity at 3.38 mm.

Location of synchrony.

The position of the synchronous population was moved along the long axis of the STN. We expressed the position as a normalized quantity with 0.0 being the most ventral-medial aspect of the STN and 1.0 being the dorsal-lateral border (Fig. 5, A–D). The long axis of the STN had a length of 10.2 mm, and the primary vector formed a compound angle of 8.75° with the trajectory of the electrode. We fixed the radius of synchronization to 3.0 mm and moved it from the ventral-medial border to the dorsal-lateral border of the STN. The mean monopolar amplitude was correlated with the gross number of synchronous neurons (r = 0.58). The maximum number of synchronous neurons (128,020, or 54.4% of the total population) occurred at a position of 0.35.

The peak in the time-domain amplitude recorded at each contact occurred when the average distance from the center of the contact to the center of the synchronous population was 1.9 mm (Fig. 5B). The time-domain amplitudes were lower in the dorsal-lateral STN because of the geometry of the nucleus boundary and the lower neural density, which resulted in fewer synchronous neurons (Fig. 5C). Beta power as a function of the position of the synchronous neurons tracked the time-domain amplitude of the respective contacts used in the bipolar recording (Fig. 5D).

The volume-matched spherical LFP model had a maximum number of synchronous neurons (164,225) at the position of 0.5 (Fig. 5G). The time-domain amplitudes exhibited a phase reversal when the center of the contact was close to the center of the synchronous population (Fig. 5F). For example, the local minima for the contact 1 monopolar amplitude coincided with a position of 0.4. The beta power then followed the synchronous population as it traversed the volume of neurons (Fig. 5H).

Model optimization.

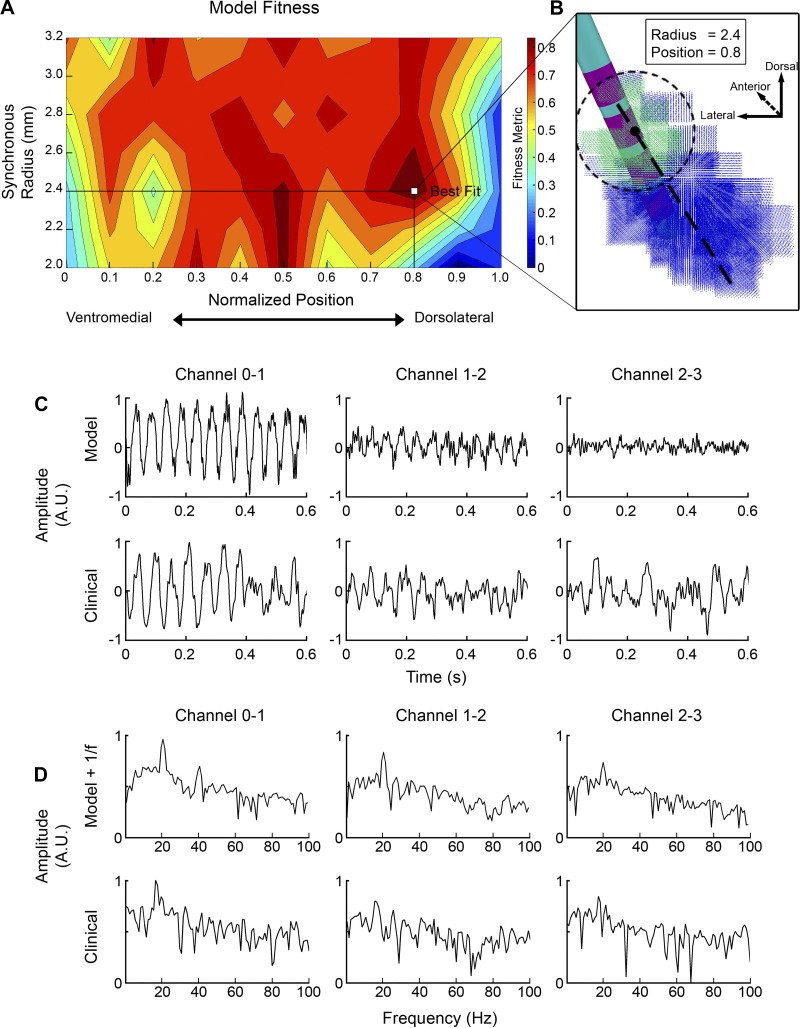
We used the patient-specific LFP model to estimate the location and radius of synchronous beta activity within the STN using clinically recorded LFPs from each of the three bipolar pairs (Fig. 6; Quinn et al. 2015). The model was swept through 77 parameter pairs of radius (ranging from 2.0 to 3.2 mm) and normalized position (ranging from 0.0 to 1.0) of synchronized activity in the STN. Model fitness was assessed using Eq. 1 (Fig. 6A). Parameter sets with low amplitude and extreme positions (close to 1 or 0) showed low model fitness, because very few neurons were receiving synchronous input in those cases. Parameters sets with a larger radius and more central positions showed high beta power; however, they poorly matched with the clinical recordings with respect to the distribution of beta power across the electrode array. One exception was an island of high fitness with a radius of ~2 mm and a position of 0.5. These model parameters corresponded to the synchronous volume approximately centered on contact 1. However, the peak model fitness was achieved at radius of 2.4 mm and position of 0.8, which corresponded to the synchronous volume approximately centered on contact 2 (Fig. 6, A and B). These optimized parameters consisted of 36,580 neurons localized in the dorsolateral aspect of the STN. The optimized model showed a high recording amplitude on contact pair 0–1 and lower amplitudes on the other pairs, similar to the clinical data (Fig. 6C). Additionally, the model power spectra compared favorably with the clinical power spectra (Fig. 6D). When compared with our naive initial STN LFP model parameters (Fig. 3), harmonics were noticeably reduced on the 0–1 contact pair and absent on other contact pairs.

Fig. 6.

Optimized subthalamic nucleus (STN) local field potential (LFP) model. A: search of the parameter space. The fitness metric incorporated coherence between the clinical and model power spectra, as well as the relative normalized beta power across the contact pairs. B: visual schematic of the optimized STN LFP model. The positions of synchronized and unsynchronized neurons are shown in green and blue, respectively. C: comparison of the time-domain results for the model and clinical LFPs. In both cases, the highest amplitude signals were recorded across contact pair 0–1. A.U., arbitrary units. D: comparison of the model and experimental power spectra. Both cases show high beta power for the contact pair 0–1. The optimized model shows much lower amplitude harmonics relative to the naive patient-specific model used in Fig. 3.

DISCUSSION

Scientific analyses of LFP data acquired from DBS electrodes have expanded rapidly over the last decade, and these results are beginning to drive novel advances in the clinical application of DBS technology. However, detailed biophysical understanding of the anatomical and electrical variables that dictate the clinically recorded LFP signals has been limited. This study provides the first quantitative estimates of the spatial extent of the recording volume and the number of neurons responsible for the beta activity commonly observed in the human STN. The model also allowed us to explore the roles of patient anatomy and neural synchrony in defining the magnitude and power of the recorded signal. Most importantly, these results were derived from first principles, with explicit representation of the synaptic input currents, neuronal spiking activity, and volume-conducted electric fields, all integrated within an anatomically realistic context (Figs. 2 and 3).

We found that monopolar recordings followed relatively simple and expected relationships; however, the patient-specific LFP model results highlight the complexities of understanding and interpreting bipolar recordings from clinical DBS electrodes (Figs. 4 and 5). Given that bipolar recordings are the preferred (or often required) method of clinical data collection (e.g., Marmor et al. 2017), the model provides some important insight that should be considered when LFP signals are used to estimate the localization of neuronal synchrony (Fig. 6). For example, the center of neural synchrony is not typically centered between the contact pair that has the greatest signal. As such, one must use all of the available recording pairs together to then determine which of the individual contacts is actually positioned most closely to the center of neural synchrony (Figs. 5 and 6). Interestingly, the optimized model predicted that the center of neural synchrony in our example patient was closest to contact 2, but it was actually stimulation through contact 1 that provided the greatest therapeutic benefit. Although this proof-of-concept study only included one patient, this result reinforces the concept that many different factors dictate the optimal contact for stimulation, and LFP-based identification of a contact associated with high neural synchrony may only be one piece of the clinical puzzle.

One key benefit of DBS LFPs is the opportunity to simultaneous recorded from multiple contacts and then use that information to help localize the source. Our conclusion that a synchronous dorsolateral region best fit the experimental recordings was not necessarily because of proximity of the synchronous population to a given contact (e.g., see Fig. 6A, position 0.2, which was very close to contact 0). Instead, the optimized model was defined using the combined signals observed on all of the contact pairs. This highlights the point that coupled integration of as many independent pieces of data as possible (e.g., imaging, anatomy, and electrophysiology) can help to constrain the number of realistic solutions that are possible for the “inverse problem” of source localization that theoretically has an infinite number of solutions.

The substantial growth in clinical STN LFP data collection for scientific analyses has provided the foundation for wide-ranging correlative associations between beta-band activity and parkinsonian symptoms (Blumenfeld and Brontë-Stewart 2015). Pragmatic translation of these scientific findings are now providing advances to the clinical practice of DBS in the form of advanced intraoperative targeting algorithms (e.g., Valsky et al. 2017) and electrode contact selection methods for therapeutic stimulation (e.g., Tinkhauser et al. 2017). In addition, the chronic recording of STN LFP beta can also be used as an electrophysiological biomarker in adaptive DBS control systems (Meidahl et al. 2017). We propose that as these various LFP-based clinical algorithms attempt to become more sophisticated, they will need to rely on a more detailed and quantitative understanding of the underlying biophysical factors dictating the recorded signals. Unfortunately, interpretation of LFPs can be influenced by many different factors. Therefore, our approach has been to focus on understanding and accounting for variables that are likely to play the biggest role in creating patient-to-patient variability in STN LFP recordings. These variables include the anatomy of the patient, the position of the electrode, and the location/size of neural synchrony. Our results show that all of these factors are important in shaping the LFP and that a patient-specific modeling approach can be used to account for these sources of variability (Figs. 4 and 5).

The LFP models created in this study are exceptionally complicated and technically demanding to implement. As such, their direct application in large-scale clinical research studies or integration into LFP-based clinical algorithms is unlikely in the foreseeable future. Nonetheless, they do represent a theoretical “gold standard” that can be used to develop and evaluate simplified, but still patient-specific, LFP models that are capable of capturing the salient features of the detailed model system while also being computationally tractable for larger scale analyses. Such simplified models could become especially useful as clinical DBS systems greatly expand the number of electrode contacts available for both stimulation and recording (Bour et al. 2015; Tinkhauser et al. 2017). This added electrode complexity provides more flexibility for therapeutic optimization but will likely also require algorithmic tools to help process and interpret the LFP data to enable identification of the optimal DBS control system for the patient. For example, if the underlying goal of a closed-loop DBS algorithm is to efficiently stimulate the neurons that are responsible for creating the beta oscillation, then the amplitude of the beta oscillation recorded at each contact provides only part of the information needed to customize the therapy to the patient. By calculating a center and radius of the synchronous population, a patient-specific LFP model can provide a “target volume” that can be used not only in defining an optimal recording configuration for chronic monitoring but also in stimulation contact selection and the tuning of stimulation amplitudes to optimize modulation of that target.

Although our patient-specific STN LFP model system is highly detailed, it still suffers from a range of limitations. One of the most important limitations in any patient-specific model of DBS is the accuracy in which the location of the electrode can be defined within the anatomy. We used commonly accepted methods in patient-specific DBS modeling with great attention to detail, but even still, the relative location of the electrode to the STN could be off by ~1 mm in any direction. These potential localization errors do not necessarily impact the general findings of this study, but they could be an important consideration for future attempts to correlate patient-specific electrode locations with anatomical regions of high neural synchrony.

One discrepancy with our model and the PC+S recordings was the model underestimating the raw signal amplitudes by a factor of ~2. If one takes the PC+S recordings as a gold standard, two physiological features may be able to reconcile this model limitation. First, human STN neurons are likely larger than the macaque STN neuron models used in our simulations. A scaling factor of 3 would be consistent with general brain size and nucleus size differences (Hardman et al. 2002), which would coincide with a larger magnitude of synaptic currents and membrane currents per neuron. Second, not all beta signals recorded by subthalamic DBS electrodes come from the STN. Volume-conducted currents from other brain regions (i.e., cortex) likely play a measurable role (Marmor et al. 2017), and the model ignores these external currents.

Another limitation of our model was the lack of an intrinsic 1/f distribution in the power spectrum, which is a common deficiency in LFP models typically attributed to ionic diffusion (Bédard and Destexhe 2009). In addition, the absence of a 1/f pattern in our model was also likely due to the homogeneity of the frequency of synaptic inputs. Replacing the constant frequency with inputs drawn from an exponential distribution can result in a 1/f pattern; however, this comes at the expense of overall model synchrony (which further exacerbates the recording amplitude limitation of the model) (data not shown). As such, the complex interplay between the heterogeneity of synaptic inputs and the 1/f distribution represent key questions for the future of LFP modeling.

Possibly the most unrealistic simplifying assumption in our analysis was the decision to represent regions of synchrony as a sphere. We viewed using this general assumption as a basic first step to begin the development of conceptual guidelines for interpreting clinical LFP signals. The model infrastructure allows for the use of any synaptic input pattern to any of the neurons and is well positioned to begin analyzing more complicated forms of synchrony. However, searching through that nearly infinite parameter space should be guided by specific anatomical connectivity patterns (i.e., hyperdirect vs. pallidal inputs) and precise electrophysiological hypotheses [i.e., high-frequency (~300 Hz) vs. low-frequency (~20 Hz) oscillations]. Therein lies the foundational motivation for developing this LFP modeling system, and this sets up the focus of our future investigations. Thankfully, parameterization of those future models will be aided by the growing opportunities to acquire simultaneous high-resolution and directional LFP recordings provided by the next generation of clinical DBS electrodes (Bour et al. 2015; Tinkhauser et al. 2017).

GRANTS

This work was supported by National Institutes of Health Grants R01 MH106173 and R01 NS086100.

DISCLOSURES

C. C. McIntyre is a paid consultant for Boston Scientific Neuromodulation and Kernel, as well as a shareholder in the following companies: Surgical Information Sciences, Autonomic Technologies, Cardionomic, Enspire DBS, and Neuros Medical.

AUTHOR CONTRIBUTIONS

N.M. and C.C.M. conceived and designed research; N.M. performed experiments; N.M., S.F.L., Z.B., H.B.-S., and C.C.M. analyzed data; N.M., S.F.L., H.B.-S., and C.C.M. interpreted results of experiments; N.M. and C.C.M. prepared figures; N.M. and C.C.M. drafted manuscript; N.M., S.F.L., H.B.-S., and C.C.M. edited and revised manuscript; N.M., S.F.L., Z.B., H.B.-S., and C.C.M. approved final version of manuscript.