Abstract
The problem of identifying functional connectivity from multiple time series data recorded in each of two or more brain areas arises in many neuroscientific investigations. For a single stationary time series in each of two brain areas statistical tools such as cross-correlation and Granger causality may be applied. On the other hand, to examine multivariate interactions at a single time point, canonical correlation, which finds the linear combinations of signals that maximize the correlation, may be used. We report here a new method that produces interpretations much like these standard techniques and, in addition, 1) extends the idea of canonical correlation to 3-way arrays (with dimensionality number of signals by number of time points by number of trials), 2) allows for nonstationarity, 3) also allows for nonlinearity, 4) scales well as the number of signals increases, and 5) captures predictive relationships, as is done with Granger causality. We demonstrate the effectiveness of the method through simulation studies and illustrate by analyzing local field potentials recorded from a behaving primate.
NEW & NOTEWORTHY Multiple signals recorded from each of multiple brain regions may contain information about cross-region interactions. This article provides a method for visualizing the complicated interdependencies contained in these signals and assessing them statistically. The method combines signals optimally but allows the resulting measure of dependence to change, both within and between regions, as the responses evolve dynamically across time. We demonstrate the effectiveness of the method through numerical simulations and by uncovering a novel connectivity pattern between hippocampus and prefrontal cortex during a declarative memory task.
Keywords: canonical correlation analysis, cross correlation, functional connectivity, kernel canonical correlation analysis, LFP
INTRODUCTION
When recordings from multiple electrode arrays are used to establish functional connectivity across two or more brain regions, multiple signals within each brain region must be considered. If, for example, local field potential (LFP) signals in each of two regions are examined, the problem is to describe the multivariate relationship between all the signals from the first region and all the signals from the second region, as it evolves across time, during a task. One possibility is to take averages across signals in each region and then apply cross-correlation or Granger causality (Brovelli et al. 2004; Granger 1969). Alternatively, one might apply these techniques across all pairs involving one signal from each of the two regions, and then average the results. Such averaging, however, may lose important information, as when only a subset of the time series from one region correlates well with a subset of time series from the other region. Furthermore, Granger causality is delicate in the sense that it can be misleading in some common situations (Barnett and Seth 2011; Ding and Wang 2014; Wang et al. 2008). We have developed and investigated a new method, which is descriptive (as opposed to involving generative models such as autoregressive processes used in Granger causality) and is capable of finding subtle multivariate interactions among signals that are highly nonstationary due to stimulus or behavioral effects.
Our approach begins with the familiar cross-correlogram, which is used to understand the correlation of two univariate signals, including their lead-lag relationship, and generalizes this in two ways: first, we extend it to a pair of multivariate signals using the standard multivariate technique known as canonical correlation analysis (CCA); second, we allow the correlation structure to evolve dynamically across time. In addition, we found that a comparatively recent variation on CCA, known as kernel-CCA (KCCA), provides a more flexible and computationally efficient framework. We call the initial CCA-based method dynamic CCA (DCCA) and the kernel-based version dynamic KCCA (DKCCA).
We assume the signals of interest are recorded across multiple experimental trials, and the correlations we examine measure the tendency of signals to vary together across trials: a positive correlation between two of the signals would indicate that trials on which the first signal is larger than average, tend also to be trials on which the second signal is larger than average. At a single point in time we could measure the correlation (across trials) between any two signals. At a single point in time we could also take any linear combination of signals in one region and correlate it with a linear combination of signals in the other region; the canonical correlation is the maximum such correlation among all possible linear combinations. A technical challenge is to find a way to compute canonical correlation while taking into account multiple time points at which the signals are collected.
In a different context, Lu (2013) proposed time-invariant weights over both multivariate signals and time points, such that the resulting vectors are maximally correlated. This does not solve satisfactorily the problem we face because it ignores the natural ordering of time and can therefore produce nonphysiological combinations. Another proposal (Bießmann et al. 2010) applies to individual trials and therefore examines correlation across time (as opposed to correlation across trials), which requires signals that are stationary (time-invariant), whereas we wish to describe the dynamic evolution of their correlation across time. Our DKCCA solution applies KCCA in sliding windows across time, similarly to the way a spectrogram computes frequency decompositions in sliding windows across time. After describing the method, we evaluate DKCCA on simulated data, where there is ground truth, and show that DKCCA can recover correlation structure where simpler averaging methods fail. We then apply DKCCA to data collected simultaneously from the prefrontal cortex and hippocampus of a rhesus macaque, and we uncover a novel connectivity pattern that is not detected by traditional averaging methods.
MATERIALS AND METHODS
In this section, we first review CCA and kernel CCA, and then describe our algorithms, DCCA and DKCCA, our artificial-data simulations, and our experimental methods.
CCA
CCA (Hotelling 1936) provides a natural way to examine correlation between two sets of N multivariate observations. The algorithm finds maximally correlated linear combinations of the variables in each set, reducing a multivariate correlation analysis into several orthogonal univariate analyses. Specifically, given two multivariate, zero mean data sets X ∈ and Y ∈ , where qx and qy are the number of variables in X and Y, respectively, CCA seeks to find canonical weights wX and wY, the coefficients for linear combinations of the columns of X and Y, respectively, such that
| (1) |
where ρ1 indicates the first canonical correlation and the first canonical weight pairs. Successive canonical correlations and weight pairs are similarly defined such that
| (2) |
additionally satisfying
| (3) |
Furthermore, p ≤ min(qx,qy) but often in practice p ≪ min(qx,qy). Essentially, each canonical weight pair from CCA projects the two multivariate sets of N observations to two univariate sets of N observations, called canonical components, from which correlation can be obtained in the usual way.
Kernel CCA
Kernel CCA (Hardoon et al. 2004) extends CCA to allow for nonlinear combinations of the variables, and it also remains numerically stable while CCA can become unstable with large numbers of variables. Importantly, even though kernel CCA applies CCA to a transformation of the data determined by the nonlinearity of interest, all calculations can be performed using inner products of the transformed data matrices. These inner products are defined by a kernel function and are collected in a matrix often called the kernel matrix. Because the resulting computations are efficient, and avoid explicit calculation of the nonlinear transformations, this is usually called the “kernel trick.” It has been studied extensively (Christopher 2016). We next make this explicit in our context.
Following the example of Hardoon et al. (2004), kernel CCA maps observations into a “feature space”
| (4) |
on which CCA is performed. Using the fact that the weights wϕ(X) and wϕ(Y) lie in the row space of ϕ(X) and ϕ(Y), respectively,
| (5) |
and substituting Eq. 5 into Eq. 1, we have
| (6) |
Rewriting ϕ(X)ϕ(X)⊤ as KX and ϕ(Y)ϕ(Y)⊤ as KY, we can express Eq. 6 as
| (7) |
with successive canonical correlations found as in plain CCA. The Gram matrices KX and KY require regularization, and the regularization parameter is typically set using cross-validation.
Instead of calculating the canonical weights, canonical components can be calculated directly using
| (8) |
In this paper we use the linear kernel, which returns weights that can be interpreted like they are in plain CCA. Even with the linear kernel, kernel CCA provides benefits when the number of variables in the data matrices is larger—in our case, much larger—than the number of observations. Kernel CCA requires the estimation and use of the kernel matrices of size N × N, rather than the much larger matrices of size qx × qx, qy × qy, and qx × qx. Furthermore, as we describe below, the Gram matrices used in kernel CCA permit a decomposition specific to our method that is not possible with plain CCA, and that allows for substantial improvement in computational speed.
Dynamic Canonical Correlation Analysis
We first describe DCCA and DKCCA. Then, we show how to integrate multiple components of CCA analysis into the DCCA framework, and determine significance of observed canonical correlations based on a permutation test.
To motivate the problem and our solution, we first describe the procedure for assessing correlation structure in the case of two univariate signals. Suppose we have two simultaneously recorded univariate time series of length T over N repeated trials collected into matrices X ∈ and Y ∈ . Let X(i,s) and Y(i,t) denote the ith trial at times s and t in X and Y, then the cross-correlation between times s and t is
| (9) |
where and . Our goal is to extend this to a multivariate version
| (10) |
where arrays X ∈ and Y ∈ collect the N multivariate time series of length T of dimensions qx and qY respectively, and X(s) ∈ and Y(t) ∈ denote slices of arrays X and Y corresponding to times s and t. The challenge is to identify linear combinations wX(s,t) and wY (s,t) for all s,t. As mentioned in the introduction, a natural first thought is to solve for wX(s,t) and wY(s,t) by using CCA for every pair of times s and t, but this leads to correlations and weights that are difficult to interpret. Alternatively we could find fixed wX(s,t) and wY(s,t) for all s,t, but this does not take into account the nonstationarity of signals in the brain. DCCA, which we now describe, solves these problems by inferring a single set of weights that modulate over time without knowing a priori the lagged correlation structure of the system.
We start by creating extended observations at each time point that are a concatenation of observations in a local window of time. Fix local window g, and let X(s′) ∈ and Y(s′) ∈ be matrices defined as
| (11) |
where [A,…,Z] indicates concatenation of matrices A,…,Z along columns. For each time point s, we run a CCA between X(s′) and Y(s′), which yields linear combination weights wX(s′) and wY(s′) of lengths qx·(2g + 1) and qy·(2g + 1), respectively (see Eq. 1). Since the CCA is run using concatenated observations matrices X(s′) and Y(s′), we can express the concatenated weights as
| (12) |
where the w′ emphasizes that these weights are not the same weights that would be obtained from a CCA with observations that are not concatenated. We then set the canonical weights for X(s) and Y(s) equal to and in Eq. 12 and calculate matrices Xproj ∈ and Yproj ∈ where
| (13) |
and the superscript label is used to denote projection. Finally, we calculate the matrix ccc as in Eq. 9 using matrices Xproj and Xproj.
In this approach, exact lagged relationships need not be established a priori. Instead, if there is a strong lagged correlation between X and Y at times s and t, then as long as |s – t| < g, this lagged relationship will be a driving factor in setting the linear combination weights for both X at time s and Y at time t (although these will not be set simultaneously). Furthermore, the strong correlation between X and Y at times s and t will drive setting the linear combination weights at time s′ where 0 < |s′ − s| < g and 0 < |s′ − t| < g, instead of wX(s′) and wY(s′) being set to greedily maximize correlation at time s′.
Extended observations are the key to discovering a priori unknown lagged cross-correlation, as they make observations within the specified local window visible to each other. To see this, if array X has observations that are independent of each other across time, and Y is a shifted copy of X, so Y(t) = X(t − k), then without creating extended observations, this procedure would only return false correlations since in the shifted case the instantaneous observations are independent (and hence uncorrelated) by design. Recovery of the actual lagged correlation without extended observations would require knowledge of the true lag, which in the above example would be k.
Although DCCA with CCA might work well in some scenarios, as described above it has some disadvantages. First, in many cases, qx·(2g + 1) ≫ N and qy·(2g + 1) ≫ N, which causes numerical instability. Second, as a result of forming concatenated matrices X(s′) and Y(s′), we must estimate a covariance matrix for all observation pairs X(s) and X(t), Y(s) and Y(t), and X(s) and Y(t) for |s – t| < 2g + 1. Finally, for inference involving trial permutations or bootstrapping, these covariance matrices must be recalculated for each simulated data set.
The first and third problems are well understood from the literature, and the solution is to use kernel CCA (KCCA) instead of CCA. In the next section, we describe DCCA with KCCA and show that not only is KCCA a solution to the first and third problems with respect to the DCCA procedure, but also the second. Furthermore, KCCA allows for nonlinear combinations over signals.
Dynamic Kernel Canonical Correlation Analysis
In theory, DKCCA proceeds as described above, but with KCCA instead of CCA. Observations are concatenated over a local window of time, s – g to s + g, and kernel matrices are computed from these concatenated observations. Weights for the concatenated observations (see Eq. 12) are derived according to Eq. 5, from which the weights at time s are extracted and matrices Xproj and Yproj are created as in Eq. 13.
As indicated in Eq. 7, the KCCA algorithm finds optimal α(s) and β(s), which from Eq. 5 we can interpret as coefficients for the linear combinations over the N replications in X(s) and Y(s), respectively [see, for instance, Hardoon et al. (2004) for details]. Because the concatenated observation matrix X[(s+1)′] contains all the observations in the matrix X(s′) with the exception of one, and likewise for matrices Y[(s+1)′] and Y(s′), α(s) and β(s) modulate smoothly over time in the DKCCA procedure. As a consequence, using Eq. 5, we have that wX(s) and wY(s) evolve smoothly over time as well. Note that the degree of smoothness depends on the smoothness of the original time series.
Calculating the canonical weights in Eq. 5, while informative in many scientific settings, is not strictly necessary. In cases where the focus lies solely on the temporal lagged correlations, Xproj(s) and Yproj(s) in Eq. 13 can be calculated directly using Eq. 8. This is especially useful when ϕ maps observations into high-dimensional or infinite-dimensional space, where the weights become difficult to interpret. Calculating Xproj(s) and Yproj(s) directly allows for a wide range of nonlinear combinations of the time series to be considered with low computational cost.
In addition to extending CCA to nonlinear combinations, KCCA allows for numerical stability when the number of signals multiplied by concatenated time points is larger than the number of trials. Also, bootstrap and permutation testing procedures are much faster with KCCA, since they amount to selection or permutation of the rows and columns of the kernel matrices. Furthermore, KCCA solves the second problem mentioned above, that of needing to estimate a covariance matrix for all observation pairs X(s) and X(t), Y(s) and Y(t), and X(s) and Y(t) for |s – t| < 2g + 1 under DCCA with CCA. Focusing for now on the case where ϕ is the identity map, we calculate the kernel matrix from Eq. 7, KX(s′) ∈ , as KX(s′) = [likewise with the kernel matrix KY(s′)]. This calculation can be decomposed as
| (14) |
and since in Eq. 7 only KX and KY need to be computed (whereas in CCA the cross-covariance terms between X and Y must be computed), then for each time point s, KX(s) and KY(s) need be computed only once, with KX(s′) and KY(s′) computed as the sum of the relevant kernel matrices. For arbitrary ϕ, the decomposition in Eq. 14 does not necessarily hold, as interactions between time points are potentially allowed to occur. To take advantage of the decomposition, we can impose a constraint on ϕ that allows for nonlinearities across time series dimensions, but not across time.
Incorporating multiple components.
Typically in CCA-based methods, it suffices to describe the procedure using only the first canonical correlation, as canonical correlations associated with components p ≥ 2 can be studied independently, or can be added to get the total canonical correlation over all components. This is because the canonical components satisfy the constraints in Eq. 3. However, in DKCCA, we do not have these guarantees. Although the constraints in Eq. 3 do apply to the canonical weights calculated from the concatenated observations (Eq. 12), they do not apply to the canonical components Xproj(s) and Yproj(s) in Eq. 13 as these are derived from extracted weights. As an analogy, a set of orthogonal bases over the interval (0,1) are not necessarily orthogonal when restricted to an arbitrary interval (a,b) ⊂ (0,1). To incorporate canonical correlations across multiple components in DKCCA, we therefore cannot add the ccc matrices calculated from each component.
We now describe a way of combining the top k correlations between components at times s and t in X and Y, respectively. Let and be the ith canonical weights for X and Y at time s, and similarly to Eq. 13, for i = 1…k, let and be the k components for X(s) and Y(t). Then,
1) Set .
2) Decompose and into a projection onto and , respectively, and the associated residual:
| (15) |
| (16) |
| (17) |
| (18) |
3) Set
| (19) |
This is almost cov[(s),(t)]; however, we have removed the covariance component cov[(s),(t)], as this is redundant. Importantly, we still allow for correlations across components, where strict orthogonalization would not.
4) For the ith canonical components, decompose (s) into a projection onto the subspace spanned by components {,…,} and its orthogonal residual, and (t) into a projection onto the subspace spanned by components {,…,} and the orthogonal residual. Calculate γi as in step 3.
5) Finally, set .
This procedure has the nice property that if it were performed on output from a vanilla CCA, for canonical correlations ρi, we have that γi = ρi.
Identifying significant regions of cross-correlation.
We generate a null distribution for cross-correlations between regions with a permutation test, combined with an excursion test. We create B new data sets by randomly permuting the order of the trials of Y, rerunning DKCCA on each of the permuted data sets. This results in matrices for i ∈ 1:B. For each entry (s,t), we have B sampled correlations from the null distribution, and say that point (s,t) is αpw(s,t)-significant if its correlation value is greater than 1 – αpw percent of the B sampled correlations. As mentioned above, the relevant kernel matrices need not be recalculated for each permuted data set. Only the order of the rows and columns of kernel matrices KY(s) are affected.
Because we are interested in broad temporal regions of correlated activity, and not isolated time point pairs, we use the B data sets from the permutation test to perform an excursion test [see Xu et al. (2011)]. We say that two αpw significant points (s,t) and (s′,t′), with either s ≠ s′, t ≠ t′, or both, belong to the same contiguous region if there exists a connected path between them such that each point along the path is also αpw significant. To perform the excursion test, we identify contiguous regions in the matrices, and for each contiguous region with mi ∈ [1…Mi] where Mi is the number of contiguous regions in the ith bootstrapped data set, we record the sum of the excess correlation above the αpw cutoff values,
| (20) |
The collection {k(i,mi): i ∈ [1…B], mi ∈ [1…Mi]} defines a null distribution over the total excess correlation for contiguous regions, from which an αregion-level cutoff value can be calculated. We consider as significant any contiguous regions Cm whose total excess correlation exceeds the αregion-level cutoff value.
Simulations
We ran several simulation scenarios to evaluate the effectiveness of the DKCCA procedure1. Each scenario simulated an experiment with two multivariate time series of dimensions 96 and 16, with 100 repeated time-locked trials. Each time series for each trial was generated from a two-dimensional latent variable model
| (21) |
where H(t) ∈ is the latent trajectory with the first and second components uncorrelated, and A(t) ∈ (where q = 96 for time series 1 and q = 16 for time series 2) is a mapping from the latent variable to the signal space, and ϵ(t) is a noise term. H(t) and ϵ(t) were both resampled for each trial, while A(t) was fixed across trials, although as is clear by the notation, was allowed to vary across time. We refer to the collection of A(t) for all t as the A-operator.
We introduced correlation between time series 1 and 2 through the first latent dimension for each time series. Let and be the sample paths of the first latent dimension for time series 1 and 2, respectively. Furthermore, let ρ(k) be a “ramp function” that is piecewise linear with ρ(0) = 0, ramps up to a plateau where it stays for a length of time, then returns to 0. Then starting at time s and for desired lag l,
| (22) |
While we kept lag l fixed across trials, we allowed the induced correlation starting time s to vary uniformly within 10 time steps to simulate small differences in the time course of brain signals with respect to the time-locked stimulus.
We sampled each latent trajectory of H for each time series, and the trajectories for each entry in the time-dynamic A-operators for each time series, as zero mean Gaussian processes with covariance kernels of the form
| (23) |
Let A1 be the A-operator for time series 1 and A2 the A-operator time series 2. For A1, A2, H1, and H2, we let σ = 1 in Eq. 23. For H1 and H2 we let λ be 40 and 20, respectively, and for A1 and A2 we set λ = 100.
Finally, ϵ(t) for each time series is simulated as a two-dimensional latent state model as in Eq. 21 in order to control spatial-dependence and long-range temporal-dependence in the noise. For each Aϵ-operator [where the subscript emphasizes that it is used to simulate the noise terms ϵ(t)], we let σ = 1 and λ = 30 in Eq. 23. For Hϵ we let λ = 80 and, across various simulation conditions on the signal-to-noise ratio, fix σnoise = σ in Eq. 23 to be between 0.2 and 2.
Experimental Methods
The experiment consisted of the presentation of one of four cue objects, each mapped to one of two associated objects. A rhesus macaque was required to fixate on a white center dot, after which one of the four object cues was shown, followed by a correct or incorrect associated object. A correct object presentation required an immediate saccade to a target, while an incorrect object presentation required a delay until a correct object was presented. The presentations of fixation, object cue, and associated objects were separated by blank intervals. Multielectrode recordings were made from both hippocampus (HPC) and lateral prefrontal cortex (PFC) to examine the roles of HPC and PFC in nonspatial declarative memory.
Each day over 1,000 trials were conducted. Electrodes were daily reimplanted into the macaque brain, hence the exact location, and number, of electrodes in the HPC and PFC varied from day to day. For the analysis of the DKCCA algorithm we only considered days in which there were at least 8 electrodes in each section, with typical numbers being between 8 and 20 per brain region. The sampling rate for each trial was 1,000 Hz. [For further details on the experimental setup and data collection, see Brincat and Miller (2016).] All procedures followed the guidelines of the MIT Institutional Animal Care and Use Committee (IACUC) and the US National Institutes of Health, and our protocols were approved by the MIT IACUC. We expand upon details relevant to analysis of the DKCCA algorithm here.
Past work has shown that for multielectrode recordings such as LFP and EEG, the use of a common pickup and the presence of volume conduction can adversely affect functional connectivity analysis [see, for example, the work of Bastos and Schoffelen (2016) and Trongnetrpunya et al. (2016) for a description of the problem and steps that can be taken to mitigate the effect]. These same issues impact DKCCA, especially when the instantaneous correlation of the contaminating signal is almost as strong as or stronger than the lagged correlation of interest, and we recommend following the guidance proposed by past work. For the current data, to minimize pickup of any specific signals through the reference, collection was made using a common reference via a low-impedance connection to animal ground.
For the analyses reported here, we filtered each trial using a Morlet wavelet centered around 16 Hz, where this frequency was determined from previous studies. It is critical in correlation based analyses to isolate the frequency band of interest, and 16 Hz was chosen for this analysis because it is in this region (the beta band) that we see the strongest LFP power and coherence effects [see Brincat and Miller (2016) for details]. Finally, we downsampled the signal to 200 Hz.
RESULTS
The goal of DKCCA was to extend dynamic cross-correlation analysis to two multivariate time series with repeated trials. The algorithm infers a linear or nonlinear combinations over the signal dimensions that 1) are interpretable, 2) are allowed to change over time, and 3) do not require prior knowledge of the lagged correlation structure. Because it uses sliding windows, the combinations can adapt to the underlying nonstationarity of the brain regions and their interactions. DKCCA can thereby recover correlation structure where averaging methods fail. In this section, we evaluate DKCCA on both simulated and real data. In simulations, we show that DKCCA is able to recover the underlying correlation structure between two highly dynamic multivariate time series under varying noise conditions, and simulate a realistic example where DKCCA recovers the correlation structure but averaging methods do not. In the real data, DKCCA detected a novel cross-correlation while the averaging methods did not.
DKCCA Analysis of Simulated Data
To illustrate DKCCA’s ability to recover dynamic cross correlation from two multivariate signals, we ran several simulations (see Eqs. 21–23) under varying noise conditions, with lag l = 20 and simulation start time s sampled for each trial uniformly between min = 310 and max = 320. We designed our simulations to verify three important properties of the algorithm: 1) that it can recover cross-correlation between highly dynamic time series, 2) that it is robust against spurious correlation, and 3) that it can recover cross-correlation in adversarial conditions, where averaging methods fail. We subsequently illustrate these properties in our analysis of the real data.
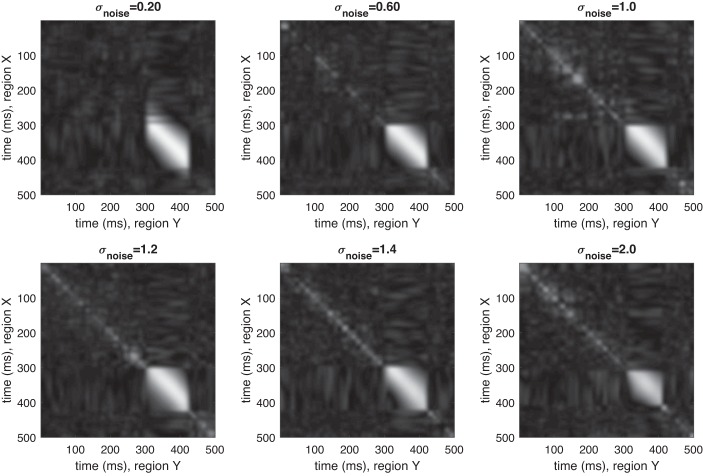
Despite the highly dynamic nature of the simulated time series, DKCCA correctly identifies the temporal region in which lagged correlation exists, and indicates no correlation outside of that region. Figure 1 shows the raw cross-correlograms for various noise levels generated from one such set of simulations. Figure 2 shows the cross-correlograms after accounting for the inference step. The magnitude displayed is excess pairwise canonical correlation after inference. As noise increases, cross-area correlated multivariate signals are more difficult to find, but DKCCA is successful even in high noise regimes. Furthermore, our simulations suggest that the method is robust for finding spurious correlations, since in Figs. 1 and 2 almost no cross-correlation is indicated outside of the regions of induced correlation.
Fig. 1.
Dynamic kernel canonical correlation analysis (DKCCA) captures lagged correlation across a variety of noise levels. Representative results for running DKCCA on simulated data with σnoise = 0.2, 0.6, 1, 1.2, 1.4, and 2 (left to right, top to bottom). y-axis is time (ms) in section X; x-axis is time (ms) in section Y. Trial length: 500 ms. True lag of 20 ms begins in each trial between 300 and 310 in section Y (280 and 290 in section X) and lasts ~80 ms. DKCCA recovers the true correlation structure well even for relatively small signal-to-noise ratio.
Fig. 2.
Excursion test for dynamic kernel canonical correlation analysis (DKCCA) correctly identifies significant regions of cross-correlation. Representative results after bootstrap and excursion test for trials from simulations with σnoise = 0.2, 0.6, 1, 1.2, 1.4, and 2 (left to right, top to bottom). y-axis is time (ms) in section X; x-axis is time (ms) in section Y. Trial length: 500 ms. True lag of 20 ms begins in each trial between 300 and 310 in section Y (280 and 290 in section X) and lasts ~80 ms. Nonzero values are excess above cutoff. Zero values indicate time-pair correlation that was at cutoff or below.
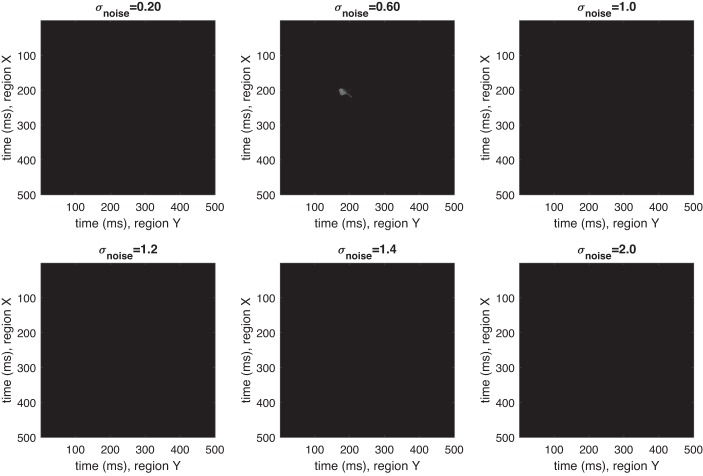
To see this more directly, we ran simulations with no cross-correlation structure, again under varying noise conditions. Results are in Fig. 3. For all analyses, we set our window size parameter, g, to be 20.
Fig. 3.
Excursion test for dynamic kernel canonical correlation analysis (DKCCA) avoids identifying spurious cross-correlation. Representative results for running DKCCA on simulated data with σnoise = 0.2, 0.6, 1, 1.2, 1.4, and 2 (left to right, top to bottom). y-axis is time (ms) in section X; x-axis is time (ms) in section Y. Trial length: 500m s. No true lead-lag relationships present.
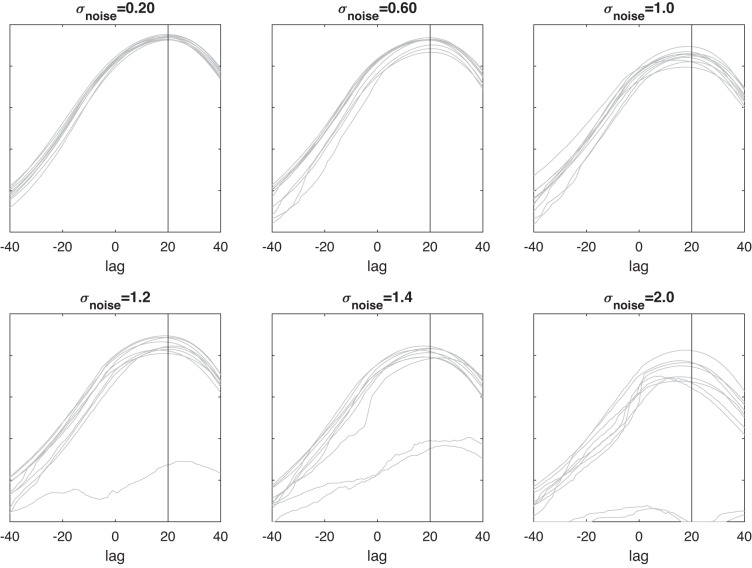
To assess DKCCA’s recovery of the correct lag, we computed a standard cross correlogram from the ccc matrix generated by the DKCCA algorithm by averaging the lagged correlations of one region with respect to the other, within the time period of induced lagged correlation. The results in Fig. 4 show that our algorithm correctly recovers the location of the maximal correlation at a lag of 20. As is expected the accuracy of the method decreases as the signal-to-noise ratio decreases.
Fig. 4.
Dynamic kernel canonical correlation analysis (DKCCA) accurately identifies the correct lag length. Each gray line is the averaged lagged correlation of area of interest for trials from simulations (10 simulations for each noise level) with σnoise = 0.2, 0.6, 1, 1.2, 1.4, and 2. Lag τ = 20 is indicated with a vertical line.
Finally we compared the performance of DKCCA to two common methods, averaging the pairwise correlations between signals (APC) and taking the correlation between the average of signals in each region (CAS). Figure 5 shows the results of the comparison with the same simulation setup as before, but with signal present in only a portion of the simulated electrodes. We achieved this by permuting the remaining electrodes across trials, thereby leaving the temporal characteristics of each electrode intact, but breaking their dependence with other electrodes in a given trial. While APC and CAS do not capture the simulated correlation structure, DKCCA does capture the correct correlation dynamics.
Fig. 5.
Dynamic kernel canonical correlation analysis (DKCCA) identifies the correct region of interest where other methods fail. Comparison of DKCCA, APC (averaging the pairwise correlations between signals), and CAS (taking the correlation between the average of signals in each region) on simulated data with signal present in only a portion of the electrodes. DKCCA correctly identifies signal, as above. APC and CAS are unable to identify signal. Note that intensity is not comparable across methods as all correlations in APC and CAS are comparatively small, so correlations have been scaled for visual presentation.
DKCCA Analysis of LFPs from PFC and HPC
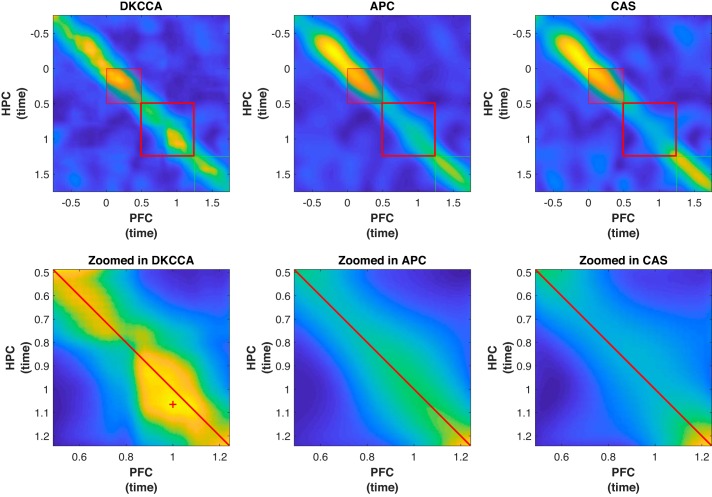
We applied DKCCA to analyze local field potential (LFP) data from the paired-association task described in Experimental Methods. In the experiment, a cue was presented, followed by a series of objects, one of which had a learned association with the cue. A rhesus macaque was required to make a saccade to a target following the display of the correct associated object, and a reward was provided as feedback following a correct saccade. In the original study, Brincat and Miller (2015) concentrated their analysis on the feedback period of each trial. We focused our analysis on the period between the initial presentation of the cue object and the appearance of the first potential associated object. In this portion of the experiment, Brincat and Miller (2015) showed there was high power in a band around 16 Hz in both HPC and PFC, and that, broadly, signal in HPC led the signal in PFC (HPC → PFC). In our analysis we 1) verify that DKCCA also identified that, broadly, HPC → PFC; and 2) compare DKCCA to standard averaging methods to show that DKCCA is better able to detect nuanced cross-correlation. In addition to 1 and 2, our analysis uncovered an interesting reversal in the lead-lag relationship between HPC and PFC that was not found by traditional averaging methods.
In our analysis we used a block of 200 trials, and a total sliding window size of 21 (g = 10) time steps, or 105 ms. We used kernels generated by setting ϕ to be the identity map. The left column of Fig. 6 shows the result of DKCCA generated from a representative set of trials. The figure shows both the ccc matrix for the full trial length (top panel) as well as the ccc matrix zoomed in to the time period corresponding to the portion of the trial between the presentation of the cue and the presentation of the associated pair (bottom panel). In the full trial, DKCCA shows strong correlation before the presentation of the cue (time −0.5 s to 0 s), and during the presentation of the cue (time 0 s to 0.5 s). Lag time varies throughout the interval before and during presentation of the cue, but generally suggests that HPC leads PFC. Correlation is weaker and more intermittent between the presentation of the cue and the presentation of the associated pair, with a noticeable temporary increase in correlation just before the associated pair presentation. While not as distinct as during and just before cue presentation, correlation during the associated pair presentation (timing 1.25 s to 1.75 s) is persistent. Although neither APC nor CAS show significant lagged activity in the time period between the presentation of the cue and the presentation of the associated pair, the zoomed cross-correlogram for DKCCA shows a burst of correlation just after time = 1 s, and in particular suggests that PFC leads HPC in that time period. The effect is significant in the magnitude of the excursion with P ≪ 0.001.
Fig. 6.
Dynamic kernel canonical correlation analysis (DKCCA) finds lagged cross-correlation where traditional methods fail. Top left: cross-correlogram created by the DKCCA algorithm on full trial from −0.75 s to ~1.75 s. The small red and green boxes show timing of display of cue and associated pairs, respectively. Bottom left: cross-correlogram from trial zoomed in to the period between the end of the cue presentation (time = 0.5 s) and the beginning of the associated pair presentation (time = 1.25 s), as indicated by the large red box on the full cross-correlogram. The red diagonal line shows time in hippocampus (HPC) = time in prefrontal cortex (PFC), and the red cross in the bottom left panel indicates the location of the maximum cross correlation in the excursion of interest. Results based on DKCCA are contrasted to the cross-correlogram and zoomed cross-correlogram created by averaging the absolute value of the pairwise cross-correlograms (APC, middle column) and those created by averaging the signals before calculating the cross-correlogram (CAS, right column). In both APC and CAS, we do not see any activity in the zoomed cross-correlograms. For display purposes, correlation magnitudes are not comparable between DKCCA, APC, and CAS as APC and CAS cross-correlations tend to be small compared with the DKCCA, so they have been rescaled.
The highly significant correlation between PFC and HPC found by DKCCA in the bottom left panel of Fig. 6 appears to be asymmetric about the diagonal. We found the point of maximal cross correlation to occur when PFC leads HPC by ~65 ms, as marked with a red cross in that figure. The within-task timing of a switch in lead-lag relationship from HPC → PFC to PFC → HPC would be roughly consistent with the timing of the lead-lag switch found in Place et al. (2016), who studied the theta band in rats. However, with our descriptive method we are unable to provide a statistical test of the lead-lag relationship. We also do not contribute to the as of yet inconclusive discussion of why the theta band is predominant in hippocampal-cortical interaction in rodents, whereas beta is predominant in primates. But despite the difference in frequencies, in both rats and primates, interactions with HPC → PFC directionality seem to be prominent early in trials, during the preparatory and cue presentation periods, but switch to PFC → HPC directionality near the time period when the cue is eliciting memory retrieval. This suggests (in both situations) that PFC may be involved in guiding memory retrieval in the HPC. Figure 6 confirms, on real data, that DKCCA can effectively recover cross-correlation, and that it has the power to detect subtle changes in the lead-lag relationship between time series, such as the reversal seen between object presentations.
We next compare the results of DKCCA to results from APC. In Fig. 6, DKCCA reports a much richer correlation structure throughout the trial than does APC. There are two places in particular where APC differs from DKCCA: first in the period before the presentation of the cue (time −0.5 s to 0 s), and second between the presentation of the cue and the associated pair (time 0.5 s to 1.25 s), where APC indicates that correlation disappears between HPC and PFC. The reason is that with APC there is a single set of weights used when combining the pairwise cross-correlations, regardless of the temporal location of those cross correlations in the trial. However, because of the dynamic nature of the brain, signal pairs do not contribute to population-level correlation activity in a consistent manner over time. In Fig. 6, even where APC does indicate correlation, it does not capture the optimal correlation structure. DKCCA, on the other hand, accommodates these changing dynamics by modulating the weights of the signals over time.
CAS has comparable performance to APC. In particular, the CAS method is unable to fully capture the dynamic cross-correlation structure both before the presentation of the cue and between the presentation of the cue and the presentation of the associated pair. APC and CAS both treat all signals with the same weight, which does not optimize for, and therefore potentially misses, dynamic cross-correlation between the two regions.
DISCUSSION
In this paper we derived and studied a pair of descriptive methods for assessing dynamic cross-correlation between two multivariate time series. DCCA extends canonical correlation analysis to three-way arrays indexed by signals, time, and trials, where the canonical weights over signals are allowed to evolve slowly over time. Because it is based on sliding windows, DCCA accommodates nonstationary time series while avoiding strong assumptions on the dynamics of the lagged correlation over time. We prefer to use the kernelized variant, DKCCA, because it scales well with a growing number of signals, incorporates nonlinear combinations, and provides computational efficiencies not available in DCCA.
Even though nonlinear kernels might provide powerful results, they are difficult to interpret. In our analyses, we have used the linear kernel, which yields weights that are interpreted identically to those in CCA while providing more stable and efficient computation.
DKCCA requires a few parameters to be set, or inferred. The first is a regularization parameter used in implementing KCCA. In one run of the DKCCA algorithm, KCCA is called multiple times, and to allow for comparisons between different entries in the ccc matrix, it is important to use a single regularization value for all KCCA calls. In our experiments, we set this global regularization value through cross-validation. The second parameter is the half-window size g. This value should be set according to scientific context, although there are a few considerations to take into account. A large g heavily smooths the kernel matrices over time. This leads to a slow evolution of α(s) and β(s) in Eq. 7 and could possibly obscure the nonstationary characteristic of the time series. On the other hand, small g might miss important lagged-correlation structure. In this paper, we did not explore optimizing g in the absence of intuition about the maximal lag of interest. We leave this for future work.
We also suggest a possible method for computational savings when the time series under consideration are long and prohibit DKCCA (or DCCA) from running in the desired amount of time. As presented in this paper, the algorithms set the weights for a single time point for each window of the sliding window. Instead, weights for j time points can be set per window. We advise that j should be much smaller than the length of the window, 2g + 1, to ensure the smoothness of weights over time. For the analyses in this paper, we set j = 1.
We validated DKCCA on both simulated and real data, comparing the results to methods commonly used to compute cross-correlation. On simulated data, DKCCA successfully captured the dynamic cross-correlation structure, even under adversarial conditions where traditional methods failed. On real data, in addition to showing more intricate dynamics where traditional methods also captured some correlation, DKCCA found cross-correlation where those methods did not, suggesting a switch in the lead-lag relationship between the hippocampus (HPC) and prefrontal cortex (PFC) in the rhesus macaque.
Signals captured from the brain are highly dynamic, demanding new statistical tools to characterize them. DKCCA provides one such tool to describe dynamic cross-correlation.
GRANTS
This work was supported by NIMH grants MH-064537 (to R. E. Kass), R37-MH-087027 (to E. K. Miller), and F32-MH-081507 (to S. L. Brincat) and The MIT Picower Institute Innovation Fund (to E. K. Miller and S. L. Brincat).
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
J.R. and R.E.K. conceived and designed research; J.R. and N.K. analyzed data; J.R., S.L.B., and R.E.K. interpreted results of experiments; J.R. prepared figures; J.R. drafted manuscript; J.R., S.L.B., and R.E.K. edited and revised manuscript; J.R., N.K., S.L.B., E.K.M., and R.E.K. approved final version of manuscript; S.L.B. and E.K.M. performed experiments.
Footnotes
Code for the DKCCA algorithm and this simulation is provided at https://github.com/jrodu/DKCCA.git.
REFERENCES
- Barnett L, Seth AK. Behaviour of Granger causality under filtering: theoretical invariance and practical application. J Neurosci Methods 201: 404–419, 2011. doi: 10.1016/j.jneumeth.2011.08.010. [DOI] [PubMed] [Google Scholar]
- Bastos AM, Schoffelen J-M. A tutorial review of functional connectivity analysis methods and their interpretational pitfalls. Front Syst Neurosci 9: 175, 2016. doi: 10.3389/fnsys.2015.00175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bießmann F, Meinecke FC, Gretton A, Rauch A, Rainer G, Logothetis NK, Müller K-R. Temporal kernel CCA and its application in multimodal neuronal data analysis. Mach Learn 79: 5–27, 2010. doi: 10.1007/s10994-009-5153-3. [DOI] [Google Scholar]
- Brincat SL, Miller EK. Frequency-specific hippocampal-prefrontal interactions during associative learning. Nat Neurosci 18: 576–581, 2015. doi: 10.1038/nn.3954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brincat SL, Miller EK. Prefrontal cortex networks shift from external to internal modes during learning. J Neurosci 36: 9739–9754, 2016. doi: 10.1523/JNEUROSCI.0274-16.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brovelli A, Ding M, Ledberg A, Chen Y, Nakamura R, Bressler SL. Beta oscillations in a large-scale sensorimotor cortical network: directional influences revealed by Granger causality. Proc Natl Acad Sci USA 101: 9849–9854, 2004. doi: 10.1073/pnas.0308538101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christopher MB. Pattern Recognition and Machine Learning. New York: Springer, 2016. [Google Scholar]
- Ding M, Wang C. Analyzing MEG data with Granger causality: promises and pitfalls. In: Magnetoencephalography, edited by Supek S, Aine CJ. Berlin: Springer, 2014, p. 309–318. doi: 10.1007/978-3-642-33045-2_15. [DOI] [Google Scholar]
- Granger CWJ. Investigating causal relations by econometric models and cross-spectral methods. Econometrica 37: 424–438, 1969. doi: 10.2307/1912791. [DOI] [Google Scholar]
- Hardoon DR, Szedmak S, Shawe-Taylor J. Canonical correlation analysis: an overview with application to learning methods. Neural Comput 16: 2639–2664, 2004. doi: 10.1162/0899766042321814. [DOI] [PubMed] [Google Scholar]
- Hotelling H. Relations between two sets of variates. Biometrika 28: 321–377, 1936. doi: 10.1093/biomet/28.3-4.321. [DOI] [Google Scholar]
- Lu H. Learning canonical correlations of paired tensor sets via tensor-to-vector projection. In: Proceedings of the 23rd International Joint Conference on Artificial Intelligence (Beijing, China, August 3–9, 2013), edited by Rossi F. Palo Alto, CA: IJCAI/AAAI Press, 2013, p. 1516–1522. [Google Scholar]
- Place R, Farovik A, Brockmann M, Eichenbaum H. Bidirectional prefrontal-hippocampal interactions support context-guided memory. Nat Neurosci 19: 992–994, 2016. doi: 10.1038/nn.4327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trongnetrpunya A, Nandi B, Kang D, Kocsis B, Schroeder CE, Ding M. Assessing granger causality in electrophysiological data: removing the adverse effects of common signals via bipolar derivations. Front Syst Neurosci 9: 189, 2016. doi: 10.3389/fnsys.2015.00189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X, Chen Y, Ding M. Estimating Granger causality after stimulus onset: a cautionary note. Neuroimage 41: 767–776, 2008. doi: 10.1016/j.neuroimage.2008.03.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu Y, Sudre GP, Wang W, Weber DJ, Kass RE. Characterizing global statistical significance of spatiotemporal hot spots in magnetoencephalography/electroencephalography source space via excursion algorithms. Stat Med 30: 2854–2866, 2011. doi: 10.1002/sim.4309. [DOI] [PMC free article] [PubMed] [Google Scholar]