Prediction of Drug–Target Binding Kinetics by Comparative Binding Energy Analysis

Abstract

A growing consensus is emerging that optimizing the drug–target affinity alone under equilibrium conditions does not necessarily translate into higher potency in vivo and that instead binding kinetic parameters should be optimized to ensure better efficacy. Therefore, in silico methods are needed to predict the kinetic parameters and the mechanistic determinants of drug–protein binding. Here we demonstrate the application of COMparative BINding Energy (COMBINE) analysis to derive quantitative structure–kinetics relationships (QSKRs) for the dissociation rate constants (k_off) of inhibitors of heat shock protein 90 (HSP90) and HIV-1 protease. We derived protein-specific scoring functions by correlating k_off rate constants with a subset of weighted interaction energy components determined from the energy-minimized structures of drug–protein complexes. As the QSKRs derived for these sets of chemically diverse compounds have good predictive ability and provide insights into important drug–protein interactions for optimizing k_off, COMBINE analysis offers a promising approach for binding kinetics-guided lead optimization.

Over the past few decades, many classical regression techniques have been developed and successfully applied to correlate the properties of a series of molecules with their biological activities to derive quantitative structure–activity relationships (QSAR).^1,2 With the availability of the three-dimensional (3D) structures of many macromolecular drug targets and data on the activities of families of compounds, these approaches have been extended in three dimensions to derive 3D-QSARs.³⁻⁶ COMparative BINding Energy (COMBINE) analysis is one such approach that has been successfully applied to a number of targets to derive target specific scoring functions based on molecular mechanics calculations to predict binding affinity and target selectivity.^{7−11,11−13} Unlike other 3D-QSAR methods, such as CoMFA³ or CoMSIA,¹⁴ COMBINE makes full, simultaneous, and systematic use of all the available information from 3D structures of receptor–ligand complexes and the measured bioactivities of compounds, by explicitly including information about the receptor–ligand interaction energies rather than only about the interaction properties of the ligands. Over the past few years, drug–target binding kinetics have gained a lot of interest from the drug discovery research community due to their influence on the time course of a drug’s effect.¹⁵ It is now increasingly recognized that the in vivo efficacy of a drug correlates better with binding kinetics than binding affinity.¹⁶ However, the molecular determinants of drug-binding kinetics are poorly understood. With the increasing number of experimental measurements of drug-binding kinetics and crystal structures of the corresponding drug–target complexes, there is great potential for using this data to derive 3D-QSKRs for medium throughput prediction of binding kinetics for novel compounds. In addition, computational methods to derive 3D-QSKRs can provide an understanding of the determinants of relatively faster or slower binding kinetics of a specific drug. These insights can help in the rational modulation of the binding kinetics during lead optimization. In a number of cases, it has been found that a drug’s efficacy directly depends on the residence time (τ = 1/k_off) of the drug-receptor complex.^16,17 For example, Maschera et al.¹⁸ and Shuman et al.,¹⁹ in their separate studies on the interaction of drug-resistant mutants of HIV-1 protease and clinical drugs, observed that the inhibition of wild type and mutant proteases was strongly correlated with the dissociation rates (k_off) of the drug–protease complexes and that the resistance mainly resulted from the increase in k_off rates. In another study, geldanamycin, a HSP90 inhibitor, was shown to have nanomolar efficacy in contrast to its micromolar affinity in vitro and its high efficacy was found to be the result of its slow k_off rate.²⁰

In this work, we apply the COMBINE analysis method to derive QSKRs for the dissociation rate constants (k_off) of chemically diverse sets of inhibitors of HSP90 and HIV-1 protease. COMBINE analysis was originally developed to derive QSARs for binding affinity; here, we provide the first demonstration of its applicability to deriving QSKRs for binding kinetic parameters. For this purpose, we studied two established and well-studied drug targets. HSP90 is a chaperone protein, known for its role in stabilizing a number of proteins essential for tumor growth, and it is therefore an anticancer target.²¹ HIV-1 protease is a primary target for anti-AIDS chemotherapy.²² Both proteins have been the subject of extensive structure-based drug discovery efforts and hence are well characterized experimentally. The two targets present different challenges for the prediction of drug-binding kinetics: they show high binding site flexibility and inhibitors with both slow and fast binding kinetics are known.^23,24

For COMBINE analysis, a set of 3D structures of ligand–receptor complexes are modeled and energy-minimized, and ligand–receptor interaction energies are computed using a classical molecular mechanics force-field. These energies are then partitioned and subjected to partial least-squares projection to latent structures (PLS) regression to derive a statistical model which correlates the activity of interest to weighted selected components of the ligand–receptor interaction energy (see eq 1). The interaction energy components are typically Lennard–Jones (LJ) and coulombic interaction terms, decomposed on a per residue basis.

1

where k is the activity of interest (e.g., K_D, k_off, k_on), Δu_i are per residue terms of the ligand–receptor interaction energy, calculated for n residues. Coefficients w_i and the constant C are determined from PLS regression.²⁵⁻²⁷ PLS is used to predict the dependent variables (activity values) from a set of predictors or independent variables (matrix of interaction energy terms) by extracting the set of orthogonal factors, latent variables, which have the best predictive power and explain the maximum covariance between the dependent and independent variables. This step is followed by a regression step where the latent variables are used to predict the dependent (activity) variables.

The data set used for the COMBINE analysis of HSP90 inhibitors consists of 70 structurally diverse inhibitors belonging to 11 different chemical classes: resorcinol, indazole, hydroxyl-indazole, aminoquinazoline, benzamide, aminopyrrolopyrimidine, 7-imidazopyridine, 7-azaindole, aminothienopyridine, 6-hydroxyindole, adenine and 2-aminopyridine (see Figure S4 in the Supporting Information).²⁸ These inhibitors bind to the ATP binding pocket in the N-terminal domain of HSP90 (N-HSP90) and block its ATPase function. The structures of the N-HSP90 in complex with inhibitors are known to have high plasticity and exist in “loop-in”, “helical”, or “loop-out” conformations which differ at the side of ATP binding site where the α-helix3 is located.^29,30 Here, 57 of the inhibitors in the data set bind to the helical conformation of N-HSP90 and 13 inhibitors bind to the loop-in conformation of N-HSP90. The k_off rate constants measured for these compounds by surface plasmon resonance (SPR) were taken from Kokh et al.,²⁸ and they span about 4 orders of magnitude (from 0.0001 to 0.83 s^–1). Co-crystallized structures of 37 HSP90–inhibitor complexes were available in the PDB database. The structures of the remaining 33 protein–inhibitor complexes were modeled by analogy, and the bound complexes were subsequently optimized using the Schrödinger software (release 2015-4, Schrödinger, LLC, New York). During the chemometric analysis, four compounds (6, 30, 65, and 69) were detected as outliers and they significantly diminished the quality of the model. Interestingly, three of these compounds (30, 65, 69) were also identified as outliers in the recent work by Kokh et al.²⁸ where the authors used τRAMD, an enhanced sampling procedure based on molecular dynamics simulations, to calculate the relative residence times of HSP90 inhibitors. These outlier compounds were not considered further here, and therefore, our final data set consisted of 66 inhibitors. For selection of the training and test sets of compounds, the inhibitors were ranked from high to low k_off values and every fifth inhibitor in the list was selected for the test set. Therefore, the resulting training set and test set consisted of 53 inhibitors (80%) and 13 inhibitors (20%), respectively. In addition, the final model was also validated using different cross-validation methods (see Table 1).

Table 1. Statistical Measures of Correlation for the COMBINE Analysis Models Derived for log(k_off) of HSP90 and HIV-1 Protease Inhibitors^a.

	HSP90			HIV-1 protease
validation	Q2	AAEV	RMEV	Q2	AAEV	RMEV
leave-one-out (LOO)	0.69	0.45	0.57	0.70	0.58	0.75
leave-two-out (L2O)	0.69	0.45	0.58	0.51	0.68	0.96
leave-three-out (L3O)	0.68	0.46	0.59	0.52	0.68	0.95
random groups of 7 (10 iterations)	0.68	0.46	0.59	0.60	0.63	0.86

^aCross-validated correlation coefficient (Q²), average absolute errors (AAE_V), and root mean squared errors (RME_V) for different validation methods are given for the PLS models derived with three latent variables for HSP90 inhibitors and six latent variables for HIV-1 protease inhibitors.

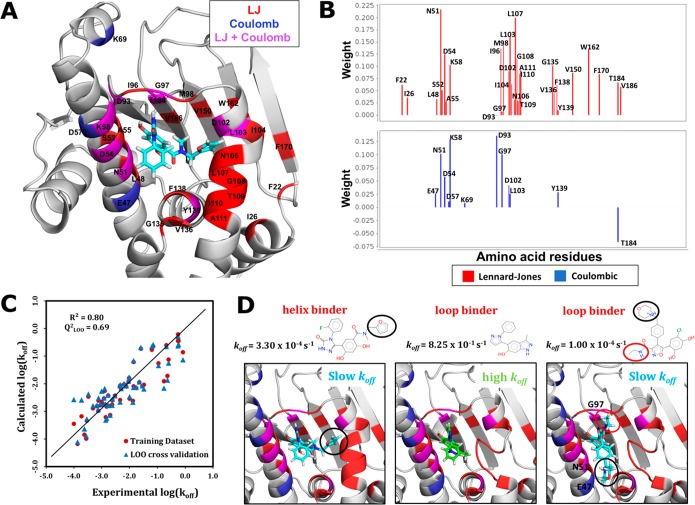
Using the gCOMBINE program,³¹ 207 coulombic and 207 LJ energy terms for all 53 HSP90 inhibitors in the training set were calculated. These interaction energies correspond to the 207 amino acid residues in the N-HSP90. Next, only those interaction energy terms that show variance across the entire training data set and have a standard deviation greater than the specified cutoff value, were selected for PLS analysis. Different cutoff values in the range of 0.2–1.0 kcal/mol were tested. The best model was obtained when a standard deviation cutoff of 0.25 kcal/mol was used, resulting in 42 inhibitor–residue interaction energy terms (12 coulombic and 30 LJ terms) to be used for PLS analysis (see Figure 1A). Then the weights (or the contributions) of these 42 energy terms and their projection over different numbers of latent variables were determined from PLS analysis by correlating the energy terms with experimental log₁₀(k_off) values (see Figure 1B). The regression coefficient R² and standard mean errors were determined for different numbers of latent variables (see Table S1 in the Supporting Information). The models were then subjected to different cross-validation techniques to access their sensitivity and predictive ability. The model with three latent variables was found to have the best predictive power and least sensitivity with a R² of 0.80 and a leave-one-out (LOO) cross-validated correlation coefficient (Q²) of 0.69. The average absolute error (AAE_T) and the root mean squared error (RME_T) for the training set were calculated to be 0.37 (log₁₀ (s^–1) units) and 0.46 (log₁₀ (s^–1) units), respectively. The model obtained has good predictive power as the correlation coefficient for the test-set (R²_PRED) with 13 compounds was calculated to be 0.86 with an AAE_P of 0.33 and RME_P of 0.37. The values of the average absolute error (AAE_V) and the root mean squared error (RME_V) for different cross-validation sets were found to be consistent for the different cross-validation methods used (Table 1).

Figure 1.

COMBINE analysis model for the k_off rate constants of HSP90 inhibitors. (A) 30 LJ and 12 coulombic protein residue–inhibitor interaction energy terms were selected based on variance over the inhibitors for deriving the PLS model. On the crystal structure (PDB ID: 5J20) of compound 11 (cyan sticks) complexed with N-HSP90 (ribbon representation), the residues are colored according to whether their coulombic (blue), LJ (red), or both coulombic and LJ (magenta) interaction energies with the bound inhibitor contribute to the model. (B) Weights for different LJ and coulombic interaction energy contributions derived from the PLS analysis (projection to 3 latent variables, the value of constant C was 0.158). (C) Plot of calculated vs experimental log(k_off) values for the training data set (R² = 0.80) and LOO cross-validation (Q² = 0.69). The straight line corresponds to y = x (ideal case). (D) Comparison of the binding modes and the key interactions for a helix-binder (compound 11, crystal structure PDB ID: 5J20), a faster dissociating loop-binder (compound 9, model based on PDB ID: 5OCI), and a slower dissociating loop-binder (compound 4, crystal structure PDB ID: 5NYI), respectively. Hydrophobic moieties (shown with a black circle in the left panel) of helix-binders occupy a transient hydrophobic cavity formed by the helix conformation of N-HSP90 and mediate strong LJ interactions with hydrophobic residues. Most of the loop binders are smaller in size and dissociate faster (middle panel). Some of the slower dissociating loop-binders have additional polar moieties (marked with red and black circles in the right panel) that mediate additional electrostatic interactions with the binding-site residues.

Nine amino acid residues: N51, D54, K58, D93, G97, D102, L103, Y139, and T184, make contributions of both coulombic and LJ interaction energies to the QSKR model (see Figures 1B and S2). The major contribution to the k_off rates comes from the LJ energies of the hydrophobic residues lining the binding pocket. Therefore, compounds with slow k_off rates tend to have bulky hydrophobic groups mediating strong LJ interactions with the nonpolar binding site residues. Most of the helix-binders are relatively bulkier in size and have slower k_off rate constants, as they have additional hydrophobic moieties which occupy a transient hydrophobic cavity formed between α-helix3 and β-strands and mediate strong van der Waals interactions with hydrophobic residues L103, I104, N106, L107, G108, T109, I110, and A111 (see Figure 1A and 1D). On the other hand, loop-binders are usually smaller in size and have relatively higher k_off rates. As also observed by Kokh et al.,²⁸ there is a good correlation (R² = 0.61) between molecular weight and k_off values for all the compounds. This correlation between k_off values and compound size is even more prominent (R² = 0.94) for the resorcinol class of compounds that bind to the helix conformation of N-HSP90.²⁸ Loop-binders that have slower k_off rates have additional polar moieties mediating coulombic interactions with amino acid residues such as N51, E47, and G97, thereby stabilizing the bound-state (see Figure 1D).

For the COMBINE analysis of HIV-1 protease, the data set consisted of 36 compounds belonging to different chemical classes such as cyclic ureas, cyclic sulfamides, linear analogues of compound B268, and nonanalogues of B268 (see Figure S5). Experimental data on kinetic rates for these compounds are available from Markgren et al.,³² and the k_off values for these compounds range from 0.00022 to 83.3 s^–1. The structures of 12 of the protein–inhibitor complexes are available in the PDB database, and the rest were modeled by introducing small substitutions into cocrystallized structures of similar compounds complexed with HIV-1 protease. Three of these inhibitors (U75875, B249, and B376), were identified as outliers. Two of these outliers: B249 and B376, which are dihydroxy analogues of compound B268, have a variety of substituents at the valine side chains of B268 and no crystal structures were available for them. These small substitutions in B268 resulted in large increases of k_off rates by almost 1000-fold, and this effect was not captured by the COMBINE analysis as the modeled complexes of these compounds were very similar to the reference structure. Therefore, we decided to exclude these compounds from our analysis. Due to the small size of the data set, all of the remaining 33 compounds were used to train the model and the model was assessed by different cross-validation techniques (Table 1).

HIV-1 protease is a homodimer with each monomer consisting of 99 amino acid residues. Therefore, for each of the 33 protease inhibitors, 198 coulombic and 198 LJ energies were calculated using gCOMBINE.³¹ To select a subset of interaction energy terms for PLS, a standard deviation cutoff range (from 0.2 to 1.0 kcal/mol) was tested and the choice of a cutoff of 0.65 kcal/mol resulted in the best model. Seventeen coulombic and 17 LJ terms that have standard deviations higher than the cutoff value were used for PLS analysis (see Figure 2A). The models were derived for different numbers of latent variables and validated using several validation methods (see Tables 1 and S4). The model with the best predictive ability and least sensitivity was obtained when projection was made to six latent variables. The R², AAE_T, and RME_T for the training set are 0.94, 0.26 (log₁₀ (s^–1) units), and 0.34 (log₁₀ (s^–1) units), respectively. The Q² value for different validation methods ranged from 0.51 to 0.70 (Table 1). Of the 17 coulombic and 17 LJ interactions considered in the PLS analysis, many make an unfavorable contribution to the dissociation kinetics (see Figure 2C). It was observed that some of the interactions of the inhibitors, specifically with the residues in the flap region of HIV-1 protease, favor fast unbinding. For example, the cyclic urea and cyclic sulfamide inhibitors have direct polar contacts with the I50 residues located in the flap regions of the HIV-1 protease dimer and have fast dissociation rates. The flaps are very dynamic in nature and are known to exist in different conformations ranging from open to semiclosed to closed. Their fast movements could lead to these small cyclic compounds being driven out of the binding pocket. The cyclic urea inhibitors A008 and DMP323 have the highest k_off rate constants, and they have hydroxyl groups that make hydrogen bonds with the amide backbone atoms of both D30 residues in the bound complexes. The interaction with D30B was identified as unfavorable by the COMBINE analysis (Figure 2C, bottom inset). The acyclic inhibitors, on the other hand, are peptidomimetic and have relatively slow dissociation rates. They do not form direct contacts with the flap residues and their aromatic groups mediate favorable LJ interactions with residues such as P81 and R08 (Figure 2C, top inset). In some of the crystal structures of acyclic inhibitors complexed with HIV-1 protease, bridging waters mediate the interaction between the inhibitors and binding site residues such as D30 and I50. While interfacial water molecules can be considered explicitly in COMBINE analysis,¹³ we omitted them in this study. Thus, the effect of the water-mediated interactions that tend to correlate with slow dissociation rates appears to be represented implicitly by direct hydrogen-bonding to the corresponding residues in the complexes of fast dissociating inhibitors having negative weights in the PLS model.

Figure 2.

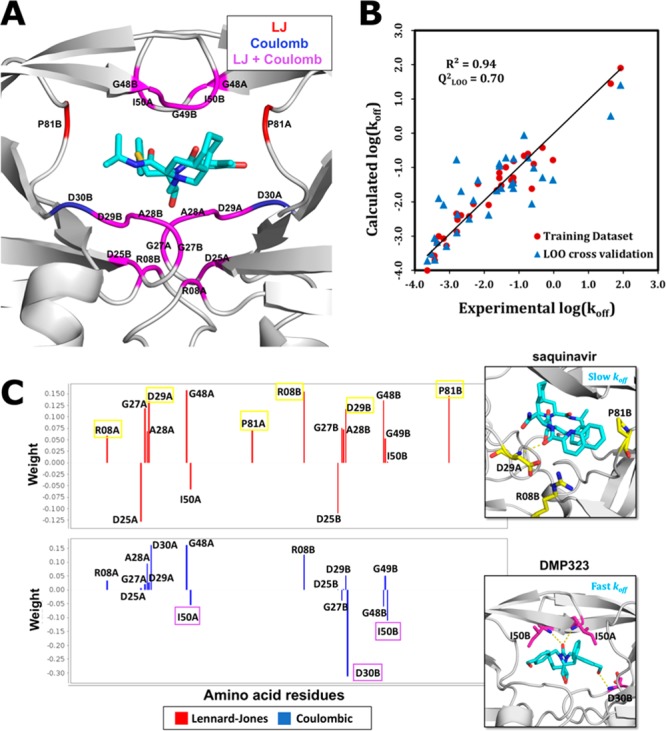
COMBINE analysis model for the k_off rate constants of HIV-1 protease inhibitors. (A) 17 LJ and 17 coulombic protein residue–inhibitor interactions were selected based on variance over the inhibitors. Residues are shown on the crystal structure (PDB ID: 1OHR) of nelfinavir (cyan sticks) bound to HIV-1 protease (ribbon representation) colored according to whether their LJ (red), coulombic (blue), or both LJ and coulombic (magenta) interaction energy terms, contribute to the PLS model. (B) Plot of calculated vs experimental log(k_off) values for the training data set (R² = 0.94) and LOO cross-validation (Q² = 0.70). The straight line corresponds to y = x (ideal case). (C) Weights for different LJ and coulombic interaction energy terms derived from the PLS analysis (projection to six latent variables, the value of constant C was 0.134). A negative weight means that an energetically favorable (negative) interaction energy term tends to shorten the residence time. The labels of some of the interaction energy terms that characterize slow and fast dissociating inhibitors are highlighted, and the corresponding residues are also shown in the inset figures. The top inset shows a few of the interactions (yellow) contributing to the long residence time of the slowly dissociating inhibitor saquinavir (k_off = 0.00023 s^–1) and the bottom inset shows the interactions (magenta) contributing to the short residence time of a very fast dissociating cyclic urea inhibitor DMP323 (k_off = 83.3 s^–1) in the crystal structures with PDB IDs 3OXC and 1QBS, respectively.

In summary, we obtained models for k_off rates with very good predictive power (Q²_LOO = 0.69, R²_PRED = 0.86 for N-HSP90 and Q²_LOO= 0.70 for HIV-1 protease) and identified the key ligand–receptor interactions that contribute to the variance in binding kinetics. These specific interaction energy components provide insights into the mechanisms of specific slow and fast dissociating classes of compounds. Additionally, COMBINE analysis could be used to predict the effect of specific mutations in the protein on the dissociation kinetics of its inhibitors. COMBINE analysis was originally developed to derive QSARs for binding affinity (or K_D, the equilibrium dissociation constant) for a congeneric series of compounds with a similar binding mode to a protein target. Here, we have not used congeneric series, but rather diverse sets of compounds with very different scaffolds and binding modes. We find that our COMBINE analysis models for K_D are not as predictive as the COMBINE models for k_off for these diverse sets of compounds (Tables S6–S9). We do however, obtain better statistics for a COMBINE model for K_D generated with a smaller data set of resorcinol compounds that inhibit HSP90 and have a similar scaffold (Table S10). A possible explanation for the better predictions for k_off than K_D may be that dissociation rates are independent of the unbound state, and therefore differences in ligand and protein desolvation and conformational free energies are not so important. The current applications to HSP90 and HIV-1 protease data sets with very diverse sets of inhibitors, using both crystal structures and modeled protein-inhibitor complexes, demonstrates the potential of COMBINE analysis as a robust QSKR approach with increasing scope for application as more data sets of measured kinetic parameters become available. COMBINE analysis complements a growing number of methods based on biomolecular simulation and machine learning to predict drug–target binding kinetics.³³ Indeed, a possible extension of the COMBINE analysis approach would be to the analysis of structures from molecular dynamics simulations, including intermediates along drug binding or unbinding pathways.

Experimental Procedures

The structures of the protein–inhibitor complexes used were crystal structures or modeled by analogy by introducing small substitutions into crystal structures of similar compounds complexed with the proteins. Preprocessing of the structures was performed with the Schrödinger suite (release 2015-4).³⁴ The force field parameters and topology files were constructed, and the systems were energy minimized using the Amber14 software.³⁵ ff14SB³⁶ was used for the proteins and the general Amber force field (GAFF) for the inhibitors. The partial atomic charges of the inhibitors were fitted using the RESP³⁷ program to the molecular electrostatic potential computed using the GAMESS program.³⁸ The gCOMBINE program³¹ was used to compute the coulombic and LJ interaction energies, decompose them on a per-residue basis, and perform chemometric PLS analysis. Methodological details are given in the Supporting Information.

Glossary

Abbreviations

COMBINE

comparative binding energy analysis

CoMFA

comparative molecular field analysis

CoMSIA

comparative molecular similarity index analysis

HSP90

heat-shock protein 90

N-HSP90

N-terminal domain of HSP90

HIV

human immunodeficiency virus

LOO

leave-one-out

QSKR

quantitative structure-kinetics relationship

ATP

adenosine triphosphate

PDB

protein data bank

PLS

partial least-squares

AAE

average absolute error

RME

root-mean squared error

SPR

surface plasmon resonance

LJ

Lennard–Jones

RMSD

root-mean-square deviation

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsmedchemlett.8b00397.

• Methods, COMBINE analysis workflow, list of HSP90 and HIV-1 protease inhibitors, calculated interaction energy terms and PLS analysis results for k_off and K_D models, formulas for statistical measures of correlation (PDF)

• Data files for HSP90 COMBINE analysis (ZIP)

• Data files for HIV COMBINE analysis (ZIP)

Author Contributions

Both authors designed the study and wrote the manuscript. G.K.G. performed the computations and analyzed the data with assistance from R.C.W.

This work was supported by the EU/EFPIA Innovative Medicines Initiative (IMI) Joint Undertaking, K4DD (Grant No. 115366) and by the Klaus Tschira Foundation.

The authors declare no competing financial interest.