Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2018 Aug 21;3(9):2199–2205. doi: 10.1021/acsenergylett.8b01227

Ultrafast Intraband Spectroscopy of Hot-Carrier Cooling in Lead-Halide Perovskites

Thomas R Hopper †, Andrei Gorodetsky †, Jarvist M Frost ‡,⊥,, Christian Müller §,#, Robert Lovrincic §,#, Artem A Bakulin †,*
PMCID: PMC6231231  PMID: 30450410

Abstract

graphic file with name nz-2018-01227m_0005.jpg

The rapid relaxation of above-band-gap “hot” carriers (HCs) imposes the key efficiency limit in lead-halide perovskite (LHP) solar cells. Recent studies have indicated that HC cooling in these systems may be sensitive to materials composition, as well as the energy and density of excited states. However, the key parameters underpinning the cooling mechanism are currently under debate. Here we use a sequence of ultrafast optical pulses (visible pump–infrared push–infrared probe) to directly compare the intraband cooling dynamics in five common LHPs: FAPbI3, FAPbBr3, MAPbI3, MAPbBr3, and CsPbBr3. We observe ∼100–900 fs cooling times, with slower cooling at higher HC densities. This effect is strongest in the all-inorganic Cs-based system, compared to the hybrid analogues with organic cations. These observations, together with band structure calculations, allow us to quantify the origin of the “hot-phonon bottleneck” in LHPs and assert the thermodynamic contribution of a symmetry-breaking organic cation toward rapid HC cooling.

In contemporary solar energy research, lead-halide perovskites (LHPs) have surged in popularity as highly efficient light-harvesting materials. The optoelectronic properties of these materials systems can be tuned by altering the composition of the “APbX3” structure, where A and X represent a monovalent cation (e.g., methylammonium (MA+); formamidinium (FA+); cesium (Cs+)) and a halide (e.g., I–; Br–; Cl–), respectively.1 Since the first demonstration of an all-solid-state perovskite solar cell (SC) in 2012,2 shortly following the first dye-sensitized analogue in 2009,3 the power conversion efficiency (PCE) of these technologies has increased at an unprecedented rate, with current records above 20%.4

Despite their impressive performance, the maximum theoretical PCE of perovskite SCs is curtailed by the Shockley–Queisser limit for single-junction SCs.5 This largely stems from the relaxation of above-band-gap “hot” carriers (HCs) to the band extrema, whereby the excess energy is dissipated as heat in the lattice.6 The hypothesized HC SC avoids this limit by utilizing the HCs before they have cooled,7 either through direct extraction or carrier multiplication. Consequently, materials with prolonged cooling times are desired as these provide a longer timespan for HC utilization. LHPs are highly regarded for their superb optical properties (hence thin films),8,9 high charge carrier mobilities/diffusion lengths,10−13 and scope for nanostructures.14−16 Multiple studies have also focused on HC dynamics in perovskites, with some indications of unusually slow cooling,17−19 making perovskites attractive candidates for HC SCs.

The prospect of these applications has prompted numerous time-resolved studies aiming to elucidate the dynamics of HCs in perovskite materials. Ultrafast spectroscopy allows the photophysics of materials to be studied immediately following photoexcitation. Optical pumping above the perovskite band gap is thought to create an initial transient excitonic state that dissociates into free carriers under device operating conditions.20 Recent extreme time resolution transient absorption (TA) investigations have reported that this event occurs on the order of 10 fs.21 Excess energy is distributed between the nascent above-band-gap free carriers until a thermalized population of HCs, with an effective temperature exceeding that of the surrounding lattice, is formed.7 Two-dimensional electronic spectroscopy was recently implemented to show that this carrier “thermalization” step occurs within 100 fs for MAPbI3 films.22 The majority of ultrafast studies on perovskites focus on cooling of HCs at later time scales (>100 fs), where the carrier and lattice temperatures equilibrate by electron–phonon coupling. Due to the polar nature of LHPs, this coupling is mainly the long-range Fröhlich dielectric interaction, which is also responsible for the polaronic character of charges in perovskites.17,23−25

Cooling of HCs to the band extrema is frequently observed in TA studies and is characterized by a red shift and delayed onset of the band edge photobleaching at early times (<1 ps).26−28 Competing Burstein–Moss and band gap renormalization effects also play a role in TA signals here and can influence the interpretation.29−31 An alternative visualization of HC phenomena is provided by a recent state-of-the-art TA microscopy study on MAPbI3, which demonstrates a slow buildup of the ground-state bleaching as well as diffusive transport (on the ∼102 nm scale32,33) of the above-band-gap states when pumping at 3.1 eV but not when pumping at the band gap.34 The existence of these energetic states has also been recognized by transient photoluminescence studies, with long-lived (∼10–100 ps) decay of the above-band-edge emission attributed to HC cooling.17,18,35,36 When pumping MAPbI3 beyond 2.6 eV, Bretschneider et al. tentatively proposed a momentum transition as the origin of the HCs.36 Frost et al. emphasize that pumping in this energy regime (i.e., far above the band gap) should be met with careful interpretation of the photophysical data, owing to the population of higher-lying electronic bands.23 The multiband nature of LHPs is well established, and the optical activity of these bands has been experimentally demonstrated.37−41 High pump fluence has also been shown to play a role in the population of additional excited states.42 Along with many-body Auger dynamics,6,28 these effects may confound the analysis of HC cooling in perovskite materials at high carrier densities.

The cooling of electrons and holes occurs within the respective conduction and valence bands, and techniques that specifically address free carrier dynamics are especially potent for observing these phenomena. From the Drude model, it is well established that mobile carriers in semiconductors exhibit an intraband response that is resonant with infrared (IR) frequencies.43 Recent visible pump–IR probe studies by Zhai et al. apparently distinguished the dynamics of excitons and free carriers in bulk perovskite films.44 Broad intraband transitions characteristic of free carrier absorption were also observed by Narra et al. in MAPbI3.45 These particular findings were echoed by Asbury and co-workers, who showed that free carriers in MAPbI3 films display a strong mid-IR absorption with respect to trap states in the ns time domain.46 Monitoring intraband IR absorption on earlier time scales can be used to study HC cooling. This was prominently demonstrated in colloidal CdSe quantum dots by Guyot-Sionnest et al., who pioneered a three-pulse approach to load carriers into the lowest excited state (1S), excite these carriers into higher-lying (1P) states, and subsequently probe the 1S repopulation.47 This method was later advanced to the fs time domain.48 Compared to the other methods above, this “pump–push–probe” (PPP) approach enables the controlled formation of HCs from an initial excited-state reservoir. Consequently, spectroscopic data can be interpreted without corrections for multiband excitation and Auger effects that are unavoidable in TA studies that use above-band-gap, high-fluence pumping. Additionally, the thermal relaxation of carriers in materials systems with different band gaps can be systematically compared without changing the initial pump conditions (as long as the initial carriers can be generated by the fixed pump).

Our work presents the first demonstration of the PPP technique toward HC cooling in perovskite-based materials. We measure the HC density-dependent cooling dynamics in five commonly studied LHPs incorporating a broad range of ubiquitous cations and halides: FAPbI3, FAPbBr3, MAPbI3, MAPbBr3, and CsPbBr3. Our results show that the HC cooling time in the studied systems spans between ∼100 and 900 fs, mainly depending on both the density of HCs and the type of cation. Both these observations and supporting band structure calculations indicate that the cooling rate is limited by the “hot-phonon bottleneck” imposed by the lattice vibrations, which are governed by the phonon spectra of the cation sublattice. These findings provide preliminary insight into materials design for prospective perovskite HC SCs.

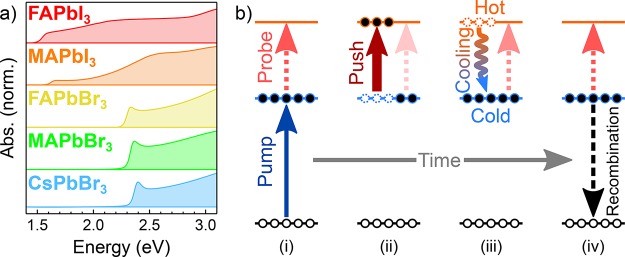
Figure 1a contains the UV–vis absorption spectra for the five LHPs under study. The A-site cation was either organic (MA+ or FA+) or inorganic (Cs+) in nature. The choice of halide (I– or Br–) in the surrounding lead-halide octahedra has a particularly dramatic effect on the optical properties of the perovskite. Namely, the position of the first (low-energy) absorption onset is blue-shifted when swapping the iodide for bromide. Additional, smaller energy shifts are afforded by substitution of the cations, which is explained elsewhere.49 The energy of the absorption onsets that we observe are in reasonable agreement with other experimental and theoretical values for the optical band gaps in the presented materials.49,50

Figure 1.

Figure 1

Open in a new tab

(a) UV–vis absorption spectra of the five LHP films under study. (b) State energy diagram, outlining the effect of the optical pulses on the carriers; (i) visible pump forms “cold” (band edge) carriers, which absorb the intraband near-IR probe; (ii) hot-carrier formation by the near-IR push; (iii) cooling of the HCs, and (iv) recovery of the probe and eventual recombination of the cold carriers.

Figure 1b outlines the concept of the PPP measurement. A visible pump creates “cold” band edge carriers. These cold carriers are detected by the intraband absorption of a low-intensity, near-IR probe. An intense near-IR (NIR) push elevates a portion of the transient electron and hole populations into higher-lying “hot” states within the conduction and valence band density of states, respectively. The depletion of the cold carrier ensemble bleaches the probe signal, which recovers as the HCs relax back to the cold states. Assuming a two-level model (hot and cold states), the time scale of this signal recovery should solely reflect the cooling lifetime, τcool, of the HCs (for a given push energy and fluence).

Figure 2a demonstrates a typical PPP transient for a MAPbI3 film, with and without the push. The action of the pulses described in Figure 1b can be directly observed here. The 2.6 eV pump creates carriers that absorb the NIR (0.6 eV) probe. In the case of the iodide-containing perovskites, the pump creates HCs (excess energy of ∼1 eV) that eventually cool to the band edges. Photoinduced absorption by the cold carriers reduces the transparency of the sample, thereby giving a negative differential transmission (ΔT/T) signal, which diminishes as the carriers recombine. Approximately 12 ps after the pump, the NIR (0.6 eV) push pulse arrives. The momentary depletion of this cold carrier ensemble by the push renders the sample transparent to the NIR probe (more positive ΔT/T), causing rapid (<100 fs) bleaching of the signal. The pronounced bleaching suggests that photoinduced NIR absorption by the HCs is relatively small. As HCs relax to the band edges, the cold carrier reservoir is repopulated and the signal recovers. The inset in Figure 2a shows the monoexponential fitting of the push-induced bleach kinetics, from which the HC cooling time, τcool, is extracted. Note that we do not discriminate the dynamics of hot electrons and holes, given their comparable effective masses.51

Figure 2.

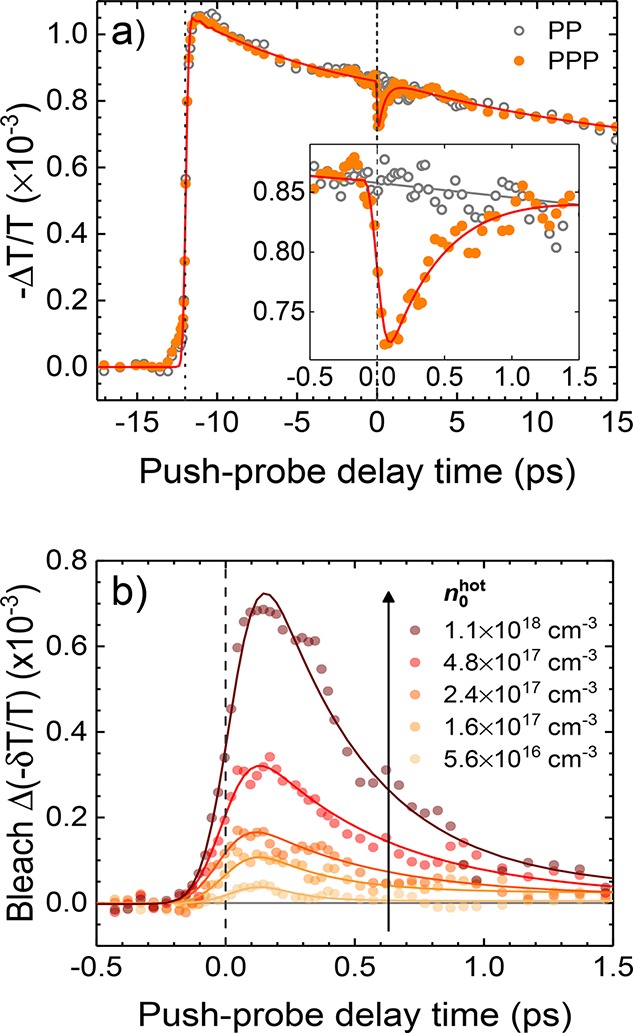
Figure 2

Open in a new tab

PPP transients for a MAPbI3 film. The pump, push, and probe energies are 2.6, 0.6, and 0.6 eV, respectively. (a) PPP (with push) and PP (without push) transients. The pump arrives 12 ps before the push. Inset: zoomed-in region to clearly show the bleaching of the PP signal by the push. The pump and push pulses were set to 0.048 and 4.8 mJ cm–2, respectively. (b) Differential transmission transients (PPP–PP) obtained from a push-fluence-dependent PPP measurement at a fixed pump fluence (88 μJ cm–2). The solid lines are Gaussian-convoluted monoexponential fits.

At the given pump fluence (48 μJ cm–2), the initial cold carrier density, n0cold, in the MAPbI3 film is calculated to be ∼2 × 1018 cm–3, based on the film thickness and optical density at 0.6 eV (Figure 1a). Fluence-dependent pump–probe (PP) results in Figure S1 reveal prominent early time recombination at higher n0, which is concordant with the onset of Auger recombination at >1018 cm–3 in previous investigations on MAPbI3.28,30 For each sample, the pump fluence was appropriately restricted in the PPP measurements to avoid this energy exchange between carriers. Furthermore, the 12 ps delay between the pump and push ensures that the majority of carriers are cold before optically reheating them with the push. Figure S2 shows that elongating the pump–push delay time does not affect the observed cooling dynamics. This suggests that any residual HCs (and associated phonons) from the pump do not strongly affect the dynamics of the reheated carriers. Further evidence for this is provided in Figure S3, which shows that the cooling does not exhibit a dependence on the excess pump energy. Therefore, the iodide- and bromide-based perovskites can be systematically studied with the same 2.6 eV pump, despite differing excess energies (∼1 and ∼0.3 eV above the respective band gaps in Figure 1a).

To explore the effect of the HC density on the cooling kinetics, we performed a push-fluence-dependent measurement. Figure 2b shows the dependence of the PPP signal on the push-induced HC density, n0hot, in MAPbI3. n0 was calculated from the product of the initial pump-induced carrier density (n0cold) and the ratio between the PP (without push) and PPP (with push) signal amplitudes at the push–probe “time zero”. The push fluence was controlled in the presented experiments, and the bleaching amplitude scales roughly linearly with n0 in all of the materials. Complementary checks were performed by varying both the pump and push intensities (Figure S4). We observed that n0hot, rather than n0, is the key parameter determining the PPP transients, which precludes the dominant role of the band edge states in the relaxation of the HCs. For MAPbI3, as well as all other studied samples, we find that τcool steadily increases with increasing n0hot. We understand this in terms of the hot-phonon bottleneck model, which presumes that the polaron charge carriers occupy a finite spatial volume. As the n0 increases, emitted phonons from one polaron interact with other polarons and their associated phonons, such that the excess energy is retained by the electronic states as opposed to flowing away into a cool lattice. This model has been invoked by a large number of previous studies on perovskite systems;23,26,27,30,31,42,52−57 however, a quantitative description of the bottleneck, as well as an understanding of the relevant phonon modes, is still lacking.

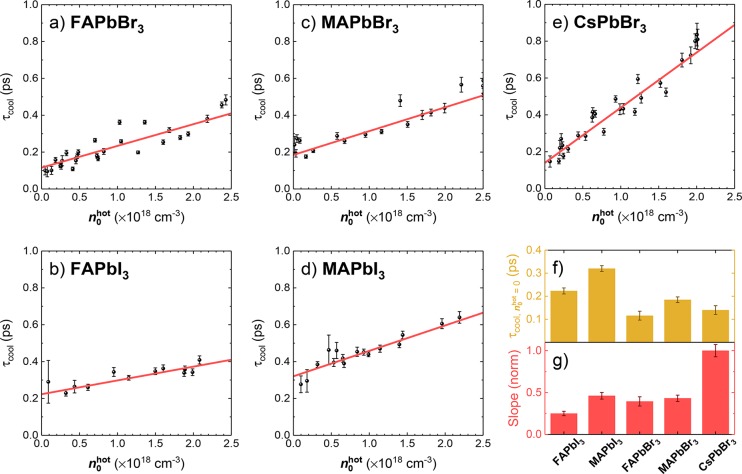
Figure 3a–e shows the derived values of τcool plotted as a function of n0hot for all studied perovskites. τcool ranges from ∼100 to 900 fs, which is in excellent agreement with values obtained from LHPs by numerous groups and techniques.12,21,24,26,30,31,33,52,53,56,58−60 For all of the materials that we studied, τcool is extended at higher n0. An instrumentally weighted linear regression was applied to each of the data sets for quantitative data analysis.

Figure 3.

Figure 3

Open in a new tab

(a–e) Fitted HC cooling time (τcool) plotted as a function of the initial HC density (n0hot) for the five perovskite material systems under study. A linear regression (red line) was applied to each of the data sets, and the extracted y-intercept (τcool, n0 = 0) and slope are presented in (f,g). All data sets were taken from PPP transients obtained with a 2.6 eV pump (<50 μJ cm–2), 0.6 eV push, and 0.6 eV probe.

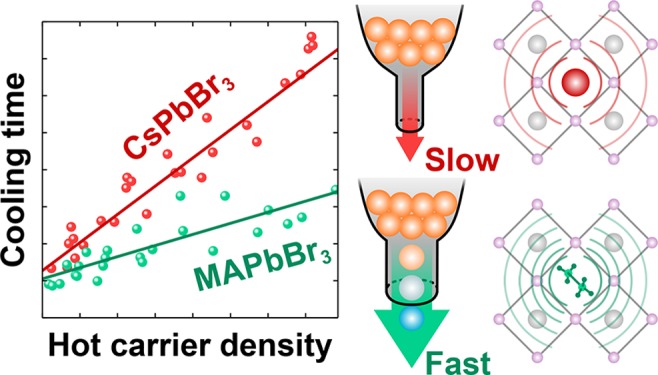
The linear dependence of τcool on n0hot has an intuitive physical meaning in the framework of the hot-phonon bottleneck model. The projection of the linear fit onto n0 = 0 can be interpreted as the cooling time for an isolated HC, in the case where the hot polarons do not overlap in space. Meanwhile, the slope of this fit reflects the sensitivity of the cooling dynamics to the polaron overlap, when the same phonons are coupled to several different charge carriers. The results in Figure 3f suggest that the cooling of a single HC might be slightly slower in the iodide-containing perovskites, though we appreciate that the error bars on these “intercept” values are large. Much more distinctively, the slope describing the relationship between τcool and n0hot is significantly steeper for the all-inorganic CsPbBr3 material, compared to the hybrid perovskites with organic cations, which all have a similar slope (Figure 3g).

The cooling at n0hot = 0 reflects the behavior of the isolated hot polaron. The polaron–phonon interaction in the Fröhlich Hamiltonian can be approximated with the Feynman variational theory.61 The Kadanoff Boltzmann equation produces a time constant for the scattering of optical phonons by this coupling.62 Recent codes63 and experimental results25 enable the calculation of these polaron parameters from materials properties. The scattering time constant has been explicitly linked to the rate of cooling.23 Though the absolute values do not exactly match, the overall faster “single-polaron” cooling time in the bromide-perovskites (Figure 3f) is also revealed by the results of the polaron scattering calculations in Figure 4a (see the SI for details of the underlying calculations). Indeed, the polarons in the bromide-perovskites should to be more strongly scattering, as indicated by their larger Fröhlich electron–phonon coupling coefficients.64 This, in turn, can be understood from the smaller optical dielectric constant in these larger band gap materials, as well as their larger effective masses (Table S1).

Figure 4.

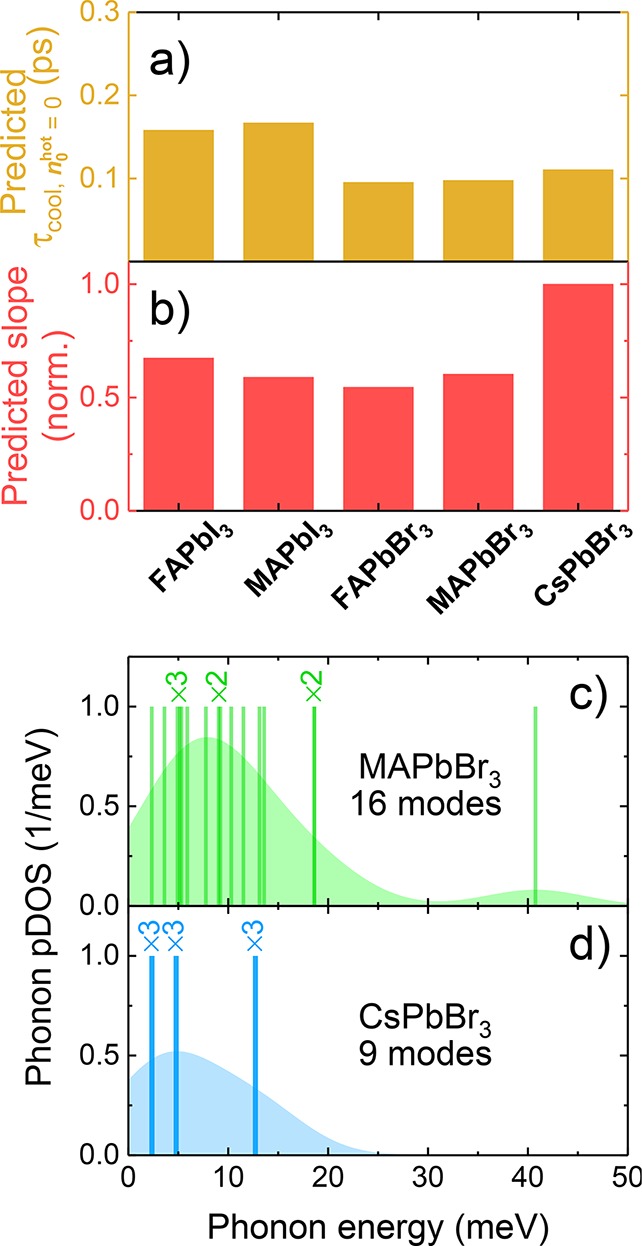
Figure 4

Open in a new tab

Prediction of the experimental trends (see Figure 3f,g). (a) Comparison of the polaron scattering times at 300 K; (b) comparison of the inverse of the per-unit cell-specific heat capacity for the five perovskites under study. The smaller specific heat capacity (steeper slope) of CsPbBr3 is ascribed to there being fewer phonon modes in the thermally accessible energy window. The energies (solid lines) and partial density of states (pDOS, shaded area, constructed from a kernel-density estimation with a Gaussian bandwidth of 10 meV) of these calculated phonon modes are compared for MAPbBr3 (c) and CsPbBr3 (d). Doubly (×2) and triply (×3) degenerate modes are labeled. Details for all of the calculations are provided in the SI.

The much steeper dependence of τcool on n0hot in the all-inorganic perovskite (Figure 3g) can be predicted by the specific heat capacity, as shown in Figure 4b. As the specific heat capacity increases, the same volume of the lattice is capable of absorbing more energy from the carriers before being heated. From a microscopic point of view, the specific heat capacity comes from the occupation of the vibrational modes by a Bose–Einstein distribution. The substitution of an organic cation by an inorganic counterpart in the perovskite lattice effectively doubles the density of states of accessible (<kBT) modes (e.g., 15 in the case of MAPbBr3 versus the 9 in CsPbBr3) by breaking the symmetry of the lattice. The extra coupled cation–lattice modes are observed as additional branches in the phonon spectra and additional density of states in the relevant thermal <kBT (25 meV) energy window (Figure 4c,d). The change in the density of states is so large that other materials parameters (including stiffening of the lattice modes from iodide- to bromide-perovskites) play a lesser role. It is noteworthy that other cation-specific properties, namely, their rotational motion and associated hydrogen-bonding behavior, have also been proposed to influence the charge carrier dynamics in perovskites.65−68 Moreover, the cation-dependent trend in cooling times that we observe (FA+ ≈ MA+ < Cs+) is congruent with a number of recent findings in the literature,24,53,59 which, alongside our work, clearly illustrates that the cation is a critical determinant in the cooling dynamics of LHPs.

A further minor effect stems from the difference in polaron size between the perovskites. Due to details of the different couplings, the polaron state is physically more or less localized. As the polaron becomes larger, a smaller nhot0 is required to reach the critical point where the polarons begin to physically overlap. Though there are multiple propagated errors by the time we are looking at such detailed parameters, we predict from the polaron theories that CsPbBr3 has the largest polaron (radius ≈ 36 Å; see Table S1), which should enhance the phonon bottleneck effect in this material. Indeed, CsPbBr3 is the material in which we measure the steepest slope (Figure 3g).

To summarize, we show that the infrared optical heating and subsequent repopulation of band edge carriers can be used to study the dynamics of HC cooling in perovskite-based materials. We report these dynamics for five common LHPs (FAPbI3, FAPbBr3, MAPbI3, MAPbBr3, and CsPbBr3) and observe that the cooling time slows with increasing HC density. Comparatively, the cooling dynamics in CsPbBr3 exhibit the strongest dependence on the HC density. We ascribe this to the smaller specific heat capacity of the fully inorganic perovskites due to the presence of fewer optical phonon modes (halving the number of modes essentially halves the cooling rate). Meanwhile, extrapolating the HC density-independent cooling time reveals a faster value for the bromide-perovskites, consistent with their stronger electron–phonon coupling. These findings reveal the key phonon modes and dynamics involved in carrier cooling through a hot-phonon bottleneck mechanism. Overall, our work highlights the critical role of the cation in the HC dynamics of LHPs, as well as the importance of careful materials design for the utilization of HCs in prospective photovoltaic applications.

Acknowledgments

We thank Sandy Ruhman and Maxim Pshenichnikov for useful discussions. A.A.B. is a Royal Society University Research Fellow. C.M. and R.L. thank the BMBF for funding (FKZ 13N13656). This project has also received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Grant Agreement No. 639750).

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsenergylett.8b01227.

  • Experimental methods, fluence-dependent pump–probe kinetics for a MAPbI3 film, pump–push–probe results at different pump–push delay times, pump–push–probe results at different pump energies, pseudocolor map describing the effect of pump and push fluence on the cooling kinetics, details of the electronic structure and lattice dynamics calculations, and table of polaron parameters obtained from the calculations (PDF)

The authors declare no competing financial interest.

Notes

The codes used in this study are openly available at DOI: 10.21105/joss.00566. Scripts to generate and plot the calculated data in this paper are available online at DOI: 10.5281/zenodo.1400794.

Supplementary Material

nz8b01227_si_001.pdf (929.2KB, pdf)

References

  1. Correa-Baena J.-P.; Abate A.; Saliba M.; Tress W.; Jesper Jacobsson T.; Grätzel M.; Hagfeldt A. The Rapid Evolution of Highly Efficient Perovskite Solar Cells. Energy Environ. Sci. 2017, 10 (3), 710–727. 10.1039/C6EE03397K. [DOI] [Google Scholar]
  2. Lee M. M.; Teuscher J.; Miyasaka T.; Murakami T. N.; Snaith H. J. Efficient Hybrid Solar Cells Based on Meso-Superstructured Organometal Halide Perovskites. Science 2012, 338 (6107), 643–647. 10.1126/science.1228604. [DOI] [PubMed] [Google Scholar]
  3. Kojima A.; Teshima K.; Shirai Y.; Miyasaka T. Organometal Halide Perovskites as Visible-Light Sensitizers for Photovoltaic Cells. J. Am. Chem. Soc. 2009, 131 (17), 6050–6051. 10.1021/ja809598r. [DOI] [PubMed] [Google Scholar]
  4. NREL Best Research-Cell Efficiences Chart. https://www.nrel.gov (accessed April 2018).
  5. Shockley W.; Queisser H. J. Detailed Balance Limit of Efficiency of p-n Junction Solar Cells. J. Appl. Phys. 1961, 32 (3), 510–519. 10.1063/1.1736034. [DOI] [Google Scholar]
  6. Herz L. M. Charge-Carrier Dynamics in Organic-Inorganic Metal Halide Perovskites. Annu. Rev. Phys. Chem. 2016, 67, 65–89. 10.1146/annurev-physchem-040215-112222. [DOI] [PubMed] [Google Scholar]
  7. Ross R. T.; Nozik A. J. Efficiency of Hot-Carrier Solar Energy Converters. J. Appl. Phys. 1982, 53 (5), 3813–3818. 10.1063/1.331124. [DOI] [Google Scholar]
  8. Kim H.-S.; Lee C.-R.; Im J.-H.; Lee K.-B.; Moehl T.; Marchioro A.; Moon S.-J.; Humphry-Baker R.; Yum J.-H.; Moser J. E.; et al. Lead Iodide Perovskite Sensitized All-Solid-State Submicron Thin Film Mesoscopic Solar Cell with Efficiency Exceeding 9%. Sci. Rep. 2012, 2, 591. 10.1038/srep00591. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Egger D. A.; et al. What Remains Unexplained About the Properties of Halide Perovskites?. Adv. Mater. 2018, 30 (20), 1800691. 10.1002/adma.201800691. [DOI] [PubMed] [Google Scholar]
  10. Wehrenfennig C.; Eperon G. E.; Johnston M. B.; Snaith H. J.; Herz L. M. High Charge Carrier Mobilities and Lifetimes in Organolead Trihalide Perovskites. Adv. Mater. 2014, 26 (10), 1584–1589. 10.1002/adma.201305172. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Stranks S. D.; Eperon G. E.; Grancini G.; Menelaou C.; Alcocer M. J. P.; Leijtens T.; Herz L. M.; Petrozza A.; Snaith H. J. Electron-Hole Diffusion Lengths Exceeding 1 Micrometer in an Organometal Trihalide Perovskite Absorber. Science 2013, 342 (6156), 341–344. 10.1126/science.1243982. [DOI] [PubMed] [Google Scholar]
  12. Xing G.; Mathews N.; Sun S.; Lim S. S.; Lam Y. M.; Grätzel M.; Mhaisalkar S.; Sum T. C. Long-Range Balanced Electron- and Hole-Transport Lengths in Organic-Inorganic CH3NH3PbI3. Science 2013, 342 (6156), 344–347. 10.1126/science.1243167. [DOI] [PubMed] [Google Scholar]
  13. Dong Q.; Fang Y.; Shao Y.; Mulligan P.; Qiu J.; Cao L.; Huang J. Electron-Hole Diffusion Lengths > 175 μm in Solution-Grown CH3NH3PbI3 Single Crystals. Science 2015, 347 (6225), 967–970. 10.1126/science.aaa5760. [DOI] [PubMed] [Google Scholar]
  14. Protesescu L.; Yakunin S.; Bodnarchuk M. I.; Krieg F.; Caputo R.; Hendon C. H.; Yang R. X.; Walsh A.; Kovalenko M. V. Nanocrystals of Cesium Lead Halide Perovskites (CsPbX3, X = Cl, Br, and I): Novel Optoelectronic Materials Showing Bright Emission with Wide Color Gamut. Nano Lett. 2015, 15 (6), 3692–3696. 10.1021/nl5048779. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Im J.-H.; Lee C.-R.; Lee J.-W.; Park S.-W.; Park N.-G. 6.5% Efficient Perovskite Quantum-Dot-Sensitized Solar Cell. Nanoscale 2011, 3 (10), 4088–4093. 10.1039/c1nr10867k. [DOI] [PubMed] [Google Scholar]
  16. Zhang Y.; Liu J.; Wang Z.; Xue Y.; Ou Q.; Polavarapu L.; Zheng J.; Qi X.; Bao Q. Synthesis, Properties, and Optical Applications of Low-Dimensional Perovskites. Chem. Commun. 2016, 52 (94), 13637–13655. 10.1039/C6CC06425F. [DOI] [PubMed] [Google Scholar]
  17. Zhu H.; Miyata K.; Fu Y.; Wang J.; Joshi P. P.; Niesner D.; Williams K. W.; Jin S.; Zhu X.-Y. Screening in Crystalline Liquids Protects Energetic Carriers in Hybrid Perovskites. Science 2016, 353 (6306), 1409–1413. 10.1126/science.aaf9570. [DOI] [PubMed] [Google Scholar]
  18. Niesner D.; Zhu H.; Miyata K.; Joshi P. P.; Evans T. J. S.; Kudisch B. J.; Trinh M. T.; Marks M.; Zhu X. Y. Persistent Energetic Electrons in Methylammonium Lead Iodide Perovskite Thin Films. J. Am. Chem. Soc. 2016, 138 (48), 15717–15726. 10.1021/jacs.6b08880. [DOI] [PubMed] [Google Scholar]
  19. Fang H.-H.; Adjokatse S.; Shao S.; Even J.; Loi M. A. Long-Lived Hot-Carrier Light Emission and Large Blue Shift in Formamidinium Tin Triiodide Perovskites. Nat. Commun. 2018, 9 (1), 243–243. 10.1038/s41467-017-02684-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. D’Innocenzo V.; Grancini G.; Alcocer M. J. P.; Kandada A. R. S.; Stranks S. D.; Lee M. M.; Lanzani G.; Snaith H. J.; Petrozza A. Excitons Versus Free Charges in Organo-Lead Tri-Halide Perovskites. Nat. Commun. 2014, 5, 3586–3586. 10.1038/ncomms4586. [DOI] [PubMed] [Google Scholar]
  21. Ghosh T.; Aharon S.; Etgar L.; Ruhman S. Free Carrier Emergence and Onset of Electron–Phonon Coupling in Methylammonium Lead Halide Perovskite Films. J. Am. Chem. Soc. 2017, 139 (50), 18262–18270. 10.1021/jacs.7b09508. [DOI] [PubMed] [Google Scholar]
  22. Richter J. M.; Branchi F.; Valduga de Almeida Camargo F.; Zhao B.; Friend R. H.; Cerullo G.; Deschler F. Ultrafast Carrier Thermalization in Lead Iodide Perovskite Probed with Two-Dimensional Electronic Spectroscopy. Nat. Commun. 2017, 8 (1), 376. 10.1038/s41467-017-00546-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Frost J. M.; Whalley L. D.; Walsh A. Slow Cooling of Hot Polarons in Halide Perovskite Solar Cells. ACS Energy Letters 2017, 2 (12), 2647–2652. 10.1021/acsenergylett.7b00862. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Miyata K.; Meggiolaro D.; Trinh M. T.; Joshi P. P.; Mosconi E.; Jones S. C.; De Angelis F.; Zhu X. Y. Large Polarons in Lead Halide Perovskites. Sci. Adv. 2017, 3 (8), e1701217. 10.1126/sciadv.1701217. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Sendner M.; Nayak P. K.; Egger D. A.; Beck S.; Muller C.; Epding B.; Kowalsky W.; Kronik L.; Snaith H. J.; Pucci A.; et al. Optical Phonons in Methylammonium Lead Halide Perovskites and Implications for Charge Transport. Mater. Horiz. 2016, 3 (6), 613–620. 10.1039/C6MH00275G. [DOI] [Google Scholar]
  26. Fu J.; Xu Q.; Han G.; Wu B.; Huan C. H. A.; Leek M. L.; Sum T. C. Hot Carrier Cooling Mechanisms in Halide Perovskites. Nat. Commun. 2017, 8 (1), 1300–1300. 10.1038/s41467-017-01360-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Li M.; Bhaumik S.; Goh T. W.; Kumar M. S.; Yantara N.; Gratzel M.; Mhaisalkar S.; Mathews N.; Sum T. C. Slow Cooling and Highly Efficient Extraction of Hot Carriers in Colloidal Perovskite Nanocrystals. Nat. Commun. 2017, 8, 14350. 10.1038/ncomms14350. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Trinh M. T.; Wu X.; Niesner D.; Zhu X. Y. Many-Body Interactions in Photo-Excited Lead Iodide Perovskite. J. Mater. Chem. A 2015, 3 (17), 9285–9290. 10.1039/C5TA01093D. [DOI] [Google Scholar]
  29. Manser J. S.; Kamat P. V. Band Filling with Free Charge Carriers in Organometal Halide Perovskites. Nat. Photonics 2014, 8 (9), 737–743. 10.1038/nphoton.2014.171. [DOI] [Google Scholar]
  30. Price M. B.; Butkus J.; Jellicoe T. C.; Sadhanala A.; Briane A.; Halpert J. E.; Broch K.; Hodgkiss J. M.; Friend R. H.; Deschler F. Hot-Carrier Cooling and Photoinduced Refractive Index Changes in Organic-Inorganic Lead Halide Perovskites. Nat. Commun. 2015, 6, 8420. 10.1038/ncomms9420. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Yang Y.; Ostrowski D. P.; France R. M.; Zhu K.; van de Lagemaat J.; Luther J. M.; Beard M. C. Observation of a Hot-Phonon Bottleneck in Lead-Iodide Perovskites. Nat. Photonics 2016, 10 (1), 53–59. 10.1038/nphoton.2015.213. [DOI] [Google Scholar]
  32. Guo Z.; Manser J. S.; Wan Y.; Kamat P. V.; Huang L. Spatial and Temporal Imaging of Long-Range Charge Transport in Perovskite Thin Films by Ultrafast Microscopy. Nat. Commun. 2015, 6, 7471. 10.1038/ncomms8471. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Nah S.; Spokoyny B. M.; Soe C. M. M.; Stoumpos C. C.; Kanatzidis M. G.; Harel E. Ultrafast Imaging of Carrier Cooling in Metal Halide Perovskite Thin Films. Nano Lett. 2018, 18 (2), 1044–1048. 10.1021/acs.nanolett.7b04520. [DOI] [PubMed] [Google Scholar]
  34. Guo Z.; Wan Y.; Yang M.; Snaider J.; Zhu K.; Huang L. Long-Range Hot-Carrier Transport in Hybrid Perovskites Visualized by Ultrafast Microscopy. Science 2017, 356 (6333), 59–62. 10.1126/science.aam7744. [DOI] [PubMed] [Google Scholar]
  35. Chen K.; Barker A. J.; Morgan F. L.; Halpert J. E.; Hodgkiss J. M. Effect of Carrier Thermalization Dynamics on Light Emission and Amplification in Organometal Halide Perovskites. J. Phys. Chem. Lett. 2015, 6 (1), 153–158. 10.1021/jz502528c. [DOI] [PubMed] [Google Scholar]
  36. Bretschneider S. A.; Laquai F.; Bonn M. Trap-Free Hot Carrier Relaxation in Lead–Halide Perovskite Films. J. Phys. Chem. C 2017, 121 (21), 11201–11206. 10.1021/acs.jpcc.7b03992. [DOI] [Google Scholar]
  37. Even J.; Pedesseau L.; Katan C. Analysis of Multivalley and Multibandgap Absorption and Enhancement of Free Carriers Related to Exciton Screening in Hybrid Perovskites. J. Phys. Chem. C 2014, 118 (22), 11566–11572. 10.1021/jp503337a. [DOI] [Google Scholar]
  38. Stamplecoskie K. G.; Manser J. S.; Kamat P. V. Dual Nature of the Excited State in Organic-Inorganic Lead Halide Perovskites. Energy Environ. Sci. 2015, 8 (1), 208–215. 10.1039/C4EE02988G. [DOI] [Google Scholar]
  39. Anand B.; Sampat S.; Danilov E. O.; Peng W.; Rupich S. M.; Chabal Y. J.; Gartstein Y. N.; Malko A. V. Broadband Transient Absorption Study of Photoexcitations in Lead Halide Perovskites: Towards a Multiband Picture. Phys. Rev. B: Condens. Matter Mater. Phys. 2016, 93 (16), 161205–161205. 10.1103/PhysRevB.93.161205. [DOI] [Google Scholar]
  40. Appavoo K.; Nie W.; Blancon J.-c.; Even J.; Mohite A. D.; Sfeir M. Y. Ultrafast Optical Snapshots of Hybrid Perovskites Reveal the Origin of Multiband Electronic Transitions. Phys. Rev. B: Condens. Matter Mater. Phys. 2017, 96 (19), 195308–195308. 10.1103/PhysRevB.96.195308. [DOI] [Google Scholar]
  41. Leguy A. M. A.; Azarhoosh P.; Alonso M. I.; Campoy-Quiles M.; Weber O. J.; Yao J.; Bryant D.; Weller M. T.; Nelson J.; Walsh A.; et al. Experimental and Theoretical Optical Properties of Methylammonium Lead Halide Perovskites. Nanoscale 2016, 8 (12), 6317–6327. 10.1039/C5NR05435D. [DOI] [PubMed] [Google Scholar]
  42. Piatkowski P.; Cohen B.; Kazim S.; Ahmad S.; Douhal A. How Photon Pump Fluence Changes the Charge Carrier Relaxation Mechanism in an Organic-Inorganic Hybrid Lead Triiodide Perovskite. Phys. Chem. Chem. Phys. 2016, 18 (39), 27090–27101. 10.1039/C6CP02682F. [DOI] [PubMed] [Google Scholar]
  43. Helm M. Infrared Spectroscopy and Transport of Electrons in Semiconductor Superlattices. Semicond. Sci. Technol. 1995, 10 (5), 557. 10.1088/0268-1242/10/5/001. [DOI] [Google Scholar]
  44. Zhai Y.; Sheng C. X.; Zhang C.; Vardeny Z. V. Ultrafast Spectroscopy of Photoexcitations in Organometal Trihalide Perovskites. Adv. Funct. Mater. 2016, 26 (10), 1617–1627. 10.1002/adfm.201505115. [DOI] [Google Scholar]
  45. Narra S.; Chung C.-c.; Diau E. W.-g.; Shigeto S. Simultaneous Observation of an Intraband Transition and Distinct Transient Species in the Infrared Region for Perovskite Solar Cells. J. Phys. Chem. Lett. 2016, 7 (13), 2450–2455. 10.1021/acs.jpclett.6b01111. [DOI] [PubMed] [Google Scholar]
  46. Munson K. T.; Grieco C.; Kennehan E. R.; Stewart R. J.; Asbury J. B. Time-Resolved Infrared Spectroscopy Directly Probes Free and Trapped Carriers in Organo-Halide Perovskites. ACS Energy Letters 2017, 2 (3), 651–658. 10.1021/acsenergylett.7b00033. [DOI] [Google Scholar]
  47. Guyot-Sionnest P.; Shim M.; Matranga C.; Hines M. Intraband Relaxation in CdSe Quantum Dots. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 60 (4), R2181–R2184. 10.1103/PhysRevB.60.R2181. [DOI] [Google Scholar]
  48. Rabouw F. T.; Vaxenburg R.; Bakulin A. A.; van Dijk-Moes R. J. A.; Bakker H. J.; Rodina A.; Lifshitz E.; Efros A. L.; Koenderink A. F.; Vanmaekelbergh D. Dynamics of Intraband and Interband Auger Processes in Colloidal Core–Shell Quantum Dots. ACS Nano 2015, 9 (10), 10366–10376. 10.1021/acsnano.5b04491. [DOI] [PubMed] [Google Scholar]
  49. Amat A.; Mosconi E.; Ronca E.; Quarti C.; Umari P.; Nazeeruddin M. K.; Grätzel M.; De Angelis F. Cation-Induced Band-Gap Tuning in Organohalide Perovskites: Interplay of Spin–Orbit Coupling and Octahedra Tilting. Nano Lett. 2014, 14 (6), 3608–3616. 10.1021/nl5012992. [DOI] [PubMed] [Google Scholar]
  50. Castelli I. E.; García-Lastra J. M.; Thygesen K. S.; Jacobsen K. W. Bandgap Calculations and Trends of Organometal Halide Perovskites. APL Mater. 2014, 2 (8), 081514. 10.1063/1.4893495. [DOI] [Google Scholar]
  51. Giorgi G.; Fujisawa J.-I.; Segawa H.; Yamashita K. Small Photocarrier Effective Masses Featuring Ambipolar Transport in Methylammonium Lead Iodide Perovskite: A Density Functional Analysis. J. Phys. Chem. Lett. 2013, 4 (24), 4213–4216. 10.1021/jz4023865. [DOI] [PubMed] [Google Scholar]
  52. Butkus J.; Vashishtha P.; Chen K.; Gallaher J. K.; Prasad S. K. K.; Metin D. Z.; Laufersky G.; Gaston N.; Halpert J. E.; Hodgkiss J. M. The Evolution of Quantum Confinement in CsPbBr3 Perovskite Nanocrystals. Chem. Mater. 2017, 29 (8), 3644–3652. 10.1021/acs.chemmater.7b00478. [DOI] [Google Scholar]
  53. Madjet M. E.; Berdiyorov G. R.; El-Mellouhi F.; Alharbi F. H.; Akimov A. V.; Kais S. Cation Effect on Hot Carrier Cooling in Halide Perovskite Materials. J. Phys. Chem. Lett. 2017, 8 (18), 4439–4445. 10.1021/acs.jpclett.7b01732. [DOI] [PubMed] [Google Scholar]
  54. Monahan D. M.; Guo L.; Lin J.; Dou L.; Yang P.; Fleming G. R. Room-Temperature Coherent Optical Phonon in 2D Electronic Spectra of CH3NH3PbI3 Perovskite as a Possible Cooling Bottleneck. J. Phys. Chem. Lett. 2017, 8 (14), 3211–3215. 10.1021/acs.jpclett.7b01357. [DOI] [PubMed] [Google Scholar]
  55. Guzelturk B.; Belisle R. A.; Smith M. D.; Bruening K.; Prasanna R.; Yuan Y.; Gopalan V.; Tassone C. J.; Karunadasa H. I.; McGehee M. D.; et al. Terahertz Emission from Hybrid Perovskites Driven by Ultrafast Charge Separation and Strong Electron-Phonon Coupling. Adv. Mater. 2018, 30 (11), 1704737. 10.1002/adma.201704737. [DOI] [PubMed] [Google Scholar]
  56. Yang J.; Wen X.; Xia H.; Sheng R.; Ma Q.; Kim J.; Tapping P.; Harada T.; Kee T. W.; Huang F.; et al. Acoustic-Optical Phonon Up-Conversion and Hot-Phonon Bottleneck in Lead-Halide Perovskites. Nat. Commun. 2017, 8, 14120. 10.1038/ncomms14120. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Kirchartz T.; Markvart T.; Rau U.; Egger D. A. Impact of Small Phonon Energies on the Charge-Carrier Lifetimes in Metal-Halide Perovskites. J. Phys. Chem. Lett. 2018, 9 (5), 939–946. 10.1021/acs.jpclett.7b03414. [DOI] [PubMed] [Google Scholar]
  58. Piatkowski P.; Cohen B.; Javier Ramos F.; Di Nunzio M.; Nazeeruddin M. K.; Grätzel M.; Ahmad S.; Douhal A. Direct Monitoring of Ultrafast Electron and Hole Dynamics in Perovskite Solar Cells. Phys. Chem. Chem. Phys. 2015, 17 (22), 14674–14684. 10.1039/C5CP01119A. [DOI] [PubMed] [Google Scholar]
  59. Bretschneider S. A.; Ivanov I.; Wang H. I.; Miyata K.; Zhu X.; Bonn M. Quantifying Polaron Formation and Charge Carrier Cooling in Lead-Iodide Perovskites. Adv. Mater. 2018, 30, 1707312. 10.1002/adma.201707312. [DOI] [PubMed] [Google Scholar]
  60. Evans T. J. S.; Miyata K.; Joshi P. P.; Maehrlein S.; Liu F.; Zhu X. Y. Competition between Hot-Electron Cooling and Large Polaron Screening in CsPbBr3 Perovskite Single Crystals. J. Phys. Chem. C 2018, 122 (25), 13724–13730. 10.1021/acs.jpcc.8b00476. [DOI] [Google Scholar]
  61. Feynman R. P. Slow Electrons in a Polar Crystal. Phys. Rev. 1955, 97 (3), 660–665. 10.1103/PhysRev.97.660. [DOI] [Google Scholar]
  62. Kadanoff L. P. Boltzmann Equation for Polarons. Phys. Rev. 1963, 130 (4), 1364–1369. 10.1103/PhysRev.130.1364. [DOI] [Google Scholar]
  63. Frost J. M. Calculating Polaron Mobility in Halide Perovskites. Phys. Rev. B: Condens. Matter Mater. Phys. 2017, 96 (19), 195202–195202. 10.1103/PhysRevB.96.195202. [DOI] [Google Scholar]
  64. Wright A. D.; Verdi C.; Milot R. L.; Eperon G. E.; Pérez-Osorio M. A.; Snaith H. J.; Giustino F.; Johnston M. B.; Herz L. M. Electron–Phonon Coupling in Hybrid Lead Halide Perovskites. Nat. Commun. 2016, 7, 11755. 10.1038/ncomms11755. [DOI] [PMC free article] [PubMed] [Google Scholar]
  65. Bakulin A. A.; Selig O.; Bakker H. J.; Rezus Y. L. A.; Müller C.; Glaser T.; Lovrincic R.; Sun Z.; Chen Z.; Walsh A.; et al. Real-Time Observation of Organic Cation Reorientation in Methylammonium Lead Iodide Perovskites. J. Phys. Chem. Lett. 2015, 6 (18), 3663–3669. 10.1021/acs.jpclett.5b01555. [DOI] [PubMed] [Google Scholar]
  66. Selig O.; Sadhanala A.; Müller C.; Lovrincic R.; Chen Z.; Rezus Y. L. A.; Frost J. M.; Jansen T. L. C.; Bakulin A. A. Organic Cation Rotation and Immobilization in Pure and Mixed Methylammonium Lead-Halide Perovskites. J. Am. Chem. Soc. 2017, 139 (11), 4068–4074. 10.1021/jacs.6b12239. [DOI] [PubMed] [Google Scholar]
  67. Taylor V. C. A.; Tiwari D.; Duchi M.; Donaldson P. M.; Clark I. P.; Fermin D. J.; Oliver T. A. A. Investigating the Role of the Organic Cation in Formamidinium Lead Iodide Perovskite Using Ultrafast Spectroscopy. J. Phys. Chem. Lett. 2018, 9 (4), 895–901. 10.1021/acs.jpclett.7b03296. [DOI] [PubMed] [Google Scholar]
  68. Fabini D. H.; Siaw T. A.; Stoumpos C. C.; Laurita G.; Olds D.; Page K.; Hu J. G.; Kanatzidis M. G.; Han S.; Seshadri R. Universal Dynamics of Molecular Reorientation in Hybrid Lead Iodide Perovskites. J. Am. Chem. Soc. 2017, 139 (46), 16875–16884. 10.1021/jacs.7b09536. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nz8b01227_si_001.pdf (929.2KB, pdf)

Articles from ACS Energy Letters are provided here courtesy of American Chemical Society

RESOURCES