No discrete start/stop signals in the dorsal striatum of mice performing a learned action

Abstract

A popular hypothesis is that the dorsal striatum generates discrete "traffic-light" signals that initiate, maintain and terminate the execution of learned actions. Alternatively, the striatum may continuously monitor the dynamics of movements associated with action execution by processing inputs from somatosensory and motor cortices. Here we recorded the activity of striatal neurons in mice performing a run-and-stop task and characterized the diversity of firing rate modulations relative to run performance (tuning curves) across neurons. We found that the tuning curves could not be statistically clustered in discrete functional groups (start or stop neurons). Rather, their shape varied continuously according to the movement dynamics of the task. Moreover, striatal spiking activity correlated with running speed on a run-by-run basis, and was modulated by task-related non-locomotor movements such as licking. We hypothesize that such moment-to-moment movement monitoring by the dorsal striatum contributes to the learning of adaptive actions and/or updating their kinematics.

Introduction

Locomotion allows animals to move around and interact with their environment, and the control of locomotion is one of the most fundamental functions of the nervous system. Generally, animals start, maintain and stop their locomotor activity according to external predictive cues or internal factors (appetite, fatigue, …). Locomotion depends primarily on neuronal circuits located in the spinal cord [1] which are under the direct influence of descending pathways from the motor cortex and brainstem [2]. Recordings of brainstem reticulospinal neurons revealed patterns of activity compatible with the presence of locomotion start, maintain and stop cells [3]. In addition, selective manipulation of brainstem V2a neurons demonstrated that this genetically defined neuronal group acts as locomotion stop neurons in freely moving mice [3,4]. Thus, it appears that the three main phases of locomotion may be controlled by traffic-light signals in the brainstem.

If the brainstem is equipped with locomotion start, maintain and stop cells, what are the descending mechanisms controlling the activity of these cells? The selective activation of striatal projection neurons forming the basal ganglia direct and indirect-pathways respectively promotes and inhibits, locomotion, through modulation of glutamatergic neurons in the brainstem mesencephalic reticular nucleus [5]. Interestingly, it has been proposed that action "start", "maintain" and "stop" signals emerged in the dorsal striatum during the learning of action sequences [6–9]. The hypothesis of discrete groups of striatal neurons that regulate learned actions like a traffic-light is appealing due to its simplicity and potential relevance for striatal disorders such as Parkinson's disease which is associated with difficulties in initiating movements [6,10]. However, it is unclear how this disembodied traffic-light hypothesis is consistent with anatomical and physiological data showing that neuronal activity in the striatum is modulated by movements of different body parts, and sensory stimulation associated with movements. Indeed, a large portion of the dorsal striatum receives somatotopically organized inputs from primary sensory and motor cortices that provide sensory feedback and motor efference signals associated with the movements of body parts, including trunk, forepaws and hindpaws, mouth, face and whiskers (in rodents) [11–17]. In addition, electrophysiological studies in rodents and non-human primates have shown that neurons in localized regions of the dorsal striatum responded to both passive and active movements of specific body parts [18–24]. Thus, the striatum may provide a moment-by-moment representation of the ensemble of movements associated with the execution of a learned action rather than triggering action initiation or termination [25].

We tested the relative validity of these two alternative functions in a new locomotion-based task in which head-restrained mice were trained to start, maintain and stop running according to external cues. After training, we recorded the spiking activity of multiple well-isolated neurons using silicon probes while mice performed this run-and-stop action and computed the average firing rate profile of the recorded neurons relative to the different run phases (referred to as tuning curve in the rest of the manuscript). If start, maintain and stop neurons exist, it should be possible to statistically separate them into groups based on the shape of their tuning curve or the time of their maximal firing rate modulations. The firing rate of start neurons should be transiently modulated before the beginning of the runs and such modulation should be distinguishable from the modulation of neurons associated with the early phases of the runs. In addition, the spiking activity of putative start neurons should be the main source of accurate decoding of the run initiation phases by ensembles of striatal neurons. Alternatively, if striatal activity mainly follows the dynamics of movements (not only locomotion-related movements but also those associated with postural adjustments and orofacial activities occurring around run initiation and termination), a continuum of tuning curves is expected. Such continuum would reflect the overlapping nature of the sequential movements of different body parts during action execution, with a tendency for transient firing rate modulations occurring around run initiation and termination and more prolonged modulations between these events. In that case, it will be difficult to separate tuning curves in functional groups (start, stop, …), even if some neurons may display a prominent modulation of their firing rate before run initiation and/or termination. Finally, if neuronal activity in the striatum primarily represents the dynamics of movements on a moment-by-moment basis, there should be a correlation with the running speed and/or others non-locomotor movements associated with the task performance (such as licking or whisking activities).

Results

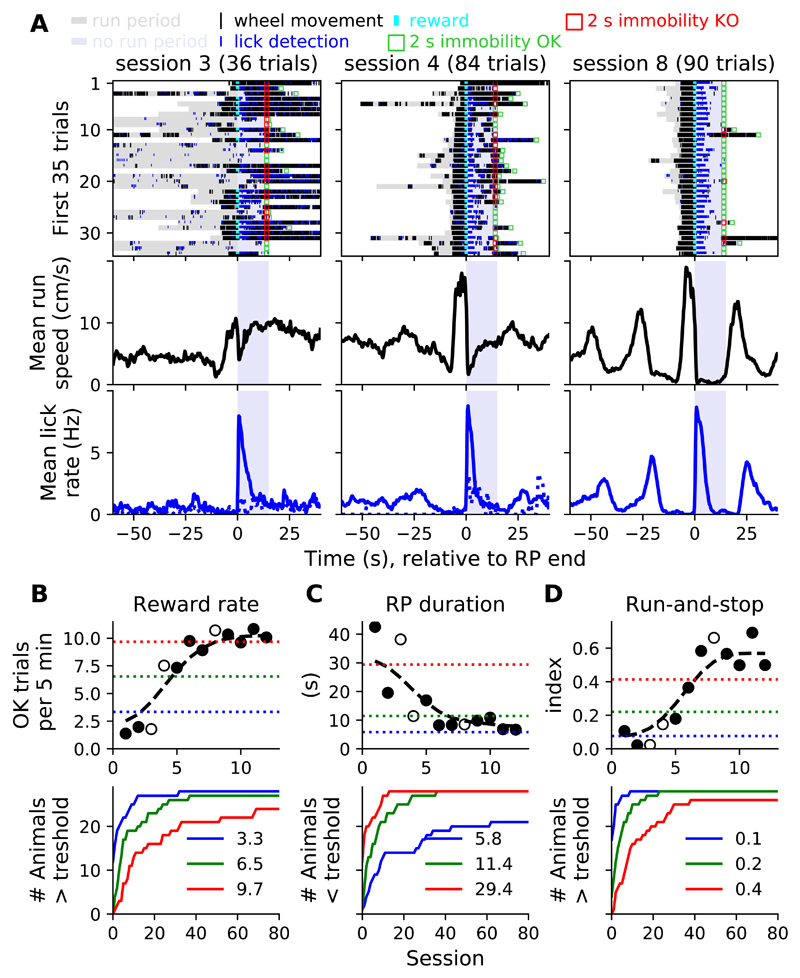
To investigate how the activity of dorsal striatum neurons is modulated during and around well-isolated epochs of locomotor activity, we developed a task in which mice, head-restrained above a free spinning wheel, performed prolonged runs interleaved with running pauses to obtain a maximum of rewards (drops of a sucrose solution, Figure S1A). The behavioral sessions consisted of several trials, divided in "Run" and "No run" periods (RP and NRP, respectively) whose durations depended on the animals' locomotor activity. During RP (signaled by a continuous white noise), mice obtained a drop of sucrose as soon as they ran for 100 cm without stopping. At the time of reward delivery, the white noise was turned off and the task transitioned to the NRP, which lasted 15 s or more. Indeed, when mice stayed immobile for at least 2 s at the end of the NRP (e.g., between 13 and 15 s after the end of the RP, Figure S1A), a new trial started (sound on). However, when mice failed to respect this 2 s immobility period, the NRP was prolonged until animals paused their locomotor activity for 2 s. A trial was considered correct if the animal ran continuously for 100 cm before the end of the RP (see illustrative trials 3-6, Figure S1B). When the mice failed to run continuously for 100 cm after 60 s in the RP, either because they did not run enough (illustrative trial 1, Figure S1B), or because multiple short runs interleaved with pauses were performed (illustrative trial 2, Figure S1B), the trials were considered as incorrect and the task transitioned from RP to NRP without reward delivery. When the mice started to run toward the end of the RP (illustrative trial 3, Figure S1B) or ran during the immobility period of the NRP (illustrative trials 4-5, Figure S1B), trials were labeled as correct even if they resulted in a low rate of reward delivery. Indeed, efficient performance consisted of short RP (the mice performed 100 cm-long runs as soon as the RP started) and 15 s-long NRP (the mice did not run at the end of the NRP, illustrative trial 6, Figure S1B). Early during training, mice ran very little and/or performed few long runs that exceeded the RP (Figure 1A, left panels). Still, mice licked consistently after reward delivery (i.e., at the beginning of the NRP) but not after non-rewarded RP (Figure 1A, lower left/middle panels). Progressively, mice became more efficient and regularly alternated between run and immobility epochs (Figure 1A, middle/right panels). To quantify the progress of the mice on a session-by-session basis, we used three complementary measures: the average rate of correct trials (i.e., the reward rate), the average duration of the RP and a Run-and-Stop index (difference between average running speeds at the end of the RP versus during the NRP, Figures 1B-1D). We extracted the 20^th, 50^th and 80^th percentiles of all values obtained across sessions (n = 2060) and animals (n = 28), for each metric. We then plotted, for each metric, how many animals had reached these performance thresholds across sessions. About half of the animals learned the task quickly and reached a high level of performance in less than 20 sessions while other animals took much longer to become proficient.

Figure 1. Mice became progressively more proficient in the run-and-stop task.

A) 3 illustrative sessions of a given mouse showing, from left to right, progressive proficiency. Locomotor and lick activities are shown during the first 35 trials (top), along with session-average running speed (middle, all trials) and lick rate (bottom, continuous and dashed lines show correct and incorrect trials, respectively) relative to RP end. Green squares indicate that the mice was immobile during the last 2 s of the No run period. Red squares indicate that the mice was moving during the last 2 s of the No run period. Session-averaged running speeds and lick rates (middle and bottom panels) took in account wheel and lick detections from adjacent trials, not shown in the top rasters (white areas). B-D) Session-by-session learning curves (top) for the example mouse shown in A for 3 behavioral metrics. Empty circles correspond to the illustrative sessions shown in A. The 3 colored horizontal dashed lines correspond to 3 performance levels defined as the 20, 50, 80 percentiles values for each metric across all animals. Cumulative number of animals passing the 3 performance levels (bottom, same color code and values as top panels). See also Figure S1.

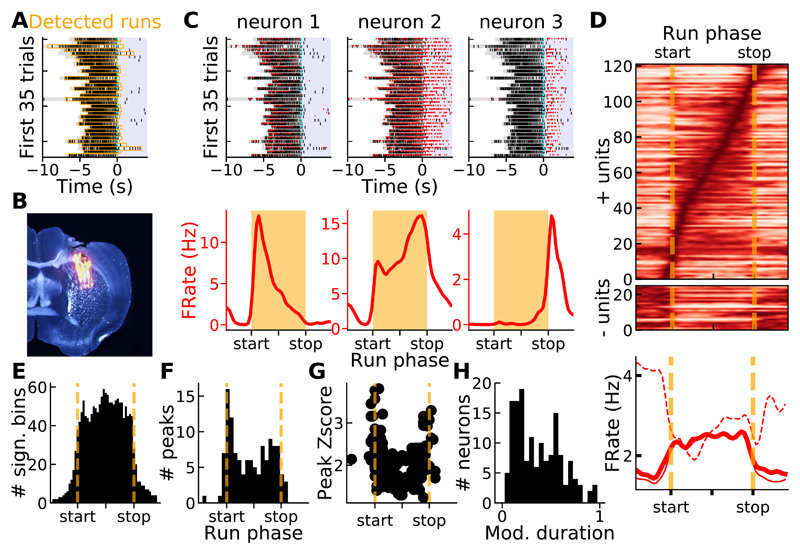
In the first training sessions, animals either rarely moved or performed runs with variable durations (Figure 1A, upper left and middle panels), precluding the isolation of a sufficient number of runs with similar durations. Thus, we focused our analysis on electrophysiological recordings performed once mice reached good proficiency in the task (see STAR Methods). To examine how the activity of individual striatal neurons were modulated relative to the different phases of the run, runs were isolated and their durations were normalized (Figure 2A and see STAR Methods). A 32-channel silicon probe targeting a region overlapping the dorsocentral and dorsolateral striatum was used to acutely record multiple single units while mice performed the task (Figure 2B and see STAR Methods). Visual inspection of the spike rasters during task performance from a few representative neurons (Figure 2C, top) and their average firing rates relative to the run phases (Figure 2C, bottom and Figure 2D; from now on average firing rates relative to the run phases are referred to as tuning curves) revealed strong modulations at different phases of the runs. A majority of neurons displayed a significant increase in their firing rate (72%, Figure 2D, top, see STAR Methods) while a minority displayed a decrease in firing rate during the runs (14%, Figure 2D, middle). Positively and negatively-modulated neuronal populations displayed a sustained increase and decrease in firing rate throughout the runs, respectively (Figure 2D, bottom). Previous studies reported prominent increases in firing rate around the beginning and end of motor sequences [6,9,26,27]. Thus, we first focused our analysis on neurons that increased their firing rate during or just around the runs (positively modulated neurons). The distribution of all the run phases associated with significant modulation of the tuning curves was uniform during the run (Kolmogorov Smirnov test for uniform distribution's statistic = 0.032, p = 0.12, Figure 2E). Still, the firing rate peaks were stronger and more numerous close to the beginning and end of the runs (Kolmogorov Smirnov test's statistic = 0.17, p = 0.0024, Figures 2F and 2G). Finally, across neurons, the durations of the modulations (normalized relative to the average run duration), were quite variable (Figure 2H). Similar results were obtained when the analysis was restricted to runs with more homogeneous durations (Figure S2, see STAR Methods). Altogether, this set of descriptive analyses revealed a trend toward stronger increases in firing rates close to the beginning and end of the runs, even if the population average firing rate increased in step-like manner throughout the runs.

Figure 2. Spiking activity of dorsal striatal neurons is strongly modulated during and around the runs.

A) Behavioral performance during a recording session (same legend as Figure 1A, licks were not detected in this experiment, orange areas indicate detected run periods). B) Histological confirmation of silicon probe position in the dorso-central striatum. C) Top, spike rasters (red) of 3 task-modulated neurons superimposed on locomotor activity (black, same session as A) aligned to reward delivery. Bottom, mean firing rates relative to normalized run phases (tuning curves). D) Averaged firing rates during normalized runs (sorted according to the peak firing rate's phase) for neurons showing significant increase (top) or decrease (middle) in firing rate. Bottom, population averaged firing rate for all (thick line), positively modulated (continuous line) and negatively modulated (dashed line) neurons. E) Distribution of all the run phases with significant positive modulation of firing rate. F) Distribution of the run phases corresponding to the peak firing rates. G) Z-scored peak firing rates versus run phases. H) Distribution of the durations (normalized relative to run duration) of the significant increases in firing rate. See also Figure S2.

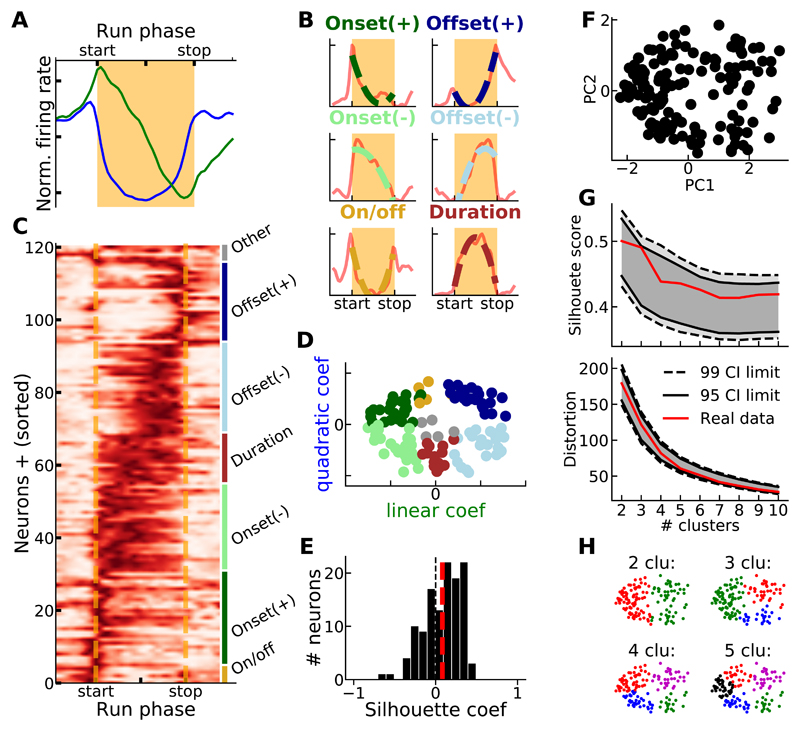
To examine if discrete groups of neurons signaled specific run phases, as predicted from the traffic-light hypothesis, we first applied Principle Components Analysis (PCA) on the tuning curves of positively modulated neurons (see STAR Methods). This analysis revealed that a combination of a quadratic function with zero linear term (first principal component) and a linear function (second principal component) comprised most (~ 70%) of the variance of these tuning curves (Figure 3A, [28]). Each tuning curve could then be fitted with a second-order polynomial function (see STAR Methods). Accordingly, tuning curves could be arbitrarily divided into 6 groups according to the sign of the curvature and the slope of the linear component of the fitting function (Figures 3B and 3C, see Table 1 in STAR Methods). Tuning curves belonging to some of these groups resembled the firing rate profile of start, stop and boundary neurons previously described (e.g., Onset+, Offset+ and On/Off neurons in Figure 3B, [6,7]). Still, separating tuning curves according to these arbitrary criteria revealed heterogeneity inside each group and similarity between certain members of different groups (Figure 3C). In order to statistically separate neurons on the basis of the most variable features of their tuning curves, we plotted the quadratic and linear coefficients of the fit functions of the tuning curves against each other. This did not reveal obvious clusters (Figure 3D). We used the Silhouette method to quantify the cohesion inside the aforementioned arbitrary groups and the separation between groups (see STAR Methods, [29]). The distribution of the silhouette coefficients of all the positively modulated neurons was centered around zero (mean Silhouette score = 0.08) and never exceeded 0.5, indicating strong overlaps between the arbitrarily defined groups (Figure 3E). Finally, we used an unsupervised approach to try to cluster the tuning curves. A k-means algorithm generated the best partitioning of the tuning curves (using their first and second principal components, Figure 3F) in k groups, with k ranging from 2 to 10 (see STAR Methods). The Silhouette score and distortion (see STAR Methods) provided a metric of the tightness and separation of the clusters generated by the algorithm. Both measures continuously decreased with k, which indicates an absence of optimal number of clusters (Figure 3G). Similar results were obtained when more principal components were used to partition the tuning curves (Figure S3). The Silhouette scores and distortion profiles for k between 2 and 10 generated from our data set, fell inside the intervals of confidence defined by the Silhouette scores and distortions generated from surrogate data sets (Figure 3G, see STAR Methods). Altogether, these results showed that, at a population level, the striatal neurons we recorded could not be divided in discrete groups according to the shape of their tuning curve (see also Figure 3H).

Figure 3. Continuous, not discrete, representation of the run phases at the population level.

A) Projections of the normalized firing rate population activity onto the first 2 principal components (PC1: blue, PC2: green) computed from the tuning curves matrix shown in C. B) Example neurons with significant linear and positive quadratic components (onset+ and offset+, top), significant linear and negative quadratic components (onset- and offset-, middle) and significant quadratic and non-significant linear components (on/off and duration, bottom). Continuous and dashed lines show the tuning curve and its corresponding fit, respectively. C) Tuning curves (sorted according to linear and quadratic coefficients, same colors as B, for positively modulated neurons. D) Scatter plot of the linear and quadratic coefficients of the tuning curve fit functions, for all positively modulated neurons (same color code as B, non-classified neurons in gray). E) Distribution of the Silhouette coefficients for data points in D. Red dashed line indicates overall Silhouette score. F) Scatter plot of the 1^st and 2^nd PC of each tuning curve with significant modulation (same data as in top and middle panels, Figure 2D). G) Silhouette score (top) and distortion (bottom) when data in F are partitioned in 2 to 10 groups, using a k-means algorithm. Confidence intervals (CIs) were generated by randomly sampling pairs of PC values from the distribution of the real data (PC1 and PC2 shown in F). H) Data in F partitioned in 2, 3, 4 or 5 groups using a k-means algorithm. See also Figure S3 and S4.

Table 1. Functional classification criteria.

pb <= 0.05				pb > 0.05
a > 0		a <= 0		pa <= 0.05		pa > 0.05
g[0] <= g[1]	g[0] > g[1]	g[0] < g[1]	g[0] >= g[1]	a <= 0	a > 0	Non classified
Positive offset	Positive onset	Negative offset	Negative onset	Duration	On/off

It is possible that the heterogeneity of the tuning curves stems from the fact that we did not separate neurons according to their putative cell-type (projection neurons, PN vs interneurons). Previous studies have shown that it is possible to separate projection neurons (PN) and fast spiking interneurons (FSI) based on the shape of their spike waveform [30]. We could not observe a clear separation between narrow and broad spike waveforms in our dataset (Figure S4A). Still, we used typical waveform criteria to separate putative PN and FSI (Figures S4A and S4B). As expected, putative FSI fired at higher rates than putative PN (Figure S4C). Still, many putative FSI fired at low frequencies (< 5Hz) perhaps due to constant firing rate modulations during the task (i.e, these putative FSI might fire at higher frequencies during home cage or sleep recordings, which could not be tested as we performed acute recordings). We found that putative PN displayed a significant increase of their firing rate before, during and after the run (Figure S4D) and their tuning curves were highly heterogeneous and did not cluster according to the linear and quadratic coefficients of their polynomial fits (Figures S4E and S4F).

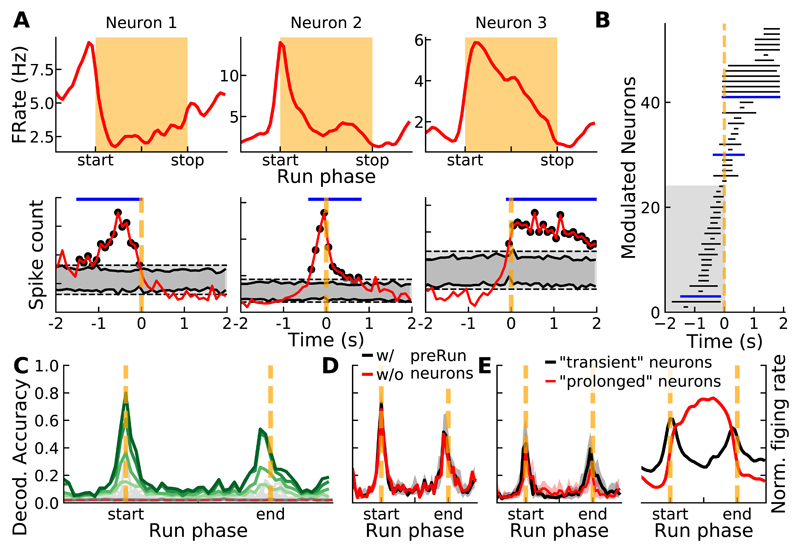
We further examined the possibility that a dedicated discrete group of neurons had its spiking activity selectively modulated before the initiation of the run and could act as "start" neurons. For all the recorded neurons, we generated a peristimulus time histogram (PSTH) of their spiking activity aligned with the time at which runs started (Figure 4A, bottom). We identified bins with significant firing rate modulations (Figure 4A, bottom, see STAR Methods). Sorting these modulations with respect to the beginning of the run revealed a continuum of modulations rather than the presence of a discrete population that fires selectively before the runs (Figure 4B).

Figure 4. Continuous representation of run initiation and decoding accuracy by striatal ensembles.

A) Top, tuning curves of 3 illustrative neurons with a peak firing rate modulation around run start. Bottom, PSTHs (same neurons as top) aligned relative to run start. Dark and light gray bands indicate pointwise and global CIs. Black dots indicate contiguous significant bins that surrounded the maximal modulation. B) Detected modulated portions of the PSTHs around run start for all the neurons, sorted in time. Modulated portions of illustrative neurons in A are shown in blue. C) Bayesian decoding accuracy of the run phases from the spiking activity of individual neurons (light gray lines, dark gray line indicates averaged individual decoding) and ensembles of increasing size (light to dark green lines indicate ensemble decoding when number of neuron is 25, 50, 100 or 146). Dashed horizontal red line indicate chance level. D) Decoding accuracy of the run phases by ensembles of neurons (size = 122 neurons) in which pre-Run neurons (shaded area in B) were excluded (red) or included (black; in this condition, the thick black line indicates median decoding accuracy over 100 ensembles and gray area shows data comprised between 5^th and 95^th percentiles). E) Left, run phases decoding accuracy by ensembles of neurons (size = 50 neurons) composed of neurons that either displayed transient (black) or prolonged (red) modulations of their firing rate (arbitrary classification based on Figure 3C, see main text). Thick lines indicate median decoding accuracy and areas show data comprised between 5^th and 95^th percentiles. Right, mean normalized firing rate for the two groups of neurons partitioned based on transient vs prolonged modulation of firing rate.

Finally, we examined how the different phases of the run (including pre and post-run phases) could be decoded from the spiking activity of the recorded striatal neurons. We used a Bayesian decoding approach (see STAR Methods) and observed that the different phases of the runs were not accurately decoded from the activity of single neurons (Figure 4C, gray lines). Decoding accuracy increased sharply around the run start and stop phases when neuronal ensembles of increasing size were considered (Figure 4C, green lines), which is expected, as the most prominent variations in firing rate occurred around these phases of the run [31]. Next, we arbitrarily defined a group of pre-Run neurons that displayed a prominent modulation of their firing rate before the start of the runs (gray area in Figure 4B). We found that the decoding accuracy was similar for same-size ensembles that either contained or lacked pre-Run neurons (Figure 4D). Finally, we compared decoding accuracy of same-size ensembles composed of transiently modulated neurons (On/Off, Onset+, Offset+, see Figure 3BC) versus ensembles composed of neurons that displayed more sustained firing rate modulations (Onset-, Duration, Offset-, see Figures 3B and 3C). Both types of ensemble similarly decoded the run start and stop phases (Figure 4E, left). This was expected as firing rate variations occurred mainly around run start and run stop phases in both cases (Figure 4E, right). Altogether this set of results demonstrates that the decoding of the initiation (termination) of the run does not uniquely rely on the activity of specialized neurons that display transient firing rate modulation locked to the initiation (termination) of the runs.

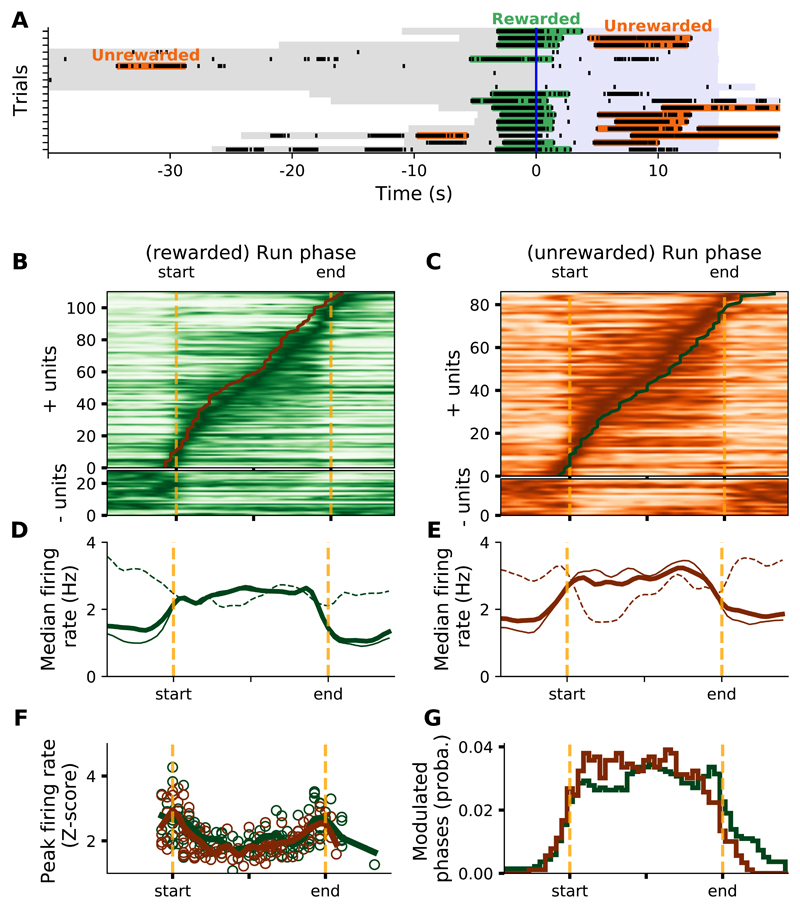
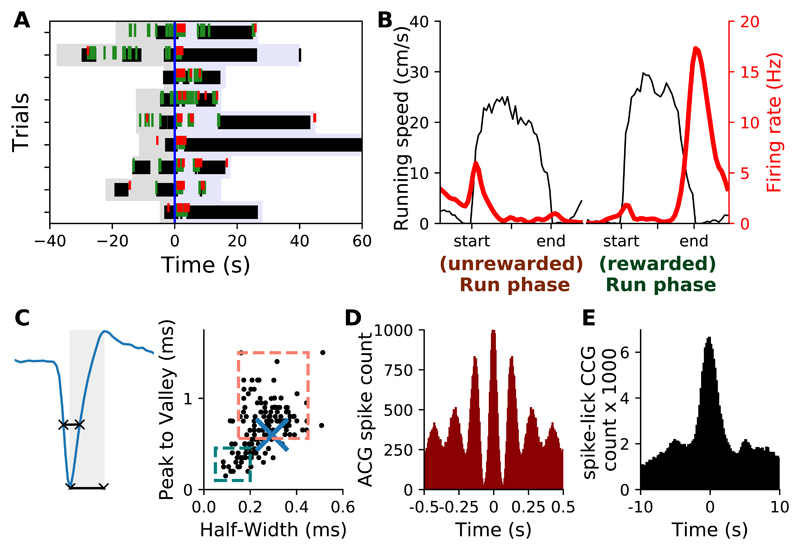
During recording sessions, mice often performed both unrewarded and rewarded runs (Figure 5A). If the main function of the striatum is to signal discrete run phases (start, maintenance and stop), firing rate modulation should be similar for both types of trials. Alternatively, if the striatum monitors the movement dynamics on a moment-to-moment basis, a differential modulation of striatal neurons activity would be expected in these types of run, as the end of rewarded runs are associated with distinct motor activities (such as licking). At a population level, fewer neurons were positively modulated toward the end of the run in unrewarded runs compared to rewarded runs (Figures 5B and 5C). This effect was not associated with a clear difference in striatal population firing rates (Figures 5D and 5E) or in the magnitude of peak firing rates modulations occurring during runs (Figure 5F) but was visible in the distribution of the significantly positively modulated phases (Figure 5G, p < 1.10^-5, two sided Kolmogorov-Smirnov). Figures 6A and 6B show an example of a neuron whose activity was stronger at the end of rewarded runs compared to unrewarded runs. This neuron's waveform was characteristic of PN (Figure 6C). Its spike timings autocorrelogram displayed prominent rhythmicity around 8Hz (Figure 6D), which is the typical licking frequency of mice. Finally, cross-correlating spiking and licking activities confirmed that this neuron fired spikes mostly when the mouse was licking (Figure 6E).

Figure 5. Population activity in rewarded and unrewarded runs.

A) Detection of rewarded (green) and unrewarded (orange) runs, in a few trials of an illustrative session. B,C) Mean firing rate for all modulated cells during rewarded (B) and unrewarded (C) runs. In B and C upper panels, continuous running lines represent the peak firing rates of all modulated neurons in unrewarded and rewarded runs, respectively. D,E) Population mean firing rates of positively-modulated (continuous line), negatively-modulated (dashed line) and all (thick line) neurons during rewarded (D) and unrewarded (E) runs. F) Z-scored peak firing rates versus run phases (circles) and population average (continuous line) for rewarded (green) and unrewarded (brown) runs. G) Distribution of all the run phases with significant positive modulation of firing rate, for rewarded (green) and unrewarded (brown) runs.

Figure 6. Licking rewards modulate spiking activity at the end of runs.

A) Behavioral activity during a few trials of a recording session and spiking activity of a neuron showing increased firing rate at the end of the runs. B) Mean firing rate during unrewarded (left) and rewarded (right). Same neuron as A. C) Mean spike waveform and waveform features of neuron in A (right, blue cross), superimposed on all recorded neurons waveform features (black dots, dashed squares indicate classical limits used to distinguish putative FSI (teal) and PN (salmon)). D) Auto-correlogram of spiking activity. E) Cross-correlogram between spiking and licking activities. Data in A-E are from the same neuron.

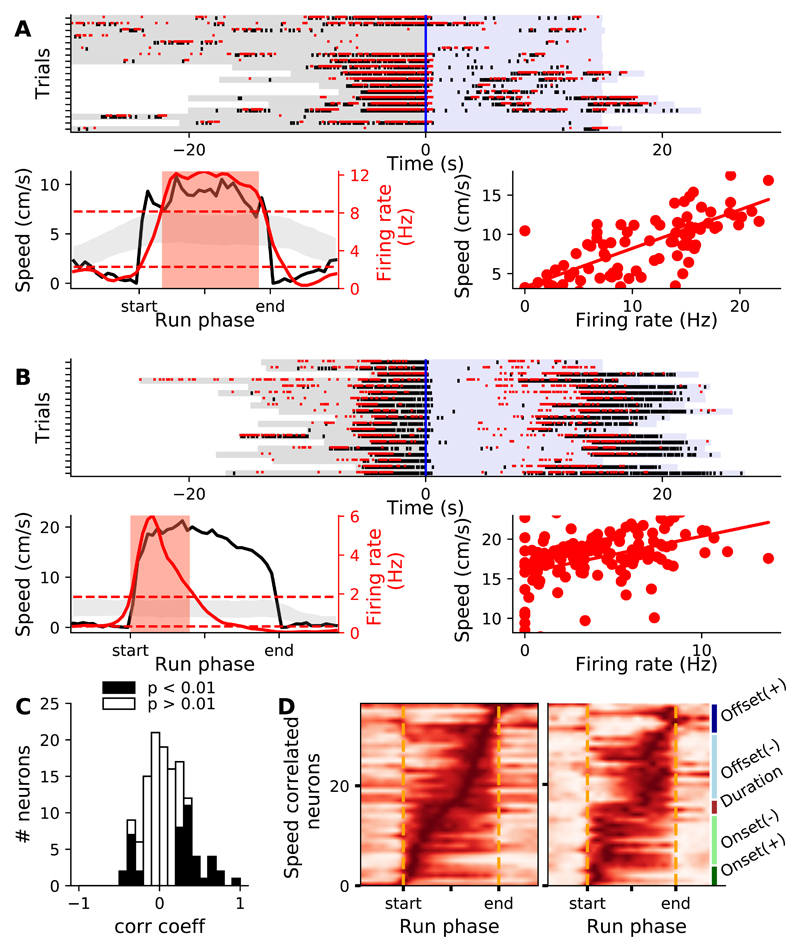
Finally, we examined if the firing rate of positively-modulated neurons correlated with the running speed, on a trial-by-trial basis [32–34]. We first determined the running phases during which the tuning curves were significantly modulated (see STAR Methods, red shaded areas Figures 7A and 7B). We then measured the correlation between firing rates and running speeds taken in the modulated run phases, on a trial-by-trial basis. We found that the firing rate of more than a third of the positively-modulated neurons was significantly correlated with the running speed (Figure 7C). Some neurons displayed prolonged modulations of their firing rate and strong correlation with running speed (Figure 7A) while others displayed more transient modulations and weaker (but still highly significant) correlations (Figure 7B). At a population level, running speed-correlated neurons displayed a wide range of tuning curves with modulations covering the whole run durations (Figure 7D). Altogether these data show that a significant fraction of striatal neurons displayed robust sensitivity to running speed across the different run phases.

Figure 7. A large fraction of striatal neurons displayed trial-by-trial correlation between firing rate and running speed.

A,B) 2 illustrative neurons with significant running speed-firing rate correlation. Top panels show rasters of spike times superimposed on wheel movement detections for a few consecutive trials. Lower-left panels show the mean firing rate (red thick line) relative to run phases, superimposed on the average running speed (black). Red area indicates phases with significant modulation of the firing rate. Dashed red lines and gray shaded area indicate, respectively, the global and pointwise CIs used to detect significant modulations (see STAR Methods). Lower-right panels show a scatter plot of speed versus firing rate taken in the modulated run epochs, across all runs. C) Distribution of Spearman correlation coefficients between firing rate and running speed, for all positively modulated neurons. D) Tuning curves for all the neurons with a significant correlation coefficient between firing rate and running speed, ordered by the phase of the peak firing rate (left), or according to the coefficients of the quadratic and linear polynomial fit functions (right).

Discussion

Here we developed a task in which mice performed prolonged runs interleaved with running pauses to maximize reward consumption. We examined how striatal neurons fired with respect to the different phases of the runs. The firing rate of the majority of neurons increased significantly around the initiation, maintenance and termination phases of the runs. Some of these modulations strikingly resembled those of start, stop or boundary-related neurons previously reported during self-paced motor sequences. However, at a population level, the shapes of single neuron average firing rates (the run-related tuning curves) varied continuously according to the task dynamics: transient modulations tended to occur around the initiation and termination of runs while more prolonged modulation occurred during the run. Consequently, it was not possible to statistically separate the recorded neurons in groups, using the shape of their tuning curve or the time of the peak firing rate modulations. In addition, a significant fraction of the run-modulated neurons showed robust trial-by-trial correlation between firing rates and running speed. We propose that, collectively, these types of modulations are not compatible with a role of the striatum in action gating or limited to action initiation. Rather the striatum may monitor on a moment-to-moment basis the dynamics of movements of the animal. Such function could be required for learning and updating the kinematics content of adaptive actions.

Early in vivo single-unit recording experiments revealed outstanding modulations of spiking activity in sensory (e.g. visual cortex) and associative (e.g., hippocampus) brain areas by specific features of the stimuli or behavior [35,36]. These studies provided powerful intuitions on the functions of these areas (e.g., in vision processing and spatial navigation). Similar efforts have been applied to understand the contribution of the striatum in the control of actions. Single-units recordings performed in the putamen of non-human primates performing overlearned short actions, such as saccades or arm reaching, revealed neuronal modulations that 1) were movement-related and covered a wide range of timings, mostly after but also before movements' initiation, 2) showed context-dependent modulations to movement and 3) were sensitive to task-relevant cues or sensory stimulation [37,38]. In contrast to this complexity of striatal responses to short actions, recordings in the dorsal striatum of rodents have revealed a predominance of modulation around the beginning and the end of learned prolonged actions such as lever press sequences or T-maze run bouts [6,7,9,26,27,39] as well as more sustained modulations during faster actions [7]. It has been proposed that these distinct forms of modulation are critical for initiating and terminating learned actions [7]. Such a "traffic-light" coding mechanism [10] supposes that start, maintain and stop signals can be unambiguously distinguished. In the example of the traffic light, if highly similar colors were used to signal start and stop, drivers might be confused and cross a road intersection while they should have stopped. Thus, a basic requirement of the traffic-light hypothesis for striatal function is that the firing rate modulations of two "start" neurons should be more similar than the firing rate modulations of a "start" and a "maintain" neuron. The classification of neurons in distinct functional groups based on their firing rate modulations requires unbiased methods to capture their variability and to quantify the degree of separability/overlap of the putative groups. Here, using principal component analysis, we found that the tuning curves' variability was well explained by a polynomial function [28]. The most informative aspects of the run-related tuning curves can thus be represented in a lower two-dimensional space defined by the curvature and linear components of the fitting functions. When considered individually, many of the tuning curves resembled previously described “start”, “stop” or “boundary-related” neurons (see Figure 3B). However, at a population level, tuning curves changed continuously and separate groups could not be isolated using either the coefficients of the fit functions or their first two principal components (Figures 3C-3G). Such a continuum of neuronal modulations was also observed when we analyzed and sorted the times of peak firing rate modulation around run initiation across neurons (Figures 4A and 4B). It is still possible to arbitrarily define groups of neurons based on the time of their peak firing modulations or the value of fit functions (Figures 3B and 3C and gray area in Figure 4B). We found that the decoding accuracy of the different run phases (including pre and post-run phases) by striatal ensembles was not compromised when we excluded neurons that exhibited prominent firing rate modulation just before the runs (Figure 4D). We also found similar encoding accuracy of the run start and stop phases by neuronal ensembles composed of neurons either displaying transient firing rate modulation around run start and stop, or prolonged modulations during the runs (Figure 4E). These result shows that, contrary to what might have been expected, neurons with firing rate modulations that peak or plateau during the runs also contribute significantly to the decoding of the initiation and termination of the runs.

The existence of start, maintain and stop signals in the striatum has been proposed from the predominance of modulations of firing rates at the beginning and ending of learned actions [6–9,26,27]. This trend is also apparent in our data (Figures 2F and 2G). In addition, we also observed that transient modulations occurred preferentially around the start and stop phases of the run while more sustained modulations occurred during the run (Figure 3C). This suggests that the impossibility to cluster neurons using the shape of their tuning curves is unlikely to stem from a difference in task design or learning level between our study and the aforementioned related works. Still, it would be interesting to examine, using large-scale chronic recording techniques, wether the separability of the tuning curves of a given neuronal ensemble evolves during task learning and automatization of the motor routine. We believe that the continuum of modulations we observed is congruent on the one hand with the movement dynamics of prolonged stereotyped actions, and on the other hand the somatotopic organization of somatosensory and motor inputs reaching the dorsal striatum (reviewed in Robbe et al. 2018). In our task, somatosensory stimuli and motor commands occurring around run initiation and termination will overlap with more sustained and stable movement dynamics associated with running. For instance, we reported a clear case in which a "run stop" neuron was primarily driven by the licking activity that occurred toward the end of rewarded runs. Here we only recorded licking activity and running wheel movements. Thus, it is possible that some of the transient modulations occurring around the beginning and the end of the runs can be triggered by brief movements, such as changes in posture or bouts of whisking activity. This possibility is supported by a recent study performed in head-fixed mice in which phasic dopaminergic signals in the dorsal striatum preceding run bouts were primarily correlated with brief whisker movements that systematically occurred prior to locomotor activity [40]. In addition, a tendency for a representation of movement-rich parts of tasks by striatal ensembles has been suggested before, in the context of spatial navigation [31]. The detection of movement-related signals around the beginning or end of learned actions will be facilitated if these actions are integrated in a larger stereotyped motor routine (e.g., whisk-run-lick, run-press-run, …). Consequently, experimental conditions associated with low level of behavioral stereotypy (such as early during training or following neuronal perturbation) are bound to be associated with weak or undetectable firing rate modulations around start/stop action phases [6,26]. A role of the dorsal striatum in providing moment-to-moment movements representation can not be overlooked, as the dorsocentral/lateral striatal regions in which we (and others) recorded neuronal activity receive massive cortical input from motor and sensory regions related to movements and stimulation of different body parts, mainly the trunk, limbs and, to a lesser extent, oro-facial regions [13,14]. Moreover, it has been shown that the spiking activity of dorsal striatal putative FSI and direct and indirect-pathway PN is strongly modulated by passive manipulations of body parts in mice and rats [23,41]. Finally, large-scale calcium imaging of both direct and indirect-pathway PN activity has revealed that distinct behavioral patterns associated with openfield exploration are fully mapped in the dorsal striatum [42]. These anatomical and physiological considerations are sufficient to explain the predominance of transient modulations during early and late phases of the runs and more sustained modulations during run, without invoking discrete start, maintain or stop signals. Such monitoring capacity is compatible with the dynamics of a network model of striatal projection neurons responding to a sequence of excitatory inputs [43].We propose that the main function of the dorsal striatum is not to gate action by sending disembodied "traffic-light" signals, but is more likely to continuously monitor the movement dynamics of different body parts during action execution.

What could be the behavioral function(s) of such movement monitoring by the dorsal striatal network? A first possibility is that it is not directly related to the control of ongoing actions but could be useful for de novo motor learning. For instance if the action-reward contingency of our task was suddenly changed, the movements dynamics representation combined with dopaminergic modulations triggered by the updated-reward contingency [44] could contribute to an exploration of different movements dynamics [45]. The continuous movements monitoring by striatal neurons could also contribute to keep track of time in an embodied manner, in agreement with previous studies reporting that the striatum multiplexes time and task-related information [32,46,47]. A given somatosensory state would automatically trigger a specific movement pattern and stereotyped task performance would result from the succession of somatosensory-motor couplings. The design of our task, in which distinct running patterns can lead to reward delivery, does not allow to examine if altered movement dynamics representation can cause variations in running behavior. However, in line with such possibility, it has been shown, in mice trained to lick in response to whisker stimulation, that an absence of whisker-evoked response in striatal neurons occurred selectively in trials in which mice failed to lick in response to the whisker stimulation [48]. Finally, because the monitoring of movement dynamics was accompanied by high correlations between firing rate and running speed on trial-by-trial basis, our results also support a role of the striatum in controlling the speed of action or vigor [28,32,49–51]. While future studies will surely delineate the exact (and possibly multiple) contribution(s) of the striatum to motor control and learning, our results add to a significant body of work suggesting that the classical view of the striatum as a key element of action selection and/or initiation must be revisited.

STAR Methods

Contact for Reagent and Resource Sharing

Further information and requests for reagents may be directed to and will be fulfilled by the Lead Contact, Dr. David Robbe (david.robbe@inserm.fr).

Experimental Model and Subject Details

All experimental procedures were conducted in accordance with the standard ethical guidelines (European Communities Directive 86/60 - EEC) and were approved by the relevant national ethics committee (Ministère de l’enseignement supérieur et de la recherche, France, Ref 00172.01). 3 types of mice were used in this study: wild-type (WT) C57BL/6J (n = 18, Charles River), Drd2-Cre (n = 10, C57BL/6J background, founder ER44, donated by Dr Valjent), and eNpHR-ChAT (n = 6, donated by Dr Beurrier, Ai39 mice were crossed with ChATcre/cre to induce eNpHR3.0 expression in cholinergic neurons). Drd2-Cre mice were included in the task learning figure (Figures 1B-1D, n = 5) and/or in the neurophysiological data analysis (n = 7). eNpHR-ChAT mice were included in the task learning figure (Figures 1B-1D, n = 6). There was no difference in the number of sessions necessary to reach proficiency in the task (Figures 1B-1D) between WT, Drd2-Cre and eNpHR-ChAT mice (correct trial rate: p = 0.09; median trial duration, p = 0.31, Run-and-stop index: p = 0.25, Kruskal-Wallis test), thus all the behavioral data of all animals, regardless of genotype were pooled together (Figure 1). Some of the Drd2-Cre and eNpHR-ChAT mice were used in yet unpublished optogenetic-based experiments that took place after training or electrophysiological recordings presented in this manuscript. Two days before fixation of head plates, mice (~ 3 months old, male) were housed individually in transparent cages located in the experimental room, with controlled temperature (22 °C) and humidity levels (60%) and maintained on a 12:12 h dark-light reverse cycle to allow experimentation during dark phase. Before training, mice were housed with ad libitum access to food and water.

Method Details

Surgical Procedures

All surgical procedures were performed under stereotaxic control and deep isoflurane anesthesia. In anticipation of head-fixed behavioral and acute electrophysiological experiments, a custom-designed head-plate was cemented on the exposed and cleaned skull of all animals (Superbond Kit, Frapident). For mice intended for electrophysiological recordings, two miniature stainless steel screws (Small Parts, size 000-120) were epidurally implanted above the cerebellum, to serve as ground and reference. A bilateral craniotomy was performed at the following coordinates relative to Bregma: 0 mm AnteroPosterior and ± 2 mm MedioLateral. The dura was not removed but protected with a layer of Kwik-Cast (WPI). Animals were given at least 1 week of recovery after the surgery before behavioral training started.

Behavioral apparatus

The behavioral apparatus consisted of a custom-made enclosure made of Mini T-slot profile beams (MakerBeam) that maintained in its center a free spinning wheel (12 cm diameter and 8 cm wide, 3D printed in la Plateforme Technologique du Pays d’Aix, Plateforme Technologique, IUT d’Aix en Provence). The enclosure design allowed to position the mice on top of the wheel via the head-plate. The wheel was covered with a layer of washable velvet and rotated around a ball-bearing shaft, allowing the mice to walk easily on the wheel (Figure S1A). Movements of the wheel were measured using a photodetector that detected the passing of the wheel spokes (Figure S1A). The number of spokes allowed the detection of rotations of the wheel, which was equivalent to 2.36 cm of linear travel. A liquid well was positioned near the mouth of the mice. The delivery of rewards (10 µl of 10% sucrose solution) was ensured through a solenoid valve, which generated an audible click at the time of opening. Mice simply collected the reward by licking. In some experiments, the licking activity was recorded using a custom-made photodetector (Figure S1A). A white noise was played through a mini loudspeaker to signal the RP (Figure S1B). The movements of the wheel, sound, lick detections and openings of the solenoid valve for reward delivery, were recorded/controlled through a custom-designed electronic board interface connected to a multifunction data acquisition device (USB-6353, National Instruments) and managed by a custom made software (LabVIEW, National Instruments).

Behavioral task and training

After recovery from the surgery (2 to 5 days), mice were handled by the experimenter every day for at least 5 days. Then, the mice were familiarized with the head-fixation/wheel apparatus during 20 min-long sessions. In these sessions, rewards were delivered manually by the experimenter as soon as the mice ran/walked for about 10 cm. Once mice performed several runs of at least 10 cm, training in the run-and-stop task started. Mice were placed on a water restriction schedule (1 ml/day, weight >= 85% of pre-training weight). Training sessions lasted 40 min, during which the experimenter was not physically present in the room. The behavioral sessions were composed of several trials, divided into "Run" and "No run" periods (RP and NRP, respectively), whose durations depended on the locomotor activity of the animals. During RP, which were signaled by a continuous white noise, mice obtained a drop of sucrose as soon as they ran for 100 cm without stopping. Operationally, stops were defined as moments during which no wheel movements were detected for more than 1 s. At the time of reward delivery, the white noise was turned off and the task transitioned to the NRP, which, depending on the locomotor activity of the animal in that period, lasted 15 s or more. Indeed, when the mice did not run (i.e., no wheel detection) for at least 2 s at the end of the NRP (between 13 and 15 s, after the end of the RP, Figures S1A and S1B), a new trial started. However, if the mice failed to respect this 2 s immobility period, the NRP was prolonged until animals paused their locomotor activity for 2 s. A trial was considered correct if the animal ran continuously for 100 cm before the end of the RP (see illustrative trials 3-6, Figure S1B). If, after 60 s in the RP, the animal failed to reach this objective, either because the run was too short (illustrative trial 1, Figure S1B), or because multiple short runs interleaved with stops were performed (illustrative trial 2, Figure S1B), the trial was considered as incorrect and the task transitioned from RP to NRP without reward delivery. The transitions between the different trials and periods of the tasks and the recording of the behavioral performance were ensured by a LabVIEW custom made software. At the end of each session, we measured the total amount of liquid delivered during the session. One hour after the training session, mice received a complementary amount of tap water to ensure they consumed at least 1 ml of liquid per day.

Acute in vivo electrophysiological recordings

Acute extracellular recordings of spiking activity were performed in the dorsal striatum while mice performed the run-and-stop task. On the recording day, mice were briefly anesthetized with isoflurane, the craniotomy was cleaned (by removing the Kwik-Cast) and the dura was removed. Mice were head-fixed above the wheel and while they woke up from the anesthesia a 32-channel silicon probe (Buzsaki32A, NeuroNexus) was slowly lowered into the brain with a precision stereotaxic arm. After reaching the dorsal striatum (DV: − 2.0 mm, relative to bregma), liquid agar (1.5%) at near body temperature was applied around the probe to seal the craniotomy and to improve the stability of the recordings. To visualize the silicon probe track in the brain, DiI Lipophilic carbocyanine dye (DiI, 42364, Sigma-Aldrich) (1-2% diluted in ethanol) was applied to the back of the tip of the probe before penetration. Recording sessions for all mice typically lasted 40 min, during which the animal performed the task. Many sessions had to be removed due to excessive drift or lack of proper behavior performance on the day of the electrophysiological recording. In this manuscript, we consider the activity of 167 neurons recorded during 30 different sessions (1 to 3 recording sessions per animals in one or two brain hemispheres) in 13 well-trained animals. Animals were considered well-trained if they performed at least 3 consecutive sessions with an average rate of correct trial > 10 correct trials/5 min).

Electrophysiological data acquisition and processing

Wide-band (0.1–8 KHz) neurophysiological signals were amplified 1.000 times via a Plexon VLSI headstage and a PBX2 amplifier and digitized at 20 kHz on two synchronized National Instruments A/D cards (PCI 6254, 16 bit resolution). Raw local field potential signals were processed off line and spike sorting was performed using a semi-automatic method, as described previously [32,52] except that we used an updated version of the klustakwik algorithm (http://klusta-team.github.io/, [53])

Histology

At the end of the experiments, mice were deeply anesthetized and transcardiacly perfused with PBS (Phosphate Buffer Solution) followed by 4% paraformaldehyde. Cresyl violet staining of coronal and sagittal sections (60 μm) was performed to confirm the position of the silicon probe during recordings through visualization of the DiI stain traces.

Quantification and Statistical Analysis

Data and Software Availability

All the analyses were performed using the Python language taking advantage of the Jupyter Notebook web interface which allowed regeneration (or modification) of the manuscript figures. A first pre-analysis step was performed to synchronize the timings of spikes of well-isolated units (see above for processing), wheel and lick events. These timings were aligned relative to the structure of the task (trial numbers, beginnings and ends of RP and NRP). The notebooks supporting these pre-analysis processing steps are available at https://bitbucket.org/davidrobbe/sales-cabonell_manuscript. All the figures of this manuscript were generated through a series of python codes, which analyze, quantify and visualize specific aspects of the behavioral and neuronal data and their relationship. These codes are entirely described in notebooks available at https://bitbucket.org/davidrobbe/sales-cabonell_manuscript. Raw electrophysiological data (unfiltered 32-channel LFPs, sampled at 20 kHz) are conserved at INMED and can be shared to any reader upon reasonable request. Processed electrophysiological data (spike times, features and IDs, behavioral data) used by the Jupyter Notebooks to generate the figures can be directly uploaded from Mendeley data (http://dx.doi.org/10.17632/rtmr3scw8j.2).

Firing rate relative to run phases (tuning curves, TCs)

Runs were detected as series of consecutive wheel movement detection times occurring in intervals < 1 s. We restricted our analysis to runs that lasted at least 2 s and shorter than 15 s (i.e., the time difference between the first and last wheel detections in a detected series was >= 2 and <= 15 s). Similar patterns of firing rate modulation were obtained if our criteria for run detection was more stringent (Figure S2). We then normalized the duration of all the runs detected during a recording session. For each session, we computed the median run duration across all the detected runs. We then divided all the runs in an equal number of bins (n_bin): n_bin = mrd x 4 where mrd is the median run duration in a session (for example, if the mrd was 6.5 s in a given session, all the runs of this session were divided in 26 (6.5 x 4) bins). For each bin, we computed the instantaneous firing rate (spike count / bin duration). We also included 3 s before and after the detected runs. These pre- and post-run epochs were divided in bins of 250 ms (i.e., 12 bins). By definition, the 1^st second before and after the detected run epochs corresponded to immobility (no detection of wheel movement) epochs. Finally, the binned firing rates of the normalized runs, and their flanking 3 s-long epochs, were averaged across all runs in a given session. TCs (such as seen in Figure 2C) were obtained by convolution of the resulting averaged/binned firing rate series with a Gaussian Kernel (σ = 1). For a single neuron, a TC could be computed for all the detected runs (Figures 2-4 and 7), or separately for rewarded and non-rewarded runs (Figures 5 and 6). Because all the TCs have the same number of bins, we refer to the bins as phases of the run. Here, phases are not circular (the 1^st phase is not equivalent to the last one). Rather, they must be understood as relative times versus the beginning and the end of the run. As a consequence, the first and last 12 phases of the TCs correspond to pre- and post-run phases.

To detect the run phases during which the spiking activity of the neurons was significantly modulated, we randomly altered the relation between spike times and wheel detection events. We constructed 500 surrogate TCs as explained above, except that for each detected run, the spike times were jittered by a value randomly chosen between “– run duration” and “+ run duration”. A global band of confidence was defined as the 5 % highest and lowest values of the 500 surrogate TCs (i.e., 2 values). A pointwise band of confidence was defined as the 5 % highest and lowest values of the 500 surrogate TCs at each point. A TC was defined as significantly modulated if it crossed the global band of confidence. The significantly modulated phases were defined as the bins corresponding to the area between the TC and the pointwise band (see examples in Figures 7A and 7B, lower left panels, and supplementary methods in [54]). Some TCs crossed both superior and inferior limits of the global band of confidence. In these cases, we transformed the TC in Z-score and the sign of the maximum absolute deviation was used to determine if the TC was positively or negatively modulated.

For all the neurons that displayed a positive significant modulation of their TC, we quantified the trial-by-trial correlation between firing rate and running speed during the modulated phases (Figure 7). In each trial, we only considered the phases corresponding to a continuous modulated part of the TC, between run start and stop. If the TC was modulated in more than one region, we only considered the phases showing the strongest modulation. In each run, we computed the average running speed (r_s) in the modulated run phases: r_s= (n_wheel-event-1)*2.356/(n_bin*bin_duration), where n_wheel-event is the number of wheel detection events in the modulated portion, n_bin is the number of modulated bins and bin_duration is the bin duration in this run. The relation between the running speed and firing rate was statistically assessed using the Spearman's rank correlation coefficient.

Functional classification of neurons

The positively modulated TCs displayed a wide range of shapes (Figures 2-4). We used PCA to capture the main determinants of this variability. The majority of the variance (70%) was contained in the first two principal components, that were well approximated by a quadratic function with or without a linear function, respectively (Figures 3A and 3B). Each neuron’s TC was approximated with a second order polynomial function g: g(x) = ax² + bx + c, where x is the normalized trial duration (0 ≤ x 0 ≤ 1), a is the quadratic coefficient, b is the linear coefficient and c is the origin value. The coefficients a and b were considered significant if their p values (pa and pb, respectively) were lower than 0.05. The TCs (i.e., the neurons) were divided into 7 putative groups according to the significance and sign of the quadratic and linear coefficients (Table 1). In brief, onset positive/negative neurons were mostly active/inactive at the beginning of the trials, offset positive/negative neurons were mostly active/inactive at the end of the trials, on/off neurons were mostly active at the beginning and end of the trials, and the duration neurons showed sustained activity. The seventh pseudo-class contained neurons with non-significant quadratic and linear coefficients.

To evaluate if the different groups could be considered as segregated entities, we considered the polynomial fit function of each TC and plotted its linear coefficient versus its quadratic coefficient (as approximations of their 1^st and 2^nd principal component value). Given that each TC was assigned to one of the 7 putative groups, we computed the Silhouette Coefficient score (SC) of all the neurons to measure the inter-dependency of the groups as: SC = (d' - d) / max (d, d') with d being the mean intra-cluster distance and d' the mean nearest-cluster distance to the considered neuron (Rousseeuw, 1987). For each TC, the SC could take a value between 1 (perfect assignment) and -1 (perfect assignment to the nearest cluster). A value near zero indicated that the TC was equally likely to belong to its assigned group/cluster or to the closest neighbor. A negative value indicated that a TC was assigned to the wrong cluster.

Unsupervised clustering of neurons based on TC profiles

We performed PCA of the tuning curves of both positively and negatively modulated neurons. A k-means algorithm (fscikit-learn python package) was used to generate the best partitioning of the tuning curves on the basis of their first and second PC (Figure 3F). We then varied the number of partition (k) between 2 and 10. The number of runs of the algorithm was set to 20 and the maximum number of iterations was 300. To quantify the quality of the clusters generated by the k-means algorithm, we used the Silhouette score as a measure of cohesion inside groups versus separation between groups (see above). We also used distortion (also referred to as inertia or within-cluster sum-of-squares), which is directly computed by the k-means algorithm. Indeed, the k-means algorithm tries to minimize distortion, which is the sum of the squared distances between each observation (pairs of PC) and its dominating centroid. To demonstrate quantitatively the lack of clusterability of the PC scatter plot (Figure 3F), we generated one thousand surrogate data sets by independently sampling pairs of PC from the distributions of the first and second PC of our tuning curve data set (i.e., independent reverse sampling from the real data set). Each surrogate data set (n = 146 pairs of PCs) was clustered using the same k-means algorithm and Silhouette scores and distortions were computed.

Peristimulus time histograms of spiking activity

For all the recorded neurons, we generated a peristimulus time histogram (PSTH) of their spiking activity aligned with the time at which runs started. We used bins of 100 ms and examined the spiking activity from 2 s before to 2 s after the beginning of all the detected runs (Figure 4A, bottom). We identified bins with significant firing rate modulations by comparing each original PSTH with one thousand surrogate PSTHs generated after randomizing the relationship between the spike trains of the neuron and the times of run start. Those surrogate PSTHs served to generate a global and a pointwise confidence intervals. The crossing of those intervals by the original PSTHs was used to isolate PSTH bins exhibiting significant modulation (same as TC analysis). From all the significantly modulated bins of a given neuron, we isolated those that surrounded the maximal firing rate modulation and that occurred from 2 s before to 2 s after the start of the runs (Figure 4A, bottom). For instance, in the case of the first illustrative neuron 1, we did not consider the significantly modulated bin around 2 s (Figure 4A, bottom).

Bayesian decoding

The decoding procedure consisted in computing the probability of the animal being in a given run phase (normalized time bin computed from run start and stop times and run duration) knowing the spiking response of a single neuron (or an ensemble of single neurons; [31]). We used the same normalization procedure of the run durations as the one used to construct the TCs and used a leave-one-out cross-validation procedure [55]. For each time bin t before, during and after the detected run (12 bins before, 28 bins during and 12 bins after the run, average bin duration = 250 ms), we first took the instantaneous firing rate xi of a neuron i in that bin at a random trial. Second, we computed the posterior probability function p (Bin = t | xi, t from 1 to 52) of the mice being at each of the 52 time bins given the tuning curve of the neuron computed from the remaining trials, assuming a uniform prior and a Poisson distribution of the spike count variability [55]. To perform decoding using an ensemble of neurons, we multiplied the individual probability functions to obtain the ensemble posterior probability, assuming independence between the ensemble members (low level of correlation between striatal neurons and pulling of neurons from different sessions). The accuracy of predicting the considered bin (run phase) t0 by an ensemble of k neurons (k>=1) was given by the mean ensemble probability of a correct estimate: p (Bin = t0 | [xi, i from 1 to k]) over 50 leave-one-out repetitions [55].

To compute the decoding accuracy of run phases, we used the trial-by-trial instantaneous firing rates relative to the normalized run phases (see above) of both positively and negatively modulated neurons (n =146 in total). For the decoding accuracy of striatal ensemble of increasing size (25, 50, 100, Figure 4C), we randomly selected 25, 50 or 100 neurons out of the total data set (146 neurons). We repeated this operation 10 times and reported the average decoding accuracy. To compare the decoding accuracy between ensembles that included or excluded the 24 pre-Run neurons (Figure 4D), the size of the ensembles was 122 neurons, for each condition. We randomly selected 122 neurons from the entire data set to generate ensembles that included the pre-Run neurons and computed the decoding accuracy of each ensemble. We repeated the procedure 100 times and reported the median decoding accuracy and the 5^th and 95^th percentiles. This was compared to the decoding accuracy obtained when we used the 122 non-pre-Run neurons (i.e., same size comparison). To compare the decoding accuracy between ensembles composed of neurons that displayed either transient or prolonged neuronal modulation (Figure 4E), we assigned positively modulated neurons into two groups. The transient group was composed of neurons classified as On/Off, Onset+ and Offset+ (53 neurons in total, Figures 3B and 3C). The prolonged group was composed of neurons classified as Onset-, Duration and Offset- (63 neurons in total, Figures 3B and 3C). We compared the decoding accuracy of ensembles of 50 neurons randomly selected from each group and repeated the operation 100 times.

Statistical tests

To statistically compare task learning rates across mice genotypes we used the Kruskal-Wallis test. To test for uniformity of distributions we used the Kolmogorov Smirnov test (Figures 2E and 2F). To test for statistical difference between two distributions, we used the two sided Kolmogorov-Smirnov test (Figure 5G). P values were reported in the main text. To test for firing rate difference between putative projection neurons and fast spiking interneurons (Figure S4C), we used the non-parametric Wilcoxon test. In this case, the p value was directly reported on the figure. The relation between the running speed and firing rate was statistically assessed using the Spearman's rank correlation coefficient (see above). P values for all the units analyzed are reported graphically (Figure 7C). The method to identify significant modulations of firing rates has been explained in detail above. The method to statistically test for the presence of functional groups, based on the shape of the neuronal tuning curves, has been described above.