Abstract
Electrocardiogram, electrodermal activity, electromyogram, continuous blood pressure, and impedance cardiography are among the most commonly used peripheral physiological signals (biosignals) in psychological studies and healthcare applications, including health tracking, sleep quality assessment, disease early-detection/diagnosis, and understanding human emotional and affective phenomena. This paper presents the development of a biosignal-specific processing toolbox (Bio-SP tool) for preprocessing and feature extraction of these physiological signals according to the state-of-the-art studies reported in the scientific literature and feedback received from the field experts. Our open-source Bio-SP tool is intended to assist researchers in affective computing, digital and mobile health, and telemedicine to extract relevant physiological patterns (i.e., features) from these biosignals semi-automatically and reliably. In this paper, we describe the successful algorithms used for signal-specific quality checking, artifact/noise filtering, and segmentation along with introducing features shown to be highly relevant to category discrimination in several healthcare applications (e.g., discriminating patterns associated with disease versus non-disease). Further, the Bio-SP tool is a publicly-available software written in MATLAB with a user-friendly graphical user interface (GUI), enabling future crowd-sourced modification to these tools. The GUI is compatible with MathWorks Classification Learner app for inference model development, such as model training, cross-validation scheme farming, and classification result computation.
Keywords: Affective computing, biosignal processing, blood pressure (BP), dimensionality reduction, electrocardiogram (ECG), electrodermal activity (EDA), electromyography (EMG), feature extraction, health informatics, impedance cardiography (ICG), machine learning, pattern recognition, quality checking
The BiosignalSpecific Processing toolbox for preprocessing and feature extraction of biosignals is based on state-of-the-art algorithms and expert feedback. This open-source toolbox supports researchers in machine learning, affective computing, and psychophysiology, providing more automatic and reliable extraction of signal-specific physiologically relevant features from different biosignals for use with a wide variety of machine learning and pattern recognition algorithms.
I. Introduction
Measures of peripheral physiological signals (biosignals), including the electrocardiogram (ECG), impedance cardio- gram (ICG), electromyogram (EMG), electrodermal activity (EDA) and continuous, noninvasive arterial blood pressure (BP) can provide rich information about peripheral physiological functioning of the body with the potential for providing insights on phenomena such as health status, sleep quality, and the affective properties of psychological experience. These measures are thus widely used as the input data for machine learning and pattern recognition algorithms focused on preventive care, diagnostics, and telemedicine, including guiding therapy [1]–[8]. For example, a support vector machine (SVM) classifier was trained on ECG signal features, such as inter-beat interval (IBI) to predict ischaemic heart disease in [2], and an SVM was trained on EDA signal features to corroborate coding by adult experimenters of groups of children who were either easy or hard to engage socially during a set of lab interaction tasks [3]. In [4], an inference model trained on EMG signal features was used to aid the diagnosis of neuromuscular disorders, and in [5], a model trained on BP signal features was used to aid in diagnosing diabetes. Valvular heart diseases have been predicted by models using ICG signal features [6] and physiological responding under stress has been studied by analyzing multimodal data comprising ECG, EMG, EDA, and ICG signal features [7]. These are just a few examples of the rapidly expanding research utilizing the information present in biosignals for machine learning and pattern recognition in healthcare and psychological science [7], [9].
Typically, in these studies, a large amount of physiological data is collected. However, to reduce the dimensionality of these data, researchers often extract specific attributes (i.e., features) from each biosignal to use as input for machine learning or pattern classification models. Identifying relevant features of a given biosignal for a specific inference tasks requires deep knowledge regarding the human biological mechanisms as well as expertise in analyzing these data [10]. Due to increasing interest in and usability of these peripheral biosignals in medical and bio-engineering research, several commercial software and open-source toolboxes have been developed to simplify the preprocessing and feature extraction required when analyzing these biosignals [10]–[12]. There are also biosignal-specific processing algorithms for ECG [12]–[14], [14], [15], EMG [16], [17], EDA [18]–[20], continuous blood pressure (BP) [21], [22] and ICG [23], [24] signal processing. However, a large portion of these software and algorithms are not designed for semi-automatic processing, and require intensive manual interventions by the users. For instance, many processing pipelines are unreliable without visual inspection and therefore demand visual inspections for basic quality checking; this is because their algorithm are not sufficiently robust to morphological variations of the biosignals and to the low signal-to-noise-ratio conditions that often arise. Moreover, details and rationale behind the choice of the processing algorithms, their implementation and parameter tuning are missing in the majorities of these works.
The present work describes an open-source Biosignal-Specific Processing toolbox (Bio-SP tool) for psychologists, neuroscientists, and researchers in affective computing, machine learning and pattern classification that can be used to process ECG, EMG, EDA, ICG and continuous BP biosignals all in one easy-to-use, MATLAB-based toolbox. Bio-SP tool extracts relevant features for each signal automatically and reliably, and has been used in affective computing studies for processing and feature extraction with peripheral physiological biosignals [7], [25]. In this paper, we provide additional background information about the Bio-SP tool.
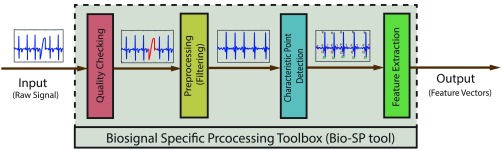
The biosignal processing pipeline employed in Bio-SP tool includes signal-specific algorithms for: (1) checking the quality of physiological data, (2) preprocessing of the biosignal data (e.g., noise filtering and artifact removal), (3) segmentation of continuous biosignal data, (4) detection of characteristic points on a biosignal waveform, and (5) feature extraction. The signal-specific algorithms employed in Bio-SP tool are developed using the current state-of-the-art in the scientific literature [13]–[24], [26] and are based on feedback received from field experts. Future iterations can incorporate or link to new signal processing tools that appear in the literature such as a new moving ensemble averaging procedure for processing ICG data (Cieslak et al., 2018).
Moreover, very few software/toolboxes have ICG processing tools that have been combined with such tools for other peripheral biosignals. Our Bio-SP tool provides the ability to process ICG and extract ICG-based signal features, such as cardiac output (CO), pre-ejection period (PEP), and stroke volume (SV), which are associated with distinctive patterns of cardiovascular response (i.e., threat vs. challenge) during motivated performance tasks [27]–[29].
The Bio-SP tool is accessible via the MathWorks File Exchange site [30]. The toolbox has been developed such that the outputted feature matrix can be employed directly by machine learning algorithms for further analysis, or even passed directly as input into the Classification Learner App provided by MATLAB.
II. Materials and Methods
We developed a set of signal-specific algorithms to extract physiologically relevant features from raw biosignals of ECG, EDA, EMG, ICG and continuous BP. To this end, for each biosignal, several layers of algorithms are implemented in consecutive order. The input-output as well as inner toolbox layers of Bio-SP tool are schematically illustrated in Fig. 1. Although, the algorithms are signal-specific, the general pipeline is similar across all five signal modalities. First, we perform basic automatic quality checking. Segments of the raw signal that are purely noise or are of low quality due to improper attachment of sensors or large movements of participants are detected and marked in red, identifying them for possible replacement or removal from the original signal. Signals then undergo a filtering process designed to remove high frequency noise (e.g., 60 Hz power-line interference) and lower frequency artifacts (e.g., limb movements). Parameters of choice for the specification of filters (filter type or bandpass values) can be tuned by users, however, we provided the recommended values for filtering parameters for each biosignal. Next, signal-specific algorithms are used to detect characteristic points of each waveform based on the prior knowledge provided by experts in these signals or existing published guidelines in this literature. Finally, relevant physiological features are extracted and outputted as a feature matrix for machine learning and pattern recognition analysis. This paper is primarily focused on the biosignal-specific feature extraction algorithms. We first describe the filtering, characteristic point detection, and feature extraction algorithms for each biosignal, and then we elaborate on the algorithms used for quality checking. Finally, we briefly introduce the tool box graphical user interface (GUI).
FIGURE 1.
Our Bio-SP tool pipeline. The input (left) to the Bio-SP tool is a raw segment of either ECG, EDA, EMG, BP, or ICG biosignal (or modality). The Bio-SP tool output (right) is the signal-specific feature vector. The Bio-SP tool itself is comprised of the following consecutive processing steps: (1) Basic quality checking of raw signals. Poor quality portions of the input signal are detected and marked in red for possible elimination or replacement. (2) Preprocessing (filtering) of raw signals for noise or artifact removal. (3) Characteristic point detection on the filtered signal based on a series of signal-specific algorithms. (4) Feature extraction as functions of characteristic points detected on the signal.
A. Dataset Description
In this work, we used a dataset from the Interdisciplinary Affective Science Laboratory in the Psychology Department at Northeastern University for algorithm development and verification. The data were recorded as part of a larger research project funded by the Army Research Institute for the Behavioral and Social Sciences (W5J9CQ-12-C-0049). Data from 107 participants (65 females) were randomly selected from a larger dataset of 260 participants. All of the physiological measures included in our Bio-SP tool were recorded from each participant while he/she was performing a series of motivated performance tasks [7]. All biosignals were recorded using BioLab v.3.0.13 (Mindware Technologies; Gahanna, OH), and were acquired on a BioNex 8-Slot Chassis with a sampling rate of 1000 Hz. We included samples of this dataset in the Bio-SP tool directory for the tutorial purposes. For further algorithm evaluation, we also employed datasets from the PhysioBank ATM website [31] as well as some datasets shared by the MIT Affective Computing group [32].
B. Biosignal #1: Electrocardiogram (ECG)
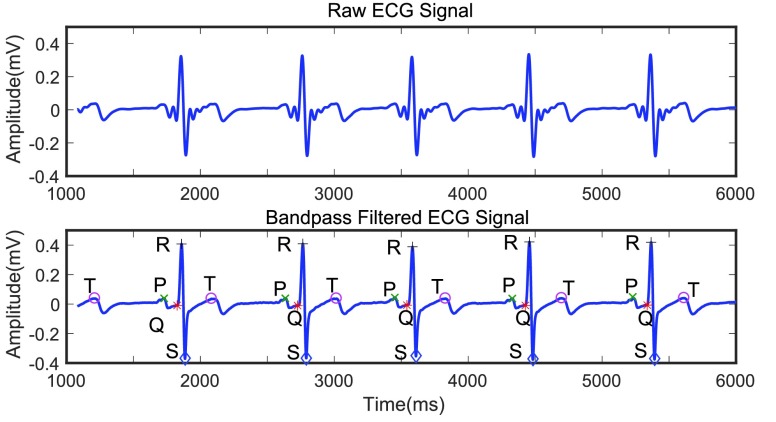
ECG is a primary diagnostic signal for detecting cardiovascular disease [33] and contains rich information relevant to human health, sleep quality, and psychological states [13]. The ECG signal comprises a consistent, complex electrical waveform that typically repeats for each heartbeat. The waveform associated with each beat contains several critical events including a P wave, a QRS complex, and a T wave (Fig. 2). Relevant physiological features can be defined by detecting these characteristic points for each heartbeat. We first use filtering to remove noise and artifacts. Then our developed robust algorithms are used to detect all important events (P, Q, R, S, T points) [30]. Finally, physiological features are calculated using these detected points.
FIGURE 2.
Raw ECG signal (top); bandpass filtered ECG signal (bottom) with the characteristic points (P,Q,R,S and T) identified on the signal.
1). ECG Preprocessing
Corruption of the ECG signal may be caused by power-line interference or baseline shifts, which can be caused by respiration or large movements of the participants or drift in the recording instruments [15], [34]. Therefore it is necessary to preprocess the ECG signal prior to applying any detection algorithm. Using an analysis of the signal power spectral density (PSD) function of ECG in our dataset, we determined that several band-pass filters, such as Elliptic, Gaussian, or Butterworth provide satisfactory performance in eliminating baseline and high-frequency noise without significantly decreasing the amplitude of the QRS complexes. Although we specified a band-pass Elliptic filter as a default option, other types of band-pass filters are also available in our GUI.
2). ECG Characteristic Point Detection
Inspired by the commonly used Pan-Tompkins algorithm [14], we developed an algorithm for robust QRS detection for ECG with the following steps:
-
Step I:
Since the human heart rate does not exceed 5 beats per second two adjacent QRS complexes cannot appear closer together than 200ms [14]. Therefore, a sliding window of 400 ms size with a step size of 1 sample can iteratively scan the entire signal. At each iteration, we find the global maximum in the sliding window and if this global maximum appears in the middle of the window, that global maximum is marked as a potential R point. By scanning the entire input ECG signal, the peaks which are likely to be R peaks are detected. The
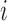 th peak is denoted by
th peak is denoted by 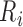 .
. -
Step II:
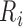 peaks that are lower in amplitude than an amplitude threshold (Amp-Thr) are eliminated. Amp-Thr is initially set to
peaks that are lower in amplitude than an amplitude threshold (Amp-Thr) are eliminated. Amp-Thr is initially set to 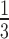 times the maximum amplitude of the first 2 seconds of the input ECG signal. To adapt to the changes in the ECG over time, upon passing sufficient R peaks from the beginning of the signal, Amp-Thr is updated to 0.75 times the mean of the amplitude of the last eight determined R peaks.
times the maximum amplitude of the first 2 seconds of the input ECG signal. To adapt to the changes in the ECG over time, upon passing sufficient R peaks from the beginning of the signal, Amp-Thr is updated to 0.75 times the mean of the amplitude of the last eight determined R peaks. -
Step III:
After scanning through all the detected adjacent R peak to R peak time intervals (R-R intervals), if any R-R interval is greater than a predefined threshold (RR-Thr), it implies that an R peak is missing. Thus, we assign a new R peak as the global maximum amplitude of the signal within the range of
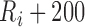 ms and
ms and 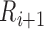 -200ms [14]. According to [14], the rate of change for adjacent R-R intervals will not exceed 166%. Thus, RR-Thr is initially set to the previous R-R interval multiplied by 1.66. Upon detecting enough R-R intervals, the RR-Thr is then updated to reflect the average of the last eight R-R intervals multiplied by 1.66.
-200ms [14]. According to [14], the rate of change for adjacent R-R intervals will not exceed 166%. Thus, RR-Thr is initially set to the previous R-R interval multiplied by 1.66. Upon detecting enough R-R intervals, the RR-Thr is then updated to reflect the average of the last eight R-R intervals multiplied by 1.66. -
Step IV:
Detection of P, Q, S, and T points are based on the locations of the detected R peaks.
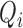 is identified as the first closest local minimum before
is identified as the first closest local minimum before 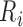 and within the interval of
and within the interval of 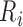 -70ms and
-70ms and 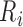 . Likewise,
. Likewise, 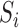 is identified as the first closest local minimum after
is identified as the first closest local minimum after 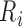 and within the interval of
and within the interval of 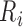 and
and 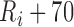 ms. The peak of the P wave,
ms. The peak of the P wave, 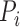 , is identified as the global maximum point found in the interval of
, is identified as the global maximum point found in the interval of 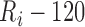 ms to
ms to 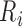 , and the peak of the T wave,
, and the peak of the T wave, 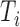 , is identified as the global maximum point found in the interval of
, is identified as the global maximum point found in the interval of 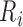 to
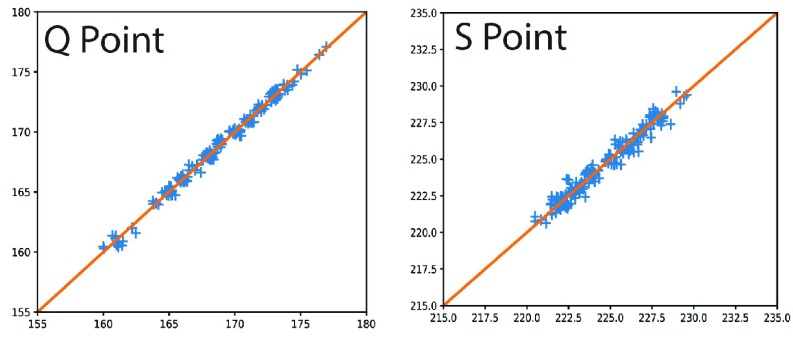
to 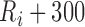 ms. The detected locations of P, Q, R, S, and T on a few sample heartbeats are shown in Fig. 2. We investigated the accuracy of our Q and S point detection algorithm by comparing the results of our automated detection algorithm with visual inspection of 1000 randomly selected heartbeat cycles from the ECG signal of 10 different participants. Results demonstrated that that almost all the Q and S points were accurately detected (see Fig. 3). Slight differences were likely caused by the lower resolution in the visualization used to mark manual detection.
ms. The detected locations of P, Q, R, S, and T on a few sample heartbeats are shown in Fig. 2. We investigated the accuracy of our Q and S point detection algorithm by comparing the results of our automated detection algorithm with visual inspection of 1000 randomly selected heartbeat cycles from the ECG signal of 10 different participants. Results demonstrated that that almost all the Q and S points were accurately detected (see Fig. 3). Slight differences were likely caused by the lower resolution in the visualization used to mark manual detection.
FIGURE 3.
Validation of detecting characteristic ECG points, with visual detection (x-axis) vs. algorithm-based detection (y-axis): Q point (left), and S point (right).
3). ECG Feature Extraction
The following morphological features were extracted based on the QRS detection:
IBIM is the mean of all inter-beat intervals (IBIs) in a segment, where each IBI is the time (ms) between adjacent R-R intervals [16].
IBISD is the standard deviation of all IBIs in the input signal segment [16].
- SDSD is defined as the standard deviation of the differences between adjacent IBIs in a signal segment [16]. SDSD may be found by the following equation:
where
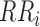 is the
is the 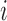 th R-R interval,
th R-R interval,  and
and  is the number of R-R intervals.
is the number of R-R intervals. - RMSSD is the square root of the mean of the sum of the squares of the differences between adjacent IBIs in a segment [17].
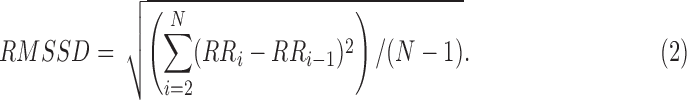
ECG-derived respiratory mean (EDRm) and standard deviation (EDRsd) [16] are related to respiratory effort. EDR is calculated based on the area of each normal QRS complex measured over a fixed window width
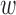 , which is determined by the interval from the PQ junction to the J(junction)-point which is the onset of repolarization phase on the ECG signal. We estimated
, which is determined by the interval from the PQ junction to the J(junction)-point which is the onset of repolarization phase on the ECG signal. We estimated 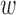 as two times the sum of the QR interval and the RS interval (
as two times the sum of the QR interval and the RS interval (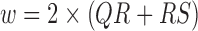 ). The mean and standard deviation of EDR (EDRm and EDRsd) are outputted as two features.
). The mean and standard deviation of EDR (EDRm and EDRsd) are outputted as two features.QR to QS ratio and RS to QS ratio, features used in cardiology, are defined as the ratio of the QR interval to the QS interval, and the ratio of the RS interval to the QS interval for each R peak, respectively.
C. Biosignal #2: Electrodermal Activity (EDA)
EDA reflects changes in the electrical conductivity of the skin that results from both internal (e.g., deep breaths) and external stimuli (e.g., sounds to which we attend) [35]. Changes in EDA reflect changes in the activity of the eccrine sweat glands, which are exclusively innervated by the sympathetic nervous system (SNS). Because of this relationship between EDA activity and SNS activity, EDA has been widely used as an indirect measure of peripheral physiological arousal [36]. The EDA signal is composed of two components, both a background, or tonic, level and phasic changes that are of shorter duration (on the order several seconds). The tonic level is referred to as the skin conductance level (SCL). The phasic changes are referred to as skin conductance responses (SCRs). SCRs can arise from stimuli external to the person (often called event-related skin conductance responses or ER-SCRs) or the responses can be non-specific meaning that there is no apparent external stimulus (non-specific or NS-SCRs) [18].
1). EDA Preprocessing
To eliminate noise, the filtering options provided for EDA in our Bio-SP tool are the same as those described above for the ECG signal (Elliptic, Gaussian and Butterworth filters). Some authors have suggested using a Gaussian filter with a low-pass frequency of 1 Hz to filter the EDA signal [19].
2). EDA Characteristic Points Detection
SCRs contained within the EDA signal can be detected by performing differentiation and subsequent convolution with a 20-point Bartlett window [20]. A Bartlett window is a triangle function represented as:
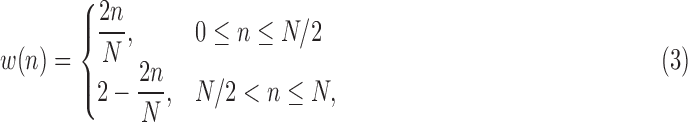 |
where 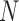 is the window size (=20) and
is the window size (=20) and 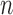 is the
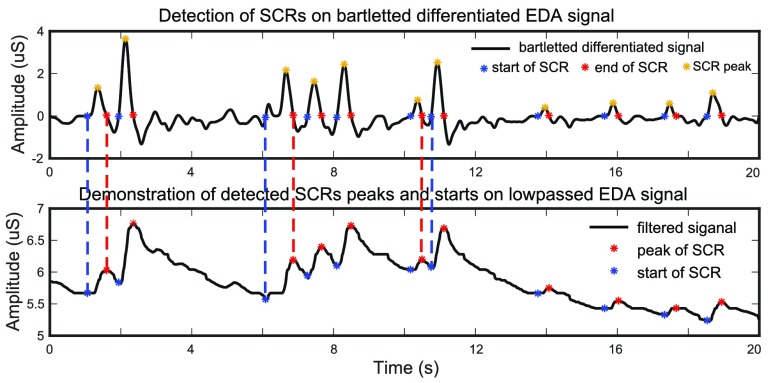
is the 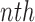 signal sample in the window. The occurrence of a SCR is detected by finding two consecutive zero-crossings, from negative to positive and positive to negative of the bartletted differentiated EDA signal (see Fig. 4). We considered negative to positive as the beginning and positive to negative as the end of each SCR. The amplitude of the SCR is obtained by finding the maximum value between these two zero-crossings, and calculating the difference between the initial zero crossing and the maximum value. Detected SCRs with amplitudes smaller than 10 percent of the maximum SCR amplitudes that are already detected on the differentiated signal will be eliminated [20]. Fig. 4 demonstrates the detection of SCRs. In Fig. 4 top, the beginning, end, and peak of each detected SCR is shown on the differentiated signal. In Fig. 4 bottom, the corresponding locations of the previously detected SCRs are provided on the original low-pass filtered signal.
signal sample in the window. The occurrence of a SCR is detected by finding two consecutive zero-crossings, from negative to positive and positive to negative of the bartletted differentiated EDA signal (see Fig. 4). We considered negative to positive as the beginning and positive to negative as the end of each SCR. The amplitude of the SCR is obtained by finding the maximum value between these two zero-crossings, and calculating the difference between the initial zero crossing and the maximum value. Detected SCRs with amplitudes smaller than 10 percent of the maximum SCR amplitudes that are already detected on the differentiated signal will be eliminated [20]. Fig. 4 demonstrates the detection of SCRs. In Fig. 4 top, the beginning, end, and peak of each detected SCR is shown on the differentiated signal. In Fig. 4 bottom, the corresponding locations of the previously detected SCRs are provided on the original low-pass filtered signal.
FIGURE 4.
Detection of SCRs on bartletted differentiated EDA signal (top) and demonstration of detected SCRs peaks and starts on low passed filtered EDA signal (bottom).
3). EDA Feature Extraction
After detecting the SCRs in the signal, the following features can be extracted:
SCR duration mean is the average of each detected SCR’s duration within a given input segment. Duration of an SCR is defined as the time (in ms) from the beginning to the end of an SCR detected in the differential signal.
SCR amplitude mean is the average of the amplitude of the detected SCRs within a given input segment.
SCR rise-time mean is the average of the SCR rise-times within a given input segment, which is defined as the time (in ms) between the beginning and the peak of an SCR.
Mean skin conductance (MSC) is the average of the low-pass filtered signal within a given input segment.
Number of detected SCRs is the number of the detected SCRs in the input segment.
Tonic SCL is the average value of the EDA signal within a given input segment, with data from the start to end of each SCR excluded from the calculation. If no SCRs are detected throughout the input segment, all the features except MSC and Tonic SCL will be outputted as NaN values.
D. Biosignal #3: Electromyography (EMG)
EMG is a measure of electrical activity, here measured at the surface of the skin, which is responsible for the activation of a skeletal muscle region [37]. In general, it is best to refer to muscle regions rather than specific muscles when using surface EMG, because the signal detected at the skin typically reflects the combined electrical changes from multiple underlying muscles. EMG is sometimes used as a diagnostic procedure to determine the health of muscles and the nerve cells that control them (motor neurons) [38]. EMG signals are also widely used to measure facial muscle activation of muscles that create facial configurations, which, despite a common assumption, do not have a one-to-one relationship with specific emotional experiences such as happiness or anger [39].
1). EMG Preprocessing
The proper choice of EMG filtering depends on the specific muscles that are being measured. For example, different filtering options are used for facial muscles vs. larger muscles in the arms/legs. Moreover, the speed/duration of the anticipated response also must be considered. For instance, different filters should be used when measuring an eye blink response relative to a sustained muscle activation over a large muscle. Thus, Bio-SP tool incorporates multiple filter options including the type of filter as well as multiple choices of cut-off frequencies that are chosen by the user. A band-pass Elliptic filter with the cut-off frequency of 10–300 Hz [40] is provided as the default filter option.
2). EMG Feature Extraction
The feature extraction implementation in this paper is based on the recommendations provided in [26] for the EMG data of larger muscle groups in the arms or legs. We refer readers interested in feature extraction of facial EMG (fEMG) signals, to the work by Fridlund and Cacioppo [41].
MAV is the mean absolute value of the EMG signal in a analysis time window with 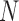 samples.
samples. 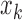 is the
is the 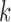 th sample in this analysis window [26]:
th sample in this analysis window [26]: 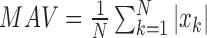 .
.
Zero crossing count is the number of times the EMG signal crosses zero within a analysis time window. It is a simple measure associated with the frequency of the signal. To avoid signal crossing counts due to low-level noise, a threshold 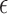 is used in deriving the count (
is used in deriving the count (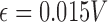 ) [26]. The zero crossing count is increased when:
) [26]. The zero crossing count is increased when:
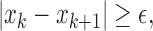 |
and
(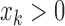 and
and 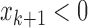 ) or (
) or (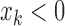 and
and 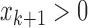 ).
).
Slope sign change is related to the signal frequency and is defined as the number of times that the slope of the EMG waveform changes sign within an analysis window. A count threshold 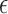 is used to reduce noise-induced counts (
is used to reduce noise-induced counts (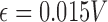 ) [26]. The slope sign count increases by one if:
) [26]. The slope sign count increases by one if: 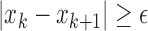 or
or 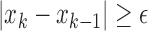 , and (
, and (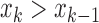 and
and 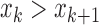 ) or (
) or (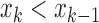 and
and 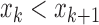 ).
).
Waveform length provides a measure of the complexity of the signal [26] and is defined as the cumulative magnitude of the EMG signal within the analysis window as 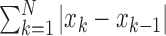
Log detector is an estimate of the exerted muscle force and its feature is defined as 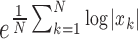 .
.
Peak amplitude is the amplitude of the maximum of the filtered EMG signal for a given epoch relative to zero voltage.
Peak latency is the time in which the maximum of the filtered EMG signal takes place.
SD is the standard deviation of the amplitudes of the filtered EMG signal.
RMS is the root mean square of the amplitudes of the filtered EMG signal for a given epoch.
E. Biosignal #4: Continuous Blood Pressure (BP)
BP in the circulatory system is a common measure because it is an important parameter relevant to the overall function of cardiovascular system. BP, the overall force of blood against the vessel walls, results from the complex, combined effects of changes in blood vessel diameter and the elasticity of the walls of the large arteries [42]. Although some researchers rely on intermittent readings of systolic and diastolic blood pressure, recent technological advances have increased the availability of devices that enable the noninvasive measure of continuous BP. Thus, it is crucial that there are automatic, robust, and accurate methods for extracting beat to beat BP features such as mean arterial pressure (MAP), systolic blood pressure (SBP), and diastolic blood pressure (DBP) from continuous BP signals.
1). BP Preprocessing
The low-pass filter frequency for continuous BP signal preprocessing should be at least 10 times higher than the heart rate and less than half of the sampling rate [43]. Since a typical resting human heart rate varies between 40 and 100 beats per minute (bpm) [44], a low-pass filter with a cut-off frequency of 40 Hz is often used for removal of high frequency artifacts in BP signals [43]. However, in our software, other filter options, similar to those provided for ECG (Elliptic, Gaussian, and Butterworth filters), are also available for preprocessing the BP signal.
2). BP Characteristic Point Detection
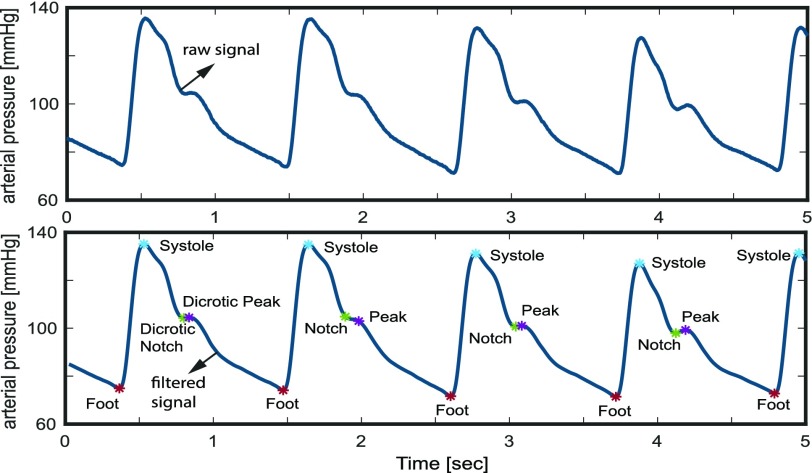
An algorithm implemented by Laurin [21] for the feature extraction of arterial blood pressure is used in this work. This algorithm, inspired by the derivatives and thresholds described by Pan and Tompkins [14] and criteria of Sun et al.
[22], primarily detects the characteristic points in the BP signal including systolic BP, diastolic BP (Foot), the dicrotic notch and the dicrotic peak (see Fig. 5). The Foot, or lowest level of BP for a given heartbeat, is defined as the BP at the time of occurrence of the maximum point in the second derivative of the BP time-series for each heartbeat. The systolic point is defined as the maximum value of the BP waveform within the time range of [0s – 0.125s] after the Foot index [21]. The dicrotic notch, which occurs due to a disruption in the flow of blood as the aortic valve closes, is defined as the BP at the minimum of the subtraction of the signal and the straight line going from systole to Foot. Finally, the dicrotic peak is defined as the BP at the minimum of the second derivative of the time-series following the dicrotic notch, within a window of size 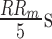 above it where
above it where 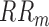 is the median heartbeat interval computed from the Foot points.
is the median heartbeat interval computed from the Foot points.
FIGURE 5.
Raw continuous blood pressure (BP) signal (Top), Corresponding low-pass filtered continuous BP signal (bottom) with the characteristic points (foot, systolic, dicrotic notch, and dicrotic peak) detected on the signal. The foot is equivalent to the diastolic BP.
3). BP Feature Extraction
Based on the extraction of these characteristic peaks, the following five physiological features are extracted [21].
Mean diastolic pressure (Foot) is the mean of all the signal values (pressures) at the Foot indices for a given epoch.
Mean systolic pressure is the mean of all the signal values (pressures) at the systolic indices for a given epoch.
Mean dicrotic peak pressure is the mean of all the signal values (pressures) at the dicrotic peak for a given epoch.
Mean dicrotic notch pressure is the mean of all the signal values (pressures) at the dicrotic notch for a given epoch.
Mean arterial pressure (MAP) represents mean signal value (in pressure) for the entire input BP signal for a given epoch.
Total peripheral resistance (TPR) is another important BP feature reflecting the overall resistance to blood flow in the systemic circulation [45]. Because the calculation of TPR also requires features extracted from the ICG signal, the description of TPR is provided in the ICG section.
F. Biosignal #5: Impedance Cardiography (ICG)
ICG is a non-invasive method used to extract estimates of stroke volume, cardiac output, and overall vascular resistance (i.e., TPR), along with systolic time intervals including pre-ejection period (PEP) and left-ventricular ejection time (LVET). Together these measures provide a more complete understanding of the full hemodynamic function of the cardiovascular system. Biosignals measured via ICG include basal thoracic impedance (Z0) and its first derivative (dZ/dt). Common features from the ICG signal include: (1) mean Z0; (2) stroke volume (SV), which is defined as the amount of blood pumped by the heart with each heartbeat (usually in units of ml); (3) cardiac output (CO), which is the volume of blood pumped by the heart per unit of time (typically as liters/minute) [46], (4) total peripheral resistance (TPR), which is the overall resistance to blood flow in the systemic circulation [45], (5) pre-ejection period (PEP), which is the time period between the electrical activity signaling the start of ventricular contraction and the onset of blood being ejecting into the aorta [47]; and (6) left ventricular ejection time (LVET), which is the time period during which blood flows through the open aortic valve. Guidelines for the collection and reporting of ICG signals are provided by [23]. Additional details on ensemble averaging methods can be found in [48], and on a new method for moving ensemble averaging in [12]. These six features can be calculated from the basal impedance (Z0), the dZ/dt, the ECG, and BP.
1). ICG Preprocessing
The preprocessing of the ICG signal includes the following steps.
Noise and artifact removal is a necessary step in preprocessing the ICG signal. A second order Elliptic band-pass filter with a low cut-off frequency of 0.75 Hz and high cut-off frequency of 40 Hz is recommended in available biosignal software, such as Biolab [49]. However, our Bio-SP tool allows the user to adjust these low and high cut-off frequencies as desired as well as to choose the filter type (Elliptic, Gaussian, or Butterworth).
Segmentation of the dZ/dt signal into beat to beat intervals is required for the ensemble averaging step. Using the R peak from the ECG signal, we considered a beat to beat interval to start at
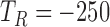 ms and to end at
ms and to end at 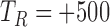 ms, where
ms, where 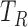 is the R peak location time in ms [23], [49].
is the R peak location time in ms [23], [49].Ensemble averaging of multiple cardiac cycles is performed to eliminate stochastically distributed noise as well as respiratory influences and movement artifacts in the dZ/dt signal [23], [48], [50]. The number of cycles is adjustable by the user and is set to 8 beats by default in the Bio-SP tool.
2). DZ/DT and ECG Point Detection
To extract features, the following points have to be identified on the dZ/dt and ECG signals:
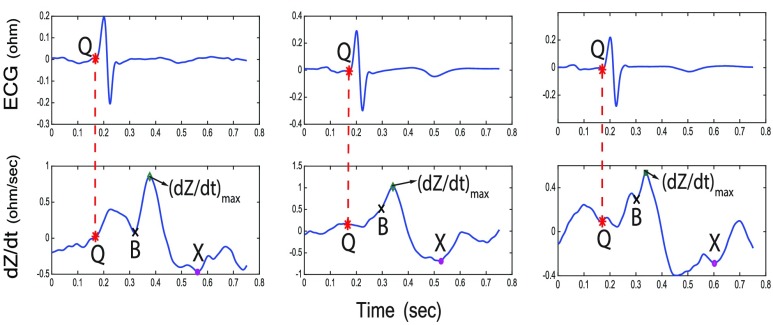
Q point time is the Q point time derived from the ECG signal (Fig. 6).
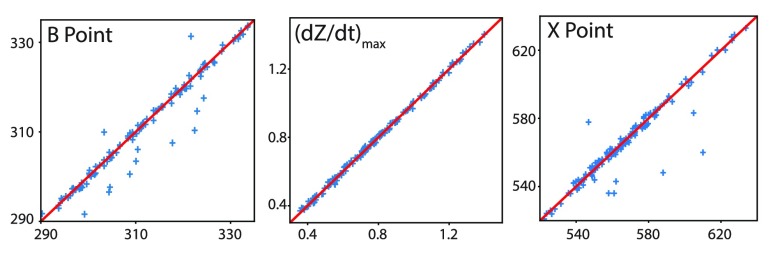
B point identification can be difficult due to variations in the morphology of the ICG signals [23]. There have been several algorithmic definitions proposed to approximate the location of the B point [23], [24], [51]. Fig. 6 illustrates three examples of the variation in the morphology of the dZ/dt waveform. In general, the B point indicates the onset of the final rapid upstroke toward the dZ/dtmax [23]. We use here a second derivative classification [24], [52] which has been used in prior literature as a method for detecting the B point. Specifically, we first calculate the second derivative of the dZ/dt signal, and then we locate the times when the maximum peak of this second derivative of the dZ/dt occurs within a small time period (80ms) before occurrence of the dZ/dtmax. This algorithm robustly detected the B point in all three of the different morphology samples illustrated in Fig. 6. To quantitatively evaluate the performance of this algorithm, we compared B points detected by this algorithm to B points detected by visual inspection and manual marking by trained scorers for 150 randomly selected cardiac cycles from 20 different participants [7]. Results shown in Fig. 7 illustrate that the automatic detection matched the visual detection with manual marking more than 90% of the time. The remaining 10% disagreement was the result of the existence of outliers as well as small, sharp notches on the dZ/dt signal that were not visible to the naked eye and therefore not detected by the human inspectors. The root-mean-square deviation (RMSD) [53] between the manual and algorithmic detection of the B point was 5.38 ms.
dZ/dtmax is identical to the global maximum value of the dZ/dt signal within one cardiac cycle. Full agreement exists between visual detection with manual marking and the detection algorithm for dZ/dtmax developed here (Fig. 7).
X point represents the closing of the aortic valve after the ejection of blood from the left ventricle of the heart [23]. Using the second derivative of the dZ/dt signal, we developed an X point detection algorithm which is robust to morphological variations in the dZ/dt signals. The X point is often defined by the point in time where the minimum dZ/dt value in one cardiac cycle is detected. However, due to variations in the morphology of the dZ/dt waveform, this does not always hold true. For instance, in Fig. 6 the selected X point is not the global minimum of the ICG signal in the right-most case. In such cases, the X point is not a minimum point but a notch in the signal (i.e., a local minimum, but not the global minimum). To capture these variations, the second derivative of the dZ/dt can be used: both global minimum points and notches (local minima) appear as peak values in the second derivative of the dZ/dt signal. Therefore, the algorithm used in this work is as follows: We search for all the peak indices for the second derivative of the dZ/dt signal in a period of time after the B point (i.e.,
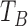 ) from 230 ms to 400 ms after
) from 230 ms to 400 ms after 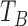 , and we choose the index that corresponds to the lowest value in the original dZ/dt signal. If no peak is found in the second derivative of the dZ/dt signal in this interval, we repeat the same procedure within a larger window from
, and we choose the index that corresponds to the lowest value in the original dZ/dt signal. If no peak is found in the second derivative of the dZ/dt signal in this interval, we repeat the same procedure within a larger window from 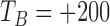 ms to 400ms. These threshold values for the time window after
ms to 400ms. These threshold values for the time window after 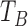 (200, 230, and 400 ms) were chosen based on the normal range for LVET values [23], [54], as well as recommendations made by experts in this area. Fig. 7 shows the result of the validation of this algorithm for automatic X point detection in the same sample dataset as used for validating the automatic B point detection algorithm. Root-mean-square deviation (RMSD) between manual- and algorithm-based detection of the X point is 10.59 ms.
(200, 230, and 400 ms) were chosen based on the normal range for LVET values [23], [54], as well as recommendations made by experts in this area. Fig. 7 shows the result of the validation of this algorithm for automatic X point detection in the same sample dataset as used for validating the automatic B point detection algorithm. Root-mean-square deviation (RMSD) between manual- and algorithm-based detection of the X point is 10.59 ms.
FIGURE 6.
Three cases of dZ/dt (bottom) with the corresponding ECG signal (top) indicating variations in the morphology of dZ/dt signal with the characteristic points identified by the algorithm. Left panel: B and X points occur at a local minimum and global minimum, respectively; Middle panel: the B point is a notch; Right panel: the X point is just a local minimum and NOT a global minimum.
FIGURE 7.
Validation of (left) B-point location, (middle) dZ/dtmax value, (right) X-point location, detected by visual inspection and manual placement (x-axis) vs. our algorithm (y-axis) for 150 randomly selected cardiac cycles.
3). ICG Feature Extraction
After detecting the characteristic points, we can compute physiological features of interest including pre-ejection period (PEP in msec), left ventricular ejection time (LVET in msec), stroke volume (SV in ml), cardiac output (CO in l/min), and total peripheral resistance (TPR in dyne-seconds 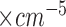 ) using the following formulas [23]:
) using the following formulas [23]:
 |
where 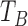 ,
, 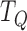 , and
, and 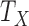 are the times (in sec) when the B, Q and X points occur, respectively.
are the times (in sec) when the B, Q and X points occur, respectively. 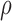 is the resistivity of blood (in ohm-cm) and is usually set to 135 ohm-cm [23].
is the resistivity of blood (in ohm-cm) and is usually set to 135 ohm-cm [23]. 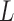 (cm) is the distance between the recording electrodes used for obtaining the dZ/dt and Z0 signals, Z0 is the mean basal Z0, and MAP is the mean arterial pressure over the same segment. Finally, the mean value of Z0 is also reported as a feature, since researchers may be interested in having an estimate of basal thoracic impedance.
(cm) is the distance between the recording electrodes used for obtaining the dZ/dt and Z0 signals, Z0 is the mean basal Z0, and MAP is the mean arterial pressure over the same segment. Finally, the mean value of Z0 is also reported as a feature, since researchers may be interested in having an estimate of basal thoracic impedance.
III. Quality Assessment of BIOSIGNALS
Signals recorded with improper sensor attachment or during large bodily movements not only provide no useful information, but they also may result in non-optimal decisions within biomedical systems (e.g., excessive emergency alarms) and/or lead to poor machine learning-based models, if they are trained on these aberrant signals. Therefore, it is necessary to implement basic signal quality assessments before the more extensive preprocessing and feature extraction described above so that these large-scale quality issues can be detected and eliminated (or properly adjudicated). Although basic data quality assessment has traditionally been done by visual inspection (coupled with manual marking of poor quality data), this approach is not feasible with the quantity of physiological data being collected in many current studies, particularly data collected under ambulatory conditions. Technological advancements in physiological sensor technology, particularly mobile sensors, increased data storage capacity and increased device battery life, together have enabled the collection of very large physiological datasets (on the order of tens of gigabytes to multiple terabytes) [7], [55]. As a result, entirely manualized visual inspection of all data should be replaced by semi-automated methods that permit the visual inspection of smaller, potentially aberrant epochs of data. There have been numerous biosignal-specific algorithms developed for the automatic quality checking of biosignals [56]–[59]. Inspired by these published algorithms, we developed algorithms for basic quality checking of ECG, BP, ICG and EDA signals in Bio-SP tool. An algorithm introduced by Moody [58] is used for the quality checking of ECG, ICG and BP, while an algorithm proposed by Kleckner [59] is used for the quality checking of EDA.
A. ECG, ICG, and BP Quality Checking
A rule-based algorithm proposed by Moody [58] was used in Bio-SP tool for ECG data quality checking. This algorithm achieved one of the highest accuracy scores in the Physionet/CinC Challenge [57]. The algorithm inspects segments of the signals based on the following three criteria:
-
(1)
If the signal is flat, it suggests that the electrodes are not well attached to the skin. Mathematically speaking, if the standard deviation of a segment of a signal is very close to zero, that segment is a flat signal.
-
(2)
The minimum, maximum, and the maximum-minimum difference values of the signal should be within an acceptable range. Values that are too small or too large also may result from improper electrode attachment or from large noise spikes in the signal [58].
-
(3)
The ECG signal remains close to a zero voltage (i.e., the isoelectric line) during much of the overall signal except during the relatively short period between the P and T waves, when the electrical activity associated with the heartbeat occurs. Therefore, the duration between these larger voltage changes should be within a specific range for high-quality signals. Specifically, given a signal segment (with the size of larger than one heartbeat), the difference between the global maximum and global minimum of its sub-segments as a random variable makes a highly positively skewed distribution. We measured the skewness using the definition provided by Groeneveld and Meeden [60]. This algorithm detects segments of the signal that are not similar to the specific shape features of a prototypical ECG signal.
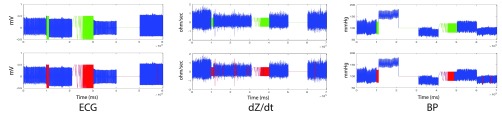
If a segment of the signal fails to meet any of these criteria, that segment will be marked as poor quality. Because ECG, dZ/dt, and continuous BP signals contain similar frequencies and patterns related to cardiac activity, we tuned the threshold parameters used for rules (1)–(3) above for ECG, and applied similar quality checking algorithms to the dZ/dt and BP biosignals. To evaluate the performance of our basic quality checking algorithms for ECG, dZ/dt, and BP, we examined how our algorithms worked on signals comprising a combination of good quality signals and synthetically-generated corrupted signals (Fig. 8). Accordingly, we created input signals containing four segments of clean biosignals from four different datasets [7], [31], [32] as well as several segments with synthetically-generated noise and with artifacts that occurred between the segments of good quality data. As shown in Fig. 8 (bottom row), our proposed algorithms robustly detected all artifactual segments (red) while correctly passing the good quality signals (blue).
FIGURE 8.
Quality checking of ECG (left panel), dZ/dt (middle panel) and continuous BP (right panel) signals. Top row: Raw signals composed of 4 different good quality segments (blue) as well as three irrelevant synthetically generated signals (green). Bottom row: Low quality signal portions detected in red color.
B. EDA Quality Checking
Using rules documented in [60] and [61], we determined invalid or poor quality data segments in the EDA signal within Bio-SP tool as follows:
-
(1)
The minimum or maximum values of the EDA signal exceed a user-specified acceptable range.
-
(2)
Changes in the EDA signal occur at a higher frequency than is physiologically plausible (e.g., faster than
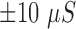 /s), where
/s), where 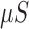 is microSiemens.
is microSiemens. -
(3)
EDA signal epochs that are within 5 s of invalid portions from rules (1) and (2) are also marked as invalid.
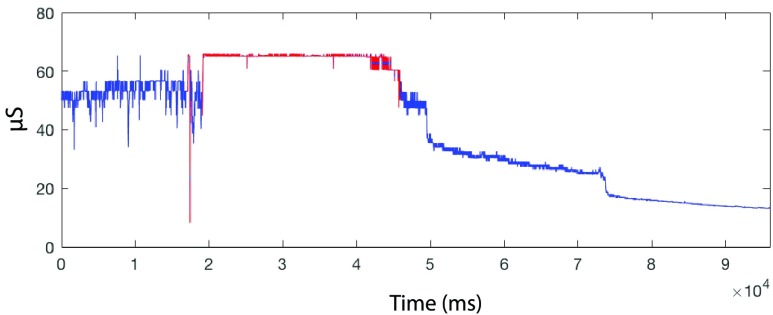
Fig. 9 illustrates sample output from our EDA quality checking algorithm on real EDA data with portions of low-quality signal marked as red. The algorithm has accurately detected both out-of-range portions (rule 1) of the signal as well as portions of the signal where the signal is changing too quickly (rule 2). The acceptable range in rule (1) may be selected by the user based on the specific characteristics of their recording equipment and amplification parameters.
FIGURE 9.
Quality checking of EDA signal on a real EDA data with portions of low quality signal which are being marked in red. The red color regions are either out-of-range (rule 1) or changing too quickly (rule 2).
In Bio-SP tool, the quality-checking algorithm, for a given input signal (ECG, dZ/dt, BP or EDA) outputs a two-column matrix indicating the corresponding start and end indices of any low-quality regions. Moreover, users can opt to have the features extracted from these segments be reported as NaNs.
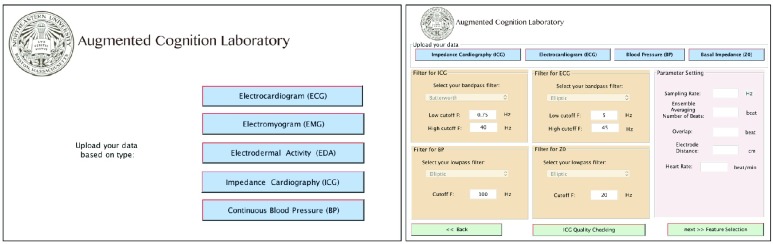
IV. Graphical User Interface (GUI)
Our Bio-SP tool produces a feature matrix extracted from each biosignal which can be further used as the input features for a variety of machine learning and pattern recognition algorithms. The GUI designed for Bio-SP tool, starts with a selection page as shown in Fig. 10 (left panel), where the user selects the type of biosignal which is to be processed. Options are: ECG, EMG, EDA, continuous BP, and ICG. By the selection of each signal modality, a second page (e.g., the ICG page, see Fig. 10 (right panel)) appears which requests the necessary raw signal inputs, filter characteristics,sampling rate and other specific parameters required for some signals.
FIGURE 10.
A snapshot of first and second pages of Bio-SP tool GUI, specialized for preprocessing of the ICG signals.
V. Conclusion
In this paper, we present our newly-developed Biosignal-Specific Processing toolbox (Bio-SP tool) for preprocessing and feature extraction of ECG, EDA, EMG, continuous BP and ICG biosignals, based on state-of-the-art algorithms reported in the scientific literature and the feedback received from experts. This open-source toolbox accommodates researchers in machine learning, affective computing, and psychophysiology to provide more automatic and reliable extraction of signal-specific physiologically-relevant features from different biosignals for use with a wide variety of machine learning and pattern recognition algorithms.
Funding Statement
This work was supported by MathWorks. The work of K. S. Quigley and J. Wormwood was supported by the Army Research Institute under Grant W911NF-16-1-0191.
References
- [1].Baumert M., Porta A., and Cichocki A., “Biomedical signal processing: From a conceptual framework to clinical applications [scanning the issue],” Proc. IEEE, vol. 104, no. 2, pp. 220–222, Feb. 2016. [Google Scholar]
- [2].Kukar M., Kononenko I., Grošelj C., Kralj K., and Fettich J., “Analysing and improving the diagnosis of ischaemic heart disease with machine learning,” Artif. Intell. Med., vol. 16, no. 1, pp. 25–50, 1999. [DOI] [PubMed] [Google Scholar]
- [3].Hernandez J., Riobo I., Rozga A., Abowd G. D., and Picard R. W., “Using electrodermal activity to recognize ease of engagement in children during social interactions,” in Proc. ACM Int. Joint Conf. Pervasive Ubiquitous Comput., 2014, pp. 307–317. [Google Scholar]
- [4].Subasi A., “Classification of EMG signals using PSO optimized SVM for diagnosis of neuromuscular disorders,” Comput. Biol. Med., vol. 43, no. 5, pp. 576–586, Jun. 2013. [DOI] [PubMed] [Google Scholar]
- [5].Barakat N., Bradley A. P., and Barakat M. N. H., “Intelligible support vector machines for diagnosis of diabetes mellitus,” IEEE Trans. Inf. Technol. Biomed., vol. 14, no. 4, pp. 1114–1120, Jul. 2010. [DOI] [PubMed] [Google Scholar]
- [6].Chabchoub S., Mansouri S., and Salah R. B., “Detection of valvular heart diseases using impedance cardiography ICG,” Biocybern. Biomed. Eng., vol. 38, no. 2, pp. 251–261, 2018. [Google Scholar]
- [7].Khalaf A.et al. (2018). Analysis of Multimodal Physiological Signals Within and Across Individuals to Predict Psychological Threat vs. Challenge. [Online]. Available: https://psyarxiv.com/96djs/ [Google Scholar]
- [8].Rajpurkar P., Hannun A. Y., Haghpanahi M., Bourn C., and Ng A. Y. (2017). “Cardiologist-level arrhythmia detection with convolutional neural networks.” [Online]. Available: https://arxiv.org/abs/1707.01836 [Google Scholar]
- [9].Lewis D., Chang B. L., and Friedman C. P., “Consumer health informatics,” in Consumer Health Informatics. Springer, 2005, pp. 1–7. [Google Scholar]
- [10].Vidaurre C., Sander T. H., and Schlögl A., “BioSig: The free and open source software library for biomedical signal processing,” Comput. Intell. Neurosci., vol. 2011, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Blechert J., Peyk P., Liedlgruber M., and Wilhelm F. H., “ANSLAB: Integrated multichannel peripheral biosignal processing in psychophysiological science,” Behav. Res. Methods, vol. 48, no. 4, pp. 1528–1545, 2016. [DOI] [PubMed] [Google Scholar]
- [12].Cieslak M.et al. , “Quantifying rapid changes in cardiovascular state with a moving ensemble average,” Psychophysiology, vol. 55, no. 4, p. e13018, 2018. [DOI] [PubMed] [Google Scholar]
- [13].Mane R. S., Cheeran A. N., Awandekar V. D., and Rani P., “Cardiac arrhythmia detection by ECG feature extraction,” Int. J. Eng. Res. Appl., vol. 3, no. 2, pp. 327–332, 2013. [Google Scholar]
- [14].Pan J. and Tompkins W. J., “A real-time QRS detection algorithm,” IEEE Trans. Biomed. Eng., vol. BME-32, no. 3, pp. 230–236, Mar. 1985. [DOI] [PubMed] [Google Scholar]
- [15].Chavan M., Agarwala R. A., and Uplane M. D., “Digital elliptic filter application for noise reduction in ECG signal,” in Proc. 4th WSEAS Int. Conf. Electron., Control Signal Process., 2005, pp. 58–63. [Google Scholar]
- [16].Bsoul M., Minn H., Nourani M., Gupta G., and Tamil L., “Real-time sleep quality assessment using single-lead ECG and multi-stage SVM classifier,” in Proc. Annu. Int. Conf. Eng. Med. Biol. Soc. (EMBC), Aug./Sep. 2010, pp. 1178–1181. [DOI] [PubMed] [Google Scholar]
- [17].de Chazal P., Heneghan C., Sheridan E., Reilly R., Nolan P., and O’Malley M., “Automated processing of the single-lead electrocardiogram for the detection of obstructive sleep apnoea,” IEEE Trans. Biomed. Eng., vol. 50, no. 6, pp. 686–696, Jun. 2003. [DOI] [PubMed] [Google Scholar]
- [18].Gamboa H. F. S. and Fred A. L. N., “An electrodermal activity psychophysiologic model,” Citeseer, 2005. [Online]. Available: https://scholar.google.com/scholar?hl=en&as_sdt=0%2C22&q=H.+Gamboa+and+A.+Fred%2C+%E2%80%98%E2%80%98An+electrodermal+activity+psychophysiologic&btnG= [Google Scholar]
- [19].Greco A., Valenza G., and Scilingo E. P., Advances in Electrodermal Activity Processing With Applications for Mental Health: From Heuristic Methods to Convex Optimization. Springer, 2016. [Google Scholar]
- [20].Kim K. H., Bang S. W., and Kim S. R., “Emotion recognition system using short-term monitoring of physiological signals,” Med. Biol. Eng. Comput., vol. 42, no. 3, pp. 419–427, 2004. [DOI] [PubMed] [Google Scholar]
- [21].Laurin A. BP_Annotate. Accessed: May 2, 2018. [Online]. Available: https://www.mathworks.com/matlabcentral/fileexchange/60172-bp-annotate [Google Scholar]
- [22].Sun J. X., Reisner A. T., and Mark R. G., “A signal abnormality index for arterial blood pressure waveforms,” in Proc. Comput. Cardiol., Sep. 2006, pp. 13–16. [Google Scholar]
- [23].Sherwood A., Allen M. T., Fahrenberg J., Kelsey R. M., Lovallo W. R., and van Doornen L. J. P., “Methodological guidelines for impedance cardiography,” Psychophysiology, vol. 27, no. 1, pp. 1–23, 1990. [DOI] [PubMed] [Google Scholar]
- [24].Shyu L.-Y., Lin Y.-S., Liu C.-P., and Hu W.-C., “The detection of impedance cardiogram characteristic points using wavelet transform,” Comput. Biol. Med., vol. 34, no. 2, pp. 165–175, 2004. [DOI] [PubMed] [Google Scholar]
- [25].Biosignal-Specific Processing (Bio-SP) Tool. Accessed: 2018. [Online]. Available: http://www.northeastern.edu/ostadabbas/software/
- [26].Tkach D., Huang H., and Kuiken T. A., “Study of stability of time-domain features for electromyographic pattern recognition,” J. NeuroEng. Rehabil., vol. 7, no. 1, p. 21, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Tomaka J., Blascovich J., Kelsey R. M., and Leitten C. L., “Subjective, physiological, and behavioral effects of threat and challenge appraisal,” J. Personality Social Psychol., vol. 65, no. 2, pp. 248–260, 1993. [Google Scholar]
- [28].Tomaka J., Blascovich J., Kibler J., and Ernst J. M., “Cognitive and physiological antecedents of threat and challenge appraisal,” J. Personality Social Psychol., vol. 73, no. 1, pp. 63–72, 1997. [DOI] [PubMed] [Google Scholar]
- [29].Quigley K. S., Barrett L. F., and Weinstein S., “Cardiovascular patterns associated with threat and challenge appraisals: A within-subjects analysis,” Psychophysiology, vol. 39, no. 3, pp. 292–302, 2002. [DOI] [PubMed] [Google Scholar]
- [30].Nabian M., Nouhi A., Yin Y., and Ostadabbas S., “A biosignal-specific processing tool for machine learning and pattern recognition,” in Proc. IEEE Healthcare Innov. Point Care Technol. (HI-POCT), Nov. 2017, pp. 76–80. [Google Scholar]
- [31].(2016). PhysioBank ATM. [Online]. Available: https://physionet.org/cgi-bin/atm/ATM
- [32].(2016). MIT Effective Computing Group. [Online]. Available: http:// affect.media.mit.edu
- [33].Bacquer D. D., Backer G. D., Kornitzer M., and Blackburn H., “Prognostic value of ECG findings for total, cardiovascular disease, and coronary heart disease death in men and women,” Heart, vol. 80, no. 6, pp. 570–577, 1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Blanco-Velasco M., Weng B., and Barner K. E., “ECG signal denoising and baseline wander correction based on the empirical mode decomposition,” Comput. Biol. Med., vol. 38, no. 1, pp. 1–13, Jan. 2008. [DOI] [PubMed] [Google Scholar]
- [35].Dawson M. E., Schell A. M., and Filion D. L., “The electrodermal system,” in Handbook of Psychophysiology, vol. 2 Cambridge, U.K.: Cambridge Univ. Press, 2007, pp. 200–223. [Google Scholar]
- [36].Perez-Rosero M. S., Rezaei B., Akcakaya M., and Ostadabbas S., “Decoding emotional experiences through physiological signal processing,” in Proc. IEEE Int. Conf. Acoust., Speech Signal Process. (ICASSP), Mar. 2017, pp. 881–885. [Google Scholar]
- [37].Benedek J. and Hazlett R., “Incorporating facial emg emotion measures as feedback in the software design process,” in Proc. Hum. Comput. Interact. Consortium, 2005 [Online]. Available: https://scholar.google.com/scholar?hl=en&as_sdt=0%2C22&q=J.+Benedek+and+R.+Hazlett%2C+%E2%80%98%E2%80%98Incorporating+facial+EMG+emotion+measures+857+as+feedback+in+the+software+design+process%2C%E2%80%99%E2%80%99+in+Proc.+Hum.+Comput.+858+Interact.+Consortium%2C+2005.&btnG= [Google Scholar]
- [38].Reaz M. B. I., Hussain M. S., and Mohd-Yasin F., “Techniques of EMG signal analysis: Detection, processing, classification and applications,” Biol. Procedures, vol. 8, no. 1, pp. 11–35, Dec. 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Barrett L. F., Salovey P., and Mayer J. D., The Wisdom in Feeling: Psychological Processes in Emotional Intelligence. New York, NY, USA: Guilford Press, 2002. [Google Scholar]
- [40].De Luca C. J., Gilmore L. D., Kuznetsov M., and Roy S. H., “Filtering the surface EMG signal: Movement artifact and baseline noise contamination,” J. Biomech., vol. 43, no. 8, pp. 1573–1579, 2010. [DOI] [PubMed] [Google Scholar]
- [41].Fridlund A. J. and Cacioppo J. T., “Guidelines for human electromyographic research,” Psychophysiology, vol. 23, no. 5, pp. 567–589, 1986. [DOI] [PubMed] [Google Scholar]
- [42].Shapiro D., Goldstein I. B., and Jamner L. D., “Effects of cynical hostility, anger out, anxiety, and defensiveness on ambulatory blood pressure in black and white college students,” Psychosomatic Med., vol. 58, no. 4, pp. 354–364, 1996. [DOI] [PubMed] [Google Scholar]
- [43].Young S. S., Computerized Data Acquisition and Analysis for the Life Sciences: A Hands-on Guide. Cambridge, U.K.: Cambridge Univ. Press, 2001. [Google Scholar]
- [44].Aladin A. I.et al. , “Relation of resting heart rate to risk for all-cause mortality by gender after considering exercise capacity (the henry ford exercise testing project),” Amer. J. Cardiol., vol. 114, no. 11, pp. 1701–1706, 2014. [DOI] [PubMed] [Google Scholar]
- [45].Etsten B. and Li T. H., “Hemodynamic changes during thiopental anesthesia in humans: Cardiac output, stroke volume, total peripheral resistance, and intrathoracic blood volume,” J. Clin. Invest., vol. 34, no. 3, pp. 500–510, 1955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Maceira A. M., Prasad S. K., Khan M., and Pennell D. J., “Normalized left ventricular systolic and diastolic function by steady state free precession cardiovascular magnetic resonance,” J. Cardiovascular Magn. Reson., vol. 8, no. 3, pp. 417–426, 2006. [DOI] [PubMed] [Google Scholar]
- [47].Goertz A. W.et al. , “Effect of 7.2% hypertonic saline/6% hetastarch on left ventricular contractility in anesthetized humans,” J. Amer. Soc. Anesthesiologists, vol. 82, no. 6, pp. 1389–1395, 1995. [DOI] [PubMed] [Google Scholar]
- [48].Kelsey R. M. and Guethlein W., “An evaluation of the ensemble averaged impedance cardiogram,” Psychophysiology, vol. 27, no. 1, pp. 24–33, 1990. [DOI] [PubMed] [Google Scholar]
- [49].Knowledge Base Impedance Cardiography. Accessed: 2017. [Online]. Available: https://support.mindwaretech.com/article-categories/imp/
- [50].Kelsey R. M., Reiff S., Wiens S., Schneider T. R., Mezzacappa E. S., and Guethlein W., “The ensemble-averaged impedance cardiogram: An evaluation of scoring methods and interrater reliability,” Psychophysiology, vol. 35, no. 3, pp. 337–340, 1998. [DOI] [PubMed] [Google Scholar]
- [51].Debski T. T., Zhang Y., Jennings J. R., and Kamarck T. W., “Stability of cardiac impedance measures: Aortic opening (B-point) detection and scoring,” Biol. Psychol., vol. 36, nos. 1–2, pp. 63–74, 1993. [DOI] [PubMed] [Google Scholar]
- [52].Árbol J. R., Perakakis P., Garrido A., Mata J. L., Fernández-Santaella M. C., and Vila J., “Mathematical detection of aortic valve opening (B point) in impedance cardiography: A comparison of three popular algorithms,” Psychophysiology, vol. 54, no. 3, pp. 350–357, 2017. [DOI] [PubMed] [Google Scholar]
- [53].Petitjean M., “On the root mean square quantitative chirality and quantitative symmetry measures,” J. Math. Phys., vol. 40, no. 9, pp. 4587–4595, 1999. [Google Scholar]
- [54].Kolev N. and Zimpfer M., “Left ventricular ejection time and end-systolic pressure revisited,” Anesthesia Analgesia, vol. 81, no. 4, pp. 890–891, 1995. [DOI] [PubMed] [Google Scholar]
- [55].Lee J. J., Knox W. B., Baumann J., Breazeal C., and DeSteno D., “Computationally modeling interpersonal trust,” Frontiers Psychol., vol. 4, no. 4, p. 893, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Satija U., Ramkumar B., and Manikandan M. S., “An automated ECG signal quality assessment method for unsupervised diagnostic systems,” Biocybern. Biomed. Eng., vol. 38, no. 1, pp. 54–70, 2018. [Google Scholar]
- [57].Morgado E.et al. , “Quality estimation of the electrocardiogram using cross-correlation among leads,” Biomed. Eng. Online, vol. 14, no. 1, p. 59, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Moody B. E., “Rule-based methods for ECG quality control,” in Proc. IEEE Comput. Cardiol., Sep. 2011, pp. 361–363. [Google Scholar]
- [59].Kleckner I. (2016). Electrodermal Activity Quality Assessment. [Online]. Available: https://github.com/iankleckner/EDAQA [Google Scholar]
- [60].Groeneveld R. A. and Meeden G., “Measuring skewness and kurtosis,” Statistician, vol. 33, no. 4, pp. 391–399, 1984. [Google Scholar]
- [61].Kleckner I. R.et al. , “Simple, transparent, and flexible automated quality assessment procedures for ambulatory electrodermal activity data,” IEEE Trans. Biomed. Eng., vol. 65, no. 7, pp. 1460–1467, Jul. 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]