Abstract
We developed an automated approach for QRS complex detection and QRS duration (QRSd) measurement that can effectively analyze multichannel electrocardiograms (MECGs) acquired during abnormal conduction and pacing in heart failure and cardiac resynchronization therapy (CRT) patients to enable the use of MECGs to characterize cardiac activation in such patients. The algorithms use MECGs acquired with a custom 53-electrode investigational body surface mapping system and were validated using previously collected data from 58 CRT patients. An expert cohort analyzed the same data to determine algorithm accuracy and error. The algorithms: 1) detect QRS complexes; 2) identify complexes of the most prevalent morphology and morphologic outliers; and 3) determine the array-specific (i.e., anterior and posterior) and global QRS complex onsets, offsets, and durations for the detected complexes. The QRS complex detection algorithm had a positive predictivity and sensitivity of ≥96% for complex detection and classification. The absolute QRSd error was 17 ± 14 ms, or 12%, for array-specific QRSd and 12 ± 10 ms, or 8%, for global QRSd. The absolute global QRSd error (12 ms) was less than the interobserver variation in that measurement (15 ± 10 ms). The sensitivity, positive predictivity, and error of the algorithms were similar to the values reported for current state-of-the-art algorithms designed for and limited to simpler data sets and conduction patterns and within the variation found in clinical 12-lead ECG QRSd measurement techniques. These new algorithms permit accurate, real-time analysis of QRS complex features in MECGs in patients with conduction disorders and/or pacing.
Keywords: Biomedical signal processing, classification algorithms, detection algorithms, electrocardiology
I. Introduction
The QRS complex measured by 12-lead electrocardiogram (ECG) is the main feature in the diagnosis of a number of cardiac pathologies. In the heart failure (HF) population, QRS complex duration (QRSd) and morphology are key criteria for assessing electrical activation in candidates for and patients with cardiac resynchronization therapy (CRT) [1], [2]. However, in spite of the clinical ubiquity of the 12-lead ECG in CRT patient care, its sensitivity to relevant electrophysiologic substrate behavior in that population is limited [3], [4]. Recently, QRS complex features measured in multichannel electrocardiograms (i.e., ECGs from arrays with 50 to 250 electrodes [MECGs]) have been investigated to describe cardiac activation in CRT patients while addressing the spatial limitations of the 12-lead ECG and with the goal of concomitantly reducing patient non-response, which affects 30% of CRT recipients [5]–[8]. However, manual evaluation of the requisite QRS complex features would be prohibitively labor-intensive in MECGs and is not even routinely performed using 12-lead ECGs [9]–[11]. An automated analysis approach is therefore needed if CRT patients are to benefit from the increased information content of QRS complex features measured in MECGs.
Automated QRS complex detection and measurement algorithms for MECGs are lacking. In body surface mapping studies using MECGs for myocardial infarction detection and for activation mapping, “semi-automated” (i.e., template matching) or completely manual QRS complex detection methods are used in combination with manual QRSd measurement [12]–[14]. Semi-automated detection strategies require the a priori identification of the QRS complex morphology of interest and have difficulty discriminating QRS complexes from T-waves [15]. In the single identified system for automated QRS complex detection in MECGs, the algorithm used was designed to detect QRS complexes during episodes of ventricular tachycardia and relied on specific features associated with that condition [16], [17]. In addition, current 12-lead ECG QRS complex detection and QRSd measurement algorithms are ill suited for translation to MECGs. Although generally characterized by high sensitivity and positive predictivity, these methods are typically validated using single-channel 12-lead ECG data from the MIT-BIH database and struggle with negative-polarity complexes, very wide complexes, and low-amplitude complexes [18], [19].
ECGs of any type acquired from HF and CRT patients exhibit all of the characteristics that conventional 12-lead ECG algorithms struggle with. The HF and CRT patient populations represent a variety of conduction delay pathologies, each of which is associated with a different QRS complex morphology and polarity. Patients with left bundle branch block (LBBB), who make up the majority of CRT recipients, are characterized by large negative peaks on ECGs because of the anterior-to-posterior direction of cardiac activation [20]. Signal amplitudes in the HF and CRT populations may also vary widely due to the large range of BMIs present in this group [21], [22]. In addition, these patients require the analysis of not only native conduction (i.e. un-paced) ECGs but also paced data. In paced patients, device settings may not uniformly affect the cardiac cycle, and associated QRS complex changes cannot be predicted or described programmatically because of the individual nature of the electrophysiologic substrate response [23]. Furthermore, CRT patients may experience any combination of native conduction breakthrough, premature ventricular contractions, premature atrial contractions, fusion beats, and paced beats during CRT. A successful QRS complex detection algorithm for use with MECGs from CRT patients must correctly identify the electrical substrate behavior (i.e., QRS complex morphology) that the patient experiences most frequently, in spite of these confounding factors.
This study describes the paired development and validation of an automated MECG QRS complex detection algorithm and an MECG QRSd measurement algorithm to address the dual challenges of automated feature detection in MECGs and the idiosyncrasies of electrical substrate behavior in the CRT population. When the algorithms are used in tandem, the QRS complex detection algorithm identifies and classifies all of the QRS complexes associated with the most prevalent conduction pattern (i.e., most prevalent complex morphology) in a given MECG recording and the QRSd measurement algorithm delineates the array-specific (i.e., anterior and posterior) and global start and end points and measures the corresponding QRSd in each complex. Algorithm performance was determined by comparing the QRS classification and QRSd measurement results with those independently acquired from an expert cohort. The algorithm described herein has been submitted for a patent [24].
II. Methods and Procedures
A. MECGs
Algorithm development and validation were performed using data collected for a previous study of advanced systolic HF patients who had received new CRT implants between 2014 and 2017 at United Heart and Vascular Clinic in St. Paul, MN. For that study, written informed consent was obtained from all patients, and the study protocol was approved by an institutional review board (IRB). Both 12-lead ECGs and MECGs were used, the latter of which were acquired with a custom ECG Belt investigational body surface mapping system (see below). Data was available from 149 patients during native conduction (CRT off) and with CRT on at a range of device settings.
Algorithm development was performed using training data from 5 patients, and data from an additional 10 patients was used for the validation step while optimizing algorithm parameters. These 15 patients included right bundle branch block (RBBB), LBBB, nonspecific intraventricular conduction delay, and complete heart block patients. Data from a separate group of 58 patients was used for the final phase of algorithm validation, as described in later sections.
The ECG Belt system has been described elsewhere [11], [12]. The investigational system consists of a multichannel amplifier, a monitor, and electrode array (Heartscape, Verathon, Seattle, WA) and customized data acquisition software (Medtronic, PLC, Minneapolis, MN). The ECG Belt electrode array consists of 53 (17 anterior and 36 posterior) unipolar ECG electrodes arranged on the torso as shown in Fig. 2. MECGs for a given condition were collected in 15- to 20-s recording at a sampling rate of 1 kHz and bit resolution of 24 bits and saved offline for subsequent analyses.
FIGURE 2.
Example average signal groups and QRS peaks. Five groups of channels with distinct morphologies were identified in the sample recording (see text). The electrodes belonging to each group are shown in black (left). The associated average signals are shown to the right of the respective torso diagram, and the identified QRS complex peaks in each average signal are indicated with blue Xs.
B. QRS Detection and QRSd Measurement Algorithms
1). Implementation of Algorithms
The following preprocessing method, QRS detection algorithm, and QRSd measurement algorithm have been implemented in comprehensive stand-alone software written in MATLAB (using MATLAB Release 2017b, The Math-Works, Inc., Natick, MA) that supports the loading and serial analysis of MECGs collected during multiple conditions from one or more patients. The data preprocessing method and both algorithms make use of built-in MATLAB functions, including those provided with the digital signal processing (DSP) system toolbox, the signal processing toolbox, and the statistics and machine learning toolbox.
A complete analysis identifies all of the QRS complexes in a given recording, classifies each complex as predominant or outlier morphology (PM or OM, respectively), delineates the array-specific (i.e., anterior and posterior) and global start and end points of each of the PM complexes, and measures the array-specific and global QRS durations. The software also automatically generates figures for ready visualization of the results of the QRS detection and QRSd measurement algorithms for each recording. In addition, we have created a second version of the software with a graphical user interface (GUI) front end for use by an operator unfamiliar with the MATLAB scripting language.
2). Data Preprocessing
Prior to analysis with the QRS complex detection algorithm, each recording underwent filtering, channel redaction, splicing, and baseline correction. Zero-phase filtering was performed with a 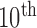 order, 0.5- to 25-Hz passband filter designed using the Matlab “window” design method [25]–[28]. An acceptable absolute (i.e., positive or negative) peak amplitude range of 0.10 to 4.0 mV, derived from 12-lead ECG data, was then applied to identify and remove channels of data from non-contacting or poorly contacting electrodes. A power spectrum analysis using the short-time Fourier transform was used to identify, remove, and splice around segments of the recording containing relatively large amounts of high-frequency noise.
order, 0.5- to 25-Hz passband filter designed using the Matlab “window” design method [25]–[28]. An acceptable absolute (i.e., positive or negative) peak amplitude range of 0.10 to 4.0 mV, derived from 12-lead ECG data, was then applied to identify and remove channels of data from non-contacting or poorly contacting electrodes. A power spectrum analysis using the short-time Fourier transform was used to identify, remove, and splice around segments of the recording containing relatively large amounts of high-frequency noise.
3). Automated QRS Complex Detection Algorithm
The QRS complex detection algorithm consists of five main stages designed to identify all of the QRS complexes in a recording and subsequently classify them as PM or OM complexes without the use of template matching or any  priori assumptions regarding QRS complex morphology. These stages are (1) channel grouping and averaging, (2) peak detection, (3) definition of QRS complex windows, (4) identification of additional complexes, and (5) classification of QRS complex morphologies. Each main substep of the detection algorithm is shown in the flowchart in Fig. 1. The criteria used to execute each substep are presented, as applicable, in Table 1. Figs. 2 and 3 illustrate the main results of each stage using data collected in an LBBB patient at AdaptivCRT (aCRT) settings during a point in time when LV-only pacing with an atrioventricular delay of 90 ms was being delivered by the CRT device. This patient had approximately two premature ventricular contractions (PVCs) per minute and frequent premature atrial contractions, which caused uneven beat-to-beat (i.e., RR) intervals. For easier visualization of signal features, only the first 7.5 s of the 15-s recording are used in Figs. 2 and 3.
priori assumptions regarding QRS complex morphology. These stages are (1) channel grouping and averaging, (2) peak detection, (3) definition of QRS complex windows, (4) identification of additional complexes, and (5) classification of QRS complex morphologies. Each main substep of the detection algorithm is shown in the flowchart in Fig. 1. The criteria used to execute each substep are presented, as applicable, in Table 1. Figs. 2 and 3 illustrate the main results of each stage using data collected in an LBBB patient at AdaptivCRT (aCRT) settings during a point in time when LV-only pacing with an atrioventricular delay of 90 ms was being delivered by the CRT device. This patient had approximately two premature ventricular contractions (PVCs) per minute and frequent premature atrial contractions, which caused uneven beat-to-beat (i.e., RR) intervals. For easier visualization of signal features, only the first 7.5 s of the 15-s recording are used in Figs. 2 and 3.
FIGURE 1.
QRS detection flowchart. The QRS detection method consists of five main stages. The alpha symbol (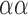 ) is used to indicate steps applied to each average signal separately. In stage 2, the steps indicated with the ± symbol are applied to the group of positive peaks (PP) and the group of negative peaks (NP) separately. In addition, the steps inside the rounded rectangle are performed for each average signal separately. In stage 3, the steps indicated with the © symbol are applied to each QRS complex separately. Also in step 3, the PR and QT intervals are approximated based on previously published equations [29], [30]. In stage 4, the previous steps indicated with the
) is used to indicate steps applied to each average signal separately. In stage 2, the steps indicated with the ± symbol are applied to the group of positive peaks (PP) and the group of negative peaks (NP) separately. In addition, the steps inside the rounded rectangle are performed for each average signal separately. In stage 3, the steps indicated with the © symbol are applied to each QRS complex separately. Also in step 3, the PR and QT intervals are approximated based on previously published equations [29], [30]. In stage 4, the previous steps indicated with the 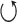 are repeated in numerical order. Parallelograms are used to indicate algorithm inputs and outputs.
are repeated in numerical order. Parallelograms are used to indicate algorithm inputs and outputs.
TABLE 1. Criteria for QRS Complex Detection Algorithm Steps.
| Step | Action | Parameter | Value/Criteria |
|---|---|---|---|
| 1a. | Relevant time segment selection | Initial length | 70 bpm cycle length A |
| Length options | Cycle length for ± 10 bpm A | ||
| 1b. | Channel grouping | Grouping criteria | Linear model fit |
| Peak polarities, magnitudes, and temporal position | |||
| Grouping over-fits | Too many small groups | ||
| Segment insufficient | Too few groups | ||
| Successful grouping | ≥3 groups of ≥3 channels | ||
| 2a. | Peak detection threshold | Threshold calculation for a given average signal | Maximum minimum peak height identified over 1,000-ms increments |
| 2b. | Peak down-selection | Peak amplitude | Group of peaks within ± 0.1 mV B |
| Peak width | Group of peaks within ± 20 ms B | ||
| 2c. | Comparison of peaks across average signals | Maximum intra-complex peak-to-peak distance | 81 ms C |
| 3. | Definition of QRS complex windows | R-R interval ranges | Cycle lengths corresponding to heart rates of 40 to 120 bpm A |
| Heart rate calculation | The heart rate associated with the most-common R-R interval range | ||
| 4. | Identification of additional complexes | Section(s) of the recording in which to detect additional peaks | Any interval between PM complexes that is larger than the calculated R-R interval |
| 5a. | Comparison of complex morphologies | Morphological features | Cross-correlation |
| Complex maximum peak amplitude and sign |
I.e., a segment length equal to the length of one cardiac cycle at a heart rate of 70 bpm (860 ms). The additional segment length options range from 1500 ms to 500 ms and correspond to heart rates from 40 to 120 bpm.
Based on precision of 12-lead ECG grid paper
Based on difference (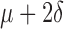 ) between paired global and widest single-lead ECG QRSd measurements (n = 150)
) between paired global and widest single-lead ECG QRSd measurements (n = 150)
Criteria without sources were determined during the development process.
FIGURE 3.
Example PM complexes. Three consecutive PM complexes identified in the sample recording (see text). The average signal for each of the five groups is shown in a different color. QRS complex peaks are indicated with black Xs. Vertical dotted lines mark the first and last peak in each complex. The RR interval is the distance (time) between the first peak in each complex and that of the following complex. The shaded area defines the broad window around each QRS complex, which is designed to encompass the leading and trailing edges of the complex.
The purpose of stage 1, channel grouping and averaging, is to create an average signal that is representative of each distinct ECG morphology present in the recording. Channel grouping and subsequent averaging leverage the redundancy of the MECGs to enhance large-amplitude, low-frequency features, which can then be used for peak detection. In order to efficiently and effectively group the channels, a time segment of data with sufficient non-isoelectric content to allow morphologic comparisons between channels must be extracted from the complete recording (see steps 1a and 1b in Fig. 1). Grouping of channels is independent of source electrode location. Fig. 2 shows the channel grouping and averaging results for the sample recording. Forty-five of the fifty-three electrodes were placed into five groups, as shown in the torso diagrams in Fig. 2. The average signal for each group is shown next to its respective torso diagram.
The purpose of stage 2 is to identify the peaks in each average signal that have features characteristic of QRS complexes and that belong to the PM complexes. QRS complex peaks are assumed to be larger in amplitude and narrower than T-wave peaks. The number of same-polarity peaks with QRS-complex-like features is used to avoid morphologic outliers (i.e., peaks from OM complexes). Peak detection is performed in each average signal separately and based on a threshold specific to that average signal. The QRS complex peaks in each average signal are indicated with blue Xs in Fig. 2. After the QRS complex peaks are identified in each average signal, peaks belonging to the same QRS complex are identified across the average signals. Fig. 3 shows the peaks in three consecutive QRS complexes in the same sample recording.
In stage 3, each QRS complex is defined by a window (i.e. broad limits) around it. QRS complex windowing is necessary for subsequent morphological comparisons between complexes. Each QRS complex window is broadly defined to ensure that the leading and trailing edges the complex are accounted for: the limits of each window are wider than the complex itself and include an interval approximately equal to the PR interval preceding the first peak in the QRS complex, the interval over which the complex peaks occur, and an interval approximately equal to the QT interval following the last peak in the complex. The complexes thus defined at the end of stage 3 are preliminarily classified as PM complexes. Fig. 3 also shows the window around each of the three QRS complexes.
The purpose of stage 4 is to identify any QRS complexes present in the recording but not identified in stage 2 and to subsequently define the windows around them. This stage is necessary to ensure that as many PM complexes are identified as possible, and it utilizes the more-informed description of PM complex features available after stage 3 to identify any complexes erroneously excluded on the basis of the information available during stage 2. Any complexes resulting from this stage are preliminarily classified as OM complexes. In stage 5, the morphologies of identified complexes are compared to finalize their classification as either PM or OM. This final comparison uses the complete QRS complex (i.e., not only the peaks) to confirm classifications. Complexes with morphologies that do not match the other complexes in their class are then reassigned as needed.
At the completion of all of the identification and classification steps, all of the QRS complexes associated with the most prevalent electrical substrate behavior have been identified, as have those associated with anomalous or ectopic behavior. This information can subsequently be used to measure the PM-to-OM complex ratio (i.e., OM complex burden), perform other analyses of the electrical substrate behavior, and/or measure the QRSd in each PM complex, as described below.
4). Automated QRS Complex Measurement Algorithm
The QRSd measurement algorithm is designed to delineate and measure the array-specific (i.e., anterior and posterior) and global QRS complex durations in each PM complex identified with the QRS detection algorithm.
Because the QRSd algorithm is designed to measure the QRSd separately in the data collected from the anterior and posterior arrays, array-specific morphologic outliers are identified prior to the application of the algorithm. The algorithm consists of five stages, which will be referred to as stages 6 through 10 for continuity with the QRS detection algorithm. The stages are (6) the identification of significant peaks in each channel, (7) the formation of array-specific peak groups, (8) the delineation of channel-specific QRS complex borders, (9) the delineation and measurement of array-specific QRS complex borders and durations, and (10) the delineation and measurement of the global QRS complex borders and duration. The substeps of the QRSd algorithm are shown in Figs. 4 and 5. The criteria used to execute each substep are presented, as applicable, in Table 2.
FIGURE 4.
QRSd measurement flowchart. The QRSd measurement algorithm consists of five main stages, which are numbered continuously with those of the detection algorithm. Parallelograms are used to indicate algorithm inputs and outputs.
FIGURE 5.
Identification of significant peaks in each channel. The identification of significant peaks in each channel is stage 6 of the QRSd measurement algorithm. The “P/F” symbol is used to indicate that the significance assessment is performed separately for the group of candidate peaks preceding the reference peak and the group following the reference peak. The  symbol is used to indicate that the significance assessment is performed for each candidate peak in turn (see Table 3).
symbol is used to indicate that the significance assessment is performed for each candidate peak in turn (see Table 3).
TABLE 2. Criteria for QRSd Measurement Algorithm Steps.
| Step | Action | Parameter | Value/Criteria |
|---|---|---|---|
| Prior to QRSd algorithm | Removal of array-specific outliers | Morphological features | Cross-correlation |
| Peak polarities, magnitudes, and temporal position | |||
| Exclusion criteria | Channel is morphologic outlier in the first, middle, and last PM complex | ||
| 6. | Identification of peak bounds | Leading or trailing peak boundary | Earlier of zero-crossing and concavity change |
| Significance assessment | Order of candidate peak evaluation | In order of ascending proximity to the reference peak | |
| Peak significance criteria | Peak position | Occurs after preceding significant peak bounds | |
| Peak amplitude | Opposite polarity of preceding significant peak | ||
| Criteria scaling factor | Ratio of candidate peak height to reference peak height | ||
| Leading and falling phase slope | Reference peak slope 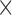 scaling factor scaling factor |
||
| Leading and falling phase curvature | Reference peak curvature 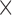 scaling factor scaling factor |
||
| 7. | Removal of array-specific peak outliers | Maximum peak-to-peak spacing | 52 ms A |
| 8. | Delineation of channel specific borders | Amplitude | <50% of the height of the closest significant peak |
| Slope | <2.5 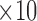 −2 mV/ms B −2 mV/ms B
|
||
| 9. | Delineation of array-specific borders | Group of normal array-specific border values | Largest group of borders within 20-ms |
| Array-specific start | Earliest in the group of array-specific normal start values | ||
| Array-specific end | Latest in the group of array-specific normal start values | ||
| 10. | Delineation of global borders | Global start | Earlier of the array-specific start values |
| Global end | Later of the array-specific end values |
Based on precision of 12-lead ECG grid paper
Based on difference (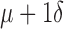 ) between paired global and widest single-lead 12-lead ECG QRSd measurements (n = 150)
) between paired global and widest single-lead 12-lead ECG QRSd measurements (n = 150)
Criteria without sources were determined during the development process
The purpose of stage 6 is to identify in each channel all significant peaks that occur within the QRS complex window, as determined with the QRS detection algorithm, to prevent cropping of important QRS complex features. Stage 6 consists of two parts for each channel (see Fig. 5): identification of the reference peak and evaluation of other candidate peaks to determine their significance. The reference peak in each channel is the largest-amplitude peak, and the other significant peaks are those that fall on either side of the reference peak and meet concavity and slope criteria that are scaled to those of the reference peak based on the ratio of a given peak’s height to that of the reference peak. Subsequently, in stage 7, two array-specific peak groups are formed: one consisting of all of the reference and significant peaks in the anterior channels and one consisting of all of the reference and significant peaks in the posterior channels.
In stages 8 to 10, the QRS complex borders (i.e., start and end points) are defined in each channel, the two pairs of array-specific borders are delineated, and the global QRS complex borders are delineated. The array-specific and global QRS durations are also measured. Fig. 6 illustrates the results of stages 8 and 9 for the anterior channels of a PM complex from the same recording shown in Figs. 2 and 3.
FIGURE 6.
Example channel-specific and array-specific QRS complex borders. Data from all viable anterior channels in the sample recording (see text) is shown for part of the QRS complex window. Significant peaks in are indicated with Xs. The channel-specific start and end borders are shown with vertical lines. Channel-specific start and end borders that do not belong to the group of normal values are indicated with black dotted vertical lines, while normal borders are indicated with color solid lines. For channels with an abnormal border, the closest significant peak is indicated with a black X. All other significant peaks are indicated in a color that matches the color of the channel-specific border. In one channel, both the start and end borders were outside those of the normal groups and that channel is shown using a dashed line. The earliest channel-specific start (“S”) and latest channel-specific end (“E”) are the anterior array-specific borders.
At the completion of the above steps, the array-specific and global QRS complex borders have been delineated, and the corresponding QRS durations have been measured for every PM complex in the recording. In addition to clinical significance of QRSd, the QRS complex borders can be used to facilitate measurement of other QRS complex features, such as the QRS integral.
C. Validation Studies
In order to evaluate the performance of the QRS complex detection and measurement algorithms in the type of data they are intended for, validation was performed using MECGs acquired in the previously described study of heart failure patients. Use of a standard 12-lead ECG database would not have been relevant to the algorithms’ intended use and no MECG databases are available. Furthermore, the number of validation studies performed was limited by the availability of the expert cohort.
1). QRS Detection Algorithm Validation
Validation studies were selected from patients in the top 20% of the study population based on clinical premature ventricular contraction (PVC) burden. First, each patient and recording were selected using a random-number generator. Second, the presence of PVCs or of other QRS complex morphologic variation in the 12-lead ECG collected at the same settings was visually confirmed. Third, the un-analyzed MECGs were visually inspected for the presence of PVCs or other QRS complex morphologic variation. Availability of validation data was limited by two factors: (1) wide-spread anti-arrhythmic use in the study population and (2) optimization of CRT percent pacing prior to 12-lead ECG and MECG collection. Twenty recordings from 8 patients were ultimately selected. The selected validation studies represent native conduction and a range of pacing configurations. Two studies with no PVCs or visible morphologic variation were included as negative controls.
This data was then independently analyzed by an expert cohort. Four cardiac device nurses and one certified cardiac device specialist scientist made up the expert cohort used to evaluate the performance of the QRS detection algorithm. Each expert had more than 5 years of experience clinically evaluating QRS complex morphologies during pacemaker, implanted cardioverter defibrillator, and CRT device interrogations. The experts’ responses were acquired using a purpose-made MATLAB GUI and digital calipers. Because of the difficulty of visually distinguishing the morphologies of 53 channels of data and because of the difference between MECGs and the single-lead ECG data used during clinical device interrogations, experts were presented with the average signals resulting from stage 1c (see Fig. 1) on a single axis for each validation study. The experts were instructed to use the digital calipers (1) to mark a window around each QRS complex in the recording and (2) to indicate any QRS complexes that appeared to be OM complexes compared to the other complexes in the recording. Respondents were asked to use the same level of precision as they would during a clinical device interrogation. Respondents had the opportunity to edit their responses for each recording before proceeding to the next validation study. Three of five experts had to concur for a QRS complex to be classified as a PM or OM complex.
The QRS complex detection algorithm was evaluated on two criteria: (1) detection of QRS complexes and (2) classification of QRS complex morphology (i.e., PM or OM). Algorithm detection and classification performance were quantified by sensitivity and positive predictivity, per the Association for the Advancement of Medical Instrumentation guidelines [31]. Classification performance was additionally assessed for accuracy. The average percent concordance for each complex classified as a PM complex in a given validation study was used as a measure of expert uncertainty. The relationships between algorithm performance, the total number of complexes, the proportion of OM complexes (OM complex burden), and the extent of expert PM classification concordance were also investigated. The execution time of the detection algorithm was measured as an indicator of practicality for real-time use.
2). QRSd Measurement Algorithm Validation
A single PM complex from each of 50 recordings during native conduction ( ) or CRT (
) or CRT (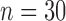 ) was blindly and randomly selected for QRSd measurement validation studies. Each recording came from a different patient, and the QRS detection and QRSd measurement groups of validation studies did not overlap. The authors checked that the complexes selected for use in validation were true QRS complexes (and not T-waves, etc.) and this check was performed blinded to the algorithm results. Due to the previously described difficulty of visually distinguishing the morphologies of 53 channels of data and the need for all channels to be accounted for in the global QRSd measurement, three research scientists with extensive backgrounds in cardiac electrophysiology made up the expert cohort used to evaluate the QRSd measurement algorithm. The experts’ responses were acquired using a purpose-made MATLAB GUI and digital calipers. For each validation study, each expert was presented with a single QRS complex identified by the algorithm and the 50 ms of data preceding and following the algorithm-determined global QRS complex borders, which were not shown. Due to preprocessing, pacing spikes were not visible in recordings collected during CRT. Data from the anterior and posterior channels was shown in colors from two different MATLAB color maps. The experts were asked to use the calipers to select the array-specific QRS start and end points for the anterior and posterior channels based on the earliest start and latest end point of the waveform in the array-specific channels [32]. The array-specific and global QRS durations were then calculated automatically and saved. Respondents had the opportunity to edit their responses for each recording before proceeding to the next validation study.
) was blindly and randomly selected for QRSd measurement validation studies. Each recording came from a different patient, and the QRS detection and QRSd measurement groups of validation studies did not overlap. The authors checked that the complexes selected for use in validation were true QRS complexes (and not T-waves, etc.) and this check was performed blinded to the algorithm results. Due to the previously described difficulty of visually distinguishing the morphologies of 53 channels of data and the need for all channels to be accounted for in the global QRSd measurement, three research scientists with extensive backgrounds in cardiac electrophysiology made up the expert cohort used to evaluate the QRSd measurement algorithm. The experts’ responses were acquired using a purpose-made MATLAB GUI and digital calipers. For each validation study, each expert was presented with a single QRS complex identified by the algorithm and the 50 ms of data preceding and following the algorithm-determined global QRS complex borders, which were not shown. Due to preprocessing, pacing spikes were not visible in recordings collected during CRT. Data from the anterior and posterior channels was shown in colors from two different MATLAB color maps. The experts were asked to use the calipers to select the array-specific QRS start and end points for the anterior and posterior channels based on the earliest start and latest end point of the waveform in the array-specific channels [32]. The array-specific and global QRS durations were then calculated automatically and saved. Respondents had the opportunity to edit their responses for each recording before proceeding to the next validation study.
The QRSd measurement algorithm was evaluated for both array-specific and global QRSd delineation and measurement. Algorithm error was quantified with both the signed and absolute paired difference between the algorithm results and the results averaged from the expert cohort, which were calculated for both array-specific and global QRS onset, offset, and duration. The errors of the anterior and posterior array-specific QRSd measurements were also compared. For native conduction validation studies (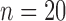 ), classification of QRSd values as narrow (<120 ms), moderate (120 to 150 ms), or wide (≥150) was evaluated using the global QRSd results. In addition, the influence on algorithm performance of QRS complex peak height (i.e., the average of the maximum anterior channel peak height and the maximum posterior channel peak height), QRS width, and the proportion of viable channels was investigated. Last, interobserver variations in array-specific and global QRSd values for the expert cohort were measured, and the relationship between interobserver variation and algorithm QRS border and QRSd measurement accuracy were investigated. The execution time of the QRSd algorithm was measured as an indicator of practicality for real-time use.
), classification of QRSd values as narrow (<120 ms), moderate (120 to 150 ms), or wide (≥150) was evaluated using the global QRSd results. In addition, the influence on algorithm performance of QRS complex peak height (i.e., the average of the maximum anterior channel peak height and the maximum posterior channel peak height), QRS width, and the proportion of viable channels was investigated. Last, interobserver variations in array-specific and global QRSd values for the expert cohort were measured, and the relationship between interobserver variation and algorithm QRS border and QRSd measurement accuracy were investigated. The execution time of the QRSd algorithm was measured as an indicator of practicality for real-time use.
3). Statistics
Data are expressed as means ± standard deviations. Student’s unpaired  -test was used to analyze unpaired data. A paired
-test was used to analyze unpaired data. A paired  -test was used to analyze differences between paired measurements when those measurements were normally distributed based on a Lilliefors test. Univariate regression was used to determine the relationships between algorithm performance and individual variables. Multivariate regression using backward stepwise elimination until all variables had a
-test was used to analyze differences between paired measurements when those measurements were normally distributed based on a Lilliefors test. Univariate regression was used to determine the relationships between algorithm performance and individual variables. Multivariate regression using backward stepwise elimination until all variables had a 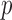 value of <0.10 was subsequently used to identify significant predictors of QRSd measurement accuracy. For all other analyses, a
value of <0.10 was subsequently used to identify significant predictors of QRSd measurement accuracy. For all other analyses, a 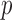 value of <0.05 was considered significant. All statistical analyses were performed using MATLAB.
value of <0.05 was considered significant. All statistical analyses were performed using MATLAB.
Pt. = patient; Se = sensitivity; P+ = positive predictivity; PM = predominant morphology; OM = outlier morphology; C = concordance; Ac = accuracy. Undetected and erroneously detected QRS complexes were not included in the calculations of the classification accuracy measures.
III. Results
A. QRS Detection Algorithm Validation
The total time for data preprocessing and analysis with the QRS complex detection algorithm was, on average, 30% of total recording length using a laptop with a 3.1 GHz Intel Core i5 processor. Table 3 shows the detection performance of the algorithm for each of the 20 validation studies. The validation studies contained a total of 267 complexes. The overall detection sensitivity of the algorithm was 98.5%, and its overall positive predictivity was 98.9%. Neither detection sensitivity nor positive predictivity was correlated with the number of complexes in the recording.
TABLE 3. Performance of QRS Detection Algorithm.
| Pt. # | Detection | Classification | |||||||
|---|---|---|---|---|---|---|---|---|---|
| QRS (#) | Se (%) | P+ (%) | PM (#) | OM (#) | C (%) | Se (%) | P+ (%) | Ac (%) | |
| 1 | 11 | 100 | 100 | 10 | 1 | 100 | 100 | 91 | 91 |
| 2 | 12 | 92 | 100 | 11 | 1 | 90 | 100 | 91 | 91 |
| 13 | 100 | 100 | 8 | 5 | 100 | 100 | 89 | 91 | |
| 3 | 28 | 100 | 97 | 25 | 3 | 91 | 88 | 100 | 89 |
| 14 | 100 | 100 | 14 | 0 | 100 | 100 | 100 | 100 | |
| 18 | 94 | 90 | 14 | 4 | 90 | 100 | 100 | 100 | |
| 4 | 13 | 100 | 100 | 12 | 1 | 100 | 100 | 100 | 100 |
| 11 | 100 | 100 | 7 | 4 | 92 | 86 | 100 | 91 | |
| 10 | 100 | 100 | 7 | 3 | 84 | 71 | 100 | 80 | |
| 5 | 13 | 100 | 100 | 12 | 1 | 100 | 92 | 100 | 92 |
| 14 | 93 | 100 | 13 | 1 | 99 | 100 | 100 | 100 | |
| 13 | 100 | 100 | 12 | 1 | 100 | 100 | 100 | 100 | |
| 13 | 100 | 100 | 11 | 2 | 97 | 100 | 92 | 92 | |
| 6 | 12 | 100 | 100 | 11 | 1 | 100 | 100 | 100 | 100 |
| 14 | 100 | 100 | 12 | 2 | 97 | 100 | 100 | 100 | |
| 12 | 100 | 100 | 12 | 0 | 95 | 92 | 100 | 92 | |
| 7 | 17 | 100 | 100 | 16 | 1 | 100 | 100 | 100 | 100 |
| 8 | 7 | 100 | 100 | 5 | 2 | 100 | 100 | 83 | 86 |
| 12 | 92 | 100 | 10 | 2 | 90 | 89 | 100 | 91 | |
| 10 | 100 | 100 | 9 | 1 | 92 | 100 | 90 | 90 | |
| Tot | 267 | 99 | 99 | 231 | 36 | 96 | 96 | 97 | 94 |
Pt. = patient; Se = sensitivity; P+ = positive predictivity; PM = predominant morphology; OM = outlier morphology; C = concordance; Ac = accuracy. Undetected and erroneously detected QRS complexes were not included in the calculations of the classification accuracy measures.
Table 3 also shows the classification performance of the QRS detection algorithm for each of the validation studies. In the studies with complexes of outlier morphology present ( ), the average burden was 16% (range, 7% to 39%). In total, the experts identified 231 complexes as PM complexes and 36 as OM complexes. The average expert classification concordance was 95.7%. The overall classification accuracy of the algorithm was 94.3%, with a sensitivity of 96% and a positive predictivity of 97.3%. The classification accuracy decreased with increasing OM complex burden (
), the average burden was 16% (range, 7% to 39%). In total, the experts identified 231 complexes as PM complexes and 36 as OM complexes. The average expert classification concordance was 95.7%. The overall classification accuracy of the algorithm was 94.3%, with a sensitivity of 96% and a positive predictivity of 97.3%. The classification accuracy decreased with increasing OM complex burden (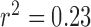 ,
, 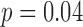 ), while expert classification concordance remained consistent as the ratio of OM to PM complexes increased (
), while expert classification concordance remained consistent as the ratio of OM to PM complexes increased (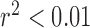 ,
, 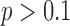 ).
).
B. QRSd Measurement Algorithm Validation
The total time for data preprocessing and analysis with both the QRS detection and the QRSd measurement algorithm was, on average, 90% of total recording length. The algorithm performance results for both array-specific and global QRS complex delineation and measurement are shown in Table 4. The average absolute algorithm error was approximately 10 ms or less for the array-specific and global QRS onsets and offsets. As shown in the histogram of the absolute error for the array-specific QRSd (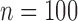 ) in Fig7A, the average absolute array-specific QRSd error was 17 ± 14 ms (
) in Fig7A, the average absolute array-specific QRSd error was 17 ± 14 ms (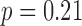 ), or 12% of the result averaged from the expert cohort. As shown in the histogram of the absolute algorithm error for global QRSd (
), or 12% of the result averaged from the expert cohort. As shown in the histogram of the absolute algorithm error for global QRSd ( ) in Fig. 7B, the average absolute global QRSd error was 12 ± 10 ms (
) in Fig. 7B, the average absolute global QRSd error was 12 ± 10 ms (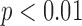 ), which was 8% of the averaged expert result.
), which was 8% of the averaged expert result.
TABLE 4. Performance of QRS Measurement Algorithm.
| Type | Parameter | QRS onset | QRS offset | QRSd |
|---|---|---|---|---|
Array-specific (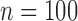 ) ) |
Mean ± Std. | 3.2 ± 13.6 | 0.3 ± 15.6 | –2.8 ± 21.7 |
 Mean Mean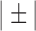 Std. Std.
|
10.0 ± 9.8 | 10.3 ± 11.7 | 16.6 ± 14.3 | |
 Median Median
|
8.5 | 7.5 | 14.0 | |
[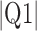 , , 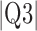 ] ] |
[4.0, 12.0] | [4.0, 12.0] | [7.0, 20.0] | |
Global (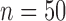 ) ) |
Mean ± Std. | 6.0 ± 9.9 | –3.9 ± 7.5 | –8.6 ± 12.4 |
 Mean Mean Std. Std.
|
8.0 ± 8.3 | 7.0 ± 4.7 | 11.6 ± 9.6 | |
 Median Median
|
7.0 | 6.0 | 10.0 | |
[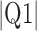 , ,  ] ] |
[3.0, 11.0] | [4.0, 9.8] | [5.0, 16.0] |
Parameters reported are mean signed or absolute (indicated by  ) error, i.e., the difference between the algorithm result and the averaged result from the expert cohort. Q1 = first quartile; Q3 = third quartile.
) error, i.e., the difference between the algorithm result and the averaged result from the expert cohort. Q1 = first quartile; Q3 = third quartile.
FIGURE 7.
Validation study results. Histogram of the absolute error for (A) the algorithm array-specific QRSd values and, (B) the algorithm global QRSd values. Seventy-six percent of algorithm array-specific QRSd values and 88% of algorithm global QRSd values were within 20 ms of the average expert values.
Seventy-six percent of algorithm array-specific QRSd values and 88% of algorithm global QRSd values were within 20 ms (half of the smallest precision on a 12-lead ECG grid) of the averaged expert results. The average absolute errors for anterior and posterior array-specific QRSd results, however, were similar (anterior, 14 ± 12 ms; posterior, 19 ± 15 ms; 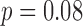 ).
).
The clinical QRSd classifications of the native conduction validation studies (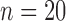 ) as narrow (<120 ms), moderate (120 to 150 ms), or wide (≥150) were the same for the algorithm and the average expert response in 19 of the 20 native conduction validation studies (95%). QRS complex peak height and expert QRSd were significant predictors of algorithm error for global QRSd (
) as narrow (<120 ms), moderate (120 to 150 ms), or wide (≥150) were the same for the algorithm and the average expert response in 19 of the 20 native conduction validation studies (95%). QRS complex peak height and expert QRSd were significant predictors of algorithm error for global QRSd ( ,
, 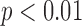 ). Increased complex peak height was associated in the multivariate model with algorithm underestimation of QRSd, while increased average expert QRSd was associated with algorithm overestimation of QRSd.
). Increased complex peak height was associated in the multivariate model with algorithm underestimation of QRSd, while increased average expert QRSd was associated with algorithm overestimation of QRSd.
The interobserver variation data for the experts’ responses is shown in Table 5. The average standard deviation of the experts’ array-specific and global QRS onset and offset results ranged from approximately 6 to 10 ms, while the standard deviations for the array-specific and global QRSd results were both about 15 ms (10%). Increased algorithm error was not associated with increased interobserver differences in the experts’ results for either array-specific or global QRSd.
TABLE 5. Interobserver Variation for QRSd Validation Studies.
| Type | Parameter | QRS onset | QRS offset | QRSd |
|---|---|---|---|---|
Array-specific (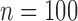 ) ) |
Mean ± Std. | 8.4 ± 7.2 | 7.9 ± 9.2 | 15.2 ± 12.0 |
| Median | 5.6 | 5.4 | 11.3 | |
| [Q1, Q3] | [3.3, 11.8] | [3.0, 10.1] | [7.0, 19.1] | |
Global ( ) ) |
Mean ± Std. | 9.6 ± 7.1 | 6.4 ± 4.4 | 15.2 ± 10.1 |
| Median | 7.3 | 5.3 | 12.9 | |
| [Q1, Q3] | [3.8, 14.3] | [3.5, 8.6] | [7.5, 19.0] |
Parameters reported are mean signed interobserver variation, i.e., the standard deviation of the results of the expert cohort. Q1 = first quartile; Q3 = third quartile.
IV. Discussion
In this study, we describe a pair of automated real-time algorithms for QRS complex detection and classification and for QRS complex delineation and measurement in MECGs acquired in the HF and/or CRT population, which is characterized (1) by complexes of both negative and positive polarities, large width, and variable amplitudes and (2) by unpredictable and inconsistent variation in complex morphology. We evaluated the performance of these algorithms using MECGs collected in real-world CRT patients and compared the algorithm results with the independently acquired results from two groups of experts. The QRS complex detection algorithm had at least 96% sensitivity and positive predictivity for QRS complex detection and classification. The accuracy of the QRS delineation and measurement algorithm was close to the interobserver variation in the expert cohort responses, similar to that of existing single-lead ECG methods [33], and similar to documented differences in QRSd results between clinical ECG machines and manual clinician measurements [34]. The QRSd measurement algorithm clinical classification accuracy was 95% in the 20 native conduction validation studies, which is better than the reported classification agreement between clinical ECG machines and doctors [34].
A. QRS Detection Algorithm Validation
The QRS complex detection algorithm was at least 96% sensitive had a positive predictivity of at least 97% for both complex detection and classification of PM and OM complexes. No previously published QRS complex detection and/or classification algorithms for MECGs were found in the literature. Reported sensitivity and positive predictivity for single-lead ECG algorithms are usually over 99% for QRS complex detection without morphologic classification [15], [33]. Fully automated real-time QRS detectors with morphologic classification (i.e., PVC detectors), however, tend to have positive predictivity and sensitivity values closer to 90% to 95% [15]. These results indicate that the QRS complex detection algorithm sensitivity and positive predictivity are similar to those reported for current state-of-the-art methods for single-channel 12-lead ECG data in spite of the additional challenges posed by MECGs acquired in CRT patients.
B. QRSd Measurement Algorithm Validation
As with the QRS complex detection algorithm, no previously developed QRSd measurement algorithms for MECGs were found in the literature. Comparison of algorithm accuracy with the expert cohort’s interobserver variation may, therefore, be the best means of assessing the QRSd measurement algorithm’s performance. The average absolute algorithm error was approximately 10 ms or less for array-specific and global QRS onset and offset, which is one-fourth of the smallest unit of precision of standard clinical 12-lead ECG grid paper (40 ms). Moreover, the algorithm global QRSd error (12 ± 10 ms) was substantially less than the interobserver variation in that measurement (15±10 ms), and the algorithm array-specific QRSd measurement was close to the interobserver variation in that measurement.
Most QRSd measurement algorithms developed for single-lead ECG data report QRS onset and offset error. Cesari et al. reported results (absolute average QRS onset difference: 10 ms; absolute average QRS offset difference: 14 ms) similar to ours for an algorithm designed for single-lead ECG data and validated with the MIT-BIH database [33]. In addition, our non-absolute average QRS onset and offset errors of 0.3 to 3.2 ms are within the results of other investigators’ single-lead ECG algorithms, for which the error ranged from 0.1 to 4.6 ms [33].
The QRSd measurement algorithm also performs well when its accuracy is compared with that of current clinical 12-lead ECG machines or the reproducibility of manual QRSd measurements made by clinicians. The average absolute algorithm error of 12 ms for our cohort of 20 native conduction and 30 paced MECG recordings is well within the range of error between a clinical ECG machine and a pair of clinicians, as reported by De Pooter et al. (7 ms and 14 ms in native and paced 12-lead ECGs, respectively). De Pooter also reported an 85% or 63% agreement between the expert clinicians and clinical ECG machines for the classification of native conduction ECGs as narrow or moderate, respectively. In our study, the agreement between the QRSd measurement algorithm and the average expert result was considerably higher, at 95%. Last, De Guillebon et al. reported that the results of three cardiologists and a clinical ECG machine were found to differ by more than 20 ms in 47% of cases [35]. In contrast, 76% of algorithm array-specific QRSd values and 88% of algorithm global QRSd values in our study were within 20 ms of the average expert result. Ultimately, the QRSd measurement algorithm border delineation and QRSd error are well matched with those of the expert cohort, reported results for state-of-the-art single-lead ECG algorithms, and variation in clinical 12-lead ECG measurement techniques.
C. Clinical Significance
The paired QRS complex detection and measurement algorithms described herein may be used to accurately identify and analyze the QRS complexes associated with the most prevalent conduction pattern in MECGs in candidates for or patients with CRT pacing. The real-time nature of these algorithms makes them viable for use in a clinical environment. The algorithms described in this paper could be used in the future not only to measure QRS complex duration but also (1) to evaluate the effectiveness of changes to pacing settings on OM complex burden, (2) to compare the characteristics of the most prevalent conduction pattern with those of anomalous or ectopic behavior, (3) to augment existing noninvasive 3D mapping systems, or (4) to measure novel QRS-based metrics of electrical dyssynchrony, such as the QRS integral.
D. Limitations
These algorithms have been developed and validated using the ECG Belt investigational body surface mapping system and not validated in another MECG system due to lack of availability. In addition, the QRS complex detection algorithm is designed for dichotomized, and not multi-class, heart beat classification. This strategy is used to provide as much flexibility as possible in the algorithm and prevent erroneous identification of PM complexes as outliers.
V. Conclusions
The paired algorithms described in this study have been specifically designed to overcome the challenges of MECGs and of conduction patterns in the CRT population. The algorithms’ QRS complex detection, classification, border delineation, and measurement results have been validated in MECGs against the independently acquired results of an expert cohort and have been found to be within accuracies comparable to those of studies done with clinical 12-lead ECG machines and to the interobserver variation of experts in the field. These methods may be used for real-time analysis and represent a key first step toward implementation of MECG methods for improved characterization of cardiac activation in HF and CRT patients.
Acknowledgment
Ms. Curtin, Dr. Burns, and Dr. Bank are authors on a patent filing describing this work.
Funding Statement
This work was supported by the Medtronic External Research Program, Medtronic plc.
References
- [1].Epstein A. E.et al. , “2012 ACCF/AHA/HRS focused update incorporated into the ACCF/AHA/HRS 2008 guidelines for device-based therapy of cardiac rhythm abnormalities,” J. Amer. College Cardiol., vol. 127, no. 3, pp. e283–e352, Jan. 2013. [DOI] [PubMed] [Google Scholar]
- [2].Brignole M.et al. , “2013 ESC guidelines on cardiac pacing and cardiac resynchronization therapy,” Eur. Heart J., vol. 34, no. 29, pp. 2281–2329, Aug. 2013. [DOI] [PubMed] [Google Scholar]
- [3].Engels E. B., Mafi-Rad M., van Stipdonk A. M., Vernooy K., and Prinzen F. W., “Why QRS duration should be replaced by better measures of electrical activation to improve patient selection for cardiac resynchronization therapy,” J. Cardiovascular Transl. Res., vol. 9, no. 4, pp. 257–265, Aug. 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Varma N., Ploux S., Ritter P., Wilkoff B., Eschalier R., and Bordachar P., “Noninvasive mapping of electrical dyssynchrony in heart failure and cardiac resynchronization therapy,” Card Electrophysiol. Clin., vol. 7, no. 1, pp. 125–134, Mar. 2015. [DOI] [PubMed] [Google Scholar]
- [5].Douglas R. A. G., Samesima N., Filho M. M., Pedrosa A. A., Nishioka S. A., and Pastore C. A., “Global and regional ventricular repolarization study by body surface potential mapping in patients with left bundle-branch block and heart failure undergoing cardiac resynchronization therapy,” Ann. Noninvasive Electrocardiol., vol. 17, no. 2, pp. 123–129, Apr. 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Guillem M. S., Brugada R., Thibault B., Climent A. M., and Millet J., “Analysis of body surface potential maps in cardiac resynchronization therapy,” in Proc. Comput. Cardiol., vol. 35, pp. 93–96, Sep. 2008. [Google Scholar]
- [7].Ploux S.et al. , “Noninvasive electrocardiographic mapping to improve patient selection for cardiac resynchronization therapy: Beyond QRS duration and left bundle branch block morphology,” J. Amer. College Cardiol., vol. 61, no. 24, pp. 2435–2443, Jun. 2013. [DOI] [PubMed] [Google Scholar]
- [8].Gage R. M., Curtin A. E., Burns K. V., Ghosh S., Gillberg J. M., and Bank A. J., “Changes in electrical dyssynchrony by body surface mapping predict left ventricular remodeling in patients with cardiac resynchronization therapy,” Heart Rhythm, vol. 14, no. 3, pp. 392–399, Mar. 2017. [DOI] [PubMed] [Google Scholar]
- [9].Barold S. S. and Herweg B., “Usefulness of the 12-lead electrocardiogram in the follow-up of patients with cardiac resynchronization devices. Part II,” Cardiol. J., vol. 18, no. 6, pp. 610–624, 2011. [DOI] [PubMed] [Google Scholar]
- [10].van Stipdonk A., Wijers S., Meine M., and Vernooy K., “ECG patterns in cardiac resynchronization therapy,” J. Atrial Fibrillation, vol. 7, no. 6, p. 1214, Apr-May 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].van Deursen C. J. M.et al. , “The value of the 12-lead ECG for evaluation and optimization of cardiac resynchronization therapy in daily clinical practice,” J. Electrocardiol., vol. 47, no. 2, pp. 202–211, Mar-Apr 2014. [DOI] [PubMed] [Google Scholar]
- [12].McClelland A. J. J., Owens C. G., Menown I. B. A., Lown M., and Adgey A. A. J., “Comparison of the 80-lead body surface map to physician and to 12-lead electrocardiogram in detection of acute myocardial infarction,” Amer. J. Cardiol., vol. 92, no. 3, pp. 252–257, Aug. 2003. [DOI] [PubMed] [Google Scholar]
- [13].Ornato J. P.et al. , “Body surface mapping vs 12-lead electrocardiography to detect ST-elevation myocardial infarction,” Amer. J. Emergency Med., vol. 27, no. 7, pp. 779–784, Sep. 2009. [DOI] [PubMed] [Google Scholar]
- [14].O’Neil B. J.et al. , “Incremental benefit of 80-lead electrocardiogram body surface mapping over the 12-lead electrocardiogram in the detection of acute coronary syndromes in patients without st-elevation myocardial infarction,” Acad. Emerg. Med., vol. 17, no. 9, pp. 932–939, Sep. 2010. [DOI] [PubMed] [Google Scholar]
- [15].Oweis R. and Al-Tabbaa B. O., “QRS detection and heart rate variability analysis: A survey,” Biomed. Sci. Eng., vol. 2, no. 1, pp. 13–34, 2014. [Google Scholar]
- [16].Potse M., Linnenbank A. C., and Grimbergen C. A., “Software design for analysis of multichannel intracardial and body surface electrocardiograms,” Comput. Methods Programs Biomed., vol. 69, no. 3, pp. 225–236, Nov. 2002. [DOI] [PubMed] [Google Scholar]
- [17].Kemmelings J. G. C., Linnenbank A. C., Muilwijk S. L. C., SippensGroenewegen A., Peper A., and Grimbergen C. A., “Automatic QRS onset and offset detection for body surface QRS integral mapping of ventricular tachycardia,” IEEE Trans. Biomed. Eng., vol. 41, no. 9, pp. 830–836, Sep. 1994. [DOI] [PubMed] [Google Scholar]
- [18].Arzeno N. M., Deng Z.-D., and Poon C.-S., “Analysis of first-derivative based QRS detection algorithms,” IEEE Trans. Biomed. Eng., vol. 55, no. 2, pp. 478–484, Feb. 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].da S Luz E. J., Schwartz W. R., Cámara-Chávez G., and Menotti D., “ECG-based heartbeat classification for arrhythmia detection: A survey,” Comput. Methods Programs Biomed., vol. 127, pp. 144–164, Apr. 2016. [DOI] [PubMed] [Google Scholar]
- [20].Sweeney M. O., Hellkamp A. S., van Bommel R. J., Schalij M. J., Borleffs C. J. W., and Bax J. J., “QRS fusion complex analysis using wave interference to predict reverse remodeling during cardiac resynchronization therapy,” Heart Rhythm, vol. 11, no. 5, pp. 806–813, May 2014. [DOI] [PubMed] [Google Scholar]
- [21].Cuspidi C.et al. , “Does QRS voltage correction by body mass index improve the accuracy of electrocardiography in detecting left ventricular hypertrophy and predicting cardiovascular events in a general population?” J. Clin. Hypertension, vol. 18, no. 5, pp. 415–421, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Kurisu S.et al. , “Electrocardiographic characteristics in the underweight and obese in accordance with the world health organization classification,” IJC Metabolic Endocrine, vol. 9, pp. 61–65, Dec. 2015. [Google Scholar]
- [23].Jia P., Ramanathan C., Ghanem R. N., Ryu K., Varma N., and Rudy Y., “Electrocardiographic imaging of cardiac resynchronization therapy in heart failure: Observation of variable electrophysiologic responses,” Heart Rhythm, vol. 3, no. 3, pp. 296–310, Mar. 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Curtin A. E., Bank A. J., Gage R. M., and Burns K. V., “Anterior and posterior electrode signals,” USPTO Patent 62 609 924, 2017.
- [25].Kligfield P.et al. , “Recommendations for the standardization and interpretation of the electrocardiogram: Part I: The electrocardiogram and its technology,” J. Amer. College Cardiol., vol. 115, no. 10, pp. 1306–1324, Mar. 2007. [DOI] [PubMed] [Google Scholar]
- [26].Aranda J. M. Jr., et al. , “QRS duration variability in patients with heart failure,” Amer. J. Cardiol., vol. 90, no. 3, pp. 335–337, Aug. 2002. [DOI] [PubMed] [Google Scholar]
- [27].Iaizzo P. A., Handbook of Cardiac Anatomy, Physiology, and Devices. New York, NY, USA: Springer, 2009. [Google Scholar]
- [28].Köhler B.-U., Hennig C., and Orglmeister R., “The principles of software QRS detection,” IEEE Eng. Med. Biol. Mag., vol. 21, no. 1, pp. 42–57, Jan-Feb 2002. [DOI] [PubMed] [Google Scholar]
- [29].Carruthers S. G., McCall B., Cordell B. A., and Wu R., “Relationships between heart rate and PR interval during physiological and pharmacological interventions,” Brit. J. Clin. Pharmacol., vol. 23, no. 3, pp. 259–265, 1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Karjalainen J., Viitasalo M., Mänttär M., and Manninen V., “Relation between QT intervals and heart rates from 40 to 120 beats/min in rest electrocardiograms of men and a simple method to adjust QT interval values,” J. Amer. College Cardiol., vol. 23, no. 7, pp. 1547–1553, 1994. [DOI] [PubMed] [Google Scholar]
- [31].Recommended Practice for Testing and Reporting Performance Results of Ventricular Arrhythmia Detection Algorithms, Assoc. Adv. Med. Instrum., Arrhythmia Monitoring Subcommittee, 1987.
- [32].Surawicz B., Childers R., Deal B. J., and Gettes L. S., “AHA/ACCF/HRS recommendations for the standardization and interpretation of the electrocardiogram: Part III: Intraventricular conduction disturbances,” J. Amer. College Cardiol., vol. 119, no. 10, pp. e235–e240, Mar. 2009. [DOI] [PubMed] [Google Scholar]
- [33].Cesari M., Mehlsen J., Mehlsen A.-B., and Sorensen H. B. D., “A new wavelet-based ECG delineator for the evaluation of the ventricular innervation,” IEEE J. Transl. Eng. Health Med., vol. 5, Jul. 2017, Art. no. 2000215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].De Pooter J., El Haddad M., Stroobandt R., De Buyzere M., and Timmermans F., “Accuracy of computer-calculated and manual QRS duration assessments: Clinical implications to select candidates for cardiac resynchronization therapy,” Int. J. Cardiol., vol. 236, pp. 276–282, Jun. 2017. [DOI] [PubMed] [Google Scholar]
- [35].De Guillebon M.et al. , “Reliability and reproducibility of QRS duration in the selection of candidates for cardiac resynchronization therapy,” J. Cardiovascular Electrophysiol., vol. 21, no. 8, pp. 890–892, Aug. 2010. [DOI] [PubMed] [Google Scholar]









