Molecular mechanisms of force production in clathrinmediated endocytosis

Abstract

During clathrin-mediated endocytosis (CME), a flat patch of membrane is invaginated and pinched off to release a vesicle into the cytoplasm. In yeast CME, over 60 proteins—including a dynamic actin meshwork—self-assemble to deform the plasma membrane. Several models have been proposed for how actin and other molecules produce the forces necessary to overcome the mechanical barriers of membrane tension and turgor pressure, but the precise mechanisms and a full picture of their interplay are still not clear. In this review, we discuss the evidence for these force production models from a quantitative perspective and propose future directions for experimental and theoretical work that could clarify their various contributions.

Eukaryotic cells create endocytic vesicles from the plasma membrane to import extracellular molecules and regulate cell surface components. This process enables a variety of vital cellular functions including nutrient uptake, cell size control, signaling protein regulation, and recycling of membrane components. Clathrin-mediated endocytosis (CME), the primary endocytic pathway, has been a subject of study in cell biology for decades, and many of the biochemical components are well understood [1–5]. What remains poorly understood is precisely how the macromolecular components cooperate to perform this mechanical work to deform the membrane.

Clathrin-mediated endocytosis involves an initial bending of the plasma membrane, elongation of the invagination, and scission of the tubule neck to form a ~ 50 nm diameter membrane vesicle that is released into the cytoplasm. The robust, regulated self-assembly of endocytic proteins in cells has been quantitatively measured in several studies and has been shown to be highly reproducible across events [6–9] (Fig. 1A). Over 60 proteins are self-assembled at the endocytic site (Table 1), including a dynamic meshwork of cytoskeletal actin filaments. Approximately 100 s before vesicle formation, clathrin and a number of membrane-binding proteins bind to a site on the plasma membrane. Recruitment of other membrane-associated proteins, followed by a burst of actin polymerization leads to the formation of a dense meshwork of short, Arp2/3branched actin filaments. The actin assembly phase leads to membrane elongation and scission of the membrane invagination within ~ 10 s.

Fig. 1.

Overview of proteins and forces in clathrin-mediated endocytosis in yeast. (A) Stages of CME membrane deformation, and spatial organization and timing of various protein modules. Membrane shapes, actin filaments, and vesicle are drawn to scale, reflecting quantitative microscopy data from yeast. Myosin-I and WASp localizations are represented by dashed lines when the reported localizations in S. cerevisiae and S. pombe differ. (B) Forces opposing CME. Turgor pressure, membrane bending and membrane tension pose significant energy barriers that must be overcome to generate a clathrin-coated pit and vesicle. Note that turgor pressure is applied isotropically to all membrane surfaces, favoring collapse of the pit and tubule, and membrane scission passes through a high-energy intermediate. Arrows are drawn to indicate the direction and order of magnitude of forces opposing CME.

Table 1.

CME protein names for yeast and mammals.

Module	Fission yeast	Budding Yeast	Mammals	Description
Early coat	SPBC800.10c, Ucp8	Ede1p	EPS15, EPS15L1	UB/EH/EF hand domain protein
	Syp1p	Syp1p	FCHO1/2, SGIP1	F-BAR domain protein
	Ubp2p	Ubp2p	-*	Ubiquitin C-terminal hydrolase 2 (fungi only)
	Ubp7p	Ubp7p	-	Ubiquitin C-terminal hydrolase 7 (fungi only)
	Chc1p	Chc1p	CLTC, CLTCL1	Clathrin heavy chain
	Clc1p	Clc1p	CLTA/B	Clathrin light chain
	Pal1p	Pal1p	-	Membrane-associated protein (fungi only)
	Apl1p	Apl1p	AP1B1, AP2B1	AP-2 adaptor complex beta subunit
	Apl3p	Apl3p	AP2A1/2	AP-2 adaptor complex alpha subunit
	Apm4p	Apm4p	AP2M1	AP-2 adaptor complex mu subunit
	Aps2p	Aps2p	AP2S1	AP-2 adaptor complex sigma subunit
Intermediate coat	End4p	Sla2p	HIP1, HIP1R	Huntingtin-interacting protein homolog
	Ent1p	Ent1/2/4p	EPN1/2/3, ENTHD1	Epsin
	Yap18p	Yap1801/2p	CALM, SNAP91, AP180	ENTH, VHS domain protein
Late coat	Pan1p	Pan1p	ITSN1/2	Actin cortical patch component with EF hand and WH2 motif (Intersectin complex)
	Shd1p	Sla1p	CIN85	Cytoskeletal protein binding (Intersectin complex)
	End3p	End3p	EPS15, EPS15L1	Actin cortical patch component (Intersectin complex)
	Lsb4p	Lsb3p, Ysc84	SH3YL1	Actin cortical patch component
	Lsb5p	Lsb5p	TOM1, TOM1L1/2	Actin cortical patch component
	Ucp3p	Gts1p	-	GTPase activating protein (fungi only)
WASp/Myo	Wsp1p	Las17p	WAS, WASL	WASp
	Vrp1p	Vrp1p	WIPF1/2, WIP	Verpolin
	Bzz1p	Bzz1p	TRIP10, FNBP1/L	F-BAR domain protein (syndapin-like)
	-	Scd5p	-	(Budding yeast only)
	Myo1p	Myo3/5p	MYO1E/F	Myosin Type I-e
	Bbc1p	Bbc1p	-	WIP family cytoskeletal protein (fungi only)
	Lsb1p	Lsb1p, PIN3	GRAP/2, GRB2	WASp binding protein
	Aim21p	Aim21p	-	Barbed end F-actin assembly inhibitor (fungi only)
	Cdc15p	Hof1p	PSTPIP1/2	Extended Fer/CIP4 (EFC) domain protein
	Cam1p	Cmd1p	CALM1/2/3/4/5	Calmodulin
Actin	Act1p	Act1p	ACTA/B/C/G/L	Actin
	Arc5p	Arc15p	ARPC5, ARPC5L	ARP2/3 complex subunit Arc5
	Arc3p	Arc18p	ARPC3	ARP2/3 complex subunit Arc21
	Arc4p	Arc19p	ARPC4	ARP2/3 complex subunit Arc4
	Arc2p	Arc35p	ARPC2	ARP2/3 complex subunit Arc34
	Arc1p	Arc40p	ARPC1A/B	ARP2/3 complex subunit Sop2
	Arp2p	Arp2p	ACTR2	ARP2/3 complex subunit Arp2
	Arp3p	Arp3p	ACTR3, ACTR3B/C	ARP2/3 complex subunit Arp3
	Dip1p	Ldb17	NCKIPSD	WISH/DIP/SPIN90 ortholog
	Abp1p	Abp1p	DBNL	Debrin ortholog
	Acp1p	Cap1p	CAPZA1/2	F-actin capping protein alpha subunit
	Acp2p	Cap2p	CAPZB	F-actin capping protein beta subunit
	Fim1p	Sac6p	LCP1, PLS1/3	Fimbrin
	Stg1p	Scp1p	TAGLN, TAGLN2/3	Transgelin
	Twf1p	Twf1p	TWF1/2	Twinfilin
	Crn1p	Crn1p	CORO1A/B/C	Coronin
	Ppk29, Ppk30, Ppk38	Ark1p, Prk1p, Akl1p	BMP2K, AAK1	Ark1/Prk1 family protein kinase
	Adf1p	Cof1p	DSTN, CFL1, CFL2	ADF/cofilin
	Aip1p	Aip1p	WDR1	Actin-binding WD repeat protein
	-	Bsp1p	-	(Budding yeast only)
	Cdc3p	Pfy1p	PFN4	Profilin
	Gmf1p	Aim7p	GMFB/G	Glia Maturation Factor
	Cap1p	Srv2	CAP1/2	Adenylyl cyclase-associated protein
	-	Aim3p	-	Budding yeast only
Scission	Hob3p	Rvs161p	BIN3	BAR adaptor protein (amphiphysin)
	Hob1p	Rvs167p	BIN1/2, AMPH	BAR adaptor protein (amphiphysin/endophilin)
	Syj1p	Inp52	SYNJ1/2	Synaptojanin
	Vps1p**	Vps1p	DNM1, DNM1L	Dynamin family GTPase
Less-well characterized	Mug137p	App1p	-	Phosphatidate phosphatase
	Mug137p	-	SHGL1/2/3	BAR adaptor protein, involved in endocytosis (predicted)
	Dlc1p	Tda2	TCTEX1D1/2/4, TCTE3, DYNLT1	Dynein light chain

^*“-” indicates no known ortholog.

^**In fission yeast, Vps1p is not recruited to endocytic patches and its role in budding yeast endocytosis needs to be resolved.

The actin meshwork and coat proteins are rapidly disassembled as the vesicle is released and diffuses into the cytoplasm [10]. A variety of these protein modules are capable of producing force, and a number of theoretical efforts have aimed to explain how the protein machinery develops over time [11,12] and how the membrane is deformed [13,14]. In recent years, several models of force production have been explored but a comprehensive account of how force is produced to achieve CME is lacking. Currently, we do not know how the various proposed force production mechanisms cooperate, synergize, and coordinate mechanical work on the membrane in a spatially and temporally controlled manner.

In this review, we focus on the model organisms budding yeast and fission yeast (Saccharomyces cerevisiae and Schizosaccharomyces pombe, respectively) which exhibit many valuable similarities and a few differences compared with other eukaryotes such as mammals. Yeast has been historically used in cell biology studies, since they are amenable to genetic manipulation, easy to handle and their proteins are well conserved with higher eukaryotes [6,15]. Yeast CME is of special interest because membrane invagination is opposed by much larger forces than in mammalian cells, due to their high turgor pressure (Fig. 1B), and therefore successful CME in yeast requires actin dynamics [16,17]—highlighting its role in force production.

In this review, we will discuss the energetic barriers to endocytosis and a variety of models that explain how cells produce sufficient force to carry out CME, focusing first on actin-based models and then on other mechanisms acting on the membrane. The redundancy and cooperation of multiple mechanisms can make CME more robust but the multitude of overlapping mechanisms often obscures our understanding of the underlying mechanisms and complicates direct experimental study or comprehensive modeling. By quantitatively assessing the experimental and theoretical support for each model, we hope to synthesize the various hypotheses and evaluate their potential for force production comprehensively.

Force and energy barriers for membrane deformation during CME

Clathrin-mediated endocytosis involves a series of morphological changes in the membrane that are opposed by the bending stiffness and surface tension of the membrane, as well as the turgor pressure of the cell. Initially, forces must be applied to bend the membrane and begin the invagination of a tubule into the cytoplasm (Fig. 1B). Later, the clathrin-coated pit (CCP) must be elongated and the tubule neck must be constricted to induce scission and release the vesicle into the cytoplasm.

Using the theory of elastic membranes developed by Helfrich [18], one can estimate that the energy required to create a vesicle from a flat membrane is larger than 500 k_BT [19,20]. The required energy is even higher in cells with increased membrane tension or turgor pressure. For instance, creating a cylindrical tube of 50 nm in diameter and 120 nm in length against a 1 MPa turgor pressure [21,22] requires an energy around 6 9 10⁴ k_BT and a force around 2000 pN.

In mammalian cells, where the turgor pressure is low, the largest energetic barrier to endocytosis is overcoming a cell’s membrane tension. Simulations with high membrane tension (~ 0.5 pN/nm) indicate that the force to pull the membrane into an elongated tube is ~ 100–200 pN [23] (Table 2). This force can be reduced to tens of piconewtons with the assistance of coat proteins that impose a specified curvature on the membrane [14]. When membrane tension is low (0.002 pN/nm), increasing the area covered by curvature-generating proteins is sufficient to induce vesiculation without applying other external forces [14]. In yeast cells, under realistic conditions of membrane tension and turgor pressure (0.2–1 MPa, [21,22]), the force required to deform the membrane into a tube is ~ 3000 pN [24,25]. Theory and experiments [24,26–28] demonstrate that the main force barrier for the formation of a CCP comes from the initial deformations of the plasma membrane into a small tubule while maintaining the tubule elongation requires a relatively smaller amount of force.

Table 2.

Force requirements for CME estimated from simulations.

Turgor pressure	Membrane tension	Curvature-generating proteins	Pulling force required	References
0	0.02 pN/nm (low)	Clathrin	15 pN	[14]
1 kPa (low)	0.5 pN/nm (high)	No	190 pN	[23]
1 kPa (low)	0.5 pN/nm (high)	BAR and clathrin	130 pN	[23]
1 kPa (low)	0.5 pN/nm (high)	Clathrin	0	[23]
0.2–1 MPa (high)	0	Clathrin	3000 pN	[24]

Differences between yeast and mammals

Turgor pressure in yeast is significantly larger than in mammals, and, therefore, a dynamic actin network is always required for successful CME in yeast [16] but is not necessarily required for CME in mammals. However, actin is required in mammalian CME in conditions where the membrane tension is increased [17]. Recent studies of mammalian CME have revealed that actin is often involved—if not required in some physiological conditions [29,30]. Actin is also involved in clathrin-independent endocytic pathways in mammals [31] but we will not discuss these pathways in this review.

Another major difference is that dynamin is required for membrane scission in mammals [32] but is not required for CME in yeast [8]. Because the precise molecular mechanism of membrane scission is not fully understood, it is possible that dynamin itself is not strictly required for CME in all organisms, especially since dynamin appeared quite late in evolution [33], and key aspects of its function could be performed instead by BAR domain proteins, the actin machinery, and other factors [34,35].

The ease of genetic manipulation in and the handling of yeast has enabled detailed quantitative microscopy studies [8–10,36,37]. In contrast, experimental results from mammalian cells have been difficult to quantitatively interpret due to the presence of redundant isoforms, incomplete knockdown experiments, and variable gene expression profiles across cells and cell lines—although these challenges are being mitigated with new genome-editing tools [38].

Actin-based mechanisms

Many lines of evidence have suggested that the actin meshwork assembled at sites of endocytosis is responsible for producing the forces necessary for membrane deformation [39]. The yeast CME machinery assembles and disassembles very rapidly (~ 20 s) and on a very short length scale (~ 250 nm), posing challenges both for experimental observation and for adapting established theories from other actin systems. Simulations of the dynamic evolution of actin during endocytosis demonstrated that the observed fast actin assembly can be explained by autocatalytic dendritic nucleation of filaments [11,40]. This model also indicated that key steps of Arp2/3 nucleation and filament capping are faster in the cell than previously reported in vitro and that severing of filaments into short pieces (rather than depolymerization alone) is necessary to account for the fast disassembly in 10 s. Thus, while actin’s biochemistry is tightly controlled and concomitant with rapid deformations of the membrane, how this biochemistry is coupled to mechanical utility is unclear. Here, we address models seeking to describe the molecular mechanisms of force production by actin, which are complex and remain unresolved.

Actin filament polymerization

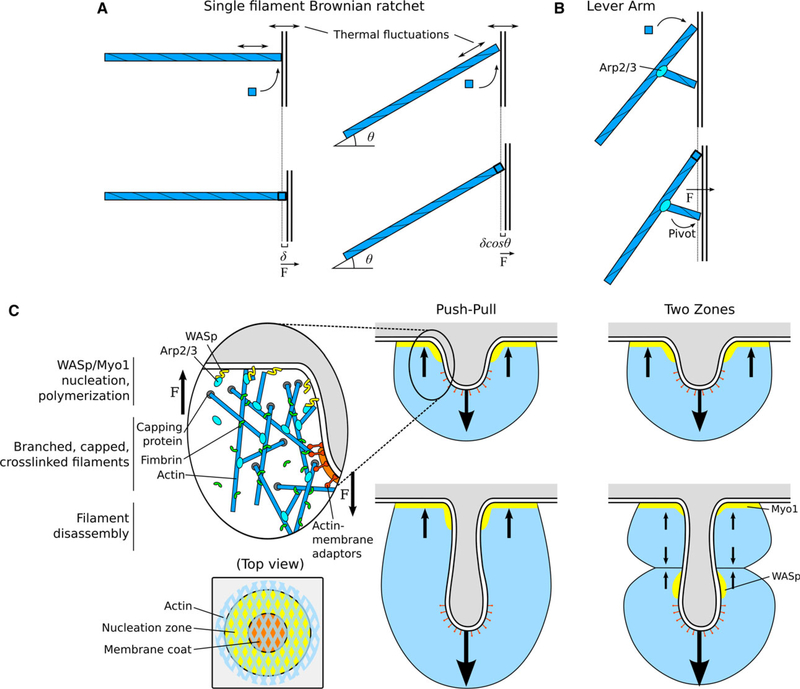
Polymerization of individual actin filaments can generate forces, and can power many forms of cell motility, such as the movement of Listeria monocytogenes and the leading edge of lamellipodia [41,42]. In the Brownian ratchet model, thermal fluctuations can create a gap between the filament’s polymerizing barbed end and the object against which actin polymerizes (Fig. 2A, left), allowing the addition of an actin monomer in that gap, which generates a net force on the object [43–45].

Fig. 2.

Actin force production by polymerization. (A) Brownian ratchet model for force production from polymerization of a single filament. Left: A single filament polymerizing against a barrier or object exerts force related to the single polymerization step distance d. Right: A filament at an angle exerts force related to the step distance dcosh. If the filament is maintained at an angle (e.g., as one branch in a meshwork), the stall force is higher but the velocity of the barrier object is lower compared with the perpendicular filament. (B) Actin polymerization force can be distributed through pivot points. Polymerizing filaments exert force not only at their barbed end but may also generate torque with branched or crosslinked filaments or membrane-bound proteins acting as a lever arm. (C) Schematic of the dendritic nucleation model for the endocytic actin meshwork. Left inset: Force production can be achieved by WASp/Myo1 nucleation at the membrane surface, actin filament branching and polymerization, capping and crosslinking, and attachment to the invaginating CCP tip to transmit force from the growing meshwork. Right: The Push-Pull model proposes an actin meshwork nucleated at the base membrane pushing toward the cytoplasm and attachment to the CCP tip pulling the membrane. Far right: The two-zone model proposes that, as the CCP elongates, two distinct zones of nucleation (by myosin-I and WASp) generate two actin meshworks that push against each other, resulting in pulling the CCP tip toward the cytoplasm. Arrows are drawn to indicate the direction of forces generated and propagated by actin filaments or meshwork.

An actin filament experiencing a load force F from the object reduces its polymerization velocity. This force–velocity relationship is $V=V_{\text{p}}{e}^{(-F\text{δ}/k_{\text{B}}T})-V_{\text{d}}$, where V_p is the polymerization velocity in the absence of force, V_d is the depolymerization velocity, and d is the elongation length of the filament by incorporation of one actin monomer. The first term of this equation describes the negative effect of a load force on the polymerization velocity. Actin polymerization is related to the concentration of monomeric actin by the relation V_p/V_d = c/c*, where c is the free actin monomer concentration and c* is the critical concentration above which polymerization dominates over depolymerization. The stalling force, which represents the maximum force that can be produced from actin polymerization and the force at which the net polymerization velocity vanishes, is F_s = (k_BT/δ) ln(c/c*).

In fission yeast, the cytoplasmic actin concentration is c ~ 20–40 μM [8,46], and for c* ~ 0.11 μM [47] and d δ 2.7 nm, individual actin filaments are predicted to have a polymerization stalling force F_s smaller than 9 pN. However, in vitro measurements of the polymerization stalling force of a single filament are around 1 pN [24,48,49], due to the lower concentration of free actin used in these experiments. We expect actin polymerization force in vivo is closer to the lower estimate of ~ 1 pN than to the upper bound of 9 pN because only a fraction of actin in the cell is free to polymerize due to the abundance of actin-associated protein complexes and cytoplasmic actin oligomers in the cell [50,51].

The previous estimates assumed that actin polymerization applies a force on a surface that is perpendicular to the axis of the filament. If instead the filament has an angle h with respect to the normal to the surface of the object, the force–velocity relationship of actin polymerization becomes $V=\cos \text{θ}\left(V_{\text{p}}{e}^{\left(-F\text{δ}\cos \text{θ}/k_{\text{B}}T\right)}-V_{\text{d}}\right)$ (Fig. 2A, right) [45]. The stalling force F_s is increased by a factor of 1/cosh at the expense of reduced velocity by a factor of cosθ.

Force production from groups of filaments

In yeast cells during endocytosis, the membrane invagination speed is about 12 nm/s and the calculated force required to sustain an elongated tube is ~ 3000 pN [24]. To achieve such a speed and force, assuming the force is equally shared among all the filaments, a population of more than 300 filaments would be needed, all nearly parallel to the membrane. If a more detailed actin population model is considered, where filaments are grouped into “working” filaments and “attached” filaments, and the spatial distribution of actin monomers is explicitly treated [45,52], the required total number of filaments is even higher. This scenario is highly implausible for CME because the required number of working filaments is far higher than the estimated eight growing filaments based on experimental data [11] and because Arp2/3-mediated branching of filaments will broaden the angular distribution. Ongoing modeling efforts will need to account for parameters unique to the endocytic site, such as the rates of nucleation, polymerization, and disassembly, as well as the specific geometries of filaments and the plasma membrane. However, many of these parameters remain to be experimentally measured in the context of CME.

Lever arm

An additional consideration of filament geometry is that the small forces generated by individual polymerizing filaments in a branched network could be amplified through a lever arm mechanism (Fig. 2B). Dmitrieff and Nedelec [53] considered the geometry of a branched filament or otherwise membrane-anchored actin filament in a meshwork, with a long arm polymerizing against the membrane and a short arm acting as a pivot point against the membrane. They proposed that the force produced by polymerization of the long filament would be transmitted by the lever arm to the pivot point, producing an amplified force as a result of the length difference of the two filaments. Such a mechanism could enhance the force output of an actin network without requiring all filaments to be actively polymerizing, but experimental evidence is still needed to determine to what extent this effect might occur.

The “push-pull” model

We have discussed how polymerization of individual actin filaments generates pushing force and how these forces can be amplified in an Arp2/3-branched actin meshwork. The two most potent Arp2/3 complex activators during CME are the C-terminal domain of WASp and myosin-I [54,55]. The intriguing question about endocytosis is precisely how actin polymerization generates forces that pull the plasma membrane toward the cytoplasm, since filaments’ barbed ends are oriented toward the plasma membrane. A number of experimental and theoretical efforts have aimed to understand the geometry and dynamics of the actin meshwork in yeast CME.

Actin nucleation and polymerization appear to be localized to a ring-shaped region on the surface of the membrane surrounding the CCP (Fig. 2C). This actin assembly profile produces forces that push against the plasma membrane and creates a retrograde flow of the actin meshwork toward the cytoplasm, which pulls the CCP via actin-binding proteins in the membrane coat.

The dynamic evolution of the membrane shape during initiation and tubular elongation has been simulated by minimizing the Helfrich bending energy of the membrane, assuming force balance between the pushing and pulling forces acting on the membrane. It is generally assumed that the membrane reaches steady state at each time step, because its relaxation times are on the millisecond timescale. Simulations by Carlsson and colleagues, which treated the actin meshwork as a continuous elastic material, were able to produce a pulling stress as large as 500 kPa on the CCP [25]. However, the result of this study implied that each growing actin filament must produce forces of 15 pN, which is significantly larger than the stalling force of individual filaments, as discussed above. Wang and Carlsson developed another model that coupled simplified actin dynamics with membrane deformation [56]. In this model, actin dynamics consist of nucleation, branching and severing, with nucleation localized only in a ring-shaped region on the plasma membrane. Negative feedback of actin branching on the number of actin nucleators (WASp) resulted in an increased actin density with reduced nucleation. They estimated that the maximum pulling force generated by the actin meshwork was ~ 725 pN, which is still smaller than the required force to initiate invagination.

The push-pull model is supported by experimental observations that WASp and myosin-I are distributed in a ring-shaped region around the CCP base in budding yeast, while the HIP1R homologs (S. cerevisiae Sla2p and S. pombe End4p), which connect actin filaments with the membrane, are concentrated inside the ring [36,57]. Ongoing experimental efforts will help determine how the actin machinery generates forces in CME, with novel geometries or previously unobserved dynamics (such as enhanced rates of assembly or turnover). Given our current understanding, it seems that other non-polymerization-based mechanisms are required to produce the missing force.

The two-zone model

In fission yeast, both WASp and myosin-I are bound to the plasma membrane, but when the CCP elongates, myosin-I remains at the base of the tubule while WASp moves inward [8,58]. These observations led to the hypothesis that two independent actin meshworks could be created, one nucleated by myosin-I at the tubule base and on by WASp along the neck (Fig. 2C, right). While actin filaments elongate, the growing meshworks expand and push against each other, and the WASp-nucleated meshwork transmits the forces to the CCP tip through its attachment via coat proteins, elongating the tubule. This idea is supported by in vivo experiments demonstrating that the presence of a single nucleator is not sufficient to elongate a CCP [58]. Live-cell super-resolution imaging showed that two zones of actin are visible before vesicle scission, and the formation of two zones requires the presence of both Arp2/3 nucleators, WASp and myosin-I [59]. Recent mathematical modeling considering the actin meshworks as a visco-active fluid and using realistic parameters showed that a two-zone model may produce forces in the 1000 pN range (Boris M. Slepchenko, Masoud Nickaeen and Thomas Pollard, personal communication). However, fluorescence microscopy in budding yeast did not detect the inward motion of WASp along the CCP neck [9,36]. Further work will be required to determine whether the twozone model is unique to fission yeast and to test whether the fusion of WASp to fluorescent proteins in budding yeast alters its dynamic localization.

Crosslinking mechanism

The actin filaments at endocytic sites are highly crosslinked by fimbrin and deletion of fimbrin results in significant defects of endocytic internalization in yeast cells [60–62]. The role of fimbrin remains unclear but it has been proposed to rigidify the actin meshwork and allow force transmission [63–65]. Another promising hypothesis is that fimbrin crosslinkers store elastic energy that could be released to drive membrane deformation in the later stages of CME [66]. Actin filaments at endocytic sites are shorter than 200 nm [11,67], which is two orders of magnitude smaller than the persistence length of actin filaments (~ 10 lm). At this length scale, actin filaments behave as virtually unbendable rods, instead of semiflexible polymers as are usually assumed in models of actin filaments in cell motility, cytokinesis, or actomyosin contraction models. Thus, even though the filaments cannot bend, filament helicity and the high fimbrin density lead to highly strained crosslinkers that can store a large amount of elastic energy (Fig. 3A). Indeed, simulations of crosslinked actin meshworks showed that the elastic energy stored in crosslinkers could account for up to 1/6 of the total energy cost of endocytosis if the crosslinkers’ stiffness is high [68]. They further showed that ordered detachment of crosslinkers could generate directed torque. Future theoretical work and simulations may determine how this energy can be used in the context of endocytosis to enhance the forces generated by actin polymerization.

Fig. 3.

Higher order force generation mechanisms. (A) Elastic crosslinkers can store energy. Due to the helical nature of actin filaments, most crosslinkers may be deformed from their optimal conformation, enabling the meshwork to convert chemical binding energy into elastic energy. (B) Models of actin meshwork as an elastic gel may reveal un-accounted-for forces of compression and friction or drag force on the membrane tubule surface. (C) Liquid phase separation mediated by disordered protein–protein interactions may exert force on the membrane surface because the interfacial energy causes the droplet to minimize its surface area for a given volume. Adhesion to the membrane surface pulls the CCP inward as the droplet grows and pushes to adopt a more spherical shape.

The elastic gel model

The mechanical properties of actin meshworks have been extensively studied in the context of bacteria motility, such as Listeria and Shigella. In vitro reconstitution using cell extracts or purified proteins have been critical to compare the different mechanisms of force production of entangled actin meshworks nucleated by the Arp2/3 complex [69,70]. In these experiments, micrometric hard (e.g., beads, rods) or deformable objects (e.g., lipid vesicles, oil droplets) were coated with an activator of the Arp2/3 complex and incubated in a solution of purified proteins or cell extract. After an initial phase where actin built up a shell around the coated object, an actin “comet tail” propelled the micron-size objects with speeds around 5 to 50 nm/s, producing forces around 100 to 1000 pN [71–73]. Some of these experiments using deformable liposomes also demonstrated that friction between the actin meshwork and lipids occasionally created long tubules that eventually snapped into smaller vesicles [71]. Mathematical modeling and later experiments showed that the Brownian ratchet model was not sufficient to explain reconstituted motility [74,75]. Better results were obtained by considering the actin meshwork as an elastic gel that builds up a circumferential tension and/or compressive forces orthogonal to the direction of movement, which are responsible for the observed teardrop shapes of lipid vesicles.

The set of proteins implicated in these motility experiments (actin, Arp2/3 complex, crosslinkers, capping proteins, etc.) is quite similar to the set of proteins required for endocytosis in yeast and therefore these elastic properties may contribute to endocytic invagination (Fig. 3B). However, the dimensions of the endocytic actin meshwork are 1–2 orders of magnitude smaller in space and 2–3 orders of magnitude shorter in time compared to the meshworks considered in these studies. It remains unclear if the results from the elastic gel model could be applied to scales relevant to CME, so future theoretical work should test if these unique geometrical constraints give rise to similar behaviors.

Myosin molecular motors

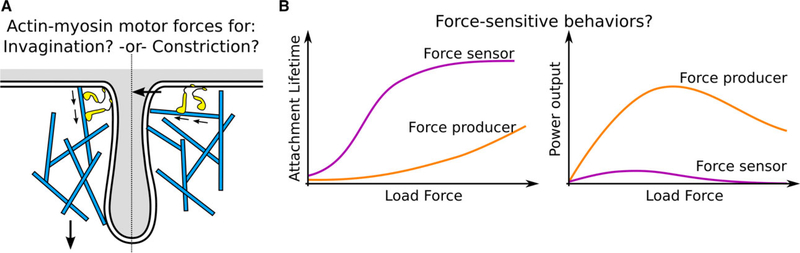
In addition to its nucleation-promoting activity (discussed above), myosin-I may generate force through its motor activity. In domain of the monomeric type-I myosin (Myo3p and Myo5p in S. cerevisiae, Myo1p in S. pombe) is required for endocytosis [55,76,77]. It is thought that myosin-I primarily contributes to elongation rather than scission of the endocytic vesicle [55,78]. However, it remains unclear whether myosin-Is are processive motors or force sensors and precisely how they contribute to endocytosis.

Myosin-Is exert their powerstroke toward the barbed end of actin filaments, producing force directed toward the pointed end. One hypothesis is that myosin-I pushes actin filaments away from the plasma membrane and helps CCP elongation [9,79] (Fig. 4A). Since each myosin-I might produce up to ~ 2 pN of force [80,81], and up to ~ 300 myosin-I molecules are present at each endocytic site in yeast [8], a generous upper bound of force produced by myosin-I motor activity is ~ 600 pN.

Fig. 4.

Myosin force production and force-sensing. (A) Depending on their relative orientation at the CCP base, myosin-I might exert force pushing the actin meshwork toward the cytoplasm (driving elongation) or compressing the meshwork toward the CCP center (driving constriction and scission). (B) Some myosin-I isoforms serve as force producers, increasing their power output under high load. Others act as force sensors, with their motor activity stalling under small load forces and remaining tightly bound under high forces. It is not known what type of behavior describes the myosin-I isoforms which are involved in CME.

Another hypothesis is that myosin-I motor activity increases the stress in the actin meshwork, turning the endocytic actin meshwork into an active elastic gel [82]. In vitro reconstitution of actomyosin networks with type-I or type-II myosins demonstrates that they can generate up to 1 MPa of tensile stress [83–86]. Alternatively, actomyosin contractility might contribute a compressive force on the membrane and pinch the membrane at scission, similar to a contractile ring [78]. However, these ideas are speculative, as it is unclear if the actin filaments are arranged in a geometry that can be compressed (i.e., antiparallel) and myosin-I’s biochemistry and mechanics might be sensitive to force. Future high-resolution imaging of actin and myosin at endocytic sites, with techniques such as cryo-electron tomography or single-molecule fluorescence, might reveal whether the geometry and motions within the endocytic actin meshwork are compatible with these hypotheses.

Generally, type-I myosin motors adjust their actin attachment lifetime, motility, power output, and duty ratio based on the direction and magnitude of force acting against their powerstroke [81] (Fig. 4B). Therefore, myosin-I may serve as a force-sensitive actinmembrane anchor. Little is known about the mechanical properties of yeast myosin-Is and their mammalian homolog, myosin-IE, which participates in endocytosis. In mammals, different myosin-I isoforms are sensitive to forces in different ways (Fig. 4B), either tightening the actin-membrane connection or altering their force production under loads of a few pN, but it is unclear which of these behaviors the endocytic myosin-I exhibits. Single-molecule force measurements on endocytic myosin-Is are needed to distinguish between force-sensitive or force-producing behavior and deepen our understanding of myosin-I’s role in endocytosis.

Membrane-binding proteins and lipid-mediated mechanisms

Many other mechanisms contribute to membrane bending, elongation, and scission during CME by lowering the barriers to pit elongation and scission, while some directly produce forces and actively deform the membrane. Binding of the curved surface of a protein or oligomer of proteins to a membrane can cause the membrane to adopt the curvature of this protein scaffold if the membrane-binding energy exceeds the energetic cost of membrane bending [20,87,88]. Membrane bending can also be achieved through steric crowding of large protein domains [89], or through the wedgelike insertion of amphipathic helices or other motifs [90]. In addition to favoring increased membrane curvature and lowering the barrier for CME pit invagination, protein scaffolds also limit lipid diffusion and create frictional forces [35], and the dynamin scaffold can actively constrict to induce membrane scission [34,91].

Membrane bending by clathrin

The clathrin cage that surrounds nascent endocytic vesicles is a polyhedral arrangement of triskelion subunits. Each triskelion is composed of three clathrin heavy chains and three clathrin light chains [2,92,93]. In yeast, clathrin appears to be important for regulating the vesicle’s size but not the membrane curvature, suggesting that clathrin is not strictly necessary for initial membrane bending or elongation [60,94,95]. However, clathrin is sufficient to induce vesicle budding in vitro [96,97]. Polymerization into a clathrin cage may yield up to ~ 40 k_BT of energy per clathrin triskelion [96,98,99], which, given that around 13 triskelia are assembled in fission yeast CME [8], suggests that up to 500 k_BT of energy could be generated by clathrin cage assembly. This value is close to the required membrane bending energy so clathrin cage formation might contribute to membrane bending for low membrane tensions. However, the observation of flat clathrin lattices in cells suggests that the polymerization energy does not directly lead to membrane curvature without contributions of other membrane-deforming mechanisms [95,100,101]. Thus, clathrin may contribute to—though not dominate—membrane bending in vivo.

Membrane bending by BAR domains

The BAR (Bin/Amphiphysin/Rvs) domains are a group of crescent-shaped membrane-binding proteins that can both sense and generate membrane curvature. Extensive studies in vivo, in vitro, and in silico have investigated the general mechanisms of BAR domains and their specific contributions to CME [102–104]. At low protein concentrations, most BAR domains sense curvature by binding to membranes that display the curvature that matches their preferred curvature. At high protein concentrations, most BAR domains generate membrane curvature by imposing a nonzero spontaneous curvature, typically around 15–40 nm radius [105,106] (Fig. 5A). In CME, several of the early membrane coat proteins contain moderately curved F-BAR domains (Fes-CIP4 homology BAR domain: Syp1/FCHo1–2, Bzz1/syndapin, Cdc15/Hof1/ PSTPIP1–2), while several proteins involved in membrane scission contain more highly curved N-BAR domains (N-terminal amphipathic helix BAR domain: Hob1–3/Rvs167–161/endophilin-amphiphysin) [107].

Fig. 5.

Membrane bending and scission. (A) Scaffolds of clathrin and BAR domain proteins can induce membrane bending by changing the spontaneous curvature of the membrane. (B) BAR domains stabilize the tubule neck but can also mediate scission by limiting lipid diffusion and creating friction forces as the tubule is pulled toward the cytoplasm. (C) Steric crowding of bulky domains favors membrane bending if there is an asymmetry of lateral pressure (left); however, the extracellular domains of CCP cargo will also be crowded in the CCP lumen, generating force that opposes invagination (right). The net energy contribution to CME will be determined by the relative sizes and densities of the intracellular and extracellular domains. (D) Dynamin assembles at the membrane tubule neck. Binding of GTP induces the helical oligomer to undergo a conformational change driving constriction, reducing the radius and elongating along the tubule axis. GTP hydrolysis leads to both scission of the membrane neck and disassembly of the dynamin scaffold (not shown).

Calculations of typical BAR domain surfaces estimate the magnitude of binding energies is around 6 to 12 k_BT per protein [87]. However, their ability to induce curvature depends on the membrane tension. In vitro experiments with the endophilin N-BAR domain show that for a low-tension membrane, tubulation occurs at a protein density of approximately 650 μm², which is equivalent to 15 proteins on a patch of membrane the size of a CCP [108]. At higher membrane tension (0.1 pN/nm), tubulation requires a density of 3000 lm², which is equivalent to about 70 proteins on a CCP, or about 10% of the membrane surface area [108]. Importantly, tubulation was not observed at membrane tensions higher than 0.25 pN/ nm [108].

These results suggest that BAR domains may be able to drive membrane bending in mammalian CME in some conditions, since membrane tension ranges from 0.003 to 0.3 pN/nm [109]. However, BAR domains are likely not sufficient to drive membrane invagination in yeast since the turgor pressure adds a much higher barrier (Table 2). This argument is supported by correlative light and electron microscopy studies of yeast CME indicating that plasma membrane bending does not begin until the actin assembly phase [110].

Molecular crowding

Contrary to the purified systems used in vitro, cell membranes are densely crowded with proteins. Membrane-associated proteins constitute around two-third of the mass of cellular membranes [111,112]. Steric clashes of bulky membrane-associated proteins exert lateral pressure, favoring membrane curvature that relieves any asymmetry [89] (Fig. 5C). Crowding can induce tubulation and scission of membranes in vitro, even with proteins containing cytoplasmic unstructured domains [113,114]. However, extracellular proteins in the cavity of the developing CCP also exert steric forces, countering those produced by cytoplasmic proteins. Above a certain point, bulky cargoes are excluded from the nascent pit [115]. The extreme case of maximal crowding at equal density on both faces of the membrane could double or triple the total energetic cost of forming a vesicle [116]. For crowding to have a major positive effect on CCP and vesicle formation, the cytoplasmic face would have to be extremely crowded and the extracellular face would have to be very sparse, but it is difficult to measure the local protein density in cells. Even if the specific force contributions are unclear, the fact that the cell membrane is extraordinarily crowded complicates the translation of results from theoretical models and reconstituted systems. Future modeling work should attempt to consider this factor, but further experimental characterization of cell membranes at endocytic sites will be needed to determine the true extent of crowding.

Other membrane curvature-generating mechanisms

Other curvature-inducing protein domains in endocytosis include ENTH (epsin N-terminal homology: epsin/ Ent1–2, Yap18/Yap1801–2/PICALM) and ANTH (AP180 N-terminal homology: Yap18/Yap1801–2/ PICALM, Sla2/End4/Hip1-Hip1R) domains that form scaffolds on the plasma membrane [117,118]. N-BAR and ENTH domains further induce curvature by wedging their amphipathic helices into the bilayer surface [20,119]. This helix insertion adds to the membranebending forces and contributes to scission. Many of these curvature-generating scaffolds also contain protein-interaction domains that enable other force production mechanisms—for example, Syp1/FCHo and Bzz1/ Syndapin recruit WASp to localize actin nucleation [58].

Membrane scission by BAR domains

BAR domains play a different role in membrane scission. In fact, protein scaffolds stabilize the highly curved tube (Fig. 5B). In vitro studies showed that the pulling force required to maintain a membrane tube from a liposome (around 20 to 50 pN depending on the tension) falls to near zero upon binding of an endophilin scaffold [120]. However, if force is applied to rapidly extend the BAR domain-coated tubule, the protein scaffold acts as a barrier to lipid flow and creates friction on the membrane, leading to scission [35], whereas uncoated tubules do not undergo scission even at excessive pulling forces [121]. Although the pulling speeds used in these experiments were an order of magnitude higher than the observed rate of tubule elongation in CME, this friction-mediated scission mechanism is likely a significant contributor to fission yeast CME and in clathrin- and dynamin-independent endocytosis in mammalian cells. Further experiments should aim to test these mechanisms in vivo where the membrane and protein scaffolds are much more complex and to dissect the interplay with other scission mechanisms such as dynamin.

Membrane scission by dynamin

In mammals and many eukaryotes, scission of the membrane neck requires the GTPase dynamin. Dynamin assembles into a helical oligomeric scaffold around the neck of the CCP at the late stages of CME [32,91]. Upon GTP binding, the oligomer twists, which reduces the radius of curvature and extends the length of the scaffolded tube, and then, GTP hydrolysis triggers membrane scission and disassembly of the dynamin scaffold (Fig. 5D). Precisely how GTP hydrolysis triggers membrane scission is debated but several plausible models have been proposed: instability at the boundary of the coated and uncoated membrane, collapse of the high-curvature tubule after the dynamin scaffold disassembles, or linear tension exerted by the extension of the tubule coat [122].

Structural studies [123,124] and fluorescence imaging in mammalian cells [125,126] showed that fewer than two full turns of the helical oligomer (26 to 40 dynamin molecules) are sufficient to carry out scission in vivo. In vitro studies indicate that long dynamin scaffolds can generate very high torque, 700 to 1000 pN*nm [127], but it is unknown how much force is exerted by the smaller one- to two-turn helical oligomers that exist in cells for CME. The energy of GTP hydrolysis (if one GTP is hydrolyzed per dynamin molecule) yields a maximum of about 100 k_BT of mechanical energy from 15 molecules of dynamin, which is sufficient to overcome the barrier of the membrane shape transition for scission [127].

Unexpectedly, no dynamin homolog is observed in fission yeast CME [8]. The budding yeast dynamin-like protein Vps1 has been reported to be involved in CME and its deletion causes defects in the timing of recruitment of several endocytic proteins [128], but other studies report that Vps1 is only rarely recruited to CME sites and its deletion mimics (but does not enhance) the defect of deleting the amphiphysin homolog Rvs167 [129]. These reports suggest that dynamin is not strictly required for membrane scission and instead the BAR domain proteins endophilin and amphiphysin (Hob1/3 in fission yeast, Rvs161/167 in budding yeast) drive membrane scission in yeast CME, as discussed above. However, it remains unclear how these and other mechanisms generate the very large mechanical forces supplied by dynamin in other organisms for membrane scission. The complex interplay of actin, BAR domain proteins, and dynamin for their recruitment, regulation, and mechanical contributions to scission are still not fully resolved but provide an exciting avenue for ongoing research [34,122].

Membrane line tension

Different lipids may segregate to form distinct phases and generate an interfacial tension within the membrane. This interfacial tension, or line tension, destabilizes the membrane shape and could facilitate budding and scission of the vesicle [130,131]. Additionally, dynamin and BAR proteins could act as barriers to lipid flow on the membrane to facilitate phase separation of lipids into tube region and vesicle region [34,132,133]. In model membrane systems, line tension generates forces on the order of 0.1–10 pN, constricting the tubule [134,135], but in complex systems with many species like the cell plasma membrane this value is likely to be significantly lower. Direct experimental observation of membrane phase separation during endocytosis in vivo is missing, and while it remains a technically challenging feat, such observations might be enabled by novel advances in lipid-specific fluorophores or super-resolution microscopy techniques. Even if it is physiologically relevant, it appears that line tension only has a minor role in producing the required force for CME.

Other putative mechanisms

Liquid phase separation

Phase-separated liquid droplets are regions with higher local concentrations of components within the structure compared to without. Droplets form when there are multivalent interactions between components, such as between proteins with modular protein-interaction domains, high charge densities, or intrinsically disordered regions [136,137]. Recent work suggests that droplets may form at endocytic structures through interactions between intrinsically disordered prion-like domains, which are found within several endocytic coat proteins [138,139]. Depending on the composition of the droplet, its surface tension might be large and the droplet will be viscoelastic [137]. Such a droplet will exert force on the membrane surface because, in order to minimize its membrane and cytosolic interfacial energy, the droplet minimizes its surface area for a given volume [139]. Adhesion to the membrane pulls the CCP inward as the droplet grows and pushes to adopt a more spherical shape (Fig. 3C). The droplet’s interfacial energy is favorable up to an invagination depth of ~ 80 nm, close to the range that the CCP moves before scission (~ 100 nm) [110,140], totaling ~ 1000 k_BT [139]. However, the interfacial energy minimum is reached at an invagination depth of ~ 40 nm, which falls short of the expected invagination depth [139]. Furthermore, it remains unclear exactly what causes, disrupts, maintains, or contributes to phaseseparated droplet formation within endocytic structures and it is especially difficult to experimentally probe the dynamic stability of droplets in endocytosis, given that the process is out of equilibrium and completed within seconds. Additional experiments, perhaps on stalled endocytic patches, are needed to probe whether the endocytic proteins indeed behave as a viscoelastic, phase-separated droplet and to determine whether different stages of endocytosis have different mechanical properties.

Local turgor pressure drop

Yeast cells maintain high concentrations of osmolytes such as glycerol, creating turgor pressure which pushes the membrane outward against the cell wall. Since the turgor pressure is proportional to the difference in concentrations of the solute between the inside and outside of the cell, the turgor pressure could be reduced if the membrane was permeable to that solute. It has been proposed that the glycerol concentration gradient could be locally equalized around individual sites of endocytosis and, thus, the turgor pressure locally reduced [141]. If an endocytic membrane patch of 45 nm diameter contained as many as 60 glycerol channels, the resulting glycerol transport could locally reduce the turgor pressure by up to 50% [141]. If the turgor pressure were reduced so drastically, much less than 3000 pN would be required for endocytosis. However, it is not clear whether glycerol channels do localize to endocytic sites, nor is it clear how the local opening of channels could be regulated throughout the stages of endocytosis. Even though the deletion of the glycerol transporter Fps1 causes a failure of ~ 40% of endocytic events [16], it is unclear if those failures are due to a global increase of turgor pressure or a loss of local turgor pressure modulation. A 50% reduction in local turgor pressure is significant, as it would reduce the amount of force required for invagination by ~ 650 pN. However, there is little support for this model and convincing experimental evidence will be difficult to acquire.

Summary

A wide variety of mechanisms are available to generate the forces needed to remodel the cell membrane to form endocytic vesicles (summarized in Table 3). While there are multiple mechanisms whose disruption can cause CME to fail, no single mechanism is solely responsible for generating the full magnitude of force required for CME in yeast. Several components add small or speculative amounts of force (BAR domains, clathrin, crowding, membrane line tension, liquid droplet, turgor pressure drop) but when combined in the context of the cell, they may make up a significant proportion of the overall required force for CME. The mechanisms that could contribute large amounts of force (actin polymerization, myosin, dynamin) have been extensively studied in vitro, but it remains unclear how the molecular organization leads to efficient and robust membrane remodeling in CME in vivo.

Table 3.

Summary of force production mechanisms in CME.

Mechanism	Stage(s)	Proteins or lipids involved*	Force or energy contribution (pN or kBT)**	References
Actin-based
Push-Pull	Initiation, elongation, scission?	Actin, WASp, Myo1, etc. Membrane anchors (End4/Sla2, etc.)	100–700 pN	[25]
Two zones	Elongation, scission?	Actin, WASp, Myo1, etc. Membrane anchors (End4/Sla2, etc.)	~ 1000 pN	[58,59] Slepchenko et al.***
Crosslinking	Elongation?, scission	Actin, Fimbrin	~ 800–8000 kBT	[68]
Elastic gel	Elongation, scission	Actin, Fimbrin	100–1000 pN	[71,73,74]
Myosins	Elongation, scission	Myosin-1e: Myo3/5 (S.c.), Myo1 (S.p.)	0 – 600 pN	[79,81]
Membrane-based
Clathrin	Initiation	Clc1, Chc1	~ 500 kBT	[8,96,98]
BAR domain proteins	Initiation, elongation, scission	Syp1/FCHo1–2, Bzz1/syndapin, Cdc15/Hof1/PSTIPIP1–2 Hob1–3/Rvs167–161/endophilinamphiphysin	20–50 pN for tube elongation, Lowers scission force to ~ 30 pN	[35,120]
Crowding	Initiation, elongation, scission	Any (Ent1/epsin, Yap18/Yap180/AP180)	1000 to 1000 pN?	[89,113,116]
Dynamin	Scission	Vps1(S.c.), none (S.p.)	~ 100 kBT	[127]
Line tension	Scission	Lipids	0.1–10 pN	[134,135]
Other putative mechanisms
Local turgor pressure drop	Initiation, elongation	Fps1 or other channels?	~ 650 pN	[141]
Phase-separated droplet	Initiation, elongation	Prion-like domains of Sla1/2, Ent1/2, Yap1801/2, etc.	~ 1200 kBT	[139]

^*See Table 1 for listing of protein names in fission yeast, budding yeast, and mammals.

^**Force production (pN) is listed for mechanisms where the direction and force output are clearly understood, or an energy amount (k_BT) is given when it is unclear how the energy is converted to mechanical force.

^***Boris M. Slepchenko, Masoud Nickaeen and Thomas Pollard (personal communication).

Perspectives and future directions

Though it appears that enough total energy could be found across the various proposed mechanisms, no single model has successfully integrated the multiple plausible mechanisms to globally account for all of the energetic barriers to CME. Theoretical estimates sometimes assume the most generous conditions from a wide range of possible parameters or invoke speculative mechanisms to lower the energy requirements, which enable their favored mechanism to produce enough force for CME on its own. However, these assumptions and simplifications are seldomly validated experimentally. In addition, the contributions from the many minor force-producing mechanisms are often simplified or ignored, precluding a wholistic view of the force generating mechanisms at play during CME. Thus, the coordination across these mechanisms throughout the process of CME remains to be resolved.

Some of these open questions will be addressable by advances in modeling or experimental methods. Increasingly detailed simulations may reveal novel mechanisms of force production such as higher order and emergent properties of actin meshwork dynamics. Future theoretical work should attempt to consider complications such as the spatial or temporal differences in properties of the plasma membrane or the changes in activity of endocytic proteins due to protein post-translational modifications, for example. In addition, the magnitudes and directions of forces produced by individual protein modules likely change during the course of CME, but since these forces remain technically challenging to directly measure in cells it has been unclear whether and how to account for this behavior in theoretical models. Future simulations should attempt to address the changes in different dominant force production mechanisms at different stages of CME. For instance, at the early stage when the membrane is flat, the organization of actin filaments to generate forces toward the cytoplasm likely differs from the later organization of actin filaments at the time of scission, perhaps producing compressive forces by other mechanisms. These changes could be driven by membrane geometry or biochemical factors, and likely depend on complex crosstalk and feedback loops within the system.

Likewise, novel experimental approaches should aim to overcome the limitations that have prevented direct measurements of several valuable quantities and parameters, such as the amount of hydrolyzed ATP and GTP, the local membrane tension at sites of CME, and the molecular orientations and forces of actin filaments and myosin motors. Electron and super-resolution fluorescence microscopy may suggest previously unobserved architectures and dynamics of the actin and membrane-scaffold protein networks. Quantitative microscopy and new observations could revise the limits of known mechanisms. For example, if the actin meshwork turns over multiple times during CME, which has been proposed [4,11,39] but not yet directly observed in physiological conditions, such an enhanced filament polymerization rate would enable a greater amount of force than what has been calculated for the currently known number of filaments.

Even if no single mechanism is sufficient to fully generate the required forces, the cooperation of multiple mechanisms may provide a more robust solution for the cell to achieve successful CME in a variety of conditions. Fully understanding the complexity of CME and the synergy between multiple coexisting force production mechanisms remains challenging, but we are confident that ongoing experimental and theoretical work will continue to illuminate this vital cellular process.

Abbreviations

BAR

Bin/Amphiphysin/Rvs

CCP

Clathrin-coated pit

CME

Clathrin-mediated endocytosis