Multiparametric Biomechanical and Biochemical Phenotypic Profiling of Single Cancer Cells Using Elasticity Microcytometer

Abstract

Deep phenotyping of cancer cells at the single-cell level is of critical importance in the era of precision medicine to advance understanding of the precise relationship between gene mutation and cell phenotype and to elucidate biological nature of tumor heterogeneity and their potential biological and clinical implications. Existing microfluidic single-cell phenotyping tools, albeit their high-throughput, high-resolution operation, are limited to phenotypic measurements of 1 – 2 selected morphological and physiological features of single cells. To address the critical need for multiplexed, informative phenotyping of live single cancer cells, herein we reported a microfluidic elasticity microcytometer for multiparametric biomechanical and biochemical phenotypic profiling of free-floating, live single cancer cells to obtain quantitative information of cell size, cell deformability / stiffness, and expression levels of surface receptors simultaneously for the same single live cancer cells. The elasticity microcytometer was implemented for single-cell measurements and comparisons of four human cell lines with distinct metastatic potentials and derived from different human tissues. An analytical model was developed from first principles for the first time to effectively convert cell deformation and adhesion information of single cancer cells encapsulated inside the elasticity microcytometer to cell deformability / stiffness and surface protein expression. Together, the elasticity microcytometer holds a great promise for comprehensive molecular, cellular, and biomechanical phenotypic profiling of live cancer cells at the single cell level, critical for studying intra-tumor cellular and molecular heterogeneity using low-abundance, clinically relevant human cancer cells.

INTRODUCTION

Cancer is the leading cause of death among men and women under 85 years of age in the United States [1]. Despite improvements in detecting and treating primary tumors, long-term survival of cancer patients is compromised by the development of metastatic lesions [2, 3]. While metastatic cancer is sometimes apparent at the time of diagnosis, most common metastatic lesions appear after a prolonged period of time following primary therapy [4, 5]. Although post-operative adjuvant therapy is designed to eradicate residual disease, secondary tumors in distant tissues can successfully evade existing therapeutic options for metastatic cancer. Thus, for cancer, there is an urgent need for new prognostic markers to distinguish tumors that will remain indolent, latent, or be eradicated from those that will metastasize.

It has now become well recognized that one of the paramount challenges facing the field of cancer prognosis is the high degree of intra-tumor cellular and molecular heterogeneity [6, 7]. With rare exceptions, spontaneous tumors originate from a single cell. Yet, at the time of clinical diagnosis, the majority of human tumors display startling heterogeneity in many cellular features, such as cell morphology, expression of cell surface receptors, and proliferative and angiogenic potential [8, 9]. Illustrating the full complexity of tumor phenotypic heterogeneity is critically important in determining and uncovering the meaning of heterogeneous features of tumor and their implications for cancer prognosis, therapeutic responses, and patient stratification.

Cell deformability under an applied load, or cell stiffness, plays critical roles in cancer metastasis [10–12]. It has been postulated that mechanical property changes in invading cancer cells may be necessary for them to squeeze into vessels (intravasate) and metastasize [13–16]. Using an optofluidic setup to deform floating cancer cells, Guck et al. [11] and Lincoln et al. [17] have first shown a significantly greater cell stiffness associated with normal breast epithelial cells (MCF-10A) when compared to benign breast carcinoma cells (MCF-7). Importantly, similar observations have been obtained recently by Remmerbach et al. [18] and Cross et al. [12] using atomic force microscopy for primary colon, lung and breast cancer cells extracted from human cancer patients. Furthermore, a link between increased cancer cell deformability and metastatic potential or invasiveness, as measured by Matrigel invasion assays, has been found by Swaminathan et al. and Coughlin et al. for patient-derived ovarian and lung cancer cells [18, 19]. Together, these studies have highlighted the usefulness of intrinsic cell stiffness as a cellular biomarker in a label-free manner that is very different from current immunohistological methods for cancer diagnosis and prognosis.

Over the past decade, there is a significant interest in the research fields of microfluidics and Bio-microelectromechanical systems (BioMEMS) in developing integrated microscale, high-throughput, high-resolution devices and platforms for rapid and precise quantifications of morphological and physiological features of free-floating mammalian cells down to the single-cell resolution [20–22]. Leveraging unique measurement methodologies, these microscale cell phenotyping tools have been successfully implemented for measurements of cell size [23], cell density / weight [24], cell deformability / stiffness [25–27], expression of cell surface receptors [28, 29], and secretion profiles [30–32] of clinically relevant human cells down to the single-cell resolution. However, the unique physical mechanisms employed by these microscale cell phenotyping devices for cell phonotypical measurements have also limited the applicability of these tools for measurements of only 1 – 2 selected morphological and physiological features of single cells albeit with high-throughput and high-resolution.

The recent excitement of precision medicine for cancer using single-cell level genomic information further require deep phenotyping of cancer cells down to the single cell level so as to help cancer biologists develop an understanding of the precise relationship between gene mutation and cell phenotype and thus tumor heterogeneity and their potential biological and clinical implications. To address the critical need for multiplexed, informative phenotyping of live single cancer cells, herein we reported a microfluidic elasticity microcytometer made of poly-dimethylsiloxane (PDMS) for high-sensitivity, multiparametric biomechanical and biochemical phenotypic profiling of free-floating live single cancer cells. The elasticity microcytometer contained arrays of funnel-shaped confining microchannels that were functionalized with specific antibodies against target cell surface antigens to trap and deform free-floating live single cells under precisely regulated hydraulic pressures. Cell trapping and deformation of each single cancer cell within confining microchannels were recorded and analyzed using analytical models developed from first principles to obtain quantitative information of cell size, cell deformability / stiffness, and expression levels of surface receptors simultaneously for the same single live cancer cells. The microfluidic elasticity microcytometer was implemented for single-cell measurements and comparisons of four human cell lines with distinct metastatic potentials and derived from different human tissues. Data obtained from this work suggested that the microfluidic elasticity microcytometer could serve as a critical component for comprehensive molecular, cellular, and biomechanical phenotypic profiling of live cancer cells at the single cell level, holding a great promise for studying intra-tumor cellular and molecular heterogeneity using low-abundance, clinically relevant human cancer cells such as circulating tumor cells (CTCs) or cancer cells obtained from fine needle biopsy.

RESULTS AND DISCUSSION

Design of elasticity microcytometer

We designed and fabricated the elasticity microcytometer to quantitatively measure both elasticity (or stiffness) and surface protein expression of free-floating, live single cancer cells. The elasticity microcytometer contained two regular arrays of 40 parallel, funnel-shaped confining microchannels with the channel width linearly decreasing from 32 μm at the channel entrance to 6 μm at the channel exit (with the channel wall tilt angle θ = 2.48º) (Fig. 1). These confining microchannels had a uniform height of 40 μm. Close to the device flow inlet, an array of blocking pillars was incorporated to mechanically push floating cells injected into the device toward the center of flow stream (Fig. 1a). Driven by a constant hydraulic pressure, free-floating, live single cancer cells then entered and flew along individual confining channels (Fig. 1b). Since epithelial cells (including both normal and cancerous ones) are normally larger than confining channel exit, the cells would eventually contact channel side walls and deform before trapped inside the confining channels (Fig. 1b). Cell penetration length L, defined as the distance between confining channel entrance and cell settling position, was recorded and analyzed for quantitative measurements of cell elasticity or stiffness at the single-cell level.

Figure 1.

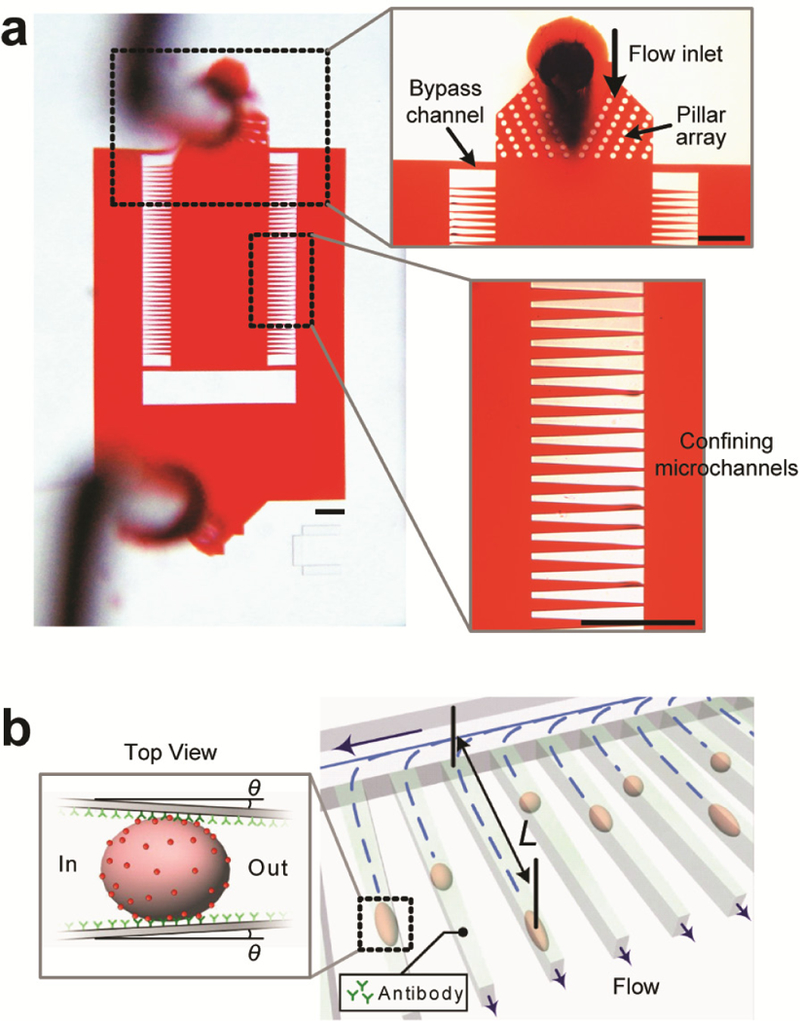
Design of elasticity microcytometer. (a) Micrographs showing layout of the elasticity microcytometer, which contained two regular arrays of identical, funnel-shaped confining channels to direct and trap live, single cancer cells. Floating single cancer cells injected into the device first passed through an array of focusing pillars (upper inset) before flowing into and becoming trapped at individual confining channels (lower inset). Scale bars, 300 µm. (b) Cell deformability and membrane protein expression were determined by measurements of penetration length L of individual cancer cells within confining channels under a constant hydraulic pressure. θ denoted the tilt angle of tapered confining channels relative to channel length direction. For inert channels coated with pluronics F-127 (see Methods), cell trapping was dictated by steric interactions of cancer cells with confining channels, resulting in L completely determined by cell size and deformability. To quantify cell surface protein expression, confining channels were functionalized with monoclonal antibodies targeting specific surface proteins. Adhesive covalent interactions between cell surface proteins and antibodies depended on both the number of covalent interactions and their bond strength, leading to a higher hydraulic pressure needed for detaching and flushing out cancer cells from confining channels.

Within the elasticity microcytometer, two bypass channels were added to the two sides of each of the confining channel arrays to ensure a steady flow condition within the device (Fig. 1a). Dimensions of bypass channels were designed to ensure a negligible fluidic resistance R_side of bypass channels compared to that of confining channels R_confining (R_side = 3.6 × 10⁻⁵ MPa·s/mm³ vs. R_confining = 8.2 × 10⁻² MPa·s/mm³, values obtained by simulation). Cell encapsulation within a confining channel could result in a maximal value of R_confining ~ ∞ under a full blockage condition within the confining channel. The overall fluidic resistance R_overall of the confining channel array would thus fall between 1 / (40 / R_confining + 2 / R_side) ≤ R_overall ≤ 1 / [(40 – N_encap) / R_confining + 2 / R_side], where N_encap denoted the number of confining channels with single cells encapsulated. R_overall varied only slightly (< 1 %) between 1.785 × 10⁻⁵ MPa·s/mm³ and 1.8 × 10⁻⁵ MPa·s/mm³, supporting the effectiveness of bypass channels to provide a steady flow condition for confining channels. It should be noted that when a cell flew into a confining channel, significant increase of fluidic resistance of that individual confining channel R_confining would result in a decreased flow rate along the confining channel, preventing other cells entering and thus encapsulation of multiple cells in the same channel (Fig. S1).

As a proof of concept, in this work epithelial cadherin adhesion molecule (EpCAM) was selected as a target cell surface antigen to demonstrate utility of the elasticity microcytometer for quantitative measurements of expression of cell surface proteins. EpCAM has been widely considered as a diagnostic and prognostic biomarker for some carcinomas [33] given its heightened expression in tumorigenic cancer cells in colon [34], gastric, breast [35, 36], lung, prostate [37], bladder [38], pancreas [39], ovarian [40] and cervical squamous epithelia [41]. Clinical studies have also shown that cancer patients with higher EpCAM expression tend to have a shorter survival [37] and lower survival rates [42]. In fact, an EpCAM-specific antibody called Catumaxomab has been approved by the European Union as a certified breast cancer therapeutic drug [43]. Although detailed molecular mechanism(s) underlying EpCAM function in tumor development and progression remains elusive, in vitro studies have shown that down-regulation of EpCAM expression by siRNA inhibits proliferation, migration, and invasion of some breast cancer cell lines [44]. Likely, over-expression of EpCAM in cancer cells is a common behavior of metastatic cells to support their proliferation, migration, self-renewal, invasiveness, anchorage-independent growth [45], and reduced cadherin-mediated cell-cell adhesion [46].

To quantitatively determine EpCAM expression of cancer cells, inner surfaces of the confining channel array were functionalized with monoclonal antibodies against EpCAM (Fig. 1b and Methods). Individual EpCAM expressing (or EpCAM+) cancer cells trapped inside confining channels would adhere to channel walls within a few min after cell encapsulation. Strength of cell adhesion depended on EpCAM expression, quantification of which was conducted by gradually increasing hydraulic pressure till encapsulated cancer cells were flushed out of confining channels. Altogether, design of the elasticity microcytometer allowed efficient, multiplexed quantitative measurements of both biomechanical and biochemical phenotypes (cell size, stiffness or deformability, and surface protein expression) of live cancer cells at the single-cell level.

Fluidic simulation of confining channel with a single cell encapsulated

Penetration distance L of a single cell with an undeformed cell diameter D_cell determined both deformed cell shape and stress (tensile and shear stresses) distribution on the cell, important characteristics related to cell stiffness. Given the small tilt angle of the confining channels (θ = 2.48º), deformed cell shape of a single cell encapsulated in the confining channel could be reasonably approximated by the Hertz’s and Tatara’s theories [47]. Since cell surfaces in contact with confining channel walls could be reasonably assumed to be spherical due to surface tension of cell membrane, the deformed cell shape for a single cell encapsulated in the confining channel could be approximated as a sphere with a diameter of D_deformed with its top and bottom roofs each chopped for a length of (D_cell – W_deformed) / 2; here W_deformed was the cell width at the penetration distance L, and W_deformed = W_out + (W_in − W_out)L / L_channel, where W_in was channel inlet width, W_out was channel outlet width, and L_channel was channel total length (Fig. 2). Assuming a constant cell volume, D_deformed could be considered as a function of L and D_cell using the relation [47]

$$\frac{4}{3}\pi {\left(\frac{D_{cell}}{2}\right)}^3\approx 2\pi {\left(\frac{D_{deformed}}{2}\right)}^2\left(\frac{W_{deformed}}{2}\right)-\frac{2}{3}\pi {\left(\frac{W_{deformed}}{2}\right)}^3\cdot$$ (1)

Therefore, we obtained

$$D_{deformed}\approx {\left[\frac{2D_{cell}^3}{3W_{deformed}}+\frac{W_{deformed}^2}{3}\right]}^{1/2}\cdot$$ (2)

With defined D_cell and L, D_deformed was calculated using Eq. (2) for an encapsulated cell at penetration distance L in a confining channel, which was further used in fluidic simulations with commercially available software (COMSOL Multiphysics 4.2) to compute relevant flow characteristics, including flow velocity and hydraulic pressure profiles around an encapsulated cell (Fig. 3a).

Figure 2.

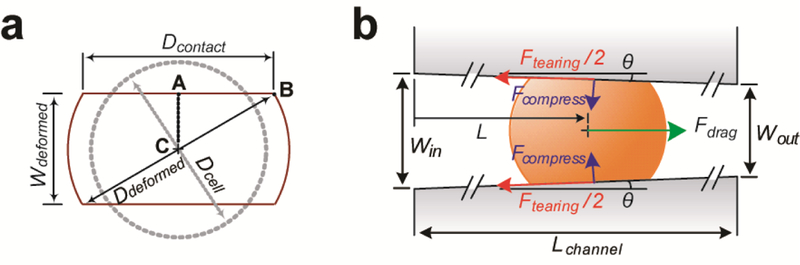
Theoretic analysis of a floating spherical cell encapsulated in a funnel-shaped confining channel. (a) Simplified geometrical representation of a single cell encapsulated in a confining channel. D_contact: diameter of cell contact area, W_deformed: width of a deformed cell, D_deformed: diameter of a deformed cell, and D_cell: diameter of an undeformed cell. (b) Free body diagram showing a cell settling inside a confining channel at a penetration length of L under a horizontal drag force F_drag. W_in: channel inlet width, W_out: channel outlet width, θ: angle of tapered channel relative to the channel length direction, L_channel: channel total length, F_tearing: tearing force acting on the cell, F_compress: compressive force acting on the cell by channel wall.

Figure 3.

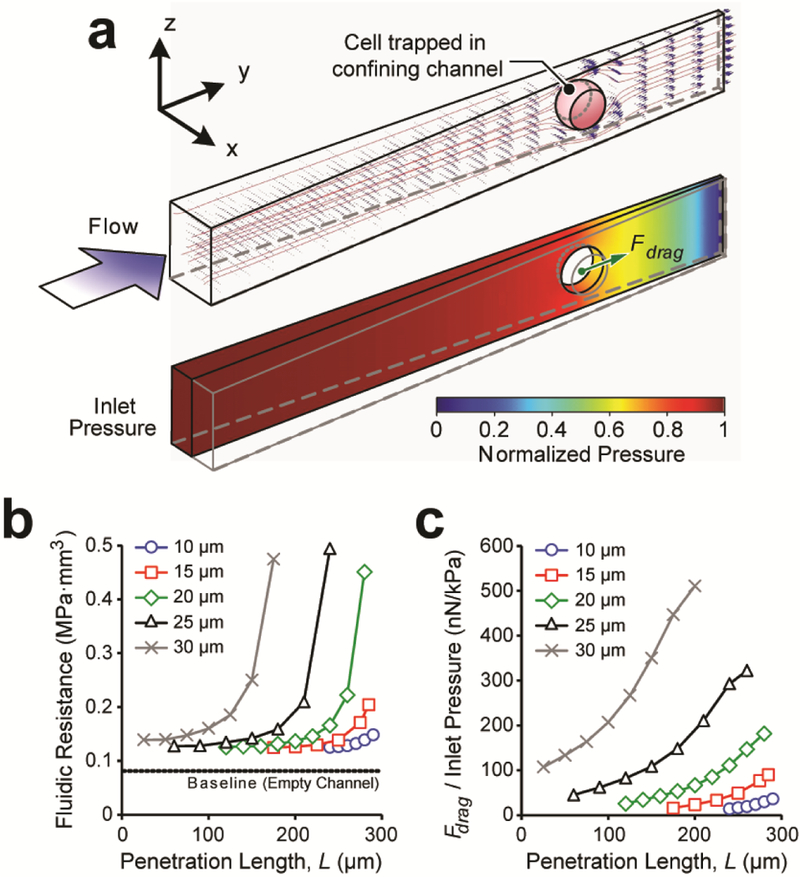
Fluid simulation of a single cell encapsulated in a funnel-shaped confining channel. (a) Representative computation model showing numerical simulations of flow velocity (upper) and pressure (lower) profiles in the confining channel. Shape and position of each cell were computed first using the Hertz’s and Tatara’s theories. (b) Flow resistance R_confining of a confining channel with a single cancer cell trapped as a function of cell diameter D_cell and penetration length L. (c) Drag force F_drag acting on a trapped cell per unit inlet hydraulic pressure as a function of cell diameter D_cell and penetration length L.

The elasticity microcytometer operated in the regime of very low Reynolds number (Re << 1). Thus, hydraulic pressure profile was proportional to flow velocity, leading to fluidic resistance of the confining channel R_confining independent of inlet pressure. Fluidic simulations suggested that R_confining increased from 0.08 MPa·s/mm³ to > 0.4 MPa·s/mm³ due to blockage of a single cell in the confining channel (Fig. 3b). Simulation results of tensile and shear stress profiles were further converted into an effective drag force F_drag acting on a deformed cell along the flow direction. We computed and summarized the ratio between the effective drag force F_drag and inlet pressure as a function of cancer cell diameter D_cell and penetration distance L in the confining channel (Fig. 3c). Importantly, this relation provided a direct mapping of key experimental parameters (i.e., cell diameter D_cell and penetration distance L) to F_drag, estimated by a bilinear interpolation approach.

Trapping of single cancer cells in inert confining channels

The elasticity microcytometer containing inert confining channels coated with pluronics F-127 was first utilized to measure penetration length L of individual cancer cells for four different human cell lines: breast cells MCF-10A, breast cancer cells MCF-7, cervical cancer cells HeLa, and prostate cancer cells PC3. MCF-7, HeLa, and PC3 are known metastatic cell lines [48–50], with MCF-7 and PC3 positively expressing EpCAM (or EpCAM+) while HeLa cells being EpCAM negative (or EpCAM-). Breast cells MCF-10A are EpCAM-. Coating of pluronics F-127 in the elasticity microcytometer could effectively block non-specific interactions between cancer cells and confining channel walls, resulting in confinement of cancer cells in confining channels completely due to steric effects.

We injected each type of cancer cells as floating single cells into the elasticity microcytometer under different gauge pressures (0.1 kPa and 0.2 kPa for all cell types, and 0.3 kPa and 0.4 kPa for MCF-10A). Micrographs of confining channels showing encapsulation of single cancer cells were recorded simultaneously (Fig. 4a). Through imaging analysis, penetration length L, deformed cell width W_deformed, and deformed cell diameter D_deformed were determined first. Undeformed cell diameter D_cell was then calculated using Eq. (1) at the single-cell level (Fig. 4a, Fig. S2). Plotting single-cell data of cell diameter and penetration length for MCF-10A, MCF-7, HeLa, and PC3 cells revealed strong linear correlations between cell diameter D_cell and penetration length L under different gauge pressures applied to the elasticity microcytometer (Fig. 4a). Ensemble averaged data of cell diameter and penetration length were further analyzed, suggesting that MCF-10A, MCF-7, HeLa, and PC3 cells had average diameters of 14.88 ± 0.56 µm, 19.81± 0.76 µm, 16.01 ± 0.62 µm, and 19.85 ± 0.69 µm, respectively (Fig. 4b), agreeing well with previous reports [51–53]. Importantly, MCF-10A cells could remain trapped inside confining channels of the elasticity microcytometer with the gauge pressure up to 400 Pa, whereas MCF-7, HeLa, and PC3 cells flew through confining channels with gauge pressure > 200 Pa (Fig. 4c). These observations were consistent with data reported by Guck et al. using optical forces that MCF-10A cells are significantly stiffer than MCF-7 cells [54, 55].

Figure 4.

Cell deformability measurement using the elasticity microcytometer with inert confining channels coated with pluronics F-127. Four cancer cell lines were assayed, including MCF-10A (n = 180), MCF-7 (n = 134), PC3 (n = 173), and HeLa (n = 105). Data was obtained from three independent experiments. (a) Microscopic images (left) showing live, single cancer cells trapped in individual confining channels under different hydraulic pressures (100 Pa and 200 Pa) as indicated. Black arrows mark individual single cells. Through imaging analysis, cell diameter and penetration length L were determined at the single-cell level and plotted against each other. Data trends were analyzed using linear least square fitting, with R² values indicated. Scale bar, 50 μm. (b) Ensemble averaged cell diameter of the four cancer cell types. Errors bars, s.e.m. * indicates P < 0.01 when comparing to the value from MCF-10A. (c) Penetration length L as a function of inlet pressure for the four cancer cell types as indicated. Errors bars, s.e.m.

Biomechanical phenotyping of cancer cells

When a single cancer cell remained trapped inside a confining channel of the elasticity microcytometer, resultant cell deformation under a steady fluidic inlet pressure was caused by compression from confining channel sidewalls. To characterize mechanical properties of cancer cells using the elasticity microcytometer, we first developed a first principles-based model to describe static deformation of cancer cells, which could be viewed as soft particles that would deform under compressive forces F_compress from confining channel walls based on the Hertz’s and Tatara’s theories [47, 56], and F_compress ≈ F_drag / (2sinθ). Herein, deformation of PDMS channel walls was neglected, since cancer cells were much softer than PDMS. Furthermore, we neglected a tearing force F_tearing caused by friction between confining channel walls and cancer cell membranes (F_tearing = ξ F_compress, where ξ was the static friction coefficient and ξ < 0.008) [57].

Cell deformability, defined as the ratio between the major and minor axes of a deforming cancer cell per unit compressive pressure F_compress [58], was first quantified using the first principles-based model. Cell deformabilities of MCF-10A, MCF-7, PC3, and HeLa cells were 2.19 ± SE0.31 kPa⁻¹, 3.08 ± SE0.19 kPa⁻¹, 3.69 ± SE0.23 kPa⁻¹, and 3.30 ± SE0.34 kPa⁻¹, respectively (Fig. 5a&b). These results agreed with previous findings that cancer cells MCF-7 and PC3 had significantly higher cell deformability than nonmalignant breast cells MCF-10A [19, 26, 59].

Figure 5.

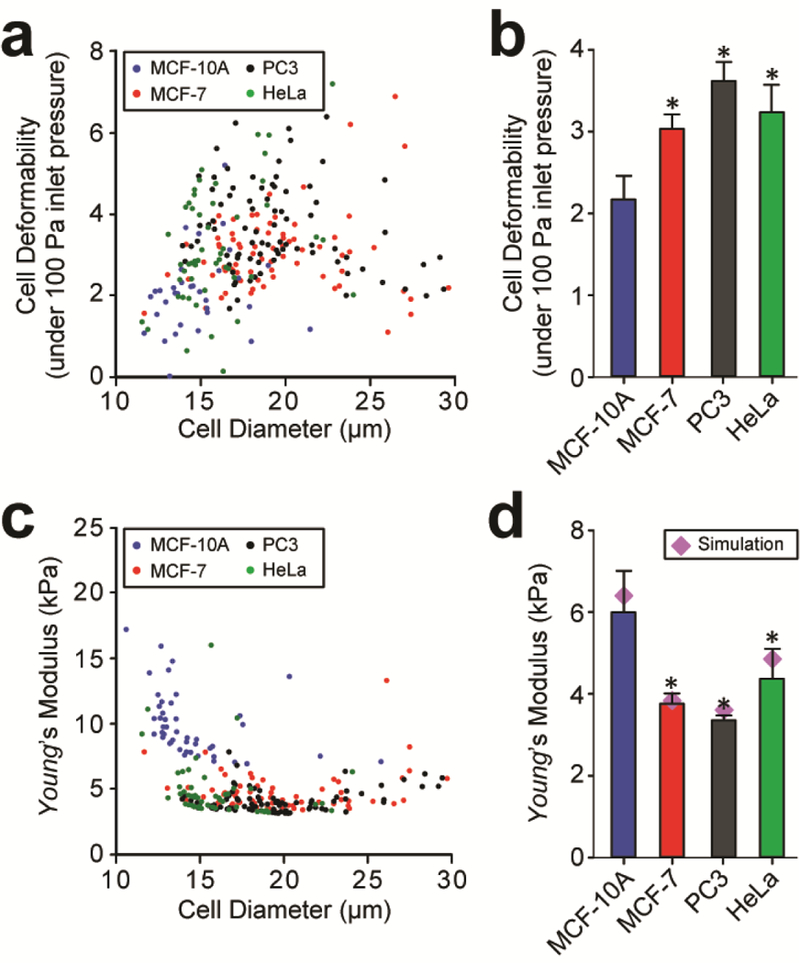
Quantification of cell deformability (a & b) and Young’s modulus (c & d) of cancer cells by the elasticity microcytometer. (a & c) Scatter plots of cell deformability (a) or Young’s modulus (c) vs. cell diameter, with each data point representing an individual cell. Data was pooled from four cancer cell lines as indicated. (b & d) Ensemble averaged cell deformability (b) and Young’s modulus (d) of the four cancer cell types. Errors bars, s.e.m. * indicates P < 0.01 when comparing to the value from MCF-10A.

Since compressive forces F_compress was related to cancer cell deformation as

$$F_{compress}=\frac{4}{3}\cdot \frac{E_{cell}}{(1-{\text{v}}_{cell}^2)}\cdot {\left(\frac{D_{cell}}{2}\right)}^{\frac{1}{2}}\cdot {\left(\frac{D_{cell}-W_{deformed}}{2}\right)}^{\frac{3}{2}},$$ (3)

where ν_cell was the Poisson’s ratio and ν_cell ≈ 0.5, E_cell was the Young’s modulus of cancer cells, E_cell could be calculated directly as

$$E_{cell}\approx \frac{9F_{drag}}{8\sin \text{θ}\sqrt{D_{cell}{(D_{cell}-W_{deformed})}^3}}.,$$ (4)

Using Eq. (4), Young’s modulus E_cell of each single cancer cell was quantified using experimental data of cell diameter D_cell and penetration distance L and simulation results of F_drag (Fig. 5c). Ensemble averaged Young’s modulus for populations of MCF-10A, MCF-7, PC3 and HeLa cells were calculated as 6.01 ± 1.01 kPa, 3.77 ± 0.22 kPa, 3.35 ± 0.13 kPa, and 4.34 ± 0.76 kPa, respectively (Fig. 5d). To verify analytical results obtained from the first principles-based model, we further conducted numerical simulations to determine the elastic modulus of cancer cells using an iterative scheme described in Methods. Simulation results of Young’s modulus for MCF-10A, MCF-7, PC3, and HeLa cells were 6.28 kPa, 3.84 kPa, 3.7 kPa, and 4.7 kPa, respectively (Fig. 5d). Simulation data demonstrated a very reasonable agreement with analytical results from the first principles-based model, supporting the validity and effectiveness of the first-principles model for calculating cell stiffness using experimental data from the elasticity microcytometer.

Quantitative measurement of EpCAM expression on single cancer cells

Using the elasticity microcytometer functionalized with anti-EpCAM, we further conducted multiparametric biomechanical and biochemical phenotypic profiling to quantify cell size, stiffness, and EpCAM expression simultaneously for single cancer cells. Suspensions of single cancer cells were prepared using trypsin (see Methods), as trypsin treatment for cell subculture has been reported with no significant effect on EpCAM expression of cancer cells [55]. Measurements of cell size and stiffness with the elasticity microcytometer were identical to the procedure described above using an inlet gauge pressure of 0.1 kPa. Immediately after initial trapping of single cancer cells in confining channels, micrographs of confining channels were recorded to determine cell diameter D_cell and cell penetration length L. Inlet pressure of 0.1 kPa was maintained for about 2 – 5 min to ensure specific antibody-antigen binding interactions between EpCAM+ cancer cells and confining channel walls, as it is known that specific antibody-antigen binding interactions typically occur within seconds [60]. Beyond this time frame, continuous trapping of EpCAM+ cancer cells in confining channels coated with anti-EpCAM for > 15 min would eventually lead to significant cell spreading on confining channel walls with enlarged cell contact areas (Fig. S3). Thus, in this work, all measurements of EpCAM expression on single cancer cells were conducted within 5 min after initial cell encapsulation.

We quantified EpCAM expression of single cancer cells based on measurements of total adhesion force generated from EpCAM / anti-EpCAM binding. After initial cell trapping, hydraulic pressure at the device inlet was increased for multiple steps (with each increment of 1 kPa) till the drag force F_drag along the channel direction generated by shear flow was sufficiently large to break all EpCAM / anti-EpCAM bonds and flush out all the trapped cancer cells from confining channels. Control experiments using inert elasticity microcytometers coated with pluronics were also conducted for comparison. Enhanced cell adhesion was clearly evident for MCF-7 and PC3 cells in anti-EpCAM-coated elasticity microcytometers, as higher gauge pressures were required for cell dislocation and removal from confining channels as compared to inert confining channels, supporting positive EpCAM expression of MCF-7 and PC3 cells (Fig. 6a). In distinct contract, for MCF-10A and HeLa cells, no notable difference was observed between anti-EpCAM-coated and pluronics-coated elasticity microcytometers when hydraulic gauge pressures were gradually increased to flush out cancer cells from confining channels, supportive of negative EpCAM expression of MCF-10A and HeLa cells (Fig. 6a).

Figure 6.

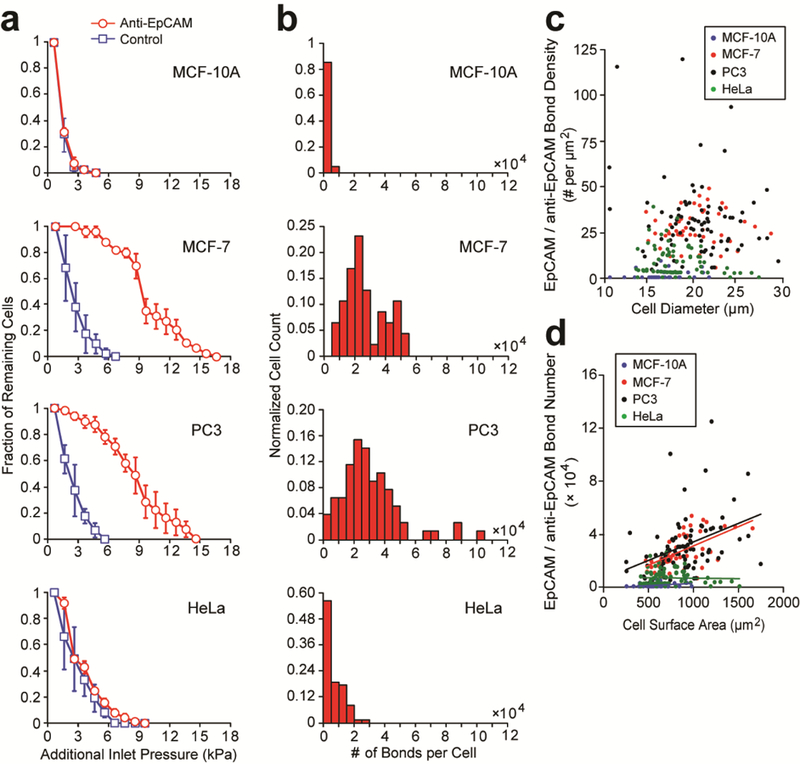
Quantification of EpCAM expression of cancer cells using the elasticity microcytometer. (a) Fraction of live single cancer cells remaining trapped in confining channels of the elasticity microcytometer as a function of additional hydraulic pressure applied to flush out cancer cells from confining channels. Confining channels were either coated with pluronics F-127 (control) or antibodies against EpCAM as indicated. Errors bars, s.e.m. (b) Histogram of the number of EpCAM/anti-EpCAM bonds for different cancer cell types as indicated. n > 50, with two separate experiments for each cell type. (c) Scatter plot of EpCAM/anti-EpCAM bond density vs. cell diameter. Each data point represents an individual cell. Data was pooled from the four cancer cell types as indicated. (d) Scatter plot of total EpCAM number vs. cell surface area. Each data point represents an individual cell. Data was pooled from the four cancer cell types as indicated.

To quantify EpCAM expression levels of cancer cells, we leveraged the first principles-based model and further considered a critical tearing force F_tearing acting on a cancer cell needed to overcome cell adhesion due to EpCAM / anti-EpCAM binding. Therefore, for cancer cell removal from confining channels, F_tearing > A_contactC_bondF_bond, where A_contact was cell contact area with confining channel walls and $A_{contact}\approx \text{π(}{D}_{deformed}^2-W_{deformed}^2)/2,C_{bond}$ was EpCAM / anti-EpCAM bond density, and F_bond denoted adhesion force of a single EpCAM / anti-EpCAM bond and F_bond ≈ 6.7 × 10⁻⁶ dynes as computed by Adams et al. using the Bell’s model [61, 62]. Given F_tearing ≈ F_dragcosθ, simulation results of F_drag from Fig. 3c was directly used to calculate critical tearing force F_tearing and thus EpCAM / anti-EpCAM bond density C_bond for each single cancer cell (Fig. 6b&c, Fig. S4).

Scatter plot of EpCAM / anti-EpCAM bond density C_bond vs. cell diameter D_cell suggested that EpCAM expression was independent of cell size for all four cancer cell types (MCF-10A, MCF-7, PC3, and HeLa) (Fig. 6c). Scatter plot of total EpCAM / anti-EpCAM bond number vs. cell surface area further revealed that for MCF-7 and PC3 cells, the total number of EpCAM / anti-EpCAM bonds was linearly proportional to cell surface area; however, for MCF-10A and HeLa cells, such linear correlation was not observable (Fig. 6d). These observations further supported positive and comparable EpCAM expression for MCF-7 and PC3 cells [63] and negative EpCAM expression for MCF-10A and HeLa cells [64]. Assuming homogenous distribution of EpCAM on cancer cell membranes, average EpCAM / anti-EpCAM bond density Cbond for MCF-10A, MCF-7, PC3, and HeLa cells were 1.36 ± 0.62 bonds/μm², 29.71 ± 2.66 bonds/μm², 34.36 ± 3.94 bonds/μm², and 9.29 ± 1.57 bonds/μm², respectively. Average total number of EpCAM / anti-EpCAM bonds on MCF-10A, MCF-7, PC3, and HeLa cells were 9.30 × 10² ± 4.27 × 10² bonds/cell, 2.71 × 10⁴ ± 0.32 × 10⁴ bonds/cell, 3.15 × 10⁴ ± 0.37 × 10⁴ bonds/cell, and 6.51 × 10³ ± 1.06 × 10³ bonds/cell, respectively. We should note that the EpCAM / anti-EpCAM bond quantities measured by the elasticity microcytometer were different from total EpCAM expression conventionally measured at the single cell level by immunostaining or fluorescence-activated cell sorting (FACS). Nonetheless, the total numbers of EpCAM / anti-EpCAM bonds on MCF-10A, MCF-7, PC3, and HeLa cells determined from the elasticity microcytometer were consistent and on the same order of magnitude with the total EpCAM expression data reported in the literature [63,64].

Two-dimensional scatter plot of EpCAM / anti-EpCAM bond density C_bond vs. cell stiffness was generated to further compare cellular phenotypes between MCF-10A and MCF-7 cells (Fig. 7). Importantly, clustering of MCF-10A and MCF-7 cells in the scatter plot clearly revealed a significant distinction between these two cell types with respect to EpCAM expression and cell stiffness. Single-cell data from MCF-10A and MCF-7 cells fell into two distinct regions in the scatter plot, supporting effective categorization of cancer cells based on multiparametric biomechanical and biochemical phenotypic profiling of single cancer cells as demonstrated in this work.

Figure 7.

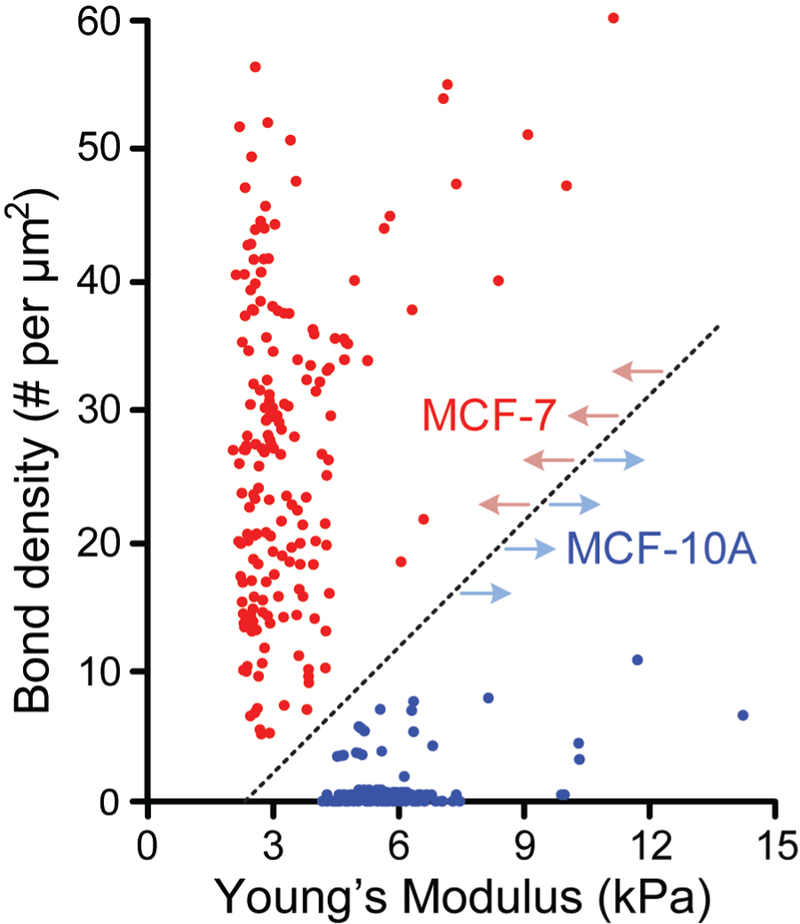
Scatter plot of EpCAM/anti-EpCAM bond density vs. Young’s modulus for MCF-10A (blue; n = 180) and MCF-7 (red; n = 134) cells. Each data point represents an individual cell. Dotted line highlights a clear separation between MCF-10A and MCF-7 populations.

CONCLUSION

In this work, a novel microfluidic elasticity microcytometer integrated with cell surface protein measurement functionality was developed and characterized for multiplexed biomechanical and biochemical phenotyping of single cancer cells. Fabrication and experimental operation of the elasticity microcytometer were simple and straightforward, supporting a future feasibility of mass production and implementation of the elasticity microcytometer for addressing critical biological and biomedical challenges involving deep phenotyping of rare human cells including rare human cancer cells at the single cell level. Importantly, an analytical model was developed from the first principles to convert cell deformation and penetration length within confining channels of the elasticity microcytometer to important cellular biomechanical and biochemical characteristics including cell deformability / stiffness and expression of cell surface receptors. The microfluidic elasticity microcytometer was implemented for single-cell measurements and comparisons of four human cell lines with distinct metastatic potentials and derived from different human tissues (MCF-10A, MCF-7, HeLa, and PC3). Cell size, cell stiffness, and EpCAM expression levels of the four human cell lines measured from the elasticity microcytometer agreed reasonably well with values reported by others. Furthermore, analytical results of cell stiffness from the first-principles model agreed well with date obtained from numerical simulations, supporting the validity and effectiveness of the first-principles model for calculating cell stiffness using experimental data from the elasticity microcytometer.

The elasticity microcytometer demonstrated in this work could finish processing 60 – 80 individual, free-floating cells from biofluidic samples within 10 min at a volume flow rate of ~20 μL /sec under a hydraulic pressure of 0.1 kPa. This sample throughput should be sufficient for clinically relevant rare human cancer cells such as CTCs or cancer cells obtained from fine needle biopsy. Sample throughput of the elasticity microcytometer could be scaled up by parallelism using multi-device processing or integrating a greater number of confining channel arrays on the same device and implementing the device under a continuous flow operation. Future development of the elasticity microcytometer platform could incorporate functional modules for quantitative measurements of single-cell viscoelasticity and dynamic friction of antigen-antibody bindings [65, 66]. Generating a linear array of confining channels with each channel arranged in series and selectively functionalized with different monoclonal antibodies would further allow simultaneous quantification of expression of multiple cell surface proteins for the same single cells [67]. These future exploration and improvement of the elasticity microcytometer platform will be critical for fulfilling its promise for deep phenotyping of live cells at the single-cell level in the era of precision medicine.

METHODS

Device fabrication

A Si wafer was first primed with hexamethyldisilazane (HMDS, AZ Electronic Materials, Branchburg, NJ) before a positive photoresist (AZ5214, AZ Electronic Materials) was spin-coated on the wafer and patterned by photolithography. The wafer was then processed with deep reactive ion etching (DRIE, STS Deep Silicon Etcher, Surface Technology Systems, Newport, UK) to generate microstructures with a depth of 20 µm on the wafer. After stripping off photoresist, the Si wafer was treated briefly with air plasma (Plasma Prep II, SPI Supplies, West Chester, PA) and silanized with vaporized (tridecafluoro-1,1,2,2,-tetrahydrooctyl)-1-trichlorosilane in a vacuum desiccator to facilitate release of molded polydimethylsiloxane (PDMS).

The elasticity microcytometer was fabricated by a ‘double casting’ process using PDMS. Briefly, PDMS pre-polymer (PDMS monomer : curing agent ratio = 10 : 1; Sylgard-184, Dow Corning, Midland, MI) was poured onto the Si mold and bake at 110 °C for 20 hr. The PDMS layer was peeled off from the Si mold before treated with air plasma and silanized. PDMS pre-polymer was poured onto the PDMS negative mold, followed by baking at 110 °C for 20 hr. After baking, the second PDMS substrate (as the final device layer) was peeled off from the negative PDMS mold, trimmed using a razor blade, and punched with inlet and outlet holes (Harris Uni-Core Dia. 0.5 mm, Ted Pella, Redding, CA). After a brief treatment with air plasma, the PDMS device layer was bonded onto a glass coverslip (VWR, VWR, Radnor, PA).

Device functionalization

Device functionalization was performed within 10 min after device fabrication, when inner surfaces of the elasticity microcytometer remained hydrophilic. To render confining channels of the elasticity microcytometer inert, non-adhesive, block copolymer pluronics F-127 (Sigma-Aldrich, St. Louis, MO) was injected into the device for 30 min to allow coating of pluronics F-127 on PDMS walls. To quantify EpCAM expression on cancer cells, the elasticity microcytometer was functionalized with monoclonal antibodies against EpCAM using the avidin-biotin chemistry [68]. Briefly, 4% (v/v) of 3-mercaptopropyl trimethoxysilane (Gelest, Morrisville, PA) in ethanol was first flushed into the elasticity microcytometer for 30 min at room temperature. The elasticity microcytometer was then rinsed with pure ethanol, before 1 mM or 0.28% (w/v) N-γ-maleimidobutyryloxy succinimide ester (GMBS) in ethanol was flushed into the device for another 15 min. After rinsing with PBS, 10 µg/mL avidin (Life Technologies Scientific, Grand Island, NY) in PBS was flushed into the elasticity microcytometer at room temperature for 30 min. The elasticity microcytometer was rinsed again with PBS, before 10 µg/mL biotinylated goat anti-human EpCAM (R&D Systems, Minneapolis, MN) in PBS with 1 (w/v) bovine serum albumin (BSA) and 0.09 % (w/v) sodium azide was flushed into the elasticity microcytometer for 30 min. Coating the elasticity microcytometer with GMBS, a heterobifunctional cross-linker, could facilitate covalent conjugation of biotinylated EpCAM antibodies and avidin. To ensure anti-EpCAM activity and avoid antibody hydrolysis processes, cell deformability assays were conducted within 3 hr after device functionalization.

Numerical simulation

Three-dimensional finite element models were constructed using commercial software (COMSOL 4.2, Burlington, MA). The models, which represented half-channel geometry due to physical symmetry, included half of a single deformed cell with different diameters (10 – 30 µm) located at prescribed penetration lengths L along the confining channel. For each model, cell shape was first computed based on the Hertz’s and Tatara’s theories. Flow velocity and pressure profiles along the confining channel were then computed to determine fluidic resistance of the confining channel R_confining as a function of cell diameter and penetration length. Simulation results of shear stress were further converted to an effective drag force F_drag acting on the deformed cell along the flow direction.

To use computational simulations to directly obtain the Young’s modulus of cancer cells, a commercial software package (Abaqus, Dassault Systems Corp., Waltham, MA) was utilized to simulate penetration length and deformation of a single cancer cell encapsulated in a confining channel. Similar to fluidic simulation, we considered a model with a half-channel geometry and half of a single deformed cell. Specifically, the computational model was discretized as meshes composed of hexahedral elements (with a characteristic length of 0.5 μm for the cell and 2 μm for channel walls, respectively). Simulations were performed for each cancer cell type using ensemble averaged data of cell diameter and penetration length obtained directly from experiments. Fluid pressure profile around the cell was configured using results from fluidic simulations. For material properties, the Young’s modulus of PDMS channel walls was set to be 2.2 MPa [69]. The cell was modeled as linear elastic, as the current study considered only the first order elastic modulus of the cell as cell stiffness. For each cell type, simulations were reiterated to obtain a cell stiffness value that could result in a penetration length consistent with ensemble averaged experimental data. Specifically, searching for proper cell stiffness values was implemented by fitting with guessed cell stiffness values and reiterative corrections using a bisection scheme.

Cell culture

Human breast epithelial cells (MCF-10A), breast cancer adenocarcinoma cells (MCF-7), prostate cancer cells (PC3) and cervical cancer cells (HeLa) were all obtained from ATCC (Manassas, VA). MCF-10A cells were cultured in Mammary Epithelial Growth Medium (MEGM; CC-3150, Lonza, New York City, NY), containing 0.4% (v/v) bovine pituitary extract (BD, Franklin Lakes, NJ), 0.1% (v/v) human epithelial growth factor (hEGF; Cell Signaling Technology, Beverly, MA), 0.1% (v/v) hydrocortisone (Sigma-Aldrich), 0.1% (v/v) insulin (Sigma-Aldrich), and 0.1% (v/v) of a reagent mixed with 30 mg/mL gentamicin and 15 μg/mL amphotericin (GA-1000, Lonza). MCF-7 and HeLa cells were cultured in high-glucose Dulbecco’s modified Eagle’s medium (DMEM; Invitrogen, Carlsbad, CA) supplemented with 10% fetal bovine serum (Atlanta Biological, Atlanta, GA), 0.5 μg/mL fungizone (Invitrogen), 5 μg/mL gentamicin (Invitrogen), 100 units/mL penicillin, and 100 μg/mL streptomycin. PC3 cells were maintained in Roswell Park Memorial Institute medium (RPMI-1640; ATCC) containing 10% fetal bovine serum, 0.5 μg/mL fungizone, 5 μg/mL gentamicin, 100 units/mL penicillin, and 100 μg/mL streptomycin. All cells were maintained at 37 °C with 100% humidity and 5% CO2. When cells reached 80% confluency, fresh 0.25% trypsin-EDTA in phosphate buffered saline (PBS) was used to re-suspend cells before subculture at a cell concentration of 3 × 10³ cells/cm². It has been reported that confluent cancer cell culture may induce lysis of EpCAM and thus affect EpCAM surface expression [70]. In addition, trypsin treatment for cell subculture has been reported to have no significant effect on EpCAM expression of cancer cells [55].

Statistics

p-values were calculated using the Student’s t-test in Excel (Microsoft, Seattle, WA).