Syntheses and Energy Transfer in Multiporphyrinic Arrays Self-Assembled with Hydrogen-Bonding Recognition Groups and Comparison with Covalent Steroidal Models

Abstract

A number of new porphyrins equipped with complementary triple hydrogen-bonding groups were synthesized in good yields. Self-assembly was investigated by NMR spectroscopy, dynamic light scattering (DLS), and atomic force microscopy (AFM). These artificial antenna systems were further characterized by stationary and timeresolved fluorescence techniques to investigate several yet unsolved questions on the mechanism of excitation energy transfer (EET) in supramolecular systems. For example, the photophysics of a simple D–U≡P–A dyad was studied, in which donor D and acceptor A are Zn^II- metalated and freebase porphyrins, respectively, and U (uracyl) and P (2,6-diacetamidopyridyl) are complementary hydrogen-bonding groups linked by flexible spacers. In this dyad, the EET occurs with about 20% efficiency with a lifetime of 14 ps. Reversal of the nonsymmetric triple hydrogen-bonding groups to give a A–U≡P–D construct results in an EET efficiency of about 25% and a lifetime of 19 ps. Thus, there is a slight directionality of EET mediated by these asymmetric triple hydrogen-bonding units tethered to flexible spacers. In polymeric systems of the type ⋯P-D-P≡U-A-U≡P-D-P⋯, or⋯U-D-U≡P-A-P≡U-D-U⋯, the EET efficiency doubles as each donor is flanked by two acceptors. Because doubling the probability of photon capture doubles the EET efficiency, there is no energy amplification, which is consistent with the “antenna effect”. For these polymeric systems, AFM images and DLS data indicate large rodlike assemblies of a few hundred nanometers, whereas the components form much smaller aggregates under the same conditions. To understand the importance of the flexible hydrogen-bonding zipper, three different covalently bridged D-B-A molecules were synthesized in which the bridge B is a rigid steroidal system and the same ester chemistry was used to link the porphyrins to each end of the steroid. The geometry inferred from molecular modeling of D-B-A indicates geometric similarities between B and some conformations of the –P≡U– supramolecular bridge. Although the EET efficiency is a factor of two greater for the steroidal systems relative to the supramolecular dyads, the rate is 50–80 times slower, but still slightly faster than that predicted by Förster-type mechanisms. Circular dichrosim (CD) spectra provide a conformational sampling of the porphyrin groups appended on the steroidal skeleton, thus allowing an estimation of the orientation factor κ for the transition dipole moments, which significantly affects the EET rate. We conclude that the flexible hydrogen-bonded linked systems are adaptive and have variable geometries with foldamers in which the D and A groups can approach well under 1 nm. In these folded conformations, a rapid EET process occurs, probably also involving a Dexter-type exchange mechanism, thus explaining the fast EET relative to the rigid steroidal compounds. This study predicts that it is indeed possible to build large supramolecular antennas and the component design and supramolecular dynamics are essential features that dictate EET rates and efficiencies.

Introduction

Life on earth depends on efficient solar-energy conversion mediated by photosynthesis. Light-harvesting by pigments, such as chlorophylls, is the first step in photosynthesis. In plants, algae, and purple photosynthetic bacteria the protein–pigment antenna complexes capture solar energy and efficiently funnel this energy to an energetic sink referred to as the reaction center. The reaction center converts the exciton into chemical energy by charge separation across a membrane by a cascade of electron-transfer steps that involve a highly specific and conserved arrangement of pigments within the protein complex. The first photosynthetic organisms appeared about 4.5 billion years ago, and evolution has optimized the process such that photosynthetic “devices” have reached over 35 % efficiency in the transformation of light energy into biochemical energy.^[1] Any effort to mimic or indeed improve photosynthesis to create solar-energy conversion devices must maximize the light harvesting and efficiently couple this process to the electron transfer that results in the production of a useful chemical or electrical potential. Silicon-based solar cells represent a functioning technology, but mass production has not led to the expected drop in manufacturing price so that solar energy production still is about ten times more expensive than conventionally produced electrical energy.^[2] During the last decade, in spite of considerable effort, nonsilicon-based artificial systems still remained at about 10 % efficiency.^[2i,j] Organic or plastic solar cells have the potential to be mass produced at much lower costs using continuous processing, and proof-of-principle devices have been demonstrated,^[3] but the efficiency is still below the commercialization value of about 6 %.^[2i] There exists a biological–inorganic hybrid approach, which for example, couples photosynthetic membranes or chloroplasts to conducting or semiconducting substrates incorporated into a device. However, this technique has met with limited success thus far because the photosynthetic pigments and apparatus are remarkably fragile once removed from their natural environment.^[2k] A more promising organic–inorganic hybrid approach is to exploit the high optical cross section and electrochemical tunability of robust organic pigments coupled to inorganic substrates with complementary band properties.^[2f,h]

Inspired by natural photosynthesis, our initial focus was to construct light-harvesting systems with increased photoncapture cross sections that enable hybrid solar cells to function even under low-light-illumination conditions.^[4] For light-harvesting purposes, an assembly of excitonically coupled chromophores that act as the antenna system must ensure that the exciton energy transfers to the trap with high efficiency.^[5] Recently, a variety of covalent multichromophoric arrays^[6] and dendrimers were elegantly synthesized as antennas and their photophysics investigated.^[7] However, complex multistep syntheses generally render the covalent systems prohibitively expensive for practical, commercially viable applications. The alternative, noncovalent approach, in which appropriately designed chromophores self-assemble into functional antenna systems obviates much of the synthetic efforts and costs. However, self-assembled systems necessitate careful consideration of organizational robustness under the application conditions as only weak intermolecular forces, such as metal ligation, hydrogen bonding, π–π interactions, and dispersion forces hold these structures together.^[8] The architecture of the chromophores should maximize energy transfer and be stable for use in potential devices. Once the self-assembly algorithm has been programmed into a molecule by equipping it with groups suitable for specific intermolecular interactions, the outcome of the process is dictated by a fine balance between kinetics and thermodynamics. As the thermodynamic structure is usually the product, the components can reassemble, thus affording an autorepair mechanism for some component of the device.

Self-assembly is also a functional principle for natural light-harvesting antennae, as illustrated by numerous studies of the antenna chlorosomes of green photosynthetic bacteria^.[9,10] These “green-sacks” encapsulate hierarchically organized aggregates of bacteriochlorophyll (BChl) c, d, or e, which also self-assemble in nonpolar solvents mediated by axial metal ligation between the bacteriochlorophyll pigments by pendant alcohols.^[11] The spectroscopic properties of bacteriochlorophylls self-assembled in vitro in the absence of any proteins are essentially identical with those of the chlorosome in vivo preparations.^[9–11] Replication of the self-assembly algorithm that operates for BChls with fully synthetic porphyrins and chlorins by using the same recognition motifs at specified positions of the tetrapyrrolic macrocycle results in similar spectroscopic signatures.^[12] Tamiaki et al. have elegantly prepared other synthetic self-assembling mimics of BChls^.[13] Because such self-assembled antenna architectures can lead to functional light-harvesting nanostructures,^[14] a deeper understanding of their energy transfer capabilities is required to optimize their use in efficient hybrid solar cells.

Herein, we report the syntheses and singlet–singlet energy transfer studies of both simple, covalently linked porphyrin dyads and self-assembled porphyrin multimers. Comparison of the excitation energy transfer (EET) efficiencies and rates of the covalently constructed donor–bridge–acceptor (D-B-A) systems to supramolecular donor–acceptor systems organized by complementary hydrogen-bond motifs allows detailed examination of the roles of linkers and recognition units in EET. The covalent systems use a steroidal bridge to link an energy-donor to an energy-acceptor moiety in different configurations of known geometry. Four fundamental issues are addressed, which prior to the present study remained ambiguous regarding EET.^[6,7,15] 1) For (D-B-A) systems self-assembled with hydrogen-bonding interactions, how does the adaptive intermolecular linkage influence the efficiency and rate of the EET process (i.e., what is the role of supramolecular dynamics)? 2) As the hydrogen-bonding motifs are heterocomplementary, there is an asymmetric link (B) between the donor and acceptor groups, and thus how does this asymmetry affect the rate and efficiency of EETof D-B-Aversus A-B-D configurations? 3) Is an antenna effect in multichromophoric arrays assembled through hydrogen bonding indeed observed when multiple donors are linked to one acceptor? 4) It has been hypothesized that chromophore and protein dynamics in both photosynthetic antenna complexes and reaction centers are essential features that allow energy and electron transfer to proceed with near quantum efficiency,^[16] yet in simple model systems the more rigid systems are generally more efficient than floppy ones.^[17] Thus, are flexible linkers detrimental for EET and should one prefer rigid architectures with optimized geometries of the transition dipole moments? In natural light-harvesting systems, the proteins are used as a scaffold for the noncovalently bound chromophores, such as chlorophylls and carotenoids, and they allow careful positioning of the transition dipoles. This last question is especially relevant in regard to the recent report by Jang et al.,^[15b] who extended the Förster formalism for EET to multichromophoric systems and applied their method to describe the energy transfer in light-harvesting 2 (LH2) complexes. The observed experimental rates in LH2 are about ten times faster than the ones predicted from the simple Förster formula.^[18] This discovery has led to controversy over whether or not for chromophores of large sizes, (i.e., chlorophylls and porphyrins, in which the center–center distance between an energy donor and an acceptor are not much larger than the molecular size of a diameter of roughly 1 nm) the Förster dipolar description of EET is still valid.

Experimental Section

Full experimental details on the AFM and DLS measurements and the synthetic procedures are given in the Supporting Information.

Time-resolved fluorescence

Single photon timing:

Preliminary measurements of the time-resolved fluorescence were performed using the single-photon-timing (SPT) method with a high temporal resolution. The SPT setup is described in detail elsewhere.^[19] The samples were excited at 552 nm with laser pulses of approximately 10 ps at a repetition rate of 4 MHz, and fluorescence was passed through the monochromator and detected at different wavelengths (using “magic angle” polarization conditions) with a fast microchannel plate photomultiplier R3809U-51 (Hamamatsu, Japan). The system response was 30 ps, thus allowing time resolution down to 3 ps using a deconvolution procedure. The decay traces were fitted using the global analysis method, as described previously,^[20] thus resulting in the decay-associated lifetime amplitudes A_i(λ) (the so-called decay-associated emission spectra (DAES)) versus wavelengths λ:^[20]

$$F\left(t,\lambda \right)=I\left(t\right)\otimes \sum _i{A}_{\text{i}}\left(\lambda \right)\text{exp}\left(-t/{\tau }_{\text{i}}\right)$$ (1)

where F(t,λ) is time- and wavelength-resolved fluorescence, I(t) is the measured instrument response function, ⊗ denotes convolution, and τ_i are lifetimes.

Streak camera:

The solutions of the investigated compounds were excited with the second harmonic light pulse (≈150 fs FWHM) from the optical parametric oscillator (OPO) at a repetition rate of 76 MHz. For the triply hydrogen-bonded systems, the excitation wavelength was tuned to 547 nm, at which the absorption ratio of the energy donor and the energy-trap moieties is maximal (≈2:1). For the covalent steroidal bisporphyrins, the optimal excitation wavelength was found to be 552 nm (≈3:1). The average incident power was approximately 5 mW, thus corresponding to a pulse energy of 65 pJ. The fluorescence signal was recorded using a combination of a spectrometer (Jobin-Yvon HR460, France; grating: 100 linesmm⁻¹) and a streak camera C568 (Hamamatsu, Japan) in the wavelength range 560–760 nm, thus covering a time interval up to 2 ns. The spectral and temporal resolutions were 2 nm and 8 ps, respectively. The streak camera was operated in the analogue integration mode. A color glass filter OG570 (Schott, USA) was used for suppressing the scattered pump light. Measured fluorescence was corrected by using independently measured spectral and temporal response functions of the filter-spectrometer-streak camera set up. The decay-associated spectra were calculated by using Equation (1) and taking into account that the fluorescence signal has not decayed completely during a single streakcamera sweep.

Results

Syntheses:

Long alkyl chains appended onto the meso positions impart a greater solubility to porphyrins than most meso aryl groups. The porphyrins were made under Lindsey^[21] conditions, in which a mixed aldehyde condensation with dodecanal, methyl 4-formyl-benzoate, and pyrrole was followed by oxidation to obtain a mixture of six porphyrins denoted by A–F in the order of their elution from a normal silica gel chromatographic column. These porphyrins (Por) bearing either undecyl groups, for increased solubility, or 4-carboxymethylphenyl groups, for further functionalization, are easily available in gram quantities (Scheme 1).^[22] After hydrolysis of the methyl ester group(s), the corresponding benzoic acids can be isolated in high yields. We were unsuccessful in obtaining porphyrin esters by direct transesterification of the methyl benzoates or through acid chloride groups using a variety of alcohols linked to recognition groups (Rec). However, under mild coupling conditions that employed EDCI and DMAP, as described by Matile et al.^[23] the desired esters were obtained in moderate but preparatively useful yields (Scheme 2) with porphyrinic monoacylureas as the by-products (see the Supporting Information).

Scheme 1.

Porphyrins A–F which are readily separated.

Scheme 2.

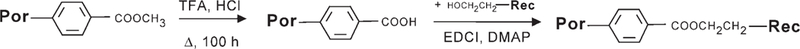
Synthesis of porphyrins equipped with recognition groups. Coupling of the recognition groups is accomplished by using dry dichloromethane as solvent.

Complementary recognition groups (Rec) capable of triple hydrogen bonding, such as 2,6-diacetamidopyridine (P) and uracyl (U), have been shown to induce self-organization into large chiral suprastructures when flexible tartaric esters are used as the core.^[24] With rigid groups such as anthracene, polymeric materials with adaptive properties may be obtained.^[25] These hydrogen-bonding motifs allow the self-assembly of a large variety of architectures^[26] depending on the topologies of the component molecules. Here freebase or Zn^II porphyrins serve as the core functional entity. The photophysical properties of both the free base and the zinc porphyrins are well established, and zinc metalloporphyrins can serve as energy donors to free base (FB) energy acceptors if the molecular or supramolecular structure is appropriate. For example, if the distance between the chromophores is below the Förster radius, a dipolar energy transfer mechanism is possible. Furthermore, a stringent condition for the likelihood of energy transfer is that a good spectral overlap between the fluorescence of the Zn donor and the absorption of the FB acceptor exists. Numerous covalently linked systems have been investigated and the energy transfer efficiency has been shown to depend on the distance, orientation, and flexibility of the linkers in the donor and acceptor moieties.^{[6, 7]} Furthermore, antenna effects, namely, by increasing the number of donors that can be excited, have also been observed.^{[6, 7]} Much scarcer are reports on noncovalent systems. Sessler et al. investigated systems in which the donor and acceptor were linked by hydrogen bonding, either doubly in a cytosine dimer or triply in a guanineadenine conjugate.^[27] This study concluded that energy transfer does indeed take place between such hydrogen-bonded assemblies and forms the basis of our efforts herein. Porphyrins with similar hydrogen-bonding motifs (uracyls and diacetamidopyridyls) grafted directly onto the meso positions of porphyrins were reported by Drain et al.^[28] This latter strategy minimizes the conformation dynamics and demonstrated the occurrence of energy transfer from a zinc porphyrin to the free base in self-assembled square arrays by steady-state fluorescence studies.

Herein, we report the design of a second generation of porphyrin assemblies that have several advantages over the previous systems, such as good availability, increased solubility, and the possibility of modular self-assembly of components in a variety of architectures. Scheme 3 presents the “tectons”^{[26, 29]} used herein for the noncovalent assembly of functional units.

Scheme 3.

Porphyrins bearing complementary recognition groups in various topological positions (e.g., on the same side of the macrocycle, 5,10–, or on opposite sides, 5,15–). Diagrams representing the chromophores and recognition groups are shown below the formulae.

Two different uracyl units (U and Uʹ) were tested for ester coupling. Although the Uʹ group, linked at the 6 position,^{[24, 25]} worked well in the conjugation to the porphyrin acids, we concentrated on the newly developed recognition group U with a linkage on the uracyl N1 atom (Scheme 4). The latter group can be prepared on a large scale from uracyl and ethylene carbonate through an adapted one-pot procedure.^[30] In addition, with no hydrogen atom at N1, U cannot form a mismatched double hydrogen bond that would complicate the analysis. Species P is a hydrogen bond donor–acceptor–donor (dad) group and U (and Uʹ) are complementary (ada) groups. The good solubility assures association constants of approximately 10³ m⁻¹ in moderately polar solvents such as chloroform or dichloromethane (Figure 2). Anhydrous conditions are essential for the reproducibility of the results as adventitious water drastically diminishes the association constant. In dry toluene, or even better in anhydrous cyclohexane, n-hexane, and n-heptane, the association constants are increased by a much greater extent but solubility, especially with large architectures, becomes problematic.

Scheme 4.

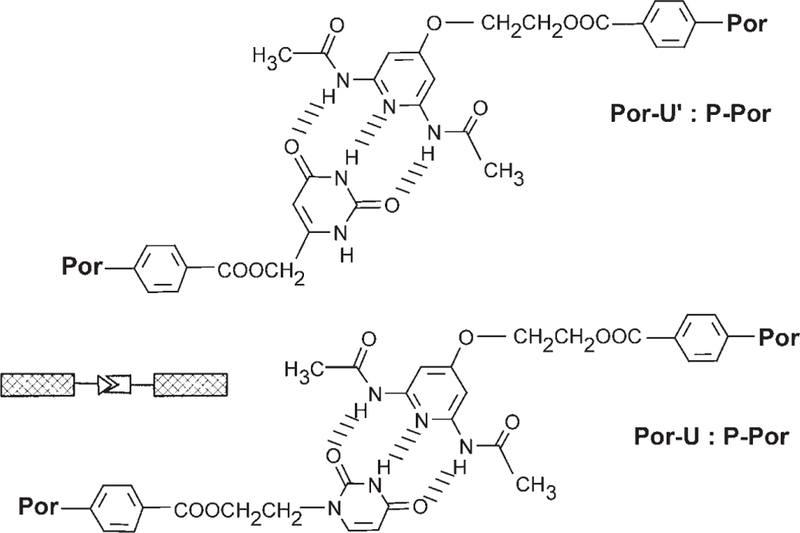
Triple hydrogen-bonding recognition groups appended onto porphyrins (Por).

Figure 2.

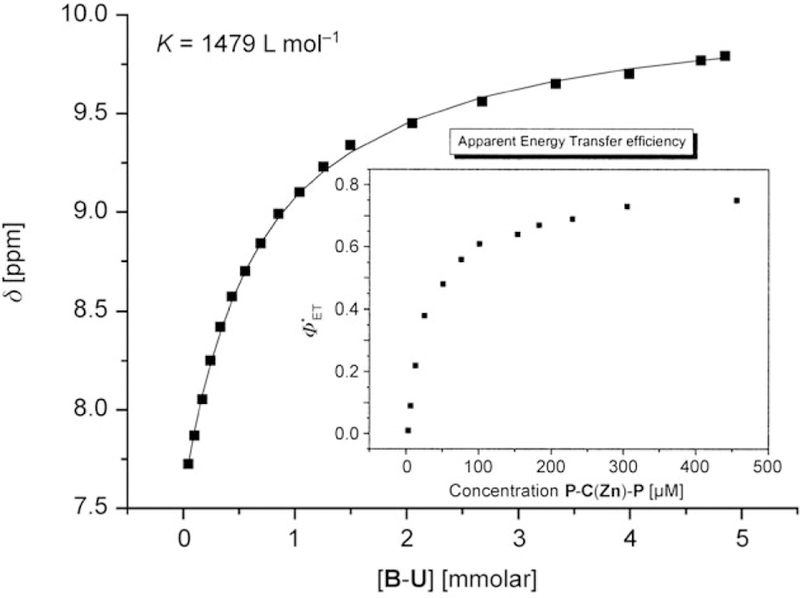
Determination of the association constant between B–P and B–U in dry CDCl₃ at 25°C (0.67mm B–P). The shift of the NH proton in B–P was monitored upon addition of B–U. For typical examples of NMR spectra and temperature dependence see Figures S2 and S3, respectively, in the Supporting Information. At 25°C this translates to about 5 kcalmol⁻¹ per binding event. Inset: The apparent decrease of efficiency of EET from P-C(Zn)-P to U-C-U in chloroform after dilution and correcting the fluorescence spectra. An equimolar mixture was diluted with dry chloroform.

These compounds allow a modular assembly of Zn^II donor porphyrins with free-base acceptor porphyrins in predefined architectures that allow the study of energy transfer and antenna effects in noncovalent supramolecular assemblies. Scheme 5 presents some possible architectures; however, it should be noted that the lengths of the polymeric arrays and other aggregates are dictated by the thermodynamics of the given equilibria under the specified conditions. The total intermolecular interactions include specific hydrogen-bonding, nonspecific dispersion, and π-stacking forces. Aggregates of the linear tapes depicted in Scheme 5, organized predominantly by π-stacking, are likely to be present at concentrations above approximately 0.1 mm, as proven by dynamic light scattering (DLS) and atomic force microscopy (AFM; representative data and images are given in the Supporting Information).

Scheme 5.

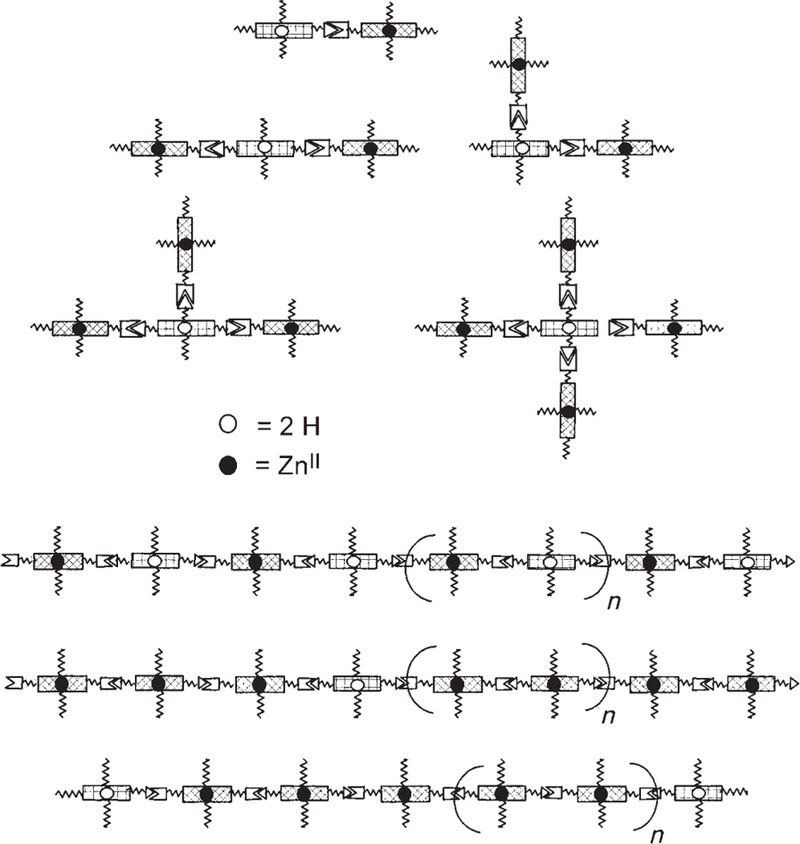
Possible self-assembled arrays and self-organized tapes using the Zn^II donor and free-base acceptor porphyrins (recognition motifs have the same symbols as in Scheme 3). The lengths of the polymeric tapes (bottom) are dictated by the equilibria under the conditions of interest. The center tape represents a statistical mixture of the donor and acceptor molecules that results in a random insertion of an acceptor molecule. The bottom tape represents a statistical mixture of capping accept-or molecules that results in a distribution of lengths.

Previous studies with the same recognition groups have shown that a fine control of the stoichiometry is needed to maximize the yields of target systems, and a mathematical model with predictive value for the degree of supramolecular polymerization has been developed.^[25a] These nanoarchitectures can afford test cases to examine the design criteria needed to maximize energy harvesting and trapping efficiency: 1) In terms of the supramolecular topology, the nonmetalated energy traps can be assembled with 1–4 donor moieties (Scheme 5, top). The traps may also be incorporated either within the assembly or as the end groups, as the diagrams in Scheme 5 (bottom) suggest. By adjusting the concentration of the traps that act as capping groups, the size distribution of the antenna can be somewhat controlled. Systematic variation in the stoichiometries of metalloporphyrins to the free base moieties allows a statistical incorporation of the traps into the linear tapes (and tape aggregates). 2) The efficiency and rate of energy transfer can be influenced by the hydrogen bonding directionality, which can be quantified by measuring the energy transfer rates (K_EET) for two self-assembled dyads: D-P≡U-A, where D–P is the donor Zn^II– pyridyl metalloporphyrin and U–A is the acceptor free-base uracyl porphyrin, and the opposite case A-P≡U-D where A–P is the acceptor and U–D is the donor (Scheme 6). 3) Quantification of the antenna effect is possible through examination of a series of related architectures. A somewhat controversial discussion of this issue exists, which is related to a semantic problem of how one actually defines the “antenna effect” (see below).

Scheme 6.

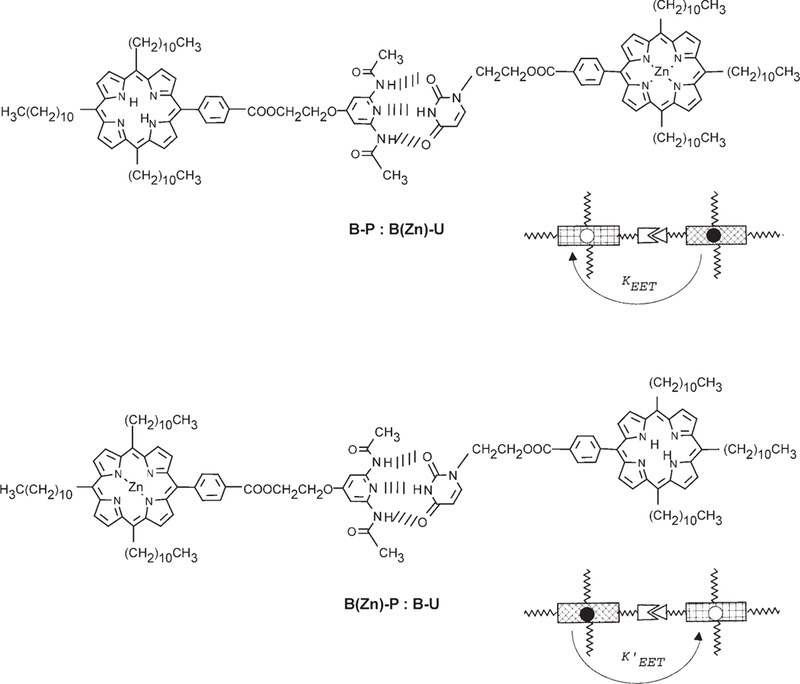
An advantage of complementary motifs is that the role of directionality through hydrogen bonding motifs (P to U or U to P) in EET processes can be assessed.

Covalent steroidal models:

The inherent complications in studying electron and energy transfer in self-assembled systems are the associated supramolecular dynamics and equilibria. Thus, the EET of three isomers of a covalently bound Zn and free base porphyrin on a 5α-androstanic skeleton were investigated to compare with similar studies on the assemblies using flexible hydrogen-bonding linkers. The rigid steroidal linker ensures a predefined geometry that depends on the 3- and 17-diastereomeric benzoates. There are four dihedral angles that can vary in these dyads of meso-benzoate-substituted porphyrins, but previous studies on similar bis(porphyrin) steroids indicate a preferred conformation.^[31] The compounds shown in Scheme 7 were synthesized using two successive esterifications. After the first coupling at the 17 position, a zinc center was inserted followed by stereospecific reduction of the 3-keto group and finally by esterification with the second free base (see the Supporting Information for synthetic details). This stepwise sequence assures regiospecific metalation that otherwise is not achievable, as attempts to monometalate a bis(free base) construct and then separate the two regioisomers (Zn/free base and free base/Zn) failed. CD spectra of the mono-Zn metalated bis-(porphyrin) species show similar excitonic couplets as those of the bis(free base) moieties on similar steroidal skeletons,^[31] except that a 10–30% intensity increase is observed (see Figure S11 the Supporting Information). Thus, similar geometries are expected in the constructs presented herein. These CD studies have shown that porphyrinic chromophores are excellent reporters of chirality over large distances.^[32]

Scheme 7.

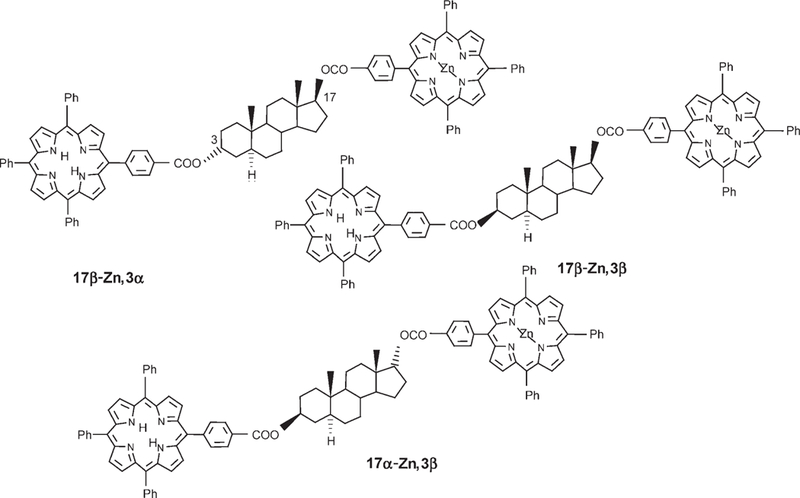
Covalent D-B-A dyads based on a 5a-androstanic skeleton are used to compare the role of the bridge in covalent versus noncovalent energy transfer.

Association studies in solution and on surfaces:

In an earlier study, it was shown that there is no energy transfer when Zn tetraphenylporphyrin (Zn/TPP) is admixed in solu-tion with its free base (TPP).^[6a] As TPP is not very soluble in chloroform or dichloromethane, we used much more soluble porphyrins bearing two undecyl groups in the 5 and 15 meso positions and two benzoate esters in the 10 and 20 meso positions (C; Scheme 1 and Scheme 8). The EET of mixtures of free base porphyrin and C(Zn) can be characterized up to concentrations similar to the ones used for the hydrogen-bonded assemblies. We have previously shown that even at millimolar concentrations there is no associa-tion in solution for C, but the shifts for the ¹H NMR resonances of the isomer with the two undecyl groups in the 5 and 10 meso-positions (D; Scheme 1) gives and indication that it π stacks strongly in this concentration range.^[22] For comparison with the steroidal compounds bearing tetraarylporphyrins, tetra-para-tolyl porphyrins (Scheme 8) were used because of their similar optical spectra. A blue shift of 5 nm is observed for both the absorption and emission bands of the meso alkyl porphyrins appended to the recognition groups with the phenyl linkers relative to typical tetraaryl porphyrins and the steroidal compounds. Even at high concentrations of these nonbonded systems, no evidence for EET was found, which is consistent with previous studies.^[6a]

Scheme 8.

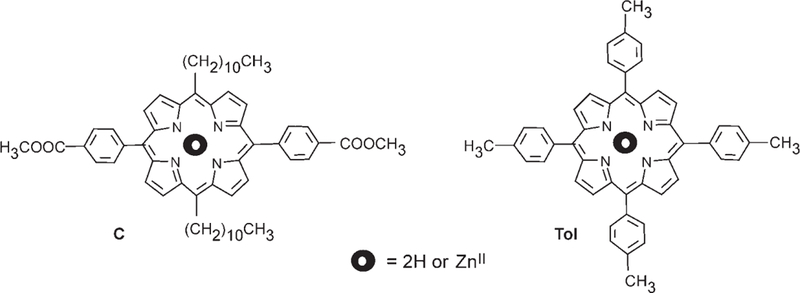
Noninteracting Zn and free-base porphyrins used as calibration standard compounds.

Ultimately, utilization of these systems in solar-energyharvesting devices will require deposition onto conducting or semiconducting surfaces—either ceramic or polymeric. The observed morphologies on surfaces are not a priori similar to those in solution because of the inherent changes in equilibria as the solvent is removed.^[33] Thus, we examined the self-organization of these molecules and mixtures drop cast onto clean glass and mica (see the Supporting information). Several key conclusions can be made: The association of molecules by homocomplementary hydrogen-bonding motifs, in this case uracyl–uracyl and diacetamidopyridyl–diacetamidopyridyl interactions, is known to occur in solution. The specific single and double hydrogen-bonding interactions between the uracyl units (and there are four possible hydrogen-bonding interactions between the pyridyl moieties with varying degrees of stability) are a few kJmol⁻¹ less stable than the heterocomplementary triple hydrogen-bonding interactions.^[28] The homocomplementary interactions become increasingly important as the concentration increases, as do nonspecific interactions, such as π stacking. These intermolecular interactions lead to aggregation of the individual component molecules as the solutions are concentrated. As expected, DLS studies of 25-mm solutions of the individual porphyrins (UCU, PCP, PC(Zn)P, UC(Zn)U) in dry chloroform at 25°C reveals that a small quantity of the compounds aggregate to form particles with similar diameters of approximately 200 nm but with varying dispersities (see Figure S15 in the Supporting Information for typical examples). Contact mode AFM studies of these individual porphyrinic compounds drop or spin cast onto glass surfaces from 25-µm solutions in CHCl₃ show a small surface density of particles that are (15±5)×(210±30) nm (height×diameter), whereas on mica surfaces the heights are somewhat smaller (see Figure S14 in the Supporting Information). Again the dispersities are different for each compound.

Because of the greater intermolecular interactions of the complimentary hydrogen-bonding motifs, it was expected, and observed, that 1:1 ratios of these compounds form larger aggregates at the same 25-µm concentrations in chloroform at 25°C than the components. Thus DLS studies indicate large amounts of 200–400-nm diameter particles for PCP≡UC(Zn)U, and 250–800-nm diameter particles of UCU≡PC(Zn)P, each with a smaller population of about 60-nm diameter particles. Contact mode AFM studies on glass and mica show a much higher surface density of the target assemblies relative to the individual compounds, with heights of approximately 20 nm and diameters of approximately 300 nm (see Figure S14 in the Supporting Information).

In solution, the nanoscaled aggregates of both the compounds and the mixtures likely contain a large amount of solvent, and are composed of numerous subdomains, as has been shown with other porphyrinic nanoparticles.^[34] Thus, upon deposition and solvent evaporation the nanoparticles collapse and can break apart into the subdomains. Fluid dynamics as the solvent evaporates also contribute to the observed morphologies. Thus, the AFM data can be considered generally consistent with the DLS data.

We examined FT-IR spectra of equimolar mixtures of B(Zn)U≡BP and B(Zn)P≡BU in concentrated and dilute solutions of dry chloroform (see Figure S4 in the Supporting Information). There was clear evidence of hydrogen bonding in the concentrated solutions by broad bands in the 3000–2200-cm⁻¹ region. Upon dilution, these bands gradually decrease as a result of dissociation, a behavior that is in parallel with the NMR spectroscopic analysis in dry chloroform (see the Supporting Information).

Photophysical studies

Steady-state spectra:

A good overlap exists between the Q absorption bands of the FB acceptor molecule B–P and the emission of the energy donor B(Zn)–U, and conversely the overlap integral is quite small in the reverse case (see Figure S1-B, blue area in the Supporting Information). This represents a sine qua non condition for a directional energy transfer. In the case of an equimolar mixture between a Zn– donor and a FB-acceptor, porphyrin energy transfer occurs only when these come close to each other, either as a result of multiple hydrogen bonding or the covalent steroidal bridge. For two noninteracting units there is no observable energy transfer in solution over a wide concentration range, as explored with the two couples C(Zn)/C and Tol(Zn)/Tol (data not shown).

Two methods can be used to assess the efficiency of the energy transfer (Φ_EET) by steady state methods. If a comparison of the fluorescence excitation spectrum monitored at the emission of the free-base acceptor (ca. 725 nm) with the absorption spectra of the mixture reveals a decreased donor absorption, an increase in FB emission as a result of EET is indicated. Alternatively, one can approximate the energytransfer efficiency according to Equation (2):^[6a]

$${\Phi }_{\text{EET}}=\left(1-F_{605}/F_{1:1}\right)\times 100$$ (2)

where F₆₀₅ is the fluorescence of the Zn donor at 605 nm, which is quenched in the case of an energy-transfer process, and F_1:1 is the fluorescence in the absence of energy transfer, that is, in a hypothetical 1:1 mixture of Zn donor and FB acceptor. The spectra of solutions of C(Zn)–C and Tol(Zn)–Tol at the same concentration, in which there is no energy transfer, has the least amount fluorescence at 605 nm, at which only the donor fluoresces. Thus, there is no quenching of the donor fluorescence upon adding increasing amounts of the free base.

Conversely, in the case of the covalent steroidal models, a relatively strong quenching of the donor fluorescence is observed. From the degree of steady-state fluorescence quenching, Φ_EET is determined to be approximately 46 and 40% for 17αZn-3β and 17αZn-3β dyads, respectively. Note that upon dilution over three orders of magnitude, the fluorescence quenching remains almost constant as the donor and acceptor cannot be taken apart (see Figure S11 in the Supporting Information). A small degree of aggregation is observed at concentrations over approximately 15 µm.

In contrast to the covalent systems, much lower Φ_EET values were determined for the supramolecular systems. Thus, for the couple B(Zn)–P≡B–U Φ_EET=27% was derived, whereas for the inversely metalated system B(Zn)–U≡B–P an even lower value of Φ_EET=19% was determined by steady-state experiments by using Equation (2). In the case when two donors can transfer energy to the same acceptor, doubling of the acceptor fluorescence is expected. In the tapes formed from U-C(Zn)-U≡P-C-P, or U-C-U≡PC(Zn)–P, the fluorescence of the free-base acceptor roughly doubles relative to the systems with single donors, thus increasing to Φ_EET=50 and 54% respectively. Figure 1 illustrates the quenching of the donor fluorescence and the concomitant increase in the acceptor fluoresence in the self-organized tapes. Under the constant illumination of the steady-state experiments, the light flux is such that only one or two chromophores of a given tape are hit at a given time during the lifetime of a few nanoseconds. If a photon hits a zinc donor in the tape, there are two neighboring acceptors; for example, the energy can be transferred to either neighboring free bases. Statistically, this behavior is similar to the two-acceptor/one-donor systems. An interpretation of the observed doubling in free base fluorescence is that the energy transfer to each neighbor is approximately equally to 25%.

Figure 1.

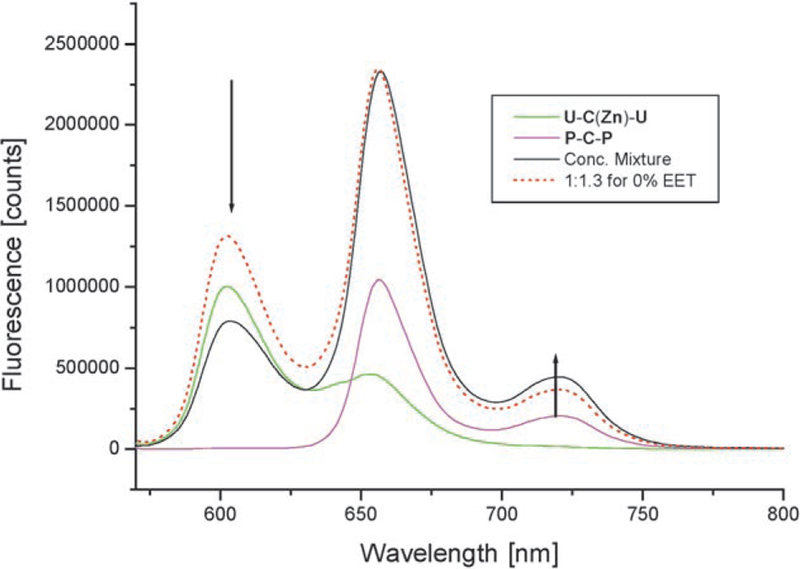
Addition of P-C-P to U-C(Zn)-U in dry chloroform. Note that considerable quenching at 605 nm occurs in comparison with a calculated 1:1.3 mixture at the same concentrations of about 2 mm and in the absence of energy transfer (dotted line). Excitation was at 550 nm and the measurement was done with a front face geometry and in a 1 cm2 cuvette. (For several other concentrations see Figure S9 in the Supporting Information).

In contrast to the steroidal models, these triply hydrogenbonded systems are in dynamic equilibrium in solution, thus a strong recovery of the donor fluorescence is observed upon dilution because the donor and acceptor dissociate. Such adaptive systems allow the possibility of fine-tuning the apparent luminescence through Φ_EET, as seen in a plot of EET versus concentration of the donor or versus the molar ratio (inset of Figure 2).

Note the very steep decrease in Φ_EET value at low concentrations of under 0.1 mm. This behavior parallels the association constant determination (Figure 2) and can be used to determine the effective association constants from the quenching efficiency of the donor fluorescence in known and optimized systems. However, the saturation curve for EET from P–C(Zn)–P to U–C–U (half maximum at ≈60 µm) differs from that of the association constant between B–P and B–U in NMR titrations (half maximum at ≈670 µm) by about a factor of 10. This difference in concentration dependence arises for several reasons. The NMR spectra indicate the formation of a dimer as each porphyrin is monotopic. The porphyrins are ditopic in the EET studies summarized in Figure 2 (inset), thus doubling the effective concentration of the recognition moieties and possibly indicating the formation of small tapes or aggregates.

Three problems with the calculation of Φ_EET values have to be taken into account: First is the deconvolution of the spectra. Fitting of the measured spectra to the sum of the components yields coefficients suitable for calculating the quenching and comparing to standard systems with no EET and of known stoichiometry. The fitting is, however, only possible at the maxima of 605 and 655 nm simultaneously and not at 725 nm. By using a gradient optimization program which finds the coefficients by a least-squares fit (over the entire spectral width) a much poorer fit is obtained. A second problem comes from the different extinction coefficients of the two components and thus absorptions at the 550 nm excitation wavelength. In the concentrated solutions, much of the emitted light gets (re)absorbed in the front face geometry used. This experimental geometry necessitates correction of the fluorescence spectra for absorption but this correction does not alter the results and in fact reveals isosbestic points. Third, the fluorescence maxima of the hydrogen-bonded complexes are blue-shifted by 2–3 nm relative to the FB emission, thus further indicating that a new complex is formed, and this behavior makes the fitting with the individual components problematic. These issues result in 20% intrinsic errors in the values for Φ_EET.

A second experiment compares the excitation spectra (at the 720-nm emission of the FB acceptor) of the self-organ-ized system to the absorption spectra of the same solution. The excitation spectrum shows reduced intensity in the Q bands as a result of the EET from the zinc–porphyrin donor (510 and 595 nm) relative to the absorption spectra in the Q band region, which clearly indicates that part of the donor excited-state energy is transferred to the FB (Figure 3). These steady-state methods clearly show that hy-drogen-bonding motifs can bring the donor and acceptor into close proximity for the time required for EET to occur.^[28] However, the kinetics reveal a more accurate pic-ture of the energy-transfer processes within these self-organized systems.

Figure 3.

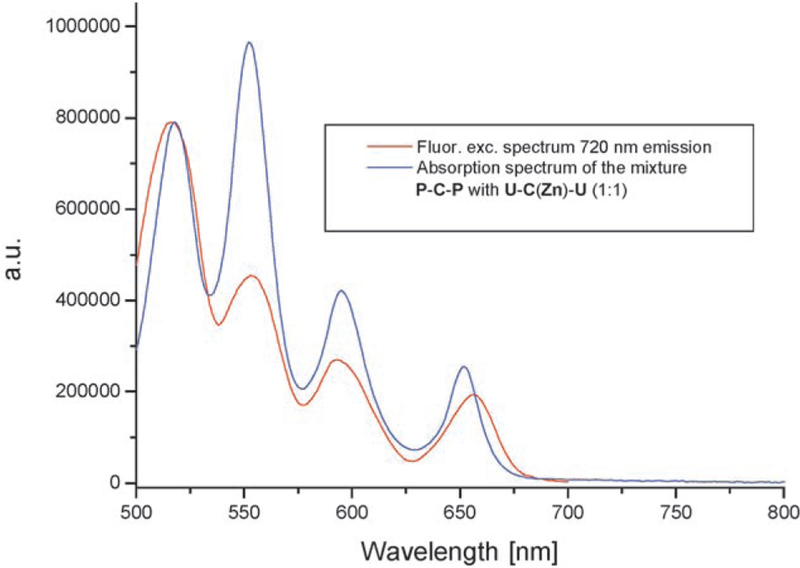
Comparison between fluorescence excitation (red trace) and ab-sorption (blue trace) spectra for a 1:1 mixture of U-C(Zn)-U≡P-C-P. The concentration was approximately 0.5 mm in chloroform at room temperature measured with a front face geometry. The spectra were scaled at the first Q maximum.

Time-resolved measurements:

Initial measurements were made in cyclohexane using a single-photon timing setup.^[19] Decay-associated emission spectra (DAES) obtained by a global analysis were used to determine the energy-transfer components.^[20] These spectra clearly indicate a decay of the donor fluorescence measured at 605 nm with a concomitant rise on the acceptor side (at ca. 730 nm), thus giving rise to the characteristic “butterfly-type” lineshape of the 16-ps DAES (Figure 4). For the inversely metalated dyad B(Zn)–P≡B–U in cyclohexane, very similar data, within the experimental error, were obtained and a 19-ps component could be assigned to the EET from the DAES (data not shown). Surprisingly, for the covalent steroidal model compounds, the EET is slower by almost two orders of magnitude. Figure 5 shows the corresponding DAES in the 17βZn–3β dyad in which the 1.35-ns component is clearly identifiable as arising from EET.

Figure 4.

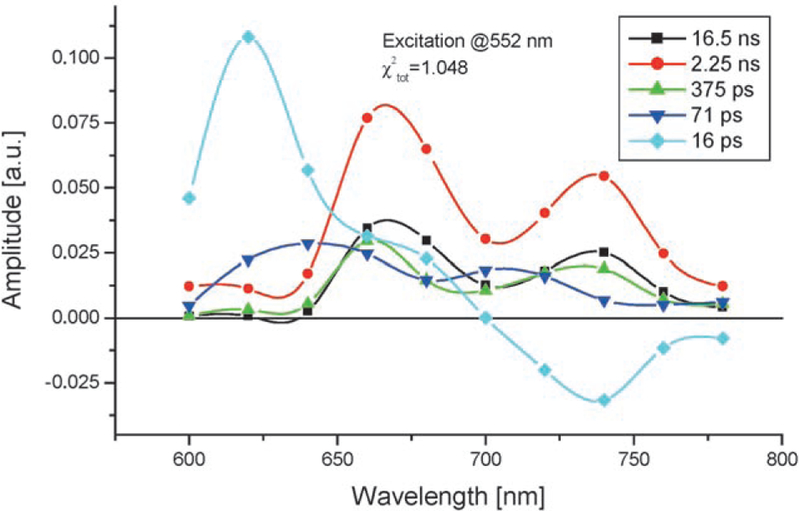
Typical DAES of the hydrogen-bonded assembly B(Zn)-U≡B-P, the concentration was 15 mm in cyclohexane. The 16 ps component can be clearly associated to the energy transfer whereas one of the other components (2.25 ns) represents the fluorescence of the FB as a result of direct excitation at 552 nm. The B(Zn)–U absorbs about three times more than the free base B–P at 552 nm.

Figure 5.

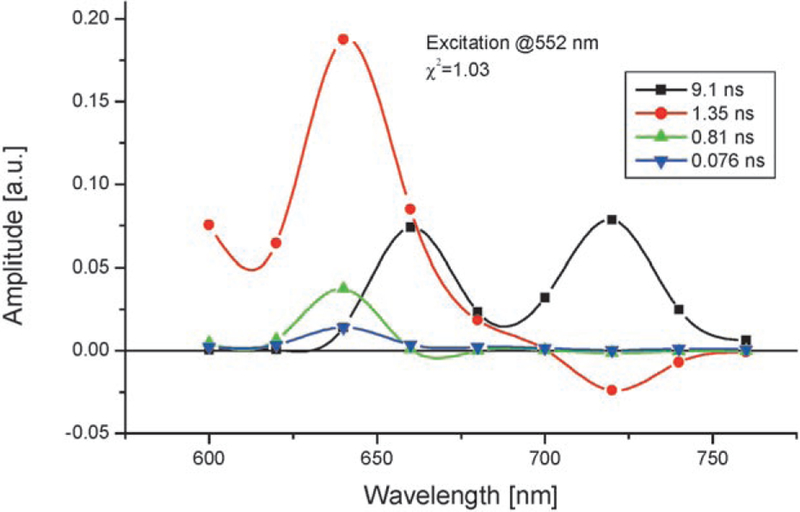
DAES of 17βZn-3β. The experimental conditions and setup are similar to the ones used to obtain the results shown in Figure 4.

From molecular modeling, the separations between the donor and acceptor porphyrins in the supramolecular systems in an extended conformation and in the steroidal covalent models appear similar, so that similar rates for the EET were expected (see below). Puzzled by the much faster EET in the triply hydrogen-bonded systems, we decided to reinvestigate these systems using a time-resolved system that employed a streak camera, which has better spectral resolution, but somewhat lower temporal resolution as there was no deconvolution performed (typical results are shown in the Supporting Information).

For the steroidal compounds, two time constants were found (see Figure 6): time constant τ₁ is between 0.91 and 1.19 ns as a result of the energy transfer from Zn–TPP to FB–TPP, as demonstrated by the DAES, which show a decay of the spectral components of the Zn–TPP moiety with a simultaneous rise in the fluorescence of the FB–TPP part of the molecule. The t₂ value is found to be on the order of several nanoseconds, thus corresponding to the decay of the FB–TPP spectral component (Figure 6).

Figure 6.

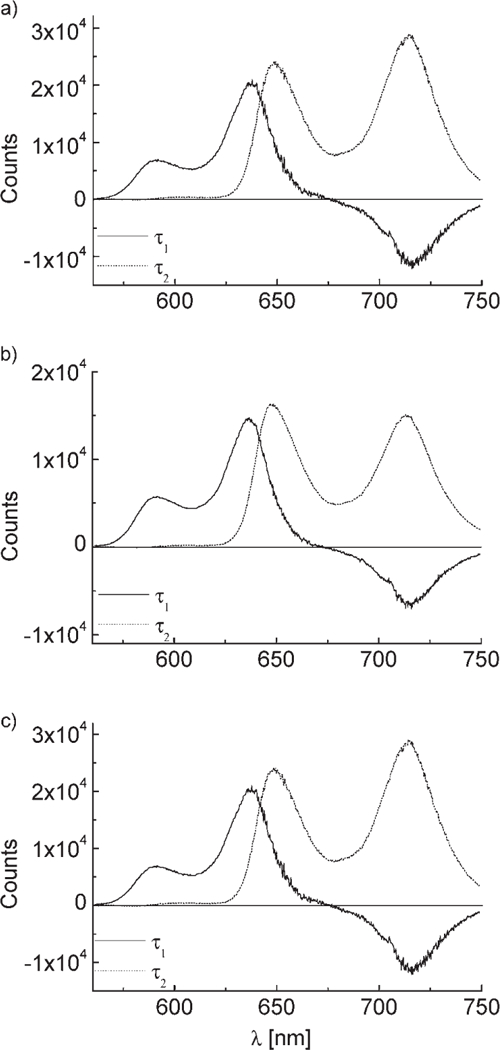
The DAES of the steroidal linked systems 17α-Zn,3β (a), 17β-Zn,3α (b), and 17β-Zn,3β (c) using the streak camera apparatus. The compounds were about 0.1mm in chloroform, excitation at 552 nm, where the Zn donor absorbs about three times more than that of the free base acceptor. Time constants (corrected for the blinking electron beam): 17α-Zn,3β (τ₁ = 0.99 ns, τ₂ = 3.7 ns, χ² = 1.426×10⁻⁴); 17β-Zn,3α (τ₁ = 0.91 ns, τ₂ = 4.2 ns, χ² = 4.208×10⁻⁵); 17β-Zn,3β (τ₁ = 1.19 ns, τ₂ = 5.4 ns, χ² = 4.892010⁻⁵).

Discussion

The much higher EET transfer rates in the triply hydrogen-bonded assemblies relative to the covalent steroidal models was surprising, thus prompting further studies. Can the well established theories for EET reconcile these results, or do we need to set boundaries for the applications of Förtser EET? Recent data on natural-light-harvesting systems suggest that a new model may be more appropriate for EET in hierarchical assemblies.^[15b]

Energy transfer in bis(porphyrin) steroidal compounds 17-Zn-TPP-3-H₂-TPP-5α-androstane-3,17-diols (17α-Zn,3β; 17β-Zn,3β; 17β-Zn,3α)

Estimation of experimental energy transfer:

The experimental EET was extracted from the set of “corrected” spectra by using Equation (2ʹ):^[6a]

$${\Phi }_{\text{EET}}=1-\frac{F^{\text{max}}}{F_{1:1}^{602}}$$ (2ʹ)

where $F_{1:1}^{602}$ is the hypothetical fluorescence intensity at 602 nm (first maximum of emission) of a 1:1 mixture of the donor and the acceptor in the absence of EET, and F^max is the observed fluorescence intensity at the maximum of emission close to 602 nm. In practice, the value of $F_{1:1}^{602}$ was evaluated starting from the emission spectra of the zinc and free base tetra-para-tolylporphyrin model compounds (Zn-Tol and H₂-Tol).^[35] The use of F^max instead of F⁶⁰² for the steroidal compounds is justified by the apparent blue shift of the first maximum of emission (by 6–7 nm) with respect to the model mixture. Thus, the use of the intensities at 602 nm instead of the maxima would lead to systematic overestimation of the experimental EET. The F^max values were estimated after normalization (from the spectrum of the 1:1 mixture of Zn-Tol and H₂-Tol) of the intensities at the second maximum of emission (around 650 nm) and by using two methods: 1) direct evaluation of F^max (at 595–596 nm); 2) three Gaussian fits of the emission profiles.^[36] The two methods give consistent values that agree within 0.01 emission units. Table 1 reports the estimated Φ_EET value for the three isomers.

Table 1.

Fluorescence parameters and experimental EET values for compounds 17β-Zn,3β, 17β-Zn,3α, and 17α-Zn,3β.

Compound	λmax [nm][a]	Fmax [a.u.][a]	ΦEET exp.[b]	ΦEET error	ΦEET calcd [%][c]	τ1 [ps]
17β-Zn,3β	595	0.11	21	±4	42	1190
17β-Zn,3α	594	0.097	31	±5	54	910
17β-Zn,3β	594	0.089	37	±6	51	990
Model 1:1	602	0.14
	595	0.189

^[a]λ^max and F^max wavelength maximum and intensity for the first emission band; F^max is obtained after normalization of the intensities at the second maximum of emission (around 650 nm). %

^[b]Φ_EET exp. represents the experimental percent energy transfer efficiency evaluated with Eqution (2ʹ).

^[c]Φ_EET represents the calculated value from the corresponding lifetimes. For a comparison of the calculated values with the experimental efficiencies determined both from the stationary fluorescence and the time resolved measurements, see the Supporting Information.

Theoretical calculation of energy transfer and geometry calculations of the steroidal compounds:

The bis(porphyrin) derivatives of 5α-androstane-3,17-diol were considered herein as useful models of the hydrogen-bonded assemblies but with less dynamic structures in solution. The molecular geometries of the 17-Zn-TPP-3-H₂-TPP-5α-androstane-3,17diols were calculated by using the Merck force field MMFF94 developed by Halgren,^[37] and the conformational space was sampled with Monte Carlo (MC) simulations.^[38] The necessity of using the MC conformational searches arises from the flexibility around the ester group and the phenylporphyrins bonds. The dihedral angles described by the two linkages (indicated by ψ and φ in Scheme 9) oscillate around the respective average values in a largely unrestricted range (–60 < ψ < 60^° and 45°<ϕ< 135^°), although only the average structures are detected on the NMR timescale. These conformational dynamics are reflected in the relative arrangement between the donor and acceptor units thence in any interaction between the two fluorophores, including the EET. The MMFF/MC calculations find a limited number of sets (two or four) of well-defined minima with ϕ_A,ϕ_D = 90° and ψ_A,ψ_D ≈±30–40° for each compound.^[39] Table 2 reports the relevant geometrical parameters evaluated for the average structures of compounds 17β-Zn,3β, 17β-Zn,α and 17α-Zn,3β (ψ = 0° and ϕ= 90°). The geometrical parameters are defined in Scheme 10.

Scheme 9.

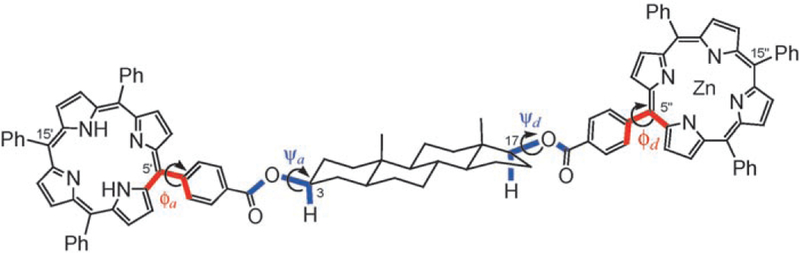
Dihedral angles defining the geometry of steroidal compounds.

Table 2.

Geometrical parameters for the average MMFF structures of compounds 17β-Zn,3β, 17β-Zn,3α, and 17α-Zn,3β.

Compound	Rad [Å][a]	θaR [°][b]	θndR [°][c]	τand [°][d]	ΦEET [%]	Lifetime [ps]
17β-Zn,3β	29.0	+28	+59	−124	21	1190
17β-Zn,3α	23.9	+60	+45	−152	31	910
17α-Zn,3β	24.8	+17	+87	+105	37	990

^[a]R_ad is the interporphyrin (donor “d” at C17, acceptor “a” at C3) center-to-center distance (if edge-to-edge distances are considered, these are approximately 10 Å smaller).

^[b]θ_aR is angle between the 5ʹ 15ʹ direction of acceptor porphyrin “a” at C3 and the interporphyrin center-to-center distance vector.

^[c]θ_ndR is angle between the vector normal to the plane of donor porphyrin “d” at C17 and the interporphyrin center-to-center distance vector.

^[d]τ_and is the projection angle between the 5ʹ−15ʹ direction of “a” and the normal to the plane of “d” (cf. Scheme 10).

Scheme 10.

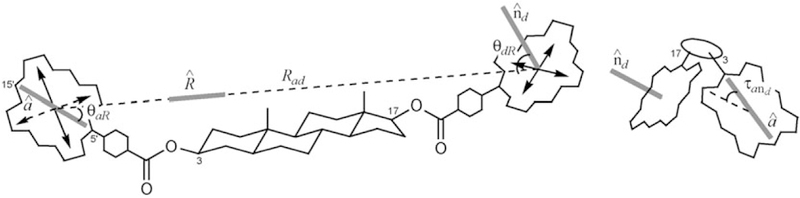
Geometrical parameters relevant to EET estimation.

It is apparent from Table 2 that the 17α-Zn,3β, isomer has a greater experimental rate of EET, even though it has a longer calculated interchromophoric distance than the 17β-Zn,3α isomer, which exhibits less efficient rate of EET. This behavior means that the orientation factors κ must play a role in determining the observed EET. Using the usual simplification κ²=2/3, which is valid for a true isotropic donor and acceptor couple, would be inaccurate.

Choice of the κ² expression:

The theoretical energy transfer is calculated through the Förster formulae given in Equations (3) and (4):

$${\Phi }_{\text{EET}}=\frac{R_0^6}{R_0^6+R_{\text{ad}}^6}$$ (3)

$$R_0^6=8.79\times {10}^{-5}\frac{Q_{\text{d}}{\kappa }^2}{n^4}J$$ (4)

where R_ad is the interchromophoric distance in Å, R₀ is the Förster distance in Å, Q_d is the donor quantum yield (0.025 for Zn-TPP in CHCl₃), n is the medium refractive index (1.4459 for CHCl₃ at 20°C), and J is the overlap integral in units of m⁻¹ cm⁻¹ nm⁴ (obtained by normalizing the donor emission spectrum to unity, thus expressing the acceptor absorption spectrum as molar absorption and reporting both in wavelengths). For the current case, it is estimated for the model compounds (Zn-Tol and H₂-Tol) J=3.26× 10¹⁴M⁻¹cm⁻¹nm⁴ (3.2×10⁻¹¹mol⁻¹cm⁶), which compares well with reported values.^[6a,40]

The choice of the most proper expression of the orientation factor for these systems is not straightforward. In fact, the Q bands of the porphyrin chromophore are known to be related to two perpendicularly oriented and degenerate (or quasi degenerate) transitions polarized in the porphyrin plane, and directed along the opposite N–N directions;^[41] these are referred to as Q_x and Q_y components.^[42] For closed-shell metallotetraphenylporphyrin systems (i.e., Zn–TPP), the Q_x and Q_y are exactly degenerate and undistinguishable (the presence of the ester group at the para position of the 5ʹʹ-phenyl in the steroidal compounds only slightly perturbs the degeneracy). Thus, the emission of the donor porphyrin at C17 must be regarded as polarized along the whole plane^.[40b] For the free-base H₂–TPP, the absorption Q_x and Q_y components are well distinguished; the lowest energy absorption bands (at about 590 and 650 nm) are defined as arising from the Qx dipole component (along the N-H–H-N direction). As the position of the pyrrole N–H atoms is fluxional on the microsecond timescale^[43] and the two possible dispositions are equally probable, both must be considered.

Thus, the energy transfer in these covalent models actually occurs between a nominally planar degenerate donor and a dipolar acceptor, to which Equation (5) is applicable^:[44]

$${\kappa }^2=\frac{1}{2}\{1+3(\widehat{a}\cdot \widehat{R})2-{[\widehat{a}\cdot {\widehat{n}}_d-3(\widehat{a}\cdot \widehat{R})(\widehat{R}\cdot {\widehat{n}}_d)]}^2\}$$ (5)

where the denotes the unit vectors of the interchromophoric distance R, the normal n_d to the donor plane, and the acceptor dipole direction a (see Schemes 9 and 10). In this situation, the range of possible κ² values is 0–2, with 0.5 being the most and 2 the least probable values.^[44]

A further spectroscopic complication is the pronounced vibronic structure of the Q bands, which makes the actual transition dipole vary with the vibrational state involved. Wavelength-dependent kinetics can probe these issues experimentally,^[45] but the theoretical description is significantly more complex.

Role of the conformational averaging:

As described above, at least four degrees of conformational freedom (ψ and ϕ dihedrals) are largely unrestricted in 17α-Zn,3β, 17β-Zn,3β and 17β-Zn,3α. As it is likely that both of these rotations occur with rates not much higher than the EET rate,^[46] the dynamics of these motions should be taken into account when calculating the theoretical EET. However, the evaluation of the EET in a static averaging regime would require calculating the κ² value for all the possible donor/acceptor arrangements,^[44] thus implying a computational effort beyond the scope of the present work. The dynamic averaging approximation has been employed in EET calculations of covalent bis(porphyrin) systems.^[40a] Analysis of CD spectra of steroidal bis-porphyrins suggests that only an average value of ±90° for ϕ_a and ϕ_d dihedrals needs to be considered.^[31] The well-known geometry of the dihedral angle between the macrocycle and meso aryl moieties of ±90° in solution is due to steric interactions between the ortho phenyl hydrogen atoms and the pyrrole β hydrogen atoms and was used for the ϕ_a and ϕ_d values in the calculation. In crystal structures, dihedral angles between 90 and 70° are most often observed.^[22a] Thus, we used the dynamically averaged conformations for the compounds 17α-Zn,3β, 17β-Zn,3β and 17β-Zn,3α to evaluate the theoretical EET. Molecular models indicate that the interchromophoric distances R_ad, which greatly affect the EET, are essentially unaffected by the allowed rotations around the ψ and ϕ angles. For the donor planar polarization, the average plane with ϕ_d=90° and ψ_d=0° was used. For the acceptor dipole, it was assumed that the rotation around the 5ʹ–15ʹ direction and the N–H dynamics discussed above would define an effective transition moment oriented along the 5ʹ–15ʹ direction itself. These assumptions lead to the parameters shown in Scheme 10 and reported in Table 3 for calculating the theoretical EET through Equations (3)–(5).

Table 3.

Calculated orientation factors κ², Förster distances R₀, and theoretical EET for compounds 17β-Zn,3β, 17β-Zn,3α, and 17α-Zn,3β.

Compound	κ2	R0 [Å]	ΦEET,calcd	ΦEET,exp	Δ [%][a]	τ1 [ps]
17β-Zn,3β	1.0	23.4	0.22	0.21	+4	1190
17β-Zn,3α	0.52	21.0	0.31	0.31	0	910
17α-Zn,3β	0.94	23.1	0.40	0.37	+7	990

^[a]Percent difference between Φ_EET,calcd and Φ_EET,exp relative to Φ_EET,exp.

Calculation of Φ_EET:

The orientation factors κ² [Eq. (5)], Förster distances R₀ [Eq. (4)], and theoretical EET [Eq. (3)] for 17β-Zn,3β, 17β-Zn,3α, and17α-Zn,3β were calculated by using the geometrical description outlined above (Table 3). Equation (5) may be expressed as a function of the geometric parameters defined in Table 2 and Schemes 9 and 10 according to Equation (6):

$${\kappa }^2=\frac{1}{2}\{1+3{\text{cos}}^2{\theta }_{\text{aR}}-{\left[\text{sin}{\theta }_{\text{aR}}\text{sin}{\theta }_{\text{ndR}}\text{cos}{\tau }_{\text{and}}-2\text{cos}{\theta }_{\text{aR}}\text{cos}{\theta }_{\text{ndR}}\right]}^2\}$$ (6)

For all compounds, the calculated EET rates agree well with the observed ones, with discrepancies below 10%. Notice that the κ² factor for 17α-Zn,3β is almost twice that of 17β-Zn,3α, thus suggesting a reason for the greater observed EET for the former despite the longer interporphyrin distance.

Conformational-energy minimization (MacroModel and HyperChem^[47]) using a combination of geometry optimizations at semiempirical (PM3) and molecular mechanics level (MM + force field) results in similar geometries to those estimated above but identifies several conformers with approximately the same energy. The κ² and EET rates for the four most stable conformers are consistent with the results in Table 3.

Energy transfer within the supramolecular assemblies and their geometry calculations:

For the assessment of the multiple conformers, the undecyl groups were removed and a second zinc atom was inserted to facilitate measurement of the center-to-center distance between the two porphyrin units. Figure 7 presents two such conformers which differ in energy by less than 1 kcal mol⁻¹ and are interconvertible without breaking the triple hydrogen bonds.

Figure 7.

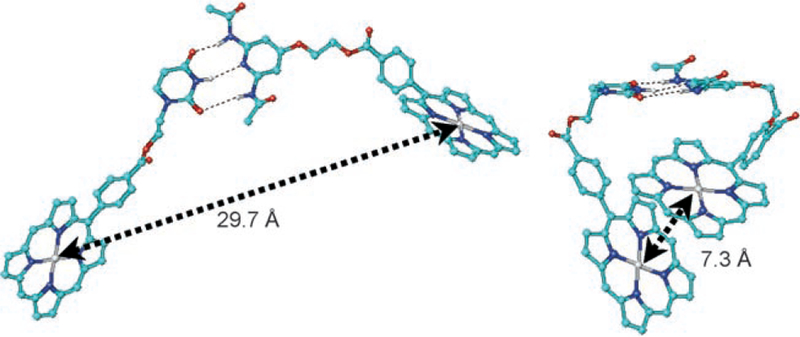
Two different conformers of B(Zn)-U≡P-B(Zn). The meso-un-decyl groups have not been included in the calculation.

Molecular dynamics (MD) simulations were run on B(Zn)-U≡P-B with the purpose of obtaining a more exhaustive conformational picture. Even starting with the molecule in an extended conformation, MD simulations in vacuo (steps of 1–2 fs) unavoidably led within 30–50 ps and at 300 K to structures with the two porphyrin units stacked.^[47b] In this favored geometry, which is similar to that showed in Figure 7 (right), the two porphyrin planes lay almost parallel to each other at a distance of 4.3–4.5 Å, with an approximate center-to-center distance of 7 Å and an offset of approximately 4 Å. MD simulations in explicit solvents, which would probably be less biased toward stacked structures, were prevented by the large system size.

The supramolecular dynamics of this hydrogen-bond assembled dimer allows for a plausible explanation of the observed photophysical properties, and a comparison with the covalent steroidal models. In the extended conformations, the center-to-center distance is comparable to that in the steroidal models and the orientation factor κ² can take similar values, which implies EET times on the order of 1 ns. Some conformations have much lower center-to-center distances, for example, under 1 nm, which indicates π–π interactions between the porphyrin macrocycles and extended orbital overlap. Alternatively, if one considers edge-to-edge distances that are more appropriate for large chromophores of size comparable to that of the separating bridge, then an extensive orbital overlap is clearly evident. This behavior could facilitate a Dexter exchange mechanism, which nominally entails a double electron transfer. In contrast to the Förster mechanism, which operates exclusively as a singlet– singlet EET, the Dexter EET can also operate between the triplet states. Upon sampling over a large number of conformers, these hydrogen-bonded dyads are in somewhat extended conformations most of the time, but can access tightly packed conformations in which a very rapid transfer takes place on the 20-ps timescale. This is roughly fifty times faster than in the covalent steroidal models and the efficiency is nearly half in the supramolecular systems because of competing processes, such as nonradiative decay and intersystem crossing to the longer lived triplet manifolds. Actually, the shorter the excited-state lifetime is, the influence of other quenching mechanisms than energy transfer should be smaller. The conclusion is that these supramolecular systems in extended conformations are minimally active in terms of EET, but within the population that adopts a packed conformation the EET takes place rapidly. However, in these closed conformations additional nonradiative processes, for example, electron transfer, can take place, lowering thus the overall transfer efficiency.

Antenna effects:

When multiple donors are present the photon capture cross section is increased and this enhances the Φ_EET. Herein, we use the definition of the antenna effect as introduced by Lehn and co-workers wherein multiple chromophores lead to a higher probability of trapping useful photons,^[48] as such there is no energy “amplification” as suggested more recently.^[7c–f]

The present study illustrates that for porphyrins, which have an area of approximately 1 nm², the center-to-center distance is only a rough approximation, especially when dynamics are considered. For these supramolecular systems, the Förster equation for EET needs to account for the distinct conformational populations: extended and π–π stacked. For the latter conformation, the EET is accelerated by almost two orders of magnitude relative to rigid covalent systems, but the efficiency was also decreased as a result of conformations with low EET and other decay pathways. Similar conclusions were drawn from studies of a rigidly linked dyad with a bipyridine spacer in which only the relative dihedral angles of the macrocycles can change, which is controlled by the metalation state of the bipyridine unit. The relative orientation of two porphyrin units on opposing sides of bipyridine linkers dictates both the electronic coupling in the ground-state and excited-state properties.^[49] Furthermore, it was recently shown that in a covalent bis(porphyrin) construct on a terpyridine skeleton, beside energy transfer, upon switching the conformation to a closed compact form, an electron-transfer process is responsible for the observed fluorescence quenching.^[50]

Conclusion

This study shows that the design of supramolecular antennas requires precise optimization of the architecture to achieve efficient excitation-energy transfer. As expected, the diacetamidopyridyl–uracyl moieties afford complementary hydrogen-bonding motifs that promote the association of the donor and acceptor molecules in moderately polar and nonpolar solvents. Metal coordination can be used to organize chromophores into more robust, less dynamic architectures, but there are both redox and heavy-atom effects that need to be considered.^[33a,51] This principle is actually used in the chlorosomes in which ligation of the central magnesium atoms in bacteriochlorophylls is the main supramolecular interaction.^[12d] Porphyrins and phthalocyanines are excellent candidates for the formation of photonic materials such as antennas as they are significantly more robust chromophores than the photosynthetic pigments, are readily synthesized, and have a rich coordination chemistry. As the size and complexity of the target systems increase, self-assembly becomes an increasingly important, if not the only, means to access large quantities of multichromophoric arrays for diverse applications. We are currently pursuing studies on photosensitizing wide bandgap semiconductors with self-assembled antenna systems with the view to fabricate hybrid solar cells that can function efficiently also under low-light illumination, in a similar manner to the chlorosomses of the green photosynthetic bacteria.