Modeling excess zeros and heterogeneity in count data from a complex survey design with application to the demographic health survey in sub-Saharan Africa

Abstract

Purpose

To show a novel application of a weighted zero-inflated negative binomial model in modeling count data with excess zeros and heterogeneity to quantify the regional variation in HIV-AIDS prevalence in sub-Saharan African countries.

Methods

Data come from latest round of the Demographic and Health Survey (DHS) conducted in three countries (Ethiopia-2011, Kenya-2009 and Rwanda-2010) using a two-stage cluster sampling design. The outcome is an aggregate count of HIV cases in each census enumeration area of each country. The outcome data are characterized by excess zeros and heterogeneity due to clustering. We compare scale weighted zero-inflated negative binomial models with and without random effects to account for zero-inflation, complex survey design and clustering. Finally, we provide marginalized rate ratio estimates from the best zero-inflated negative binomial model.

Results

The best fitting zero-inflated negative binomial model is scale weighted and with a common random intercept for the three countries. Rate ratio estimates from the final model show that HIV prevalence is associated with age and gender distribution, HIV acceptance, HIV knowledge, and its regional variation is associated with divorce rate, burden of sexually transmitted diseases and rural residence.

Conclusions

Scale weighted zero-inflated negative binomial with proper modeling of random effects is shown to be the best model for count data from a complex survey design characterized by excess zeros and extra heterogeneity. In our data example, the final rate ratio estimates show significant regional variation in the factors associated with HIV prevalence indicating that HIV intervention strategies should be tailored to the unique factors found in each country.

1. Introduction

AIDS is one of the most significant public health problems around the world.¹ Since the inception of the epidemic, there have been over 70 million persons infected with HIV with approximately 35 million AIDS-related deaths.^1,2 Among the estimated 35.3 million people living with HIV,² sub-Saharan Africa is the region most affected with over 25 million HIV cases which constitutes about 5% of the adult population in this region.³

HIV prevalence in sub-Saharan Africa varies regionally. In west and central Africa, HIV prevalence is lower than in east and southern Africa, with HIV prevalence below 2% in most countries in this region. In east and southern Africa, HIV prevalence is above 5% in many countries.⁴ Due to several prevention and intervention strategies, the rate of HIV infection is improving in many countries.^5,6 In some countries, HIV prevalence has recently declined, but in the majority of countries, the epidemics appears to have stabilized with constant prevalence rates. For example, the HIV prevalence in Kenya fell from approximately 14% to 5% over the past 20 years⁷ while Ethiopia and Rwanda have seen little variation in prevalence over time. Recent data from DHS (Demographic and Health Survey) show that HIV prevalence estimate in Kenya was 6.7% in 2003 and 6.4% in 2010, while the estimate in Ethiopia it was 1.4% in 2000 and 1.5% in 2011. In Rwanda, it was 3.0% in 2000 and 2010.

Researchers are increasingly paying attention to characteristics that affect regional HIV prevalence in Sub-Saharan Africa. Most of the studies on HIV prevalence undertaken in some sub-Saharan African countries using DHS or other smaller surveys are country-specific and mostly descriptive in nature. There are no studies that use standardized multi-country data to assess the issue of regional variation in sub-Saharan Africa.

The main goal of this study is therefore to show a novel application of a weighted zero-inflated negative binomial model (ZINB) in modeling count data with extra heterogeneity to examine factors (demographic, socio-economic, behavioral, HIV knowledge, and stigma) associated with regional variation in HIV-AIDS prevalence in sub-Saharan Africa. The novelty is the model accounts for the complex sampling design nature of the data (two-stage cluster sampling design) and for the clustering of observed count responses by ‘‘census enumeration area’’ (CEA) and country in addition to zero-inflation. The primary outcome is defined as an aggregated count of HIV positive people in a country-specific CEA standardized by CEA specific population size as an off-set. We hypothesize that some combination of the risk factors discussed above can be used to quantify the regional variation in HIV prevalence.

2. Materials and methods

2.1. Data and study design

Our analyses are based on data from the latest round of the DHS conducted from 2008 to 2011 in three countries (Ethiopia, Kenya and Rwanda). The surveys were household-based and used a two-stage sample design. At the first stage, a stratified sample of CEAs is selected with probability proportional to size, and at the second stage, households are selected by equal probability in the selected CEAs.⁸ In the selected households, all women of reproductive age (15–49) are eligible for an individual interview. Sub-samples of men are included in the survey, generally by interviewing all men in every second or third household.⁹

Measures assessed in the DHS included age, sex, education, and the relationship of the subject to the head of the household. There was a separate questionnaire for women and men used to collect the information on a wide range of topics, such as background characteristics, marriage and sexual activity, knowledge of AIDS, etcetera. In DHS surveys, testing for HIV infection was conducted for survey participants. A men’s questionnaire was administered to all eligible males in one-third of the households, a subsample often used in DHS surveys. In these same households, all respondents were asked to give a few drops of blood to be tested in a laboratory for HIV. The HIV test results of those eligible and who consented were anonymously linked to the interview information mentioned above.¹⁰ Thus, the data used for analysis include eligible participants aged 15 to 49 years who had the HIV test. Table 1 shows the number of enumeration areas (or clusters) and HIV test sample size (men and women) in each of the three countries considered in this study.

Table 1.

Sample size for the demographic and health survey (DHS) conducted in Ethiopia, Kenya and Rwanda in 2008–2011.

Country	Year	Enumeration Area/clusters	Women	Men	Total
Ethiopia	2011	624	15,517	11,869	27,386
Kenya	2008/2009	400	3811	2907	6718
Rwanda	2010	492	6952	5666	12,618

2.2. Definition of variables used in the study

We used cluster-level information for both the outcome and predictor variables. Both the outcome variable and the risk factors were aggregated for each CEA to generate cluster-level information. This allowed us to get more stable values of the variables that are less affected by measurement error. Except for country and location of residence (whether the cluster is urban or rural); the cluster-level variables are derived as the weighted proportion of individuals who have specific characteristics in the cluster. Key variables used in analyses are as follows:

HIV prevalence: the number of people who tested positive in each cluster, or census enumeration area standardized by eligible population size. Respondent’s HIV status was determined with serologic testing among respondents who consented to HIV testing.

Gender: percentage of males and female in the cluster. Male is percentage of males.

Marital status: percentage of single, married, and divorced members in a cluster.

HIV knowledge: percentage in each category answering correctly to a standard battery of knowledge questions: very low AIDS knowledge (0–20% correct answers), low AIDS knowledge (20–40% correct answers), medium AIDS knowledge (40–60% correct answers), and high AIDS knowledge (60–100% correct answers).

HIV acceptance (antonym of HIV stigma): is the number of positive answer to 4 questions related to accepting attitudes toward those living with HIV/AIDS. Respondents were asked the following four questions: Are you willing to care for family member with the AIDS virus in the respondent’s home? Would you buy fresh vegetables from shopkeeper who has the AIDS virus? Would you not want an HIV-positive status of a family member to remain secret? Do you think a female teacher with the AIDS virus and is not sick should be allowed to continue teaching? Percentage of people who have positive response to one, two, three or all of the questions is calculated.

STI symptom prevalence: is defined as percentage of people with any self-reported signs or symptoms of sexually transmitted infections, such as genital discharge or genital ulcer.

Multiple sexual partners: has three categories relating to the number of self-reported sexual partners in the past 12-months: (1) none, (2) one, (3) two or more.

Media usage: is defined as the proportion of people who reported using any of the three media (television, radio, or newspaper) more than 1 h per week.

2.3. Statistical models

We use a general count regression modeling approach with negative binomial (NB) and ZINB models fitted with and without random effect scenarios. These were used to account for clustering by CEA and country and re-scaled weights to account for the complex survey design used to collect the data. Given that the subjects in the study have all voluntarily provided blood samples to be tested, the pathways to have zero count for each CEA could be because the sampled subpopulation was not susceptible to HIV infection or the whole CEA population were healthier resulting in a sample with zero count of HIV positive people. Thus, the excess zero model is appropriate. The general framework of analysis can be described as follows.

Let y_ij denote the count of HIV positive people for cluster j (j = 1,…,n_i) in country i (i = 1,…,K) that has a sample of size N_ij. We formulate a generalized linear mixed model with random effects and offset as follows

$$E(y_{ij}|X_{ij})=g^{-1}\left({\beta }_0+{\beta }_1{X}_{ij}+u_i+v_{ij}\right)\times N_{ij}$$ (1)

where X_ij is a vector of covariates, and $u_i\sim N\left(0,{\sigma }^2\right)$ is the random effect for the between country variability and $v_{ij}\sim N\left(0,{\sigma }_i^2\right)$ are CEA specific random effects for the within country CEAs variability that are uncorrelated with u_i and g is a log link function which leads the model parameters β to have a log rate ratio interpretation. In our case, since K = 3 is small and the countries are not a random sample of the sub-Saharan African countries, we excluded u_i.

Typically Poisson regression is used to model count data where observations are assumed to be independent and the number of cases has variance equal to the mean for each level of the covariates. However, in practice, either the independence or equal mean and variance assumption is often violated, mostly leading to overdispersion (when the variance is greater than the conditional mean). Thus, we consider a NB model that handles the problem of overdispersion and that does not assume an equal mean and variance assumption. In certain cases, overdispersion may not be sufficiently modeled via the extra parameter in NB. Thus, we consider including random effects into the NB model to account for overdispersion and clustering.

Another challenge with modeling count data is the issue of excess zeroes. Zero-inflated models such as ZINB can be used for modeling the excess zeros. The ZINB model is a mixture of NB model for the count part (Y_ij) and a logit model for the excess zeros. For responses from country i (i = 1,2,3) and cluster j (j = 1,…,n_i), we can assume Y_ij ∼ 0 with probability q_ij and Y_ij ∼ NB(λ_ij, ѱ) with probability 1 − q_ij, where λ_ij is the location parameter and is the scale parameter. The zero-inflated model can be formulated as a two part model as follows¹¹

$$\log \{q_{ij}/(1-q_{ij})\}={\alpha }_0+{\alpha }_1{X}_{ij}+v_{ij}^{\prime }$$ (2)

$$\log ({\lambda }_{ij})=\log (N_{ij})+{\beta }_0+{\beta }_1{X}_{ij}+v_{ij},i=1,2,3;j=1,\mathrm{\dots },n_i$$ (3)

The corresponding likelihood functions for the two parts can be given by

$$P(Y_{ij}=0)=q_{ij}+(1-q_{ij}){(1+\frac{{\lambda }_{ij}}{r})}^{-r}$$ (4)

$$P(Y_{ij}=y)=(1-q_{ij})\frac{\Gamma (y+r)}{y!\Gamma (r)}{\left(1+\frac{{\lambda }_{ij}}{r}\right)}^{-r}{\left(1+\frac{r}{{\lambda }_{ij}}\right)}^{-y},y=1,2,\mathrm{\dots }$$ (5)

Right now we have ZINB,¹² the parameters in the ZINB model have conditional or latent class interpretations, which correspond to a susceptible subpopulation at risk for the condition (in our case HIV) with counts generated from a NB distribution and a non-susceptible subpopulation that provides the extra or excess zeros.¹² This population mean conditional on being non-zero can be given as E (Y_ij) = λ_ij (1 − q_ij). Thus, the ZINB model parameters are not well suited for quantifying the effect of an explanatory variable in the overall mixture population. We modified the marginalized zero-inflated Poisson¹³ to implement a marginalized ZINB that is suitable to model the population mean count directly, allowing straightforward inference for overall covariate effects.¹⁴

2.4. Estimation of parameters

Estimation of parameters is made using PROC NLMIXED (SAS 9.4) in which a marginal likelihood function of the form below is used.¹⁵ NLMIXED treats the below pseudo-likelihood as a true likelihood and evaluates it using adaptive quadrature. For $\theta =\left({\beta }_0,{\beta }_1,{\alpha }_0,{\alpha }_1\right)$ and ${\zeta }_{ij}=\left(v_{ij},{v^{\prime }}_{ij}\right)$

$$m\left(\theta \right)=\sum _{i=1}^3\log \int \exp \left\{\sum _{j=1}^{n_i}{w^{\prime }}_{ij}\log f\left(y_{ij}|\theta ,X_{ij},{\zeta }_{ij}\right)g\left({\zeta }_{ij}\right)\text{d}{\zeta }_{ij}\right\}$$ (6)

where X_ij is a matrix of observed predictors, ζ_ij are country-specific random intercepts uncorrelated with covariates such that ζ_ij ~ N(0, Σ) .

The function f (θ) = − log m(θ) is minimized over θ numerically via the Newton-Raphson algorithm in order to estimate θ and the ${w^{\prime }}_{ij}$ is re-scaled cluster weight of the j-th cluster and i-th country and N_ij is included as an offset term. In complex surveys, when including weights in the pseudo likelihood to account for unequal selection probabilities, previous studies have shown that weights need to be scaled. Some simulation studies have also shown that the scaling methods provide better (less biased and smaller variance) estimates than using unweighted analyses.^16–18 Among the scaling methods proposed by those studies, scaling the weights so that the new weights sum to the cluster sample size provided the least biased estimates.^15,16 Thus, weight is rescaled as follows

$${w^{\prime }}_{ij}=w_{ij}{n}_i/\sum _j{w}_{ij}$$ (7)

where w_ij is the sum of the individual level weights within the j-th cluster and i-th country, n_i is the number of clusters in i-th country. The individual level sampling weights were calculated as the ratio of the household sampling weight and individual response rate, where the individual response rate reflects the proportion of people who had valid test results from those who were eligible for the test.⁸ The sum of the individual weights reflects the CEA size.

The log likelihood function log f (y_ij|θ, X_ij, ζ_ij) is given by

$$\begin{gathered} \log f\left(y_{ij}|\theta ,X_{ij},{\zeta }_{ij}\right)=\sum _{y_{ij}=0}\log [q_{ij}+(1-q_{ij}){\left(1+\frac{{\lambda }_{ij}}{r}\right)}^{-r}] \\ +\sum _{y_{ij}>0}\left[\log \left(1-q_{ij}\right)+\log \frac{\Gamma \left(y_{ij}+r\right)}{\Gamma \left(y_{ij}+1\right)\Gamma (r)}+y_{ij}\log \left(\frac{{\lambda }_{ij}}{r}\right)-(y_{ij}+r)\log \left(1+\frac{{\lambda }_{ij}}{r}\right)\right] \end{gathered}$$ (8)

The variances for the random effect can vary by country or can be homogenous across the three countries. In the latter, the random effects assume equal heterogeneity of the CEAs across the three countries which is only useful when responses within each country are equally correlated. When there are differences in the correlation of responses across countries, a country-specific random effect is needed. These additional assumptions lead to different forms of Σ and add extra computational and modeling effort. We would like to note that NLMIXED treats the pseudo-likelihood as a true likelihood and computes the standard errors which could be biased when the sample size is small. A solution to this could be to use a sandwich estimator. However, our sample size is very large and we do not expect the bias to be non-negligible.

We fit six different regression models which include NB and (ZINB), and marginal ZINB (mZINB) with and without random effect. The random effect is included to account for the correlation of outcomes due to clustering by country (Ethiopia, Kenya, Rwanda) in two different ways; either by including a random intercept or alternatively by including a country-specific random intercept in each model. These models also include individual sampling weights to adjust for nonresponse and to restore representativeness of the sample. Due to the expected extra heterogeneity, Poisson models were not applicable.

2.5. Model selection and diagnostics

We use AIC and BIC, which deal with the trade-off between the goodness of fit and complexity of the models, to choose the best fitting model among the different models and further assessment of the goodness of fit for the final model is made via the Pearson goodness of fit statistic.¹⁹ A model with a smaller value of AIC, BIC, and a Pearson statistic close to one is considered a better fit to the data. We used SAS 9.4 to manage the data and fit all the models.

3. Results

Table 1 shows the number of enumeration areas (or clusters) and HIV test sample size (men and women) in each of the three countries considered in this study. Table 2 shows the weighted distribution of the sample by each of the variables included in the analysis to model HIV prevalence in each country. Adult prevalence of HIV was 1.5% in Ethiopia, 6.3% in Kenya, and 3.0% in Rwanda (p < 0.001). The gender distribution in all the three countries is similar with the proportion of males at around 46% (p 0.179). The age distribution is also very similar in the three countries with the younger age groups (15–19 years, 20–24 years, 25–29 years) consisting of 20% of the weighted sampled population in each cluster and the older age groups (30–34 years, 35–39 years, 40–44 years, 45–49 years) consisting of 13%, 11%, 8% and 7%, respectively.

Table 2.

Weighted distribution of census enumeration area level sample characteristics for Ethiopia (ET), Kenya (KE) and Rwanda (RW) from DHS 2008–2011.

Characteristic	All countries (%)	Country			2 sided p value
		ET (%)	KE (%)	RW (%)
HIV prevalence	2.6	1.5	6.3	3.0	<0.001
Gender
Male	45.8	46.1	45.7	45.1	0.179
Residence
Rural	78.6	76.8	75.3	84.2	<0.001
Use of media
At least 1 h/day	75.3	93.0	95.6	0.3	<0.001
STI burden
Have STI burden	3.9	2.8	3.8	6.3	<0.001
HIV knowledge					<0.001
<20%	3.7	5.8	1.9	3.4	<0.001
20%–<40%	7.7	7.2	21.9	1.1	<0.001
40%–<60%	21.0	15.4	72.7	5.5	<0.001
>=60%	67.6	71.6	3.4	93.1	<0.001
Number of partners					<0.001
0	38.3	37.7	29.1	44.3	<0.001
1	59.4	60.4	65.9	53.6	<0.001
>=2	2.4	1.9	5.0	2.1	<0.001
Marital status
Single	37.7	34.4	38.8	44.5	<0.001
Married	55.3	58.6	53.6	48.8	<0.001
Divorced	7.0	7.0	7.6	6.7	0.064
HIV acceptance					<0.001
No positive response (no acceptance)	5.3	7.9	2.7	1.1	<0.001
Positive response to 1 question	12.9	18.2	7.7	4.1	<0.001
Positive response to 2 questions	23.3	30.0	19.2	11.1	<0.001
Positive response to 3 questions	44.3	34.1	51.6	62.7	<0.001
Positive response to 4 questions	14.1	9.8	18.9	21.0	<0.001
Age group					<0.001
15–19	23.6	23.9	22.6	23.7	0.097
20–24	18.8	18.0	19.6	20.1	<0.001
25–29	18.1	18.5	16.3	18.3	<0.001
30–34	12.5	12.1	14.2	12.6	<0.001
35–39	11.2	12.3	9.7	9.6	<0.001
40–44	8.3	8.1	9.5	8.3	0.001
45–49	7.4	7.2	8.1	7.5	0.047
Education level					<0.001
No education	28.4	41.0	6.2	13.0	<0.001
Primary	53.0	45.2	54.8	68.7	<0.001
Secondary	13.7	8.3	30.5	16.5	<0.001
More than secondary	4.9	5.5	8.5	1.7	<0.001

There is variation among the three countries in terms of education level (p < 0.001) with Kenya leading in the weighted proportion of people with secondary or higher education level. The weighted proportion of people with no education is the highest in Ethiopia (41%) followed by 13% in Rwanda and 6% in Kenya. The weighted proportion of rural clusters is the lowest at about 75% in Kenya, while it is over 77% in Ethiopia and 84% in Rwanda (p < 0.001). Analysis of adult marital status shows that the weighted proportion of people with single status in Ethiopia is less than Kenya by 4% and Rwanda by 10%, while the proportion of married people is higher by 5% and 10%, respectively (p < 0.001) with no differences in the weighted proportion of divorced people (p 0.06). Kenya has the lowest percentage of people who have no sexual partners, but the weighted percentage of people with more than one partner is almost twice that of Ethiopia and Rwanda (p < 0.001). The weighted percentage of media usage also varies by country with Ethiopia at 75%, while it is over 90% in Kenya and Rwanda (p < 0.001).

Compared to Kenya, adults in Rwanda and Ethiopia have more HIV-related knowledge with the majority of people in both countries answering over 60% of HIV questions asked in the survey correctly (p < 0.001). Stigma towards HIV is also different among the three countries. The results show that people in Kenya and Ethiopia have more positive attitudes towards people with HIV than in Rwanda (p < 0.001); with more conservative views in Ethiopia (less than 10% people have positive answer for all four stigma questions in the survey). On the other hand, the weighted proportion of people with STI symptoms is the highest in Rwanda and lowest in Ethiopia (p < 0.001).

Figure 1 is a histogram that shows the distribution of clusters by HIV prevalence in the three countries. Here, we see that the concentration of HIV prevalence by cluster varies across countries, with the biggest range in Kenya (0–47%) where there are clusters with prevalence as low as zero and as high as 47%, followed by Rwanda (0– 23%), and Ethiopia (0–17%). The proportion of clusters with zero prevalence of HIV is the highest in Ethiopia at 70% followed by Rwanda at 55% and Kenya at 45% (Figure 2).

Figure 1.

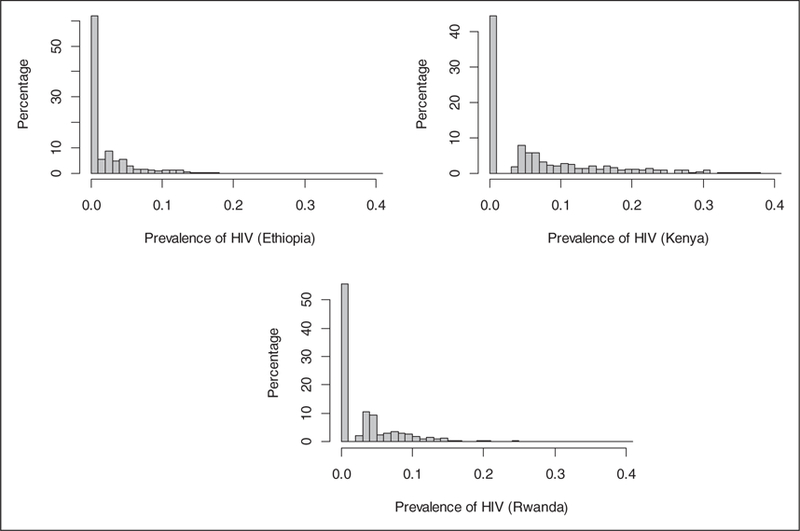
Percentage of CEAs (y-axis) by prevalence of HIV or proportion of HIV cases (x-axis); DHS survey results for Ethiopia, Kenya and Rwanda; 2008–2011.

Figure 2.

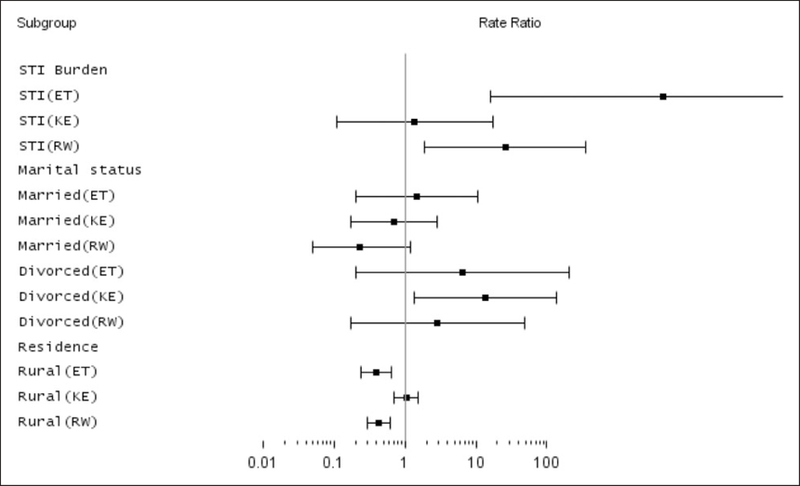
Forest plot of RRs estimated via ZINB; DHS survey results for Ethiopia, Kenya and Rwanda; 2008–2011.

Table 3 shows the model fit statistics for AIC and BIC and Pearson Chi-square. The AIC value for NB is 4045 with a Pearson chi-square to degree of freedom ratio of 1.21 and the corresponding numbers for ZINB are 3898 and 1.37, respectively. When a common random intercept is included, the AIC for the NB decreases to 3860 and the AIC for ZINB decreases to 3836. The over-dispersion parameter estimates for the NB and ZINB with a common random intercept are 0.75 and 0.90, respectively. The corresponding AIC values with country-specific random intercept for NB and ZINB are 3976 and 4019, respectively. Comparing all these models, the ZINB model with random common intercept appears to be the best fit using both statistical information criteria and Pearson statistic. This demonstrates the fact that ZINB coupled with a common random intercept fits the heterogeneity in the aggregate counts in our data example better than the other models. The common random intercept is indicating the homogeneity of the extra variability in the cluster specific HIV counts that is captured by the random intercept for each of the three countries. We hypothesized that there will be an underlying mixing distribution for the country-specific random effects.

Table 3.

Model comparison using AIC, BIC and Pearson Chi-Square; DHS survey results for Ethiopia, Kenya and Rwanda;2008–2011.

	AIC	BIC	Pearson Chi-Square/DF	Significant predictors
Model without random effect
NB	4045	4241	1.21	Gender stigma age partners media STI*country marital*country residence *country
ZI-NB	3898	4132	1.37	Gender stigma age partners media STI*country marital*country residence *country
mZI-NB	3932	4165	1.26	Gender stigma age partners knowledge media STI*country marital*country residence *country
Model with random effect(random intercept)
NB	3860	4056	0.75	Gender stigma age STI*country marital*country residence *country
ZI-NB	3836	4075	0.90	GENDER stigma age partners STI*country marital*country residence *country
mZI-NB	3862	4101	0.88	Gender stigma age partners knowledge STI*country marital*country residence *country
Model with random effect(country-specific random intercept)
NB	3976	4183	1.25	Stigma age partners STI residence *country
ZI-NB	4019	4258	1.18	Stigma age partners marital STI*country residence *country
mZI-NB	4012	4261	1.35	Gender stigma age partners media STI*country marital*country residence *country

Note:AIC, Akaike information criteria; BIC, Bayesian information criteria; NB, negative binomial; ZINB, zero-inflated NB; mZI-NB, marginalized ZINB; HNB, hurdle NB. Models are fitted using Proc NLMIXED, SAS 9.4.

Interestingly, although the models produce somewhat different estimates of the rate ratios (RRs), most of them identify country, gender, rural residence, proportion with STI, number of partners, marital status, attitude towards HIV, interaction between country and STI, interaction between country and residence, interaction between country and marital status to be significantly associated with HIV prevalence (see Figure 2). All other interactions with county were not statistically significant and hence not included in the final model.

Table 4 (first three columns) describes the RR estimates and 95% CI from the marginal ZINB model. The RR has marginal interpretation as any regular RR estimates from a NB model. Higher proportion of males, HIV knowledge, HIV acceptance, older age, higher number of sexual partners, higher proportion of people with STI, higher divorced rate, and rurality of residence are all associated with HIV prevalence. The association between HIV prevalence with STI burden, divorce rate and rurality of residence was different by country For example, the rate of HIV prevalence in Kenya and Rwanda is 4.8 (0.88, 26.03) times and 6.02 (2.11, 17.22) times of the rates in Ethiopia. Census enumeration areas with a higher proportion of males are associated with lower HIV prevalence (RR 0.07 95% CI: 0.03–0.21). Compared to those census enumeration areas with higher proportion of people with no sexual partners, census enumeration areas with higher proportion of people with one or more partners are associated with higher prevalence of HIV (RR 6.52 for two or more and RR 1.95 for one or more). HIV acceptance (low stigma) is highly associated with HIV prevalence wherein census enumeration areas with high level of HIV acceptance showing higher prevalence of HIV. CEAs with higher proportion of STI (p < 0.05), high divorce rate status (p < 0.05), and that are rural (p < 0.05) are associated with HIV prevalence differentially by country. In Ethiopia, census enumeration areas with higher proportion of people with STI compared to those without STI are 4366 (CI: 16.1,∞) times more likely to have higher prevalence of HIV, while the ratios for Kenya and Rwanda are RR 1.4 (p = 0.81) and RR 25.9 (p = 0.02), respectively. The positive association between HIV prevalence and census enumeration areas with a higher proportion of divorced people is the highest in Kenya (RR 13.7, p = 0.03), followed by Ethiopia (RR 6.5, p = 0.29), and Rwanda (RR 2.89, p = 0.46). In all three countries, CEAs with higher proportion of divorced or widowed people have higher HIV prevalence compared to those with higher proportion of married or single people. Rurality of the census enumeration area is associated with lower rate of HIV prevalence in Ethiopia (RR 0.39, p < 0.01) and Rwanda (RR 0.43, p < 0.01), while in Kenya there is no significant difference between the people living in urban and rural areas (RR = 1.04, p = 0.83).

Table 4.

Parameter estimates of zero-inflated negative binomial (ZINB) and marginal ZINB Models for HIV prevalence; DHS survey results for Ethiopia, Kenya and Rwanda; 2008–2011.

	Random Effect marginal ZINB			Random Effect ZINB
Variablesa	Rate ratio	95% CI	2 sided P value	Rate ratio	95% CI	2 sided P value
Kenya	4.80	0.88,26.03	0.07	2.38	0.59,9.61	0.22
Rwanda	6.02	2.11,17.22	<0.01	2.81	1.2,6.55	0.02
Gender
Male	0.07	0.03,0.21	<0.01	0.38	0.15,0.98	0.04
Use media at least 1 h per week	1.90	0.55,6.56	0.31	2.50	0.83,7.55	0.11
HIV knowledge
20%–<40%	0.03	0,0.73	0.03	0.11	0.01,2.16	0.15
40%–<60%	0.06	0,1.1	0.06	0.26	0.02,3.74	0.32
>=60%	0.03	0,0.47	0.01	0.53	0.04,7.16	0.63
Number of partners
1	1.95	0.55,6.89	0.30	5.57	1.68,18.5	0.01
>=2	6.52	0.71,59.7	0.10	4.56	0.69,30.2	0.12
HIV acceptance
Positive response to 1 question	346.37	13.2,9087.91	<0.01	25.05	1.49,420.1	0.03
Positive response to 2 questions	3835.67	181.36,81121.23	<0.01	149.65	11.68,1917.93	0.01
Positive response to 3 questions	3558.16	177.01,71517.68	<0.01	205.35	16.76,2515.94	<0.01
Positive response to 4 questions	13377.11	643.55,278062.17	<0.01	578.54	44.37,7543.19	<0.01
Age
20–24	0.42	0.11,1.6	0.20	0.40	0.12,1.4	0.15
25–29	0.30	0.07,1.29	0.11	0.30	0.08,1.19	0.09
30–34	0.56	0.12,2.77	0.48	0.44	0.1,1.91	0.27
35–39	0.32	0.05,1.97	0.22	0.39	0.07,2.1	0.27
40–44	0.13	0.02,0.86	0.03	0.16	0.03,0.93	0.04
45–49	0.05	0.01,0.38	<0.01	0.06	0.01,0.35	<0.01
Education
Primary	0.77	0.27,2.22	0.63	1.13	0.44,2.87	0.80
Secondary	0.93	0.28,3.11	0.91	0.97	0.35,2.63	0.94
More than secondary	0.22	0.05,1.01	0.05	0.46	0.11,1.84	0.27
STI burden
People with STI burden(ET)	4366.43	16.11,1183397.39	<0.01	649.11	5.04,83600.1	0.01
People with STI burden(KE)	1.37	0.11,17.48	0.81	1.14	0.1,12.77	0.92
People with STI burden(RW)	25.90	1.88,356.84	0.02	11.40	1.02,126.99	0.05
Marital status(country)
Married(ET)	1.49	0.2,10.78	0.69	1.51	0.27,8.44	0.64
Married(KE)	0.71	0.17,2.89	0.63	1.86	0.49,7.04	0.36
Married(RW)	0.23	0.05,1.17	0.08	0.56	0.14,2.22	0.41
Divorces(ET)	6.50	0.2,209.68	0.29	8.90	0.51,155.04	0.13
Divorces(KE)	13.72	1.36,138.28	0.03	29.98	5.79,155.29	<0.01
Divorces(RW)	2.89	0.17,48.52	0.46	1.09	0.18,6.52	0.93
Residence(country)
Rural(ET)	0.39	0.24,0.64	<0.01	0.44	0.29,0.67	0.01
Rural(KE)	1.04	0.71,1.54	0.83	0.81	0.57,1.17	0.27
Rural(RW)	0.43	0.3,0.62	<0.01	0.44	0.34,0.56	<0.01

Note: CI, Confidence interval; STI, sexually transmitted diseases; ET, Ethiopia; KE, Kenya; RW, Rwanda.

^aReference group for each variables: country: Ethiopia, gender: female, HIV knowledge: answer less than 20%, positive stigma: no positive attitudes towards the related questions, age: 15–19, education: no education, STI: no STI in each CEA, marital status: singles in each CEA, residence: urban in each CEA, number of partners: zero partners.

We have also fitted a random effects ZINB model and the results are reported in the last three columns of Table 4 and Figure 2. It is important to note that the RR estimates do not have the same interpretation as those from the marginal ZINB. These RRs have an interpretation of the association between HIV prevalence and covariates for the latent class of individuals that are considered to be at risk of HIV/AIDS.

Table 5 shows odds ratio estimates from the random effects ZINB and mZINB models which have very similar values. Each estimate compares the odds of being an excess zero to the odds of not being an excess zero in each CEA as a function of selected covariates. Consistent with Figure 1, the odds of excess zero counts is not different by country. Clusters with excess of negative tests (zeros) are more likely to have lower number of divorces, lower number of people with two or more partners and lower proportion of people with STI.

Table 5.

Odds ratio estimates from the excess zero-part of the random effect ZINB model, DHS survey results for Ethiopia, Kenya and Rwanda; 2008–2011.

	Excess zero model marginal ZINB			Excess zero model ZINB
Variablesa	Odds ratio	95% CI	2 sided P value	Odds ratio	95% CI	2 sided P value
Intercept	0.17	0.02,1.13	0.08	0.16	0.02,1.16	0.07
Country
Kenya	1.03	0.38,2.82	0.95	0.96	0.33,2.81	0.94
Rwanda	1.05	0.13,8.81	0.96	1.22	0.16,9.66	0.85
STI burden
People with STI burden	0.02	0.01,34.29	0.26	0.02	0.01,54.67	0.33
Marital status
Married	0.87	0.03,25.16	0.93	1.03	0.02,43.59	0.99
Divorces	0.01	0.00,0.04	<0.01	0.01	0.00,0.05	<0.01
Number of partners
1	4.73	0.33,68.33	0.25	3.78	0.26,55.73	0.33
>=2	0.01	0.00,0.2	<0.01	0.01	0.00,0.2	0.01

Note: CI, Confidence interval; STI, sexually transmitted diseases.

^aReference group for each variables: : country: Ethiopia, STI: no STI in each CEA, marital status: singles in each CEA, residence: urban, number of partners: zero partners in each CEA.

4. Discussion

In this analysis, we show a novel application of a scale weighted ZINB with and without random effect to analyze count data from a survey of three countries. We show how to fit these advanced statistical models using SAS and how to select the model that best accounts for clustering of the count responses by CEA as well as the complex survey nature of the data to study factors associated with regional variation in HIV prevalence. We also estimate and report marginalized RRs of the fitted ZINB model to get estimates that have same interpretation as regular RRs from NB models.

While there have been many prior country-level examinations of factors associated with HIV prevalence available in the literature, there has been scant examination of regional variations in factors associated with HIV prevalence. Understanding the variations in HIV prevalence, the factors that are associated with differences across countries can help to develop more appropriate intervention strategies. Challenges to examining regional variation in HIV prevalence patterns include limitations in availability of harmonized data by time, content, and region; and methodological design constraints that introduce multiple levels of geographic nesting within available data, leading to challenges in statistical analyses due to cluster-driven dependency across observations. In this analysis, we have been able to compile a harmonized dataset (by time, content, region) and also identify a robust estimation model that well specifies the predictors of HIV prevalence for three countries in sub-Saharan African region. Importantly, we found there are indeed significant differences across these countries in the patterns of HIV prevalence. In particular, the role of sexually transmitted infection, rural presence and distribution of HIV, and marital status were significantly different across Kenya, Ethiopia and Rwanda. This suggests that the intervention response to the HIV epidemic across these countries should be tailored to the distinct nature of the epidemic in each setting.

Kenya is characterized by a much larger HIV epidemic with higher penetration into rural areas, and where divorced and widowed persons are at heightened risk of HIV infection. Ethiopia is experiencing a much more rural concentrated epidemic with significant correlation also found between HIV and other sexually transmitted infections. Rwanda’s HIV epidemic is characterized by a moderate but significant association between both HIV and STI, and HIV and divorced marital status. Like Ethiopia, HIV is much more concentrated geographically in Rwanda. In addition, HIV prevalence in both Rwanda and Ethiopia was higher in rural than in urban areas.

Across countries, based on the final ZINB model with random effects, we found that lower HIV prevalence was associated with older age and male gender. The prevalence of HIV was also lower among singles and higher among previously married (widowed, divorced or separated). Within each country, urban census enumeration areas had higher prevalence of HIV infection (Ethiopia: 4.2 versus 0.6 in DHS2011, Kenya: 7.3 versus 6.1 in DHS2009, Rwanda: 7.1 versus 2.3 in DHS2010). These findings are consistent with the results from previous studies,^20–23 except for the effect of rural residence and marital status which showed some variation by country in other studies.²³

Consistent with our findings, other studies have found that having multiple sexual partners is associated with increased risk of HIV prevalence.^24,25 Our results suggest that having more sexual partners in the recent 12 months is associated with HIV prevalence. Similar to previous findings, HIV acceptance is strongly associated with HIV prevalence. Genberg and colleagues found that stigma (opposite of HIV acceptance) has a negative correlation with HIV prevalence in a quantitative study in three countries in sub-Saharan Africa and Thailand.²⁶ In a study by Winskell et al.,²⁷ the association between HIV stigma and HIV prevalence was similar to our findings. The positive association we see between HIV acceptance and HIV prevalence can be due to the fact that people who live in areas with higher prevalence may have more opportunities to socially interact with the HIV-infected people, and hence accept the realities of living with HIV positive people. This could be explained by the high level of HIV prevention education provided in areas with higher HIV prevalence.

While we believe that the veracity of the results presented here is robust, there are some limitations that should be mentioned. First, the analysis is limited to three countries and can be increased to more than three with additional computational resources given the complex models we are using for analysis. However, the results may not necessarily apply to countries that are not included in the study. Second, despite the fact that our modeling strategies accounted for the complex nature of the survey data from multiple countries and the aggregation of the outcomes and covariates by census enumeration area reduce the impact of measurement error and missing data, there is a possibility that our results might be affected by non-response bias. However, there was no difference in the demographic distribution of those who declined or were missed in the sampling compared to the people who participated in the surveys. We do not expect an unmeasured bias to be introduced in the analyses.^28,29 This potential problem has been reported in a DHS study of Zambia³⁰ where selection bias underestimated the HIV prevalence estimates. It is important to note that aggregation of the individual data into CEA level does not make us lose too much information since analysis assuming Bernoulli distribution (individual level) and assuming Binomial distribution (CEA aggregate data which are sum of Bernoulli) with CEA specific probability are equivalent as long as a correct modeling approach such as generalized linear mixed model is used. In fact, the CEA aggregated data helps to reduce the impact of measurement error and missing data and are less likely to be affected by ecological fallacy.

5. Conclusions

In this analysis, we show that a scale weighted ZINB with proper modeling of random effects can be used to account for zero-inflation, clustering of count responses as well as the complex survey nature of the data. While it requires further simulation studies to understand the operational characteristic of these models, it can be inferred from our study that the scale weighted ZINB model can be applied in other areas of biomedical research in which responses are measured in clusters using a complex survey design, for example, in modeling of number of days of missed primary activities due to illness,³¹ study of outpatient psychiatric service use,³² and study of malaria infection.³³