The mouse eye lens was used as a model for multiscale transfer of loads. In the lens, compressive strain is distributed across specific lens tissue microstructures, including the extracellular capsule, as well as the epithelial and fiber cells. The removal of high loads resulted in complete recovery of most, but not all, microstructures.
Abstract
The understanding of multiscale load transfer within complex soft tissues is incomplete. The eye lens is ideal for multiscale mechanical studies because its principal function is to fine-focus light at different distances onto the retina via shape changes. The biomechanical function, resiliency, and intricate microstructure of the lens makes it an excellent nonconnective soft tissue model. We hypothesized that strain applied onto whole-lens tissue leads to deformation of specific microstructures and that this deformation is reversible following load removal. For this examination, mouse lenses were compressed by sequential application of increasing load. Using confocal microscopy and quantitative image analysis, we determined that axial strain ≥10% reduces capsule thickness, expands epithelial cell area, and separates fiber cell tips at the anterior region. At the equatorial region, strain ≥6% increases fiber cell widths. The effects of strain on lens epithelial cell area, capsule thickness, and fiber cell widths are reversible following the release from strain. However, the separation of fiber cell tips is irreversible at high loads. This irreversible separation between fiber cell tips leads to incomplete whole-lens resiliency. The lens is an accessible biomechanical model system that provides new insights on multiscale transfer of loads in soft tissues.
INTRODUCTION
An understanding of the multiscale relationship between macro- and microlevel mechanics is essential for determining how tissue mechanical properties emerge from specific tissue microstructures (Dumont and Prakash, 2014). The multiscale transfer of load in soft tissues has been previously characterized in studies that use isolated portions of connective tissues (such as tendon, meniscus, and annulus fibrosis) (Bruehlmann et al., 2004; Upton et al., 2008; Desrochers and Duncan, 2010; Han et al., 2013). In these connective tissues, the proportion of strain applied at the tissue level is largely to completely attenuated by the extracellular matrix (ECM) before it reaches the small number of cells embedded within a large amount of ECM (Bruehlmann et al., 2004; Han et al., 2013). For a more complete understanding of microscale load transfer in tissues, studies that examine how loads are distributed within more complex tissues that have a vastly different microstructural cellular composition and organization than connective tissues are needed.
The eye lens serves as an ideal model to develop new insights into the multiscale transfer of mechanical loads in tissues for several reasons. The lens is a soft, transparent tissue in the anterior chamber of the eye that changes shape to fine-focus light from different distances onto the retina to generate a clear image. Thus, the optical function of the lens is closely tied to its mechanical function. The biomechanical stiffness of soft tissues (Candiello et al., 2010; Tsujii et al., 2017; Lampi and Reinhart-King, 2018), including the lens (Baradia et al., 2010; Hozic et al., 2012; Cheng et al., 2016a), increases with age. Increased biomechanical tissue stiffness in the aging lens diminishes its ability to change shape, resulting in presbyopia and the need for reading glasses (Heys et al., 2004). There is little known about the cellular and molecular mechanisms that regulate microstructural deformability and whether age-related changes in microstructural deformability result in the reduced ability for lens shape change. Therefore, determining the transfer of loads during bulk lens shape change will provide a foundation for understanding the role that anatomical microstructure may play in lens pathology as well as the general relationship between microstructure and age-related stiffening of soft tissues. Another property that could provide additional insights into multiscale load transfer is lens resiliency. Release from tensional strain in vivo leads to lens rounding. While the effect of mechanical unloading has recently been shown in cells (Bonakdar et al., 2016), the effect of unloading on microstructures within a tissue system has not been determined. Thus, the lens also provides an opportunity to investigate microstructure during release from various magnitudes of mechanical loads.
The lens serves as an important model of multiscale load transfer, because it is a predominantly cellular tissue, with a microstructural composition and organization dramatically different from connective soft tissues (Upton et al., 2008; Desrochers and Duncan, 2010; Han et al., 2013; Szczesny and Elliott, 2014). The only ECM present in the lens is a thin basement membrane, known as the lens capsule. The capsule, which is rich in type IV collagen, surrounds the entire organ (Lovicu and Robinson, 2004). Inward from the capsule are the lens cells, which have intricate shapes and are highly organized (Wanko and Gavin, 1959; Cheng et al., 2017b). A monolayer of epithelial cells covers the anterior hemisphere of the lens and is attached to the capsule. Lifelong lens growth is facilitated by continuous proliferation and differentiation of equatorial epithelial cells into newly formed fiber cells. Fiber cells migrate and elongate into thin, ribbon-like cells extending from the anterior to posterior pole, and new layers of fiber cells are added onto older generations of fiber cells in concentric shells. At the poles, fiber cell tips from the opposing sides of the lens meet to form the anterior and posterior suture cell–cell junctions (Kuszak et al., 1984, 2006; Kuszak and Zoltoski, 2006). Thus, determination of multiscale load transfer in the lens will aid in elucidating tissue responses to load for complex and predominantly cellular tissues.
In this study, we examined the hypothesis that compressive strain leads to reversible deformation of lens microstructural dimensions. We developed new quantitative methodology to examine lens capsule thickness, epithelial cell area, fiber cell widths, and fiber tip organization during, as well as recovery from, compression in live mouse lenses. This analysis has allowed us to characterize multiscale load transfer in the lens. We show that, in contrast to connective tissues (Bruehlmann et al., 2004; Upton et al., 2008; Desrochers and Duncan, 2010; Han et al., 2013), load was not only transferred to the lens matrix (capsule), but also throughout the lens epithelial and fiber cells. We also determined that whole-lens resiliency was incomplete following the release from high loads and that this corresponded to incomplete recovery of fiber cell–tip organization. Other microstructural features, however, such as capsule thickness and equatorial fiber widths, were completely recovered following release from high loads, suggesting that the inability of tissues to recover from load could be due to failure of specific microstructures. The lens model provides a robust system to develop insights into multiscale load transfer onto cells through a thin matrix that will result in a better understanding of how biomechanical tissue properties emerge from specific tissue microstructures.
RESULTS
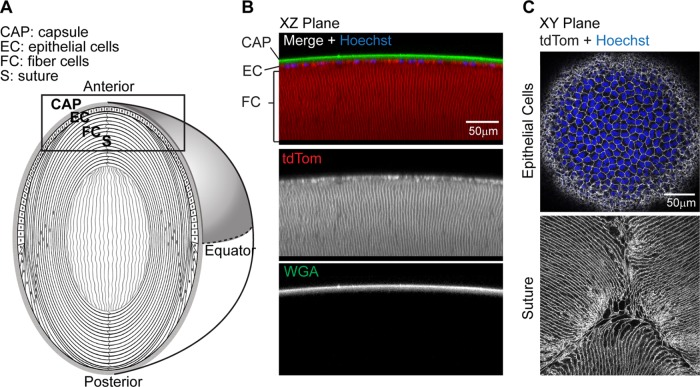
tdTomato labeling of mouse lenses allows live visualization of the lens anterior
We used mice expressing tandem dimer-Tomato (B6.129(Cg)-Gt(ROSA) (hereafter referred to as tdTomato) to visualize plasma membranes of the cells in live lenses. These mice have been genetically engineered to express tdTomato protein fused to connexin 43 and driven by the chicken β-actin core promoter with a cytomegalovirus enhancer (the tdTomato-connexin 43 communication is disabled) (Campbell et al., 2002; Muzumdar et al., 2007). This results in membrane targeting of tdTomato and allows for visualization of cell morphology by confocal fluorescence microscopy.
Although expression of tdTomato in these mice is ubiquitous, the expression can be variable depending on tissue type (Muzumdar et al., 2007). Therefore, we examined whether the tdTomato expression was present at epithelial and fiber cell plasma membranes in the anterior region of live mouse lenses (as depicted in Figure 1A). We observed that tdTomato labeling is bright and stable and can be easily observed in lens cells as deep as 150 μm from the capsule surface (Figure 1B). Additionally, the characteristic cobblestone morphology of the anterior epithelial cell monolayer and the fiber cell tips at the Y-shaped sutures of mouse lenses (Kuszak et al., 1984; Cheng et al., 2017b) are apparent with endogenous tdTomato labeling (Figure 1C).
FIGURE 1:
tdTomato-labeled membranes in mouse lenses allow live-cell confocal imaging. (A) Diagram of lens anatomy showing lens capsule (CAP), epithelial cells (EC), fiber cells (FC), and suture (S). The lens anterior region is boxed, and the lens equator is indicated by the dashed horizontal line. (B) Sagittal optical section (x,z-plane view) of reconstructed confocal z-stacks of the lens anterior showing epithelial cells and fiber cell membranes labeled with tdTomato (red), lens capsule stained with WGA (green), and epithelial cell nuclei stained with Hoechst (blue). (C) Single optical sections (x,y-plane view) of tdTomato-labeled membranes of lens epithelial and fiber cells (grayscale), showing Hoechst-stained nuclei (blue) in the epithelium (top) and the anterior fiber cells meeting at the suture (bottom).
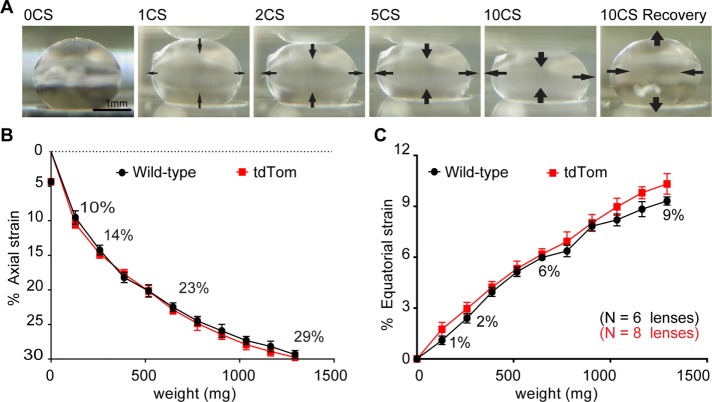
Biomechanical properties of wild-type and tdTomato lenses
tdTomato is targeted to the plasma membrane, and because cell membrane properties contribute to cell mechanical properties (Heidemann and Wirtz, 2004), we next sought to determine whether tdTomato membrane labeling alters the bulk biomechanical properties of the lens. To perform this analysis, we sequentially applied increasing axial load in the form of glass coverslips onto tdTomato (Figure 2A) or wild-type C57BL/6 mouse lenses. This method of compression allows for precise and reproducible measurement of lens strain (Baradia et al., 2010; Gokhin et al., 2012; Cheng et al., 2016a). To determine axial and equatorial strain, we measured axial and equatorial diameters before (d0) and during (dl) load. We then calculated strain “ε” using the formula ε = 100 × (dl − d0)/d0. We determined that, at any given load tested, there are no differences (p > 0.05) in axial strain between wild-type and tdTomato lenses (Figure 2B). For subsequent experiments, we used a range of strains by applying 1, 2, 5, or 10 coverslips onto lenses. These loads result in axial strains of 10, 14, 23, and 29% in mouse lenses, respectively.
FIGURE 2:
The effect of coverslip compression on mouse lens axial and equatorial strain. (A) Sagittal-view images of tdTomato mouse lens compressed by the indicated number of coverslips (CS) and following the removal of 10 coverslips (10CS recovery). Arrows on images indicate direction of lens shape changes at the anterior, posterior, and equator. Mean (B) axial and (C) equatorial strains (±SEM) as a function of coverslip weight for wild-type and tdTomato mouse lenses. Strain was calculated using ε = 100 × (dl− d0)/d0, where d0 is initial lens axial or equatorial diameter and dl is axial or equatorial diameter when loaded. The application of 1, 2, 5, and 10 coverslips (129.3 mg per coverslip) provided a range of strains that were used for the remainder of this study. Numbers are percent strain calculated for the indicated numbers of coverslips.
Lenses behave according to the Poisson effect, such that axial compression also results in equatorial expansion (Bailey et al., 2010; Gokhin et al., 2012; Cheng et al., 2016a). Measurements of equatorial strain of the lens during compression reveal that, at any given load, the magnitude of axial strain (Figure 2B) is greater than equatorial strain (Figure 2C). The application of 1, 2, 5, and 10 coverslip loads results in equatorial strains of 1, 2, 6, and 9% in mouse lenses, respectively. Similar to axial strain, at any given load tested, there are no differences (p > 0.05) in equatorial strain between wild-type and tdTomato lenses (Figure 2C).
Bulk lens dimensions recover only partially at higher strains
To examine whether the amount of strain affected the ability to recover shape after release from compression, we determined whether there were differences between prestrain and postrelease axial and equatorial lens diameters. Initial studies indicated that there were no differences in recovery of axial diameter between tdTomato and wild-type mouse lenses (Supplemental Figure S1); therefore, we pooled data from tdTomato and wild-type lenses. Release from 10% axial strain (1 coverslip load) results in complete axial diameter recovery, as there is no significant difference (p > 0.05) between pre- and postrelease strain axial lens diameters (Figure 3A). Release from axial strains ≥14% (loads ≥2 coverslips), however, results in only partial recovery of axial diameter, as the postrelease from strain axial diameter is significantly less compared with the prestrain axial diameter. Release from axial strains of 14% (2 coverslips load), 23% (5 coverslips load), and 29% (10 coverslips load) led to postrelease axial diameters that were 98.0 ± 1.0% (p = 0.01), 96.5 ± 2.8% (p = 0.03), and 95.9 ± 1.1% (p < 0.001) those of prestrain axial diameters, respectively (Figure 3B).
FIGURE 3:
Recovery of bulk lens axial and equatorial dimensions following release from strain. (A) Plots of axial (top row) and equatorial (bottom row) diameters of lenses pre- and poststrain. (B) Bar graphs showing that axial diameter recovery (percentage of post- to preaxial diameter) progressively decreased with increasing strain. (C) Bar graphs showing that average postrelease from strain diameter (±SEM) is greater than preequatorial diameter when lenses are strained with 9% equatorial strain. *, p < 0.05; ***, p < 0.001.
Similar to recovery of lens axial diameter, recovery of lens equatorial diameter was complete at lower equatorial strains. Release from equatorial strains ≤6% (≤5 coverslips load) results in complete return of equatorial diameter to prestrain levels with no significant difference (p > 0.05) between preload and postrelease equatorial diameters. Release from 9% equatorial strain (10 coverslips load), however, results in partial return of equatorial diameter, as the postrelease lens equatorial diameter is significantly higher (p < 0.001) than the prestrain axial diameter (Figure 3A), by 1.9% (Figure 3C).
Recovery from high strains was incomplete, which suggests that increasing strain may lead to progressive tissue damage. Our data show that compression with 10% axial strain in mouse lenses does not cause irreversible damage to bulk lens shape. Ten percent axial strain is within the range of physiological primate lens shape changes during accommodation calculated from in vivo measurements (Jackson, 1907; Doyle et al., 2013; Marussich et al., 2015). Because 10% strain approximates the deformation that lenses could experience in vivo, for the rest of this study, we focused primarily on the microstructural changes that occur at 10% axial strain. To provide additional insights into the microstructural changes that occur at high loads, we also examined the effects of higher levels of strain.
Lens flattening caused by strain results in a reversible decrease in capsule thickness
Isolated human lens capsules are highly elastic and can stretch up to ∼108% (Fisher, 1969b; Krag et al., 1997), even more so than other types of collagenous connective tissue (Oxlund and Andreassen, 1980). This propensity to undergo strain has led to the speculation that capsules stretch during lens flattening (Fisher, 1969a). To examine the effect of axial strain on capsule deformation, we determined capsule thickness in the anterior region of lenses (as depicted in Figure 4A) by performing line scan analysis (Figure 4B) on three-dimensional (3D) reconstructed images of capsules stained with wheat germ agglutinin (WGA) fluorescent conjugate, before, during, and after the release from strain (Figure 4C). In our reconstructed images, we determined that WGA staining is present throughout the lens capsule and was most intense at the top surface (Figure 4C). There is less staining for WGA in the underlying epithelial cells. In contrast to WGA staining, tdTomato labels the underlying epithelial cell membranes but not the capsule. These mutually exclusive labeling properties of WGA for the capsule and tdTomato for epithelial cells allow for precise measurement of capsule thickness by line scan analysis (Figure 4B). Fluorescent line scan profiles reveal a WGA peak corresponding to the intense top-surface staining of the capsule and a tdTomato peak corresponding to the basal surface of the epithelial membranes adjacent to the bottom surface of the capsule. The difference in distance between the two peaks is therefore capsule thickness.
FIGURE 4:
Lens axial strain leads to a reversible decrease in anterior capsule thickness. (A) Diagram depicting anterior capsule and epithelial cells. (B) Capsule thickness was determined by line scan data from images. Line scans demonstrate a single WGA (green) peak that corresponds to the top surface (TS) of the capsule and a tdTomato (red) peak that corresponds to the basal side (BS) of epithelial cells adjacent to the capsule. The distance between green and red peaks represents capsule thickness. (C) Images of WGA-stained capsule (green) and tdTomato (tdTom)-labeled underlying epithelial cells (red) in a sagittal optical section (x,z-plane view) from 3D reconstructions of confocal z-stacks. Line scans, indicated by dashed vertical gray line, with the taper of the dashed line indicating the direction of line scan. (D) Repeated-measures dot plots of capsule thickness from unstrained (0%), strained, and recovered lenses. (E) Average change in capsule thickness (±SEM) calculated from data in D, normalized to capsule thickness at 0% axial strain. *, p < 0.05; **, p < 0.01; ***, p < 0.001.
We observed that anterior capsule thickness is variable between individual lenses (Figure 4D), in keeping with previous findings for C57BL/6 wild-type mice of similar ages (Danysh et al., 2008). Owing to this inherent variability, we used a repeated-measure analysis on individual lenses to determine the effects of strain. We determined that the application of 10% axial strain significantly decreases capsule thickness, with thickness reduced on average by 9.9 ± 3.0% (Figure 4E). Following removal of load, capsule thickness returns to unstrained levels (Figure 4, D and E).
Increasing axial strains beyond 10% further decreased capsule thickness (Figure 4B). The decrease in capsule thickness at 29% axial strain (the highest strain used in this study) (Figure 4D) is significantly greater than the decrease in capsule thickness at 10% axial strain (p < 0.05) (Figure 4E). On average, 29% axial strain decreased capsule thickness by 25.8 ± 4.3%. Furthermore, even at 29% axial strain, capsule thickness recovers completely following release from load, such that there is no significant difference (p = 0.99) in capsule thickness between unloaded capsules and those recovered from 10% axial strain. These findings extend previous studies on isolated capsules (Fisher, 1969a,b; Krag et al., 1997) by demonstrating that capsules are also highly elastic in native, intact, live lens tissues.
Lens flattening caused by strain leads to a reversible increase in epithelial cell area
Next, we sought to determine whether axial strain propagated into the cellular regions of the lens by examining anterior epithelial cells located beneath and attached to the lens capsule. For this examination, we identified a region of interest (ROI) of an identical population of epithelial cells from images taken before, during, and after release from 10% strain (Figure 5A). Measurement of the ROI areas before and during strain revealed that the application of 10% axial strain leads to an increase in ROI area (Figure 5, A and B).
FIGURE 5:
Lens axial strain leads to a reversible increase in anterior epithelial cell area. (A) x,y extended view of the midregion of tdTomato epithelial cells from unstrained (0%), 10% strained, and recovered lenses after release from strain. Total cell area (ROI area) was measured, and the average cell area was calculated by dividing ROI area by total cell number as indicated below images. (B) Overlay of cell area at 0% strain (white area) on top of cell area at 10% strain (gray area), demonstrating an increase in area with strain. (C) Repeated-measures dot plots of average epithelial cell area from individual unstrained (0%), 10% strained, and recovered lenses. (D) Average change in epithelial cell area (±SEM) was calculated from data shown in C, normalized to the epithelial area at 0% strain. **, p < 0.01.
To determine average cell area for individual epithelial cells, we divided the ROI area by the total number of cells within the ROI (Figure 5A). In keeping with a previous study that used C57BL/6 wild-type mice of a similar age (Shi et al., 2014), we determined that average epithelial cell area is variable between lenses (Figure 5C). Owing to this inherent variability in epithelial cell area, a repeated-measures analysis on individual lenses was used to determine the effects of strain. The application of 10% axial strain significantly increases cell area (Figure 5C), with an average increase in area of 7.0 ± 1.1% (Figure 5D). Furthermore, following removal of 10% axial strain, epithelial cell area returns to unstrained levels (Figure 5, C and D). Unlike in the capsule, where additional strain results in progressive reductions to capsule thickness (Figure 4C), there are no further increases in epithelial cell area by increasing strain beyond 10% (Supplemental Figure S2). Even at 29% axial strain, the increase in epithelial cell area was not different from the increase in epithelial cell area at 10% axial strain (p = 0.24). Our results demonstrate that axial compression propagates into the epithelial cell layer, and epithelial cells expand their areas to near-maximal levels at ∼10% axial strain.
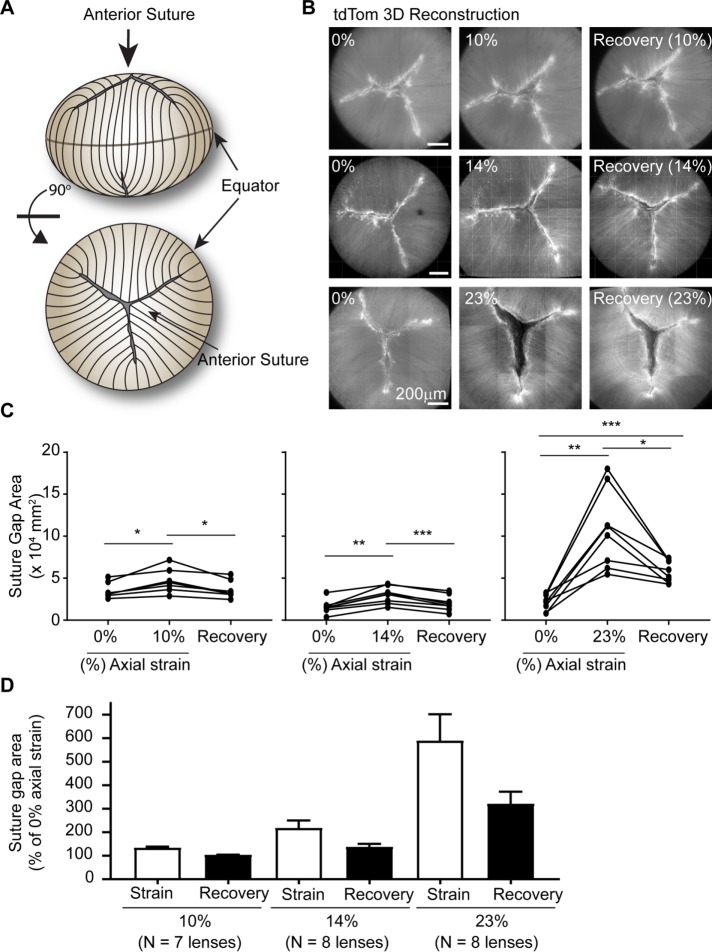
Fiber cell–tip separation at the suture progressively increases with applied strain and is not completely reversible at high loads
Underlying the anterior epithelial cells, the apical tips of fiber cells meet to form the suture, which is typically a three-branched, Y-shaped suture in mouse lenses (Kuszak et al., 2006) (as depicted in Figure 6A). To determine whether the application of axial strain affects the anterior fiber cell tips at the suture, we examined the suture in lenses before, during, and after the release from strain. Fiber cell–tip separation was quantified by manually tracing the area between fiber cell tips in 3D reconstructions of confocal z-stacks of lens sutures (Supplemental Figure S3). We defined the area of this outlined region as the “suture gap area.”
FIGURE 6:
Lens axial strain leads to an irreversible increase in suture gap area at higher strains. (A) Diagram of lens indicating anterior suture in side view and rotated 90° forward for top view of Y-shaped suture. (B) En face images of tdTomato (tdTom) fiber cells at anterior suture from 3D reconstructions of confocal z-stacks in lenses before (left column), during (middle column), and after release from (right column) strain. Axial strains of 10% (top row), 14% (middle row), or 23% (bottom row) are shown. The area between opposing fiber cell tips was outlined on images and was defined as the suture gap area (see Supplemental Figure S3). (C) Repeated-measures dot plots showing the effect of coverslip loading and removal on lens suture gap area for individual lenses. (D) Average change in suture gap area (±SEM) was calculated from data shown in C, normalized to suture gap area at 0% strain. *, p < 0.05; **, p < 0.01; ***, p < 0.001.
We determined that the sutures of tdTomato mouse lenses are variable. Approximately 27% of tdTomato lenses have sutures with four, rather than the typical three, branches (Supplemental Figure S3). Additionally, the suture gap area is variable between lenses. Therefore, due to the inherent suture variability, a repeated-measures analysis on individual lenses was used to determine the effects of strain. The application of 10% axial strain significantly increases suture gap area. Following removal of 10% axial strain, the suture gap area returns to its original size (Figure 6, B and C). The amount of fiber cell–tip separation at the suture depends on the applied strain (Figure 6D), with axial strains of 10, 14, and 23%, the suture gap area increased by 1.4-, 2.2-, and 5.9-fold over the unloaded control, respectively. The suture gap area completely recovers back to its original size after release from 10% or 14% axial strain. However, the suture gap area only partially recovers after release from 23% axial strain, with the suture gap remaining 3.2-fold larger than the unstrained control (Figure 6, B–D). The application of 29% axial strain also increases suture gap area, which only partially recovers after removal of strain (unpublished data). These findings indicate that axial strain affects suture structure in mouse lenses, causing separation of fiber tips leading to an increase in the suture gap area. While these effects are reversible at low axial strains (≤14%), they are irreversible at higher axial strains (≥23%), suggesting damage occurs to the suture at higher strains, consistent with previous qualitative observations (Baradia et al., 2010).
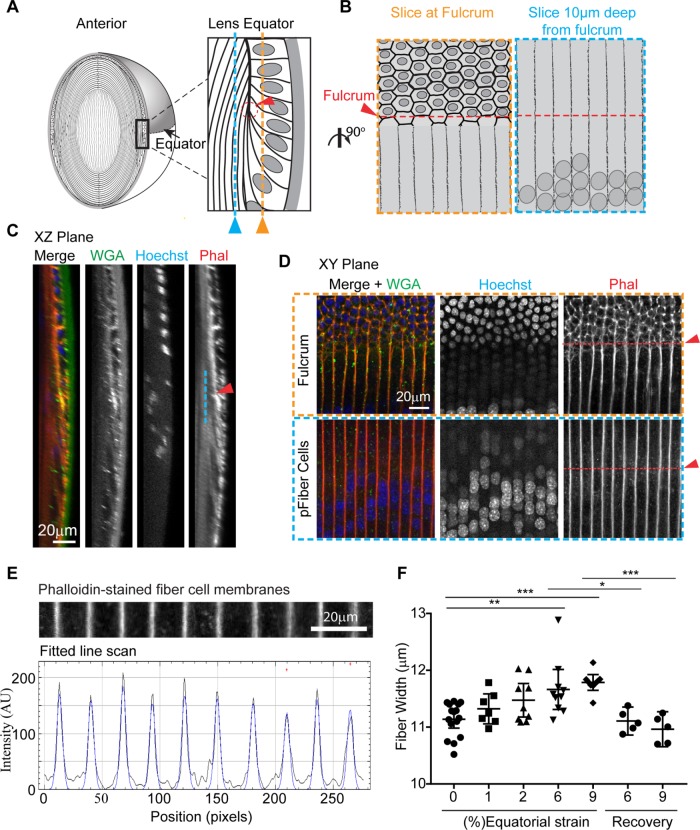
Lens flattening caused by strain leads to a reversible increase in equatorial fiber cell width
When lenses are compressed axially, they expand equatorially (Baradia et al., 2010; Gokhin et al., 2012; Cheng et al., 2016a). We determined that axial strains of 10, 14, 23, and 29% correspond to equatorial strains of 1, 2, 6, and 9%, respectively (Figure 2). At the lens equator, long, thin fiber cells are aligned perpendicular to the direction of equatorial strain; therefore, fiber cell widths might be expected to expand during axial lens flattening. To examine fiber cell widths, we fixed lenses as they were strained by application of coverslip loads. When fixed under strain, lenses maintain their flattened shape (Supplemental Figure S4). The use of fixed lenses enables orientation of lenses so that the equatorial region is in proximity to the microscope objective, which is necessary for optimum imaging of the individual fiber cells. Fixed lenses were then permeabilized and stained with WGA for the capsule, Hoechst for cell nuclei, and rhodamine–phalloidin for visualization of F-actin at fiber cell membranes (Cheng et al., 2017b). The tdTomato fluorescence signal is not well preserved following paraformaldehyde fixation (Bianchi et al., 2015), and we determined that the staining of fiber cell membrane–associated F-actin with phalloidin resulted in superior signal-to-noise ratio as compared with the images of fixed tdTomato-labeled fiber cells at the equator (unpublished data). This superior labeling of F-actin at membranes is the reason for conducting this portion of the study in wild-type lenses rather than tdTomato lenses.
Because fiber cell widths change with depth in the lens, we standardized the depth at which we measured fiber cell widths in unstrained and strained lenses. For depth standardization, we located the lens fulcrum or modiolus where the apical tips of elongating fiber cells anchor before cell elongation (Zampighi et al., 2000; Sugiyama et al., 2009; Cheng et al., 2013) and measured fiber widths within the fiber cell mass at ∼10 μm inward from the fulcrum (∼4 cell layers deep), as depicted in Figure 7, A and B. The fulcrum was identified at the equator based on concentrated F-actin staining (Cheng et al., 2013) in x,z-plane views of sagittal optical sections of 3D reconstructions from confocal z-stacks (red arrow in Figure 7, A and C). In single optical sections en face (x,y-plane view), the fulcrum could also be identified by a change in cell organization (revealed by the F-actin at cell boundaries) and by nuclear alignment (red arrow in top panel in Figure 7, B and D). Fiber cell widths were measured through line scan analysis of F-actin signal intensity across a line perpendicular to the fiber cell lengths, at the level of the fulcrum, and 10 μm deep from the fulcrum. On the resultant line scan profiles of F-actin fluorescence intensity, the periodic signals mark the cell boundaries. These signals were analyzed computationally to obtain high spatial accuracy in determination of fiber widths by peak-to-peak analysis (Gokhin and Fowler, 2017).
FIGURE 7:
Lens equatorial strains of 6 or 9% lead to increased equatorial fiber widths. (A) Diagram depicting equatorial region of lens (left), with equatorial region boxed and magnified (right) to indicate the location of the optical section at the epithelial to fiber cell transition (orange) at the fulcrum (red), and the location of the optical section used to measure fiber cell widths 10 μm deep from the fulcrum (blue). (B) Diagram depicting x,y plane of an optical section showing epithelial to fiber transition (left, outlined in orange dashed box) The fulcrum can be determined by the change in nuclear organization and cell morphology (red arrow and dashed line), and fiber widths were measured at the fulcrum position in an optical section ∼10 μm deep from fulcrum (right, outlined in blue dashed box). (C) A 3D sagittal reconstruction of confocal z-stacks, in x,z-plane view, of lens equator showing fulcrum (red arrowhead) and peripheral fiber cells ∼10 μm deep from the fulcrum (blue line). (D) Single optical section (x,y-plane view) shows the epithelial to fiber transition (top) and the peripheral fiber cell layer (pFiber cells) ∼10 μm deep in this region (bottom), as depicted schematically in B. The pFiber cells shown in the bottom panels are from the region marked by the blue dashed line in A and B; arrowhead indicates the x,z position of the fulcrum. (E) For calculation of fiber cell width, fitted line scan analysis of F-actin intensity across fiber cell membranes at the level of the fulcrum was performed. The distances between F-actin peaks represent fiber cell widths in pixels, which were converted to distance in microns. (F) Dot plots demonstrating the effect of compression on lens fiber width. Each dot represents the average fiber cell width from one lens. *, p < 0.05; **, p < 0.01; ***, p < 0.001 as compared with unstrained, 0% strain lenses.
We determined that, in unstrained lenses, fiber cells are 11.1 ± 0.1 μm wide. At 6% equatorial strain, fiber width increased to 11.7 ± 0.2 μm (Figure 7F). At 9% equatorial strain, fiber width increased to 11.8 ± 0.1 μm. Thus, fiber cell width increased ∼4.7 and 5.8% on average, at 6 and 9% equatorial strains on the lens, respectively. Despite trends toward increasing fiber width even at equatorial strains of 1% (p > 0.99) or 2% (p = 0.15), these fiber widths at 1 or 2% strain were not statistically different from unstrained fiber widths. Following removal of either 6 or 9% equatorial strain, fiber width returned to unstrained levels. Thus, fiber cells at the equator respond to whole-lens axial compression by increasing in width, and upon release of strain, fiber cells recover completely.
DISCUSSION
This study provides new insights into microscale transfer of loads. The distribution of strain differs within the lens as compared with connective soft tissue (tendon, meniscus, annulus fibrosis). In connective tissues, mechanical stress is shielded by the matrix, and strain is largely/completely attenuated before reaching the cells (Bruehlmann et al., 2004; Fang and Lake, 2015). However, in the eye lens, strain is transferred onto the cells, thereby increasing epithelial cell areas and fiber widths (Figure 8). Lens cells form a mass of highly organized and interconnected cells that allow study of force transmission between neighboring cell types and across the bulk tissue. Our work also indicates that microstructures within a tissue respond to mechanical unloading. At low levels of strain (≤14% axial strain), there is complete recovery in bulk lens tissue and all microstructural dimensions. However, at high loads (≥23% axial strain), where bulk tissue recovery is incomplete, there is also incomplete recovery of the suture gap area. The recovery of other microstructures from high loads was not affected. Thus, specific microstructures have different propensities to bear and recover from load.
FIGURE 8:
Summary diagram of the effects of axial and equatorial strains on mouse lens shape and capsule and cellular morphologies. Low compressive strains reversibly reduce capsule thickness and increase anterior epithelial cell area and separation of fiber cell tips at the anterior suture. High compressive strains reversibly increase fiber cell widths at the equator, but irreversibly separate fiber cell tips at the anterior suture.
We find that lens capsule thickness decreases with axial strain and recovers completely following release from strain (Figure 8). The ability of the capsule to reversibly deform with applied strain may not come as a surprise because it has been well documented that isolated capsules are viscoelastic (Fisher, 1969b; Halfter et al., 2013). Our observations of intact, and not isolated, lens capsules provide additional support for capsule deformability in situ. We also show that capsule thickness decreases progressively with increasing strains. Even at 29% axial strain, the highest level of strain applied, the capsule completely recovers to its original thickness following the release from load. This demonstrates the high propensity for the mouse lens capsule to undergo strain. Intriguingly, in a previous study, it was determined that isolated bovine capsules can undergo up to 76% strain, and young human capsules can undergo up to 108% strain (Halfter et al., 2013). The mechanical strength and viscoelasticity of lens capsules is thought to be due to type IV collagen polymer structure, a hexagonal network that forms the main component of capsules across species, including mice and humans (Schmut, 1978; Danysh and Duncan, 2009; Halfter et al., 2013).
Loads applied to the anterior of the lens propagate through the lens capsule to the underlying epithelial cells, which respond to 10% bulk axial strain by expanding their cell area (Figure 8). Lens anterior epithelial cells have a specialized network of actin and myosin organized in polygonal arrays that are thought to generate tensional forces to allow for load bearing (Rafferty and Scholz, 1985, 1989; Rafferty et al., 1990). Our findings that the epithelial cell area increases with lens flattening is consistent with the idea that the lens epithelial cells are load bearing. Additionally, when lenses are released from 10% strain, the epithelial cell area decreases and returns to its prestrain area. An interesting question that arises from these data is whether the lens rounding is a consequence of the tension generated by the actin–myosin polygonal arrays in the epithelial cells, as previously hypothesized (Rafferty and Scholz, 1985, 1989; Rafferty et al., 1990). Alternatively, the decrease in epithelial cell area may instead be a consequence of forces generated from bulk lens rounding. Although it has been shown that actomyosin disruption can affect the biomechanical response of chick lenses to bear load (Won et al., 2015), future experiments that specifically perturb the actin–myosin network in either epithelial or fiber cells of lenses under mechanical stress will be required to address this question. Beyond 10% strain, we did not detect a further increase in epithelial area, possibly due to the variability of anterior epithelial cell areas at higher loads. This variability may arise due to localized epithelial cells sinking into the suture gap at high loads, leading to a decrease in cell area of epithelial cells directly above the suture, but an increase in cell area of epithelial cells away from the suture (unpublished data).
Application of load at the lens posterior, resulting in whole-lens flattening, causes an increase in fiber cell width at the equator. Notably, unlike the lens capsule and epithelial cells, which change their dimensions at low load (1 coverslip), fiber cells increased their width only at higher loads (≥5 coverslips). This could be due to the magnitude of strain being greater axially than equatorially at any given load, as shown here and previously (Cheng et al., 2016a). With 1 coverslip, the equatorial strain is only 1%, whereas axial strain is 10%. Although there is a trend toward small increases in fiber cell widths at 1 and 2% equatorial strain, a power analysis reveals that detection of such small differences would require a very large lens sample size (N = 104 and 58 for 1 and 2% equatorial strain, respectively). Nevertheless, we detected an increase in fiber cell widths at 6 and 9% equatorial strain with our lens sample sizes (N = 9 and 10 for equatorial strains of 6 and 9%, respectively). The increase in fiber widths may not come as a surprise. The hexagonal shapes and formation of complex interlocking protrusions of the mature fiber cells (Dickson and Crock, 1972; Willekens and Vrensen, 1981; Cheng et al., 2016b) imply a cellular architecture optimized for load bearing by analogy to other hexagonally shaped structures, such as in lung alveoli and trabecular bone, that can undergo large deformations (Gibson et al., 1982). We also determined that the increase in fiber cell width is completely reversible following release from strain. The complete recovery of fiber width is consistent with bulk lens equatorial recovery, which was also complete at 6% equatorial strain and nearly complete at 9% equatorial strain. Because 9% equatorial strain is already beyond the physiological equatorial strain that accommodative lenses would experience in vivo (Jackson, 1907; Ziebarth et al., 2007; Marussich et al., 2015), we did not examine the effect of higher loads to determine whether greater equatorial strains led to incomplete recovery.
Compression of lenses results in fiber tip separation at the sutures. As sutures have been shown to provide an extracellular pathway for the directed delivery of molecules to the lens core through the lens microcirculation system (Vaghefi et al., 2012), our findings lead to the speculation that mechanical loading could facilitate molecule delivery through fiber tip separation. However, further experiments are required to examine this. Our results also showed that fiber cell–tip separation at the suture is irreversible at axial strains ≥23%. These findings are similar to those of Baradia et al. (2010), who showed that, in 4-wk-old C57Bl/6 wild-type mouse lenses, fiber cell tips irreversibly separated when lenses were compressed by 200 μm with a specialized confocal microscope objective (Baradia et al., 2010). Damage at the suture could explain the incomplete bulk recovery of whole-lens shape observed at high strains. These observations of damage raise the question, Are mouse lenses, and specifically the fiber cell tips at the sutures, at the ages used in the present study and by Baradia and colleagues, still undergoing maturation and therefore unable to tolerate strain? In support of this idea, older, more mature fiber cells that are approximately >70 μm deep from the anterior surface do not appear to separate at the suture in 6- to 9-wk-old mice (unpublished data). However, it is unclear whether this is due solely to fiber cell maturity or to dissipation of loads with distance inward. Therefore, examination of lenses from older mice may give more direct insight into this question.
This study provides a framework to examine multiscale transfer of strain in lenses of other species. Mouse and primate lenses have similar biomechanical characteristics, including the increase in lens modulus with age (Manns et al., 2007; Ziebarth et al., 2007; Scarcelli et al., 2011; Cheng et al., 2016a), as well as similar capsule and cellular structures (Wanko and Gavin, 1959; Rafferty and Scholz, 1985; Kuszak et al., 2006; Danysh and Duncan, 2009). Thus, mouse lenses are a suitable starting point to develop methodologies and determine characteristics of multiscale transfer. Also, mice can be genetically engineered, and the use of tdTomato mice was advantageous to allow for the identification of microstructures in live lenses in this study. However, mouse lenses are presumed to have limited ability for shape change in vivo (Rafferty and Scholz, 1989; Baradia et al., 2010). There are also microstructural differences between mouse and accommodating (primate) lenses (Kuszak et al., 2006; Kuszak and Zoltoski, 2006). Whereas mouse lenses typically have sutures with three or four branches, accommodative primate lenses have sutures shaped in a complex star pattern with multiple branches. In addition, mouse lens fiber cells form well-aligned sutures between concentric fiber cell layers, while in primate lenses, suture patterns are offset between concentric layers. Therefore, loads may be more effectively transmitted across the multiple suture branches and offset layers in primate lenses. Furthermore, scanning electron microscopy studies show that lens fiber cell–tip morphologies in primate lenses and mouse lenses are different. The fiber cell tips in accommodative lenses taper at their ends and have been proposed to allow fiber cell tips to slide over one another during lens shape changes (Kuszak and Zoltoski, 2006). Mouse lens fiber cell tips, on the other hand, have little taper and limited overlap and are therefore unlikely to slide over each other (Kuszak et al., 2006; Kuszak and Zoltoski, 2006). The lower number of suture branches and reduced tip adhesive area in mouse lens fiber cell tips could explain why the mouse lens suture separates at high loads. Studies evaluating the effect of load on suture morphology and fiber cell tips in primate lenses, and whether any damage occurs to the suture under load, will provide insight into species-specific differences.
Further work is required to confirm whether the microstructural changes we noted with lens compression are similar to microstructural deformations upon lens stretch. In vivo forces on the lens arise from radial tension generated by zonular fibers that attach to the lens capsule at the equator. Radial lens–stretching devices have been used to stretch lenses from larger species (human, monkey, pig) (Pierscionek, 1995; Manns et al., 2007; Reilly et al., 2009). These devices change bulk lens shape by exerting tensile force on zonular fibers. However, because mice have diminutive zonules, we used lens compression in this study. Thus, for mouse lenses, mathematical modeling would be required to determine the differences in local deformations caused by lens compression as compared with stretch. However, the broad effects on bulk lens shape change (decrease in axial diameter and expansion of equatorial diameter) are comparable for compression or stretch. Therefore, we speculate that similar general microstructural deformations would occur with lens stretch. Future experiments comparing compression with stretch of primate lenses are required to test this speculation.
In conclusion, our study establishes a relationship between whole-tissue biomechanics and specific microstructures in the lens model. Gross lens shape change caused by strain results in microstructural-level changes in all the regions of the lens that we examined. This provides critical information that will be useful in expanding current biomechanical models of lens shape changes (Reilly and Ravi, 2010; Reilly, 2014; Wang et al., 2017). Furthermore, the identification of a relationship between microstructure and tissue biomechanics supports the idea that age-dependent microstructural alterations, such as an increase in stiffness of cells or matrix (Starodubtseva, 2011; Lacolley et al., 2017), could have biomechanical consequences at the tissue level. Our methodology could be adapted to further determine which specific molecules, present in either matrix or cells, affect soft tissue biomechanics. Thus, the lens is a novel robust model that will allow in-depth studies to elucidate the complexities of soft tissue multiscale load transfer.
MATERIALS AND METHODS
Mice
Wild-type and Rosa26-tdTomato mice tandem dimer-Tomato (B6.129(Cg)-Gt(ROSA) (tdTomato) (Jackson Laboratories) in the C57BL/6J background between the ages of 6 and 9 wk were used for experiments. The tdTomato mice express tdTomato protein fused in frame to connexin 43 (Muzumdar et al., 2007). Genotyping confirmed that the mice were wild-type for Bfsp2/CP49. Breeding and care of mice were conducted in accordance with an approved animal protocol from the Scripps Research Institute. Following euthanasia, eyes were enucleated from mice and placed in a dissection dish in phosphate-buffered saline (PBS) (137 mM NaCl, 2.7 mM KCl, 8.1 mM Na2HPO4, 1.5 mM KH2PO4, pH 8.1). All experiments were performed at room temperature in PBS. We did not observe any obvious changes in lens transparency during experiments.
Lens dissections
For investigation of bulk mechanical properties of lenses and to image the equatorial regions of fixed lenses, complete lens dissection was performed (Cheng et al., 2016a). Lenses were dissected from mouse eyes under oblique illumination of a dissecting microscope. Briefly, the optic nerve was removed from freshly enucleated eyes using microdissection scissors. Then, fine straight tweezers were inserted into the remaining hole where the optic nerve entered the eye, and scissors were used to cut from the posterior halfway around the eye to the anterior region. Finally, the lens was then gently pushed out by applying pressure to the uncut side of the eye.
For investigation of the anterior regions of the live lens, partial lens dissection was performed. Partial lens dissection minimizes mechanical damage that can occur at the anterior region with complete dissection. For partial lens dissection, an incision was first made at the cornea–sclera junction of the eye using the tip of a scalpel blade (#11; Feather Safety Razor, Osaka, Japan). Next, microdissection scissors were inserted into the incision, and small cuts were made all the way around the eye along the cornea–sclera junction. Following removal of the cornea, the iris was gently peeled off the lens using fine forceps to expose the anterior region (Supplemental Figure S5, anterior view). Next, the optic nerve was cut off using scissors as close to the eye as possible. Finally, scissors were inserted through the hole where the optic nerve entered the eye and used to cut halfway up the posterior region of the eye and then circumferentially around the eye equator, exposing the posterior regions of the lens (Supplemental Figure S5, posterior view). Following this partial lens dissection, the eye lens with an attached band of the surrounding equatorial eye tissue remained (Supplemental Figure S5, side view).
Biomechanical compressive testing of lenses
Bulk compressive properties of lenses were assessed by sequential application of glass coverslips onto the completely dissected lens as previously described (Gokhin et al., 2012; Cheng et al., 2016a). Briefly, lenses were placed in PBS within a divot of a custom-made loading chamber that was situated underneath a dissecting microscope. Side views of the lens were captured through a 45° angled mirror placed at a fixed distance from lens. Images were acquired through a digital camera mounted onto the microscope. Coverslips, with an average weight of 129.3 mg, were applied sequentially, one at a time, onto the lenses. The lenses were compressed for 2 min to allow for stress-relaxation equilibration before image acquisition. The axial and equatorial diameters were measured on images using FIJI software. Lens diameters were converted from pixels to metric (mm) units using the mirror edge (length of 5 mm) for calibration. Percentage strain was calculated using the formula ε = 100 × (dl − d0)/d0, where ε is either axial or equatorial strain, dl is the axial or equatorial diameter at a given load, and d0 is the axial or equatorial diameter at the unstrained (0% strain) state. Lens bulk recovery or resilience was calculated from axial diameter values using the formula recovery = df/d0, where df is the axial or equatorial diameter of the lens following the release from a given load.
Effect of compression on anterior region of lens
Confocal examination of lens anterior regions under compression was performed on live, partially dissected, tdTomato lenses. Immediately following dissection, lenses were stained with fluorescent CF640 dye conjugated to WGA (Biotium, Fremont, CA) (1:100) and Hoechst 33342 (Biotium) (1:500) in PBS to visualize the lens capsule and epithelial cell nuclei, respectively. After 15 min, stained live lenses were then transferred onto glass-bottomed culture dishes (10-mm microwell; MatTek, Ashland, MA) in 3 ml of PBS supplemented with 1.8 U of Oxyrase (Oxyrase, Mansfield, OH). To prevent movement of lenses during imaging, lenses were immobilized in the culture dishes within a 2-mm-diameter circular divot that was created, using a biopsy punch, in a thin layer of agarose (4% wt/vol in PBS). Unconfined compression was applied by sequential application of microscope glass coverslips onto the lenses.
Effect of compression on equatorial region of lens
The effect of strain on equatorial fiber cell widths was investigated in fixed lenses. Completely dissected lenses were placed in 3 ml of PBS and immobilized within an agarose divot, as above. Coverslips were then applied to compress the lenses, as above. After 2 min of compression, the strained lenses were fixed by adding 1 ml of 16% paraformaldehyde to PBS (to achieve a final concentration of 4% paraformaldehyde). After 30 min, coverslips were removed, and lenses were incubated in the 4% paraformaldehyde fixative for an additional 90 min. Fixed lenses were washed in PBS, placed in permeabilization/blocking solution for 30 min, and then stained with WGA (1:100), rhodamine–phalloidin conjugate (Thermo Fisher Scientific, Waltman, MA) (1:20), and Hoechst 33342 (1:500) for 2 h. Lenses were washed in PBS three times for 5 min and then immobilized on their equatorial edges by placement within an agarose wedge (Cheng et al., 2017a).
Confocal microscopy and image analysis
Imaging was performed on a Zeiss 880 laser-scanning confocal microscope (Zeiss, Germany) using a 10× air C-Apo W 0.45NA objective, a 20× air Plan-Apo 0.8 NA objective, or a 40× oil Plan-Apo 1.4 NA objective. z-Stacks were acquired at a digital zoom of 0.6 or 1.0, with z-step sizes of 0.7 μm (10× or 20× objective) and 0.3 μm (40× objective). Raw images were processed using either Zen (Zeiss) or FIJI software. The 3D reconstructions were performed on z-stack data using Arivis Vision4D (Arivis AG) software. Morphometric image analysis was performed using FIJI software. Detailed explanations of the morphometric analysis are provided in the Results section. Briefly, capsule thickness was calculated by line scan analysis of x,z plane–view images to obtain intensity distributions of WGA staining (capsule) and tdTomato labeling (cell membranes) from the outside of the lens across the capsule to the epithelium. For measurement of epithelial cell area, an ROI containing an identical population of cells was identified in x,y images that were taken before, during, and after the release from strain. Average cell area was calculated by dividing the ROI area by the total number of cells within the ROI. Suture gap areas were measured by manually outlining sutures on 3D reconstructed images of tdTomato-labeled fiber cells from the outer layers down to 100 μm depths. Fiber cell widths of fiber cell membranes stained with rhodamine–phalloidin were determined at the lens equator, ∼10 μm inward from the fulcrum, using FIJI with the Distributed Deconvolution (Ddecon) (available at www.scripps.edu/fowler) plug-in. Ddecon deconvolutes fluorescent line scan profiles into a Gaussian point-spread function using a mathematical algorithm for deconvolution. The mathematical algorithm is based on the diffractive properties of light and predictive models providing high spatial precision (Gokhin and Fowler, 2017). The Z-line predictive model was used in the analysis of fiber cell width.
Statistical analysis
Each experiment was replicated on at least four separate occasions. The noted sample size (N) represents the number of lenses used for each experiment. The lenses, represented by N, were not all necessarily from different mice, as preliminary studies showed that the variance in the biomechanical properties between lenses from the same mice is not significantly different from the variance between lenses from different mice. Paired t tests were used to detect differences between two groups of data. Differences between multiple groups in live lenses were detected using a one-way repeated measures analysis of variance followed by a multiple-comparisons test with a Sidak’s adjustment post hoc. For analysis of differences between multiple groups in fixed lenses, a one-way analysis of variance followed by a multiple-comparisons test with a Bonferroni adjustment post hoc was used.
Supplementary Material
Acknowledgments
We thank Michael Amadeo, Dorothy DeBiasse, and Alyssa Mendenhall for assistance with assessment of lens biomechanics. This work was supported by National Eye Institute Grant R01 EY017724 to V.M.F. and a Natural Sciences and Engineering Research Council of Canada (NSERC) postdoctoral fellowship to J.P.
Abbreviations used:
- 3D
three-dimensional
- ECM
extracellular matrix
- PBS
phosphate-buffered saline
- ROI
region of interest
- tdTomato
tandem dimer-Tomato
- WGA
wheat germ agglutinin.
Footnotes
This article was published online ahead of print in MBoC in Press (http://www.molbiolcell.org/cgi/doi/10.1091/mbc.E18-01-0035) on April 10, 2018.
REFERENCES
- Bailey ST, Twa MD, Gump JC, Venkiteshwar M, Bullimore MA, Sooryakumar R. (2010). Light-scattering study of the normal human eye lens: elastic properties and age dependence. IEEE Trans Biomed Eng , 2910–2917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baradia H, Nikahd N, Glasser A. (2010). Mouse lens stiffness measurements. Exp Eye Res , 300–307. [DOI] [PubMed] [Google Scholar]
- Bianchi R, Teijeira A, Proulx ST, Christiansen AJ, Seidel CD, Rulicke T, Makinen T, Hagerling R, Halin C, Detmar M. (2015). A transgenic Prox1-Cre-tdTomato reporter mouse for lymphatic vessel research. PLoS One , e0122976. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bonakdar N, Gerum R, Kuhn M, Sporrer M, Lippert A, Schneider W, Aifantis KE, Fabry B. (2016). Mechanical plasticity of cells. Nat Mater , 1090–1094. [DOI] [PubMed] [Google Scholar]
- Bruehlmann SB, Hulme PA, Duncan NA. (2004). In situ intercellular mechanics of the bovine outer annulus fibrosus subjected to biaxial strains. J Biomech , 223–231. [DOI] [PubMed] [Google Scholar]
- Campbell RE, Tour O, Palmer AE, Steinbach PA, Baird GS, Zacharias DA, Tsien RY. (2002). A monomeric red fluorescent protein. Proc Natl Acad Sci USA , 7877–7882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Candiello J, Cole GJ, Halfter W. (2010). Age-dependent changes in the structure, composition and biophysical properties of a human basement membrane. Matrix Biol , 402–410. [DOI] [PubMed] [Google Scholar]
- Cheng C, Ansari MM, Cooper JA, Gong X. (2013). EphA2 and Src regulate equatorial cell morphogenesis during lens development. Development , 4237–4245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng C, Fowler VM, Gong X. (2017a). EphA2 and ephrin-A5 are not a receptor-ligand pair in the ocular lens. Exp Eye Res , 9–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng C, Gokhin DS, Nowak RB, Fowler VM. (2016a). Sequential application of glass coverslips to assess the compressive stiffness of the mouse lens: strain and morphometric analyses. J Vis Exp , 53986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng C, Nowak RB, Biswas SK, Lo WK, FitzGerald PG, Fowler VM. (2016b). Tropomodulin 1 regulation of actin is required for the formation of large paddle protrusions between mature lens fiber cells. Invest Ophthalmol Vis Sci , 4084–4099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng C, Nowak RB, Fowler VM. (2017b). The lens actin filament cytoskeleton: diverse structures for complex functions. Exp Eye Res , 58–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Danysh BP, Czymmek KJ, Olurin PT, Sivak JG, Duncan MK. (2008). Contributions of mouse genetic background and age on anterior lens capsule thickness. Anat Rec (Hoboken) , 1619–1627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Danysh BP, Duncan MK. (2009). The lens capsule. Exp Eye Res , 151–164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desrochers J, Duncan NA. (2010). Strain transfer in the annulus fibrosus under applied flexion. J Biomech , 2141–2148. [DOI] [PubMed] [Google Scholar]
- Dickson DH, Crock GW. (1972). Interlocking patterns on primate lens fibers. Invest Ophthalmol , 809–815. [PubMed] [Google Scholar]
- Doyle L, Little JA, Saunders KJ. (2013). Repeatability of OCT lens thickness measures with age and accommodation. Optom Vis Sci , 1396–1405. [DOI] [PubMed] [Google Scholar]
- Dumont S, Prakash M. (2014). Emergent mechanics of biological structures. Mol Biol Cell , 3461–3465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fang F, Lake SP. (2015). Multiscale strain analysis of tendon subjected to shear and compression demonstrates strain attenuation, fiber sliding, and reorganization. J Orthop Res , 1704–1712. [DOI] [PubMed] [Google Scholar]
- Fisher RF. (1969a). Elastic constants of the human lens capsule. J Physiol , 1–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisher RF. (1969b). The significance of the shape of the lens and capsular energy changes in accommodation. J Physiol , 21–47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gibson LJ, Ashby FRS, Schajer GS, Robertson CI. (1982). The mechanics of two-dimensional cellular materials. Proc R Soc Lond B Biol Sci , 25–42. [Google Scholar]
- Gokhin DS, Fowler VM. (2017). Software-based measurement of thin filament lengths: an open-source GUI for distributed deconvolution analysis of fluorescence images. J Microsc , 11–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gokhin DS, Nowak RB, Kim NE, Arnett EE, Chen AC, Sah RL, Clark JI, Fowler VM. (2012). Tmod1 and CP49 synergize to control the fiber cell geometry, transparency, and mechanical stiffness of the mouse lens. PLoS One , e48734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halfter W, Candiello J, Hu H, Zhang P, Schreiber E, Balasubramani M. (2013). Protein composition and biomechanical properties of in vivo-derived basement membranes. Cell Adh Migr , 64–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han WM, Heo SJ, Driscoll TP, Smith LJ, Mauck RL, Elliott DM. (2013). Macro- to microscale strain transfer in fibrous tissues is heterogeneous and tissue-specific. Biophys J , 807–817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heidemann SR, Wirtz D. (2004). Towards a regional approach to cell mechanics. Trends Cell Biol , 160–166. [DOI] [PubMed] [Google Scholar]
- Heys KR, Cram SL, Truscott RJ. (2004). Massive increase in the stiffness of the human lens nucleus with age: the basis for presbyopia? Mol Vis , 956–963. [PubMed] [Google Scholar]
- Hozic A, Rico F, Colom A, Buzhynskyy N, Scheuring S. (2012). Nanomechanical characterization of the stiffness of eye lens cells: a pilot study. Invest Ophthalmol Vis Sci , 2151–2156. [DOI] [PubMed] [Google Scholar]
- Jackson E. (1907). Amplitude of accommodation at different periods of life. Cal State J Med , 163–166. [PMC free article] [PubMed] [Google Scholar]
- Krag S, Olsen T, Andreassen TT. (1997). Biomechanical characteristics of the human anterior lens capsule in relation to age. Invest Ophthalmol Vis Sci , 357–363. [PubMed] [Google Scholar]
- Kuszak JR, Bertram BA, Macsai MS, Rae JL. (1984). Sutures of the crystalline lens: a review. Scan Electron Microsc 1369–1378. [PubMed] [Google Scholar]
- Kuszak JR, Mazurkiewicz M, Jison L, Madurski A, Ngando A, Zoltoski RK. (2006). Quantitative analysis of animal model lens anatomy: accommodative range is related to fiber structure and organization. Vet Ophthalmol , 266–280. [DOI] [PubMed] [Google Scholar]
- Kuszak JR, Zoltoski RK. (2006). Focus on Eye Research: The Mechanism of Accommodation at the Fiber Level, Hauppauge, NY: Nova Science Publishers, 117–132. [Google Scholar]
- Lacolley P, Regnault V, Segers P, Laurent S. (2017). Vascular smooth muscle cells and arterial stiffening: relevance in development, aging, and disease. Physiol Rev , 1555–1617. [DOI] [PubMed] [Google Scholar]
- Lampi MC, Reinhart-King CA. (2018). Targeting extracellular matrix stiffness to attenuate disease: from molecular mechanisms to clinical trials. Sci Transl Med , eaao0475. [DOI] [PubMed] [Google Scholar]
- Lovicu FJ, Robinson ML. (2004). Development of the Ocular Lens, Cambridge, UK: Cambridge University Press. [Google Scholar]
- Manns F, Parel JM, Denham D, Billotte C, Ziebarth N, Borja D, Fernandez V, Aly M, Arrieta E, Ho A, Holden B. (2007). Optomechanical response of human and monkey lenses in a lens stretcher. Invest Ophthalmol Vis Sci , 3260–3268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marussich L, Manns F, Nankivil D, Maceo Heilman B, Yao Y, Arrieta-Quintero E, Ho A, Augusteyn R, Parel JM. (2015). Measurement of crystalline lens volume during accommodation in a lens stretcher. Invest Ophthalmol Vis Sci , 4239–4248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muzumdar MD, Tasic B, Miyamichi K, Li L, Luo L. (2007). A global double-fluorescent Cre reporter mouse. Genesis , 593–605. [DOI] [PubMed] [Google Scholar]
- Oxlund H, Andreassen TT. (1980). The roles of hyaluronic acid, collagen and elastin in the mechanical properties of connective tissues. J Anat , 611–620. [PMC free article] [PubMed] [Google Scholar]
- Pierscionek BK. (1995). Age-related response of human lenses to stretching forces. Exp Eye Res , 325–332. [DOI] [PubMed] [Google Scholar]
- Rafferty NS, Scholz DL. (1985). Actin in polygonal arrays of microfilaments and sequestered actin bundles (SABs) in lens epithelial cells of rabbits and mice. Curr Eye Res , 713–718. [DOI] [PubMed] [Google Scholar]
- Rafferty NS, Scholz DL. (1989). Comparative study of actin filament patterns in lens epithelial cells. Are these determined by the mechanisms of lens accommodation? Curr Eye Res , 569–579. [DOI] [PubMed] [Google Scholar]
- Rafferty NS, Scholz DL, Goldberg M, Lewyckyj M. (1990). Immunocytochemical evidence for an actin-myosin system in lens epithelial cells. Exp Eye Res , 591–600. [DOI] [PubMed] [Google Scholar]
- Reilly MA. (2014). A quantitative geometric mechanics lens model: insights into the mechanisms of accommodation and presbyopia. Vision Res , 20–31. [DOI] [PubMed] [Google Scholar]
- Reilly MA, Hamilton PD, Perry G, Ravi N. (2009). Comparison of the behavior of natural and refilled porcine lenses in a robotic lens stretcher. Exp Eye Res , 483–494. [DOI] [PubMed] [Google Scholar]
- Reilly MA, Ravi N. (2010). A geometric model of ocular accommodation. Vision Res , 330–336. [DOI] [PubMed] [Google Scholar]
- Scarcelli G, Kim P, Yun SH. (2011). In vivo measurement of age-related stiffening in the crystalline lens by Brillouin optical microscopy. Biophys J , 1539–1545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmut O. (1978). The organization of tissues of the eye by different collagen types. Albrecht Von Graefes Arch Klin Exp Ophthalmol , 189–199. [DOI] [PubMed] [Google Scholar]
- Shi Y, De Maria A, Lubura S, Sikic H, Bassnett S. (2014). The penny pusher: a cellular model of lens growth. Invest Ophthalmol Vis Sci , 799–809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Starodubtseva MN. (2011). Mechanical properties of cells and ageing. Ageing Res Rev , 16–25. [DOI] [PubMed] [Google Scholar]
- Sugiyama Y, Akimoto K, Robinson ML, Ohno S, Quinlan RA. (2009). A cell polarity protein aPKCλ is required for eye lens formation and growth. Dev Biol , 246–256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szczesny SE, Elliott DM. (2014). Interfibrillar shear stress is the loading mechanism of collagen fibrils in tendon. Acta Biomater , 2582–2590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsujii A, Nakamura N, Horibe S. (2017). Age-related changes in the knee meniscus. Knee , 1262–1270. [DOI] [PubMed] [Google Scholar]
- Upton ML, Gilchrist CL, Guilak F, Setton LA. (2008). Transfer of macroscale tissue strain to microscale cell regions in the deformed meniscus. Biophys J , 2116–2124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vaghefi E, Walker K, Pontre BP, Jacobs MD, Donaldson PJ. (2012). Magnetic resonance and confocal imaging of solute penetration into the lens reveals a zone of restricted extracellular space diffusion. Am J Physiol Regul Integr Comp Physiol , R1250–R1259. [DOI] [PubMed] [Google Scholar]
- Wang K, Venetsanos DT, Wang J, Augousti AT, Pierscionek BK. (2017). The importance of parameter choice in modelling dynamics of the eye lens. Sci Rep , 16688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wanko T, Gavin MA. (1959). Electron microscope study of lens fibers. J Biophys Biochem Cytol , 97–102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Willekens B, Vrensen G. (1981). The three-dimensional organization of lens fibers in the rabbit. A scanning electron microscopic reinvestigation. Albrecht Von Graefes Arch Klin Exp Ophthalmol , 275–289. [DOI] [PubMed] [Google Scholar]
- Won GJ, Fudge DS, Choh V. (2015). The effects of actomyosin disruptors on the mechanical integrity of the avian crystalline lens. Mol Vis , 98–109. [PMC free article] [PubMed] [Google Scholar]
- Zampighi GA, Eskandari S, Kreman M. (2000). Epithelial organization of the mammalian lens. Exp Eye Res , 415–435. [DOI] [PubMed] [Google Scholar]
- Ziebarth NM, Wojcikiewicz EP, Manns F, Moy VT, Parel JM. (2007). Atomic force microscopy measurements of lens elasticity in monkey eyes. Mol Vis , 504–510. [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.