Skip to main content
PMC home page
Molecular Biology of the Cell logoLink to Molecular Biology of the Cell
. 2018 Aug 8;29(16):2005–2011. doi: 10.1091/mbc.E18-03-0154

Probing cellular mechanics with acoustic force spectroscopy

Raya Sorkin a,b,†,*, Giulia Bergamaschi a,†, Douwe Kamsma a, Guy Brand a, Elya Dekel c, Yifat Ofir-Birin c, Ariel Rudik c, Marta Gironella d, Felix Ritort d, Neta Regev-Rudzki c, Wouter H Roos b, Gijs J L Wuite a,*
Editor: Dennis Dischere
PMCID: PMC6232971  PMID: 29927358

Abstract

A large number of studies demonstrate that cell mechanics and pathology are intimately linked. In particular, deformability of red blood cells (RBCs) is key to their function and is dramatically altered in the time course of diseases such as anemia and malaria. Due to the physiological importance of cell mechanics, many methods for cell mechanical probing have been developed. While single-cell methods provide very valuable information, they are often technically challenging and lack the high data throughput needed to distinguish differences in heterogeneous populations, while fluid-flow high-throughput methods miss the accuracy to detect subtle differences. Here we present a new method for multiplexed single-cell mechanical probing using acoustic force spectroscopy (AFS). We demonstrate that mechanical differences induced by chemical treatments of known effect can be measured and quantified. Furthermore, we explore the effect of extracellular vesicles (EVs) uptake on RBC mechanics and demonstrate that EVs uptake increases RBC deformability. Our findings demonstrate the ability of AFS to manipulate cells with high stability and precision and pave the way to further new insights into cellular mechanics and mechanobiology in health and disease, as well as potential biomedical applications.

INTRODUCTION

Mechanical forces participate in the regulation of a large number of biological processes, ranging from the nanoscale (e.g., molecular motors) to the cellular level. Several examples include synthesis of proteoglycans by chondrocytes in response to external loads (Bachrach et al., 1995) or the impact of the substrate’s viscoelastic properties on cell division, morphology, and function (Engler et al., 2006; Evans et al., 2009; Denning and Roos, 2016). In red blood cells (RBCs), mechanics plays a key role, as these cells have a unique ability to undergo repeated large deformations on passing through microcapillaries (Mohandas and Evans, 1994). Moreover, structural and mechanical changes in cells often occur upon disease, including anemia (Maciaszek and Lykotrafitis, 2011), spherocytosis (Jacob et al., 1971), diabetes (Ernst and Matrai, 1986), neurodegeneration (Fang et al., 2014), cancer (Cross et al., 2007), fibrosis (Liu et al., 2010), or malaria (Suresh et al., 2005; Suresh, 2006). As the mechanical response of cells has been shown to change under the influence of these diseases, such changes in stiffness could potentially be used as biomarkers for a large number of pathologies (Hoffman et al., 2011).

Methodology to study the mechanical properties of cells has developed rapidly over the past few decades. Magnetic bead cytometry (Crick and Hughes, 1950) and micropipette aspiration were among the first methods used for cell mechanics studies, as pressure application on RBC with a micropipette allowed the first measurements of their resistance to deformation (Rand and Burton, 1964). Later, RBC deformation was studied by applying flow in microfluidic devices (Skalak and Branemark, 1969; Noguchi and Gompper, 2005; Wan et al., 2008) and recent advances allow for fast mechanical phenotyping of large cell populations (Otto et al., 2015). Because fluid flow devices did not always deliver the accuracy needed, many single-cell methods to probe cell mechanics have been employed; optical tweezers stretching of RBCs (Dao et al., 2003) revealed that the shear modulus of RBCs increases up to 10-fold during malaria parasite infection (Suresh et al., 2005). AFM measurements of sickle cell disease RBCs revealed that the Young’s modulus of these pathological erythrocytes was approximately three times higher than in normal cells (Maciaszek and Lykotrafitis, 2011). Further, analysis of thermal fluctuations (flicker spectroscopy) of RBC membranes provides valuable insights into their mechanics (Park et al., 2010b). Very recently, real-time deformability cytometry and flicker spectroscopy measurements demonstrated that malaria parasite binding to RBCs leads to a reduction in the bending modulus of the cell membrane, thus effectively reducing the energy barrier to invasion (Koch et al., 2017). While single-cell methods provide very valuable information, they are often technically challenging and lack the high data throughput needed to distinguish differences in heterogeneous populations, while fluid-flow high-throughput methods miss the accuracy to detect subtle differences.

In this work, we present a novel approach to probe cell mechanics using AFS. AFS is a recently introduced single-molecule technique that distinguishes itself by a high experimental throughput, a wide range of forces that can be applied, and an unmatched range of force loading rates (Sitters et al., 2015; Kamsma et al., 2016). We now introduce an approach where AFS is used to apply well-controlled force up to 500 pN to cells confined between a microsphere and a surface. With our approach, we were able to follow 30–50 single cells in parallel in real time, while exchanging the buffer and probing changes in their mechanical properties. This method can be used to probe various cells and subcellular structures. The average size of the particles may be selected between 0.2 and 10 μm. Moreover, we have previously estimated the time response of AFS to be in the order of 1 µs (Sitters et al., 2015), meaning that experiments are limited to the time response of the biological system. Long-term measurements are also possible (hours or even days), due to the inherent stability of the method. To validate our approach, we apply chemical treatments of known effect, 5-cholesten-3β-ol-7-one (7-KC) and formaldehyde (FA), and show that following these treatments, significant changes in RBC mechanics are detected.

After validation of our method, we examined the effect of extracellular vesicles (EVs) uptake on RBCs mechanics. EVs, secreted by all cell types, comprise a heterogeneous group of vesicles of different sizes and intracellular origins that are able to transfer signaling molecules, such as nucleic acids, proteins, and lipids, between cells (Kastelowitz and Yin, 2014). EVs are involved in maintenance of normal homeostasis as well as the spread of a wide range of diseases (Barteneva et al., 2013; El Andaloussi et al., 2013a,b; Ofir-Birin et al., 2017). In RBCs, membrane-shed EVs are released in vivo as well as under blood bank storage conditions (Greenwalt, 2006). EVs from RBCs promote coagulation and macrophage uptake and may also have immunosuppressive activities (Alaarg et al., 2013), while during malaria infection, parasites in RBCs communicate via exosome-like vesicles (Regev-Rudzki et al., 2013). We ask whether presence of a high concentration of EVs in the vicinity of RBCs might affect cell mechanics. To address this question, we incubate healthy RBCs with EVs derived from RBCs and demonstrate that this treatment increases RBC deformability.

RESULTS AND DISCUSSION

Acoustic stretching of RBC can be recorded and quantitatively analyzed

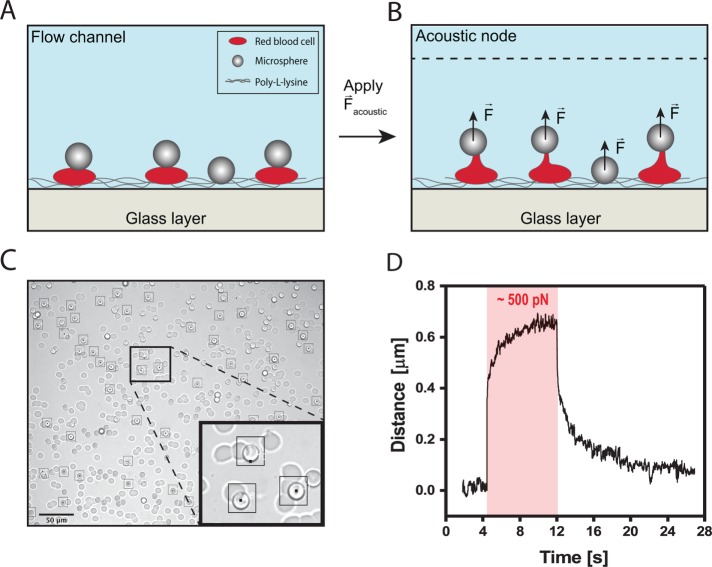
Here we use AFS to probe the mechanical properties of RBCs. To apply forces on single cells using AFS, cells are confined between a microsphere and the glass surface of the AFS chip (see Figure 1A; see Materials and Methods for the setup). The procedure we employ is as follows: the chamber of the AFS chip is functionalized with poly-l-lysine (see Materials and Methods). Next, fresh RBCs from healthy donors are introduced into the flow chamber (at 4% vol/vol), where they precipitate and then stick immediately to the bottom of the chamber. Next, silica microspheres (6.84 µm in diameter) modified with concanavilin-A are introduced into the flow chamber, precipitate randomly and in some cases attach on top of RBCs (Figure 1C). Last, when the voltage is turned on, an acoustic field is generated, and the beads are pulled toward the acoustic node, thereby stretching the RBCs (Figure 1B). Relatively large silica microspheres are used for high imaging contrast compared with the RBC (see Figure 1C) to enable tracking of the microspheres in three dimensions. Also, silica has a higher acoustic contrast factor compared with RBC (Settnes and Bruus, 2012); as the silica microsphere and the RBC have roughly the same volume, the force experienced by the RBC due to the acoustic field is significantly lower than the pulling force generated by the silica microsphere on the RBC. The microspheres are tracked in three dimensions using a tracking software as described previously (Kamsma et al., 2016). In parallel to tracking of beads on top of cells, stuck beads on the flow chamber surface are monitored to correct for the long-term drift. A microsphere on top of an RBC can be tracked with an accuracy of ∼20 nm SD in x, y, and z, as measured on cells in resting state (Supplemental Figure S1). Owing to the interference of the RBC, the tracking accuracy is decreased compared with previously reported values (Sitters et al., 2015). Typically, several tens of RBCs with microspheres attached on top could be tracked in one field of view (Figure 1C; black squares mark the cells that were tracked during the course of one experiment). In a typical experiment, a constant load is applied (a force clamp) on the RBC, and their elongation over time is recorded, as shown is Figure 1D.

FIGURE 1:

FIGURE 1:

Open in a new tab

Principle of AFS measurements on RBCs. (A) Illustrative image of the experiment; RBCs are confined between the surface and silica microspheres. (B) The acoustic force is turned on, pushing the microspheres upwards and thereby pulling on RBCs. (C) Digital camera image of a typical field of view in a pulling experiment. Tens of microspheres on top of the RBCs can be individually tracked (indicated with black squares). Scale bar is 50 μm. (D) Typical trace of a RBC response to the application of constant force (red area illustrates a force step of ∼500 pN). The extension of the RBC is tracked over time, demonstrating a three-phasic viscoelastic response. When the acoustic force is switched off, viscoelastic relaxation is observed.

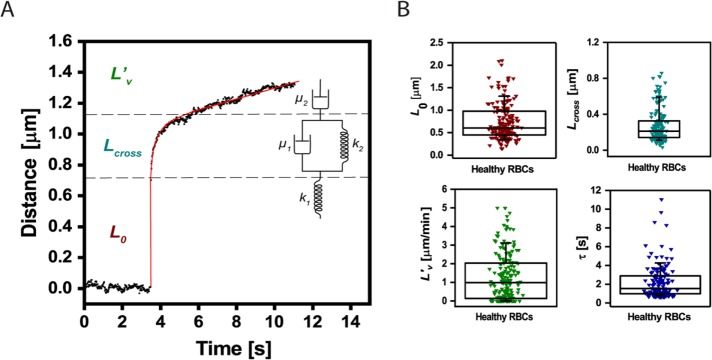
Following the application of a force step, the cells exhibit a three-phase creep response, as shown in Figure 2A: an instantaneous elastic response, then a retarded elastic response, followed by a viscous flow behavior. This type of response can be described by a simple viscoelastic model consisting of springs and dashpots (as illustrated in the inset of Figure 2A), a four-parameter model termed Burger’s viscoelastic model (Rand, 1964):

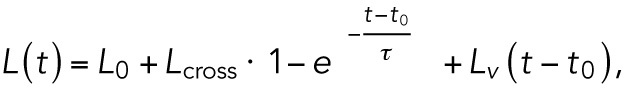graphic file with name mbc-29-2005-e001.jpg(1)

FIGURE 2:

FIGURE 2:

Open in a new tab

Quantification of RBCs viscoelastic behavior in response to acoustic force pulses. (A) Cellular extension (black dots) can be fitted by means of the Burger’s model (red line). The distance–time curve can then be decomposed using the Burger’s model (see springs and dashpots mechanical analogue), including the instantaneous linear extension L0 (F/k1), a viscous response described by a characteristic time τ (µ1/k2), a viscous elongation Lcross (F/k2), and an extrusion velocity L′v (F/µ2) (see Materials and Methods for detailed description; F is the applied force). (B) Distribution of the parameters L0 (0.6 μm, 90% CI [0.34–1.3]), Lcross (0.21 μm, 90% CI [0.11–0.59]), τ (1.27 s, 90% CI [0.74–4.26]) and L′v (0.99 μm/min, 90% CI [1.35 × 10–11–3.12]), as computed from the fitting of AFS data collected for healthy RBCs to Burger’s model. The box plots report median lines and the 10/90% interval.

where L0 (F/k1) is the instantaneous elastic elongation, Lcross (F/k2) is the retarded elastic behavior, τ (µ1/k2) is the characteristic time constant of the retarded elastic behavior, and L′v (F/µ2) the long-term viscous flow. Modeling compliance by a simple combination of elastic and viscous elements, denoted by springs and dashpots, was previously used in a range of experiments, such as for lipid vesicles in fluid flow (Guevorkian et al., 2015), microrheological measurements on cells (Bausch et al., 1998, 1999), and AFM studies of cell mechanics (Wu et al., 1998; Yango et al., 2016). Based on this analysis, as detailed under Materials and Methods, the viscoelastic behavior of cells can be described by the above-mentioned four parameters. The distributions of these parameters for normal RBC are shown in Figure 2B. One hundred sixty-nine cells from five separate experiments on normal healthy RBC are depicted in these plots, demonstrating the large distribution due to biological variation and further stressing the necessity to probe many cells to depict differences resulting from cell treatments or pathologies. Further, we test whether the overall deformation cells undergo is linear by summing the creep and relaxation responses, as shown in Supplemental Figure S2. As can be seen in Supplemental Figure S2, this sum is roughly constant with time, indicating that the deformation is indeed linear, and hence the use of a linear viscoelastic model is justified.

To establish experimental parameters that can affect RBC mechanics, we first examined the effect of time. We discovered that RBC show stiffening after 2 h (Supplemental Figure S3). L0 is significantly lower after 3 h, while τ and other parameters are significantly lower after 2 h (Supplemental Figure S3). Interestingly, while the values of the different parameters are changing with time, there is a correlation between L0 and Lcross values; when plotting L0 as a function of Lcross at t = 0 and t = 4 h, the average slope is the same for both cases: 0.32 (Supplemental Figure S4). The slope is equal to the ratio of elastic coefficients, 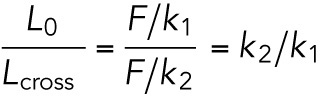Inline graphic, which appears to be conserved and time independent.

We note that the error in the parameter estimation is 30% for τ and only 2% for L0, as explained in detail under Materials and Methods. Reported values of characteristic time constant τ in similar experiments vary widely in the literature, discrepancies that are often attributed to varying time scales and frequencies of experiments (Haase and Pelling, 2015). The instantaneous elastic response L0 is more intuitive to interpret, as shorter elongation directly correlates to higher stiffness. Furthermore, the determination of L0 is more robust, because it does not depend on the other fit parameters. We convert the elastic elongation data to elastic coefficient values (in N/m units) by dividing the applied force by the elongation distance. This is enabled by a force calibration, performed by quantifying and averaging the response of freely suspended beads to force, a procedure we term “shooting beads,” as previously described (Kamsma et al., 2016) and explained under Materials and Methods and shown in Supplemental Figure S5.

The median elastic coefficient value for healthy RBCs in our experiments is 0.58 nN/μm (90% confidence interval [CI] [0.27–1.01 nN/μm]). When comparing this value to the literature, it is in a similar range but softer than previously reported values for fibroblasts, ∼3 mN/m (Yango et al., 2016), which is expected, as RBCs are more deformable. This value is close to previously reported values for membrane tension in RBC under strong adhesion to polylysine (∼1 mN/m) and higher than the shear elastic modulus of the RBC membrane skeleton (∼0.01 mN/m) (Hategan et al., 2003). Strong adhesion of RBCs to polylysine contributes to cell membrane tension, which leads to resistance of the adherent cell to pushing and pulling (Hategan et al., 2003; Sen et al., 2005). This effect should be considered when performing cell mechanics measurements on surface attached cells and especially in the case of RBC that lack tension modulation mechanisms. To address the effect of surface attachment on the mechanical parameters extracted from our data, we have performed measurements on RBC attached to 0.001 mg/ml poly-l-lysine. We observed an increase in the L0 values obtained from these measurements, indicating greater deformability of the RBC as a result of a less-strong surface attachment. Moreover, the spread in the results increased for the lower polylysine concentration, likely due to variation in the adhesion of the RBC to the surface (Supplemental Figure S6). As the poly-l-lysine coating is an important factor in our measurements, we take special care to keep the concentration and application procedure constant thought all measurements reported in this work.

The observed stiffening of RBCs with time can possibly be attributed to exhaustion of the available glucose. This explanation is further supported by RBC mechanical measurements in phosphate-buffered saline (PBS) and Ringer’s buffer supplemented with glucose, as shown in Supplemental Figure S7. RBCs in Ringer’s buffer show a significantly larger elastic elongation L0 in the glucose-containing buffer (measurements performed immediately on RBC introduction in the flow cell). This is consistent with several studies that demonstrated that ATP driven cytoskeleton forces lead to membrane softening in RBCs (Gov and Safran, 2005; Betz et al., 2009; Park et al., 2010a; Rodriguez-Garcia et al., 2015), as consumption of ATP promotes spectrin-actin dissociation due to phosphorylation of protein-4.1 (Ling et al., 1988; Bennett, 1989; Manno et al., 2005). Therefore, all the next measurements are performed in glucose-supplemented Ringer’s buffer immediately after introducing the RBCs into the flow chamber and for no longer than 2 h.

Chemically induced changes in cell mechanics can be directly measured and quantified

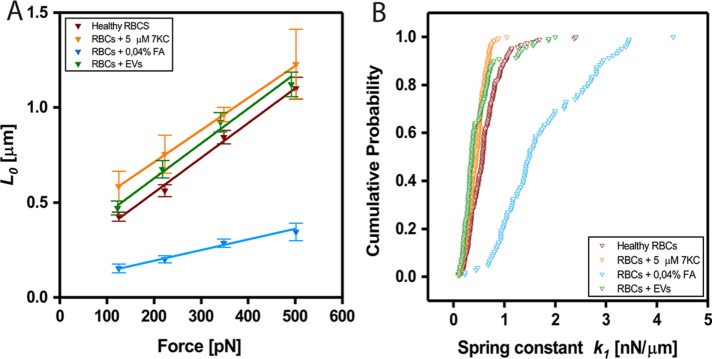
To validate the ability of our method to depict mechanical changes in RBC, we next applied chemical treatments with known mechanical effects: FA, a well-known cross-linking agent that is expected to stiffen cells (Braet et al., 1998), and 5-cholesten-3β-ol-7-one (7KC), a cholesterol analogue that is expected to soften the cell membrane (Koch et al., 2017). Both treatments were found to induce the expected effects; FA treatment significantly stiffened the RBC, as is evident from the smaller elongation (L0 values) at different applied forces (Figure 3A). 7KC also induced the expected effect, as is evident from the larger elongation (L0 values) at different applied forces (Figure 3A). Cumulative distributions of the elastic coefficients k1 (F/L0) for force clamps of ∼350 pN are shown in Figure 3B. As the differences between the healthy RBC, the 7KC treated RBC, and the vesicle-treated RBC (explained in detail below) are not very large, we have employed a rigorous statistical test to compare the distributions of the values for the different cells. The Kolmogorov–Smirnov statistical test, a nonparametric test that quantifies the distance between empirical distributions of two data sets, was used (see Materials and Methods). The distributions of k1 values for each of the treatments were found to be significantly different from the normal RBCs with p < 0.005. Detailed distributions of all the fitting parameters are shown in Supplemental Figure S8.

FIGURE 3:

FIGURE 3:

Open in a new tab

Quantification of mechanical changes on addition of chemicals or EVs. (A) Force dependence of instantaneous elongations L0 for healthy RBCs treated with formaldehyde (0.04%), 7K-C (5 μM), and vesicles. Linear fits yielded values of yhealthy = 0.0018x + 0.19, y7KC = 0.0017x + 0.37, yFA = 0.0006x + 0.08, yEVs = 0.0018x + 0.26. (B) Cumulative probability distributions of measured elastic coefficient k1 per cell (nN/μm) computed for force clamps of ∼350 pN. For healthy RBCs, the median value of k1 was found to be 0.58 nN/μm (90% CI [0.27–1.01 nN/μm]); RBCs treated with 0.04% formaldehyde, 1.50 nN/μm (90% CI [0.81–2.95 nN/μm]); 5 μM 7K-C, 0.45 nN/μm (90% CI [0.21–0.68 nN/μm]); and cells exposed to RBC vesicles; 0.36 nN/μm (90% CI [0.19–0.85 nN/μm]); p < 0.005 (as determined by KS statistical test; see Materials and Methods).

To better understand these effects, stiffening induced by FA treatment and softening induced by 7KC treatment, we should consider the unique structure of RBCs. The membrane of an RBC is tightly attached to an underlying skeleton, a pseudohexagonal meshwork of spectrin, actin, and other proteins. Formaldehyde reacts mostly with primary amines (lysine) and thiols (cys­teine), forming methylene bridges (Thavarajah et al., 2012) between proteins. This treatment affects only the membrane skeleton and cytosolic proteins, most abundant of which is haemoglobin, and does not affect mechanical properties of lipid membranes. 7KC is a cholesterol analogue that has a ketone group on carbon-7 and thus interferes with acyl chain packing and reduces membrane order. Unlike FA, this treatment does not affect the cytoskeleton and cytosolic proteins but only the lipid membrane. It seems from our analysis that both cytoskeleton and membrane modifications affect the viscoelastic parameters, and therefore we cannot easily disentangle these effects. We do, however, observe a more dramatic effect following FA treatment.

RBC-derived vesicle uptake increases cell deformability

After successful validation of our method, we sought to examine the effect of incubation of RBCs with RBC-derived EVs on cell mechanics. To this end, we first introduced cells and microspheres into the flow cell, as explained before, and then exchanged the buffer with a buffer containing EVs derived from other RBCs (10 μl at a concentration of 1012 particles/ml; see Materials and Methods). Immediately on vesicle introduction, the mechanical properties of the RBCs were probed. We expected that vesicles in the vicinity of RBC might be taken up by the RBC and thereby change cell deformability. As RBCs do not have internal organelles, such as endoplasmic reticulum (ER) and Golgi, we expect that uptake of vesicles might increase the surface area of the cell membrane and thereby alter the mechanical response. We find that this treatment indeed induces a change in RBC mechanical response: lower elastic coefficient values are obtained after vesicle treatment (Figure 3, A and B, and Supplemental Figure S7A). A possible explanation for this increased deformability is that there is simply more available membrane to be pulled, due to incorporation of the vesicle lipids into the cell membrane. Interestingly, the long-term viscous flow (L′v) following vesicle treatment is significantly larger than for untreated RBC (Supplemental Figure S7C), similarly to the effect of 7KC, thus further supporting the explanation of increased membrane surface area. This finding may have implications in pathology, as in several disease states the concentrations of EVs are significantly elevated. For example, EV concentrations were significantly increased in trauma patients compared with healthy controls (Kuravi et al., 2017), and EV concentration was found to be 40-fold higher in breast cancer patients compared with healthy females (König et al., 2018). Further, elevated levels of EVs were measured in plasma of malaria-infected children compared with healthy controls (Combes et al., 2004). As there are known changes in cell mechanics, as well as in EV levels in several pathologies, there may exist a link between the two. For example, during malaria infection, RBCs become stiffer (Suresh et al., 2005). At the same time, the concentration of EVs (in this case, they are a mixture of both exosomes from the parasite and membrane shed vesicles from the RBCs) is known to increase about 10-fold (Mantel et al., 2013; Regev-Rudzki et al., 2013). A possible explanation may be that infected cells that harbor parasites have increased vesiculation and become stiffer by losing membrane. These vesicles, while having many possible roles (Regev-Rudzki et al., 2013; Mantel et al., 2016; Sisquella et al., 2017), may also be taken up by healthy bystander RBC, which would become softer as a result of such uptake. This softening will, in turn, allow easier entry of the parasite into these bystander cells, thus facilitating invasion. We intend to further investigate this idea in the future.

To conclude, we demonstrated that AFS can be successfully applied for cell mechanics measurements by stretching multiple cells under constant force and quantitatively analyzing the cell compliance response. We have validated our method by applying chemical treatments of known effect, and we explored the effect of EVs uptake on RBC mechanics. This leads to the discovery of increased cell deformability following EV treatment. Our findings demonstrate the ability of AFS to manipulate cells with high stability and precision and pave the way to further new insights into cellular mechanics and mechanobiology in health and disease, as well as potential biomedical applications.

MATERIALS AND METHODS

Sample preparation

Blood was collected on the day of each experiment from healthy donors by a finger pricking technique (iHealth glucose meter lancing device). RBCs were diluted to 4% vol/vol in 500 µl of Ringer’s buffer (32 mM HEPES, 125 mM NaCl, 5 mM KCl, 1 mM MgSO4, 1 mM CaCl2, 5 mM glucose, pH 7.4) and used within 2 h after extraction. To allow surface attachment of RBCs, the AFS flow cell was first functionalized with poly-l-lysine (0.1 mg/ml, incubated for 30 min; Sigma-Aldrich, P4707). Then RBCs were flushed into the flow cell where they descended by gravitation and attached directly to the bottom surface. The flushing procedure was repeated until an optimal working coverage of RBCs was reached (∼1500 cells per mm2; see Figure 1C). Then, functionalized silica microbeads (described below) were flushed into the flow chamber, where they descended to the bottom surface and attached in nonspecific locations (see Figure 1, A and C). We address in the supplementary information and Supplemental Figure S9 the effect of neighboring cells on our measurements. All measurements were performed at a physiologically relevant temperature of 37°C, using a temperature control module (AFS-TC, LUMICKS). For data obtained with formaldehyde, 7KC and EVs, the sample is prepared as described above, and then chemicals of interest are flushed in the flow chamber.

Microsphere functionalization

Silica microspheres (6.84 µm in diameter, 1% wt/wt; Bangs Labs, SS06000) were first washed by 3% (vol/vol) dilution in PBS, followed by centrifugation at 500 × g (for 2 min) and removal of supernatant. Then, microspheres were surface activated by incubation in 3% HCl (10 min). After washing in PBS and centrifugation (500 × g for 2 min), microspheres were functionalied by incubation with concanavalin A (1 mg/ml; Sigma-Aldrich C5275) for 30 min at 4°C. Finally, the microspheres were washed and resuspended in 500 µl Ringer’s buffer.

The setup

An AFS microfluidic chip consists of a monolithic glass chip with a fluid channel inside and a piezoelectric element on top. These microfluidic chips are custom fabricated by LUMICKS B.V (Sitters et al., 2015). For imaging, an inverted bright-field microscope is used, as described in Kamsma et al. (2016). Digital camera images were recorded, and the x, y, and z coordinates of all the tracked microspheres were determined in real time. The x and y positions were obtained by quadrant interpolation (van Loenhout et al., 2012) and the z position by means of a look-up table (Gosse and Croquette, 2002).

Data fitting

The RBCs response to a fixed force F shows a steep linear increase, followed by a slower elongation; this behavior can be described by means of a Burger’s mechanical model, comprising a Kelvin-Voigt body connected in series to a second dashpot (damping coefficient µ1) and spring (spring constant k1). To quantify the RBCs viscoelastic response, the data are fitted to Burger’s model using Eq. 1. The fitting parameters L0, Lcross, τ, and L′v are extracted using a custom-made Python script (https://gitlab.com/sorkin.raya/Cellular-mechanics-AFS/tree/master) as follows: The data can be divided into two regions; the first region includes the fast vertical jump that happens right at the onset of the applied force, while the second region includes the viscoelastic and the long-range viscous flow. The end of the jump, that is, the start of the second region, is found by examination of the derivative of the distance with respect to time right after the onset of force. The second region is then fitted to the model (Eq. 1 without the first elastic spring L0) by least-squares regression. The uncertainty of the fitted parameters is mostly due to the uncertainty in the separation of the two regions, that is, the determination of the transition from regime 1 to regime 2, as seen clearly in Figure 2A. Therefore, to estimate the error in the extracted parameters, six different adjacent time points are picked around the most likely end of jump time. For each of these possible end-of-jump points, we fit the data and find the parameters that we then average. Since the jump only lasts for several data points (the jump lasts less than 0.1 s or 6 sample points), this is an overestimation of the error. Doing this procedure for the normal RBC data for 348 pN force clamp results in the following errors in the extracted parameters: Lcross, 10%, τ, 30%, L′v, 5%, and L0, 2%.

Sample collection and size

To test for day-to-day variability, experiments were repeated on 6 different days for healthy cells in Ringer’s, 5 d for healthy cells in PBS, 4 d for 5 µM 7KC (3 d for 50 μM 7KC), 3 d for 0.04% FA experiments, and 2 d for EVs treatment. The number of donors for the experiment was three for healthy and EVs treatments, while blood from two different donors was used for 7KC and FA experiments. The sample size (number of cells studied) per experimental condition is as follows: Nhealthy = 191, N7KC = 153, NFA = 104, and NEVs = 113. Traces for which the fit failed have been discarded and do not appear in the sample size count.

Statistical analysis

Normality of the data sets was tested with a Shapiro–Wilk normality test. None of the data sets was found to be normally distributed (p < 0.005); hence the use of a nonparametric (with no assumption for normality) test.

Statistical significance of the results was determined by a two-samples Kolmogorov–Smirnov test. This is a two-tailed nonparametric test that quantifies the distance between the empirical distributions of two data sets, where the null hypothesis states that the two samples are drawn from the same distribution.

Addition of chemicals

To induce stiffening, 0.04% wt/vol (in Ringer’s buffer) formaldehyde (Sigma-Aldrich F8775) was flushed into the flow cell. Similarly, to induce RBCs softening, 5 μM of 5-cholesten-3β-ol-7-one (Sigma C2394) was added to the chamber. In both cases, measurements were performed after a brief incubation time of 5–10 min on addition of the chemicals.

Vesicles experiments

Human erythrocytes at 4% haematocrit were incubated in RPMI-HEPES supplemented with 0.5% (wt/vol) Albumax (Invitrogen). Vesicles were isolated from RBC supernatant by differential centrifugation as previously described (Regev-Rudzki et al., 2013)

Supplementary Material

Click here for additional data file. (1,013.1KB, pdf)

Acknowledgments

R.S. acknowledges support through Human Frontier Science Program (HFSP) postdoctoral fellowship LT000419/2015, as well as support through the Israeli National Postdoctoral Award for Advancing Women in Science and the L’Oreal UNESCO award for advancing women in science. W.H.R. acknowledges the support of a Nederlandse Organisatie voor Wetenschappelijk Onderzoek Vidi grant.

Abbreviations used:

AFS

acoustic force spectroscopy

EVs

extracellular vesicles

RBCs

red blood cells

Footnotes

This article was published online ahead of print in MBoC in Press (http://www.molbiolcell.org/cgi/doi/10.1091/mbc.E18-03-0154) on June 21, 2018.

REFERENCES

  1. Alaarg A, Schiffelers RM, van Solinge WW, van Wijk R. (2013). Red blood cell vesiculation in hereditary hemolytic anemia. Front Physiol , 365. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Bachrach NM, Valhmu WB, Stazzone E, Ratcliffe A, Lai WM, Mow VC. (1995). Changes in proteoglycan synthesis of chondrocytes in articular cartilage are associated with the time-dependent changes in their mechanical environment. J Biomech , 1561–1569. [DOI] [PubMed] [Google Scholar]
  3. Barteneva NS, Fasler-Kan E, Bernimoulin M, Stern JNH, Ponomarev ED, Duckett L, Vorobjev IA. (2013). Circulating microparticles: square the circle. Bmc Cell Biol . [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bausch AR, Möller W, Sackmann E. (1999). Measurement of local viscoelasticity and forces in living cells by magnetic tweezers. Biophys J , 573–579. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Bausch AR, Ziemann F, Boulbitch AA, Jacobson K, Sackmann E. (1998). Local measurements of viscoelastic parameters of adherent cell surfaces by magnetic bead microrheometry. Biophys J , 2038–2049. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Bennett V. (1989). The spectrin-actin junction of erythrocyte-membrane skeletons. Biochim Biophys Acta , 107–121. [DOI] [PubMed] [Google Scholar]
  7. Betz T, Lenz M, Joanny JF, Sykes C. (2009). ATP-dependent mechanics of red blood cells. Proc Natl Acad Sci USA , 15320–15325. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Braet F, Rotsch C, Wisse E, Radmacher M. (1998). Comparison of fixed and living liver endothelial cells by atomic force microscopy. Appl Phys A-Mater , S575–S578. [Google Scholar]
  9. Combes V, Taylor TE, Juhan-Vague I, Mege JL, Mwenechanya J, Tembo M, Grau GE, Molyneux ME. (2004). Circulating endothelial microparticles in Malawian children with severe falciparum malaria complicated with coma. J Am Med Assoc , 2542–2544. [DOI] [PubMed] [Google Scholar]
  10. Crick FHC, Hughes AFW. (1950). The physical properties of cytoplasm—a study by means of the magnetic particle method. 1. Experimental. Exp Cell Res , 37–80. [Google Scholar]
  11. Cross SE, Jin YS, Rao J, Gimzewski JK. (2007). Nanomechanical analysis of cells from cancer patients. Nat Nanotechnol , 780–783. [DOI] [PubMed] [Google Scholar]
  12. Dao M, Lim CT, Suresh S. (2003). Mechanics of the human red blood cell deformed by optical tweezers. J Mech Phys Solids , 2259–2280. [Google Scholar]
  13. Denning D, Roos WH. (2016). Elucidating the molecular mechanisms underlying cellular response to biophysical cues using synthetic biology approaches. Cell Adhes Migr , 540–553. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. EL Andaloussi S, Maeger I, Breakefield XO, Wood MJA. (2013a). Extracellular vesicles: biology and emerging therapeutic opportunities. Nat Rev Drug Discov , 348–358. [DOI] [PubMed] [Google Scholar]
  15. El Andaloussi S, Mäger I, Breakefield XO, Wood MJA. (2013b). Extracellular vesicles: biology and emerging therapeutic opportunities. Nat Rev Drug Discov , 347. [DOI] [PubMed] [Google Scholar]
  16. Engler AJ, Sen S, Sweeney HL, Discher DE. (2006). Matrix elasticity directs stem cell lineage specification. Cell , 677–689. [DOI] [PubMed] [Google Scholar]
  17. Ernst E, Matrai A. (1986). Altered red and white blood cell rheology in type II diabetes. Diabetes , 1412–1415. [DOI] [PubMed] [Google Scholar]
  18. Evans ND, Minelli C, Gentleman E, LaPointe V, Patankar SN, Kallivretaki M, Chen XY, Roberts CJ, Stevens MM. (2009). Substrate stiffness affects early differentiation events in embryonic stem cells. Eur Cells Mater , 1–14. [DOI] [PubMed] [Google Scholar]
  19. Fang YQ, Iu CYY, Lui CNP, Zou YK, Fung CKM, Li HW, Xi N, Yung KKL, Lai KWC. (2014). Investigating dynamic structural and mechanical changes of neuroblastoma cells associated with glutamate-mediated neurodegeneration. Sci Rep , 7074. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Gosse C, Croquette V. (2002). Magnetic tweezers: micromanipulation and force measurement at the molecular level. Biophys J , 3314–3329. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Gov NS, Safran SA. (2005). Red blood cell membrane fluctuations and shape controlled by ATP-induced cytoskeletal defects. Biophys J , 1859–1874. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Greenwalt TJ. (2006). The how and why of exocytic vesicles. Transfusion , 143–152. [DOI] [PubMed] [Google Scholar]
  23. Guevorkian K, Manzi J, Pontani LL, Brochard-Wyart F, Sykes C. (2015). Mechanics of biomimetic liposomes encapsulating an actin shell. Biophys J , 2471–2479. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Haase K, Pelling AE. (2015). Investigating cell mechanics with atomic force microscopy. J R Soc Interface , 20140970. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Hategan A, Law R, Kahn S, Discher DE. (2003). Adhesively-tensed cell membranes: lysis kinetics and atomic force microscopy probing. Biophys J , 2746–2759. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Hoffman BD, Grashoff C, Schwartz MA. (2011). Dynamic molecular processes mediate cellular mechanotransduction. Nature , 316–323. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Jacob HS, Ruby A, Overland ES, Mazia D. (1971). Abnormal membrane protein of red blood cells in hereditary spherocytosis. J Clin Invest , 1800–1805. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Kamsma D, Creyghton R, Sitters G, Wuite GJL, Peterman EJG. (2016). Tuning the music: acoustic force spectroscopy (AFS) 2.0. Methods , 26–33. [DOI] [PubMed] [Google Scholar]
  29. Kastelowitz N, Yin H. (2014). Exosomes and microvesicles: identification and targeting by particle size and lipid chemical probes. Chembiochem , 923–928. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Koch M, Wright KE, Otto O, Herbig M, Salinas ND, Tolia NH, Satchwell TJ, Guck J, Brooks NJ, Baum J. (2017). Plasmodium falciparum erythrocyte-binding antigen 175 triggers a biophysical change in the red blood cell that facilitates invasion. Proc Natl Acad Sci USA , 4225–4230. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. König L, Kasimir-Bauer S, Bittner A-K, Hoffmann O, Wagner B, Santos Manvailer LF, Kimmig R, Horn PA, Rebmann V. (2018). Elevated levels of extracellular vesicles are associated with therapy failure and disease progression in breast cancer patients undergoing neoadjuvant chemotherapy. OncoImmunology , e1376153. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Kuravi SJ, Yates CM, Foster M, Harrison P, Hazeldine J, Hampson P, Watson C, Belli A, Midwinter M, Nash GB. (2017). Changes in the pattern of plasma extracellular vesicles after severe trauma. PLoS ONE , e0183640. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Ling E, Danilov YN, Cohen CM. (1988). Modulation of red-cell band-4.1 function by camp-dependent kinase and protein kinase-C phosphorylation. J Biol Chem , 2209–2216. [PubMed] [Google Scholar]
  34. Liu F, Mih JD, Shea BS, Kho AT, Sharif AS, Tager AM, Tschumperlin DJ. (2010). Feedback amplification of fibrosis through matrix stiffening and COX-2 suppression. J Cell Biol , 693–706. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Maciaszek JL, Lykotrafitis G. (2011). Sickle cell trait human erythrocytes are significantly stiffer than normal. J Biomech , 657–661. [DOI] [PubMed] [Google Scholar]
  36. Manno S, Takakuwa Y, Mohandas N. (2005). Modulation of erythrocyte membrane mechanical function by protein 4.1 phosphorylation. J Biol Chem , 7581–7587. [DOI] [PubMed] [Google Scholar]
  37. Mantel PY, Hjelmqvist D, Walch M, Kharoubi-Hess S, Nilsson S, Ravel D, Ribeiro M, Gruring C, Ma SY, Padmanabhan P, et al (2016). Infected erythrocyte-derived extracellular vesicles alter vascular function via regulatory Ago2-miRNA complexes in malaria. Nat Commun , 12727. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Mantel PY, Hoang AN, Goldowitz I, Potashnikova D, Hamza B, Vorobjev I, Ghiran I, Toner M, Irimia D, Ivanov AR, et al (2013). Malaria-infected erythrocyte-derived microvesicles mediate cellular communication within the parasite population and with the host immune system. Cell Host Microbe , 521–534. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Mohandas N, Evans E. (1994). Mechanical properties of the red cell membrane in relation to molecular structure and genetic defects. Annu Rev Biophys Biomol Struct , 787–818. [DOI] [PubMed] [Google Scholar]
  40. Noguchi H, Gompper G. (2005). Shape transitions of fluid vesicles and red blood cells in capillary flows. Proc Natl Acad Sci USA , 14159–14164. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Ofir-Birin Y, Heidenreich M, Regev-Rudzki N. (2017). Pathogen-derived extracellular vesicles coordinate social behaviour and host manipulation. Semin Cell Dev Biol , 83–90. [DOI] [PubMed] [Google Scholar]
  42. Otto O, Rosendahl P, Mietke A, Golfier S, Herold C, Klaue D, Girardo S, Pagliara S, Ekpenyong A, Jacobi A, et al (2015). Real-time deformability cytometry: on-the-fly cell mechanical phenotyping. Nat Methods , 199–202. [DOI] [PubMed] [Google Scholar]
  43. Park Y, Best CA, Auth T, Gov NS, Safran SA, Popescu G, Suresh S, Feld MS. (2010a). Metabolic remodeling of the human red blood cell membrane. Proc Natl Acad Sci USA , 1289–1294. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Park Y, Best CA, Badizadegan K, Dasari RR, Feld MS, Kuriabova T, Henle ML, Levine AJ, Popescu G. (2010b). Measurement of red blood cell mechanics during morphological changes. Proc Natl Acad Sci USA , 6731–6736. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Rand RP. (1964). Mechanical properties of the red cell membrane: II. Viscoelastic breakdown of the membrane. Biophys J , 303–316. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Rand RP, Burton AC. (1964). Mechanical properties of the red cell membrane. I. Membrane stiffness and intracellular pressure. Biophys J , 115–135. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Regev-Rudzki N, Wilson DW, Carvalho TG, Sisquella X, Coleman BM, Rug M, Bursac D, Angrisano F, Gee M, Hill AF, et al (2013). Cell-cell communication between malaria-infected red blood cells via exosome-like vesicles. Cell , 1120–1133. [DOI] [PubMed] [Google Scholar]
  48. Rodriguez-Garcia R, Lopez-Montero I, Mell M, Egea G, Gov NS, Monroy F. (2015). Direct cytoskeleton forces cause membrane softening in red blood cells. Biophys J , 2794–2806. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Sen S, Subramanian S, Discher DE. (2005). Indentation and adhesive probing of a cell membrane with AFM: theoretical model and experiments. Biophys J , 3203–3213. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Settnes M, Bruus H. (2012). Forces acting on a small particle in an acoustical field in a viscous fluid. Phys Rev E , 016327. [DOI] [PubMed] [Google Scholar]
  51. Sisquella X, Ofir-Birin Y, Pimentel MA, Cheng L, Abou Karam P, Sampaio NG, Penington JS, Connolly D, Giladi T, Scicluna BJ, et al (2017). Malaria parasite DNA-harbouring vesicles activate cytosolic immune sensors. Nat Commun , 1985. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Sitters G, Kamsma D, Thalhammer G, Ritsch-Marte M, Peterman EJG, Wuite GJL. (2015). Acoustic force spectroscopy. Nat Methods , 47–50. [DOI] [PubMed] [Google Scholar]
  53. Skalak R, Branemark PI. (1969). Deformation of red blood cells in capillaries. Science , 717–719. [DOI] [PubMed] [Google Scholar]
  54. Suresh S. (2006). Mechanical response of human red blood cells in health and disease: some structure-property-function relationships. J Mater Res , 1871–1877. [Google Scholar]
  55. Suresh S, Spatz J, Mills JP, Micoulet A, Dao M, Lim CT, Beil M, Seufferlein T. (2005). Connections between single-cell biomechanics and human disease states: gastrointestinal cancer and malaria. Acta Biomaterialia , 15–30. [DOI] [PubMed] [Google Scholar]
  56. Thavarajah R, Mudimbaimannar VK, Elizabeth J, Rao UK, Ranganathan K. (2012). Chemical and physical basics of routine formaldehyde fixation. J Oral Maxillofac Pathol , 400–405. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. van Loenhout MTJ, Kerssemakers JWJ, De Vlaminck I, Dekker C. (2012). Non-bias-limited tracking of spherical particles, enabling nanometer resolution at low magnification. Biophys J , 2362–2371. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Wan JD, Ristenpart WD, Stone HA. (2008). Dynamics of shear-induced ATP release from red blood cells. Proc Natl Acad Sci USA , 16432–16437. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Wu HW, Kuhn T, Moy VT. (1998). Mechanical properties of L929 cells measured by atomic force microscopy: effects of anticytoskeletal drugs and membrane crosslinking. Scanning , 389–397. [DOI] [PubMed] [Google Scholar]
  60. Yango A, Schape J, Rianna C, Doschke H, Radmacher M. (2016). Measuring the viscoelastic creep of soft samples by step response AFM. Soft Matter , 8297–8306. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Click here for additional data file. (1,013.1KB, pdf)

Articles from Molecular Biology of the Cell are provided here courtesy of American Society for Cell Biology

RESOURCES