Significance
Major experimental research efforts have gone into investigating general principles governing self-assembly under nonequilibrium driving. However, in contrast to equilibrium scenarios, where the system tends to find local minima in the free-energy landscape, there is no equivalent theoretical framework for systems operating far from equilibrium. Inspired by many examples of nonequilibrium self-assembly in living systems, we set out to explore the added benefits achieved by nonequilibrium driving and identify distinctive collective phenomena that emerge in this regime. We demonstrate the interplay between the assembly speed, kinetic stability, and relative population of dynamical attractors, aiming to provide insights into nonequilibrium self-assembly processes and lay the foundations for understanding biomolecular cases as well as for designing examples.
Keywords: nonequilibrium self-assembly, local driving, self-healing, stored structures
Abstract
Many biological systems rely on the ability to self-assemble different target structures using the same set of components. Equilibrium self-assembly suffers from a limited capacity in such cases, due to an increasing number of decoy states that grows rapidly with the number of targets encoded. Moreover, improving the kinetic stability of a target at equilibrium carries the price of introducing kinetic traps, leading to slower assembly. Using a toy physical model of interacting particles, we demonstrate that local driving can improve both the assembly time and kinetic stability of multitarget self-assembly, as well as reduce fluctuations around the target configuration. We further show that the local drive can result in a steady-state probability distribution over target structures that deviates from the Boltzmann distribution in a way that depends on the types of interactions that stabilize the targets. Our results illustrate the role that nonequilibrium driving plays in overcoming tradeoffs that are inherent to equilibrium assemblies.
Many biological processes rely on the ability to self-assemble multiple structures using the same set of components. Examples range from the variety of protein chaperones, cochaperones, and chaperonins that orchestrate protein folding (1–3) to the protein components of chromatin (mainly histones) whose modifications regulate gene expression through conformational changes (4–6). In the former example, the protein quality control system must handle a huge diversity of denatured protein products including folding intermediates, amorphous aggregates, amyloid fibrils, and more, with each case requiring the recruitment of different members of the regulatory system. In the latter example, different local modifications of the long histone tails can change the global conformation of the nucleosome, rendering certain genes accessible for transcription. The common feature of both cases is the flexibility of the components and their ability to rearrange themselves into different global structures with desired functions while undergoing conformational changes. Efforts to mimic nature in this context include the design of switchable smart materials that can change their shape and properties in response to external stimuli (7) such as heat (8), pH (9, 10), and laser irradiation (11–13), with a goal of allowing for the self-assembly of different structures depending on the conformation or morphology of the configurable building blocks (14–17).
Another typical characteristic of biological self-assembly is self-healing, that is, the ability to correct for a wrong state on the way to the desired final structure (18). For example, microtubules, which govern intracellular transport and polarity, polymerize in the growing phase by binding tubulin dimers to the positive end and can also self-repair a damaged site by incorporating free tubulin dimers into a defect location, with both processes fueled by guanosine triphosphate (GTP) hydrolysis (19, 20).
Self-healing is just one of many aspects of self-assembly in the biological context that operate far from equilibrium while constantly absorbing work from its environment (21). Nonequilibrium driving forces fuel the essential hallmarks of life such as growth, self-replication, and adaptation (22–24), all of which rely on interactions at the molecular level which allow biological building blocks to bind and self-assemble, while discriminating between right and wrong states (25). At present, it is accepted that a general understanding of the fundamental tradeoffs governing nonequilibrium self-assembly is much needed, yet only just beginning to emerge (26–32). For example, several studies showed an improvement in a self-assembly outcome using time-dependent interactions (33–37). Others showed self-assembly structures that adapt to a particular external drive of acoustic waves (38), electrical fields (39, 40), or light (41). Further studies provided design principles for self-assembly processes driven by chemical potential excess (29) and suggested dissipative adaptation as the underlying mechanism governing self-organization in driven systems (23).
In contrast, equilibrium self-assembly is well understood as a process of relaxation toward equilibrium, characterized by the minimization of the free energy (42–45). In this regime, a self-assembly target can be encoded by specific interactions between particles and their designated neighbors in the target structure. An example of such a programmable equilibrium self-assembly is DNA origami (46, 47). Self-assembly processes of this type are similar to memory retrieval in associative neural networks with specific short-range interactions (48), and a major challenge of the equilibrium framework from this perspective is the limitation on storage capacity. Just as associative memory models have a finite number of memories that can be encoded and retrieved with high fidelity (48–50), so too is there an upper limit to the possible number of structures that can be encoded by specific interactions within a shared pool of monomer building blocks (51, 52).
Inspired by the molecular architecture of living things, we set out to explore the opportunities and challenges of self-healing self-assembly in the nonequilibrium regime, using a toy physical model. Self-assembly goals are encoded through specific interactions between monomers; however, in analogy to different conformations adopted by proteins, each particle can adopt one of several internal states. Interparticle interactions are dependent on the internal state of members of the interacting pair. Within this framework, different target structures are encoded through the specific interactions between the particles when all of the components adopt a particular internal state.
A local, self-healing drive is incorporated through the tendency of a particle to adopt an internal state that matches those of its neighbors. The goal of this type of driving is to establish assembly targets (memories) as dynamical attractors which autonomously emerge during the exploration of the configuration space, in a manner loosely inspired by intracellular signaling cascades (53, 54). A system thus described can be thought of as an associative memory model of an unsupervised stochastic neural network (55), i.e., a Boltzmann machine, with added nonequilibrium dynamics which further stabilize the encoded memories. As such, the system can wander around in the configuration space, and if a partially assembled seed happens to form, it can be fully assembled with the help of the local drive.
In what follows, we discuss equilibrium tradeoffs and constraints that can be overcome in the nonequilibrium regime. Our model highlights global-scale phenomena that arise from a driving force with a simple local rule. Specifically, we show that the local driving can accelerate the assembly, increase the stability of the assembled target, and reduce fluctuations around it, as well as demonstrate how local minima in the free-energy landscape are differentially affected by the drive.
Model of Interacting Particles on a Lattice with Multiple Stored Targets
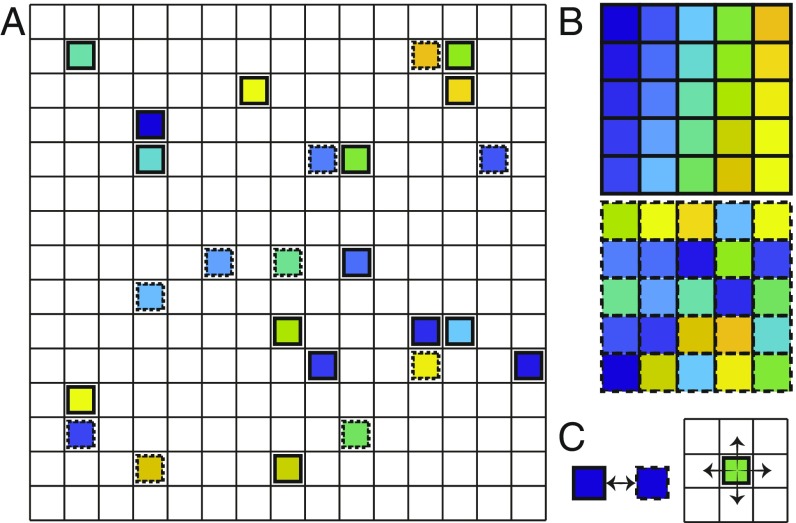
Our model consists of distinguishable particles, with possible internal states, , placed on a 2D square lattice of size , where each site can be either unoccupied or occupied by a single particle (Fig. 1A). When two particles, and , occupy adjacent lattice sites, they exhibit nearest-neighbors (n.n.) interaction of magnitude . The system has stored targets, corresponding to the internal states of the particles, where each target is defined as a unique spatial arrangement of the particles positions on the lattice, all with internal state (Fig. 1B). The targets are encoded by the n.n. interactions: Particles of the same internal state experience a strong attraction, , if they are n.n. according to a target structure, and a weak attraction, , otherwise:
| [1] |
If, on the other hand, n.n. particles are of different internal states , then
| [2] |
The total energy of the system is thus defined as
| [3] |
where the summation is over n.n.
Fig. 1.
Model system illustration. (A) An example of a lattice of size , occupied by particles with possible internal states identified by either solid or dashed lines. The particles are distinguishable, denoted by the unique color of each one. (B) Two target structures corresponding to all of the particles being in one of the two possible internal states. Each structure has a unique spatial configuration of the particles. (C) In each iteration a physical move on the lattice (Right) followed by an internal state switching (Left) is attempted. The trial moves are accepted with probability that depends on the energy differences as described in the main text.
The dynamics are simulated using a single-particle Monte Carlo Metropolis algorithm (56). Initially, the particles are placed randomly on the lattice. Each iteration, a particle is chosen at random, as well as a random direction of the four possibilities: up, down, right, or left (Fig. 1C). If the destination site is occupied or outside the boundary of the lattice, the move is rejected. Otherwise, the energy difference between the proposed and current configurations is calculated and the attempted move is accepted with probability according to the Metropolis criterion (56)
| [4] |
which guarantees detailed balance, where the temperature was chosen to be for all of the simulations, with a Boltzmann constant . After each attempted physical move, a particle is chosen at random again, along with a new random internal state, different from its current one (Fig. 1C). The internal state switch is accepted with probability according to Eq. 4 as well.
Equilibrium Tradeoffs
Equilibrium assembly faces an unavoidable tradeoff that pits speed against stability (30); while stronger interactions favor the target state, interactions that are too strong will slow down the rearrangements needed to find the target state.
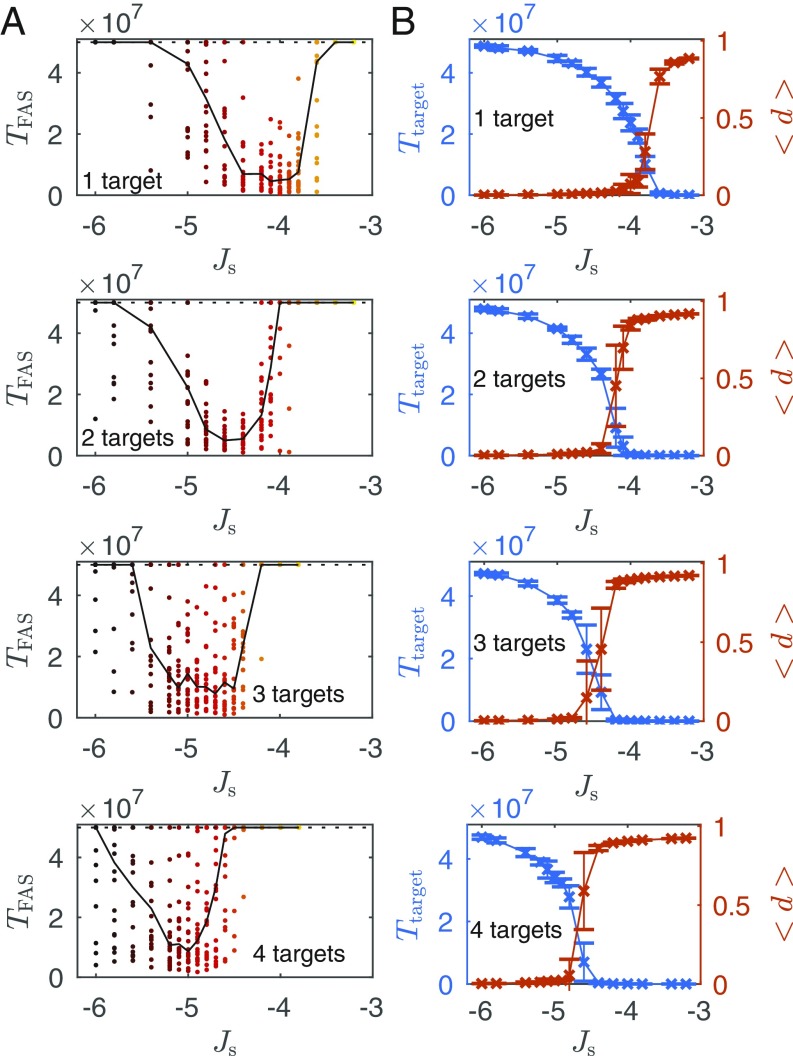
To demonstrate this, simulations were run for targets, with particles and lattice size . The weak interaction was set to be , and the strong interaction was varied between and . The lattice was initialized with random positions of the particles, and their initial internal states were chosen randomly when applicable. During each realization, we tracked the first time (measured in Monte Carlo steps) in which one of the targets was assembled, , and found particular values for the strong interaction that gave rise to the fastest assembly, depending on the number of targets encoded (Fig. 2A). As the number of targets increased, stronger attraction was needed to achieve the fastest assembly. For interaction energies that are too weak, the system remained in a homogeneous phase, whereas interaction energies that are too strong resulted in multiple kinetic traps that hindered a successful assembly of the target. These results agree with previous work of multicomponent equilibrium self-assembly (57, 58), guided by designed interactions, showing that high-yield assembly occurs even in the presence of nonspecific (undesigned) interactions as long as their scale is sufficiently separated from the specific interactions and that the distribution of the specific interactions is narrow (in our case, all of the values of the specific interactions are identical, ).
Fig. 2.
Equilibrium constraints. (A) First assembly time of a target, , as a function of the strong interaction energy for one, two, three, and four possible targets (Top to Bottom, respectively). Each circle represents a result from one realization (20 in total for each interaction value) with random initial conditions. The black dotted line is the total simulation time, and the black solid curve tracks the median of the first assembly time as a guide for the eye. (B) Time spent at the target, , for simulations initialized at one of the target structures (blue crosses, left y axis), and the mean distance from the target, (orange crosses, right y axis), as a function of the strong interaction energy for one, two, three, and four possible targets (Top to Bottom, respectively). The data points are averages over 20 realizations with identical initial conditions. Error bars are 1 SD.
To quantify target stability, we monitored the amount of time spent at a target and the mean deviation from it along a realization. We defined a distance measure from the target, , to be the normalized Hamming distance (59) between the current microstate and the target, i.e., the fraction of particles that are in the correct spatial location according to a specific target. We initialized the simulations at one of the targets and tracked the amount of time the system spent at the initial target state, , as well as the average distance from the target along each realization (Fig. 2B). As expected, the strong interaction energy value that gave rise to the fastest assembly was right at the cusp of the melting point, above which the time spent at the initial target diminished significantly and the mean distance from the target increased dramatically.
These results demonstrate some of the constraints in an equilibrium system of self-assembly, namely, increased stability comes at the price of slower assembly. Further, there is not a single value of the interaction energy that can accommodate an increasing number of target structures encoded through the interparticle interaction energies. Given a specific value of , there is a very limited range of number of targets that can be assembled within a time-limited process.
Next, we set to explore the benefits of nonequilibrium driving force in this context.
Local Driving Force
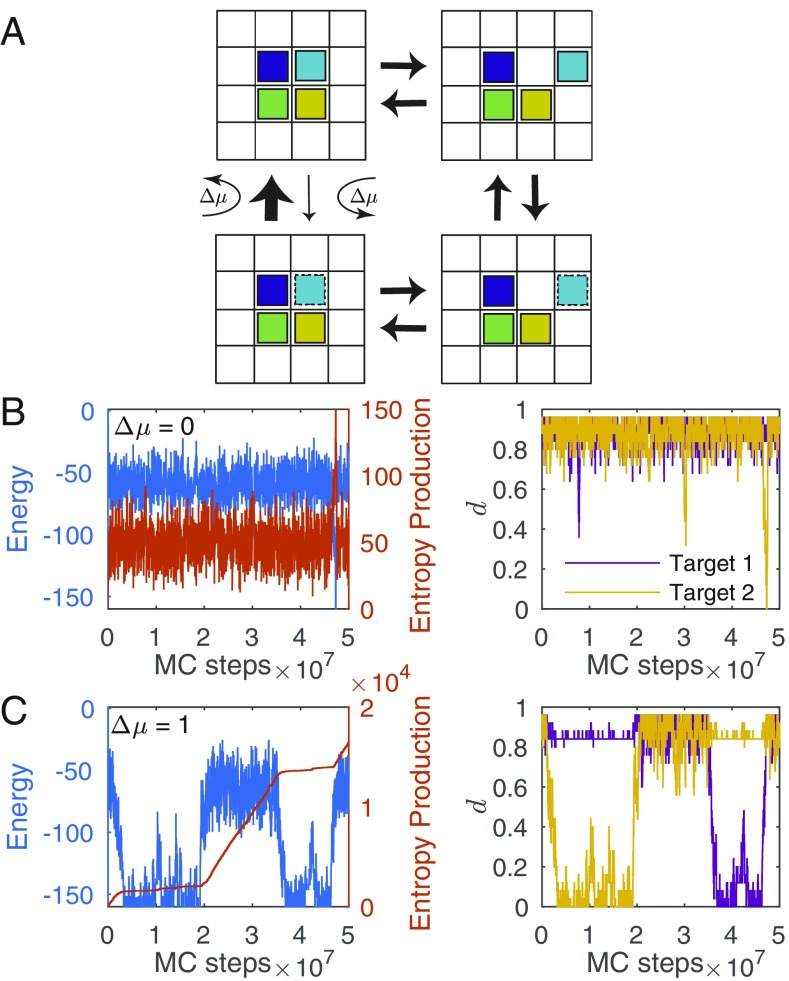
We added a local driving force which affects the probabilities of accepting or rejecting trial moves of switching internal states. Coupling to the external drive depends only on the local environment of the randomly chosen particle: If the particle has two or more neighbors with the same internal state, the drive increases the acceptance probability of a trial move that results in the particle flipping to the same state as its neighbors and decreases the acceptance probability of a trial move that results in the particle flipping away from the same state as its neighbors to a different one (Fig. 3A). In contrast, the physical moves of the particles remain unaffected.
Fig. 3.
Local nonequilibrium drive. (A) Illustration of the effect of the driving force in a cycle that breaks detailed balance. (Top Left) Four neighboring particles with the same internal state (solid line). (Top Right) One of the particles was detached from the cluster. (Bottom Right) The detached particle flipped to a different internal state (dashed line). (Bottom Left) The particle retuned to its previous location within the original cluster. The arrows between these transitions represent Metropolis acceptance probabilities. The transitions between Top Left and Bottom Left microstates are accepted with either increased or decreased probabilities, corresponding to the thicker and thinner arrows, respectively. (B and C) Typical realization of the simulation for targets in detailed balance, (B), and with the local drive (C). B and C, Left show the energy along the simulation as a function of the Monte Carlo (MC) step number (blue curve, left y axis) and the entropy production (orange curve, right y axis). B and C, Right show the distance from target 1 (purple curve) and target 2 (yellow curve) as a function of the MC step number. For an assembled target, .
Effectively, the drive either decreases or increases the barrier heights between each two microstates in which a particle with two or more neighbors with the same internal state is trying to change its own to or switch away from , respectively. Let us stress that flipping into the same internal state as neighboring particles is not always energetically favored. For example, if a particle with an internal state has two neighbors with internal states , which are also its n.n. according to target , and it is attempting to switch to internal state , then for this attempted move is positive given that the particles are not n.n. according to target . If a particle has four neighbors, two of which have internal states , and the other two have internal states , the coupling to the drive when trying to flip to or from state or occurs with probability one-half. Such a drive is considered to be self-healing, as it pushes to “correct” for wrong internal states.
Compared with Eq. 4, the modified probability for accepting an internal state-switching trial move is now
| [5] |
where the and − signs in the argument of the exponent correspond to increased and decreased acceptance probability, respectively, and denotes the value of the drive. For , detailed balance no longer holds. This driving force can be thought to result from a chemical potential gradient of a molecule which catalyzes or suppresses the reaction. An effect of this kind could potentially relate to an ATPase chaperone-like activity, such that upon binding to a particular (i.e., nonnative) conformation of a protein substrate, ATP hydrolysis catalyzes a conformational change to its native state.
Typical realizations of the simulation with targets (and internal states) are shown in Fig. 3 B and C for and , respectively. For , the system spends most of the simulation time away from the target structures, as evident from the high energy and distance values. If a target is eventually assembled, it is not stable and is immediately disassembled. For , however, not only is the assembly time shorter, but also the system stabilizes an assembled target for longer. In addition to the energy and distance values, we also track the entropy production along each realization, by adding up the log ratio of the probabilities of each move and its reverse (60–62). For the detailed balance example, , the entropy production rate is zero throughout almost all of the realization, whereas in the driven case, , the total entropy production is constantly increasing, with lower rates when a target is assembled compared with the exploration phase.
We now turn to quantifying these qualitative effects to emphasize the benefits of the nonequilibrium driving.
Nonequilibrium Speedup and the Entropic Cost
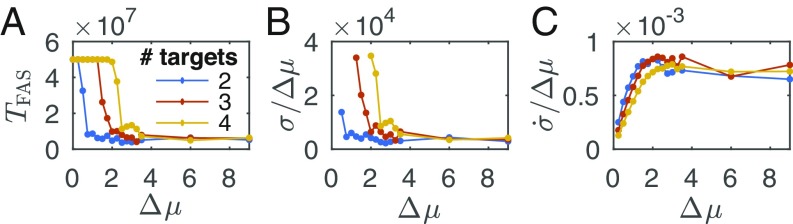
To test the effect of the local driving force, we ran the simulations for targets (corresponding to internal states), with particles and a lattice size of , for various drive values ranging between 0 and 9, while keeping the value of the strong interaction energy fixed at . The specific value for was chosen owing to being within the range of values resulting in the fastest assembly time of a single target (Fig. 2A, Top). Our goal was to accelerate the assembly time using the local drive and demonstrate it breaks the built-in tradeoff between speed and structural stability that is observed in equilibrium self-assembly (30). While stronger interactions (higher absolute values of ) increase target stability, interactions that are too strong compromise the assembly speed.
In the case of detailed balance (), there were only a few assembly events within the simulation duration, which became rarer to nonexistent for increasing number of targets (Fig. 4A and SI Appendix, Fig. S1A). This is consistent with the results presented in Fig. 2, showing that rapid assembly requires stronger interactions as the number of targets increases. In addition, our results agree with the analysis of a similar equilibrium self-assembly system by Murugan et al. (51), estimating the number of targets that can be encoded and retrieved with high fidelity of a comparable system to be of order 1 (more details are in SI Appendix).
Fig. 4.
Nonequilibrium gain. (A) Median first assembly time, , of one of the encoded targets, as a function of the driving-force value for two (blue), three (red), and four (yellow) encoded targets. The median was taken over 20 realizations. The total time of each simulation is Monte Carlo steps. (B) Median of the total entropy production up to the first assembly time normalized by the the driving-force value, , as a function of the driving-force value. (C) Median of the entropy production rate normalized by the the driving-force value, , as a function of the driving-force value.
When the local drive is introduced, the first assembly time, , decreases with increasing drive value, where more targets require higher forcing for similar assembly times. A comparison between the median assembly times as a function of the driving force clearly shows the higher drive value needed for the larger number of targets encoded (Fig. 4A). Moreover, targets can be stabilized for longer periods of time with increasing drive value, where more encoded targets require higher forcing (SI Appendix, Fig. S2A). Even for binding energies , for which target assembly is the fastest at equilibrium, the local drive reduces thermal fluctuations around the target structure (SI Appendix, Fig. S2B). This demonstrates the contribution of an external drive to the feasibility of self-assembly with shared components encoding several structures. The drive both accelerates the assembly and increases target stability. Additionally, stronger drive always leads to a comparable or better performance. In contrast, although increasing the attraction energy up to a certain value improves target stability and accelerates the assembly, further increase would slow down the assembly.
Looking at the total entropy production up to the first assembly time, , normalized by the drive value, as a function of the drive value, we see a decreasing trend, indicating that fewer entropy-producing cycles are needed to achieve assembly for higher driving forces (Fig. 4B and SI Appendix, Fig. S1B). This occurs despite the fact that the entropy production rate, defined as , increases as a function of the drive strength even when normalized by the drive strength (Fig. 4C), indicating a more efficient assembly for higher driving forces.
In the simulations described so far for particles and lattice size of , there were only a handful of successful assemblies within the duration of a single realization. To better explore the configuration space we reduced the system size for the following set of simulations.
Deviation from Boltzmann Ratio
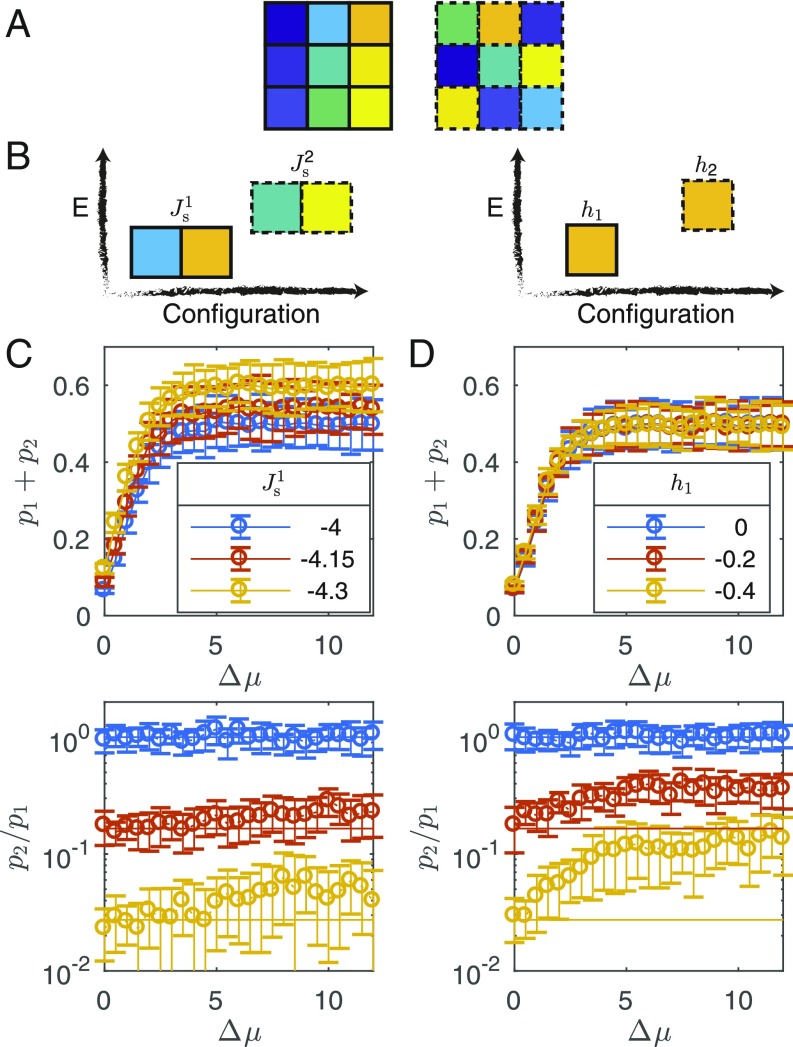
We ran an additional set of simulations for targets, particles, and a lattice size of . The smaller system size allowed us to better sample the configuration space and benefit from better statistics. The two target assemblies were of square shape, with different spatial arrangement of the nine particles, excluding the central particle that was identical for the two targets (Fig. 5A).
Fig. 5.
Target bias. (A) Two targets of particles each. The central particle is identical for both targets. Corner particles in one target are on the middle location of the edges in the other one. (B) A bias between the two targets is introduced, either by modifying the strong attractive interaction between neighboring particles (Left) or by modifying the internal energies of the two internal states (Right). (C and D) The normalized simulation time spent in either target 1 or target 2 (Top) and the ratio between them (Bottom) for binding-energy bias (C) and internal energy bias (D). The solid line in C and D, Bottom represents the corresponding Boltzmann ratio.
To study the relative probabilities of the two targets with the nonequilibrium drive described above, we further introduced a bias that favored one of the target assemblies over the other. Our goal here was to understand how the driving affected the relative populations of local free-energy minima when these minima were stabilized or destabilized with respect to each other by differing mechanisms.
In one case, we modified the strong binding energy of target 1, , by increasing its strength relative to target 2, which was kept constant, , thus favoring the former (Fig. 5B). This could correspond to a scenario in which an environmental change, such as the introduction of a new solute, could alter the effective attraction among monomers in the assembly. In this scenario, the only difference in the Hamiltonian is the definition of given in Eq. 1,
| [6] |
where denotes the strong attractive interaction for the two targets, . A typical realization with different binding energies bias is shown in SI Appendix, Fig. S3. In the detailed balance case, , there are many assembly events, with an obvious preference for target 1, which has stronger interaction energy compared with target 2. In the driven case, , the system spends more time in one of the assembled states compared with the undriven simulation, again with an obvious preference for target 1.
In the other case of applying a bias between free energy wells, we assigned a different internal energy value to the two possible internal states corresponding to the two targets. Specifically, we lowered the internal energy of being in state 1, , for each particle, relative to the internal energy of being in state 2 which was kept constant, , thus favoring the former (Fig. 5B). This mechanism of destabilization could correspond to the introduction of a small ligand that binds preferentially to each monomer in its preferred conformational state. For this case of assigning an internal energy for each particle, the total energy of a configuration now includes an additional term,
| [7] |
where is the internal energy of the internal state of particle .
We ran the simulations for the two cases of the applied bias, for different values of the driving force ranging from to . During each realization we tracked the relative normalized time spent at each of the two targets, and , respectively, to test the joint effect of the bias and the drive (Fig. 5 C and D). For both cases the total time spent at either of the targets, , increased with increasing the drive until a plateaued value. The upper bound of is controlled by the strength of the binding interaction, as evident from comparing the case of different binding energies (Fig. 5C, Top) to the case of different internal energies (Fig. 5D, Top), in which the binding energy was held constant for the two targets. The upper bound of stems from the fact that above a certain drive value, the particles effectively cannot flip their internal state once they are bound to two or more neighbors with the same conformation. Hence, the only route of escape from a target state, or any cluster, is by breaking the strong interaction energies between the neighbors, while forbidding the path of first flipping the internal state to reduce the interaction strength and subsequently leaving the cluster. Thus, the strong interaction energy value determines the upper limit of in this case.
We now turn our attention to the relative probability between being at target 2 and being at target 1, i.e., , as a function of the drive for different bias values (Fig. 5 C and D, Bottom). As expected, when there is no bias, this ratio is one, , regardless of the drive value (blue curve), whereas in the presence of a bias toward target 1, the ratio is smaller (red and yellow curves). Further, comparing the ratio to the corresponding Boltzmann factor (solid curves), , where and are the energies of the system when at target 1 or target 2, respectively, we see an agreement when there is no drive . However, when increasing the drive in the presence of the bias toward target 1, we surprisingly see a deviation from the Boltzmann ratio favoring target 2, . This deviation is more pronounced for the case of different internal energies (Fig. 5D, Bottom), compared with the case of different binding energies (Fig. 5C, Bottom).
To shed light on the mechanism governing the enrichment of the least-favored target compared with the Boltzmann ratio, we focus on the lowest energy levels for both cases of different binding energies, and different internal energies, corresponding to single-particle fluctuations—internal-state flips or detachment from the target. While the energy level spacings are similar for target 1 in both cases, the energy level spacings for target 2 are smaller in the case of different internal energies compared with different binding energies (SI Appendix, Fig. S4). This feature is not limited to the target size studied here, but is generally manifested for larger systems as well. An intuitive explanation can be given by inspecting the Hamiltonians corresponding to the two cases. Let us consider a specific example of the energy gap between a microstate where all of the particles adopt the internal state 2 and are spatially arranged according to target 2, referred to as the ground state, and a similar microstate except for a single particle at one of the corners which adopts the internal state 1, referred to as the first excited state. The energy difference between the ground state and the first excited state originating from the quadratic term in the Hamiltonian (first term in Eq. 7) is identical for both cases of different binding energies and different internal energies; however, in the latter case, the second term in the Hamiltonian also contributes, rendering the gap smaller owing to the lower internal energy of internal state 1 compared with state 2.
We fitted the data of the deviation from the Boltzmann ratio according to to find the saturation value, (SI Appendix, Fig. S5). In the interest of describing the deviation from a unifying perspective, given the different features of the energy spectra described above, we plotted the deviation value at saturation, , as a function of a factor which captures the ratio of the relative populations of single-particle fluctuations from the target compared with the ground state between the two targets,
| [8] |
where , , and denote the energies of the microstates corresponding to a corner, an edge, or a bulk particle flipping its internal state to the “wrong” conformation, and , , and are the corresponding degeneracies of these microstates, for targets and , respectively. Further, and are the energies of the microstates corresponding to a corner or an edge particle detaching from the target cluster, for targets and , respectively (the “2” prefactor associated with the term stems from the fact that a corner particle can detach from the target in two different directions). The degeneracies are , corresponding to four corner particles regardless of the total number of particles ; , corresponding to the number of edge particles excluding the corners; and , corresponding to the number of bulk particles. Further simplification of the factor is in SI Appendix.
We have found that both data point sets, for different binding energies and for different internal energies, collapse onto a single curve when plotting the saturation value, , as a function of (SI Appendix, Fig. S6). To further validate the scaling of the saturation value with , we combined both cases. We repeated the simulations for different internal energies (similar to Fig. 5D and SI Appendix, Fig. S5A) in the addition of a different binding-energy bias; i.e., and . The deviation from the Boltzmann ratio was fitted in a similar way, and the saturation value, , was plotted as a function of (SI Appendix, Fig. S6). This dataset also follows the same scaling as the datasets from the previous simulations, in support of our model.
The scaling of with the total number of particles, , was calculated for particular values of the binding-energy bias and for the internal energy bias (SI Appendix, Fig. S7). We found that was decreasing with down to a constant asymptotic value, correlating to a higher saturation value and stronger deviation from the Boltzmann ratio for larger . For , only the terms with a prefactor that scales as , i.e., , contribute to , so .
The difference in the deviation from the Boltzmann ratio between the cases of different internal energies and different binding energies can be elucidated by focusing on the first excited state, corresponding to a single corner particle flipping its internal state. Plotting as a function of either or for different internal energies and different binding energies, respectively, illustrates the difference between them; namely, it increases for target 1 and decreases for target 2 in the former case, whereas it increases for target 1 and remains unchanged for target 2 in the latter case (SI Appendix, Fig. S8). Similar qualitative behavior also appears for and (SI Appendix, Eq. S1). Thus, we conclude that local nonequilibrium driving leads to stronger deviation from the Boltzmann distribution in cases where the different free-energy wells’ relative stability is determined by the energies of monomeric internal states rather than by binding energies between monomers. The effect originates in the fact that the drive makes a bigger difference to target stability in instances where the Boltzmann distribution samples near-target states more frequently because of small excitation gaps.
Summary
We have demonstrated some of the constraints of an equilibrium self-assembly system that can be overcome by introducing a local driving force. When different targets are encoded through specific short-range interactions between the same set of components, there is a limit to how many targets can be encoded such that an assembly event can take place within a finite amount of time. When increasing the number of targets, rapid assembly requires stronger interaction energies to dominate over the entropic contribution to the free energy. Thus, given a set value of the interaction, too many encoded targets can lead to frustration, such that making all of the desired targets more favorable than off-pathway traps becomes impossible. Increasing the attraction between the building blocks, on the other hand, both accelerates equilibrium assembly and improves target stability. However, increasing the interaction strength above the value leading to the fastest assembly possible, while further reducing fluctuations around an assembled target structure, slows down the assembly process due to kinetic traps.
Previous studies have shown that fluctuating or reconfigurable conformation of monomeric building blocks can facilitate the self-assembly of a particular structure given some external bias toward one of the internal states of the monomers (7, 14). Other studies have shown that high-yield self-assembly of a particular structure encoded by specific interactions between its (distinguishable) building blocks occurs at a finite regime of the parameter space (interaction strength, temperature, etc.) (57, 58). In this line of studies, the self-assembly was a relaxation process toward equilibrium, obeying detailed balance, or guided by a global drive (such as a temperature change). In our case, we combined the approaches and modeled a system of distinguishable particles, each of which can switch between several internal states. Further, instead of having a global external stimulus that would favor one target structure over the others, we included a local driving force that affects the internal state of a particle based on its local environment.
The local drive pushes particles to adopt the internal state of their neighbors, to which we refer as a self-healing property. Here, we worked with a constant value for the strong interaction energy which facilitated the fastest assembly of a single target at equilibrium, even though this value increased with increasing number of targets. Nonetheless, we have been able to demonstrate that when multiple targets are encoded, a driving force such as the one considered here promoted target retrieval by accelerating the assembly and reducing fluctuations even though the interaction energy was not varied with the number of targets.
We have also shown that, although nonequilibrium mechanisms are not always more effective necessarily at meeting their goals when dissipation of energy from an external drive is increased (63), in this case, a multitarget equilibrium self-assembly with suboptimally weak interaction energy shows increased efficiency of self-assembly with increasing external drive strength. Indeed, the number of entropy-producing cycles needed for target assembly decreases with increasing drive strength. This increased effectiveness results from the drive’s consistent ability to convert external work into local pushes toward the assembled state. The underlying mechanism of the drive is its ability to lead the stochastic dynamics to randomly choose one of the optional target structures, by biasing a cluster of particles to adopt a particular internal state that encodes a specific spatial arrangement (i.e., a target structure) through the interparticle interactions.
The self-healing drive also nontrivially affects the relative stability of different targets when there is an applied bias that favors one target over the other. We observed, however, that the strength of this effect depends on the mechanism by which the relative stability of targets is determined and points to monomeric conformational stability as the more sensitive case. These findings may provide guidance to designers of nonequilibrium self-assembly schemes and inspire the next generation of reconfigurable smart material. Further, our results may offer insight into the potential impact of driving on macromolecular complexes in the living cell.
Materials and Methods
The numerical simulations were run using Matlab parallelized code, where each realization consisted of Monte Carlo steps. Two sets of parameters were used, either or . The targets were of square shape, and , respectively, such that the central particle was identical in all of the targets in each of the cases. The central particle was held in place, at the center of the lattice, throughout the simulations. When calculating the distance measure between a specific microstate and a target structure, the normalized Hamming distance was taken to be the minimal value over all of the members of the target symmetry group generated by a reflection and a rotation.
Supplementary Material
Acknowledgments
The authors acknowledge valuable discussions with and insightful comments from Jordan M. Horowitz, Sumantra Sarkar, Hridesh Kedia, Todd R. Gingrich, Sarah E. Marzen, Tal Kachman, Jeremy A. Owen, Jacob M. Gold, David F. Theurel, Robert A. Marsland, Pavel Chvykov, Weishun Zhong, and Pankaj Mehta. G.B. and J.L.E. are funded by the James S. McDonnell Foundation Scholar Grant 220020476.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1805769115/-/DCSupplemental.
References
- 1.Glover JR, Lindquist S. Hsp104, hsp70, and hsp40: A novel chaperone system that rescues previously aggregated proteins. Cell. 1998;94:73–82. doi: 10.1016/s0092-8674(00)81223-4. [DOI] [PubMed] [Google Scholar]
- 2.Bukau B, Horwich AL. The hsp70 and hsp60 chaperone machines. Cell. 1998;92:351–366. doi: 10.1016/s0092-8674(00)80928-9. [DOI] [PubMed] [Google Scholar]
- 3.Tyedmers J, Mogk A, Bukau B. Cellular strategies for controlling protein aggregation. Nat Rev Mol Cell Biol. 2010;11:777–788. doi: 10.1038/nrm2993. [DOI] [PubMed] [Google Scholar]
- 4.Cedar H, Bergman Y. Linking DNA methylation and histone modification: Patterns and paradigms. Nat Rev Genet. 2009;10:295–304. doi: 10.1038/nrg2540. [DOI] [PubMed] [Google Scholar]
- 5.Bártová E, Krejčí J, Harničarová A, Galiová G, Kozubek S. Histone modifications and nuclear architecture: A review. J Histochem Cytochem. 2008;56:711–721. doi: 10.1369/jhc.2008.951251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Karlić R, Chung HR, Lasserre J, Vlahoviček K, Vingron M. Histone modification levels are predictive for gene expression. Proc Natl Acad Sci USA. 2010;107:2926–2931. doi: 10.1073/pnas.0909344107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Nguyen TD, Jankowski E, Glotzer SC. Self-assembly and reconfigurability of shape-shifting particles. ACS Nano. 2011;5:8892–8903. doi: 10.1021/nn203067y. [DOI] [PubMed] [Google Scholar]
- 8.Gong T, et al. Thermally activated reversible shape switch of polymer particles. J Mater Chem B. 2014;2:6855–6866. doi: 10.1039/c4tb01155d. [DOI] [PubMed] [Google Scholar]
- 9.Yoo JW, Mitragotri S. Polymer particles that switch shape in response to a stimulus. Proc Natl Acad Sci USA. 2010;107:11205–11210. doi: 10.1073/pnas.1000346107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Tu F, Lee D. Shape-changing and amphiphilicity-reversing Janus particles with pH-responsive surfactant properties. J Am Chem Soc. 2014;136:9999–10006. doi: 10.1021/ja503189r. [DOI] [PubMed] [Google Scholar]
- 11.Link S, Burda C, Nikoobakht B, El-Sayed MA. Laser-induced shape changes of colloidal gold nanorods using femtosecond and nanosecond laser pulses. J Phys Chem B. 2000;104:6152–6163. [Google Scholar]
- 12.Bisker G, Minai L, Yelin D. Controlled fabrication of gold nanoparticle and fluorescent protein conjugates. Plasmonics. 2012;7:609–617. [Google Scholar]
- 13.Warshavski O, Minai L, Bisker G, Yelin D. Effect of single femtosecond pulses on gold nanoparticles. J Phys Chem C. 2011;115:3910–3917. [Google Scholar]
- 14.Whitelam S, et al. The impact of conformational fluctuations on self-assembly: Cooperative aggregation of archaeal chaperonin proteins. Nano Lett. 2008;9:292–297. doi: 10.1021/nl8029306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Batista VM, Miller MA. Crystallization of deformable spherical colloids. Phys Rev Lett. 2010;105:088305. doi: 10.1103/PhysRevLett.105.088305. [DOI] [PubMed] [Google Scholar]
- 16.Lewandowski W, Fruhnert M, Mieczkowski J, Rockstuhl C, Górecka E. Dynamically self-assembled silver nanoparticles as a thermally tunable metamaterial. Nat Commun. 2015;6:6590. doi: 10.1038/ncomms7590. [DOI] [PubMed] [Google Scholar]
- 17.Sacanna S, et al. Shaping colloids for self-assembly. Nat Commun. 2013;4:1688. doi: 10.1038/ncomms2694. [DOI] [PubMed] [Google Scholar]
- 18.Hess H, Ross JL. Non-equilibrium assembly of microtubules: From molecules to autonomous chemical robots. Chem Soc Rev. 2017;46:5570–5587. doi: 10.1039/c7cs00030h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Mitchison T, Kirschner M. Dynamic instability of microtubule growth. Nature. 1984;312:237–242. doi: 10.1038/312237a0. [DOI] [PubMed] [Google Scholar]
- 20.Aumeier C, et al. Self-repair promotes microtubule rescue. Nat Cell Biol. 2016;18:1054–1064. doi: 10.1038/ncb3406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Schrödinger E. What Is Life?: With Mind and Matter and Autobiographical Sketches. Cambridge Univ Press; Cambridge, UK: 1992. [Google Scholar]
- 22.England JL. Statistical physics of self-replication. J Chem Phys. 2013;139:121923. doi: 10.1063/1.4818538. [DOI] [PubMed] [Google Scholar]
- 23.England JL. Dissipative adaptation in driven self-assembly. Nat Nanotechnol. 2015;10:919–923. doi: 10.1038/nnano.2015.250. [DOI] [PubMed] [Google Scholar]
- 24.Perunov N, Marsland RA, England JL. Statistical physics of adaptation. Phys Rev X. 2016;6:021036. [Google Scholar]
- 25.Mehta P, Lang AH, Schwab DJ. Landauer in the age of synthetic biology: Energy consumption and information processing in biochemical networks. J Stat Phys. 2016;162:1153–1166. [Google Scholar]
- 26.Grzybowski BA, Wilmer CE, Kim J, Browne KP, Bishop KJ. Self-assembly: From crystals to cells. Soft Matter. 2009;5:1110–1128. [Google Scholar]
- 27.Grzelczak M, Vermant J, Furst EM, Liz-Marzán LM. Directed self-assembly of nanoparticles. ACS Nano. 2010;4:3591–3605. doi: 10.1021/nn100869j. [DOI] [PubMed] [Google Scholar]
- 28.Whitelam S, Jack RL. The statistical mechanics of dynamic pathways to self-assembly. Annu Rev Phys Chem. 2015;66:143–163. doi: 10.1146/annurev-physchem-040214-121215. [DOI] [PubMed] [Google Scholar]
- 29.Nguyen M, Vaikuntanathan S. Design principles for nonequilibrium self-assembly. Proc Natl Acad Sci USA. 2016;113:14231–14236. doi: 10.1073/pnas.1609983113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Marsland R, England JL. Active regeneration unites high- and low-temperature features in cooperative self-assembly. Phys Rev E. 2018;98:022411. doi: 10.1103/PhysRevE.98.022411. [DOI] [PubMed] [Google Scholar]
- 31.Grünwald M, Tricard S, Whitesides GM, Geissler PL. Exploiting non-equilibrium phase separation for self-assembly. Soft Matter. 2016;12:1517–1524. doi: 10.1039/c5sm01922b. [DOI] [PubMed] [Google Scholar]
- 32.Rotskoff GM, Geissler PL. 2017. Robust nonequilibrium pathways to microcompartment assembly. arXiv:1709.00321.
- 33.Fullerton CJ, Jack RL. Optimising self-assembly through time-dependent interactions. J Chem Phys. 2016;145:244505. doi: 10.1063/1.4972861. [DOI] [PubMed] [Google Scholar]
- 34.Sherman ZM, Swan JW. Dynamic, directed self-assembly of nanoparticles via toggled interactions. ACS Nano. 2016;10:5260–5271. doi: 10.1021/acsnano.6b01050. [DOI] [PubMed] [Google Scholar]
- 35.Heinen L, Walther A. Celebrating soft matter’s 10th anniversary: Approaches to program the time domain of self-assemblies. Soft Matter. 2015;11:7857–7866. doi: 10.1039/c5sm01660f. [DOI] [PubMed] [Google Scholar]
- 36.Taylor SL, Evans R, Royall CP. Temperature as an external field for colloid–polymer mixtures: ‘Quenching’ by heating and ‘melting’ by cooling. J Phys Condens Matter. 2012;24:464128. doi: 10.1088/0953-8984/24/46/464128. [DOI] [PubMed] [Google Scholar]
- 37.Tagliazucchi M, Weiss EA, Szleifer I. Dissipative self-assembly of particles interacting through time-oscillatory potentials. Proc Natl Acad Sci USA. 2014;111:9751–9756. doi: 10.1073/pnas.1406122111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Bachelard N, et al. Emergence of an enslaved phononic bandgap in a non-equilibrium pseudo-crystal. Nat Mater. 2017;16:808–813. doi: 10.1038/nmat4920. [DOI] [PubMed] [Google Scholar]
- 39.Kondepudi D, Kay B, Dixon J. End-directed evolution and the emergence of energy-seeking behavior in a complex system. Phys Rev E. 2015;91:050902. doi: 10.1103/PhysRevE.91.050902. [DOI] [PubMed] [Google Scholar]
- 40.Jun JK, Hübler AH. Formation and structure of ramified charge transportation networks in an electromechanical system. Proc Natl Acad Sci USA. 2005;102:536–540. doi: 10.1073/pnas.0406025102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Palacci J, Sacanna S, Steinberg AP, Pine DJ, Chaikin PM. Living crystals of light-activated colloidal surfers. Science. 2013;339:936–940. doi: 10.1126/science.1230020. [DOI] [PubMed] [Google Scholar]
- 42.Whitesides GM, Mathias JP, Seto CT. Molecular self-assembly and nanochemistry: A chemical strategy for the synthesis of nanostructures. Science. 1991;254:1312–1319. doi: 10.1126/science.1962191. [DOI] [PubMed] [Google Scholar]
- 43.Breen TL, et al. Design and self-assembly of open, regular, 3D mesostructures. Science. 1999;284:948–951. doi: 10.1126/science.284.5416.948. [DOI] [PubMed] [Google Scholar]
- 44.Whitesides GM, Boncheva M. Beyond molecules: Self-assembly of mesoscopic and macroscopic components. Proc Natl Acad Sci USA. 2002;99:4769–4774. doi: 10.1073/pnas.082065899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Zhang Z, Glotzer SC. Self-assembly of patchy particles. Nano Lett. 2004;4:1407–1413. doi: 10.1021/nl0493500. [DOI] [PubMed] [Google Scholar]
- 46.Zheng J, et al. From molecular to macroscopic via the rational design of a self-assembled 3D DNA crystal. Nature. 2009;461:74–77. doi: 10.1038/nature08274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Ong LL, et al. Programmable self-assembly of three-dimensional nanostructures from 10,000 unique components. Nature. 2017;552:72–77. doi: 10.1038/nature24648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Zhong W, Schwab DJ, Murugan A. Associative pattern recognition through macro-molecular self-assembly. J Stat Phys. 2017;167:806–826. [Google Scholar]
- 49.Hopfield JJ. Neural networks and physical systems with emergent collective computational abilities. Proc Natl Acad Sci USA. 1982;79:2554–2558. doi: 10.1073/pnas.79.8.2554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.McEliece R, Posner E, Rodemich E, Venkatesh S. The capacity of the hopfield associative memory. IEEE Trans Inf Theory. 1987;33:461–482. [Google Scholar]
- 51.Murugan A, Zeravcic Z, Brenner MP, Leibler S. Multifarious assembly mixtures: Systems allowing retrieval of diverse stored structures. Proc Natl Acad Sci USA. 2015;112:54–59. doi: 10.1073/pnas.1413941112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Huntley MH, Murugan A, Brenner MP. Information capacity of specific interactions. Proc Natl Acad Sci USA. 2016;113:5841–5846. doi: 10.1073/pnas.1520969113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Thomas GM, Huganir RL. MAPK cascade signalling and synaptic plasticity. Nat Rev Neurosci. 2004;5:173–183. doi: 10.1038/nrn1346. [DOI] [PubMed] [Google Scholar]
- 54.Pawson T, Nash P. Assembly of cell regulatory systems through protein interaction domains. Science. 2003;300:445–452. doi: 10.1126/science.1083653. [DOI] [PubMed] [Google Scholar]
- 55.Amit DJ. Modeling Brain Function: The World of Attractor Neural Networks. Cambridge Univ Press; Cambridge, UK: 1992. [Google Scholar]
- 56.Newman M, Barkema G. Monte Carlo Methods in Statistical Physics. Clarendon Press; Oxford, UK: 1999. [Google Scholar]
- 57.Hedges LO, Mannige RV, Whitelam S. Growth of equilibrium structures built from a large number of distinct component types. Soft Matter. 2014;10:6404–6416. doi: 10.1039/c4sm01021c. [DOI] [PubMed] [Google Scholar]
- 58.Jacobs WM, Reinhardt A, Frenkel D. Rational design of self-assembly pathways for complex multicomponent structures. Proc Natl Acad Sci USA. 2015;112:6313–6318. doi: 10.1073/pnas.1502210112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Yanushkevich SN, Shmerko VP. Introduction to Logic Design. CRC Press; Boca Raton, FL: 2008. [Google Scholar]
- 60.Bisker G, Polettini M, Gingrich TR, Horowitz JM. Hierarchical bounds on entropy production inferred from partial information. J Stat Mech Theory Exp. 2017;2017:093210. [Google Scholar]
- 61.Seifert U. Stochastic thermodynamics, fluctuation theorems and molecular machines. Rep Prog Phys. 2012;75:126001. doi: 10.1088/0034-4885/75/12/126001. [DOI] [PubMed] [Google Scholar]
- 62.Van den Broeck C, Esposito M. Ensemble and trajectory thermodynamics: A brief introduction. Phys A. 2015;418:6–16. [Google Scholar]
- 63.Baiesi M, Maes C. Life efficiency does not always increase with the dissipation rate. J Phys Commun. 2018;2:045017. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.