Critical computational analysis illuminates the reductive-elimination mechanism that activates nitrogenase for N₂ reduction

Significance

This report critically evaluates the mechanism by which nitrogenase cleaves the N≡N triple bond. It assesses the thermodynamic driving force provided by the accompanying, apparently “wasteful,” reductive elimination of an H₂, and explains how the enzyme mechanistically couples exothermic H₂ formation to endothermic triple-bond cleavage in a nearly thermoneutral equilibrium process, thereby preventing the “futile” generation of two H₂ without N₂ reduction. This evaluation rests on a critical assessment of the density functional theory flavors needed to properly treat nitrogenase, and a demonstration that to prevent spurious disruption of FeMo-co upon 4[e⁻/H⁺] accumulation, one must employ a nitrogenase structural model that includes all residues interacting directly with FeMo-co, either via specific H-bond interactions, nonspecific electrostatic interactions, or steric confinement.

Abstract

Recent spectroscopic, kinetic, photophysical, and thermodynamic measurements show activation of nitrogenase for N₂ → 2NH₃ reduction involves the reductive elimination (re) of H₂ from two [Fe–H–Fe] bridging hydrides bound to the catalytic [7Fe–9S–Mo–C–homocitrate] FeMo-cofactor (FeMo-co). These studies rationalize the Lowe–Thorneley kinetic scheme’s proposal of mechanistically obligatory formation of one H₂ for each N₂ reduced. They also provide an overall framework for understanding the mechanism of nitrogen fixation by nitrogenase. However, they directly pose fundamental questions addressed computationally here. We here report an extensive computational investigation of the structure and energetics of possible nitrogenase intermediates using structural models for the active site with a broad range in complexity, while evaluating a diverse set of density functional theory flavors. (i) This shows that to prevent spurious disruption of FeMo-co having accumulated 4[e⁻/H⁺] it is necessary to include: all residues (and water molecules) interacting directly with FeMo-co via specific H-bond interactions; nonspecific local electrostatic interactions; and steric confinement. (ii) These calculations indicate an important role of sulfide hemilability in the overall conversion of E₀ to a diazene-level intermediate. (iii) Perhaps most importantly, they explain (iiia) how the enzyme mechanistically couples exothermic H₂ formation to endothermic cleavage of the N≡N triple bond in a nearly thermoneutral re/oxidative-addition equilibrium, (iiib) while preventing the “futile” generation of two H₂ without N₂ reduction: hydride re generates an H₂ complex, but H₂ is only lost when displaced by N₂, to form an end-on N₂ complex that proceeds to a diazene-level intermediate.

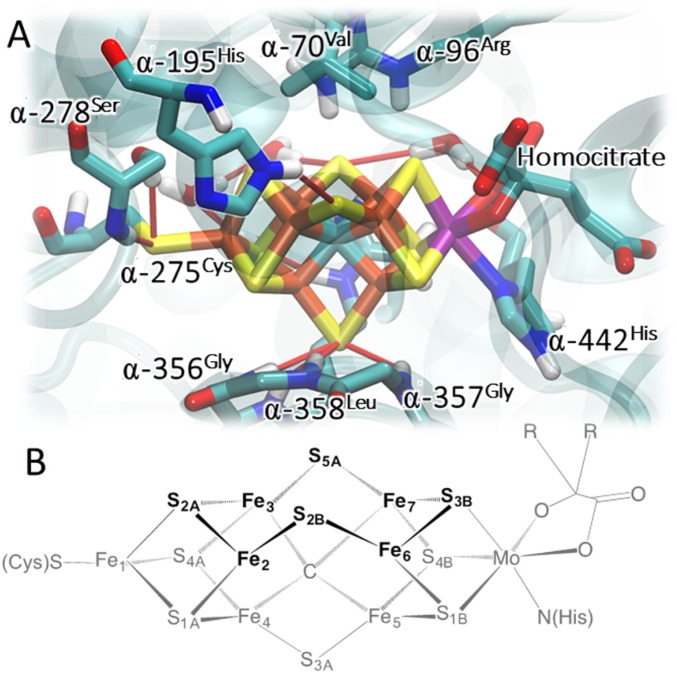
Biological nitrogen fixation is one of the most challenging chemical transformations in biology, the conversion of N₂ to ammonia. The catalyst for biological N₂ fixation, the metalloenzyme nitrogenase, is known in three different forms (1) with the most abundant being the Mo-dependent enzyme, which is composed of the electron-donating Fe protein and the catalytic MoFe protein. The Fe protein, a homodimer, delivers one electron at a time during transient association with the MoFe protein heterotetramer with dissociation of the two proteins driven by the hydrolysis of two ATP to two ADP/P_i per electron transfer (ET) event (2). The reduction of N₂ takes place on the [7Fe–9S–Mo–C–homocitrate] FeMo-cofactor (FeMo-co) in the active site of the MoFe protein (Fig. 1), with the [8Fe–7S] P-cluster in the MoFe protein acting as an ET intermediary.

Fig. 1.

Structure of the FeMo-co binding pocket as obtained from MD simulations (22) (A) and schematic representation of FeMo-co (standard atom numbering) (B). For simplicity, only the polar H atoms are shown. The color coding of atoms is as follows: rust, Fe; yellow, S; cyan, C; purple, Mo; red, O; blue, N; light gray, H. Hydrogen bonds are shown as thin red sticks. The cartoon representation of the protein in cyan color is reported with the purpose to highlight the surrounding protein environment. The N₂ access channel is indicated with the thick blue arrow.

Lowe and Thorneley put forward a kinetic model for catalysis by the MoFe protein, including rate constants for formation of each intermediate state, designated as E_n, where n indicates the number of electrons and protons accumulated. This scheme incorporates a controversial limiting stoichiometry:

$${\mathrm{N}}_2+8e^{-}+16\mathrm{ATP}+8{\mathrm{H}}^{+}\to 2\mathrm{N}{\mathrm{H}}_3+{\mathrm{H}}_2+16\mathrm{ADP}+16{\mathrm{P}}_{\mathrm{i}},$$ [1]

with an obligatory formation of 1 mol of H₂ per mole of N₂ reduced, and a corresponding requirement of 8[e⁻/H⁺], not 6, and as a result, the apparently “wasted” hydrolysis of 4 ATP (3–5).

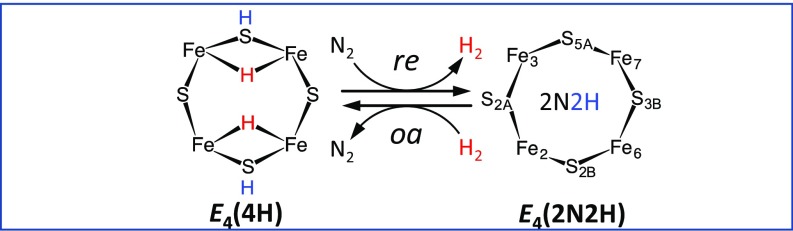
In recent years, we have demonstrated (6, 7) that this stoichiometry arises because activation of nitrogenase for N₂ reduction involves the accumulation of four reducing equivalents at the active-site FeMo-co (4) to form a state with two [Fe–H–Fe] bridging hydrides and two sulfur-bound protons, denoted E₄(4H), the Janus intermediate, and that breaking the N≡N triple bond requires the reductive elimination (re) of H₂ from E₄(4H) (6–9). This process corresponds to the forward direction of the equilibrium in Fig. 2, which leads to the formation of a diazene-level N₂ reduction product [denoted as E₄(2N2H)]; the reverse of this reaction is the oxidative addition (oa) of H₂ with release of N₂ (6). EPR/electron nuclear double resonance (ENDOR) and photophysical measurements established re/oa as central to the mechanism of the wild-type enzyme and showed it to be a nearly isoergic (ΔG = −8 kJ/mol), kinetically accessible process (8, 9). Photophysical measurements further suggested that during re activation of nitrogenase, E₄(4H) and E₄(2N2H) are likely connected via an H₂-bound intermediate [E₄(H₂)] (9). These studies provide an overall framework for understanding the mechanism of nitrogen fixation by nitrogenase. However, they directly pose a number of fundamental questions that are addressed computationally in this report. First, we address the “protonation isomers” at the E₄ level of electron accumulation, in particular the disposition of the two [Fe–H–Fe] moieties of the mechanistically central E₄(4H) intermediate. This contentious question has not been resolved experimentally, and its computational examination has required us to carry out a critical evaluation of the computational methodology required to study the nitrogenase catalytic mechanism. Computational studies of nitrogenase (10–22), mostly based on broken-symmetry (BS) density functional theory (DFT), have provided a wealth of information about the electronic structure of the FeMo-co (resting) state E₀ (14, 15). However, early work was constrained by the uncertainty as to the existence/identity of the cofactor central atom, and the limited size of the structural models adopted (10–13, 16, 18). Recently, computational investigations have begun to use larger structural models of the catalytic pocket (20, 21, 23–27). However, these included studies addressing the structure of E₄(4H) that advanced novel mechanistic proposals that are difficult to reconcile with the chemical expectations and experimental evidence. Notably, work by Siegbahn (20, 23), Rao et al. (21), and McKee (22) suggested the protonation of the FeMo-co central carbon atom during catalysis, while Siegbahn (20, 23) even proposed a Fe-bound methyl intermediate as the central E₄ catalytic species. Very recently, Einsle and coworkers (28) were able to solve the structure of the as-isolated VFe protein and observed replacement of the S_2B sulfide that bridges Fe₂–Fe₆. This led them to propose the two hydrides of E₄(4H) state bridge the Fe₂–Fe₆ center, and that this is the state that reductively eliminates H₂, leaving a vacant binding site for N₂. This proposal likewise needs computational assessment.

Fig. 2.

Schematic of the reductive-elimination (re)/oxidative-addition (oa) mechanism. 2N2H indicates a diazene-level N₂ reduction product.

To evaluate these proposals and in so doing answer fundamental questions of nitrogenase catalysis, we have carried out an in-depth evaluation of a variety of DFT flavors, structural models, and oxidation states of the resting state, and show that the proper incorporation of all interactions with the protein environment that envelops FeMo-co at the enzyme active site is critical to stabilize FeMo-co and prevent its disruption upon protonation. The resulting structural model is then used to characterize the alternative E₄ “protonation isomers,” including, but not limited to, characterization of the ground-state structure of E₄(4H). In doing this, we are led to consider the hemilability of Fe–S bonds during catalysis (28–30).

With this foundation, we are able to answer two of the key unresolved mechanistic questions: (i) what is the overall thermodynamic driving force for the process by which ATP-coupled electron delivery (Eq. 1) leads to N₂ reduction with loss of H₂ at the E₄ mechanistic stage; (ii) how does the enzyme mechanistically prevent the even more favorable production of a second H₂ without reduction of N₂, namely, how is re of H₂ mechanistically coupled to cleavage of the N≡N triple bond.

Computational Methods

Structural Models.

The FeMo-co strongly interacts with the surrounding protein environment mostly via hydrogen bonding and electrostatic interactions. Therefore, any quantitative computational investigation of its activity must include a realistic representation of the enzymatic pocket. In particular, as shown in Fig. 1, in addition to the coordination bonds with ligands, Fe₁-α-275^Cys, Mo-α-442^His (Azotobacter vinelandii numbering) (2), and Mo-R-homocitrate, FeMo-co engages several hydrogen bonds with the protein backbone, side chains, and water molecules present in the enzymatic pocket, which are known to be abundant near the FeMo-co (31). Some of these interactions are not evident from a simple investigation of the available crystallographic structures, as they are a representation of the most populated configuration at the temperature at which they were solved (typically 100 K). At room temperature, a multitude of local minima very close in free energy are accessible, and this conformational complexity finely tunes chemical reactivity.

In the present work, we use a structural model of nitrogenase based on submicrosecond force-field–based molecular dynamics (MD) simulations (32). The model includes all of the residues interacting directly with FeMo-co both via specific H-bond interactions and nonspecific electrostatic interactions (Fig. 1), while the rest of the protein is described with a polarizable continuum (33). Five different structural models of decreasing complexity were examined (SI Appendix, Fig. S1).

Model (a).

The full model (a) includes the FeMo-co with truncated modifications of the α-275^Cys, α-442^His ligands (Azotobacter vinelandii numbering), R-homocitrate, and all of the MoFe protein residues and water molecules that engage hydrogen-bonding interactions with the FeMo-co, or are known to be important of the catalytic activity (α-70^Val and α-96^Arg). Cysteine, histidine, arginine, valine, and R-homocitrate residues were modeled as methylthiolate, imidazole (or 4-methyl-imidazole), methylguanidinium, and tert-butyl and dimethyl glycolate, respectively. Recent reports highlighted that the protonation state of the homocitrate may influence the electronic properties of FeMo-co (24, 25). In the present study, homocitrate was considered fully deprotonated. Arginines were considered protonated, whereas the effect of both neutral (δ- and ε-form) and protonated forms of α-442^His was explored. The backbone of α-356^Gly, α-357^Gly, 358^Leu, and α-359^Arg, which interacts with FeMo-co via N–H hydrogen bonds, was modeled as a methylammine terminated triglycine. α-278^Ser forms hydrogen bonds with FeMo-co with both the side chain and the backbone N–H, and it was included in full as C-methylated serine. The steric confinement exerted by the protein matrix on α-70^Val and α-96^Arg was included by adding one ethane molecule next to α-70^Val at the location of the backbone C atoms of α-66^Gly, the side chain of α-98^Asn, the backbone of α-70^Val and α-69^gly, and a bridging water molecule (SI Appendix, Fig. S1A). It is important to point out that it is crucial to include the residues around α-70^Val and α-96^Arg to avoid unrealistic, large conformational reorganization of residues as observed in other reports (20, 23). The C atoms of the ethane molecule were kept fixed at their equilibrium distance. The atoms at the locations where the residues were truncated were also fixed during the geometry optimizations. The list of the frozen atoms is provided in SI Appendix, section S7.

Starting from the full model (a), we generated four additional models by progressively deleting residues, as follows.

Model (b).

Model (b) deletes all water molecules interacting with FeMo-co (SI Appendix, Fig. S1B).

Model (c).

Model (c) further deletes the backbone of α-356^Gly, α-357^Gly, 358^Leu, and α-359^Arg (SI Appendix, Fig. S1C).

Model (d).

Model (d) additionally omits the side chain and the backbone N–H of α-278^Ser (SI Appendix, Fig. S1D).

Model (e).

Model (e) further removes the residues α-70^Val, α-96^Arg, and α-359^Arg, yielding a minimal model that includes only FeMo-co and its ligands α-275^Cys, α-442^His, and Mo-R-homocitrate (SI Appendix, Fig. S1E).

The initial position of atoms was obtained from previous MD simulation studies (32). Specifically, we performed a clustering analysis of the MD trajectory to find groups of similar frames, and then adopted the frame closest to the center of the largest group (representing about the 80% of the configurational space of the residues included in the quantum-mechanical model). The representative MD configuration we adopted for the present study contains the same number of water molecules present in the starting Protein Data Bank (PDB) structure (2). The validity of the adopted structural model is discussed in detail below. We will show that it is imperative to include all of the residues interacting with FeMo-co, that is, model (a), to obtain meaningful mechanistic predictions. In particular, the protein cage helps stabilize the FeMo-co and avoid artifacts such as those reported in recent investigations, where the protonation of the central carbide up to CH₃ (20, 23), with consequent disruption of the cofactor, was found very favorable and erroneously proposed to be a key catalytic step.

Electronic Structure Calculations.

BS-DFT.

It is commonly accepted that BS-DFT calculations represent a good compromise between computational efficiency and accuracy, and DFT has been widely applied to the study of FeMo-co. Noodleman and coworkers (14) reported an exhaustive search for the lowest-energy electronic wavefunction of FeMo-co in the S = 3/2 E₀ state for a minimal active-site model, which corresponds to model (e) described above, including only FeMo-co and its ligands. It was shown that, as expected, the E₀ (S = 3/2) state maximizes the antiferromagnetic coupling between the Fe centers. Later, Harris and Szilagyi (16) showed that both pure generalized gradient approximation (GGA) and hybrid functionals consistently reproduce Noodleman’s results. Recent large-scale calculations carried out by Bjornsson and coworkers (26, 27) corroborated these early studies. We note that, although BS-DFT is effective in resolving the questions of nitrogenase function addressed here, the approximate nature of the adopted functionals, coupled with the single determinant framework of the theory, is unable to capture finer quantitative details associated with the complex transformations at the FeMo-co, as noted below.

For each E_n, there are various possible patterns that maximize the antiferromagnetic coupling, which are in the absence of the potential due to the protein environment equienergetic. The asymmetry of the protein environment breaks the degeneracy of these spin patterns. As shown in SI Appendix, Fig. S2, the energy difference between patterns can be as high as 23 kJ/mol for E₀. Similar differences are found for the other E_n states investigated. In the following, for each E_n, the lowest energy spin pattern was adopted.

The present DFT calculations explored seven exchange and correlation functionals: BP86, BLYP, PBE, B3LYP, PBE0, M06, and M06-2X, primarily focusing on the GGA BP86 (34–36) functional and the hybrid B3LYP functional (37–39). However, a result discussed without explicit mention of functional is derived with BP86 for reasons discussed in SI Appendix, section S3. The Ahlrichs VTZ basis set was used for all Fe atoms (40), the Los Alamos National Laboratory basis set LANL2TZ with an effective core potential was employed for the Mo atom (41), and the 6-311++G** basis set was employed for all atoms coordinated to metal atoms, including protic and hydridic hydrogen atoms and all of the atoms with which they interact via a covalent bond or a hydrogen bond, and finally the 6-31G* basis set (42) was adopted for all other atoms. All calculations were performed with the NWChem quantum chemistry package (43).

Oxidation state.

Various different oxidation states for Fe centers of the FeMo-co in the E₀ (S = 3/2) have been proposed over the years. There is now general consensus (27, 44) that the proper oxidation state of E₀ is [Mo³⁺3Fe²⁺4Fe³⁺]. The majority of the calculations presented in this work were performed on E₀ in this oxidation state. However, for a better assessment of the general validity of our results, selected E₀ and E₄ species were also investigated for an electron counting corresponding to the more oxidized E₀ (S = 3/2) state, [Mo³⁺1Fe²⁺6Fe³⁺]. The current consensus is that FeMo-co in E₀ has a low-spin Mo(III) (27, 44), consistent with ENDOR measurements that show small hyperfine couplings to ⁹⁵Mo (27). In all of our calculations on E₀, Mo has a very low spin density, regardless of the exchange and correlation functional that is adopted (as described directly below) (SI Appendix, Tables S2 and S3). In E₄, we again find a Mo(III) oxidation state, but the metal ion can assume low- or high-spin configurations depending on the location of the hydrogen atoms and the functional employed, with GGA functionals (e.g., BP86) preferentially yielding low spin configurations (low spin densities) and hybrid functionals (e.g., B3LYP) favoring high spin states (higher spin densities; SI Appendix, Tables S4–S11). ⁹⁵Mo ENDOR experiments on E₄(4H) have shown small ⁹⁵Mo couplings in E₄, little changed from the Mo hyperfine coupling in E₀, which not only implies the persistence of the Mo(III) oxidation state, but also suggests that the low spin state persists as well (45, 46). In that sense, the ENDOR measurements support the choice of the GGA functionals as being most appropriate for the present investigation.

Spin states.

Spectroscopic investigations have provided the spin state of various intermediates in the Lowe–Thorneley kinetic model, notably for this report, E₀, E₂, and both E₄(4H) and E₄(2N2H). As recently established (47), not only E₀ but also the E₂ intermediates have a total spin S = 3/2, while the two E₄ intermediates have S = 1/2 (6). Therefore, calculations were performed for the observed S = 3/2 spin state (E₀ and E₂) and the two S = 1/2 (E₄) states within the BS approach (16). Because of the single-determinant nature of BS-DFT, what is calculated are not the pure S = 3/2 or S = 1/2 spin states, but rather a mixed determinant with M_S = 3/2 or M_S = 1/2 components (27, 44). This is an important point that should be kept in mind, as the energies of the proper pure spin states can be quite different from the BS-DFT energies. Clearly, all of the many DFT studies reported in the literature suffer from the same problem. The energy of the pure spin states can be estimated using the Heisenberg spin ladder framework (14, 15, 48–50), which might be problematic for the FeMo-co because of the large exchange coupling constants (14, 15). A few recent pioneering studies point the way beyond DFT in addressing the nitrogenase problem (51–53). Conclusions drawn below are tempered by this recognition. For a more straightforward comparison between computation and experiment, we will still refer to the S = 3/2 and S = 1/2 state for E₀ and E₄, rather than M_S = 3/2 and M_S = 1/2, respectively.

Initial guesses were constructed according to the spin configurations of SI Appendix, Table S1 from atomic guesses corresponding to Fe²⁺ (S = 2), Fe³⁺ (S = 5/2), and Mo³⁺ (S = 3/2; different choices yielded similar results). Three BS solutions were shown to maximize the antiferromagnetic coupling between spins in the E₀ (S = 3/2) state [see SI Appendix, Fig. S2, corresponding to the state BS7 proposed by Noodleman and coworkers (14)]; initial geometries were optimized for the antiferromagnetic coupling with the lowest energy (16, 27). Then, for each E_n state and its isomers that are considered (see below), all of the 35 possible BS solutions were explored at both BP86 and B3LYP level (SI Appendix, Table S1). There are eight magnetic centers in FeMo-co (1Mo³⁺, 3Fe²⁺, and 4Fe³⁺). In the absence of an external magnetic field, we can set the spin of one of the centers (for instance, Mo) arbitrarily either up or down, which leaves a total of 7!/(4!·3!) = 35 possible spin up and spin down combinations for both S = 1/2 and 3/2 total spin states, if we do not distinguish the specific location of Fe²⁺ and Fe³⁺ centers. For a more detailed discussion, see ref. 27. Finally, the geometry of the BS solutions within 20 kJ/mol from the lowest-energy solution was further optimized for E₀, the first four lowest-energy E₄ protomers, the protonated CH E₄ isomer (see below), and all of the diazene-level N₂ reduction E₄ states.

Medium effects.

The COSMO polarizable dielectric continuum (33) was used to describe the protein environment not explicitly considered in our structural models along with atomic radii according to ref. 54. A dielectric continuum should be always used with care, as the dielectric properties of a protein are ill defined. Ideally, one could assume that the larger the adopted structural model is, the smaller the dependence on the dielectric constant of the continuum. In the present work, two dielectric constants were examined, ε = 4 and 10. As shown in SI Appendix, the energy differences between E₄ isomers calculated with our largest structural model show little dependence (smaller than 10 kJ/mol) on the choice of ε, in contrast to what observed for the smaller models, where far larger variations are observed. This result suggests that the residues included in our largest model indeed well describe the local environment of FeMo-co. All of the energies discussed in this paper are calculated for ε = 4, as we think this is more appropriate to describe the hydrophobic protein scaffold beyond the outer coordination sphere of FeMo-co.

Free-energy corrections.

Free-energy corrections were estimated using harmonic vibrational frequencies after projecting out the spurious imaginary frequencies associated with the frozen atomic positions.

Exploration of possible pathways for interconversion of E₄ isomers and H₂ release.

The size of the working structural model [model (a)] precluded a full transition state search based on vibrational frequencies. We estimated the energetic barrier associated with equilibria between the lowest-energy E₄ isomers, E₄(4H), E₄(4H)^(b), E₄(4H)^(c), and E₄(2H;H₂), using a simple line search based on constrained geometry optimizations, whereby a given Fe/H distance is gradually varied between the limiting values assumed in two targeted E₄ species. In a similar manner, we studied the release of H₂ from E₄(2H,H₂) and E₄(2H,H₂;N₂) by a stepwise increase of the distance between Fe₂ and the center of mass of the H₂ molecule. In all of the cases, for each targeted distance, the position of all atoms was relaxed, except for the atoms at the truncation points, as discussed in Structural Models above.

Results

We investigated five structural models of the nitrogenase active site [models (a) to (e)], with the extent of incorporating interactions with the protein environment pictured in Fig. 1 increasing in the order, model (e) → model (a), using a variety of DFT flavors, various protonation states of FeMo-co, as well as different oxidation states for E₀. The majority of the calculations were performed starting from the electron count associated with the “oxidized” Mo³⁺3Fe²⁺4Fe³⁺ E₀ (S = 3/2) oxidation state with α-195^His doubly protonated. The latter choice was based on pK_a values estimates for the doubly protonated α-195^His higher than 10. The pK_a of α-195^His was estimated from the free energy for transferring either the ε- or δ-proton for the protonated α-195^His to histidine in water, for which an accurate value of the pK_a is available. This calculation was performed using our largest model. For completeness, selected structures were also analyzed for the more oxidized [Mo³⁺1Fe²⁺6Fe³⁺] E₀ (S = 3/2) state and for neutral α-195^His.

The structure and the corresponding energetics of various critical E₄ protonation states were calculated at both BP86 and B3LYP level of theory. We found that the two functionals provide a similar picture of the energy landscape of the E₄ isomers; differences will also be discussed. Because BP86 predicts a low-spin Mo(III) state for both E₀ and E₄, consistent with the available ENDOR data and X-ray/computational studies (27, 44), as well as for other reasons to be given below, the energies discussed here refer to this functional unless noted; B3LYP energies are nonetheless given as appropriate. A detailed discussion on the performance of these and other functionals is presented in SI Appendix, section S3.

Because of the large number of possible isomers, the energetic comparisons mostly included only the total electronic energy and continuum corrections for the protein environment, that is, without including zero-point energy and vibrational corrections to free energy, as their inclusion would have required computationally very expensive vibrational frequency calculations for a large number of structures. Rather, frequency calculations were performed only on the low-lying intermediates of mechanistic significance.

Protonation States of E₄.

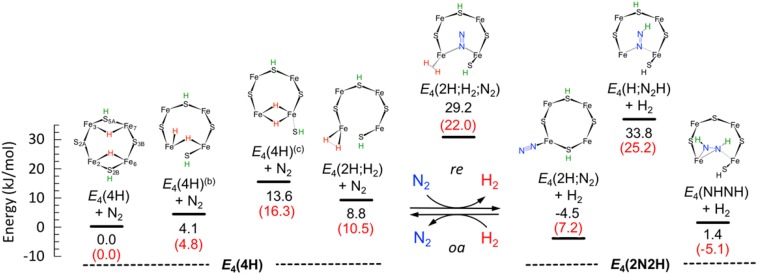
Previous computational studies on a simplified model of nitrogenase (19), which included only FeMo-co and its ligands, revealed that μ₂-S atoms are preferentially protonated over μ₃-S atoms and that accumulation of [e⁻/H⁺] pairs starting from E₀ proceeds by the alternate protonation of μ₂-S atoms and Fe atoms. Examination of a number of possible protonation states for the extended model (a) confirmed these initial observations. The relative energetics and the structure of all of the E₄ states we analyzed is reported in SI Appendix, Fig. S3, while the states relevant to the present discussion are listed in Fig. 3. The computations here performed on model (a) indicate that, among the three μ₂-S atoms, protonation of S_5A and S_2B (located on the reactive face; Fig. 1) is more favorable than the protonation of S_3A, which is located in a protein matrix cleft and receives hydrogen bonds from the protein backbone (Fig. 1). There are three low-lying E₄ states that differ by the location of one hydride (Fig. 3). Consistent with low-temperature ENDOR results (6, 7), and in keeping with previous exploratory calculations (9), the lowest-energy state has two hydrides asymmetrically bridging Fe₂–Fe₆ and Fe₃–Fe₇, and two protonated sulfur atoms (S_5A and S_2B). We will refer to this state as E₄(4H).

Fig. 3.

Relative free energy (black) and energy (red) of various E₄ species potentially involved in FeMo-co reductive activation and the breaking of the N₂ triple bond. Protic and hydridic hydrogens are indicated in green and red, respectively.

The next state, indicated as E₄(4H)^(b), lies only ΔE = 4.8 kJ/mol higher then E₄(4H), and differs from it in that the Fe₂–H–Fe₆ bridging hydride has migrated to Fe₂ in E₄(4H)^(b), with Fe₆ thus binding a terminal hydride and acting as one terminus of the hydride bridge. Next higher in energy (ΔE = 10.5 kJ/mol) is a dihydride species E₄(4H)^(c) with both hydrides bridging the Fe₂–Fe₆ centers, similar to the E₄ intermediate recently proposed by Einsle for the FeV-cofactor in the vanadium nitrogenase (28). Slightly higher in energy still (ΔE = 16.3 kJ/mol) we found a dihydrogen intermediate E₄(2H;H₂) with a strongly activated dihydrogen moiety [d(H–H) = 1.00 Å, vs. 0.7 Å for the isolated molecule] located on Fe₂.

As schematically depicted in Fig. 3, the E₄ isomers containing two hydrides bound in some way to the Fe₂ have the Fe₂–S_2B bond broken or partially broken. In addition, E₄(4H)^(c) Fe₂–Fe₆ dibridged dihydride has a very elongated Fe₆–S_2B bond [2.72 Å vs. 2.32 and 2.48 Å in E₄(4H) and E₄(4H)^(b), respectively]. In the next section, we will comment on the possible role of the hemilabile Fe–S bond(s) in the activity of nitrogenase. Addition of dispersion corrections (55–57) has only a minimal effect on this ladder of states. For instance, the relative BP86-D3 (56, 57) energies of the four low-energy E₄ states are 0, 12.2, 14.3, and 20.7 kJ/mol. At B3LYP level of theory, only E₄(4H), E₄(4H)^(c), and E₄(2H;H₂) were identified as lowest-energy isomers. Instead, E₄(4H)^(b) was found to be unstable. Indeed, geometry optimizations started from the E₄(4H)^(b) BP86 structure yielded either the E₄(2H;H₂) state, which is located at +27.5 kJ/mol above E₄(4H), or the E₄(4H)^(c), which is nearly degenerate with the E₄(4H) being located at only 2.8 kJ/mol above it. A simple line search for a possible pathway connecting these states carried out at the BP86 level of DFT indicates that the migration of the hydride between Fe₃ and Fe₇ in the lowest-lying E₄(4H) to Fe₂ of E₄(4H)^(b) (ΔE^‡ ∼ 29 kJ/mol), and of one of the two hydrogens between Fe₂ and Fe₆ in E₄(4H)^(b) to Fe₂ in E₄(4H)^(b) [ΔE^‡ ∼ 14 kJ/mol relative to E₄(4H)] is facile.

In computations with the large model (a) of Fig. 1, we found that protonation of the central carbide, with the concomitant formation of a deformed E₄(3H,CH) FeMo-co state (Fig. 4 and SI Appendix, Fig. S3), is extremely unfavorable (ΔE = +121.4 kJ/mol). Using hybrid functionals, such as B3LYP, the energy of E₄(3H;CH) decreases considerably but still remains far above E₄(4H) (ΔE = +81.6 kJ/mol). Also for this isomer, addition of dispersion corrections (55–57) has only a small effect. For example, the BP86-D3 energy relative to E₄(4H) is +106.6 kJ/mol. This finding is in contrast to recent reports by Siegbahn (20, 23), Rao et al. (21), and McKee (22) that E₄(3H;CH) is lower in energy than E₄(4H) (20–23). Frequency calculations on the first four low-energy states E₄(4H), E₄(4H)^(b), E₄(4H)^(c), and E₄(2H;H₂) allowed estimation of free energies, and confirmed the relative ordering discussed above, and locate E₄(4H)^(b), E₄(4H)^(c), and E₄(2H;H₂) at ΔG = 4.1, 13.6, and 8.8 kJ/mol above the E₄(4H) baseline, respectively, as shown in Fig. 3.

Fig. 4.

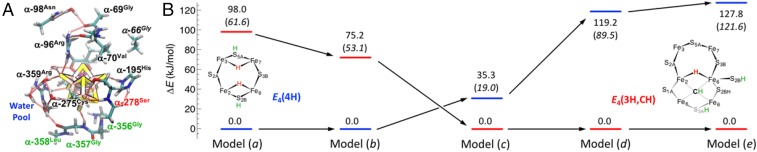
Effect of the enzymatic environment around FeMo-co on the relative stability of the bridging hydride state E₄(4H) and C-protonated state E₄(3H,CH). (A) Models used in the present study, with the labels of the residues sequentially removed from the full model (a): highlighted in blue [model (b)], green [model (c)], red [model (d)], and black [model (e)], respectively (SI Appendix, Fig. S1). (B) Corresponding relative electronic energy (no polarizable continuum corrections applied) as obtained from DFT/BP86 and DFT/B3LYP level of theory (values in parentheses).

Geometry optimizations of these states with neutral, rather than protonated, α-195^His provide similar qualitative ordering, but with E₄(4H)^(b), and E₄(2H;H₂) located only at ΔE = 4.1 and 8.3 kJ/mol from E₄(4H). Finally, analysis of E₄(4H), E₄(4H)^(b), E₄(2H;H₂), and E₄(3H,CH) based on the assumption that the resting-state E₀ (S = 3/2) exhibits an electron count corresponding to the oxidation state [Mo³⁺1Fe²⁺6Fe³⁺] provided a similar energy ordering with E₄(4H)^(b), E₄(2H;H₂) at only ΔE = 5.7 and 7.1 kJ/mol above E₄(4H), while E₄(3H,CH) is more than ΔE = 140 kJ/mol above E₄(4H).

Taken altogether, our computations show that likely there are at least four low-lying E₄ isomers in equilibrium with each other. Although the energy difference between them is small and well within typical DFT errors, the finding that the state with the lowest energy has two [Fe–H–Fe] bridging hydrides, E₄(4H), is consistent with the conclusion from low-temperature ENDOR measurements (6), while the characterization of a low-lying H₂ complex, E₄(2H;H₂), possibly involved during reductive elimination of the hydrides of E₄(4H), is consistent with recent photophysical studies showing that re of H₂ involves such a complex (8, 9).

Role of the FeMo-Co Environment.

The major improvement in the present computations compared with other recent mechanistic studies (20–23) is that we incorporated the entire protein envelope around FeMo-co, including the full set of hydrogen-bonding interactions from both protein residues and water molecules (Fig. 1). To obtain a detailed understanding of the importance of the different interactions, we examined structural models (b) through (e) of progressively decreasing complexity (Fig. 4). These unambiguously shows that the local environment around FeMo-co plays a crucial role in stabilizing the cofactor and controlling the reaction pathway.

SI Appendix, Fig. S1 depicts the five levels of incorporating the protein environment of FeMo-co adopted in the present work: (i) represents the full (largest) model employed in our study, which includes all residues enclosing FeMo-co (see Methods for listing), and, in particular all of the residues interacting via H-bonding and electrostatic interactions (Fig. 1); (ii) eliminates the water molecules interacting with FeMo-co; (iii) additionally eliminates the backbone of the residues H-bonded to the bottom of FeMo-co; (iv) also removes the side chain and the backbone N–H of α-278^Ser, thus eliminating most of the H bonds to FeMo-co; and (v) shows a minimal model, which includes only the cofactor and its ligands. The models adopted by Siegbahn (20, 23) and Rao et al. (21) are similar to our models (c) and (d), in that they lack the majority of the H-bond cage around FeMo-co, while McKee’s model (22) is identical to our minimal model (e). In particular, although Rao et al. (21) performed a multiscale quantum-chemical study that included the full protein scaffold, they still missed the majority of the active-site interactions, as they simply adopted one of the available X-ray structures and neglected the presence of water, which is known to be present near the FeMo-co (31). Any realistic model must include hydrogen bonding from water as well as the protein residues, and most of the H-bonding network becomes apparent only after computationally relaxing the protein in its aqueous environment at room temperature. The representative MD configuration (32) we adopted in the present study contains the same number of water molecules present in the starting PDB structure (2). However, in our model, FeMo-co has been evolved according to MD simulations during which hydrogen bonds form the water molecules and protein residues; the most representative configuration has been chosen for the calculation as described in Computational Methods.

As shown in Fig. 4, with the resulting full model (a), the native-like FeMo-co core of E₄(4H) is about 98 kJ/mol (BP86) or 62 kJ/mol (B3LYP) more stable than the (deformed) C-protonated E₄(3H,CH) core at this level of [e⁻/H⁺] accumulation. The progressive elimination of protein cage around the cofactor reverses the order; elimination of the five water molecules present on one of the FeMo-co sides lowers the gaps between E₄(4H) and E₄(3H,CH) to 75 kJ/mol (BP86) or 53 kJ/mol (B3LYP) in favor of E₄(4H). Removal of the backbone chain on the bottom of the cofactor in model (c) (i.e., opposite to the FeMo-co Fe_2,3,6,7 catalytic face) makes E₄(3H,CH) more stable than E₄(4H) by 35 kJ/mol (BP86). Elimination of α-278^Ser (which engages H bonds with FeMo-co trough the side-chain OH and the backbone NH) in model (d) brings the energy gap to 119 kJ/mol (BP86) or 89 kJ/mol (B3LYP) in favor of the E₄(3H,CH); the situation is even more extreme with the minimal model (e), where the open core is over 120 kJ more stable at both BP86 and B3LYP levels of theory. From the trend of the relative stability of E₄(4H) to E₄(3H;CH), it is evident that all of the residues at the active site play an important stabilizing role on E₄(4H). Although the progression of Fig. 4 presents a clear trend in the energetics, which shows the open core to be irrelevant to function, quantitatively, even these results might not yet be at convergence. In all likelihood, more extended models should be used to properly describe the highly anisotropic protein environment beyond the second coordination sphere of the FeMo-co, as included in the present study. Indeed, it has been shown for other systems, such as the photosystem II (58–60), that the field arising from the highly heterogeneous protein scaffold finely tunes activity.

We note that Siegbahn’s original model (20) corresponded roughly to our model (d), but in a recent communication (23), he extended his initial structural model to match the size of our largest model, in response to some experimental data from our team suggesting an equilibrium involving a dihydrogen species [the E₄(2H;H₂) species discussed below] (9). The results with the larger model repeated Siegbahn’s former observation of a favorable protonation of the central carbon. However, although the size (number of atoms) of his expanded model (23) is comparable with ours, this new model is fundamentally identical to the original one (20) in that it does not incorporate crucial interactions with the protein residues and water molecules around the FeMo-co core; the additional residues are only around the homocitrate tail. Thus, our study demonstrates that it is only the failure to incorporate the protein envelope encapsulating FeMo-co that results in an open FeMo-co core upon [e⁻/H⁺] delivery, and that inappropriately appears to make protonation of the central carbon atom thermodynamically favorable.

However, what is the actual role of the protein environment? To what degree are the H-bonding interactions energetically stabilizing the core of the reduced FeMo-co, and to what degree does the protein confining cage stabilize its geometry? To better characterize which effect dominates, for each of the models (a) to (d), we removed all of the protein residues and water molecules and recalculated the energies without relaxing the geometries of FeMo-co (SI Appendix, Fig. S4). Indeed, using the geometry of FeMo-co from models (a) and (b), we obtain that E₄(4H) is still more stable than E₄(3H;CH) by ΔE^(el) = 105.8 and 89.8 kJ/mol (BP86), respectively (difference in the total energy without PCM corrections); in contrast, using the geometry of FeMo-co from model (c), which lacks the protein residues on the bottom of the FeMo-co, we obtain the reverse result with E₄(3H;CH), now more stable than E₄(4H) by ΔE^(el) = 63.3 kJ/mol. In model (d), the stability of FeMo-co from model E₄(3H;CH) relative to that of E₄(4H) increases to 151.9 kJ/mol, a value that is close to the value obtained directly with model (e), with FeMo-co of E₄(3H;CH) more stable than that of E₄(4H) by ΔE^(el) = 132.4 kJ/mol. Regarding the FeMo-co geometry itself, going from model (a) to model (e), a contraction of the majority of the Fe–S distances is observed for E₄(4H) (up to 4% for the Fe₁–S_1A and Fe₇–S_4B), while an expansion of most of the Fe–S distances is observed for E₄(3H;CH) (up to 3% for Fe₃–S_5A and Fe₆–S_1B).

Remarkably, the change in the difference in energies between FeMo-co in the E₄(4H) and E₄(3H;CH) states with the model occurs almost exclusively through changes in the energy of E₄(3H;CH); the energy of E₄(4H) is rather insensitive to the size of the model, varying by less than 20 kJ/mol passing from model (a) to model (e). This can be clearly appreciated from the data reported in SI Appendix, Fig. S4, where the energy of FeMo-co in the E₄(4H) and E₄(3H,CH) states as obtained from the five models studied here are compared with that of FeMo-co in the E₀. These results indicate that the protein envelope is (as might have been expected) complementary to the geometry of the closed-core FeMo-co observed in the resting state, and that the protein scaffold enforces this geometry upon FeMo-co all along the catalytic cycle, quite likely with the benefit that it prevents the enzyme from destroying its active-site cluster through carbide protonation to form CH₄. Our analysis indicates that all of the protein envelope around of FeMo-co is responsible for the stabilization of E₄(4H) over E₄(3H;CH), but with a more prominent role of the residues on the bottom, which appear to structurally confine the cofactor, preventing the decomposition upon reduction seen in the computations that do not include them (20, 23). Further details of the role of the protein environment in stabilizing the cofactor and determining the actual mechanism of N₂ reduction are presented in SI Appendix.

Fe–S Bond Hemilability.

We analyzed the structures of all four lowest-energy E₄ electron-accumulation isomers, E₄(4H), E₄(4H)^(b), E₄(4H)^(c), and E₄(2H;H₂), which are very close in energy, and in addition the structure of E4(3H;CH). As can be seen from SI Appendix, Table S13, all of the bond distances for FeMo-co in the E₄ states are similar to those in E₀, with two notable exceptions. The first one is the expected marked elongation in Fe₃–C and Fe₇–C distances in the extremely high-energy E₄(3H;CH) species (1.6 and 1.3 Å relative to E₀, respectively) as a consequence of the disruption of FeMo-co upon protonation of the central carbon. In contrast, for all of the species that are potentially energetically accessible and mechanistically important, the Fe–C bond lengths change by less than 0.1 Å relative to E₀. In short, in energetically accessible states, the Fe–C bonds are maintained.

The second exception is the Fe₂–S_2B bond for some isomers with protonated S_2BH. Generally, we observe that protonation of an S atom bound to two metal ions causes a maximum increase of the Fe–S bonds of 0.1–0.2 Å, while protonation of an S atom bound to three metal ions causes a maximum lengthening of the Fe–S bond up to 0.4 Å. In keeping with this behavior, in E₄(4H) where Fe₃/Fe₇ is bridged both one of the two bridging hydrides and by the protonated S_5B, the Fe₃–S_5B bond elongates by 0.2 Å and the bond to Fe₇ by less than 0.1 Å. The second hydride of E₄(4H) bridges Fe₂/Fe₆, as does the protonated S_2B. However, in contrast, the Fe₂–S_2B bond in E₄(4H) elongates by almost 0.4 Å. This bond is actually broken in the low-energy isomers E₄(4H)^(b), E₄(4H)^(c), and E₄(2H;H₂), with the Fe₂–S_2B distance increased by about 1.6 Å in these cases. Higher-energy isomers again are characterized by an increase of the Fe₂–S_2BH bond distance, in line with the other Fe–S bonds of S bound to two metal ions. In the double-bridged Fe₂/Fe₆ dihydride E₄(4H)^(c), also the Fe₆–S_2B distance considerably elongates, being about 0.40 Å longer than in E₄(4H). The behavior of the Fe₆–S_2B in E₄(4H)^(c) is even more dramatic at the B3LYP level of theory, whereby the Fe₆–S_2BH bond further elongates and, when 195^His doubly protonated, the S_2BH deprotonates and H₂S is formed upon proton transfer from 195^His, which remains coordinated to Fe₆. Release of S_2B (as HS⁻) via the formation of a doubly bridged Fe₂/Fe₆ dihydride, similar to E₄(4H)^(c), has been recently proposed to be central for N₂ activation in vanadium nitrogenase (28).

What differentiates the behavior of S_5B and S_2B in E₄(4H) is likely to be in some part the presence of the H bond to S_2B from 195^His; in the low-lying states with broken Fe–S_2B bond, rearrangement of the bridging hydrides makes S_2B unique. We hypothesize that, as proposed for some H₂-producing catalytic systems (29, 30), the hemilability of the Fe–S_2B bond is important to creating an efficient H₂ re pathway with the concomitant binding of N₂ in which Fe₂ first binds both hydrides, and then forms H₂. We conclude, anticipating the results presented in the next section, that upon release of H₂ and binding of N₂, the Fe₂–S_2B bond is restored. The reversible breaking of this Fe–S bond further demonstrates its hemilabile nature. To the best of our knowledge, this behavior of the Fe–S bond in nitrogenase has been proposed previously only by Einsle and coworkers (28).

Thermodynamics of N₂ Activation.

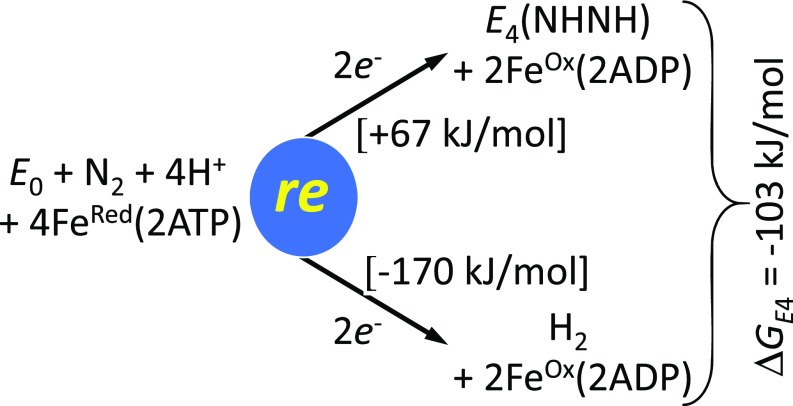
It is possible to achieve a profound understanding of the thermodynamic necessity of coupling H₂ formation via re to cleavage of the N≡N triple bond by looking at the overall process for the formation of any of the diazene-level intermediates [E₄(2H;N₂), E₄(H;N₂H), or E₄(NHNH)] from E₀. Focusing just on the formation of E₄(NHNH), as displayed in Fig. 5, the overall process is exergonic by ΔG_E4 = −103 kJ/mol at pH 7 (a detailed discussion on how this value was calculated is presented in SI Appendix, section S5). What makes this process so favorable can be understood by decomposing it into the two parts shown in Fig. 5: (i) the endergonic formation of E₄(NHNH) from E₀, N₂, 2H⁺, and 2e⁻, the latter provided by the Fe protein and the hydrolysis of four ATPs, with ΔG_DZ = +67 kJ/mol; and (ii) the exergonic formation of H₂ from 2H⁺, and 2e⁻, again provided by the Fe protein with ATP hydrolysis, with ΔG_H2 = −170 kJ/mol. Thus, although direct formation of E₄(NHNH) without generation of H₂ is thermodynamically unfavorable, nitrogenase couples this unfavorable reaction of N₂ with a highly favorable one, generation of H₂, resulting in an overall exergonic process to drive N₂ fixation. Following Bucket and Thauer (61), this process may therefore be viewed as “cluster-based electron bifurcation,” in which two hydride electron pairs split, with an exergonic reaction involving one pair (H₂ formation) driving an endergonic reaction involving the other (N₂ triple-bond cleavage).

Fig. 5.

The energetics of formation of E₄(NHNH) from the enzymatic reactants and its decomposition into two individual two-electron, two-proton processes, each involving the hydrolysis of 2ATP: N₂ binding and formation of E₄(NHNH); release of H₂ formed by re from E₄(4H). These are coupled through displacement by N₂ of the H₂ formed by re.

N₂ Activation by Reductive Elimination.

MD simulations (32) showed that access of small substrates to the active site is very facile and suggested that N₂ and H₂ are always present in the catalytic pocket near the Fe₂–Fe₆ edge confined by α-70^Val and α-195^His. Guided by these simulations, possible N₂ binding sites were explored for the four low-lying E₄(4H), E₄(4H)^(b), E₄(4H)^(c), and E₄(2H;H₂) isomers, using the BP86 functional. First, geometry optimizations were performed constraining the N₂ molecule to stay at a Fe–N₂ distance typical of metal–N₂ molecular complexes. Then the structures were relaxed without the constraint. All attempts to find a stable N₂-bound state to either E₄(4H), E₄(4H)^(b), or E₄(4H)^(c) failed. In contrast, E₄(2H;H₂), resulting from the reductive formation of H₂, with retention of the H₂ bound to the doubly reduced FeMo-co core, reacts with N₂ to form a asymmetrically bridged, end-on Fe₂–(N₂)–Fe₆ adduct, E₄(2H;H₂;μ-N₂), reminiscent of the side-on, end-on N₂ bridging mode reported for a few classes of complexes (62, 63). The E₄(2H;H₂;μ-N₂) state is ΔG = 29.2 kJ/mol above E₄(4H) (Fe₂–N and Fe₆–N distances of 1.87 and 2.07 Å, respectively) (Fig. 3). Upon formation of E₄(2H;H₂;μ-N₂), the H₂ becomes less activated, with the H–H distance shortening from 1.00 Å in E₄(2H;H₂) to 0.84 Å and a concomitant reduction of the Fe₂–S_2B bond of 0.2 Å. Release of H₂ from E₄(2H;H₂;μ-N₂), yielding the E₄(2H;N₂) state with N₂ bound end-on to Fe₂ and restoration of the Fe₂–S_2B bond, is thermodynamically favorable (ΔG = −33.7 kJ/mol; Fig. 3).

The energy barrier for H₂ release from both E₄(2H;H₂) and E₄(2H;H₂;μ-N₂) was estimated using the line search approach discussed in Methods. A monotonic increase of energy was obtained when exploring elimination of H₂ from E₄(2H;H₂) with the search carried out until the energy had increased by over 50 kJ/mol, increasing the Fe₂–H distance from its equilibrium value of about 1.5 to 3.5 Å. This is a consequence of the high energy of the E₄(2H)* FeMo-co state, with its doubly reduced Fe core produced by H₂ loss. In short, the H₂-bound state, E₄(2H;H₂), is readily formed by re of the two hydrides of E₄(4H), but it does not release that H₂. In contrast, a barrier of only about 28 kJ/mol was estimated for H₂ release from E₄(2H;H₂;μ-N₂) when using the same constrained optimization approach, with an estimated Fe₂–H₂ distance at the transition state of 2.1 Å (SI Appendix, Fig. S5). Although at this point the computations do not definitively discriminate between a concerted and stepwise process, the striking difference observed between E₄(2H;H₂;μ-N₂) and E₄(2H;H₂) offers an explanation for the experimental report of an H₂ complex as an intermediate in re, with H₂ lost only upon N₂ binding. The computations also explain the implication drawn from HD formation during turnover under N₂ and D₂, that H₂ is released only concomitant with binding of N₂ (4, 8, 9).

The pictorial representation of all of the states discussed here is shown in SI Appendix, Fig. S6, and an animation provided as Movie S1 illustrates the proposed overall process of re of the hydrides to form H₂, followed by the described reaction with N₂ leading to release of the H₂. Although, as noted, the data reported in Fig. 3 are obtained at BP86 level, the B3LYP functional provides a consistent picture (SI Appendix, Fig. S7).

To understand the role of re, we further analyzed the bonding and the electron distribution in the various E₄ species. Previous analysis of the electronic properties of the E₂(2H) state (19), carried out within the natural bond orbital (NBO) framework (64, 65), indicated that the Fe–H can be described as polarized covalent bonds, with charge buildup on the H atom of about −0.2e, as expected from the difference in electronegativity of the atoms involved. The same is true for the E₄(4H) and E₄(4H)^(b) intermediates. Nonetheless, as shown in SI Appendix, Fig. S4, the two Fe–H bonds in E₄(4H) and E₄(4H)^(b), whether involving bridging or terminal hydrides, each can be viewed as two-electron covalent bonds that together store the four reducing equivalents. As also discussed in SI Appendix, Fig. S4, upon formation and release of H₂, two electrons are first stored in and then depart with the H₂ molecule. This process leaves two reducing equivalents (i.e., electrons) on the FeMo-co core, which is at the heart of the re mechanism (6, 7, 9): as the H₂ molecule forms, two reducing equivalents become available for binding and activating N₂, explaining why only E₄(2H; H₂) is able to bind N₂.

The NBO analysis indicates that in this double adduct, the two remaining reducing equivalents are distributed within the FeMo-co core, primarily on the Fe; the Mo valency does not change. The N₂ moiety receives a fraction of the reducing equivalents via π-acceptor (FeMo-co-to-N₂) interactions: N₂ assumes an overall net negative charge of −0.29 e, nearly equally distributed between the two N atoms. Extension of the NBO analysis to the end-on Fe₂–(N₂) moiety (62) of E₄(2H;N₂) reveals that the bond between Fe₂–(N₂) is characterized by negligible σ-donor interactions (N₂-to-FeMo-co) and large π-acceptor (FeMo-coto-N₂) interactions. Thus, according to the NBO formulation, the σ-charge transferred from N₂ to FeMo-co is about 0.01 e, while the charge backtransferred to N₂ because of π-acceptor effects is 0.29 e, which results in a large net fractional negative charge on N₂ (−0.41 e according to NBO atomic charge partitioning). The N–N bond distance in E₄(2H;N₂) is d(N–N) = 1.14 Å, only 0.04 Å longer than in the free molecule (SI Appendix, Fig. S6). This contrasts with the bond elongation observed in typical metal dinitrogen complexes, where N–N is considered “strongly” activated at d(N–N) > 1.20 Å (66). However, in contrast to the majority of the model dinitrogen complexes, protonation of the distal N atom in E₄(2H;N₂) is thermodynamically accessible, being endergonic by 24.2 kJ/mol, while no protonation of the proximal N atom was found. We do not discuss the protonation mechanism of N₂, which is the subject of an ongoing investigation. However, our analysis suggests that the first proton most likely is delivered by the protonated S_2B, which in turn is promptly reprotonated by α-195^His, the first of two instances in this investigation where this residue acts as a proton “buffer” (see below). We remark that histidine is often used to rapidly shuttle protons in enzymes, a prototypical example being carbonic anhydrase (67).

Upon N₂ protonation, the N–N distance increases to 1.27 Å and the N₂H moves from Fe₂ to a bridging position between Fe₂ and Fe₆ (SI Appendix, Fig. S6). The second protonation of N₂ is exergonic by ΔG = −12.4 kJ/mol, with the resulting transdiazene-bound intermediate E₄(η²-NHNH) + H₂ located at ΔG = +1.4 kJ/mol from E₄(4H) + N₂. The diazene moiety asymmetrically binds side-on between Fe₂ and Fe₆ with Fe₂–N₁, Fe₂–N₂, and Fe₆–N₂ distances of about 1.92, 1.88, and 1.96 Å. Remarkably, the N–N distance (1.39 Å) is considerably longer than the distance in the isolated transdiazene molecule (1.25 Å) calculated at the same level of theory.

On the basis of these purely thermodynamics considerations, the present calculations suggest that formation of the dihydrogen adduct E₄(2H;H₂), followed by N₂ binding and loss of H₂, leads to a diazene-level intermediate E₄(2N2H) with an overall equilibrium free energy consistent with the experimental free-energy change ΔG of approximately −8 kJ/mol (8). Thus, depending on which of the two E₄(2N2H) isomers is the equilibrium product of the re of H₂ and binding of N₂, the computations yield the following (Fig. 3):

$$E_4\left(4H\right)+N_2\rightleftarrows E_4\left(2\mathrm{N}2\mathrm{H}\right)+{\mathrm{H}}_2;\mathrm{\Delta }G=-4.5\hspace{0.17em}\mathrm{kJ}/\mathrm{mol}\hspace{0.17em}\mathrm{or}\hspace{0.17em}1.4\hspace{0.17em}\mathrm{kJ}/\mathrm{mol}.$$ [2]

The former ΔG value refers to the formation of E₄(N₂), the latter to the formation of E₄(NHNH) (ΔG = −17.7 or 19.9 kJ/mol at B3LYP level; SI Appendix, Fig. S7); the relative free energy of these two states is within the computational error. Regardless of this minor uncertainty, the present result is very important, as it clearly supports and illuminates the experimentally proposed re mechanism by indicating that the formation of the diazene-level E₄(2N2H) intermediates, in particular the diazene-bound intermediate E₄(NHNH), is indeed essentially thermoneutral as reported (8) and becomes thermodynamically accessible through the re/oa equilibrium process. This is a truly remarkable enzymatic achievement, as the noncatalytic direct hydrogenation of N₂ to form diazene is endergonic by more than 200 kJ/mol (68).

An explanation for the stability of the FeMo-co diazene-bound intermediate E₄(NHNH) is provided by the NBO analysis of this state (SI Appendix, Tables S14 and S15), which reveals that the diazene moiety interacts with FeMo-co via π(N=N) → d*(Fe₂) and d*(Fe₆) charge donation, and that these strong bonding interactions considerably stabilize this highly energetic species. Because of these strong interactions in the E₄(NHNH) intermediate with the Fe₂ and Fe₆ centers, the π character of the N–N bond of the diazene is lost and replaced with Fe–N bonds resulting from 3d(Fe) [with a smaller extent of s(Fe)] and p(N) mixing. This enables the stepwise protonation of the N₂ moiety to yield first E₄(H; N₂H) and then E₄(NHNH), during which the Fe₂–N and Fe₃–N interaction intensify and the Fe₂–S_2B bond breaks, with the sulfur picking up a proton from α-195^His. Upon removal of the N₂H or NHNH fragments, the cluster returns to the E₁(H) or E₀ state, respectively, the Fe₂–S_2B bond is restored, and the proton is returned to α-195^His. We hypothesize that the hemilability of the Fe–S bond is important for the overall catalytic efficiency: in addition to facilitating the re of H₂, it allows the formation of a Fe–N bond and therefore helps stabilize the otherwise highly unstable N₂H and NHNH intermediates. The NBO analysis of all of the E₄(2N2H) states, quantifying the conclusions drawn above, is summarized in SI Appendix, Tables S14 and S15.

Discussion and Conclusion

We have carried out an extensive BS DFT study of N₂ activation by nitrogenase. The analysis of structural models of the FeMo-co environment with a wide range of complexity reveals that the utilization of model (a), which incorporates the complete array of direct interactions of FeMo-co with its surrounding protein envelope, is required to give meaningful results, and to prevent disruption of FeMo-co that has accumulated 4[e⁻/H⁺], through the protonation of the central carbide. We find that this E₄ state exhibits a variety of low-lying isomers, with the lowest in energy being E₄(4H), which has two [Fe–H–Fe] bridging hydrides, as observed in low-temperature ENDOR measurements (4) of the single conformer captured when the enzyme is freeze-trapped under turnover conditions. Because of the single determinant nature of BS-DFT, these results provide only a qualitative idea of the energy landscape of the possible E₄ states. However, with this in mind, the results are suggestive that at ambient temperatures there may be a dynamic equilibrium among the four E₄ isomers, E₄(4H), E₄(4H)^(b), E₄(4H)^(c), and E₄(2H;H₂). We also found that the re of H₂ by E₄(4H) to form the H₂-bound complex E₄(2H;H₂) has a low barrier (ΔE^‡ ∼ 22 kJ/mol). Although this value represents a coarse approximation to true activation energy, it is consistent with the experimental evidence and suggests that, at room temperature, E₄(4H) and E₄(2H;H₂) should be in fast equilibrium (Fig. 3), illuminating the recent finding that an H₂ complex forms during re of the hydrides of E₄(4H). Notably, we found that the re/oa equilibrium of Eq. 2, in which the loss of H₂ is coupled to N₂ binding and the possible formation of a diazene-level intermediate E₄(2N2H), in particular to the diazene E₄(NHNH) intermediate itself, is nearly equi-ergic, in close agreement with the recent direct measurement of this equilibrium (8). In this process, E₄(4H) undergoes re of H₂ but retains the H₂ as the dihydrogen adduct E₄(2H;H₂), which can revert to E₄(4H) by oa of the H₂; only after binding N₂, forming E₄(2H;H₂;N₂), does the enzyme release H₂ and proceed on to hydrogenated forms of N₂. Indeed, any attempt to eliminate H₂ directly from E₄(2H;H₂) failed. Instead, we found a low barrier for the release of H₂ from E₄(2H;N₂; H₂) (ΔE^‡ ∼ 28 kJ/mol).

The thermodynamic analysis of N₂ bond cleavage shows that, although direct formation of E₄(NHNH) without generation of H₂ is thermodynamically unfavorable, nitrogenase couples this unfavorable reaction of N₂ with the highly favorable generation of H₂, resulting in an overall exergonic process to drive cleavage of the N≡N triple bond. However, thermodynamically, it is clearly far more favorable to simply generate two H₂ by hydride protonation, returning the enzyme to E₀, than to generate only one H₂ while carrying out the unfavorable N₂ reduction. The key to catalytic nitrogen fixation by nitrogenase thus is the mechanistic coupling of the endergonic formation of E₄(2N2H) to the exergonic release of one H₂. That coupling of the two processes is captured in Fig. 5. The E₄(4H) form(s) can undergo re of H₂ to form E₄(2H;H₂), thereby capturing the free energy of H₂ formation as reducing power of this state’s doubly reduced FeMo-co. However, experiment shows this high-energy E₄ state does not by itself release H₂; if it did, D₂ would react with the state produced, even in the absence of N₂, contrary to observation (16). As the present computations now show, it is the binding of N₂ to the reductively activated H₂ complex E₄(2H;H₂) state that mechanistically couples re of H₂ to N₂ reduction: N₂ binding induces the loss of H₂ and leads to N₂ reduction with formation of E₄(NHNH) (Figs. 3 and 5). Although the exergonic production of H₂ provides the thermodynamic driving force for the endergonic cleavage of the N≡N triple bond, it is the mechanistic coupling of N₂ binding with the release H₂ formed by re of the E₄(4H) bridging hydrides that is the true heart of the re mechanism of nitrogenase catalysis.

Supporting Information

Please see SI Appendix for a schematic representation of the structural models adopted in the present study; relative energy of possible spin configuration for the E₀ state; representation of relevant E_n states; relative energies of BS solutions and spin populations for E₀ and selected E₄ states as obtained at BP86 and B3LYP level of theory; statistical data on the deviations from the crystal structure of Fe–Fe, Fe–C, and Fe–S distances in the E₀ state calculated using different exchange and correlation functionals; structural data of the E_n states; benchmark of DFT exchange and correlation functionals; analysis of the protein environment and stability of FeMo-co; natural bond orbitals analysis of selected E₄ states; a discussion on the calculation of the energetics reported in Fig. 5; and Cartesian coordinates of the structures calculated in the present study. Please see Movie S1 for an animation showing the mechanism for H₂ re and N₂ binding as inferred from the present study.