Abstract
Advances in neurobiology suggest that neuronal response of the primary visual cortex to natural stimuli may be attributed to sparse approximation of images, encoding stimuli to activate specific neurons although the underlying mechanisms are still unclear. The responses of retinal ganglion cells (RGCs) to natural and random checkerboard stimuli were simulated using fast independent component analysis. The neuronal response to stimuli was measured using kurtosis and Treves–Rolls sparseness, and the kurtosis, lifetime and population sparseness were analyzed. RGCs exhibited significant lifetime sparseness in response to natural stimuli and random checkerboard stimuli. About 65 and 72% of RGCs do not fire all the time in response to natural and random checkerboard stimuli, respectively. Both kurtosis of single neurons and lifetime response of single neurons values were larger in the case of natural than in random checkerboard stimuli. The population of RGCs fire much less in response to random checkerboard stimuli than natural stimuli. However, kurtosis of population sparseness and population response of the entire neurons were larger with natural than random checkerboard stimuli. RGCs fire more sparsely in response to natural stimuli. Individual neurons fire at a low rate, while the occasional “burst” of neuronal population transmits information efficiently.
Keywords: Sparse coding, Independent component analysis, Kurtosis, Sparsity
Introduction
The sensory system is responsible for processing the sensory information. The commonly recognized sensory systems include visual, auditory, olfactory, taste and touch systems (Field 1994; Kandel and Schwartz 2013). Visual inputs play a critical role in primates’ response to the external environment, and in a normal individual, over 70% information is derived visually (Treichler 1967). Visual system is one of the most widely and intensely studied sensory systems, as well as the most complex sensory nervous system; however the underlying visual mechanism is yet to be elucidated (Jessell Thomas et al. 2000; Rieke et al. 1997; Yan et al. 2016; Barranca et al. 2014). The surrounding visual information is processed in the retina, lateral geniculate nucleus, visual cortex, and other regions of the central nervous system (Schiller 1986; Gross 1994; Qiu et al. 2016). A large number of biological experiments are focused on the lateral geniculate and visual cortex of the visual system. The anatomical structures and functional properties of the retina have been studied comprehensively. Stimulation can be defined and the corresponding neuronal responses recorded easily. Therefore, in recent years, investigations are increasingly focused on the study of the retina (Bartsch et al. 2008; Maturana et al. 2014). The retina is the most investigated area in the brain, retinal mechanisms and responses have been studied with a great accuracy (Khoshbin-e-Khoshnazar 2014; Maturana et al. 2016; Urakawa et al. 2017). There are many models of retina which are accessible in the literature. They include detailed biophysical mechanisms as well as computationally efficient and abstract models (Qureshi et al. 2014; Touryan et al. 2005). The most computationally effective model is a set of models each of which represent a single cell (Reich and Bedell 2000). The reduction of theory would be a good idea to study the distribution of retinal responses, their properties general across all cells and dependency between responses of different retinal cells. Such information may help us to omit obtaining redundant information of responses by means of numerical integration and thus improve simulation speed with minor assumptions induced. So studying general properties such as response sparseness is of a great importance (Bakouie et al. 2017; Gravier et al. 2016).
A majority of the visual neuroscientists used random stimuli with simple statistical properties and stimulation patterns (such as light spots or light bars) to study the characteristics and coding mechanism of the neurons (Atick 1992; Felsen et al. 2005). However, animals and humans live in the natural as well as a rather environment. The retina is located in a complex visual environment and is naturally optimized to process the natural stimuli (Kandel and Schwartz 2013; Jessell Thomas et al. 2000). Although natural scenes are viewed as simple superposition of different types of stimuli, neuronal responses are not simple. Therefore, we cannot determine the mechanism of neuronal processing and coding of complex natural visual stimuli accurately using simple stimuli. Thus, natural stimuli are vital for exploring the perception of the human brain (Felsen et al. 2005; Simoncelli and Olshausen 2001; Felsen and Dan 2005).
Since information processing and transfer in the brain are restricted by energy metabolism, the nervous system may use energy-efficient strategies to deal with information, especially visual information processing and coding (Barlow 1961; Mizraji and Lin 2017). Recent advances in neurobiology suggested that neuronal response of the primary visual cortex (V1) to natural stimuli might be attributed to a sparse approximation of images and encoding stimuli to activate the specific neurons (Olshausen and Field 1996; Simoncelli 2003; Olshausen and Field 1997). Sparse coding refers to the activation of a subset of neurons at a specific period in response to a stimulus. Consecutively, single neuronal activities are primarily maintained at a low level during stimulation (Olshausen and Field 2004; Zheng et al. 2016; Lewick 2002). Sparse coding is essential for the processing of visual information; it reduces the number of neurons involved, saves energy consumption, improves the efficacy of information transmission and enhances the ability of information processing (Hubel and Wiesel 1997; Peters et al. 2017). In recent years, visual information processing and coding have been comprehensively investigated and the results (Lewick 2002; Hubel and Wiesel 1997; Peters et al. 2017; Vinje and Gallant 2002) allow simulation of the visual system in silico. Combining the data and results obtained by neurophysiologists using signal processing and computing theory facilitates the simulation of visual system by computers in order to resolve the challenges encountered in image processing (Huberman et al. 2008; Pillow et al. 2008; Tozzi and Peters 2017).
So far, there are many studies on the RGCs. Kameneva et al. use the Hodgkin–Huxley model to simulate morphological and physiological characteristics of RGCs (Kameneva et al. 2016). Hadjinicolaou et al. established a linear and non-linear model that predicts the response of RGCs under multi-electrode array stimulation (Hadjinicolaou et al. 2016). Wohrer and Kornprobst proposed virtual retina software which can simulate large-scale simulation of up to 100,000 neurons with good physiological characteristics (Wohrer and Kornprobst 2009). These experiments show that we can simulate the relevant characteristics of RGCs very well through the computer.
Fast Independent Component Analysis (FASTICA) is a unique sparse coding algorithm invented by Hyvärinen and Hoyer (Hyvarinen 1999; Hoyer and Hyvarinen 2000; Hyvarinen et al. 2001). It is a fast iterative algorithm based on an orthogonal rotation of pre-whitened data, using a fixed-point iteration scheme that maximizes the non-Gaussianity of the rotated components. The convergence of FASTICA is rapid, and independent of the step-size. In authors’s previously published paper,standard sparse coding and sparse coding based on FASTICA have been simulated, and the time of training bases, the convergence speed of objective function and the sparsity of coefficient matrix were compared respectively. The results show that sparse coding based on FASTICA is more effective than standard sparse coding. In addition, many experiments have proved that FASTICA can simulate sparse coding very well (Wang and Wang 2017; Hyvärinen 1999).
Methods
The basic idea of FASTICA is to determine the matrix to maximize non-Gaussianity with projection steps ( projected onto ).
The FASTICA involves the following steps:
Whitening and centralizing the input data and we can obtain processed data .
Random initialization of Projection matrix .
, where (.) = (.), is an averaging operation.
Each iteration of the process is
Normalization:
Repetition of step 3 until convergence is obtained.
After the above steps we can get the projection matrix, the initial characteristic matrix can be obtained by the following formula:
| 1 |
Then the resulting initial feature matrix is brought into the following process:
-
7.
Initialize the coefficient matrix .
-
8.
According to given , solve to minimize .
-
9.
According to the given , solution to minimize .
-
10.
Record the value of the coefficient corresponding to each pixel in the 1000 small image blocks, stop the iteration after 100 iterations, otherwise repeat step 8.
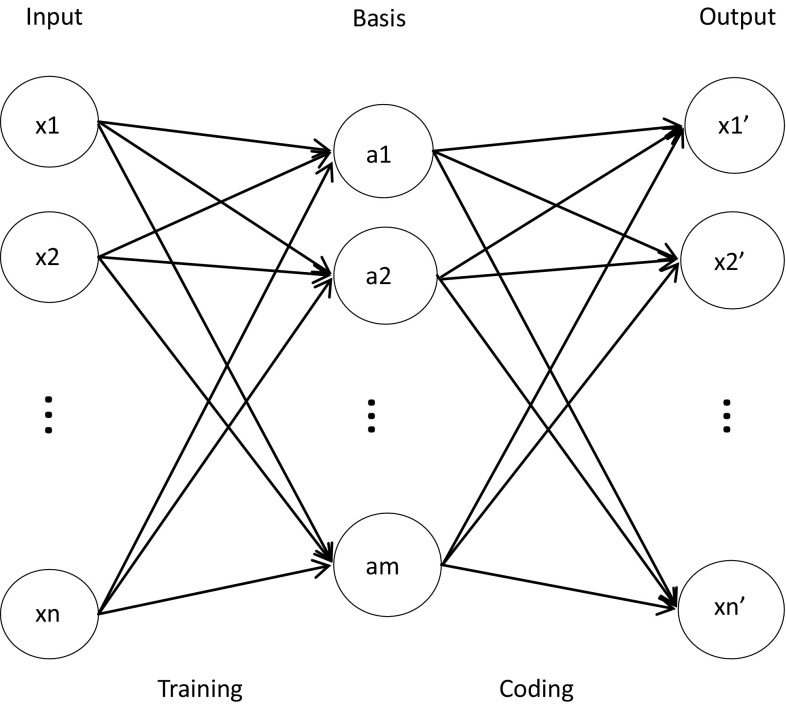
Here we did not use gaussian function because tanh function has better versatility (Hyvarinen et al. 2001; Hyvarinen and Hoyer 2002).We established a sparse coding model in order to describe the FASTICA algorithms effectively (Fig. 1).
Fig. 1.
Sparse coding model. The model consists of three layers: input, basic function and output. Data is fed into the input layer and trained by FASTICA to obtain basic functions, which are converted to output data through coding process
In the experiments, training samples consist of a sample of 10 image patches of 512 × 512 pixels sampled from natural images. We selected 10,000 mini-patches of 10 × 10 pixels from 10 images (each image 1000) randomly. Taking into account the computational speed and time cost, we randomly selected 1000 small blocks from the above 10,000 small blocks for experiments. The extracted small image blocks are taken as input data and processed through a sparse coding model based on FASTICA. The number of fixed iterations is 100, and finally the feature matrix and its corresponding coefficient matrix are obtained. It should be noted that the purpose of this paper is to simulate the temporal and spatial responses of ganglion cells under different stimuli through sparse coding based on FASTICA. Therefore, we consider each pixel of 1000 mini-patches of images as a ganglion cell and ignore visual field of neurons, and the coefficient corresponding to each pixel is the distribution of ganglion cells. The total number of pixels and corresponding ganglion cells are 100,000. The iterations equivalent to the experiment time in a physiological experiment, each iteration corresponds to the activation of all 100,000 ganglion cells for image stimuli. Due to the “fire or not” of neuronal action potentials, we do not consider the size of the coefficient for each pixel, we just consider the value of the coefficient is nonzero or zero. (zero means a ganglion cell is not activated and no action potential is generated, nonzero means a ganglion cell is activated and generated an action potential). So in this paper we consider a non-zero value as 1 in order to simplify the calculation.
Two types of stimuli are discussed in this study: natural scenes and random checkerboard stimuli, compared with the natural stimuli. Natural stimuli comprise of the sample with 10-image patches measuring 512 × 512 pixels derived from natural images. Conversely, the random checkerboard stimuli consist of 64 × 64 patches measuring 8 × 8 pixels. The brightness of each patch generated by the random sequence is graded on a scale of 0–1, with 1 representing black and 0 denoting white. The RGC was simulated by training the FASTICA algorithm with either natural scenes or random checkerboards. Then using the outputs of the trained model to simulate the responses to either natural scenes or random checkerboards. The reason why we use random checkerboard stimuli is that the artificial stimuli used in physiological experiments are random checkerboard stimuli. Checkerboard image stimuli was used in physiological experiments to measure the receptive field of ganglion cells, and the ganglion cells were compared with the response of random checkerboard stimulation and natural image stimulation at the same time. Since we want to compare the simulated experimental data with the physiological experimental data, we also used checkerboard stimuli, not white noise stimuli.
Statistical analysis
The neuronal response to stimuli was measured using kurtosis (Willmore and Tolhurst 2001). Kurtosis is the fourth moment of distribution at the peak. The value of kurtosis is close to zero for a Gaussian distribution and a high positive value is related to heavy-tailed peak distribution, similar to that in sparse neuronal response.
| 2 |
Sparseness can be defined as lifetime and population sparseness. The fourth moment of the response distribution of a single neuron in response to stimuli was used for the quantification of the lifetime sparseness (). Exposure to stimuli evokes neuronal responses … … , and the lifetime sparseness, is obtained by the following equation:
| 3 |
where and represent the mean and standard deviation of the responses, respectively. A distribution manifests high positive kurtosis if it contains several small responses (as compared to the standard deviation ), and only a few large responses. A large value implies short neuronal firing, and most often the absence of firing
Similarly, the distribution of the firing rate of the neuronal population in response to stimuli can be used to quantify the population sparseness (), which is calculated as follows:
| 4 |
where denotes the number of neurons, is the firing rate of the entire population of neurons to a single stimulus, and represent the mean and standard deviation of the firing rates, respectively. The population sparseness is indicated by the distribution of responses of the entire coding population of N neurons to a single stimulus. A large value indicates limited neuronal firing, and a majority of the neurons do not fire in response to a single stimulus.
Treves et al. proposed an alternative to lifetime sparseness and population sparseness (Treves and Rolls 1991). Similar to kurtosis, the parameter measures the shape of response distribution. However, it is appropriate only for responses (such as those of real neurons), which range from 0 to + . The Treves–Rolls sparseness is obtained by the following equation:
| 5 |
The sparseness value is subtracted from 1 in order to obtain that increases with rising population sparseness:
| 6 |
The parameter is used to characterize the lifetime response of single neurons () and the population response of the entire neurons () in response to stimuli. If the measure was used to represent M different responses generated by a single neuron in response to different stimuli (Eq. 1), the proportion of strong responses is closely related to lifetime kurtosis of the specific neuron. The value of is between 0 and 1. A large suggests the more sparse the discharge activity of a single neuron under stimulation, the neuron does not issue action potentials for most of the time under stimulation. A large value suggests firing by a small number of neurons and most of the neurons do not respond to a single stimulus.
Student’s t test was employed for the comparison of the statistical results.
Results
Simulation of responses in single RGCs
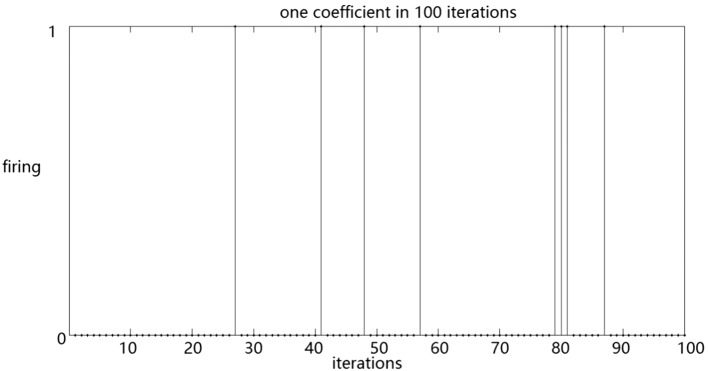
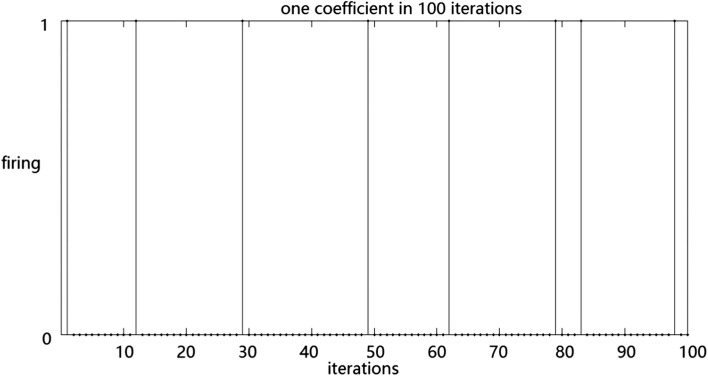
We simulated the responses of single RGCs to stimuli. Consequently, RGCs showing an enhanced response to natural stimuli and random checkerboard stimuli was selected. The kurtosis was calculated, and the values were 5.111 and 1.308, respectively. These results suggested that the RGCs exhibits a significant lifetime sparseness in response to natural and random checkerboard stimuli. The RGCs fires sparsely in response to natural stimuli. In addition, we calculated the Treves–Rolls sparseness of the RGCs, and the values were 0.587 and 0.418, respectively. The resulted also showed that the RGCs fires more sparsely in response to natural stimuli than random checkerboard stimuli. The responses of a ganglion cell to natural stimuli and random checkerboard stimuli are shown in Figs. 2 and 3.
Fig. 2.
The distribution of a ganglion cell under natural image stimulation
Fig. 3.
The distribution of a ganglion cell under random checkerboard stimulation
Horizontal axis represents the duration of the experiment and the vertical axis represents the response of the RGCs: 1 indicates neuronal firing, and 0 denotes the absence of response. Each vertical line indicates a single spike.
Simulating the population response of RGCs
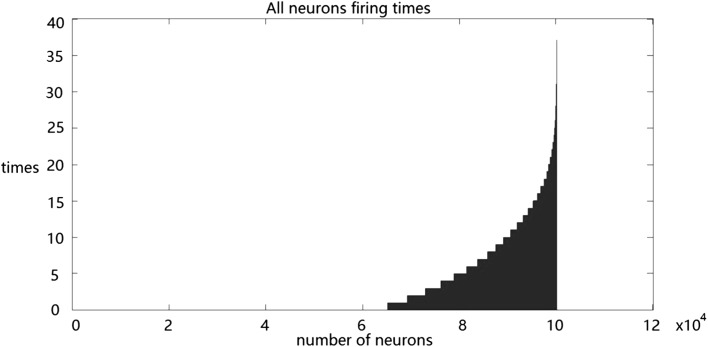
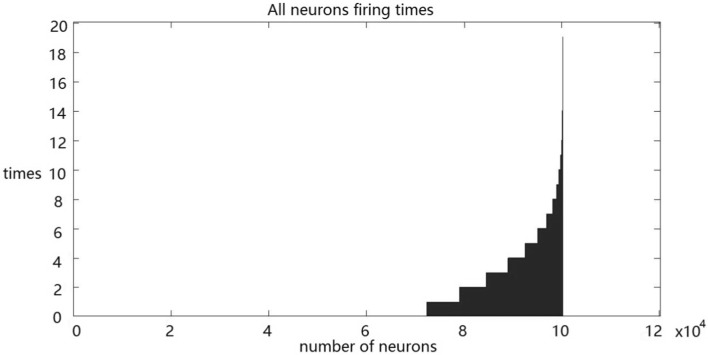
Next, we simulated the population response of RGCs to stimuli. The statistical results show that approximately 65% of the RGCs do not fire and nearly 6% fire more than 15 times constantly in response to natural stimuli (Fig. 4). About 72% of the RGCs do not fire, and all the RGCs fire less than 15 times in response to random checkerboard stimuli continually (Fig. 5).
Fig. 4.
Population response of RGCs to natural stimuli
Fig. 5.
Response of RGCs population to random checkerboard stimuli
The lifetime sparseness of single neurons is an interesting property, which is not identical to population sparseness. Population sparseness is an instantaneous response of the population, whereas lifetime sparseness is defined as the lifetime response of an individual cell. We compared the population response of RGCs to different stimuli quantitatively using population sparseness parameters and . Next, we simulated the response of RGCs population to natural stimuli and determined that the was 5.019. Interestingly, the RGCs fire substantially less in response to the random checkerboard stimuli than natural stimuli. However, the was 1.499 corresponds to random checkerboard stimuli suggesting that the “burst” of action potentials of single neurons primarily contribute to the sparse representation of the population of RGCs. Subsequently, the Treves–Rolls sparseness of population response to natural stimuli and random checkerboard stimuli was evaluated, and the values were found to be 0.578 and 0.319, respectively. The results also suggested that in response to natural stimuli, individual neurons fire at a low rate, while the occasional “burst” of neuronal population transmits information efficiently.
The statistical results of lifetime sparseness (, ) and population sparseness (, ) of the neuronal activities in response to natural and random checkerboard stimuli are shown in Table 1, together with the results recorded from the chicken RGCs (Zhang et al. 2010). We observe the simulation data are more consistent with the results of real biophysical experiments recorded in the chicken RGCs. Results of this paper do not correspond to experimental data presented in Table 1, because our experiment is a simulation experiment and quoted data is from a physiological experiment. It is normal that the data of two experiments are not completely consistent, but the result of the two is the same. For example, the data of natural stimuli is larger than random checkerboard stimuli in simulation experiment in Table 1, and the data of natural stimuli is also larger than random checkerboard stimuli in chicken retinal experiment. Although the values of the two experiments were different, they all showed that the response of ganglion cells under natural image stimulation were more sparse.
Table 1.
Results of simulation and chicken retinal experiments
| Simulation experiment | Population response of RGCs | ||||
|---|---|---|---|---|---|
| Natural stimuli | 5.111 | 0.587 | 5.019 | 0.578 | 65% show negative response |
| Random checkerboard stimuli | 1.308 | 0.418 | 1.499 | 0.319 | 72% show negative response |
| Chicken retinal experiment | Population response of RGCs | ||||
|---|---|---|---|---|---|
| Natural stimuli | 8.827 | 0.802 | 10.250 | 0.852 | 68% show negative response |
| Random checkerboard stimuli | 3.780 | 0.777 | 3.500 | 0.802 | 73% show negative response |
Results of the lifetime sparseness (,) and population sparseness (,) of the neuronal activities in response to natural and random checkerboard stimuli
It should be noted that since the method of modelling and experimental are different, the values of modelling and experimental results are also different. Although there are discrepancies in the values between modelling and experimental data, the results of modelling and experimental are consistently. In our simulation experiment the outputs of neurons were 0 or 1, a burst of neural activity means multiple 1 values in less continuous iterations. The exact statement here about a burst of neural activity is the high frequency firing of a single ganglion cell. Here we correspond 100 iterations in our simulation experiment to a period of time in a physiological experiment. More in detail, 100 iterations in our simulation correspond 192 s of stimulation in the reference (Zhang et al. 2010).
The differential response of RGCs in response to natural and random checkerboard stimuli is explained by Theunissen et al. (2001). The study recorded neural response in the V1 of awake macaques, using natural spatiotemporal statistics, and also in response to a dynamic grating sequence stimulus. In addition, the fitted nonlinear receptive field models were established using each of these data sets and their varying response to natural visual stimuli compared. Although reference (Theunissen et al. 2001) is about cortical neurons, we think this explanation can also be applied to the retinal, because we believe that the main reason is the difference between the natural image and the random check-board image, which may not be related to the structural difference of cortical neurons and retinal. On average, the model using the natural stimulus predicted the visual response more than two times as accurately as the model fit using artificial stimulus. During natural stimulation, the temporal responses often showed a stronger late inhibitory component, indicating the effect of nonlinear temporal summation during natural vision. The natural stimuli are also strongly related spatially and temporally in contrast to synthetic stimuli. RGC receptive fields reduce the relevance between natural stimuli spatially and temporally, thereby, decreasing the number of neurons involved. Sparse coding can make neurons fire less times or reduce the number of activated neurons to represent enough information, and the efficacy of information transmission was improved. More in detail, sparse coding can reduce the energy consumption of action potentials produced by neurons. Since the brain consumes a certain amount of energy per unit time, less activated neurons or action potentials means less energy to represent a particular stimulus. Therefore, retinal processing of natural stimuli improves the efficiency of information transmission.
Discussion
We simulated the responses of RGCs to natural and random checkerboard stimuli using FASTICA. Also, kurtosis, lifetime and population sparseness were investigated and analyzed. These results were in agreement with biophysical experiments involving chicken RGCs.
First, the RGCs exhibited the significant lifetime sparseness in response to natural stimuli and random checkerboard stimuli. About 65 and 72% of the RGCs do not fire continually in response to natural and random checkerboard stimuli, respectively. The results showed that RGCs might respond to stimuli by sparse coding.
Second, we calculated the kurtosis and the Treves–Rolls sparseness of the RGCs in response to natural and random checkerboard stimuli. Consequently, both and values were larger in the case of natural than random checkerboard stimuli. The results show that the RGCs fires sparsely in response to natural stimuli.
Third, the population of RGCs fires much less in response to random checkerboard stimuli than natural stimuli. However, and values were larger with natural than random checkerboard stimuli. The results suggested that in response to natural stimuli, individual neurons fire at a low rate, while the occasional “burst” of neuronal population transmits information efficiently.
Finally, about 6% of the RGCs fire more than 15 times in response to natural stimuli while all of the RGCs fire less than 15 times in response to random checkerboard stimuli continuously. This phenomenon indicated that RGCs coding stimulates the information depending on a small number of RGCs that fire at a high frequency.
The responses of RGCs to natural and random checkerboard stimuli were simulated using FASTICA. We investigated and analyzed kurtosis, lifetime and population sparseness. The results of these simulation experiments were consistent with those of the biophysical experiments involving chicken RGCs indicating their reliability. The natural stimulus inputs are derived from the training set of natural scenes in this paper. In making a case for the robustness of the study, since presumably mammals have a vast set of “training inputs”, sparse coding was facilitated even for inputs beyond previously observed scenes. Although checkerboard image stimuli was used in physiological experiments to measure the receptive field of ganglion cells, we did not consider receptive fields for simplicity.
The results suggested that RGCs may represent stimuli by sparse coding. Sparse coding facilitates the retinal processing of natural visual information efficiently and improves the efficacy of information transmission. It also ensures optimal balance between metabolic energy consumption and efficiency of information transmission and was found to be conceptually similar to energy coding; thus, it uses minimal energy (Wang and Zhu 2016; Wang et al. 2017; Hasenstaub et al. 2010). The fewer the number of active neurons in a neural network, the less energy the network cost. Studies have shown that sparse neural coding patterns reflect the maximization of energy efficiency, that is, consume little energy to encode information (Levy and Baxter 1999; Laughlin 2001). Our study is mainly a simulation experiment without physiological studies, because biophysical mechanisms are too complicated and many mechanisms are not yet clear (Protopapa et al. 2016; Momtaz and Daliri 2016). We are simply trying to simulate and perform a simple analysis on a simplified ganglion cell activity using an artificial neural network, so biophysical mechanisms were not investigated in the study.
Since presumably mammals have a vast set of “training inputs”, sparse coding is facilitated even for inputs beyond previously observed scenes. Nevertheless, some complex mechanisms in the simulation experiments was not investigated. However, the results of simulation suggested the feasibility of in silico modeling of the visual system. Although the current simulation experiments illustrated the proof of concept, additional studies are essential to validate these findings.
Acknowledgements
This study was funded by the National Natural Science Foundation of China (Nos. 11232005, 11472104).
Appendix
Sparse coding
Sparse coding includes a class of unsupervised methods for learning sets of complete bases for efficient data representation. The aim of sparse coding is to develop a set of basic vectors that represent an input vector as a linear combination of the basic vectors:
| 7 |
where represents input data, is base matrix, is column i in , which represents the basic functions. denotes coefficient matrix. With a complete basis, is no longer uniquely determined by the input vector . Therefore, we introduced the additional criterion of sparsity in sparse coding. We define sparsity in terms of few non-zero components or few components not close to zero. The choice of sparsity as a desired characteristic in our representation of the input data is motivated by the observation that most sensory data such as natural images may be described as the superposition of a small number of atomic elements such as surfaces or edges. Other justifications such as comparisons of the properties of the primary visual cortex have also been advanced.
We define the sparse coding cost function using a set of n input vectors as follows:
| 8 |
where represents basic function, is coefficient, is input data, is a constant, denotes a sparsity cost function, which penalizes for being far from zero. Usually a common choice for the sparsity cost is the L1 penalty , but it is non-differentiable when basic function equals 0, therefore, we selected sparsity cost , wherein is a constant.
We interpret the first term of the sparse coding objective as a reconstruction term, which uses the algorithm to provide a good representation of x and the second term as a sparsity penalty, which is a sparce representation of . The constant is a scaling constant determining the relative importance of these two contributions.
In addition, it is possible to make the sparsity penalty arbitrarily small by scaling down and scaling up using a large constant. To prevent this event, we constrain to be less than the constant C.
The full sparse coding cost function including our constraint is as follows:
| 9 |
However, the constraint of cannot be enforced using simple gradient-based methods. This constraint is weakened to a “weight decay” term designed to keep the entries of small. Therefore, we added the constraints to the objective function to provide a new objective function:
| 10 |
where is input data, is base matrix, is coefficient matrix, and are constants.
The objective function is non-convex, and hence impossible to optimize well using gradient-based methods. However, given , the problem of finding that minimizes is convex. Similarly, given , the problem of finding that minimizes is also convex suggesting an alternative to optimize for a fixed , and then optimizing with a fixed .
The analytic solution of is obtained as follows:
| 11 |
The analytic solution of is provided by:
| 12 |
Therefore, the learning equation of basic function is represented by:
| 13 |
The learning equation of coefficient is as follows:
| 14 |
Using the simple iterative algorithm on a large dataset (including 10,000 patches) results in prolonged iterations and convergence of the algorithm. To increase the rate of convergence by accelerating the iteration, the algorithm may be run on mini-patch selecting a mini-patch random subset of 1000 patches from the 10,000 patches.
A faster and better convergence may be obtained via initialization of the feature matrix before using gradient descent (or other methods) to optimize the objective function for given . In practice, initializing randomly at each iteration results in poor convergence unless a good optimum is found for before optimizing for . A better way to initialize involves the following steps:
Random initialization of
- Repetition until convergence
- Selection of a mini-patch random subset.
- Initialization of with , dividing the feature by the the corresponding basic vector in .
- Finding that minimizes for the in the previous step.
- Determination of that minimizes for the found in the previous step. Using this method, good local optima can be reached relatively quickly.
We obtained the base matrix trained by FASTICA. Using the FASTICA method, we derived the coefficient matrix and the objective function values through traditional sparse coding. We selected a convex function for the sparsity cost in objective function, where = 0.01 and = 0.3. Since the base matrix in objective function was obtained and normalized by FASTICA, equals 1. does not affect the optimization of the objective function, and therefore, = 0.
References
- Atick JJ. Could information theory provide an ecological theory of sensory processing? Network. 1992;22(1–4):4–44. doi: 10.3109/0954898X.2011.638888. [DOI] [PubMed] [Google Scholar]
- Bakouie F, Pishnamazi M, Zeraati R, Gharibzadeh S. Scale-freeness of dominant and piecemeal perceptions during binocular rivalry. Cogn Neurodyn. 2017;11:319–326. doi: 10.1007/s11571-017-9434-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barlow HB. Possible principles underlying the transformation of sensory messages. Cambridge: MIT Press; 1961. pp. 217–234. [Google Scholar]
- Barranca VJ, Kovacic G, Zhou D, et al. Sparsity and compressed coding in sensory systems. PLoS Comput Biol. 2014;10(8):e1003793. doi: 10.1371/journal.pcbi.1003793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartsch U, Oriyakhel W, Kenna PF, Linke S, Richard G, Petrowitz B, Humphries P, Farrar GJ, Ader M. Retinal cells integrate into the outer nuclear layer and differentiate into mature photoreceptors after subretinal transplantation into adult mice. Exp Eye Res. 2008;86(4):691–700. doi: 10.1016/j.exer.2008.01.018. [DOI] [PubMed] [Google Scholar]
- Felsen G, Dan Y. A natural approach to studying vision. Nat Neurosci. 2005;8(12):1643. doi: 10.1038/nn1608. [DOI] [PubMed] [Google Scholar]
- Felsen G, Touryan J, Han F, et al. Cortical sensitivity to visual features in natural scenes. PLoS Biol. 2005;3(10):e342. doi: 10.1371/journal.pbio.0030342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Field DJ. What is the goal of sensory coding? Neural Comput. 1994;6(4):559–601. doi: 10.1162/neco.1994.6.4.559. [DOI] [Google Scholar]
- Gravier A, Quek C, Duch W, Wahab A, Gravier-Rymaszewska J. Neural network modelling of the influence of channelopathies on reflex visual attention. Cogn Neurodyn. 2016;10:49–72. doi: 10.1007/s11571-015-9365-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gross CG. How inferior temporal cortex became a visual area. Cereb Cortex. 1994;4(5):455. doi: 10.1093/cercor/4.5.455. [DOI] [PubMed] [Google Scholar]
- Hadjinicolaou AE, Cloherty SL, Kameneva T, et al. Frequency responses of rat RGCs. PLoS ONE. 2016;11(6):e0157676. doi: 10.1371/journal.pone.0157676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasenstaub A, Otte S, Callaway E, et al. Metabolic cost as a unifying principle governing neuronal biophysics. Proc Natl Acad Sci USA. 2010;107(27):12329. doi: 10.1073/pnas.0914886107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoyer PO, Hyvarinen A. Independent component analysis applied to feature extraction from colour and stereo images. Netw Comput Neural Syst. 2000;11(3):191–210. doi: 10.1088/0954-898X_11_3_302. [DOI] [PubMed] [Google Scholar]
- Hubel DH, Wiesel TN. Functional architecture of macaque monkey visual cortex. Proc R Soc Lond B. 1997;198:1–59. doi: 10.1098/rspb.1977.0085. [DOI] [PubMed] [Google Scholar]
- Huberman AD, Feller MB, Chapman B. Mechanisms underlying development of visual maps and receptive fields. Annu Rev Neurosci. 2008;31:479–509. doi: 10.1146/annurev.neuro.31.060407.125533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hyvarinen A. Survey on independent component analysis. Neural Comput Surv. 1999;2(4):94–128. [Google Scholar]
- Hyvärinen A. Fast independent component analysis with noisy data using Gaussian moments. Proc Int Symp Circuits Syst. 1999;5:V57–V61. [Google Scholar]
- Hyvarinen A, Hoyer PO. A two-layer sparse coding model learn simple and complex cell receptive fields and topography from natural images. Vis Res. 2002;41(18):2413–2423. doi: 10.1016/S0042-6989(01)00114-6. [DOI] [PubMed] [Google Scholar]
- Hyvarinen A, Hoyer PO, Mika OI. Topographic independent component analysis. Neural Comput. 2001;13(7):1527–1558. doi: 10.1162/089976601750264992. [DOI] [PubMed] [Google Scholar]
- Jessell Thomas M, Kandel Eric R, Schwartz JH. Principles of neural science. 5. New York: McGraw-Hill; 2000. pp. 533–540. [Google Scholar]
- Kameneva T, Maturana MI, Hadjinicolaou AE, et al. RGCs: mechanisms underlying depolarization block and differential responses to high frequency electrical stimulation of ON and OFF cells. J Neural Eng. 2016;13(1):016017. doi: 10.1088/1741-2560/13/1/016017. [DOI] [PubMed] [Google Scholar]
- Kandel E, Schwartz J. Principles of neural science. 5. New York: McGraw-Hill; 2013. [Google Scholar]
- Khoshbin-e-Khoshnazar MR. Quantum superposition in the retina: evidences and proposals. NeuroQuantology. 2014;12(1):97–101. doi: 10.14704/nq.2014.12.1.685. [DOI] [Google Scholar]
- Laughlin SB. Energy as a constraint on the coding and processing of sensory information. Curr Opin Neurobiol. 2001;11(4):475–480. doi: 10.1016/S0959-4388(00)00237-3. [DOI] [PubMed] [Google Scholar]
- Levy WB, Baxter RA. Energy efficient neural codes Neural codes and distributed representations. Cambridge: MIT Press; 1999. pp. 531–543. [DOI] [PubMed] [Google Scholar]
- Lewick M. Efficient coding of natural sounds. Nat Neurosci. 2002;5:356–363. doi: 10.1038/nn831. [DOI] [PubMed] [Google Scholar]
- Maturana MI, Kameneva T, Burkitt AN, et al. The effect of morphology upon electrophysiological responses of RGCs: simulation results. J Comput Neurosci. 2014;36(2):157–175. doi: 10.1007/s10827-013-0463-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maturana MI, Apollo NV, Hadjinicolaou AE, et al. A simple and accurate model to predict responses to multi-electrode stimulation in the retina. PLoS Comput Biol. 2016;12(4):e1004849. doi: 10.1371/journal.pcbi.1004849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mizraji E, Lin J. The feeling of understanding: an exploration with neural models. Cogn Neurodyn. 2017;11:135–146. doi: 10.1007/s11571-016-9414-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Momtaz HZ, Daliri MR. Predicting the eye fixation locations in the gray scale images in the visual scenes with different semantic contents. Cogn Neurodyn. 2016;10:31–47. doi: 10.1007/s11571-015-9357-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olshausen BA, Field DJ. Emergence of simple cell receptive properties by learning a sparse code for natural images. Nature. 1996;381:607–609. doi: 10.1038/381607a0. [DOI] [PubMed] [Google Scholar]
- Olshausen BA, Field DJ. Sparse coding with an over complete basis set: a strategy employed by V1. Vision Res. 1997;37:3313–3325. doi: 10.1016/S0042-6989(97)00169-7. [DOI] [PubMed] [Google Scholar]
- Olshausen BA, Field DJ. Sparse coding of sensory inputs. Curr Opin Neurobiol. 2004;14:481–487. doi: 10.1016/j.conb.2004.07.007. [DOI] [PubMed] [Google Scholar]
- Peters JF, Tozzi A, Ramanna S, et al. The human brain from above: an increase in complexity from environmental stimuli to abstractions. Cogn Neurodyn. 2017;11(1):1–4. doi: 10.1007/s11571-016-9419-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pillow JW, Shlens J, Paninski L, Sher A, Litke AM. Spatio-temporal correlations and visual signaling in a complete neuronal population. Nature. 2008;454:995–999. doi: 10.1038/nature07140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Protopapa F, Siettos CI, Myatchin I, Lagae L. Children with well controlled epilepsy possess different spatio-temporal patterns of causal network connectivity during a visual working memory task. Cognitive Neurodynamics. 2016;10:99–111. doi: 10.1007/s11571-015-9373-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qiu XW, Gong HQ, Zhang PM, et al. The oscillation-like activity in bullfrog ON-OFF retinal ganglion cell. Cogn Neurodyn. 2016;10(6):481. doi: 10.1007/s11571-016-9397-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qureshi TA, Hunter A, Al-Diri B. A Bayesian framework for the local configuration of retinal junctions. IEEE Comput Vis Pattern Recogn. 2014;167:3105–3110. [Google Scholar]
- Reich LN, Bedell HE. Relative legibility and confusions of letter acuity targets in the peripheral and central retina. Optom Vis Sci Off Publ Am Acad Optom. 2000;77(5):270–275. doi: 10.1097/00006324-200005000-00014. [DOI] [PubMed] [Google Scholar]
- Rieke F, Warland D, van Steveninck RR, et al. Spikes: exploring the neural code. Cambridge: MIT; 1997. [Google Scholar]
- Schiller PH. The central visual system. Vision Res. 1986;26(9):1351. doi: 10.1016/0042-6989(86)90162-8. [DOI] [PubMed] [Google Scholar]
- Simoncelli EP. Vision and the statistics of the visual environment. Curr Opin Neurobiol. 2003;1(13):144–149. doi: 10.1016/S0959-4388(03)00047-3. [DOI] [PubMed] [Google Scholar]
- Simoncelli EP, Olshausen BA. Natural image statistics and neural representation. Annu Rev Neurosci. 2001;24:1193–1216. doi: 10.1146/annurev.neuro.24.1.1193. [DOI] [PubMed] [Google Scholar]
- Theunissen FE, David SV, Singh NC, et al. Estimating spatio-temporal receptive fields of auditory and visual neurons from their responses to natural stimuli. Network. 2001;12(3):289. doi: 10.1080/net.12.3.289.316. [DOI] [PubMed] [Google Scholar]
- Touryan J, Felsen G, Dan Y. Spatial structure of complex cell receptive fields measured with natural images. Neuron. 2005;45(5):781. doi: 10.1016/j.neuron.2005.01.029. [DOI] [PubMed] [Google Scholar]
- Tozzi A, Peters JF. From abstract topology to real thermodynamic brain activity. Cogn Neurodyn. 2017;11(3):283. doi: 10.1007/s11571-017-9431-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Treichler DG. Are you missing the boat in training aids? Film Audio-Visual Commun. 1967;1:14–16. [Google Scholar]
- Treves A, Rolls ET. What determines the capacity of auto associative memories in the brain? Network. 1991;2:371–397. doi: 10.1088/0954-898X_2_4_004. [DOI] [Google Scholar]
- Urakawa T, Bunya M, Araki O. Involvement of the visual change detection process in facilitating perceptual alternation in the bistable image. Cogn Neurodyn. 2017;11(9):1–12. doi: 10.1007/s11571-017-9430-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vinje W, Gallant J. Natural stimulation of the non-classical receptive field increases information transmission efficiency in V1. J Neurosci. 2002;22:2904–2915. doi: 10.1523/JNEUROSCI.22-07-02904.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang G, Wang R. Sparse coding network model based on fast independent component analysis. Neural Comput Appl. 2017;13:1–7. [Google Scholar]
- Wang RB, Zhu YT. Can the activities of the large scale cortical network be expressed by neural energy? Cogn Neurodyn. 2016;10(1):1–5. doi: 10.1007/s11571-015-9354-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang YH, Wang RB, Zhu YT. Optimal path-finding through mental exploration based on neural energy field gradients. Cogn Neurodyn. 2017;11(1):99–111. doi: 10.1007/s11571-016-9412-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Willmore B, Tolhurst DJ. Characterizing the sparseness of neural codes. Network. 2001;12(3):255–270. doi: 10.1080/net.12.3.255.270. [DOI] [PubMed] [Google Scholar]
- Wohrer A, Kornprobst P. Virtual Retina: a biological retina model and simulator, with contrast gain control. J Comput Neurosci. 2009;26(2):219–249. doi: 10.1007/s10827-008-0108-4. [DOI] [PubMed] [Google Scholar]
- Yan RJ, Gong HQ, Zhang PM, He SG, Liang PJ. Temporal properties of dual-peak responses of mouse RGCs and effects of inhibitory pathways. Cogn Neurodyn. 2016;10(3):211–223. doi: 10.1007/s11571-015-9374-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang YY, Jin X, Gong HQ, Liang PJ. Temporal and spatial patterns of retinal ganglion cells in response to natural stimuli. Prog Biochem Biophys. 2010;37(4):389–396. doi: 10.3724/SP.J.1206.2009.00617. [DOI] [Google Scholar]
- Zheng HW, Wang RB, Qu JY. Effect of different glucose supply conditions on neuronal energy metabolism. Cogn Neurodyn. 2016;10(6):1–9. doi: 10.1007/s11571-016-9401-5. [DOI] [PMC free article] [PubMed] [Google Scholar]