Graph analysis of functional brain network topology using minimum spanning tree in driver drowsiness

Abstract

A large number of traffic accidents due to driver drowsiness have been under more attention of many countries. The organization of the functional brain network is associated with drowsiness, but little is known about the brain network topology that is modulated by drowsiness. To clarify this problem, in this study, we introduce a novel approach to detect driver drowsiness. Electroencephalogram (EEG) signals have been measured during a simulated driving task, in which participants are recruited to undergo both alert and drowsy states. The filtered EEG signals are then decomposed into multiple frequency bands by wavelet packet transform. Functional connectivity between all pairs of channels for multiple frequency bands is assessed using the phase lag index (PLI). Based on this, PLI-weighted networks are subsequently calculated, from which minimum spanning trees are constructed—a graph method that corrects for comparison bias. Statistical analyses are performed on graph-derived metrics as well as on the PLI connectivity values. The major finding is that significant differences in the delta frequency band for three graph metrics and in the theta frequency band for five graph metrics suggesting network integration and communication between network nodes are increased from alertness to drowsiness. Together, our findings also suggest a more line-like configuration in alert states and a more star-like topology in drowsy states. Collectively, our findings point to a more proficient configuration in drowsy state for lower frequency bands. Graph metrics relate to the intrinsic organization of functional brain networks, and these graph metrics may provide additional insights on driver drowsiness detection for reducing and preventing traffic accidents and further understanding the neural mechanisms of driver drowsiness.

Introduction

Drowsiness during driving is considered a major threat that endangers the life of drivers, Studies have repeatedly shown that traffic accidents due to drowsy driving has become a serious problem in the society (Chen et al. 2015; Filtness et al. 2017; He et al. 2017). In many countries, drowsy driving is identified as a contributing factor in a significant proportion of road transport accidents and the number of collisions and fatalities caused by this risky behavior has remained high over the past decades (Tefft 2012; Vanlaar et al. 2008). The National Highway Traffic Safety Administration estimated that driver drowsiness caused 100,000 accidents each year in the US (Rau 2005). Moreover, Smith et al. (2005) found that young adult drivers felt drowsy during driving accounted for 23% of the cases after a 4-week follow-up study. Usually, drowsiness is considered to be a state that varies between wakefulness and sleep, and fatigue is considered as a feeling of reduced alertness that is associated with drowsiness, which affects the ability to perform a driving task (Craig et al. 2006). Therefore, the detection of drowsiness while driving is important for avoiding accidents and hazards on the road (Smith et al. 2005).

Several countermeasures based on physiological variables like Electrooculogram (EOG), Electroencephalogram (EEG), Electromyogram (EMG) and Electrocardiogram (ECG) have been adopted in an attempt to monitor driver drowsiness (Fu and Wang 2014; Wang et al. 2014). Among the aforementioned physiological responses, EEG is considered a reliable indicator in estimating a driver’s status because of closely related to mental activity (Khasnobish et al. 2017; Zhang et al. 2017). Hence recent investigations are working more and more on detection of drowsiness based on EEG signal. Jap et al. (2009) assessed the four EEG activities as possible indicators for drowsiness detection during a monotonous driving session, and they found that a slight decrease in alpha band power and an obvious decrease in beta band power over time. A novel fuzzy mutual-information (MI)-based wavelet packet transform feature extraction method to classify the driver drowsy state was studied by Khushaba et al. (2011). Additionally, Kar et al. (2010) introduced a method based on Shannon’s entropy measures on the recorded EEG signals of drivers to quantify drowsiness during simulated driving and actual driving.

So far, previous investigations are mainly based on energy entropy or power, whose performances are susceptible to EEG amplitude because the research methods are related to amplitude. While phase lag index (PLI) estimates consistency of phase difference between two time series which is expected to be less sensitive to the influence of volume conduction and amplitude effects (Wu et al. 2013). Thus it has been widely used in neuroscience studies, such as abnormalities in developmental dyslexia (Gonzalez et al. 2016), Alzheimer’s disease (AD) (Yu et al. 2016), functional networks changed by Chinese Guqin music (Wu et al. 2013), etc. Hence, phase lag index (PLI) seems to be an effective approach for neuronal information communication between different brain regions (Gonzalez et al. 2016; Yu et al. 2016). Viewed from this perspective, it may reveal more information about drowsiness by studying the phase lag index between different brain regions.

The goal of the current study is to compare and examine functional network connectivity and organization between alert state and drowsy state during simulated driving using the electroencephalogram (EEG). Previous studies have investigated the functional connectivity between brain regions, and Xu et al. found that functional connectivity among brain regions are related to drowsiness caused by prolonged driving (Xu et al. 2017). Kong et al. utilized the phase synchronization to explore the differences between alert state and drowsy state (Kong et al. 2017). Although being widely used in some areas and having distinguished between alert and drowsy state of mind, most conventional brain network characteristics depend on the number of links in the network, and the estimated network topology is hence biased by the choice of the threshold, which limits a meaningful comparison of network topology between individuals or groups (Stam et al. 2014). It is noted that although Van et al. once suggested that normalizing the network parameters through comparison against network parameters for surrogate networks can avoid threshold problems (van Wijk et al. 2010); this approach still cannot eliminate the problem of bias.

Here, we adopt a novel method-minimum spanning tree (MST) to construct brain networks to explore the differences between alert state and drowsy state. The MST is a simplified representation of a stable network core of the original network with minimized connection cost, and it connects all the nodes in the original weighted network without forming circles or loops. In this way, due to the same number of nodes and links of MSTs, the network properties between groups are directly compared, which avoids the aforementioned methodological biases (Stam et al. 2014; van Wijk et al. 2010). Collectively, MST analysis is far superior to conventional network analysis as (1) it eliminates the problem of bias; (2) it provides a normalized comparison between conditions or groups; and (3) it integrates small-world property with scale-free property (hubs) (Tewarie et al. 2015).

The present study examines brain network connectivity patterns for frequency bands of interest, utilizing MST indices, in participants with the simulator driving while engage in crowded road driving and monotonous driving tasks. EEG data are also obtained from the 30 scalp electrodes for the whole brain. It is hypothesized that driver drowsiness would significantly modulate functional brain network reorganization in different frequency bands. Specifically, we seek to find sensitive and specific biomarkers of brain network topology properties such as MST degree, MST diameters, etc. Comparing to existing literatures, the highlights of this paper lie in the following two aspects. (1) We employ phase lag index (PLI) as a measure for phase synchronization to analyze the driver drowsiness rather than the EEG amplitude information. (2) Unlike conventional network topology that is biased by the choice of the threshold, we use minimum spanning tree (MST) analysis as a way to characterize and compare EEG network, avoiding the aforementioned methodological biases. Importantly, it provides a new and more accurate method to visualize EEG functional networks.

The paper is organized as follows. In “Methods” section, we briefly describe the experimental details and EEG data employed in this work. Results of the study are presented in “Results” section and discussed in “Discussion” section.

Methods

Participants

All of the experiments were carried out in accordance to and with the approval of the local ethical committee of the Northeastern University (NEU) Institutional Review Board. Subjects are recruited from the postgraduate students at the School of Mechanical Engineering and Automation, NEU. Fifteen male participants aged between 24 and 30 years agree to participate in the study. Their average age is 26.200 (SD = 1.935 years). According to their self-reports, none of the participants has any neurological or psychiatric disorder. All have normal or corrected to normal vision and normal hearing. All the participants own their driving licenses, driving at least once a week during the last 2 years (average of 5500 km per year). They are asked to sleep adequately (at least 8 h) before the experiment and are told not to drink coffee, alcohol or tea during the experiment. They receive 10-yuan for participation in the experiment and provide informed written consent prior to entering the experiment.

Task and procedure

Participants are instructed to drive the driving simulator in a quiet and isolated room. To adjust for individual differences in skill level, they are allowed to be familiarized with the simulator driving and practice driving. During the whole experiment, participants are instructed to avoid unnecessary movements to reduce artifacts in the physiological data recording (Fu et al. 2016). The outline of the experiment setup is shown in Fig. 1. The driving simulator equipment consists of a large screen showing other cars, the current speed, other road stimuli, etc. and a car frame with a steering wheel, horn, clutch, brake pedal, accelerator, manual shift, chair and turn signal (see Fig. 1). The equipment also provides engine noise as well as nearby traffic noise, which has the same performance as real vehicles. The distance from the participant to the screen was about 120 cm.

Fig. 1.

The outline of the experiment setup (a), electrode cap (b), and EEG raw data (c)

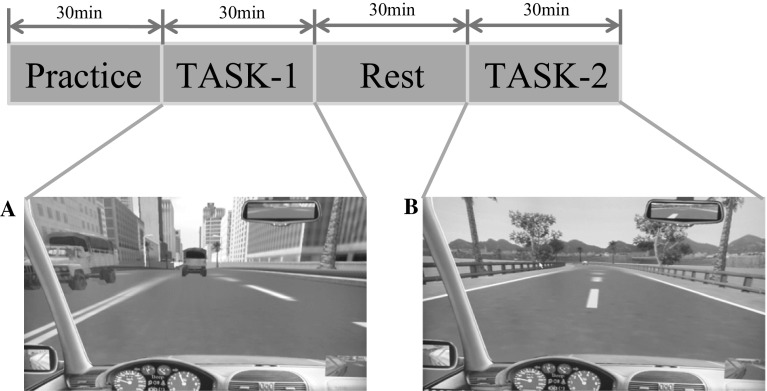
Each experiment contains two tasks; TASK-1 and TASK-2, respectively (see Fig. 2). In order to avoid the influence of circadian fluctuations, the experiments are scheduled at the same time each day, starting at about 17:00 and finishing at about 19:30. TASK-1 is the first condition in which each participant is asked to drive in a crowded bi directional and four-lane road in the city. All the participants are required to keep the motor vehicle on the track as accurately as possible to avoid other vehicles and obey traffic regulations to ensure that they are not penalized. In TASK-1, participants need to pay attention to other vehicles changing lane in crowded roads. Concerning the TASK-2, it is a monotonous driving stage, in which per participant has to drive at the speed of about 60 km/h on a two-lane road without any visual distraction. Compared to the crowded roads in the city, they are more likely to fall into drowsiness under the requirement of the speed limit and monotonous driving task. TASK-1 is separated from the TASK-2 by half an hour for the rest of the participants.

Fig. 2.

Experiment set-up with practice trials and two task blocks, TASK-1 (a) and TASK-2 (b). For details, see text please

During the whole experiment, the blink frequency based on EOG is recorded to validate the level of drowsiness. Also, other drowsy signs such as yawning and nodding are obtained manually by an observer to validate the drowsiness. After each driving task, participants’ state levels of subjective drowsiness are assessed immediately by Karolinska Sleepiness Scale (KSS) (1 = extremely alert, 9 = very sleepy) (He et al. 2017). The KSS is a well-validated measure of subjective state-related drowsiness.

Data recording

In the processing of the simulated driving experiment, the EEG signals for each participant in each task are extracted through the 30-channel brain computer interface (BCI) system. More specifically, the EEG signals are recorded from 30 scalp electrodes with an electrode cap, which are arranged according to the international 10–20 standard. Horizontal and vertical eye positions are recorded by electrooculography (EOG) using 4 electrodes positioned around eyes (Wang et al. 2016). Meanwhile, a mid-forehead electrode serves as ground and two additional electrodes are placed on the left and right mastoids. Electrode impedances are below 5 kΩ, and Neuroscan amplifiers are set for band pass at 0.01–70 Hz and data are sampled at a rate of 1000 Hz. Experiments with amplifier blocked are removed from the EEG data (Evans et al. 2011). Furthermore, prior to EEG quantitative analysis, eye movement correction protocols (Zhao et al. 2017) are applied to the entire set of recorded data to remove the DC shift and eye movement artifacts. Blink artifacts in the EEG recordings are removed by using a regression analysis in combination with artifact averaging implemented algorithm in Scan 4.3. Subsequently, the data in TASK-1 between 1th and 3th min and in TASK-2 between 28th and 30th min out of those of 30 min for each participant are selected for further preprocessing. For each task, the 2-min EEG signals from 30 channels are segmented into 3-s epochs (3000 sample points per epoch), resulting in 40 epochs for each participant.

Functional connectivity analysis

As a measure of functional connectivity between all 30 electrodes of EEG channels, the phase lag index (PLI) is adopted to calculate the asymmetry of the distribution of instantaneous phase differences between two EEG signals, making it less likely to be contaminated by an active reference electrode (Stam 2014). The instantaneous phase difference between two signals can be determined using the analytical signal based on the Hilbert transformation. Furthermore, the PLI is acquired from time series of phase differences $(\mathrm{\Delta }\phi \left(t_k\right)$, $k=1\cdots N)$, as follows

$$PLI=\left|〈\text{sign}\left[sin(\mathrm{\Delta }\phi (t_k))\right]〉\right|$$ 1

Here | | denotes the absolute value, and < > indicates the mean value. Moreover, sign is the signum function. The PLI ranges between 0 (no phase coupling, or coupling with a phase difference centered on $0\pm \pi$) and 1 (perfect phase coupling).

A square 30 × 30 PLI-weighted matrix is constructed by calculating the PLI value between all pairs of 30 EEG channels for each epoch in each frequency band, using common frequency bands by wavelet packet transform (WPT): delta-range (0–4 Hz), theta-range (4–8 Hz), alpha-range (8–12 Hz), and beta-range (12–32 Hz). Analyses of functional connectivity and subsequent brain network topology analysis are performed for these bands separately with MATLAB R2014a.

Minimum spanning tree analysis

The minimum spanning tree (MST) is an unconventional sub-graph as obtained from a weighted matrix which connects all nodes of the network but has no circle or loop. In this work, the MST is constructed based on the above-mentioned PLI adjacency matrix by applying effective greedy algorithm, that is, Kruskal’s algorithm. Briefly, this algorithm first orders the weights (defined as: 1/PLI) of all links in an ascending order. We start the construction of the MST with the link with the highest PLI value since we are interested in the strongest connections in the network, and then we add the following highest link PLI value until all 30 nodes are linked in a loop-less sub-graph consisting of 29 links. If adding a new link results in the creation of a cycle, this link should be ignored in the process.

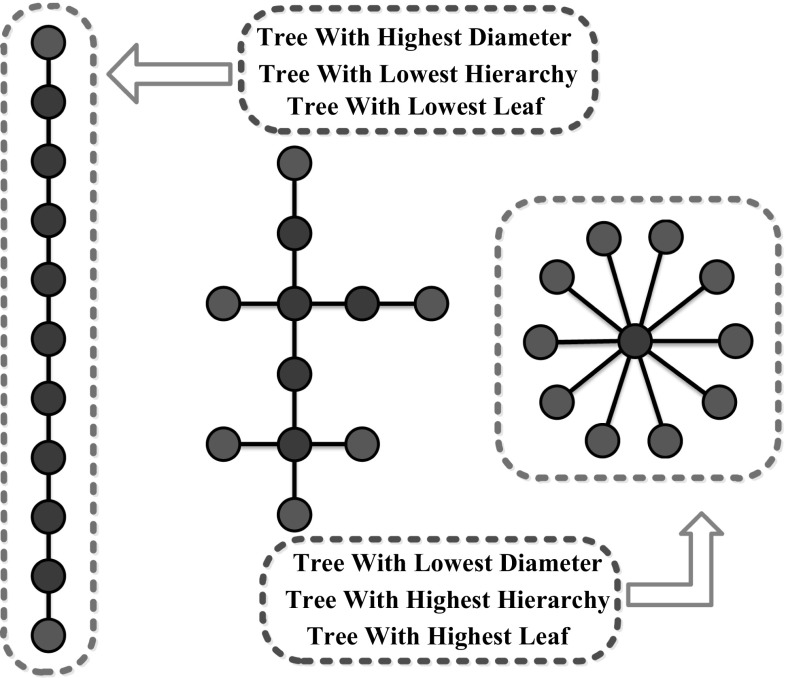
Compared to the conventional network metrics, the MST has the advantage that it abandons the need to choose an arbitrary threshold to reconstruct the graph. Moreover, the MST also has a much more uncomplicated structure since it concentrates on the most significant sub-graph and avoids bias. A brief description of all MST metrics used in this paper is listed in Table 1 [definitions are based on (Stam et al. 2014)]. And examples of tree topologies including the two extreme forms are illustrated in Fig. 3. In this work, the aforementioned metrics characterizing the MST of each epoch and condition are computed.

Table 1.

MST network metrics

Symbol	Concept	Explanation
N	Nodes	Number of nodes in the MST
M	Links	Number of links in the MST
D	Degree	Number of neighbors for a given node in the MST
L	Leaf fraction	Fraction of leaf nodes in the MST where a leaf node is defined as a node with degree one
d	Diameter	Longest shortest path in the MST
Ecc	Eccentricity	Longest distance between a reference node and any other node
BC	Betweenness centrality	Fraction of all shortest paths that pass through a particular node
k	Kappa	Measure of the broadness of the degree distribution
Th	Tree hierarchy	A hierarchical metric that quantifies the trade-off between large scale integration in the MST and the overload of central nodes
R	Degree correlation	Correlation between the degrees of a node and the degree of the neighboring vertices to which it is connected

Fig. 3.

Examples of tree topologies including the two extreme forms. They are all composed of 11 nodes and 10 edges. Leaf nodes are indicated in blue, and all other nodes are red. The MST on the left is known as a line-like tree with the lowest leaf number which is 2, a highest diameter which is 10 and low tree hierarchy. The MST on the right is known as a star-like tree with the highest leaf number which is 10, a lowest diameter which is 2 and high tree hierarchy. The MST in the middle is an intermediate configuration between these two extremes with the leaf number which is 6. (A color version of this Fig. can be viewed online.)

Statistical analysis

Topological network differences between two driving tasks (crowded road driving and monotonous driving) are compared by means of the t-test for the PLI values for each frequency band separately. Additionally, the t-test is also used to examine group (alertness and drowsiness) differences of the MST network metrics for each frequency band separately. Here, the p values below 0.05 are considered significant. Statistical analyses are performed using SPSS for windows. The methods and steps involved in this study are illustrated schematically in Fig. 4.

Fig. 4.

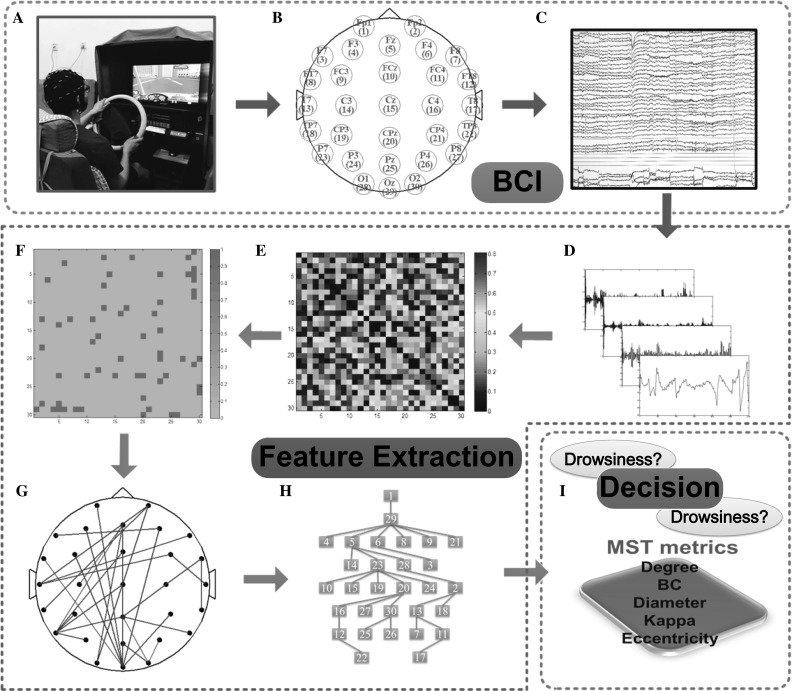
Schematic illustration of the procedure involved in this study. The simulated driving in the experiments is presented in (a). Then EEG signals are recorded from electrodes, which are arranged according to the international 10–20 standard, illustrated in (b), 30-channel EEG time series of 2 min of 1 subject are displayed in Scan 4.3 software, as shown in (c). Illustrated in (d), the wavelet package analysis is employed to the EEG signal to get common frequency bands. Weighted functional connectivity matrix constructed by the phase lag index for each frequency band, as shown in (e). Then the Kruskal’s algorithm is applied to obtain the minimum spanning tree (MST) matrix (f). Subsequently, the resulting loopless graph is displayed on a scalp projection (g). MST represented as a tree is shown in (h), which shows the hierarchical structure of the graph. Finally, MST metrics can be computed such as degree, betweenness centrality (BC), diameter, kappa and eccentricity (i). And finally, the state of the drivers will be judged based on the MST metrics

Results

Subjective and objective evaluation

The KSS is a well-validated measure of subjective state-related drowsiness. Participants are asked to evaluate how drowsy they currently feel on a 9-point ordinal scale. As shown in Table 2, the KSS score is generally increased from 2.667 ± 1.384 (M ± SD) in TASK-1 to 7.467 ± 0.694 in TASK-2. Also, KSS score varies significantly with driving tasks (p < 0.001). Moreover, drowsy signs such as yawning and nodding were observed frequently in all the participants during the driving TASK-2. Meanwhile, the blink frequency per minute obtained based on EOG are significantly increased from 12.800 ± 1.373 to 19.933 ± 2.120 (see Table 2). The subjective and objective indicators illustrated that experiment manipulation is successful to incur states of drowsiness.

Table 2.

KSS score and blink frequency across all the participants

Measures	TASK-1		TASK-2		p value
	M	SD	M	SD
KSS	2.667	1.384	7.467	0.694	< 0.001
Blink frequency (per minute)	12.800	1.373	19.933	2.120	< 0.001

M mean, SD standard deviation

Functional connectivity

The PLI values are calculated for each frequency band, and all results from the statistical analyses are presented in Table 3. Functional connectivity analysis yields significant between group effects in the delta frequency band. PLI, reflecting the relative phase distribution’s asymmetry, is significantly lower in alert state (M = 0.286, SD = 0.067) relative to drowsy state (M = 0.367, SD = 0.109) in the delta frequency band, p = 0.00002, which indicates a less asymmetry of the phase difference distribution in alert state compared to drowsy state. It is interesting that there are no significant differences in functional connectivity for all other frequency bands.

Table 3.

Analysis of variance for network metrics

Frequency band	Index	Alert state		Drowsy state		p value
		M	(SD)	M	(SD)
Delta	PLI	0.286	(0.067)	0.367	(0.109)	0.00002*
	Degree	0.277	(0.092)	0.325	(0.110)	0.022*
	Eccentricity	0.261	(0.052)	0.245	(0.054)	0.147
	BC	0.713	(0.085)	0.771	(0.095)	0.001*
	Kappa	3.406	(0.802)	3.772	(0.961)	0.041*
	R	− 0.401	(0.131)	− 0.409	(0.142)	0.774
	Diameter	0.330	(0.070)	0.313	(0.068)	0.213
	Leaf	0.606	(0.084)	0.629	(0.082)	0.175
	Th	0.427	(0.059)	0.412	(0.067)	0.233
Theta	PLI	0.215	(0.044)	0.227	(0.048)	0.221
	Degree	0.264	(0.071)	0.309	(0.106)	0.014*
	Eccentricity	0.263	(0.053)	0.236	(0.042)	0.006*
	BC	0.712	(0.071)	0.747	(0.089)	0.033*
	Kappa	3.276	(0.491)	3.65	(0.857)	0.009*
	R	− 0.421	(0.095)	− 0.401	(0.097)	0.318
	Diameter	0.332	(0.071)	0.296	(0.056)	0.007*
	Leaf	0.608	(0.075)	0.63	(0.067)	0.122
	Th	0.429	(0.055)	0.425	(0.051)	0.715
Alpha	PLI	0.213	(0.05)	0.201	(0.04)	0.158
	Degree	0.296	(0.098)	0.281	(0.098)	0.804
	Eccentricity	0.235	(0.048)	0.251	(0.062)	0.184
	BC	0.738	(0.09)	0.73	(0.083)	0.413
	Kappa	3.422	(0.788)	3.441	(0.873)	0.842
	R	− 0.354	(0.144)	− 0.387	(0.14)	0.682
	Diameter	0.296	(0.065)	0.317	(0.082)	0.195
	Leaf	0.62	(0.08)	0.611	(0.085)	0.533
	Th	0.432	(0.061)	0.421	(0.059)	0.999
Beta	PLI	0.138	(0.025)	0.135	(0.031)	0.62
	Degree	0.305	(0.114)	0.292	(0.106)	0.53
	Eccentricity	0.239	(0.044)	0.247	(0.052)	0.405
	BC	0.753	(0.078)	0.726	(0.082)	0.093
	Kappa	3.665	(0.958)	3.564	(0.935)	0.594
	R	− 0.401	(0.118)	− 0.403	(0.138)	0.943
	Diameter	0.303	(0.058)	0.312	(0.068)	0.477
	Leaf	0.63	(0.069)	0.624	(0.093)	0.708
	Th	0.421	(0.053)	0.432	(0.062)	0.348

PLI phase lag index, BC betweenness centrality, R degree correlation, Th tree hierarchy

Bold text represents significant results (p < 0.05)

Minimum spanning tree

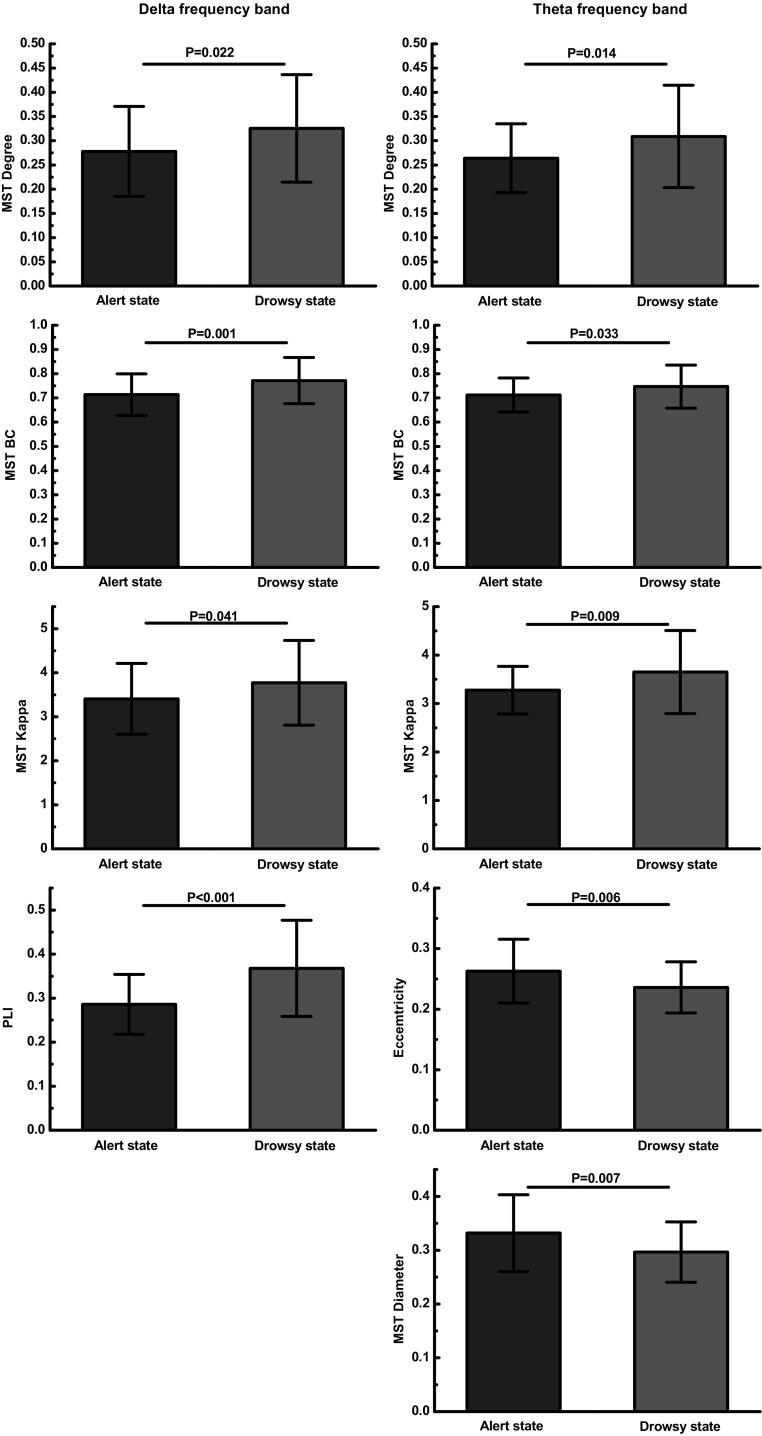
MST analysis yields significant between group effects in delta frequency band (see Table 3 and Fig. 5). Degree, representing the number of neighbors for a given node within the network, is significantly lower in alert state (M = 0.277, SD = 0.092) relative to drowsy state (M = 0.325, SD = 0.110), p = 0.022. The group effect on betweenness centrality (BC), reflecting the fraction of all shortest paths that pass through a particular node, is also significant, p = 0.001, indicating higher BC in drowsy state (M = 0.771, SD = 0.095) compared to alert state (M = 0.713, SD = 0.085). The group effect on kappa, relating to the broadness of the degree distribution, just reaches significance, p = 0.041, suggesting a trend for higher kappa in drowsy state (M = 3.772, SD = 0.961) relative to alert state (M = 3.406, SD = 0.802). The major finding is that significant differences in the delta frequency band for three graph metrics suggesting network integration and communication between network nodes are increased from alertness to drowsiness. Together, our findings also suggest a more line-like configuration in alert states and a more star-like topology in drowsy states.

Fig. 5.

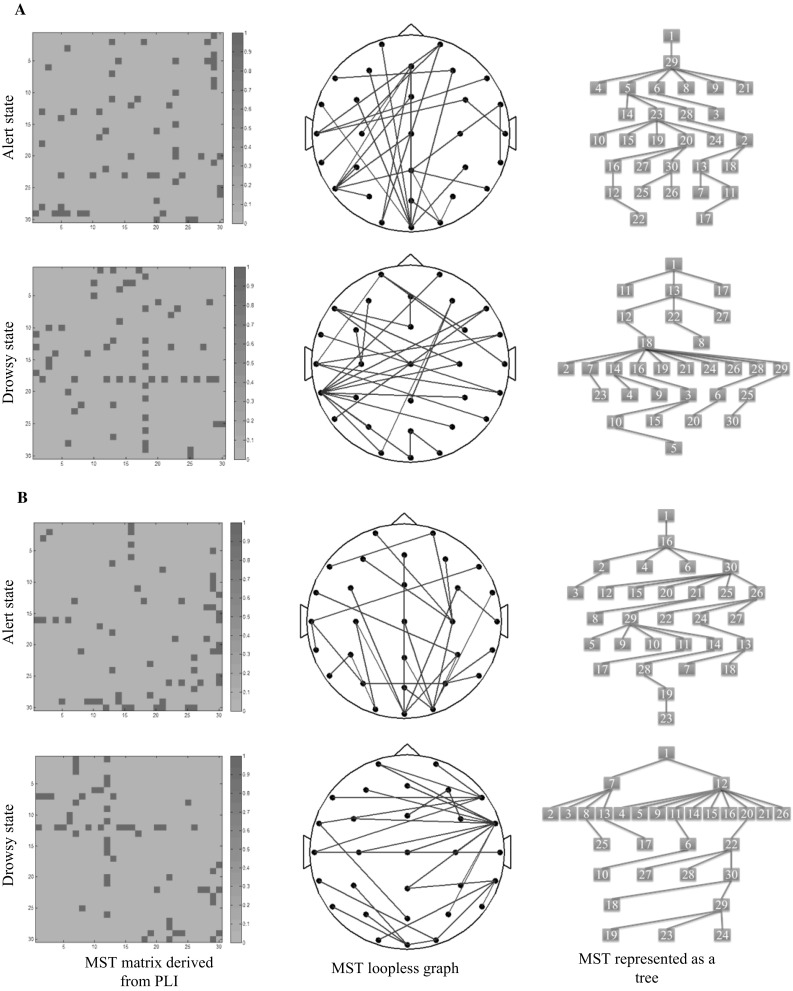
MST matrices derived from PLI matrices (left column), MST loopless graph, viewed from the top (middle column) and MST represented as a tree (right column) for alert and drowsy state for the delta frequency band (a) and theta frequency band (b), respectively. The MST matrices are 30 × 30 square matrices, where X axis and Y axis represent the corresponding EEG channels. A color scale, from blue (0) to pink (1) reflects the strength of the value respectively. Abbreviations: MST, minimum spanning tree; PLI, phase lag index. (A color version of this Fig. can be viewed online.)

For the theta frequency band, the group effects on degree, BC and kappa are significantly lower in alert state compared to drowsy state, p = 0.014, p = 0.033 and p = 0.009, respectively (see Table 3 and Fig. 3). The group effect on eccentricity, describing how efficient information is communicated from the least central node, is significantly higher in alert state (M = 0.263, SD = 0.053) relative to drowsy state (M = 0.236, SD = 0.042), p = 0.006. The group effect on diameter, representing the efficiency of communication between the nodes, is also significant, p = 0.007, indicating higher diameter in alert state (M = 0.332, SD = 0.071) relative to drowsy state (M = 0.296, SD = 0.056). These group differences are displayed in Fig. 6. In general, these results indicate a more integrated network organization in drowsy state compared to alert state in the theta frequency band. Group effects in all other measures and frequency bands are not significant.

Fig. 6.

Group differences for MST metrics. Left column represents MST metrics in delta frequency band and right column represents MST metrics in theta frequency band. Abbreviations: MST, minimum spanning tree; BC, betweenness centrality; PLI, phase lag index

Discussion

In this study, to analyze the topological characteristics of brain networks in alert state and drowsy state, we conduct simulated driving tasks and apply MST analysis derived from the PLI to EEG signal. The differences are most pronounced in the delta and theta frequency band, especially for delta frequency band, in which a significantly higher PLI is found for drowsy state compared to alert state. That is, the PLI analyses reveal differences in connectivity strength between the two states. This is consistent with the study that a higher level of connectivity strength in subjects who have poorer performance in attentional performance tasks is observed (Breckel et al. 2013). Researchers have reported that cognitive processing during the driving process is positively related to the coherence levels of the brain. More specifically, coherence levels are increased as the cognitive processing capacity becomes higher, but, on the other hand, the cognitive skills can be impaired by drowsiness induced by prolonged, monotonous driving (Lal et al. 2003). This can be explained from the perspective of the compensation mechanisms hypothesis. That is, when drowsiness is increased during driving, the synchronization of brain activity will also increase to prevent drowsiness aggravation.

Previous studies have employed EEG coherence to characterize the synchronization activities between different brain regions during monotonous driving (Lal and Craig 2002). Zhao et al. reported that that coherence levels are relatively increased at some brain regions after a monotonous driving session for the four frequency bands (Zhao et al. 2017). Whereas they described an increase in alpha and beta frequency band coherence, not found in our study. This discrepancy could be related to the method of measuring phase synchronization. The coherence may be affected by field spread, volume conduction, or alterations in power. Here, we calculate weighted connectivity matrices using the PLI, which is relatively unaffected by these factors (Porz et al. 2014; Stam et al. 2007).

The MST analyses yielded between groups differences in network organization as revealed in delta and theta frequency band (see Table 3, Figs. 5 and 6). More specifically, the differences are most pronounced in the delta band, in which MST leaf, degree, and kappa are increased and a significantly higher betweenness centrality (BC) is found for drowsy state compared to alert state. Since no other study has previously investigated the driver drowsiness using the minimum spanning tree (MST), whereas a relevant consideration when interpreting the current results is the relation between MST analysis and conventional network analysis. Tewarie et al. found that these two measures are strongly related to path length by performing an extensive and systematic series of simulation studies (Tewarie et al. 2015). MST leaf is negatively related to path length. Furthermore, when driver drowsiness was induced, a decrease in path length was observed (Kar and Routray 2013). The decrease in characteristic path length denotes better correlation between different areas of the brain, indicating lack of alertness. Accordingly, our findings are consistent with these recent studies. The MST analysis shows a higher leaf indicating more network integration for drowsy state compared to alert state. In addition, there are significant group differences for degree, betweenness centrality (BC) and kappa suggesting more communication between nodes of the network in drowsy state compared to alert state. More specifically, Nodes with a high degree may be considered ‘hubs,’ that is, crucial regions on the functional brain network (van Dellen et al. 2015); Nodes with a high BC are considered ‘hub nodes’ based on their importance for global communication in the network.

In terms of the extreme tree topologies, the network alterations in drowsy state suggest a more star-like MST network configuration (see Fig. 5), which indicates a more integrated network topology. These findings are in accordance with previous functional connectivity studies (Klimesch 1996; Kong et al. 2017) suggesting that subjects present more connections between functional units when they are in drowsy state, especially for delta frequency band. Additionally, it is generally accepted that delta waves are highly related with sleep and represent the unconscious (Klimesch 1999; Kong et al. 2017; Zhao et al. 2017). Therefore, delta frequency band takes an important role in classifying the drowsy state and alert state in our study.

It is interesting that we find not only significant differences for MST metrics in delta frequency band but also two other MST metrics in theta frequency band. That is, for theta frequency band, there is a significant group difference for MST diameter suggesting more communication between nodes of the network in drowsy state compared to alert state. Furthermore, the reduced MST eccentricity suggests that the least central nodes of the network become more important in drowsy state. Together, these results indicate, for theta frequency band, a more path-like configuration in alert state and a more star-like topology in drowsy state (see Fig. 5). Tewarie et al. observed that MST diameter is positively related to path length (Tewarie et al. 2015). Just as discussed previously, the driver drowsiness level is also positively related to path length (Kar and Routray 2013). Hence, it can be concluded that MST diameter is positively related to path length. This finding is consistent with a recent study that investigated the topology of structural networks in which a shorter path length is observed for drowsy state relative to alert state (Kar and Routray 2013).

It should be emphasized that the main group differences in network organization are found in delta and theta frequency band. Whereas Kong and colleagues did not find such significant phenomenon in theta frequency band (Kong et al. 2017). This could be related to computational differences between MST and conventional network. More specifically, the MST concentrates on the connectivity backbone of the network, thereby neglecting weaker and noisier connections (Stam et al. 2014; Tewarie et al. 2015). Additionally, the MST allows an unbiased comparison of networks with a different density and hence resulting in a more robust network characterization (Tewarie et al. 2015). This may allow the MST to better detect subtle network alterations that are present between drowsy state and alert state, but cannot be detected yet with the more conventional network.

Differences in functional network topology between drowsy state and alert state may reflect the ability of the brain to modulate either drowsiness or alertness. Distinguishing the conventional EEG power analysis (Kiroj and Aslanjan 2005) and conventional network analysis (Zhao et al. 2017), the novelty of the current study lies in the fact that the MST graph theory is employed to gain more understanding of the reorganization of brain networks with the variation of drowsiness. When drowsiness occurs, the brain regional synchronous activities are increased significantly in the delta and theta frequency band, which accordingly induces the changes in brain network configurations. The current results are consistent with previous studies on functional and scaling aspects of oscillatory activity. In terms of general properties of the brain as an oscillatory system, research suggests that lower frequencies recruit large networks whereas high oscillations are more confined to smaller networks (Buzsaki and Draguhn 2004). More specifically, it is proposed that synchronous activity of slow oscillations mediates long range integration between several cortical areas (von Stein and Sarnthein 2000).

This study demonstrates that how drowsiness modulates brain network configuration. We employ minimum spanning tree (MST) analysis as a way to investigate and compare the different brain network topologies between the drivers’ alert and drowsy states. Our results indicate that significant differences in the delta frequency band for three graph metrics and in the theta frequency band for five graph metrics suggesting network integration and communication between network nodes are increased from alertness to drowsiness. Together, our findings also suggest a more line-like configuration in alert states and a more star-like topology in drowsy states. These findings provide the first evidence that the functional brain network constructed by MST is linked with driver drowsiness, which plays a significant role in further understanding the neural mechanisms of driver drowsiness.