Abstract
Excessive synchronization of neurons in cerebral cortex is believed to play a crucial role in the emergence of neuropsychological disorders such as Parkinson’s disease, epilepsy and essential tremor. This study, by constructing a modular neuronal network with modified Oja’s learning rule, explores how to eliminate the pathological synchronized rhythm of interacted busting neurons numerically. When all neurons in the modular neuronal network are strongly synchronous within a specific range of coupling strength, the result reveals that synaptic plasticity with large learning rate can suppress bursting synchronization effectively. For the relative small learning rate not capable of suppressing synchronization, the technique of nonlinear delayed feedback control including differential feedback control and direct feedback control is further proposed to reduce the synchronized bursting state of coupled neurons. It is demonstrated that the two kinds of nonlinear feedback control can eliminate bursting synchronization significantly when the control parameters of feedback strength and feedback delay are appropriately tuned. For the former control technique, the control domain of effective synchronization suppression is similar to a semi-elliptical domain in the simulated parameter space of feedback strength and feedback delay, while for the latter one, the effective control domain is similar to a fan-shaped domain in the simulated parameter space.
Keywords: Bursting synchronization, Synaptic plasticity, Nonlinear delayed feedback control, Modular neuronal network
Introduction
Synchronization is a well-known phenomenon of collective dynamics between interacted elements (Pikovsky et al. 2002; Boccaletti et al. 2002; Zhou et al. 2016; Zhang et al. 2016; Zhao et al. 2018; Sun et al. 2018). In recent years, synchronization in the field of neuroscience has attracted a lot of attention (Rakkiyappan et al. 2016; Ngouonkadi et al. 2016; Yang and Wang 2016; Shi et al. 2017; Kim and Lim 2017a, b; Dharani et al. 2017). Theoretical study together with experimental evidence has demonstrated that synchronization of neuronal activity appears in different part of mammalian cerebral cortex (Engel et al. 1991; Singer 1993, Singer and Gray 1995), causing many normal brain function as well as pathological physiological mechanisms (Engel et al. 2001). On one hand, synchronization has been suggested to play an important role in the mechanisms of neuronal signaling and information processing within different brain areas (Singer 1993). On the other hand, synchronization is not always desirable for the fact that abnormally strong synchronization could be the cause of severely neurological diseases like epilepsy, Parkinson’s disease and other neuropsychological diseases (Bergman and Deuschl 2002; Nini et al. 1995). For instance, resting tremor in Parkinson’s disorder is caused by a pacemaker-like ensemble of neurons firing in a periodical and synchronized style (Alberts et al. 1969). Hence, suppressing such undesirable synchronized behavior of interacted neurons has become a challenging problem of neuroscience. In addition, biophysical energy has been constructed which can simulate the neural activities of neurons and large scale cortical networks (Wang and Zhu 2016; Wang et al. 2017).
Recently, some strategies have been proposed to eliminate this undesirable synchronized firing of neuronal system. Clinically, deep brain stimulation (DBS) at high frequencies has been an accepted practice to the standard treatment of movement disorders like Parkinson’s disease (Benabid et al. 1991). Since the understanding of systems effects and cellular mechanisms is deficient, this type of therapy is still controversial. Moreover, its treatment effect may decrease over time and it may cause side effects (Baizabal-Carvallo et al. 2014; Rodriguez-Oroz et al. 2005; Volkmann et al. 2009). Thus, mild stimulation techniques are desired to suppress synchronized dynamics of coupled neurons. Rosenblum and Pikovsky (2004) have proposed linear delayed feedback to control synchrony in ensembles of coupled oscillators, and bounded regions of de-synchronization have been detected in the parameter plane of feedback amplification and feedback delay. Yang et al. (2016) have studied the impact of linear differential feedback control on bursting synchronization in a modular neuronal network, and found that small feedback delay in the coupling can enhance differential feedback control to suppress bursting synchronization. However, the applicability of the linear feedback method to DBS is limited for the risk of unintentional boosting of synchronization (Popovych et al. 2005). Nonlinear delayed feedback control including differential feedback control and direct feedback control is also a significant clinical need for mild stimulation techniques that eliminate pathological synchronization. Popovych et al. (2005, 2006) Popovych and Tass (2010) have proved that nonlinear delayed feedback control can effectively eliminate the abnormal synchronization in neuronal system. Yu (2010) has found that nonlinear delayed feedback control can achieve a complete de-synchronization in a global-coupled neuronal network, which is effective even in the case of strong coupling and is robust against parameter variations. Wen et al. (2011) have also reported that nonlinear delayed feedback signals can make de-synchronization effectively in a small-world network composed of map-based neurons.
Note that synaptic plasticity is a biological process of neuronal system that adjusts the strength of connection between neurons (Donald 1949; Martin et al. 2000a, b; Munakata and Pfaffly 2004; Delgado-García et al. 2016; Wei et al. 2017). It is shown that for discrete neural circuits including the hippocampus and amygdala synaptic plasticity is a popular feature, which regulates synaptic efficacy as various time scales from milliseconds to minutes (Sigurdsson et al. 2007; Martin et al. 2000a, b). However, for most exiting works, the weights of synapses among neurons are always kept constant to simplify the neuronal network model. As a matter of fact, in the growth of neurons together with the learning and memorizing processes, the weights of synapses among connected neurons keep updated rather than hold constant (Oja 1982, 2008; Pérez and Uchida 2011; Robert et al. 2010). Now, some simplified learning rules regulating synaptic weights, such as Hebbian learning rule, Oja’s rule or modified Oja’s rule, STDP (SpikeTiming-Dependent Plasticity) rule (Kim and Lim 2017a, b), have been proposed. The Oja’s learning rule as a modified Hebb learning rule can make the updated weights have good convergence. Recent scientific research has devoted to studying synaptic plasticity with the Oja’s learning rule not only in artificial neural networks but also in biological neural network (Munakata and Pfaffly 2004; Jankovic et al. 2008; Han et al. 2011). For example, Han et al. (2011) have discussed the effects of synapse learning coefficient on synchronization in small-world neuronal network where the synapse plasticity is regulated by Oja’s learning rule. Morevover, synaptic plasticity can be used as a mild and effective way to destroy the pathological synchronization process (Hauptmann and Tass 2009; Pfister and Tass 2010; Yang et al. 2017). Hauptmann and Tass (2009) have reported that neuronal network may switch from a stable pathologically synchronized state to a stable desynchronized state by decreasing the mean synaptic weights. Pfister and Tass (2010) have derived the analytical conditions for spike-timing dependent plasticity to lead a network into a desynchronized state in recurrent networks. Yang et al. (2017) have numerically investigated that how the synaptic plasticity influences the collective bursting dynamics in a modular neuronal network, and found that bursting synchronization between interacted neurons is a little suppressed by the increase in synaptic learning rate.
Motivated by the above findings, firstly this present study constructs a model of neuronal network with synaptic plasticity, in which synaptic plasticity is regulated by modified Oja’s learning rule and the neuronal network is of modular structure. A modular neuronal network(i.e., a network with several sub-networks) may be a good candidate computational model for simulating brain network for recent neuroanatomic studies in macaque monkeys and cats suggesting that connectional features between regions of cerebral cortex are arranged into modular structure (Zamora-Lopez et al. 2009; Hilgetag et al. 2000). The brain’s firing activity can show the forms at different time scales (Yeates et al. 2017), such as spiking and bursting. Then, the significant influences of synaptic plasticity and nonlinear delayed feedback control on suppressing bursting synchronization in this modular network are explored by numerical simulations. In detail, we investigate how synaptic plasticity eliminates strong bursting synchronization when the considered modular network is free of control, and then analyze how the nonlinear delayed feedback control affects bursting synchronization when synaptic plasticity is not competent to suppress synchronization.
Mathematical model
To begin with, a modular network is introduced in this section. Firstly, it is assumed that there consist of sub-networks, and each of which is small-world network obeying the random bordering procedure proposed by Newman and Watts (1999). Then, starting from a regular ring-like network of nodes where each node is connected to its nearest neighbors, add shortcuts between non-nearest nodes with intra-cluster probability . After generating all the sub-networks, nodes in different sub-networks are randomly connected with inter-cluster probability . By doing this, a framework of modular network is constructed. The parameters of network configuration are fixed at , in this study, in which and denote intra-cluster probability for the two sub-networks, respectively.
The Courbage–Nekorkin–Vdovin (CNV) model, as a new map-based model of neural activity, was proposed by Courbage et al. (2007, 2012), and its governing equation is as follows
| 1 |
in which specifies the dynamics of the membrane potential and is the corresponding recovery variable. As indicated in the references (Courbage and Nekorkin 2010, Maslennikov and Nekorkin 2014), is Heaviside step function, and , is given by inverse N-shaped function. The parameter defines the time scale of recovery variable. is constant external stimulus associated with the excitability properties of neuron. The parameters and control the threshold properties of neuron. It has been shown that the CNV model can exhibit rich neural activity such as chaotic spiking, subthreshold oscillations and tonic spiking.
On the basis of the CNV model, this study builds a mathematical model of modular neuronal network with synaptic plasticity, as shown in the following:
| 2 |
in which (, ) represents the membrane potential of neuron in sub-network and is the corresponding recovery variable. In order to make the isolated CNV neuron produce spiking bursting activity, the parameters are taken as respectively. is the global coupling strength. The synaptic threshold and synaptic reversible potential are selected as and , respectively. is a connectivity matrix. In detail, if neuron in sub-network is connected with neuron in sub-network, otherwise and . Here a modified Oja’s learning rule is employed to describe changes of synaptic weights between neurons. denotes the change in synaptic weights from neuron in sub-network to neuron in sub-network at time . represents the learning rate, which reflects how quickly the synaptic weights update in response to neuron activation. denotes the updated synaptic weights form neuron in sub-network to neuron in sub-network at time . Specifically, if there is a connection between neuron in sub-network and neuron in sub-network.
Based on the mean field and , a complex mean-field of this network is obtained, where is the imaginary unit: . can be regarded as the mean value of state variable of all neurons, reflecting the main macroscopic features of the collective amplitude and phase dynamics of this modular neuronal network. The control term is the real part of nonlinear delayed feedback control signal , i.e., . This technique of nonlinear delayed feedback control, proposed by Popovych et al. (2005, 2006), includes two procedures, i.e., nonlinear differential feedback control
| 3 |
and nonlinear direct feedback control
| 4 |
where is feedback strength and is feedback delay, is the conjugate of complex mean-field with time delay .
Simulation results
In this manuscript, numerical simulation of the considered modular neuronal network is carried out by the explicit Euler technique. Initial states of membrane potential and recovery variable are set to be arbitrary number of interval [0, 1], and initial synaptic weights are set to be 1. To guarantee statistical accuracy, all the numerical results, except for spatiotemporal patterns of the modular network, are obtained by averaging over 10 different realizations.
First we discuss how the coupling strength influences bursting synchronization of interacting neurons when the considered modular network is free of synaptic plasticity and nonlinear delayed feedback control. Then how synaptic plasticity eliminates strong bursting synchronization is investigated when the considered modular network is free of control. Finally, the effect of nonlinear delayed feedback control on bursting synchronization is discussed when the considered modular network is of synaptic plasticity with relative small learning rate.
To describe the neuronal dynamics vividly, the order parameter is employed to quantify bursting synchronization of the modular network, which is introduced as follows:
| 5 |
where indicates the burst phase for neuron in the sub-network at time . The burst phase is defined as
| 6 |
in which denotes the moment of the burst of the neuron in the sub-network. Larger indicates a higher degree of bursting synchronization of the modular neuronal network. Specially, when the burst phases nearly coincide and when the burst phases correlate weakly. In addition, the variance of mean field is also used to depict the degree of bursting synchronization in the modular neuronal network. Higher degree of bursting synchronization is characterized by large-amplitude oscillation of mean field, which results in larger variance . On the contrary, small-amplitude fluctuation of mean-field as well as smaller variance indicates lower degree of bursting synchronization.
Figure 1(a) depicts the dependence of order parameter on coupling strength when the considered modular network is free of synaptic plasticity, i.e., . It is clear that with the increase of , the order parameter gradually increases, and when exceeds a critical value (). That is to say, coupled neurons in the modular network can achieve bursting synchronization when is large enough. Correspondingly, the variance of mean-filed versus coupling strength is depicted in Fig. 1(b). The increases as is increased, which further implies that bursting synchronization can be induced by large coupling strength in the modular network.
Fig. 1.

a The order parameter and b the variance as a function of coupling strength when the modular network is absence of synaptic plasticity and nonlinear delayed feedback control. It is seen that bursting synchronization can be induced by large coupling. When calculating and , the solution of Eq. (2) for the first 3000 times is considered as transient state
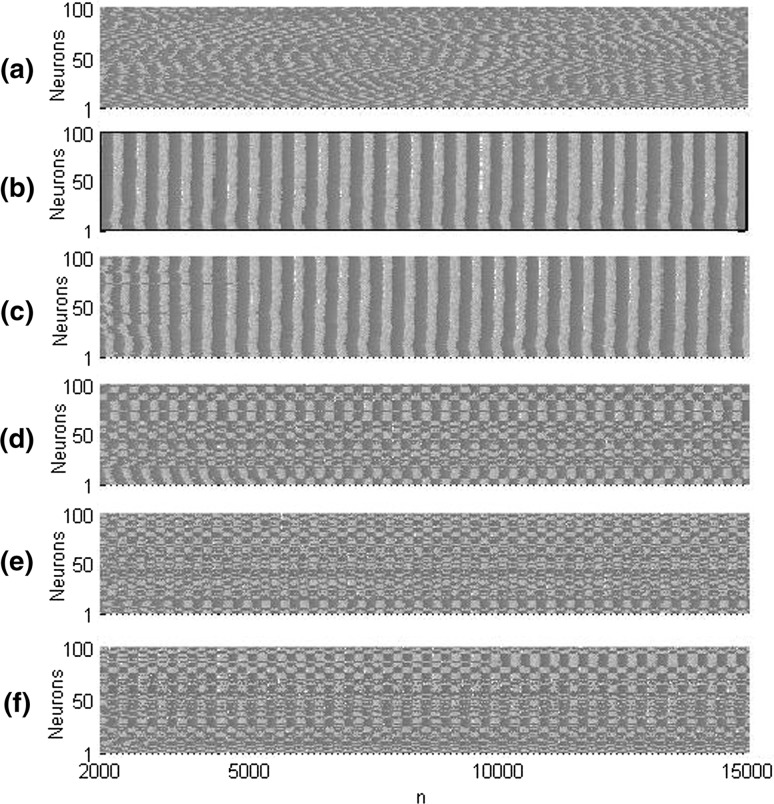
The above result can be further verified by some typical spatiotemporal patterns of the modular network. When neurons are uncoupled (i.e. ), the spatiotemporal pattern, shown in Fig. 2(a), presents a non-synchronous firing state of isolated neurons. However, when the coupling strength is large enough (e.g. ), a regular spatiotemporal pattern is depicted in Fig. 2(b), indicating that all coupled neurons are in synchronized bursting state, which further confirmed that bursting synchronization can be induced by large coupling strength in the modular network.
Fig. 2.
Spatiotemporal patterns of the modular network when a , , b , c , , d , , e , and f , . As increases, the synchronized patterns of the modular network are gradually destroyed
Suppressing bursting synchronization by synaptic plasticity
The above statement has indicated that large coupling can induce bursting synchronization in the modular network. In fact, excessively synchronized bursting rhythm of coupled neurons may be linked with some pathological conditions, such as epilepsy, essential tremor and Parkinson’s disease (Bergman and Deuschl 2002; Nini et al. 1995). Hence, suppressing such undesirable synchronized behavior of neuron population may have great significance for neuropathological study. In what follows, how synaptic plasticity controls this kind of strongly synchronous rhythm is firstly discussed when the considered modular network is free of nonlinear delayed feedback control.
Due to learning rate reflects how quickly the synaptic weights update in response to neuron activation, we first discuss how the learning rate of synaptic plasticity affects the synchronized dynamics utilizing some typical spatiotemporal patterns of the modular network qualitatively. As shown in Fig. 2(b), the modular network is in the state of bursting synchronization when and . Figure 2(c–f) depict the spatiotemporal patterns of the modular network when learning rate is and , respectively. When the synaptic plasticity is present, as shown in Fig. 2(c) when , all the coupled neurons are still basically bursting synchronized for smaller . When the learning rate increases to , Fig. 2(d) depicts that the status of bursting synchronization is a little depressed. With the further increase of learning rate (e.g.), synchronized bursting rhythms of coupled neurons are seriously destroyed, shown in Fig. 2(e–f), which implies that synaptic plasticity with larger learning rate can effectively eliminate the bursting synchronized rhythms in this modular network.
The qualitative analysis in Fig. 2 implies that larger learning rate can suppress bursting synchronization in the modular network effectively. To account for this phenomenon quantitatively, Fig. 3(a) depicts the evolution of order parameter during the course of learning rate . From this figure, it can be seen that along with the increase of , the order parameter firstly decreases and then wanders gradually at a smaller value of 0.1. It means that strong bursting synchronization in the modular network can be eliminated by larger learning rate effectively, moreover, the de-synchronous state of this modular network can be gradually maintained in a plausible context. Furthermore, Fig. 3(b) depicts the contour of order parameter as a function of the parameters of coupling strength and learning rate . Obviously, for the values of coupling strength lying in a specific region (i.e., ), the modular network in the absence of synaptic plasticity is in a synchronized bursting state, however, decreases rapidly and wanders at smaller value as the learning rate is increased from to . This result is similar with that of , which indicates that synaptic plasticity with larger learning rate can suppress bursting synchronization effectively when the coupling strength is within a specific range of .
Fig. 3.

a The order parameter as a function of learning rate when . b The contour plot of order parameter as a function of coupling and learning rate . It is seen that larger learning rate can suppress bursting synchronization effectively when the coupling is within a specific range. When calculating , the solution of Eq. (2) for the first 3000 times is considered as transient state
When the considered modular network is subjected to synaptic plasticity, how the synaptic weights are varied is further discussed. Figure 4 demonstrates the membrane potential of two connected neurons, the corresponding synaptic weights between them and the ensemble-averaged synaptic weights of the whole network (defined as ). The left three figures for the case of C = 0.03, L = 0.01 and the right three ones for the case of C = 0.03, L = 0.18. It can be seen that synaptic weights change as a function of neurons’ activity levels. In detail, if neuron in sub-network and neuron in sub-network are simultaneously active, the weights between them are strengthen, in contrast, the weights between them are weaken. Thus the ensemble-averaged synaptic weights for the former case are higher and they are lower for the latter case. This result is consistent with the basic notion of Hebbian learning that ‘units that fire together, wire together’.
Fig. 4.

The membrane potential of two connected neurons in the considered neuronal network, the corresponding synaptic weights and the ensemble-averaged synaptic weights of the whole network. The left three figures for the case of C = 0.03, L = 0.01 and the right three ones for the case of C = 0.03, L = 0.18
Suppressing bursting synchronization by nonlinear delayed feedback control
Though synaptic plasticity can suppress bursting synchronization in this modular network effectively when learning rate is large enough, synaptic plasticity has not enough capacity to suppress bursting synchronization when the learning rate is relatively small. In this case, we introduce the nonlinear delayed feedback control into this modular network and investigate how the synchronized bursting state of coupling neurons is suppressed by the technique of nonlinear delayed feedback control. Setting the coupling strength and the learning rate , Fig. 3(a) can indicate that the modular network is in the synchronized bursting state. Now, the control term consisting of nonlinear differential feedback control (Eq. (3)) and nonlinear direct feedback control (Eq. (4)) is switched on at time to control this kind of synchronized rhythms, respectively.
Nonlinear differential feedback control
Firstly, the nonlinear differential feedback control (Eq. (3)) is applied to the synchronized bursting neurons in this modular network to study the effect of de-synchronization. When the control parameters of nonlinear differential feedback signal are fixed at , the time series of the mean field is depicted in Fig. 5(a). One can see that once the differential feedback controller is switched on the large-amplitude oscillations of mean field quickly change to small-amplitude fluctuation, which indicates that synchronized rhythms in this modular network are no longer exhibited and the nonlinear differential feedback control can suppress bursting synchronization between interacted neurons. Figure 5(b) shows the membrane potential of two arbitrary neurons under the control of nonlinear differential feedback. Obviously, the bursting synchronized rhythms between neurons are eliminated after the control, but the amplitude and frequency of individual neurons are almost unchanged, which indicates that de-synchronization by nonlinear differential feedback does not affect normal discharge of individual neurons.
Fig. 5.
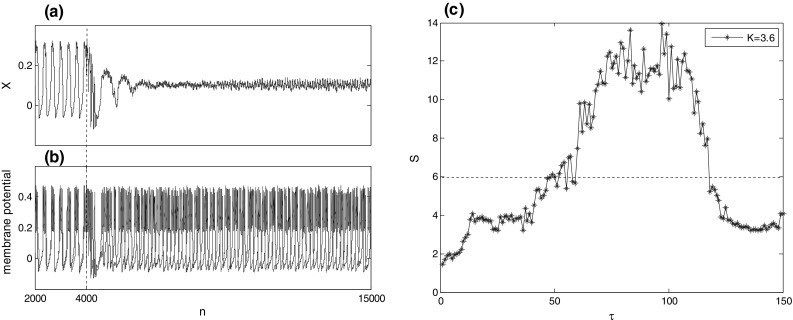
The evolution of (a) mean filed and (b) membrane potential of two arbitrary neurons when the nonlinear differential feedback with is switched on at time . (c) Suppression coefficient versus feedback delay when . When calculating , the solution of Eq. (2) for the first 5000 times is considered as transient state. It can be seen that bursting synchronization can be suppressed when feedback delay is appropriately tuned
In what follows, to quantitatively measure the effectiveness of the control procedure on suppressing bursting synchronization, the suppression coefficient is introduced as follows:
| 7 |
where and are the mean fields in the absence and presence of the feedback control, respectively. Note that the larger is the value of , the more efficient will be the feedback control on suppressing bursting synchronization. In this study, it is assumed that parameter region with large value of is considered as control domain of effective synchronization suppression.
Suppression coefficient as a function of feedback delay is illustrated in Fig. 5(c) when the feedback strength is fixed at . As we can see that basically increases firstly and then decreases upon increasing feedback delay. Moreover, exceeds the desynchronized threshold () when the delay is within the interval of , which means that bursting synchronization in the modular network can be suppressed effectively when feedback delay is tuned to appropriate interval of . This result can be further verified qualitatively by some typical mean fields of the modular network when . In the case of , Fig. 6(a) presents large-amplitude oscillation of mean field indicating that neurons in the modular neuronal network burst synchronously in phase. When the feedback delay is adjusted into the interval of , as shown in Fig. 6(b–d) for , the amplitude of mean field gets very small which implies that bursting synchronization can be suppressed when feedback delay is appropriately tuned.
Fig. 6.
Mean field of the modular network for different feedback delay with : a , b , c , d . It can be seen that bursting synchronization can be suppressed when feedback delay is appropriately tuned
What is more, suppression coefficient versus feedback delay for other feedback strengths such as is depicted in Fig. 7(a). Similar with that of , one can see that, for sufficiently large (e.g., ), bursting synchronization of the modular network can be suppressed by differential feedback control when feedback delay is within the interval of . For intermediate (e.g., ), the nonlinear differential feedback control achieves de-synchronization at an relative small interval of feedback delay compared with that of . However, for sufficiently small (e.g., ), the nonlinear differential feedback control can’t suppress bursting synchronization for the simulated feedback delay. In order to get a global visual effect, the contour plot of suppression coefficient on the two key parameters of feedback strength and feedback delay is further depicted in Fig. 7(b). Obviously, for some positive feedback strength, the differential feedback control can effectively suppress bursting synchronization when feedback delay is properly adjusted. Moreover, the higher feedback strength , the larger interval of feedback delay to suppress bursting synchronization. Vividly, the control domain of effective synchronization suppression by differential feedback control is similar to a semi-elliptical domain in the simulated parameter space of and .
Fig. 7.
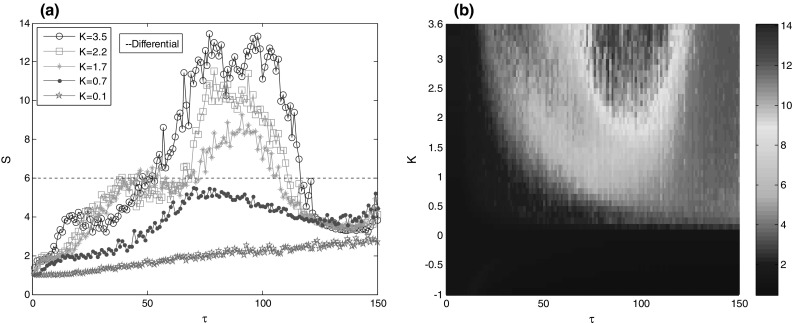
a Suppression coefficient versus feedback delay for different . b The contour plot of suppression coefficient versus and . When calculating , the solution of Eq. (2) for the first 5000 times is considered as transient state. The control domain of effective synchronization suppression by differential feedback control is approximately characterized by a semi-elliptical domain in the simulated parameter space
Nonlinear direct feedback control
Similar with the case of nonlinear differential feedback control, in this section, we employ nonlinear direct feedback control (Eq. (4)) to suppress burst synchronization in the modular network. The mean field is displayed in Fig. 8(a) when the parameters of nonlinear direct feedback signal are fixed at . One can see that the mean field quickly changes to noise-like small-amplitude fluctuation once the direct feedback controller is switched on at time , which implies that bursting synchronization can be suppressed effectively by nonlinear direct feedback control in the modular network. As shown in Fig. 8(b), though bursting synchronized rhythms between two arbitrary neurons are eliminated under the control of nonlinear direct feedback, the amplitude and frequency of each neuron are almost unchanged, which indicates that de-synchronization by nonlinear direct feedback does not affect normal discharge of individual neuron. To account for this phenomenon quantitatively, Fig. 8(c) presents the evolution of suppression coefficient during the course of feedback delay when the feedback strength is fixed at . It can be seen that decreases basically as feedback delay is increased, moreover, exceeds the desynchronized threshold when the feedback delay is about within the interval of , which means that bursting synchronization in the modular network can be suppressed effectively when feedback delay is tuned to an appropriate interval of . Furthermore, this result is verified qualitatively by some typical mean fields of the modular network when feedback delay is and . For the feedback delay lying in the region , Fig. 9(a–c) show that mean field present small-amplitude noise-like fluctuation, which implies that bursting synchronization can be suppressed when feedback delay is appropriately tuned. On the contrary, the large-amplitude oscillation of mean field for , displayed in Fig. 9(d), indicates that all neurons in the modular network are still burst synchronized in phase.
Fig. 8.

The evolution of (a) mean filed and (b) membrane potential of two arbitrary neurons when the nonlinear direct feedback with is switched on at time . (c) Suppression coefficient versus feedback delay when . When calculating , the solution of Eq. (2) for the first 5000 times is considered as transient state. It can be seen that bursting synchronization can be suppressed when feedback delay is appropriately tuned
Fig. 9.
Mean field of the modular network for different feedback delay with : a , b , c , d . It can be seen that bursting synchronization can be suppressed when feedback delay is appropriately tuned
In addition, dependence of suppression coefficient on feedback delay for other feedback strengths such as is depicted in Fig. 10(a). Similar with that of , for sufficiently small (e.g., ), bursting synchronization of the modular network can be suppressed by direct feedback control when the feedback delay is about within the domain . For intermediat (e.g., ), the nonlinear direct feedback control achieves de-synchronization at an relative small interval of feedback delay compared with that of . However, for sufficiently large (e.g., ), the direct feedback control can’t suppress bursting synchronization even in the whole domain of simulated feedback delay. In order to have a good visual effect, the contour plot of suppression coefficient on the two key parameters of feedback strength and feedback delay is further depicted in Fig. 10(b). Obviously, for some negative feedback strength, the direct feedback control can effectively suppress bursting synchronization when feedback delay is appropriately tuned. Moreover, the lower feedback strength , the larger interval of feedback delay to suppress bursting synchronization. Vividly, the control domain of effective synchronization suppression by direct feedback control is approximately characterized by a fan-shaped region in the simulated parameter space of and .
Fig. 10.

a Suppression coefficient versus feedback delay for different . b The contour plot of suppression coefficient versus and . When calculating , the solution of Eq. (2) for the first 5000 times is considered as transient state. The control domain of effective synchronization suppression by direct feedback control is similar to a fan-shaped region in the simulated parameter space
Conclusions and discussion
Based on a modular neuronal network with modified Oja’s learning rule, this study has explored how to suppress burst synchronized rhythm of coupled neurons. Through numerical simulations, the results first illustrate that all the neurons can be strongly synchronized when the coupling strength is within a specific range. Note that strongly synchronized bursting rhythm may be linked to some pathological conditions. Then synaptic plasticity is introduced to control bursting synchronization, and the results reveal that synaptic plasticity with large learning rate can eliminate bursting synchronization effectively. When the synaptic plasticity is not capable of suppressing synchronization, the nonlinear delayed feedback control including nonlinear differential feedback control and nonlinear direct feedback control is further proposed to reduce the synchronized bursting state of coupled neurons. The results demonstrate that nonlinear differential feedback control together with nonlinear direct feedback control can eliminate bursting synchronization significantly when the control parameters of feedback strength and feedback delay are properly adjusted. More interestingly, the control domain of effective synchronization suppression is approximately characterized by a semi-elliptical domain in the simulated parameter space for differential feedback control, while the effective control domain is approximately characterized by a fan-shaped domain for direct feedback control. It’s worth mentioning that recently Popovych et al. (2017a, b), combining the desynchronizing delayed feedback approach with the high-frequency deep brain stimulation technique, has proposed a pulsatile delayed feedback stimulation to suppress neuronal synchronization. They have found that depending on the stimulation parameters this pulsatile delayed feedback control can have different impact on the collective dynamics of considered networks. Especially in the parameter space of stimulation delay and intensity, they have demonstrated a certain periodic structure, where several desynchronization regions emerge when the feedback delay increases. This proposed technique is quite novel for demand-controlled desynchronization stimulation, which motivates us to explore other desynchronization method and similar periodic structure of desynchronization regions especially for neuronal network with synaptic plasticity.
Acknowledgements
This work is partially supported by the National Natural Science Foundation of China (Grant No. 11572180), the Fundamental Funds Research for the Central Universities (Grant Nos. GK201602009, GK201701001).
References
- Alberts WW, Wright EW, Feinstein B. Cortical potentials and parkinsonian tremor. Nature. 1969;221:670–672. doi: 10.1038/221670a0. [DOI] [PubMed] [Google Scholar]
- Baizabal-Carvallo JF, Kagnoff MN, Jimenez-Shahed J, Fekete R, Jankovic J. The safety and efficacy of thalamic deep brain stimulation in essential tremor: 10 years and beyond. J Neurol Neurosurg Psychiatry. 2014;85:567–572. doi: 10.1136/jnnp-2013-304943. [DOI] [PubMed] [Google Scholar]
- Benabid AL, Pollak P, Gervason C, Hoffmann D, Gao DM, Hommel M. Long-term suppression of tremor by chronic stimulation of ventral intermediate thalamic nucleus. Lancet. 1991;337:403–406. doi: 10.1016/0140-6736(91)91175-T. [DOI] [PubMed] [Google Scholar]
- Bergman H, Deuschl G. Pathophysiology of Parkinson’s disease: from clinical neurology to basic neuroscience and back. Mov Disord. 2002;17:S28–S40. doi: 10.1002/mds.10140. [DOI] [PubMed] [Google Scholar]
- Boccaletti S, Kurths J, Osipov G, Valladares DL, Zhou CS. The synchronization of chaotic systems. Phys Rep. 2002;366:1–101. doi: 10.1016/S0370-1573(02)00137-0. [DOI] [Google Scholar]
- Courbage M, Nekorkin VI. Map based models in neurodynamics. Int J Bifurcat Chaos. 2010;20:1631–1651. doi: 10.1142/S0218127410026733. [DOI] [Google Scholar]
- Courbage M, Nekorkin VI, Vdovin LV. Chaotic oscillations in a map-based model of neural activity. Chaos. 2007;17:043109. doi: 10.1063/1.2795435. [DOI] [PubMed] [Google Scholar]
- Courbage M, Maslennikov OV, Nekorkin VI. Synchronization in time-discrete model of two electrically coupled spike-bursting neurons. Chaos Soliton Fract. 2012;45:645–659. doi: 10.1016/j.chaos.2011.12.018. [DOI] [Google Scholar]
- Delgado-García José M., Sánchez-Campusano Raudel, Fernández-Lamo Iván, Gruart Agnès. Advances in Cognitive Neurodynamics (V) Singapore: Springer Singapore; 2016. Dynamic Patterns of Cortical Activation During Different Types of Learning Tasks and Unpredictable Situations; pp. 119–125. [Google Scholar]
- Dharani S, Rakkiyappan R, Cao J, Alsaedi A. Synchronization of generalized reaction-diffusion neural networks with time-varying delays based on general integral inequalities and sampled-data control approach. Cogn Neurodyn. 2017;11:1–13. doi: 10.1007/s11571-017-9438-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donald (1949) The organization of behavior. vol 9, pp 213–218
- Engel AK, Kreiter AK, Konig P, Singer W. Synchronization of oscillatory neuronal responses between striate and extrastriate visual cortical areas of the cat. Proc Natl Acad Sci India. 1991;88:6048. doi: 10.1073/pnas.88.14.6048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engel AK, Fries P, Singer W. Dynamic predictions: oscillations and synchrony in top-down processing. Nat Rev Neurosci. 2001;2:704–716. doi: 10.1038/35094565. [DOI] [PubMed] [Google Scholar]
- Han F, Lu QS, Meng X, Wang J. Synchronization of small-world neuronal networks with synapse plasticity. Dordrecht: Springer; 2011. pp. 295–299. [Google Scholar]
- Hauptmann C, Tass PA. Cumulative and after-effects of short and weak coordinated reset stimulation: a modeling study. J Neural Eng. 2009;6:016004. doi: 10.1088/1741-2560/6/1/016004. [DOI] [PubMed] [Google Scholar]
- Hilgetag CC, Burns GA, O’neill MA, Scannell JW, Young MP. Anatomical connectivity defines the organization of clusters of cortical areas in the macaque and the cat. Philos Trans R Soc Lond Ser B. 2000;355:91–92. doi: 10.1098/rstb.2000.0551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jankovic M, Martinez P, Chen Z, Cichocki A. Modified modulated Hebb-Oja learning rule: a method for biologically plausible principal component analysis. Berlin: Springer; 2008. pp. 527–536. [Google Scholar]
- Kim SY, Lim W. Dynamical responses to external stimuli for both cases of excitatory and inhibitory synchronization in a complex neuronal network. Cogn Neurodyn. 2017;11:1–19. doi: 10.1007/s11571-017-9441-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim SY, Lim W. Effect of spike-timing-dependent plasticity on stochastic burst synchronization in a scale-free neuronal network. Cogn Neurodyn. 2017;1:1–28. doi: 10.1007/s11571-017-9470-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin SJ, Grimwood PD, Morris RGM. Synaptic plasticity and memory: an evaluation of the hypothesis. Ann Rev Neurosci. 2000;23:649. doi: 10.1146/annurev.neuro.23.1.649. [DOI] [PubMed] [Google Scholar]
- Martin SJ, Grimwood PD, Morris RG. Synaptic plasticity and memory: an evaluation of the hypothesis. Ann Rev Neurosci. 2000;23:649. doi: 10.1146/annurev.neuro.23.1.649. [DOI] [PubMed] [Google Scholar]
- Maslennikov OV, Nekorkin VI. Modular networks with delayed coupling: synchronization and frequency control. Phys Rev E. 2014;90:012901. doi: 10.1103/PhysRevE.90.012901. [DOI] [PubMed] [Google Scholar]
- Munakata Y, Pfaffly J. Hebbian learning and development. Dev Sci. 2004;7:141–148. doi: 10.1111/j.1467-7687.2004.00331.x. [DOI] [PubMed] [Google Scholar]
- Newman MEJ, Watts DJ. Renormalization group analysis of the small-world network model. Phys Lett A. 1999;263:341–346. doi: 10.1016/S0375-9601(99)00757-4. [DOI] [Google Scholar]
- Ngouonkadi EBM, Fotsin HB, Nono MK, Fotso PHL. Noise effects on robust synchronization of a small pacemaker neuronal ensemble via nonlinear controller: electronic circuit design. Cogn Neurodyn. 2016;10:385–404. doi: 10.1007/s11571-016-9393-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nini A, Feingold A, Slovin H, Bergman H. Neurons in the globus pallidus do not show correlated activity in the normal monkey, but phase-locked oscillations appear in the mptp model of parkinsonism. J Neurophysiol. 1995;74:1800. doi: 10.1152/jn.1995.74.4.1800. [DOI] [PubMed] [Google Scholar]
- Oja E. A simplified neuron model as a principal component analyzer. J Math Biol. 1982;15:267–273. doi: 10.1007/BF00275687. [DOI] [PubMed] [Google Scholar]
- Oja E. Oja learning rule. Scholarpedia. 2008;3:3612. doi: 10.4249/scholarpedia.3612. [DOI] [Google Scholar]
- Pérez T, Uchida A. Reliability and synchronization in a delay-coupled neuronal network with synaptic plasticity. Phys Rev E. 2011;83:0619151. doi: 10.1103/PhysRevE.83.061915. [DOI] [PubMed] [Google Scholar]
- Pfister JP, Tass PA. STDP in oscillatory recurrent networks: theoretical conditions for desynchronization and applications to deep brain stimulation. Front Comput Neurosc. 2010;4:22. doi: 10.3389/fncom.2010.00022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pikovsky A, Rosenblum M, Kurths J. Synchronization: a universal concept in nonlinear science. Am J Phys. 2002;70:655. doi: 10.1119/1.1475332. [DOI] [Google Scholar]
- Popovych OV, Tass PA. Synchronization control of interacting oscillatory ensembles by mixed nonlinear delayed feedback. Phys Rev E. 2010;82:026204. doi: 10.1103/PhysRevE.82.026204. [DOI] [PubMed] [Google Scholar]
- Popovych OV, Hauptmann C, Tass PA. Effective desynchronization by nonlinear delayed feedback. Phys Rev Lett. 2005;94:164102. doi: 10.1103/PhysRevLett.94.164102. [DOI] [PubMed] [Google Scholar]
- Popovych OV, Hauptmann C, Tass PA. Control of neuronal synchrony by nonlinear delayed feedback. Biol Cybern. 2006;95:69–85. doi: 10.1007/s00422-006-0066-8. [DOI] [PubMed] [Google Scholar]
- Popovych OV, Lysyansky B, Tass PA. Closed-loop deep brain stimulation by pulsatile delayed feedback with increased gap between pulse phases. Sci Rep. 2017;7:1033. doi: 10.1038/s41598-017-01067-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Popovych OV, Lysyansky B, Rosenblum M, Pikovsky A, Tass PA. Pulsatile desynchronizing delayed feedback for closed-loop deep brain stimulation. PLoS ONE. 2017;12:e0173363. doi: 10.1371/journal.pone.0173363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rakkiyappan R, Premalatha S, Chandrasekar A, Cao JD. Stability and synchronization analysis of inertial memristive neural networks with time delays. Cogn Neurodyn. 2016;10:437–451. doi: 10.1007/s11571-016-9392-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robert S, Zucker RS, Regehr WG. Short-term synaptic plasticity. Annu Rev Neurosci. 2010;12:13–31. doi: 10.1146/annurev.ne.12.030189.000305. [DOI] [PubMed] [Google Scholar]
- Rodriguez-Oroz MC, Obeso JA, Lang AE. Bilateral deep brain stimulation in Parkinson’s disease: a multicentre study with 4 years follow-up. Brain. 2005;128:2240–2249. doi: 10.1093/brain/awh571. [DOI] [PubMed] [Google Scholar]
- Rosenblum M, Pikovsky A. Delayed feedback control of collective synchrony: an approach to suppression of pathological brain rhythms. Phys Rev E. 2004;70:041904. doi: 10.1103/PhysRevE.70.041904. [DOI] [PubMed] [Google Scholar]
- Shi JC, Luo M, Huang CS. Cooperative effect of random and time-periodic coupling strength on synchronization transitions in one-way coupled neural system: mean field approach. Cogn Neurodyn. 2017;11:1–8. doi: 10.1007/s11571-016-9419-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sigurdsson T, Doyère V, Cain CK, Ledoux JE. Long-term potentiation in the amygdala: a cellular mechanism of fear learning and memory. Neuropharmacology. 2007;52:215–227. doi: 10.1016/j.neuropharm.2006.06.022. [DOI] [PubMed] [Google Scholar]
- Singer W. Synchronization of cortical activity and its putative role in information processing and learning. Ann Rev Physiol. 1993;55:349–374. doi: 10.1146/annurev.ph.55.030193.002025. [DOI] [PubMed] [Google Scholar]
- Singer W, Gray CM. Visual feature integration and the temporal correlation hypothesis. Annu Rev Neurosci. 1995;18:555–586. doi: 10.1146/annurev.ne.18.030195.003011. [DOI] [PubMed] [Google Scholar]
- Sun ZK, Zhao NN, Yang XL, Xu W. Inducing amplitude death via discontinuous coupling. Nonlinear Dyn. 2018;92:1185–1195. doi: 10.1007/s11071-018-4117-1. [DOI] [Google Scholar]
- Volkmann J, Albanese A, Kulisevsky J. Long-Term effects of pallidal or subthalamic deep brain stimulation on quality of life in Parkinson’s Disease. Mov Disorders. 2009;24:1154–1161. doi: 10.1002/mds.22496. [DOI] [PubMed] [Google Scholar]
- Wang RB, Zhu YT. Can the activities of the large scale cortical network be expressed by neural energy? a brief review. Cogn Neurodyn. 2016;10:1–5. doi: 10.1007/s11571-015-9354-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang YH, Wang RB, Zhu YT. Optimal path-finding through mental exploration based on neural energy field gradients. Cogn Neurodyn. 2017;11:99–111. doi: 10.1007/s11571-016-9412-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei H, Bu YJ, Dai DW. A decision-making model based on a spiking neural circuit and synaptic plasticity. Cogn Neurodyn. 2017;1:1–17. doi: 10.1007/s11571-017-9436-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wen J, Wang J, Yu HT, Deng B, Wei X (2011) Nonlinear delayed feedback control for effective desynchronization of small-world neural networks. vol 1416, pp 2743–2747
- Yang XL, Wang MM. The evolution to global burst synchronization in a modular neuronal network. Mod Phys Lett B. 2016;30:1650210. doi: 10.1142/S0217984916502109. [DOI] [Google Scholar]
- Yang XL, Hu LP, Sun ZK. How time-delayed coupling influences differential feedback control of bursting synchronization in modular neuronal network. Nonlinear Dyn. 2016;86:1797–1806. doi: 10.1007/s11071-016-2993-9. [DOI] [Google Scholar]
- Yang XL, Wang JY, Sun ZK. The collective bursting dynamics in a modular neuronal network with synaptic plasticity. Nonlinear Dyn. 2017;10:1–10. [Google Scholar]
- Yeates P, Woolf K, Benbow E, Davies B, Boohan M, Eva K. A randomised trial of the influence of racial stereotype bias on examiners’ scores, feedback and recollections in undergraduate clinical exams. Bmc Medicine. 2017;15:179. doi: 10.1186/s12916-017-0943-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu HT. Nonlinear delayed feedback for effective desynchronization of discrete neural network. J Dyn Ctrl. 2010;8:375–380. [Google Scholar]
- Zamora-Lopez G, Zhou CS, Kurths J. Graph analysis of cortical networks reveals complex anatomical communication substrate. Chaos. 2009;19:015117. doi: 10.1063/1.3089559. [DOI] [PubMed] [Google Scholar]
- Zhang Y, Pan XC, Wang RB, Sakagami M. Functional connectivity between prefrontal cortex and striatum estimated by phase locking value. Cogn Neurodyn. 2016;10:245–254. doi: 10.1007/s11571-016-9376-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao NN, Sun ZK, Xu W. Amplitude death induced by mixed attractive and repulsive coupling in the relay system. Eur Phys J B. 2018;91:20. doi: 10.1140/epjb/e2017-80463-2. [DOI] [Google Scholar]
- Zhou B, Liao XF, Huang TW. Event-based exponential synchronization of complex networks. Cogn Neurodyn. 2016;10:423. doi: 10.1007/s11571-016-9391-3. [DOI] [PMC free article] [PubMed] [Google Scholar]