Coherent phenomena in photosynthetic light harvesting: part one—theory and spectroscopy

Abstract

The role of non-trivial quantum mechanical effects in biology has been the subject of intense scrutiny over the past decade. Much of the focus on potential “quantum biology” has been on energy transfer processes in photosynthetic light harvesting systems. Ultrafast laser spectroscopy of several light harvesting proteins has uncovered coherent oscillations dubbed “quantum beats” that persist for hundreds of femtoseconds and are putative signatures for quantum transport phenomena. This review describes the language and basic quantum mechanical phenomena that underpin quantum transport in open systems such as light harvesting and photosynthetic proteins, including the photosystem reaction centre. Coherent effects are discussed in detail, separating various meanings of the term, from delocalized excitations, or excitons, to entangled states and coherent transport. In particular, we focus on the time, energy and length scales of energy transport processes, as these are critical in understanding whether or not coherent processes are important. The role played by the protein in maintaining chromophore systems is analysed. Finally, the spectroscopic techniques that are used to probe energy transfer dynamics and that have uncovered the quantum beats are described with reference to coherent phenomena in light harvesting.

Introduction

A large international collaborative effort has been underway in the last decade to understand interference patterns, or coherence, seen in spectroscopic analyses of light harvesting systems. Although the nature of the quantum interferences (or ‘beats’) has been widely explored, many ambiguities remain. This is largely because of the difficulty in accurately teasing apart vibrational and electronic quantum coherent mechanisms when energies are (near) resonant. Most researchers have suggested that in light harvesting systems exhibiting quantum beats, the transfer of excitation energy between excited electronic states harbours coherent entangled states comprising a mixture of both electronic and vibrational degrees of freedom called vibronic states.

Quantum mechanics is the basis of matter and biological systems are hence, at least trivially, quantum mechanical. Non-trivial quantum mechanical effects such as entanglement, however, are very delicate and are lost quickly in hot, wet environments like living cells. A current point of interest questions how far quantum mechanical effects and correlations can extend in time and space, and biological systems are an excellent playground in which to search.

Coherent quantum beats have been observed in most light harvesting systems, where the coherences are stable over a time scale that is commensurate with the relevant energy transfer times. Gaining an understanding of the engineering principles behind the possible maintenance of this delicate quantum concert is paramount to many applications. Many theoretical studies highlight that having a tuned amount of quantum coherence in disordered light harvesting systems can enhance energy transfer efficiency and robustness far more than would be the case of energy incoherently hopping between chromophores (the Förster limit). Making light harvesting processes as efficient and robust as possible would be a key evolutionary advantage, especially for deep sea dwellers where photon flux is minimal. Determining if and how coherence is used and selected for by photosynthetic organisms is an open question as quantum phenomena are inherent in chromophores that are tightly packed. This is the most challenging problem faced in these studies, with the possibility that it may not be feasible to determine definitively whether quantum coherence is under evolutionary selection.

General description of biological light harvesting

The input energy for photosynthesis comes from sunlight. The output is the generation of a stable chemical energy source, i.e. ATP. The key photosynthetic complex in energy transduction is the photosystem, which includes the core reaction centre. The reaction centre accepts the energy input from light and uses it to drive charge separation, which then powers the downstream processes ultimately generating ATP.

In all stages, the photosynthetic complexes consist of a set of light-active organic molecules called chromophores that are embedded in a protein or protein complex. The protein itself does not interact directly with light or the electronic excitation produced by light in the chromophore molecules. Instead, the protein acts as a scaffold, setting the conformation of the chromophores, limiting their potential motion and arranging the chromophores into specific separations and orientations, presumably to control and direct energy transfer processes between the chromophores.

A simple photosynthetic organism could just use a single reaction centre to both capture solar energy and separate charges. However, such an apparatus would be a poor light harvester because reaction centres absorb few photons (low cross-section) in a limited range of frequencies. To live in low light environments, organisms have evolved elaborate light harvesting systems and antennae that solve both of these problems. They increase the capture cross-section and they increase the spectral coverage resulting in high photon capture efficiency of the organism as a whole (i.e. nearly all photons incident on the organism result in a charge separation in the reaction centre).

With the evolution of light harvesting proteins and antenna complexes comes the caveat that energy needs to be efficiently transferred between the chromophores in a way that nearly all excitations result in a charge separation event at the reaction centre. Understanding the mechanisms by which this is achieved is the key concern of this review.

Timescales and length scales

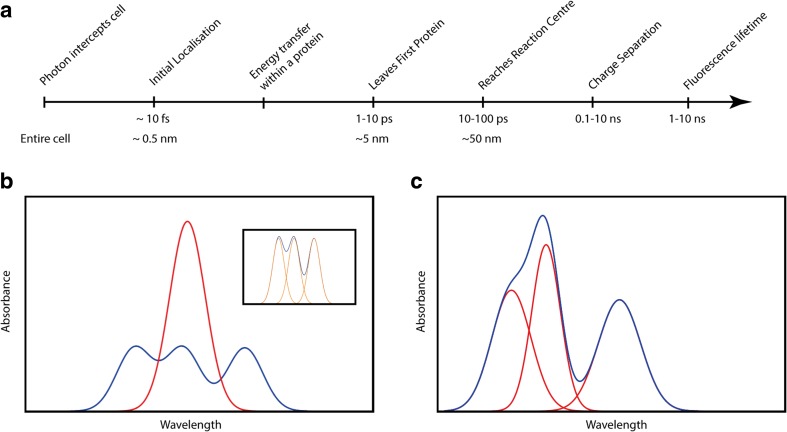
Solar energy can be viewed as a stream of photons. For a single cell, only one solar photon is likely to impinge on the cell during the timescale of energy transfer of a single excitation. The coherence volume of this photon is much larger than cellular dimensions, meaning that the photon can interact with all suitable chromophores in a single cell. From a quantum mechanical perspective, the photon will initially excite all resonant chromophores within the coherence volume in a superposition of states; however, this collective excitation will decay on femtosecond time scale resulting in the excitation being localised to a single protein system. The excitation is localised so rapidly because the phase relationships between chromophores imparted by the oscillating electric field of the photon are almost instantaneously lost. This is because weakly interacting chromophores in the coherence volume lose track of each other due to environmental perturbations (vibrations) slightly altering the energy of the excitation on the chromophore; the further away the chromophores are, the greater the effect. Within the excited protein system (typically 3–10 nm length scale), the excitation is transferred from the initial excitation to some final acceptor on a timescale of roughly 1–10 ps (Fig. 1a). Usually, there will be several transfer steps between light harvesting proteins that are likely to be in physical contact with each other; thus, the excitation will travel up to about 50 nm until it finally reaches a reaction centre (10–100 ps). Charge separation within the reaction centre takes place on a timescale of 0.1–10 ns. Throughout light harvesting, the chromophores can lose energy via fluorescence, which typically has a lifetime of 1–10 ns. Thus, to prevent energy loss via fluorescence, the passage from initial photon capture to charge separation in the reaction centre must occur within this timeframe.

Fig. 1.

a Typical timeline and length scales for photosynthetic energy transfer. b The net effect (blue) of having energetically identical chromophores (red) that are strongly interacting in a toy system of three chromophores. The inset highlights that the new absorption spectrum of the three chromophores is produced by a new set of now energetically different states (orange). c The net effect (blue) of packing multiple different non-interacting chromophores (red) into a light harvesting system in a toy system of three chromophores

Quantum processes in light harvesting proteins and energy transfer

From a quantum mechanical perspective, the chromophores embedded in a protein may not act as independent systems. Simply, two chromophores that are strongly coupled will act as a single light absorbing system. Coupling produces two possible excited states, one with lower energy and one with higher energy than that of the single chromophore. This coupling broadens the excitation spectrum of the lone chromophore, increasing the spectral range of the light harvesting system (Fig. 1b). Light harvesting proteins also use additional strategies for increasing their spectral range. The simplest approach is to incorporate a series of different chromophores, each with a distinct absorption spectrum (Fig. 1c).

A second area where quantum mechanical phenomena are likely to be important in light harvesting is in the process of energy transfer. Within a light harvesting complex, the excitation must be transferred to the final acceptor in a fast, efficient and robust way to ensure that the energy is not lost to the environment. Two extreme models for energy transfer involve either quantum coherent phenomena or a semi-classical Förster resonance energy transfer (FRET) mechanism. The latter has the excitation moving irreversibly from donor chromophore to acceptor chromophore whilst in the former, the excitation resides simultaneously on multiple chromophores before decohering and localising on some final acceptor. The current debate centres on the extent to which energy transfer processes involve quantum coherent phenomena versus the FRET model or perhaps an intermediate model between the two extremes.

Coherence as a wave phenomenon

Coherence is a property of waves. Two waves (or two points on the same wave) are coherent if the phase difference between them is constant. The phase of the waves in question is important as certain spatio-temporal features, such as momentum and energy, define the phase of a wave. When two waves are coherent, their properties have non-local correlations and information is shared between them. Furthermore, when waves are coherent they are able to produce stable interference phenomena. Waves decohere under the influence of a random external perturbation, meaning correlations in their properties decay in space and time.

Take the example of waves in a bay. At small enough distances, the crest of a single wave is at the same distance from the shore. However, due to variations in the environment such as currents under the water, boats and/or rocks on the seafloor, the position to the shore at two points of the crest of the wave can lead or lag each other. We say that the system has acquired a random phase—meaning that the evolution of the wave has advanced or retarded from where its evolution without perturbation would be. As the wave approaches the shore, the time at which the wave breaks (a crude example of a spatio-temporal property of the system) can be very different at different points given random perturbations from the environment. At length scales orders of magnitude smaller than the size of the beach, the breaking point is highly correlated as the phase difference would be minimal. The scale over which the waves share a degree of correlation is the coherence time/length. These scales are important measures in the study of quantum processes in light harvesting as they highlight the scales over which quantum phenomena can persist.

Demystifying quantum behaviour

At the most fundamental level, the universe behaves in way that is counter to our macroscopic intuitions. At the scale of proteins and small molecules, quantum behaviour becomes evident and important because all fundamental interactions and behaviours in the universe are quantum mechanical. Proteins are shaped by the orbitals of their electrons, which are constrained by quantum mechanics. Trivial effects can occur because of the short length and time scales involved. The interest in quantum phenomena in light harvesting arises from the apparent ability of these systems to sustain non-trivial quantum superpositions at greater scales (long coherence times ≳ 100 fs and greater spatial extent ≳ 1 nm) as well as other non-trivial quantum effects in reaction centres and rhodopsins.

Logical differences at different scales

Quantum mechanics predicts physical correlations that are larger than those allowed by classical logic and probability. A dictum of classical probability and logic is that a given system has a set of states along with a set of probabilities, which may be made deterministic by some unknown parameters. Take the example of the coin toss. In this system, we can ascribe a probability to the outcome of heads or tails; however, the outcome can be completely determined at any time if all the parameters of the system (such as velocities of air molecules and the force imparted by the tossing hand) are known. In quantum mechanics, we deal with a different kind of probability where systems can intrinsically be in both states at once and only when measured does the system collapse to a single state. At first glance, this does not appear like it would make any measurable difference to the outcome of an experiment; however, this leads to some striking quirks in correlations and behaviours of systems and to the conclusion that the “quantum coin” must be both heads and tails at the same time.

Quantum measurement and superposition

One of the key features of quantum mechanics is quantum superposition. Particles are capable of being in many states at once or going through many processes at the same time. It is not merely that part of the system is in a specific state; it is that the whole system is in many states concurrently. To illustrate this, consider the example of a particle in a box. Classically, if we peeked inside the box we can find out the position and momentum of the particle and from then on we could predict the position and momentum of the particle deterministically. Conversely, if we had a quantum particle and we peeked inside the box, we could never predict the evolution of the particle deterministically. The state we saw was merely one realisation of the superposition of the position and momentum states of the particle. Classically, we are used to looking at large numbers of particles forming macroscopic objects or objects with large energies where quantum effects are lost (with the exception of some finely tuned experiments). It is at the smallest scales where quantum effects play a prominent role. An electron in its orbital around an atom or molecule is in a superposition of all possible position states around the nucleus with the same energy.

The states of interest in this discourse are superpositions of electronic states. Orbitals are one example of energy eigenstates of a quantum system. Energy eigenstates are stationary in time and represent states corresponding to specific amounts of energy. Energy eigenstates are of particular interest as they represent the basis for time evolution of systems in quantum mechanics. Generally, a system evolving in time will evolve through superpositions of its various energy eigenstates. Once a system is in a superposition it can produce many wave-like features. In the time evolution of an energy eigenstate, the state will have a phase proportional to the energy of the state which is unobservable when only one state is involved. When a system is in a superposition of energy eigenstates, the system will accrue a phase proportional to the energy difference of the constituent states. The net effect is that these states interfere with one another and the outcome of a suitable experiment can show oscillatory behaviour. This quantum interference is a hallmark of a quantum process and represents the wave nature of matter (given that interference properties are present in wave phenomena).

Quantum entanglement

When considering systems with more than one subsystem (such as a collection of chromophores) even further correlations are introduced. Entanglement can be understood by considering two people, who are given a “quantum ball” each. They know that there can only be one red quantum ball and one blue quantum ball. If one person looks at the quantum ball they have (which in this instance appears red), then the second person immediately knows they have a blue quantum ball without looking at it. The subtlety here is that when the people received the quantum ball, the ball itself did not have a specific colour (as opposed to a classical ball, which must have a colour). Only upon observation was the quantum ball coloured either red or blue and, at the same time, the other ball is coloured blue or red without being observed. The quantum ball is not as abstract as it sounds—electron spin behaves in this manner.

Entangled states are states of multipartite systems that are correlated. Entanglement is just a non-separable superposition of multiple subsystems. Consider a system of two entangled chromophores that bear a single excitation (sufficient energy to excite a single chromophore). When a measurement is made, the excitation can either be on chromophore I (and not on chromophore II) or on chromophore II (and not on chromophore I). This is entanglement in action—the information about chromophore I is intrinsically linked to the excitation state of chromophore II, however, is also just a superposition of the possible states of the complete system. Information about the state of the subsystem is not separable as it depends on the whole system. The corollary of this is that interactions between two subsystems by definition means that the subsystems share information about each other, and hence, entanglement is generated.

For the more biologically inclined

In order to understand the nature of the debate about the role of quantum coherence in energy transfer and light harvesting, an understanding of both quantum mechanics and modern femtosecond laser spectroscopy is required. The two following sections provide a common language to describe and explain these phenomena and to provide an interpretation of the results observed from physical experiment. As such, they are steeped in modern physics and physical chemistry. The more biologically oriented reader may wish to skip directly to the second part of this review “Coherent Quantum Phenomena In Photosynthetic Light Harvesting Part Two: Observations In Biological Systems” (Rathbone et al. 2018).

Describing quantum states

In order to analyse quantum systems, we need a language in which we can talk about their states. This section is produced as a guide to many of the papers referenced which use spectroscopic techniques to probe light harvesting systems and theoretical techniques to model them. The first step in building a framework for analysing quantum dynamics is to note that quantum systems have a special type of probability that contains interference. In classical probability, a vector is assigned to the probabilities corresponding to the states of a system. In quantum mechanics, a density matrix, ρ, can be constructed where the diagonal elements are the “classical” probabilities or populations and the off-diagonal elements or coherences contain the interference information between the corresponding states. For the systems of interest, only discrete states of chromophores are dealt with, making the analogy to a matrix concrete. Broadly, this can be expanded to systems that are continuous. Composite systems can also be described by considering all combinations of states within this framework. A single element of the density matrix is often written as either ⍴_ab or as ∣a >  < b∣ meaning the a^th row and b^th column. For light harvesting systems, the interest is in electronic and vibrational states of the ensemble of molecules. Hence, the density matrix can contain the complete set of combinations of all electronic states and vibrational states in the system. Another technical point is that the density matrix can describe the ensemble state or thermal average of a system, as in the analyses via spectroscopic methods, which involve ensembles of particles, often obscuring interference.

We are interested in the dynamics of quantum systems, so how the density matrix evolves in time is important. We describe quantum systems using a Master equation. Two examples of Master equations are below—Eq. 1 and Eq. 2). These equations contain a coherent term and an incoherent term. The coherent evolution of any quantum system is governed by an operator known as the Hamiltonian (H), which encodes the energies of each state and the interaction energies between all states. For discrete systems, the Hamiltonian is another matrix which forms a special product with the density matrix called a commutator. States that are stationary in time, after forming a product with the Hamiltonian, will produce a density matrix that is the same as the input density matrix; otherwise, they will mix and generate superpositions. In an isolated quantum system, the system states will continue to mix via the interactions between states, given by the Hamiltonian, and the state of the system, defined by the density matrix, will oscillate between states ad infinitum. The Hamiltonian, hence, can generate coherences (off-diagonal terms) between non-stationary states and, therefore, wave-like transport through the system.

For light harvesting systems, only the electronic and vibrational states of the light harvesting molecules (chromophores) are of interest; however, these states also interact with the protein, the solvent and sunlight. These components are not included in the density matrix as it would make the problem intractable. Instead, a second mathematical object (also a matrix) which will be referred to as the Lindbladian (L) needs to be included, which encodes how the parts of the density matrix interact with the environment (the protein, the solvent and sunlight). The Lindbladian is a special case where we assume that the interaction between system and environment is Markovian (the environment has no memory). More general formalisms are available to us, however, these are generally more complex. As there is no information in the density matrix about the degrees of freedom of the environment or the coherent correlations that are generated between the system and the environment, the coherent interactions between the system and the environment would appear to be incoherent in this mathematical framework. The form of the Lindbladian is often either heuristically derived or can be exactly determined by considering a density matrix that contains the states of the environment. In essence, the Linbladian describes how energy and information are removed by the environment and how correlations are lost between the states of the system. We stress here that there is a certain level of artifice in defining the boundary between system and environment and this is a long-standing issue in quantum mechanics. As all interactions are inherently coherent, why does the macroscopic world appear incoherent? At least experimentally, in light harvesting systems one need not worry about this question.

The two dynamical objects (i.e. the Hamiltonian and the Lindbladian) produce very different effects. The Hamiltonian entrains coherence and interference in the system whilst the Lindbladian has a decohering effect by mixing the system with the environment, thereby removing interference between states—collapsing the system (described by the density matrix) to a single realisation of its superposition. The Hamiltonian evolution has a wavelike character produced by coherent interactions and possesses the imaginary unit i (=√-1) to describe rotations through the space of states. The Lindbladian evolution, however, is not wavelike and is more of an incoherent decay and renewal process. The two components of this decay are referred to as dissipation (the relaxation of populations of states) and dephasing (the decay of superpositions). The equation describing the evolution of the density matrix is given below (where concatenation is matrix multiplication and the dagger means the complex conjugate and transpose of the matrix) in the approximation that the environment and system are uncorrelated (or Markovian—which is not always true when very short time scales are involved).

$$\frac{d\mathrm{\rho }}{\mathrm{d}t}=-i\left(\mathrm{H\rho }-\mathit{\rho H}\right)+\mathit{L\rho }{L}^{†}-\rho L^{†}L-L^{†}\mathit{L\rho }$$ 1

Furthermore, many theoretical explorations do not use this formalism but opt for that of the Redfield master equation. The two formalisms are nearly equivalent but different fields (that of quantum optics and chemistry) have a preferred use of one or the other as different approximations are more valid in different systems of interest and ensure that the solutions to these equations are well behaved. The Redfield approach is as follows: the coherent evolution of the system under its Hamiltonian is exactly the same and denoted by the frequency related to the energy difference between states; however, the Lindblad operators are replaced with the Redfield tensor which is another matrix-like object that takes elements of a density matrix, mixes them, and spits an element back out. The elements of the Redfield tensor represent the time correlation of the chromophore environment’s states and hence how the correlations between the system and chromophore environment are retained within the chromophore environment over time and the possibility of the reinjection of correlations to different parts of the system over time.

$$\frac{d{\mathrm{\rho }}_{\mathit{ab}}}{\mathit{dt}}=-i{\omega }_{\mathit{ab}}{\mathrm{\rho }}_{\mathit{ab}}+\sum _{a^{\prime }{b}^{\prime }}{R}_{\mathit{ab};a^{\prime }{b}^{\prime }}{\mathrm{\rho }}_{a^{\prime }{b}^{\prime }}$$ 2

When a^’ = b^’ and a = b, this represents transfer via the environment between populations. When a^’ = a and b^’ = b this represents dephasing, which is the decoherence process where coherences are destroyed by the environment. When a^’ ≠ b^’ and a = b or vice versa, this represents transfer between coherences and populations. Lastly when a^’ ≠ b^’ and a ≠ b, this represents transfer between coherences.

Coherence and decoherence in quantum systems

The term quantum coherence alludes to the wave nature of states in matter. Broadly speaking, it refers to the persistence of quantum behaviour at the scales of interest, namely the preservation of superpositions of states which lead to quantum interference. Quantum processes under the influence of a random external perturbation decohere over time leading to a loss of quantum correlations, just as with classical waves. By interaction with the environment governed by the irreversible master equation dynamics, the system decoheres into a state that is stochastically selected by the perturbation. The environment can be thought of as making a measurement which collapses the superposition to a single state. It should be stressed that it is not by some virtue of consciousness that the system collapses to a single state. There is a little more complexity to this, as the environment itself must be governed by quantum mechanics and there is a blurred line between it and the system. The subtlety here is a long-standing problem in physics, namely, why does the whole universe not appear as one coherent quantum system. As with wave phenomena, the scale over which quantum coherence is maintained is referred to as the coherence time or length. This is the most important measure for studies into quantum effects in biology as it provides us with a scale over which quantum processes can take place coherently to produce effects that affect the efficiency and robustness of energy transport in these systems.

Once entangled with the environment (or other parts of the system), any originally superposed sub-states are lost as the information shared between them is irreversibly altered—a process tending to increase entropy. When the energy scale of the Hamiltonian is larger than that of the Lindbladian, the system will tend toward being coherent for a longer time and vice versa. To achieve efficiency and robustness in photosynthetic light harvesting, organisms have discovered strategies to: engineer transfer of energy faster than decoherence; generate geometries that are capable of maintaining coherent states; or use entanglement with the environment to their advantage.

Deeper exploration of energy transport between chromophores

Given the laws of quantum mechanics, we understand the fundamental processes involved in the evolution of quantum states over chromophores. Here, we will walk through a toy model describing the physical mechanisms by which solar energy is funnelled via photosynthetic antennae of phototrophic organisms to the reaction centre. An important tool in understanding the energy transfer dynamics of light harvesting systems is the knowledge of scale. Scales of energy, length and time offer information needed to understand whether or not coherence is present and relevant. The following toy model will explore the relevance of transport phenomena given the scales of light harvesting complexes and relies on a few recent reviews (Scholes et al. 2012; Mirkovic et al. 2016) that provide valuable information not given here. Mechanisms specific to particular light harvesting systems will subsequently be assessed in more detail with the data in the subsequent article (Rathbone et al. 2018).

Firstly, the case where excitations are strongly localised to single chromophores is considered. Solar photons are captured by light harvesting antenna by their absorption, subsequently exciting electronic states, vibrational states and/or vibronic states (entangled electronic and vibrational states) of chromophores to higher energy levels. A way to think about this interaction is that the oscillating electric field of the photon interacts with the electronic states of the molecule upon absorption and an electron in the molecule oscillates from the ground to the excited state. The excitation is then transferred between chromophores via Coulombic coupling between the electric fields produced by one molecule and the electronic transition densities (the probability of a transition between states) of another in a similar manner as photon absorption. In a classical sense, the electric field of the excited chromophore interacts with that of the acceptor chromophore. The electric fields induce excitation by interacting with the electronic states involved in the transition of the molecule exchanging the excitation. At long enough distances, the fields involved are dipolar and the interaction energy is low compared with the interactions with the environment, which might decohere any superposition.

The picture described in the preceding paragraph is the Förster transfer limit, which has a further proviso that vibrations are at equilibrium. For general light-activated systems, we move away from the notion of transition dipoles in favour of the average interaction energy for the transfer of excitation. This scheme is used because, for closely packed chromophores, the interaction is not dipolar as the chromophore is extended in space and hence the electric field will be felt differently across the molecule. Furthermore, this scheme is preferred as the molecules are by and large static and variations to the excitation energy can be treated as random perturbations from the environment.

The energetic constraint that both chromophores must be at least near resonant (i.e. they have the same transition energy) is also important for energy to be able to be transferred. Some energy can escape or be absorbed via the generation or absorption of phonons (vibrational wave packets). Generally, quantum mechanical processes require energetic resonance to satisfy energy conservation.

For any interaction to take place, it must be coherent at least on a time scale which is proportional to the inverse of the energy of the interaction. A rough calculation of this timescale using Heisenberg’s uncertainty principle, places the coherence time for interactions between chromophores and light to be on the order of 1 fs. In the Förster regime, excitations merely hop from one chromophore to another until the reaction centre is reached and it is assumed that any phase information and electronic or vibrational coherence has decayed by dephasing and relaxation on a timescale far shorter than the time scale of exchange of excitation (the “hops”). The excited states in photosynthetic light harvesters have very short lifetimes (on the order of nanoseconds) before they fluoresce, which limits the timescale by which the excitation must reach its target, and thus, predictions of Förster theory may not suffice.

Excitons

The quantum object moving between chromophores created by the absorption of a photon cannot really be thought of as the electron. It is the excitation itself that is transferred between chromophores. Broadly speaking, these excitations are referred to as excitons and are part of a broader class of objects called quasiparticles. Quasiparticles are not fundamental particles but some quantum state that behaves as though it is a particle. This may sound like an odd and unnecessary distinction to make, however, it is an important one.

Further subtlety arises from quantum systems containing multiple, strongly coupled components. Recall the Hamiltonian and the electronic orbital, and more deeply consider why the electron is spread over many states of position at once. The reason is that the Hamiltonian contains coupling terms between the position states (meaning that the Hamiltonian has off diagonal elements). Within a collection of chromophores, there are electronic couplings between them which results in a new set of delocalised states (similar to that of an electronic orbital except, in this example, the probability lies on distinct, specific chromophore sites and not across space). This new set of states are the system’s natural excitons that will be generated by excitation from a discrete packet of energy that is confluent with the energy of the state. Also note that if a system has uncoupled elements (chromophores), then the excitons for these elements will just be excitations of specific (uncoupled) chromophore sites and not superpositions among them. The excitons are the natural states of the system in an energy basis as they will not evolve into a different state over time. Mathematically, without a decohering environment, the Hamiltonian will take the density matrix describing these states, mix them and then return exactly the same density matrix as an output (they are stationary in time and the energy of interactions does not perturb them). All the different possible exciton states give rise to the energy spectrum of a quantum system.

One other remarkable thing happens from the superposition of two (or more) chromophore states to produce stationary states: the energy spectrum of the joint system of two coupled chromophores is far different from that of the two lone chromophores (Fig. 1b). For example, uncoupled chlorophyll molecules embedded in a protein matrix all have very similar near resonant energy levels for their excited states. Thus, the absorption spectrum would contain a single peak in the absence of coupling. However, due to coupling between the subsystems (individual chromophores), the energies of the resonant excited states split into a set of states with energies higher and lower than the isolated chromophores. The degree to which the energy levels split is proportional to the coupling strength, thus, the stronger the coupling, the broader the spectrum. In the weak coupling limit, the exciton energies would be approximately the chromophore excitation energies given the weak to non-existent mixing between states. Hence, it must be stressed that the excitation energies seen in spectroscopic analysis of these systems are not necessarily the energies related to each individual chromophore, but rather the energies of the set of delocalised excitons in the system.

The broad absorption spectra that result from coupling may be an evolutionary reason for the near-ubiquitous presence of strongly coupled chromophore dimers and multimers in light harvesting systems. Generally, light harvesting systems exhibit excitons that are on the order of 2–4 chromophores, with the exception of the chlorosome which has excitons covering a larger number of chromophores. The excitation is transferred between the excitons via Coulombic coupling whereby excitons hop between coherent clusters of chromophores (the excitons) in an incoherent fashion. This is the essence of both supertransfer and generalised Förster theory.

In addition a more subtle effect can take place when the donor clusters and acceptor clusters are coherent. When they retain phase information about each other, the cluster can then sample multiple energy transfer pathways simultaneously and, later on, an end state can be selected from the superposition. This excitation energy transfer mechanism is wavelike and hence different pathways can constructively and destructively interfere. This then presents a more efficient way of channelling excitations from an initially excited chromophore to a final acceptor chromophore both in space and in energy.

Quantum coherence between the exciton states may now allow the excitation to funnel to the global minimum (the final acceptor chromophore) instead of getting stuck in local energetic minima (trap states). However, there are caveats to this that are discussed below. Instead of the transfer and coherence between excited states of each chromophore, the transfer and coherence between excitons (the number of exciton states in the system is equal to the number of chromophores that generate them) must be considered. An overlap between different excitons over the set of chromophore sites exists, thus population transfer can then be funnelled by this overlap downhill with respect to energy. This implies that even incoherent exciton dynamics are more efficient than chromophore to chromophore transfer.

Vibrational coherence

The vibrational states of molecules are also of importance in describing the quantum state of the system. Just as coherences between electronic states can play an important role in the dynamic evolution of the system, so too can coherent superpositions of vibrational modes. This can involve a singly excited vibrational mode in the ground or excited electronic state and it may involve different vibrational modes on the same molecule. Vibrations on different chromophores can also occur in tandem and can hence be coupled and phase locked (coherent) or exist across many chromophores. The role of vibrations and vibrational coherence is made more complex by the superposition of different vibrational modes across different electronic states of the molecule and between molecules. These vibrational coherences can be observed spectroscopically through Raman transitions and can be difficult to discern from electronic coherence between states separated by similar energy values. These vibrational coherences can be particularly important in electronic energy transfer when their energy matches the energy gaps between excitons. In this case, the additional vibrational energy brings excited chromophore states into resonance that would not be otherwise. In some cases, the coupling between electronic and vibrational states can be so strong that they are no longer separable. In these instances, alterations to the nuclear structure distort the electronic orbitals, which affect the vibrational states and we cannot approximate electronic states as separate from vibrational states. In such cases the mixed, inseparable states are referred to as vibronic states.

Vibronic states

In vibronic states (which appear frequently in light harvesting systems), information about the quantum state depends on the whole system (i.e. the vibrational states plus the electronic states). In the case described above, where the vibrational mode has energy equal to the energy gap between electronic states, the vibronic coupling can be particularly strong, which can have some significant effects for light harvesting. Firstly, the electronic states can borrow coherence lifetime from the vibrational states with which they are entangled, leading to vibronic coherences (that is, a coherent superposition between vibronic states which can be more vibrational or more electronic in character), which can remain coherent longer than purely electronic coherences. Secondly, vibronic states can effectively enhance spectral overlap between electronic (excitonic) states and enhance resonant energy transfer. This effect can be enhanced by the possible phase locking of the vibrational coherences on different but identical chromophores leading to synchronised fluctuations. The phase locked behaviour can be generated either by mechanical contact (close packed chromophores) or electromagnetic interactions (oscillations in electric field of an effector molecule caused by changes in charge density from the vibrations can force oscillations in a detector molecule).

Types of coherence

In quantum systems, the type of coherence that is produced is dependent on the basis set of states that harbour the coherence. These coherences can be over any state—electronic, vibrational or vibronic. Firstly, coherence in the site/chromophore basis refers to exciton states—the delocalised states that are stationary when evolved by the Hamiltonian. Excitons (site coherences) are ubiquitous in light harvesting systems and are generally produced when strong coupling between chromophores is present and generates splittings in the energy levels. Secondly, coherence between excitons are states that are superpositions in the energy basis (basis of stationary states—excitons or vibronic states). These coherences are what can be observed through quantum beats in spectroscopic experiments as they represent oscillations between two energy basis states (excitons) with different energies. A laser excites the system via its excitons and hence observed features of the system will also be between excitons. Lastly, states that undergo coherent processes (when dephasing from the environment is smaller than the interaction energy of the said process) harbour process coherence. This is the case where outcomes are quantum mechanical and produce quantum superpositions and can evolve superpositions themselves. All of these types of coherence can be represented as off-diagonal elements of a density matrix in some basis. Furthermore, if we were to represent the density matrix of the system in the site basis, off diagonal elements would reference coherences between sites (excitons). If the density matrix were represented in the energy basis, off diagonal elements would represent coherences between excitons, and so on.

Decoherence

Environmental interactions with the chromophoric system come in two flavours, both of which cause fluctuations and heterogeneity in the electronic structure of the chromophores and have implications for the coherence scales of the excitons and their interactions. The first effect is dynamic disorder in which the environment changes phase relationships already present between excitons. Dynamic disorder localises the state to a smaller region if the energy from environmental interactions is larger than the energy of interactions between chromophores or excitons. This means there is a separability of timescales between energy transfer and localisation timescales. In this regime, the exciton remains at least partially delocalised when the exciton is at thermal equilibrium with the environment. Under strong localisation conditions, the electronic states are dressed with environmental fluctuations. Hence, phase relationships between any states are lost much faster than the transfer time, localising the state and placing the system into an equilibrium state determined by the Boltzmann distribution under thermal conditions.

The second effect is static disorder which arises from heterogeneity of chromophore excitation energies, altering the Hamiltonian and thus the stationary states. This localisation effect takes place when the difference between chromophore excitation energies is larger than the coupling strength—when the electronic state transition is away from resonance. As such, chromophores with different energies tend not to mix whereas chromophores that already have the same energy are already resonant and hence can mix fully providing the interaction energy is larger than the environmental perturbations. Interestingly, however, disorder induced by the environment can also bring prior non-resonant chromophores into resonance by shifts in the chromophore excitation energies.

Differences in chromophore excitation energies can either be due to having different molecular species (chromophores) in the system or via different local perturbations of the electrostatic environment from the protein environment surrounding identical chromophores in a system. Furthermore, very slow (picosecond—estimating the speed of sound in a protein as ~ 2 nm/ps (Nogly et al. 2018)) conformational dynamics can lead to a similar effect as the local electrostatic environment slowly changes, shifting the chromophore excitation energy. In many light harvesting systems discussed in the subsequent article (Rathbone et al. 2018), the environmental interaction energy is of the same order as the electronic coupling meaning that the Förster regime is not applicable given the inability to separate time and energy scales. The effect produced here is that the interactions between chromophores and environment place the system in a regime that allows just enough quantumness to produce some non-trivial effects over the energy transfer time scale. For circumstances where long range transfer is required between weakly coupled chromophores, however, the Förster regime is perfectly applicable. Even within a single system, there may be a subset of chromophores that are weakly coupled in the Förster regime to a subset of more strongly coupled chromophores that harbour quantum exotica. In the subsequent article (Rathbone et al. 2018), we will see that there are indeed examples of this in nature (namely the eighth chromophore of the FMO complex).

In perfect quantum systems without noise, the excitons in the system may be found in a superposition and hence may suffer destructive interference at the trap site/chromophore depending on the initial superposition, thereby making energy funnelling impossible. Furthermore, considering a complex energetic landscape through space, an excitation cannot go up (too far) in energy if it is at a local minimum. Only if the exciton is already higher in energy and is in a superposition of energetically lower lying states can it funnel to a global trap.

In energetically disordered systems (such as light harvesting antennae), a fluctuating environment that induces a robustly tuned level of dephasing can also be beneficial. Perfectly coherent transport produces rapid localization due to the lack of order and correlations in energies of the system (known as Anderson localisation) and an infinitely incoherent system produces what is called the quantum Zeno effect (where the excitation state cannot travel anywhere as it is constantly being measured/localised by the environment) (Rebentrost et al. 2009). The fluctuating environment can also be thought of as transiently bringing chromophore excitation energies into resonance (de-trapping). Furthermore, partial spatial and energetic order can enhance transport by providing structure that allows for transport of excitations to converge to a key acceptor chromophore.

There is considerable debate concerning how quantum coherence can aid the efficiency of exciton transport. The argument that a light harvesting system will sample many pathways simultaneously and select the most energy efficient one (given the state of the environment) may not need to be invoked. Instead, starting at a high energy state away from a local energetic minimum, that system may stochastically select the global energetic minimum in an incoherent manner with greater probability instead of being trapped in a local minimum and fluorescing. Of course, having a coherent superposition of a local trap and non-trap state would mean that the system has a probability of moving away from the local trap instead of the ‘classical’ case where it is stuck until it fluoresces or FRETs. The role of quantum coherence in increasing efficiency remains one of the greatest open questions.

Protein and solvent effects

Whilst the light-active molecules that support the excitons are the chromophores, the effects of the environment surrounding the chromophores are important in governing their behaviour. The environment, in this case, is composed of the surrounding protein and the solvent (or cellular medium) supporting the protein. Effects due to this protein and solvent environment can induce alterations to chromophore coherence and energy transfer. Firstly, the environment may not be purely Markovian; that is, the time scale for relaxation of the environment is longer than the energy transfer time (environment correlation time being the length of time until the system reaches thermal equilibrium and loses memory). In this case, the environment can remove phase relations via discrete vibrational wave packets and then reinject the phase information and energy at a later time, reinvigorating coherence. If the time scale of environment correlations is far smaller than the energy transfer time, then the energy transfer process can be assumed Markovian.

Generally, continuum low frequency modes permeate the protein and determine the time scale of decoherence of the chromophores and timescale of equilibration of vibrations. Furthermore, when chromophores are embedded in the same protein matrix their local environments are now correlated meaning that vibrations in the environment may influence the chromophores in the same or similar manner. This further implies that non-equilibrium fluctuations taken up by the protein from one chromophore can be injected into another, providing another albeit semi-classical coherence mechanism. For chromophores separated by distances comparable to even a fraction of a protein, this effect would be negligible, because the time over which mechanical perturbations propagate is small compared with interaction times. The prediction of the speed with which a disturbance propagates through a protein is reported to be on the order of 5 nm/ps (Young et al. 2013) and direct measurements of the speed of protein disturbances using time-resolved crystallography via X-ray free electron laser (in bacteriorhodopsin) is on the order of 2 nm/ps (Nogly et al. 2018). Locally, protein disturbance may influence energy transfer via specific vibrations but it is unlikely that any globally concerted dynamics will occur, especially due to dissipation and perturbation from the solvent. Hence, vibrational coherences between molecules cannot be transferred mechanically via the protein and must propagate electromagnetically. The effect of the protein would then be to ensure the local electrostatic environments allow for similar molecular vibrations and hence coherence, if at all.

Given the speed of sound in a protein, any mechanical coupling between chromophores not in close contact is likely to occur on the picosecond timescale or longer. Thus, the protein is unlikely to act as a mechanical coupling mechanism for coherent energy transfer. Instead, the protein plays a major role in “straight jacketing” the chromophores by providing a scaffold that is quasi-rigid on the energy transfer timescale. As such, it will tune the chromophores via both setting their conformations and determining their electrostatic environments. This is likely to have a significant impact on the electronic energy levels of each chromophore and thus support resonances and hence coherence.

Charge separation

Once the excitation reaches the reaction centre, we encounter something new. In the space of ‘possible system states’, charge transfer states need to be included. These states describe the system when an electron is stripped from the electron donor and the electron itself is transferred between the final few chromophores. This is the crucial step that enables all subsequent biochemical reactions in photosynthesis. Whilst the mechanism is different to excitation energy transfer, the approach to modelling the dynamics with phenomenological time constants and coupling strengths is not and is influenced by all the same conditions as excitation energy transfer. The various charge transfer states can also remain in a superposition of the reaction centre exciton states for a similar length of time. We will see in the subsequent manuscript (Rathbone et al. 2018) with the presented data that this may affect the pathway taken during charge separation and electron transport.

The peak absorption of the reaction centre lies on the reddest edge of the visible spectrum (the lowest energy), meaning that charge separation occurs using the lowest activation energy that photons from the sun can provide (note that the infrared photons are filtered out through vibrational absorption by water). This means that the energy from photons higher (bluer) in energy than what the reaction centre can absorb can only be transferred to the reaction centre once the excess energy is carried off by the environment. In many cases, the antenna complexes can capture these bluer photons and the excitation can be funnelled down in energy to the reaction centre meaning that a larger number of photons can now be harvested and thus increase the efficiency of the system (i.e. the ratio of photons in/electrons out is increased). Any single excitation cannot produce two separate charge separation events. Hence, the goal of the antennae and the reaction centre is to efficiently convert a photon to a charge separation—the excitation need only have enough energy to push the electron over the potential energy barrier for tunnelling, which is provided by the specific energy gap of the final acceptor before charge transfer.

Photoprotection

Of brief noteworthiness is the ability for photosynthetic organisms to alter their light harvesting properties based on the availability of photons. The risk of oxidative damage is significantly increased when photosynthesis goes into overproduction and when triplet states are produced. Photosynthetic organisms have myriad ways to decrease photosynthetic light harvesting by altering energy transfer. This often involves a protein light switch and accessory proteins that decrease the efficiency of light harvest via quenching (Roach and Krieger-Liszkay 2012; Ballottari et al. 2013), tuned carotenoid-chlorophyll interactions (Di Valentin and Carbonera 2017) or possibly the use of triplet states which phosphoresce after long lifetimes and are often unable to be transported (Kim et al. 2007). Photoprotection may be as important as the need for efficient energy transfer and hence energy transfer and photoprotective pathways may often compete.

The photosynthetic process

Within the framework presented, transport phenomena appear to lie in a regime where time scales and energy scales for competing processes are commensurate. Evolutionary optimization of light harvesting must follow a trade-off between increasing the capture cross section for photons, efficiency of transport from capture to charge separation and robustness to changes in the local environment. Increasing capture cross section reduces transfer efficiency by increasing the distance an excitation must travel to reach the reaction centre and increasing efficiency by tuning the system decreases robustness to perturbations in the chromophore environment and conformational states of the protein. In general, quantum coherent effects are possibly confined intra-protein and would not be expected to exist inter-protein unless the proteins are components of a larger, stable complex. Hence, nature has found suitable trade-offs leading to competing mechanisms working on similar time and energy scales.

Experimental probes and spectroscopic signatures in light harvesting systems

The term spectroscopy shares the same roots as the word spectre, which is rather fitting for modern optical studies. By using spectroscopic techniques, we are looking at short lived “ghosts” in optically active systems that give us hints of quantum mechanisms behind energy transfer. Linear spectroscopies (such as absorbance and fluorescence) highlight only the initial and final states of energy transfer through light-activated molecules and obscure the myriad internal dynamics of these systems. In the chromophores of interest here, optical photons are responsible for the excitation of electronic states (excitation of an electron from one orbital to a higher orbital and its subsequent fluorescence being the emission of a photon from the electron returning to its initial state). Vibrational modes of chromophores can be excited by infrared region photons which generate a resonance between nuclei and driving them into an oscillatory behaviour. Furthermore, vibrational modes can be excited in optical experiments via Raman scattering where the photon’s energy excess is released as a vibration.

Clever spectroscopic techniques have been developed to probe deeper into the quantum mechanisms in complex molecules to understand the internal dynamics between the initial and final states. Our goal using these spectroscopic techniques is to search for coherences (non-classical off-diagonal elements of our system’s density matrix), excitation energy transfer on populations (diagonal elements) and how they evolve in time and mix with one another. The two main spectroscopic techniques that allow one to probe the internal dynamics of light harvesting systems are transient absorption (TA) and two-dimensional electronic spectroscopy (2DES), with many variations thereof that broadly fall into the category of pump-probe techniques (Berera et al. 2009). These facilitate the visualisation of various spectroscopic effects such as ground state bleaching, excited state absorption and stimulated emission independently with high temporal resolution. Below is merely a nuts and bolts overview of methodologies and their interpretations within the framework of quantum mechanics. Other methods—namely circular dichroism spectroscopy, infrared and Raman spectroscopies—are helpful in understanding the energetic structure of the excitonic and vibrational states of light harvesting systems, respectively. These are auxiliary to the two main techniques mentioned and do not provide information concerning the coherent structure of energy transport within light harvesting systems, hence, will only be mentioned in passing.

All pump-probe techniques have some shared features. Most rely on femtosecond pulsed laser light and some require a defined phase relationship between the incoming light pulses. A typical transient absorption experiment begins with the excitation of a sample with a broad-spectrum pulse (a broad spectrum offering high time resolution). The system is then left to evolve according to its Hamiltonian plus perturbations from the environment. At a later time, a second pulse—generated from the same source—interacts with the system and an absorption spectrum is measured. This is repeated, building up time slices of absorption spectra. These absorption spectra are compared to the equilibrium absorption spectrum, with changes to the absorption spectra occurring due to the state of the system. This may involve a decreased absorption at some energy because the electronic state at that energy is already excited. By following changes to the absorption spectra over time, a picture of the energy transfer pathways and dynamics can be built up. The presence of coherences (vibrational, vibronic, or electronic) can lead to oscillations in the amplitude of the transient absorption spectra as the delay between pump and probe is varied. The frequencies of the oscillations are found either by Fourier analysis or by fitting the time evolution to a sinusoidal function and hence determining the energy associated with the oscillation (coherence) in question. The associated decay of the sinusoid provides the decoherence time of the specific coherence. The phase and amplitude changes of signal oscillations across the detection wavelength are of importance in pump-probe methods in determining the origin of coherent oscillations. Phase flips and amplitude dips across a region of maximum emission or excitation are indicative of excited state and ground state coherence features, respectively, although there are some obscurities. The frequencies associated with the coherent oscillations can then be matched to exciton energy gaps and vibrational frequencies to assign coherent features to a plausible origin.

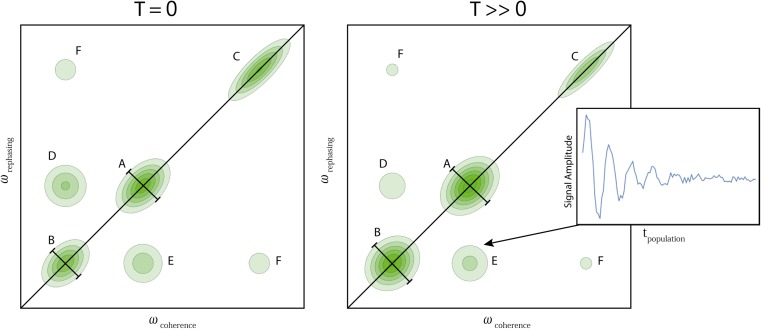
2DES is an extension of TA and akin to 2D NMR spectroscopy, the difference being the wavelength of electromagnetic radiation used (visible/near-infrared light versus radio waves) and the quantum state being excited (Jonas 2003; Cheng and Fleming 2008). In this method, three pulses are incident on the sample. The first pulse excites the system into a coherence between the ground and excited state and oscillates with the energy difference between them. After the coherence time τ a second pulse is incident on the sample which excites the system into a population state (diagonal state in the energy basis density matrix). Then, after the population time T a third pulse excites the system into a coherence between excited states. A signal is then emitted at the rephasing time t and data is collected by interfering the signal with a fourth pulse allowing access to amplitude and phase information. The coherence, τ, and rephasing, t, time axes are then Fourier transformed to produce what is essentially an excitation-emission spectrum with time slices at different population times, T. What one ends up with is a correlation map of states as a function of the population time (Fig. 2). Spectral peaks that lie along the diagonal correspond to absorption and emission from the same state and can arise from stimulated emission, ground state bleach or coherence pathways. As a function of population time, diagonal peaks can decay as the specific excited state is depopulated (either by returning to the ground state or transferring energy to another state) and/or as the ground state is repopulated. Coherence pathways will lead to oscillations of the amplitude and/or phase changes of the diagonal peak as a function of T (oscillations in populations), the magnitude of which will decay as the coherence decays. Cross peaks in the 2D spectra correspond to absorption and emission from different states and highlight interactions between the states. They can arise from ground state bleach, excited state absorption, energy/population transfer or coherence pathways. In the first two cases the amplitude of cross peaks will rise with the initial excitation, and decay in the same manner as diagonal peaks. For cross peaks arising from energy transfer, they will rise as a function of T as energy is transferred from a higher energy state to the lower energy one, and decay as this population subsequently relaxes to a lower energy state. For coherence pathways, the phase and/or amplitude of the cross peaks will oscillate as for peaks appearing on the diagonal (Fig. 2, inset).

Fig. 2.

Typical, yet highly simplified 2DES absolute value spectra with three excitons (A, B and C) of which A and B and B and C are coupled through time. A and B anti-diagonal width increase shown, C decay of states of high energy, D and E anti-correlated oscillations across the diagonal with decay including an example signal through the population time (inset) and F oscillation and decay in phase

As can be seen from this very preliminary identification of the different contributions to a 2D spectrum, there is a lot of information packed in, and it can be difficult to separate all of the different contributions. To overcome this limitation several approaches have been developed. Firstly, the spectra can be broken into rephasing/photon-echo (R) and non-rephasing (NR) spectra which correspond mathematically to different orderings of the first two pulses. This can be achieved by choosing specific geometries in the experimental setup as the incoming (three incident pulses) and outgoing signal wave vectors must conserve momentum. These geometries are called boxCARS and boxCARS parallelogram. A Fourier transform of the data over the population time (providing the sampling rate does not suffer aliasing) leads to positive and negative frequency components, whose symmetries or lack thereof can provide information about the coherences involved. Because the amplitude and phase of the electric field is measured, 2DES spectra also provide details of the the real and imaginary parts of the third-order susceptibility (related to the dielectric function) of the sample. The real part is corresponding to absorption and emission processes and the imaginary part is corresponding to the dispersion/refraction of light. For studies of light harvesting systems, the imaginary part is often neglected.

The trade-off of 2DES is that, whilst providing a lot more information, it is generally much harder to interpret. Many competing pathways can produce very similar spectroscopic results, making it difficult to disentangle the competing internal dynamics of the system. The internal steps that lead to the signal generation in these systems are often described by Feynman-Liouville pathways. The spectroscopic data is thus typically accompanied by a model of the system dynamics from which these pathways and the generated spectra can be simulated. This model can then be compared with the data to better understand the dynamics observed and the origin of any coherences.

The distinction between R and NR spectra becomes important here as different pathways result in different effects in each spectrum. Generally speaking, electronic coherences will appear as oscillations on NR diagonals and R cross peaks whilst vibrational coherences will appear as oscillations with no preferred position on the R and NR spectra. However, vibrational coherences can in fact masquerade as electronic coherences in certain circumstances when the energy difference between vibrational and electronic levels are in resonance (or possibly arising from vibronic states) which can obfuscate analyses. Additionally, the phase of coherent oscillations belonging to different peaks in 2DES spectra can help elucidate the origin of coherences. For example, electronic coherences in general will have a π/2 phase flip between diagonal and off diagonal peaks of the same energy indicating oscillatory transfer of populations (there are, however, some ambiguities with this, as with transient absorption). There are also some more subtle ways to gain information about the dynamics of the system: firstly, the width of diagonal peaks along the anti-diagonal (that is, the homogeneous linewidth; see Fig. 2 diagonal peaks A and B) contains information about the broadening due to the environment and its change over time correlates to the dephasing rate, and secondly, vibrational wave packets can produce oscillations in the ellipticity of the peaks observed.

To gain further insight into the origins of coherent oscillations one can tune the polarisation of the pulse sequence, which can enhance and suppress different Feynman-Liouville pathways. In TA spectroscopy, the pump and probe pulses can either be parallel or perpendicular to one another with respect to polarisation. From the two signals, one can then can find the anisotropy (the normalised difference between the polarisations), which highlights the difference between the spectra over detection wavelength and time. Rapid decay of the anisotropy is indicative of the presence of exciton delocalisation over a number of chromophores. The mere presence of exciton effects is highlighted by an initial anisotropy of 0.4–0.8 whereas individual, randomly oriented dipoles will only give a maximum anisotropy of 0.4. In 2DES, the two commonly used polarisation schemes are all-parallel (AP) and double-crossed (DC) sequences. The AP scheme allows the generation of signal from most pathways, including coherences involving a single exciton state, or different levels within a vibrational manifold. The DC scheme suppresses pathways where the coherence involves states with parallel transition dipoles from the ground state, and hence, vibrational modes and intramolecular coherences will not be observed. An intricacy arises, however, where certain coherent mixtures of vibrational and electronic states (vibronic states) can produce what appear to be electronic coherences in the DC spectra. With subsequent analysis of NR and R spectra in both these schemes, one can ascribe vibronic coherence to the oscillations observed by searching for signatures that show otherwise paradoxical characteristics of both vibrational and electronic coherence.

One can also isolate spectroscopic effects by changing the spectral shape of the pulses in the sequence. In one-colour experiments, all pulses will have the same spectra; however, in two-colour experiments, the different pulses can have different spectral characteristics. Within the scheme of two-colour studies, one can selectively excite/probe different quantum states and, hence, the coherences generated between them. An alternative approach has been to use ultrabroadband light, which can excite/probe multiple states and their coherence(s), but with lower specificity. The advantage of this approach is that the information content in the 2D spectrum is greater, but the associated problem is that it can be more difficult to pull it all apart and understand all of the dynamics.

Interestingly, the density matrix obtained by spectroscopic analysis is the ensemble average of the system, and hence obscures variations in properties of the individual complexes. The density matrix also takes into account the thermal ensemble statistics of the quantum states not just quantum interference. Some members of the ensemble may be more or less delocalised than others, and hence, averaging will obscure the effects this produces. Notably, coherences can last much longer than seen in the density matrix due to this averaging. One can extract the distribution of coherence times by performing single molecule variants of pump probe technique, however, many of these experimental methods are still being developed and have teething issues. Many variations on the theme of multiphoton spectroscopy exist based on these set-ups and will be merely referred to in the subsequent paper (Rathbone et al. 2018), all of which have the same flavour described above but with tweaks that tease out specific quantum mechanical effects.

One further issue is that of coherent light. All of these methods require illumination by a coherent light source. Hence, excitation by laser light will generate defined phase relationships between chromophores and a coherent superposition of energy states whereas illumination by sunlight will give rise to a statistically independent mixture of excited states with different energies and adornments of vibrational states. This may or may not be an issue when considering the density of excitations in a sample used for spectroscopy. If excitations generated by separate events are non-interacting, then the coherence between sites generated by excitonic splitting may not be destructively influenced by random phase of incoherent illumination. Furthermore, given the density of excitations in laser illuminated samples (0.1 photons/ns for a 5-nm diameter protein), it is unlikely that multiphoton events will occur where destructive interference effects may be present, and hence, transfer pathways obscured. Similarly, this is the case for incoherent illumination—there are no multiphoton events on single chromophores. Even further still, all realisations of the different transfer pathways are present in the ensemble which may destroy coherent effects via destructive interference or at least obscure coherence in any experiment. However, laser pulses are spectrally coherent which means that the phases of the photons at different energies are correlated, whereas the phases of sunlight are completely uncorrelated. Hence, there is an obligate phase relationship imposed a priori on the system by the laser excitation as the phases of each excited chromophore state are correlated.

Finally, another element of spectroscopic experimentation is that it is often done at cryogenic temperatures to reduce inhomogeneous broadening. This changes the chromophore environment correlation time increasing the coherence time of the system. Hence, many of the coherence times reported represent upper limits and should be taken with a grain of salt.

Conclusion to part one

We have now built up a framework within which one can understand the spectroscopic signals observed when probing biological light harvesting systems. It is evident that there are many complex and competing mechanisms at play in light harvesting systems. The most complex of which is the interplay between coherent quantum mechanisms and decoherence from environmental effects. Part one has also discussed some of the practical limitations and technical aspects of making spectroscopic measurements of light harvesting protein systems. In part two (Rathbone et al. 2018), we will explore observations made in real biological systems and the possible origins of quantum coherences and their effects.

Conflict of interest

Harry W. Rathbone declares that he has no conflicts of interest. Jeffery A. Davis declares that he has no conflicts of interest. Katharine A. Michie declares that she has no conflicts of interest. Sophia C. Goodchild declares that she has no conflicts of interest. Neil O. Robertson declares that he has no conflicts of interest. Paul M.G. Curmi declares that he has no conflicts of interest.

Ethical approval

This article does not contain any studies with human participants or animals performed by any of the authors.