Abstract
Direct molecular dynamics (MD) simulation with ab initio quantum mechanical and molecular mechanical (QM/MM) methods is very powerful for studying the mechanism of chemical reactions in a complex environment but also very time-consuming. The computational cost of QM/MM calculations during MD simulations can be reduced significantly using semiempirical QM/MM methods with lower accuracy. To achieve higher accuracy at the ab initio QM/MM level, a correction on the existing semiempirical QM/MM model is an attractive idea. Recently, we reported a neural network (NN) method as QM/MM-NN to predict the potential energy difference between semiempirical and ab initio QM/MM approaches. The high-level results can be obtained using neural network based on semiempirical QM/MM MD simulations, but the lack of direct MD samplings at the ab initio QM/MM level is still a deficiency that limits the applications of QM/MM-NN. In the present paper, we developed a dynamic scheme of QM/MM-NN for direct MD simulations on the NN-predicted potential energy surface to approximate ab initio QM/MM MD. Since some configurations excluded from the database for NN training were encountered during simulations, which may cause some difficulties on MD samplings, an adaptive procedure inspired by the selection scheme reported by Behler was employed with some adaptions to update NN and carry out MD iteratively. We further applied the adaptive QM/MM-NN MD method to the free energy calculation and transition path optimization on chemical reactions in water. The results at the ab initio QM/MM level can be well reproduced using this method after 2–4 iteration cycles. The saving in computational cost is about 2 orders of magnitude. It demonstrates that the QM/MM-NN with direct MD simulations has great potentials not only for the calculation of thermodynamic properties but also for the characterization of reaction dynamics, which provides a useful tool to study chemical or biochemical systems in solution or enzymes.
INTRODUCTION
Understanding the mechanism of chemical reactions in solution or enzymes at a molecular level is a challenging task in computational chemistry because of the large number of degrees of freedom. The free energy change or potential of mean force rather than potential energy change during a reaction process in a complex environment is a central quantity. In general, molecular dynamics (MD) simulations from tens of picoseconds to hundreds of nanoseconds are necessary to achieve converged statistical sampling for free energy calculations. The change in electronic structures in bond forming or breaking processes requires in addition a quantum mechanical description such as density functional theory (DFT) on the system, which limits the MD application to a small number of atoms for a short time. The combined quantum mechanical and molecular mechanical (QM/MM) method, first proposed by Warshel and Levitt, provides a multiscale computational tool to allow a reliable quantum mechanical calculation on the active site with a realistic modeling of the complex environment.1–5 Although the QM/MM model has been further developed for decades with great success to study many biological and chemical reactions,6–10 it requires electronic structure calculations at each step during MD samplings. Semiempirical QM (SQM) such as AM1 and the self-consistent charge density functional tight binding (SCC-DFTB) methods can be employed to reduce the computational cost on QM/MM calculations and perform direct MD for several nanoseconds, but the results may be less reliable in some cases because of the approximations introduced to SQM models.11–14 On the purely empirical side, a number of approaches such as EVB, ReaxFF, and multisurface adiabatic reactive molecular dynamics were also developed with significant success to describe the dissociation and formation of chemical bonds in a wide range of complex systems without expensive QM calculations, but these methods still introduce a dependence on empirical formalism and parameters for the active site.15–17 Calculation and sampling at an ab initio level are usually required.
Several new methods address the challenges of direct QM/MM MD simulations in different ways, either “static” or “dynamic”. In the class of static approaches, a direct phase space sampling is restricted at the MM or SQM/MM level, which is several orders of magnitude faster than ab initio calculations. It is also possible to obtain approximate reaction free energy changes without direct QM/MM MD as in the QM/MM minimum free-energy path (QM/MM-MFEP) method to minimize the reaction path on the free energy surface of the QM degrees of freedom.18–21 In the QM/MM-MFEP method, the MD samplings on the QM subsystem were replaced by geometry optimizations in an environment with a fixed MM ensemble. However, some additional expensive calculations on the dynamic contributions of the QM subsystem were usually necessary. Another typical static approach is the quantum mechanical thermodynamic-cycle perturbation, in which the free energy profile from SQM/MM MD was corrected to the target ab initio QM/MM level using free energy perturbations.22 The use of non-Boltzmann Bennett reweighting schemes or nonequilibrium work techniques can achieve a better convergence on MD samplings and further decrease the amount of ab initio calculations.23,24 However, the influence of different sampling spaces at two levels of theory cannot be neglected completely in many cases. In the class of dynamic approaches, the discrepancies between the potential energies at two levels are reduced after low-level MD simulations, and then the thermodynamic properties can be calculated based on a direct configurational space sampling on the optimized potential energy surface (PES) with higher accuracy. This class of methods can be further divided into “reparametrization” and “interpolation” styles. In the former, a refinement procedure was designed to adjust some parameters in an existing low-level model to match the high-level calculations on a specific system. Maurer et al. reported a force matching protocol to parametrize biomolecular nonpolarizable force fields to reproduce several properties from QM/MM simulations.25 Plotnikov et al. developed a paradynamics approach to make the EVB potential close to the ab initio potential gradually.26 Zhou and Pu proposed an iterative force matching method to fit some specific reaction parameters in the semiempirical PM3 model to Hartree–Fock on some selected configurations along the reaction path.27 In the latter, the ab initio PES can be represented with an interpolation scheme and then applied to MD evolution. For example, the difference between SQM/MM and ab initio QM/MM potential energies can be approximated as a spline function of a predefined reaction coordinate (RC).28 Another example is the interpolated PES, in which the global PES was constructed using a Taylor expansion on the potential energies of some collected geometries combined with an interpolation weighting function.29,30 Several applications of these dynamic approaches have demonstrated their success,31,32 but there are still some concerns in practice, such as the restriction of function forms in the low-level models for reparametrization and the difficulty to capture the coupling between QM and MM subsystems for interpolation.
To overcome the limitation originated from the physical approximations or fitness functions as discussed above, machine learning techniques such as neural network (NN) are being increasingly used as a sophisticated force field for molecular simulations.33–37 The first goal on machine-learning-based QM/MM simulations is to describe potential energy landscapes with an ab initio accuracy and a force field computational cost. Behler et al. designed a high-dimensional neural network and applied the NN potentials to various systems such as bimetallic nanoparticles and bulk water in the past decade.38–40 In the generalized neural network representation, the total potential energy was expanded as a sum of atomic energies, and each atomic contribution was dependent on its local chemical environment that can be described with a set of symmetry functions as input vectors of NN. Ramakrishnan et al. reported a Δ-machine learning method, in which the difference between low-level and high-level QM calculations was predicted as a correction term using a kernel-based machine learning technique.41 Inspired by these approaches, we recently developed a QM/MM-NN method to predict the potential energy difference between SQM/MM and ab initio QM/MM based on the training data points from SQM/MM MD simulations.42 The free energy changes along the reaction coordinate at the high level were obtained subsequently using a reweighting scheme. Its reliability and efficiency have been demonstrated in our previous work, but the lack of direct configurational space samplings on the high-level QM/MM PES is an inherent deficiency that may lead to statistical errors. The characterization of transition path and reaction dynamics also requires direct MD simulations rather than energy corrections. Therefore, the second goal on machine-learning-based simulations is to perform MD evolution on a self-adaptive NN-predicted PES. Li et al. presented a machine learning method to predict QM atomic forces on materials processes.43 The database for machine learning was growing during MD with a “learn-on-the-fly” strategy, in which additional QM calculations were necessary only when “something new” configurations were encountered. Botu et al. constructed an adaptive, generalizable, and neighborhood informed force field with a machine learning multistep workflow to accelerate ab initio MD for materials simulations.44–46 However, the predictions on chemical or biochemical QM/MM systems have more difficulties because the geometrical changes during a reaction process in solution or enzymes are usually larger and more complex. The MD evolution on a rough NN-predicted PES without tuning carefully may even cause numerical instability. Recently a force-based machine learning method for direct QM/MM MD simulations was developed in our group.47 At each MD step using SQM/MM, an internal force was predicted and added along RC directions to correct the difference of atomic forces between SQM/MM and ab initio QM/MM along RC. The free energy profiles at the ab initio QM/MM level for two testing systems were obtained. However, the force prediction presented in the work was not perfect, and an update on the machine learning model during MD simulations was absent. In addition, the atomic forces rather than energy were predicted directly in the above papers, which hampers a general statistical theory and requires additional energy estimations. Alternatively, Behler et al. developed an adaptive selection scheme for NN-driven MD, in which the database continuously grows when the configurations with diverging NN predictions are sampled and then the high-dimensional NN potentials are retrained on-the-fly.36,37 This scheme can significantly improve the transferability of a preliminary NN model constructed using a small initial database, especially if the NN is applied to explore a new configurational space.
In order to accomplish the second goal of machine-learning-based QM/MM simulations at the ab initio level, in this work we developed a method to perform direct QM/MM MD simulations by combining our QM/MM-NN model reported previously42 and an iterative protocol based on the adaptive selection scheme reported by Behler.36,37 The new method is a dynamic scheme of QM/MM-NN and named as QM/MM-NN MD. Similar to our previous work, a neural network model is first constructed based on the sampled configurations from SQM/MM simulations. The difference between SQM/MM and ab initio QM/MM potential energies is predicted for any configuration. Furthermore, the difference on atomic forces can be calculated based on the functions of energy difference in NN. The QM/MM MD simulations are then performed on the NN-predicted PES in this work. After visiting the approximated high-level configurational space, an iterative procedure is implemented to extend the database for NN training and update the NN-predicted PES for MD evolution in the next iteration cycle. Finally, the free energy calculation or reaction path optimization based on MD samplings is converged at a highly accurate result compared to ab initio QM/MM level. The theory of QM/MM-NN MD will be described in the next section, followed by simulation details, results, and discussions.
THEORY
Structure of QM/MM-NN.
Based on the high-dimensional neural network model reported by Behler et al.,38 we have developed a QM/MM-NN method with modifications for QM/MM calculations.42 We will briefly review the QM/MM-NN method. The schematic structure of a typical QM/MM-NN was illustrated in Figure 1 in our previous paper with more details and discussions.42
Figure 1.
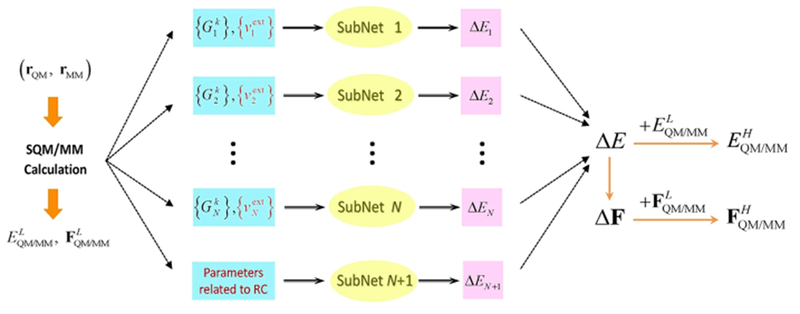
Schematic structure of QM/MM-NN for a system containing N atoms in the QM subsystem. Here rQM and rMM are respectively the Cartesian coordinates of the atoms in the QM and MM subsystem, {} is the symmetry function that depends on rQM, i denotes the QM atoms, k denotes different radial and angular functions with different hyperparameters, and {} is the external electrostatic potential at QM grids close to atom i as a function of rQM and rMM. After semiempirical QM/MM calculations with rQM and rMM, the total potential energy and the corresponding forces on all QM and MM atoms at the low level are known. Then the energy difference between two levels as ΔE is predicted with QM/MM-NN, and the derivative of ΔE with respect to rQM and rMM is calculated analytically. Finally, the total potential energy and the corresponding forces on all QM and MM atoms at the high level is obtained. The differences on the input variables of NN compared to our previous work42 are highlighted in red.
In the QM/MM method, the whole system is divided into a QM subsystem containing the active site and an MM subsystem containing the rest. The total potential energy is written as
| (1) |
where EQM is the quantum mechanical energy of the QM subsystem, EMM is the molecular mechanical energy of the MM subsystem, and , , and are the coupling terms between QM and MM subsystems including electrostatic, van der Waals (vdW), and covalent interactions, respectively. The sum of the first two terms is calculated from an effective QM Hamiltonian as follows
| (2) |
where
| (3) |
is the Hamiltonian of QM subsystem in vacuum determined by the QM model, Zi is the nuclear charge of QM atom i, ql is the point charge of MM atom l, ri and rl are the positions of atom i and l, respectively, and ρ(r′) is the electron density of QM subsystem. The remaining terms in eq 1 are calculated with MM force fields. Consider two QM/MM models in which only the QM methods are different. One is the high-level model that achieves higher accuracy at an expensive computational cost, such as an ab initio QM/MM method. Another is the low-level model that is more efficient but less accurate, such as a semiempirical QM/MM method. The high-level total potential energy can be expressed as the low-level total potential energy with a correction term, that is,
| (4) |
where and are the high-level ab initio and low-level semiempirical QM Hamiltonian in vacuum, respectively, and ΨH and ΨL are the electronic wave functions obtained from the corresponding QM calculations with MM charges embedded.
The potential energy difference between ab initio and semi-empirical QM/MM methods, that is, the correction term in eq 4, is denoted as
| (5) |
In our QM/MM-NN, ΔE is predicted as the output of NN model. The ab initio QM/MM potential and atomic forces can be hereby approximated from the SQM/MM calculation and NN prediction, both of which are several orders of magnitude faster than ab initio methods. In the high-dimensional neural network scheme, ΔE can be represented as
| (6) |
where N is the number of QM atoms. Here the whole network is divided into N + 1 subnets. The first N subnets are the atomic subnets, each describing the atomic contribution of atom i, while the last one is ΔEN+1, the RC subnet describing the contribution of reaction coordinate. Note that ΔEN+1 was denoted as ΔERC in our previous paper. Following the standard neural network scheme, we have
| (7) |
for the ith subnet, where k and j denote the nodes in input and hidden layers with the total number of M and L in the ith subnet, respectively, is the input variable in the kth node in the input layer, Wijk and wij are the weight parameters connecting two nodes in neighboring layers, bij and bi are the bias weights of hidden and output layers, and f(x) is the nonlinear function such as the hyperbolic function used in this paper. Here the subnet has one hidden layer for simplicity, but it can be extended directly to more complex structures.
As shown in eq 5, ΔE is a function of the positions of QM and MM atoms. The input variables for N atomic subnets, that is, in eq 7 if 1 ≤ i ≤ N, are classified into two groups in order to capture the influence of QM and MM degrees of freedom, respectively. The first group includes the atom-centered symmetry functions that describe the local chemical environment of each QM atom with the relative positions of other neighboring QM atoms. Two types of symmetry functions involving radial and angular functions are used in this work. The radial function of atom i is
| (8) |
where fc(Rij) is the cutoff function such as
| (9) |
Rij is the distance between QM atom i and j, and Rc, Rs, and η are hyperparameters of NN. The angular function of atom i is
| (10) |
where θijk is the angle that consists of atom i, j, and k, Rij, Rjk and Rik denote the distances between two atoms, and ξ is another hyperparameter of NN. Several radial and angular functions with different sets of (η, ξ) are used in each atomic subnet. More details on symmetry functions have been discussed in Behler’s papers.48,49 The second group of input variables includes the external electrostatic potentials at different QM grids, which are generated from the surrounding MM charges, that is,
| (11) |
where ql and rl are the point charge and position of MM atom l, respectively, and rm is the position of QM grid m close to atom i, which is expressed as a linear combination of the positions of QM atom i and other QM atoms in the current work. More complex representations such as electrostatic multipole moments centered on solute atoms or a set of radial and spherical harmonic basis functions50,51 can be also applied to expand the MM polarization effect. In spite of the function form, the key point to design this input feature is to decrease the thousands of MM degrees of freedom to a low-dimensional data representation.
The RC subnet was introduced to describe the information on reaction coordinates in a more explicit way. On one hand, the predefined RC can capture the major physical or chemical change in molecular processes. On the other hand, definition on the accurate RC is very challenging for many chemical reactions, and thus, an approximate RC in a low-dimensional space is often constructed in practice. To exploit the guidance of RC and overcome its limitation, we employed several parameters related to RC as the input variables of RC subnet, that is, in eq 7 for i = N + 1. A typical input feature can involve not only internal coordinates but also solvent variables or virtual coupling parameters.52,53 Its choice is very flexible because increasing the number of input nodes in NN is much easier than increasing the dimensionality of RC in MD samplings.
It is worthwhile to point out that there are three changes on the structure of QM/MM-NN compared with our previous method. The first one is due to the feature that different subnets are built for different atoms in QM/MM-NN. This is not a problem for energy predictions on our testing systems because most of QM atoms can be distinguished from others according to the molecular graph of the QM subsystem, while the “identical” atoms defined as the QM atoms that are indistinguishable based on molecular topology, such as the hydrogen atoms connected to the same heavy atom in the QM subsystem, can be permuted in advance to satisfy a predefined order of their bond lengths. For MD simulations, however, it will cause some errors since the NN-predicted PES is discontinuous at the configurations in which the bond lengths related to identical atoms are equal. A possible choice is to keep different subnets for different atoms but introduce an exchange scheme with a smooth switch function during MD.54 As an alternative, we assigned the same subnet to identical atoms in this work in order to maintain permutation invariance, which may cause a slight loss of the accuracy of NN as a compromise. Note that the definition of identical atoms is different from that in Behler’s work in which all atoms of the same element were described identically in the high-dimensional NN model.38 The permutation invariance is also considered on the positions of QM grids in eq 11 and the input variables in the RC subnet. The second change is to replace the Mulliken charges on QM atoms by the MM electrostatic potentials at QM grids to avoid the complicated and expensive calculation on the gradient of QM atomic charges.55,56 The third change is to introduce more parameters such as internal coordinates to the input features in the RC subnet, which is useful to collect the “chemically novel” configurations more efficiently. The schematic structure of the present QM/MM-NN used in this paper is illustrated in Figure 1.
Adaptive MD Procedure with QM/MM-NN.
In comparison with potential energy predictions using QM/MM-NN, MD simulations on the NN-predicted PES are more difficult because of two factors. First, the overlap between the sampling spaces at two levels of theory may be poor. In other words, any neural network model based on the training points in the SQM/MM sampling space cannot imply the same degree of accuracy for the data points in the ab initio QM/MM sampling space. Second, the error on the atomic force prediction of any configuration during MD may dominate the following samplings and cause failure on simulations. A schematic view of one-dimensional potential energy surfaces predicted with low-level, high-level, and NN models is illustrated in Figure 2. In the region in shadow, the NN-predicted PES is consistent with that obtained using the high-level model, while the results of the low-level model have a large amount of deviation. In the region out of shadow, however, the energy changes along coordinate at the low level and high level have a similar tendency qualitatively, while the NN model gives a completely incorrect representation since the configurations in this region are excluded from the training points for NN. In addition, the simulation using QM/MM may come across a convergence problem on electronic structure calculations when a configuration with high energy is encountered at one MD step based on the NN. It may be more frequent during the simulation on chemical reactions in aqueous solution because the degrees of freedom in these systems are flexible.
Figure 2.

Schematic view of potential energy surfaces with high-level QM/MM (blue), low-level QM/MM (orange), and QM/MM-NN (red). The range of coordinates of the configurations for NN training is in shadow. For the samples within the interval of training points, the QM/MM-NN PES is much more accurate than the low-level result compared with the high-level QM/MM PES. For the samples outside the boundary of the database, the low-level QM/MM PES is similar to the high-level reference qualitatively, but the QM/MM-NN prediction is completely incorrect, which may cause convergence failure and/or numerical instability during MD evolution on the NN-predicted PES.
In the present work, two features are considered to improve the performance on MD simulations on the NN-predicted PES. First, when a configuration sampled in QM/MM-NN MD is outside the database for NN training, it should be appended to the database with a probability in order to adjust the NN model. Second, the propagation on the configuration outside NN database should be treated carefully, which requires a compromise between the computational cost and accuracy on QM/MM calculation at the present integration step. In this paper, an adaptive algorithm is implemented on the basis of the adaptive selection scheme36,37 with some adaptions to the above features of QM/MM-NN in order to update NN and repeat MD iteratively. We outline the procedure as follows:
- Initialization steps
-
(1)Define the reaction coordinate that involves one or a set of collective variables of the system and perform SQM/MM MD simulations in different sampling windows along RC.
-
(2)Select several snapshots randomly from SQM/MM MD trajectories in step 1 and calculate their ab initio QM/MM potential energies to build the initial database for NN training.
-
(1)
- Iteration steps
-
(3)Construct the QM/MM-NN based on the current database with the combined genetic and steep-descent optimization algorithms reported in our previous work.42
-
(4)Perform QM/MM MD simulations on the NN-predicted PES using QM/MM-NN obtained in step 3. At one MD step, each NN input variable in eq 7 is first calculated and compared with its boundary determined by the data points in the current training set. Then, the positions and velocities of all atoms are propagated forward in time in three cases:
-
(a)Each input variable is inside its boundary. In this case, the QM/MM potential energy is obtained using eqs 4–7, and the corresponding force acting on atom i is denoted as and calculated as
where atom i belongs to either QM or MM sub-system, ri is the position of atom i, N is the number of QM atoms, j denotes the subnets, k denotes the input nodes with the total number of M in each subnet, is the low-level force calculated with SQM/MM, ΔE is the potential energy difference between SQM/MM and ab initio QM/MM, ΔEj is the atomic energy contribution of the jth subnet defined in eq 7, and is the input variable in the kth input node in the jth subnet as discussed in the above subsection. Note that is easy to calculate since has been written as an explicit function of atomic positions.(12) -
(b)Any input variable as a symmetry function (that is, the first group of input features in the atomic subnet) or any input variable in the RC subnet is outside its boundary. In this case, the QM/MM potential energy and forces are calculated using the low-level SQM/MM model, and the current configuration is saved in preparation for the extension of NN database.
-
(c)Any input variable as an MM electrostatic potential at a QM grid (that is, the second group of input features in the atomic subnet) is outside its boundary, but other input variables mentioned in case b are inside. In this case, the QM/MM potential energy and forces are calculated as case a, but the current configuration is saved as case b in preparation to extend the database. In the rest of this paper, the collection of configurations satisfying case b will be called the “outside QM boundary”, and that satisfying either case b or c will be called the “outside NN boundary”.
-
(a)
-
(5)Calculate the properties interested, for example, the free energy change along RC or the optimized transition path connected two stable states, on the basis of MD samplings in step 4, and check the convergence with the results obtained in the previous iteration cycle. Stop if converged and the number of the sampled configurations outside the boundary in the current cycle is small enough; otherwise, go to step 6.
-
(6)Select several snapshots from the configurations saved in step 4 randomly, calculate their ab initio QM/MM potential energies, and add them to the current database. Different types of strategy can be employed to select the data points. Here we used three criteria. First, the numbers of additional data points from different sampling windows should be in proportion to the numbers of configurations outside the boundary in the corresponding windows. Second, the data points selected from the same trajectory should be at least 100 MD integration steps apart in order to reduce the correlation. Finally, different probabilities for random selections should be assigned to different types of input features. For example, the convergence of iterations was observed to be accelerated when the input variables in the RC subnet have priority over others. For simplicity, the total number of additional snapshots at each iteration cycle is set as the same as that in the initial database unless the sampled configurations outside the NN boundary in the current cycle is insufficient to reach the number under the above criteria, which may take place in the second last cycle for our testing systems.
-
(7)Repeat steps 3–6 until convergence.
-
(3)
It should be emphasized that the idea of adaptive machine learning model during MD simulations is not new. For example, Csányi et al. reported a “learn-on-the-fly” scheme in which the accuracy of the interatomic potentials was monitored and improved using new QM data.57 Recent works include different adaptive schemes used for diverse machine learning models such as Gaussian process,43 linearly parametrized interatomic potentials,58 and high-dimensional NN models.36,37 The motivation of the present work is to perform NN-driven QM/MM MD simulations at the ab initio level by combining an appropriate adaptive scheme with QM/MM-NN. Compared with the previous adaptive selection scheme for NN,37 it is worthwhile to discuss two features. First, the QM/MM-NN potential is fixed during MD samplings at each iteration cycle and retrained using both existing and additional configurations after MD, which can be called a “macroiteration”. In comparison, in the previous works the energy function was usually adjusted immediately to mimic the high-level model when a new conformation was sampled,37,58 which can be called a “microiteration”. The latter may be the only choice if the total potential energy rather than the energy difference between two levels was predicted with NN, because the failure on MD simulations would take place very frequently after encountering a chemically novel configuration. In our QM/MM-NN scheme, however, the low-level forces can be applied in such a case to continue less accurate but numerically stable MD samplings. On one hand, there are some practical advantages of the macroiteration procedure herein. The number of NN reoptimizations is as small as the number of iteration cycles. The additional configurations can be selected more systematically, which is useful to obtain more representative data points with a lower correlation. The communication between different MD trajectories becomes unnecessary even if parallel simulations such as umbrella sampling were performed. On the other hand, the microiteration procedure can decrease the total number of MD steps and further improve the efficiency of QM/MM-NN MD. Second, new configurations are detected based on the boundaries of input variables of NN in this work, while the uncertainty analysis based on a machine-learning ensemble was suggested as a better choice because of the presence of insufficiently sampled regions where all input variables are inside their boundaries and the lack of a regular high-dimensional grid of data points.37,59 However, our results on QM/MM solvation free energy calculations using different machine-learning models show that the uncertainty analysis may also lead to failure on MD simulations, while the criterion based on the current boundary seems more robust. Since both algorithms on the credibility of machine learning predictions are imperfect without any rigorous theory foundation, how to identify and explore insufficiently sampled regions with NN is still an open problem.
SIMULATION DETAILS
To evaluate the reliability of this method, we first calculated the free energy changes along a predefined reaction coordinate for two aqueous systems with different QM/MM models. One system is the SN2 reaction of CH3Cl+Cl− → Cl− + CH3Cl in water; the other is the intramolecular proton transfer reaction for glycine as in water. For the SN2 reaction, the complex of CH3Cl + Cl− was set as the QM subsystem and solvated in a cubic water box of 48 Å × 48 Å × 48 Å. For the proton transfer reaction, the glycine molecule was set as the QM subsystem and solvated in a cubic box of 64 Å × 64 Å × 64 Å. The MM subsystem for the SN2 and proton transfer reactions contains 3600 and 8650 water molecules, respectively. For both reactions, the TIP3P water model was applied under periodic boundary condition,60 and the CHARMM22 force field was employed to calculate the QM/MM vdW interactions.61 The cutoff distance for nonbonded interactions for the SN2 and proton transfer reactions was set as 14 and 12 Å, respectively. The DFT method with B3LYP hybrid functional62,63 and 6-31G(d) basis set and the SCC-DFTB method with the second-order formulation (DFTB2/MIO)12,64 were selected as the high-level and low-level QM models, respectively. Note that we chose the two QM models based on the difference of the QM/MM MD simulation results, while their comparisons with experiments are not important for our purpose presently. It should be also noted that the newly issued versions of DFTB such as DFTB3/3OB can provide more accurate results for a wide range of organic molecules.65,66 The MD simulations using umbrella sampling were carried out after geometry optimization on solute in gas phase and solvent equilibration. For the SN2 reaction, the reaction coordinate was chosen as z = dCCl1 − dCCl2, where dij is the distance between atom i and j, and the umbrella samplings with 37 windows centered from z = −2.5 to 2.5 Å were applied. For the proton transfer reaction of glycine, the reaction coordinate was chosen as z = dNH − dOH, where H is the transferred proton, and the umbrella samplings with 25 windows centering from z = −1.5 to 1.5 Å were applied. The free energy changes along z were calculated with the weighted histogram analysis method.67,68 For both reactions, the MD simulations at the DFTB2/MIO/MM and B3LYP/6-31G(d)/MM levels were performed for 50 ps for each window, respectively. The same simulation times were applied to QM/MM-NN MD in each cycle. The MD integration time step was set as 1 fs, and the system temperature was maintained at 300 K with a Berendsen thermostat.69
To demonstrate the capability of the direct QM/MM-NN MD simulations, we next optimized the reaction path for the first system on the free energy surface using the finite-temperature string (FTS) method, which was first developed by E et al.70,71 The improved FTS version in collective variable (CV) space72 was used in this work to capture the dynamic contributions of the whole system to the free energy. More details on FTS, which involve the MD evolution on the energy landscape with a reflecting boundary condition at the boundary of the Voronoi cell, the calculation on the average position of each image in CV space, and the smoothing and reparametrization processes on the string, can be seen in the related paper.72 For the SN2 reaction, the bond lengths dCCl1 and dCCl2 were selected as two CVs and represented on the string. The optimized geometries of reactant and product were set as the end points of the string, and 48 images were interpolated as the intermediates along the string in two-dimensional CV space. The position of each image was updated each 10 MD steps. A half-side harmonic restraint was added on the direction of dCCl1 − dCCl2 with a force constant of 20 kcal⋅mol−1⋅Å−2 when its value is less than −2.5 Å or more than 2.5 Å. Three QM/MM models, two low-level methods as AM1/MM and DFTB2/MIO/MM and one high-level method as B3LYP/6-31G(d)/MM, were employed. The FTS calculations at the SQM/MM and ab initio QM/MM levels were performed for 2 × 104 optimization steps, respectively. The same steps were applied to QM/MM-NN MD in each cycle. The convergence of the string at low levels was further checked with longer simulations for 1 × 105 optimization steps. The MD integration time step was set as 1 fs and the system temperature was maintained at 300 K using Langevin dynamics.73 All simulations for the SN2 reaction system were implemented using an in-house QM4D program package74 combined with GAUSSIAN 03 program75 for DFT calculations and Amber SQM (version 14) program76,77 for AM1 and DFTB calculations. All simulations for glycine were implemented using QM4D combined with GAUSSIAN 03 for DFT calculations.
RESULTS AND DISCUSSION
Free Energy Calculation on SN2 Reaction in Water.
In the initialization steps, the database for NN training was constructed based on DFTB2/MIO/MM MD simulations in the same way as that in our previous work.42 The training set was set up with 20 samples from each window, that is, with the total number of data points as 380. Additional 20 samples from each window were adopted to build the testing set. Note that only 19 windows centered from z = −2.5 to 0.0 Å were used in the database because of the symmetry of this reaction along the reaction coordinate. Besides the subnets of hydrogen atoms as discussed above, the NN parameters in the subnets for two chlorine atoms are identical for permutation invariance. In each atomic subnet, 5 radial and 5 angular functions were employed with the hyperparameters of (ηC ηH ηCl, ξC ξH ξCl) as follows: (0.120, 0.300, 0.060, 0.120, 0.300, 0.060), (0.160, 0.400, 0.080, 0.160, 0.400, 0.080), (0.200, 0.500, 0.100, 0.200, 0.500, 0.100), (0.256, 0.556, 0.156, 0.400, 0.700, 0.300), and (0.312, 0.612, 0.212, 0.600, 0.900, 0.500). The units of η are bohr−2. The values of Rc and Rs were set as 6.0 and 0.0 Å, respectively. In all atomic subnets, the electrostatic potentials on the positions of 66 QM grids in total were introduced to represent MM environment. In the RC subnet, the bond lengths dCCl1 and dCCl2 and the angle that consists of C, Cl1, and Cl2 were selected as the input variables. For this system, we defined two sets of identical atoms using the same atomic subnet, respectively. One includes three hydrogen atoms, another includes two chlorine atoms. It happens to be equivalent to the case in which all atoms of the same element are identical in NN38 because of the small number of the QM degrees of freedom and the symmetry of this reaction. The root mean squared errors (RMSEs) for the potential energy differences between DFTB2/MIO/MM and B3LYP/6-31G(d)/MM on the training and testing sets were 1.03 and 1.09 kcal/mol, respectively (see Table 1). The values are similar to that in our previous paper using a similar NN model with different input variables (1.15 and 1.16 kcal/mol).42
Table 1.
Root Mean Squared Errors (kcal/mol) of Training and Testing Sets with Q2 Values (in Parentheses)a and Percentages of MD Samples outside the Boundary of the Database (%)b in Different Iteration Cycles for SN2 Reaction with Corrections from DFTB2/MIO/MM to B3LYP/6-31G(d)/MM
| RMSE |
percentage outside boundary |
|||
|---|---|---|---|---|
| training set | testing set | NN boundary | QM boundary | |
| cycle 1 | 1.03 | 1.09 (0.766) | 28.6 | 27.8 |
| cycle 2 | 0.99 | 1.07 (0.789) | 1.6 | 0.7 |
| cycle 3 | 1.00 | 1.06 (0.749) | 0.2 | <0.1 |
, where and are the predicted and reference values of QM/MM potential energy difference between two levels for the ith sample in the testing set, respectively, and is the average of
The explanations of outside QM boundary and outside NN boundary are in step 4 in the subsection Adaptive MD Procedure with QM/MM-NN in the section Theory.
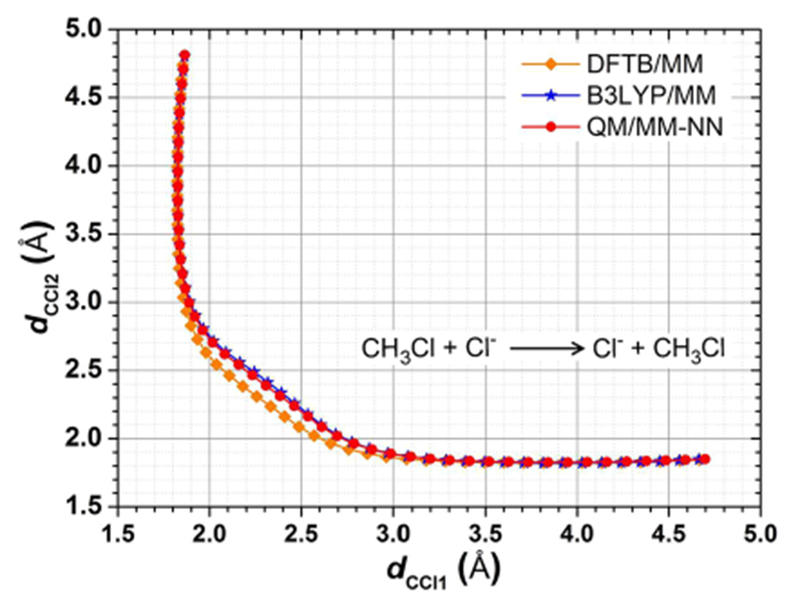
The free energy barrier was estimated as 26.8 and 22.0 kcal/mol from DFTB2/MIO/MM and direct B3LYP/6-31G(d)/MM MD simulations, respectively. The constructed NN was applied to perform MD simulations with the algorithm in step 4. The free energy barrier was calculated as 22.8 kcal/mol, which is similar to the results obtained at the high level. However, 28.6% of the configurations in all trajectories were outside NN boundary, and the major portion (27.8%) was outside the QM boundary and calculated at the DFTB2/MIO/MM level for MD evolution. Therefore, we performed the iteration steps to adapt NN with the growing database and repeat MD simulations on the updated NN-predicted PES. The free energy changes along the reaction coordinate were shown in Figure 3a. It can be seen that the free energy changes obtained in the second and third cycle were very similar, in which the barrier heights were estimated as 21.7 and 21.8 kcal/mol, respectively. As shown in Table 1, the percentage of MD samples outside NN and QM boundary in the second cycle was decreased to 1.6% and 0.7%, respectively, and that in the third cycle was 0.2% and less than 0.1%, respectively. The RMSEs on the training and testing sets for the updated NNs were 1.0–1.1 kcal/mol. The QM/MM-NN MD simulations can achieve convergence after two iteration cycles, and the converged free energy profile agrees well with that obtained using direct ab initio QM/MM MD (see Figure 3b). A small discrepancy within 0.5 kcal/mol along the free energy profiles from DFTB2/MIO/MM and QM/MM-NN MD simulations was observed between Berendsen and Langevin thermostats, which indicates a slight dependence of the present calculations on the statistical mechanical ensemble associated with thermostats.
Figure 3.

Potential of mean force for the SN2 reaction. (a) Convergence of QM/MM-NN MD during iteration steps. Different colors and shapes represent different iteration cycles. (b) Comparison between low-level QM/MM, high-level QM/MM, and QM/MM-NN. Different colors and shapes represent different methods (orange diamond DFTB2/MIO/MM MD; red circle QM/MM-NN MD in the third iteration cycle; blue star direct B3LYP/6-31G(d)/MM MD).
Three types of calculations are involved in our approach. The first type is DFTB2/MIO/MM and NN-driven MD simulations. It has been well-known that DFTB is usually 100–1000 times faster than DFT.64,78,79 The QM/MM-NN prediction requires only a small fraction more than the computation needed for DFTB. For this reaction, we performed DFTB2/MIO/MM MD for 50 ps in the initialization steps and NN-driven MD (i.e., DFTB2/MIO/MM MD with NN corrections at each MD step) for totally 150 ps during 3 cycles in the iteration steps. Therefore, the computational cost on all MD simulations is about 0.4–4.5% of that on the direct ab initio QM/MM MD for 50 ps using DFT with medium sized basis sets. The second type is the B3LYP/6-31G(d)/MM single point calculations in order to construct the database for NN training. As discussed in our previous work, 20 samples from each window are sufficient for training, which requires 20 ab initio QM/MM calculations.42 No more than this number of samples were appended to the database after MD simulations in each iteration cycle, and thus, the computational cost on all ab initio QM/MM calculations is about 0.1–0.2% of that on direct ab initio QM/MM MD. The third type is the optimization on the parameters of QM/MM-NN. On one hand, its efficiency is determined by the implemented training algorithm,80–83 which is an active research topic but outside the scope of this work. On the other hand, a single NN covering the whole range of reaction coordinate is optimized in our method to predict the potential energy of any configuration in any window. Therefore, the NN optimization spends much less CPU time compared with the umbrella samplings with 20–40 windows. For this system, the CPU time on all NN optimizations in the initialization and iteration steps is less than 0.1% of that on direct ab initio QM/MM MD. In summary, the total CPU time on QM/MM-NN MD to simulate this reaction is about 0.5–5.0% of that on the high-level QM/MM MD, showing the saving in computational cost as around 2 orders of magnitude.
Free Energy Calculation on Proton Transfer Reaction for Glycine in Water.
The ab initio QM/MM potential energies of glycine with different conformations from zwitterion to neutral form during the proton transfer process were predicted with NN. The training set was constructed with 20 samples from each window during SQM/MM simulations, that is, with the total number of data points as 500. Additional 20 samples from each window were employed for the testing set. In each atomic subnet, 5 radial and 5 angular functions were used with the hyperparameters of (ηC ηO, ηN, ηH, ξC ξO, ξN, ξH) as follows: (0.480, 0.120, 0.480, 0.120, 0.480, 0.540, 0.600, 0.360), (0.640, 0.160, 0.640, 0.160, 0.640, 0.720, 0.800, 0.480), (0.800, 0.200, 0.800, 0.200, 0.800, 0.900, 1.000, 0.600), (0.856, 0.256, 0.856, 0.256, 1.000, 1.100, 1.200, 0.800), and (0.912, 0.312, 0.912, 0.312, 1.200, 1.300, 1.400, 1.000). The units of η are bohr−2. The values of Rc and Rs were set as 6.0 and 0.0 Å, respectively. In all atomic subnets, the electrostatic potentials on the positions of 190 QM grids in total were introduced to represent MM environment. In the RC subnet, the bond lengths dNH and dOH and the angle that consists of N, H, and O were selected as the input variables, where H is the transferred proton. For this system, we defined two sets of identical atoms using the same atomic subnet, respectively. One involves two hydrogen atoms in NH2, and another involves two hydrogen atoms in CH2. For all heavy atoms and the transfer proton, different subnets were applied to different atoms. In the initialization steps, the RMSE on the training set was 1.03 kcal/mol, and that on the testing set was 1.22 kcal/mol (see Table 2), which are comparable with the accuracy reported in our previous paper (1.22 and 1.25 kcal/mol).42
Table 2.
Root Mean Squared Errors (kcal/mol) of Training and Testing Sets with Q2 Values (in Parentheses) and Percentages of MD Samples outside the Boundary of the Database (%) in Different Iteration Cycles for Proton Transfer Reaction of Glycine with Corrections from DFTB2/MIO/MM to B3LYP/6-31G(d)/MM
| RMSE |
percentage outside boundary |
|||
|---|---|---|---|---|
| training set | testing set | NN boundary | QM boundary | |
| cycle 1 | 1.03 | 1.22 (0.972) | 53.3 | 50.3 |
| cycle 2 | 1.15 | 1.30 (0.969) | 4.4 | 1.2 |
| cycle 3 | 1.17 | 1.23 (0.977) | 1.5 | 0.2 |
| cycle 4 | 1.18 | 1.24 (0.976) | 0.8 | <0.1 |
| cycle 5 | 1.18 | 1.26 (0.973) | 0.3 | <0.1 |
The free energy difference and barrier were estimated as −7.6 and 5.3 kcal/mol with DFTB2/MIO/MM MD simulations, respectively, while the corresponding values calculated using direct B3LYP/6-31G(d)/MM MD were 8.1 and 10.2 kcal/mol, respectively. The latter predicts the predominant form of aqueous glycine as zwitterion correctly. Applying the NN model constructed based on DFTB2/MIO/MM samplings to perform MD simulations, the free energy difference and barrier were obtained as 0.4 and 7.7 kcal/mol, respectively, both of which were underestimated compared with the high-level free energy calculation. As shown in Table 2, more than half (53.3%) of the configurations from all windows were outside NN boundary, and the major portion (50.3%) was outside QM boundary. During the second cycle of the iteration steps, the percentage of MD samples outside NN and QM boundary was decreased respectively to 4.4% and 1.2%, but the free energy profile was a little overestimated, where the difference and barrier were 8.9 and 10.7 kcal/mol, respectively. As shown in Figure 4a, the convergence can be achieved after four iteration cycles. The free energy difference and barrier were estimated respectively as 7.7 and 9.9 kcal/mol in the last cycle, in which 0.3% and less than 0.1% of configurations were outside NN and QM boundary, respectively. The free energy changes along the entire reaction path are consistent with the results using direct ab initio QM/MM MD (see Figure 4b). The RMSEs for the updated NNs were 1.1–1.3 kcal/mol. Again, the difference on the free energy profiles between Berendsen and Langevin thermostats was within 0.5 kcal/mol.
Figure 4.

Potential of mean force for the proton transfer reaction of glycine. (a) Convergence of QM/MM-NN MD during iteration steps. Different colors and shapes represent different iteration cycles. (b) Comparison between low-level QM/MM, high-level QM/MM, and QM/MM-NN. Different colors and shapes represent different methods (orange diamond DFTB2/MIO/MM MD; red circle QM/MM-NN MD in the fifth iteration cycle; blue star direct B3LYP/6-31G(d)/MM MD).
The savings in computational cost on this system can be estimated in the same way as discussed above. First, the DFTB2/MIO/MM and NN-driven MD simulations were carried out for 50 and 250 ps in the initialization and iteration steps, respectively, which consume the computational time as about 0.6–7.0% of that on direct ab initio QM/MM MD for 50 ps. Second, the number of iteration cycles was increased to five, so the computational cost on ab initio QM/MM calculations to build the database is about 0.2–0.4% of that on direct ab initio QM/MM MD. Finally, the CPU time on NN optimizations was observed as around 0.2–0.4% of that on direct ab initio QM/MM MD for this system. The computations on NN training are more expensive than that for the first system because of a larger number of atomic subnets and more input variables for MM representation in each atomic subnet for aqueous glycine. The total CPU time for QM/MM-NN MD simulations is about 1–8% of that on the high-level QM/MM MD, showing a computational saving of about 10–100.
For this system, it can be seen that the free energy profile in the third cycle is similar to the converged result. For example, the free energy difference and barrier were respectively 8.2 and 9.9 kcal/mol, which have a small difference within 0.5 kcal/mol from the corresponding values in the last cycle. During MD simulations in this cycle, the percentage of the configurations outside NN and QM boundary was only 1.5% and 0.2%, respectively. The same tendency was observed for the first system in the second iteration cycle. It suggests that the free energy changes calculated in the iteration cycle of QM/MM-NN MD may be good enough when the percentage of MD samples outside QM boundary is less than 1% and/or that outside NN boundary is less than 2%. The application of the looser criterion can further reduce the computational cost on this method by 25–35%.
Transition Path Optimization on SN2 Reaction in Water.
The transition path connecting the reactant and product of the SN2 reaction of the first system was optimized using the FTS method72 in the two-dimensional CV space that consists of two bond lengths as dCCl1 and dCCl2. The bond lengths between C and Cl in the transition state can be further identified from FTS because this reaction is symmetric along dCCl1–dCCl2, which leads to dCCl1 = dCCl2 in the transition state independent of the model applied to potential energy calculations. The locations of the optimized strings in CV space are dissimilar using different QM methods. The C–Cl bond length in the transition state was calculated as about 2.17, 2.28, and 2.36 A at the AM1/MM, DFTB2/MIO/MM, and B3LYP/6-31G(d)/MM levels, respectively. In addition, the FTS optimization using AM1/MM underestimates the C–Cl bond length in CH3Cl in the reactant and product regions by about 0.1 Å compared with that using the two other methods.
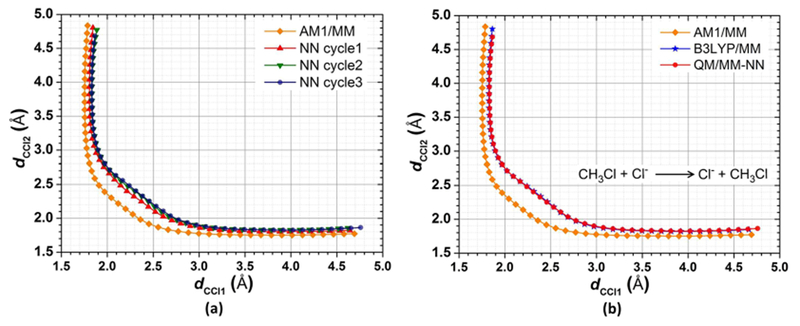
We used DFTB2/MIO/MM as the low-level SQM/MM method. The existing NN model that has been constructed iteratively during umbrella sampling on the same system was applied directly. The algorithm in step 4 was followed. At each MD step in FTS, the potential energy difference between DFTB2/MIO/MM and B3LYP/6-31G(d)/MM for the current configuration was predicted with NN, and then, the positions and velocities of all atoms were propagated on the NN-predicted PES. The iterative procedure to update NN was absent during the FTS calculation. As shown in Figure 5, the deviation of the optimized transition path at the DFTB2/MIO/MM level from that at the ab initio QM/MM level can be reduced significantly with NN corrections. It indicates that an existing NN model constructed during an adaptive procedure can be used for different sampling algorithms for various purposes as long as the same low-level and high-level QM/MM methods are applied to the same system.
Figure 5.
Transition path for the SN2 reaction with FTS optimization in two-dimensional collective variable space without the adaptive procedure. Different colors and shapes represent different methods (orange diamond DFTB2/MIO/MM; red circle QM/MM-NN with the existing NN model that has been constructed iteratively during umbrella sampling along one-dimensional reaction coordinate dCCl1–dCCl2, see subsection Free Energy Calculation on SN2 Reaction in Water in section Results and Discussion; blue star B3LYP/6-31G(d)/MM).
To further validate the performance of our adaptive procedure, we next employed AM1/MM as the low-level model, which has a larger deviation from the optimized transition path at the ab initio QM/MM level, and then implemented the adaptive procedure of QM/MM-NN MD during FTS optimizations. The potential energy difference between AM1/MM and B3LYP/6-31G(d)/MM for any sampled configuration in FTS was predicted with the adaptive NN. Starting from FTS calculations at the AM1/MM level, the initial training set was generated with 20 samples from each image along the string, that is, with the total number of data points as 1000. Additional 20 samples from each image were selected for the testing set. Note that an “image” in FTS is analogous to a “window” in umbrella sampling. In each atomic subnet, 7 radial and 7 angular functions were introduced with the hyperparameters of (ηC ηH, ηCl, ξC ξH ξCl) as follows: (0.080, 0.200, 0.040, 0.080, 0.200, 0.040), (0.120, 0.300, 0.060, 0.120, 0.300, 0.060), (0.160, 0.400, 0.080, 0.160, 0.400, 0.080), (0.200, 0.500, 0.100, 0.200, 0.500, 0.100), (0.256, 0.556, 0.156, 0.400, 0.700, 0.300), (0.312, 0.612, 0.212, 0.600, 0.900, 0.500), and (0.368, 0.668, 0.268, 0.800, 1.100, 0.700). The units of η are bohr−2. Other hyperparameters of NN were set as the same as that reported in the first subsection in this section. As shown in Table 3, the RMSEs on the training and testing sets in the initialization steps were 0.75 and 0.80 kcal/mol, respectively. Applying this NN to FTS and following the MD algorithm in step 4, we obtained a string with a small deviation from the high-level result. The percentage of the samples outside NN and QM boundary in all trajectories was 31.6% and 30.6%, respectively (see Table 3). The iteration steps were then performed to update NN and repeat FTS optimizations for 2 × 104 steps in each cycle. As shown in Figure 6, the strings obtained in the second and third cycle were very similar and in good agreement with the ab initio QM/MM optimized reaction path. Less than 0.1% of configurations were outside NN and QM boundary in the last cycle. The RMSEs for the updated NN were 0.7–0.8 kcal/mol. The savings in CPU time are comparable with that during umbrella samplings on the same system, again 2 orders of magnitude faster than the high-level FTS calculations.
Table 3.
Root Mean Squared Errors (kcal/mol) of Training and Testing Sets with Q2 Values (in Parentheses) and Percentages of MD Samples outside the Boundary of the Database (%) in Different Iteration Cycles for SN2 Reaction with Corrections from AM1/MM to B3LYP/6-31G(d)/MM
| RMSE |
percentage outside boundary |
|||
|---|---|---|---|---|
| training set | testing set | NN boundary | QM boundary | |
| cycle 1 | 0.75 | 0.80 (0.942) | 31.6 | 30.6 |
| cycle 2 | 0.75 | 0.80 (0.973) | 0.6 | <0.1 |
| cycle 3 | 0.70 | 0.81 (0.968) | <0.1 | <0.1 |
Figure 6.
Transition path for the SN2 reaction with FTS optimization in two-dimensional collective variable space. (a) Convergence of QM/MM-NN during iteration steps. Different colors and shapes represent different iteration cycles. (b) Comparison between low-level QM/MM, high-level QM/MM, and QM/MM-NN. Different colors and shapes represent different methods (orange diamond AM1/MM; red circle QM/MM-NN in the third iteration cycle; blue star B3LYP/6-31G(d)/MM).
Further Improvements and Extensions.
The accuracy and efficiency of the present method can be further improved in three aspects. The first one is a better modeling of the neural network. For example, the sampled configurations can be classified based on the clustering technique or structure-based sampling,84,85 which would be useful to optimize the size of the growing database to further reduce the computational cost on ab initio calculations and NN optimizations. The cutoff function in eq 9 can be also improved on account of the discontinuity of its second derivative at the cutoff distance. Figure S1 shows good energy conservation on both examples with a total energy drift smaller than 5 × 10−7 kcal/mol per atom per picosecond during a 20 ps NVE simulation, which indicates the reliability of the present cutoff function for our testing systems. Other switch functions with continuous first and second derivatives are better than that in eq 9, particularly for some more complex reactions with a large QM subsystem.48,86,87 In addition, although we focus exclusively in this paper on neural networks, there are many other machine learning approaches such as kernel ridge regressions combined with a Coulomb matrix descriptor to construct a sophisticated potential energy surface efficiently.88,89 A systematic assessment of different machine learning potentials for QM/MM MD simulations would be addressed in the future. The second aspect is the application of advanced MD techniques. For example, the enhance sampling such as the generalized ensemble methods90,91 can be introduced for more uniform distribution and increase the sampling space of data points for training. Special care should be also taken on the reliability of the statistical mechanical ensemble associated with QM/MM MD simulations.92 Finally, it can be expected that the time savings on QM/MM-NN MD would be increased significantly if more expensive QM models such as coupled cluster methods were applied at the high level. The transferability of QM/MM-NN among several QM models was validated by choosing different low-level (e.g., DFTB3/3OB/MM) and high-level (e.g., CCSD(T)/aug-cc-pvtz/MM) methods. The preliminary results listed in Tables S1 and S2 were obtained using the aforementioned initial database for our first and second testing examples and the same hyperparameters without further tuning. Almost all RMSEs are less than 1.5 kcal/mol, which indicates a great potential to extend QM/MM-NN MD to the maximum QM accuracy.
CONCLUSIONS
In summary, in order to achieve the accuracy of ab initio QM/MM yet at the computational cost similar to SQM/MM approaches, we developed a new method to advance our previous QM/MM-NN method to QM/MM MD simulations by employing an adaptive procedure. First, a QM/MM-NN model was generated after SQM/MM simulations to predict the potential energy difference between SQM/MM and ab initio QM/MM for any configuration. Based on our original QM/MM-NN method reported recently, several modifications on the input variables of NN were applied for MD evolution. Second, MD simulations on the NN-predicted PES were carried out. The reliability of NN prediction on diverse configurations encountered during simulations was analyzed carefully. Some of the chemically novel configurations excluded from the current training set were selected and added to the database, and then, the QM/MM-NN model was retrained with the growing training and testing sets. Finally, MD simulations were repeated on the updated QM/MM-NN PES. The adaptive procedure was performed iteratively until the NN-predicted potentials and the properties under research achieved a convergent result.
Free energy calculations on two chemical reactions in water and reaction path optimization on one aqueous system were carried out for computational validations on this method. The RMSEs for the predicted QM/MM potential energies were around 0.7–1.3 kcal/mol. The free energy changes along the reaction coordinate and the optimized transition path in collective variable space were obtained using QM/MM-NN MD, which are in excellent accordance with the results at the high-level ab initio QM/MM level. The convergence of the adaptive procedure was achieved after 2–4 iteration cycles, showing a speed-up of about 2 orders of magnitude compared with the direct B3LYP/6-31G(d)/MM MD. The QM/MM-NN MD provides great potentials to study a broad range of biochemical systems in complex environment using long time simulations. As a dynamic scheme of QM/MM-NN, we expect this method to be particularly useful for the characterization of reaction dynamics for interesting applications, such as the discovery of new reactive channels,93,94 the identification of reaction coordinates and pathways,71,95,96 and the kinetics study with transition path samplings.97–99
Supplementary Material
ACKNOWLEDGMENTS
Financial support from the National Institute of Health (R01 GM061870-13) is gratefully appreciated. L.S. acknowledges the helpful suggestions and comments on machine learning from Hao Wang and Pan Zhang.
Footnotes
Supporting Information
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.7b01195.
Tables S1 and S2 for the RMSEs of training and testing sets for the SN2 and proton transfer reactions using different QM models at the two levels. Figure S1 for the energy evolution of representative trajectories during NVE simulations on the SN2 and proton transfer reactions using DFTB2/MIO/MM with QM/MM-NN corrections (PDF)
The authors declare no competing financial interest.
REFERENCES
- (1).Warshel A; Levitt M Theoretical studies of enzymic reactions: Dielectric, electrostatic and steric stabilization of the carbonium ion in the reaction of lysozyme. J. Mol. Biol 1976, 103, 227–249. [DOI] [PubMed] [Google Scholar]
- (2).Senn HM; Thiel W QM/MM Methods for Biomolecular Systems. Angew. Chem., Int. Ed. 2009, 48, 1198–1229. [DOI] [PubMed] [Google Scholar]
- (3).Chung LW; Sameera WMC; Ramozzi R; Page AJ; Hatanaka M; Petrova GP; Harris TV; Li X; Ke Z; Liu F; Li H-B; Ding L; Morokuma K The ONIOM Method and Its Applications. Chem. Rev 2015, 115, 5678–5796. [DOI] [PubMed] [Google Scholar]
- (4).Pezeshki S; Lin H Recent developments in QM/MM methods towards open-boundary multi-scale simulations. Mol. Simul. 2015, 41, 168–189. [Google Scholar]
- (5).Lu X; Fang D; Ito S; Okamoto Y; Ovchinnikov V; Cui Q QM/MM free energy simulations: recent progress and challenges. Mol. Simul. 2016, 42, 1056–1078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (6).Zhang Y; Liu H; Yang W Free energy calculation on enzyme reactions with an efficient iterative procedure to determine minimum energy paths on a combined ab initio QM/MM potential energy surface. J. Chem. Phys. 2000, 112, 3483–3492. [Google Scholar]
- (7).Hu P; Wang S; Zhang Y How Do SET-Domain Protein Lysine Methyltransferases Achieve the Methylation State Specificity? Revisited by Ab Initio QM/MM Molecular Dynamics Simulations. J. Am. Chem. Soc. 2008, 130, 3806–3813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (8).Hu P; Wang S; Zhang Y Highly Dissociative and Concerted Mechanism for the Nicotinamide Cleavage Reaction in Sir2Tm Enzyme Suggested by Ab Initio QM/MM Molecular Dynamics Simulations. J. Am. Chem. Soc. 2008, 130, 16721–16728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (9).Kamerlin SCL; Haranczyk M; Warshel A Progress in Ab Initio QM/MM Free-Energy Simulations of Electrostatic Energies in Proteins: Accelerated QM/MM Studies of pKa, Redox Reactions and Solvation Free Energies. J. Phys. Chem. B 2009, 113, 1253–1272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (10).Brunk E; Rothlisberger U Mixed Quantum Mechanical/Molecular Mechanical Molecular Dynamics Simulations of Biological Systems in Ground and Electronically Excited States. Chem. Rev. 2015, 115, 6217–6263. [DOI] [PubMed] [Google Scholar]
- (11).Dewar MJS; Storch DM Development and use of quantum molecular models. 75 Comparative tests of theoretical procedures for studying chemical reactions. J. Am. Chem. Soc. 1985, 107, 3898–3902. [Google Scholar]
- (12).Elstner M; Porezag D; Jungnickel G; Elsner J; Haugk M; Frauenheim T; Suhai S; Seifert G Self-consistent-charge density-functional tight-binding method for simulations of complex materials properties. Phys. Rev. B: Condens. Matter Mater. Phys. 1998, 58, 7260–7268. [Google Scholar]
- (13).Silva-Junior MR; Thiel W Benchmark of Electronically Excited States for Semiempirical Methods: MNDO, AM1, PM3, OM1, OM2, OM3, INDO/S, and INDO/S2. J. Chem. Theory Comput 2010, 6, 1546–1564. [DOI] [PubMed] [Google Scholar]
- (14).Akimov AV; Prezhdo OV Large-Scale Computations in Chemistry: A Bird’s Eye View of a Vibrant Field. Chem. Rev. 2015, 115, 5797–5890. [DOI] [PubMed] [Google Scholar]
- (15).Warshel A; Weiss RM An empirical valence bond approach for comparing reactions in solutions and in enzymes. J. Am. Chem. Soc. 1980, 102, 6218–6226. [Google Scholar]
- (16).van Duin ACT; Dasgupta S; Lorant F; Goddard WA III ReaxFF: A Reactive Force Field for Hydrocarbons. J. Phys. Chem. A 2001, 105, 9396–9409. [Google Scholar]
- (17).Nagy T; Yosa Reyes J; Meuwly M Multisurface Adiabatic Reactive Molecular Dynamics. J. Chem. Theory Comput. 2014, 10, 1366–1375. [DOI] [PubMed] [Google Scholar]
- (18).Hu H; Lu Z; Yang W QM/MM Minimum Free-Energy Path: Methodology and Application to Triosephosphate Isomerase. J. Chem. Theory Comput. 2007, 3, 390–406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (19).Hu H; Lu Z; Parks JM; Burger SK; Yang W Quantum mechanics/molecular mechanics minimum free-energy path for accurate reaction energetics in solution and enzymes: Sequential sampling and optimization on the potential of mean force surface. J. Chem. Phys. 2008, 128, 034105. [DOI] [PubMed] [Google Scholar]
- (20).Hu H; Yang W Free Energies of Chemical Reactions in Solution and in Enzymes with Ab Initio Quantum Mechanics/Molecular Mechanics Methods. Annu. Rev. Phys. Chem. 2008, 59, 573–601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (21).Hu H; Yang W Development and application of ab initio QM/MM methods for mechanistic simulation of reactions in solution and in enzymes. J. Mol. Struct.: THEOCHEM 2009, 898, 17–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (22).Rod TH; Ryde U Quantum Mechanical Free Energy Barrier for an Enzymatic Reaction. Phys. Rev. Lett. 2005, 94, 138302. [DOI] [PubMed] [Google Scholar]
- (23).König G; Hudson PS; Boresch S; Woodcock HL Multiscale Free Energy Simulations: An Efficient Method for Connecting Classical MD Simulations to QM or QM/MM Free Energies Using Non-Boltzmann Bennett Reweighting Schemes. J. Chem. Theory Comput. 2014, 10, 1406–1419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (24).Hudson PS; Woodcock HL; Boresch S Use of Nonequilibrium Work Methods to Compute Free Energy Differences Between Molecular Mechanical and Quantum Mechanical Representations of Molecular Systems. J. Phys. Chem. Lett. 2015, 6, 4850–4856. [DOI] [PubMed] [Google Scholar]
- (25).Maurer P; Laio A; Hugosson HW; Colombo MC; Rothlisberger U Automated Parametrization of Biomolecular Force Fields from Quantum Mechanics/Molecular Mechanics (QM/MM) Simulations through Force Matching. J. Chem. Theory Comput. 2007, 3, 628–639. [DOI] [PubMed] [Google Scholar]
- (26).Plotnikov NV; Kamerlin SCL; Warshel A Paradynamics: An Effective and Reliable Model for Ab Initio QM/MM Free-Energy Calculations and Related Tasks. J. Phys. Chem. B 2011, 115, 7950–7962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (27).Zhou Y; Pu J Reaction Path Force Matching: A New Strategy of Fitting Specific Reaction Parameters for Semiempirical Methods in Combined QM/MM Simulations. J. Chem. Theory Comput. 2014, 10, 3038–3054. [DOI] [PubMed] [Google Scholar]
- (28).Ruiz-Pernía JJ; Silla E; Tuñón I; Martí S; Moliner V Hybrid QM/MM potentials of mean force with interpolated corrections. J. Phys. Chem. B 2004, 108, 8427–8433. [Google Scholar]
- (29).Ischtwan J; Collins MA Molecular potential energy surfaces by interpolation. J. Chem. Phys. 1994, 100, 8080–8088. [Google Scholar]
- (30).Rhee YM Construction of an accurate potential energy surface by interpolation with Cartesian weighting coordinates. J. Chem. Phys. 2000, 113, 6021–6024. [Google Scholar]
- (31).Doemer M; Maurer P; Campomanes P; Tavernelli I; Rothlisberger U Generalized QM/MM Force Matching Approach Applied to the 11-cis Protonated Schiff Base Chromophore of Rhodopsin. J. Chem. Theory Comput. 2014, 10, 412–422. [DOI] [PubMed] [Google Scholar]
- (32).Kim CW; Rhee YM Constructing an Interpolated Potential Energy Surface of a Large Molecule: A Case Study with Bacteriochlorophyll a Model in the Fenna-Matthews-Olson Complex. J. Chem. Theory Comput. 2016, 12, 5235–5246. [DOI] [PubMed] [Google Scholar]
- (33).Blank TB; Brown SD; Calhoun AW; Doren DJ Neural network models of potential energy surfaces. J. Chem. Phys. 1995, 103, 4129–4137. [Google Scholar]
- (34).Handley CM; Popelier PLA Potential Energy Surfaces Fitted by Artificial Neural Networks. J. Phys. Chem. A 2010, 114, 3371–3383. [DOI] [PubMed] [Google Scholar]
- (35).Handley CM; Behler J Next generation interatomic potentials for condensed systems. Eur. Phys. J. B 2014, 87, 152. [Google Scholar]
- (36).Behler J Constructing high-dimensional neural network potentials: A tutorial review. Int. J. Quantum Chem. 2015, 115, 1032–1050. [Google Scholar]
- (37).Behler J First Principles Neural Network Potentials for Reactive Simulations of Large Molecular and Condensed Systems. Angew. Chem., Int. Ed. 2017, 56, 12828–12840. [DOI] [PubMed] [Google Scholar]
- (38).Behler J; Parrinello M Generalized Neural-Network Representation of High-Dimensional Potential-Energy Surfaces. Phys. Rev. Lett. 2007, 98, 146401. [DOI] [PubMed] [Google Scholar]
- (39).Artrith N; Kolpak AM Understanding the Composition and Activity of Electrocatalytic Nanoalloys in Aqueous Solvents: A Combination of DFT and Accurate Neural Network Potentials. Nano Lett. 2014, 14, 2670–2676. [DOI] [PubMed] [Google Scholar]
- (40).Morawietz T; Singraber A; Dellago C; Behler J How van der Waals interactions determine the unique properties of water. Proc. Natl. Acad. Sci U. S. A 2016, 113, 8368–8373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (41).Ramakrishnan R; Dral PO; Rupp M; von Lilienfeld OA Big Data Meets Quantum Chemistry Approximations: The Δ-Machine Learning Approach. J. Chem. Theory Comput. 2015, 11, 2087–2096. [DOI] [PubMed] [Google Scholar]
- (42).Shen L; Wu J; Yang W Multiscale Quantum Mechanics/Molecular Mechanics Simulations with Neural Networks. J. Chem. Theory Comput. 2016, 12, 4934–4946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (43).Li Z; Kermode JR; De Vita A Molecular Dynamics with On-the-Fly Machine Learning of Quantum-Mechanical Forces. Phys. Rev. Lett. 2015, 114, 096405. [DOI] [PubMed] [Google Scholar]
- (44).Botu V; Ramprasad R Learning scheme to predict atomic forces and accelerate materials simulations. Phys. Rev. B: Condens. Matter Mater. Phys. 2015, 92, 094306. [Google Scholar]
- (45).Botu V; Ramprasad R Adaptive machine learning framework to accelerate ab initio molecular dynamics. Int. J. Quantum Chem. 2015, H5, 1074–1083. [Google Scholar]
- (46).Botu V; Batra R; Chapman J; Ramprasad R Machine Learning Force Fields: Construction, Validation, and Outlook. J. Phys. Chem. C 2017, 111, 511–522. [Google Scholar]
- (47).Wu J; Shen L; Yang W Internal force corrections with machine learning for quantum mechanics/molecular mechanics simulations. J. Chem. Phys. 2017, 147, 161732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (48).Behler J Atom-centered symmetry functions for constructing high-dimensional neural network potentials. J. Chem. Phys. 2011, 134, 074106. [DOI] [PubMed] [Google Scholar]
- (49).Jose KVJ; Artrith N; Behler J Construction of highdimensional neural network potentials using environment-dependent atom pairs. J. Chem. Phys. 2012, 136, 194111. [DOI] [PubMed] [Google Scholar]
- (50).Handley CM; Hawe GI; Kell DB; Popelier PLA Optimal construction of a fast and accurate polarisable water potential based on multipole moments trained by machine learning. Phys. Chem. Chem. Phys. 2009, 11, 6365–6376. [DOI] [PubMed] [Google Scholar]
- (51).Bartók AP; Kondor R; Csányi G On representing chemical environments. Phys. Rev. B: Condens. Matter Mater. Phys. 2013, 87, 184115. [Google Scholar]
- (52).Hu H; Yang W Elucidating Solvent Contributions to Solution Reactions with Ab Initio QM/MM Methods. J. Phys. Chem. B 2010, 114, 2755–2759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (53).Wu P; Hu X; Yang W Λ-Metadynamics Approach To Compute Absolute Solvation Free Energy. J. Phys. Chem. Lett. 2011, 2, 2099–2103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (54).Chen J; Xu X; Xu X; Zhang DH A global potential energy surface for the H2 + OH → H2O + H reaction using neural networks. J. Chem. Phys. 2013, 138, 154301. [DOI] [PubMed] [Google Scholar]
- (55).Morita A; Kato S Ab Initio Molecular Orbital Theory on Intramolecular Charge Polarization: Effect of Hydrogen Abstraction on the Charge Sensitivity of Aromatic and Nonaromatic Species. J. Am. Chem. Soc. 1997, 119, 4021–4032. [Google Scholar]
- (56).Lu Z; Yang W Reaction path potential for complex systems derived from combined ab initio quantum mechanical and molecular mechanical calculations. J. Chem. Phys. 2004, 121, 89–100. [DOI] [PubMed] [Google Scholar]
- (57).Csányi G; Albaret T; Payne MC; De Vita A “Learn on the Fly”: A Hybrid Classical and Quantum-Mechanical Molecular Dynamics Simulation. Phys. Rev. Lett. 2004, 93, 175503. [DOI] [PubMed] [Google Scholar]
- (58).Podryabinkin EV; Shapeev AV Active learning of linearly parametrized interatomic potentials. Comput. Mater. Sci. 2017, 140, 171–180. [Google Scholar]
- (59).Peterson AA; Christensen R; Khorshidi A Addressing uncertainty in atomistic machine learning. Phys. Chem. Chem. Phys. 2017, 19, 10978–10985. [DOI] [PubMed] [Google Scholar]
- (60).Jorgensen WL; Chandrasekhar J; Madura JD; Impey RW; Klein ML Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar]
- (61).MacKerell AD Jr; Bashford D; Bellott M; Dunbrack RL Jr; Evanseck JD; Field MJ; Fischer S; Gao J; Guo H; Ha S; Joseph-McCarthy D; Kuchnir L; Kuczera K; Lau FTK; Mattos C; Michnick S; Ngo T; Nguyen DT; Prodhom B; Reiher WE; Roux B; Schlenkrich M; Smith JC; Stote R; Straub J; Watanabe M; Wiorkiewicz-Kuczera J; Yin D; Karplus M All-Atom Empirical Potential for Molecular Modeling and Dynamics Studies of Proteins. J. Phys. Chem. B 1998, 102, 3586–3616. [DOI] [PubMed] [Google Scholar]
- (62).Lee C; Yang W; Parr RG Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B: Condens. Matter Mater. Phys. 1988, 37, 785–789. [DOI] [PubMed] [Google Scholar]
- (63).Becke AD Density functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar]
- (64).Cui Q; Elstner M; Kaxiras E; Frauenheim T; Karplus M A QM/MM Implementation of the Self-Consistent Charge Density Functional Tight Binding (SCC-DFTB) Method. J. Phys. Chem. B 2001, 105, 569–585. [Google Scholar]
- (65).Gaus M; Cui Q; Elstner M DFTB3: Extension of the Self-Consistent-Charge Density-Functional Tight-Binding Method (SCC-DFTB). J. Chem. Theory Comput. 2011, 7, 931–948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (66).Gaus M; Goez A; Elstner M Parametrization and Benchmark of DFTB3 for Organic Molecules. J. Chem. Theory Comput. 2013, 9, 338–354. [DOI] [PubMed] [Google Scholar]
- (67).Ferrenberg AM; Swendsen RH Optimized Monte Carlo data analysis. Phys. Rev. Lett. 1989, 63, 1195–1198. [DOI] [PubMed] [Google Scholar]
- (68).Kumar S; Rosenberg JM; Bouzida D; Swendsen RH; Kollman PA The weighted histogram analysis method for free-energy calculations on biomolecules. I The method. J. Comput. Chem. 1992, 13, 1011–1021. [Google Scholar]
- (69).Berendsen HJC; Postma JPM; van Gunsteren WF; DiNola A; Haak JR Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar]
- (70).E W; Ren W; Vanden-Eijnden E Finite Temperature String Method for the Study of Rare Events. J. Phys. Chem. B 2005, 109, 6688–6693. [DOI] [PubMed] [Google Scholar]
- (71).Ren W; Vanden-Eijnden E; Maragakis P; E W Transition pathways in complex systems: Application of the finite-temperature string method to the alanine dipeptide. J. Chem. Phys. 2005, 123, 134109. [DOI] [PubMed] [Google Scholar]
- (72).Vanden-Eijnden E; Venturoli M Revisiting the finite temperature string method for the calculation of reaction tubes and free energies. J. Chem. Phys. 2009, 130, 194103. [DOI] [PubMed] [Google Scholar]
- (73).van Gunsteren WF; Berendsen HJC A Leap-frog Algorithm for Stochastic Dynamics. Mol. Simul. 1988, 1, 173–185. [Google Scholar]
- (74).Hu X; Hu H; Yang W QM4D: An integrated and versatile quantum mechanical/molecular mechanical simulation package. http://www.qm4d.info/ (accessed 2018).
- (75).Frisch MJ; Trucks GW; Schlegel HB; Scuseria GE; Robb MA; Cheeseman JR; Montgomery JA Jr.; Vreven T; Kudin KN; Burant JC; Millam JM; Iyengar SS; Tomasi J; Barone V; Mennucci B; Cossi M; Scalmani G; Rega N; Petersson GA; Nakatsuji H; Hada M; Ehara M; Toyota K; Fukuda R; Hasegawa J; Ishida M; Nakajima T; Honda Y; Kitao O; Nakai H; Klene M; Li X; Knox JE; Hratchian HP; Cross JB; Bakken V; Adamo C; Jaramillo J; Gomperts R; Stratmann RE; Yazyev O; Austin AJ; Cammi R; Pomelli C; Ochterski JW; Ayala PY; Morokuma K; Voth GA; Salvador P; Dannenberg JJ; Zakrzewski VG; Dapprich S; Daniels AD; Strain MC; Farkas O; Malick DK; Rabuck AD; Raghavachari K; Foresman JB; Ortiz JV; Cui Q; Baboul AG; Clifford S; Cioslowski J; Stefanov BB; Liu G; Liashenko A; Piskorz P; Komaromi I; Martin RL; Fox DJ; Keith T; Al-Laham MA; Peng CY; Nanayakkara A; Challacombe M; Gill PMW; Johnson B; Chen W; Wong MW; Gonzalez C; Pople JA Gaussian 03, Revision D.02; Gaussian, Inc.: Wallingford, CT, 2004. [Google Scholar]
- (76).Seabra G. d. M.; Walker RC; Elstner M; Case DA; Roitberg AE Implementation of the SCC-DFTB Method for Hybrid QM/MM Simulations within the Amber Molecular Dynamics Package. J. Phys. Chem. A 2007, 111, 5655–5664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (77).Walker RC; Crowley MF; Case DA The implementation of a fast and accurate QM/MM potential method in Amber. J. Comput. Chem. 2008, 29, 1019–1031. [DOI] [PubMed] [Google Scholar]
- (78).Cui Q; Elstner M Density functional tight binding: values of semi-empirical methods in an ab initio era. Phys. Chem. Chem. Phys. 2014, 16, 14368–14377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (79).Gruden M; Andjeklovic L; Jissy AK; Stepanovic S; Zlatar M; Cui Q; Elstner M Benchmarking density functional tight binding models for barrier heights and reaction energetics of organic molecules. J. Comput. Chem. 2017, 38, 2171–2185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (80).Riedmiller M; Braun H A direct adaptive method for faster backpropagation learning: the RPROP algorithm. IEEE International Conference on Neural Networks 1993, 586. [Google Scholar]
- (81).Wu J; Mei J; Wen S; Liao S; Chen J; Shen Y A self-adaptive genetic algorithm-artificial neural network algorithm with leave-one-out cross validation for descriptor selection in QSAR study. J. Comput. Chem. 2010, 31, 1956–1968. [DOI] [PubMed] [Google Scholar]
- (82).Gastegger M; Marquetand P High-Dimensional Neural Network Potentials for Organic Reactions and an Improved Training Algorithm. J. Chem. Theory Comput. 2015, 11, 2187–2198. [DOI] [PubMed] [Google Scholar]
- (83).Goodfellow I; Bengio Y; Courville A Deep Learning; MIT Press: 2016. [Google Scholar]
- (84).Rodriguez A; Laio A Clustering by fast search and find of density peaks. Science 2014, 344, 1492–1496. [DOI] [PubMed] [Google Scholar]
- (85).Dral PO; Owens A; Yurchenko SN; Thiel W Structure-based sampling and self-correcting machine learning for accurate calculations of potential energy surfaces and vibrational levels. J. Chem. Phys. 2017, 146, 244108. [DOI] [PubMed] [Google Scholar]
- (86).Leach A Molecular Modelling: Principles and Applications; Prentice Hall: 2001. [Google Scholar]
- (87).Shen L; Hu H Resolution-Adapted All-Atomic and Coarse-Grained Model for Biomolecular Simulations. J. Chem. Theory Comput. 2014, 10, 2528–2536. [DOI] [PubMed] [Google Scholar]
- (88).Rupp M; Tkatchenko A; Müller K-R; von Lilienfeld OA Fast and Accurate Modeling of Molecular Atomization Energies with Machine Learning. Phys. Rev. Lett. 2012, 108, 058301. [DOI] [PubMed] [Google Scholar]
- (89).Hansen K; Montavon G; Biegler F; Fazli S; Rupp M; Scheffler M; von Lilienfeld OA; Tkatchenko A; Muller K-R Assessment and Validation of Machine Learning Methods for Predicting Molecular Atomization Energies. J. Chem. Theory Comput. 2013, 9, 3404–3419. [DOI] [PubMed] [Google Scholar]
- (90).Okamoto Y Generalized-ensemble algorithms: enhanced sampling techniques for Monte Carlo and molecular dynamics simulations. J. Mol. Graphics Modell. 2004, 22, 425–439. [DOI] [PubMed] [Google Scholar]
- (91).Gao YQ An integrate-over-temperature approach for enhanced sampling. J. Chem. Phys. 2008, 128, 064105. [DOI] [PubMed] [Google Scholar]
- (92).Hu H; Liu H Pitfall in Quantum Mechanical/Molecular Mechanical Molecular Dynamics Simulation of Small Solutes in Solution. J. Phys. Chem. B 2013, 117, 6505–6511. [DOI] [PubMed] [Google Scholar]
- (93).Wang L-P; Titov A; McGibbon R; Liu F; Pande VS; Martinez TJ Discovering chemistry with an ab initio nanoreactor. Nat. Chem. 2014, 6, 1044–1048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (94).Wang L-P; McGibbon RT; Pande VS; Martinez TJ Automated Discovery and Refinement of Reactive Molecular Dynamics Pathways. J. Chem. Theory Comput. 2016, 12, 638–649. [DOI] [PubMed] [Google Scholar]
- (95).Li W; Ma A Recent developments in methods for identifying reaction coordinates. Mol. Simul 2014, 40, 784–793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (96).Peters B Reaction Coordinates and Mechanistic Hypothesis Tests. Annu. Rev. Phys. Chem. 2016, 67, 669–690. [DOI] [PubMed] [Google Scholar]
- (97).Bolhuis PG; Chandler D; Dellago C; Geissler PL Transition Path Sampling: Throwing Ropes Over Rough Mountain Passes, in the Dark. Annu. Rev. Phys. Chem. 2002, 53, 291–318. [DOI] [PubMed] [Google Scholar]
- (98).Fu X; Yang L; Gao YQ Selective sampling of transition paths. J. Chem. Phys. 2007, 127, 154106. [DOI] [PubMed] [Google Scholar]
- (99).Zhang J; Zhang Z; Yang YI; Liu S; Yang L; Gao YQ Rich Dynamics Underlying Solution Reactions Revealed by Sampling and Data Mining of Reactive Trajectories. ACS Cent. Sci. 2017, 3, 407–414. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


