Time-gated Scintillator Imaging for Real-time Optical Surface Dosimetry in Total Skin Electron Therapy

Abstract

Purpose

To measure surface dose by remote time-gated imaging of plastic scintillators.

Methods

A novel technique for time-gated, intensified camera imaging of scintillator emission was demonstrated, and key parameters influencing the signal were analyzed, including distance, angle and thickness. A set of scintillator samples was calibrated by using thermo-luminescence detector response as reference. Examples of use in total skin electron therapy are described.

Results

The data showed excellent room light rejection (signal-to-noise ratio of scintillation SNR ≈ 470), ideal scintillation dose response linearity, and 2% dose rate error. Individual sample scintillation response varied by 7% due to sample preparation. Inverse square distance dependence correction and lens throughput error (8% per meter) correction were needed. At scintillator-to-source angle and observation angle < 50°, the radiant energy fluence error was smaller than 1%. The achieved standard error of the scintillator cumulative dose measurement compared to the TLD dose was 5%.

Conclusions

The results from this proof-of-concept study documented the first use of small scintillator targets for remote surface dosimetry in ambient room lighting. The measured dose accuracy renders our method to be comparable to thermo-luminescent detector dosimetry, with the ultimate realization of accuracy likely to be better than shown here. Once optimized, this approach to remote dosimetry may substantially reduce time and effort required for surface dosimetry.

Introduction

In-vivo surface dosimetry is a valuable tool to determine the accuracy of doses delivered during external beam radiation therapy (EBRT), because of the complexity of dose estimation at boundaries, and for independent verification of delivery on the patient[1]. Currently established surface dosimeters, such as film, thermo-luminescent or optically-stimulated luminescence dosimeters (TLDs, OSLDs, resp.), alanine dosimeters [2, 3], silicon diode [4] or MOSFET dosimeters [5], or scintillator fibers [6] requires lengthy readout procedures and/or exhibit issues with handling and detector fixation. In the case of total skin electron therapy (TSET), dose monitoring is routinely assessed according to Quality Audit guidelines of Task Group 23 [1], requiring a measurement of dose at the umbilicus in one of the initial treatments. The reason is that there are reported 15–60% dose variations observed across the skin surface of the body [7, 8]. Lengthy application of dosimeters onto patient’s compromised skin prior a physically demanding treatment, laborious and lengthy dose readout, and/or increased chance of error during post-treatment dosimeter handling are the main motivations to search for an easy-applicable, real-time dosimetry [9]. In this study we demonstrate for the first time the use of a remote camera to directly read out the surface dose from thin plastic scintillators is demonstrated for the first time, indicating that remote estimation could be done in a seamless manner.

The development of time-gated imaging during radiotherapy was originally driven by the research of real-time Cherenkov radiation imaging in ambient room lighting [10–12]. By gating the imager only during the microsecond pulses of clinical linear accelerators (linacs), the ambient background light is suppressed by a factor of 1000, making scintillation or low-intensity Cherenkov [13] imaging feasible in normal room light conditions.

Our hypothesis is that an image of well-calibrated thin scintillators, affixed on patient’s skin, could provide accurate surface dose measurements[1]. In this work, direct imaging of plastic scintillators via remote time-gated imaging is shown for optical-dose reporting with excellent linearity and high luminescent quantum yield of plastic scintillators to perform real-time surface dosimetry. We defined the dose calculation procedure, characterized scintillation output according to the relative dose, dose rate, and geometry, and calibrated using independent TLD measurements. Finally, we recorded the scintillator emission during a clinical TSET treatment to demonstrate the practical dose accuracy and the viability of our method for clinical use.

Methods and Materials

Scintillators

A 1 mm thick EJ-240 scintillator (Eljen Technology, TX, USA) was cut to 2.5×2.5 cm² (sample #7–10) and 5×5 cm² (sample #5 and #6) samples. The back side and edges of each scintillator were painted with white reflective paint Eljen EJ-510.

Radiation Source

The characterization of the scintillators was performed on a Varian 2100CD (Varian Medical Systems, CA, USA) medical linac. The calibration and clinical imaging experiment was performed on a Varian Trilogy linac. For sample characterization measurements, the 2100CD linac was used with up to 1000 MU/min dose rate and 6 MeV electrons. Before characterization and calibration experiments, the scintillators were mounted on a solid water phantom with thickness of 5 cm.

TLD dosimetry

TLDs were chosen as a reference dosimeter due to their ability to both repeatedly (within 2%) and accurately (within 5%) measure dose, and because TLD dosimetry was a verified standard at our clinic at the time of study. For scintillation dose readout calibration, the TLDs (TLD-100 rods, Ø1×6 mm, ThermoFischer Scientific, MA, USA) were affixed to the solid water phantom or TSET frame and read out after each treatment. Post-irradiation, TLDs were annealed at 93°C for 15 minutes and read-out by thermo-luminescence detector (Harshaw Nuclear Systems Model 2000, ThermoFischer Scientific, MA, USA). Finally, TLDs were reset by being placed in a furnace at 400°C for one hour followed by lab oven at 93°C for two hours. The absolute dose response of all TLDs was determined to 5% absolute dose deviation by an independent calibration using an Exradin P11 (Standard Imaging, WA, USA) parallel-plate ionization chamber according to AAPM TG-51 protocol.

Patient Treatment

All procedures for imaging subjects were approved by the Dartmouth Institutional Review Board (IRB) and management of the data and patient followed the approved protocol. After informed patient consent, the patients were imaged during their routine TSET treatment, which was delivered per standard institutional protocol using a modified Stanford technique, a 6 MeV HDTSe⁻ electron beam without spoiler, source-to-surface distance SSD=3 m, with isocenter dose rate 888 cGy/min and 36 × 36 cm field size. The prescribed total dose was 1800 cGy in 200 cGy/cycle. While affixing the scintillators directly on the patient was under a separate IRB review at the time of the study, the scintillator samples were attached to the frame supporting the patient in order to demonstrate the feasibility of our method in clinical conditions.

Imaging system

A PI-MAX4 1024i (Princeton Instruments, NJ, USA) intensified charge-coupled device (ICCD) camera coupled with an f/1.4, 24 mm lens (Canon, Japan) was used to image the interaction area. The camera was operated at 100× intensifier gain and cooled to −20°C. The rising edge of a klystron current signal (KLYI) from the linac was used as the trigger event. The intensifier was gated by a pulsed signal with 4 µs gate width, delayed by 1.3 µs after the trigger event. This gating acted as a fast shutter, allowing the photons to be collected only during the duration of electron pulse from linac. This way, we suppressed accumulating photons from the scene when the beam is off (99.9% of total time), therefore increasing the signal-to-background ratio by three orders of magnitude. The acquisition gate delay and duration included approx. 0.3 µs safety margins before and after the actual electron pulse in order to avoid underestimation of dose. The exposure time of the CCD was driven by a pre-defined number of 25 linac pulses (accumulations-on-chip, AOC).

Imaging of the dose delivery resulted in a temporal stack of scintillation images. The resulting stack was background-subtracted, flat-field corrected and summed to create a single frame with the cumulative scintillation intensity. In the characterization and calibration experiments, a background image was taken for each scintillation image using the same dose delivery and acquisition parameters, except for a 500 µs gate pulse delay. The intensifier gating was delayed after the X-ray/scintillation pulse and the camera captured a room-light scene with de-excited scintillators. In patient imaging, a static background image was taken before and after the irradiation.

Absolute dose calculation

Under clinically relevant conditions, the scintillation light output, expressed by radiant energy fluence Φ_s (J m⁻²), is expected to be directly proportional to the received dose D [14]:

$$D=k_D{\mathrm{\Phi }}_s,$$ (1)

assuming ideal scintillator emission isotropy, the scintillation-dose linearity, and an electronic equilibrium established in the scintillator volume. The dose conversion factor, k_D, includes the electron mass collision stopping power of the scintillator, as well as several unit-less factors that contribute to the scintillator image formation. An illustration of the typical imaging setup, geometry parameters, and relevant radiometric terms used in the dose calculation is shown in Fig. 1.

Fig. 1.

The schematic overview (a) and geometry (b) for radiation source, imaging camera and scintillator sheet. An example scintillator image (c) shows the intensity of scintillation radiant flux, Q_s, measured as a sum of all intensity values within the thresholded image, as well as the scaled radiant energy fluence, Φ_s, measured as an average intensity value from an interior region-of-interest (ROI) of the scintillator image.

Typically, a time-integrated image of the flat isotropic scintillator (Fig. 1.b) may directly provide a scaled radiant energy fluence Φ_s (DN, digital number) by measuring the average pixel intensity values from within an inner region-of-interest (ROI). However, measuring Φ_s from an image of a small scintillator could be limited in practice due to an insufficient image resolution. A second approach to measure scaled Φ_s requires summing the pixel intensity values from a ROI that is larger than the scintillator’s outline, and normalizing the summed value by the projected scintillator area. This second approach requires knowledge of the observation angle and scintillator-to-camera distance. We describe the absolute dose calculation using the latter technique. The measured quantity will then be the total scintillation photon energy collected by the imaging system:

$${\mathrm{Q}}_s=A\mathrm{\Omega }{k}_c{\mathrm{\Phi }}_s$$ (2)

where A is the scintillator area and Ω is the solid angle projected by the imaging system subtended by the scintillator outline in the direction of the camera optical axis. The imaging system sensitivity is contained in the linear constant k_c and can be factored out during dose calibration, avoiding a rigorous measurement of absolute radiant energy fluence Φ_s [J/cm²] and electron energy-dependent constant k_D. The chosen approach also requires calibration due to the projected solid angle Ω, which depends on scintillator-camera distance d and angle θ of scintillator normal to camera optical axis:

$$D=k_c\frac{{\mathrm{Q}}_s}{\text{cos }\theta }{\left(\frac{d}{d_c}\right)}^2.$$ (3)

Here, the dose calibration factor k_c would be acquired at an angle θ = 0 and at a specific scintillator-camera distance d_c. Eq. 3 would be sufficient for an ideal isotropically-emitting scintillator with uniform dose distribution throughout the scintillator volume. However, these approximations might not hold true at large observation angles θ and source-to-scintillator angles ρ (typically θ, ρ > 45°). At large observation angles θ, one could expect a decrease of the observed radiant energy due to refractive index mismatch at the scintillator-air boundary. In addition, at large angles ρ one could observe the dose buildup effect, and therefore the scintillation radiant energy fluence would increase. We introduce the additional observation angle factor k_θ (θ) and source-to-scintillator angle factor k_ρ (ρ) to illustrate the extent of these effects:

$$D=k_c\frac{{\mathrm{Q}}_s}{\text{cos }\theta }{\left(\frac{d}{d_c}\right)}^2{k}_{\theta }(\theta )k_{\rho }(\rho ),$$ (4)

where both factors k_θ and k_ρ can be described as inverse values of normalized radiant energy:

$$k_{\theta }(\theta )=\frac{{\mathrm{\Phi }}_{\theta 0}}{\mathrm{\Phi }(\theta )},k_{\rho }(\rho )=\frac{{\mathrm{\Phi }}_{\rho 0}}{\mathrm{\Phi }(\rho )},$$ (5)

The angular profile of radiant energy fluence is normalized to the Φ_θ0 or Φ_ρ0 values at angles θ and ρ, respectively, at which the radiant energy error due to off-angle measurement drops below the standard error of the radiant energy measurement.

Lastly, an additional scintillator-camera distance calibration shall be carried out to mitigate a small but non-negligible effect of lens throughput at different focal distance values. The lens throughput effect may be approximated to first order by a factor k_l (d), yielding the final dose calculation formula:

$$D=k_c{k}_l(d)\frac{{\mathrm{Q}}_s}{\text{cos }\theta }{\left(\frac{d}{d_c}\right)}^2{k}_{\theta }(\theta )k_{\rho }(\rho ).$$ (5)

The radiant energy fluence values were measured as an average value of pixels from an ROI defined inside the cumulative scintillator image (Fig. 1). The radiant energy values were measured as a sum of pixel intensity values above 50% intensity threshold in the cumulative scintillator image. This threshold was chosen to eliminate the remaining background noise, but also to eliminate scintillation signal crosstalk in the occasions when the scintillators were packed closely together (namely during the angular and distance dependence measurements). The geometrical parameters and linac settings used in characterization experiments and clinical imaging are summarized in Table 1.

Table 1.

The summarized geometrical parameters and linac settings used in this study.

Experiment	Linac output MU	Linac output rate MU/min	Field Size cm2	SSD cm	d cm	θ deg	ρ deg	Fig. no.
Dose response linearity	10–900	888	36×36	300	400	15	0	2.a
Dose rate dependence	300	100–1000	20×20	300	400	15	0	2.b
Source-to-scintillator angle	50	888	20×20	100	250	0	40–75	2.e
Observation angle dep.	50	888	20×20	100	250	45–80	0	2.e
Distance dependence	50	888	20×20	100	70–330	0	35	2.c,d
Absolute dose calibration	303, 909	888	36×36	300	400	16.5	0	2.f
Clinical imaging	3× 303	888	36×36	300	380–441	13, 24	0	5

Dose response calibration

The absolute dose response calibration of the scintillator imaging system would typically consist of placing the scintillator on a back-scattering water-equivalent phantom along with a group of TLDs or OSLDs. The scintillator-camera distance and angle would be measured or calculated from a calibration pattern on the phantom. A scintillation intensity-dose response would then be recorded for varying doses delivered to the phantom (Absolute dose calibration in Table 1), and at two or more scintillator-camera distances (Distance dependence in Table 1). Using the rearranged Eq. 5, it is possible to obtain the dose calibration factor k_c at recorded scintillator distance d = d_c and observation angle θ, provided that the angles θ and ρ would be small enough to rule out the factors k_θ and k_ρ. By empirical calibration of absolute response factor k_c we avoided to perform rigorous measurement of absolute radiant energy fluence Φ_s in units of J/cm² and electron energy-dependent constant k_D.

Results

First, we present the scintillator readout-dose linearity and its dependency on dose rate, distance, sources-cintillator angle, and scintillator-camera angle. Second, we show the calibration results. Third, we demonstrate the clinical application of remote surface dosimetry during a TSET treatment session.

I. Characterization

Scintillation-Dose linearity

To evaluate the scintillator emission response linearity, a range of effective doses (defined in linac output monitor-units, MU, corresponding to an approximate range of 1 cGy to 1 Gy) was deposited to the samples using parameters in Table 1. As plotted in Fig. 2.a, the radiant energy fluence was measured as a mean intensity of the inner ROI of scintillator image, expressed per pixel area. The linear model data fit (lines in Fig. 2.a) revealed a perfect (R² = 1) linear dependence of measured radiant energy fluence on the delivered dose.

Fig. 2.

The dependence of scintillation output on a) linac output and b) on linac output rate. c) The distance dependence of lens throughput factor and d) of corrected radiant energy. e) Scintillation response at varying observation angle θ and linac angle ρ. In e), an inverse of correction factors is plotted to represent the deviations of measured radiant energy fluence. f) Absolute dose calibration of scintillators using reference TLD measurements. Dashed lines represent fitted linear function, yielding absolute dose conversion factor k_c. Scintillator sample numbers are annotated on the right side of the graphs.

Dose Rate Dependence

Since the camera is acquiring the images in a non-overlapping mode, the scintillator’s light output is left undetected during the CCD read-out periods, which may lead to the dose rate dependence of measured signal. We delivered 300 MU (approximately 0.34 Gy) of 6 MeV electrons at different linac output rates according to Tab.1. The measured effective dose rate response is plotted in Fig. 2.b, exhibiting a standard deviation of 2% from the mean value. However, the dose rate dependence would be negligible for majority of the electron treatments, because the prescription requires electron delivery under constant dose rates.

Distance Dependence

First, we assessed the distance dependence of the lens throughput. The average radiant energy fluence normalized to the fluence at 1 m distance is plotted in Fig. 2.d. We observed an 8% decrease per 1 m distance (revealed by linear fit of data in Fig. 2.c). The lens throughput factor must correct for this decrease, therefore we set k_l(d) = 1.08d. Only after the lens throughput correction, the distance dependency of the measured radiant energy matched the expected 1/d² fall-off (Fig. 2.d). The distance versus corrected radiant energy data were fitted with power functions, yielding an exponent value of 2.04±0.05. Therefore, both the lens throughput correction factor k_l(d) and square root law distance scaling factor (d/d_c)² are required in Eq. 5, and the distance dependence can be corrected in real measurement scenarios.

Scintillator-camera angle

The radiant energy fluence values (Fig. 2.e) showed a deviation from the expected constant profile at angles larger than 50°. This deviation, which corresponds to the inverse of observation angle factor k_θ⁻¹ in Eq. 5, appears to have a similar fall-off among all tested samples. We verified that this factor is sufficient to correct the energy fluence values to match (1% precision) an ideal constant profile as expected in an isotropic emitter, allowing the use of cosine correction of radiant flux in Eq. 5 for absolute dose calculation.

Source-scintillator angle

At large angles ρ between the electron beam direction and scintillator’s normal (ρ > 50°), the buildup effect within the scintillator would cause a non-uniform spatial distribution of dose and the scintillation signal, leading to possible surface dose over-estimation, as demonstrated in Fig. 2.e. The data in Fig. 2.e were normalized to the value of Φ_ρ0 at an angle ρ=35°.

II. Absolute Dose Calibration

After the characterization, we subjected the scintillators to an absolute dose calibration and evaluated the rearranged Eq. 4 to obtain the dose calibration factors k_c. We arranged the samples on a phantom with dosimetric reference TLDs (±5% accuracy) placed adjacent to each scintillator. The measured fluence values (Fig. 2.f) were fitted by a linear model, defined by Eq. 4. The geometrical parameters were as noted in Tab. 1, and the parameters k_θ and k_ρ were set equal to 1 according to Fig. 2.e. The fit yielded dose calibration factors k_c which are listed in the inset of Fig. 2.f.

III. Clinical TSET radiation dosimetry

One patient receiving total skin electron beam therapy (TSET) was imaged with the scintillators and the TLDs adhered on the wooden support frame during the treatment for mycosis fungoides. The TLD-100 rods were placed adjacent to the scintillators to provide an independent surface dose measurement. Since the IRB approval of affixing the scintillators directly on the patient was under review at the time of study, we demonstrate the feasibility for clinical use by measuring surface dose to the support frame during an actual clinical therapy session.

The camera was positioned on a tripod at a distance of 4 m from the frame and at angle of 18° to allow full view of the patient, as seen in Fig. 3. The institutional protocol used six positions with dual fields – linac angle of 289.5° and 250.5° for the upper and lower portion of the body, respectively. Both TLDs and scintillators were kept on the frame during the whole daily irradiation session, so as not to interfere with patient treatment under the IRB approved protocol. Single frame snapshots of the 7 frames-per-second scintillation/Cherenkov image stream (blue overlay) are displayed over a grayscale background in Fig. 4.

Fig. 3.

TSET imaging of a subject was done with frame-mounted scintillators (a) highlighted by arrows and a sample number. Image (a) is composed of grayscale background image and blue overlay of background-subtracted, cumulative scintillation/Cherenkov image. In the background-subtracted cumulative image (b), Cherenkov radiation from the patient and frame markers are observed together with brighter scintillation signals. The scintillators are annotated by the remotely measured cumulative dose value. Cherenkov emission from patient is partially blocked by cloth garment.

Fig. 4.

Example images of the TSET subject treated by upper and lower radiation fields in 3 positions, using the Stanford technique. Each image show the frame-mounted scintillator signals, and Cherenkov photon emission from the patient’s skin, which was effectively blocked by the patient’s shorts.

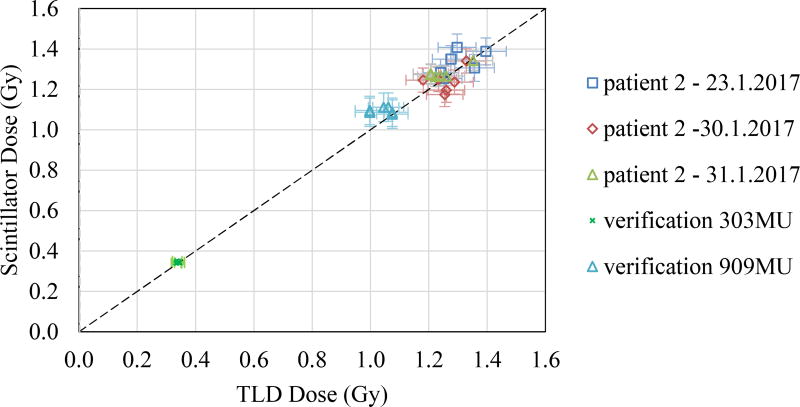
For cumulative dose analysis, the recorded image streams were background-subtracted and summed over the whole daily session. The scintillator-based absolute dose values were calculated using Eq. 4, and plotted against the TLD values in Fig. 5.

Fig. 5.

TLD dose values plotted against the scintillation-based dose values, obtained during 3 days of TSET treatment. TLD dose uncertainties are plotted as horizontal error bars, and scintillator dose standard deviations (1σ) from reference TLD measurements are plotted as vertical error bars.

The scintillator-based absolute doses were reported with a sample standard deviation of 5%. An attempt to calculate the absolute doses based solely on the radiant energy fluence Ψ_s (Eq. 1) led to a sample standard deviation of 11%.

Discussion

The plastic scintillators were expected to be linear at the clinically relevant dose rates [15] of < 1 Gy/s [16] and <1 kGy total delivered doses [17]. We observed a perfect linearity (R²=1). The radiant energy fluence was found to vary between the used samples by 7%. The radiant energy fluence of larger 5×5 cm² scintillators was 20% higher than the fluence from 2.5×2.5 cm² samples, suggesting partial absorption and/or light piping effect at the scintillator boundaries. This is consistent with the fact that the circumference-area ratio of smaller scintillator was 2× larger than of 5×5 cm² scintillator. Imperfections in reflective paint layer preparation may also contribute to sample-to-sample response differences. The radiant fluence deviated by up to 2% depending on the set linac dose rate.

The absolute dose measurement was based on the readout of total radiant energy emitted by the scintillator. As this approach required a calibration including the observation solid angle, the error of absolute dose measurement was influenced by the distance and angle measurement error. As an example, a 1% absolute dose measurement error due to distance estimation in a typical TSET geometry (4 m camera to patient distance) would require a distance measurement margin of 2 cm. With a 1 mm thin slab scintillator, the scintillator-to-source angle and observation angle shall be kept under 50° to achieve <1% radiant energy fluence error. After an angular dependence calibration, the measured radiant energy had to be scaled by the cosine of the observation angle. As an example, a 1% absolute dose measurement error from a scintillator at 15° observation angle would require angular measurement error of 13%. The simulated clinical dosimetry study revealed that we achieved sample standard deviation of 5% of absolute dose measurement, when we used the TLD dose readout as a reference. The largest sources of error were empirically found to be the distance measurement and lens throughput. The latter factor depends on focal distance adjustment accuracy. Image-based distance measurement and operating the lens at larger aperture f-number would have positive effect on the accuracy of absolute dosimetry. The effect of image signal-to-noise ratio (SNR) on the dosimetry accuracy was not addressed. Owing to the gated imaging technique, we achieved SNR ≈ 470 in our clinical measurement, yielding a negligible 0.2% error contribution.

While most of the uncertainties above can be minimized by careful calibration and optical setup, measuring the observation angle may be the most limiting factor. In this experiment, we used 2.5×2.5 cm² and 5×5 cm² scintillator plates, which may me too large to be attached on skin. In a more practical setup, e.g. with 1 mm thick scintillator disks with diameter of 1 cm, the angle measurement accuracy may be limited due to camera resolution. In that case, we see the use of scaled radiant energy fluence, estimated from a fit of the scintillator image with a suitable model function. This approach may be superior to the currently used method, if the scintillators will be designed as Lambertian emitters. In addition, frame-by-frame fitting would provide real-time dose readout, and therefore minimize the motion-induced artifacts.

The practical benefit of the presented remote scintillator dosimetry lies in the real-time dose readout capability. The dose values can be calculated during the treatment, and cumulative values may be recorded along with a cumulative Cherenkov image and stored as a clinical record of the treatment. Once a software tool is developed for extracting values from the images, aside from scintillator application, no additional clinical/technical work would be required, thereby eliminating the time spent during dose readout (in the case of TLDs, OSLDs, and alanine detectors) and manual dose reporting.

Compared to the established techniques, remote scintillator dosimetry can provide fast readout (comparable to MOSFET and diode dosimeters, faster than OSLD, TLD, or alanine dosimeters), minimal sensitivity to humidity (with respect to alanine), tissue equivalency (with respect to diode and MOSFET), low dose-rate dependency (with respect to diode dosimeters), ease of application (with respect to tethered detectors). The main disadvantage of this presented technique is that it does not provide dose readout for sites outside of the field-of-view, or on surfaces tangential to the camera’s optical axis. The design of the scintillator should be optimized to eliminate or minimize angular dose dependency. Since the standard accuracy goal of delivering the therapy is within 5% of the dose prescribed, with regard to a controlled factors, the achieved uncertainty reported here is already rendering the technique suitable for TSET dosimetry, alongside with TLDs (5% typ.), OSLDs (3% typ.), alanine dosimeters (4% typ.), diode dosimeters (1% typ.), or MOSFET dosimeters (5% typ.) [4, 18].

Conclusions

This study experimentally demonstrated for first time that wide-field time-gated imaging could be used for remote dosimetry in ambient room lighting. The calibration of the camera system to the scintillator targets allowed us to measure surface dose during a clinical treatment with accuracy of 5% (1σ) against reference TLD dose values. It is likely that future refinements to this methodology could be found to reduce this number. In principle, this could be one of the most efficient ways to recover surface dosimetry in a manner which minimally impacts clinical time.