Contributions of reader- and text-level characteristics to eye-movement patterns during passage reading

Abstract

The present research presents a novel method for investigating how characteristics of texts (words, sentences and passages) and individuals (verbal and general cognitive skills) jointly influence eye-movement patterns over the time-course of reading, as well as comprehension accuracy. Fifty-one proficient readers read passages of varying complexity from the Gray Oral Reading Test, while their eye-movements were recorded. Participants also completed a large battery of tests assessing various components of reading comprehension ability (vocabulary size, decoding, phonological awareness, and experience with print), as well as general cognitive and executive skills. We used the Random Forests non-parametric regression technique to simultaneously estimate relative importance of all predictors. This method enabled us to trace the temporal engagement of individual predictors and entire predictor groups on eye-movements during reading, while avoiding the problems of model overfitting and collinearity, typical of parametric regression methods. Our findings both confirmed well-established results of prior research and pointed to a space of hypotheses that is as yet unexplored.

Eye-movements during passage reading are susceptible to at least three sources of variability, stemming from i) the cognitive and linguistic ability of the reader him/herself; ii) linguistic properties of the text itself; and iii) the dynamic requirements of the reading task itself. While the first two have been well studied in the literature, they are typically not examined jointly (but see Rayner, 1998, 2009 and the literature review below). The third, which requires the coordinated uptake of perceptual information (i.e., identification of lines and circles that constitute symbols) as well as the timely integration of various levels of information in the process of creating a coherent meaning representation, has only recently received direct attention (e.g., Goswami, 2011) but this work has not focused on eye-movements as a gateway for information uptake. These three sources – labeled here as Reader, Text, and Time – are known to interact (see the literature review below), and thus the ideal state of knowledge about reading for comprehension as reflected in eye-movements would require understanding of what we informally label here the Reader × Text × Time interaction. This amounts to achieving, through behavioral measurement, joint time-locked specification of cognitive, linguistic, perceptual, and visuo-oculomotor components on eye-movement behavior. Recently, an argument has been made that such specification is incomplete without estimates of the relative contributions of those components over time (e.g., Calvo & Meseguer, 2002; Kliegl et al., 2004; Kliegl et al., 2006; Kuperman & Van Dyke, 2011). Mapping the major predictors of reading behavior – along with their temporal locus, absolute effect size (in milliseconds, pixels or likelihood rates), and relative importance among other predictors would provide an important benchmark for the development of computational models of eye-movement control. Indeed, Rayner included models such as this under the “mixed model” rubric in his (1978) classification of existing and theoretically possible accounts (see Kliegl et al., 2006). Yet no studies were available to populate this rubric in the 1978 review and, as argued in Kliegl et al. (2006) and below, very few studies have directly pursued this line of research in the following 40 years.

A practical explanation for this lacuna is that the statistical machinery required to analyze such a complex dataset has simply not been available until now. The present study takes advantage of recent advances in machine learning techniques to estimate and visualize the relative importance of the reader- and text-driven variability in eye-movements over time. We utilize the Random Forests method, which surpasses traditional linear regression methods in its ability to manage two problems inherent to this type of dataset: collinearity among predictors and model overfitting (see Matsuki, Kuperman, & Van Dyke, 2016 for further discussion). In the remainder of the Introduction, we review briefly the literature that informs the joint specification of components of reading, provide motivation for establishing their relative importance, and formulate the goals of our study.

Reader, Text and Time as major causes of variability in reading behavior have been in the focus of eye-movement research since its inception, and particularly so since the introduction of the modern eye-tracking technology (Huey, 1908; Rayner, 1998; 2009; Tinker, 1946). The fine temporal resolution of eye-tracking, as well as the saccadic nature of reading with a clearly defined sequence of saccades and fixations on the target, makes the eye-movement record one of the few behavioral indices for the timing of cognitive processes. The correspondence between eye-movement measures and the temporal order of reading processes is not isomorphic, yet allows for a meaningful separation of early and late stages of word processing: see Clifton, Staub, and Rayner (2007) and Tables 3 and 4 in Boston, Hale, Kliegl, Patil, and Vasishth (2008) for a detailed description of eye-movement measures, the hypothesized cognitive processes, and references. Studies investigating the interaction of reader variables and temporal measures of eye movements (Reader × Time) go back to Buswell’s classic study (1922; data reproduced in Findlay & Gilchrist, 2003), which demonstrated a gradient decrease in the mean number of fixations per line, fixation durations, and regressions per line associated with an increase in years of schooling and exposure to print. Further developmental and clinical research has mapped out systematic differences between-subject variability in eye-movements during reading across the life-span (e.g., Blythe, 2014; Laubrock, Kliegl, & Engbert, 2006; Rayner, Castelhano, & Yang, 2009; Schroeder, Hyönä, & Liversedge, 2015); within and across writing systems (see Liversedge et al., 2016; Rayner, Li, Williams, Cave, & Well, 2007); across levels of specific verbal and broad cognitive skills (see review by Rayner, Abbott, & Plummer, 2015), as well as between impaired (primarily, reading-impaired) and non-clinical groups (for dyslexia, see Eden, Stein, Wood & Wood, 1994; Hawelka, Gagl, & Wimmer, 2010; Pavlidis, 1985).

Even more abundant are demonstrations of the correlation between eye-movement patterns and complexity at multiple levels of linguistic representation (Text × Time). In the last half century, much research has reported systematic changes in fixation times, fixation counts, or the rate of regressive saccades, skips or blinks as a function of text complexity (cf. Rayner & Pollatsek, 1989), its discourse structure (Hyönä, 1995), complexity and ambiguity of syntactic structure at the sentence level (Clifton & Staub, 2011), predictability of a word in its context (Staub, 2015), word frequency and length (Rayner & Duffy, 1986; Inhoff & Rayner, 1986), properties of sublexical (morphological and other) units (Ashby & Rayner, 2004; Bertram, 2011; Hyönä, 1995) and many other linguistic variables (cf. Rayner, 2009).

Similarly, studies of interactions between linguistic and participant characteristics (Reader × Text) in eye movement control during reading date back at least three decades (Pavlidis, 1985; Rayner, 1985; Schilling, Rayner, Chumbley, 1998). Both historical and recent research into interactions between Text properties and individual differences in eye-movements during reading and related tasks is surveyed in Radach and Kennedy (2013); Rayner (1998, 2009); Rayner, Abbott and Plummer (2015) and Rayner, Pollatsek, Ashby, and Clifton (2012) reviews. For related empirical and computational research focused on the stability and variability in oculomotor characteristics of readers, see also Henderson and Luke (2014), Reichle et al. (2013), Veldre and Andrews (2014), and Vorstius, Radach, and Lonigan (2014). A relevant rich body of knowledge is also available in educational psychology for relationships between untimed or less time-sensitive tests of component skills and reading for comprehension and the moderating role of individual characteristics (cf. among others Garcia & Cain’s (2014) meta-analysis).

To sum up, the empirical base of research in eye-movement control in reading is capital, illuminating both the individual sources of variability in reading behavior (Reader, Text and Time) and their two-way interactions, with little attention to three-way interactions. Yet surprisingly little effort has been directed towards creating what Rayner (1978) referred to as “mixed models”, i.e. models that would (a) consider oculomotor, perceptual, cognitive and linguistic influences jointly and (b) simulate their time-course, effect sizes, and relative importance. To our knowledge, only three papers contributed to point (b) so far. Reichle et al. (2013) and Mancheva et al. (2015) incorporated age and skill variability into visuo-oculomotor and linguistic parameters of the computational E-Z Reader model of eye movement control to simulate reading behavior in children and adults of varying ability, and Laubrock, Kliegl and Engbert (2006) implemented age-related differences in visual acuity, processing speed and inhibitory control to account for the effects of aging on reading behavior in the SWIFT model.

For point (a), we identified only five relevant empirical papers. Four of these estimated relative contributions of word length, frequency of occurrence and (except one) predictability in context to the variance in eye-movements representing the entire time-course of word reading. Calvo and Meseguer (2002) used the sentence reading task in Spanish (with additional context-priming conditions) to calculate the unique variance associated with the three lexical predictors in multiple regression models fitted to eye-movements to words n, n−1, and n+1. Kliegl, Grabner, Rolfs and Engbert (2004) used the data of the Potsdam Sentence Corpus to estimate effect sizes of word length, frequency and predictability based on unstandardized regression coefficients from the aggregation of participant-specific multiple regression models (Lorch & Myers, 1990). Kliegl, Nuthmann and Engbert (2006) used the same sentence-reading corpus in German (with a large number of readers) to assess the unique amount of variance that the length, frequency and predictability of words n, n – 1 and n + 1, along with other oculomotor factors, explained in the eye-movements to word n, as indicated by the repeated-measures multiple regression models. The studies largely agreed that word length exerts the strongest and most pervasive effect across the entire eye-movement record (except for first fixation duration, Kliegl et al., 2004). Predictability showed a weaker effect than length, which was confined to later processing stages, and the frequency effect was the weakest and had an early temporal locus.

More recently, the sentence-reading study in English by Kuperman and Van Dyke (2011; Figure 6 in that article) compared relative contributions of word length and frequency and two individual-differences measures (rapid automatized letter naming and word identification). The comparison of standardized regression coefficients associated with these predictors in the generalized linear mixed-effects models revealed that measures of individual variability overshadowed contributions of lexical factors at early processing stages (first and single fixation duration) and were stronger predictors than lexical frequency across the entire eye-movement record. The effect of word length dominated in the cumulative measures (second pass duration and total reading time). Finally, von der Malsburg, Kliegl, and Vasishth (2016) carried out analyses of scanpaths on the Potsdam Sentence Corpus and investigated how variation in readers’ age would interact with word length and measures of syntactic processing effort (i.e., surprisal and retrieval cost). The finding that older readers showed a smaller effect of syntactic processing difficulty was interpreted as indicating an age-associated shift in reading strategies that is driven less by syntax and more by world and discourse knowledge. Taken together, this body of work made the first step toward disentangling contributions of a selected group of text- and reader-level variables and their distribution over time, thus providing benchmark data for empirical research and computational modeling.

The current paper furthers this line of empirical research by reporting the relative importance of a large number of the text-level and reader-level variables over the full time-course of reading measures. We depart from the earlier studies in three crucial ways. First, we adopt the practice common in educational psychology and applied linguistics of assessing verbal, cognitive, and psychophysical skills via a comprehensive battery of standardized skill assessments (see Kuperman & Van Dyke, 2011 for motivation). This allows for a more precise pinpointing of the specific cognitive or linguistic skills that underlie reading behaviors at specific points in a text. For example, we can ask whether phonological awareness, syntactic ability, or working memory is most critical for explaining variance in particular eye-movement measures and for particular linguistic material. Connecting this reader-level variability to specific skills supports a more refined account of the factors that drive the “where” and “when” parameters of eye-movements during reading.

Our second departure from previous work is to employ full texts with increasing lexical, syntactic and discourse-level complexity. This is an advance from previous work which has almost exclusively examined sentence-only reading, and is important because eye-movements while reading sentences embedded in paragraphs have been shown to differ from those associated with reading the same sentences in isolation (e.g., Radach, Huestegge, & Reilly, 2008; Wochna & Juhasz, 2013). In particular, typographic cues such as line-breaks and screen/page boundaries invoke semantic integration processes even when these do not coincide with clause boundaries (Al-Zanoon, Dambacher, & Kuperman, 2016; Kuperman, Dambacher, Nuthmann, & Kliegl, 2010; LaVasseur et al., 2006). Thus, the use of full texts allows for a more ecologically valid assessment of eye-movements, together with the reader characteristics that drive them.

Finally, the complexity of this dataset, with its multiple assessments of reader skill and multiple variables indexing text complexity surpasses previous work, but at the same time represents a challenge for traditional analysis methods. Classical techniques (such as generalized linear regression) work well in “low-dimensional” scenarios, where the number of observations (n) is much greater than the number of variables (p) in a given data set. In cases where the situation is reversed and p is much greater than n (“high-dimensional” scenarios), classical techniques will fail either due to model overfitting or not having enough degrees of freedom. The Random Forests method, a non-parametric regression technique (Strobl, Malley, & Tutz, 2009) based on principles from machine learning, enables us to retain the descriptive advantage provided by our multiple skill assessments with a sample size typical of laboratory-based eye-movement studies. Rather than being forced to resort to data-compression methods such as the principal components or factor analysis, where the separability of various skills may become overshadowed by their common verbal core, this method allows us to evaluate the importance of each skill assessment individually. This will shed light on the relative contributions of linguistic and cognitive skills as well as maintain distinctions important for reading instruction (cf. Rayner, Foorman, Perfetti, Pesetsky, & Seidenberg, 2001). Thus, our use of this method in the current study has the added benefit of demonstrating its utility for examination of individual differences.

The Random Forests method differs from traditional techniques in that it is an atheoretical, data-driven method (see Matsuki et al., 2016, for further comparisons with linear regression methods.) We view this as an important advantage, in that it opens the possibility of discovering novel effects and interactions that might be overlooked in studies with a more narrow theoretical focus, or which incorporate only a small number of factors. In so doing, we introduce a method that responds to Tukey’s (1977) argument that the confirmatory hypothesis-testing aspect of statistical data analysis is incomplete and often misguided without the equally worthwhile and complementary effort of using data to suggest hypotheses to test. Our hope is that this study will serve as a model for the wider application of the Random Forests method as a means of generating hypotheses in psychological science.

In what follows we first report the methods of the corpus collection and the Random Forests method. Then, in three analyses we assess relative contributions of reader- and text-level variables to explaining eye-movement behavior and its time-course. Analysis 1 focuses on eye-movements to individual words. Analysis 2 zooms in on behavior reflecting integrative sentence processing by applying our approach to sentence-final words (motivated by Hyönä, Lorch, & Kaakinen, 2002; Kaakinen & Hyönä, 2007). Finally, Analysis 3 reports global eye-movement patterns at the text level in order to explore variability in passage-level reading behavior. Relative contributions of predictors are considered both individually (Analyses 1A, 2 and 3A) and in interaction with other strong predictors of reading effort (Analyses 1B and 3B). Since this study is exploratory in its nature, we do not aim to posit and validate specific hypotheses. Instead, we present the results of each comprehensive analysis in its entirety and highlight particular associations that are consistent with well-established phenomena in the eye-tracking literature—these can be seen as confirmatory analyses. We will also highlight novel findings produced by the Random Forests method, which describe the relative contributions and interactions of text- and reader-level variables to the reading effort. Where possible, we follow up on these findings with linear regression-based analyses to see whether novel patterns can be confirmed with more traditional methods.

Methods

Participants

A total of 65 (54 females and 11 males; age ranging from 17 to 27) undergraduate students at McMaster University (Hamilton, ON, Canada) participated in the study for a course credit. All the participants reported that they had not been diagnosed with learning or cognitive impairments, and had normal or corrected-to-normal vision. The data from two non-native English speakers were excluded. The data of two other participants were excluded because the microphone failed to properly record the acoustic output of either the letter or digit serial naming tasks. The eye-movement records of 10 additional participants were unusable due to excessive signal loss or equipment issues. Therefore, only the data of 51 participants (40 females) were analyzed. The study was approved by the McMaster Research Ethics Board (protocol 2011-165).

Procedure

Eye-tracking tasks

For the eye-tracking phase of the study, participants were seated in a comfortable chair approximately 65 cm in front of an NEC MultiSync LCD 17 inch computer monitor with a resolution of 1600 × 1200 and screen refresh rate of 60 Hz. Tahoma 50 point font was used for presentation of Rapid Automatized Naming stimuli (see Supplementary materials S1) and Tahoma 30 point font for text passages, resulting in 2.8 characters subtending 1 degree of visual angle. Eye-movements were recorded with an EyeLink 1000 desktop eye-tracker (SR Research, Kanata, Ontario, Canada) with a sampling rate of 1000 Hz. Calibration was performed using a series of nine fixed targets distributed around the display, followed by a 9-point accuracy test to validate eye position. Stimuli were viewed binocularly, but eye-movement data from only one eye was analyzed. Prior to the presentation of the trial stimuli, a dot appeared on the monitor screen, 20 pixels to the left of the position of the first symbol in a grid used in the RAN task, or the first word in the passage. Once the participant had fixated on it, the trial would begin. Drift correction took place at the beginning of each trial and calibration was monitored, and redone if necessary, by the researcher, throughout the data collection. Articulatory responses for the RAN read-aloud tasks were recorded through a Dynex DX28 headset using an ASIO-compatible Creative Sound Blaster X-Fi Titanium HD sound card, guaranteeing a fixed audio latency of 10 ms.

Skill tests

Participants completed non-computerized cognitive and reading assessments in a quiet lab room. The assessments tested cognitive and reading skills such as subjective indices of reading habits, print exposure, reading efficiency, vocabulary size, rapid automatized naming (RAN), and finger tapping. Table 1 lists all of the assessments used in the study. For motivation of participant-level variables and detailed procedure, see Supplementary materials S1. The tests were administered in the same order for all participants.

Table 1.

Descriptive statistics of composite participant-level characteristics, and references to component tests. Labels used for predictors are given in italics.

Test	Reference	Predictor	Min	Max	Median	M	SD
Comparative reading habits survey	Acheson, D. J., Wells, J. B., & MacDonald, M. C. (2008). New and updated tests of print exposure and reading abilities in college students. Behavior Research Methods, 40(1), 278-289.	Comparative reading habits (sum of all the subcomponents)	15	28	23	22.52	3.30
Author Recognition Test and Magazine Recognition Test,	Acheson, D. J., Wells, J. B., & MacDonald, M. C. (2008). New and updated tests of print exposure and reading abilities in college students. Behavior Research Methods, 40(1), 278-289.	Print exposure (sum of Author and Magazine Recognition Test scores)	4	48	16	17.66	9.57
Test of Word Reading Efficiency	Torgesen, J. K., Wagner, R., & Rashotte, C. (1999). TOWRE–2 Test of Word Reading Efficiency.	Reading efficiency	80	120	102	100.93	10.67
Vocabulary Size Test	Nation, I.S.P. and Beglar, D. (2007) A vocabulary size test. The Language Teacher 31, 7: 9-13.	Vocabulary size	20	71	56	53.07	11.87
The Wechsler Abbreviated Scale of Intelligence™ (WASI)	Wechsler, D. (1999). Wechsler abbreviated scale of intelligence. Psychological Corporation.	WASI verbal IQ	87	133	109	107.65	11.17
		WASI reasoning IQ	71	124	107	104.45	12.44
Rapid automatized naming time (RAN)	Denckla, M. B., & Rudel, R. (1974). Rapid automatized naming of pictured objects, colors, letters and numbers by normal children. Cortex, 10(2), 186-202.	RAN naming time (sum of the mean-centered time spent reading letter and number RAN grids)	−10.21	23.60	−0.42	−0.37	6.34
Eye-movement records on RAN grid.	Denckla, M. B., & Rudel, R. (1974). Rapid automatized naming of pictured objects, colors, letters and numbers by normal children. Cortex, 10(2), 186-202.	Mean total reading time for RAN	116	502	200	223	77
		Mean regression rate for RAN	69	200	119	120	30
		Mean skipping rate for RAN	59	201	98	101	25
Finger Tapping	Carello, C., LeVasseur, V. M., & Schmidt, R. C. (2002). Movement sequencing and phonological fluency in (putatively) nonimpaired readers. Psychological Science, 13(4), 375-379.	Tapping means (Inter-tap interval in tapping tasks, mean; averaged across four different measures of tapping)	119	277	167	171	34
		Tapping SDs (Inter-tap interval in tapping tasks, SD; averaged across four different tapping measures)	31	95	61	59	16

To obtain both online and offline measures of reading comprehension, participants read a number of passages (stories 7-14) from the Gray Oral Reading Tests version 4, (GORT, Wiederhold & Bryant, 2001) kit, and answered five multiple choice questions after each passage. Story 4 with its questions from Form A was used as a practice trial for all participants. The text continued to be displayed until the participant pressed a key to signal that they had finished reading, which triggered the presentation of the first of five multiple choice questions. Each question appeared on the screen with five answer choices labeled by the numbers 1-5. Once a participant clicked on a number key, the next question appeared until all five questions had been displayed and answered. After answers to all five questions had been recorded, the next trial began until all texts had been read and the questions answered. Each text and question occupied exactly one screen; the longest text occupied 11 lines. Ample breaks were provided to minimize participants’ fatigue: The entire experiment lasted no longer than 120 minutes.

Variables

Since our examination addressed different aspects of eye-movement behavior, our choice of the unit of analysis, as well as the list of dependent and independent variables, varied across Analyses 1 – 3. Table 2 summarizes those choices.

Table 2.

The descriptive statistics of eye-movement measures for each Analysis differing in the unit of anlysis, and the predictors used in each Analysis.

	Unit of analysis	Dependent Variables	N	Min	Max	Mean	SD	Predictors
Analysis 1	Word	Skipping	16295	0	1	0.21	0.41	All text- and participant-level predictors (19 total)
		Fixation position, pixels	12762	0	195.9	48.63	32.84
		First fixation duration, ms	12762	51	991	221	98
		Gaze duration, ms	12762	51	1782	263	155
		First-pass regression	12762	0	1	0.16	0.36
		Regression path duration	12762	51	29407	583	1168
		Total reading time, ms	12762	51	2913	399	285
Analysis 2	Word (sentence final words only)	Skipping	1876	0	1	0.26	0.44	All text-level predictors except forward transitional probability, and all participant-level predictors (18 total)
		Fixation position	1388	0	230.5	55.88	39.42
		First fixation duration	1388	6	1114.0	212.34	106
		Gaze duration	1388	15	1959.0	262.08	168
		First-pass regression	1388	0	1	0.25	0.43
		Regression path duration	1388	24	31479	963	2248
		Total reading time	1388	15	2804	419	327
Analysis 3	Passage	Total number of skips (per word)	243	0.14	0.60	0.33	0.09	GORT Complexity index and all participant-level variables (13 total)
		Total number of fixations (per word)	243	0.50	2.02	1.16	0.30
		Total number of regressions (per word)	243	0.01	0.33	0.15	0.05
		Total reading duration (per word)	243	103.00	511.63	251.90	74.31
		Comprehension score (per passage)	243	0.00	5.00	3.54	1.29

Dependent variables

Eye-movement measures were collected while reading GORT passages. The current study looked at the following measures at the word level: first fixation position (position of the initial fixation of words from the left-most bound of the words, in pixels), first fixation duration¹, gaze duration (summed duration of all fixations landing on the word before the gaze leaves the word for the first time), first-pass regression rate (a binary indicator of whether the first pass ended in a regressive saccade), regression path duration (also known as go-past time, i.e., summed duration of all fixations starting on the word until the gaze leaves the word to the right for the first time, including the time spent regressing back to earlier parts), total reading time (summed duration of all fixations landing on the word), and skipping rate (a binary indicator of whether the word is skipped). Since we often encountered a situation when one of the first exploratory fixations on a screen was to the middle or end of the text, a disproportionately high share of words appeared as if they were skipped during the first pass on the word. For this reason, we defined skipped words as words that were not fixated at all during a trial, rather than not fixated during the first pass. The listed eye-movement measures, applied to all words in the passage, reflected the effort of word recognition in context (Analysis 1A,B). The same set of measures was considered for sentence-final words, in order to quantify the effort of integrating words in a sentence into a unified semantic representation (Analysis 2). For Analysis 3, the dependent variables at the passage level included the following five measures: total number of skips, total number of fixations, total number of fist-pass regressions, and total reading duration per passage, and accuracy of responses to comprehension questions. Because of the different passage lengths, the former four measures were normed by the number of words in each passage. Table 2 lists the dependent variables and number of data points considered in each Analysis.

Independent variables: Participant properties

The skill test battery incorporated seven diverse tasks, with multiple subtasks, representing major hypothesized components of reading comprehension ability (vocabulary size, decoding, phonological awareness, rapid automatized naming (RAN), and experience with print), as well as general cognitive (IQ) and executive (tapping) skills. These tasks gave rise to 12 behavioral measures of Reader variables: Table 1 contains a summary of the measures with respective citations, and Supplementary materials S1 provide motivation for including those components.

Independent variables: Text properties

In addition, seven different text-specific characteristics were considered: word length (in characters), word frequency, word position in passage, surprisal², backward bigram frequency (i.e., the frequency of co-occurrence of each word with a preceding word), forward bigram frequency (i.e., the frequency of co-occurrence of each word with a following word), and complexity of GORT passages (henceforth text complexity).

Word frequency counts were obtained from the 51 million-token SUBTLEX-US corpus of subtitles to US films and media (Brysbaert & New, 2009). Word length and frequency as lexical-level variables were complemented by five variables that define the role of word in context, i.e. at the level of discourse. Word position was defined as the ordinal position of each word in the passage, numerically coded from 1 to the total number of words in a passage. This is a measure of how much of the passage context the reader has been exposed to, and how much it can influence processing of an individual word. Since this measure is rarely considered in eye-tracking studies of reading (but see related explorations of sentence length effects in Cop, Drieghe, & Duyck, 2015; Liversedge et al., 2016), we highlight its role in our analyses below. As described below, we systematically removed the words that were displayed in the left-most and the right-most positions on a line of text. Thus, the actual values for the word position runs from 2 to the total number of words in the paragraph, with values for the left-most and right-most words missing in between.

Surprisal (Hale, 2001; Levy, 2008) is a measure of the extent to which the occurrence of a given word is unexpected given the previous words of a sentence, and is hypothesized to capture the cognitive effort required to process a word in its context. A few studies (e.g., Boston, Hale, Kliegl, Patil & Vasishth, 2008; Boston, Hale, Kliegl & Vasishth, 2011; Demberg & Keller, 2008; von der Malsburg, et al., 2016) have shown that surprisal is a useful predictor of sentence processing difficulty. Similar arguments were made regarding transitional probabilities (McDonald & Shillcock, 2003; but see Frisson, Rayner, & Pickering, 2005). To obtain surprisal estimates for each word, we first tagged Parts-of-Speech (POS) of each word in each sentence in our texts using the Stanford POS tagger (Toutanova et al., 2003). The POS tags of the texts were then supplied to the HumDep Version 3.0 software package (Boston, 2013), which generates word-level surprisal as its output using the dependency parsing algorithm by Nivre (2004). Backward and forward bigram frequency (defined above) were estimated from the Corpus of Contemporary American English (Davies, 2008).

Finally, text complexity is a measure of the lexical and syntactic complexity of the read passage. We supplied texts 7-11 from the GORT standardized assessment as inputs into the Coh-Metrix online tool (McNamara, Louwerse, Cai, & Graesser, 2013), which provides numeric indices of the coherence of the text based on such linguistic measures as readability, syntactic complexity, lexical diversity, and referential cohesion. The resulting estimates of the lexical and syntactic difficulty of the texts, as well as their readability, indicated a constant gradient increase along multiple indices of complexity as a function of the text’s ordinal number in the test kit. We considered that number (7 to 11) as an overall index of the text complexity. Table 3 lists the descriptive summaries of the text properties.

Table 3.

Descriptive statistics of text-level predictors.

Text-level predictor	Min	Max	Median	M	SD
Word length	3	15	6	6.63	2.32
Frequency (log10)	0.00	5.50	2.80	2.88	1.19
Backward bigram frequency (log10)	0.00	5.49	1.97	1.82	1.60
Forward bigram frequency (log10)	0.00	5.48	1.65	1.60	1.54
Surprisal	0.00	9.76	1.63	1.99	1.68
Word Position	2	164	68	71	41.34

Statistical methods

Random Forests

In the current study, the relative importance of predictors was investigated through a statistical technique known as Random Forests (Breiman, 2001; Strobl, Malley, & Tutz, 2009; see Matsuki et al., 2016 for a tutorial review). The method of Random Forests is a generalization of the decision tree method, in which the data space is recursively partitioned (usually a binary split) according to the value of one of the predictor variables, such that the observations within a partition become more and more homogeneous. Random Forests builds multiple decision trees using random samples of observations for each tree and (at each split point) random samples of predictors. The outcome of a decision tree is a set of split points and associated hierarchically nested predictive rules, for instance, “If Text complexity > 9, and if Reading efficiency > 108, then mean total reading duration = 237 ms.” The decision tree is powerful yet highly flexible as it can model any type or distribution of dependent variable without explicit specification (i.e., continuous, ordinal, or binary). Decision trees are also robust against outliers and variation in the distribution and type of predictors (Steinberg & Colla, 1995), however they can suffer from potential overfitting, losing generalizability. The Random Forests technique solves this shortcoming by adding two layers of random sampling. First, it utilizes a procedure referred to as bagging (bootstrap aggregating) where multiple decision trees are fit to random (often bootstrapped) samples of observations, and the predictions from each tree are then aggregated to provide more fine-grained prediction than is available from any single tree. Second, a random subset of predictors is chosen when determining each split point, so that all predictors would have a chance of contributing to the model’s prediction. In this way, the uniqueness of each tree within the forest is maximized, which results in lowering the generalization error of the forest.

As demonstrated in earlier research (Matsuki et al., 2016; see also Strobl et al., 2009; Tagliamonte & Baayen, 2012), the Random Forests technique can capture functional relations between dependent variables and predictors even in datasets with a small number of observations and a large number of predictors while avoiding two problems common for parametric regression approaches: overfitting and collinearity. This feature of the method affords a definitive advantage to the Random Forests method in the task of simultaneously comparing contributions of numerous predictors. In a generalized multiple regression model, this estimation would have been inaccurate either because of a low number of observations per predictor (see discussion in Analysis 3A and Harrell, 2001) or because of the astronomically high levels of collinearity between predictors (condition number χ > 200 in all analyses below).

The flexibility of the Random Forests technique can also be seen in the fact that no specialized mechanisms are required to capture random effects or clustered data (c.f. Hajjem, Bellavance, & Larocque, 2014; Karpievitch, et al., 2009), For example, because the predictors used in the current study vary at levels of participant, word or passage, the observations from the same cluster (formed, for instance, by arbitrarily chosen values of Text complexity = 10 and Reading efficiency = 109) will end up in the same terminal node of the tree by design, effectively generating a hierarchical structure similar to crossed random effects. Matsuki et al., (2016) verified that this method of treating observations as nested under participants consistently explained approximately the same amount of variance as the upper-bound of the linear regression-based methods (see Dilts, 2013; Hajjem et al, 2014, for similar observations).

Assessment of Relative Importance with Random Forests

Because the individual trees in a Random Forests model are not based on the same subset of the data, it is not suitable to use stepwise model comparison for estimation of relative importance, as might be done with linear regression models. Instead, relative importance of predictors in Random Forests can be estimated through the procedure of variable permutation and model refitting. For each predictor, random permutation of its values is performed such that any existing correlation of the predictor with the dependent variable is broken. If a tree has breakpoints based on a predictor A but no breakpoints based on B, randomly swapping the value of A should greatly affect the tree’s prediction accuracy, but doing the same on B should have no effect. Thus, if the predictor is important, the prediction accuracy of the model should drop substantially. On the other hand, the prediction accuracy of the model after random permutation would remain unchanged if the predictor has little or no importance. Thus, the difference between the prediction accuracy of the models fit to the pre-permutation data and the post-permutation data reflect the importance of the predictor. Because Random Forests models can capture complex interactions, the relative importance of variables does not simply reflect the direct relation between the dependent variable and one of the predictor variables (i.e., the predictor’s main effect). It can also reflect a substantial contribution of the predictor to interactions with other predictors.

Crucial parameters in the application of Random Forests are the number of trees to be built (commonly referred to as ntree) and the number of randomly sampled predictor variables used to select each split point (commonly referred to as mtry). The values of these parameters are known to influence model stability—that is, since Random Forests models incorporate random sampling and permutation, their outcomes are necessarily subject to random variation. In the current study, the value of ntree was set to 1,000 in all models. It is common to use for values of mtry either the square-root of the number of predictors (Breiman, 2001), or one-third of the number of predictors (Liaw & Wiener, 2002). To address the issue of stability, we follow the method suggested by Genuer, Poggi, and Tuleau-Malot (2010), which is to run multiple sets of models with the mtry parameter varying between these two commonly used values with a step of 1 (e.g., for a model with 19 predictors, mtry would take values 4, 5, and 6; for the number of predictors in each analysis, see Table 2). The results of each run are averaged to obtain a stable outcome.

The outcomes are expressed as numeric values of variable importance. These values are not comparable between Random Forests models, as each model will have its own scale of importance. What is of interest in the model outcomes then are not the actual scores of the predictors’ importance, but rather the relative rank of the predictors: These are informative and comparable across models.

All analyses in the current study were conducted using the statistical software package R version 3.1.0 (R Core Team, 2014). We used the Random Forests algorithm implemented in cforest function of the party package version 1.0-21 (Hothorn, Buehlmann, Dudoit, Molinaro, & Van Der Laan, 2006; Strobl, Boulesteix, Zeileis, & Hothorn, 2007; Strobl, Boulesteix, Kneib, Augustin, & Zeileis, 2008). For an additional tutorial on model fitting and interpretation, see Matsuki et al., (2016). Also, see Supplementary materials S5 to this paper for the code and data used to produce Random Forests models and visualizations.

Results and Discussion

Analysis 1: Reading comprehension at the word-level

In this analysis, word in a passage was the unit of analysis. The original data contained 33,455 data points, which come from a total of 243 passages that did not feature excessive blinking, skipping, and signal loss throughout the passages (12 of the 255 [51 participants × 5 passages] passages were removed). To be consistent with previous work (e.g., Kliegl et al., 2004), we excluded all fixations on words that were displayed in the left-most and the right-most positions on a line of text (5,574 data points). Because eye-movement patterns on the closed-class function words have been shown to differ from those on content words (e.g., Kliegl et al., 2004), we also removed all fixations that landed on closed-class function words so as to simplify our discussion (199 words in total; 10,763 data points). We then removed words that do not appear in the word frequency list of the 51 million-token SUBTLEX-US corpus (534 data points). This resulted in 16,295 data points. The dataset for the measure of skipping (a binary indicator of whether the word is skipped) is based on these 16,295 data points. Finally, we removed fixations shorter than 50 ms which are more likely to be associated with oculomotor programming rather than cognitive processes (Morris, 1984), as well as fixations longer than 1000 ms, gaze duration longer than 1800 ms, and total reading time longer than 3000 ms (3,533 data points altogether; all upper thresholds were set to cut off the top 1% of the duration distribution). The remaining data pool of fixated words contained 12,762 points. In what follows we report the relative importance of predictors considered individually (Analysis 1A), and the relative importance of predictors in an interaction with word length as a strong co-determiner of eye-movements (Analysis 1B).

Analysis 1A: Relative importance of individual predictors in the word-level analysis

Skipping

We demonstrate our method of depicting the results of Random Forests modelling using the eye-movement measure of skipping as an illustrative example; results for other measures will be presented in summary form via the heat-maps described below. We chose skipping because it is the earliest index of eye-movement behavior that a word can elicit and this measure is central for empirical and theoretical research into oculomotor control (cf. reviews by Brysbaert, Drieghe, & Vitu, 2005; Drieghe, Rayner, & Pollatsek, 2005). Figure 1A displays a sorted list of relative importance scores for each independent variable, derived via the permutation method presented above with skipping rate as the dependent variable. Each score is represented as a mean and standard error resulting from multiple runs of Random Forests models with different values of the mtry parameter (ranging between 4 and 6 for this model with 19 parameters). Both this Random Forests model and all subsequent ones demonstrated a high degree of stability of predictions across multiple runs and small values of standard errors for each predictor.

Figure 1.

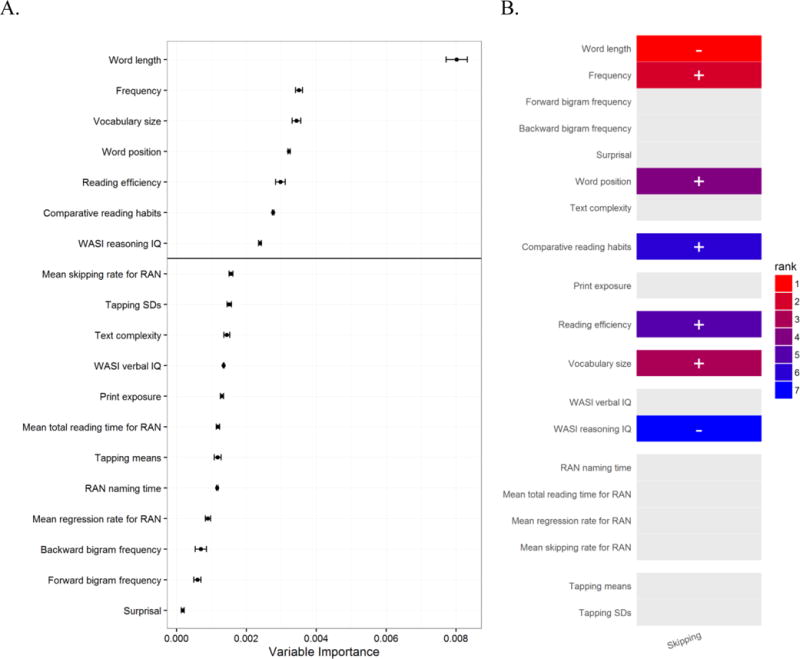
Relative variable importance obtained from Random Forests models for skipping rate at the word level (Analysis 1). A. The variable importance scores are plotted in ascending order to show the rotated ‘Scree plot’, with the solid black horizontal line indicating the threshold chosen through visual inspection. Error bars represent the standard error of variable importance scores obtained from multiple runs of forests with different mtry parameters. B. A heat map representation of the variable importance where only variables above the threshold are colored according to their rank.

To simplify the process of comparing results across eye-movement measurements, we re-plotted the information shown in Figure 1A as a heat-map (see Figure 1B) using the following two steps. First, we determined a threshold for variable importance by visually inspecting the gap in the sorted list of relative importance scores (shown as a horizontal line in Figure 1A). This is conceptually similar to the scree test in factor analysis (Cattell, 1966) in which a threshold is determined visually at the gap in the steepness of a line connecting the sorted values of variance (or eigenvalues) associated with the factors (see Supplementary Material S2 for more detail). Note that this is not at all equivalent to a determination that certain predictors are more or less statistically significant, but is simply an expedient method for focusing attention on the most important predictors. Second, we generated a heat-map-like image where color-coding reflects ranked relative importance of variables.

Thus, for the skipping dependent measure, seven predictors had importance scores that were distinguishable from the rest. Figure 1B displays these seven predictors with cells for the relevant predictors color-coded by their rank (with red as the top ranked and blue as the bottom ranked), while the remaining predictors are shown in grey. We further organize our results in Figure 1B so that text characteristics (top 7 cells) are separated from participant characteristics (all other cells below the white-space break). That is, rather than listing predictors by order of importance (as in Figure 1A), the rows in Figure 1B are partitioned into the 7 subgroups of measures described in Table 1, with text characteristics presented at the top followed by the 6 different skills assessed by our battery measures. The signs in the colored cells indicate the directionality of the relation between skipping and each predictor, which were obtained by calculating the rank-order correlation between the predictor and the dependent variable (see Supplementary Material S2 for more detail).

To aid interpretation of this set of results, we report the rank-order correlations between skipping and each of the seven predictors with a relatively high importance: Word length, ρ = −0.20, p < .001, word frequency, ρ = 0.13, p < .001, vocabulary size, ρ = 0.06 p < .001, word position in passage, ρ = 0.01, p > .2, reading efficiency, ρ = 0.05, p < .001, comparative reading habits, ρ = 0.05, p < .001, and reasoning IQ, ρ = −0.05, p < .001. Reported p-values were adjusted for multiple comparisons (in this case, 7 comparisons) using the False Discovery Rate method (Benjamini & Hochberg, 1995). We stress that–given the potential non-linear or interactive nature of functional relations in the data–simple correlations reported as polarity signs in the heat maps occasionally produce unintuitive directions for effects, see Supplementary materials S2 for details. However, since correlations are obtained independently of the Random Forests modeling they do not reflect on the utility of this non-parametric machine-learning method. Correlations can only be seen as supplementary information regarding the association between the two variables in question.

Replicating prior findings

The Random Forests analysis revealed that the most important predictor of Skipping was word length, and the correlation sign indicated that shorter words were skipped more often, corroborating a well-established observation in the literature (Brysbaert, Drieghe, & Vitu, 2005; Kliegl, Grabner, Rolfs, & Engbert, 2004; Rayner & McConkie, 1976; Rayner, Sereno, & Raney, 1996; Rayner, Slattery, Drieghe, & Liversedge, 2011). Word frequency was second in its relative importance, and the correlation sign showed increasingly frequent skipping for more frequent words. The finding was also consistent with the experimentally established direction of the effect, and the robust prior finding that the effect of word frequency on skipping rate tends to be weaker than the effect of word length (Kliegl, Grabner, Rolfs, & Engbert, 2004; Rayner, Slattery, Drieghe, & Liversedge, 2011). One key difference between the current and the previous observations is that in previous studies, the effect of word frequency is commonly seen after controlling for the length of words. Yet the correlation between length and frequency is no concern for a Random Forests model which uses a full permutation and thus considers all variables independently; see also Analysis 1B for a length × frequency interaction. Despite methodological differences, the Random Forests analysis is consistent with analyses of variance (including generalized regression) in prior research and emphasizes the reliability of the present method.

Novel findings

Four skill measures—Vocabulary size, Reading efficiency, Comparative Reading habits, and reasoning IQ—were identified as being of high importance for predicting skipping (Figure 1A), and these represent novel findings in the eye-movement literature. Readers with a greater ability to efficiently decode orthographic codes into phonological ones (Reading efficiency), as well as readers with larger vocabulary sizes were more likely to skip words. Likewise, readers who self-reported as being more proficient and avid readers (Comparative reading habits) were more likely to skip words. These results are intuitive, suggesting that skipping is a strategy preferred by those with better command of grapheme-to-phoneme correspondences or who have a more developed mental lexicon, which may support more efficient extraction of upcoming parafoveal information that can be used to direct eye-movements past known information (Veldre & Andrews, 2015). A less intuitive finding was one showing that a higher non-verbal IQ leads to a lower skipping rate. This role of non-verbal IQ seemed to recur in later analysis, and we speculate that readers with higher non-verbal IQ are more likely to be attentive and read the documents more thoroughly, thus showing a lower skipping rate.

Finally, the word position in passage was revealed in this analysis to be an important predictor of skipping, despite a non-significant correlation between the two measures. We defer a detailed discussion of this effect to Analysis 1B under Effects of word position in text.

All dependent variables

Figure 2 extends the presentation of results to all eye-movement dependent variables, which were concatenated into one plot to allow easy comparison across measures. The eye-movement measures are ordered in columns according to the time course of reading, and are further grouped into early measures (first fixation position, first fixation duration, and gaze duration), and late measures (first-pass regression, regression path duration, and total reading time). Skipping rate is its own group. Color coding in each column indicates the relative ranks of the independent variables identified as important predictors of a given dependent variable (see above). Thus, the seven predictors of skipping rate above the cut-off elbow point in Figure 1 are represented as colored tiles (with red as the top rank) in the leftmost column of Figure 2.

Figure 2.

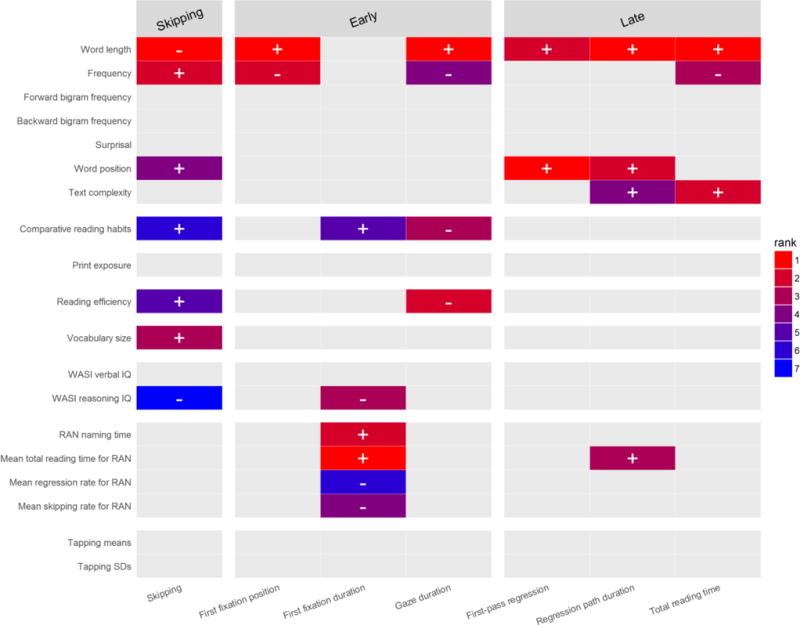
Heat map of the relative importance of text- and participant-level predictors of word processing effort across the eye-movement record.

The relative importance heat map in Figure 2 enables visual examination of how the set of predictors as a group, as well as a sole predictor alone, contribute to either select measures of reading behavior or throughout the entire time course of reading. First, we highlight the data patterns in Figure 2 that corroborate well-established findings of the literature on eye-movement control in reading, and then proceed to novel findings.

Confirmatory findings

One of the robust observations in the eye-tracking literature is a large degree of dissociation between the spatial (“where”) and temporal (“when”) aspects of saccadic planning and execution (cf. Morrison, 1984; Rayner & McConkie, 1976; Findlay & Walker, 1999; Rayner, 1998; Vainio, Hyönä, & Pajunen, 2009). Figure 2 reveals that variables that rank highly as predictors of first fixation position on a word were in a complementary distribution with those identified as important for first fixation duration. First fixation position was strongly influenced by the text properties of word length and word frequency, while its duration is modulated by properties of the reader. This finding strongly corroborated the independence between the “where” and the “when” of eye-movements in reading. It also gave rise to a novel observation. Measures of reading efficiency, RAN performance and vocabulary size have been shown by Kuperman and Van Dyke (2011) to reliably affect initial landing position (with more proficient readers landing further into the word) in a cohort of non-college-bound readers. However, no individual difference measure came out as an important predictor in the current cohort of (presumably more proficient) undergraduate readers. This suggests that – at least among proficient readers – individual variability is a minor causal factor for the accuracy of saccadic planning and execution as compared to length and frequency of the target to-be-fixated word.

Furthermore, in prior characterizations of the role that text variables play in English, Finnish, German and Spanish, word length would invariably emerge as a strong predictor for all eye-movement measures, with the exception of the earliest measure, first fixation duration (Calvo & Meseguer, 2002; Hyönä & Olson, 1995; Kliegl et al., 2004; Kliegl et al., 1983; Rayner & McConkie, 1976). Also Kuperman and Van Dyke (2011) have observed that the impact of length was relatively small in first fixation duration and single fixation duration (as compared to the impact of reader-level predictors), but was the strongest of all predictors in gaze duration and total reading time. Additionally, the contribution of word frequency in Kuperman and Van Dyke’s data was found to be smaller than that of word length, with the discrepancy in their effect sizes increasing from the early to late eye-movement measures (cf. Figure 6 in Kuperman & Van Dyke, 2011). Our present results as displayed in Figure 2 faithfully replicate this earlier body of findings. Word length emerged in our data as a pervasive and highly ranked predictor for virtually all eye-movement measures. As word length increased, readers tended to fixate further into words, spend more time fixating words, and skip them less often. However, as in prior studies (e.g., Kliegl et al., 2004), word length was not an important predictor of the duration of the first fixation on the word. We also found that the relative importance of word frequency was dwarfed by that of word length, and the rank difference between the two variables increased towards late measures such as regression path duration and total reading time. To sum up, our method confirmed the well-established time-course of comparative contributions of word length and frequency in codetermining reading behavior as established across languages and skill levels (proficient undergraduate readers and non-college-bound young adults).

Novel findings

Time-course of Reader and Text effects on word recognition

While it is possible to discuss each specific effect represented by a colored cell or lack thereof in the heat map of Figure 2, here we restrict ourselves to a broad overview of data patterns. Highly-ranked predictors (i.e., colored tiles) in Figure 2 suggest differential effects of Reader and Text properties on early (first fixation and gaze duration) and late (regression path duration and total reading time) eye-movement durational measures. Participant characteristics mainly drive variability in early measures and are absent as important predictors from late eye-movement measures. While not a formal test, patterns observed in the heatmap reveal many more colored (important) tiles in early vs late measures, 8 vs 1 respectively. Conversely, Text variables surface more often as predictors of late, and not early, eye-movement measures: 2 vs 8 colored tiles, respectively. A general advantage in reading and cognitive skills – indexed as higher IQ, better reading efficiency, or faster or more consistent RAN performance – was associated with shorter first fixation durations and gaze durations, and had little to no influence on later reading measures.

Correlation signs also pointed to a counterintuitive inflation of first fixation durations for readers who self-reported as more proficient readers. A follow-up analysis in Supplementary materials S3 (and Figure S2) demonstrates that this apparent inflation is spurious and occurs because simple correlations are ill-equipped to model the interactive and non-linear effects which in fact characterize this data. This reiterates our point that it is more instructive to focus simply on the ranking outcome of the Random Forests analysis and treat the absolute direction of any correlation that may exist as only a rough indication of the effect’s polarity. (The calculation of correlations is done outside of the Random Forests framework and do not reflect on the reliability of the method itself.)

Among Text variables, words and texts that were linguistically more complex were associated with higher regression rates, longer regression path durations and total reading times. Words further into the text also led to higher skipping and regression rates as well as longer regression path durations (see the section Effects of word position in text in Analysis 1B for further discussion). Pitted against received interpretations of eye-movement measures (Boston et al., 2008, Clifton, Staub, & Rayner, 2007), these novel findings suggest a previously unattested temporal localization for sources of influence on word recognition in context. Variability between readers is influential for early word decoding and word identification processes. Properties of texts and, surprisingly, even properties of words only play a secondary role in these early stages. Conversely, inter-reader variability is dwarfed by text properties in the later stages of integrating words into context and resolving ambiguities. We return to this observation in further Analyses and in the General Discussion.

Analysis 1B: Interactions in the word-level analysis

For our exploratory method to be of utility, we need to demonstrate the ability to consider interactions of variables, beyond the description of the “overall” importance of Reader and Text variables provided above. There are two reasons for this. First, there is a wealth of evidence that Reader variables interact with Text variables as reading comprehension unfolds in time (see Introduction for references). Second, the importance metric we used here indicates the importance of predictors relative to other predictors in the Random Forests model, but does not provide the absolute size of their effects. Consequently, the presence of one strong predictor with an exceedingly high relative importance score may make the importance of all other predictors look trivial. In addition, a single predictor with a very high relative importance score may affect the calculation of the cut-off point that determines which predictors in the Random Forests model are considered important, resulting in some strong predictors going unrecognized. In our data, an example of such a predictor is word length and its very high relative importance for skipping rate, first fixation position, gaze duration, regression rate, regression path duration, and total reading time. Analysis 1B addresses both the ability to model interactions in a more transparent manner and the specific influence of word length by implementing an interaction of each text- and participant-level predictor by word length, across all dependent variables.

Although we focus on word length, the analytical approach we follow here is a general one, through which an interaction between any variable of interest and all remaining predictors may be examined. We do this by partitioning the data based on values of the variable of interest (here, word length) and fitting separate sets of Random Forests models to each partition of the data. By examining the ranking of predictors within each partition, we can observe analogues of a “simple main effect” (i.e. the ranking of a predictor in one partition is the same as in other partitions), an “interaction” (i.e. rankings of a predictor in different partitions are substantially different), or a “null effect” (i.e. a predictor is considered trivial in all partitions).

Previous studies have indicated that word length interacts with several individual-level predictors. For instance, Kuperman and Van Dyke (2011) have shown that readers with better word identification and rapid automatized naming skills tended to show smaller effects of word length on durational eye-movement measures (also see, among others, Hawelka, Gagl, & Wimmer, 2010). In this analysis, we chose to split the data for each eye-movement measure into two partitions based on the median split of word length. The dataset containing only short words (less than 6 characters) had 9,089 data points available for identifying skipping and 6,556 data points available for measures based on fixated words. The dataset with long words (6 characters or more) had 7,206 data points for skipping and 6,206 data points for all the other measures. If some predictors were to interact with word length, we expect a discrepancy between the short and long words in either rank orders of those predictors or the directionality of the relation between the predictor and eye-movement measures.

Methods

All aspects of the statistical modeling were identical to those of Analysis 1A, with one exception. Word length was not included as one of the predictors during model fitting. Thus, for this analysis, there were a total of 19 independent variables. The model fitting procedures and the heat-map generation procedures were adjusted accordingly to accommodate this change. One key difference in the resulting heat map is the arrangement of columns. In the current analysis, there are two columns per each dependent variable: one reporting the rankings of relative variable importance obtained from the subset of data containing only the short words (less than 6 characters) and another reporting the rankings obtained from the remaining subset with the long words.

Results and Discussion

Figure 3 illustrates the relative importance of predictors for each eye-movement measure, separately for each subset of data containing short and long words. As we have speculated, many patterns that were absent in Analysis 1A have emerged, as a larger number of predictors previously overshadowed by the strength of the length predictor now demonstrated higher importance. This occurred particularly for the eye-movement measures for which world length was the most (or second-most) important predictor in the previous analysis 1A (i.e., all but first-fixation duration).

Figure 3.

Heat map of the relative importance of text- and participant-level predictors of word processing effort across the eye-movement record. Separate models were fit to the subset of the data containing long words (more than 6 character long) and short words.

Figure 3 enables us to identify patterns of interaction (via color/sign discrepancy in adjacent cells) across the entire space of predictors and the time-course of reading. To continue with skipping rate as our example, most of the important predictors of skipping (frequency, comparative reading habits, reading efficiency and the non-verbal reasoning component of IQ) were found to strongly affect shorter rather than longer words. We observed a stronger rank order correlation between skipping rate, frequency and non-verbal IQ in shorter words rather than longer words (Frequency: ρ = 0.08, p < .001 for short vs. ρ = 0.03, p < .02 for long words; nonverbal IQ: ρ = −0.06, p < .005 for short vs. ρ = −0.04, p < .01 for long words). There was no significant numeric difference between short and long words in how strongly skipping rate correlated with comparative reading habits and reading efficiency (ρ = 0.05, p < .001). The length by frequency interaction is in line with a robust observation that short frequent words have the highest skipping rate (Drieghe et al., 2005; Rayner, Sereno, Raney, 1996); however other interactions are new and merit further investigation. For instance, word position in text showed an interaction with word length. The direction of this functional relationship changed from shorter to longer words, suggesting readers skipped shorter words more often and longer words less often when progressing through the text. A further examination of this interaction is provided below under Effects of word position in text.

Differences in relative importance among skill measures between the length-based partitions were evident in most other dependent measures (see especially first fixation position, first fixation duration, gaze duration, regression path duration and total reading time). In the absence of word length as a competitor for relative importance, the pattern observed above whereby Reader variables dominated early durational measures and Text variables dominated later ones was still found, both with respect to the number of important predictors and in their relative importance (shown in color). However, Figure 3 shows that interactions of these variable-types with length did not follow the same strict dichotomy, as effects of the reader variables (e.g., IQ, RAN, Vocabulary Size) were observed in later measures (e.g., first pass regressions, regression path duration, and total reading time), and even appeared as the most highly ranked variables for the latest measures (i.e., regression path duration and total reading time.)

Confirmatory findings

As in Analysis 1A, we refrain from exhaustively describing the role of individual predictors throughout the time-course of reading, although this information is available from a close inspection of Figure 3. Here we focus on two findings that are especially noteworthy. First, we note that the effect of four measures of RAN performance (i.e., RAN naming times and total reading time, regression and skipping rate during RAN) was primarily found in shorter words, coming out as an important predictor of first fixation and gaze duration (see Figure 3 for rankings and Table 4 for rank-order correlations). This advantage in predictive power for shorter words is intuitive when one considers that shorter words have little morphological and phonological complexity, and therefore may evoke the same surface-level visual processing required in RAN tasks, where one simply has to identify single letters, digits or short words.

Table 4.

Rank-order correlation (ρ) and associated p-value (adjusted for multiple comparisons using the false discovery rate method) for the relation between two eye-movement measures and four rapid automatized naming (RAN) measures for short and long words.

	Short		Long
	ρ	p-value	ρ	p-value
First Fixation Duration
RAN name time	0.05	<0.01	−0.01	0.64
Mean total reading time for RAN	0.02	0.12	0.02	0.23
Mean regression rate for RAN	−0.03	0.07	−0.01	0.47
Mean skipping rate for RAN	−0.01	0.35	−0.02	0.20
Gaze Duration
RAN name time	0.05	<0.01	0.01	0.37
Mean total reading time for RAN	0.03	0.08	0.03	0.08
Mean regression rate for RAN	−0.03	0.07	−0.02	0.31
Mean skipping rate for RAN	−0.01	0.42	−0.02	0.23

Second, text complexity either exclusively affected longer words (total reading time) or showed a comparable level of relative importance for shorter and longer words (first fixation position and regression path duration). For instance, as the complexity of text increased, there was a greater increase in total reading time for words that are longer (ρ = 0.15, p < .001), but a much less pronounced change for shorter words (ρ = 0.03, p < .01). This is indicative of increased effort for processing long words embedded in texts that are lexically, syntactically or inferentially complicated: this effort is apparent in measures that indicate both word recognition (first fixation position) and integration in context (regression path duration, total reading time; see below). We interpret this finding as suggesting that word recognition is influenced not only by processing the word in its immediate context, but also by the difficulty of incrementally building and maintaining more complex structures at the sentence and discourse-level. This observation is in line with earlier investigations demonstrating the influence of global context on word and sentence processing effort (see Huestegge & Bocianski, 2010; Radach, Huestegge, Reilly, 2008; Pynte & Kennedy, 2006; and Teng, Wallot, & Kelty-Stephen, 2016).

Novel findings: Effects of word position in text

As in Analysis 1A, we demonstrate the utility of the Random Forests method for generating new data-driven hypotheses by highlighting novel findings. Word position is ranked very highly as a predictor of skipping in our analysis (Figure 3), yet to our knowledge, the influence that word position in a text has on eye-movements is largely unstudied (but see Kuperman et al., 2010; Pynte & Kennedy, 2006 and related work by Al-Zanoon et al., 2016; Cop, Drieghe, & Duyck, 2015; Liversedge et al., 2016). This section summarizes our findings in relation to this variable. As described earlier, we found that the effect of word position on skipping rate showed different signs for shorter versus longer words. Closer investigation of this apparent interaction revealed this as an instance where correlation signs can be misleading due to the non-monotonicity of the relation (see Supplementary materials S3). Figure 4 (top left panel) shows local regression (loess) curves fitted to skipping rate and reveals that the effect changes as a quadratic U-shaped function of word position in text, such that skipping rate dropped gradually until about 50 words into the text, and then gradually increased toward the end of the passage. The dotted linear fit in Figure 4 which determines the sign of the linear correlation apparently does not capture the true underlying relation. A generalized mixed effect model confirmed that word position has a significant second-degree polynomial relationship with skipping rate (Word Position: b = 6.22, SE = 4.38, z = 1.42, p > .15; Word Positionˆ2: b = 21.75, SE = 4.93, z = 4.42, p < .001), with longer words showing a steeper parabola (Word Positionˆ2: b= 28.25) than shorter words (Word Positionˆ2: b = 15.26; Length contrast × Word Positionˆ2 = 12.99, SE = 4.86, z = 2.67, p < .001; see Supplementary materials S4 for details of model fitting procedure). As shown in the remaining panels in Figure 4, we visually examined the pattern at each level of text complexity, and found a similar pattern across all passages, which varied in complexity, number of words and distributions of word lengths. We tentatively conclude that readers tended to engage in a riskier reading behavior but gradually increased their attention after the first few sentences (at regions roughly equivalent to the 50th word). One explanation for this behavior is that readers are initially seeking to establish the topic of the text and activate the relevant schema, after which they settle into more careful reading behavior (Graesser, 1981).

Figure 4.

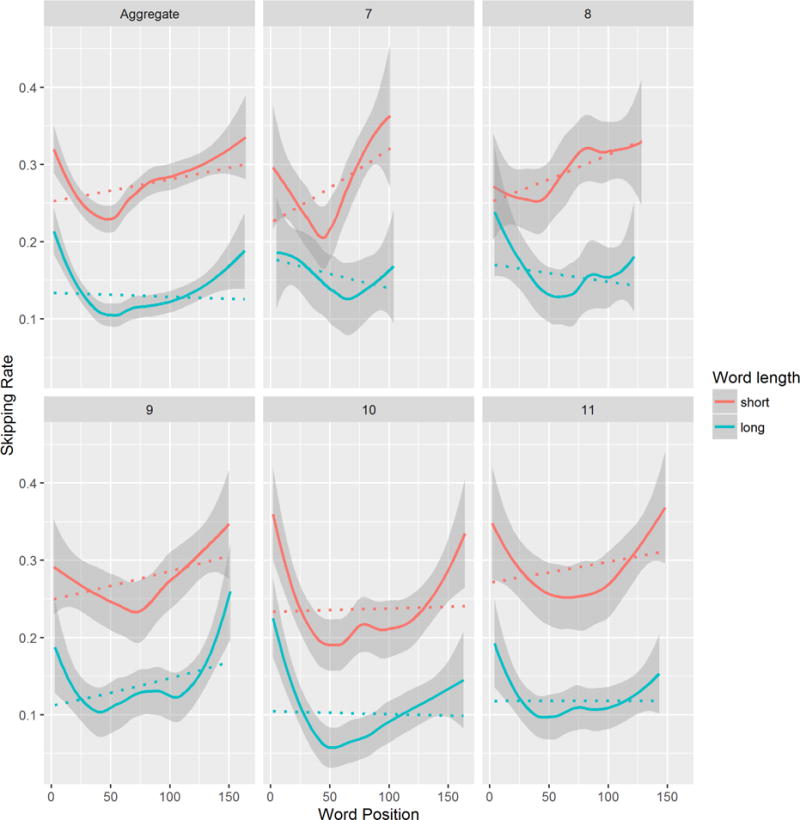
Skipping rate as a function of word position for longer words and shorter words. The top left panel (“aggregated”) is based on an entire dataset, whereas other panels only include datasets with a corresponding GORT passage number. Dotted lines are based on the fit of generalized linear models with a binomial link function, and solid lines are based on the fit of local regression (loess).

Similar observations were true for the effect of word position on regression path duration, where opposite correlation signs for shorter and longer words were a by-product of underlying non-monotonic patterns (loess fits not shown).

A different type of interaction between word position and word length was observed for total reading time, where shorter words showed a similar total reading time throughout a text with a slight decrease toward the later part of the passage, while longer words were read faster the further they were into the text. A generalized mixed effect model shows that there was a significant interaction between the word position and total reading time such that word position stood in a second-degree polynomial relation when the word is longer (Word Position: b = −7.57, SE= 1.52, t = −4.97, p < .001; Word Positionˆ2: b = 3.31, SE = 1.45, t = 2.29, p < .05), but not when the words are shorter (Word Position: b = −3.50, SE= 1.36, t = −2.57, p < .05; Word Positionˆ2: b = −1.43, SE = 1.25, t = −1.15, p > .25). Figure 5 illustrates this pattern both when aggregated across passages (top left panel) as well as across passages with different levels of text complexity (other panels of Figure 5). Clearly, total reading times for shorter words do not change widely through the passage, whereas total reading times for longer words gradually decrease toward the later part of a text. An additional observation here is that the magnitude of this decreasing trend for longer words seems to change across passages of different text complexity, with a greater rate of change in more complex passages than less complex ones. In summary, these findings show that the position of a word within an passage has a unique influence on whether they are fixated or not, and for how long.

Figure 5.

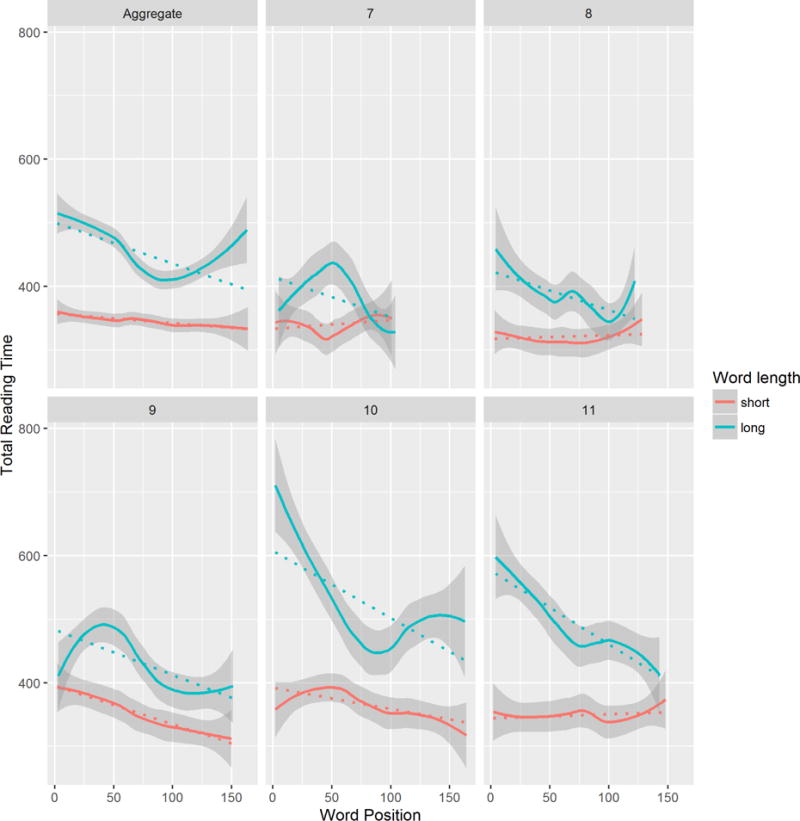
Total reading time as a function of word position for longer words and shorter words. The top left panel (“aggregated”) is based on an entire dataset, whereas other panels only include datasets with a corresponding GORT passage number. Dotted lines are based on the fits of linear models, and solid lines are based on the fits of local regression (loess) models.

Analysis 2: Sentence-final words

Real-time word processing is only one of the processes that reading for comprehension recruits. The analysis below concentrates on the effort of processing entire sentences, which includes the building of a syntactic structure, resolution of lexical and structural ambiguities, integration of words into a unified semantic representation, and integration with a larger discourse. These cognitive demands specific to the sentence-level have been repeatedly shown to lead to sentence- or clause wrap-up effects – the tendency to spend more time reading the sentence- or clause-final words (Hill & Murray, 2000). It has been traditionally argued that wrap-up effects reflect integrative processes related to updating the discourse representation (Just & Carpenter, 1980). More recent accounts of wrap-up effects additionally emphasize the role of early oculomotor responses to punctuation marks or internal prosody (Hill & Murray, 2000; Hirotani, Frazier, & Rayner, 2006; Warren, White, & Reichle, 2009). Regardless of the theoretical stance, the notion that a substantial part of integrative processing occurs at the sentential or clausal boundaries suggest the possibility that eye-movement patterns at those regions may be influenced differently or more greatly by individuals’ cognitive abilities and/or reading experience (Hyönä et al., 2002; Kaakinen and Hyönä, 2007). Thus, Analysis 2 aims to investigate the Reader × Text × Time interaction in sentence-final words, and investigate whether it contrasts with the patterns observed in Analysis 1 where individual words were considered.

Methods

All aspects of statistical modeling were identical to those of Analysis 1A, with the exception of the number of dependent and independent variables. The dependent variables for this analysis consisted of the six eye-movement measures identical to Analysis 1A (see Table 2 for comparative summary). However, only the eye-movements recorded on the final words of the sentences in each passage were considered. The number of data points varied across passages as the number of sentences in the passages differed, ranging from 6 to 11 (M = 7.7). The independent variable of forward transitional probability was removed because its value was always 0 for sentence-final words. In addition to the remaining 18 independent variables used in Analysis 1, we added 4 additional text-level variables that reflect syntactic complexity of the sentence and the overall difficulty of words in the sentences, and might be of influence for wrap-up effects. These were: sentence length, number of verbs in the sentence, average word length, and average word frequency³.

Results and Discussion

The data pool consisted of 1,876 data points. The heat map in Figure 6 displays outcomes of Random Forests models fitted to eye-movements to sentence-final words. Patterns in Figure 6 generally replicated those shown in Figure 2 (Analysis 1A), but with a few additional findings for the newly added predictors. This is not surprizing as the data set for this analysis is essentially a subset of that used in Analysis 1A.

Figure 6.

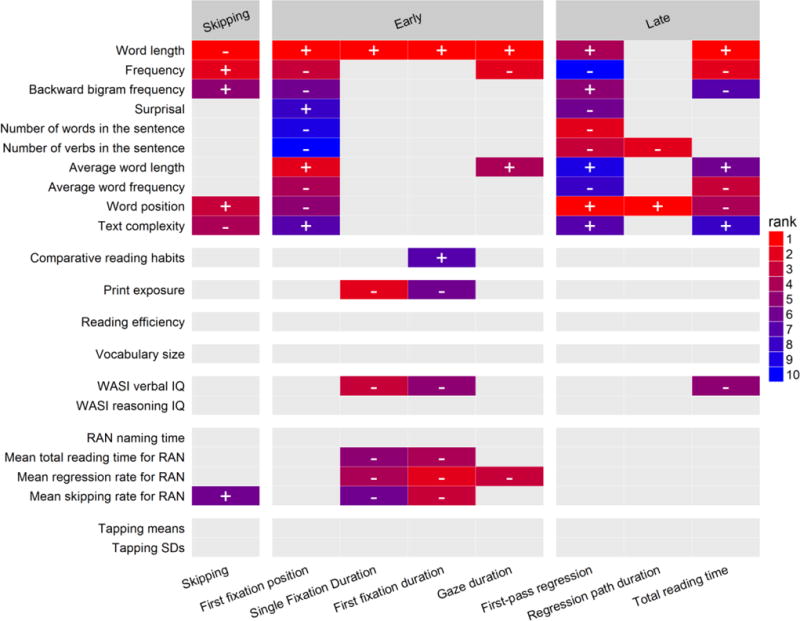
Heat map of the relative importance of text- and participant-level predictors of word processing effort across the eye-movement record at the sentence final words.

There was a clear separation of the where and when decision, as indicated by the complementary distribution of highly ranked predictors for first fixation position versus first fixation duration (with the exception of word length that was important in both measures). Likewise, the effect of word length was salient in its relative importance across all eye-movements measures. Word position also influenced all eye-movement measures except early durational measures. Furthermore, the influence of Reader variables was confined to early eye-movement measures (i.e., first fixation duration), while Text variables were more predictive in late, rather than early, durational eye-movement measures.

Despite the overall similarity, there were several key differences between the patterns observed in sentence-final words versus all words. Thus, all Text characteristics shown in Figure 6 – whether they reflected properties of words as such, their local contexts or an entire discourse – were more pronounced in their relative importance in the sentence-final words, as compared to all words, especially at the early stages of reading. This discrepancy is interesting as it highlights the ability of the Random Forests method to capture substantial empirical differences in the processing of any word in a passage versus the processing that takes place at the sentence-final word, which focuses on discourse-level integration.

The directions of effects were generally as expected: more difficult sentence-final words (i.e., words that were longer, less frequent, or less predictable) came with lower skipping rates, longer processing times, and higher regression rates. Likewise, the complexity of the context in which the sentence-final words occurred (number of words and verbs in the sentence, average word length and frequency, and text complexity) influenced processing times and regression rate in the same way, such that final words of more complex sentences were read more slowly and with a higher regression rate. For instance, there was a positive effect of text complexity on regression path duration (ρ = 0.11, p < .001) and total reading time (ρ = 0.16, p < .001). These findings are consistent with the classic interpretation of wrap-up effects in which increased integrative processing leads to an inflation of reading time.

The position of a sentence-final word closer to the end of a passage came with shorter fixations on the word, which was likely due to a higher degree of contextual constraint and a concomitant higher predictability of word and sentence meanings. Such words also came with higher regression rates and longer regression path durations. This is not surprising given that more material becomes available for regressive saccades as the eyes move towards the passage end.

In sum, the integrative operations at sentence-final words reflected a greater role of text-variables over reader variables compared with the analysis of mid-sentence words. This was especially true for variables that reflect the contribution of local sentence context (cf. surprisal, backward transitional probability) and of the entire discourse (text complexity and word position). While generally absent from the earliest durational measure (first fixation duration), all Text properties were important predictors of the remaining time-course of reading for comprehension. Because of the small size of the dataset, we do not examine interactions of Reader and Text variables with word length or any other variable.

Analysis 3A: Relative importance of predictors at the passage level

The most global unit of analysis for reading comprehension is the entire text passage. We considered eye-movements aggregated at the passage level as online indices of the global comprehension effort that expository texts elicit, and answers to comprehension questions as indices of the quality of comprehension. One potential challenge in this kind of analysis is that the number of observations relative to the number of the predictors is quite small, often termed the “small n large p” problem. A small ratio (e.g., smaller than 15 to 1, Harrell, 2001) can result in overfitting and the accompanying loss of generalizability in statistical models. Unlike traditional linear regression-based methods, the Random Forests method does not have the problem of overfitting in the “small n large p” situation (see Matsuki et al., 2016 for detailed examination). Thus, we can apply the same approach as previous analyses without concern. Analysis 3A characterized the overall contribution of individual variability and text complexity on passage-level reading, while Analysis 3B zoomed in on interactions of individual differences measures with text complexity.

Methods

All aspects of the statistical modeling were identical to those of Analysis 1, with the exception of the number of dependent and independent variables, as described below (see Table 2). The model fitting procedures and heat-map construction procedure were adjusted accordingly.

Variables

Dependent variables for the current analysis consisted of five measures aggregated at the passage-level: We obtained one data point per participant for each of GORT stories 7-11. One variable was an individual’s comprehension score. Participants responded to five questions following each of the five passages under consideration (stories 7-11 in GORT), to a total of 25 responses. Comprehension scores were calculated for each passage as a by-participant sum of correct responses to comprehension questions. The other four dependent variables were: total number of skips, total number of fixations, total number of first-pass regressions, and total reading duration per passage. Since passages were of different lengths, all measures were normalized by the number of words.

For the independent variables, there were total of 13 test measures. Unlike the earlier analyses, all the word-level properties (word length, frequency and position in passage, as well as a word’s transitional probability and surprisal) were not considered as they were irrelevant at the level of passage. Text complexity was the only text property we retained as a predictor of passage reading effort.

Results and Discussion

Originally, a total of 255 data points (51 participants × 5 passages) were obtained for each dependent variable. As described in Analysis 1, we removed 12 data points because it was difficult to retain any fixation data due to excessive blinking, skipping, or the loss of signal throughout the passages. This yielded a total of 243 data points.

Figure 7 illustrates the relative importance of predictors of eye-movements and comprehension scores aggregated at the passage level.

Figure 7.

Heat map of the relative importance of complexity and participant-level predictors of passage-level processing effort.

The overall direction of effects was as expected: more proficient readers (i.e., those with better performance in cognitive and verbal tasks and faster or more consistent performance in timed tasks like RAN and tapping) showed an increased skipping rate, shorter inspection times, smaller number of fixations, and higher accuracy of comprehension. The non-verbal component of the WASI IQ test was the only exception, where better performance led to a lower skipping rate, ρ = −.29, p < .001, and inflated number of fixations, ρ = .27, p < .001 (see discussion of the same finding in Analysis 1A).

Every group of predictors contributed to one or more indices of passage-level reading, supporting the notion that reading is a multi-faceted task that recruits multiple physiological, cognitive and perceptual abilities. Several measures exclusively predicted online (eye-movement) reading measures (viz., comparative reading habits, reading efficiency, verbal and reasoning IQ, mean skipping rate for RAN, and tapping means and SDs.) Relationships between these measures and eye-movements have not previously been investigated, to our knowledge, and so further experimentation is needed to understand these results. The findings of exclusivity with the two IQ measures are surprising, as verbal IQ at least has previously been found to relate to offline comprehension (e.g., Van Dyke, Johns, & Kukona, 2014). Two measures had their impact exclusively on the offline measure (comprehension questions): print exposure and vocabulary size. The importance of these assessments was not surprising: The benefit of more extensive word knowledge and experience with printed materials has been robustly established (Stanovich, 1986), however an exclusive effect has not previously been observed. A more surprising finding was that the effects of print exposure (measured via the Author or Magazine Recognition Tests) were not important predictors of online measures at the passage level, even though these effects on eye-movements to words are reported as robust (e.g., Choi, Lowder, Ferreira, & Henderson, 2015; Falkauskas & Kuperman, 2015; Lowder & Gordon, 2017; Moore & Gordon, 2015). This highlights complementarity between techniques aiming at establishing whether a single predictor explains a non-trivial amount of variance (e.g., regression) and those aiming at identifying how important a single predictor is relative to others (e.g., Random Forests). Our results suggest that in the face of other strong predictors in our dataset, print exposure was not sufficiently important to meet our reporting cutoff for any online measure.

Offline comprehension was additionally affected by text complexity and RAN naming time, both of which also influenced online eye-movement variables. The appearance of RAN as a high-ranking variable is consistent with a massive literature demonstrating a strong predictive relationship between RAN and general reading ability (cf. Norton & Wolf (2012) for a review), however the link to offline comprehension is surprising because this research is based on online (timed) word or text reading tasks, rather than assessments of the products of comprehension. Indeed, a recent study utilizing multiple versions of the RAN task aimed at decomposing its components of saccadic planning, lexical retrieval and articulation observed no association between any version of RAN and offline comprehension questions identical to those used here (Kuperman, Van Dyke, & Henry, 2016).

Text complexity was an important predictor of both offline and online measures of comprehension. More complex texts elicited a larger number of fixations, which were longer in duration. They also resulted in lower accuracy in comprehension questions. This finding is consistent with an extensive literature examining complexity effects as operationalized in a variety of different ways (e.g., Crossley et al., 2017; Gibson, 1998; McNamara, Graesser, & Louwerse, 2012; Perfetti & Stafura, 2014; Van Dyke, 2007). To understand the behavior of this important predictor more thoroughly, we probe interactions with complexity below.

Analysis 3B: Interactions with text complexity at the passage level

Since text complexity was a consistently strong predictor of both online and offline indices of passage comprehension, we investigated its potential interactions with Reader variables. We adopted the procedure similar to Analysis 1B by partitioning the data into subsets that contain texts with low complexity (Complexity 7, 8, and 9; a total of 148 data points) and high complexity (Complexity 10 and 11; a total of 95 data points). We selected the break-point for the partitioning based on the observation that the by-complexity average of each dependent measure shows a consistent modulation at level 10 (see Figure 8).

Figure 8.

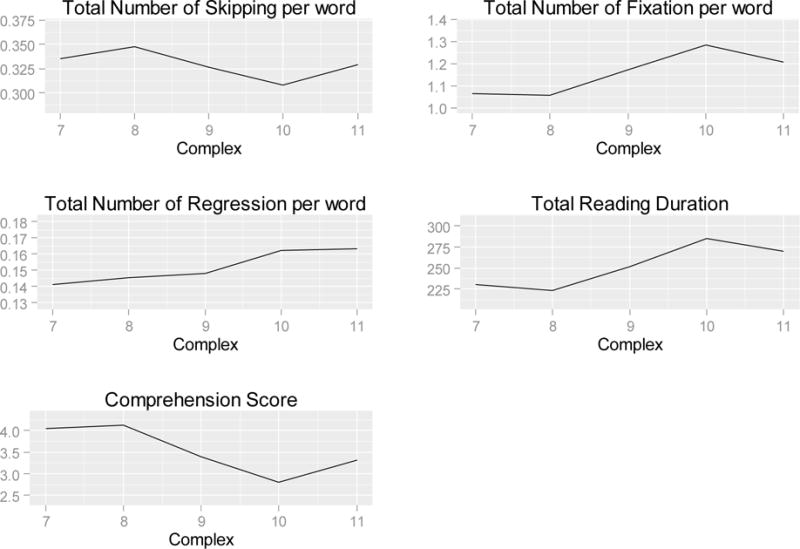
Line plots of means of total number of skipping, total number of fixation, total number of regression, total reading duration, and comprehension scores per each level of Text complexity. Passages 10 and 11 are qualitatively different from other passages.

The heat map of the relative importance of variables in Figure 9 largely replicated the patterns we reported in Analysis 3A. The directions of effects were as expected (with the exception of reasoning IQ described above). The dissociation between individual differences measures that were important for predicting only online indices of reading effort vs those that predicted both online and offline indices was the same as reported above. However, the investigation of interactions with text complexity enabled us to refine some of our prior observations. Notably, the same measures mentioned above exclusively predicted online reading measures (viz., comparative reading habits, reading efficiency, verbal and reasoning IQ, mean skipping rate for RAN, and tapping means and SDs,) however there were no measures that exclusively predicted the offline comprehension measure. While unimportant for predicting eye-movements in the presence of complexity as a predictor, vocabulary size (and to a more limited extent, print exposure) revealed an interactive behavior whereby each came out as an important predictor only in less complex texts (except in total number of fixations, where vocabulary was also a high-ranking predictor of more complex texts, although not ranked as highly as in less complex texts. Figure 10 provides a detailed description of these interactive effects for the vocabulary measure on total number of skips, total number of fixations, total reading duration and offline comprehension score.

Figure 9.

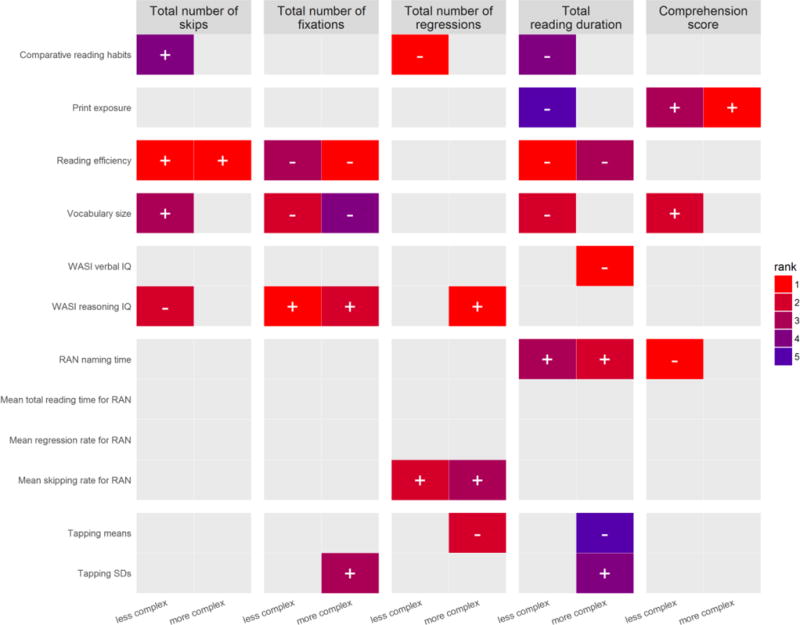
Heat map of the relative importance of complexity and participant-level predictors of passage-level processing effort and comprehension score. Separate models were fit to the subset of the data containing less complex (GORT passage number 7, 8, and 9) and more complex passages (10 and 11).

Figure 10.

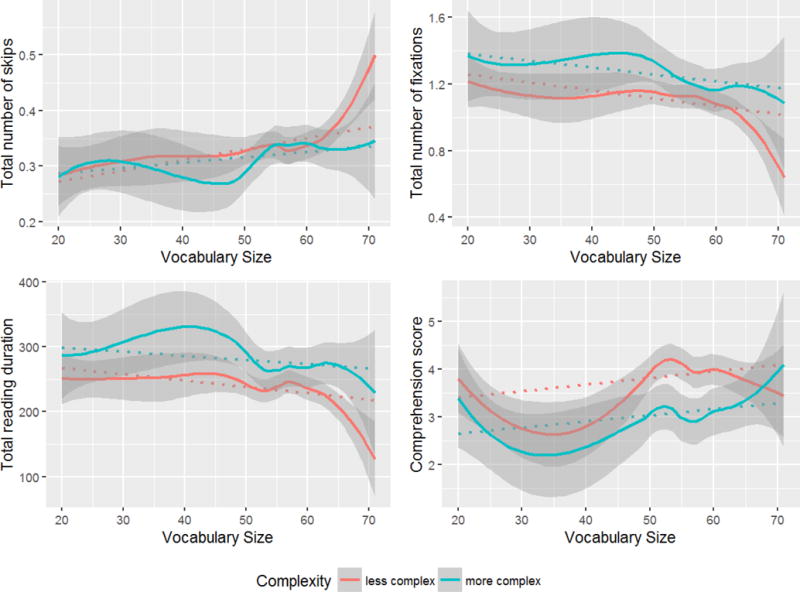
Total number of skips, total number of fixations, total reading duration, and comprehension score as a function of vocabulary size for less (7, 8, and 9) and more (10 and 11) complex GORT passages. Dotted lines represent linear regression lines from the models fitted to an entire dataset, whereas solid lines represent the fits of local regression (loess) models.

The patterns of modest modulation for high complexity texts in Figure 10 may suggest a floor effect, i.e., more complex texts presented lexical, syntactic and logical complexity that was similarly difficult for all individuals, even though participants varied widely in their lexical knowledge. For less complex texts, we observed a tendency for participants with higher vocabulary size to show a larger number of skips (ρ = 0.24, p < .005), a lower number of fixations (ρ = −0.27, p < .005), and shorter total reading time (ρ = −0.24, p < .001) when reading less complex texts. These effects were more modest, and often statistically unreliable, for more complex texts: number of skips (ρ = 0.21, p < .05), number of fixations (ρ = −0.18, p = .07), and shorter total time of reading (ρ = −0.12, p = .24). This suggests that a lower level of lexical difficulty was a better discriminator between individuals with smaller and larger vocabularies. This possibility is corroborated by a stronger role of comparative reading habits in less rather than more complex texts. Individuals varying in subjective estimates of their own reading proficiency showed behavior that fit their estimates in relatively accessible texts, but not in texts that appeared to be equally difficult for all readers.

Taken together, Analyses 3A and 3B were consistent with previous experimental work in demonstrating the importance of text complexity as a consistent predictor of both online and offline comprehension measures. Furthermore, the analysis pointed to distinctive interactions between text complexity and a number of other Reader variables—especially vocabulary size, reading efficiency, and IQ, raising the possibility that the interactions with reading efficiency and IQ, though not vocabulary size, may have a differential presence in online vs. offline assessments of reading.

General Discussion

The primary goal for this investigation was to jointly characterize the roles of individual variability and linguistic complexity in determining eye-movement behavior throughout the time course of reading. In the Introduction we motivated the need to synthesize knowledge of how and when multiple components of the reading effort contribute to predicting that effort (cf. Calvo & Meseguer, 2002; Kliegl et al., 2004; Kliegl et al., 2006; Kuperman & Van Dyke, 2011, Rayner, 1978). Current models of eye-movement control during reading rely predominantly on a few text-based predictors of reading effort (most notably, word frequency, length, and predictability) as benchmark constraints against which models can be evaluated. We suggested that more comprehensive computational models would benefit from benchmark specifications that depict the contributions of a broader range of Reader- and Text-level variables over Time. This paper demonstrates the application of a non-parametric data-mining technique (Random Forests) to identify these crucial interactions. Using this technique, we evaluated the relative importance of a large battery of individual differences scores and text (word, sentence and discourse) properties on eye-movements at the word, sentence and passage level, as well as on offline indices of comprehension quality. We sought to confirm previous benchmark results using this method, and—in the spirit of Tukey’s (1977) distinction between confirmatory and exploratory analysis—generate hypotheses that would lead to further experimentation.

Some of the patterns we observed indeed corroborated well-established facts from reading research. These include a dissociation between the where and when aspects of saccade planning, replication of effects that lexical benchmark predictors have on the eye-movement record; and confirmation of the relative contributions of word length and other benchmark word-level properties over the time-course of reading (cf. Rayner, 1998 and references above). This convergence of findings between traditional analyses of variance and the non-parametric Random Forests regression technique is a reassurance of the validity of the latter method. Other patterns we found constitute novel hypotheses, which we summarize below.

Temporal localization of Reader and Text influences

Across Analyses 1A, 1B and 2 we observed a robust dissociation between early and later stages of word processing (as gauged by the eye-movement record) in their susceptibility to variability in individual vs. text-level properties. Reader-level measures were consistently important in predicting variance in early durational measures which have typically been associated with the efficiency of oculomotor control, as well as the application of grapheme-phoneme correspondence rules during word decoding. Conversely, the influence of text-level measures was paramount in later eye-movement measures, which have primarily been associated with integrating a word into a broader representation of the text’s meaning. This temporal localization of sources of variation in eye-movements is novel and poses a new challenge to models of oculomotor control in reading. To accommodate these findings, models will need to adopt additional parameters to account for reader-level variables (as done in only a few so far, e.g., Mancheva et al., 2013; Laubrock et al., 2006 and Reichle et al., 2013) and ensure that both reader- and text-level parameters can accommodate the dynamically changing relative importance of the reader- and text-level effects throughout the time-course of reading.

Online vs offline measures of reading comprehension

Reading comprehension ability is typically assessed via “off-line” measures—that is, multiple-choice tests that ask readers to interpret text passages after they were read (e.g., Kaufman Test of Educational Achievement (Kaufman, 2014); Nelson-Denny Reading Test (Brown, Fishco, & Hanna, 1993); Woodcock-Johnson Passage Comprehension (Schrank, Mather, & McGrew, 2014); etc.) Yet, our examination of overall passage reading (Analysis 3B) showed a greater tendency for Reader-level variables to be important predictors of online measures of reading (eye-movements) compared to the offline comprehension score (15 to 4 in Figure 7). Indeed, a number of variables (comparative reading habits, reading efficiency, verbal and reasoning IQ, skipping rate for RAN, and mean and SD tapping) were ranked highly only for online measures, even when text complexity was taken into account. As noted above, further research is necessary to replicate these exclusivity findings, as—to our knowledge—these measures have not previously been employed in experimental studies of online reading. Even IQ, which is a very common individual differences assessment, mostly appears in eye-tracking research as a subject selection criterion and not as a covariate (e.g., Olson, Kliegl, & Davidson, 1983). Nevertheless, a highly practical conclusion can already be drawn: off-line assessments are necessarily far removed from actual reading processes, and may implicate skills that have little to do with actual reading (e.g., reasoning, strategic problem solving, etc.) Our findings demonstrate that skill differences are evident in online measures during passage comprehension, pointing to a need for new assessments that can directly pinpoint variability in passage-level reading skills (e.g., reference resolution, coherence monitoring, etc.) independently of more general cognitive skills invoked by traditional question-answering assessments.

Additional new observations

Our atheoretical data-mining method detected several interactions that have an empirical value and may serve as targets for confirmatory empirical analysis and future computational modeling. For instance, the position of words within a passage was an important predictor of word skipping and total reading times, and interactions of this variable with word length were observed. A U-shaped effect of word position on skipping rate showed a minimum at around 50 words into a passage, regardless of the total number of words per passage. Accompanied with a gradual decrease in total reading time for longer words throughout passages, this might indicate readers shift from deep (or attentive) to shallow (or good-enough) processing (Ferreira & Patson, 2007). The questions of whether this behavior pattern is accidental (due to defocused attention or mind wandering) or strategic, and whether this behavior is specific to the current choice of reading materials, await further investigation.

We also observed that text complexity was most important as a predictor for longer words. Such words tend to be less frequent and have more intricate morphological and phonological structures. This suggests that the overall processing load of relatively complex texts (coming from the need to recognize more difficult words, resolve more diverse and difficult syntactic dependencies and reconcile more intricate logical structures) especially inflates the processing effort for difficult words. To our knowledge, the interaction of word complexity (defined as word length, frequency, morphological complexity or contextual predictability) by text complexity has not been studied, and might be a fruitful research venue to pursue (for related claims, see Huestegge & Bocianski, 2010; Pynte & Kennedy, 2006; and Radach, Huestegge, & Reilly, 2008).

Equally important for mapping future research directions is the knowledge of variables that were not important predictors of the eye-movement record. For instance, measures of a word’s predictability in local context (surprisal, as well as backward and forward bigram frequency) only showed an appreciable influence in sentence-final words, and for word recognition or passage reading. This does not imply that such measures do not merit investigation, nor does it imply that the measures would be statistically unreliable if entered as predictors into a regression model. What this weak influence suggests – if replicated across other datasets – is that these specific predictability measures contribute much less than other Text-level or Reader-level variables to explaining variance in the eye-movement data.

Limitations

The empirical base of this paper is a single eye-tracking study of 51 undergraduate students. Typically, a study like this would be analyzed for main effects of one or two variables (e.g., word length and predictability) and possibly an interaction between these variables and a small selected set of individual differences measures. Our data-mining technique enabled us to use the dataset to simultaneously quantify relative contributions of multiple variables, across the entire time-course and an offline measure of reading comprehension. It is fully understood that some of the patterns we report above may be specific to this dataset, and further replication and confirmatory studies – with different sample sizes, populations, and reading materials – are necessary before the current findings have been fully validated. In addition, although the current study used data splitting as a way to investigate the interaction of a strong predictor with all the other predictor variables (i.e., word length in Analysis 1B and complexity in Analysis 3B), this approach may not always be feasible for all interactions. We note, however, that providing such a general method was not our goal. Rather, we aimed to point out the most important predictors both for the data overall, and in specific subsets. Those that do not come out as important are likely not to interact with other variables either, and are unlikely to yield reliable interactions in confirmatory analysis. Given this, we believe that the current results from Random Forests models can illustrate which predictors are important and should be considered in further investigations.

On a more technical note, exploratory data analysis using Random Forests is still in its early stage. Furthermore, supplemental tools that we applied to aid our interpretation of their outcomes (e.g., sign of the rank-order correlation coefficient for the directionality, and median-splitting for investigation of interactions) are by no means optimal and have not achieved universal acceptance within the Random Forests modeling community. We opted for the rank-order correlation coefficient as an ad-hoc method of indicating directionality of relations because relative importance scores alone provide no insight into this aspect of the data. This ad-hoc method, however, was occasionally too simplistic and provided outcomes that did not reflect the true underlying pattern (viz. when non-linear patterns were present). Further development of methods for quantifying and interpreting patterns within data partitions will provide more sophisticated ways to approach the same or similar questions.

Conclusion

Our method of evaluating the relative importance of predictors gave rise to a wealth of observations, which both confirmed the prior state of knowledge about oculomotor behavior and generated new hypotheses. We believe that some of these hypotheses will inform not only the “where” and “when” aspects of the eye-movement record, but also its “what” aspect, that is, they will point to Text-level and Reader-level variables of importance for the temporal and spatial characteristics of reading behavior. We further suggest that many of the novel hypotheses generated here (e.g., localization of variability in early vs. late or online vs. offline measures and linguistic properties such as word position as sources of variability) represent fruitful areas for future research. Random Forests provide a method of capitalizing on the multidimensionality and richness within even a modest-sized dataset, and its ability to use patterns in such data to generate novel hypotheses has particularly promising implications for advancing clinical and educational research.