Rapid and Quantitative Chemical Exchange Saturation Transfer (CEST) Imaging with Magnetic Resonance Fingerprinting (MRF)

Abstract

Purpose

To develop a fast magnetic resonance fingerprinting (MRF) method for quantitative chemical exchange saturation transfer (CEST) imaging.

Methods

We implemented a CEST-MRF method to quantify the chemical exchange rate and volume fraction of the N_α-amine protons of L-arginine (L-Arg) phantoms and the amide and semi-solid exchangeable protons of in vivo rat brain tissue. L-Arg phantoms were made with different concentrations (25–100 mM) and pH (pH 4–6). The MRF acquisition schedule varied the saturation power randomly for 30 iterations (phantom: 0–6 μT; in vivo: 0–4 μT) with a total acquisition time of ≤2 minutes. The signal trajectories were pattern-matched to a large dictionary of signal trajectories simulated using the Bloch-McConnell equations for different combinations of exchange rate, exchangeable proton volume fraction, and water T1 and T2 relaxation times.

Results

The chemical exchange rates of the N_α-amine protons of L-Arg were significantly (p<0.0001) correlated with the rates measured with the Quantitation of Exchange using Saturation Power method. Similarly, the L-Arg concentrations determined using MRF were significantly (p<0.0001) correlated with the known concentrations. The pH dependence of the exchange rate was well fit (R²=0.9186) by a base catalyzed exchange model. The amide proton exchange rate measured in rat brain cortex (34.8±11.7 Hz) was in good agreement with that measured previously with the Water Exchange spectroscopy method (28.6±7.4 Hz). The semi-solid proton volume fraction was elevated in white (12.2±1.7%) compared to gray (8.1±1.1%) matter brain regions in agreement with previous magnetization transfer studies.

Conclusion

CEST-MRF provides a method for fast, quantitative CEST imaging.

INTRODUCTION

Chemical Exchange Saturation Transfer (CEST) MRI (1–3) uses selective radio-frequency (RF) pulses to saturate the magnetization of exchangeable protons on a variety of molecules and macromolecules, including proteins, which due to fast chemical exchange with bulk water results in a decreased water MRI signal. CEST has proven to be a powerful tool for imaging a wide range of disease states and pathologies. For example, the amide proton CEST contrast from endogenous proteins has been used to distinguish tumor progression from radiation necrosis in a gliosarcoma rodent model (4) and in clinical glioma patients (5,6), detect early response to temozolomide (7) and radiation therapy (8) in glioblastoma rodent models, evaluate tumor grade and cellularity of clinical glioma patients (9), distinguish benign and atypical meningiomas in clinical subjects (10), and detect changes in pH during stroke that may provide insight into the viability of the ischemic penumbra (11–13). In addition, a number of exogenous diamagnetic CEST imaging probes have been identified including lysine rich proteins (14,15), glucose (16–18), creatine (19,20), glycosaminoglycans (21), barbituric acid (22), thymidine analogs (23), iodinated compounds (24,25), imidazoles (26), salicylic acid analogs (27–29), and anthranillic (30) analogs. Glucose and iodinated CEST imaging probes are currently under clinical evaluation for monitoring tumor perfusion (31,32) and tumor acidosis (33), respectively. However, efficient methods for quantification of the chemical exchange rates and exchangeable proton volume fractions are needed to produce high quality pH and volume fraction maps required to move many of these studies forward.

In a traditional CEST experiment, the frequency offset of the RF saturation pulse is stepped across the water resonance to generate a CEST Z-spectrum of signal intensity as a function of saturation frequency offset. The Magnetization Transfer Ratio asymmetry (MTR_asym), or CEST contrast, is then calculated from the difference between the signal intensities (S) acquired with negative (ω⁻) and positive (ω⁺) frequency offsets from water as given by equation 1.

$${\mathit{MTR}}_{\mathit{asym}}=\frac{S({\omega }^{-})-S({\omega }^{+})}{S_0}$$ [Eq. 1]

However, CEST MRI suffers from several limitations including long image acquisition times and the qualitative nature of the CEST contrast, which depends on many factors, including the chemical exchange rate (k_ex), volume fraction of the exchangeable solute protons (f_s), water longitudinal relaxation rate (R_1w), RF saturation time (t_sat), and the RF saturation efficiency (α), which in turn depends on the saturation power (B₁), water transverse relaxation rate (R_2w), and k_ex, as given in equation 2 (34).

$$\begin{gathered} {\mathit{MTR}}_{\mathit{asym}}=\frac{\alpha ·f_s·k_{ex}}{R_{1w}+\alpha ·f_s·k_{ex}}\left(1-e^{-(R_{1w}+\alpha ·f_s·k_{ex})·t_{\mathit{sat}}}\right) \\ \alpha =\frac{{\left(\gamma B_1\right)}^2}{{\left(\gamma B_1\right)}^2+k_{ex}\left(k_{ex}+R_{2w}\right)} \\ {f}_s=\frac{[\mathit{exchangeable}\mathit{proton}]}{2·[H_{2}O]} \end{gathered}$$ [Eq. 2]

Analysis of the MTR_asym is further complicated by the presence of Nuclear Overhauser Enhancement (NOE) effects attributed to aliphatic exchangeable protons between −2 to −5 ppm from water, CEST effects from amine exchangeable protons between 2–3 ppm from water, and very broad magnetization transfer (MT) effects due to semi-solid, macromolecular exchangeable protons centered at approximately −2.5 ppm.

Therefore, while a number of methods have been developed for quantifying chemical exchange rates, including the Quantitation of Exchange using Saturation Power (QUESP) (35–37), Quantitation of Exchange using Saturation Time (QUEST) (35), Quantitation of Exchange using Saturation Power and Time (QUEPT) (37), RF-power based ratiometric CEST (PRCEST) (25,38,39), Frequency Labeled Exchange Transfer (FLEX) (40,41), and NMR line width fitting (42,43) methods, these methods have typically only been employed for studying simple phantom chemical exchange systems and not in vivo tissue where the large number of exchangeable proton pools that must be modeled greatly complicates the data analysis. Most in vivo measurements of endogenous amide proton chemical exchange rates have been determined from fitting of the CEST Z-spectrum, which again depends on adequately modeling the many exchangeable proton pools and requires long image acquisition times. Clinical translation of CEST methods would therefore benefit greatly from the development of more quantitative, specific and rapid CEST methods.

A recently developed Magnetic Resonance Fingerprinting (MRF) method has been used for the rapid quantification of tissue T1 and T2 relaxation times (44) and for the multiparametric estimation of brain hemodynamic parameters such as cerebral blood flow (45). The MRF method varies the image acquisition parameters to generate unique signal trajectories for different quantitative tissue parameters. The experimental trajectories are then matched to a large dictionary of signal trajectories simulated using the Bloch equations for different combinations of tissue parameters. The MRF method allows for the simultaneous quantification of multiple parameters in a short acquisition time period. Here we extend the MRF approach by incorporating chemical exchange into the Bloch equation simulations, and report the use of a fast CEST-MRF method for generating quantitative exchange rate and proton volume fraction maps of N_α-amine exchangeable protons of L-arginine phantoms with different concentrations (25–100 mM) and pH (pH 4–6), and of endogenous amide and semi-solid exchangeable protons of in vivo rat brain tissue.

METHODS

L-Arginine Phantoms

A set of phantoms was prepared with various L-arginine (L-Arg) concentrations by dissolving L-Arg (Sigma-Aldrich, St. Louis, MO) in pH 4 or pH 5 buffer (BDH, London, UK) at concentrations of 25, 50 or 100 mM. In addition, a set of phantoms with varying pH was prepared by titrating a 50 mM, pH 4 L-Arg solution with NaOH to a pH of 4.0, 4.5, 5.0, 5.5 or 6.0. The N_α-amine of L-Arg has a chemical shift of +3 ppm with respect to the water resonance and has 3 equivalent exchangeable amine protons. The different L-Arg solutions were placed in 2 ml glass vials with sets of 3 vials placed into 50 ml Falcon tubes with 2% agarose gel surrounding the vials. Phantoms were imaged at a room temperature of 20°C.

Animal Preparation

All animal experiments and procedures were performed in accordance with the NIH Guide for the Care and Use of Laboratory Animals and were approved by the Institutional Animal Care and Use Committee of the Massachusetts General Hospital. A male Wistar rat (Charles River Labs, Wilmington, MA) was anesthetized with 1–2% isolflurane in 50:50 O₂:medical air mixture and placed prone on a home-built rat MRI cradle with ear and bite bars to secure the rat head. Respiration rate and temperature were monitored with a small animal physiological monitoring system (SA Instruments, Inc., Stony Brook, NY) and a body temperature of 37°C was maintained by blowing warm air in the bore of the magnet.

Magnetic Resonance Imaging

Phantom Study

Single-slice, single-shot CEST gradient Echo Planar Images (EPI) were acquired on a 4.7 T MRI scanner (Bruker Biospin, Billerica, MA) with a 35 mm inner diameter birdcage volume coil (Bruker Biospin, Billerica, MA). The CEST-MRF acquisition schedule (shown schematically in Figure 1A) was designed to keep the saturation pulse frequency offset fixed at the amine (L-Arg α-NH₃: +3 ppm) exchangeable proton frequency, and randomly vary the saturation power for 30 iterations, with amplitude between 0–6 μT. The maximum saturation power limits were chosen to fully saturate the exchangeable proton and maximize the CEST contrast. The phantom image acqusition parameters were: saturation pulse length = 3000 ms, TE/TR=21/4000 ms, flip angle (FA) = 60°, matrix 100×100, field of view (FOV) = 30×30 mm, number of averages (NA) = 1. The total MRF image acquisition time was 2 minutes for the phantom study.

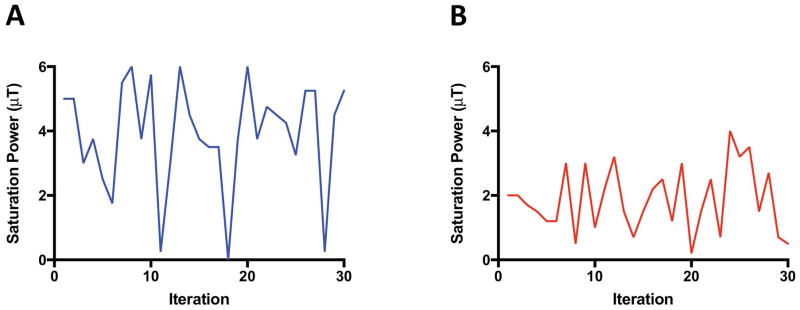
FIG. 1.

Schematic of the CEST-MRF acquisition schedule. The saturation pulse power was varied for 30 iterations ranging from (A) 0–6 μT for the L-Arginine phantoms and (B) 0–4 μT for the in vivo rat brain. For the phantom study a 3 sec saturation pulse was used with the saturation frequency offset fixed at 3 ppm, corresponding to the frequency of the N_α-amine exchangeable protons. For the in vivo study, a 2.5 sec saturation pulse was used with the saturation frequency offset fixed at 3.5 ppm, corresponding to the frequency of the amide exchangeable protons.

The amine proton chemical exchange rates were independently measured with the QUantification of Exchange using Saturation Power (QUESP) MRI method (35). Single-shot QUESP-EPI images were acquired at saturation frequency offsets of ±3 ppm with saturation powers ranging from 0–6 μT in 1 μT increments. The QUESP image acquisition parameters were: saturation pulse length = 3000 ms, TE/TR = 21/15000 ms, FA = 90°, matrix = 100×100, FOV = 30×30 mm, NA = 1.

T1 maps were generated from variable repetition time (VTR) images acquired with repetition times TR = 7500, 5000, 3000, 1500, 800, 400, 200, and 50 ms. VTR image acquisition parameters were: TE = 6.5 ms, FA = 90°, matrix = 100×100, FOV = 30×30, NA = 1. T2 and T2* maps were generated from multi-echo spin-echo and multi-echo gradient-echo images, respectively. Spin-echo acquisition parameters consisted of TR=2000 ms, 25 echoes with an initial echo-time of TE_init=20 ms and echo spacing of ΔTE=20 ms, FA=90°, matrix=100×100, FOV = 30×30, and NA=1. Gradient-echo acquisition parameters consisted of TR=1000 ms, 20 echoes with TE_init=4 ms and ΔTE=40 ms, FA=90°, matrix=100×100, FOV=30×30 mm and NA=1.

In Vivo Study

In vivo single-slice, single-shot CEST gradient Echo Planar Images (EPI) were acquired on a 4.7 T MRI scanner (Bruker Biospin, Billerica, MA) with a rat brain, 4-channel, phased array-receive coil (Bruker Biospin, Billerica, MA) and a 72 mm quadrature birdcage volume transmit coil (Bruker Biospin, Billerica, MA). The CEST-MRF acquisition schedule (shown schematically in Figure 1B) was designed to keep the saturation pulse frequency offset fixed at the amide (+3.5 ppm) exchangeable proton frequency, and randomly vary the saturation power for 30 iterations, with amplitude between 0–4 μT. The maximum saturation power limit was chosen to fully saturate the exchangeable proton and maximize the CEST contrast. A lower maximum saturation power limit was used for the in vivo studies than for the L-Arg phantom studies due to the expected slower exchange rate of the endogenous amide protons compared to the L-Arg pH 6 amine exchangeable proton. The in vivo image acquisition parameters were: saturation pulse length = 2500 ms, TE/TR = 21/3500 ms, FA = 90°, matrix 80×80, FOV = 40×40 mm, NA = 1. The total MRF image acquisition time was 1.75 minutes.

T1 maps were generated from VTR images acquired with TR = 4000, 2000, 1500, 1000, 750, 400, and 100 ms. VTR image acquisition parameters were: TE = 7.5 ms, FA = 90°, matrix = 80×80, FOV = 40×40, NA = 1. T2 and T2* maps were generated from multi-echo spin-echo and multi-echo gradient-echo images, respectively. Spin-echo acquisition parameters consisted of TR=2000 ms, 25 echoes with TE_init=9 ms and ΔTE=9 ms, FA=90°, matrix=80×80, FOV=40×40 mm and NA=1. Gradient-echo acquisition parameters consisted of TR=800 ms, 8 echoes with TE_init=4 ms and ΔTE=5.5 ms, FA=90°, matrix=80×80, FOV=40×40 mm and NA=1.

MRF Dictionary Generation

Large MRF dictionaries of simulated signal intensity trajectories for a given acquisition schedule were generated using a custom-written MATLAB (Mathworks, Natick, MA) program. The dictionary simulations were performed using a vectorized, sparse matrix implementation of the Bloch equations modified to include chemical exchange between the water proton pool and both the solute (amide or amine) and semi-solid proton pools. Bloch equation simulations were performed for all possible combinations of a range of chemical exchange rates, exchangeable proton volume fractions, and water T1 and T2 relaxation times. Different dictionaries were used for the phantom (2-pool model) and in vivo (3-pool model) studies due to the different ranges of exchange rates observed and due to the absence of a semi-solid proton pool in the phantom experiments. The parameter increment step sizes in the respective dictionaries were chosen to be as small as possible without making the dictionary size too large and hence the computation times required excesssively long (>1 hour).

For the phantom studies the amine proton chemical exchange rate was varied from 100 to 1400 Hz in 10 Hz increments, the amine proton concentration was varied from 10 to 120 mM in 5 mM increments, the water T1 was varied from 2500 to 3300 Hz in 50 Hz increments, and the water T2 was varied from 600 to 1200 ms in 50 ms increments. The value for the amine proton T1 of the L-Arg phantoms was set to be approximately the same as the experimentally measured water T1 (2800 ms), while the amine T2 (40 ms) was selected from the best match between the experimental signal trajectory and a simulated MRF dictionary where the water and amine proton T1 were fixed and the amine T2 was varied from 20–60 ms in 10 ms increments. Generation of the ~670,000 dictionary entries required 61 minutes and 298 MB of storage on a 2.7 GHz Intel Core i7 MacBook Pro with 16 GB 1600 MHz DDR3 memory.

For the in vivo studies, the amide proton exchange rate was varied from 50 to 150 Hz in 5 Hz increments, the amide proton concentration was varied from 100 to 1000 mM in 50 mM increments, the semi-solid proton exchange rate was varied from 5 to 100 Hz in 5 Hz increments, and the semi-solid proton concentration was varied from 2 to 30 mM in 2 mM increments. The water T1 and T2 relaxation times were fixed to the experimentally measured values (T1= 1450 ms, T2=60 ms), the amide and semi-solid T1 were set to be the same as the water T1, and the semi-solid T2 was set to 40 μs.

Data Analysis

For MRF experiments, the measured signal trajectories were normalized by their norms and matched voxelwise to the pre-computed CEST-MRF dictionary by selecting the entry with the largest vector dot product. For the QUESP experiments, the MTR_asym at 3 ppm frequency offset was calculated and plotted as a function of saturation power. A custom-written MATLAB program was used to fit the saturation power curves for the exchange rate and water T1 and T2 using the lsqcurvefit function in MATLAB with the fit function defined by the Bloch equations. The L-Arg concentrations were kept fixed at the known concentrations. The 95% confidence intervals for the QUESP fit parameters were calculated from the residual and the jacobian matices using the nlparci MATLAB function. T1 maps were generated from an exponential fit of the variable TR signal intensity as a function of TR using a non-linear least squares fitting algorithm implemented in a custom-written MATLAB program. Similarly, T2 and T2* maps were generated by exponential fitting of the signal intensity as a function of echo time using a non-linear least squares fitting algorithm implemented in a custom-written MATLAB program. The Pearson correlation coefficients between the the MRF and QUESP determined chemical exchange rates, the MRF and known L-Arg concentrations, and the MRF and VTR determined T1 relaxation times were calculated in Prism 6 (GraphPad Software, Inc, La Jolla, CA). In addition, the pH dependence of the CEST-MRF determined exchange rate was fit to the acid/base catalyzed exchange model (46,47) as given by equation 3, where k₀ is the spontaneous exchange rate, k_a is the acid catalyzed exchange rate, and k_b is the base catalyzed rate.

$$k_{ex}=k_0+\left(k_a\times {10}^{-pH}\right)+\left(k_b\times {10}^{pH-\mathit{pKw}}\right)$$ [Eq. 3]

All statistical analyses were performed with Prism 6 (GraphPad Software, Inc, La Jolla, CA) with p<0.05 considered as significant. MRF matched parameter values for a given region-of-interest are reported as the mean ±standard deviation.

Sensitivity Analysis

A Monte Carlo analysis was used to test the sensitivity of the amide proton chemical exchange rate (k_sw) and the semi-solid proton volume fraction (f_ss) of the 3-pool CEST model to errors in the fixed input parameters to the model, including the water T1 (T1_w), water T2 (T2_w), semi-solid T2 (T2_ss) and the saturation pulse B1. First, the uncertainties in the fixed input parameters were modeled by sampling a large range of T1_w (1000–2000 ms), T2_w (20–80 ms), T2_ss (20–60 ms) and B1 scaling factors (0.8–1.2) using the Latin hypercube sampling Matlab function lhdesign. Next, Bloch equation simulations of signal trajectories using the Monte Carlo sampled input parameter values were performed for a fixed amide proton exchange rate and volume fraction of 35 Hz and 0.55%, respectively, and a semi-solid proton exchange rate and volume fraction of 50 Hz and 9.09%, respectively. These fixed amide and semi-solid exchange parameters represent the “ground truth” values. Finally, the sensitivity of the amide proton exchange rate, or the semi-solid proton volume fraction, to uncertainties in the fixed 3-pool model input parameters was assessed individually for each of the four input parameters by matching the Monte Carlo simulated signal trajectories to dictionaries that contained a range of k_sw, or a range of f_ss, but that fixed the particular input parameter of interest (T1_w, T2_w, T2_ss or B1) while allowing the other 3 input parameters to vary as detailed in supporting information Table S1. Since the Monte Carlo simulated signal trajectories contain a range of input parameter values, fixing one of the input parameter values in the matching dictionary will lead to errors in the matched k_sw or f_ss. To examine the error introduced into k_sw or f_ss by combinations of errors in the various input parameters the signal trajectories were also matched to dictionaries in which different combinations of the four input parameters were either fixed or varied (see supporting information, Table S1). For each dictionary the matched amide exchange rate (k_sw), or semi-solid proton volume fraction (f_ss), was compared to the true values (k_sw=35 Hz, f_ss =9.09 %) for each fingerprint and the average value across all Monte Carlo simulated fingerprints was calculated for each case.

To assess the sensitivity of the matched amide exchange rate to noise, signal trajectories were also generated for a Monte Carlo sampled range of amide proton exchange rates (1–80 Hz) with all other parameters (T1_w, T2_w, T1_ss, T2_ss, k_ssw, f_ss, T1_s, T2_s, f_s, and B1) fixed. Varying levels of zero-mean Gaussian noise were then added to each Monte Carlo simulated signal trajectory. The amide proton exchange rate (k_sw) was reconstructed from each noisy signal trajectory and the average value across all fingerprints was compared to the true value.

The ability of the proposed CEST-MRF method to simultaneously quantify both the MT and CEST exchange parameters with saturation at a single offset frequency was also evaluated for a large number of different combinations of Monte Carlo sampled amide proton and semi-solid exchange rates and volume fractions. The exchange parameters selected by the Monte Carlo sampling were used to generate simulated signal trajectories that were then reconstructed using a preliminary implementation of a trained neural network as described previously (48). The error in the reconstruction was assessed by comparison to the true values.

Discrimination of CEST-MRF and CEST Z-spectrum acquisition schedules

The capacities of two different MRF acquisition schedules – a variable saturation power schedule (used in this study) and a variable saturation frequency offset schedule (corresponding to a traditional CEST Z-spectrum) – to efficiently discriminate between different exchangeable proton concentrations and exchange rates were assessed by forming the dot-product correlation of the dictionaries with themselves, similar to previous work in the literature (49–51). Dictionary simulations for the variable saturation power acquisition schedule were performed using the L-Arg phantom acquisition schedule (Fig. 1A). Dictionary simulations for the CEST Z-spectrum schedule kept the saturation power fixed at 4 μT and varied the saturation frequency offset from +5 to −5 ppm in 0.25 ppm increments. Simulations were performed for five different exchangeable proton concentrations of 75, 150, 300, 600, and 900 mM with the exchange rate varied from 0–1000 Hz in 10 Hz increments. The low concentrations (75, 150, 300 mM) were chosen to match the range of L-Arg concentrations used experimentally (25, 50, 100 mM) as there are 3 equivalent N_α-amine protons per L-Arg.

The discriminability of the water T1 relaxation times and exchangeable proton concentrations of the variable saturation power schedule was also calculated for the same five exchangeable proton concentrations with the water T1 varied from 2500–3300 ms in 20 ms increments.

RESULTS

CEST-MRF of L-Arginine Phantoms

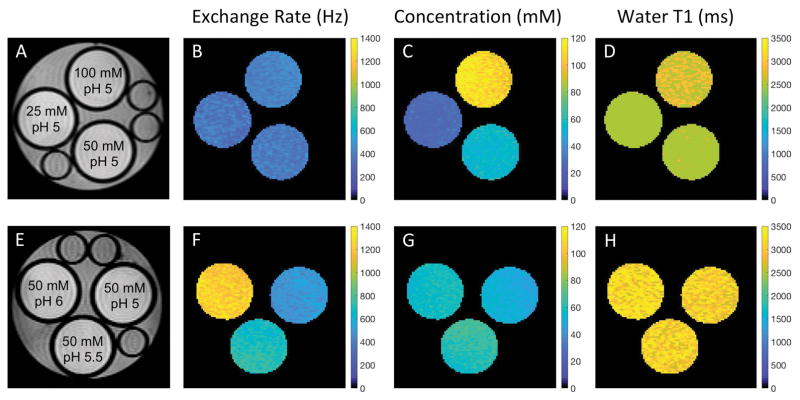
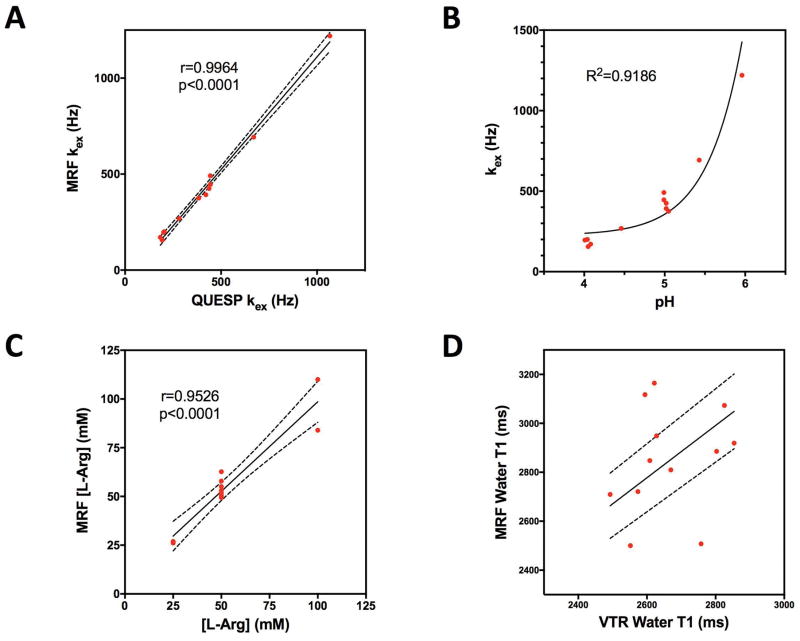
CEST-MRF matched exchange rate, L-Arg concentration and water T1 maps are shown in Figure 2 for representative phantoms with either varying L-Arg concentration (Fig. 2, top row) or varying pH (Fig. 2, bottom row). For the L-Arg phantoms, there was a significant correlation (r=0.9964, p<0.0001) between the QUESP and CEST-MRF measured amine proton exchange rates (Fig. 3A). The pH dependence of the exchange rate (Fig. 3B) was well fit (R²=0.9186) by the acid/base-catalyzed chemical exchange model given by equation 3 with k₀=252.2 Hz, k_a=1.42×10⁻¹⁶ Hz, k_b=1.06×10¹¹ Hz, and pK_w=13.97, consistent with base catalyzed proton exchange.

FIG. 2.

(A,E) Proton density images of representative L-arginine phantoms with varying concentrations (top row) and pH (bottom row) along with the associated quantitative chemical exchange rate (B,F), L-arginine concentration (C,G), and water T1 (D,H) maps generated from the MRF matching. The quantitative values for all phantom vials are reported in Table 1.

FIG. 3.

(A) The MRF determined exchange rates for the N_α-amine protons of L-Arg were significantly correlated (r=0.9964, p<0.0001) with the exchange rates determined with the QUESP method. (B) The pH dependence of the chemical exchange rate was well fit (R²=0.9186) by the base catalyzed proton exchange model (Eq. 3). (C) The MRF determined L-Arg concentrations were significantly correlated (r=0.9526, p<0.0001) with the known concentrations. (D) The water T1 relaxation times measured by MRF and a variable repetition time (VTR) method were not significantly correlated, however, the MRF determined relaxation times were all within ±20% of the VTR values. The dashed lines represent the 95% confidence interval.

A significant correlation (r=0.9526, p<0.0001) was also observed between the CEST-MRF and known L-Arg concentrations as shown in Figure 3C. The slight discrepancies in the matched L-Arg concentrations for the 100 mM L-Arg concentration phantoms are likely due to the relatively poor fingerprinting schedule efficiency as discussed below. While the CEST-MRF matched water T1 values were not significantly correlated (r=0.2207, p=0.4906) with the VTR measured T1 values (Fig. 3D), the CEST-MRF T1 values were all within ±20% of those measured by the VTR method. In general, the CEST-MRF T1 values tend to overestimate the VTR T1 values. A summary of the mean (±standard deviation) chemical exchange rates, L-Arg concentrations and water T1 relaxation times determined by the different measurement methods for regions-of-interest (ROIs) drawn for each phantom vial is given in Table 1.

Table 1.

Comparison of the CEST-MRF determined L-Arg concentrations, amine proton chemical exchange rates and water T1 relaxation times with the known concentrations, QUESP measured exchange rates, and variable TR (VTR) measured T1 relaxation times, respectively, for the various L-Arg phantoms. The mean ±standard deviation was calculated for the ROI drawn around each vial.

pH	[L-Arg] (mM)		kex (Hz)		Water T1 (ms)
	known	MRF	QUESP	MRF	VTR	MRF
4.05	25	26.1±6.7	193.9±57.0	156.2±44.5	2492.8±51.8	2709.2±143.9
4.08	50	49.4±7.0	183.7±21.7	170.7±23.9	2802.9±60.0	2885.7±154.3
4.01	100	84.0±9.6	200.4±30.4	196.2±21.4	2628.3±52.6	2949±152.0
4.04	50	51.7±6.8	204.5±31.1	200.4±29.4	2669.7±55.7	2809.6±141.6
4.46	50	53.1±5.2	281.8±28.9	268.5±31.5	2608.3±50.2	2847.6±159.1
4.99	50	50.3±3.2	444.3±33.0	446.0±34.3	2854.1±58.7	2919.5176.2
5.05	25	26.9±2.7	384.2±61.1	375.5±53.6	2551.9±51.73	2500±0
5.02	50	55.1±3.4	420.9±45.3	392.4±39.5	2757.9±59.1	2507.7±34.6
5.02	100	110.0±6.4	437.8±82.7	424.5±30.7	2573.6±48.1	2721±197.3
4.99	50	50.4±2.9	444.1±86.7	491.5±40.9	2825.7±52.1	3073.2±244.6
5.43	50	62.7±3.6	670.0±120.8	692.6±50.6	2594.5±50.1	3117.4±229.3
5.96	50	57.9±3.4	1066.8±148.7	1219.4±65.0	2621.6±48.2	3164.4±222.3

CEST-MRF of In Vivo Rat Brain

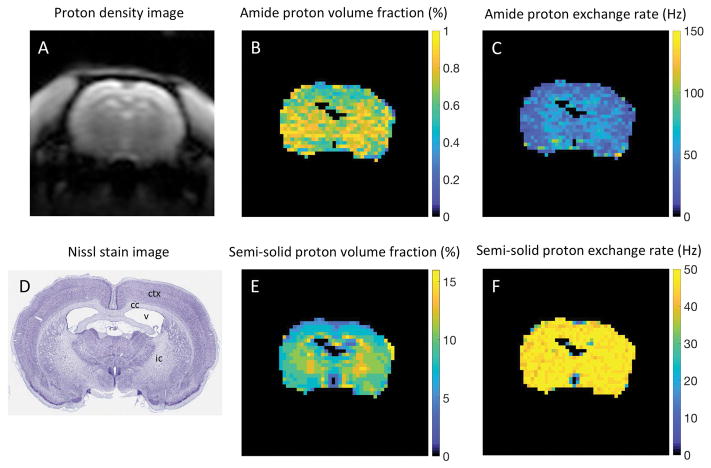
CEST-MRF matched amide and semi-solid proton chemical exchange rates and exchangeable proton volume fraction maps for the in vivo rat brain (n=1) along with the associated proton density image and Nissl stained rat brain section from the brainmap.org rat atlas (52) are shown in Figure 4. The average values for the matched parameters in white (corpus callosum and internal capsule) and gray (cerebral cortex) matter regions of interest are shown in Table 2. An average endogenous amide proton exchange rate of 34.8±11.7 Hz was measured in the rat brain cortex (Fig. 4C) in good agreement with that measured previously (28.6±7.4 Hz) with the Water EXchange spectroscopy (WEX) method (53). The semi-solid proton pool volume fraction map demonstrated elevated volume fraction in white matter (12.2±1.7%) compared to gray matter (8.1±1.1%) brain regions (Fig. 4E). The regions of elevated white matter semi-solid proton volume fraction are in good agreement with the Nissl stained histology tissue section (Fig. 4B), where neuronal cell bodies of gray matter, but not white matter fiber tracts, are preferentially stained.

FIG. 4.

(A) Proton density image and (D) corresponding Nissl stained rat brain section with the ventricle (v), cortex (ctx), corpus callosum (cc), and internal capsule (ic) identified. MRF matched (B) amide proton volume fraction and (C) chemical exchange rate maps and semi-solid (E) proton volume fraction and (F) chemical exchange rate maps of in vivo rat brain tissue. The average cortex amide proton exchange rate determined from MRF (34.8±11.7 Hz) was in good agreement with that measured previously using the water exchange spectroscopy (WEX) method (28.6±7.4 Hz). The semi-solid proton volume fraction was elevated in white (12.2±1.7%) compared to gray (8.1±1.1%) matter brain regions in agreement with literature values.

Table 2.

CEST-MRF determined amide and semi-solid proton chemical exchange rates (k) and volume fractions (f) for gray (GM) and white matter (WM) regions of in vivo rat brain tissue.

	Cortical GM	Subcortical WMa
Amide ksw (Hz)	34.8±11.7	47.9±11.6
Amide fs (%)	0.61±0.13	0.76±0.09
Semi-solid kssw (Hz)	47.1±4.0	48.6±2.4
Semi-solid fss (%)	8.1±1.1	12.2±1.7

^aaverage of corpus callosum and internal capsule

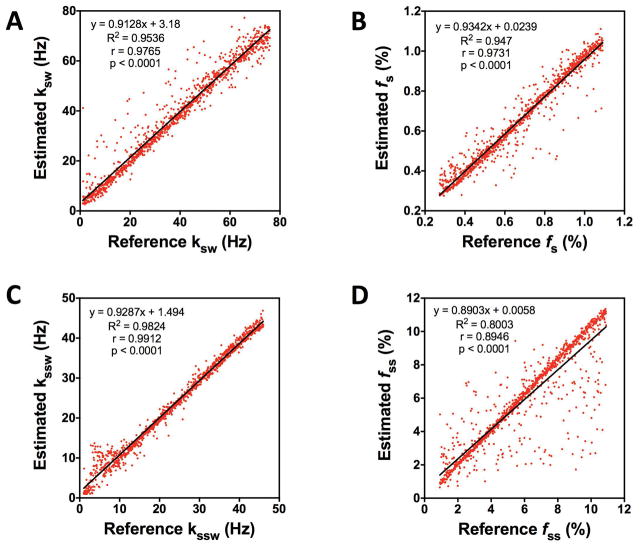
To demonstrate the uniqueness of the MRF signal trajectories for different combinations of amide and semi-solid proton exchange parameters, and the ability of CEST-MRF to separate out the two different proton pool exchange components, we performed simulations of signal trajectories with a wide range of Monte Carlo sampled amide and semi-solid proton exchange parameters, reconstructed the exchange parameter maps using a neural network trained on a sparse dictionary, and assessed the error in the matched values for each trajectory. A comparison between the MRF estimated amide proton and semi-solid exchange rates and volume fractions and the true values is shown in Figure 5. The estimated parameters showed excellent agreement with the true values for k_sw, k_ssw, and f_s. The MRF estimated k_sw, k_ssw, and f_s were all significantly (p<0.0001) correlated with the true, reference values with Pearson correlation coefficients of r=0.9765, r=0.9912, and r=0.9731, respectively. The MRF estimated f_ss parameters were also significantly (p<0.0001) correlated to the true values with a Pearson correlation coefficient of 0.8946, but showed greater dispersion likely due to the smaller number of f_ss values sampled in the neural network training dictionary. The excellent agreement between the MRF estimated and the true exchange parameters validates the feasibility of simultaneous reconstruction of MT and CEST chemical exchange parameter maps.

Fig. 5.

The uniqueness of signal trajectories simulated for a large number of different combinations of Monte Carlo sampled amide proton exchange rates (k_sw) and volume fractions (f_s) and semi-solid proton exchange rates (k_ssw) and volume fractions (f_ss) is demonstrated by the significant (p<0.0001) correlations observed between the true, reference exchange parameter values and the values estimated from MRF matching. Correlation of the MRF estimated amide proton (A) exchange rates and (B) volume fractions with the true, reference exchange rates and volume fractions. Correlation of the MRF estimated semi-solid proton (C) exchange rates and (D) volume fractions with the true, reference exchange rates and volume fractions. The linear regression fit of the data points is given by the solid black line for all plots.

MRF Acquisition Schedule Efficiency

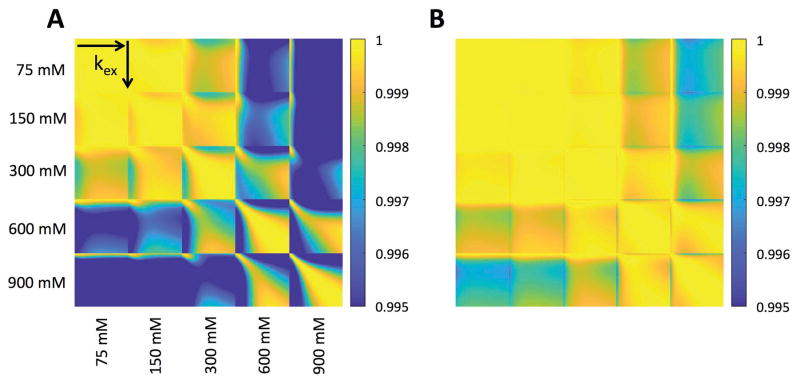
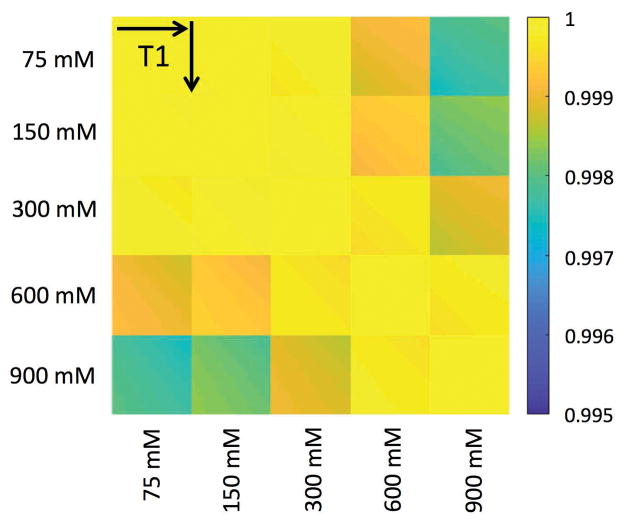
The dictionary correlation matrices for the CEST-MRF and Z-spectrum acquisition methods are shown in Figure 6. For norm normalized signal trajectories, a vector dot product of unity represents a perfect match between two signal trajectories. For an ideal MRF acquisition schedule, a signal trajectory simulated for a particular exchange rate and proton volume fraction would be perfectly correlated only with itself (i.e., a vector dot product of one) and have a poor correlation (low vector dot product) with all other signal trajectories simulated for other combinations of proton exchange rate and volume fraction. The CEST-MRF correlation plots, however, demonstrate relatively poor discrimination of exchange rates, in particular at low exchangeable proton concentrations where trajectories with different exchange rates all have vector dot products very close to unity. Much better discrimination is, however, observed for the CEST-MRF acquisition schedule (Fig. 6A) than for the CEST Z-spectrum schedule (Fig. 6B). The discrimination of the water T1 relaxation times and exchangeable proton concentrations of the CEST-MRF acquisition schedule is shown in Figure 7. Very poor T1 discrimination is observed indicating that the CEST-MRF saturation power acquisition schedule is relatively insensitive to T1 variations over the range of T1 values simulated (2500–3300 ms).

FIG. 6.

Correlation of the MRF simulated dictionary with itself for MRF acquisition schedules that varied either (A) the saturation pulse power or (B) the saturation pulse frequency offset, corresponding to a traditional CEST Z-spectrum. The correlation was performed for 5 different exchangeable proton concentrations (75, 150, 300, 600, and 900 mM) with the chemical exchange rate varied for each concentration from 0–1000 Hz in 10 Hz increments. Better chemical exchange rate and concentration discrimination was observed with the variable saturation power acquisition schedule than with the CEST Z-spectrum acquisition schedule.

FIG. 7.

Correlation of the MRF simulated dictionary with itself for the variable saturation power acquisition schedule. The correlation was performed for 5 different exchangeable proton concentrations (75, 150, 300, 600, and 900 mM) with the water T1 relaxation time varied for each concentration from 2500–3200 ms in 20 ms increments. The variable saturation power acquisition schedule demonstrated little sensitivity to the water T1.

Sensitivity Analysis

Monte Carlo simulations of the sensitivity of the in vivo amide proton chemical exchange rate (k_sw) and the semi-solid proton volume fraction (f_ss) to uncertainties in the 3-pool model input parameters that were fixed in the CEST-MRF dictionary simulations – namely the water T1 (T1_w) and T2 (T2_w), semi-solid T2 (T2_ss), and B1 – are shown in Table 3. Signal trajectories were simulated for fixed amide and semi-solid proton exchange parameters, but a range of Monte Carlo sampled T1_w, T2_w, T2_ss and B1 input parameters representing large uncertainties in each of the input parameters. Thus fixing the value of a particular input parameter of interest (T1_w, T2_w, T2_ss or B1) in the dictionary used to match the Monte Carlo simulated trajectories will lead to errors in the matched amide and semi-solid proton exchange parameters. The mean ±standard deviation of the amide proton exchange rate and the semi-solid proton volume fraction are reported for different matching dictionaries that were generated with different combinations of variable and fixed T1_w, T2_w, T2_ss and B1 parameters. Unsurprisingly, dictionary reconstructions that contained a range of values for each input parameter yielded the smallest error (1.1% for k_sw and 5.7% for f_ss). Fixing each parameter in turn, errors in T1_w were found to have the largest impact on the exchange rate (11.5%) and semi-solid proton volume fraction (8.2%), demonstrating the sensitivity of these parameters to errors in T1_w. We do note, however, that the Monte Carlo simulations sampled a very large range of T1_w’s (1000–2000 ms) that represent ±30% of the nominal T1_w value (1450 ms), indicating that the matched exchange parameters are not particularly sensitive to errors in T1_w. The largest error in the amide proton exchange rate (27.0%) was observed when the T1_w, T2_w, and B1 were set to fixed nominal values. Interestingly, the error in the amide proton exchange rate was smaller (6.5 %) when all of the parameters under study (T1_w, T2_w, T2_ss and B1) were set to fixed values implying that errors in different model input parameters can cancel each other out leading to a smaller total error in the matched exchange parameter maps. In contrast to the exchange rate, the largest error for the semi-solid proton volume fraction (8.2%) was observed when only the T1_w was kept fixed. Finally, we note that the matched parameters were immune to the addition of moderate (SNR>20) levels of noise, since only the best matching fingerprint is selected among all dictionary entries. For highly noisy data, the error will depend on the dictionary bin size i.e. the sampling density. This is because high noise can cause the signal to match to signal trajectories with parameter values neighboring to the true ones, which, for a sparsely sampled dictionary, can result in significant errors in the matched values.

Table 3.

Mean value (±standard deviation) and percent error induced in the amide proton exchange rate (k_sw) or the semi-solid proton volume fraction (f_ss) by errors in the water T1 (T1_w), water T2 (T2_w), semi-solid T2 (T2_ss) and B1 parameters considered individually and in all possible combinations.

	Variable ksw		Variable fss
Fixed parameters	Mean ksw (Hz)	Error (%)	Mean fss (Hz)	Error (%)
None	35.4±4.4	1.1	10.6±2.8	5.7
T1w	39.0±11.3	11.5	10.8±3.5	8.2
T2w	37.6±9.0	7.3	10.2±3.2	1.6
T2ss	36.7±11.2	4.8	9.9±3.7	0.9
B1	37.1±10.1	5.9	10.3±3.4	3.4
T1w, T2w	42.8±19.4	22.1	10.0±4.1	0.4
T1w, T2ss	39.3±16.9	12.3	9.8±3.6	1. 7
T1w, B1	41.8±16.5	19.3	10.6±3.6	5.8
T1w, T2w, T2ss	42.5±21.6	21.5	9.9±4.2	0.6
T1w, T2w, B1	44.5±22.6	27.0	9.8±4.3	1.9
T2w, T2ss, B1	39.9±25.0	13.9	10.7±5.5	7.4
All	37.3±30.1	6.5	9.7±4.7	2.7

The same Monte Carlo simulations were also performed for a traditional CEST Z-spectrum acquisition schedule. Significantly greater errors were observed for the amide proton exchange rate (20.1 %) and semi-solid proton volume fraction (31.9 %) in the CEST Z-spectrum matching when all four input parameters (T1_w, T2_w, T2_ss and B1) were fixed. This again suggests that the CEST-MRF method provides greater discrimination and is less sensitive to errors in the fixed input parameters of the 3-pool exchange model.

The sensitivity of the matched parameters to B0 inhomogeneity was not included in the Monte Carlo sensitivity analysis as B0 inhomogeneity effects are scaled out by the trajectory normalization. This is demonstrated in supporting information Figure S1 where the experimental MRF signal trajectories were matched to dictionaries generated with different B0 offsets ranging from +0.15 ppm (+30 Hz) to −0.15 ppm (-30 Hz). We note that in vivo experimental B0 field maps observed a maximum B0 shift of ±10 Hz. As summarized in supporting Table S2, very little error is introduced in any of the matched parameters due to B0 field offset (<±5% error). The lack of sensitivity of the CEST-MRF method to B0 shifts is due to the use of a fixed saturation frequency offset and the normalization of the trajectory by the trajectory norm. So long as we are saturating within the relatively broad amide proton resonance, slight offsets in the irradiation position due to B0 field inhomogeneity will only result in a slightly different scaling of the signal trajectory for a given voxel, which will be normalized out when taking the norm of the trajectory for the dot product matching. In contrast, slight shifts of the CEST Z-spectrum due to B0 field inhomogeneity can result in large differences in the MTR_asym due to the image subtraction performed for the positive and negative paired saturation frequency offsets.

DISCUSSION

This study is the first application of MR Fingerprinting for the simultaneous quantification of proton chemical exchange rates and volume fractions. A previous study by Geades et al did use a pre-calculated look-up table of Bloch equation simulated Z-spectra to fit experimental Z-spectra, acquired with three different saturation powers, and extract proton volume fractions (54). However, due to the very large number of proton pools required to simulate the full Z-spectrum, a very coarse dictionary was used with only 8 different proton volume fractions for each of the NOE (aliphatic), CEST (amide) and MT (semi-solid) proton pools, 5 water T1 relaxation times and 3 B1 fields. All other parameters, including all chemical exchange rates, were fixed. Our CEST-MRF approach, in which the saturation frequency offset is fixed and the saturation power is varied, provides several advantages over fitting or matching of traditional CEST Z-spectra. First, the CEST-MRF method is specific for the CEST (amide or amine) and MT (semi-solid) proton pools only. This greatly simplifies the analysis and allows finely sampled dictionaries to be used that can accurately quantify both the exchange rates and volume fractions of the CEST and MT exchangeable proton pools. Second, the experimental acquisition time is significantly reduced compared to a traditional CEST Z-spectrum. We have chosen an acquisition schedule with 30 iterations of the saturation power, which required less than 2 minutes to acquire. With further optimization of the acquisition schedule (50) even shorter acquisition times may be achievable. Third, the different exchangeable proton pools are sensitive to different RF saturation powers depending on their respective chemical exchange rates. Varying the RF saturation power provides simultaneous sensitivity to the various exchange rates of the different proton pools. Fourth, the CEST-MRF method is relatively insensitive to B0 field inhomogeneity since slight shifts in irradiation position within the exchange broadened amide proton resonance will only result in a constant scaling factor of the MRF signal trajectory, which will be normalized out when taking the trajectory norm. Fifth, as demonstrated by the dictionary correlation plots (Fig. 6) and the Monte Carlo sensitivity analysis, the CEST-MRF method provides greatly improved discrimination and reduced errors in the proton exchange rates and volume fractions compared to a traditional CEST Z-spectrum. The very poor discrimination and large uncertainties observed for the traditional CEST Z-spectrum may partly explain the very wide range of exchange rates and volume fractions that have been reported in the literature for the endogenous amide (k_ex=20–280 Hz, f_s=0.1–1.0%) (11,53–57) and semi-solid (k_ex=1–160 Hz, f_ss=3–30.0%, see supporting information, Table S3) proton pools of in vivo brain tissue.

While the CEST-MRF saturation power acquisition schedule displayed improved discrimination relative to the CEST Z-spectrum schedule, the schedule of saturation powers used in this work was selected at random and is likely far from optimal. This is reflected in the relatively poor discrimination of concentration and exchange rate observed in the correlation plots shown in Figure 6 implying strong similarity between signals arising from different tissue parameters. Nevertheless, excellent agreement was observed in L-Arg phantoms between the amine proton exchange rates and L-Arg concentrations calculated with MRF-CEST and those obtained with alternative techniques (Table 1). This can be attributed to the dictionary matching reconstruction since only the dictionary entry with the greatest dot product value is selected. Hence, acquisitions with poor discrimination can still yield accurate matches provided the signal-to-noise ratio (SNR) is sufficiently high to permit distinguishing similar signal evolutions. For a given SNR level, however, the discriminability can provide an a priori measure of the expected quality of the estimated tissue parameters.

The very poor CEST-MRF discrimination observed for the water T1 of the phantoms (Fig. 7) is consistent with the lack of a significant correlation between VTR and MRF determined T1. The lack of T1 sensitivity is not surprising for the CEST-MRF acquisition schedule used in this study, which only varied the saturation power and used a relatively long, constant repetition time (TR). This has the advantage that it simplifies the analysis, but at the cost of impaired T1 sensitivity. However, if accurate T1 maps are desired, sensitivity to T1 could be increased by varying additional acquisition parameters such as the TR and RF flip angle as originally demonstrated by Griswold and coworkers (44).

As discussed above, a wide range of endogenous amide proton exchange rates in brain tissue (20–280 Hz) have been reported in the literature (11,53–57). The water exchange spectroscopy (WEX) method should, however, provide the most accurate measurement of the amide proton exchange rate as the amide proton pool is specifically and directly probed (53) rather than being obtained from a large multiparametric fit of the CEST Z-spectrum. We allowed the amide proton exchange rate of the CEST-MRF dictionary to vary over a large range (5–150 Hz) encompassing most of the literature reported values and found good agreement between the in vivo amide proton exchange rate measured by CEST-MRF (34.8±11.7 Hz) and the previously reported water exchange (WEX) spectroscopy method (28.6±7.4 Hz) (53).

Similar good agreement was observed between our CEST-MRF matched semi-solid proton volume fractions (f_ss) in gray (8.1±1.1%) and white matter (12.2±1.7%) rat brain tissue and the values reported in MT studies (see supporting information, Table S3) of rat (58–60), mouse (61,62), dog (63), bovine (64) and human brain tissue (65–68) with gray matter volume fractions ranging between 5–8% and white matter volume fractions between 10–15%. Variability in the semi-solid volume fractions was observed in human studies with some studies reporting significantly elevated gray (13%) and white (26%) matter semi-solid proton volume fractions (69,70), while others reported significantly lower gray (3–4%) and white matter (6–9%) volume fractions (54,57). However, in all cases an elevated semi-solid proton volume fraction was observed in white matter compared to gray matter brain tissue, consistent with the increased semi-solid lipid content of myelinated white matter fiber tracts. Previous MT studies have shown a strong correlation between f_ss and histological measures of myelin fraction (58,61,71,72).

While the CEST-MRF saturation power acquisition schedule displayed relatively poor discrimination (Fig. 6), improved discrimination can be obtained by optimization of the acquisition schedule as was previously demonstrated for MRF (50) and multi-inversion EPI (49) sequences. The optimization consists of searching the hyperspace of acquisition parameters to find the set that maximizes the discrimination. Each of the acquisition parameters (saturation power, saturation frequency offset, saturation pulse length, TR, FA, etc.) represents an additional degree of freedom that can be used to improve the discrimination further. Importantly, improved discrimination can yield accurate estimation of the tissue parameters using only a small number of acquisitions, which translates directly into reduced acquisition times. This is an active area of research that will be explored in future studies.

Despite the very large parameter ranges (errors) used in the Monte Carlo sensitivity analysis, the error in the amide exchange rate was, at worst, 27%. The finite dictionary sampling density used in this study contributed to this error, which can be mitigated using Deep Learning strategies described below. The water T1 had the greatest contribution to the amide proton exchange rate error. This is in accordance with prior studies demonstrating the dependence of the CEST contrast on the longitudinal relaxation rate (13,73,74). In contrast we found no sensitivity of the matched exchange parameters to B0 field inhomogeneity.

An important challenge in the matching or optimization of CEST-MRF data is the large dictionaries that are required. This problem is particularly acute for in vivo acquisitions where the four-pool model contains up to fourteen nominally independent parameters hence theoretically requiring a fourteen dimensional dictionary. In this study a four dimensional dictionary with ~670,000 entries was used to limit the compute time needed. Nevertheless, larger dictionaries could provide improved accuracy and simultaneous estimation of additional parameters. Dictionary compression and fast matching methods (75,76) could be used to reduce the post-processing time. Unfortunately, those methods still require the full dictionary to first be generated prior to compression and may be ineffective on optimized acquisition schedules where similarities between the measured signals are minimized. Instead, recent work in Deep Learning based MRF reconstruction may be used to overcome this problem (48) through training of a neural network with sparse dictionaries that can be used to reconstruct the acquired CEST-MRF data. Deep Learning methods also yield continuous valued parameter maps and eliminate the discretization artifacts in dictionary matching caused by the large intervals used in some of the dictionary parameter ranges.

CONCLUSION

CEST-MRF provides a method for fast, quantitative CEST imaging. Despite the relatively poor CEST-MRF discrimination, excellent agreement was observed between CEST-MRF and alternative methods for the proton exchange rates and volume fractions of both L-Arg phantoms and in vivo rat brain tissue. Optimization of the MRF acquisition schedule should lead to further improvements in the discrimination of chemical exchange rates and exchangeable proton volume fractions.

Supplementary Material

Supp info

FIG. S1. Error (%) induced in the amide proton exchange rate (k_sw), amide proton volume fraction (f_s), semi-solid proton exchange rate (k_ssw) and semi-solid proton volume fraction (f_ss) due to B0 field shifts ranging from +0.15 to −0.15 ppm (±30 Hz).

Table S1. Dictionary parameter ranges (min:increment:max) used for matching the Monte Carlo simulated signal trajectories. Dictionaries used either a variable amide proton chemical exchange rate (k_sw) or a variable semi-solid proton volume fraction (f_ss). A total of 12 different dictionaries were generated in each case with all possible combinations of variable and fixed water T1 (T1_w), water T2 (T2_w), semi-solid T2 (T2_ss) and B1 scaling factor parameters. The solute amide proton T1 (T1_s), T2 (T2_s) and volume fraction (f_s) and the semi-solid exchange rate (k_ssw) were fixed for all dictionaries with T1_s=1450 ms, T2_s=1 ms, f_s =0.55% and k_ssw=50 Hz.

Table S2. rror induced in the matched amide proton chemical exchange rate (k_sw) and volume fraction (f_s) and the semi-solid proton exchange rate (k_ssw) and volume fraction (f_ss) for different B0 field shifts.

Table S3. Semi-solid, macromolecular proton volume fractions (f_ss) of gray (GM) and white matter (WM) brain tissue reported in the literature.