Students Are Rarely Independent: When, Why, and How to Use Random Effects in Discipline-Based Education Research

Abstract

Discipline-based education researchers have a natural laboratory—classrooms, programs, colleges, and universities. Studies that administer treatments to multiple sections, in multiple years, or at multiple institutions are particularly compelling for two reasons: first, the sample sizes increase, and second, the implementation of the treatments can be intentionally designed and carefully monitored, potentially negating the need for additional control variables. However, when studies are implemented in this way, the observations on students are not completely independent; rather, students are clustered in sections, terms, years, or other factors. Here, I demonstrate why this clustering can be problematic in regression analysis. Fortunately, nonindependence of sampling can often be accounted for with random effects in multilevel regression models. Using several examples, including an extended example with R code, this paper illustrates why and how to implement random effects in multilevel modeling. It also provides resources to promote implementation of analyses that control for the nonindependence inherent in many quasi-random sampling designs.

BACKGROUND

Recent calls to continue, expand, and improve undergraduate science teaching are being answered (Freeman et al., 2014), and these advances in classroom teaching are being assessed with studies that evaluate the effectiveness of classroom interventions (National Research Council, 2012). The use of regression analysis in these studies to determine the quantitative comparative impact of classroom interventions has been heralded as best practice (Theobald and Freeman, 2014), but when implementing regression approaches, it is important to recognize that classroom interventions are often clustered or nested in a way that makes the observations not truly independent—this means that simple regression is often not the best strategy.

In a truly randomized trial (often referred to as a randomized control trial), subjects are independent from one another. For example, medical trials are frequently randomized at the individual level (i.e., they are truly randomized): participants are randomly assigned to treatments—some individuals receive the trial drug (treatment) and some individuals receive a placebo (control). In education research, however, this type of experimental design is not always possible. Instead, a common experimental protocol is to measure student outcomes when an intervention is administered to different sections. For example, as described in the extended example presented later, treatment is randomized by section, not by student, resulting in multiple control sections and multiple treatment sections. When the outcome is measured on students (not sections), student observations are not truly independent from one another. Instead, students within a section share experiences that are not shared across sections.

This kind of nonindependence is common in quasi-random experimental designs and is important to account for: incorrectly assuming independence of observations can shrink standard errors in a way that overestimates the accuracy of estimates (Raudenbush and Bryk, 2002; Gelman and Hill, 2007; DeLeeuw and Meijer, 2008). A common way to account for this type of clustering is by fitting multilevel models that include both fixed effects (parameters of interest, e.g., “treatment”) and random effects (variables by which students are clustered, in this example, “section”; Gelman and Hill, 2007; Bolker et al., 2009). Multilevel models are so named because they account for variation at multiple levels—level 1 with fixed effects (treatment) and levels 2+ with random effects (section, year, etc.).

This paper is intended to be a starting point, and reference, for discipline-based education researchers who employ nonindependent sampling designs (e.g., cluster-level randomization). It details when multilevel models are necessary and how to implement multilevel models in R (R Core Team, 2017).¹ There are several clarifying notes throughout the text, including a glossary (Table 1) that defines common terminology (with terms bolded in the text upon first use; e.g., estimate, parameter, quasi-random, variation have all been introduced before this point), and a graphical workflow for multilevel modeling (Figure 1). This paper is not an exhaustive review of multilevel modeling and relies heavily on texts published in other fields: Gelman and Hill (2007), Raudenbush and Bryk (2002), Zuur et al. (2009), and Burnham and Anderson (2002).

TABLE 1.

Glossary of terms used throughout the paper (terms are bolded in the text at first use)

Term	Definition	Example/synonym/application
Complex model	Used to mean a model that includes all likely ­parameters, including parameters that explicitly test the hypothesis of interest	Example: Score ∼ SAT + Sex + Treatment + ­Sex*Treatment This model includes SAT as a likely parameter that explains score and an interaction between Sex*Treatment and tests whether the treatment has a disproportional effect on students of different sexes.
Converge	The process of reaching a solution. Maximum likelihood estimation attempts to find the parameter values that maximize the likelihood function given the observations. If the parameter values cannot be found, the model will not converge.	When models do not converge, R will report a warning or an error message.
Estimate	Verb: A model estimates the effects of the parameters. Noun: An approximation of a parameter derived from a sample of individuals	The estimated coefficient in a regression estimates (i.e., approximates) the relationship between performance and SAT scores for a sample of college students.
Intraclass correlation (ICC)	The amount of clustering, or nonindependence, within a variable	ρ (“rho”); the ratio of between-cluster variance to total variance
Overfit model	A model that considers too many parameters; the penalty of adding an extra parameter vs. the additional variation explained has not been appropriately weighed.	A saturated model is an example of an extreme example of an overfit model. A model does not have to be saturated to be overfit. Opposite: underfit model.
Parameter	The true value [of something] for all individuals in a population	The parameter is the true relationship between SAT scores and performance for all college students in the country. (A model estimates this value from data from a subset of the whole population; see “Estimate.”)
Pseudo-replication	Replication when replicates are not statistically independent	Example: if students are nested in sections, students are not independent, so observations on students exhibit pseudo-replication.
Quasi-random	When a study is randomized, but not at the level where observations are made	Example: observations are made on student outcomes, treatments are randomized at the section level. Results in pseudo-replication. As opposed to randomized
Saturated model	A model that includes as many parameters as data points	Saturated models should be avoided; see “Overfit model.”
Underfit model	A model that does not have enough variables to explain the data	Example: not including prescore as a predictor when modeling postscore
Variance	The square of the SD of a sample; describes how far each value in the data set is from the mean	σ2 (where σ is the SD of the sample)
Variation	A general term describing the amount of variability in something; it is measured by various quantities, including variance.	Synonyms: spread, dispersion, scatter, variability

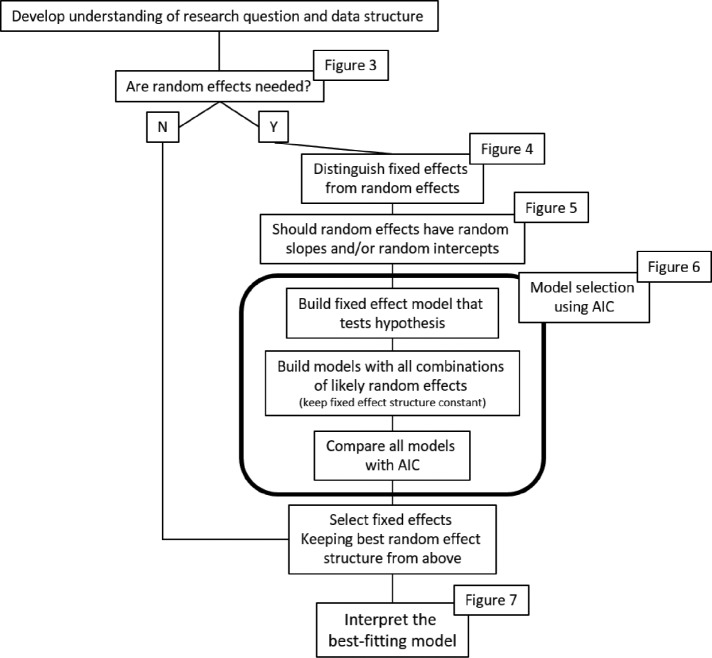
FIGURE 1.

Workflow for multilevel modeling and a guide to using this paper. Each “decision point” in this figure represents a critical step in multilevel modeling and corresponds to a section in the paper and a figure and is illustrated with the extended example. R code for analyzing the data from the extended example can be found in Appendix 3 in the Supplemental Material (data are in Appendix 4). The code details calculating the ICC (helpful in determining whether random effects are needed), using model selection to select the appropriate random effect structure, and using model selection to select the appropriate fixed effects.

While using an extended example to motivate the need for multilevel modeling (Figure 2 graphically represents the experimental design in the extended example), this essay has several stages. First it builds a case for multilevel modeling: it uses examples to describe two common cases for random effects (Figure 3) and provides reasoning behind random effects. Second, it details the how to select the appropriate random effect structure: which variables work best as random or fixed effects (Figure 4), what is the difference between the two types of random effects (Figure 5), and how to use model selection to determine the best random effect structure (Figure 6). Finally, the essay, concludes by using R to analyze the data and interpret the results from the extended example (Figure 7).

FIGURE 2.

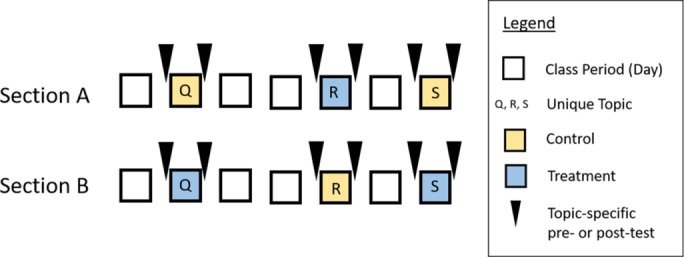
Experimental design in the extended example. Squares represent class days (note that there were more class days in the course and the spacing between interventions is not to scale). Experimental treatment and control are color coded as yellow and blue, respectively. Unique topic is indicated with the letters “Q,” “R,” and “S.” The pre- and posttests (black triangles) on each day were identical. The fact that students took a posttest three times made the students “repeated measure” and warranted students being treated as random effects. Additionally, students were clustered in sections (and section was not synonymous with intervention), so section was tested as a possible random effect. The experimental design was unbalanced, such that section A received the control twice and the treatment once, whereas section B received the treatment twice and the control once.

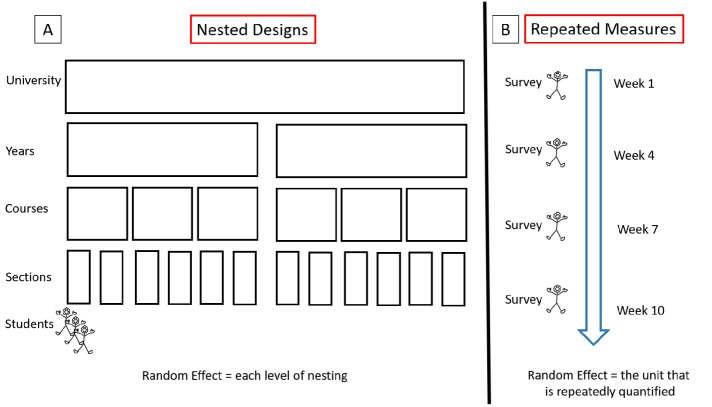
FIGURE 3.

Random effects are important to include when modeling data from (A) nested design studies and (B) repeated-measures studies. In both nested designs and repeated measures, the outcome is quantified on the student level. (Note that this is not always the case in DEBR studies; e.g., a researcher may be interested in which courses have the highest proportion of women, in which case the outcome is likely measured on the section level.) In the nested design illustration (A), students are nested in sections, which are nested in courses, which are nested in years, which are nested in universities. Each of these nested levels, or clusters, is important to account for with random effects. Similarly, in the repeated-measures study (B), the outcome (students’ survey responses) is quantified on the student level, and students take the survey four times. In this case, it is important to account for the fact that students are repeated, so student 1 on survey 1 is not independent from student 1 on survey 2. Including a student random effect accounts for this nonindependence within a student.

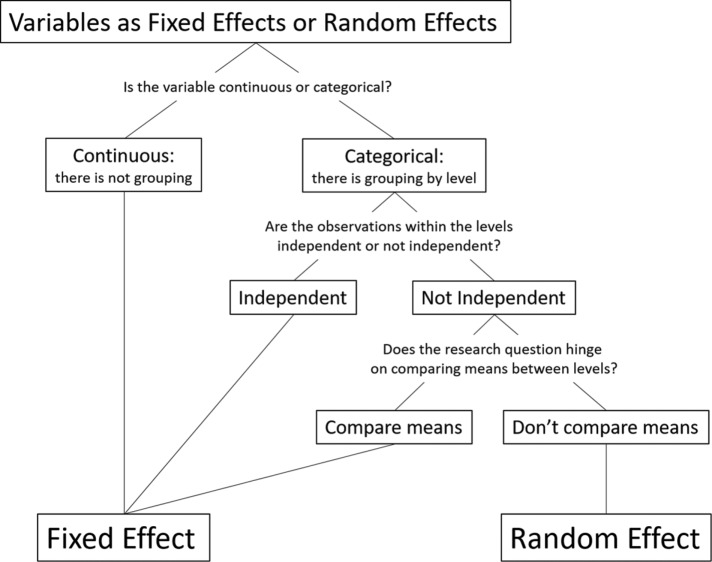
FIGURE 4.

Researchers can build intuition to determine whether variables should be included as fixed effects or random effects by asking three questions and following this decision tree.

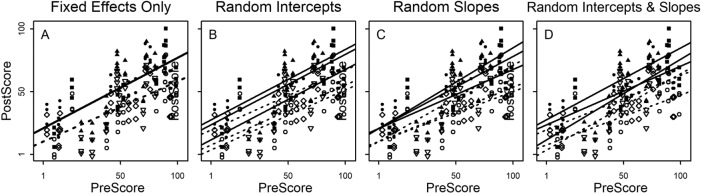
FIGURE 5.

Depending on the structure of the data, a fixed effects–only model (A) may not be the best model. There are three main ways to specify random effects in multilevel models: (B) as random intercepts, in which the slope is the same for all groups, but the intercepts vary for each group; (C) as random slopes, in which the intercept is the same for all groups, but the slopes vary for each group; and (D) as random intercepts and random slopes, in which all groups are allowed to have different slopes and different intercepts. Illustrated here, students (points) are nested in six sections (illustrated by the six combinations of filled/unfilled symbols in different shapes). There are two treatments, illustrated by filled and unfilled symbols. The lines show how each approach models the relationship between PreScore and PostScore. In a fixed effects–only model (A), a single regression line is fit for the treatment (filled) and control (unfilled symbol), ignoring sections; in a random effects model (B–D), separate regression lines are fit for each section. In the random intercepts model (B), the intercepts are allowed to vary by section but not the slopes (thus, the lines are parallel); in the random slopes model (C), the slopes are allowed to vary for each section, but not the intercepts (thus, all the lines start at the same place); and in the random intercepts and random slopes model (D), both the intercepts and the slopes are allowed to vary for each section. The overall model fit in B–D is essentially the weighted average of the regression lines for each group and is not shown.

FIGURE 6.

Steps in random effect model selection, as recommended by Zuur et al. (2009) and Burnham and Anderson (2002). This example was implemented in R.

FIGURE 7.

R output from code in Figure 3: (A) step 3 of model selection (comparing AIC values for each model that was fit); (B) model 1, which did not include any random effects; and (C) the best-fitting multilevel model with student as the only random effect. Note that treatment was retained in the final model, noting a treatment effect and supporting the hypothesis that the treatment is positively correlated with postscore.

A Note about Terminology: Different resources (and statisticians) refer to multilevel models with varying terminology. The three most common terms are 1) “multilevel models,” because the fixed and random effects in the models account for variation coming from multiple levels (e.g., grade point average and section); 2) “mixed models,” because the models include a mix of fixed effects and random effects; and 3) “hierarchical models,” for two reasons, first because there is sometimes a hierarchy to the data (e.g., when students are clustered in sections, courses, and universities) and second because the model itself has hierarchy (e.g., within-­section regressions at the bottom, controlled for by the random effects at the upper-level model). For the purposes of this paper, these models will be referred to as multilevel models, as in Gelman and Hill (2007). While ostensibly interchangeable with the term “multilevel modeling,” the other two terms can lead to confusion: simply because of terminology, mixed models are sometimes erroneously confused with mixture models (which are entirely different), and the data in multilevel models are not always hierarchical. For example, it is unclear which level is “higher,” universities or years and a hierarchy need not be explicitly assigned. Thus, the flexibility and clarity of the term “multilevel models” makes it the obvious choice. Additionally, in this paper, “random effects” or “random factors” are used interchangeably. Note that the typical abbreviation for random effect is “RF,” short for random factor.

EXTENDED EXAMPLE: EXPERIMENTAL DESIGN

The extended example presented here will be the motivating and illustrative example for the remainder of the paper. The data come from a real class in a real experiment. The specifics of the experiment have been removed for illustrative purposes.

Imagine that a group of researchers at a large university wanted to know whether a classroom intervention improved student performance. They implemented an experiment on three different days in two sections of a single course; on each day, one section was assigned the “control” and the other the “treatment.” Students from each section experienced both the treatment and the control, but for logistical reasons, one got the control twice (and the treatment once) and the other section got the treatment twice (and the control once). The three instances of the experiment occurred on three separate days when class material covered three unique topics. The researchers wanted to know whether the treatment helped students learn more, as measured by their scores on a posttest. There were three pre- and posttests (one for each topic) for each student, because the experiment was implemented on three separate days.

A CASE FOR MULTILEVEL MODELING

Understanding the Research Question and Data Structure

First, we need to determine whether our study is appropriate for multilevel modeling, which requires understanding the hypothesis being tested and the process by which the data were collected (Figure 1). In other words, what is the research question and what is the structure of the data that are being used to answer the question? It is worth emphasizing that primers, flowcharts, and step-by-step instructions in statistics are not an excuse or replacement for thinking critically about the experimental design, data, or analysis decisions. Each analytical decision should be based on sound rationale about whether it is the most appropriate decision given the goals of the analysis and the circumstances of the study.

Two Common Cases for Random Effects.

There are two common data structures in discipline-based education research (DBER) that necessitate using multilevel models to control for nonindependence in sampling: 1) nested or clustered designs (Figure 3A) and 2) repeated measures (Figure 3B). In nested designs, students are clustered, or nested. For example, in the extended example, students are clustered in sections. Because of this clustering, students within each section are not independent from one another. Specifically, students within a section often share a number of attributes that are not shared by other sections, such as instructor, time of day, exams, classroom environment, number of missed classes because of holidays, and so on. This nonindependence can be illustrated, albeit with an extreme example, when thinking about students in each of those sections taking an exam: if the fire alarm were to sound when students in one section were taking the exam, but not in the other section, it is likely that students’ scores in the fire alarm section would be impacted, but not the scores of students in the other section.

In a statistical context, nonindependence alters the effective sample size (n). When observations of 50 students (i.e., 50 data points) are not independent, n is not considered to be 50. Rather, the effective sample size is a function of how correlated, or how dependent, the observations are with one another. Because standard errors are a direct function of sample size (when n increases, standard errors decrease), ignoring the nonindependent nature of observations underestimates the variance or overestimates the accuracy of the effect (Raudenbush and Bryk, 2002; Gelman and Hill, 2007). This type of clustering/nesting pertains not only to sections but can continue through multiple levels of clustering, because students are nested in courses, within terms (e.g., semesters or quarters), within years, within universities, and so on (Figure 3A). When there is clustering in an experimental design, it is important to account for each level of clustering (e.g., instructors, quarters, years, universities) with random effects.

Another common study design that necessitates multilevel models is a repeated-measures design wherein the same students take the same assessment or the same survey multiple times (Figure 3B). Conceptually, this is akin to an assessment being “nested” within students. In the extended example, each student took a posttest three times (once for each of three topics). It is important to account for the nonindependence of responses by the same individual student. Specifically, Student A’s responses on the first posttest are likely to be more similar to his or her own responses on the second posttest than to Student B’s responses on the posttests. Similarly, if researchers are interested in whether students’ perception of group dynamics changes as time in class progresses, they might administer the same “group dynamics survey” three times (once early, midway, and late in the course; Figure 3B). Again, it is necessary to account for the nonindependence in student responses in a model that includes “time in course” as a predictor and survey response as the outcome. Including a student random effect in both of these cases accounts for the nonindependence of these repeated student measures.

The Reasoning behind Random Effects.

The general purpose of regression analysis is to explain the observed variation in an outcome. There are three primary sources of variation that researchers try to explain (or reduce) when implementing experiments and modeling outcomes: process variance, observation error, and estimation error. Process variance is variation that can be accounted for with random effects. It describes the variation in the outcome variable that is caused by “nuisance” variables that might impact outcomes but are otherwise unaccounted for. For example, there are differences between sections (and the converse: similarity within sections), and there are differences between individual students (e.g., an interest in gardening might impact student performance on a plant biology assessment). Frequently, process variance is important to account for, but is not in itself of interest to researchers, and thus is accounted for with random effects.

Observation error comes from imprecision in measurements. To account for this kind of error in data sets, researchers can employ various methods, for example, by gathering validity and reliability evidence for survey use (American Educational Research Association et al., 2014). Furthermore, observation error can be exacerbated if observations (i.e., data) are missing. Keeping all observations in data sets instead of restricting the set such that some students are omitted reduces post hoc volunteer bias. As Brownell and colleagues (2013, p. 177) describe, volunteer bias is a condition wherein there are “unobserved systematic differences between two conditions which will bias results.” In other words, when students volunteer to participate in an intervention, it is entirely possible that these volunteers are different from nonvolunteers. These differences can bias the study results. Extending that idea here, post hoc volunteer bias is the condition wherein the data set is limited in a nonrandom way, resulting in a final data set that includes data that do not accurately describe the whole population. This can lead to biased conclusions (see Rosenthal and Rosnow [1975] and Heckman [1979] for technical details).

Finally, estimation error comes from the precision (or imprecision) of the parameters included in models. Do Scholastic Aptitude Test (SAT) scores really control for all of the prior preparation a student had before entering the class? Does the model include enough control variables? Collecting and adding more controls, or fixed effects, and including those as covariates—for example, by including a student’s score on a placement test as well as an SAT score to account for prior preparation—and including demographic variables in models can reduce estimation error (see Theobald and Freeman [2014] for a thorough description). There will always be unavoidable variation that causes estimation error, but control variables can help limit it.

Another way to think of sources of variance is in general terms. There are three primary sources of variance in education data: 1) things researchers are explicitly testing and can measure (e.g., whether a student received the intervention), 2) things researchers are not testing but might want to control for and can measure (e.g., student’s SAT scores or clustering in sections), and 3) things researchers want to control for but cannot explicitly measure (i.e., the nonindependence between students in the same section).

Selecting a Random Effects ­Structure

Variables as Random Effects or Fixed Effects.

There are two primary ways to determine whether variables should be specified as random effects or fixed effects: 1) building intuition and 2) quantitative assessment.

Building Intuition.

There are three questions an analyst should ask while building intuition to determine whether a variable should be modeled as a random effect or a fixed effect (Figure 4): 1) Is the variable continuous or categorical? 2) Are the observations within the levels (i.e., groups) of the variable independent? 3) Does the research question hinge on comparing the means between the levels (i.e., groups) of the variable?

Is the variable continuous or categorical? Random effects can only handle data that are categorical. This is logical, because a random effect accounts for the nonindependence between observations within a group. Thus, random effects are grouping (or clustering) variables, and groups are, by definition, categories. If a continuous variable is specified as a random effect, each value will be considered a category. For example, in the extended example, prescore (on a test that was identical to postscore) was collected. If prescore is specified as a random effect, all students who have a prescore of 52% will be in a group and all students who have a prescore of 55% will be in another group. This, of course, is not the appropriate way to handle prescore.

Are the observations within the levels (i.e., groups) of the variable independent? Observations that are independent should be specified as fixed effects, not random effects: random effects are grouping variables, and the underlying definition of a grouping variable is that the observations within the groups are not independent. For example, there is not likely to be a strong grouping of women within a course. In other words, students within a section are not independent, but there is not likely to be additional grouping by sex in a course; thus, sex is most often a fixed effect, not a random effect.

On the other hand, observations that are not independent need to be in the model but can be specified as either fixed or random effects. For example, in the extended example, observations within a topic are not independent; thus, topic needs to be in the model. Topic can be specified as a fixed effect or a random effect. The drawback of including group (e.g., topic) as a fixed effect is that this can reduce power and weaken statistical inference when there are a large number of groups (Bolker, 2008). When there are a large number of groups, including group as a random effect is advantageous.

Does the research question hinge on comparing the means between the levels (i.e., groups) of the variable? If a variable has two levels (e.g., although gender can include multiple categories, sex is frequently treated as having two levels: male and female), and the research question asks whether the levels of the variable are different (e.g., whether males respond differently from females) then the variable (sex, with male and female as levels) needs to be specified as a fixed effect. Random effects in multilevel modeling estimate the variance between the groups, not the mean of each group, so statistical comparisons of means generally come from fitting variables as fixed effects.

In summary, some variables are better suited as fixed effects than random effects, and some variables could be either, depending on the research question. Assuming the research question does not hinge on comparisons between levels in these groups, the variables that are most commonly specified as random effects in DBER studies include: section, year (categorical), course, instructor, and student (in repeated-measures studies). Variables that are most commonly specified as fixed effects in DBER studies include: treatment, proxies for student ability (SAT, ACT, placement exam, prescore, etc.), and student demographics (ethnicity, gender, etc.).

In the extended example, a student random effect should be necessary, because students took part in each day of the experiment and thus have multiple posttests. Therefore, students are designated as “repeated measures” in this design (Figure 3B). In addition, a section random effect would account for the nonindependence of sections, because students are clustered in sections; thus, a section random effect should be necessary (Figure 3A).

Quantitative Assessment.

There are two quantitative ways to determine whether a variable should be treated as a random effect: 1) with model selection (which is described at length later) and 2) with the intraclass correlation (ICC). The ICC is a measure of the clustering in a variable. Specifically, it is ρ (“rho”), the ratio of between-cluster variance to total variance:

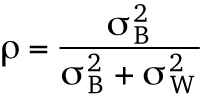where 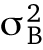is the variance between the clusters and 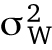is the within-cluster variance. When ρ = 0, there is no clustering, and when ρ = 1, there is complete clustering. There are no hard-and-fast rules about ρ values that dictate random effects; however, the rule of thumb states that random effects are most effective when ρ > 0.05 (Gelman and Hill, 2007; Hedges and Hedberg, 2007). In other words, when ρ is well into single-digit percentiles (ρ < 0.05), a random effect may not be necessary.

The ICC is calculated from null models that include only the random effect of interest: outcome ∼ 1 + (RF). Although lme4 in R does not automatically calculate ρ, the values that are used to calculate it are part of the standard R output from the summary(mod) command. R code that accompanies the extended example (Appendix 3 in the Supplemental Material) includes a calculation of the ICC for student repeated measures and section in the example data.

Three Types of Random Effects Models.

There are many kinds of and ways to specify random effects in R (see Bates, 2010; Bates et al., 2015, 2018 for details). For simplicity, we will focus on three of the most common types. The random effects models discussed to this point are models with random intercepts; additionally, there are models with random slopes and models with both random intercepts and random slopes. Figure 5 illustrates a model without fixed effects (Figure 5A) and the three main types of random effects models. Random intercepts models allow each grouping variable (e.g., section in nested designs and students in repeated measures, as in the extended example) to have its own intercept but keeps the slope equivalent for each group (Figure 5B). The interpretation of these models is that the average for each group is different, but the relationship with the predictors is the same.

In the extended example, when modeling postscore (as an outcome) and section as a random effect, a random intercepts model allows each section to have a different mean postscore but dictates that the treatment has the same relationship with postscore in each section (Figure 5B). Conversely, a random slopes model (Figure 5C) allows the relationships between the predictors and outcome to vary by grouping variable but forces the starting place to be the same. For example, a random slopes model allows the relationship between treatment and postscore to be different for each section, but assumes that the mean postscore is the same for each section. Finally, random slopes and intercepts models (Figure 5D) dictate that each section is allowed a unique mean (intercept) and a unique relationship/impact of treatment. The mathematical mechanics of these models can be found in Appendix 1 in the Supplemental Material.

In the extended example, it is most likely that there is not anything about section that would suggest that the treatment, or any other variable, would differentially impact students’ postscores—both were taught by the same instructor only 1 hour apart. This means that the slope of treatment (or any other variable) should not vary by section, thus dictating that the slope of the random effect should be fixed. At the same time, it is definitely possible that each section will have a different mean postscore, implying that the intercepts are likely to be different. Testing section as a random effect with a fixed slope and random intercept is the most intuitive approach for this study design (i.e., a model that corresponds to Figure 5B).

Similarly, it is most likely that students’ postscores will be affected by the intervention in the same way but that each student’s postscore will be different. This is an argument to include student as a random effect with a fixed slope and random intercept. In other words, the impact of the treatment (or any other variable in the model) on the postscore (slope) is likely to be the same, regardless of student, whereas each student may well have a different score overall (intercept).

Just as specifying variables as fixed effects or random effects comes from a combination of understanding and strategy, knowing whether to model random effects as random intercepts, random slopes, or both comes from a combination of understanding and strategy. Specifically, determining which structure (random intercepts and/or slopes) to use comes from understanding the question the model is trying to answer and the structure of the data (often as a result of the way in which the data were collected). Is it likely that the relationship between the variable of interest and the outcome is different for each grouping variable? If so, test with model selection (see next section) whether a random slope fits best. Is it likely that the relationship between the variable of interest and the outcome is the same but that the mean for each grouping variable may be different? If so, test whether a random intercept fits best. If, after building understanding of the question and the data, there is still uncertainty about whether to include random effects as random slopes or random intercepts, model selection can help inform that decision and is a useful next step.

Model Selection Using Akaike’s Information Criterion (AIC).

After understanding which random effects could be included in the model, model selection (or ICC) can be used to formally test which random effects should be included in the model. The primary goal when modeling is to interpret a model that fits the data well (Figure 1; Burnham and Anderson, 2002). If a model with poor fit is interpreted, then inference, including presence, direction, or magnitude of the effect, can be inaccurate or misleading. Determining the best-fitting model, thus the appropriate model to interpret, takes a combination of selecting the best random effects structure then selecting the best fixed effects. Before selecting fixed effects, one must first select the random effects structure (Zuur et al., 2009).

One commonly used strategy to determine model fit and the most appropriate random effect structure, given a study question, is derived from model selection. Zuur et al. (2009) and Burnham and Anderson (2002) describe model selection at length (primarily with examples from ecology, wherein individuals are frequently clustered in blocks or plots as a way of subsampling populations). Here, best practices from these two authorities are combined and summarized to become recommendations in DBER practice.

Selecting the best random effect structure for your data requires three steps:

1. Build a fixed effects–only model that explicitly tests the hypothesis. In the extended example, the hypothesis is that the treatment will be correlated with an increased postscore, controlling for prescore and topic. (Note: If the hypothesis were that women will disproportionally benefit from the intervention, then the model needs to include the gender by treatment [sex*treatment in R] interaction.)

2. Build models with all the fixed effects from step 1 and all likely combinations of random effects (including a model with no random effects) by removing random effects singularly and in combination.

3. Compare all of the models from steps 1 and 2 using AIC (or AICc, which is AIC with a correction for small sample size; i.e., when the ratio of the sample size to number of estimated parameters is less than 40; for details, see Burnham and Anderson, 2002).

Information criterion (e.g., AIC and AICc) provide a relative measure of “goodness of fit” for models explaining the same data. There are many types of information criterion an analyst can use while conducting model selection (e.g., Bayesian information criterion [i.e., BIC], Hannan-Quinn information criterion [i.e., HQIC]). The performance of each criterion in model selection depends on the data, the model assumptions, and the modeling circumstances (Gurka, 2006; Whittaker and Furlow, 2009). For simplicity, AIC is primarily discussed and is employed in the extended example.

As with all information criterion calculation, AIC weighs how well the model fits and how complex the model is. In short, the more parameters included in a model, the better the model will describe the data. However, at some point, the marginal gain of including another parameter or the added benefit compared with the penalty of additional parameters is negligible, so the additional parameters only add unnecessary complexity. AIC formally calculates this trade-off by considering the maximum likelihood of a model and including a “penalty” for the number of parameters. The simplest models with the lowest AIC values are considered the best-fitting models, with the important caveat that models within ΔAIC of 2 are considered to have equivalent fit (Burnham and Anderson, 2002). With this caveat in mind, the true goal of model selection is parsimony: balancing the trade-off between maximum likelihood and number of parameters, thus threading the needle between underfit and overfit models (Burnham and Anderson, 2002).

AIC values can be either positive or negative, so models with the lowest value are best fitting, not models with the value closest to zero. It is also important to emphasize that AIC is a relative comparison; comparison of models using AIC values is valid only when the models are describing the same data. In DBER, that means the same students need to be present in all the models. Students can be lost from a model if they do not have measurements for all variables. For example, students who did not take the SAT, do not have an SAT score; a model that includes SAT as a factor will omit students without an SAT score. This is an example of post hoc volunteer bias as described above. AIC is often built into R packages (including base R) and therefore can be easily calculated. Additionally, the R packages glmulti (Calcagno, 2015) and AICcmodavg (Mazerolle, 2017) have explicit functions to calculate AIC and AICc.

The final step of model selection is selecting the appropriate fixed effects. The intricacies of this step of model selection are beyond the scope of this paper. However, briefly, selecting fixed effects can be done with backward selection or forward selection. Importantly, in both strategies, all models have the same random effect structure, as determined by steps 1–3. When employing backward selection, first fit a model with all possible fixed effects and the best random effect structure, then remove the fixed effects singularly; candidate models are compared using AIC. In forward selection, the simplest model (with the selected best random effect structure) is fit and fixed effects are added singularly; candidate models are compared using AIC. There are automated functions in R to perform model selection with fixed effects, but not all can be applied to multilevel models fit in lme4. Typically, these functions compare all possible combinations of fixed effects and therefore may select a different final model than one based on selection by singularly removing parameters. It is worth noting that some practitioners criticize these automated functions for being too exploratory or too similar to “fishing for significance” (Burnham and Anderson, 2002); therefore, they should be used with extreme caution or avoided.

Three points are worth making about using model selection when fitting multilevel models. First, fitting multilevel models using restricted maximum likelihood has become so commonplace that it is the default in the lme4 package (i.e., REML = T is the default). It is generally accepted that restricted maximum likelihood is best suited for accurately estimating variance parameters (e.g., random effects), but it is highly dependent on the fixed effects included in the model. For this reason, it is considered best practice to select random effects using restricted maximum likelihood (the default in lme4) but to select the fixed effects with maximum likelihood by adding REML = F in the model command. Finally, when interpreting the final model, it is best to refit it with REML = T to get the most precise estimates. This nuance is demonstrated in the extended example.

Second, interpreting p values from multilevel model output is not considered best practice. Calculating the p value requires an accurate t statistic, which relies on an accurate measure of the degrees of freedom in a model; this is not straightforward in multilevel models (Bates, 2010). In fact, the model output from a multilevel model fit with lme4 will not report a p value. While it is possible to estimate a p value (from the reported corrected t statistic) or to calculate it in other ways, this is not considered wise (more details are provided in Appendix 2 in the Supplemental Material). Thus, model selection or multimodel inference is the preferred mode of hypothesis testing when fitting multilevel models. When performing model selection, each model that is fit can be considered a distinct hypothesis that is supported (or rejected) by determining how well the model fits compared with other models (i.e., other hypotheses).

Third, there is some debate in the literature about whether AIC is the most appropriate information criterion to use when fitting multilevel models (see Gurka [2006] for details). Participating in this debate is beyond the scope of this paper, but there is evidence that AIC performs as well or better than other information criteria in selecting the correct multilevel model in many circumstances (Gurka, 2006; Zuur et al., 2009). Furthermore, using AIC to select the best-fitting multilevel models that have been fit in lme4 with the lmer and glmer function in R is currently supported (Zuur et al., 2009).

Additional Notes

Note 1.

To account for clustering with random effects, the clustering needs to be independent of the treatment. For example, in the extended example, two sections got both treatments. Another common experimental design is for two or more sections to be named as the control sections and two or more different sections to be named as the treatment sections (as illustrated in Figure 5). In each of these cases, including a section random effect will account for some student clustering, and the overall treatment effect can still be estimated. On the other hand, if an experiment had just one section of the control and one section of the treatment, it is inappropriate to include a section random effect, because the treatment is synonymous with section. Here, the random effect will attribute the effect of the treatment to “nuisance” differences between sections, effectively sabotaging the effect of treatment completely. The better experimental design is to replicate the experiment such that there are multiple sections of the control and multiple sections of the treatment, or to randomize treatment to students instead of sections. When the preferred experimental design is not possible, making random effects inappropriate, controlling for student nonequivalence is paramount; this is described at length in Theobald and Freeman (2014).

Note 2.

As a general rule of thumb, a random effect needs several groups (levels) to be effective; however, there is no clear, quantitative definition of “several.” That said, there is no harm in testing random effects with as few as two groups; it is possible these models will not converge, but if they do, they will likely converge at equivalent estimates as models without random effects (Gelman and Hill, 2007). In other words, a model that converges reaches a solution, whereas a model that does not converge never reaches a solution; R will report nonconvergence with a warning or error. If a model has random effects with too few groups, the solution reached will be equivalent to a solution reached when random effects are not included. Conversely, not including a random effect when one is needed can have several unfortunate ramifications: first, it can falsely increase your sample size by treating all observations as independent when they are not; second, it can overestimate the accuracy of your estimate; and ultimately, it can mask relevant effects, as illustrated in the extended example below. In short, testing possible random effects is usually a good idea—there is greater harm in not including a random effect that is necessary than including a random effect that is not necessary (Gelman and Hill, 2007).

Note 3.

Many different types of outcome data (e.g., binomial, Poisson) can be accommodated in multilevel models with standard R packages. Table 2 includes a list of outcome data types (continuous, binary, etc.) that are common in DBER studies. The corresponding name of fixed effects–only models and multilevel models, the R package in which the multilevel models are implemented, and example syntax for building the models in R are also included in the table. In addition, several DBER papers have implemented random effects well and have detailed their justification and implementation. These papers include studies that use random effects to account for repeated measures, typically students (Eddy et al., 2014; Linton et al., 2014; Wright et al., 2016; Theobald et al., 2017; Wiggins et al., 2017), and studies that use random effects to account for clustering, either by class, quarter, or instructor (Freeman et al., 2011; Eddy et al., 2014; Wright et al., 2016).

TABLE 2.

Random effects can be implemented in regression models that model various types of outcome variables^a

				Implementation in R
Outcome data type	Example in DBER	Regression type (R function)	With random effect (R function)	R package	R syntax
Continuous	Exam points	Linear model (lm)	Linear mixed effects model (lmer)	lme4b	Mod ← lmer(outcome ∼ predictor, data = data)
Binary (0/1; yes/no)	Pass/fail	Binomial (glm)	Generalized linear mixed effects model (glmer)	lme4b	Mod ← glmer(outcome ∼ predictor, family = binomial, data = data)
Proportion	Proportion of classes attended	Binomial (glm, family = binomial)	Generalized linear mixed effects model (glmer)	lme4b	Mod ← glmer(cbind(numerator, denominator) ∼ predictor, family = binomial, data = data)
Count	Number of hand-raises	Poisson (glm, family = Poisson)	Generalized linear mixed effects model (glmer)	lme4b	Mod ← glmer(outcome ∼ predictor, family = Poisson, data = data)
Likert; categorical ordinal	Agree–neutral–­disagree	Proportional odds or ordered logit (polr)	Cumulative link mixed model (clmm)	ordinalc	Mod ← clmm(as.factor(outcome) ∼ predictor, data = data)

^aSome of the most common types of discipline-based education research (DBER) outcome variables can be categorized as continuous, binary, proportion, count, or on a Likert scale. This table shows the most common types of data in DBER and the corresponding implementation of multilevel models in R, including a recommended R package and corresponding syntax for model specification.

^bBates et al., 2018.

^cChristensen, 2018.

EXTENDED EXAMPLE ANALYSIS

In summary, the extended example describes an experiment wherein researchers test the hypothesis that the postscore is correlated with treatment, controlling for prescore and topic. Controlling for pretest in a linear regression (as opposed to using gains or change scores) should be considered best practice, as it is the best way to determine that observed differences are a result of the true treatment effect (i.e., the effect of the intervention) and not student characteristics (Theobald and Freeman, 2014). Given that student mastery is often variable by topic (i.e., because different topics are harder than others or different assessments are better than others), the analyst controls for topic with a fixed effect (topic in the extended example has three levels: Q, R, S). Furthermore, the experimental design dictates that the analyst tests random effects for section (as a nested design, section has two levels: A and B; Figure 3A) and students (as repeated measures; Figure 3B).

The code and data used in this analysis can be found in Appendices 3 and 4, respectively, and also in the online github repository: https://github.com/ejtheobald/Multilevel_Modeling.

Specifying Variables

When building models with factor variables in R (i.e., variables with discrete levels or categories), the analyst can choose the reference group for each comparison. Here, treatment is coded as 1 and control as 0, so control is the reference: the output will show the effect of the treatment relative to the effect of the control. Similarly, topic is coded as Q, R, and S. Q is (arbitrarily) the reference (because it comes first in the alphabet), so the output will show the effect of Topic R relative to Q and the effect of Topic S relative to Q. If the analyst desires other comparisons (e.g., Topic S relative to Topic R), the function relevel in base R enables this comparison (R Core Team, 2017).

The R syntax for coding random effects in the package lme4 (Bates et al., 2018) follows the structure (x₁|x₂). The term to the left of the | indicates a random slope (e.g., x₁), while the term to the right of the | indicates a random intercept (e.g., x₂). When one or the other of those terms is not needed, replace the term with a 1. Here, the analyst tests two random effects: students as a random intercept (1|StudentID) and section as a random intercept (1|Section).

Note: If it were likely that the relationship between treatment and outcome varies by section, a random effect with section as a random slope (and fixed intercept) would take the form (0+Treatment|Section), and section with a random slope and random intercept would take the form (Treatment|Section) (Bates et al., 2015). There are many ways to specify other random effects in lme4, and these are explained at length in the package documentation (e.g., Bates, 2010; Bates et al., 2015, 2018). Here, intuition does not support testing random slopes, because there is no a priori reason to suspect that treatment will have a differential effect on the postscores of students in the two sections.

An important note about data structure: when modeling data that are nested (e.g., section within course within year), it is important to consider how levels are indicated in the raw data. For example, if there are five sections in the same course in 3 years, the data can either be indicated as Year 1, Section 1–5; Year 2, Section 1–5; and Year 3, Section 1–5; or Year 1, Section 1–5; Year 2, Section 6–10; and Year 3, Section 11–15. Note the section numbers either start over in each year (option 1) or are continuous (option 2). Either strategy will yield the same result, but the R syntax for specifying models with these two different data structures is different. For the purposes of this paper, data are structured such that sections are continuous (i.e., no two sections have the same number and every section has a globally unique identifier). For details on how to specify models with data where sections start over, see Bates (2010) and Bates et al. (2015).

Model Selection Using AIC

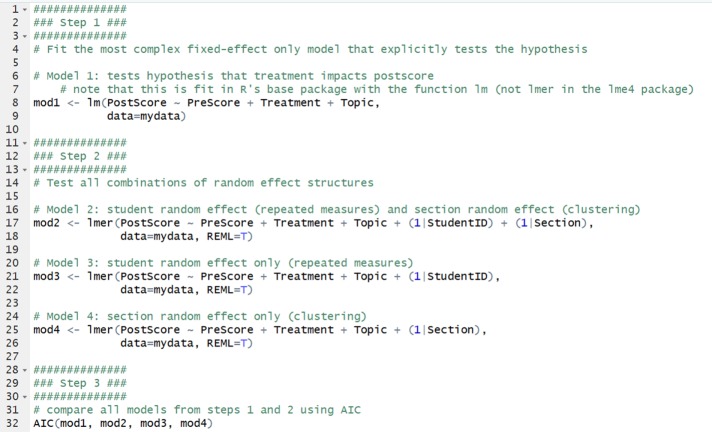
The first step in model selection (Figure 1) is to fit a fixed effects–only model that tests the hypothesis; this step is illustrated here as well as in Figure 6 (step 1, lines 1–9):

mod1: PostScore ∼ Treatment + PreScore + Topic

This model models PostScore as a function of (noted with the “∼”) Treatment, controlling for PreScore and Topic. This model explicitly tests the hypothesis that treatment impacts the PostScore. Model 1 was fit using the lm function in R’s base package (Figure 6, step 1, lines 1–9), because lmer can fit only multilevel models (R Core Team, 2017; Bates et al., 2018).

The second step (Figure 1) is to fit three additional models, with all the possible combinations of random effects (Figure 6, step 2, lines 11 – 26):

mod2: PostScore ∼ PreScore + Treatment + Topic + (1|StudentID)

mod3: PostScore ∼ PreScore + Treatment + Topic + (1|Section)

mod4: PostScore ∼ PreScore + Treatment + Topic + (1|StudentID) + (1|Section)

Students (identified by their unique student ID, “StudentID”) and sections are included as random effects with random intercepts and fixed slopes. Models 2 through 4 were fit using the function lmer in the lme4 package in R (Bates et al., 2018).

Finally, the third step (Figure 1) is to compare the four models using AIC to determine which model fits best (Figure 6, step 3, lines 28–32).

Interpreting Results

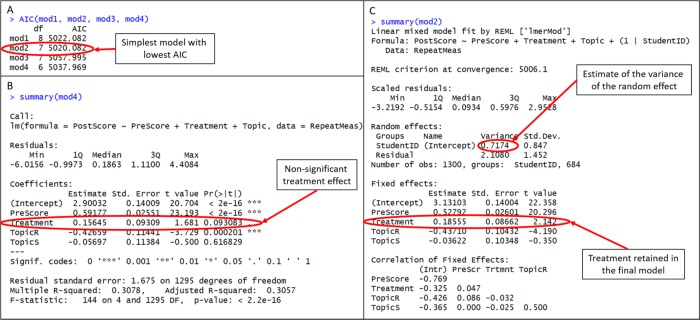
Recall that the goal of modeling is to interpret the best-fitting model (Figure 1), and the best-fitting model has the lowest AIC. Models within ΔAIC = 2 are considered to have equivalent fit (Burnham and Anderson, 2002), so if ΔAIC ≤ 2, the model with the fewest number of parameters (i.e., the simplest model) is selected (Burnham and Anderson, 2002). Here, mod3, containing the student random effect to account for repeated measures, was selected as best fitting (Figure 7A).

After determining the model with the most appropriate random effect structure (mod3), the analyst selects the best fixed effects that explain the data (Figure 1). This procedure is identical to selecting the random effects (except for also specifying REML = F) and is detailed in the R code in Appendix 3 in the Supplemental Material.

The best-fitting model is the model that includes a student random effect (to account for the repeated measures) and Pre-Score, Topic, and Treatment as fixed effects (Figure 7; Appendix 3 in the Supplemental Material). Section was not retained as a random effect, which is not surprising, given its ICC is 1.9e^-14—essentially zero (Appendix 3 in the Supplemental Material).

Interpreting the best-fitting model to answer the research question, the researchers conclude that students who received the treatment performed, on average, 0.186 points better than students who received the control, all else being equal (Figure 7C). This inference comes from the retention of treatment in the best-fitting model (i.e., the model that contains treatment has the lowest AIC). Note that, although it is possible to consider the t statistic to test the hypothesis, according to the author of the lme4 package, it is not wise. See Appendix 2 in the Supplemental Material for details and Bates (2010) for technical details.

Looking at the rest of the output (Figure 7C), the student random effect has an estimated variance of 0.7174. Remember that a random effect is not estimating a slope parameter, but rather only a variance parameter, so there is not a “beta coefficient” in the output, only an estimate of variance. It is from this variance parameter that an ICC is calculated. The ICC for the student repeated measures is calculated in the code found in Appendix 3 in the Supplemental Material and is 0.455. This indicates that the within-student answers are highly correlated compared with the between-student answers, further justifying the inclusion of StudentID as a random effect. Finally, the other fixed effects in the model (PreScore and Topic R and Topic S, both of which are being compared with Topic Q) indicate that treatment is not the only factor that influences PostScore.

For illustrative purposes, Figure 7B also shows the output of a fixed effects–only model. Without a random effect (in the fixed effects–only model), the effect of treatment is masked at conventional significance levels, p < 0.05 (Figure 7B, p = 0.09 for Treatment). Only when controlling for the student repeated measures with a student random effect does the treatment effect become apparent (Figure 7C). In other words, getting the random effect structure right is not only a matter of protecting against spurious conclusions driven by pseudo-replication and lower-than-correct standard errors, but it actually helps detect effects that can be concealed by confounding structure in the data.

In this case, the nonsignificance of treatment when the student random effect is omitted and the retention of treatment when the student random effect is retained are likely artifacts of the experimental design: because the design was unbalanced (section B got the treatment twice), using a fixed effects–only model makes the treatment effect more dependent on who the students are in section B. Students who got the treatment more often might be slightly less proficient students, so without a random effect, it might seem as though the treatment does not have a substantial impact. Controlling for prescore (as well as other covariates that are not included in the data: course grade, SAT score, etc.) corrects for some of this variation but not all of it, because it does not account for the individual students themselves. A student random effect helps to better account for variation among students by accounting for the repeated measures, thus the unbalanced design.

CONCLUSIONS

Observations in DBER studies that employ quasi-experimental designs are rarely truly independent: subjects are frequently clustered in sections, courses, or years or are often sampled more than once. This kind of nonindependence of observations artificially inflates sample size, thus shrinking standard errors in a way that overestimates the accuracy of estimates. Therefore, statistical methods that cluster observations and account for this nonindependence of errors are necessary. Multilevel regression modeling, which includes fixed and random effects, can account for this clustering and can lead to more accurate estimates of treatment effects. Random effects should be specified and tested within each level of clustering (e.g., each group in clustered studies). Random effects can be incorporated into many of the regression models that are most commonly employed in DBER.