Size matters: height, cell number and a person's risk of cancer

Abstract

The multistage model of carcinogenesis predicts cancer risk will increase with tissue size, since more cells provide more targets for oncogenic somatic mutation. However, this increase is not seen among mammal species of different sizes (Peto's paradox), a paradox argued to be due to larger species evolving added cancer suppression. If this explanation is correct, the cell number effect is still expected within species. Consistent with this, the hazard ratio for overall cancer risk per 10 cm increase in human height (HR₁₀) is about 1.1, indicating a 10% increase in cancer risk per 10 cm; however, an alternative explanation invokes an indirect effect of height, with factors that increase cancer risk independently increasing adult height. The data from four large-scale surveillance projects on 23 cancer categories were tested against quantitative predictions of the cell-number hypothesis, predictions that were accurately supported. For overall cancer risk the HR₁₀ predicted versus observed was 1.13 versus 1.12 for women and 1.11 versus 1.09 for men, suggesting that cell number variation provides a null hypothesis for assessing height effects. Melanoma showed an unexpectedly strong relationship to height, indicating an additional effect, perhaps due to an increasing cell division rate mediated through increasing IGF-I with height. Similarly, only about one-third of the higher incidence of non-reproductive cancers in men versus women can be explained by cell number. The cancer risks of obesity are not correlated with effects of height, consistent with different primary causation. The direct effect of height on cancer risk suggests caution in identifying height-related SNPs as cancer causing.

1. Introduction

Humans and mice have approximately the same aged-corrected incidence of cancer [1]. However, based on the multistage model of carcinogenesis, in which cancer originates via the progressive loss of genetic regulation within cells due to the accumulation of a cancer-specific set of mutations (figure 1), this observation raises a logical problem first clearly articulated by Peto [2]. He noted that, if all else is equal, large long-lived animals should experience a massively higher incidence of cancer than small short-lived ones because increasing the number of cells (size) and increasing the number of times they divide (longevity) increase the likelihood of least one cell accumulating the mutations that initiate cancer. However, there is no such strong tendency of large long-lived mammals to be more cancer prone [3], although the effect may be weaker in birds [4]. This lack of fit of the data to expectation is called Peto's paradox [5]; however, the paradox is resolved if species subject to selection for larger body size and/or greater longevity evolve additional layers of cancer suppression [5,6]. For example, compared with mice, human fibroblasts require more mutational events to become transformed [7], large and long-lived rodents have additional, and in some cases unique, anti-cancer mechanisms [8], and it has been proposed that retrogene copies of TP53 reduce cancer incidence in elephants [3].

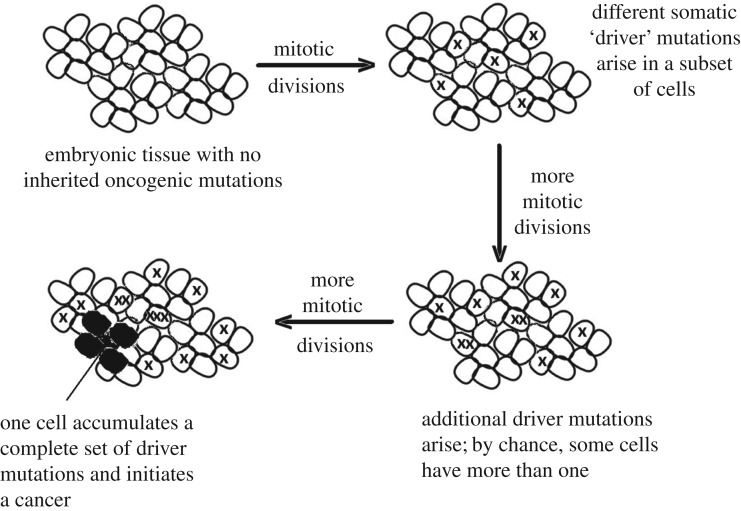
Figure 1.

The multistage model of carcinogenesis. In the simplest form of the multistage model, cancer originates following the accumulation in a single cell of a cancer-specific set of driver mutations. These mutations may be a mix of DNA mutations, epigenetic reprogramming and/or chromosomal alterations. The probability of cancer depends upon the number of dividing cells, the number of divisions that each cell lineage undergoes, the somatic mutation rate, and the number of driver mutations required.

As a result, the combination of the multistage model with this adaptive evolution leads to the prediction (1) that larger individuals within a species will be more prone to cancer due to their greater cell number, but (2) that larger species will generally have no such tendency due to their evolutionarily enhanced levels of cancer suppression. This evolutionary resolution of Peto's paradox (prediction 2) is expected only if the underlying assumption of the multistage model (prediction 1) is correct (i.e. that more cells and greater longevity indeed result in more somatic mutation). Consistent with the longevity effect, we know that, for most cancers, risk increases dramatically with age, but what about the effect of more cells? Within a species there are two sources of cell number variation that can be examined: body size variation among individuals; and tissue size variation within individuals.

Recently, there has been an extensive discussion in the literature about the correlation between tissue-specific cancer risk and estimates of the total lifetime stem cell divisions (lscd) within those tissues (e.g. [9,10]). Since lscd is the product of stem cell number and lifetime divisions per cell, these two components can be separated, and a significant effect of stem cell number can be identified [11], suggesting that tissues with more stem cells have a higher risk of cancer. However, this association is confounded by important tissue-specific differences in the number and nature of driver mutations required to induce different cancers [11–13], and an earlier study showed no association with overall cell number across organs, using the proxy of organ weight [14]. Tissue differences in cancer suppression are expected because large and/or rapidly dividing tissues are predicted to evolve enhanced cancer suppression for the same reason that enhanced cancer suppression is expected to evolve in large and/or long-lived species (i.e. to reduce the loss of Darwinian fitness due to cancer [5]). To minimize this expected variation among tissues, Noble et al. [11] grouped anatomically similar tissues and found that within them the correlation with lscd was consistent with the multistage model, a result that provides the best evidence to date of a cell number effect.

The confounding issue of tissue-specific differences can be avoided by comparing the same tissue in individuals of differing size, since, in mammals, changes in body size are generally due to differences in cell number; only slowly dividing cells such as neurons appear to respond by changing their volume [15]. Thus larger individuals are expected to have a higher overall cancer risk. While we can expect natural selection to favour added cancer suppression mechanisms in large relative to small species, there is no expectation of enhanced cancer suppression in large relative to small individuals within a single species. The members of a single species share the same gene pool, and hence share the same average level of cancer suppression. Exceptions could arise only (a) if the gene pool was geographically sub-divided, leading to local adaptive changes in size and hence potentially to the level of cancer suppression, and (b) if some alleles increasing size within a species had a pleiotropic effect of reducing cancer risk. Based on current data such pleiotropy seems unlikely, especially given that the best documented example of an apparent pleiotropic effect on height and cancer risk (Laron syndrome, discussed below), has the opposite effect of reducing the cancer risk of small individuals [16,17].

Albanes and colleagues proposed 30 years ago that there was a link between human height and the incidence of cancer [18–20]. However, humans do not vary greatly in height, and many other factors can influence cancer risk, so it needed large datasets to effectively test both the overall height–cancer relationship and the effect of height on specific cancers. Furthermore, until fairly recently, analyses of the effect of human body size on cancer risk generally focused on the risks resulting from obesity (see [21]), rather than on the potential effect of height. However, large datasets now exist from studies tracking hundreds of thousands of individuals and they have provided overwhelming evidence that height is a risk factor for most cancers [22–25]. This conclusion is supported in another species, the domestic dog, where different breeds vary enormously in their typical weight (greater than 25-fold) and cancer risk increases with breed size [26,27].

Many factors, genetic and environmental, affect human height and hence increase cell number, but under the ‘direct effect’ hypothesis derived from the multistage model, the effector remains cell number. An alternative possibility is that the association is indirect, where height, as a proxy for cell number, is not causal. For example, it has been suggested that the height/cancer association arises from factors acting early in life that affect both height and cancer risk separately, such as nutrition, health or social conditions early in life [19,28,29]. It is often proposed that these factors act by determining the levels of growth-determining hormones such as IGF-I levels, and that these hormones, acting early in life, are the causal agents [23,28]. It has also been proposed that chronic exposure to high levels of insulin and IGF-I throughout life is the causal factor driving the links between cancer and both height and obesity [30]. Note that, while early-life levels of growth-determining hormones affect height, under the indirect-effect hypothesis these factors are assumed to cause an increase in cancer risk via some other route unrelated to height.

Publications noting the effect of height on the incidence of cancer generally discuss both the direct and indirect hypotheses; however, the question of how these hypotheses can be distinguished has been left unanswered. The goal of the present work is to provide the first test of these alternatives by comparing the best available data to predictions of the direct-effect hypothesis, predictions derived from a model of multistage carcinogenesis. The expectation is that the increase in cancer risk with height will be predictable from the allometric relationship between cell number and height. In contrast, most of the indirect-effect hypotheses are not model based and hence do not make specific a priori quantitative predictions. One exception is the hypothesis that taller individuals experience a higher rate of cell division, which in turn leads to a higher risk of cancer [22]. There is evidence of height-related differences in the level of the mitogenic hormone IGF-I [31–33], and an increased rate of cell division with height has some direct support [34]. Given the link between cell division and somatic mutation [18], the magnitude of any effect can be predicted from the multistage model.

The direct-effect hypothesis makes two important predictions that can be quantified using an appropriate model of multistage carcinogenesis. First, the model predicts a specific rate of increase in overall cancer risk with height. Second, it predicts that the magnitude of effect of height on cancer risk should be general across all or nearly all cancers, since an increase in height typically results in an increase in the size of organs (as measured by weight) [35]. Although some tissue-specific variation in the effect of height on specific cancers is expected depending on how the cell number in the at-risk tissue scales with height, the pattern seen in specific cancers should, in general, mirror the predicted overall effect. If the height effects on specific cancers do fit closely to the predictions of the direct-effect hypothesis then it can be concluded that changes in cell number account for most, if not all, of the effect of height on cancer risk. Moreover, it would provide further validation of the multistage model of carcinogenesis.

2. Material and methods

To test the predictions of the direct-effect hypothesis, data from large-scale surveillance projects were required to test the observed effect of height on cancer risk across multiple cancers against predictions derived from a general model of multistage carcinogenesis. The criteria used to select studies were (1) at least 10 000 total cancer cases in each sex tracked; and (2) a rigorous estimation of the effect of height on multiple types of cancer using a Cox proportional-hazards regression model that factored out any association between age and height, plus other appropriate variables. The resulting relationship between height and cancer risk is usually expressed as the hazard ratio (defined as the change in the instantaneous probability of cancer occurring at some age due to a difference in height), measured per 10 cm increase in height (HR₁₀) [23] or per 5 cm [24,25], or as the relative risk (the change in the probability of experiencing cancer by some age due to a difference in height), again usually standardized for a 10 cm increase in height (RR₁₀) [22]. In the case of cancer occurrence, typically a rare event, HR₁₀ is equal to the relative risk (RR₁₀), as shown below.

For each cancer category recorded in at least two of the studies for a given sex, a weighted geometric mean of the change in HR₁₀, HR₅ (transformed to HR₁₀) or RR₁₀ was calculated, with values inversely weighted by the sample variance, so that the variance of the pooled mean is the sum of the sample weights.

(a). Modelling multistage carcinogenesis

The concept of multistage carcinogenesis (figure 1) was introduced by Nordling [36], who used the fit of data on the age-specific incidence of cancer deaths to a simple mutational model to suggest that most cancers resulted from the accumulation of seven mutations. However, more than 20 years later, the incidence of retinoblastoma was shown to fit a ‘two-hit’ model [37], indicating that the number of mutational hits (M) was variable. This two-hit model included an explicit link between the incidence of retinoblastoma and three parameters: the number of at-risk cells, the number of cell divisions that they underwent and the somatic mutation rate. The model (which applied to a growing tissue) was later generalized to allow an arbitrary number of mutational hits in either growing or non-growing tissue [5]. For a non-growing tissue, the probability of a specific cancer (p) over a lifetime of length T is determined by the accumulation in a single cell of the M somatic driver mutations required to initiate the cancer (figure 1). This depends upon the number of dividing cells (C), the rate of division (k) and the somatic mutation rate per cell division (u), so that the lifetime number of divisions per cell is defined by K = kT (i.e. product of the rate of cell division and time). In its most general form, the model defines the cancer risk as

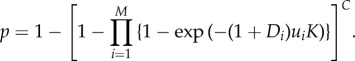2.1

Equation (2.1) incorporates the possibility that each of the M driver mutations may differ in its somatic mutation rate (u_i), and whether or not the associated genetic change is recessive (D_i = 0, a classic tumour suppressor) or dominant (D_i = 1, a protooncogene) [5].

Assuming the incidence of the cancer is relatively low (i.e. small p), equation (2.1) can be usefully (and very accurately) approximated by

2.2

This form allows us to investigate how the incidence of cancer is altered as we change parameters, such as C, the number of at-risk cells in a given tissue, and k, the rate at which those cells divide [5].

To further understand the model in terms of some recent literature that has focused on lifetime cell divisions lscd [9,10], it is useful to simplify equation (2.2) and assume that cancer suppression is controlled by a set of M/2 autosomal tumour suppressor genes (requiring M driver mutations to inactivate them all), each with the same risk of mutational failure (u) per copy. If it is assumed that the cells at-risk for initiating cancer are the stem cells then

2.3

where lscd = KC = kTC. This form makes it clear that while the risk of accumulating a specific set of M mutations in a single cell lineage doubles if we double the cell number C, it more than doubles (by 2^M) if we double the number of lifetime divisions (K). Because M is known to vary among tissues, lscd is not a reliable metric for predicting cancer risk unless differences among tissues are taken into account [11–13].

As noted above, the effect of height on cancer risk can be expressed in two ways: as a relative risk (RR) or as a hazard ratio (HR). These two measures, although closely related are generally slightly different; however, in the case of rare events they converge. This can be shown by differentiating equation (2.2) with respect to time to get the rate of cancer incidence:

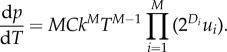2.4

Equation (2.2), the probability of cancer by time T, and equation (2.4), the instantaneous probability of cancer at time T, show that for two individuals differing in height the equations are identical except for their value of C. This leads to a simple relationship that defines both RR (equation (2.2)) and HR (equation (2.4)), assuming that height affects cell number but not the rate of cell division:

2.5

where it is assumed that the two individuals differ by y units of height around their mean height of h, and the exponent b defines the allometric relationship between height and cell number [27]. However, if the rate of cell division also varies with height, then comparing a tall and short individual, we have, from both equations (2.2) and (2.4),

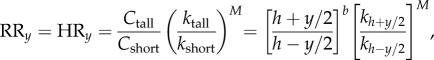2.6

where k_h is the division rate at height h. Equation (2.6) shows that any effect of division rate is amplified by the exponent M, the number of driver mutations required to initiate a given cancer. Given that large, rapidly dividing tissues are the most susceptible to somatic mutation and hence are predicted to have the largest M [5], these are the tissues most likely to show the effects of any subtle increase in cell division rate with height.

(b). Scaling height to cell number

The relationship between height and overall body mass is generally calculated using the body mass index (BMI), where b = 2, although scaling based on fat-free mass (considered here as a proxy for cell number) may be somewhat less in men, with estimates of b = 1.86 ± 0.10 for men, and 2.05 ± 0.09 for women [38]. The allometric scaling of different organs with height varies, and although estimates are complicated by the covariation of height and weight, they appear to range from roughly linear (b = 1) (e.g. brain) to volumetric (b = 3) (e.g. spleen) (see [39]). The effect of these allometric differences is not large, given the relatively narrow range of human height, so that b = 2 remains a good initial approximation.

3. Results

(a). More cells, more cancer: a quantitative test of the direct-effect hypothesis on overall cancer risk

Equation (2.5) can be used to predict the relationship between height and cancer risk expected under the direct-effect hypothesis that cell number is causal. Assuming, from [38], average heights of 162 cm (64 inches) for women and 175 cm (69 inches) for men, with sex-specific allometric values (b) of 2.05 (women) and 1.86 (men), then the expected change in hazard for a 10 cm change in height, measured as a 5 cm shift above and below the mean, is 13% for women and 12% for men, i.e. HR₁₀ = 1.13 (women) or 1.11 (men). These values define the model-based prediction of the effect of height on cancer risk based on changes in cell number.

To test these predictions against human data, four large-scale studies of women [22–25], and three studies of men [23–25] satisfied the criteria defined above. In estimating the effect of height, all four studies incorporated the potential confounding effects of age, BMI, and smoking, and, where relevant, menopausal status.

The mean estimate of HR₁₀ for overall cancer risk in these studies was 12% for women and 9% for men (figure 2; electronic supplementary material, table S1). A similar value of 10% for men was obtained by Green et al. [22] in their meta-analysis, a value that holds after excluding the Sung et al. [25] data to make it independent of the estimate in electronic supplementary material, table S1. Thus, there is a very close fit between observation (12% women; 9% men) and expectation (13% women; 11% men) for the increase in overall cancer risk with height, based solely on the assumption that height increases cell number.

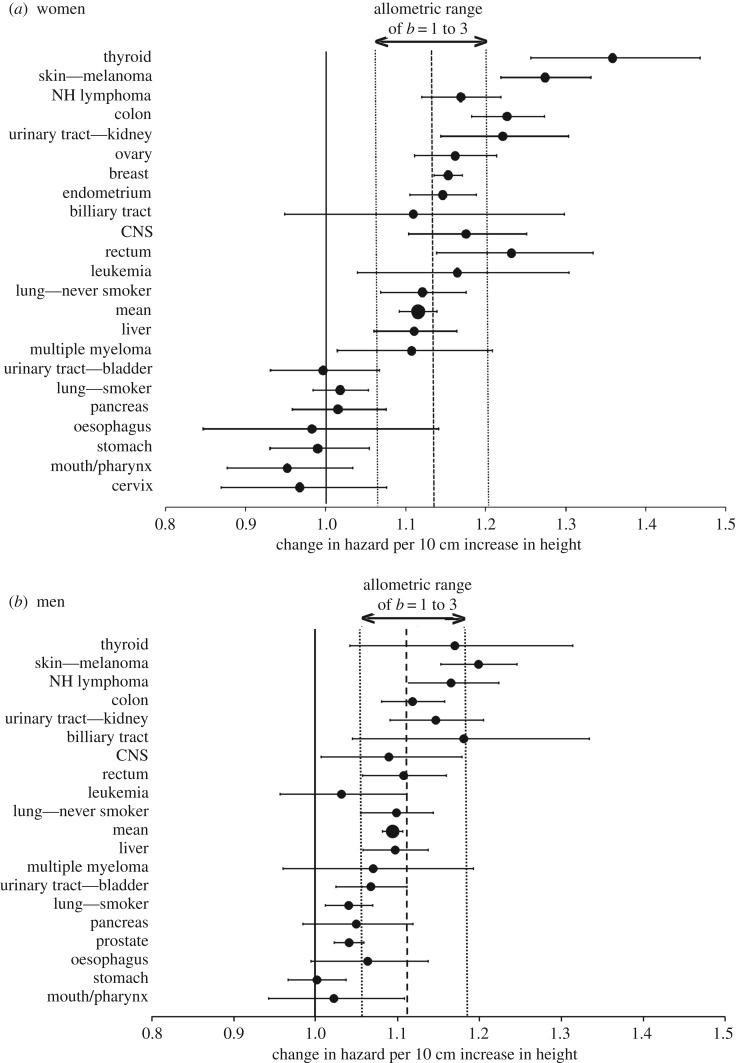
Figure 2.

A comparison of the observed and predicted effect of height on the risk of specific cancers: the observed hazard ratio (HR₁₀) and 95% confidence interval linking a 10 cm increase in height to the increased risk of specific cancers, showing only cancers included in at least two of the target studies (for women [22–25]; for men [23–25]). The vertical lines illustrate: no effect of height (HR₁₀ = 1.00; solid line); the average HR₁₀ predicted from the multistage model based on the allometry of human height to overall body mass, which is used as a proxy for cell number (dashed line); and (3) the predicted effect based on the expected extremes of organ cell number allometry to height: linear, b = 1 (lower dotted line); and volumetric, b = 3 (upper dotted line). For data sources, see electronic supplementary material, table S1.

(b). The effect of height across different cancer types

Under the direct cell-number hypothesis, the increase in overall cancer with height reflects an increase in cancer risk across all cancers. Combining data across the four large-scale cancer surveillance studies [22–25] gave results for 23 different cancer categories (including lung cancer separated by smoker/never-smoker) that were documented in at least two of the studies (electronic supplementary material, table S1). Of the 23 categories, when separated by sex, 64% of HR₁₀ values in women (14/22) and 68% of HR₁₀ in men (13/19) were significantly greater than one, indicating an increase in cancer risk with height (figure 2). Combined across both sexes, the figure increases to 78%, with significant effects in 14/18 cancers occurring in both sexes, plus 4/5 sex-specific ones (electronic supplementary material, table S1). No cancers had HR₁₀ values significantly less than one (figure 2).

As noted earlier, the allometry of organ size to height can deviate slightly from b ≈ 2, within about 1 ≤ b ≤ 3 [39]. From equation (2.5), this range predicts 1.06 ≤ HR₁₀ ≤ 1.19 for men and 1.06 ≤ HR₁₀ ≤ 1.20 for women. These upper limits are only significantly exceeded by two cancer types: thyroid cancer and melanoma in women (figure 2). Combined across the two sexes, melanoma is the only cancer to significantly exceed the upper threshold (electronic supplementary material, table S1).

The finding of high HR₁₀ for melanoma is of particular interest because of the largely two-dimensional nature of the skin, with the surface area of the body generally considered to scale at approximately b = 1.5 (see [40], assuming the BMI relationship of b = 2 linking height and body weight). This value leads to an expected HR₁₀ of 1.09, a value that is significantly exceeded by both male and female melanoma estimates in figure 2. It is also exceeded by the non-melanoma estimates in both sexes from the Me-Can study (1.25 women, 1.21 men) [24], and the pooled melanoma/non-melanoma skin cancer estimate from the Korean study (also 1.25 women, 1.21 men) [25], estimates that were not included in figure 2. Thus, based on the available data, skin cancer appears to show a consistent relationship to height that is too strong to be adequately described by the cell-number hypothesis in its simplest form.

Thyroid cancer also exhibits an unusually high HR₁₀ suggesting that it may fall into this same category; however, the results were highly variable. The Korean data showed a very strong effect (HR₁₀ of 1.54 in women and 1.35 in men) [25] not apparent in the two other studies with data: HR₁₀ of 1.03 in women and 1.10 in men [23], and HR₁₀ of 1.28 in women and 0.96 in men [24].

The observation that the Korean data showed a high HR₁₀ for thyroid cancer relative to the other studies suggested looking at the data for other notable geographical differences. The four studies used populations from the UK [22], the US [23], Norway, Sweden and Austria [24], and Korea [25], and examining all of the pairwise differences in HR₁₀ for significant differences (corrected for multiple testing) revealed four such cases involving two types of cancer in women (out of a total of 94 comparisons) and one case in men (out of 42 comparisons) (electronic supplementary material, table S2). One of the female cases involved the high HR₁₀ measured in the Korean data for thyroid cancer (relative to the US). The remaining three cases in women were due to the low (but significant) estimated increase in breast cancer with height (=1.09) in the US relative to the higher estimates in the other three populations (UK 1.17, Norway, Sweden and Austria 1.23, Korea 1.39). The single male example of heterogeneity was for prostate cancer where a small effect of height in the US (=1.02) was significantly less than the estimate from the Norway, Sweden and Austria data (=1.10), and less than the Korean estimate of 1.17, but not significantly so. Overall the geographical heterogeneity between the HR₁₀ estimates among the populations was very limited.

(c). Melanoma, cell division and height

Data for the majority of cancers are consistent with the direct-effect hypothesis that the effect of height on cancer risk is due to increased cell number. However, the data for melanoma, and perhaps for skin cancer in general, show a relationship to height that is too strong to be explained solely by cell number changes. A second factor that could also contribute to the height effect is the rate of cell division during regular tissue renewal in adults [22]. The magnitude of this effect can be quantified using equation (2.6). Assuming that for melanoma b = 1.5, giving HR₁₀ = 1.09 based on cell number, then if M (the number of driver mutations) is in the range of 4–6 (estimated at M = 4, with other epithelial cancers M = 5–7 [13]) the increase in division rate for a 10 cm increase in height would only have to be 2–3% to reach the observed HR₁₀ of 1.24 (electronic supplementary material, table S1). If b or M is larger, then the required increase in division rate is even less.

The level of circulating IGF-I (a mitogen) in adults is positively correlated with their height [31–33]. While IGF-I has been implicated in the indirect-effect hypothesis due to its multiple roles in early development, it is possible that the IGF-I level in adults has a direct effect on cancer risk via an increase in the rate of cell division. For example, a significant correlation has been found between IGF-I levels and the proliferation rate of colon epithelial cells in vivo [34], and of both adult fibroblasts [41] and epidermal keratinocytes [42] in culture.

This association may be responsible of the low cancer rates observed in individuals with growth hormone receptor deficiency (GHRD) mutations resulting in Laron syndrome. They have an IGF-I deficiency and much reduced stature, typified by a mean adult height of about 118 cm (women) or 124 cm (men) [43]. Based on equation (2.5), these heights would predict about a 50% reduction in cancer risk relative to individuals of average stature. The results of two independent studies suggest that such individuals have a reduction in cancer risk greater than 50% [16,17], consistent with unusually low adult cell division rates reducing the cancer rate below that expected based purely on their stature.

(d). Sex differences in cancer risk

It has long been recognized that men have a higher overall risk of cancer than women [44]. After excluding sex-related cancers, men suffer a roughly 35–55% higher overall risk of cancer (see [45]). While environmental differences may play a role in some of the male excess risk, such differences are not sufficient to account for this consistent pattern [46].

The link between cancer risk and height within each sex suggests that this effect may cause at least part of the sex difference in cancer incidence [44,46]. Using equation (2.5), the expected sex difference based only on a cell number effect is 17% (i.e. HR₁₀ = 1.17), assuming a sex difference in height of 13 cm (175 cm versus 162 cm) and using the BMI exponent (b = 2). This value of 17% is in very close agreement with a statistical estimate of 19% for the effect of height on the sex differences in overall cancer risk [45], suggesting that (a) the sex difference in height, while contributing substantially to the sex difference in cancer risk, fails to account for the majority of the effect, and (b) the effect of height on the sex difference in overall cancer risk can be entirely explained by a cell number difference.

Domestic dogs also show higher rates of cancer in males. A 73% higher rate in males, averaged across the five most common cancer types (excluding mammary gland cancer), was found in non-neutered animals [47]. The average sexual dimorphism across breeds is similar to that seen in humans, ranging from an average of about 1.04 in small dogs to 1.08 in large dogs for shoulder height [48], so as in the case of humans, cell number changes cannot account for most of the effect.

(e). Genetics, height and cancer risk

The height variation typically observed in human populations has a large genetic component, raising the possibility of height variation appearing as cancer-causing variation. While the effect per height locus is generally expected to be small, caution is needed in interpreting the results of ever larger (and hence more powerful) genome-wide association studies (GWAS). Recent genetic analyses have indeed identified loci associated with height variation that link to testicular germ-cell tumour [49], breast cancer [50], post-menopausal breast cancer and colorectal cancer [51], and prostate cancer [52]. Adherence to the indirect-effect hypothesis suggests that these height effect loci are having a pleiotropic effect on cancer risk; however, the direct-effect hypothesis, which is strongly supported by the present analysis, leads to the expectation that genetic height variation affects cancer risk only through its effect on height, and as such provides little or no new insight into cancer risk.

(f). Body mass index and height

A recent assessment [21] of the link between obesity, as measured by BMI, and cancer risk observed that obesity is associated with many metabolic and endocrine changes, and that the strongest evidence implicates sex hormone metabolism and chronic inflammation in obesity related cancer. Given the hypothesis that the effect of height on cancer is primarily mediated via cell number, then the effects of obesity and height should be uncorrelated. In contrast, the indirect-effect hypothesis implicating chronic exposure to insulin and IGF-I predicts that the two effects would be correlated [30]. Excluding the subdivided data for breast cancer in women and for oesophageal and lung cancers (where there are no directly comparable estimates), there is no correlation evident in women (r = −0.024, d.f. = 16, p = 0.92 ns) or men (r = 0.328, d.f. = 14, p = 0.21 ns) (electronic supplementary material, figure S1).

4. Discussion

In the first quantitative test of the direct-effect hypothesis in which human height is viewed as a proxy for cell number, it has been shown that data from four large-scale cancer surveillance projects [13,14,16,17] linking height with cancer risk generally match very closely to expectation. This predicted effect of height due only to changes in cell number versus the observed HR₁₀ values for overall cancer risk was 1.13 versus 1.12 for women and 1.11 versus 1.09 for men, and, combined across the sexes, a significant height effect was found for 18/23 cancer categories examined. This result has important consequences. First, it provides further validation of the model of multistage carcinogenesis which is founded on the assumption that more cells will lead to an increased cancer risk. As such, it reinforces the view that the absence of a body size/cancer risk among species [3] requires an adaptive explanation (i.e. that cancer suppression is an evolving trait [5,6]). Second, it provides an important null hypothesis for understanding the height–cancer risk associations observed across different cancers in humans, since both a stronger and a weaker than expected dependence of cancer risk on height suggest that additional factors may be acting. For example, 2 of the 18 cancers occurring in both sexes (and none of the five sex-specific cancers) had HR₁₀ estimates (combined across the sexes) above the upper bound of the expected range (approx. 1.19): thyroid cancer (1.26) and melanoma (1.24) (electronic supplementary material, table S1).

One possible explanation of an enhanced effect of height on cancer risk is an increased cell division rate in tall individuals [22], possibly stemming from the relationship between adult IGF-I levels and height. Consistent with this proposal is the observation noted above that the very low cancer rate in individuals with Laron syndrome (who have an IGF-I deficiency and short stature) may be due to the effects of both reduced cell number and a reduced rate of cell division. Any link between cell division rate and cancer is expected to be most apparent in tissues that have the highest values of M (the number of driver mutations; see equation (2.6)), since M acts to amplify effect of a change in cell division rate. A high M is expected in tissues that are large and divide continuously throughout life, such as the skin, since as a result they have a high lifetime risk of somatic mutation [5,6]. It was shown that a 2% increase in the cell division rate per 10 cm gain in height (mediated through an increase in IGF-I) could probably account for the excess risk of melanoma. Unlike the cell number effect, which is not amenable to any therapeutic control since cell number cannot be changed, if high adult levels of IGF-I are indeed implicated in some of the increased cancer risk (due to increased cell division), then in extreme cases it may be possible to therapeutically ameliorate the effect.

This cell division rate explanation seems unlikely to apply to thyroid cancer, which exhibited high variability in HR₁₀ among the studies, with very high values found only in the Korean study [14]. Given this geographical variability, and the high mean HR₁₀, the strong height effect warrants further investigation, especially since thyroid cancer is close to three times as common in women as in men (see [46]). Notwithstanding the variability in thyroid cancer rates, the values of HR₁₀ were generally consistent across the different geographical populations tracked in the studies examined (4 in women, 3 in men).

The sex difference in overall cancer rate was also shown to be greater than expected based on cell number differences. This effect can only account for about one-third of the increased male cancer risk, in agreement with a previous independent statistical estimate [45].

It is also important to understand why a few cancers showed no apparent relationship to height. Of the 18 cancers scored in both sexes, only four showed no significant increase with height in either sexes (pancreas, oesophagus, stomach and mouth/pharynx; figure 2) and showed no significant increase in the combined two-sex estimate, and of five sex-specific cancers, one showed no significant increase (cervix) (electronic supplementary material, table S1). It is possible that in these tissues cell numbers do not scale with body size, but this seems unlikely. Another possibility is that the underlying pattern may be masked by significant associations of these cancers with environmental factors, a possibility previously suggested by Albanes [53] to account for the apparent absence of a height effect in organs affected by smoking. Indeed, the lung cancer HR₁₀ in individuals who smoked is significantly less (in the two-sex estimate) than the association seen in never-smokers (electronic supplementary material, table S1). It is notable that the risk of cervical cancer is strongly increased by HPV infection [54], and a range of environmental factors are known to influence the risk of gastric cancers (see [55]). The potential role of infection, especially early in life, in reducing the height–cancer link may also be important in this context. For example, exposure to Helicobacter pylori early in life is associated with poor childhood growth, and this effect could contribute to the absence of a positive height link to gastric cancer [28]. However, for the present, the question of why some cancers are exceptional in showing no apparent relationship to height must remain an open one.

Breast size is not usually considered a risk factor for breast cancer; however, in contrast, breast cancer is significantly associated with height (HR₁₀ = 1.15). However, there is now substantial evidence that increasing breast size does increase risk (see [56]), especially when the baseline measurement is made in young, relatively lean women [57].

The indirect hypothesis is often based on the assumption that height is a proxy for early life events [19,28,29], leading to an emphasis on the importance of childhood nutrition, psychosocial stress and illness. While the indirect hypothesis may be relevant in some situations, the close fit of data to expectations derived from changes in cell number using a model of multistage carcinogenesis indicates that the increased cancer risk associated with height is due primarily to an increase in cell number. This direct effect of cell number on the risk of oncogenic somatic mutations should be seen as the ‘null’ against which data should be compared before invoking additional factors beyond height itself. One possible secondary effect implicated in the case of melanoma is an increased rate of cell division during adult life, an effect that under the multistage model is, like increased cell number, expected to lead to an increase in oncogenic somatic mutations.

Data accessibility

All data are published elsewhere and summarized in the online electronic supplementary material.

Competing interests

I have no competing interests.

Funding

I received no funding for this study.