Bayesian latent time joint mixed-effects model of progression in the Alzheimer's Disease Neuroimaging Initiative

Abstract

Introduction

We characterize long-term disease dynamics from cognitively healthy to dementia using data from the Alzheimer's Disease Neuroimaging Initiative.

Methods

We apply a latent time joint mixed-effects model to 16 cognitive, functional, biomarker, and imaging outcomes in Alzheimer's Disease Neuroimaging Initiative. Markov chain Monte Carlo methods are used for estimation and inference.

Results

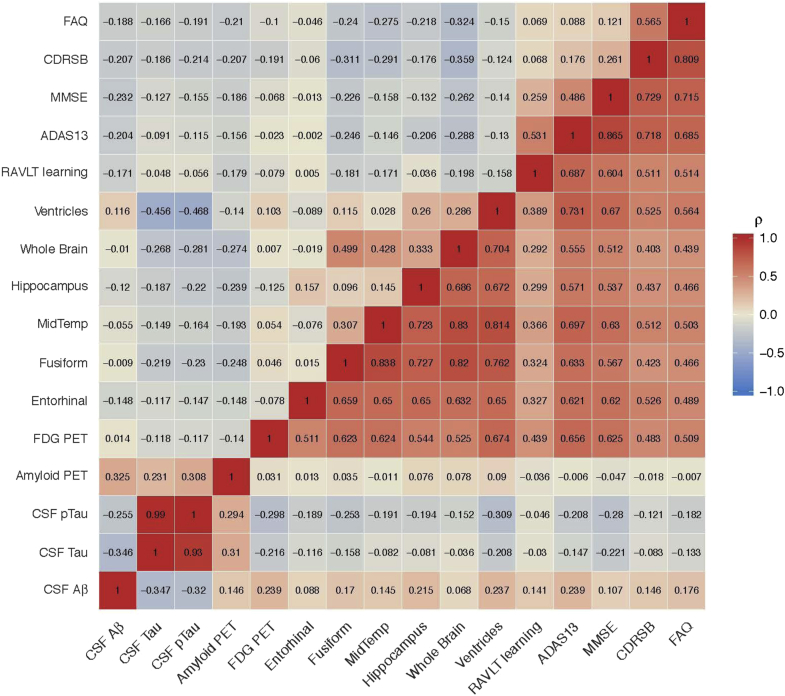
We find good concordance between latent time and diagnosis. Change in amyloid positron emission tomography shows a moderate correlation with change in cerebrospinal fluid tau (ρ = 0.310) and phosphorylated tau (ρ = 0.294) and weaker correlation with amyloid-β 42 (ρ = 0.176). In comparison to amyloid positron emission tomography, change in volumetric magnetic resonance imaging summaries is more strongly correlated with cognitive measures (e.g., ρ = 0.731 for ventricles and Alzheimer's Disease Assessment Scale). The average disease trends are consistent with the amyloid cascade hypothesis.

Discussion

The latent time joint mixed-effects model can (1) uncover long-term disease trends; (2) estimate the sequence of pathological abnormalities; and (3) provide subject-specific prognostic estimates of the time until onset of symptoms.

1. Introduction

It is important to determine the long-term dynamics of markers of Alzheimer's disease (AD) to better understand disease progression and to identify the ideal timing of potential interventions and preventative approaches [1]. Long-term dynamics are especially crucial for neurodegenerative diseases such as Parkinson's disease and AD, as therapeutic interventions are more likely to be effective in the earliest disease stages [2]. Patterns of disease progression can be explored in data sets capturing the natural history of markers of AD. Such data sets are longitudinal, in the sense, that they contain repeated measurements at multiple time points on multiple individuals. The main difficulty in deriving models of disease progression from such data sets is that individuals progress to different stages of disease at different ages and the age of disease onset is generally unknown. The onset of symptoms of AD may vary from 40 to 80 years of age, and the pathology may evolve over decades. Moreover, the onset of the disease pathology does not correspond with the onset of the symptoms [3].

Many methods exist for estimating trajectories from longitudinal observations of individuals over a given biologically common time span. For example, generalized linear or nonlinear mixed-effects models [4], [5] can model repeated measures based on time from a given event (e.g., birth or administration of an intervention). A reference time (point of origin) is required to fit these mixed-effects models, which may be implied by the experimental design. However, in studies of diseases that occur over long periods of time, we often sample individuals at different stages of disease and observe short-term longitudinal “snapshots” [6] of disease trajectories. Epidemiological studies with biologically heterogeneous subpopulations might not have a manifest biological event, which could serve as a reference time common to all subjects. Using traditional longitudinal models would require registering the data for each individual to a common event before analysis. We focus on the situation where such a common reference event is unknown and the estimation of “latent disease time” is required.

The Alzheimer's Disease Neuroimaging Initiative (ADNI) is a multicohort longitudinal study in which volunteers diagnosed as cognitively healthy or with various degrees of cognitive impairment have been followed up since 2005 [7]. The ADNI battery includes serial neuroimaging, cerebrospinal fluid (CSF), and other biomarkers, as well as clinical and neuropsychological assessments. Participants returned for repeated assessments after 6 months, 1 year, and every year thereafter. Time of onset of dementia, a potential reference “time zero”, is recorded for subjects with or transitioning to dementia, but these reference times are subjective and may be unreliable. Furthermore, subjects who are cognitively normal (CN) or with mild cognitive impairment may not be followed up long enough to observe clinical transitions.

A primary motivation for our work was to derive a data-driven version of the progression curves hypothesized by Jack et al. [8], [9]. They pointed out that individual biomarkers develop on their own time course and do not become abnormal simultaneously. They proposed a long-term model of the AD pathological cascade and specifically hypothesized the trajectory of several key biomarkers during the decades preceding the onset of dementia symptoms. The hypothesized figure (Figure 2 in Jack et al [8]) has been highly influential in the field of AD research. This figure shows the key markers of disease progressing on a common vertical scale from normal to abnormal, with clinical disease stage on the horizontal scale. Ideally, one would test the hypothesized model of Figure 2 in [8] by enrolling a large cohort of CN subjects and by collecting biomarkers, cognitive, and functional assessment results for decades. The subjects who progress to AD in such a study could be used to model the long-term biomarker progression of the disease. Until such a study could be conducted, we are limited to analyze relatively short-term studies such as ADNI.

Mixed-effects models incorporating fixed effects and subject-specific random effects have been used to study the Alzheimer's Disease Assessment Scale–Cognitive subscale [10], [11], the principal cognitive assessment tool in Alzheimer's dementia studies. Schulam et al. developed a spline model that incorporates longitudinal clustering and modeling of individual level effects to investigate trajectories of scleroderma markers [12]. Although these models analyzed each measure separately, adequately characterizing disease progression benefits from the modeling of multiple outcomes simultaneously, especially if trajectories across multiple measures are correlated and if the relative timing of changes in each outcome is informative about disease progression. Young et al (2014) [13] used an event-based probabilistic model to determine the ordering of changes in longitudinal biomarker measures. This method characterized longitudinal biomarker trajectories in a discrete framework rather than a continuous one. Donohue et al (2014) [6] proposed a semiparametric regression model in a multivariate framework to characterize the longitudinal trajectories of a set of cognitive, CSF, and neuroimaging-based biomarkers. Although this approach modeled multiple outcomes in a unified framework by introducing an individual-specific latent time shift parameter that is shared across outcomes, the method did not incorporate covariates for fixed effects or consider the correlation among outcomes.

We apply a latent time joint mixed-effects model (LTJMM) to characterize biomarker trajectories in disease progression [14]. This model extends mixed-effects models to include an individual-specific latent time shift, which is shared across all of an individual's outcomes and represents the extent of their long-term disease progression. Although similar to others (e.g., Jedynak et al [15] and Donohue et al [6]), this model also accommodates covariates for fixed-effects and is implemented in a Bayesian framework. The Bayesian framework allows flexible but rigorous interrogation of the posterior distribution to make inferences about long-term disease dynamics and the potential propagation of treatment effects from early biomarkers to downstream cognitive and functional measures. Jointly modeling all the outcomes in a multivariate framework not only considers the inter- and intra-subjects variations but also takes into account the associations between outcomes.

2. Methods

2.1. Study data

Data were acquired from the ADNI database, which has been tracking outcomes of volunteers diagnosed as CN, subjective memory concern, early mild cognitive impairment, late mild cognitive impairment (LMCI), and mild-to-moderate dementia (AD) since 2005, and contain demographic and clinical information from 55 research centers in the United States and Canada. The main goal of ADNI has been to test whether the ADNI battery such as serial magnetic resonance imaging (MRI), positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessments can be combined to measure the progression of MCI and early AD.

For the current analysis, we consider 16 outcomes that have been known to be associated with the progression of AD. The outcomes include CSF tau and amyloid-β (Aβ) 1–42; phosphorylated tau (p-tau); PET imaging of amyloid deposition and glucose metabolism in the brain; FreeSurfer volumetric MRI summaries of the hippocampus, whole brain, entorhinal cortex, ventricles, fusiform gyrus, and middle temporal gyrus; the 13-item Alzheimer's Disease Assessment Scale; the Mini–Mental State Examination; the Functional Activities Questionnaire; the Rey Auditory Visual Learning Test, and the Clinical Dementia Rating Scale Sum of Boxes. More details on these measures in ADNI are available in Petersen et al (2010) [7]. Fixed-effect covariates for each outcome include demographic factors: age, sex, education, and apolipoprotein E ɛ4 (APOE ɛ4) carrier status (presence of an APOE ɛ4 allele). Diagnostic category is a somewhat subjective interpretation of the clinical presentation (excluding CSF and imaging data) of the individuals by their physician and hence was not included as a covariate in our model. As will be demonstrated later, one advantage of our model is that latent time estimates could provide a continuous alternative to diagnosis.

Our analysis aims to compare the long-term trends of the outcomes on a comparable scale and make conclusions about the temporal ordering of their emergence. The quantile scale is commonly used to obtain a common scale. Therefore, before fitting our model, we first transformed the raw outcome measures into quantiles normalized to range from 0 (least severe) to 1 (most severe). Quantiles were calculated using the empirical cumulative distribution function by weighting according to the inverse proportion of observations from each diagnostic category for each outcome. Because the diagnostic groups are not represented equally, such a weighted quantile transformation allows an approximation of the quantiles from a sample with equal numbers of each diagnosis. The quantiles were then transformed by the inverse Gaussian quantile function. The resulting approximate z-scores will be used for model fitting.

2.2. Latent time joint mixed-effects model

Li et al (2017) [14] proposed the LTJMM to jointly model multivariate longitudinal data. In this work, we employ the LTJMM to provide smooth estimates of the longitudinal course of disease severity, assess the relationship between different markers, and further characterize evolution of disease markers in the progression of disease. We denote y_ijk as the outcome k observed at occasion j for individual i, where i = 1,…, n, j = 1,…, q_ik and k = 1,…, p. Suppose all outcomes are longitudinally measured continuous outcomes, the model is given by

$$y_{ijk}={\mathit{x}}_{ijk}^{\text{'}}{\mathit{\beta }}_k+{\gamma }_k\left(t_{ijk}+{\delta }_i\right)+{\alpha }_{0ik}+{\alpha }_{1ik}{t}_{ijk}+{\epsilon }_{ijk}\text{,}$$ (1)

where x_ijk represents a set of possibly time-varying covariates, and β_k and γ_k are the traditional coefficients for covariates and “long-term” progression time. The time shift δ_i is shared among outcomes for each subject, quantifying the progression of subject i relative to the population, and is assumed to follow ${\delta }_i\sim N\left(0,{\sigma }_{\delta }^2\right)$. The measurement error term ${\epsilon }_{ijk}\sim N\left(0,{\sigma }_k^2\right)$ accounts for outcome-specific variance. The parameters α_0ik and α_1ik are the subject and outcome-specific random intercept and slope. The model with multivariate random effects has the advantage of reflecting dependency among outcomes. However, fitting the model with univariate random effects is computational faster and also has advantages in practice. In this study, we will explore assuming the random effects follow both univariate and multivariate Gaussian distributions with zero means. In our application, all the outcomes are oriented to be increasing with time, and thus we assume γ_k > 0, k = 1, 2, …, p. We place a constraint on Eqn (1) to ensure identifiability: $\sum _{k=1}^p{\alpha }_{0ik}=0$ for all individuals i = 1, 2, …, n.

Estimation and inference are obtained using a Bayesian method. Results of parameter estimates are reported as posterior mean and 95% credible intervals. Analyses are implemented in Stan [16]. We compute the deviance information criterion [17], the widely applicable information criterion [18], [19], [20], and the leave-one-out cross-validation information criterion [21], [22] for model comparison. We refer to Li et al (2017) [14] for more details of the LTJMM and Bayesian implementation. The Stan code for model specifications and related tools for estimation and prediction are available as an R package from https://bitbucket.org/mdonohue/ltjmm.

3. Results

3.1. Exploratory analysis

Our data consist of a subset of 1554 participants that were diagnosed at their first visit with CN ($N=404$, 26%), subjective memory concern ($N=105$, 6.76%), early mild cognitive impairment ($N=285$, 18.34%), LMCI ($N=487$, 31.34%), and AD ($N=273$, 17.57%). There were 702 (45.17%) female subjects in which 288 were APOE ɛ4 carriers. Maximum follow-up is currently as long as about 11 years. Descriptive statistics for the raw values of 16 outcomes by baseline diagnostic category and the length of follow-up by outcome are provided in Supplementary Tables S0 and S1.

The data are grouped by individual and sorted by age at observation time. Raw values are transformed into a quantile scale using a weighted empirical cumulative distribution function. The raw values that correspond to the resulting quantiles are provided in Supplementary Table S2. Fig. 1 (top) shows the longitudinal measurements of the 16 outcomes over age (in years) for all participants. Additional exploratory graphical analyses are available in Supplementary Material (see Supplementary Figs. S1 and S2).

Fig. 1.

Subject-level observed and predicted severity. The top panel shows spaghetti plots of the observed quantiles of each outcome from all subjects in the Alzheimer's Disease Neuroimaging Initiative with respect to their age over time. The bottom panel shows modeled trajectories for these same subjects from the fitted LTJMM with respect to the sum of age and estimated latent time, δ. The colors indicate diagnostic severity at first observation, from cognitively normal (blue) through dementia (red). Abbreviations: PET, positron emission tomography; CSF, cerebrospinal fluid; P-tau, phosphorylated tau; Aβ, amyloid-β; RAVLT, Rey Auditory Visual Learning Test; MidTemp, middle temporal gyrus; FDG, fluorodeoxyglucose; ADAS13, Alzheimer's Disease Assessment Scale (13-item version); MMSE, Mini–Mental State Examination; CDRSB, Clinical Dementia Rating Scale Sum of Boxes; FAQ, Functional Activities Questionnaire; LTJMM, latent time joint mixed-effects model.

3.2. Latent time joint mixed-effects model

The LTJMMs with univariate and multivariate Gaussian random effects (denoted as model I and II) were fitted, respectively. All the transformed outcomes were modeled as Gaussian with identity link. The priors specified for model parameters are as discussed in Section 2.2. The estimated potential scale reduction factors $\hat{R}$ are below 1.1 for all parameters, indicating successful convergence. Table 1 summarizes the posterior estimates of the key model parameters based on posterior mean and 95% credible intervals. Table 2 summarizes the model comparison results. Model II is chosen as the best model with lower deviance information criterion, widely applicable information criterion, and leave-one-out cross-validation information criterion; and model II has smaller value of effective number of parameters than model I, indicating less model complexity.

Table 1.

Posterior mean and 95% credible intervals of parameters for the proposed LTJMM it to 16 outcomes from the ADNI

Parameter	Posterior mean (95% CI)	Parameter	Posterior mean (95% CI)	Parameter	Posterior mean (95% CI)
Hippocampus		CSF tau		MidTemp
Intercept	−3.885 (−4.375, −3.358)	Intercept	−0.992 (−1.530, −0.454)	Intercept	−3.028 (−3.510, −2.486)
Age	0.054 (0.048, 0.059)	Age	0.015 (0.009, 0.021)	Age	0.043 (0.037, 0.048)
APOE ɛ4	0.353 (0.261, 0.448)	APOE ɛ4	0.475 (0.367, 0.579)	APOE ɛ4	0.291 (0.203, 0.386)
Sex	−0.303 (−0.390, −0.222)	Sex	0.095 (−0.002, 0.194)	Sex	-0.096 (−0.188, −0.011)
Education	−0.007 (−0.023, 0.008)	Education	−0.025 (−0.043, −0.008)	Education	−0.011 (−0.027, 0.005)
Latent time	0.056 (0.051, 0.063)	Latent time	0.025 (0.020, 0.030)	Latent time	0.058 (0.052, 0.064)
σ1	0.133 (0.130, 0.136)	σ7	0.147 (0.141, 0.154)	σ13	0.168 (0.165, 0.172)
ADAS13		CSF p-tau		RAVLT learning
Intercept	−1.038 (−1.490, −0.547)	Intercept	−0.818 (−1.341, −0.285)	Intercept	−0.416 (−0.869, 0.066)
Age	0.024 (0.019, 0.029)	Age	0.012 (0.006, 0.018)	Age	0.017 (0.011, 0.022)
APOE ɛ4	0.401 (0.327, 0.474)	APOE ɛ4	0.536 (0.430, 0.639)	APOE ɛ4	0.367 (0.292, 0.444)
Sex	−0.250 (−0.326, −0.179)	Sex	0.069 (−0.027, 0.168)	Sex	−0.262 (−0.336, −0.191)
Education	−0.051 (−0.065, −0.037)	Education	−0.025 (−0.042, −0.008)	Education	−0.044 (−0.058, −0.031)
Latent time	0.059 (0.054, 0.066)	Latent time	0.026 (0.021, 0.031)	Latent time	0.050 (0.044, 0.056)
σ2	0.326 (0.319, 0.332)	σ8	0.116 (0.111, 0.122)	σ14	0.659 (0.647, 0.671)
FDG PET		Whole Brain		MMSE
Intercept	−1.839 (−2.392, −1.281)	Intercept	−4.590 (−5.053, −4.095)	Intercept	−1.308 (−2.005, −0.534)
Age	0.028 (0.022, 0.034)	Age	0.063 (0.058, 0.068)	Age	0.030 (0.021, 0.037)
APOE ɛ4	0.411 (0.320, 0.498)	APOE ɛ4	0.231 (0.138, 0.321)	APOE ɛ4	0.584 (0.469, 0.700)
Sex	−0.178 (−0.271, −0.089)	Sex	−0.198 (−0.283, −0.115)	Sex	−0.262 (−0.379, −0.149)
Education	−0.023 (−0.039, −0.006)	Education	−0.005 (−0.021, 0.011)	Education	−0.097 (−0.118, −0.076)
Latent time	0.052 (0.046, 0.058)	Latent time	0.052 (0.047, 0.058)	Latent time	0.083 (0.075, 0.093)
σ3	0.292 (0.282, 0.303)	σ9	0.139 (0.136, 0.141)	σ15	1.051 (1.033, 1.070)
Amyloid PET		CDRSB		Fusiform
Intercept	−0.372 (−0.913, 0.185)	Intercept	−0.624 (−1.518, 0.353)	Intercept	−2.742 (−3.229, −2.234)
Age	0.001 (−0.005, 0.007)	Age	0.013 (0.003, 0.023)	Age	0.040 (0.035, 0.046)
APOE ɛ4	0.697 (0.594, 0.803)	APOE ɛ4	0.764 (0.609, 0.909)	APOE ɛ4	0.273 (0.184, 0.365)
Sex	0.142 (0.042, 0.240)	Sex	−0.309 (−0.466, −0.162)	Sex	−0.089 (−0.181, 0.002)
Education	−0.007 (−0.025, 0.010)	Education	−0.079 (−0.108, −0.052)	Education	−0.017 (−0.034, −0.001)
Latent time	0.030 (0.025, 0.036)	Latent time	0.120 (0.110, 0.133)	Latent time	0.050 (0.044, 0.056)
σ4	0.282 (0.269, 0.296)	σ10	0.662 (0.650, 0.674)	σ16	0.185 (0.181, 0.189)
CSF Aβ		Entorhinal		Standard deviation of latent time
Intercept	−2.131 (−2.912, −1.307)	Intercept	-2.295 (−2.810, −1.773)	σδ	10.679 (9.625, 11.602)
Age	0.020 (0.011, 0.029)	Age	0.034 (0.029, 0.039)
APOE ɛ4	0.915 (0.776, 1.057)	APOE ɛ4	0.356 (0.262, 0.448)
Sex	−0.142 (-0.275, −0.010)	Sex	0.431 (0.344, 0.521)
Education	−0.005 (-0.029, 0.019)	Education	−0.035 (−0.051, −0.020)
Latent time	0.046 (0.039, 0.055)	Latent time	0.049 (0.044, 0.055)
σ5	0.416 (0.392, 0.441)	σ11	0.345 (0.337, 0.353)
FAQ		Ventricles
Intercept	−2.382 (−3.337, −1.355)	Intercept	−4.954 (−5.439, −4.428)
Age	0.027 (0.016, 0.037)	Age	0.066 (0.061, 0.071)
APOE ɛ4	0.806 (0.646, 0.956)	APOE ɛ4	0.194 (0.098, 0.294)
Sex	−0.347 (−0.507, −0.195)	Sex	−0.343 (−0.435, −0.247)
Education	−0.064 (−0.093, −0.036)	Education	0.007 (−0.010, 0.024)
Latent time	0.125 (0.114, 0.138)	Latent time	0.047 (0.042, 0.053)
σ6	0.846 (0.830, 0.861)	σ12	0.058 (0.057, 0.059)

Abbreviations: ADNI, Alzheimer's Disease Neuroimaging Initiative; LTJMM, latent time joint mixed-effects model; APOE ɛ4, apolipoprotein E; PET, positron emission tomography; CSF, cerebrospinal fluid; P-tau, phosphorylated tau; Aβ, amyloid-β; RAVLT, Rey Auditory Visual Learning Test; MidTemp, middle temporal gyrus; FDG, fluorodeoxyglucose; ADAS13, Alzheimer's Disease Assessment Scale (13-item version); MMSE, Mini–Mental State Examination; CDRSB, Clinical Dementia Rating Scale Sum of Boxes; FAQ, Functional Activities Questionnaire.

Table 2.

Model comparison results for the LTJMMs under two different assumptions of random effects

Model	DIC	pDIC	WAIC	pWAIC	LOOIC	pLOOIC
I	72,346.68	26,374.40	72,040.75	21,073.00	78,708.15	24,406.70
II	66,244.56	23,652.62	66,177.87	19,339.56	71,038.37	21,769.81

Abbreviations: LTJMM, latent time joint mixed-effects model; DIC, deviance information criterion; WAIC, widely applicable information criterion; LOOIC, leave-one-out cross-validation information criterion.

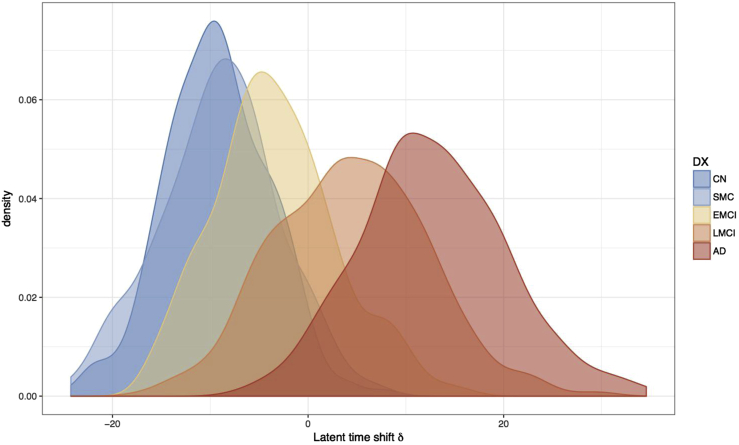
Fig. 1 shows the subject-level observations with respect to age (top) and predictions according to the sum of age and estimated latent time (bottom). From the observations, we notice that age explains variance in these outcomes. The bottom panel shows that the predictions provide a reasonable smooth of the observations, and latent time provides a reasonable ordering of individuals according to disease severity. The posterior mean (95% credible interval) for the standard deviation of latent time parameters is 10.679 (9.625 to 11.602) years, as shown in Table 1. Fig. 2 displays a density plot for the posterior mean of the subject-specific latent time by diagnosis at first ADNI visit. This figure indicates that the latent time estimates are temporally sorting individuals in a manner that is consistent with physician diagnosis, although diagnostic category is not included in the model. Latent time estimates provide a continuous alternative to diagnosis which is objectively derived from a comprehensive model of longitudinal measures of disease. Fig. 3 shows the posterior mean of correlation parameters for random intercepts (diagonal upper left) and random slopes (diagonal lower right), reflecting the inherent pairwise association between outcomes. We find that there are moderate or strong positive correlations of change between many outcomes. Most of the outcomes have weak correlations of random intercepts. Interestingly, change in fibrillar amyloid burden as assessed by 18F-florbetapir shows a moderate correlation with change in CSF tau (ρ = 0.310) and p-tau (ρ = 0.294) and weaker correlation with Aβ₄₂ (ρ = 0.176). In comparison to amyloid PET, change in volumetric magnetic resonance imaging summaries (e.g., ventricular volume) is more strongly correlated with cognitive measures (e.g., ρ = 0.176 for ventricles and Alzheimer's Disease Assessment Scale–Cognitive subscale). Evaluation of the model fit and the assumptions of latent time and random effects are available in Supplementary Material (see Supplementary Figs. S3–S6).

Fig. 2.

Distribution of the subject-specific latent time shifts. The estimated latent time shifts are colored by baseline diagnostic group, a variable not included in the model. This plot suggests that the time shifts are well aligned and consistent with diagnostic criteria. The density plot also demonstrates that there is much overlap of the diagnostic criteria with respect latent time. Abbreviations: CN, cognitively normal; SMC, subjective memory concern; EMCI, early mild cognitive impairment; LMCI, late mild cognitive impairment; AD, probable Alzheimer's disease with mild-to-moderate dementia.

Fig. 3.

Posterior mean correlations among random intercepts (diagonal upper left) and random slopes (diagonal lower right). Abbreviations: PET, positron emission tomography; CSF, cerebrospinal fluid; P-tau, phosphorylated tau; Aβ, amyloid-β; RAVLT, Rey Auditory Visual Learning Test; MidTemp, middle temporal gyrus; FDG, fluorodeoxyglucose; ADAS13, Alzheimer's Disease Assessment Scale (13-item version); MMSE, Mini–Mental State Examination; CDRSB, Clinical Dementia Rating Scale Sum of Boxes; FAQ, Functional Activities Questionnaire.

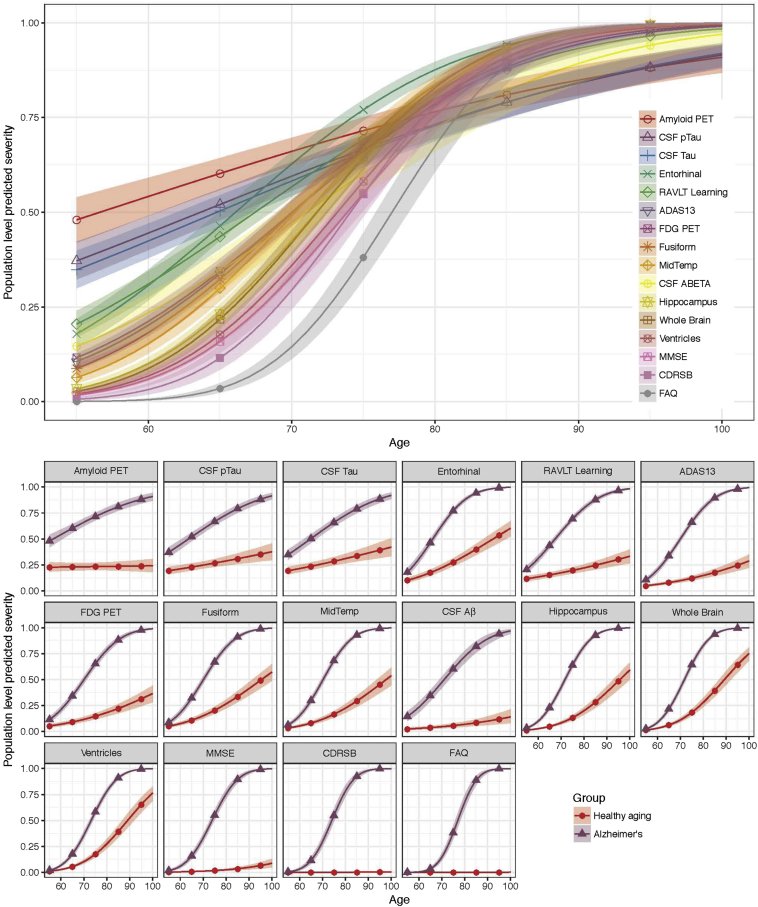
The average “long-term” predicted trajectories of severity are displayed in Fig. 4. The depicted curves are for female APOE ɛ4 carriers with the mean education and the average age in the LMCI diagnostic group. The predicted trajectories indicate the ordering of disease progression for the 16 outcomes. By considering the severity level 0.5 as a benchmark, the ordering of outcomes is as described in the legend of Fig. 4 (upper panel). For example, amyloid PET and CSF p-tau attain severity 0.5 about 10 or more years earlier than Clinical Dementia Rating Scale Sum of Boxes and Functional Activities Questionnaire. The bottom panel shows the same trajectories for progressive Alzheimer's with contrasting hypothetical trajectories for healthy aging. To obtain the hypothetical estimates for healthy aging, the effect of latent time is forced to be zero to isolate the effect of age.

Fig. 4.

Modeled population-level severity. The top panel shows the modeled average trajectories. The depicted evolution is for female APOE ɛ4 carriers with the ADNI mean education and the average age of the LMCI group. The bottom panel shows the same trajectories for progressive Alzheimer's (blue triangles) with contrasting trajectories for healthy aging (red dots). For the latter, the effect of latent time is forced to be zero to isolate the effect of age. Abbreviations: PET, positron emission tomography; CSF, cerebrospinal fluid; P-tau, phosphorylated tau; Aβ, amyloid-β; RAVLT, Rey Auditory Visual Learning Test; MidTemp, middle temporal gyrus; FDG, fluorodeoxyglucose; ADAS13, Alzheimer's Disease Assessment Scale (13-item version); MMSE, Mini–Mental State Examination; CDRSB, Clinical Dementia Rating Scale Sum of Boxes; FAQ, Functional Activities Questionnaire; ADNI, Alzheimer's Disease Neuroimaging Initiative; APOE ɛ4, apolipoprotein E ε4; LMCI, late mild cognitive impairment.

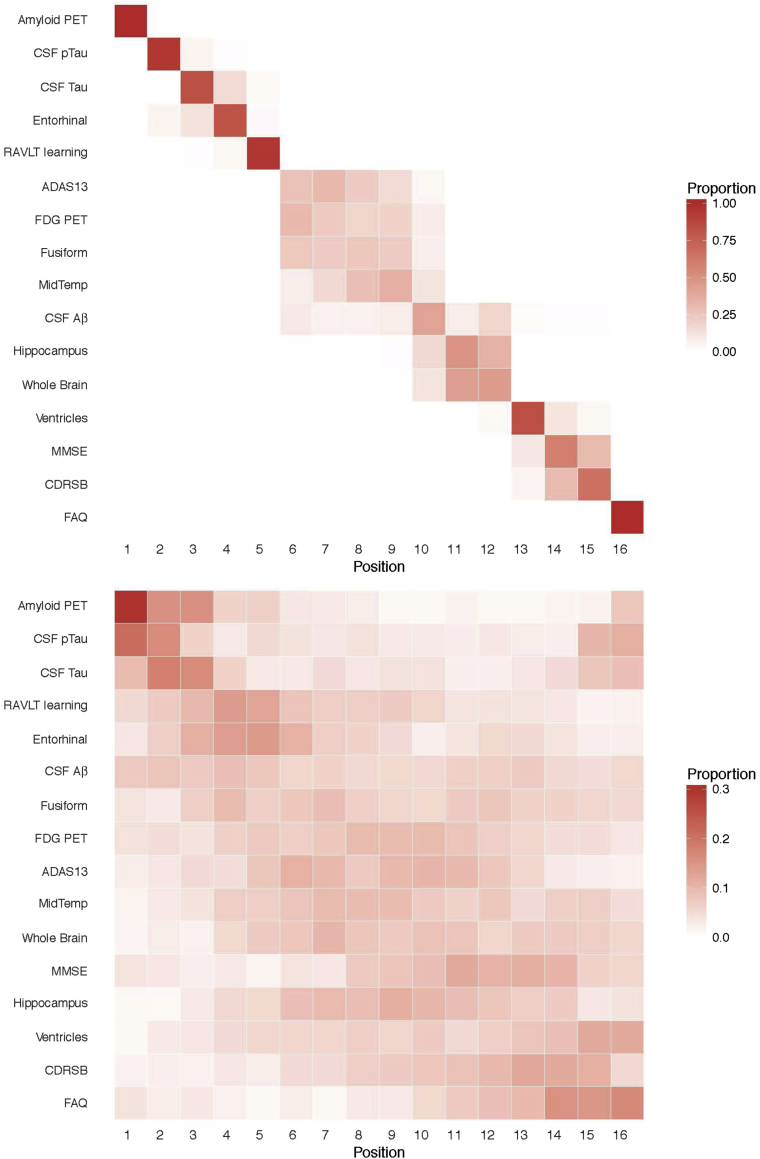
In Fig. 5, each entry of the positional variance diagram represents the proportion of samples in which a particular outcome appears in a particular position in the central ordering, ranging from 0 in white to 1 in red. In Fig. 5 (top), we study the positional variance of ordering for the female APOE ɛ4 carriers with the mean education and the average age of the LMCI group inferred by population-level predictions of the LTJMM based on the posterior samples of each parameter, followed by computing the central ordering for each sample. A red diagonal corresponds to high certainty in the ordering of outcomes, such as amyloid PET, CSF p-tau, and tau. The off-diagonal shaded blocks in this diagram indicate that the outcomes permute, indicating uncertainty in the estimation of central ordering. In Fig. 5 (bottom), we obtained the ordering of outcomes for APOE ɛ4 carriers in the data from the subject-level predictions of the LTJMM. The figure represents the distribution of the estimated subject-level ordering of outcomes. We also conducted a simulation study to assess the model performance and to find out how often the orderings of markers could be correctly estimated. The estimated marker orderings for the simulations demonstrated that our method could recover the true ordering reasonably well. For example, for 84% of the simulated data sets the model correctly identified the first marker. For details of the simulation study, please refer to Supplementary Material (see Supplementary Note S1, Figure S8, Table S3).

Fig. 5.

Positional variance diagram of the central ordering. The x-axis is the event position. The top panel shows the population-level positional variance diagram of the central ordering for the female APOE ɛ4 carriers. The bottom panel shows the subject-level positional variance diagram of the central ordering for the APOE ɛ4 carriers. Abbreviations: PET, positron emission tomography; CSF, cerebrospinal fluid; p-tau, phosphorylated tau; Aβ, amyloid-β; RAVLT, Rey Auditory Visual Learning Test; MidTemp, middle temporal gyrus; FDG, fluorodeoxyglucose; ADAS13, Alzheimer's Disease Assessment Scale (13-item version); MMSE, Mini–Mental State Examination; CDRSB, Clinical Dementia Rating Scale Sum of Boxes; FAQ, Functional Activities Questionnaire; APOE ɛ4, apolipoprotein E ε4.

4. Discussion

In this work, we apply an LTJMM to characterize the long-term disease dynamics from cognitively healthy to dementia using data from the ADNI. The LTJMM provides two key advantages over standard mixed-effects models for applications of multicohort studies of neurodegenerative disease. The first advantage is the ability to estimate disease course across a wide spectrum of the disease across the multiple cohorts or diagnostic groups. Fig. 4 demonstrates this ability and conveys a pathological cascade, which is consistent with prevailing theories: amyloid and tau abnormalities followed by cortical thinning, cognitive and FDG PET deficits, brain atrophy, and finally, loss of function. The lower panel of Fig. 4 shows the same estimates for progressive disease compared with estimates of hypothetical disease-free aging. The feature of the model, which allows this modeling across diagnostic categories, is the individual-specific parameters for latent disease time. We find that these parameters act as a continuous variable underlying the categorical diagnosis (Fig. 2) and allows for robust estimation of average pattern of disease progression as hypothesized by Jack et al. [8], [9]. The second advantage of the LTJMM is the ability to model several outcomes at once and inspect their correlations in level (intercepts) and rates of change (slopes), as demonstrated in Fig. 3. In this parameterization, the correlations are not dependent on observation or latent time. This provides easy to interpret summary measures utilizing all the data but might mask some temporal dynamics in correlation. Future work will explore this model extension.

The model is a parsimonious extension of joint mixed-effect models, adding subject-specific latent time parameters. Single-outcome mixed-effect models are the ubiquitous workhorse of longitudinal data analysis. They are robust, flexible, and their assumptions and parameterizations are generally well understood. The LTJMM shares these qualities, and the additional assumptions required for latent time are relatively weak. More flexible temporal trends (e.g., polynomial splines) are possible within the model framework but do not seem supported by ADNI data (Fig. 1).

In general, our findings are consistent with the amyloid cascade hypothesis. We find evidence of amyloid abnormalities first. The seemingly unexpected ordering of CSF Aβ might be explained by the higher within- and between-individual variability observed with CSF Aβ_1–42, as seen in Fig. 1. Consistent with our finding, Bouallègue et al. [23] found that amyloid PET appeared “more powerful than CSF markers for AD grading and MCI prognosis in term of cognitive decline and AD conversion” in an analysis of ADNI data. It is likely that other common CSF summaries, such as the ratio of tau to Aβ_1–42, might demonstrate a relatively earlier appearance of abnormality than Aβ alone. Not surprisingly, functional impairment occurs last. In between amyloid and function, there is much overlap. One reason for this is the apparent heterogeneity of disease progression. That is, not every individual follows the average disease trends. The model can be used to explore subgroups that demonstrate disease dynamics that differ from the average pattern. Future work will formalize this concept with mixture modeling. We will also leverage the model to improve prognostic prediction and to identify clinical trial populations and individuals most likely to benefit from a given intervention.

Research in Context.

• 1.Systematic review: The authors reviewed the existing literature using traditional sources for biomedical and statistical research journal articles, with search terms “Alzheimer's disease,” “joint mixed-effects models,” “long-term disease dynamics,” “longitudinal biomarker trajectories,” and “multicohort longitudinal data”.
• 2.Interpretation: We characterize long-term disease dynamics from cognitively healthy to dementia by applying a latent time joint mixed-effects model. The model can uncover long-term disease trends, estimate the sequence of pathological abnormalities, and provide subject-specific prognostic estimates of the time until onset of symptoms. Our findings are in general agreement with prevailing theories of the Alzheimer's disease amyloid cascade.
• 3.Future directions: The model can be applied to explore subgroups that demonstrate disease dynamics that differ from the average pattern. Future work will formalize this concept with mixture modeling. We will also leverage the model to improve prognostic prediction and to identify populations expected to experience the maximum benefit from a given intervention.