Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2018 Oct 4;122(43):24917–24923. doi: 10.1021/acs.jpcc.8b07283

Angle-Independent Polariton Emission Lifetime Shown by Perylene Hybridized to the Vacuum Field Inside a Fabry–Pérot Cavity

Jürgen Mony 1, Manuel Hertzog 1, Khushbu Kushwaha 1, Karl Börjesson 1,*
PMCID: PMC6234983  PMID: 30450150

Abstract

graphic file with name jp-2018-07283f_0006.jpg

The formation of hybrid light–matter states in optical structures, manifested as a Rabi splitting of the eigenenergies of a coupled system, is one of the key effects in quantum optics. The hybrid states (exciton polaritons) have unique chemical and physical properties and can be viewed as a linear combination of light and matter. The optical properties of the exciton polaritons are dispersive by nature, a property inherited from the photonic contribution to the polariton. On the other hand, the polariton lifetime in organic molecular systems has recently been highly debated. The photonic contribution to the polariton would suggest a lifetime on the femtosecond time scale, much shorter than experimentally observed. Here, we increase the insights of light–mater states by showing that the polariton emission lifetime is nondispersive. A perylene derivative was strongly coupled to the vacuum field by incorporating the molecule into a Fabry–Pérot cavity. The polariton emission from the cavity was shown to be dispersive, but the emission lifetime was nondispersive and on the time scale of the bare exciton. The results were rationalized by the exciton reservoir model, giving experimental evidence to currently used theories, thus improving our understanding of strong coupling phenomena in molecules.

Introduction

Strong exciton–photon coupling has manifested itself in recent years as a unique method for tuning chemical, physical, and optical properties of organic molecules as well as inorganic compounds. Vacuum fluctuations in surface plasmons or Fabry–Pérot (FP) cavities provide a large enough electromagnetic field to enter the strong exciton–photon coupling regime without an external electromagnetic field needed, resulting in a myriad of possible applications. When a molecular exciton couples strongly to the vacuum field, new hybrid polaritonic states are formed.1−4 The physical and chemical properties of the formed hybrid states can be radically different from those of the uncoupled molecules. A vast variety of molecules have been coupled to vacuum fluctuations, e.g., J-aggregates,5,6 crystals,7 two-dimensional materials,8,9 carbon nanotubes,10,11 liquid crystals,12 single molecule,13 nanofluidic cavity,14 nanowires,15 proteins,16 and even living bacteria.17 Applications of strongly coupled systems have previously been focused on polaritonic lasing,18 Bose–Einstein condensates,19 quantum computing,20 higher-order harmonic generation,21 organic light-emitting diode devices,22 and quantum fluids of light.23 Recent investigations have shown changes in transport,24,25 coherence length,26 chemical rate constant,27 reactivity landscapes,28 rate constants of energy transfer,29−31 phase transition,32 quantum yield,33 photo-oxidation,34 IR emission,35 and selective manipulation of excited states,36 showing an incredible scope of possible uses of the phenomena. Furthermore, recent theoretical investigations have shown possible changes in photochemical reactions,37 charge transport,38 singlet fission,39 and chemical reactions.40,41

A characteristic feature of polaritons is their dispersive behavior. The properties of polaritons are inherited from the molecular exciton and the cavity (Fabry–Pérot or plasmonic) used to create the polariton. In fact, the dispersivity of the system is often used to prove that the strong coupling regime is reached, and to determine the photonic/excitonic contribution to the polariton. The energy of the molecular exciton (Eexc) is inherently nondispersive, whereas the energy of the cavity resonance (Ec) depends on the angle of incidence (θ) and can be expressed as42

graphic file with name jp-2018-07283f_m001.jpg 1

where E0 is the energy of the cavity at normal incidence and neff is the effective refractive index. The dispersive behavior of the cavity resonance is inherited by the polaritonic states, and can be modeled by a coupled harmonic oscillator Hamiltonian. In this study, a molecule exhibiting two vibronic energy levels is coupled to a single cavity mode. The used Hamiltonian therefore contains two excitonic terms and one photonic term43

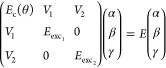graphic file with name jp-2018-07283f_m002.jpg 2

where α, β, and γ are the mixing coefficients of the system (Hopfield coefficients) and V1, V2 are the interaction potentials (the coupling strength divided by 2), which are proportional to the transition dipole moment of the coupled exciton and the square root of the molecular concentration. Solving the eigenvalues of the Hamiltonian yields the energy of each polaritonic branch, and solving the eigenvectors yields the photonic (|α|2) and excitonic (|β|2, |γ|2) weights for each branch.

In eq 2, the energy of the cavity is angle dependent; thus, the energy of the formed polaritonic states is also angle dependent. Consequently, both the magnitude and the envelope of absorption/emission of polaritons are strongly angle dependent, which has been verified on a number of occasions.44,45 However, less effort has been made toward examining the dispersivity of polariton lifetimes. Hitherto, only one report exists that examines the angular dependence of the polaritonic emission lifetime, arising from molecular excitons strongly coupled to the vacuum field. Using cyanine J-aggregates strongly coupled to the vacuum field in a significantly negatively detuned cavity at 20 K, no angular dependence of the polaritonic emission lifetime was detected. Theoretically, the lifetime of the polariton (τLP) is dispersive and can be expressed as a superposition of the lifetime of the electronically excited state of the molecule (τexc) and the lifetime of the photon inside the cavity (τc) weighted by the Hopfield coefficients

graphic file with name jp-2018-07283f_m003.jpg 3

At resonance, eq 3 suggests that the polariton lifetime is on the same time scale as the shortest component, i.e., the cavity (about 10 fs for the cavities used in this study). However, experimental results indicate a much longer lived polariton.33,46 A model in which the kinetics of populating the emissive lower polaritonic state is slower compared to the emission from the lower polaritonic state has explained this observation.47 The so-called exciton bath theory, where internal relaxation rather than the emissive properties of the lower polaritonic state govern the observed emission kinetics, suggests that the lifetime of emission cannot be calculated a priori. Having this picture in mind, eq 3 poorly captures the process and no angle dependence on the lifetime of emission is expected.

Here, we demonstrate experimentally that the lifetime of polaritonic emission is independent of the angle of emission, irrespective of cavity tuning. To do so, a Fabry–Pérot (FP) cavity consisting of two silver mirrors sandwiching a tetra-tert-butylperylene (ttb-perylene) containing polystyrene (PS) layer was constructed. We start by showing that the strong coupling regime is reached by examining the dispersive behavior of the transmission and steady-state emission of the cavities. Subsequently, the polaritonic emission lifetime as a function of emission angle was investigated, showing no dependence on the angle. Finally, time-resolved emission spectra (TRES) were recorded to prove that all emissive processes are captured, thus showing that the time resolution of our setup is high enough to capture the process. The experimentally shown independence of the polaritonic emission lifetime on emission angle is an important experimental verification of the current theoretical model, in which the bottleneck of polariton emission is the rate of polariton population.47

Materials and Methods

Cavity Preparation

The cavities were prepared on glass substrates, which were cleaned by sonicating them first in an alkaline solution (0.5% Hellmanex in distilled water) for 15 min and afterward in water and in ethanol for 1 h. After oven-drying, a silver mirror was deposited on the glass substrates by vacuum sputtering deposition (HEX, Korvus Technologies). To prepare the active polymer layer, a stock solution (20 mg/mL) of tetra-tert-butylperylene in toluene and a stock solution (40 mg/mL) of polystyrene (Sigma-Aldrich, Mw 280 000) were mixed together having a tetra-tert-butylperylene/polystyrene ratio of 1:4. The resulting solution was afterward spin-coated (Laurell Technologies WS-650) onto the silver mirror for 45 s at different speeds for varying the thickness. As the last step, a second sliver mirror was deposited on top of the polymer layer by vacuum sputtering deposition. The fabricated cavity was kept under nitrogen in the dark to avoid any oxidation of the silver mirrors or aging of the sample.

Optical Spectroscopy

The dispersive steady-state transmission spectra were recorded by a standard spectrophotometer (Lambda 650, PerkinElmer) having a variable angle accessory. The angle-dependent steady-state emission and emission lifetimes were measured using two liquid light guides connected to a spectrofluorometer (FLS 1000, Edinburgh Instruments). The light from the fiber guiding the excitation light was focused on the sample, and the emitted light was focused on the entrance of the second fiber, which was placed at different angles and was used to guide the light back to the detector of the spectrofluorometer. For the emission lifetime measurements, a pulsed laser diode (Edinburgh Instruments) was used having an excitation wavelength of 405 nm.

Results and Discussion

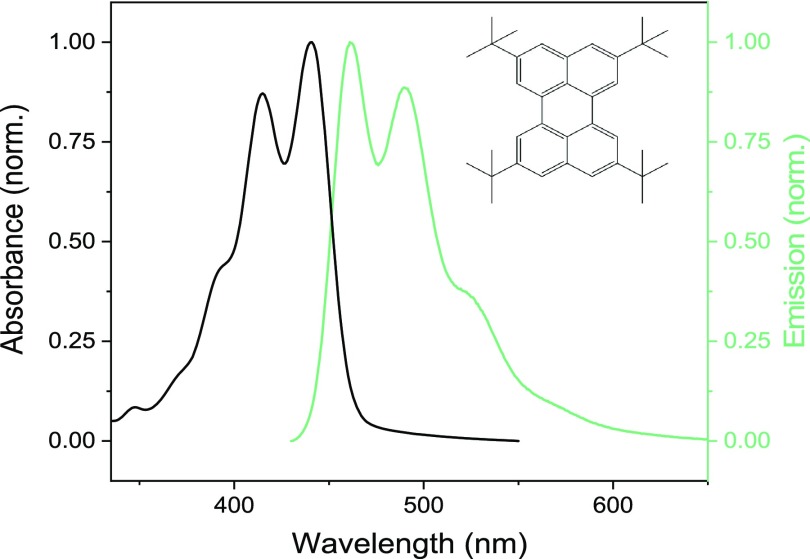
For the investigation of the angle-dependent emission lifetime in the strong coupling regime, the choice of chromophore is of high importance. To enter the strong coupling regime, the interaction between the molecular exciton and the electromagnetic field needs to be sufficiently large. In a Fabry–Pérot (FP) cavity having a predefined mode volume, the coupling strength is determined by the magnitude of the transition dipole moment of the molecular transition and the concentration of the molecule inside the cavity (eq 2). Furthermore, to probe the emission lifetime, the excited state of the molecule needs to be significantly long. In this study, tetra-tert-butylperylene (ttb-perylene) was chosen because of the following reasons: (1) It is a strong chromophore with an emission spectrum mirror imaging the absorbance spectrum (Figure 1). Hence, no big conformal changes occur in the excited state and the transition dipole moments of emission and absorption are therefore of similar magnitude. (2) A high concentration in a polymer matrix can be gained without showing excimer emission (which is present in unsubstituted perylene) because of the steric hindrance of the four tert-butyl groups. Thus, exciton–exciton coupling among molecules is negligible and is therefore absent in eq 2. A Fabry–Pérot cavity was constructed, containing ttb-perylene dissolved in polystyrene (PS) in a mass ratio of 1:4, sandwiched by two Ag mirrors. The chosen mass ratio was regarded as an optimum between a high concentration and as low as possible aggregation-induced quenching, which occurs at very high concentrations (Figure S1). At this concentration, the system is well within the strong coupling regime, and the excited state lifetime is long enough to be recorded using time-correlated single photon counting. Thus, ttb-perylene is an excellent chromophore for studying the angle dependence of the polaritonic lifetime.

Figure 1.

Figure 1

Open in a new tab

Absorption and emission spectra of tetra-tert-butylperylene (ttb-perylene) in a polystyrene matrix, at a mass ratio of 1:4 at room temperature. The inset shows the molecular structure of ttb-perylene.

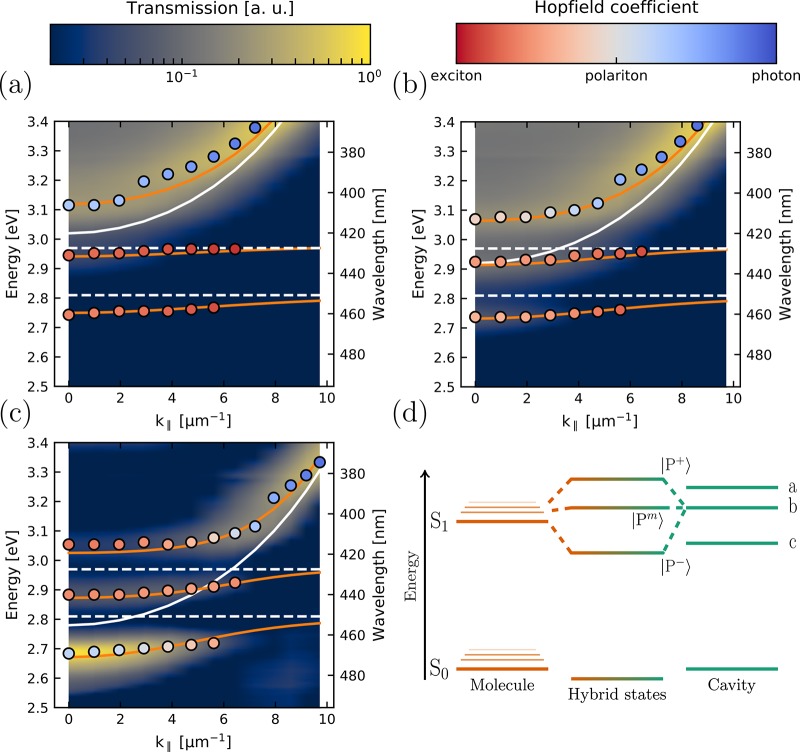
In the strong exciton–photon coupling regime, the molecular exciton is hybridized with a cavity mode, forming the polaritonic states. The energy matching between the exciton and the cavity mode governs the relative photonic/excitonic contribution to the formed polaritonic states (eq 2). Tuning of the cavity mode can thus be used to shape the properties of the polariton. Figure 2a–c shows the transmission as a function of angle for three cavities with varying thickness of the ttb-perylene/PS layer (for individual spectra of the cavity c, see Figure S2). As the thickness changes, the resonance also changes and thus the tuning of the cavities (Figure 2d). With a red tuned cavity, the photonic contribution to the lower polaritonic state (P−) is larger as compared to the excitonic contribution and vice versa. The coupled-oscillator model was used to determine the photonic contribution to P− (the Hopfield coefficients) from the dispersion plots in Figure 2a–c. Because the absorption spectrum of ttb-perylene (Figure 1) contains two equally strong vibronic peaks, we modeled the system using three coupled harmonic oscillators (eq 2). The photonic contributions to P− were calculated to be 0.19, 0.32, and 0.60 for cavities a, b and c, respectively. Furthermore, the Rabi splitting was considerably larger than the full width at half-maximum value of the exciton for all cavities (Table S1). Thus, three cavities, all well into the strong coupling regime, having different photonic contributions (which contributes to the dispersivity of the system) to the emissive P− state were constructed.

Figure 2.

Figure 2

Open in a new tab

(a–c) Dispersion plot of the tetra-tert-butylperylene-loaded cavities having different tunings. The dots represent the measurement data having different colors depending on the calculated Hopfield coefficients, where red stands for excitonic contribution and blue for photonic contribution. The lines are the fits for the different branches. (d) Jablonski diagram representing the transition of a molecule, having two equally strong vibronic transitions strongly coupled to the cavity mode, leading to the formation of three new hybrid states P+, Pm, and P–. The tunings of cavities a, b, and c are indicated in the diagram.

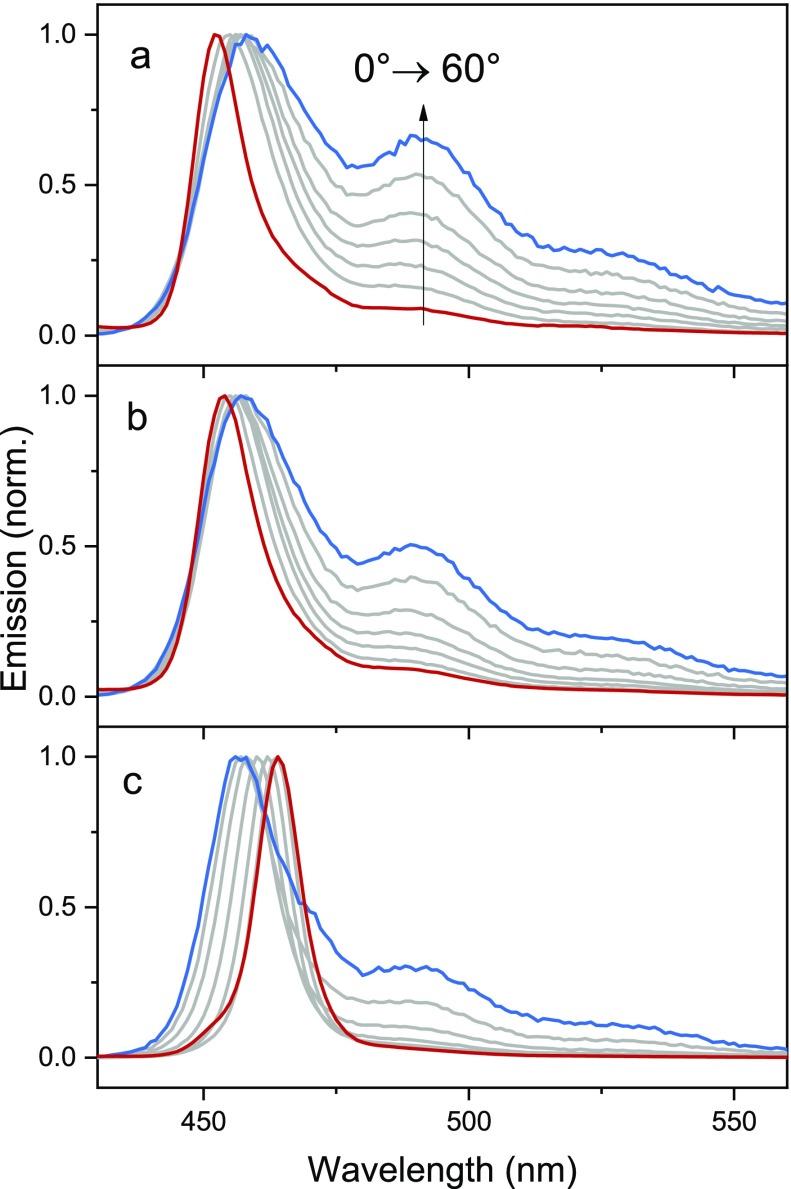
The polariton transmission exhibits a dispersive behavior and so does the polariton emission. Cavities a–c have a photonic contribution to the emissive P− state going from low to high (0.19, 0.32, and 0.60) at normal incidence. Emission from the cavity originates both from the lower polariton and from the bare exciton. As the angle of emission increases, the cavity resonance is blue tuned and the intensity of emission lowers; thus, the relative contribution of ttb-perylene emission increases. Figure 3 shows normalized cavity emission (when exciting at normal incidence) at different angles of emission. For all cases, at normal incidence the emission is sharp and overlaps in wavelength with the transmission spectrum of P− (Figure S3). Thus, the bandwidth of polaritonic emission is considerably narrower as compared to the vibronically structured emission from a bare ttb-perylene film (Figure 1). As the angle of emission increases, the intensity of the emission decreases (Figure S4) and is either blue- or red-shifted. Perhaps more interestingly, the intensity resembles more and more that of uncoupled ttb-perylene at large angles. This is most clearly seen at longer wavelengths (λ > 490 nm), where a perfect match between cavity and bare film emission can be seen (Figure S5). Thus, this indicates that the emission at longer wavelengths is due to a substantial light leakage of excimer emission through the cavity mirrors rather than the finite width of the lower polariton branch. Furthermore, the similarity with uncoupled ttb-perylene emission is the highest for cavity a, which has the lowest photonic contribution to P−. In summary, irrespective of tuning, the polariton emission is angle dependent, going from a strong sharp emission at normal incidence to a weak broad more excitonic-like emission at larger angles.

Figure 3.

Figure 3

Open in a new tab

Normalized emission spectra of the three (a–c) tetra-tert-butylperylene-loaded cavities at different angles (between 0° (red line) and 60° (blue line)) showing a shifting polaritonic emission peak at around 460 nm and an excitonic emission peak at 490 nm staying at the same position when varying the detection angle.

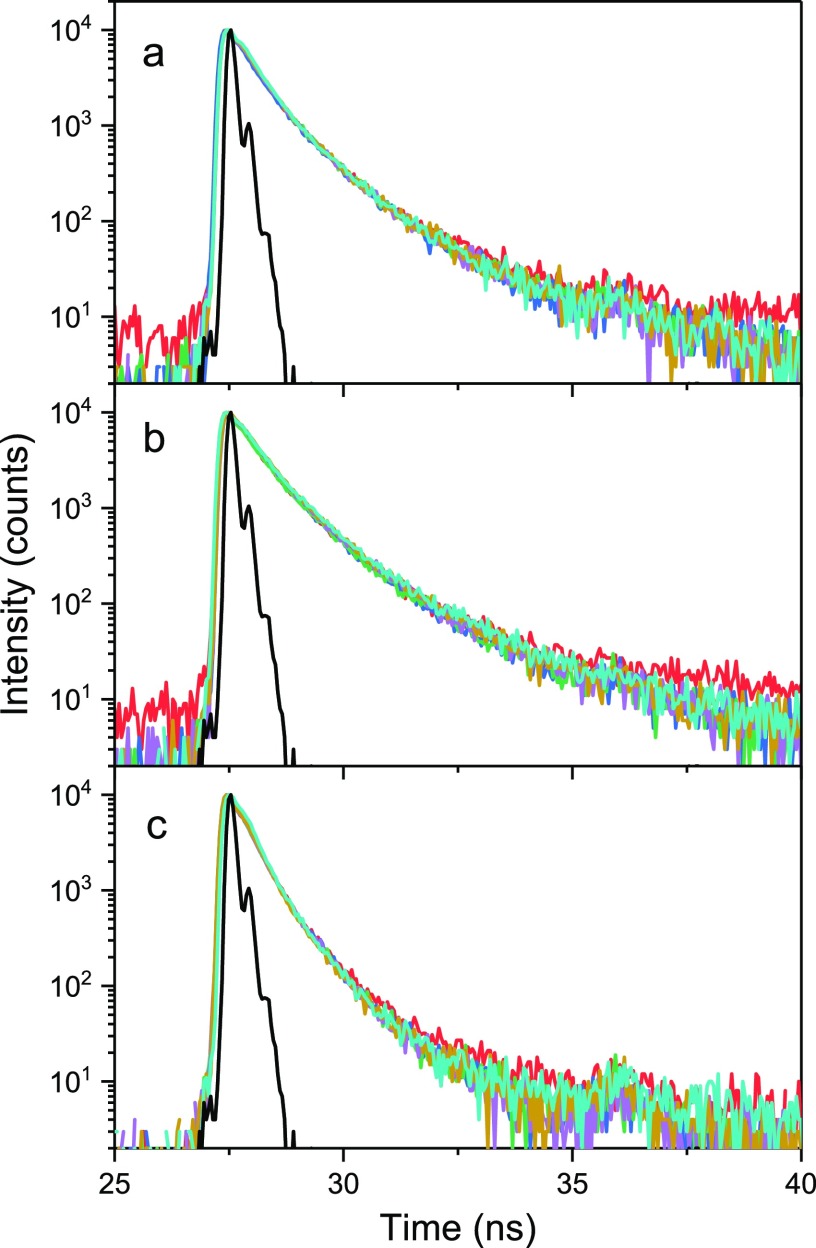
Both the emission and the transmittance of the polaritonic states show a dispersive behavior. Therefore, it is of interest to experimentally determine whether the lifetime of the polaritonic states also exhibits an angle dependence. According to eq 3, the emission lifetime should depend on the angle of emission. However, the exciton bath theory suggests that internal relaxation is the rate-limiting step in the emission process,47 thus predicting an emission lifetime independent of emission angle, even though the emission spectrum is not. Figure 4 shows the polariton emission (recorded at 460 nm) as a function of time for cavities a–c, at varying detection angles. No change in the lifetime with regard to detection angle can be observed. The polaritonic average lifetimes for cavities a, b, and c being 0.38 ± 0.02, 0.46 ± 0.03, and 0.41 ± 0.01 ns, respectively, indicate no substantial change in polariton lifetime with varying photonic/excitonic contribution to P−. To compare, time-resolved emission decays were also recorded at 490 nm, where the envelope of emission is more excitonic like (Figure S6, Tables S2–S7). Also here, no angular dependence can be seen, even though a slight increase in excited state lifetime is observed. Thus, the emission lifetime from the uncoupled molecules is also angle independent. Furthermore, the emission lifetime of a bare film of ttb-perylene was determined to be 0.21 ns, considerably shorter as compared to the polaritonic lifetime. To observe whether the bare exciton can be thermally populated by the lower polaritonic state, the relative ratio of the polaritonic and excitonic emissions at different temperatures was determined. No temperature dependence could be found. In summary, the lifetime of polariton emission is independent of the emission angle and the photonic contribution to the P− state. Thus, eq 3 does not capture the nature of polaritonic emission well. Instead, the polariton is either much more exciton like than predicted by eq 3 or the kinetics of populating the polariton is slow, as predicted by the exciton bath theory.

Figure 4.

Figure 4

Open in a new tab

Emission lifetime traces of tetra-tert-butylperylene-loaded cavities (a–c) measured at different angles between 10 and 60° and the internal machine response (black). The decays show no change of fitted lifetime within the same cavity when varying the detection angle.

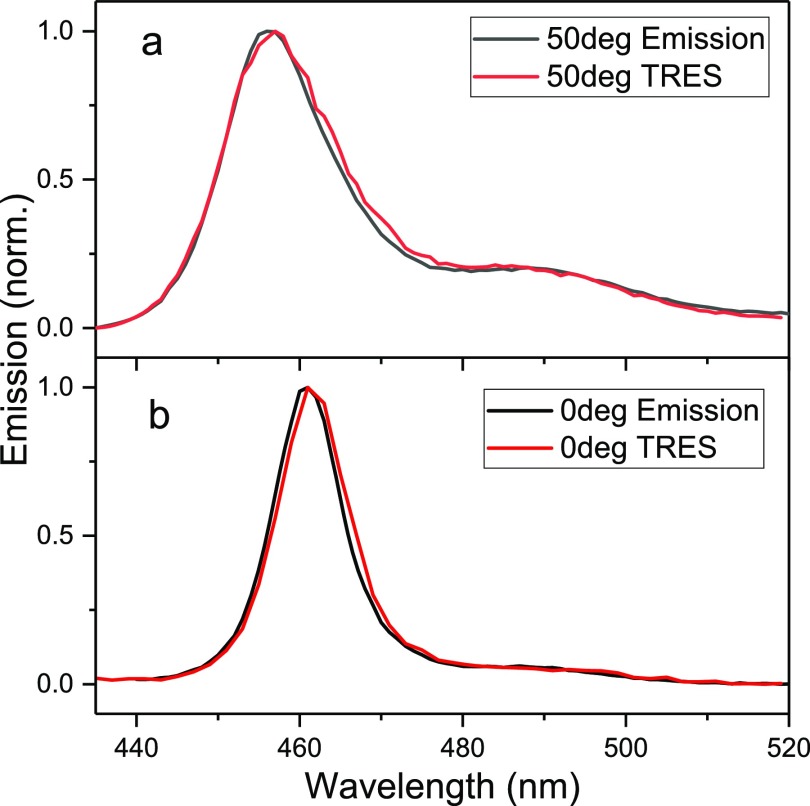
According to eq 3, the lifetime of the lower polaritonic state should be short, about 20 fs (assuming a photonic Hopfield coefficient of 0.5). Longer observed lifetimes can instead be viewed as a bottleneck for populating the emissive P− state from the exciton bath (dark states in energy in between the upper and lower polaritonic states). Nevertheless, when probing a complicated system such as this, it is important to ensure that the time resolution of the setup is high enough to capture the polariton emission. Time-resolved emission spectra (TRES, Figure S7) were used to observe whether all emissive processes were captured during the emission lifetime experiments. In a TRES experiment, an emission decay is measured for each emission wavelength, covering the whole emission profile. Each decay was integrated over the measurement time, and the resulting spectral envelope was compared to the one of the steady-state emissions at the specific angle of emission (Figures 5 and S8). If the time resolution of the system is too low, a deviation between these two spectra is expected. However, from the overlay shown in Figure 5, a perfect match between the steady-state data and the integrated TRES decays is observed, irrespective of the emission angle. Therefore, the time resolution of the system is high enough and the conclusion that the emission lifetime of polaritonic states is angle independent is valid.

Figure 5.

Figure 5

Open in a new tab

Comparison of the integrated time-resolved emission (red) and the steady-state emission (black) of cavity c at the angles of (a) 0° and (b) 50°.

Conclusions

We have shown that the lifetime of polariton emission is angle independent, irrespective of cavity tuning. To do this, a Fabry–Pérot cavity was constructed containing ttb-perylene strongly coupled to the vacuum field. Transmission through the cavity as well as the steady-state emission exhibited a strongly dispersive behavior, whereas the emission lifetime was constant and on the subnanosecond time scale. The long and nondispersive lifetime of polariton emission is not compatible with a pure exciton/photon superposition. However, it is compatible with the exciton bath theory, thus validating that the present theoretical models capture the nature of polaritonic states.

Acknowledgments

K.B. acknowledges the European Research Council (ERC-2017-StG-757733), the Swedish Research Council, and the Swedish Foundation for Strategic Research (ICA14-0018) for financial support.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcc.8b07283.

  • Emission spectra and emission lifetime decays; angle resolved transmission spectrum; Hopfield coefficients; quality factors and linewidths; normalized transmittance and emission spectra; pre-exponential factors, lifetimes, calculated average lifetime (PDF)

Author Contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.

Supplementary Material

jp8b07283_si_001.pdf (1,017.5KB, pdf)

References

  1. Lidzey D. G.; Bradley D. D. C.; Skolnick M. S.; Virgili T.; Walker S.; Whittaker D. M. Strong exciton--photon coupling in an organic semiconductor microcavity. Nature 1998, 395, 53–55. 10.1038/25692. [DOI] [Google Scholar]
  2. Ebbesen T. W. Hybrid Light-Matter States in a Molecular and Material Science Perspective. Acc. Chem. Res. 2016, 49, 2403–2412. 10.1021/acs.accounts.6b00295. [DOI] [PubMed] [Google Scholar]
  3. Törmä P.; Barnes W. L. Strong coupling between surface plasmon polaritons and emitters: a review. Rep. Prog. Phys. 2014, 78, 013901 10.1088/0034-4885/78/1/013901. [DOI] [PubMed] [Google Scholar]
  4. Ribeiro R. F.; Martinez-Martinez L. A.; Du M.; Campos-Gonzalez-Angulo J.; Yuen Zhou J. Polariton Chemistry: controlling molecular dynamics with optical cavities. Chem. Sci. 2018, 9, 6325–6339. 10.1039/C8SC01043A. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Wenus J.; Ceccarelli S.; Lidzey D. G.; Tolmachev A. I.; Slominskii J. L.; Bricks J. L. Optical strong coupling in microcavities containing J-aggregates absorbing in near-infrared spectral range. Org. Electron. 2007, 8, 120–126. 10.1016/j.orgel.2006.06.006. [DOI] [Google Scholar]
  6. Hobson P. A.; Barnes W. L.; Lidzey D. G.; Gehring G. A.; Whittaker D. M.; Skolnick M. S.; Walker S. Strong exciton–photon coupling in a low-Q all-metal mirror microcavity. Appl. Phys. Lett. 2002, 81, 3519–3521. 10.1063/1.1517714. [DOI] [Google Scholar]
  7. Kéna-Cohen S.; Davanço M.; Forrest S. R. Strong Exciton-Photon Coupling in an Organic Single Crystal Microcavity. Phys. Rev. Lett. 2008, 101, 116401 10.1103/PhysRevLett.101.116401. [DOI] [PubMed] [Google Scholar]
  8. Wang S.; Li S.; Chervy T.; Shalabney A.; Azzini S.; Orgiu E.; Hutchison J. A.; Genet C.; Samor P.; Ebbesen T. W. Coherent Coupling of WS2 Monolayers with Metallic Photonic Nanostructures at Room Temperature. Nano Lett. 2016, 16, 4368–4374. 10.1021/acs.nanolett.6b01475. [DOI] [PubMed] [Google Scholar]
  9. Flatten L. C.; He Z.; Coles D. M.; Trichet A. A. P.; Powell A. W.; Taylor R. A.; Warner J. H.; Smith J. M. Room-temperature exciton-polaritons with two-dimensional WS2. Sci. Rep. 2016, 6, 33134 10.1038/srep33134. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Graf A.; Tropf L.; Zakharko Y.; Zaumseil J.; Gather M. C. Near-infrared exciton-polaritons in strongly coupled single-walled carbon nanotube microcavities. Nat. Commun. 2016, 7, 13078 10.1038/ncomms13078. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Gao W.; Li X.; Bamba M.; Kono J. Continuous transition between weak and ultrastrong coupling through exceptional points in carbon nanotube microcavity exciton–polaritons. Nat. Photonics 2018, 12, 362–367. 10.1038/s41566-018-0157-9. [DOI] [Google Scholar]
  12. Hertzog M.; Rudquist P.; Hutchison J. A.; George J.; Ebbesen T. W.; Börjesson K. Voltage-Controlled Switching of Strong Light-Matter Interactions using Liquid Crystals. Chem. - Eur. J. 2017, 23, 18166–18170. 10.1002/chem.201705461. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Chikkaraddy R.; de Nijs B.; Benz F.; Barrow S. J.; Scherman O. A.; Rosta E.; Demetriadou A.; Fox P.; Hess O.; Baumberg J. J. Single-molecule strong coupling at room temperature in plasmonic nanocavities. Nature 2016, 535, 127–130. 10.1038/nature17974. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Bahsoun H.; Chervy T.; Thomas A.; Börjesson K.; Hertzog M.; George J.; Devaux E.; Genet C.; Hutchison J. A.; Ebbesen T. W. Electronic Light–Matter Strong Coupling in Nanofluidic Fabry–Pérot Cavities. ACS Photonics 2018, 5, 225–232. 10.1021/acsphotonics.7b00679. [DOI] [Google Scholar]
  15. Wang X.; Shoaib M.; Wang X.; Zhang X.; He M.; Luo Z.; Zheng W.; Li H.; Yang T.; Zhu X.; Ma L.; Pan A. High-Quality In-Plane Aligned CsPbX3 Perovskite Nanowire Lasers with Composition-Dependent Strong Exciton–Photon Coupling. ACS Nano 2018, 12, 6170–6178. 10.1021/acsnano.8b02793. [DOI] [PubMed] [Google Scholar]
  16. Vergauwe R. M. A.; George J.; Chervy T.; Hutchison J. A.; Shalabney A.; Torbeev V. Y.; Ebbesen T. W. Quantum Strong Coupling with Protein Vibrational Modes. J. Phys. Chem. Lett. 2016, 7, 4159–4164. 10.1021/acs.jpclett.6b01869. [DOI] [PubMed] [Google Scholar]
  17. Coles D.; Flatten L. C.; Sydney T.; Hounslow E.; Saikin S. K.; Aspuru-Guzik A.; Vedral V.; Tang J. K.-H.; Taylor R. A.; Smith J. M.; Lidzey D. G. A Nanophotonic Structure Containing Living Photosynthetic Bacteria. Small 2017, 1701777 10.1002/smll.201701777. [DOI] [PubMed] [Google Scholar]
  18. Kéna-Cohen S.; Forrest S. R. Room-temperature polariton lasing in an organic single-crystal microcavity. Nat. Photonics 2010, 4, 371–375. 10.1038/nphoton.2010.86. [DOI] [Google Scholar]
  19. Cookson T.; Georgiou K.; Zasedatelev A.; Grant R. T.; Virgili T.; Cavazzini M.; Galeotti F.; Clark C.; Berloff N. G.; Lidzey D. G.; Lagoudakis P. G. A Yellow Polariton Condensate in a Dye Filled Microcavity. Adv. Opt. Mater. 2017, 5, 1700203 10.1002/adom.201700203. [DOI] [Google Scholar]
  20. Hennessy K.; Badolato A.; Winger M.; Gerace D.; Atatüre M.; Gulde S.; Fält S.; Hu E. L.; Imamoğlu A. Quantum nature of a strongly coupled single quantum−cavity system. Nature 2007, 445, 896–899. 10.1038/nature05586. [DOI] [PubMed] [Google Scholar]
  21. Chervy T.; Xu J.; Duan Y.; Wang C.; Mager L.; Frerejean M.; Münninghoff J. A. W.; Tinnemans P.; Hutchison J. A.; Genet C.; Rowan A. E.; Rasing T.; Ebbesen T. W. High-Efficiency Second-Harmonic Generation from Hybrid Light-Matter States. Nano Lett. 2016, 16, 7352–7356. 10.1021/acs.nanolett.6b02567. [DOI] [PubMed] [Google Scholar]
  22. Christogiannis N.; Somaschi N.; Michetti P.; Coles David M.; Savvidis Pavlos G.; Lagoudakis Pavlos G.; Lidzey David G. Characterizing the Electroluminescence Emission from a Strongly Coupled Organic Semiconductor Microcavity LED. Adv. Opt. Mater. 2013, 1, 503–509. 10.1002/adom.201300017. [DOI] [Google Scholar]
  23. Carusotto I.; Ciuti C. Quantum fluids of light. Rev. Mod. Phys. 2013, 85, 299–366. 10.1103/RevModPhys.85.299. [DOI] [Google Scholar]
  24. Orgiu E.; George J.; Hutchison J. A.; Devaux E.; Dayen J. F.; Doudin B.; Stellacci F.; Genet C.; Schachenmayer J.; Genes C.; Pupillo G.; Samor P.; Ebbesen T. W. Conductivity in organic semiconductors hybridized with the vacuum field. Nat. Mater. 2015, 14, 1123–1129. 10.1038/nmat4392. [DOI] [PubMed] [Google Scholar]
  25. Rozenman G. G.; Akulov K.; Golombek A.; Schwartz T. Long-Range Transport of Organic Exciton-Polaritons Revealed by Ultrafast Microscopy. ACS Photonics 2018, 5, 105–110. 10.1021/acsphotonics.7b01332. [DOI] [Google Scholar]
  26. Spano F. C. Optical microcavities enhance the exciton coherence length and eliminate vibronic coupling in J-aggregates. J. Chem. Phys. 2015, 142, 184707 10.1063/1.4919348. [DOI] [PubMed] [Google Scholar]
  27. Thomas A.; George J.; Shalabney A.; Dryzhakov M.; Varma S. J.; Moran J.; Chervy T.; Zhong X.; Devaux E.; Genet C.; Hutchison J. A.; Ebbesen T. W. Ground-State Chemical Reactivity under Vibrational Coupling to the Vacuum Electromagnetic Field. Angew. Chem., Int. Ed. 2016, 55, 11462–11466. 10.1002/anie.201605504. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Hutchison J. A.; Schwartz T.; Genet C.; Devaux E.; Ebbesen T. W. Modifying Chemical Landscapes by Coupling to Vacuum Fields. Angew. Chem., Int. Ed. 2012, 51, 1592–1596. 10.1002/anie.201107033. [DOI] [PubMed] [Google Scholar]
  29. Zhong X.; Chervy T.; Wang S.; George J.; Thomas A.; Hutchison James A.; Devaux E.; Genet C.; Ebbesen Thomas W. Non-Radiative Energy Transfer Mediated by Hybrid Light-Matter States. Angew. Chem., Int. Ed. 2016, 55, 6202–6206. 10.1002/anie.201600428. [DOI] [PubMed] [Google Scholar]
  30. Georgiou K.; Michetti P.; Gai L.; Cavazzini M.; Shen Z.; Lidzey D. G. Control over Energy Transfer between Fluorescent BODIPY Dyes in a Strongly Coupled Microcavity. ACS Photonics 2018, 5, 258–266. 10.1021/acsphotonics.7b01002. [DOI] [Google Scholar]
  31. Coles D. M.; Somaschi N.; Michetti P.; Clark C.; Lagoudakis P. G.; Savvidis P. G.; Lidzey D. G. Polariton-mediated energy transfer between organic dyes in a strongly coupled optical microcavity. Nat. Mater. 2014, 13, 712–719. 10.1038/nmat3950. [DOI] [PubMed] [Google Scholar]
  32. Wang S.; Mika A.; Hutchison J. A.; Genet C.; Jouaiti A.; Hosseini M. W.; Ebbesen T. W. Phase transition of a perovskite strongly coupled to the vacuum field. Nanoscale 2014, 6, 7243–7248. 10.1039/C4NR01971G. [DOI] [PubMed] [Google Scholar]
  33. Wang S.; Chervy T.; George J.; Hutchison J. A.; Genet C.; Ebbesen T. W. Quantum Yield of Polariton Emission from Hybrid Light-Matter States. J. Phys. Chem. Lett. 2014, 5, 1433–1439. 10.1021/jz5004439. [DOI] [PubMed] [Google Scholar]
  34. Munkhbat B.; Wersäll M.; Baranov D. G.; Antosiewicz T. J.; Shegai T. Suppression of photo-oxidation of organic chromophores by strong coupling to plasmonic nanoantennas. Sci. Adv. 2018, 4, eaas9552 10.1126/sciadv.aas9552. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Chervy T.; Thomas A.; Akiki E.; Vergauwe R. M. A.; Shalabney A.; George J.; Devaux E.; Hutchison J. A.; Genet C.; Ebbesen T. W. Vibro-Polaritonic IR Emission in the Strong Coupling Regime. ACS Photonics 2018, 5, 217–224. 10.1021/acsphotonics.7b00677. [DOI] [Google Scholar]
  36. Stranius K.; Hertzog M.; Börjesson K. Selective manipulation of electronically excited states through strong light–matter interactions. Nat. Commun. 2018, 9, 2273 10.1038/s41467-018-04736-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Galego J.; Garcia-Vidal F. J.; Feist J. Suppressing photochemical reactions with quantized light fields. Nat. Commun. 2016, 7, 13841 10.1038/ncomms13841. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Hagenmüller D.; Schachenmayer J.; Schütz S.; Genes C.; Pupillo G. Cavity-Enhanced Transport of Charge. Phys. Rev. Lett. 2017, 119, 223601 10.1103/PhysRevLett.119.223601. [DOI] [PubMed] [Google Scholar]
  39. Martínez-Martínez L. A.; Du M.; F. Ribeiro R.; Kéna-Cohen S.; Yuen-Zhou J. Polariton-Assisted Singlet Fission in Acene Aggregates. J. Phys. Chem. Lett. 2018, 9, 1951–1957. 10.1021/acs.jpclett.8b00008. [DOI] [PubMed] [Google Scholar]
  40. Feist J.; Galego J.; Garcia-Vidal F. J. Polaritonic Chemistry with Organic Molecules. ACS Photonics 2018, 5, 205–216. 10.1021/acsphotonics.7b00680. [DOI] [Google Scholar]
  41. Martínez-Martínez L. A.; Ribeiro R. F.; Campos-González-Angulo J.; Yuen-Zhou J. Can Ultrastrong Coupling Change Ground-State Chemical Reactions?. ACS Photonics 2018, 5, 167–176. 10.1021/acsphotonics.7b00610. [DOI] [Google Scholar]
  42. Deng H.; Haug H.; Yamamoto Y. Exciton-polariton Bose-Einstein condensation. Rev. Mod. Phys. 2010, 82, 1489–1537. 10.1103/RevModPhys.82.1489. [DOI] [Google Scholar]
  43. Holmes R. J.; Forrest S. R. Strong Exciton-Photon Coupling and Exciton Hybridization in a Thermally Evaporated Polycrystalline Film of an Organic Small Molecule. Phys. Rev. Lett. 2004, 93, 186404 10.1103/PhysRevLett.93.186404. [DOI] [PubMed] [Google Scholar]
  44. Houdré R.; Weisbuch C.; Stanley R. P.; Oesterle U.; Pellandini P.; Ilegems M. Measurement of Cavity-Polariton Dispersion Curve from Angle-Resolved Photoluminescence Experiments. Phys. Rev. Lett. 1994, 73, 2043–2046. 10.1103/PhysRevLett.73.2043. [DOI] [PubMed] [Google Scholar]
  45. Ballarini D.; De Giorgi M.; Gambino S.; Lerario G.; Mazzeo M.; Genco A.; Accorsi G.; Giansante C.; Colella S.; D’Agostino S.; Cazzato P.; Sanvitto D.; Gigli G. Polariton-Induced Enhanced Emission from an Organic Dye under the Strong Coupling Regime. Adv. Opt. Mater. 2014, 2, 1076–1081. 10.1002/adom.201400226. [DOI] [Google Scholar]
  46. Canaguier-Durand A.; Genet C.; Lambrecht A.; Ebbesen T. W.; Reynaud S. Non-Markovian polariton dynamics in organic strong coupling. Eur. Phys. J. D 2015, 69, 24. 10.1140/epjd/e2014-50539-x. [DOI] [Google Scholar]
  47. Lidzey D. G.; Fox A. M.; Rahn M. D.; Skolnick M. S.; Agranovich V. M.; Walker S. Experimental study of light emission from strongly coupled organic semiconductor microcavities following nonresonant laser excitation. Phys. Rev. B 2002, 65, 195312 10.1103/PhysRevB.65.195312. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp8b07283_si_001.pdf (1,017.5KB, pdf)

Articles from The Journal of Physical Chemistry. C, Nanomaterials and Interfaces are provided here courtesy of American Chemical Society

RESOURCES