An experimental test of the mutation-selection balance model for the maintenance of genetic variance in fitness components

Abstract

Despite decades of research, the factors that maintain genetic variation for fitness are poorly understood. It is unclear what fraction of the variance in a typical fitness component can be explained by mutation-selection balance (MSB) and whether fitness components differ in this respect. In theory, the level of standing variance in fitness due to MSB can be predicted using the rate of fitness decline under mutation accumulation, and this prediction can be directly compared to the standing variance observed. This approach allows for controlled statistical tests of the sufficiency of the MSB model, and could be used to identify traits or populations where genetic variance is maintained by other factors. For example, some traits may be influenced by sexually antagonistic balancing selection, resulting in an excess of standing variance beyond that generated by deleterious mutations. We describe the underlying theory and use it to test the MSB model for three traits in Drosophila melanogaster. We find evidence for differences among traits, with MSB being sufficient to explain genetic variance in larval viability but not male mating success or female fecundity. Our results are consistent with balancing selection on sexual fitness components, and demonstrate the feasibility of rigorous statistical tests of the MSB model.

1. Introduction

The maintenance of genetic variation for fitness has been called one of the most important unresolved issues in evolutionary biology [1,2]. Despite the action of natural selection, populations harbour significant genetic variation for fitness-related traits [3]. A number of possible sources of variation exist, including deleterious mutations, beneficial alleles on their way to fixation and balancing selection, including environmental heterogeneity in selection. The relative importance of these factors is unknown, and will determine how genomes and populations evolve [4].

Deleterious mutation-selection balance (MSB) is arguably the most general explanation for genetic variance in fitness because all populations experience mutation. The question is whether MSB alone can account for the standing variation. Answering this question requires knowing how much variation would be expected from MSB alone. In a population at equilibrium, the rate at which mutation reduces mean fitness will equal the rate at which selection increases mean fitness, which in turn is equal to the genetic variance in fitness [5]. Thus, under MSB the standing genetic variance in fitness should be equal to the rate of fitness decline per generation in a mutation-accumulation experiment (mutational decline). This idea is described more formally below, and can be found in various incarnations in the literature [6–10]. If there is any other source of genetic variation apart from deleterious mutations, then the observed level of standing variation will exceed the rate of mutational decline.

Although estimates of mutational decline and standing variance exist for a number of traits (particularly in D. melanogaster), they are generally estimated in different experimental populations with different genetic backgrounds using different methodologies, which is far from ideal, especially given the considerable variation in some quantitative genetic parameters among populations [8,11]. In addition, the effects of new mutations are often assessed in the homozygous state; because new mutations will rarely be found in the homozygous state in a randomly mating population, it is their heterozygous effects that are most relevant. Homozygous mutational decline can only be used to infer the heterozygous equivalent after making tenuous assumptions about average dominance.

Despite these challenges, several attempts have been made to qualitatively test alternative models for the maintenance of genetic variation using data from numerous sources [7–9,11]. These investigations point to an important role of deleterious mutation in maintaining variation, but they cannot statistically evaluate the adequacy of the MSB model. While these studies have provided valuable insights, their conclusions are often limited by the quality and quantity of available data, leading these authors and others to call for experiments that directly address the MSB hypothesis [12–14]. Here, we outline some theoretical and empirical issues relevant to such experiments and use this approach to study the sources of standing genetic variation in a D. melanogaster laboratory population.

Populations in the laboratory, which are generally maintained in constant conditions for many generations, may be unlikely to harbour certain kinds of genetic variation because heterogeneity in selection will be minimal, and beneficial mutations on their way to fixation will be rare if the population is well adapted. (Moreover, there is reason to believe that beneficial alleles that eventually become fixed may make a relatively small contribution to standing variance [8].) However, although the environment may be relatively constant, alleles in sexual populations will be expressed in both males and females, and may be subject to intra-locus sexually antagonistic (SA) selection. This type of balancing selection may be a particularly important source of variation in well-adapted populations [15].

Although the existence of SA alleles has been established, it remains an empirical challenge to quantify their contribution to the standing genetic variance in fitness, relative to other sources of variation. If alleles under SA balancing selection are common, deleterious mutation should account for a smaller fraction of the genetic variance in sex-specific fitness components than in non-sex-specific fitness components. In other words, SA is expected to generate ‘excess' genetic variance beyond that attributable to deleterious mutations. To test this idea, we collected data on standing variance and the rate of change due to mutation accumulation (MA) for larval viability, male mating success, and female fecundity. We studied heterozygous second chromosomes (approx. 37% of the genome) on a common isogenic background, and measured mutational decline and standing variance in the same way within each fitness component.

2. Theoretical background

The theoretical background motivating this experiment has been described by others [6–10], and we present a summary of the major points here. We present an additive model formulation below; an analogous multiplicative formulation where traits are measured on a log scale is given in the electronic supplementary material.

In a large panmictic population, the equilibrium frequency of a deleterious mutation at a given locus will be q* ≈ μ/(hs), where μ is the mutation rate and hs is the coefficient of selection against heterozygotes [16]. This assumes that μ ≪ hs so q* ≪ 1; thus, the frequency of heterozygotes is approximately 2q* and the frequency of homozygous mutants is negligible. If the non-mutant value of trait z is k, and the heterozygous trait value is k(1 − a), at equilibrium the expected trait value is 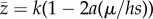. We assume that the effect of a mutation on trait z is some fraction c of its effect on total fitness, i.e. a = chs, so that .

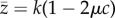Consider the additive genetic variance in trait values relative to the trait mean, 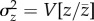, also called ‘evolvability' [3]. If mutation is the only source of variation, at equilibrium 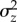at one locus will be 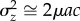, ignoring terms of O(μ²). Summing over n loci in the genome, if the variance at each site is small and assuming there is no epistasis [9] and no covariance between the mutation rate and the mutational effect, the total standing genetic variance in relative z is 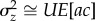where U is the mutation rate per genome. When the trait is fitness itself, c = 1, a = hs, and 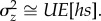Note this is equal to the rate of change in mean relative fitness due to one generation of mutation in the absence of selection, ΔM_w, which can be estimated in an MA experiment [17]. This result implies that, when the effects of mutation and selection are at equilibrium, the rate of decline in fitness due to mutation must equal the rate of increase in fitness due to selection, which is given by the additive genetic variance in fitness [5], or, for a trait, the additive genetic covariance between the trait and fitness [18]. A corresponding result is that deleterious mutations contribute little in the way of dominance variance, relative to additive variance, so that most genetic variance will be additive under MSB ([10], pp. 184–185). Under the null hypothesis that deleterious mutations completely account for standing variation, we expect no ‘excess' variance, i.e. 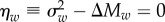. Thus η_w > 0 is an indication that there is more standing genetic variation than can be explained by MSB alone.

For traits that are components of fitness, standing variance will also depend on c:

where C[a,c] is the covariance between a and c. While ΔM_z can be estimated directly in an MA experiment, the other terms are more difficult to determine. Observations of positive mutational correlations among fitness components (e.g. [19–22]) suggest pleiotropy is generally positive, such that the average deleterious mutation will have a smaller effect on a single fitness component than on total fitness, i.e. , although this is not necessarily the case for all loci. Positive pleiotropy also suggests that C[a,c] will be positive and not too large, i.e. mutations with greater effects on a given fitness component will tend to have greater effects on total fitness. Therefore, ΔM_z alone would overestimate because , but would underestimate 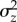because UC[a,c] > 0. However, given realistic values the first bias will tend to be larger, such that ΔM_z will tend to overestimate 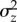, particularly when is not very close to 1, which is likely to be the case; a formal analysis of these biases is given in [8]. This bias means that the rate of mutational decline will tend to overestimate the expected variance in a given trait under MSB because the frequency of mutations will be reduced through selection on additional fitness components that are not accounted for by ΔM_z (i.e. 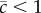). The test of MSB for a fitness component, , will therefore be conservative.

It may be possible to reduce this conservative bias by estimating . If j components of fitness are measured, a very simple estimate of for trait z is the mutational decline in the trait relative to the mutational decline in all fitness components, i.e. . This assumes that fitness components are multiplicative but that mutational effects on individual traits are sufficiently small that the total fitness effect can be approximated via the sum across all fitness components. Even when all fitness components have been measured, this approach can over- or underestimate (because E[a]/E[s] ≠ E[a/s]). If an important fitness component has not been measured, Σ_jΔM_j < ΔM_w, and so ΔM_z/Σ_jΔM_j will tend to overestimate . Again, this would lead to a conservative test of 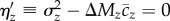. We obtained estimates of 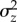and ΔM_z for three fitness components (traits), as described below to test the MSB hypothesis.

3. Material and methods

(a). Overview

Our goal was to estimate the rate of mutational decline, ΔM_z, and the standing additive genetic variance in relative trait values, 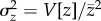, for each of three major fitness components: viability, female fecundity, and male mating success. We examined each trait in a number of MA lines, in their corresponding controls, and in an outbred laboratory population (Dahomey). In each case, focal second chromosomes were tested in the heterozygous state on a common isogenic background, allowing us to compare traits and sources of variance while minimizing background effects. All reported estimates refer to haploid second chromosomes. Details of line preparation and trait measurement protocols are given in the electronic supplementary material, and crossing procedures are shown in electronic supplementary material, figures S1 and S2.

(b). Experimental lines

We measured ΔM_z in lines that accumulated mutations for 52 generations. The MA procedure used to generate these lines is described elsewhere [23]. Briefly, an initially isogenic focal second chromosome marked with bw was replicated into many independent MA lines. Each MA line was maintained by crossing a single heterozygous male to four outbred stock females each generation, thereby maximizing the amount of drift and rendering selection ineffective; marker alleles were used to identify the relevant chromosomes (electronic supplementary material, figure S1A,B). The same initial chromosome was also maintained in three separate control populations of 450 adults each. This moderate population size should limit MA. Following MA, crosses were performed to situate the focal second chromosomes from 51 MA lines and 57 control chromosomes on an isogenic background (electronic supplementary material, figure S1C; any MA lines with evidence of recombination during MA [24] were not included in this study). For each line, we assessed each trait in six replicates for a total of approximately 678 replicates per trait. The lines used in this experiment are inferred to contain an average of 18.6 mutations each [24]. In the homozygous state, these MA chromosomes cause significantly reduced viability [23] and adult reproductive fitness [20].

We measured 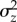among second chromosomes derived from virgin females collected at random from the outbred laboratory population. Crosses were performed to situate each chromosome on the same isogenic background described above (electronic supplementary material, figure S2A), minimizing among-line selection and ensuring that each line ultimately contained only a single focal chromosome haplotype. In addition, second chromosomes remained heterozygous throughout the experiment, minimizing selection against genotypes bearing recessive lethal or deleterious alleles. For each of 133 such lines, we assessed each trait in six replicates, for a total of approximately 798 replicates per trait.

(c). Trait measurements

Viability was estimated as the probability of survival to adulthood in competition with a standard genotype. Standing variance in viability was assessed in two blocks of 67 and 66 lines respectively. Male mating success was estimated as the proportion of standard females that mated (as assessed via offspring production) with focal males in competition with marked males, under male-biased sex ratio conditions, in a period of time that did not allow females to mate multiply. These assays were performed in two blocks for the MA group, with non-overlapping sets of mutant and control lines in each block (block 1 : 29 control lines, 25 MA lines; block 2 : 28 control lines, 26 MA lines). Similarly, two blocks were performed for the assay of standing variance in this trait, of 67 and 66 lines respectively. Female fecundity was estimated as early-life egg production, where focal females competed with standard females for access to a limited amount of live yeast [25]. Note that our measures of male mating success and female fecundity are independent of larval viability. Details on trait measurements are given in the electronic supplementary material.

(d). Data analysis

To estimate means and variance components on a log scale (see the electronic supplementary material) we fit generalized linear mixed models using MCMCglmm [26] in R [27], using non-informative priors (variances∼0, nu = –2), and a burn-in phase of 10⁶ iterations. Subsequent iterations were stored such that the autocorrelation among stored values was less than 0.1 for all model parameters and the final number of stored iterations was 10⁴. To test for a difference between two parameters of interest (e.g. ΔM_z and 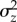) we sampled without replacement from the posterior distribution of each parameter and determined the 95% credible interval (CI) for the distribution of their differences (e.g. 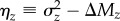). We consider 95% CIs that do not include zero to indicate a significant difference.

The response variable for viability was the ratio of focal offspring, n_focal, to standard offspring, n_standard. When modelled using a binomial link function, the model scale logit(n_focal/(n_focal + n_standard)) is equivalent to log(n_focal/n_standard). The response variable for female fecundity was number of eggs produced, modelled using a Poisson (log) link. The response variable for male mating success was the ratio of the number of females that mated with focal males to the number of females that mated with standard males in each replicate, modelled using a binomial link. Each trait and group of lines (MA lines, MA controls, outbred lines) was modelled separately, with a random effect of genotype (line).

Block did not have a significant effect on viability in outbred lines (p = 0.78), and was dropped from that model. Block had a significant effect on male mating success in outbred lines (p < 1 × 10^–5), and controls (p < 0.05), and a marginally non-significant effect in MA lines (p = 0.06). However, there was no significant difference in genetic variance between blocks in any of these groups (5000 bootstrap replicates, all p > 0.35). We, therefore, modelled male mating success with a main effect of block on the intercept only.

We estimated for each trait as the among-line (genetic) variance among outbred lines on the log scale. We estimated ΔM_z as (E[y_control] – E[y_MA])/52, where y = log(z) and 52 is the number of MA generations, as well as the mutational variance, ΔV_z = V[y_MA]/52. The ‘excess' variance in a trait beyond that expected under MSB alone was estimated as 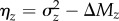. When comparing excess variance across traits we standardized η_z by the expected standing variance, ΔM_z (i.e. β_z = η_z/ΔM_z). To account for selection on multiple traits, we estimated E[c_z] for each trait as , where the subscripts v, m, and f represent viability, male mating success, and fecundity, respectively, and the coefficients of ½ reflect the sex-limited nature of some fitness components. We then estimated excess variance as .

We also used MCMCglmm to examine the standing and mutational genetic correlations among traits using priors expected to be uninformative for random effect correlations (inverse-Wishart; G: variances = 0.02, covariances = 0, nu = 4; R: variances ∼ 0, covariances = 0, nu = –2; MCMCglmm vignette). Models were conducted with a burn-in phase of 10⁶ iterations followed by 10⁸ iterations with a thinning interval of 6000, leaving 16 667 values in the posterior distribution such that autocorrelation among stored values was less than 0.1 for all model parameters. Trait correlations were determined after transformation to the original measurement scale by integration. To compare mutational and standing correlations we sampled 10⁵ values from each posterior distribution. We also estimated phenotypic correlations among line means between pairs of traits, which will differ from the genetic correlations due to estimation error (attenuation). For male mating success line means were first standardized by subtracting the block mean. Phenotypic correlations were compared between groups by bootstrapping with 10⁴ replicates.

(e). Maximum likelihood

Inferences from the analyses above assume the ideal MA control. In reality, the control populations for the MA experiment could potentially evolve over the course of MA. Though purifying selection will prevent deleterious mutations from fixing in control populations, such mutations will appear and segregate at a low level, reducing the average fitness of the controls below their initial value, downwardly biasing our estimates of ΔM. To estimate the most probable initial control values we fit a maximum-likelihood model (see the electronic supplementary material), where both the MA and control trait means and variances depend on the underlying mutation rate and the effects of mutations on each trait. We evaluated the likelihood of a given set of parameters using generalized linear mixed model functions implemented in lme4 [28], using Nelder-Mead optimization with bbmle [29], repeating the optimization 50 times with random starting values.

4. Results

Means and genetic variances for each trait on the original scale of measurement are given in electronic supplementary material, table S1, and estimates of quantitative genetic values are shown in figure 1 and electronic supplementary material, table S2. Our estimates of mutational decline and standing variance are consistent with previously reported values [9,11,17]. For each trait, we examined the posterior distribution of observed standing variances and the variance expected under MSB (figure 1). We scale excess variance η_z to mean expected variance E[ΔM_z] to facilitate comparison among traits. We cannot reject MSB for larval viability, where excess variance is low (η_j/E[ΔM_j]: mean 0.22, CI [–1.17, 2.16]). However, we find evidence for excess variance in male mating success, where the 95% CI does not overlap zero (η_m/E[ΔM_m]: mean 10.16, CI [0.11, 24.15]). The 95% CI for female fecundity slightly overlaps zero (η_f/E[ΔM_f]: mean 5.81, CI [–0.34, 14.26]) but 96% of the posterior probability mass is associated with excess variance (η_f > 0). The combined evidence from the adult fitness components indicates significant excess variance (i.e. 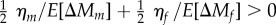; mean 7.99, CI [1.78, 16.06]), and the excess variance in the adult fitness components was significantly greater than the excess variance for viability (i.e. 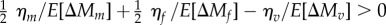; mean 7.77, CI [1.30, 16.08]). Our point estimates indicate that MSB explains only 9% and 15% of the standing genetic variance in male mating success and female fecundity, respectively, but 82% of the variance in larval viability.

Figure 1.

Standardized posterior density distributions for the genetic variance expected under mutation-selection balance (red) and the genetic variance observed (blue) for male mating success (a), female fecundity (b), and larval viability (c). The text in each panel describes the posterior means and 95% credible intervals based on quantiles; sample sizes (N) refer to total replicate trait measurements across either 133 outbred lines or 108 MA/control lines (51 MA lines plus 57 control lines).

Because our estimates of 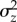are constrained to be non-negative but our estimates of ΔM_z are not, it is possible for this difference to create a bias towards finding positive η_z. ΔM_z represents the expected amount of variance so negative values are arguably non-sensical. Repeating the analysis with negative ΔM_z values replaced with zero or removed does not qualitatively affect the results.

The comparisons above ignore two likely sources of bias, which will act in opposite directions. First, mutations will generally have greater effects on total fitness than their effects on any one fitness component (i.e. 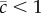), which would lead us to underestimate excess variance. Second, the appearance of deleterious mutations in control populations could not be prevented in our experiment, which would lead us to underestimate ΔM and overestimate excess variance. To address these issues we first used maximum likelihood to estimate the original trait values of the MA control genotype (electronic supplementary material, table S3), and used these adjusted control values to re-estimate ΔM for each trait. Next, we used the revised ΔM values to estimate for each trait (finding , , and ), and tested the null hypothesis 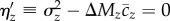. The net effect of these adjustments does not substantially alter the results described above, and we obtain similar evidence for excess variance in male mating success (mean 7.63, CI [0.14, 18.09]) and female fecundity (mean 2.64, CI [–0.06, 6.36]; 97% of posterior probability mass is associated with excess variance) but not larval viability (mean 0.65, CI [–0.60, 2.46]). There is significant excess variance combining evidence from adult traits (mean 5.14, CI [1.06, 10.67]), and greater amounts of excess variance for adult traits than for viability (mean 4.48, CI [0.04, 10.15]). Our adjusted estimates indicate that MSB explains 12%, 33%, and 86% of the standing genetic variance in male mating success, female fecundity, and larval viability, respectively.

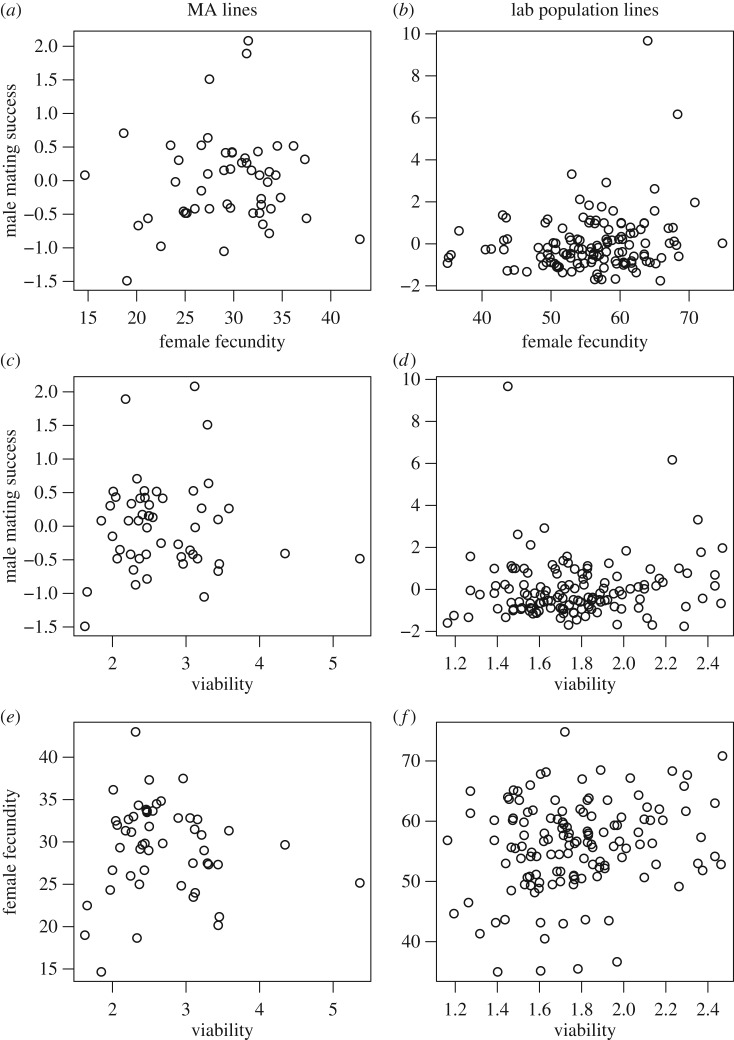
If the presence of excess standing genetic variance in adult sexual traits reflects the presence of SA alleles we would expect to find a negative standing genetic correlation between these traits, or at least that the standing genetic correlation is lower than the mutational correlation. However, the genetic correlations (table 1) are all positive and not significantly different from zero, and there is no evidence of a difference between mutational and standing genetic correlations for any pair of traits (CIs for all differences overlap zero). Although the phenotypic correlations are generally smaller than the genetic correlations (figure 2 and table 1), we detected significant standing correlations between viability and female fecundity (r = 0.21, t = 2.41, p < 0.05), and between male mating success and female fecundity (r = 0.20, t = 2.30, p < 0.05). There is no evidence of a difference between mutational and standing phenotypic correlations for any pair of traits (bootstrapping; p > 0.40).

Table 1.

Summary of genetic and phenotypic (line mean) correlation estimates for each pairwise trait combination, for mutation-accumulation (MA) lines and the standing population.

group	traitsa	genetic correlation [95%CIb]	line mean correlation [95%CIc]
MA	m–f	0.118 [–0.518, 0.679]	0.077 [–0.211, 0.354]
	m–v	0.117 [–0.514, 0.674]	0.000 [–0.278, 0.301]
	f–v	0.079 [–0.458, 0.577]	–0.045 [–0.339, 0.245]
standing	m–f	0.172 [–0.348, 0.606]	0.197 [0.045, 0.328]
	m–v	0.182 [–0.300, 0.598]	0.096 [–0.107, 0.329]
	f–v	0.278 [–0.108, 0.600]	0.206 [0.036, 0.368]

^aTraits are viability (v), male mating success (m), and female fecundity (f).

^bBayesian credible interval.

^cConfidence interval.

Figure 2.

Phenotypic means for MA lines (a,c,e) and standing laboratory population lines (b,d,f), plotted for each pair of traits. Note that values for male mating success are standardized by the group mean within each block.

5. Discussion

We tested the hypothesis that genetic variance is maintained by MSB, and our results indicate the presence of additional sources of genetic variance in adult sexual fitness components, but not viability. The strengths of our study are that we examined several major fitness components, measured mutational decline and standing genetic variance using a common genetic background and measurement procedures, and that we avoided assumptions regarding dominance by measuring the fitness effects of mutations in the heterozygous state.

We are not aware of any other study with this combination of features. A partial exception is a study of the nematodes Caenorhabditis elegans and C. briggsae [30], which examined the ratio of the mutational variance to the standing genetic variance (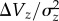) for lifetime fitness and body size across populations of each species. This ratio approximates the average strength of selection against heterozygous mutations under MSB [6]. However, if some standing variance is due to non-mutational sources then these values will be downwardly biased, and our results suggest that this could be the case for some traits, particularly male mating success. Huang et al. [31] used a similar approach to compare mutational and standing variance in quantitative traits in D. melanogaster (e.g. bristle number), and concluded that simple models of mutation-stabilizing-selection balance are insufficient to account for standing variance.

Others have made important contributions to this question by comparing mutational parameters and standing genetic variance from numerous sources, typically experiments using D. melanogaster. Houle et al. [7] examined the ratio of standing variance to mutational variance, , which approximates the ‘persistence time' of new mutations in a population under MSB [32]. They reasoned that life-history traits, which are under strong directional selection, should show reduced 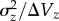relative to metric traits, which tend to be under weaker selection. Consistent with MSB, they found that the persistence time for life-history traits was significantly lower than that of metric traits. Houle et al. [7] discuss several challenges they faced, including the unavailability of estimates of 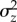and from the same population, possible bias resulting from using estimates based on homozygous rather than heterozygous mutations, and the use of standing variance measures from populations potentially not at equilibrium. Along similar lines, Houle [11] found that 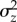and 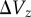were highly correlated across traits, as expected if 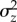is largely determined by mutational input. However, the necessary standardization of traits may have introduced some autocorrelation to this relationship [11].

Charlesworth & Hughes [9] considered the relationship 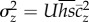expected under MSB (see their equation 19.6), equivalent to the relationship we tested. They used the best available estimates of U, , and from disparate sources to calculate expected σ² under MSB. By comparison with observed values of σ², they suggested that mutation likely contributes one-third to two-thirds of the genetic variation in a typical life-history trait. Our results (35% of variance explained on average, or 44% after adjustment for bias) are consistent with their conclusion. Using a similar approach, Charlesworth [8] concluded that most Drosophila populations show higher standing variance for viability than expected under MSB, but of the traits we studied viability shows the least evidence for excess variance. A strength of the meta-analyses described above [7–9,11] is that averaging over populations and traits may provide a more robust representation of the parameters of interest at the species level. However, this approach might also obscure real variation among traits or populations in the extent of non-mutational genetic variance.

Using a different method based on the effect of artificial selection on the mean value and inbreeding depression in a trait [33], there is evidence that intermediate-frequency alleles contribute to variation in flower size and male fitness in Mimulus guttatus [34,35] and early fecundity in D. melanogaster [14]. Although it provides a qualitative test only, this approach is relatively assumption free, and it would be valuable to apply it to compare more traits and populations. Additional evidence comes from the observation that mutation does not seem to completely explain the effects of inbreeding on life-history traits [9]. Overall, these comparisons indicate that the MSB model may often be insufficient to account for standing genetic variation. The data are inconsistent with heterozygote advantage across all traits, so any excess variance is likely due to balancing selection in the form of antagonistic pleiotropy (leading to net heterozygote advantage), heterogeneity in selection, or frequency-dependent selection [9].

We found evidence of excess variance in our study but no support for sexual antagonism as the cause, though our confidence in the latter result is low due to the uncertainty in each correlation estimate. Perhaps the excess variance in male mating success and female fecundity is due to antagonistic pleiotropy with fitness components not measured in this experiment (e.g. adult survival, sperm competitive ability). Another possible explanation arises from the fact that the conditions of the fitness assays do not represent selection on these fitness components exactly as it occurs in the laboratory population. For example, if the effects of mutations on a given fitness component had a larger effect in the assay conditions than in the laboratory population, this would inflate our estimates of mutational decline and standing variance, but would have a greater effect on standing variance, giving the false impression of excess variation. Our results could, therefore, be explained by our adult fitness assays being more selective than reality and our viability assays being less selective. Our fitness assays seem a reasonable approximation of fitness as it occurs in the laboratory population but these assays are not identical to the conditions under which the population was maintained, and do not consider the effects of multiple mating and postcopulatory sexual selection. Selection on both larval and adult fitness components can be sensitive to assay conditions [25,36]. In this respect, Drosophila populations with maintenance regimes that can be more precisely replicated in fitness assays would be preferable (e.g. [19,37]).

Although our data represent one of the more controlled tests to date of MSB in fitness components, several empirical limitations of our study should be considered. First, new mutations that arose in the control populations during the MA procedure cause us to underestimate mutational decline and overestimate excess variance; we attempted to account for this in our maximum-likelihood model but this is not an ideal solution. Second, we chose to measure mutational decline and standing genetic variance in three traits at once, which placed a practical limit on the number of independent genotypes we could manipulate and examine. Nevertheless, we gained some statistical power by combining evidence across traits. Third, we measured standing variation on only an autosomal part of the genome. This was partly done for practical reasons: we wanted to compare standing variation with mutational variation, which arose on the second chromosome in our MA lines, and we wanted to avoid complications due to hemizygosity in males. However, we might have detected stronger departures from MSB if we had included variation on the sex chromosomes, which may be enriched for alleles with SA effects [37,38].

Our findings indicate that, within our particular laboratory population, MSB is inadequate to explain levels of standing genetic variance in some fitness components, but not others. Comparing fitness components in this respect may lead to greater insight into the sources and genetic basis of non-mutational variation.

Data accessibility

Data from this research is available in the Dryad Digital Repository: https://doi.org/10.5061/dryad.2p7qb12 [39].

Authors' contributions

N.S. and A.A. designed experiments, analysed the data, and wrote the manuscript; N.S. performed experiments. All authors gave final approval for publication.

Competing interests

We have no competing interests.

Funding

This research was funded by the Natural Sciences and Engineering Research Council of Canada.