Structural Characterization of Single-Stranded DNA Monolayers Using Two-Dimensional Sum Frequency Generation Spectroscopy

Abstract

DNA-covered materials are important in technological applications such as biosensors and microarrays, but obtaining structural information on surface-bound biomolecules is experimentally challenging. In this paper, we structurally characterize single-stranded DNA monolayers of poly(thymine) from 10 to 25 bases in length with an emerging surface technique called two-dimensional sum frequency generation (2D SFG) spectroscopy. These experiments are carried out by adding a mid-IR pulse shaper to a femtosecond broad-band SFG spectrometer. Cross peaks and 2D line shapes in the 2D SFG spectra provide information about structure and dynamics. Because the 2D SFG spectra are heterodyne detected, the monolayer spectra can be directly compared to 2D infrared (2D IR) spectra of poly(thymine) in solution, which aids interpretation. We simulate the 2D SFG spectra using DFT calculations and an excitonic Hamiltonian that relates the molecular geometry to the vibrational coupling. Intrabase cross peaks help define the orientation of the bases and interbase cross peaks, created by coupling between bases, and resolves features not observed in 1D SFG spectra that constrain the relative geometries of stacked bases. We present a structure for the poly(T) oligomer that is consistent with the 2D SFG data. These experiments provide insight into the DNA monolayer structure and set precedent for studying complex biomolecules on surfaces with 2D SFG spectroscopy.

GRAPHICAL ABSTRACT

INTRODUCTION

Immobilized DNA on a material surface is the foundation of many types of DNA microarrays and biosensors.^1–3 In microarrays, the molecular recognition properties of DNA make it useful for gene-expression profiling, pathogen detection, genotyping, detecting protein−DNA interactions, and more.⁴ DNA-functionalized interfaces are also important for self-assembled DNA nanostructures that are being developed for applications in peptide recognition, molecular-scale computation, drug delivery, and protein structure determination.^5–9 However, the thermodynamics of DNA base pairing is not the same for oligomers tethered to a surface as it is in solution, presumably due to surface effects and oligomer packing.^10,11 Thus, the structure of single-stranded DNA (ssDNA) and double-stranded DNA (dsDNA) in monolayers are of tremendous interest because structure influences binding which in turn impacts device design.

Many techniques have been used to study monolayers of DNA on material surfaces. Imaging techniques such as atomic force microscopy (AFM) and scanning-tunneling microscopy (STM) provide insight into surface densities,¹² heterogeneity,¹³ DNA monolayer thickness and orientation,¹⁴ voltage-induced structural changes,^15,16 and hybridization.^12,17 In general, ssDNA is more difficult to image compared to dsDNA because it is less rigid, though both have been studied.¹⁸ Spectroscopic techniques are also often applied to surface-bound DNA. Fluorescence spectroscopy has been used to measure DNA monolayer heterogeneity,¹⁹ structural properties,²⁰ and hybridization.²¹ X-ray photoelectron spectroscopy (XPS) can determine the surface density of DNA molecules and detect different binding orientations.²² Of particular relevance to our study are surface vibrational spectroscopies such as infrared reflection absorption spectroscopy (IRRAS), sum frequency generation (SFG), and surface-enhanced Raman (SERS) that have been used to investigate a variety of systems.^23–26 These techniques are useful for structural characterization at a surface because molecular structures relate directly to vibrational frequencies and other observables.²⁷ Plus, polarization-sensitive measurements can help determine mode orientation relative to surfaces.²⁸ IRRAS has been used to track DNA monolayer deposition and distinguish between chemisorbed and physisorbed nucleobases.^29–31 Sum frequency generation has been used to look at changes in DNA orientation between air and water and also as a function of ionic strength.^32,33 Surface-enhanced Raman spectroscopy has been employed to detect DNA hybridization.³⁴

Perhaps the most studied DNA monolayer is poly(thymine) oligomers (oligo(dT)), which are used in devices for separating mRNA and serve as model systems.^35,36 Oligo(dT) and other polynucleotides have been studied with AFM, SFG, IRRAS, XPS, UV−vis, and dynamic light scattering.^{17,22,30–33,37–39} Many structures have been proposed, with most agreeing that dense monolayers of oligo(dT) on gold have chains that stand upright from the surface. Of these experiments, near-edge X-ray absorption fine structure spectroscopy is perhaps the most informative, which gives information about average tilt angle and amount of disorder.^38,40,41 From these experiments it was concluded that short oligo(dT) oligomers of length 5 had ordered monolayers with bases that preferentially orient mostly parallel to the gold surface but that oligomers of length 25 or longer were disordered like polyelectrolyte brushes.⁴² In a technique more similar to ours, SFG was used to study oligo(dT₅), which also concluded that short chain monolayers contain some amount of base ordering.³²

In this paper, we investigate ssDNA monolayers of oligo(dT) on gold surfaces using 2D infrared (2D IR) and two-dimensional sum frequency generation (2D SFG) spectroscopies. 2D IR has previously been used to investigate DNA.^43–49 2D IR and 2D SFG spectroscopies provide many more observables than one-dimensional vibrational spectroscopies like IRRAS and SFG, such as cross-peaks caused by coupling between vibrational modes, 2D line shapes which report on homogeneous and heterogeneous environments, anharmonic shifts that identify secondary structures, lifetimes that are sensitive to solvation, polarization schemes that give relative bond angles, energy transfer between coupled modes, and ultrafast time resolution that reports on dynamics.^50–55 Isotropic distributions of molecules produce no SFG signal, so molecular ordering is also detected with this technique.⁵⁶ In addition, vibrational modes that do not appear in 1D SFG spectra, such as vibrations on structurally disordered chromophores, can still be probed through cross-peaks in 2D SFG spectra.³¹ These additional quantities provide much more insight into molecular structure than the typical frequencies and intensities measured with one-dimensional spectroscopies.^31,32,38 It is especially advantageous to measure heterodyne-detected 2D SFG spectra (HD 2D SFG), as compared to homodyne-detected spectra, because the spectra can be directly compared with 2D IR spectra of bulk samples, which is valuable for assigning peaks and detecting structural and dynamic differences between bulk and surface-bound species.⁵³ For samples on gold and other reflective surfaces, heterodyne detection is straightforward because the inherent nonresonance background can be used as a local oscillator. As a result, a standard broad-band SFG spectrometer can be easily converted into a HD 2D SFG spectrometer simply by adding a mid-IR pulse shaper.⁵⁷

Using these two techniques, we measure oligo(dT) oligonucleotides of chain lengths 10, 15, and 25 in bulk and as monolayers on gold. Simulations of our data constrain the range of nucleobase orientations relative to the surface and the stacking geometry of nucleobases and provide insight into conformational ordering as a function of DNA chain length. We find that the thymine bases have an absolute conformational ordering relative to the gold surface even for ssDNA chain lengths up to 25 nucleotides. Measured spectra most closely match thymine bases that are tilted with C = O groups projecting in opposite directions onto the surface normal. Cross-peaks assigned to coupling between neighboring bases are consistent with bases that are horizontally and vertically shifted relative to one another. We believe that ordering and orientation is most likely linked to how the molecule is connected to the surface, how the bases are constrained relative to each other on the DNA backbone, and the packing density. We propose a model for the ssDNA where the phosphate backbone extends away from the surface with DNA bases projecting C4 = O4 downward toward the surface and C2 = O2 away from the surface.

METHODS

In this section we provide only brief descriptions of our methods. Complete experimental details involving sample preparation and characterization, linear spectroscopy measure-ments, and detailed nonlinear spectroscopy setups are organized in the Supporting Information.

1.1. Sample Preparation.

Oligo(dT) oligonucleotides of length 10, 15, and 25 with 5′ C₆ S−S thiol modifiers were synthesized, HPLC purified by the Biotechnology Center at University of Wisconsin—Madison, and used as received. For brevity, these DNA oligomers are referred to as (dT)₁₀^-SH, (dT)₁₅^-SH, and (dT)₂₅^-SH. All DNA oligomers had liable hydrogen atoms replaced with deuterium atoms by two rounds of H/D exchange where lyophilized DNA powders were dissolved in 99.9% pure D₂O, left overnight at room temperature, and then freeze dried. All samples were prepared in D₂O buffer (described in section 1.1.1) rather than H₂O because D₂O has lower absorbance in the 1600−1700 cm⁻¹ range.

1.1.1. DNA Monolayers on Gold Substrates.

We prepared oligo(dT) monolayers on gold substrates using a well-established method.³¹ D₂O CaCl₂−TE buffer solution was prepared with 1 M CaCl₂, 10 mM Tris, and 1 mM EDTA in 99.9% pure D₂O and set to pH = 7 using concentrated DCl in D₂O. Lyophilized DNA powders were dissolved in D₂O CaCl₂−TE buffer to give a final concentration of 3 μM DNA as verified by UV−vis. A ∼1 cm² fresh gold substrate (purchased from amsbio −100 nm Au on 5 nm Ti on Si ⟨100⟩ wafer) was submerged in 2 mL of the buffered 3 μM DNA solution and placed in an oven incubator at 37 °C for at least 40 h. The deposition solution was contained in a sealed vial, and no noticeable evaporation of the solution was observed. Note that the protective S−(CH₂)₆OH groups of the 5′ thiol-modified oligomers were not removed before reaction with gold in accordance with previously published work.^31,32,38 After deposition, the gold substrate was removed and rinsed thoroughly with 99.9% pure D₂O to remove salts and loosely bound DNA. The substrate was blown dry with flowing N₂ immediately afterward. These samples were used for 2D SFG, IRRAS, and XPS experiments (see the Supporting Information for IRRAS and XPS methods). XPS measurements are a close match to those previously reported. The O/N atomic ratio indicates less than 1 water molecule per base, if any, is present in the dehydrated films. Details for the XPS analysis are given in the Supporting Information, section 2.1.

1.1.2. Solution DNA Samples

Solution DNA samples for both 2D IR and FTIR experiments were prepared by dissolving lyophilized DNA powder in D₂O CaCl₂−TE buffer to a final concentration of 1.45 mM. A 1 μL amount of the DNA solution was placed between two CaF₂ windows separated with a 50 μm thick spacer and enclosed in a sample holder.

1.1.3. Dehydrated DNA Samples

Dehydrated DNA samples for 2D IR, FTIR, and Raman experiments were prepared by dissolving lyophilized DNA powder in 99.9% pure D₂O to a final concentration of 1.45 mM (see the Supporting Information for FTIR and Raman methods). A 1 μL amount of solution was placed on a CaF₂ window and allowed to air dry at atmosphere for 30 min. Afterward, the sample deposited on the CaF₂ window was placed under vacuum in a lyophilizer at 0.060 Torr for 40 h. The dehydrated DNA samples were deposited from pure D₂O rather than D₂O CaCl₂−TE buffer because excess dried salts cause scattering in 2D IR measurements.

1.2. 2D SFG and 2D IR Spectroscopies

The 2D SFG and 2D IR spectrometers are similar to those that have been previously described.⁵³ Briefly, a regeneratively amplified Ti:sapphire laser (Coherent Libra) output femtosecond pulses at a 1 kHz repetition rate. Three-quarters of the 800 nm output pumped an optical parametric amplifier (TOPAS) followed by home-built AgGaS₂ difference frequency generation setup to produce mid-IR light centered at ∼5.8 μm. A CaF₂ window was used to split the mid-IR pulse into a pump and probe beam path. About 95% of the light was sent through a Ge acousto-optic pulse shaper to create the E₁ and E₂ pump mid-IR pulses for both the 2D SFG and 2D IR experiments. The remaining 5% was used as the E₃ probe mid-IR pulse.

For the 2D SFG experiments, the 800 nm light that was not used for mid-IR generation was frequency narrowed using a 1 nm fwhm interference filter centered at 805 nm. The visible pulse and mid-IR pulses were focused and overlapped at the sample as shown in Figure 1. The angle of incidence for the visible pulse was θ_vis = 65° and for the mid-IR pulses θ_IR = 75° from normal. The visible pulse and all mid-IR pulses were p-polarized to collect a ppppp 2D SFG signal. Monolayers of 4-mercaptobenzoic acid were used to phase the 2D SFG spectra, which also relates the phase of the peaks to the absolute molecular orientation as described in the Supporting Information.

Figure 1.

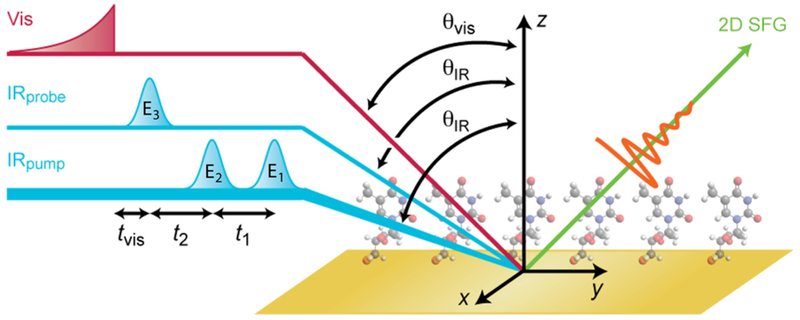
2D SFG spectroscopy pulse sequence and beam geometry. Mid-IR probe and visible pulses are aligned in the same yz plane, while mid-IR pump pulses are displaced slightly along the x axis. All pulses are polarized along the z axis (p polarized).

For the solution 2D IR experiments, a 32-pixel MCT array was used for detection; the limiting probing frequency range was from 1586 to 1713 cm⁻¹, the edge of which is represented by dashed lines in Figure 4c. The 2D IR experiments on dehydrated (dT)₂₅-SH were collected with perpendicularly polarized pump and probe pulses (ZZYY) in order to minimize interference between the signal and the pump light scattered in the signal direction.⁵⁹ Detail experimental setups are described in the Supporting Information.

Figure 4.

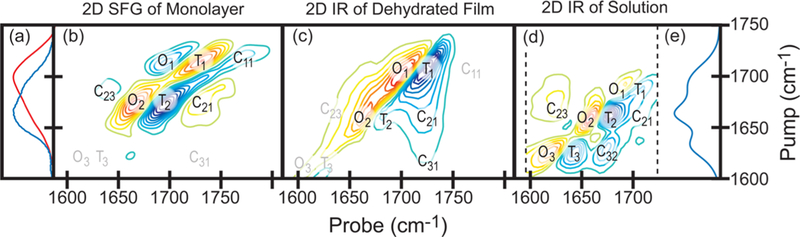
Spectra of (dT)₂₅-SH monolayers, films, and solutions. (a) IRRAS (red) and Raman (blue) spectra of the dehydrated film. (b) 2D SFG spectrum of a monolayer on gold. (c) 2D IR spectrum of the dehydrated film. (d) 2D IR and (e) FTIR spectra in D₂O CaCl₂−TE buffer. Dashed lines indicate the limits of the probe frequency range in d. Peak labels in gray labels represent approximate positions when peaks are weak or nonexistent. Labels refer to T1, T2, and T3 modes, with C_ij being the corresponding cross peaks. All spectra are normalized to the most intense peak and plotted from −1 to +1 with contour steps of 10%, omitting the zero level contour line.

1.3. Density Functional Theory (DFT) Calculations and Mode Assignments

DFT calculations were carried out on deoxythymidine using the B3LYP functional and 6–311G(d,p) basis set using Gaussian 09.⁶⁰ To match our experiments, the H atom attached to the N3 atom in the thymine ring was replaced in the calculation with a D atom. We also performed calculations at the same level of theory on deoxythymidine with three D₂O molecules associated with the carbonyl and N3-D groups, as has been done previously, to explore the difference between hydrated and dehydrated measurements.⁴⁵ Hessian calculations were performed after geometry optimizations to get the anharmonic-corrected mode frequencies, transition dipoles, and Raman polarizability tensors.

The optimized geometries and transition dipole moment vectors for both hydrated and dehydrated deoxythymidine are shown in Figure 2. Transition dipole moment vectors are shown for the three normal modes of interest in this paper that are in the 1600−1750 cm⁻¹ range. These normal modes are described below and referred to as T1, T2, and T3 in descending order of frequency. The contributions of C2 = O2, C4 = O4, and C5 = C6 stretches to each of these modes are given in Table S3 for both hydrated and dehydrated bases. Our calculations are consistent with previous studies on dehydrated DNA.⁶¹

Figure 2.

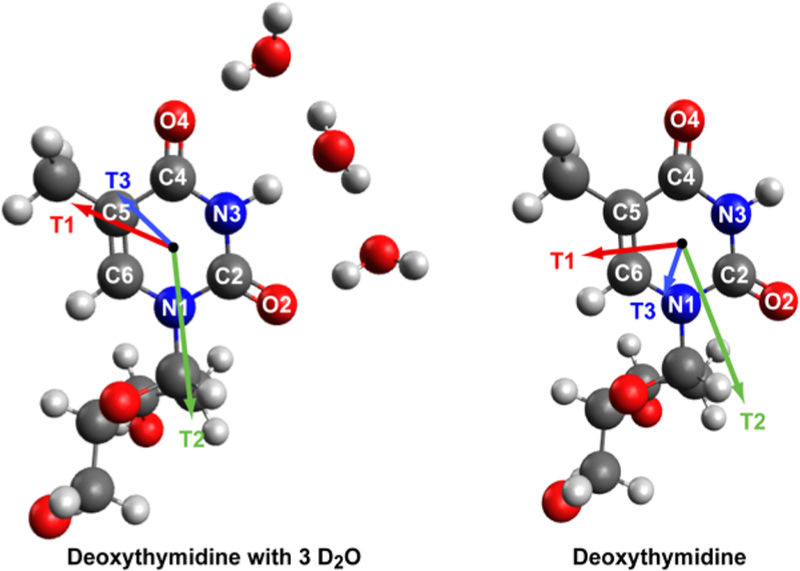
Hydrated and dehydrated deoxythymidine-optimized geometries and transition dipole moment vectors. Direction of vectors for T1 (red), T2 (green), and T3 (blue) are shown. Vector lengths are scaled in each case to indicate the relative strength of calculated transition dipoles.

1.4. 2D SFG Simulated Spectra

We simulate the 2D SFG spectra of ssDNA monolayers in two ways. The first model we present is an uncoupled base model. In this model, we assume no coupling between thymine bases so that a single thymine base is all that is necessary to obtain relative intensity between peaks, the peak signs, and the peak patterns. The purpose of this model is to approximate the single base orientation relative to the surface by matching simulations to experimental spectra. As justified below, all 2D SFG simulations use the DFT calculation results for dehydrated deoxythymidine because the oligo(dT) monolayers are found to have vibrational characteristics of dehydrated oligo(dT) films.

The second model includes coupling between thymine bases. In this simulation, we are still only concerned with the T1, T2, and T3 modes of each thymine base. We model the coupling between four bases, because we find this model adequately reproduces the major features of the experimental spectra. Coupling terms are included between every pair of bases with the coupling constants between any two bases calculated using transition dipole coupling. With four bases (base A, B, C, and and three local modes per base (T1, T2, and T3) there are 12 local modes of interest that are transformed into 12 exciton modes in our model (i.e., the one-exciton block of the Hamiltonian is of size 12-by-12). Before diagonalization, the local mode frequencies are along the diagonal and coupling terms, β, are off-diagonal elements. Coupling between degenerate local modes will cause much larger shifts than coupling between local modes separated by ∼40 cm⁻¹, and so we neglect coupling constants between different types of local modes (e.g., between T1 and T2). Simulation details are provided in the Supporting Information.

RESULTS

2.1. Mode Assignments from DFT and IR Spectroscopies

Hydration plays an important role in the normal modes of thymine bases,^62,63 which must be characterized to properly interpret and model the data presented in this paper. In this section, we present FTIR spectra of (dT)₂₅-SH in solution and of a dehydrated film on a CaF₂ window. We also present the IRRAS spectrum of a (dT)₂₅-SH monolayer on gold, which matches the samples studied with 2D SFG spectroscopy. The comparison between the hydrated and the dehydrated samples allows us to assign the vibrational modes and conclude that little to no water solvates the carbonyl groups in the dehydrated monolayers measured with 2D SFG spectroscopy, as we explain below.

For the solution phase sample, thymine bases have three major vibrational bands in the 1600−1750 cm⁻¹ region, as (blue). These modes are mainly C = O and C = C stretches.^{45 ,64–67} The three vibrational peaks absorb at 1691, 1664, and 1634 cm⁻¹, which is comparable to previously published frequencies for thymidine 5′-monophosphate and (dT)₁₂ in solution.^45,65 We will refer to these modes as T1, T2, and T3 (from highest to lowest frequency) as has been done before.⁴⁵

The IRRAS spectrum of a dehydrated (dT)₂₅-SH monolayer on a gold surface is shown in Figure 3 (red). This monolayer is the same sample used to collect the 2D IR spectrum below (Figure 4c). There is a major peak at 1700 cm⁻¹, a second large overlapping peak at 1667 cm⁻¹, and a third vibrational peak that is a small shoulder in this spectrum but more prevalent in the FTIR spectrum.

Figure 3.

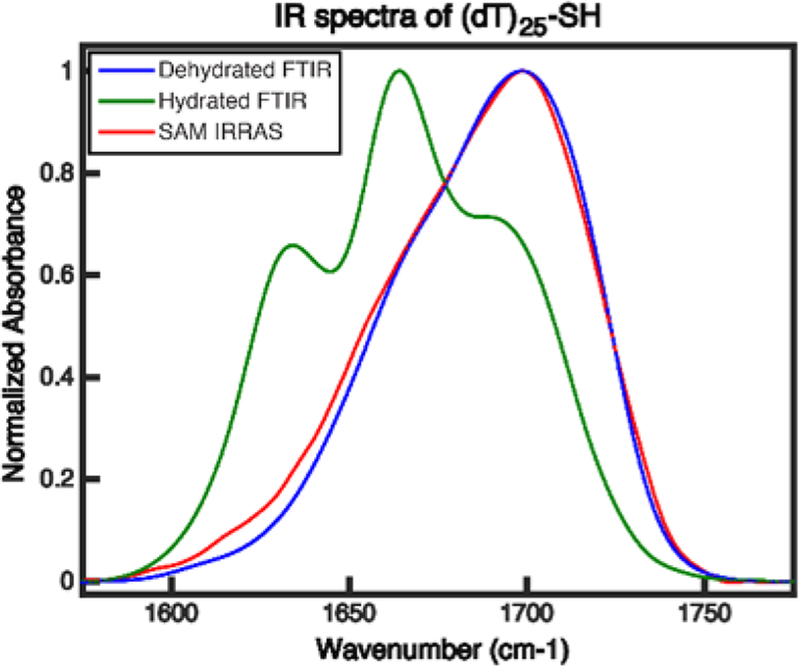
IR spectra of (dT)₂₅-SH. FTIR of (dT)₂₅-SH in D₂O CaCl₂−TE buffer (green), FTIR of dehydrated (dT)₂₅-SH film (blue), and IRRAS of (dT)₂₅-SH monolayer on gold (red). Small residual backgrounds are fit with a linear line and subtracted off each spectrum.

The monolayer and solution phase spectra of (dT)₂₅-SH are very different, which we conclude is due to the difference in solvation. Solvation is largely responsible for the difference between the FTIR and IRRAS spectra. Our conclusion largely stems from the FTIR spectrum shown in Figure 3 (green line) of a thin film dehydrated (dT)₂₅-SH. Even though it is not a monolayer, it closely matches the IRRAS spectrum (Figure 3, green line). DFT calculations show that when deoxythymidine is dehydrated, the normal modes and transition dipole moment vectors are different than in the hydrated case (Figure 2). When hydrated, the T1 mode is mostly C2 = O2 stretching. When dehydrated, one-third of the oscillator strength comes from the C4 = O4 stretch. Dehydration increases local mode mixing, because the C2 = O2 and C4 = O4 local mode stretches have more similar frequencies when there is no hydrogen bonding to water. The T2 mode is also much more delocalized across both carbonyl stretches when dehydrated. In contrast, the T3 mode becomes more localized on the C = C stretching when dehydrated. The detailed vibration mode analysis is found in the the Supporting Information.

With these spectra and DFT calculations in hand, we assign the peaks considering two main points. First, in accordance with our DFT calculations, the T1, T2, and T3 modes stay in the same relative frequency ordering upon dehydration. Second, increases in vibrational frequency are typical when going from hydrated to dehydrated samples because of changes in hydrogen bonding.⁶⁸ In the calculation using 3 water molecules, hydration shifts the modes to lower frequency, which is what we observed in our experiment. For these reasons, we assign the highest frequency peak at 1700 cm⁻¹ to the T1 mode, the peak at 1667 cm⁻¹ to the T2 mode, and the shoulder between 1610 and 1630 cm⁻¹ to the T3 mode (which we also observe below with cross peaks) in the dehydrated samples. We do not consider the relative peak amplitudes in our assignment because the IRRAS and FTIR spectra differ in their orientation and the polarization of the infrared light (IRRAS is only measured with p-polarized light).

The similarity between the IRRAS and the FTIR spectra are surprisingly similar, which raises an interesting scientific point. One would not necessarily expect these two spectra to match, because the IRRAS spectrum is collected with p-polarized light and so only measures the projection of the transition dipoles on the axis perpendicular to the surface following the so-called surface selection rules,^69,70 whereas the transmission FTIR of the film has no such rules. The similarity of the two spectra is interesting because it indicates one of two possible scenarios for the monolayer sample. The monolayer could be so disordered that the surface selection rules makes no difference to the intensities. Or the monolayer could be ordered in such a way that the T1 and T2 projections onto the surface normal are accidentally equal to the ratio of the transition dipole strengths. The mathematical argument of the two cases can be found in the Supporting Information, section 3.2. However, simply put, we know that the latter has to be true because we have nonzero SFG signal.

In summary, we conclude that the (dT)₂₅-SH monolayers studied here are dehydrated to such an extent that there is little to no water surrounding or hydrogen bonded to the carbonyl groups of the bases that are our probe of structure. Therefore, we use the transition dipoles of dehydrated deoxythymidine in our subsequent discussion and modeling.

2.2. Spectral Features Observed in 2D Spectra

In this section, we present 2D SFG spectra of the (dT)₂₅-SH monolayer on gold, whose spectra can now be interpreted in the context of the mode assignments, frequencies, and relative intensities of the FTIR spectra. While the focus of this paper is interpreting the 2D SFG spectrum to probe the structure and dynamics of the monolayer, 2D IR spectra of hydrated solutions and dehydrated films of (dT)₂₅-SH are also shown to aid in the interpretation of the spectra. A one-to-one comparison is possible between the 2D SFG and the 2D IR spectra because the same infrared pulse sequences are used for each spectra and because all spectra are collected with heterodyne detection.^51–53

Shown in Figure 4 are 2D SFG spectra of the (dT)₂₅-SH monolayer on gold, 2D IR spectra of the dehydrated (dT)₂₅-SH film, and 2D IR spectra of (dT)₂₅-SH in D₂O. All spectra shown are collected for a waiting time of t₂ = 0. The corresponding 1D spectra are shown in Figure 4 as well.

Consider the 2D IR spectrum of (dT)₂₅-SH in solution (d) and its corresponding FTIR spectrum (e). Each peak of the 3 peaks in the FTIR spectrum creates as pair of out-of-phase peaks along the diagonal. One of the two peaks lies on the diagonal itself, which is created by a transition to the ν = 1 fundamental (T_i), while the other is created by a transition from the fundamental to the first overtone(O_i), ν = 2. We label each pair of peaks with their corresponding T_i mode. The cross peaks also have positive and negative peaks pairs. However, interference with the much more intense diagonal peaks often obscures one of the two peaks. We label cross peaks with C_ij, which refers to the cross peaks between T_i and T_j mode. Note that the first index (i) refers to pumping mode, and the second index (j) refers to the probing mode.

The diagonal peaks of the 2D IR spectra closely reflect its corresponding 1D spectra, as one expects because 2D IR peaks scale with the transition dipole as μ⁴, but intensities in 2D SFG spectra do not scale like absorption spectra. The peak intensity of 2D SFG is proportional to the product of the transition dipole (μ) and Raman tensor (α). As a result, the product of the Raman and IRRAS spectra in Figure 4a qualitatively match the fundamental peaks in the 2D SFG spectra in Figure 4b. Furthermore, molecular orientation and centrosymmetric averaging can also eliminate diagonal peaks. On the basis of the linear spectra, we also added labels in gray that represent 2D SFG peaks with weak or nonexistent intensity. Also notice that the sign of the T1 diagonal peaks in the 2D SFG spectra are reversed from those in the 2D IR spectrum, which is a measure of the molecular orientation. We explain these observations in more detail in the Discussion.

Cross peaks in 2D SFG and 2D IR spectra are caused by coupling between vibrational modes. In this system, the observed cross peaks could come from coupling between nearby bases (interbase couplings) or form within the same base (intrabase coupling) or both. The 2D IR spectrum of hydrated (dT)₂₅-SH closely resembles the spectrum of thymidine 5′-monophosphate in D₂O buffer,⁴⁵ suggesting that intramolecular couplings play the dominate role, at least for the 2D spectrum in the hydrated sample. Interestingly, there is a cross peak (C₁₁) in the 2D SFG spectrum of monolayer film that cannot be explained by coupling between any of the three modes discussed above. For reasons that become clear later on, we assign this cross peak to intermolecular between T1 vibrational modes on neighboring thymine bases, creating T1 bright and dark states. Detailed description of the spectra can be found in section 2.2 of the Supporting Information.

Although not the focus of this study, the 2D line shapes of the peaks are elongated in the dehydrated samples but mostly round in the hydrated samples. Elongation is a measure of the inhomogeneity of the vibrational bands, indicating a larger degree of environmental and/or structural diversity in the dehydrated samples.

2.3. 2D SFG Spectroscopy as a Function of ssDNA Length

As mentioned in the Introduction, it has previously been concluded that large differences in base ordering occurs between short and longer chain oligo(dT) monolayers.³⁸ To explore this prior conclusion, we compared 2D SFG spectra of monolayers made from (dT)₁₀-SH, (dT)₁₅-SH, and (dT)₂₅-SH, shown in Figure 5 for t₂ = 0 fs. The (dT)₂₅-SH spectrum is reproduced from Figure 4b above.

Figure 5.

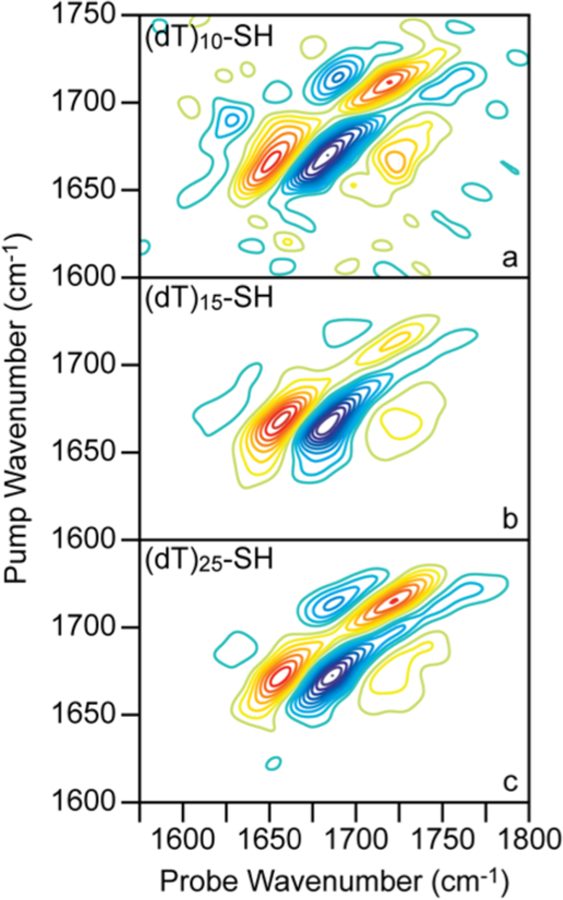
2D SFG spectra of (dT)₁₀-SH, (dT)₁₅-SH, and (dT)₂₅-SH monolayers on gold. 2D SFG spectra at t₂ = 0 fs for (a) (dT)₁₀-SH, (b) (dT)₁₅-SH, and (c) (dT)₂₅-SH. All spectra are normalized to the most intense peak and plotted from −1 to +1 with contour steps of 10%. Zero level contours are omitted002E

Overall, the peak patterns and signs in the spectrum of (dT)₂₅-SH are observed for the shorter chain oligo(dT) monolayers as well. Thus, the peak assignment remains the same in all three cases.

DISCUSSION

3.1. General Interpretation of the 2D SFG Spectra

As briefly mentioned above, heterodyne-detected 2D SFG spectra can be interpreted much like 2D IR spectra. The peak positions give the frequencies of the fundamental and overtone transitions and thus the anharmonicities and couplings of the vibrational modes. However, the peak intensities follow different scaling laws. The peak pairs can be 180° out-of-phase with the 2D IR peaks, the intensities can be very different or nonexistent, and cross peaks between two coupled modes do not have to appear both above and below the diagonal. These differences have been described previously in the context of symmetry selection rules.^53,72 We summarize this previous discussion and generalize to vibrational modes with different transition dipoles and hyperpolarizability, which has not been described previously. We outline these effects with respect to the experiments reported here.

Consider p-polarized laser beams at grazing angle so that the field of the laser pulses are polarized along the Z axis of the laboratory frame. Further consider a molecule with a single mode, A, that has a transition dipole $\left(\stackrel{\rightharpoonup }{{\mu }_A}\right)$ and Raman tensor $\left(\overleftrightarrow{{\alpha }_A}\right)$ .The probability for each of the three infrared laser beams to interact with the molecule is given by the angle between the electric field and the transition dipole, $\left|\stackrel{\rightharpoonup }{{\mu }_A}\right|\cdot \cos {\theta }_{\mu ,Z}\equiv {\mu }_{A,Z\cdot }$ Likewise, the probability that the visible pulse will interact with the molecule is given by the projection with the polarizability, which is more abstract but we will call α_A,ZZ. The total signal strength scales as the product of all 4 interactions

$$I_{AA}\propto {\alpha }_{A,ZZ}{\mu }_{A,Z}{\mu }_{A,Z}{\mu }_{A,Z}=\left({\alpha }_{A,ZZ}{\mu }_{A,Z}\right)\cdot {\mu }_{A,Z}^2$$ (1)

where we clustered the terms into the two IR pump pulses and the IR and visible probe pulses. The “probe” pulses are those found in a typical linear SFG experiment. This equation gives the intensity for the diagonal peak of mode A. For a system with a second mode, B, the intensity of its diagonal peak would be

$$I_{BB}\propto \left({\alpha }_{B,ZZ}{\mu }_{B,Z}\right)\cdot {\mu }_{B,Z}^2$$ (2)

Cross peaks are created by two laser pulses interacting with mode A and the other two with mode B. In this case, there are two possibilities. Two of the infrared pulses can interact with A and the third IR and the fourth visible pulse interact with mode B or vice versa. Thus, the cross peaks will have intensities that scale as

$$\begin{array}{l}{I}_{BA}\propto \left({\alpha }_{A,ZZ}{\mu }_{A,Z}\right)\cdot {\mu }_{B,Z}^2\\ I_{AB}\alpha \left({\alpha }_{B,ZZ}{\mu }_{B,Z}\right)\cdot {\mu }_{A,Z}^2\end{array}$$ (3)

These equations explain why the cross peaks on opposite sides of the diagonal do not need to be of equal intensity. Consider the specific case when $1>\left({\alpha }_{A,ZZ}/{\alpha }_{B,ZZ}\right)>\left({\mu }_{A,Z}/{\mu }_{B,Z}\right)$ . Then the diagonal peaks for A will be much smaller than for B, and the cross peaks in the upper quadrant will be smaller than in the lower quadrant, as shown in Figure 6.

Figure 6.

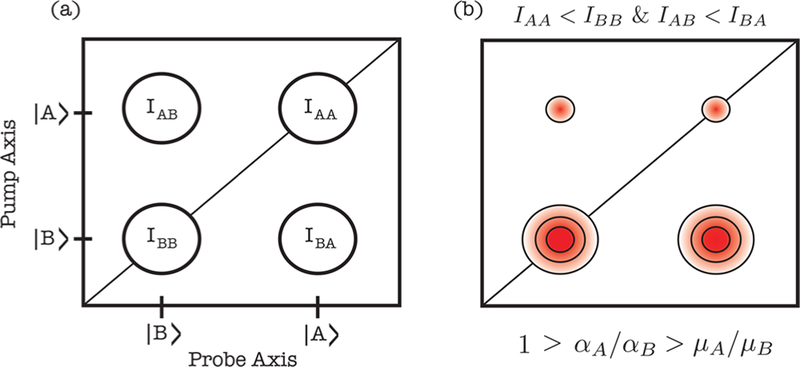
Simplified 2D SFG spectrum with two modes A and B. (a) Fundamental peaks of a two mode system. (b) The asymmetric peak pattern matches our experimental observation. The equation below is one of the conditions for this asymmetric pattern.

This peak pattern is similar to that observed experimentally between the T1 and the T2 modes that create the cross peak C₂₁ in the lower quadrant of Figure 4b. The quantitative simulations presented in section 3.2 below confirm this interpretation (although for a slightly different reason: T1 has a larger Raman tensor than T2 but not large enough to offset the difference in transition dipole strength, which is the second condition in Figure S13(a)). Other scenarios of peak patterns are shown in the the Supporting Information for various ratios of transition dipole and Raman tensor strengths.

Equations 1–3 also explain how different pairs of peaks can have different signs in the 2D SFG spectra. Since ${\mu }_{A,Z}=\left|\stackrel{\rightharpoonup }{{\mu }_A}\right|\cdot \cos {\theta }_{\mu ,Z}$, if the transition dipole points up then this term will have a positive sign and if it points down then it is negative. Likewise, for the Raman tensor term. The total signal is the product of the two and thus depends on the orientation of the molecule with respect to the laser fields. The IR pump term in eqs 1–3 $\left({\mu }_{A,Z}^{2}or{\mu }_{B,Z}^2\right)$ is always positive. Thus, the diagonal peaks are signed similar to the signals of SFG spectra measured with heterodyne detection. Equations 1–3 also show that the cross peaks will have the same sign as the diagonal peaks along the SFG probe axis. For instance, peaks T₁ and C₂₁ in Figure 4 b are both positive since they are corresponding to the same ω_probe at ∼1720 cm⁻¹ (T1 mode). Thus, the phase of the cross peaks helps assign the diagonal peaks to which they are correlated even if the diagonal peaks are too weak to be observed. For example, in Figure 4b, the negative C₂₃ cross peak reveals that the diagonal peaks of the T₃ mode are negative, which is consistent with the base orientation in our simulations. Peak C₁₁ is a cross peak with a dark T1 excitonic mode, as we explain below, but even so can still have nonzero intensity in a 2D SFG spectrum as previously explained.⁵³ A method is also given in the Supporting Information for calibrating the phase to the absolute molecular orientation.

The above discussion is for a single molecule. For an ensemble, we need to average over the molecular orientations, which is often mathematically written by adding brackets, such as for eq 1

$$I_{AA}\propto \langle {\alpha }_{A,ZZ}{\mu }_{A,Z}{\mu }_{A,Z}{\mu }_{A,Z}\rangle$$ (4)

At an interface, molecules will often be randomly oriented in the plane of the surface (e.g., azimuthally distributed). In this situation, the ensemble average does not change any of the above equations. However, molecular orientations at different tilts to the plane will have different signal strengths and so contribute differently to the ensemble average. Isotropic distributions will have equal tilts both above and below the plane which will cancel each other and give zero signal, just as in 1D SFG spectroscopy. However, in 2D SFG spectroscopy, an isotropic mode can still absorb the infrared pump pulses and so can be detected by cross peaks to SFG active modes, as has been described previously.^53,71

For the more general case of laser beams with arbitrary directions and polarizations, the projections are not only along Z but along X and Y as well. In this situation, the signal intensity can be written as

$$I_{p,q}\propto {\chi }_{IJKLM}^{\left(4\right)}=\langle {\alpha }_{q,IJ}{\mu }_{q,K}{\mu }_{p,L}{\mu }_{p,M}\rangle$$ (5)

with I, J, K, L, and M being indexes for the laboratory frame coordinate. In the literature, this is often written as a product of the tensor product of the molecular response in the molecular frame with the ensemble average of the orientation in the laboratory frame

$$I_{p,q}\propto \langle R_{Ii}{R}_{Jj}{R}_{Kk}{R}_{Ll}{R}_{Mm}\rangle \cdot {\alpha }_{q,ij}{\mu }_{q,k}{\mu }_{p,l}{\mu }_{p,m}$$ (6)

which is the method we use to simulate the spectra below.

3.2. Uncoupled Base Model Gives Single Thymine Base Orientation

The spectra and DFT calculations presented above already provide a qualitative interpretation of the data. To more quantitatively interpret the spectra, we simulate the data using an exciton model described in the Methods. Using this model we can determine base orientations that produce 2D SFG signals consistent with the experiment.

As a first step, we calculate 2D SFG spectra for all possible orientations of a single thymine base and model the three vibrational modes, T1, T2, and T3. We use the coordinate system in Figure 7a. In this coordinate system, the X−Y plane represents the flat gold surface in the experiment while the z axis is normal to the surface. We use Eular angles (ψ,θ,φ) to describe the nucleobase orientation. We further assume that the monolayer has azimuthal symmetry,³⁸ so there are only two degrees of freedom (ψ,θ) that define each simulated spectrum. We define the two angles ψ and θ as follows: the ψ angle is the rotational angle around the T3 mode vector, and the θ angle is the angle from the positive z axis to the T3 mode vector. When ψ = 0° and θ = 0°, the T3 mode vector is aligned along the positive z-axis direction and the T1 mode vector is in the yz plane (projection along the positive y axis). When φ = 0° and 0° < θ < 180°, the T3 mode vector is tilted within the xz plane. We simulated 2D SFG spectra for all thymine base orientations by scanning through the ψ angle from 0° to 360° in steps of 1° and the θ angle from 0° to 180° in steps of 1°. Each spectrum is convoluted with a 2D line shape function for comparison to experiment.

Figure 7.

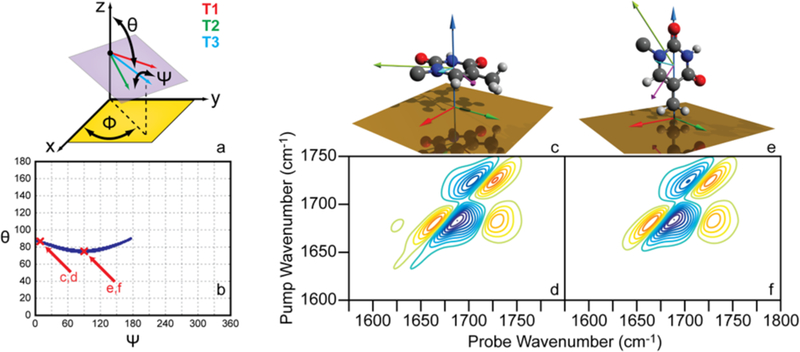
Simulated 2D SFG spectra of an uncoupled single thymine base. (a) Coordinate system for the single thymine base scan. The thymine base plane is represented by the purple surface with T1 (red), T2 (green), and T3 (blue) vectors shown. (b) Orientation (ψ,θ) plot with configurations that produce simulated 2D SFG spectra within the outlined criteria shown as blue dots. The two positions marked with red cross marks correspond to the orientations and spectra shown in Figure 6c, d and Figure 6e, f, respectively. (c) Thymine base in (ψ = 10°, θ = 86°) conformation, and (d) corresponding simulated 2D SFG spectrum. (e) Thymine base in (ψ = 90°, θ = 75°) conformation, and (f) corresponding simulated 2D SFG spectrum.

In order to determine which orientations are consistent with the experimental result, we use the experimental peak signs and relative intensities as constraints. For example, from the experimental 2D SFG spectrum of (dT)₂₅-SH (Figure 4b) we see that the T1 and T2 fundamental peaks have a relative ratio of 0.75 ± 0.05 and are of opposite sign with T1 positive and T2 negative. The other constraint is the intensity of T3. Of all the possible orientations, only the orientations marked with the blue dots in Figure 7b match these three criteria. Thus, the base is confined in θ to angles spanning the range from 74° to 90° and ψ spans from 3° to 176°. Two example orientations that produce spectra that meet the experimental criteria help to demonstrate the determined base orientation solution space. These two orientations are denoted with red marks in Figure 7b. These orientations were chosen because they represent the two extremes of the solution space: a mainly parallel and perpendicular base.

Consider the nearly parallel base given by (ψ = 10°, θ = 86°) and its simulated 2D SFG spectrum (Figure 7c and 7d). Even though the base is mainly parallel to the gold surface, it is still rotated around the T3 vector so that the T1 and T2 vectors project onto the z axis in opposite directions, creating diagonal peaks with opposite signs for these two modes.

The perpendicularly oriented base agreed equally well with experiment (Figure 7e and 7f). The only major difference is the intensity. The perpendicular orientation is about 3500 times larger than the nearly parallel orientation (see Figure S12). In principle, experimental signal intensity could be used to determine which orientation is a better model for the base orientation. However, in our 2D SFG measurements, absolute signal intensity is difficult to quantify because we have no absolute point of reference for signal size.

Optimizing a geometry by matching the intensities and phases of the diagonal peaks is similar to methods for matching 1D SFG spectroscopy.⁷² Polarization might also be used, but it does not work well on gold surfaces.^71,73 A difference between fitting 1D and 2D spectra is that the cross peaks must also match for a good 2D fit, which provides additional constraints. For example, ψ is determined not only from the intensities of both diagonal peaks but also from the C₂₁ cross peak. Thus, there are more observables to fit than available in linear spectroscopies. In the next section, we also model the C₁₁ cross peak, which is resolving a vibrational mode not apparent in 1D SFG or IR experiments.

3.3. Coupled Base Model Gives Relative Orientation of Thymine Bases

Thus far we have not accounted for the effect of coupling between DNA bases, which gives additional structural constraints. The coupling between DNA bases in double-stranded helices is very large (∼4−14 cm⁻¹) between both hydrogen-bonded (paired) bases and stacked bases.^43,45,61 Coupling shifts vibrational frequencies and creates cross-peaks in 2D IR spectra.^44,47,49 In our 2D SFG experiments, if the bases of (dT)_n-SH stack then we would presumably see similar effects. The C₁₁ cross peak cannot be modeled using only a monomer, and Fermi resonances or accidental degeneracies are very rare in this frequency range. In this section, we show that peak C₁₁ can be explained by base stacking.

The C₁₁ cross peak appears at ω_pump = 1715 and ω_probe = 1755 cm⁻¹. It has no counterpart on the quadrant above the diagonal, and so it must be correlating two modes in a scenario similar to Figure 6 in which mode B is much more intense in the 2D SFG spectrum than mode A. Moreover, the sign of C₁₁ is negative, indicating that the higher frequency mode must also have a negatively phased diagonal peak. It is not obvious from the 1D SFG or IR spectra that there is a mode at 1755 cm⁻¹. Thus, this cross peak is providing new information not easily obtainable without 2D SFG spectroscopy.

Coupling between stacked bases can explain the C₁₁ cross peak, which in turn provides additional structural information. To simulate this cross peak we use a model with four bases (bases A, B, C, and D). Overall, each configuration can be represented by orientational angles for each base and coordinates that define the position of the bases $\left(e.g.,{\psi }_A,{\theta }_A,{\phi }_A,x_A,y_A,Z_A,\mathrm{...},Z_D\right)$ . However, only a few conformations are possible that will create a cross peak consistent with C₁₁ and a peak pattern in Figure 6. Vibrational coupling redistributes oscillator strength. In a multibase model, to get a bright mode at a lower frequency than a dark mode, the coupling constant must be negative, which would be created by thymine bases with a vertical displacement, as expected for an oligomer strand with stacked based. By this reasoning we can build a multibase configuration that produces a simulated 2D SFG spectrum in very good agreement with the experimental spectrum, as we show below.

We find that stacking 4 bases in the conformation shown in Figure 8a predicts a 2D SFG spectrum in reasonable agreement with experiment. This conformation has monomer angles of (ψ_i,θ_i) = (135°, 80°) with each base translated from its neighbor by 2.2 Å along the y axis, by 2.7 Å along z, and 0.3 Å along x to give a center-to-center base distance of 3.5 Å. This conformation is similar to that found for the thymine bases in a T-A double helix taken from the Protein Data Bank structure 1D98, shown in Figure 8c. In this conformation, the nearest-neighbor coupling terms are β_{T1i − T1j} = −5.10 cm⁻¹, β_{T2i − 2j} = −6.36 cm⁻¹, and β_{T3i − T3j} = 3.37 cm⁻¹, according to a transition dipole model. In these simulations, a C₁₁ cross peak occurs because of coupling between bright and dark T1 modes that are excitonally delocalized across several bases, as observed experimentally. The phase of the C₁₁ cross peak also matches the experiment, although its intensity is about ∼3 times smaller than that observed in the experiment. More realistic distributions of structures might add diagonal and off-diagonal disorder that would increase the cross peak size by slightly breaking the symmetry (we multiply the cross peak by 3× in Figure 8b for better visualization). Adjusting the geometries did not increase the intensity of the C₁₁ cross peak. Thus, to within the accuracy of the transition dipole coupling model (which is imperfect for stacked bases), an oligomer with a structural conformation similar to that found for thymine in double-stranded DNA gives reasonable agreement with experiment, with the additional constraint being supplied by the C₁₁ cross peak.

Figure 8.

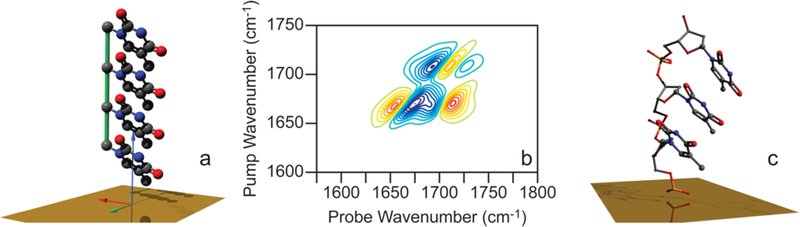
Simulated 2D SFG spectra of four coupled thymine bases. (a) Configuration of four coupled bases with monomer orientation (ψ_i,θ_i) = (135°, 80°), and (b) corresponding simulated 2D SFG spectrum. (c) Oligo(dT) DNA segment from B-type dsDNA (PDB = 1D98) extending from surface in 5′ to 3′ direction and oriented for comparison to a. Spectra are plotted the same as the experimental spectra above.

We point out that our coupled model gives constraints on the relative base geometry and thus the structure of the oligomer but is insensitive to the tilt of the strand. The tilt of the strand alters the absolute intensity of the 2D SFG spectrum but not the features in the same way that the base orientation alters the absolute intensity, as discussed in section 3.2. A tilt of 0°, as shown in Figure 8a, creates a footprint that gives the surface coverage estimated from XPS (discussed in the Supporting Information). Thus, our final structural model is built from intensities and phases of diagonal and cross peaks that constrain thymine base orientation, a cross peak that is consistent with stacking typical of thymine bases, and a tilt angle set to match surface coverage measurements.

3.4. 2D SFG Spectroscopy as a Function of ssDNA Length Reveal Consistent Thymine Base Ordering

We now turn to the 2D SFG measurements in Figure 5 made from different lengths of oligo(dT) monolayers.³⁸ These spectra are remarkably similar to one another, which suggests that they all have similar structures.

We also measured surface coverage using XPS (Figures S1 and S2 and Tables S1 and S2) for comparison to the relative SFG intensities for each length of oligomer (Figures S9 and S11). Interestingly, we find a much larger variability in SFG signals than we do for XPS. XPS only varies by ∼5%, while the SFG intensity varies as much as 40% (Figure S11), measured for precisely the same samples.

The difference between XPS and SFG intensities provides insight into ordering at the surface. Like XPS, SFG intensity scales with surface coverage but SFG intensity also depends on molecular ordering. In principle, two samples could have identical surface coverages and XPS signals but very different SFG intensities if one was ordered while the other was not. The data shown here illustrates this effect. Thus, SFG spectroscopy is much more sensitive to structure than XPS, albeit blind to absolute surface coverage.

The comparison between the XPS and the SFG measurements suggests that there are ordered and disordered regions of oligomers. AFM¹⁴ and STM¹⁵ measurements often observe domains, some of which are more ordered than others, or, it could be that bases closest to the surface are more ordered than bases at the end of the oligomers.⁷⁴ Nonetheless, the SFG signal is larger for (dT)₂₅-SH than (dT)₁₀-SH monolayers (which is also reflected in the relative 2D SFG intensities as well). Thus, longer oligomers do indeed have a larger number of ordered bases. In the future, isotope labeling or using chains of varying sequence could give further insight into base ordering by probing structure at well-defined locations along the oligomer length or calibrants could be used to quantitate the SFG signals. Either way, our data is inconsistent with (dT)₂₅-SH forming polyelectrolyte brushes, as previously suggested.⁴²

CONCLUSION

We presented for the first time 2D SFG experiments on single-stranded DNA monolayers. Our experiment utilizes a mid-IR pulse shaper and broad-band mid-IR pulses to collect heterodyne-detected 2D SFG spectra of monolayers that can be directly compared to 2D IR spectra of bulk samples. We also quantitatively assessed the range of possible structures consistent with the 2D SFG spectra. Diagonal peaks and intramolecular cross peaks were used to constrain the absolute orientation of the bases. Intermolecular cross peaks, caused by coupling between bases, were used to determine that bases are stacked in an arrangement similar to stacking found for poly(T) in double-stranded DNA. We showed that the diagonal peaks in the 2D SFG spectra provide similar information to that obtained with linear SFG spectroscopy, the cross peaks provide more rigorous structural constraints, and in the case of the intermolecular cross peaks they provide entirely new structural information about base stacking. While other investigations of oligo(dT) monolayers concluded that oligomers with 25 or more bases result in disordered polyelectrolyte brushes,⁴² we showed that oligomers of 10, 15, and 25 bases have similar, well-ordered, structures over spans that increase with oligomer length.

This paper focused on model polythymine oligomers, but the approach is also applicable to more general sequences and double-stranded helices as well. All four DNA bases are strongly coupled, whether stacked or hydrogen bonded, in DNA single-and double-stranded oligomers.^43,61,75 Moreover, 2D IR spectroscopy and calculations have been used over recent past years to develop sophisticated coupling models for linking DNA structure to experimental spectra, similar to structure/ coupling methods developed for peptides.^{44,45 ,49} In fact, 2D SFG experiments analogous to those presented here have also been made on peptide monolayers.⁵³ Thus, the experimental methodology and theoretical underpinnings are now in place to begin sophisticated investigations into biological structures at interfaces using 2D SFG spectroscopy.