Active Deep Learning with Fisher Information for Patch-wise Semantic Segmentation

Abstract

Deep learning with convolutional neural networks (CNN) has achieved unprecedented success in segmentation, however it requires large training data, which is expensive to obtain. Active Learning (AL) frameworks can facilitate major improvements in CNN performance with intelligent selection of minimal data to be labeled. This paper proposes a novel diversified AL based on Fisher information (FI) for the first time for CNNs, where gradient computations from backpropagation are used for efficient computation of FI on the large CNN parameter space. We evaluated the proposed method in the context of newborn and adolescent brain extraction problem under two scenarios: (1) semi-automatic segmentation of a particular subject from a different age group or with a pathology not available in the original training data, where starting from an inaccurate pre-trained model, we iteratively label small number of voxels queried by AL until the model generates accurate segmentation for that subject, and (2) using AL to build a universal model generalizable to all images in a given data set. In both scenarios, FI-based AL improved performance after labeling a small percentage (less than 0.05%) of voxels. The results showed that FI-based AL significantly outperformed random sampling, and achieved accuracy higher than entropy-based querying in transfer learning, where the model learns to extract brains of newborn subjects given an initial model trained on adolescents.

1. Introduction

Image segmentation plays an important role for extracting quantitative imaging markers of disease for improved medical diagnosis and treatment. CNNs have been shown to be promising for medical image segmentation [1]. However, they require large training sets to be able to generalize well. In medical applications, labels are often only available for limited subjects who come from a healthy group with a specific age range. Models trained on this population will not perform well in subjects from a different age group (such as newborns or children), subjects imaged on a different scanner or subjects with a specific disease. In order to generalize models, annotating more images is crucial. Due to costly efforts needed for medical annotation, active learning (AL) seems imperative enabling us to build generalizable models with the smallest number of additional annotations. Generally speaking, AL aims to select the most informative queries to be labeled among a pool of unlabeled samples.

Among AL algorithms used for medical image segmentation, uncertainty sampling has been one of the popular methods [2, 3], which queries the most uncertain samples to be labeled. It has recently been used with neural networks, where uncertainty was measured based on sample margins [4] or bootstrapping [5]. For the same purpose, Wang et al. [6] used entropy function but mixed it with weak labels. In addition, more sophisticated objectives such as Fisher information (FI) has theoretically been shown to be beneficial for active learning [7–9]. FI measures the amount of information carried by the observations about the underlying unknown parameter. An earlier work [10] successfully applied FI in medical image segmentation using logistic regression. However, FI based objective functions for AL have not previously been applied to CNN models mainly because of the significantly larger parameter space of deep learning models which leads to intractable computations for evaluating FI.

In this paper, we propose a modified version of FI-based AL for image segmentation with CNN. Modification of FI-based approach is towards making the queries even more informative by making them as diverse as possible. We observe that using the selected queries to fine-tune only the last few layers of a CNN can effectively improve the initial model performance, and thus there is no need for blending with weak labels. Furthermore, we leverage the very efficient backpropagation methods that exist for gradient computation in CNN models to make evaluation of FI tractable. We formulate the proposed diversified FI-based AL for the application of CNN based patch-wise brain extraction and compared it with two baselines, random sampling and entropy-based querying (uncertainty sampling), within two scenarios: semi-automatic segmentation and universal active learning. Our results show that the proposed methods significantly outperform random querying and can effectively improve the performance of a pre-trained model by querying a very small percentage (less than 0.05%) of image voxels. Finally, we show that the FI-based method outperforms entropy-based approach when active querying is used for transfer learning.

2. Methods

We explain our AL method in the context of a single querying iteration, when a parameter estimate $\widehat{\mathit{\theta }}$ is already available from an initial labeled data set. We assume that the CNN model is capable of providing us with the class posterior probability $\mathbb{P}(y|\widehat{\mathit{\theta }},x)$. In each iteration, selected queries will be labeled by the expert and the model will be updated. This process repeats using the updated model. Throughout this section, $\mathcal{U}=\left\{x_1,\dots ,x_n\right\}$ denotes the unlabeled pool of samples and $Q\subseteq \mathcal{U}$ is the (candidate) query set. The goal in a querying iteration is to generate (no more than) k > 0 most informative queries.

2.1. FI-based AL

Fisher information (FI), defined as ${\mathbb{E}}_{x,y}\left[{\nabla }_{\mathit{\theta }}\text{log}\mathbb{P}(y|x,{\mathit{\theta }}_0){\nabla }_{\mathit{\theta }}^{\top }\text{log}\mathbb{P}(y|x,{\mathit{\theta }}_0)\right]$, measures the amount of information that an observation carries about the true model parameter θ₀ ∈ ℝ^τ. Trace of (inverse) FI serves as a useful active learning objective [8, 9], where it is optimized with respect to a query distribution q defined over the pool $\mathcal{U}$ (hence q_i is the probability of querying $x_i\in \mathcal{U}$). Different approximations can be introduced for tractability [7, 10]. Here, we follow the algorithm in [11] (originally used for logistic regression), which aims to solve

$$\underset{q\in {[0,1]}^n}{\text{arg}\text{min}}\text{tr}\left[I_q{\left({\mathit{\theta }}_0\right)}^{-1}\right].$$ (1)

This optimization has a non-linear objective, but it can be reformulated in the form of a semi-definite programming (SDP) problem [12].

2.2. Diversified FI-based AL

Although (1) takes into account the interaction between different samples, it is not obvious how much diversity it includes within Q. In order to further encourage a well-spread probability mass function (PMF) and more diverse queries, we included an additional covariance-dependent term −λtr [Cov_q[x]] into the objective, where λ is a positive mixing coefficient. Unfortunately, adding this term to the objective prevents us from forming a linear SDP. In order to keep the tractability, we constrain ourselves to zero-mean PMFs, i.e., ${\mathbb{E}}_q[x]=0$. This constraint makes the covariance term linear with respect to q_i’s:

$$\underset{q\in {[0,1]}^n}{\text{arg}\text{min}}\text{tr}\left[I_q{\left({\mathit{\theta }}_0\right)}^{-1}\right]-\lambda \sum _{i=1}^n{q}_i{x}_i^{\top }{x}_i\text{s}.\text{t}.\sum _{i=1}^n{q}_i{x}_i=0.$$ (2)

Following an approach similar to [11], we can get the following linear SDP:

$$\begin{gathered} \underset{q\in {[0,1]}^n,t\in {ℝ}^{\tau }}{\text{arg}\text{min}}{t}_1+\dots +t_{\tau }-\lambda \sum _{i=1}^n{q}_i{x}_i^{\top }{x}_i \\ \text{s}.\text{t}.\sum _{x_i\in \mathcal{U}}{q}_i{x}_i=0\&\left[\begin{array}{cc}{\sum }_i{q}_i{A}_i& e_j\\ e_j^{\top }& t_j\end{array}\right]\succcurlyeq 0,j=1,\dots ,\tau . \end{gathered}$$ (3)

where t₁, …, t_τ are auxiliary variables, e_j is the j-th canonical vector, and A_i ∈ ℝ^{τ × τ} is the conditional FI of x_i, defined as

$$A_i:=\sum _{y=1}^c\mathbb{P}(y|x_i,{\mathit{\theta }}_0){\nabla }_{\mathit{\theta }}\text{log}\mathbb{P}(y|x_i,{\mathit{\theta }}_0){\nabla }_{\mathit{\theta }}^{\top }\text{log}\mathbb{P}(y|x_i,{\mathit{\theta }}_0)$$ (4)

Since θ₀ is not known, it is replaced by the available estimate $\widehat{\mathit{\theta }}$. Finally, (2) can be slow when n (pool size) and τ (parameter length) are very large, which is usually the case for CNN-based image segmentation. In order to speed up, we moderate both values by (a) downsampling $\mathcal{U}$ by only keeping β most uncertain samples [13, 11], and (b) shrinking the parameter space by representing each CNN layer with the average of its parameters. When the querying PMF q is obtained, k samples will be drawn from it and the distinct samples will be used as the queries.

3. Experimental Results

We applied the proposed method and the baselines for CNN based patch-wise brain extraction. We use tag random for random querying, entropy for entropy-based querying, and Fisher for FI-based querying with λ = 0.25,β = 200. In entropy, we used Shannon entropy as the uncertainty measure. Our data sets contain T1-weighted MRI images of two groups of subjects: (a) 66 adolescents from age 10 to 15, and (b) 25 newborns from the Developing Human Connectome Project [14]. The CNN model used in our experiments is shown in Fig. 1. Inputs are axial patches of size 25 × 25 × 1. The feature vectors x_i in (3) are extracted from output of the second FC layer.

Fig. 1.

Architecture of the CNN model used for brain extraction

We first trained an initial model using randomly selected patches from three adolescent subjects and used it to initialize AL experiments, where k is set to 50. Each querying iteration started with an empty labeled data set ${\mathcal{L}}_0$ and an initial model ${\mathcal{M}}_0$. At iteration i, ${\mathcal{M}}_{i-1}$ was used to score samples and select the queries. Labels of the queries were added to ${\mathcal{L}}_{i-1}$ to form ${\mathcal{L}}_0$, which was used to update ${\mathcal{M}}_{i-1}$ by fine-tuning only the FC layers. Accordingly, when computing conditional FI’s in (4), we only computed gradients for the FC layers. Next we discuss two general scenarios in evaluating the performance of AL methods.

3.1. Active Semi-automatic Segmentation

Here, the goal is to refine the initial pre-trained model to segment a particular subject’s brain by annotating the smallest number of additional voxels from the same subject. For the sake of computational simplicity, we used grid-subsampling of voxels with a fixed grid spacing of 5, resulting in pool of unlabeled samples with size ~200,000 for adolescent and ~350,000 for newborn subjects. We evaluated the resultant segmentation accuracy for the specific subject after each AL iteration over grid voxels. We also reported the initial/last segmentations over full voxels after post-processing the segmentations with CRF (for newborns), Gaussian smoothing (with standard deviation 2), morphological closing (with radius 2) and 3D connected component analysis.

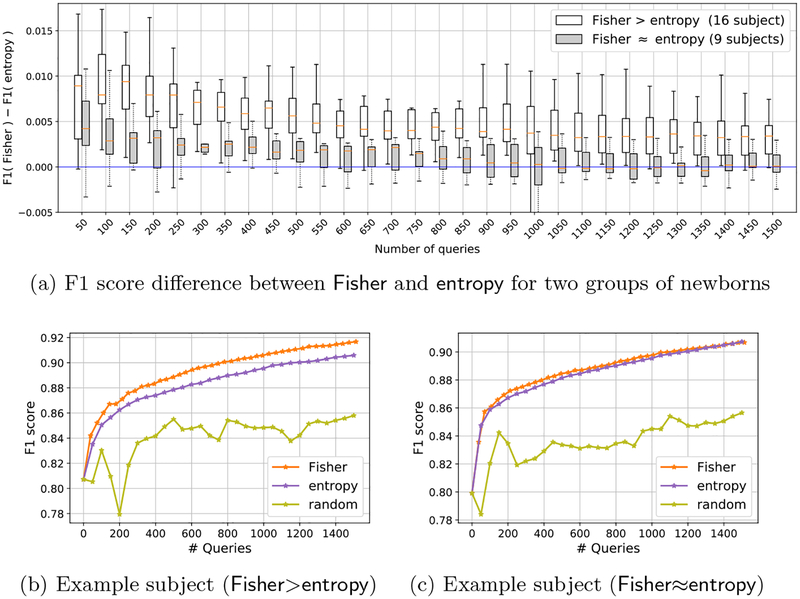
Table 1 shows mean and standard deviation of F1 scores in different querying iterations from 25 newborns and 63 adolescents (after excluding three images used in training ${\mathcal{M}}_0$). This table shows that Fisher and entropy raised the performance significantly higher than random, and increased the initial F1 score by labeling less than 0.05% of total voxels. Whereas, random decreased the average score in the early iterations, which implies potential negative effect of bad query selection. This table shows a slight difference between Fisher and entropy when considering all the images collectively. However, we observed that Fisher actually outperformed entropy in more than 60% of the newborn subjects (16 out of 25), while performing almost equally on the others. Figure 2(a) shows box plots of the difference between F1 scores of Fisher and entropy for these two groups of subjects, where the white boxes are mostly in the positive side.

Table 1.

F1 scores of the models obtained from querying iterations of different AL algorithms. The scores of intermediate querying iterations are based on grid samples, whereas the initial and final scores are reported based on full segmentation.

	Adolescents			Newborns
Initial	85.73 ± 3.91			79.93 ± 2.92
# Queries	Fisher (%)	entropy (%)	random (%)	Fisher (%)	entropy (%)	random (%)
100	87.11 ± 3.04	86.85 ± 3.29	82.61 ± 5.05	84.26 ± 2.86	83.33 ± 2.84	76.4 ± 6.22
500	90.9 ± 2.07	90.62 ± 2.16	85.28 ± 3.48	86.92 ± 2.37	86.47 ± 2.29	80.75 ± 2.96
1000	92.42 ± 1.76	92.57 ± 1.64	86.71 ± 2.88	88.11 ± 2.23	87.89 ± 2.12	82.12 ± 2.84
1500	93.57 ± 1.37	93.5 ± 1.39	87.78 ± 2.44	89.07 ± 2.02	88.82 ± 2	83.11 ± 2.85
Final	95.21 ± 0.94	95.15 ± 0.9	91 ± 1.48	90.24 ± 1.84	89.88 ± 1.72	86.92 ± 2.2

Fig. 2.

F1 scores reported separately for two groups of newborn subjects, when Fisher>entropy and Fisher≈entropy. The box-plots consider all subjects in each group, whereas the F1 curves in (b) and (c) are for one sample subject from each group.

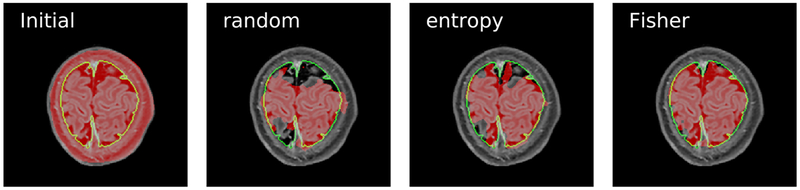
The improvements in F1 scores are shown for two selected subjects, one from each group, in Figs. 2(b) and 2(c). Furthermore, in order to visualize how differences in F1 scores may reflect in segmentations, we also showed in Fig. 3 segmentation of a slice of the subject associated with Fig. 2(b). Observe that the pre-trained model from adolescent subjects falsely classified skull as brain, since brains of adolescent and newborn subjects look very different in their T1-weighted contrast. After AL querying, the methods could better distinguish these regions but random and entropy have much more false negatives than Fisher.

Fig. 3.

Segmentation of a slice using ${\mathcal{M}}_0$ and models obtained in active semi-automatic segmentation of the newborn for which F1 curves are shown in Fig. 2(b). Green boundaries show the ground-truth segmentation and red regions are the resulting brain extraction.

3.2. Universal Active Learning

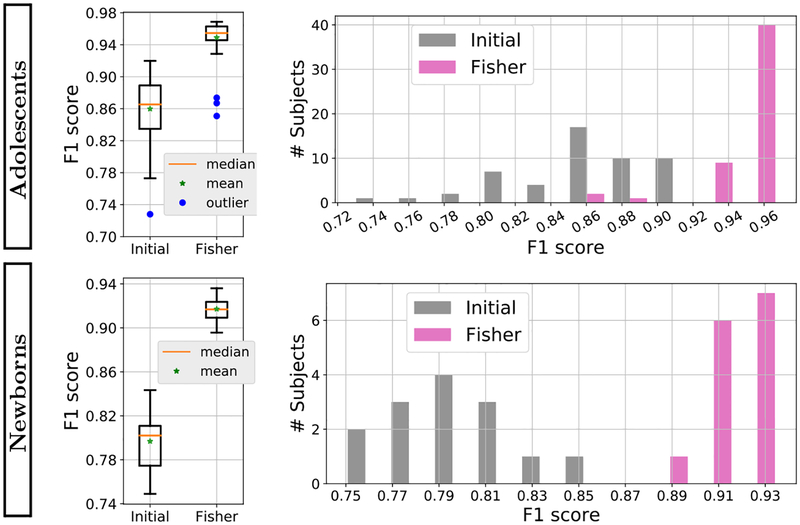
In this section, we used FI-based AL sequentially on a subset of new subjects to further improve the initial CNN model in order to achieve a universal model that can be used to segment all other subjects in the same data set. The goal was to show that FI-based querying method is able to result a more generalizable model. We ran a sequence of FI-based AL over 11 subjects in each data set, such that the initial model of querying iterations over one subject was the final model obtained from the previous subject. The pre-trained model ${\mathcal{M}}_0$ described above was used to initialize the AL algorithm for the first image. For each subject, we continued running the querying iterations with k = 50 until 1,500 queries were labeled. The resulting universal model was then tested on the remaining unused subjects in the data set. Note that for the newborn dataset the problem is a transfer learning scenario, where an initial pre-trained model from the adolescent data set was updated using the proposed AL approach to achieve improved performance in the newborn dataset. Results from test subjects reported in Fig. 4 show that the initial model is significantly improved after labeling a very small portion (less than 0.02%) of the voxels involved in the querying.

Fig. 4.

Statistics of F1 scores of universal models resulting from sequence of FI-based querying over 11 images and the initial model ${\mathcal{M}}_0$ over the test images of adolescent and newborn subjects. The box-plots and histograms show that except for a few adolescent outliers, the F1 scores are significantly increased by our proposed FI-based AL.

4. Conclusion

In this paper, we presented active learning (AL) algorithms based on Fisher information (FI) for patch-wise image segmentation using CNNs. In these new algorithms a diversifying term was added to the querying objective based on the FI criterion; where efficient FI evaluation was achieved using gradient computations from backpropagation on the CNN model. In the context of brain extraction, the proposed AL algorithm significantly outperformed random querying. We also observed that FI worked better than entropy in transfer learning, where we actively fine-tuned a pre-trained model to adapt it to segment images from a patient group with different characteristics (age, pathology, scanner) than the source data set. FI-based querying was also successfully applied for creating universal CNN models for both source (adolescent) and target (newborn) data sets, to label minimal new samples while achieving large improvement in performance.