The causal inference framework: a primer on concepts and methods for improving the study of well-woman childbearing processes

Abstract

The causal inference framework and related methods have emerged as vital within epidemiology. Scientists in many fields have found that this framework and a variety of designs and analytic approaches facilitate the conduct of strong science. These approaches have proven particularly important for catalyzing knowledge development using existing data, and addressing questions for which randomized clinical trials are neither feasible nor ethical. The study of healthy women and normal childbearing processes may benefit from more direct and deliberate engagement with the process of inferring causes and, further, may be strengthened through use of methods appropriate for this undertaking. The purpose of this primer, in tandem with the accompanying second paper, is to provide the reader an introduction to causal inference concepts and methods, aimed at the clinician scientist, and offer details and references supporting further application of epidemiology knowledge. The causal inference framework and associated methods hold promise for generating strong, broadly representative, and actionable science to improve the outcomes of healthy women during the childbearing cycle and their children.

INTRODUCTION

Scientists investigating questions about well-woman pregnancy, labor, and birth outcomes frequently face challenges specific to the study of healthy people and normal, physiologic processes. Causal inference is an existing approach for addressing these scientific challenges, but its uptake in perinatal research is relatively recent. This paper is the first in a series of two that will review the causal inference framework and describe 4 methods emerging from this framework that are especially relevant for investigating healthy childbearing.¹ These articles will provide researchers with an accessible introduction to the causal inference framework and key methods, as well as references where the interested reader can pursue further information (ie, theoretical, statistical, and computational elements). Our target audience includes both readers familiar with pregnancy and childbirth who possess training in basic multivariable statistical modeling and clinicians seeking to interpret translational science.

The study of healthy childbearing processes in women at low risk of complications is emerging as a subject of interest in perinatal epidemiology and health services research.^2–4 This emergence, in tandem with health policy promoting physiologic birth⁵ and midwifery care for women at low risk of complications,^6–8 demarcates a time of scientific challenge and opportunity. The science of perinatal processes and outcomes among healthy women must expand to keep pace with these changes and refine clinical care and policy. Simultaneously, there is growing awareness that experimental research design has important limitations when seeking to answer certain clinical questions.^9,10

Questions regarding physiologic childbearing processes and outcomes can be particularly challenging to address with experimental designs for several reasons. Most healthy women in both high and low-resource settings will experience excellent pregnancy and birth outcomes, even under less than optimal circumstances.^11–13 Hence poor outcomes are rare and thus more difficult to study due to insufficient numbers. Consequently, research on these topics requires large sample sizes, often difficult to achieve. Additionally, many pregnant and laboring women have strong preferences about the kind of care they receive and what happens to them during pregnancy, labor, and birth, making them less willing to be randomized or to persist in randomized studies.¹⁴

Further, compelling arguments have been made that women experiencing unmedicated labor frequently have strong instincts when birthing.¹⁵ There is a rich midwifery tradition and emerging science regarding what helps women who choose to birth without epidural analgesia to follow these instincts and ‘let go’ of higher order brain processing, allowing autonomic processes to be more manifest.^15,16 Complying with study protocols during unmedicated labor (eg, maintaining protocol-driven birthing positions) forces women to stay engaged with higher order brain processing and may increase stress factors that can modify the labor course.¹⁷ As well, women experiencing unmedicated labor may find labor instincts to be so compelling that they are unable to comply with study protocols. All of these points highlight pragmatic and ethical issues when using experimental design in these areas of research. In experimental studies of childbearing among healthy women, willingness to be randomized and the ability to adhere to study protocols in itself selects a sample unlikely to represent the population of healthy birthing women. These factors make healthy pregnancy, labor, and birth questions particularly problematic to study with randomized controlled trials (RCTs), an issue previously identified.¹⁵

This concern about randomization is reflected in various critiques^18–20 of the clinical equipoise principle,²¹ which proposes genuine uncertainty regarding optimizing care for an individual as the primary ethical basis justifying an RCT. Importantly, there is unlikely to be clear consensus for how to apply the clinical equipoise principle to the study of physiologic labor and birth, which are medical and health events but are also personal, emotional, and spiritual experiences, and where various professional birth attendant norms (eg, midwifery versus family practice) coexist.

For all of these reasons, methods from the causal inference framework should be explored as one approach for advancing strong, clinically-relevant, well-woman perinatal science. The purpose of this first paper is to: a) define causal inference, b) provide a brief history of the causal inference framework and associated methods, c) review an example of how such methods have strengthened research in a different area of science, and d) introduce the reader to 2 approaches for causal inference that are particularly relevant to the study of well-women and low-risk perinatal processes: directed acyclic graphs (DAGS), and propensity score analysis.

WHAT IS CAUSAL INFERENCE?

Causal inference is the process of determining that a cause led to an effect. It is a broad scientific framework rather than a set of methods; nevertheless, specific methods are frequently associated with causal inference. It is multi-disciplinary, with roots in philosophy, statistics, epidemiology, economics, and computer science.^22–26 The scientific techniques and concepts within this framework include a set of statistical and epidemiological methods that aim to formalize the assumptions required to assign causality. Thereby the process of framing answerable causal questions and estimating the association between cause and effect is improved.^27,28

Some of these approaches make use of the philosophical concept of the counterfactual.²⁷ The factual is what has happened (eg, the girl bumped the table [cause], then the glass fell [effect]). The counterfactual is what has not happened but what might have happened if conditions were different (eg, the girl bumped the table but grabbed the glass [cause with different, counterfactual condition], then the glass did not fall [counterfactual effect]). The causal inference framework frequently uses the counterfactual (the outcome that did not occur but would likely have occurred if the cause had occurred differently) to conceptualize and inform analysis of the relationship between cause and effect under different exposure or treatment conditions. A causal perspective affects both research design and analysis.²⁹

History

The history of etiological thinking is likely longer than our recorded account of it, but 18^th century philosopher David Hume is frequently considered a forebear of modern causal thinking. His formulation of a cause as something that “if the first object had not been, the second never had existed”²⁵ remains influential in much causal thinking, including the counterfactual framework,³⁰ which is often (although not exclusively³¹) a central tool in the study of causation. Because etiological thinking and the causal inference framework do not emerge from a single discipline, assembling a linear chronology of these concepts is challenging. However, some landmark concepts and tools stand out, including: 1) the counterfactual framework (also called the potential outcomes framework),³² 2) causal diagrams,^33–35 3) epidemiologic causal criteria,³⁶ 4) quasi-experimental designs (eg, instrumental variables and regression discontinuity methods),^37,38 5) the sufficient-component cause model,³⁹ 6) propensity score methods,²⁶ and 7) the g-methods.^40,41 It is important to recognize that RCTs are themselves a tool for causal inference. The approaches described above may be (but are not exclusively⁴²) employed by investigators when an RCT is not feasible, ethical, or desirable, and their broader use can open previously unexplored avenues for addressing important perinatal questions.

Methods for causal inference emerge from multiple analytical traditions, and not all are quantitative methods. What connects many methods and much of the thinking on causal inference is a rigorous accounting of specific assumptions required to propose that a relationship is causal or even that it is possible to evaluate a given causal question with a given dataset (ie, that a causal effect is identifiable). Valid statistical estimation and inference rely on assumptions. In a parallel but distinct process, causal inference invokes assumptions, only some of which are testable, and evaluates the extent to which these assumptions may be met so that causality may be inferred.⁴³ To demonstrate the utility of causal thinking and methods, we describe how researchers in another scientific field have used these approaches to advance knowledge.

Case Examples of Causal Inference

The causal inference framework is frequently used in social epidemiology to study social determinants of health. For example, research has examined how features of residential neighborhoods (eg, built environment, economic opportunity or deprivation) are associated with the health status of neighborhood inhabitants,⁴⁴ but there are considerable challenges in determining whether these associations are causal, and if so, the strength of the causal association.

Randomized experiments of neighborhood residence exist but are extremely rare, so investigators have used other appropriate methods to analyze the effect of neighborhood residence on health to assess causality.⁴⁵ For example, Sampson and colleagues wanted to understand the effect of disadvantaged neighborhoods on children’s verbal cognitive ability. Because of the logistical challenges of randomizing families to live in disadvantaged versus advantaged neighborhoods, the research team used an approach designed to isolate causal effects. They applied inverse probability of treatment weighting (an analytical technique especially well-suited to control for time-dependent confounding)⁴⁰ to a longitudinal dataset following children in Chicago. This was done to demonstrate both the observations and corresponding set of exposure and confounding variables within the dataset with which a causal effect could be identified (given that not all causal questions will be answerable in a given dataset), and the causal effect of low-resource neighborhoods on children’s verbal ability.⁴⁶ They showed that living in a severely disadvantaged neighborhood had a negative causal impact on children’s verbal cognitive ability, an effect approximately equivalent to missing one year or more of school. They also demonstrated that a causal effect was not identifiable in their entire sample because an insufficient number of white and Latino children were exposed to the highest levels of neighborhood disadvantage. Thus valid comparison between neighborhood disadvantage levels for these children could not be made, and the authors only estimated an effect among African American children.

Studies using similar data structures and/or analytical approaches have advanced knowledge of neighborhood health effects, an area of investigation where causal effects are particularly challenging to isolate.^45,47,48 The scope of the challenges confronting the estimation of causal effects in well-woman childbearing research is similar. Specifically, just as it is generally unfeasible and unethical to randomize families to reside in a certain neighborhood, it may be equally so to randomize women to receive pregnancy or childbirth care that they would not choose.

As exemplified in this example, the process of engaging with causal inference can be disappointing: it could reveal that the available data set may not enable the investigator to address all research questions. This dataset and the analytical approach enabled effect estimation among African American children, but were inadequate for inferring causes for white and Latino children. Causal inference is a framework that supports the iterative process of determining what scientific questions can and cannot be addressed given a specific dataset and analytical technique. Thus, use of this framework might help a research team conceptualize study plans that are informed by the limitations of an existing data set and by the limitations and assumptions of the proposed methodologies, to enable asking (and ideally, answering) a causal question.

To provide a perinatal analogy to the above example (ie, a question for which a causal effect may not be identifiable), consider the example of obesity in pregnancy. Suppose a researcher has a cross-sectional dataset containing measurements of pre-pregnancy maternal body mass index (BMI), pregnancy outcomes, and confounders. The researcher wishes to examine the causal effect of pre-pregnancy BMI on birthweight. Using a regression model the researcher estimates that each unit of BMI change is associated with 20 grams of infant birthweight. She multiplies the BMI coefficient by -10 to determine the effect of weight loss of 10 BMI units (eg, from an obese BMI of 33, to a normal weight BMI of 23), and concludes that infants would be 200 grams smaller under such a scenario.

Now suppose that the researcher was able to go back and collect additional, longitudinal weight measurements in the 10 years before conception, and these additional data revealed that BMI frequently increases (and rarely decreases) over time, and the maximum weight loss in the 10-year preconception period was 3 BMI units. This would demonstrate that the aforementioned scenario of a 10-unit decrease is extremely unlikely to occur in the real world, as indeed it is. There is not consensus that causal questions must correspond to observed or observable interventions.⁴⁹ However, it does bear considering: what does it mean to use our data to estimate an effect that we never observe in that dataset and/or may never be observed in reality? If the researcher wishes to formulate a causal question that can be observed in the empirical data, he or she may choose to reframe the question of interest as the effects of a 10 BMI-unit increase rather than a decrease. Another approach would be to extrapolate the calculated association to a hypothetical population whose BMI units are decreased through some other mechanism (eg, an intervention that prevented development of obesity). An explicit causal inference framework can help to select identifiable, meaningful questions and to estimate effects to answer them.

TWO METHODOLOGICAL APPROACHES PARTICULARLY RELEVANT TO THE STUDY OF HEALTHY WOMEN AT LOW-RISK FOR COMPLICATIONS

Directed Acyclic Graphs

Directed acyclic graphs (DAGs) are causal diagrams to improve research design and also to identify an optimal analytic approach, particularly when the research question involves complex causal chains.^34,35 DAGs are akin to conceptual frameworks, with formal rules for defining causal effects and various forms of bias. As such, DAGs make unstated relationships between variables explicit, thereby informing the choice of which variables to collect, differentiating confounders from mediators (and therefore determining which variables to control for), explaining and identifying selection bias, and supporting effective communication between researchers. For the consumer of research, creating a DAG can help to clarify if a study accurately represents clinical realities. DAGs are useful at various study stages and can be created prior to data collection and again before analysis. While DAGs are not the only method of accomplishing these goals, the visual nature and simplicity of DAGs can be very helpful and can be applied to any study design (eg, both prospective and retrospective) and data source.

Using DAGs to identify confounders

Suppose a research team wishes to analyze if the length of time a woman is upright versus recumbent during labor impacts her length of time in active labor. A straightforward, unadjusted analysis requires only comparison of how much time a woman was upright versus how much time she was reclining and length of labor. A DAG could be used to improve this research. In Figure 1, arrow 1 is the causal path of interest, representing our study question. The causal effect must go from the exposure (maternal positioning) to outcome (length of labor). Using a DAG assists the researchers in mapping out other variables that might influence these relationships. For example, if there was someone in the room both encouraging the woman to assume upright positions (arrow 2) and also encouraging the woman in other ways, apart from her position, that are speeding her labor (arrow 3), then this encouragement, not the woman’s position, may be leading to a shorter time in active labor (ie, a confounding bias).

Figure 1.

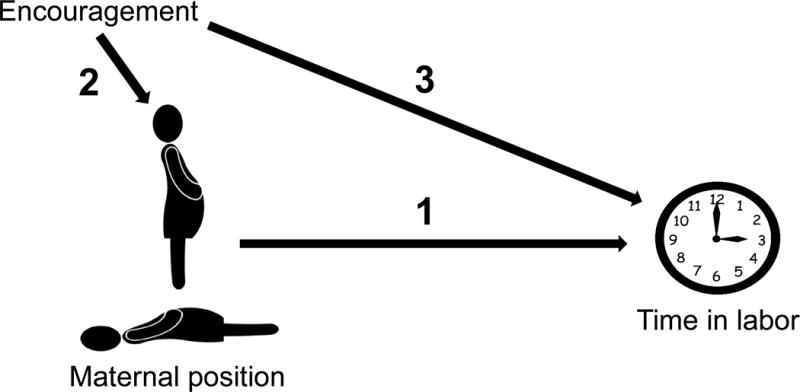
DAG representing the causal question of interest, the effect of labor position on length of labor (arrow 1) and demonstrates a confounder of the main association, encouragement during labor (arrow 2 + arrow 3)

Together, arrows 2 and 3 form another pathway connecting exposure and outcome. However, it is not an arrow pointing out of the exposure (maternal positioning), rather it points into or predicts the exposure and also the outcome (length of labor). For this reason, this arrow is termed a backdoor arrow into the exposure: arrows 2 and 3 create a backdoor path, evidence of confounding. When DAGs identify a backdoor path, it is essential that one variable on this path be blocked. This could be accomplished either by fixing one variable on the pathway (eg, no encouragement given during the labor process) or controlling for encouragement during statistical analysis (eg, regression modeling). In this example, controlling for encouragement during labor, prevents this unblocked backdoor path from introducing confounding bias into estimation of the causal effect of the exposure on the outcome. In practice, identifying whether a backdoor path connecting exposure and outcome is unblocked (ie, can introduce confounding) is more complex; we refer the reader elsewhere for a detailed discussion of this topic.⁵⁰

Using DAGs to differentiate confounders from mediators

DAGs can also help identify confounders (ie, variables associated with exposure that also cause the outcome and result in mixing of effects) versus mediators (ie, variables on the causal pathway between exposure and outcome). Using our previous example of an upright versus recumbent position during labor, another variable that might be considered is fetal descent. It is difficult to imagine how fetal descent might influence whether a laboring woman assumes an upright or a recumbent position (eg, if a fetus is descending rapidly, a woman may assume various positions to cope with this sensation, either upright or recumbent). But it is plausible that when a woman is upright, factors such as gravity and motion of the pelvis might speed fetal descent and that this fetal descent would lead to more rapid labor progress. Because fetal descent may be affected by maternal positioning during labor (but is extremely unlikely to affect whether a woman is upright or recumbent), and fetal descent might plausibly influence the length of time in labor, it is a mediator and therefore should not be controlled during analysis (Figure 2).

Figure 2.

DAG representing the direct effect of maternal position on time in labor (represented by the curved arrow) and the indirect effects mediated by fetal descent (represented by the straight arrows).

Using strictly data-based definitions of confounding without reference to a causal structure (eg, if including a variable in the statistical model changes the magnitude of the effect size by 10%, then consider it a confounder) can lead to incorrectly identifying mediators as confounders.⁵¹ Controlling for mediators frequently obscures, or masks, the overall relationship between exposure and outcome. Confusion regarding which variables are confounders and which are mediators has resulted in decades of inappropriate control of variables, inaccurate study results, or new sources of bias (termed over-adjustment bias).⁵² For example, recent research has revealed mis-estimation of the relationship between small-for-gestational-age neonates and increased risk for adiposity; this was caused by adjusting for mediators (eg, height).⁵³ DAGs help elucidate the true underlying causal structures, thereby informing more appropriate analytical strategies and avoiding these kinds of errors.^54,55

Using DAGs to identify selection bias

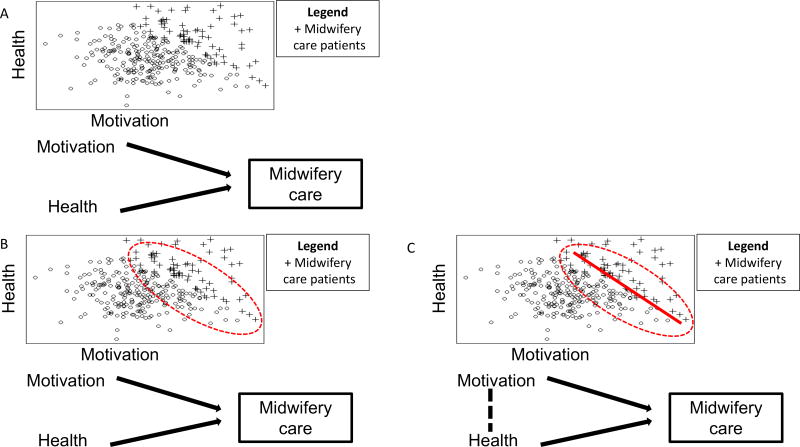
DAGs can also identify selection bias in a study design or analysis plan; to demonstrate we have adapted an example from Morgan and Winship to demonstrate how.²⁴ Suppose that the researchers are conducting their research in a population in which women’s motivation to have a vaginal birth and their health status are completely unrelated (Figure 3 a). However, their study is only recruiting women who receive midwifery care (Figure 3 b). This creates a relationship between these 2 previously unrelated factors in this selected sample (Figure 3 c). In the language of DAGs, we have conditioned on a collider, which is a variable caused by 2 other variables. In this example, midwifery care is the collider. This DAG shows us that within this study population, selection bias causes 2 variables to be associated which are unrelated in the general population: health and motivation for vaginal birth are now related to each other. Specifically, the negative trend line evident in the selected sample indicates an inverse association (Figure 3c), in contrast with the absence of trend in the entire population (Figure 3a).

Figure 3.

3a: Women’s motivation to have a vaginal birth and their health status are completely unrelated, represented by no line between motivation and health. 3b: Women choosing and receiving midwifery care are often both healthier and have higher motivation for a vaginal birth than the general population, represented by arrows from motivation and health into midwifery care. 3c: As a result of selecting women for study inclusion based on a factor (eg, receiving midwifery care) that is caused by 2 other variables (high health and/or high motivation for vaginal birth), there is now a relationship between these 2 previously unrelated factors in this selected sample.

The conditions in this example demonstrate one way that bias emerges in a study. Selection bias is most clear when considering the women who either have low levels of motivation to have a vaginal birth or are unhealthy. Women with low motivation for vaginal birth must be very healthy to have been included in the study population. And women with poor health must have high motivation for vaginal birth to have been included in the study population. This intuitively describes the inverse association (Figure 3c) between the 2 variables in our sample that create a collider.

The general effect of this selection bias (ie, sampling study participants in such a way that unrelated factors in the population become related in the sample) is to distort associations in the sample. To understand how, consider the original study question, that of labor positioning on labor duration. Due to qualities of the women more likely to choose and be appropriate to receive CNM care, an association is created between the exposure (labor position) and the outcome (labor duration) [Figure 4 a, b, and c]. Thus, selection bias is introduced into our study, resulting in incorrect estimates of the association between exposure and outcome (Figure 4 d).

Figure 4.

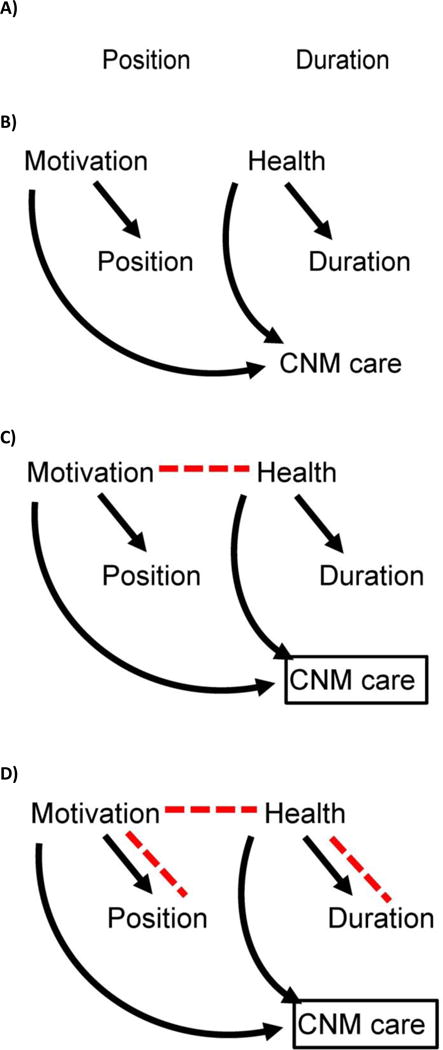
4a: Assume there is no association between the labor position and duration. Lack of causal association between labor position (exposure) and labor duration (outcome) in the second hypothetical study is shown by no arrows or lines connecting them. 4b: Suppose that women who are especially motivated to birth vaginally are also eager to try things during labor that they have heard might help them birth vaginally, such as standing or walking. So, these highly motivated women might be both especially interested in being midwifery patients (and thus potentially in the study) and also especially interested in being upright during labor. Motivation for a vaginal birth predicts labor position and CNM care, and maternal health predicts labor duration and CNM care, but there is still no association between labor position and labor duration. 4c: In parallel, suppose that healthier women have more efficient labors. So, these healthier women might be both especially interested in being midwifery patients (and thus potentially in the study) and also more likely to have rapid labors (assume for simplicity that these are the only associations in our causal system). There may be no association between the exposure (maternal position in labor) and outcome (length of time in active labor) in our population, but when we restrict analysis to women receiving midwifery care, we distort the association between motivation and health status, which in turn opens a new backdoor path between exposure and outcome. In a study restricting to CNM patients (represented by the box around CNM care), motivation and health will be associated (red dashed arrow), because CNM care is a collider. 4d: The new pathway between motivation and health in the sample of CNM patients (not present in the overall population) creates a new, biasing pathway between maternal position and duration of labor (red dashed lines): this is selection bias.

Although the causal system behind this research question has been simplified to enhance clarity, mapping out these associations with a DAG helps a research team identify such biases, which in turn guides data collection and analysis. Further, the simplifications inherent in such exercises are not a shortcoming of DAGs, rather they are shortcomings of our data sources and analytical approaches. DAGs merely serve to clarify when these shortcomings exist and ensure that the simplifications a research team incurs as a normal part of the research process are the most strategic ones. In sum, DAGs are one approach that helps researchers design and conduct a valid study through: 1) forcing an articulation of how variables fit together; 2) defining which variables should be controlled and which should not, and 3) identifying potential selection bias.

Propensity Score Analysis

While DAGs provide a graphical tool to represent the causal system underlying a research question so that study validity is enhanced, propensity score techniques are a set of analytical methods for estimating causal effects that make use of Rosenbaum’s propensity score.²⁶ Like many analytical approaches for causal inference, propensity scores are most common in secondary data analysis but have application in primary data collection as well.⁵⁶ A propensity score is the probability that a participant received a treatment based on observed, measurable baseline characteristics. In the context of physiologic birth research, it expresses the probability that an individual woman would have chosen or been exposed to one exposure setting or another (eg, upright versus recumbent labor positioning). For the researcher, propensity score analysis helps to minimize differences between the exposure groups. For the consumer of research, propensity score analysis increases confidence that any significant study findings are more likely related to the influence of the effect being studied rather than pre-existing differences in the women who were compared. In an RCT with 2 treatment settings (eg, group versus individual prenatal care) that were assigned randomly at equal probability, every woman would have the same probability (50%) of having received a treatment. If randomization was successful, no other factor would affect a woman’s probability of receiving treatment. In observational studies, the treatment assignment mechanism is considerably more complex as individuals and care providers select treatments based on multiple factors, which can create confounding bias. Propensity score analysis involves explicitly modeling how treatment and non-treatment groups were formed, to control for these complex and multi-variable factors. In this way, propensity score analysis decreases confounding bias (sometimes referred to as treatment selection bias,⁵⁷ but distinct from the selection bias described above).⁵⁸ There are at least 4 ways to conduct propensity score analyses (ie, propensity score estimators) including: 1) covariate adjustment using the propensity score, 2) stratification on the propensity score, 3) propensity-score matching, and 4) inverse probability of treatment weighting using a variation of the propensity score. Description of each approach is beyond the scope of this paper but we refer the interested reader to other literature.⁵⁹

Using Propensity Scores to increase balance between two groups

To provide an example, suppose a researcher wishes to evaluate the association between participation in group prenatal versus individual prenatal care (exposure) and perinatal outcomes. However, in this retrospective study, women self-selected to model of prenatal care based on their preferences and background (eg, race, age, and educational background). This confounding makes it difficult to ascertain if it is the model of care or something inherent in the women that explains observed associations. Suppose that the researcher finds that women who received group prenatal care had lower odds of cesarean birth compared to women who received individual prenatal care, but is unsure if this association owes to group prenatal care or if women who choose group prenatal care have other characteristics lowering their risk for cesarean. Appropriate application of propensity score analysis increases a research team’s certainty that any association seen is due to the effect of the studied exposure (model of prenatal care) on the outcome (cesarean).

In each of the 4 propensity score estimators (matching, adjustment, stratification, and inverse-probability weighting),⁵⁹ the first analytic step is to generate propensity scores for all study participants. This involves using what is known about study participants (ie, all known characteristics), to calculate the probability that each participant would have chosen group prenatal care. Continuing this example, consider one individual from the data set (Figure 5, participant 1): a woman who is nulliparous, 28 years old, married, and white who chose group prenatal care. Based on the characteristics of the entire sample of women who did and who did not choose group prenatal care, a propensity score (0.75) representing the likelihood that this woman would have chosen group prenatal care can be generated. Being a probability, the range of the propensity score is zero to one, and this relatively large propensity score indicates that, based on her characteristics, this woman was likely to have chosen group prenatal care, as she did in reality. Moving now to consider the next participant who is also nulliparous and is 29-year-old, single, and white, but chose individual care (Figure 5, participant 2). This woman is demographically similar to the prior participant who chose group prenatal care (eg, her race, age, and parity are similar), but she chose the alternative exposure setting (individual care). This intuition is borne out by this second woman’s propensity score, which shows that based on the characteristics of all women in this sample, this individual was also quite likely to have chosen group prenatal care (probability=74%).

Figure 5.

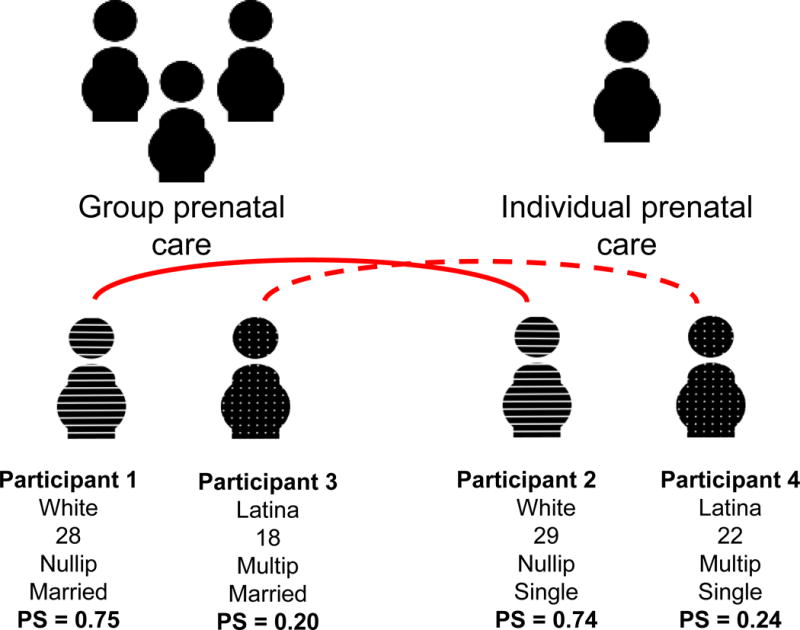
Figure describing characteristics and corresponding propensity score for 4 women, 2 who self-selected to group prenatal care and 2 who self-selected to individual prenatal care, and indicating which 2 women are matched during propensity score analysis- both solid and interrupted lines connect pairs

Now consider the third study participant (participant 3): she is a woman who is multiparous, Latina, 18 years old, married and who chose group care. Because so many of the other women in this sample who chose group care are dissimilar from this individual, her propensity score is low, just 20%. This indicates that someone sharing her characteristics was unlikely to have chosen group prenatal care. Lastly, consider a fourth woman with similar characteristics to the third study participant (22-year-old, single, multiparous, Latina) who chose individual care (participant 4). This woman also had a low propensity for choosing group prenatal care, 24%.

These hypothetical study participants demonstrate how propensity scores represent the probability that each participant in the entire sample would have chosen the designated treatment arm (group prenatal care) of the study. In this way, rather than identifying and adjusting separately for each confounder (eg, race, maternal age, etc), propensity scores condense the many characteristics proposed to be related to women’s choices (or, the vector of confounders) into a single variable which describes how likely a participant was to have been “exposed.” The propensity score can be considered a synthesis of all confounders related to choosing group versus individual prenatal care so that the investigator may compare women who are exposed to those who are unexposed but who are alike on this single, complex variable. In this example, participants 1 and 3 were exposed and participants 2 and 4 were unexposed, so if one wishes to assess the effect of exposure on outcome, either participant 2 or 4 could be chosen as the comparator for participant 1. The propensity score indicates that woman 2 is a better “match” for woman 1 than woman 4 is (ie, she is very similar across a range of confounders, but differs by her exposure status). This is the broad analytical principle underlying RCTs, and propensity scores use an additional analytical step to mimic this design so that it may be applied to observational data. Using the propensity-score matching estimator, women who had similar propensity to choose group prenatal care are matched during analysis (Figure 5, dotted and solid lines). This process is technical and there are numerous approaches for modeling the propensity score and selecting a matched observation; we refer the interested reader elsewhere for details on the mechanics of and options available for this process.^60–62

This matching enables comparison of women who have more similarities and who differ only by exposure setting. By comparing women who are similar, there is less possibility that confounding characteristics that may have affected each group assignment (self-selection) might be driving outcomes. Decreasing confounding bias increases our conviction that causality explains calculated associations. Propensity scores may also be used to determine whether there is ample data support to answer a given question; there may be samples where there are no or few exposed women to match to unexposed women. This circumstance is similar to the neighborhood effects study discussed previously, in which white and Latino children were never exposed to the highest neighborhood deprivation, meaning that this causal question could not be addressed in these sub-populations due to lack of data support. When this occurs, causal inference may be tenuous or impossible, owing to “non-positivity” or failure to satisfy the experimental treatment assignment assumption.^63,64 Put more simply, if a woman’s chance of getting group prenatal care is so high that no women receiving individual prenatal care have a comparable propensity score, then it may not be possible to infer a causal effect of the exposure among this woman and other women like her. Propensity score analysis helps identify instances of this structural confounding⁶⁵ and suggests alternative questions, approaches, and statistical quantities of interest.

Because propensity score analysis explicitly assesses and accounts for confounding bias in a rigorous and multi-dimensional manner, an investigator is likely to: 1) identify observations and combinations of variables within the data where causal inference is not feasible, 2) select a causal question that can be answered given the dataset, and 3) balance confounders between the exposure groups in the remaining data. Collectively, this process increases the investigator’s assurance in the estimation of the causal relationship between the treatment and the outcome, because the method helped clearly define an answerable causal question and minimized alternative sources of explanation (eg, confounding bias).

DISCUSSION

The causal inference framework and associated methods hold great promise for well-woman pregnancy and childbearing science. To date, such methods have been more commonly applied in epidemiology, biostatistics, and economics. But the applications in well-woman perinatal science are wide in scope and their potential to broaden understanding of healthy processes during pregnancy and childbirth is great. Causal inference is not the solution for every research question: some questions are not causal in nature (eg, predictive and descriptive questions), and the analytical techniques associated with causal inference may not be well-suited to a given research question or data structure. However, using rigorous methods in a causal framework does encourage the investigator to: 1) explicitly state the specific causal question, 2) rigorously determine whether a given data resource is capable of answering this question (eg, are causal assumptions met?), 3) deliberately design a statistical analysis plan that will estimate a result that corresponds to the research question, and finally 4) clearly state what competing explanations besides causality may underlie an association (ie, is there bias due to assumptions not being met?).

The demand for midwifery care has grown in recent years and is likely to further expand, thus opening opportunities for wider growth of this model of maternity care. Well-woman perinatal science must keep pace with clinical and policy changes, to provide relevant, valid research supporting and guiding the care of healthy US women during childbearing. We posit that using an explicit causal framework will help perinatal scientists to choose high-impact questions with direct real-world applications and then thoughtfully match these research questions to appropriate data resources and methods, catalyzing understanding of physiologic pregnancy and childbirth processes. This advancement will in turn benefit the care that healthy pregnant and laboring women receive, providing the strongest evidence base to maximize well-woman childbearing outcomes.

QUICK POINTS.

• This paper is the first in a series that reviews emerging approaches for addressing scientific challenges encountered with the investigation of pregnancy, labor, and birth outcomes.

• Causal inference is a broad scientific framework rather than a set of methods; however, specific methods are often associated with causal inference.

• Directed acyclic graphs (DAGs) and propensity score analysis are methods frequently used for causal inference that may be especially relevant to the study of healthy women and physiologic childbearing.

• The causal inference framework and associated methods hold great promise for generating strong, broadly representative, and actionable science to improve the outcomes of healthy women and their children.