The dynamic receptive fields of retinal ganglion cells

Abstract

Retinal ganglion cells (RGCs) were one of the first classes of sensory neurons to be described in terms of a receptive field (RF). Over the last six decades, our understanding of the diversity of RGC types and the nuances of their response properties has grown exponentially. We will review the current understanding of RGC receptive fields (RFs) mostly from studies in mammals, but including work from other vertebrates as well. We will argue for a new paradigm that embraces the fluidity of RGC RFs with an eye toward the neuroethology of vision. Specifically, we will focus on (1) different methods for measuring RGC RFs, (2) RF models, (3) feature selectivity and the distinction between fluid and stable RF properties, and (4) ideas about the future of understanding RGC RFs.

1. Introduction

The most outstanding feature in the present analysis is the flexibility and fluidity of the discharge patterns arising in each receptive field.… Stability […] disappears when one or more of several parameters, such as the adaptation level, stimulus intensity, and area of illumination, are changed singly or in combination. In the absence of a fixed pattern from the whole receptive field, it does not appear accurate enough to speak of “on, ” “on-off” or “off” fibers in the cat’s retina.

-Steven Kuffler (1953)

Remarkably, Steven Kuffler in the first description of receptive fields in a mammalian retina, already realized the fluidity of the concept of a receptive field (Kuffler, 1953). Sixty-five years later, we are still grappling with the difficulty of capturing concisely and completely how the visual world is encoded in the firing patterns of retinal ganglion cells (RGCs).

Another insight in Kuffler’s 1953 paper that was decades ahead of its time was that a complete understanding of the visual code of the retina must capture how populations of RGCs signal together. The retina has emerged as one of the premier systems for the study of population codes (Meister, 1996; Shlens et al., 2008), but we will restrict our discussion here to the RF properties of individual RGCs, an enormous field on its own. The early history of RFs as a tool to characterize visual neurons has been reviewed elsewhere (Spillmann, 2014), and recent reviews have focused on RGC typology (Sanes and Masland, 2015) and principles of retinal computation (Gollisch and Meister, 2010). As our understanding of RGCs has improved, a set of studies over the last several years has brought new emphasis to the concept of RF fluidity. Fluidity of RGC computations with light adaptation was the focus of another recent review (Rivlin-Etzion et al., 2018). We will discuss RGC RFs from this new perspective.

Conservation of RGC structure and function across species

While understanding the function of human RGCs is an important long-term goal of retinal research, we rely on animal models, so it is important to take stock of our current understanding of cross-species homology. Conscious visual perception in humans and non-human primates is dominated by the fovea, where the midget system with single cone resolution was a relatively recent evolutionary adaptation. In the peripheral retina, there are a wide variety of RGC types across many vertebrate species. Morphological similarity has been a key criterion for determining possible homologies between RGC types in different species, and compelling correspondence has been established from humans to non-human primates, to cats, and to rabbits (Goodchild et al., 1996; Rodieck, 1998; Sivyer et al., 2011). Studies have estimated similar RGC morphological diversity in primate (Dacey et al., 2003), cat (Boycott and Wassle, 1974; Isayama et al., 2000), rabbit (Rockhill et al., 2002), rat (Huxlin and Goodchild, 1997), and mouse (Kong et al., 2005; Sun et al., 2002; Völgyi et al., 2009). In several cases, functional parallels between species have also been established. Melanopsin expressing RGCs serve non-image forming visual functions in a set of pathways conserved across human (Provencio et al., 2000), non-human primate (Dacey et al., 2005), rat (Hannibal et al., 2014), mouse (Hattar et al., 2002), and chick (Bailey and Cassone, 2005). A functionally similar RGC type in rabbit, mouse, and non-human primates has been hypothesized to play a role in smooth pursuit eye movements (Puller et al., 2015). Orientation selectivity (OS) is conserved in rabbit, mouse, and even teleost fish (Antinucci et al., 2016), and the OS computation in these different species may even involve morphologically homologous amacrine cells (Bloomfield, 1994; Hoshi and Mills, 2009; Nath and Schwartz, 2017; Wagner and Wagner, 1988).

This review will include results from many of these species, with an emphasis on mouse, where genetic tools have led to a recent explosion in new information about RGC types, circuits, and computations. Much of the data in this field comes from ex vivo preparations in which the retina is preserved in a light-responsive state outside of the animal. In rodents, the firing properties of RGCS measured in vivo in the optic nerve (Nobles et al., 2012) and ex vivo (Pang et al., 2003) are quite comparable. Several recent studies have also made direct links between RGC firing patterns measured ex vivo and responses in retino-recipient brain areas, like dorsal lateral geniculate nucleus, measured in vivo (Piscopo et al., 2013; Román Rosón et al., 2018; Tikidji-Hamburyan et al., 2015).

Despite these encouraging signs suggesting that ex vivo preparations from a variety of animals share structural and functional motifs with the human retina, we should keep in mind the limitations that come from this set of model systems. RGC measurements from non-primates are likely to be poor comparisons for perceptual tasks involving the fovea that make up the majority of human psychophysics. The human peripheral retina – which contains the overwhelming majority of retinal area, diversity of RGC types, brain targets, and evolutionary history – is largely homologous to the retina of other species. Since reading has become a central part of our sensory experience and we are most aware of our conscious visual perception, much work in visual neuroscience has focused on the fovea. It is important to remember, when thinking about the diversity of RGC types and functions, that most of the circuitry linking photoreception to behavior lies outside the perceptual pipeline from retina to thalamus to cortex.

Defining a receptive field

The visual world is multi-dimensional and contains a wide variety of features. As the sole visual input to the brain, RGCs represent the behaviorally relevant complexity of the visual world in their spike trains. Unlike the pixel representation of a visual scene captured by the photoreceptors, RGCs transmit highly processed visual information about motion, shape, color, size, contrast, etc. The mammalian retina contains ~100 different types of interneurons that process visual signals into ~40 parallel channels defined by each RGC type (Baden et al., 2016; Bae et al., 2018; Masland, 2012; Sanes and Masland, 2015). The most general definition of a RGC RF would be a complete understanding of the stimulus to response relationship – the map between spatiotemporal patterns of light and RGC spikes.

Given the complexity of retinal circuits, a concise definition of the receptive field of a RGC includes simplifying assumptions and is necessarily incomplete. The central simplifying assumption in defining a receptive field is that it represents a static entity. We know that there are numerous sites of adaptation throughout the retina (Baccus and Meister, 2002; Rieke and Rudd, 2009), so any static RF represents, at best, a snapshot of the system in a particular steady state. Section 4 will probe this assumption in detail, exploring which aspects of RFs change with stimulus conditions and which are invariant.

Even for a static RF representation, there are tradeoffs associated with additional simplifying assumptions. In Section 3, we will examine a range of RF models from the simplest center-surround difference-of-Gaussians to substantially more detailed models. Models of RFs, of course are based on data, so before examining the models, we will discuss the various methods that have been employed to measure RGC RFs (Fig. 1) and the different kinds of data they provide.

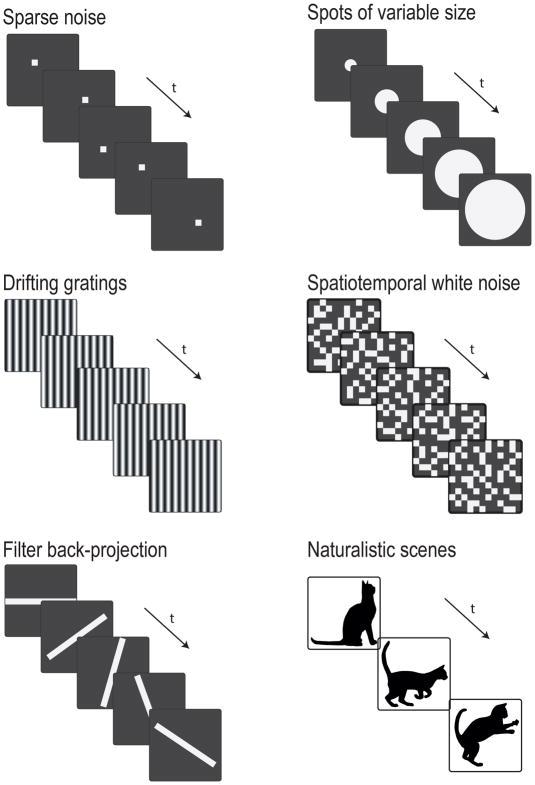
Figure 1. Stimuli used for measuring RGC RFs.

2. Methods for measuring RGC receptive fields

The first-order classification of a RGC RF is generally made on the basis of the polarity of its light response. RGCs are classified as ON, OFF, or ON-OFF based on whether their firing rate increases at the onset of a light stimulus, the offset of the stimulus, or both (Sanes and Masland, 2015). A lesser-known fourth class of RGCs is the suppressed-by-contrast (SbC) RGCs, which decrease their steady firing at both light onset and offset (Jacoby et al., 2015; Levick, 1967; Mastronarde, 1983; Sivyer et al., 2011, 2010; Tien et al., 2015; Troy et al., 1989). After polarity, receptive field size is emphasized in RGC classification because the size of the receptive field has been associated with perceptual acuity (Dowling, 1967; Peichl and Wassle, 1979). The kinetics of RGC light responses (i.e. transient verses sustained) is another aspect of their RFs that has helped researchers distinguish between RGC types and describe their different functions (Baden et al., 2016; Caldwell and Daw, 1978; Lee, 1996; Levick, 1967; Silveira et al., 2004). We will see that other aspects of RGC responses (e.g. contrast sensitivity, spatial frequency sensitivity) and selectivity for specific features (e.g. direction of motion or orientation) are less commonly included in typical RFs, but they are vital in appreciating and predicting the full range of RGC light responses.

Methods for measuring RGC RFs have typically focused on the three aspects of light responses mentioned above: polarity, size, and kinetics. Not all methods are appropriate for all three properties, and we will emphasize how the RF one measures depends on methodology (Peichl and Wassle, 1979). There are also tradeoffs in experimental speed, parallelization, and precision (see Table 1).

Table 1.

Method	ON-OFF separable	Spatial resolution	Kinetic information	Dataset Size requirements	Parallelizable	Data on subunits	Other considerations
Sparse Noise	Yes	Can be high but scales experiment time	Yes	Medium	Only for a few cells	No	Spatial RF depends on spot size and intensity
Spots of Variable Size	Yes	Low	Yes	Low	No	No	Center size conflated with surround strength
Drifting Gratings	No	Low to Medium	Limited	Low to Medium	Yes	Size but not location	Response to motion may differ from static RF
Spatiotemporal White Noise	No with STA; Yes with more complex analyses	Dependent on checker size	Limited	High	Yes	Yes, with recent analysis tools	Spatial resolution conflated with surround strength
Filter Back-Projection	Yes	Low to Medium	Yes	Medium	Yes, but experiment time scales with map area	No	Projection artifacts
Naturalistic Scenes	Yes	Medium	Yes	Very high	Yes	Yes in theory, but not shown experimentally	Computationally demanding, and optimal solution is not guaranteed

Sparse noise

The measurement of RGC RFs in mammals began with Kuffler’s (1953) characterization of cat RGCs. He employed a method now known as “sparse-noise” (Brown et al., 2000; Jones et al., 1987; Reid et al., 1997). A small exploratory spot of light is randomly placed over the visual world and the response of the neuron is recorded (Daw, 1968; Kuffler, 1953; Rodieck and Stone, 1965). The spatial extent of the receptive field is defined as the region in which the spot elicits a response. A key advantage of the sparse-noise method is that the distribution of responses is easily interpreted into the receptive field. The method also enables the experimenter to probe the polarity of the RGC, even allowing for the simultaneous measurement of separate ON and OFF RFs for ON-OFF cells. Sparse noise offers information about response kinetics only if each presentation of the exploratory spot is sufficiently long in duration, increasing the time of the experiment. Disadvantages of the sparse noise method include that it takes many repetitions and spatial locations to generate a robust receptive field, that it is not easily parallelizable (i.e. only one or possibly several cells can be measured at a time), and that the estimate of receptive field size is dependent on the size and intensity of the exploratory spot (Field and Chichilnisky, 2007).

Spots of various sizes

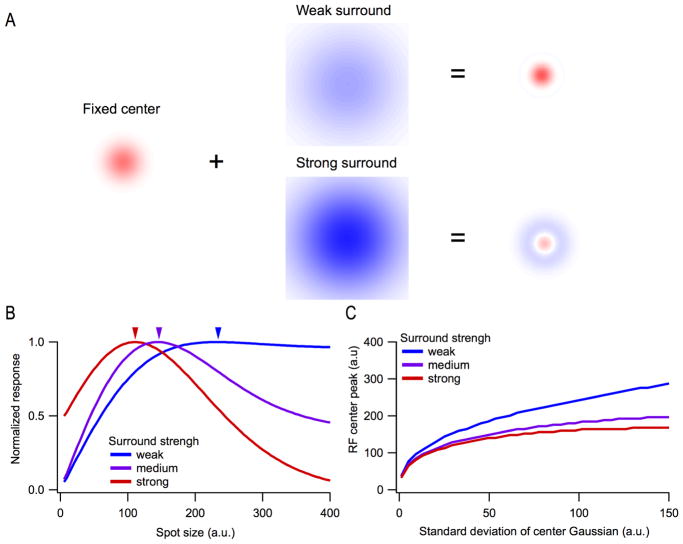
One method that naturally follows from sparse noise is using spots of various sizes (Enroth-Cugell and Lennie, 1975; Partridge and Brown, 1970; Peichl and Wassle, 1979; Sakmann and Creutzfeldt, 1969; Wiesel, 1960). Spots of different diameters are presented at a fixed location, and the smallest spot size that generates the maximal response is designated as having measured the size of the center of the receptive field. This method is highly interpretable and can rapidly offer information about polarity, size, and kinetics. The major disadvantage of this method is that it assumes circular symmetry, estimating the size but not the shape of the RF. Fine spatial structure and orientation selectivity cannot be measured by the spots-of-various-size method. Since the spots must be aligned to the RF center for the measurement to be valid, it is not robust to alignment errors, and it is not parallelizable at all; only one RGC can be measured at a time. Additionally, this method conflates the strength of suppression in the RF surround with the size of the center (Fig 2).

Figure 2. Estimated RF center size can depend on surround strength.

(A) Schematic of the sum of a fixed RF center with either a weak or a strong surround. (B) A model of normalized response (integral of RF) as a function of spot size for 3 different strengths of the surround. The RF center size is fixed. This is the response one would measure with the spots-of-varying-size technique. Arrowheads indicate the spot size giving the peak response, often used as a measure of the RF center size. (C) Relationship between the standard deviation of the RF center Gaussian and the estimated RF size from the peak response for 3 different surround strengths as in (B).

Drifting gratings

Enroth-Cugel and Robson developed an alternative method for measuring receptive fields involving drifting gratings (Enroth-Cugell and Robson, 1966). A sinusoidal drifting grating represents a single spatial frequency. The authors measured contrast sensitivity at different spatial frequencies of the grating. They then used the inverse Fourier transform to convert their measurements from the frequency domain to the spatial domain, thus estimating a spatial receptive field. This method was revolutionary at the time, and it allowed for rapid measurement of the spatial RF with a stimulus to which most RGCs respond robustly. The drifting gratings method is also suitable for measuring many RFs simultaneously, making it useful for large-scale multi-electrode array recordings or calcium imaging studies (Borghuis et al., 2011; DeVries, 1999). Another advantage of this method that has led to its adoption in cortex is that, when gratings are presented at different orientations, it provides measurements of orientation and direction selectivity (De Valois et al., 1982). Despite these advantages, measuring a RGC RF using drifting gratings also has several disadvantages. Like the spots-of-various-size method, it does not resolve fine substructure within the RF center, and it conflates suppressive surround strength with center size. It also offers little information about response kinetics, since firing is controlled by the modulation frequency of the stimulus. Finally, while presenting a moving stimulus is useful to activate RGCs robustly, measuring a static spatial RF from a moving stimulus relies on the assumption that flashed images and moving objects are represented similarly in the retina. While this has been shown to be a reasonable assumption for certain RGCs in the regime of low contrast and low spatial frequency (Cooper et al., 2016), static and moving stimuli have also been shown to be represented differently in many retinal circuits (Berry et al., 1999; Chen et al., 2013; Kim and Kerschensteiner, 2017; Kuo et al., 2016; Manookin et al., 2018; Schwartz et al., 2007; Vaney et al., 2012; Zhang et al., 2012)

Spatiotemporal white noise

Building on the linear systems approach of Enroth-Cugel and Robson, spatiotemporal white noise has become the most common stimulus employed to investigate RGC RFs (Brown et al., 2000; Chichilnisky, 2001; DeAngelis et al., 1995; Devries and Baylor, 1997; Field et al., 2010; Field and Chichilnisky, 2007; Gauthier et al., 2009; Reid et al., 1997; Yu and De Sa, 2003). In this method, a “checkerboard” with randomly flickering squares is presented to the retina and spike responses are recorded from RGCs. The straightforward method of spike-triggered-averaging (STA) – computing the mean stimulus sequence preceding a spike for each RGC – allows researchers to measure RFs from many cells in parallel. Using small checkers can reveal fine structure in spatial RFs, and response kinetics can be inferred from the mean temporal filter of the center pixels for each cell. These advantages have made spatiotemporal white noise the method of choice for most RGC RF mapping studies, and variations have been developed, including circular annuli (Fransen and Borghuis, 2017; Sakai and Naka, 1987), full field contrast flicker to investigate temporal responses in isolation (Fukada, 1971; Manookin et al., 2015), and random color checkboards to measure the contributions of individual cones (Field et al., 2010).

Despite the ubiquity of the spatiotemporal white noise STA approach, several important disadvantages limit interpretations of RFs measured by this method. One critical limitation of the standard STA approach is that it does not reveal separate ON and OFF RF components for ON-OFF cells. ON-OFF cells are classified as either ON or OFF based on which polarity dominates, and a perfectly balanced ON-OFF RF would cancel completely. This problem can be mitigated to some extent by more sophisticated analyses of the spike-triggered stimulus ensemble (Cantrell et al., 2010; Fairhall et al., 2006) – an issue we will return to below in our discussion of RF models.

Kinetic information is also limited in the spatiotemporal white noise method. One can extract a temporal kernel from the RF center pixels, but the kernel predominantly represents information near the temporal frequency of the stimulus (i.e. the refresh rate of the checkerboard). The STA computation filters out both high and low temporal frequencies. This is a general problem in applying a linear analysis, like STA, to the nonlinear responses of RGCs, and we will explore the issue of nonlinearities in space and time in greater detail in the next section.

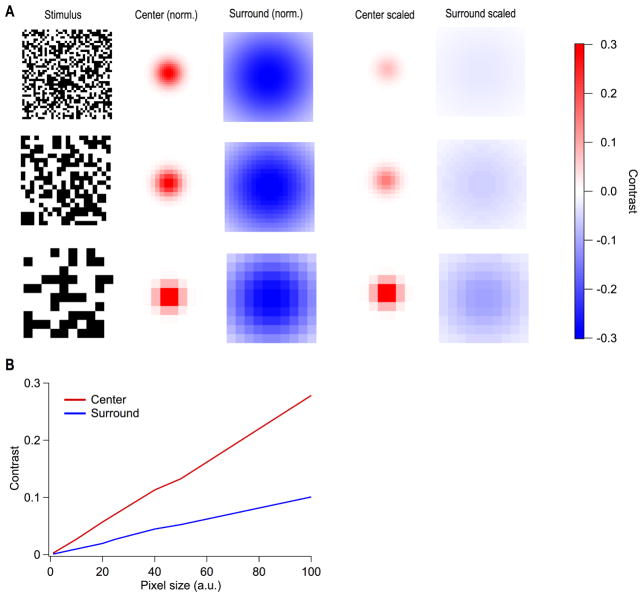
Finally, there is a tradeoff between the resolution of the stimulus (checker size) and the activation strength of different components of the RGC RF. Checkers that are very small compared to the RF center allow for fine resolution RF maps but create low total contrast across the RF center, so many cells respond weakly or not at all. The size vs. resolution tradeoff is even more problematic in the RF surround because its large integration area corresponds to extremely low contrast for small checkers. Thus, it is difficult to measure RF surrounds with spatiotemporal white noise, and estimates of center vs. surround strength are confounded by the choice of stimulus resolution (Fig. 3). The opposite problem occurs with excessive activation of a suppressive surround. Some RGC types are suppressed completely for wide-field stimuli and are, thus, silent for spatiotemporal white noise (Jacoby and Schwartz, 2017; Zhang et al., 2012).

Figure 3. Measurement of RF center and surround strength vary with the spatial resolution of a spatiotemporal white noise stimulus.

(A) Example white noise stimuli at 3 spatial resolutions along with the RF center and RF surround sampled at each resolution. The final 2 columns show the RF center and surround measurements again, but scaled by their relative strength based on the contrast of the stimulus within the center and surround, respectively. Contrast scale corresponds to these last 2 columns. (B) The relationship between the pixel size of the white noise stimulus and the contrast elicited in the RF center and RF surround.

Filter back-projection

A recently introduced method called filter back-projection (FBP) combines some of the advantages of sparse noise with the parallelizability of spatiotemporal white noise (Johnston et al., 2014). As opposed to randomly flashing spots, bars are flashed at different positions and at five or more orientations. The receptive field can then be computed using a method from X-ray scans called the inverse radon transform (Radon, 1986). Like the related sparse noise method, FBP allows for the separate measurement of ON and OFF components of the RF and the kinetics of RGC responses can be measured for sufficiently long stimulus durations. Unlike the classical sparse noise method, FBP is suitable for parallel measurements of RGC RFs on a multi-electrode array or by functional calcium imaging (although, unlike spatiotemporal white noise, experiment time scales with the total area being mapped). Because the stimuli are long bars, FBP is particularly useful for measuring orientation-selective RFs. While it is generally more efficient than spatiotemporal white noise at measuring the basic shapes of RGC RFs, FBP is limited in its ability to resolve fine structure within the RF. Another disadvantage is that it is prone to projection artifacts, which appear as streaks in the spatial RF map.

Naturalistic stimuli

The natural visual world contains spatio-temporal correlations unlike pure Gaussian white noise (Eickenberg et al., 2012; Nirenberg et al., 2001; Pitkow and Meister, 2012). Therefore complex, naturalistic stimuli are used to investigate responses to more physiological stimuli that the visual sensory neurons might encounter in the wild (Kastner et al., 2015; Katz et al., 2016). These naturalistic stimuli have included natural temporal-chromatic movies with space removed (van Hateren et al., 2002), generated white-noise with long range spatio-temporal correlations (Pitkow and Meister, 2012), naturalistic motion stimuli (Leonardo and Meister, 2013), natural movie scenes (Haider et al., 2010; Nirenberg et al., 2001), even incorporating eye movements (Turner and Rieke, 2016). Using naturalistic stimuli invalidates the assumption of zero stimulus correlations that is required for linear STA-like analyses. Several analysis modifications have allowed researchers to adapt STA-like techniques to naturalistic stimuli. These include generalized linear models (Heitman et al., 2016), and removal of stimulus autocorrelation (Lesica et al., 2008). Most of these methods have had limited success, so theorists have devised a new set of tools to search for feature selectivity with stimuli of arbitrary statistics.

One such tool, called maximally informative dimensions (MID) involves an iterative search through stimulus space to find the dimensions that maximize the mutual information between the stimulus and the spike train (Sharpee et al., 2002). In theory, MID can find multiple selective dimensions in stimulus space given arbitrary natural stimuli. The disadvantages are that it requires a lot of data (~10⁵ spikes), and the parameter space is non-convex, so there is no guarantee that a search algorithm will find the optimal solution. A variant of MID, called quadratic mutual information, has also been used to extract RGC filters from natural scenes (Katz et al., 2016). While the data requirements for this method are substantially less than for MID, it only revealed single spatiotemporal filters for each RGC that were not qualitatively different than the STA. Deep learning has also been employed in recent work to reveal aspects of retinal circuitry in the context of natural scenes (Maheswaranathan et al., 2018).

Closed loop experiments

All the RF measurement techniques we have discussed so far rely on recordings of spike responses from RGCs. Whole-cell recordings of synaptic currents in RGCs have also been measured and used to construct a class of RF models we will consider in the next section (Gregory W. Schwartz et al., 2012), but such recordings are much rarer and more labor intensive than spike recordings and do not scale to large numbers of simultaneously recorded cells. Additionally, the spiking output of RGCs is the signal ultimately sent to the brain, so a complete RF model should use spiking as the end point. One disadvantage of using spikes as the output measure is that nonlinearities associated with spike generation – including rectification at zero and saturation at high firing rates – can interfere with the experimenter’s ability to measure underlying nonlinearities in the spatiotemporal RF filter.

The closed-loop, iso-response, method allows an experimenter to separate the output (spiking) nonlinearity from upstream nonlinearities using a RGC spike recording. In this method, an online algorithm measures the spike response to each stimulus presentation, and iteratively alters the stimulus to achieve a target response amplitude (Bölinger and Gollisch, 2012). For example, consider a target response of 10 spikes. If a spot of a certain size and contrast elicited 6 spikes, the spot could be made larger or the contrast increased on the next trial. If making the spot larger reduced the response to 4 spikes, the algorithm would instead test a smaller spot. Thus, the algorithm can define the iso-response contour: the dimension in stimulus space that elicits the fixed response. In the early days, closed-loop experiments were often used to detect thresholds; for example Enroth-Cugel determined the minimum contrast necessary to elicit a detectable difference in firing (Enroth-Cugell and Robson, 1966). Even Kuffler’s recordings of cat RGC RFs used a version of the closed loop technique (Kuffler, 1953). By maintaining a fixed response throughout the measurement, closed-loop experiments can thus reveal nonlinear RF mechanisms without interference from the output nonlinearity.

The usefulness of the closed-loop approach is related to the size of the stimulus space to be explored. Defining iso-response contours while varying one or two parameters of the stimulus is feasible, but measuring contours in three or higher dimensional stimulus space becomes experimentally unrealistic due to the exponential growth of the space. Thus, the closed-loop approach is a powerful tool to that can be applied as part of many of the different RF measurement methods described above. For example, an iso-response contour could map the spatial RF in a spots-of-variable-size type of experiment in which the experimenter also varied contrast. The resulting space would offer a measure of how much more contrast is required to make the cell fire for a non-optimal spot size.

3. Receptive field models

RGC RF models have progressed dramatically from the canonical concepts of center and surround to elaborate circuit models incorporating the many distinct cell types of the retina. The purposes for RF models have also progressed. What began as a fundamental and abstract field attempting links to human perception now lies at the frontier of translational systems neuroscience. Even with his uncanny insight, Kuffler could not have predicted that models of RGC RFs would one day be programmed into computers connected to electronic prosthetics to restore sight to the blind (Eiber et al., 2013; Ong and da Cruz, 2012; Weiland et al., 2005).

While the goals of RF modeling have changed, we will use three broad criteria as a common measuring stick: predictive power, biological realism, and generalizability. Not all RF models were designed with these goals in mind, and indeed no current model succeeds completely at all three, but they nonetheless provide useful comparisons.

Predictive power is the ability for a model to predict the response of a RGC to a 2particular set of visual stimuli.

Biological realism is the degree to which the components of the RF model correspond to known biological components of retinal circuits (i.e. cells, synapses, receptors, ion channels, signaling pathways). The models that are most successful in biological realism are not necessarily the most detailed. There is always a tradeoff between the simplifying assumptions in higher-level models and the explosion of free parameters in lower-level models.

Generalizability is a measure of the transfer of predictive power across stimuli. RF models are generally built from RGC responses to a small set of stimuli, thus they often fail to predict responses to stimuli outside this set. The set of possible visual stimuli is infinite, so of particular importance in considering generalizability will be “naturalistic” stimuli that attempt to capture aspects of the visual world for which RGCs evolved.

Difference of Gaussians

One of the most influential concepts in sensory neuroscience is the idea that RFs can be modeled as a difference of Gaussians (DoG). In the retina, the first DoG model of RGC RFs is attributed to (Rodieck and Stone, 1965). For a single polarity (ON or OFF) RGC, the spatial extent of the RF center is modeled as a two-dimensional Gaussian, and the surround is modeled as another two-dimensional Gaussian with much larger extent and opposite (suppressive) polarity. The DoG model has remained extremely popular because it is concise – it only needs three parameters to define the size of each Gaussian and their relative strength – and it is easily fit from any of the RF measurements described above.

Along with the simplicity of the DoG model come several critical limitations. It is a model of space only without a temporal component, so on its own, it does not offer information about kinetics, e.g. to distinguish between transient and sustained RGC types, or to predict the response to a moving object. The DoG model also assumes a single polarity (ON or OFF) RF, so ON-OFF and SbC RGC cannot be described.

The predictive power of DoG models is limited by several of its core assumptions. First, it assumes circular symmetry in both the RF center and surround (though it can be extended to elliptical shapes for RF center and surround with four additional parameters). While most RGC RFs are reasonably circularly symmetric, some, like orientation-selective (OS) RGCs are highly asymmetric (Bloomfield, 1994; Hammond, 1974; Joesch and Meister, 2016; Kim et al., 2008; Nath and Schwartz, 2016; Venkataramani and Taylor, 2016, 2010). Even non-OS RGCs deviate from elliptical shapes at high resolution (Gauthier et al., 2009). Second, the surround can only suppress the center response. While this is the most common first-order understanding of the surround for most RGCs, numerous “non-classical” surround effects have been described, including the shift-effect (McIlwain, 1966), a polarity switch from surround stimulation (Geffen et al., 2007), a complete absence of surround (Zhao et al., 2014), disinhibition past the classical RF (Chao-Yi et al., 1992), and size-dependent latency shifts beyond the RF center (Mani and Schwartz, 2017).

Finally, and perhaps most importantly, the DoG model is spatially linear. The responses of stimuli at different locations sum linearly, and positive and negative contrasts in the RF cancel. Spatial linearity is a key assumption in many RF models despite the fact that it was shown to be incorrect in most cases even in Kuffler’s early work (Kuffler, 1953) and again by Enroth-Cugell and Robson for “Y” cells, which were the majority of cells encountered (Enroth-Cugell and Robson, 1966). The degree of success of spatially linear models like the DoG model in predicting RGC responses depends somewhat on the response regime of the RGC being modeled. Some studies have used low contrast and/or low spatial frequency stimuli, specifically to keep cells within their linear regime (Cooper et al., 2012; Enroth-Cugell and Robson, 1966), but measurements of natural scenes show a very large dynamic range of contrast and spatial frequency (Frazor and Geisler, 2006; Mante et al., 2005). We will explore spatially nonlinear RF models at the end of this section.

While the DoG model makes no explicit connection to circuit mechanisms in the retina, it is sometimes (over) interpreted as a circuit model in which the RF center corresponds to excitation from bipolar cells and the RF surround corresponds to inhibition from amacrine cells. Generalizability in the DoG model is limited mostly by its assumption of spatial linearity. For the subset of RGCs that are spatially linear (or probed in the linear regime), it can provide a reasonable prediction of the spatial pattern of RGC activation, but it fails for RGCs with nonlinear RFs when probed with naturalistic patterns (Frazor and Geisler, 2006; Heitman et al., 2016).

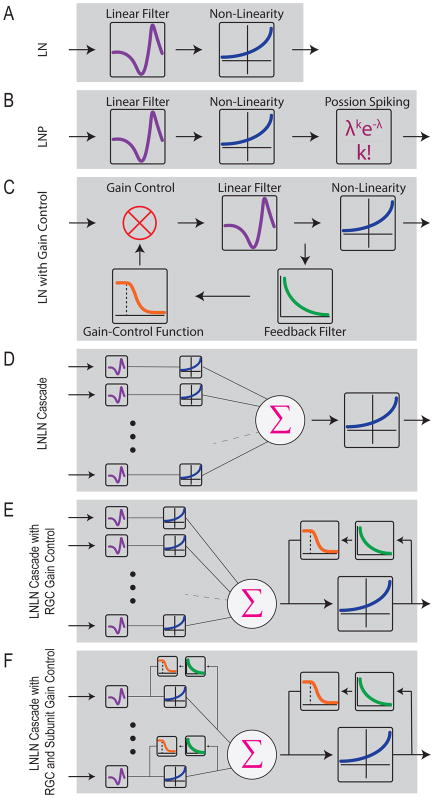
Linear-nonlinear (LN) models

Linear spatial RF models, like the DoG, were soon extended into the time domain. As described above, many RF estimation methods include a kinetic component. To make a RF model in time and space, the kinetics of the response are used to construct a temporal filter. The details of temporal filter construction depend on the RF measurement. Once constructed, the temporal filter is used along with the spatial filter to model the firing rate of a RGC responding to any spatiotemporal pattern of light.

The first spatiotemporal models using a linear temporal filter revealed a fundamental flaw: the models predicted unrealistic firing rates. For example, if an ON-center DoG model is probed with a dark spot (negative contrast), it will produce a negative value, which, when passed through a linear temporal filter, predicts that the RGC fires at a rate less than zero. On the opposite end of the contrast scale, purely linear models also predict increasing firing rates ad infinitim.

Both negative firing rates (a lack of rectification) and unrealistically high firing rates (a lack of saturation) can be fixed by introducing a static nonlinearity between the linear spatiotemporal RF model and the firing rate prediction (Chichilnisky, 2001; Victor and Shapley, 1979a). This solution gave rise to what is known as the linear-nonlinear (LN) class of RGC RF models (Fig. 4). Another important advantage of the static nonlinearity is that it allows predictions of both ON and OFF responses from a single spatiotemporal RF, because the nonlinearity can predict positive firing rates for both positive and negative filter activation values. While the ON and OFF RFs must share the same spatial structure and the same temporal filter in such a model, it at least allows ON-OFF RGCs to be included.

Figure 4. Schematics of the classes of RGC RF models.

(A–C) Spatially linear models. (D–F) Spatially nonlinear models.

LN models of RGCs are very common because their parameters, including the static nonlinearity, are easily estimated from data (Chichilnisky, 2001), and they offer good predictive power for a restricted set of stimuli. Despite their strengths, LN models fail to generalize for many classes of stimuli, including naturalistic stimuli. Importantly, the static nonlinearity in LN models follows the spatiotemporal model, so LN models still assume spatial linearity. The spatial linearity assumption is responsible for many of the generalization failures of LN models (Heitman et al., 2016).

Like the DoG model, the LN model makes no explicit connection to circuit mechanisms; and also like the DoG model, it has, nonetheless, been interpreted as a circuit model. The static nonlinearity is often associated with spike generation in the RGC, since spike generation rectifies the minimum firing rate at zero and limits the maximum firing rate by the refractory period. While spike generation certainly contributes to the static nonlinearity measured in the LN model, additional nonlinear circuit elements (notably the synapses from bipolar cells) also contribute (Demb et al., 2001; Schwartz and Rieke, 2011)

Incorporating gain control

Most RGC RF modeling efforts over the last two decades have started with the LN model and introduced additional elements to improve the model’s predictive power for particular stimuli. Some of the most successful additions have involved mechanisms for gain control (Fig. 4). In this context, gain control is any process that reduces the firing rate of a RGC temporarily following a period of high activity. The most typical stimulus parameters that cause changes in gain are intensity and contrast (reviewed by Rieke and Rudd, 2009). While neurons change state on a continuum of timescales, gain control is typically distinguished from adaptation on the basis of its fast timescale. For RGCs, gain control mechanisms act within the duration of the temporal filter – typically less than 250 ms – all the way down to the several millisecond timescale of spikes (Rieke and Rudd, 2009). Thus, modeling gain control is the first quantitative attempt to capture some of the dynamic nature of RGC RFs, but only in a limited context.

Early work recognized the importance of gain control in capturing the firing patterns of RGCs to spatial and temporal modulations of light (Shapley and Victor, 1981, 1978). More recently, gain control has been used in models of RGC responses to moving objects (Johnston and Lagnado, 2015). A LN model incorporating a gain control term was successful in capturing motion anticipation: the tendency of populations of RGCs to overcome upstream lag and fire with the leading edge of a moving object (Berry et al., 1999). On the finer timescale of the refractory period following individual spikes, models have incorporated a spike feedback term following a Poisson spike generator (Pillow et al., 2005) and have introduced post-spike “coupling terms” in a generalized linear model (GLM) framework to account for interactions among RGCs (Pillow et al., 2008). LN models with gain control have been quite successful at improving the predictive power in the temporal domain (van Hateren et al., 2002), but they remain largely unable to generalize to naturalistic scenes with large spatiotemporal correlations (Heitman et al., 2016; Maheswaranathan et al., 2018)

Gain control has several appealing correlate biological mechanisms in neurons. On the shortest timescale, well-known biophysical mechanisms, like Na⁺ channel inactivation and the opening of delayed rectifier K⁺ channels, contribute to the refractory period following each spike (Weick and Demb, 2011). Voltage-gated conductances in the RGC with slightly longer timescales, like Ca²⁺-activated K⁺ channels, can reduce gain on the timescale of tens of milliseconds (Hotson and Prince, 1980). Gain control mechanisms have been found at many levels in retinal circuits (Baccus and Meister, 2002; Kim and Rieke, 2003), so it is certainly an oversimplification to assume that all of the effect captured in such a model is the result of mechanisms in the RGC itself. A kinetic (Markov state) model was added to the standard LN model to account for contrast adaptation with more explicit connections to biological mechanism than in previous models (Ozuysal and Baccus, 2012). A recent paper returned to the mechanistic basis for the gain control responsible for motion anticipation and found that it relies on postsynaptic inhibition to the dendrites of RGCs (Johnston and Lagnado, 2015).

Multi-pathway LN models

As mentioned above, ON-OFF RGCs are modeled in only a rudimentary way in standard LN models by introducing a non-monotonic nonlinearity following a single temporal filter. More recent models of ON-OFF RGCs have used separate spatiotemporal filters and separate nonlinearities for the ON and OFF channels (T Gollisch and Meister, 2008; Tim Gollisch and Meister, 2008) Using the spatiotemporal white noise stimulus, one can use the spike-triggered covariance (STC) matrix rather than simply its mean (the STA) to extract separate ON and OFF filters (Cantrell et al., 2010; Fairhall et al., 2006). In addition to ON and OFF, the STC approach can reveal separate spatial filters, each with their own temporal components (Fairhall et al., 2006).

While it is very powerful in theory, STC requires much more data than STA, and in practice, it rarely produces more than two well-defined filters before reaching noise level (Fairhall et al., 2006; Liu and Gollisch, 2015). Nonetheless, multi-pathway LN models, whether fit from STC or constructed based on assumptions about the separate pathways and fit with another method, have been useful in capturing some of the properties of RGCs that are missed with standard LN models (Baccus et al., 2008; T Gollisch and Meister, 2008; McFarland et al., 2013; Zhang et al., 2012).

In some cases, multi-pathway LN models are inspired by the structure of retinal circuits. ON-OFF RGCs receive ON and OFF input from different sets of bipolar cells, so a two-pathway LN model has a clear rationale. Other examples of multi-pathway LN models have been built to match known circuit elements, like separate excitatory and inhibitory pathways (Baccus et al., 2008; Kastner and Baccus, 2013). The multiple filters that emerge from STC are generally less well connected to particular circuit elements.

Spatially nonlinear RF models

All the RF models we have considered thus far share the assumption of linear spatial integration, even though early work on RGC RFs revealed strong spatial nonlinearities (Enroth-Cugell and Robson, 1966; Hochstein and Shapley, 1976; Kuffler, 1953). The biological basis for nonlinear spatial integration involves rectified synapses from bipolar cells (Demb et al., 2001, 1999; Schwartz and Rieke, 2011). Victor and Shapley led the way measuring and modeling nonlinear spatial integration in RGCs (Shapley and Victor, 1979; Victor and Shapley, 1979b, 1979a). Their work was later extended by Enroth-Cugell and Freeman to form the pooled subunits model (Enroth-Cugell and Freeman, 1987).

Variations on this influential model have evolved into the LNLN cascade models that consistently outperform spatially linear RGC models for a variety of stimuli from white noise (Real et al., 2017) to object motion (Baccus et al., 2008; Ölveczky et al., 2003), to natural scenes (Gollisch, 2013; Heitman et al., 2016). Additional gain control elements at the level of individual subunits have been added in recent versions of these models to help predict responses to moving objects (Chen et al., 2014) and white noise (Real et al., 2017). The need for gain control at the level of the subunits matches experimental data showing that contrast gain control is sometimes localized on the scale of bipolar cells (Brown and Masland, 2001; Garvert and Gollisch, 2013), though it can also have components on the scale of the RGC RF (Garvert and Gollisch, 2013; Khani and Gollisch, 2017). Gap-junctional coupling between bipolar cells (via AII amacrine cells) is another addition to these models inspired by experimental data, and it has been important in capturing motion sensitivity in mouse and primate RGCs (Kuo et al., 2016; Manookin et al., 2018). Another recent model added a delay in the spatial pooling of subunits in the RF surround to account for the extra synapse between amacrine cells and RGCs (Real et al., 2017). Figure 4 summarizes the structure of some of the variants of LN models that have been used to model RGC RFs.

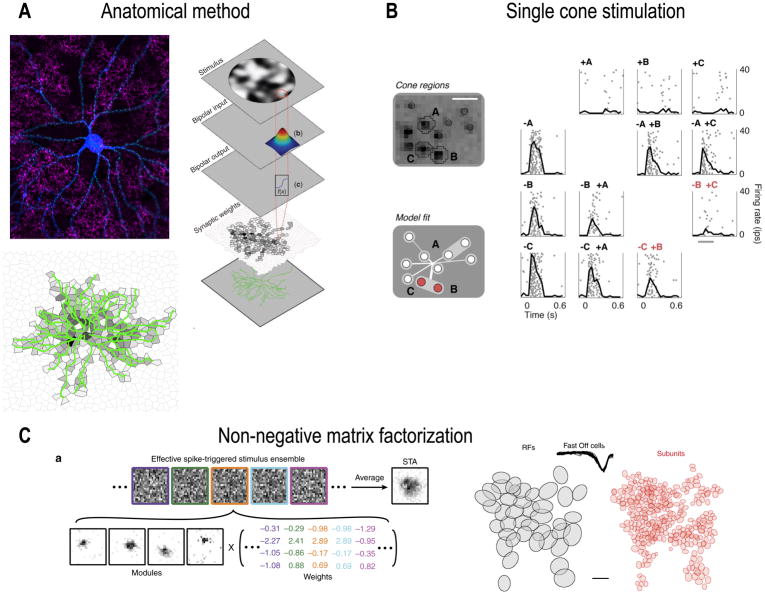
While the sizes, temporal filters, and nonlinearities of the subunits in LNLN cascade models are estimated with reasonable reliability by fitting the models to RGC spike data, determining the spatial location of each subunit in two-dimensions has proved to be much more difficult (Fig. 5). Because the subunit weights to the RGC do not conform to the Gaussian ideal, determining their locations at high resolution is critical to achieve predictive power for complex spatiotemporal stimuli (Gregory W Schwartz et al., 2012). An anatomical strategy was used in one study to predict the number of synapses received from each bipolar cell based on a traced image of the RGC dendrites. While this model predicted responses to arbitrary spatial images, it is not feasible to have a full morphological reconstruction of the RGC in most cases (Gregory W Schwartz et al., 2012). Another recent approach used stimulation of individual cones to map the locations of bipolar cells synapsing onto primate midget RGCs. The method required only the RGC spikes as input data, but was a somewhat special case since midget RGCs receive less than 10 bipolar cell inputs (Freeman et al., 2015). Using only standard spatiotemporal white noise and an analysis method called non-negative matrix factorization, Liu et al., were able to map the bipolar subunit locations in salamander RGC RFs, also a case in which the number of subunits is ~10 (Liu et al., 2017).

Figure 5. Methods for estimating subunit locations.

(A) In the anatomical method, a RGC cell fill (blue) is combined with a marker of synapses (green) and a stain for a particular bipolar cell type (magenta). A model estimates the number of synapses from each bipolar cell based on the dendritic morphology of the RGC. Adapted from (Gregory W. Schwartz et al., 2012). (B) The single cone stimulation method presents small spots of light aligned to the locations of cones. By presenting pairs of spots and measuring whether the responses combine linearly or nonlinearly in the RGCs, the experimenters were able to infer the locations of RF subunits. Adapted from (Freeman et al., 2015). (C) The non-negative matrix factorization technique is an analytical method that can be applied to data from spatiotemporal white noise experiments (left). The panel at the rights shows the linear RF (gray) and the corresponding subunit RFs (red) estimated from a multi-electrode-array recording in salamander retina. Adapted from (Liu et al., 2017).

4. Feature selectivity: fluidity versus invariance

Kuffler realized years ahead of his time that RGC RFs are “flexible” and “fluid”. Is the effort to build a generalizable RGC model then a Sisyphean task? Surely there are limits on the fluidity of RGC RFs, because the retina, despite its complexity, is still a primary sensory system with little feedback from the rest of the brain. This small amount of feedback comes from neuromodulatory retinopetal projections (Gastinger et al., 2006). The information conveyed by each RGC type must be stereotyped across individuals, because RGCs project selectively to many distinct targets in the brain, and these projection patterns appear to be genetically predetermined (Dhande and Huberman, 2014). Which aspects of a RGC’s response are stable, and which are fluid?

We will argue that the answer to this question is connected to the concept of feature selectivity. The idea that RGCs act as detectors for specific, behaviorally relevant, features of the visual world was developed in parallel with the early history of RF modeling (Barlow, 1961; Lettvin et al., 1959; Levick, 1967). Invariance is central to the view of RGCs as feature detectors. If particular RGCs encode behaviorally relevant features, those representations should be robust to other changes in the visual scene, like luminance, contrast, and noise. Another conclusion that follows from this line of reasoning is that some of the RF properties that researchers typically measure and model, like response polarity, size, and kinetics, may be fluid if they are not part of the key feature selectivity of the RGC. In this section, we will review a collection of recent reports on the fluidity of RGC RFs under different stimulus conditions, pointing out both the aspects of the RF that change and those that remain invariant.

Response polarity

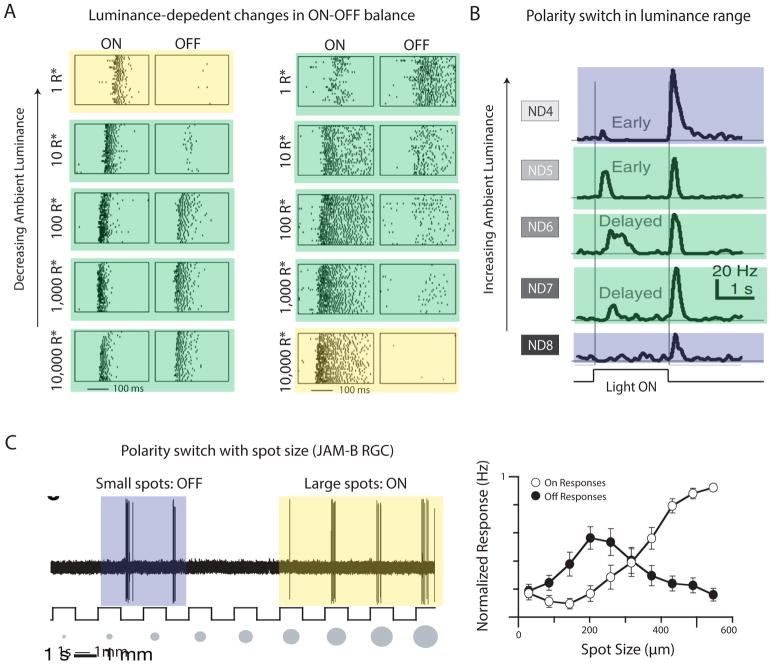
Countless studies have used response polarity as a defining feature to classify RGCs, but recent evidence has shown that this aspect of RFs is not stable across illumination levels (Rivlin-Etzion et al., 2018). Tikidji-Hamburyan et al. showed that cells classified as ON at one luminance can become ON-OFF at another luminance (Tikidji-Hamburyan et al., 2015). Similarly, cells classified as OFF could develop an additional ON response in certain luminance regimes. These results were confirmed in both mouse and pig retina and in retino-recipient dorsal lateral geniculate nucleus in vivo. Concurrent with this study, another group reported a similar luminance-dependent switch in ON:OFF ratio in three mouse RGC types (Pearson and Kerschensteiner, 2015).

Interestingly, one of the RGC types that showed this ON:OFF switching behavior was a direction-selective (DS) type presumed to be equivalent to previously described ON-OFF DS RGCs. While its ON:OFF contrast ratio switched with luminance, its direction preference did not. Orientation-selectivity (OS) also remained stable across luminance (Pearson and Kerschensteiner, 2015). Perhaps the luminance invariance of DS and OS is an indication that these properties are the core feature selectivity of these particular RGC types. One of the RGC types shown in the Tikidji-Hamburyan et al. study to change from OFF to ON-OFF with luminance, called the OFF-transient alpha, has been implicated in selectivity for looming dark objects (Münch et al., 2009) and for image recurrence following saccades (Krishnamoorthy et al., 2017). It remains unknown whether these types of feature selectivity are invariant in OFF-transient alpha RGCs across luminance.

Properties other than luminance have also been shown to elicit ON:OFF switching behavior in RGCs. Several types of RGCs in mouse have been shown to switch polarity depending on stimulus size, including the JAM-B RGC (Kim et al., 2008) and the “high definition” (HD1 and HD2) RGCs (Jacoby and Schwartz, 2017) (Fig. 6). Transient stimulation of the surround with a phase shift of a grating can also change the RF center filter of some RGCs from OFF to ON (Geffen et al., 2007).

Figure 6. Polarity switches in RGCs with stimulus conditions.

(A) Spike rasters from 2 RGCs responding to ON and OFF contrast steps across 5 log units of luminance. Polarity switches are indicated by shading for ON (yellow), ON-OFF (green) and OFF (blue) polarity. Adapted from (Pearson and Kerschensteiner, 2015). (B) The firing rate of a RGC that becomes ON-OFF in a limited luminance range. Adapted from (Tikidji-Hamburyan et al., 2015). (C) The response polarity of JAM-B RGCs depends on stimulus size. Adapted from (Kim et al., 2008).

Spatial RF

Spatial properties of RGC RFs, like the size of the RF center and strength of the RF surround, have long been known to vary with luminance (Barlow, 1957; Barlow and Levick, 1969; Creutzfeldt et al., 1970; Enroth-Cugell and Lennie, 1975; Enroth-Cugell and Robson, 1966; Enroth-Cugell and Shapley, 1973; Farrow et al., 2013; William N Grimes et al., 2014; Ogawa et al., 1966; Reitner et al., 1991; Troy et al., 1999). Circuit mechanisms for these effects include luminance-dependent changes in gap-junction coupling in both the outer retina (DeVries and Schwartz, 1989; Lasater, 1987; Xin and Bloomfield, 1999) and the inner retina (Bloomfield et al., 1997; Hu et al., 2010), and luminance-dependent recruitment of spiking amacrine cells (Farrow et al., 2013). Since electrical coupling in the retina can be modulated by time of day independent of luminance, spatial components of RGC RFs are even subject to circadian regulation (Jin and Ribelayga, 2016; Ribelayga et al., 2008; Zhang et al., 2015).

Kinetics

In addition to its effects on polarity and space, luminance has long been known to alter the kinetics of RGC responses. Responses tend to become more transient and have shorter latency as luminance increases (Ogawa et al., 1966; Tikidji-Hamburyan et al., 2015). These accelerations of the light responses with increasing luminance are largely attributed to a switch from rod-dominated to cone-dominated transduction and subsequent kinetic changes within the cone phototransduction cascade (Attwell et al., 1984; Elias et al., 2004; Euler and Masland, 2000; Murphy and Rieke, 2011; Sharpe et al., 1993). Accelerations of circuit components downstream of photoreceptors also contribute to kinetic changes in RGC light responses with luminance (Dunn et al., 2007; Dunn and Rieke, 2006).

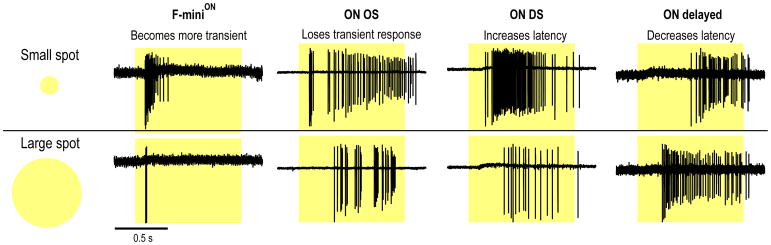
Luminance-dependent changes in kinetics are often ignored in RGC RF models designed to describe the steady state in a fixed luminance range, but what if another property of the light stimulus alters response kinetics? For some RGCs, response kinetics depends on the size of a visual stimulus (Fig. 7). These kinetic changes with increased spot size can manifest as the loss of a transient component, as in ON OS RGCs (Nath and Schwartz, 2016) or the response becoming more transient, as in F-mini^ON RGCs. Response latency can also depend on stimulus size. ON DS RGCs increase in latency for larger spots while ON delayed RGCs show decreased response latency (Mani and Schwartz, 2017).

Figure 7. RGCs respond with different kinetics to small and large spots of light.

Four examples of RGC light responses to a spot of light (darkness to 200 isomerizations per rod per second) presented for 1 sec. Top traces show responses to spots covering only the RF center (120 μm for the F-mini^ON and 200 μm for the oher cells. Bottom traces show responses from the same four cells to a full-field spot (1200 μm) covering the RF center and surround.

Spatial linearity

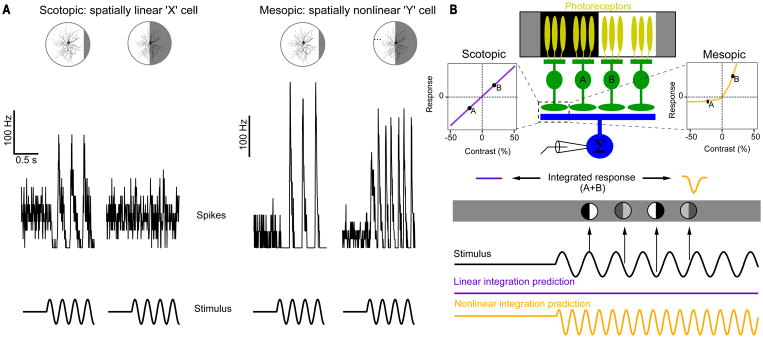
After response polarity, size, and kinetics, perhaps the most commonly used characteristic to distinguish RGC types is whether they integrate space linearly (called “X” cells) or nonlinearly (“Y” cells) (Enroth-Cugell and Robson, 1966). One cell type in mouse, called the ON-alpha RGC, has been show to integrate over space nearly linearly in low luminance and highly nonlinearly in high luminance (Fig. 8)(William N. Grimes et al., 2014). The site of this switch was localized to the output synapses from ON cone bipolar cells, which become more rectified (hence nonlinear) in bright conditions. Another result of this mechanistic change at the bipolar cell synapse is a change in the shape of the contrast sensitivity function of the RGC.

Figure 8. Linear verses nonlinear spatial integration in RGCs can depend on luminance.

(A) Example of the same ON-alpha responding to a contrast-reversing grating in scotopic and mesopic luminance. This is the same stimulus originally used to classify linear (X) vs. nonlinear (Y) RGCs (Enroth-Cugell and Robson, 1966). (B) A schematic of how a change in rectification at bipolar cell output synapses can account for a change in spatial integration in a RGC. Figure adapted from (William N. Grimes et al., 2014).

5. The next generation of measuring, modeling, and understanding RGC RFs

A decade ago, one of us had aspirations of writing a review about all that was wrong with the current state of RGC RF models until his graduate mentor asked a simple question, “What is the new framework you will propose?” This question promptly ended the review before it began; it’s always easier to tear down old theories than to build new ones. Admittedly, our answer to his compelling question remains incomplete, but it is now at least informed by our answers to several related questions.

Can a unified computational framework capture the diversity of RGC RF properties?

Perhaps not. Researchers in the early days of work on RGCs described them in two very different ways. Lettvin and colleagues famously described a set of detectors for specific behaviorally relevant features of the visual world in “What the Frog’s Eye Tells the Frog’s Brain” (Lettvin et al., 1959). Much of the rest of the field moved instead in the direction of describing RGCs in the language of signal processing from engineering, as input-output layers of linear filters, nonlinear transformations, and feedback loops (see Fig. 4). The signal processing perspective and its possible implications for a framework of the population code of the retina were first considered in the visionary work of Horace Barlow (Barlow, 1961), inspired by Simon Laughlin’s work on predictive coding (Laughlin, 1981, 1989; Srinivasan et al., 1982) and codified in the theoretical work of Atick and Redlich (Atick and Redlich, 1990). This framework was based on the concept of efficient coding: imagining the population of RGCs as an efficient coder of certain properties of a visual scene, effectively reducing the redundancy that exists because of the high degree of spatiotemporal correlation in natural scenes. While the efficient coding hypothesis persists (Nirenberg et al., 2001), especially over the last decade there has been an accumulation of evidence that redundancy reduction might be the wrong framework for thinking about retinal computation. Consider that each location in visual space is sampled by 2–3 RGCs of ~40 different types (Bae et al., 2018). A system that evolved to represent each pixel 80–120 times in its output does not seem to be optimized for redundancy reduction. Instead, the literature is full of examples of specialized computations in RGCs that were shaped by selective pressure to extract behaviorally relevant signals robustly. We have slowly returned to attempts to catalogue what an animal’s eye tells an animal’s brain. In a vague sense, this still represents an efficient code, but only through the lens of the full set of behavioral demands of an animal’s visual system – a lens whose overwhelming majority remains obscured in our current understanding. In the absence of a framework for the visual repertoire of the brain, perhaps it is counterproductive to try to impose a unifying framework on the diversity of computations that exist among RGCs.

Do RGCs encode multiple features of the visual world depending on context?

Of course they must. Even with the ~40 different RGC channels, there must be substantial multiplexing to convey the entirety of the information necessary for higher order visual processing in the spikes of the optic nerve. The requirements of vision also vary dramatically with the context of both the stimulus and behavior. What is less clear is how we come to terms with multiplexed RGC codes in our descriptions and models of RFs. Some progress has been made in describing the response patterns of RGCs to moving stimuli. The same RGCs can report either the smooth motion of an object through their RF centers or the sudden reversal of the object distant to the RF center (Schwartz et al., 2007). The multiplexed code for object motion was analyzed recently in more detail in a single type of RGCs in rat retina (Deny et al., 2017). In the broader sense, the field still grapples with the difference between selectivity and exclusivity. For example, ON-OFF DS RGCs are highly selective for a particular direction of motion, but they also respond robustly at the onset and offset of a flashed spot of light. Surely the brain does not misinterpret every spike from an ON-OFF DS RGC responding to a static object as evidence of motion in its preferred direction.

Can invariance inform our intuitions about the features that RGCs extract from the visual world?

It can and it should. The dynamic ranges of parameters in the visual world are enormous – 10 orders of magnitude of luminance (Rodieck, 1998), ~4 orders of magnitude of contrast (Frazor and Geisler, 2006; Mante et al., 2005), and multiple sizes and speeds of objects. It is extremely difficult to make a circuit out of biological elements that is robust over a large dynamic range. Finding such invariance in a RGC provides strong evidence that selective pressure played a role in establishing its feature selectivity. There are several examples of such invariance in RGCs. ON-OFF DS RGCs employ a variety of mechanisms to maintain their selectivity across a large range of luminance, speed, contrast, and in the presence of background noise (Chen et al., 2016; Nowak et al., 2011; Poleg-Polsky and Diamond, 2016; Sethuramanujam et al., 2016). OFF OS RGCs maintain orientation selectivity across seven orders of magnitude of luminance and a wide range of spatiotemporal frequencies (Nath and Schwartz, 2017). Small bistratified RGCs in primates are blue-yellow color opponent in a variety of different stimulus contexts (Dacey and Lee, 1994; Field et al., 2007). Evolutionary conservation can also be a sign of behaviorally relevant feature selectivity in a RGC type. Object motion sensitive RGCs have similar dendritic morphology and circuit mechanisms in a variety of species (Jacoby and Schwartz, 2017; Kim and Kerschensteiner, 2017; Puller et al., 2015; Venkataramani et al., 2014; Zhang et al., 2012).

On the other hand, RGC computations that are not robust offer a hint that there may remain an undiscovered aspect of feature selectivity. JAM-B RGCs were characterized as DS (Kim et al., 2008) in a narrow luminance regime (Joesch and Meister, 2016) before it was discovered that they encode OS invariant to luminance (Nath and Schwartz, 2017). F-mini^ON RGCs were reported to be weakly DS over a limited range of speeds (Rousso et al., 2016). Perhaps they are more robustly selective for a different visual feature. For the vast majority of RGCs, robust and invariant feature selectivity remains to be discovered.

Can we work backward from the brain and behavior to discover the salient features encoded by RGCs?

Yes, and we should use a comparative approach. The latest estimate is that RGCs project directly to 59 different brain regions in mouse (Martersteck et al., 2017)! Similarly extensive retinal projection patterns have been reported in other species, with many conserved targets (Campbell et al., 1967; Hannibal et al., 2014; Major et al., 2003; Matteau et al., 2003; Reiner et al., 1996; Robles et al., 2014; Shimizu et al., 1994). This extreme diversity in the targets of RGCs must mean that visual signals are used in a host of innate behaviors distinct from conscious perception, and the conservation of these pathways suggests that they drove RGC feature selectivity throughout evolution (Fig. 9). Two of the most compelling success stories linking RGCs to behavior come from studies that worked backward from specific retino-recipient brain areas to discover the specific RGC types influencing the known functional roles of these brain regions.

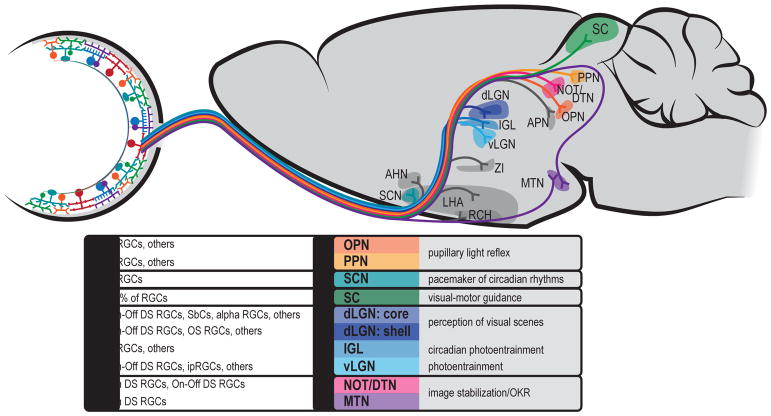
Figure 9. A subset of retinorecipient areas of the brain.

Well studied brain regions are in color and listed with their known RGC inputs and their behavioral function. Less well understood regions are shown shaded in gray.

Abbreviations: AHN: Anterior Hypothalamic Nucleus, APN: Anterior Pretectal Nucleus, IGL: Intergeniculate Leaflet, LGN: Lateral Geniculate Nucleus, LHA: Lateral Hypothalamic Area, MTN: Medial Terminal Nucleus, NOT/DTN: Nucleus of the Optic Tract/Dorsal Tegmental Nucleus, OPN: Olivary Pretectal Nucleus, PPN: Pedunculopontine Nucleus, RCH: Retrochiasmatic Area, SC: Superior Colliculus, SCN: Suprachiasmatic Nucleus.

By the 1990s it had become clear that a signal from the retina was required to entrain the circadian system to the light-dark cycle, and that this signal remained in people with extensive rod and cone loss (Zaidi et al., 2007). David Berson and colleagues injected a retrograde tracer in the super chiasmatic nucleus (SCN), the master regulator of the circadian clock, and looked for labeled RGCs. They discovered a new type of RGCs that, surprisingly, contained their own phototransduction cascade, independent from rods and cones, using the photopigment melanopsin (Berson et al., 2002). These ganglion cell photoreceptors are now called intrinsically photosensitive (ip)RGCs, and they are specialized to integrate light signals over time to measure total luminance (Milner and Do, 2017; Wong, 2012). Subsequent work has revealed that ipRGCs comprise multiple subtypes with specific roles in both image-forming vision and several non-image forming visual behaviors (Chen et al., 2011; Ecker et al., 2010; Güler et al., 2008; Schmidt et al., 2014).

Another example of intuition from neuroethology driving a discovery about RGCs is the tracing of cells projecting to the accessory optic system (AOS). Image stabilization during eye, head, and body movements requires a set of nuclei, collectively called the AOS, which receive both vestibular and visual input (Dhande et al., 2013; Gauvain and Murphy, 2015; Oyster et al., 1980; Simpson, 1984; Yonehara et al., 2009, 2008). Retrograde tracing studies from the AOS to the retina revealed a set of RGCs, called ON DS RGCs, which are selective to the direction of motion across the retina (Oyster et al., 1980). Unlike the previously identified ON-OFF DS RGCs, ON DS RGCs have large RFS and are specialized to report the slow speeds that drive the visual input for image stabilization before the vestibular system takes over at higher speeds (Ackert et al., 2006; Yonehara et al., 2009).

Future directions and conclusions

The study of RGC RFs over the last six decades has been a fascinating journey. From the beginning, Kuffler realized that a static representation would not be sufficient, but it has proved difficult to capture the dynamics of RGCs in a succinct way. Along the way, we have come to appreciate the enormous diversity of RGC types and the equally impressive diversity of their targets in the brain. The next generation of our understanding of RGCs should embrace both the dynamic nature of RGC RFs and both aspects of their diversity. Drawing inspiration from how specific RGCs evolved to serve particular behavioral needs may reveal the core computations of the visual system.

Glossary

AOS

Accessory Optic System

DoG

Difference of Gaussians

DS

Direction Selective

FBP

Filtered Back Projection

GLM

Generalized Linear Model

HD1/HD2

High Definition 1/High Definition 2

JAM-B

Junctional Adhesion Molecule B

LN

Linear Nonlinear

LNP

Linear Nonlinear Poisson

LNLN

Linear Nonlinear, Linear Nonlinear

MID

Maximally Informative Dimensions

OS

Orientation Selective

RF

Receptive Field

RGC

Retinal Ganglion Cell

ipRGC

intrinsically photosensitive RGC

SbC

Suppressed by Contrast

SCN

Suprachiasmatic Nucleus

STA

Spike Triggered Average

STC

Spike Triggered Covariance