Item-Score Reliability in Empirical-Data Sets and Its Relationship With Other Item Indices

Abstract

Reliability is usually estimated for a total score, but it can also be estimated for item scores. Item-score reliability can be useful to assess the repeatability of an individual item score in a group. Three methods to estimate item-score reliability are discussed, known as method MS, method ${\lambda }_6$, and method CA. The item-score reliability methods are compared with four well-known and widely accepted item indices, which are the item-rest correlation, the item-factor loading, the item scalability, and the item discrimination. Realistic values for item-score reliability in empirical-data sets are monitored to obtain an impression of the values to be expected in other empirical-data sets. The relation between the three item-score reliability methods and the four well-known item indices are investigated. Tentatively, a minimum value for the item-score reliability methods to be used in item analysis is recommended.

Introduction

This article discusses the practical usefulness of item-score reliability. Usually, reliability of test scores rather than item scores is considered, because test scores and not individual item scores are used to assess an individual’s ability or trait level. The test score is constructed of item scores, meaning that all the items in a test contribute to the test-score reliability. Therefore, individual item-score reliability may be relevant when constructing a test, because an item having low reliability may not contribute much to the test-score reliability and may be a candidate for removal from the test. Item-score reliability (Wanous, Reichers, & Hudy, 1997, cited 2000+ times in Google Scholar, retrieved on July 27, 2017) is used in applied psychology to assess one-item measures for job satisfaction (Gonzalez-Mulé, Carter, & Mount, 2017; Harter, Schmidt, & Hayes, 2002; Nagy, 2002; Robertson & Kee, 2017; Saari & Judge, 2004; Zapf, Vogt, Seifert, Mertini, & Isic, 1999) and burnout level (Dolan et al., 2014). Item-score reliability is also used in health research for measuring, for example, quality of life (Stewart, Hays, & Ware, 1988; Yohannes, Willgoss, Dodd, Fatoye, & Webb, 2010) and psychosocial stress (Littman, White, Satia, Bowen, & Kristal, 2006), and one-item measures have been assessed in marketing research for measuring ad and brand attitude (Bergkvist & Rossiter, 2007). However, the psychometric theory of item-score reliability appears not to be well developed, and because of this and its rather widespread practical use, we think item-score reliability deserves further study.

Currently, instead of item-score reliability researchers use several other item indices to assess item quality, for example, the item-rest correlation (Nunnally, 1978, p. 281), also known as the corrected item-total correlation, the item-factor loading (Harman, 1976, p. 15), the item-scalability coefficient (Mokken, 1971, pp. 151-152), and the item-discrimination parameter (Baker & Kim, 2004, p. 4). Although useful, these indices are not specifically related to the item-score reliability. Therefore, we also investigated the relation between these item indices and item-score reliability in empirical-data sets.

Let $X_i$ be an item score indexed $i(i=1,\dots ,J)$, and let X be the test score, which is defined as the sum of the J item scores, that is, $X=\sum _{i=1}^J{X}_i$. The context of our work is classical test theory. The three methods we use and briefly discuss are all based on the reliability definition proposed by Lord and Novick (1968, p. 61). To estimate item-score reliability, method MS (Molenaar & Sijtsma, 1988) uses data features related to nonparametric item response theory (IRT; Mokken, 1971, pp. 142-147), and the other two methods use estimation procedures based on multiple regression (method ${\lambda }_6$; Guttman, 1945) and correction for attenuation (method CA; Wanous et al., 1997; Wanous & Reichers, 1996). Consistent with classical test theory, item-score reliability for any item i, denoted by ${\rho }_{\mathrm{ii}\prime }$, is defined as the product-moment correlation between two independent replications of the same item in the same group of people. Because independent replications are unavailable in practice, ${\rho }_{\mathrm{ii}\prime }$ cannot be estimated directly by means of a sample correlation $r_{\mathrm{ii}\prime }$. Zijlmans, Van der Ark, Tijmstra, and Sijtsma (2017) identified three promising methods for the estimation of item-score reliability, which are method MS, method ${\lambda }_6$, and method CA. Their simulation study results suggested that method MS and method CA have little bias. Method ${\lambda }_6$ produced precise estimates of ${\rho }_{\mathrm{ii}\prime }$, but systematically underestimated ${\rho }_{\mathrm{ii}\prime }$, suggesting the method is conservative.

Little is known about the item-score reliability values one can expect to find in empirical data and which values should be considered acceptable for an item to be included in a test. We estimated MS, ${\lambda }_6$, and CA values for the items in 16 empirical-data sets to gain insight into empirical-data values one may expect to find when analyzing one’s data. We also estimated the item-rest correlation, the item-factor loading, the item scalability, and the item discrimination in these empirical-data sets, and compared their values with the values of the three item-score reliability methods.

This article is organized as follows: First, we discuss item-score reliability methods MS, λ₆, and CA, and the item-rest correlation, the item-factor loading, the item scalability, and the item discrimination. Second, the different sets of empirical data for which the seven item indices were estimated are discussed. Third, we discuss the results and their implications for the practical use of the three item-score reliability methods.

Method

Item-Score Reliability Methods

The following definitions (Lord & Novick, 1968, p. 61) were used. In the population, test score X has variance ${\sigma }_X^2$. True score T is the expectation of an individual’s test score across independent replications of the same test, and represents the mean of the individual’s distribution of test scores, known as his or her propensity distribution (Lord & Novick, 1968, pp. 29-30). The deviation of test score X from true score T is the random measurement error, E; that is, $E=X-T$. Because T and E are unobservable, their group variances ${\sigma }_T^2$ and ${\sigma }_E^2$ are also unobservable. Furthermore, to define the test score’s reliability, classical test theory uses the concept of parallel tests to formalize independent replications of the same test in the same group. Two tests with test scores X and $X\prime$ are parallel (Lord & Novick, 1968, p. 61) if (a) for each person v, true scores are equal, $T_v=T{\prime }_v$, implying at the group level that ${\sigma }_T^2={\sigma }_{T\prime }^2$, and (b) for both tests, test-score variances are equal, ${\sigma }_X^2={\sigma }_{X\prime }^2$. The definition implies that measurement-error variances are also equal, ${\sigma }_E^2={\sigma }_{E\prime }^2$.

Using the definition of parallel tests, test-score reliability is defined as the product-moment correlation between test scores X and $X\prime$, and denoted by ${\rho }_{\mathrm{XX}\prime }$. Correlation ${\rho }_{\mathrm{XX}\prime }$ can be shown to equal the proportion of observed-score variance that is true-score variance or, equivalently, one minus the proportion of observed-score variance that is error variance. Because variances are equal for parallel tests, the result holds for both tests. We provide the result for test score X, that is,

$${\rho }_{\mathrm{XX}\prime }=\frac{{\sigma }_T^2}{{\sigma }_X^2}=1-\frac{{\sigma }_E^2}{{\sigma }_X^2}.$$

Considering Equation (1) for an item score produces the item-score reliability, defined as

$${\rho }_{\mathrm{ii}\prime }=\frac{{\sigma }_{T_i}^2}{{\sigma }_{X_i}^2}=1-\frac{{\sigma }_{E_i}^2}{{\sigma }_{X_i}^2}.$$

The two terms on the right-hand side of Equation (2) each contain an unknown. We briefly discuss three methods to approximate item-score reliability based on one test administration. Approximations to Equation (1) are all lower bounds, meaning they have a negative discrepancy relative to reliability (Sijtsma & Van der Ark, 2015). For Equation (2) the situation is less obvious. Method λ₆ appears to be a strict lower bound, but for methods MS and CA in some situations positive bias cannot be ruled out and more research is needed (Zijlmans et al., 2017). If the item response functions coincide, method MS equals the item-score reliability (Zijlmans et al., 2017); and for method CA particular choices, not to be outlined here, lead to the conclusion that items must be essentially $\tau$-equivalent (Lord & Novick, 1968, p. 51).

Method MS

Let ${\pi }_i$ be the marginal proportion of the population obtaining a score of 1 on item i and ${\pi }_{\mathrm{ii}\prime }$ the marginal proportion of the population scoring a 1 on both item i and an independent replication of item i denoted by $i\prime$. For dichotomous items, Mokken (1971, p. 143) rewrote item reliability in Equation (2) as (right-hand side):

$${\rho }_{\mathrm{ii}\prime }=1-\frac{{\pi }_i-{\pi }_{\mathrm{ii}\prime }}{{\pi }_i(1-{\pi }_i)}=\frac{{\pi }_{\mathrm{ii}\prime }-{\pi }_i^2}{{\pi }_i(1-{\pi }_i)}.$$

One estimates proportion ${\pi }_i$ from the data as the fraction of 1 scores, but for estimating ${\pi }_{\mathrm{ii}\prime }$ one needs an independent replication of the item next to the scores on the first administration of the same item. Because independent replications are unavailable in practice, Mokken (1971, pp. 142-147) proposed two methods for approximating ${\pi }_{\mathrm{ii}\prime }$ by deriving information not only from item i but also from the next more-difficult item $i-1$ (which has the univariate proportion ${\pi }_{i-1}<{\pi }_i$ closest to ${\pi }_i$), the next easier item $i+1$ (which has the univariate proportion ${\pi }_{i+1}>{\pi }_i$ closest to ${\pi }_i$), or both items. Mokken (1971, pp. 146-147) assumed that items $i-1$ and $i+1$ were the two items from the test that were the most similar to item i, and thus were the most likely candidates to serve as approximate replications of item i. To gain more similarity, he also required that the items in the test were consistent with the double monotonicity model, which assumes a unidimensional latent variable $\theta$, local independence of the item scores conditional on $\theta$, and monotone nondecreasing and nonintersecting item response functions. Estimating ${\pi }_{\mathrm{ii}\prime }$ uses the following principle (also see Sijtsma, 1998).

Let $P_i(\theta )$ denote the item response function of item i and let $P_{i\prime }(\theta )$ be the item response function of a replication of item i, and notice that by definition $P_i(\theta )=P_{i\prime }(\theta )$. Furthermore let $G(\theta )$ denote the cumulative distribution of the latent variable $\theta$; then

$${\pi }_{\mathrm{ii}\prime }={\int }_{\theta }{P}_i(\theta )P_{i\prime }(\theta )G(\theta ).$$

Next, $P_{i\prime }(\theta )$ in the integrand is replaced by the linear combination

$${\tilde{P}}_{i\prime }(\theta )=a+b{P}_{i-1}(\theta )+c{P}_{i+1}(\theta ),a,b,\mathrm{and}c\mathrm{are\; constants}.$$

We refer to Mokken (1971, pp. 142-147) for the choice of the constants a, b, and c. His Method 1 uses only one neighbor item to item i and his Method 2 uses both neighbor items. Let ${\tilde{\pi }}_{\mathrm{ii}\prime }$ be an approximation to ${\pi }_{\mathrm{ii}\prime }$ in Equation (3). Inserting ${\tilde{P}}_{i\prime }(\theta )$ from Equation (5) in the integrand of Equation (4) and then integrating yields

$${\tilde{\pi }}_{\mathrm{ii}\prime }=a+b{\pi }_{i-1,i}+c{\pi }_{i,i+1}.$$

Equation (6) contains only observable quantities and can be used to approximate item-score reliability in Equation (3) for items that adhere to the double monotonicity model. Sijtsma and Molenaar (1987) proposed method MS as an alternative to Mokken’s Methods 1 and 2 to obtain statistically better estimates of test-score reliability, Molenaar and Sijtsma (1988) generalized all three methods to polytomous items and Meijer, Sijtsma, and Molenaar (1995) proposed the item-score reliability version. The method for estimating item-score reliability of polytomous items is similar to the method for dichotomous items and hence is not discussed here. Item-score reliability based on method MS for both dichotomous and polytomous items is denoted ${\rho }_{\mathrm{ii}\prime }^{\mathrm{MS}}$ and estimated following a procedure discussed by Zijlmans et al. (2017).

Method ${\lambda }_6$

Guttman (1945) proposed test-score reliability method ${\lambda }_6$, which Zijlmans et al. (2017) adapted to the item-score reliability method denoted by ${\rho }_{\mathrm{ii}\prime }^{{\lambda }_6}$. For this adapted method, the residual error from the multiple regression of item i on the remaining $J-1$ item scores serves as an upper bound for error variance in the item score; hence, the resulting item-score reliability is a lower bound for true item reliability. Let ${\sigma }_{{\epsilon }_i}^2$ denote the residual error of the multiple regression of item $X_i$ on the remaining $J-1$ item scores. Method ${\lambda }_6$ is defined as

$${\rho }_{\mathrm{ii}\prime }^{{\lambda }_6}=1-\frac{{\sigma }_{{\epsilon }_i}^2}{{\sigma }_{X_i}^2}.$$

Method CA

Method CA is based on the correction for attenuation (Lord & Novick, 1968, pp. 69-70; Nunnally & Bernstein, 1994, p. 257; Spearman, 1904). The method correlates an item score and a test score both allegedly measuring the same attribute (Wanous & Reichers, 1996). The item score can be obtained from the same test on which the test score was based, but the test score may also refer to another test measuring the same attribute as the item. The idea is that by correlating two variables that measure the same attribute or nearly the same attribute, one approximates parallel measures; see Equation (2). Let ${\rho }_{\mathrm{ii}\prime }^{\mathrm{CA}}$ be the item-score reliability estimate based on method CA. Let ${\rho }_{X_i{R}_{(i)}}$ be the correlation between the item score and the sum score based on the other items in the test, also known as the rest score and defined as $R_{(i)}=X-X_i$. Let ${\alpha }_{R_{(i)}}$ be the reliability of the rest score, estimated by reliability lower bound coefficient $\alpha$ (e.g., Cronbach, 1951). Method CA estimates the item-score reliability by means of

$${\rho }_{\mathrm{ii}\prime }^{\mathrm{CA}}=\frac{{\rho }_{X_i{R}_{(i)}}^2}{{\alpha }_{R_{(i)}}}.$$

Item Indices Currently Used in Test Construction

Well-known item-quality indices used in test construction are (a) the item-rest correlation, also known as the corrected item-total correlation (Lord & Novick, 1968, p. 330); (b) the loading of an item on the factor which it co-defines (Harman, 1976, p. 15), in this study called the item-factor loading; (c) the item scalability (Mokken, 1971, pp. 148-153); and (d) the item discrimination (Baker & Kim, 2004, p. 4; Hambleton & Swaminathan, 1985, p. 36). For each of these four indices, rules of thumb are available in the psychometric literature that the researcher may use to interpret the values found in empirical data and make decisions about which items to maintain in the test.

Item-Rest Correlation

The item-rest correlation is defined as the correlation between the item score $X_i$ and the rest score $R_{(i)}$, and is denoted ${\rho }_{X_i{R}_{(i)}}$. In test construction, the item-rest correlation is used to define the association of the item with the total score on the other items. Higher item-rest correlations within a test result in a higher coefficient $\alpha$ (Lord & Novick, 1968, p. 331). Rules of thumb for minimally required values of item-rest correlations are .20, .30, or .40 for maximum-performance tests (also known as cognitive tests) and higher values for typical-behavior tests (also known as noncognitive tests; De Groot & Van Naerssen, 1969, pp. 252-253; Van den Brink & Mellenbergh, 1998, p. 350). The literature does not distinguish dichotomous and polytomous items for this rule of thumb and is indecisive about the precise numerical rules of thumb for typical-behavior tests. The item-rest correlation is also used for the estimation of item-score reliability by means of method CA (see Equation 8).

Item-Factor Loading

To obtain the item-factor loading ${\lambda }_i$, a one-factor model can be estimated. Because the data consist of ordered categorical scores (including dichotomous scores), polychoric correlations are used to estimate the factor loadings (Olsson, 1979). Let ${\xi }_i^{*}$ be a latent continuous variable measuring some attribute, ${\upsilon }_i$ the intercept of item i, $\eta$ the factor-score random variable, and $E_i$ the residual-error score for item i. The ith observation is defined as

$${\xi }_i^{*}={\upsilon }_i+{\lambda }_i\eta +E_i.$$

We assume a monotone relation between $X_i$ and ${\xi }_i^{*}$ where thresholds are used to define the relationship between $X_i$ and ${\xi }_i^{*}$. For simplicity, only integer values are assigned to $X_i$, see Olsson (1979) for further details. Minimum item-factor loadings of .3 to .4 are most commonly recommended (Gorsuch, 1983, p. 210; Nunnally, 1978, pp. 422-423; Tabachnick & Fidell, 2007, p. 649). For this recommendation, no distinction is made between dichotomous and polytomous items.

Item Scalability

The $H_i$ item-scalability coefficient is defined as follows (Mokken, 1971, p. 148; Sijtsma & Molenaar, 2002, p. 57; Sijtsma & Van der Ark, 2017). Let ${\mathrm{Cov}}_{\max }(X_i\mathrm{,}{R}_i)$ be the maximum covariance and ${\rho }_{max}$ the maximum correlation between item score $X_i$ and rest score $R_{(i)}$, given the marginal frequencies in the $J-1$ two-dimensional cross tables for item i and each of the other $J-1$ items in the test. The $H_i$ coefficient is defined as

$$H_i=\frac{\mathrm{Cov}(X_i,R_{(i)})}{{\mathrm{Cov}}_{\max }(X_i,R_{(i)})}.$$

Dividing both the numerator and denominator of the ratio in Equation (10) by ${\sigma }_{X_i}{\sigma }_{R_{(i)}}$ results in

$$H_i=\frac{{\rho }_{X_i{R}_{(i)}}}{{\rho }_{\max }}.$$

Hence, $H_i$ can be viewed as a normed item-rest correlation. The $H_i$ coefficient can attain negative and positive values. Its maximum value equals 1 and its minimum depends on the distributions of the item scores but is of little interest in practical test and questionnaire construction. Moreover, in the context of nonparametric IRT where $H_i$ is used mostly, given the assumptions of nonparametric IRT models, only nonnegative $H_i$ values are allowed whereas negative values are in conflict with the nonparametric IRT models. For all practical purposes, Mokken (1971, p. 184) proposed that item-scalability coefficients should be greater than some user-specified positive constant c. Items with $H_i<c$ have relatively weak discrimination and should be removed from the test. Sijtsma and Molenaar (2002, p. 36) argue that in practice items with H_i values ranging from 0 to 0.3 are not useful because they contribute little to a reliable person ordering for all types of items. Henceforth, we call the H_i item-scalability coefficient the item scalability.

Item Discrimination

Many parametric IRT models define an item-discrimination parameter. For example, the graded response model (Samejima, 1969, 1997) contains discrimination parameter ${\alpha }_i$ (not to be confused with Cronbach's coefficient α; see Equation8). In addition, let ${\delta }_{\mathrm{ix}}$ be the location parameter for category $x(x=1,2,\dots ,m)$ of item i. The graded response model is defined as

$$P(X_i\ge x|\theta )=\frac{\exp [{\alpha }_i(\theta -{\delta }_{\mathrm{ix}})]}{1+\exp [{\alpha }_i(\theta -{\delta }_{\mathrm{ix}})]}.$$

Equation (12) represents the cumulative category response function, and an item scored $0,\dots ,m$ has m such functions, for $x=1,\dots m$. The discrimination parameter ${\alpha }_i$ is related to the steepest slope of the item’s cumulative category response function. Higher $\alpha$ values indicate that the item better distinguishes people with respect to latent variable $\theta$. For dichotomous items, Baker (2001) proposed the following heuristic guidelines for discrimination parameters under a logistic model: ${\alpha }_i<0.35$, very low; $0.35\le {\alpha }_i<0.65$ low; $0.65\le {\alpha }_i<1.35$, moderate; $1.35\le {\alpha }_i<1.70$, high; and ${\alpha }_i\ge 1.70$, very high.

Several authors (e.g., Culpepper, 2013; Gustafsson, 1977; Nicewander, 2018) proposed reliability in the context of an IRT framework. The relationship of item-score reliability versions based on these proposals to discrimination parameters in several IRT models may not be clear-cut or at least rather complex. Lord (1980) argued that the relationship between item discrimination and IRT-based item-score reliability is far from simple and differs for most IRT models.

Empirical-Data Sets

We selected 16 empirical-data sets collected by means of different tests and questionnaires and representing a wide variety of attributes. In each data set, for each item we estimated item-score reliability by means of each of the three item-score reliability methods. The two goals were to compare the values of the different methods to find differences and similarities, and to derive guidelines for reasonable values to be expected in the analysis of empirical data. We also compared the values for the three item-score reliability methods with the item-rest correlation, the item-factor loading, the item scalability, and the item discrimination. The goal was to investigate whether the item-score reliability and the other four item indices identified the same items as weak or strong relative to the other items in a scale.

Five data sets came from tests measuring maximum performance and 11 data sets came from questionnaires measuring typical behavior. A detailed overview of the data sets can be found in the Appendix. Table 1 provides a classification of the tests and questionnaires by maximum performance and typical behavior, and also by number of items and number of item scores. It was impossible for the authors to get a hold on a typical data set for each cell in Table 1, basically because several combinations of test properties are rare in practice. For example, maximum performance is usually measured using tests containing more than 10 dichotomously scored items, but not by means of shorter tests and rarely by means of tests containing polytomously scored items or the combination of both properties. Hence, for the maximum-performance category we were unable to find data sets with fewer than 10 items or containing polytomous item scores. For the typical-behavior category, we were unable to obtain dichotomous-item data sets with fewer than 20 items. Such data sets are expected to be rare in practice, and because they are rare we did not consider their absence damaging to the conclusions of this study. Tests and questionnaires for which we were able to obtain data sets differed with respect to number of items, number of answer categories (and number of item scores), and sample size. The adjective checklist (ACL; Gough & Heilbrun, 1980) and the HEXACO personality inventory (abbreviated HEX; Ashton & Lee, 2001, 2007) contained scores from 22 and 24 subscales, respectively. We considered the ACL and the HEX different data clusters and within each cluster we analyzed the subscale data separately. The other 14 data sets all referred to a single scale, and were considered a third data cluster, denoted the various-data cluster.

Table 1.

Overview of the Empirical-Data Sets Arranged by Number of Items and Number of Item Scores.

No. of items	Maximum performance		Typical behavior
	No. of Item Scores		No. of Item Scores
	2	>2	2	>2
≤10				SAT SES ACL HEX
10 < J < 20	TRA			COP SEN DS14 LON
≥20	VER BAL IND RAK		CRY TMA	WIL

Note. See the Appendix for the descriptions of the data sets.

Analysis

The three item-score reliability methods and the four accepted item indices were estimated for each data set. Listwise deletion was used to accommodate missing values. Within the three data clusters scatter plots were generated for each combination of the seven item indices, showing the relationship between all possible pairs of item indices.

The three item-score reliability methods use different approaches, but are all intended to approximate true item-score reliability in Equation (2). Hence, we were interested to know the degree to which the three methods produced the same numerical values. Numerical identity was expressed by means of the coefficient of identity (Zegers & Ten Berge, 1985), which runs from −1 to 1, with higher positive values meaning that the values of the two indices studied are more alike, and the value 1 meaning that they are numerically identical. The product-moment correlation provides identity up to a linear transformation, thus it does not provide the exact information we were interested in but it was also given because it is well known and provides approximately, albeit not precisely, the information required. When assessing the relationship between an item-score reliability method and each of the other four item indices or among the latter four indices, one needs to realize that indices in each pair estimate a different parameter. Hence, in considering the degree to which two different indices suggest item quality is in the same direction, an ordinal association measure is sufficient. We used Kendall’s $\tau$ to express this association, and even though it was not quite optimal for our purposes, we provided the product-moment correlation for completeness.

To investigate what values can be expected for the item-score reliability methods at the cutoff values for the other item indices, we regressed each of the three item-score reliability methods on each of the four item indices, thus, producing 12 bivariate regression equations. This enabled us to estimate the item-score reliability at the cutoff value of the item index (.3 for item-rest correlation, .3 for item-factor loading, .3 for item scalability, and .7 for item discrimination), for every combination of item-score reliability method and item index giving an indication of what a good cutoff value would be for the values estimated by the item-score reliability methods.

For estimating the item-score reliability methods, R code (R Core Team, 2016) was used, which was also employed by Zijlmans et al. (2017). The package lavaan (Rosseel, 2012) was used for estimating the item-factor loadings, the package mokken was used for estimating the $H_i$ coefficient (Van der Ark, 2007, 2012), and the package ltm was used for estimating the discrimination parameters (Rizopoulos, 2006) using the two-parameter logistic model for dichotomous data and the graded response model for polytomous data.

Results

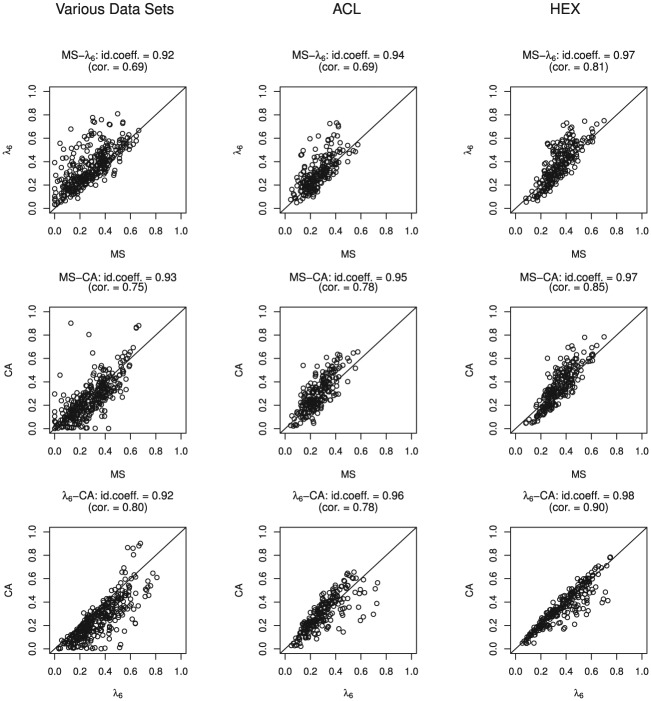
For method MS, the values of the item-score reliability estimates ranged from .00 to .70 (mean .29), for method ${\lambda }_6$, values ranged from .03 to .81 (mean .34), and for method CA, values ranged from .00 to .90 (mean .30). For the three data clusters, Figure 1 shows the scatter plots for pairs of item-score reliability methods. The identity coefficient for all pairs of item-score reliability methods exceeded .9. The plots show more scatter for the various-data cluster. For the ACL and HEX data clusters, the scatter shows stronger association. In all three data sets, in many cases method ${\lambda }_6$ had higher values than methods MS and CA. Product-moment correlations between item-score reliability methods were higher than .70 for all combinations and all data clusters. In the HEX data cluster correlations exceeded .80.

Figure 1.

Scatter plots for the three data clusters comparing the item-score reliability estimates for methods MS, ${\lambda }_6$, and CA.

Note. id. coeff. = identity coefficient; cor = correlation between two method estimates. See the Appendix for a description of the data sets.

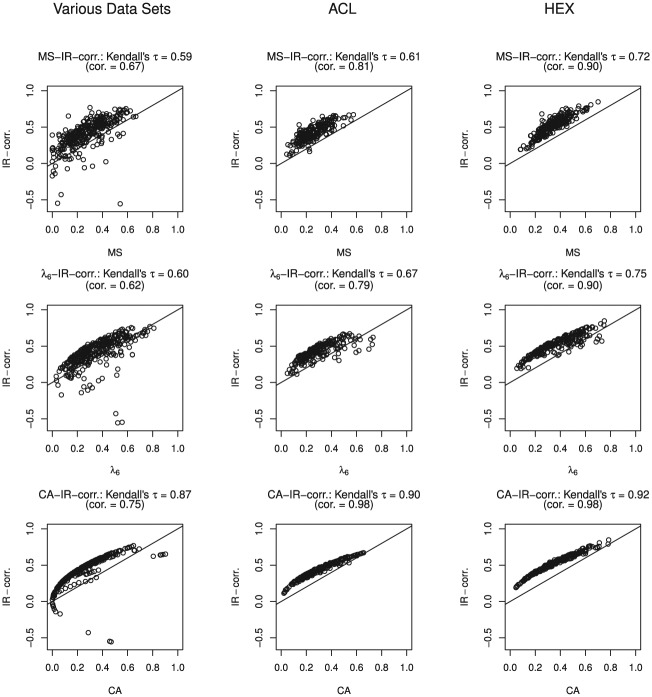
Figure 2 shows the scatterplots comparing item-rest correlation with the three item-score reliability methods. Method CA produced positive values when item-rest correlations were negative. The positive values resulted from squaring the item-rest correlation, see Equation (8). Kendall’s $\tau$ exceeded .87 for item-rest correlation and method CA in all three data clusters, while the other two item-score reliability methods showed lower values for Kendall’s $\tau$, with a maximum of .75. Item-rest correlations correlated highly with item-score reliability values in the ACL and HEX data clusters, but lower in the various-data cluster.

Figure 2.

Scatter plots for the three data clusters comparing the item-score reliability methods with the item-rest correlation (IR-corr.).

Note. cor = correlation between two method estimates. See the Appendix for a description of the data sets.

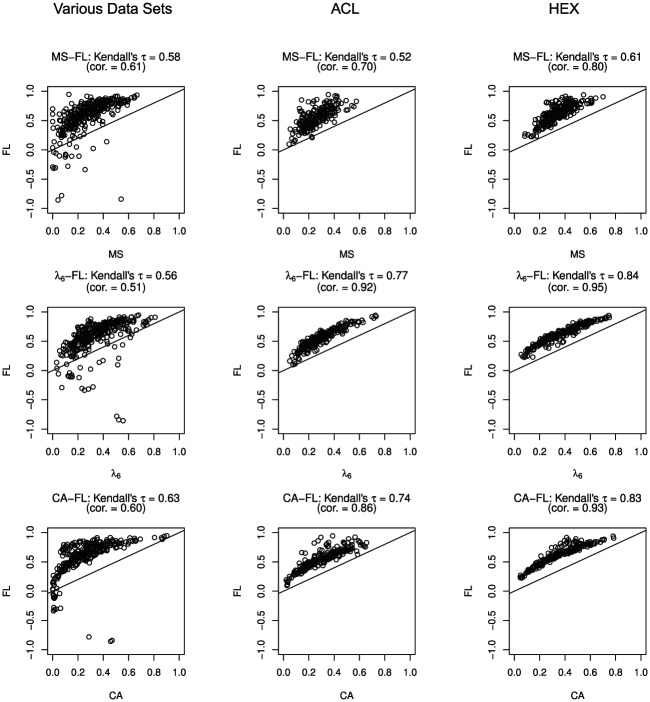
Figure 3 shows the relationship between the item-factor loadings and the three item-score reliability methods. Because most of the scatter lies above the 45-degree line, in many cases the item-factor loading was higher than the three item-score reliability estimates. In the ACL and HEX data clusters, Kendall’s $\tau$ was highest between item-factor loading and method ${\lambda }_6$ (>0.78). In the various-data cluster, Kendall’s $\tau$ was highest, equaling .63, between the item-factor loading and method CA. In the HEX data cluster, the correlation between item-factor loading and item-score reliability methods was highest, followed by the ACL data cluster. The various-data cluster showed the lowest correlations between item-factor loading and item-score reliability methods.

Figure 3.

Scatter plots for the three data clusters comparing the item-score reliability methods with the item-factor loading (FL).

Note. cor = correlation between two method estimates. See the Appendix for a description of the data sets.

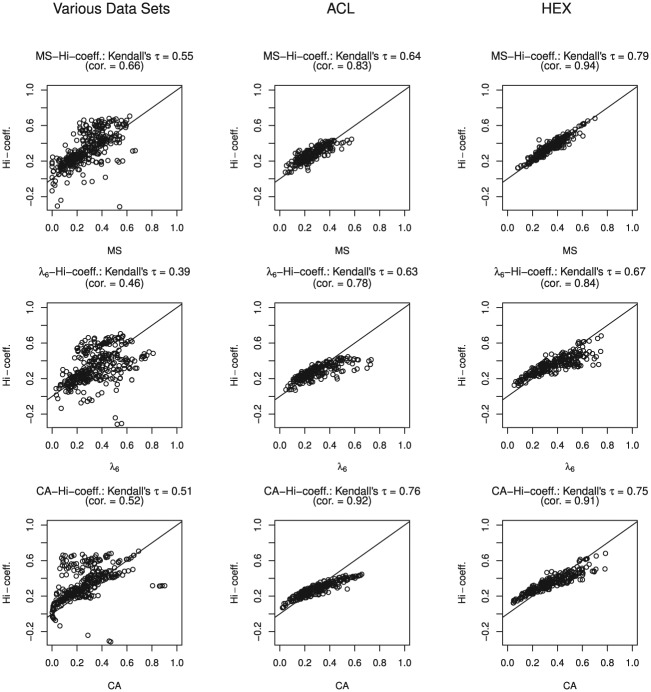
Figure 4 shows the relationship between item scalability $H_i$ and the three item-score reliability methods. Negative $H_i$ values corresponded with positive CA values, resulting in scatter similar to Figure 2. In the various-data cluster, Kendall’s $\tau$ was lower and the scatter showed more spread than in the ACL and HEX data clusters, where Kendall’s $\tau$ showed higher values in excess of .63. In the various-data cluster, correlations between $H_i$ values and the three reliability methods were relatively low, ranging from .46 to .66. In the ACL and HEX data clusters correlations were higher, ranging from .78 to .94.

Figure 4.

Scatter plots for the three data clusters comparing the item-score reliability methods with the $H_i$ coefficient ($H_i$-coeff.).

Note. cor = correlation between two method estimates. See the Appendix for a description of the data sets.

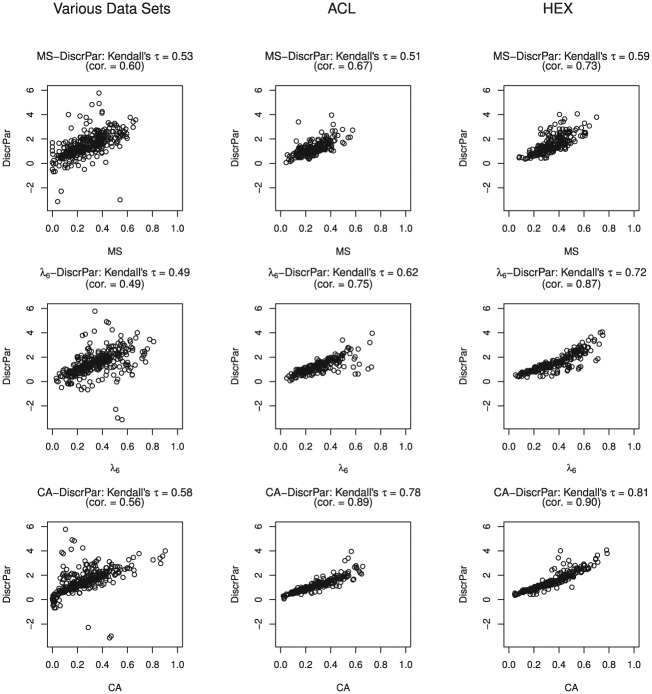
Figure 5 shows the relationship between item discrimination and the three item-score reliability methods. A discrimination value equal to 10.77 in data set RAK was assessed to be an outlier and was removed from the scatter plot. The next largest discrimination value in this data cluster was 5.7 and the mean estimated discrimination was 1.5. Kendall’s $\tau$ between discrimination and CA values was highest for the ACL and HEX data clusters. Kendall’s $\tau$ between item discrimination and MS values was lowest, with values of .53, .51 and .59 for the various-data cluster, the ACL data cluster, and the HEX data cluster, respectively. The correlation between item discrimination and item-score reliability was lower in the various-data cluster than in the ACL and HEX data clusters. In the various-data cluster, correlations ranged from .49 to .60, and in the ACL and HEX data clusters correlations ranged from .67 to .90.

Figure 5.

Scatter plots for the three data clusters comparing the item-score reliability methods with the discrimination parameter (DiscrPar).

Note. cor = correlation between two method estimates. See the Appendix for a description of the data sets.

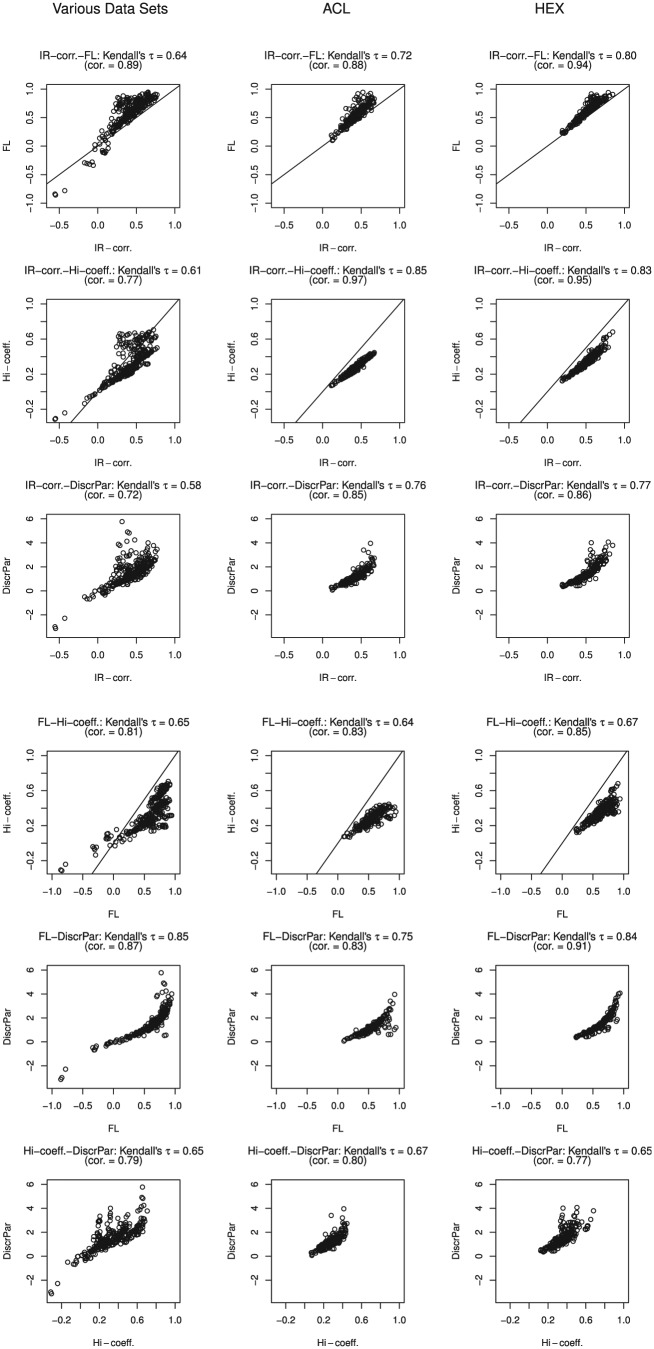
Figure 6 shows the relationship between item-rest correlation, item-factor loading, item scalability, and item discrimination. Kendall’s $\tau$ was highest between item discrimination and item-factor loading in the ACL and HEX data clusters. In these data clusters, correlations were high for the four accepted item indices. Item-rest correlation and item-factor loading correlated higher than .9 in all three clusters. In the ACL and HEX data clusters, item-rest correlation and item scalability also correlated higher than .9.

Figure 6.

Scatter plots for the three data clusters comparing the item-rest correlation (IR-corr.), item-factor loading (FL), the $H_i$ coefficient ($H_i$-coeff.), and the discrimination parameter (DiscrPar).

Note. cor = correlation between two method estimates. See the Appendix for a description of the data sets.

Table 2 provides the results for the bivariate regression estimating the three item-score reliability coefficients by the cutoff values of four other item indices. The item-factor loading estimated the lowest item-score reliability values: .18 for method MS, .20 for method ${\lambda }_6$, and .15 for method CA. The $H_i$ coefficient estimated the highest item-score reliability values: .28 for method MS, .33 for method ${\lambda }_6$, and .28 for method CA.

Table 2.

Estimates of the Three Item-Score Reliability Methods Based on the Cutoff Values of the Other Four Item Indices obtained Using a Bivariate Regression Analysis.

	Method MS	Method ${\lambda }_6$	Method CA
Item-rest correlation	.20	.24	.17
Item-factor loading	.18	.20	.15
$H_i$ coefficient	.28	.33	.28
Item discrimination	.22	.25	.20

Discussion

We estimated item-score reliability methods MS, ${\lambda }_6$, and CA in various empirical-data sets, and investigated which values the researcher may expect to find in his empirical-data set. The identity-coefficient values between the three item-score reliability methods were all higher than .9. The product-moment correlations between the three item-score reliability methods yielded values in excess of .7. Identity values in excess of .9 suggest that the three item-score reliability methods yielded nearly identical values, suggesting a high degree of interchangeability of methods for item selection. We conclude that in practice the three item-score reliability methods can be used interchangeably. The three item-score reliability methods have the same computing time, but methods ${\lambda }_6$ and CA are much simpler to program.

The relationships between the three item-score reliability methods and the four accepted item indices showed a strong association between the item-rest correlation and the item-score reliability methods, especially method CA. This result can be explained by the relation between method CA and the item-rest correlation (Equation 8). The other associations between the item-score reliability methods and the other item indices are weaker. For the other four item indices, the researcher can use available rules of thumb to decide when an item is a candidate for revision or for elimination from a test. Based on investigating a polytomous single-item measure with five response categories, Wanous et al. (1997) suggested using a lower bound of .7 for the item-score reliability. Given the values that were obtained for the items in the empirical-data sets we selected, and given the results from the bivariate linear regression, we conjecture that this requirement may be too stringent in practice: Instead, a value of .3 would be a realistic lower bound for item-score reliability.

We found that ${\lambda }_6$ values often exceeded MS and CA values. In a simulation study, Zijlmans et al. (2017) found that for many conditions in the experimental design, method ${\lambda }_6$ underestimated the true item-score reliability whereas methods MS and CA were almost unbiased, which seems to contradict the results of the present study. An explanation may be that our data sets do not fit in any of the experimental conditions Zijlmans et al. (2017) investigated, making a comparison between the two studies awkward. Our data sets were multidimensional, with relatively large numbers of items that had a considerable variation in discrimination. Zijlmans et al. (2017) studied the factors dimensionality, variation in discrimination within a test, and test length separately, and found that for the multidimensional data, for unequal discrimination, and for many items, the differences between methods MS, ${\lambda }_6$, and CA were either absent or less clear than in other experimental conditions. Hence, a combination of these factors may have caused the relatively high ${\lambda }_6$ values in the present study. In future research, these conditions, which are realistic for most data sets, should be studied further in a fully crossed simulation design.

Values we found for accepted item indices in empirical data could serve as a starting point for a simulation study that further investigates the relationship between item-score reliability and accepted item indices. Furthermore, little knowledge about the relation between item-score reliability and test-score reliability is available, rendering the investigation of this relationship urgent. Also, the effect of omitting items with low item-score reliability on the total-score reliability should be investigated.

Appendix

Appendix.

Overview of the Data Sets

Data set	Attribute	N	J	m+ 1	Percentage missingness	Recoded items	Reference
1 VER	Verbal intelligence by means of verbal analogies	990	32	2	0	—	Meijer, Sijtsma, and Smid (1990)
2 BAL	Intelligence by balance scale problem-solving	484	25	2	0	—	Van Maanen, Been, and Sijtsma (1989)
3 CRY	Tendency to cry	705	23	2	0	—	Vingerhoets and Cornelius (2001)
4 IND	Inductive reasoning	484	43	2	1.24	—	De Koning, Sijtsma, and Hamers (2003)
5 RAK	Word comprehension	1641	60	2	0	—	Bleichrodt, Drenth, Zaal, and Resing (1985)
6 TRA	Transitive reasoning	425	12	2	0	—	Verweij, Sijtsma, and Koops (1999)
7 COP	Strategies for coping with industrial malodor	828	17	4	0	—	Cavalini (1992)
8 WIL	Willingness to participate in labor union action	496	24	5	0	—	Van der Veen (1992)
9 SEN	Sensation seeking tendency	441	13	7	0	—	Van den Berg (1992)
10 DS14	Type D personality	541	14	5	0.13	1 - 3	Denollet (2005)
						1 - 3 - 4
11 TMA	Taylor Manifext Anxiety Scale	5,410	50	2	0.97	9 -12 -18 - 20 - 29	Taylor (1953)
						32 - 38 - 50
12 LON	Loneliness	7,440	11	3	0.58	1 - 4 - 7 - 8 -11	De Jong Gierveld and Van Tilburg (1999)
13 SAT	Satisfaction with life	7,423	4	5	0.43	—	Diener, Emmons, Larsen, and Griffin (1985)
							Pavot and Diener (1993)
14 SES	Rosenberg Self-Esteem Scale	47,974	10	4	0.43	3 - 5 - 8 - 9 -10	Rosenberg (1965)
15 ACL	Personality traits	433	218	6	0	—	Gough and Heilbrun (1980)
16 HEX	HEXACO Personality Inventory	22,786	240	8	<0.01	—	Ashton and Lee (2001, 2007)