Abstract
Common variant heritability has been widely reported to be concentrated in variants within cell-type-specific noncoding functional annotations, but little is known about low-frequency variant functional architectures. We partitioned the heritability of both low-frequency (0.5%≤MAF<5%) and common (MAF≥5%) variants in 40 UK Biobank traits across a broad set of functional annotations. We determined that non-synonymous coding variants explain 17±1% of low-frequency variant heritability ( ) versus 2.1±0.2% of common variant heritability ( ). Cell-type-specific noncoding annotations that were significantly enriched for of corresponding traits were similarly enriched for for most traits, but more enriched for brain-related annotations and traits. For example, H3K4me3 marks in brain dorsolateral prefrontal cortex explain 57±12% of vs. 12±2% of for neuroticism. Forward simulations confirmed that low-frequency variant enrichment depends on the mean selection coefficient of causal variants in the annotation, and can be used to predict effect size variance of causal rare variants (MAF<0.5%).
Introduction
Common variant (minor allele frequency (MAF) ≥5%) trait heritability has been widely reported to be concentrated into noncoding functional annotations that are active in relevant cell-types or tissues, with a limited role for common coding variants1–8. Although common variants explain the bulk of heritability9–11, low-frequency variants can have larger per-allele effect sizes than common variants when impacted by negative selection9–17, and may thus yield important biological insights even though the heritability they explain is modest6,7.
Recent large genome-wide association studies (GWAS) have identified low-frequency variants with large per-allele effect sizes and reported an excess of genome-wide significant low-frequency variants in coding regions18–21, implying that low-frequency coding variants have larger effect sizes than other low-frequency variants. However, the relative contribution of low-frequency coding variants to low-frequency variant heritability is currently unknown. For cell-type-specific noncoding variants, discovery of genome-wide significant low-frequency variants has been limited, and their contribution to low-frequency variant heritability is also unknown. Dissecting low-frequency variant functional architectures can shed light on the action of negative selection across functional annotations and inform the design of low-frequency and rare variant association studies14,22.
To investigate functional enrichments of low-frequency variants (defined here as 0.5%≤MAF<5%), we extended stratified LD-score regression5,23 (S-LDSC) to partition the heritability of both low-frequency and common variants; our method produces robust (unbiased or slightly conservative) results in simulations. We applied our method to partition the heritability of low-frequency and common variants in 40 heritable traits from the UK Biobank24–26 (average N=363K UK-ancestry samples) across a broad set of coding and noncoding functional annotations5,6,8,23,27–31. We performed forward simulations to connect estimated low-frequency and common variant functional enrichments to the action of negative selection, and to predict the effect size variance of causal rare variants (MAF<0.5%) within each functional annotation.
Results
Overview of methods
S-LDSC5,23 is a method for partitioning the heritability causally explained by common variants across overlapping discrete or continuous annotations using genome-wide association study (GWAS) summary statistics for accurately imputed variants and a linkage disequilibrium (LD) reference panel. Here, we extended S-LDSC to partition the heritability causally explained by low-frequency variants using GWAS summary statistics for accurately imputed and poorly imputed variants. We included separate annotations for low-frequency and common variants, and used WGS data from 3,567 UK10K samples18 as an LD reference panel to ensure accurate LD information for low-frequency variants in the UK-ancestry target samples analyzed in this study (see Methods).
We jointly analyzed 163 annotations (referred as the “baseline-LF model”), including 33 main binary annotations, MAF bins, and LD-related annotations (Supplementary Table 1 and Supplementary Table 2; see Methods). We note that the inclusion of MAF- and LD-related annotations implies that the expected causal heritability of a SNP is a function of MAF and LD. We first estimated the heritability causally explained by all low-frequency variants () and the heritability causally explained by all common variants (). For the 33 main binary annotations, we computed their low-frequency variant enrichment (LFVE), defined as the proportion of causally explained by variants in the annotation divided by the proportion of low-frequency variants that lie in the annotation, and common variant enrichment (CVE), defined analogously. Further details of the method are provided in the Methods section. We have released open-source software implementing the method, and have made our annotations publicly available (see URLs).
Simulations of extending S-LDSC to low-frequency variants
Although S-LDSC has previously been shown to produce robust results for partitioning common variant heritability using overlapping binary and continuous annotations23,32, we performed additional simulations to assess our extension to low-frequency variants. We first confirmed that S-LDSC with the UK10K LD reference panel produced unbiased heritability estimates for variants with MAF≥0.5% in simulations using UK10K target samples (see Supplementary Figure 1, Supplementary Table 3, and Supplementary Note). We subsequently performed more realistic simulations using target samples from the UK Biobank interim release24, so that LD (and MAF) in the target samples and UK10K LD reference panel do not perfectly match (see Methods and Supplementary Figure 2). S-LDSC was run either by restricting regression variants to accurately imputed variants (i.e. INFO score33 ≥0.99), as we recommended previously5, or by including all variants (regardless of INFO score). We focused our simulations on two representative annotations spanning roughly 1% of the genome: coding and enhancer. We considered various MAF-dependent architectures34,35, and conservatively specified our generative model to be different from the additive model assumed by S-LDSC (see Methods). For each of the two annotations, we simulated scenarios with no functional enrichment (“No Enrichment”) and scenarios with CVE roughly equal to 7× and lower LFVE (“Lower LFVE”), similar LFVE (“Same Enrichment”), or higher LFVE (“Higher LFVE”), respectively. For both annotations, we observed that including all variants in the regression produced slightly conservative LFVE estimates and unbiased LFVE/CVE ratio estimates, while restricting to accurately imputed variants produced upward biases (Figure 1, Supplementary Table 4). The slightly conservative and LFVE estimates are due to LD-dependent architectures (coding and enhancer variants have lower than average levels of LD, as do other enriched functional annotations23), as we observed nearly unbiased estimates when creating shifted annotations with average levels of LD (see Methods and Supplementary Figure 3). We thus recommend including all variants in the regression when running S-LDSC using the baseline-LF model. Our simulations indicate that this method is robust (unbiased or slightly conservative) in estimating low-frequency and common variant functional enrichments and LFVE/CVE ratios across a wide range of genetic architectures, even in the presence of poorly imputed variants, a target sample that does not exactly match the UK10K LD reference panel, and a MAF-dependent architecture that does not match the additive model assumed by S-LDSC.
Figure 1: Simulations to assess low-frequency variant enrichment estimates.
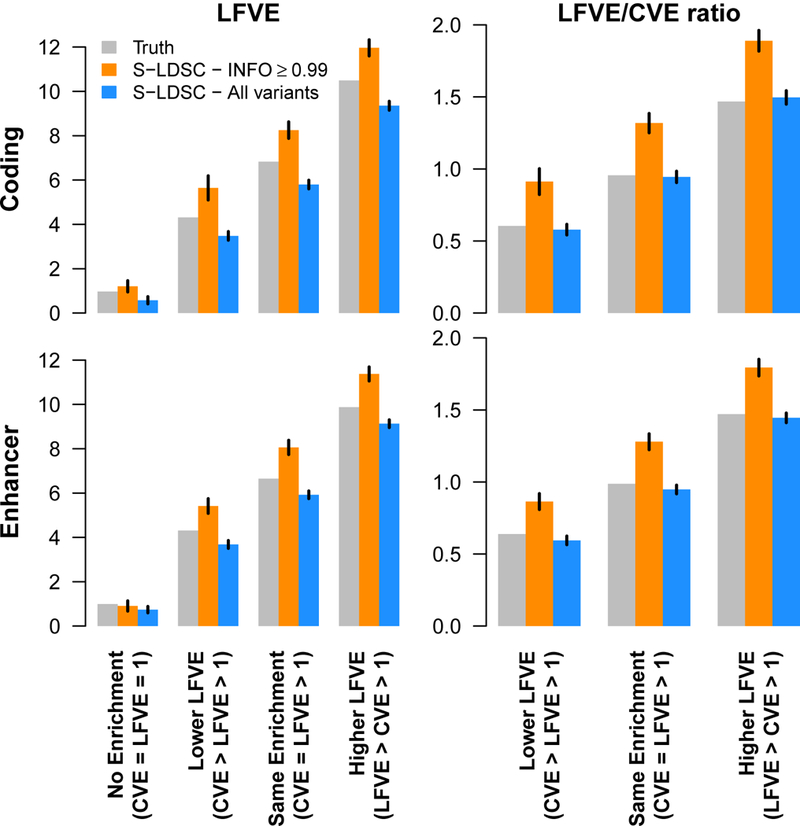
We report estimates of LFVE and LFVE/CVE ratio in simulations under a coding-enriched architecture (first row) or enhancer-enriched architecture (second row). We considered four different simulation scenarios (see main text). S-LDSC was run either by restricting regression variants to accurately imputed variants (S-LDSC – INFO ≥ 0.99), or by including all variants (S-LDSC – All variants). We do not report LFVE/CVE ratio for the No Enrichment simulation (CVE=LFVE=1) due to unstable estimates; however, all analyses of real traits in this paper focus on annotations with significant CVE. Results are averaged across 1,000 simulations. Error bars represent 95% confidence intervals. Numerical results for , , LFVE, CVE and LFVE/CVE ratio are reported in Supplementary Table 4.
Low-frequency functional architecture of UK Biobank traits
We applied S-LDSC with the baseline-LF model to 40 polygenic, heritable complex traits and diseases from the full UK Biobank release25 (average N=363K; Supplementary Table 5). Analyses were restricted to the set of 409K individuals with UK ancestry25 to ensure a close ancestry match with the UK10K LD reference panel. Summary statistics were computed by running BOLT-LMM v2.3 (ref.26) on imputed dosages, and made publicly available (see URLs). S-LDSC results were meta-analyzed across 27 independent traits (average N=355K; see Supplementary Note). We observed a roughly linear relationship between estimates of and (Figure 2 and Supplementary Table 5), with low-frequency variants explaining 6.3±0.2× less heritability and having 4.0±0.1× lower per-variant heritability than common variants on average. These ratios are consistent with a model in which the variance of per-normalized genotype effect sizes is proportional to (where p is the minor allele frequency; refs.34,35) with α=−0.37 (95% confidence interval [−0.40;−0.34]; similar to previous α estimates from raw genotype-phenotype data10,11), and consistent with a model in which low-frequency variants have smaller per-variant heritability but larger per-allele effect sizes10,11,23,34,35 (Supplementary Figure 4).
Figure 2: Common variant heritability ()and low-frequency variant heritability ()estimates for 40 UK Biobank traits.
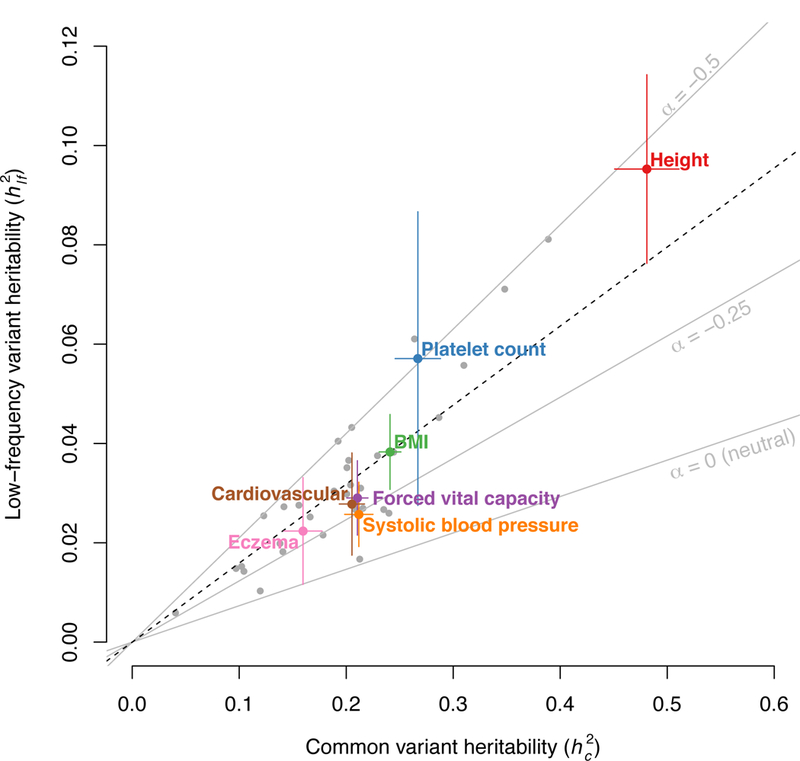
We report and estimated by S-LDSC with the baseline-LF model for 40 UK Biobank traits (for binary traits, estimates are on the liability scale), with 7 representative independent traits highlighted. Error bars represent 95% confidence intervals. The dashed black line represents the ratio between and meta-analyzed across 27 independent traits (1/6.3). Grey lines represent expected ratios for different values of α (see main text). Error bars represent 95% confidence intervals. Numerical results are reported in Supplementary Table 5.
We compared the LFVE and CVE of the 33 main binary functional annotations of the baseline-LF model, meta-analyzed across traits (Figure 3, Supplementary Table 6). LFVE were highly correlated to CVE (r=0.79) and larger than CVE on average (regression slope =1.85). We identified 9 main functional annotations with significantly different LFVE and CVE (Figure 3, Supplementary Table 6). Non-synonymous variants had the largest LFVE and largest difference vs. CVE (5.0× ratio; LFVE=38.2±2.3×, vs. CVE=7.7±0.9×; P=3×10−36 for difference). As non-synonymous variants comprise 0.45% of low-frequency variants vs. only 0.27% of common variants due to strong negative selection on non-synonymous mutations36,37 (see below), this difference is even larger when comparing the proportion of heritability they explain (8.2× ratio; 17.3±1.0% of , vs. 2.1±0.2% of ; P=5×10−47). Non-synonymous variants predicted to be deleterious by PolyPhen-2 (ref.29) had larger LFVE and LFVE/CVE ratio than non-synonymous variants predicted to be benign (Supplementary Figure 5).
Figure 3: Functional low-frequency and common variant architectures across 27 independent UK Biobank traits.
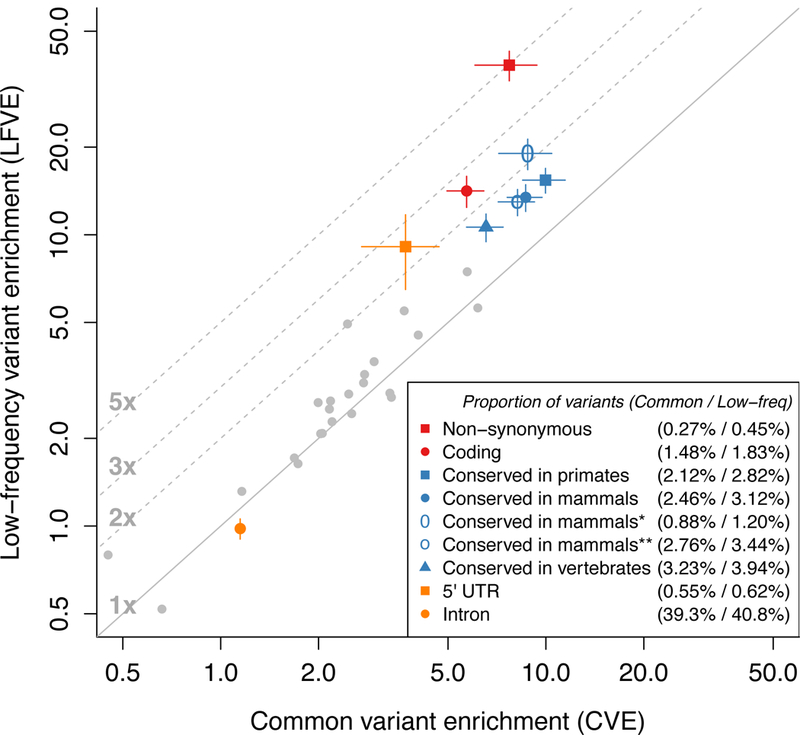
We plot LFVE vs. CVE (log scale) for the 33 main functional annotations of the baseline-LF model (meta-analyzed across the 27 independent traits), highlighting annotations for which LFVE is significantly different from CVE. Numbers in the legend represent the proportion of common / low-frequency variants inside the annotation, respectively. The first three conserved annotations are based on phastCons elements27, Conserved in mammals* is based on GERP RS scores28 (≥4), and Conserved in mammals** is based on Lindblad-Toh et al.30. The promoter flanking annotation has (non-significantly) negative LFVE and is not displayed for visualization purposes. The solid line represents LFVE=CVE; dashed lines represent LFVE=constant multiples of CVE. Error bars represent 95% confidence intervals. Numerical results are reported in Supplementary Table 6.
We also observed LFVE significantly larger than CVE for coding variants (2.5× ratio; P=1×10−18), 5’ UTR (2.5× ratio; P=1×10−4) and the five main conserved annotations27,28,30 (ratios 1.5×-2.2×; each P<5×10−7; Figure 3, Supplementary Table 6). Surprisingly, phastCons regions conserved in primates27 were more enriched than phastCons regions conserved in vertebrates or conserved in mammals27 (even though regions conserved in more distant species may be viewed as more biologically critical). We observed that the significantly larger LFVE (compared to CVE) for all 5 conserved annotations is mainly due to conserved regions that are coding, and that coding enrichments are similar for regions conserved across different species (Supplementary Figure 6). Finally, we observed significantly smaller LFVE than CVE for intronic variants (0.85× ratio; P=8×10−5). These results were generally consistent across the 40 UK Biobank traits analyzed (Supplementary Figure 7).
We also observed significantly larger enrichment/depletion for LFVE than for CVE in the first and/or last quintile of LD-related continuous annotations related to negative selection23 (Supplementary Figure 8 and Supplementary Table 7); our forward simulations from ref.23 confirmed larger effects of low-frequency variants in these LD-related annotations (Supplementary Table 8). Overall, our results suggest that LFVE is substantially larger than CVE only for annotations that are strongly constrained by negative selection, as the strongest differences were observed for coding and non-synonymous variants, which are known to be under strong negative selection36,37. A more detailed interpretation of the LFVE/CVE ratio is provided below (see Forward simulations).
Cell-type-specific enrichments of low-frequency variants
We sought to investigate the contribution to low-frequency variant architectures of cell-type-specific (CTS) annotations1–6 (i.e. reflecting regulatory activity in a given cell type) with excess contributions to common variant architectures. For each of the 40 UK Biobank traits, we selected the subset of 396 CTS Roadmap annotations6 with statistically significant common variant enrichment after conditioning on (non-CTS annotations in) the baseline-LD model5,8 (see Methods). We selected a total of 637 trait-annotation pairs, with at least one CTS annotation for 36 of 40 traits (25 of 27 independent traits) (Supplementary Table 9); the 637 CTS annotations contained 2.7% of common variants and 3.0% of low-frequency variants on average (Supplementary Table 10). We analyzed each of these trait-annotation pairs using the baseline-LF model (Figure 4a and Supplementary Table 10). For the 25 trait-annotation pairs with the most statistically significant CVE for each of the 25 independent traits (critical CTS annotations), LFVE and CVE were similar, with LFVE 1.12±0.13× larger than CVE on average (other definitions of critical CTS annotations produced similar conclusions; see Supplementary Figure 9).
Figure 4: Low-frequency and common variant architectures of cell-type-specific (CTS) annotations.
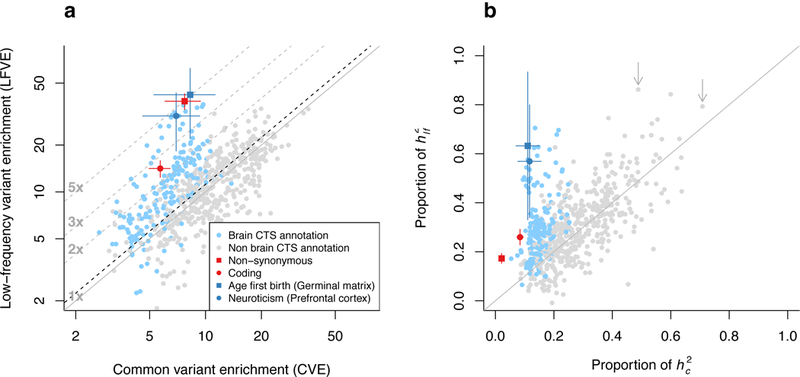
For 637 trait-annotation pairs with conditionally statistically significant common variant enrichment, we report (a) LFVE vs. CVE (log scale) and (b) proportion of vs. proportion of explained. The dashed black line in (a) represents the regression slope for 25 critical CTS annotations for independent traits (see main text). Brain-specific annotations are denoted in blue. Two trait-H3K4me3 annotation pairs with LFVE significantly larger than CVE are denoted in dark blue (see main text); error bars represent 95% confidence intervals. The two arrows in (b) denote All autoimmune diseases (H3K4me1 in Regulatory T-cells; left arrow) and Monocyte count (H3K4me1 in Primary monocytes; right arrow) (see main text). Results for coding and non-synonymous annotations (meta-analysis across 27 independent traits) are denoted in red; error bars represent 95% confidence intervals. Numerical results are reported in Supplementary Table 10.
We observed Bonferroni-significant differences (after correcting each trait for 1–53 annotations tested) for two traits. The most significant trait-annotation pairs were neuroticism and H3K4me3 in brain dorsolateral prefrontal cortex, vs. CVE=8.3±1.5×; P=0.001; 63.2±15.4% of , vs. 11.1±2.0% of ). We note that these results are not driven by the fact that H3K4me3 marks are often located in 5’ UTR and exons38 (Supplementary Table 10). Interestingly, these two annotations (and 55 of all 62 CTS annotations with LFVE/CVE>2) are brain-specific, implicating stronger selection against variants impacting gene regulation in brain tissues (see Forward simulations and Discussion).
While CTS annotations generally have only moderately large LFVE (e.g. smaller than non-synonymous variants; Figure 4a), they often explain a large proportion of (e.g. larger than non-synonymous variants; Figure 4b) due to large annotation size, as with common variant enrichment. In particular, H3K4me1 in regulatory T-cells (3.7% of low-frequency variants) explains 86.2±20.8% of for All autoimmune diseases (vs. 3.4% of common variants explaining 48.9±9.1% of ), and H3K4me1 in primary monocytes (4.8% of low-frequency variants) explains 79.3±18.1% of for monocyte count (vs. 4.6% of common variants explaining 70.8±8.6% of ; Figure 4b and Supplementary Table 10). Thus, CTS annotations often dominate low-frequency architectures, analogous to common variant architectures5,8.
Larger non-synonymous enrichments in genes under selection
Recent studies have identified gene sets that are depleted for non-synonymous variants31,39. To further investigate the connection between functional enrichment and negative selection, we stratified the CVE and LFVE of non-synonymous variants (Figure 3a) based on the strength of selection on the underlying genes. We considered 5 bins of estimated values of selection coefficients for heterozygous protein-truncating variants31 (shet), with 3,073 protein-coding genes per bin, and added annotations based on non-synonymous variants within each bin to the baseline-LF model (see Methods). We determined that both the LFVE and CVE of non-synonymous variants correlated strongly with the predicted strength of selection on the underlying genes (Figure 5 and Supplementary Table 11). In particular, we observed extremely strong enrichments for non-synonymous variants in genes under the strongest selection (bin 1: LFVE=102.0±7.9× and CVE=41.5±4.8×). However, the LFCE/CVE ratio was smaller for non-synonymous variants in genes under the strongest selection (bin 1: 2.5×) than in genes under the weakest selection (bins 4+5: 5.8×); we discuss this surprising result below (see Forward simulations). We obtained similar results when stratifying non-synonymous variants in genes under varying levels of selective constraint based on other related criteria (Supplementary Figure 10).
Figure 5: Low-frequency and common variant enrichments for non-synonymous variants vary with the strength of selection on the underlying genes.
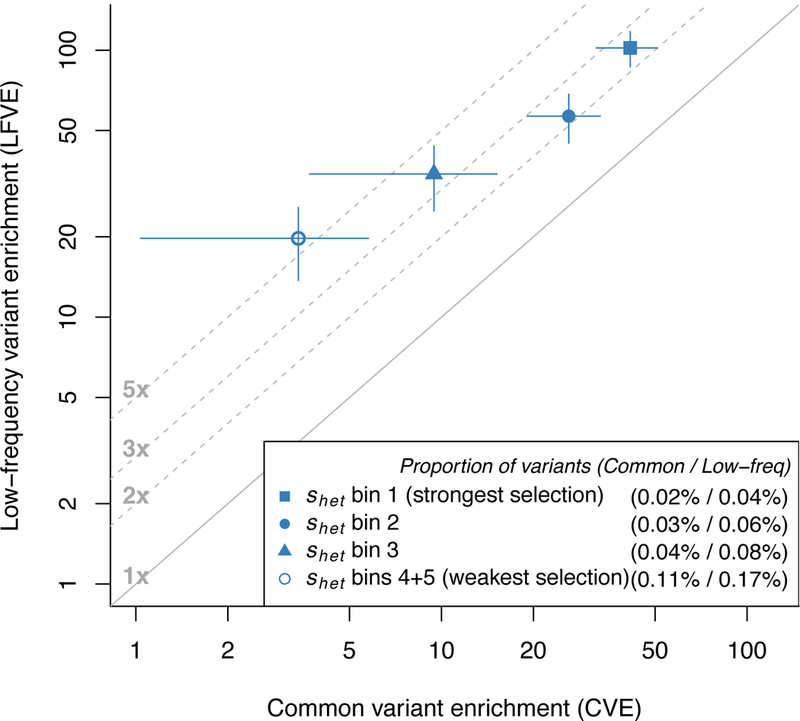
We report LFVE vs. CVE (log scale) for non-synonymous variants in 5 bins of shet (see main text), meta-analyzed across 27 independent UK Biobank traits; bins 4+5 are merged for visualization purposes. Numbers in the legend represent the proportion of common / low-frequency variants inside the annotation, respectively. The solid line represents LFVE=CVE; dashed lines represent LFVE=constant multiples of CVE. Error bars represent 95% confidence intervals. Numerical results for each bin are reported in Supplementary Table 11.
Forward simulations confirm role of negative selection
We hypothesized that the LFVE and CVE of different functional annotations would be informative for the action of negative selection, which constrains strongly selected variants to lower frequency9–17. To investigate this, we performed forward simulations40 using a genetic architecture involving annotations mimicking non-synonymous variants (1% of the simulated genome), functional noncoding variants (1%), and ordinary noncoding variants (98%), with different respective distributions of selection coefficients s (Supplementary Figure 11). For each of these three annotations we specified the probability for a de novo variant to be deleterious (πdel), the mean selection coefficient for de novo deleterious variants () and the probability for a deleterious variant to be causal for the trait (πdel:causal); the probability for a de novo variant to be causal for the trait is π=πdel·πdel:causal. Per-allele trait effect sizes were specified to be proportional to|| where parameterizes the coupling between selection coefficient and trait effect size in the Eyre-Walker model12, implying that only deleterious variants have nonzero effects (see Methods). We investigated how the LFVE and CVE of the functional noncoding annotation varied as a function of the values of and π for that annotation. To achieve a realistic simulation framework, we fixed the remaining values of πdel, and π for the three annotations, as well as the value of , to values that we fit using our UK Biobank estimate of 4.0× larger per-variant heritability for common vs. low-frequency variants, as well as the LFVE and CVE of non-synonymous variants (38.2× and 7.7×, respectively). Specifically, we fixed πdel=60% for the functional noncoding annotation (similar results for πdel=40%; see Methods); πdel=80% (ref.13), =−0.003 (ref.13) and π=8% for the non-synonymous annotation; πdel=40%, =−0.0001 and π=4% for the ordinary noncoding annotation; and =0.75. We note that our fitted value of is larger than previous estimates11,13,15,16 (see Discussion).
We determined that the CVE of the functional noncoding annotation in our simulations depends on both and π (Figure 6a), while the LFVE/CVE ratio depends primarily on (Figure 6b). When de novo deleterious variants are under strong selection (≥−0.0003, corresponding to LFVE/CVE ratio ≥1.2×; Figure 6b), the CVE depends primarily on π (Figure 6a), as the mean selection coefficient of deleterious common variants varies only weakly with (since most deleterious common variants have s<<||; Figure 6c). Finally, we observed that functional noncoding annotations with similar CVE and LFVE tend to have causal variants with slightly stronger selection coefficients (i.e. ≈−0.0002) than ordinary noncoding causal variants (=−0.0001), for which LFVE is lower than CVE (Figure 6b). We note that the LFVE/CVE ratio can be used to infer the mean selection coefficient of deleterious causal variants as a function of MAF (see Figure 6c), because this ratio depends primarily on and because the selection coefficients of de novo deleterious causal variants are drawn from a distribution with mean .
Figure 6: Forward simulations enable inferences about negative selection and rare variant architectures.
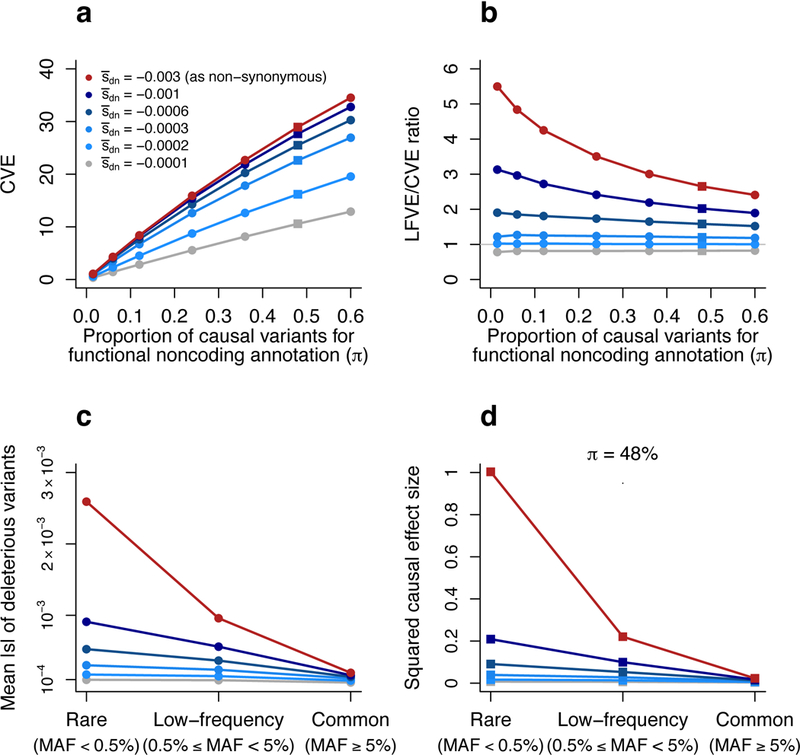
Results are based on forward simulations involving an annotation mimicking functional noncoding variants, as well as other annotations (see text). (a,b) We report the CVE (a) and LFVE/CVE ratio (b) of the functional noncoding annotation as a function of the mean selection coefficient for de novo deleterious variants () and the probability of a de novo variant to be causal (π) for this annotation. and π values for non-synonymous and ordinary noncoding annotations are described in the main text. (c) We report the mean absolute selection coefficient of deleterious variants in the functional noncoding annotation as a function of and MAF (rare, low-frequency, common). (d) We report the mean squared per-allele effect size of causal variants in the functional noncoding annotation (normalized by the mean squared per-allele effect size of rare causal non-synonymous variants) as a function of and MAF (rare, low-frequency and common). Red lines denote the value =−0.003 used to simulate non-synonymous variants, grey lines denote the value =−0.0001 used to simulate ordinary noncoding variants (see main text). The value π=48% used in (d) (see Methods) is denoted via squares in (a) and (b). Numerical results are reported in Supplementary Table 12.
Our forward simulations provide an interpretation of the LFVE/CVE ratios of different functional annotations that we estimated for UK Biobank traits and annotations. First, they confirm that non-synonymous variants (which are strongly deleterious41: large πdel and ||) can have a limited contribution to common variant architectures (2.1% of ) but a large contribution to low-frequency variant architectures (17.3% of ) (Figure 3a). Second, they indicate that the proportion of causal variants (π) is larger for critical cell-type-specific (CTS) annotations than for non-synonymous variants (based on their CVE; Figure 4a), but that the causal variants in critical CTS annotations have only slightly larger selection coefficients than ordinary noncoding variants, except for some brain annotations that are under much stronger selection (much larger ||, based on their LFVE/CVE ratios; Figure 4a). Third, they explain the extremely large CVE for non-synonymous variants inside genes predicted to be under strong negative selection31 (large shet; Figure 5), which are expected to correspond to genes with an extremely large proportion of deleterious non-synonymous variants (large πdel, implying large π=πdel·πdel:causal). However, despite extremely large CVE and LFVE, this class of variants had a smaller LFVE/CVE ratio than that of non-synonymous variants inside genes predicted to be under weak selection (Figure 5), a surprising result that appears to suggest a smaller(Figure 6b) despite the extremely large value of πdel. We performed additional forward simulations to show that a larger || doesnot produce larger LFVE/CVE ratios for annotations with extremely large values of πdel, for which the ratio between the proportion of low-frequency variants that are deleterious and the proportion of common variants that are deleterious is reduced to 1 (Supplementary Figure 12).
Although our focus is primarily on low-frequency variants (0.5%≤MAF<5%), we also used our forward simulation framework to draw inferences about rare variant (MAF<0.5%) architectures of noncoding functional annotations, based on LFVE and CVE estimates from UK Biobank (Figure 4a). Specifically, we compared the mean squared per-allele effect size of rare causal variants in annotations mimicking functional noncoding variants and non-synonymous variants, respectively. We inferred disproportionate causal effects of rare variants in annotations under very strong selection (||=−0.003, similar to non-synonymous variants13), with mean squared causal effect sizes 11×, 26× and 60× larger than annotations with ||=−0.0006, ||=−0.0003 and ||=−0.0002, respectively (Figure 6d and Supplementary Table 12; similar results for different choices of π, Supplementary Figure 13). These results indicate that an annotation with large CVE needs to have even larger LFVE (e.g. LFVE/CVE ratio ≥2×, corresponding to ||≤−0.0006; Figure 6b) in order to harbor rare causal variants with substantial mean squared effect sizes (e.g. only an order of magnitude smaller than rare causal non-synonymous variants; Figure 6d). Unfortunately, most of the non-brain CTS annotations that we analyzed do not achieve this ratio (Figure 4a), motivating further work on more precise noncoding annotations (see Discussion).
Discussion
In this study, we partitioned the heritability of both low-frequency and common variants in 40 UK Biobank traits across numerous functional annotations, employing an extension of stratified LD score regression5,23 to low-frequency and common variants that produces robust (unbiased or slightly conservative) results. Meta-analyzing functional enrichments across 27 independent traits, we highlighted the critical impact of low-frequency non-synonymous variants (17.3% of , LFVE=38.2×) compared to common non-synonymous variants (2.1% of , CVE=7.7×). Other annotations previously linked to negative selection, including non-synonymous variants with high PolyPhen-2 scores29, non-synonymous variants in genes under strong selection31, and LD-related annotations23, were also significantly more enriched for as compared to . Finally, at the trait level, we observed that CTS annotations6,8 also dominate the low-frequency architecture, and that significant CVE tend to have similar LFVE, or larger LFVE for brain-related annotations and traits. This last observation implicate the action of negative selection on low-frequency variants affecting gene regulation in the brain, and is consistent with the interaction between brain enhancers and genes under stronger purifying selection18, and with the excess of rare de novo mutations in regulatory elements active in fetal brain in patients with neurodevelopmental disorders43. We showed via forward simulations that the CVE of an annotation depends primarily on its proportion of causal variants (π), while its LFVE/CVE ratio depends primarily on the mean selection coefficient for de novo deleterious variants (), and thus to the mean selection coefficient of causal variants (Figure 6). These conclusions are consistent with previous studies of the role of selection9–17, including pleiotropic selection17, in maintaining variants with large effects on complex traits at low frequencies. Overall, our work quantifies the relationship between the strength of selection in specific functional annotations (both coding and noncoding) and low-frequency and common variant enrichment for human diseases and complex traits, providing an interpretation of the enrichments estimated for UK Biobank traits and annotations.
Our results on low-frequency variant functional architectures have several implications for downstream analyses. First, our results provide guidance for the design of association studies targeting low-frequency variants. Non-synonymous variants should be strongly prioritized at the low-frequency variant level21, as they explain a large proportion of and directly implicate causal genes (and specifically implicate core disease genes rather than peripheral genes7), avoiding the challenge of mapping noncoding variants to genes42,44. However, we observed that all coding and UTRs variants jointly explained only 26.8±1.9% of (Supplementary Table 6), providing an upper bound of the proportion of low-frequency signal captured by whole-exome sequencing (WES) studies. This underscores the advantages of large GWAS (with imputed genotypes obtained using large reference panels), compared to WES or exome chip data, for querying low-frequency variation16. Furthermore, using functionally informed association tests that assign higher weight to low-frequency non-synonymous variants or CTS annotations should significantly improve power in these analyses4,20,45. Second, our results provide guidance for the design of association studies targeting rare (MAF<0.5%) variants, which require large sequencing datasets14. While WES datasets have been successfully used to detect new coding variants, genes and gene sets associated to human diseases and complex traits, there is an increasing focus on WGS that can capture rare noncoding variants. However, our LFVE and CVE results for critical CTS annotations (Figure 4), coupled with our predictions of causal rare variant effect size variance (Figure 6d), suggest that in most instances these annotations do not harbor causal variants with large mean squared effect sizes (with brain-related annotations and traits as a notable exception; also see ref.43), highlighting the need for more precise noncoding annotations for prioritization in WGS. As a first step towards this goal, we estimated the LFVE and CVE of annotations constructed using a wide range of recently developed noncoding variant prioritization scores46–50. We identified only one annotation, defined using the top 0.5% of Eigen scores48, with an LFVE/CVE ratio significantly larger than 1 (1.7× ratio; LFVE=22.0±2.2×, vs. CVE=13.0±1.4×; P=7×10−4 for difference; Supplementary Figure 14). However, even for this annotation, the LFVE/CVE ratio <2 again implies that this annotation does not harbor causal variants with substantial mean squared effect sizes (only an order of magnitude smaller than rare causal non-synonymous variants; Figure 6d). Third, our results were consistent with strong coupling between selection coefficient and trait effect size (Eyre-Walker coupling parameter12 =0.75; robust to error bars in LFVE and CVE estimates, see Supplementary Figure 15), implicating a larger impact of negative selection on complex traits than previously reported11,13,15,16 and much larger effect sizes for rare variants in functional annotations with strong selection coefficients. This can be explained by the fact that our inference procedure explicitly allows different distributions of selection coefficients for non-synonymous and noncoding variants (=−0.003 and =−0.0001, respectively; Supplementary Figure 16). Finally, the different LFVE/CVE ratios that we inferred for different functional annotations suggest that it may be appropriate to allow annotation-specific α values when using the α model (per-normalized genotype effect size proportional to (; refs.10,11,34,35). In the extreme case of non-synonymous variants, we explored different choices of α values for non-synonymous and other variants, and determined that a value of α=−1.10 for non-synonymous variants and α=−0.30 for other variants provided the best fit our UK Biobank heritability and enrichment results (Supplementary Table 13).
Although our work has provided insights on low-frequency variant architectures of human diseases and complex traits, it has several limitations (see Supplementary Note). Despite these limitations, our low-frequency and common variant enrichment results convincingly demonstrate and quantify the action of negative selection across coding and noncoding functional annotations.
Methods
Extension of S-LDSC to low-frequency variants.
S-LDSC5,23 is a method for partitioning heritability explained by common variants across overlapping annotations (both binary and continuous23) using GWAS summary statistics. More precisely, S-LDSC models the vector of per normalized genotype effect size β as a mean-0 vector whose variance depends on D continuous-valued annotations :
| 1 |
where αd (j) is the value of annotation ad at variant j, and represents the per-variant contribution of one unit of the annotation αd to heritability. We can thus perform a regression to infer the values of using the following relationship with the expected statistic of variant j:
| 2 |
where is the LD score of variant j with respect to continuous values αd(k) of annotation αd, rjk is the correlation between variant j and k in an LD reference panel, N is the sample size of the GWAS study,and b is a term that measures the contribution of confounding biases51. Then, the heritability causally explained by a subset of variants S can be estimated as . We note that this definition, used here to define and estimate and , is different from the definition of “SNP-heritability” (ref.52), which refers to the heritability tagged by a set of genotyped and/or imputed variants.
To allow different effects for low-frequency and common variants inside a functional annotation αd, we modeled the variance of the per normalized genotype effect sizes using different for these two categories of variants. In a case where we consider Df functional annotations, we write:
| 3 |
where (resp. ) is an indicator function with value 1 if variant j is a low-frequency (resp. common) variant, and 0 otherwise, (resp. ) represents the per-variant contribution of one unit of the annotation αd to the heritability explained by low-frequency (resp. common) variants. These parameters can be estimated using S-LDSC by writing equation (3) in the form:
| 4 |
where (resp. ) is an annotation equals to αd(j) if variant j is a low-frequency (resp. common) variant and 0 otherwise. In all analyses we also added one annotation containing all the variants, 5 MAF bins for low-frequency variants, and 10 MAF bins for common variants in order to take into account MAF-dependent effects23,53,54.
For each functional binary annotation of interest αd, we compared its low-frequency variant enrichment (LFVE) and common variant enrichment (CVE), defined as the proportion of (resp. ) explained by the annotation, divided by the proportion of low-frequency (resp. common) variants that are in the annotation (see Supplementary Note for a justification of the denominator). Standard errors were computed using a block jackknife procedure5. We note that these computations did not include the heritability causally explained by rare variants (MAF<0.5%).
Application of S-LDSC was performed using 3,567 unrelated individuals of UK10K data set18 (ALSPAC and TWINSUK cohorts) as an LD reference panel. This choice was made in order to ensure a close ancestry match between the target sample used to compute summary statistics (UK Biobank) and the LD reference panel (UK10K), as LD patterns of low-frequency variants are expected to vary across European populations55,56 (see Supplementary Note for more information on our application of S-LDSC). The main differences of our application of S-LDSC compared to standard S-LDSC analyses on common variants are summarized in Supplementary Table 14.
Baseline-LF model and functional annotations.
We considered 34 main functional annotations from the baseline-LD model v1.1 (27 binary and 7 continuous annotations, including LD-related annotations; refs.5,23,57,58), including coding, UTR, promoter and intronic regions, the histone marks monomethylation (H3K4me1) and trimethylation (H3K4me3) of histone H3 at lysine 4, acetylation of histone H3 at lysine 9 (H3K9ac) and two versions of acetylation of histone H3 at lysine 27 (H3K27ac), open chromatin as reflected by DNase I hypersensitivity sites (DHSs), combined chromHMM and Segway predictions (which make use of many Encyclopedia of DNA Elements (ENCODE) annotations to produce a single partition of the genome into seven underlying chromatin states), three different conserved annotations, two versions of super-enhancers, FANTOM5 enhancers, typical enhancers, and 6 LD-related continuous annotations (see Supplementary Table 1).
In order to further dissect the set of coding variants, a major focus of this study, we annotated each coding variant using ANNOVAR59, and added one synonymous and one non-synonymous annotation to our model. We also added three new annotations based on phastCons27 conserved elements (46 way) in vertebrates, mammals and primates, and one annotation based on flanking bivalent TSS/enhancers from Roadmap data6 (see URLs). These 6 new annotations led to a total of 33 main binary annotations (see Supplementary Table 1).
We included 500 bp windows around each binary annotation and 100 bp windows around four of the main annotations, leading to a total of 74 main functional annotations. Then, all annotations were duplicated for low-frequency and common variants as described in equation (4), except for the predicted allele age annotation60 (which had too many missing values for low-frequency variants). Finally, we included one annotation containing all variants, 10 common variant MAF bins (as in the baseline-LD model23) and 5 low-frequency variant 5 MAF bins. We thus obtained a set of 163 total annotations. We refer to this set of annotations as the “baseline-LF model” (see Supplementary Table 2), which we used for all of our S-LDSC analyses. More details on the baseline-LF model are provided in the Supplementary Note.
We note that the inclusion of MAF and LD-related annotations in this model implies that the expected causal heritability of a SNP is a function of MAF and LD. More details on LD-related heritability models are provided in the Supplementary Note.
Simulations using UK Biobank target samples to assess extension of S-LDSC to low-frequency variants.
To assess possible biases in heritability and enrichment estimates under a more realistic scenario, we simulated quantitative phenotypes from chromosome 1 of UK Biobank interim release dataset with imputed variants from thousand genomes61 and UK10K18 (113,851 unrelated individuals, 1,023,655 variants with allele counts greater or equal to 5 in UK10K). First, we randomly sampled integer-valued genotypes from UK Biobank imputation dosage data. Second, we set trait heritability to h2=0.5, selected M=100,000 causal variants, and performed simulations under a coding-enriched architecture by simulating the variance of per-normalized genotype effect sizes proportional to , where 1jcoding (resp.1j noncoding )is an indicator function taking the value 1 if variant j belongs (resp. does not belong) to the coding annotation,p is the frequency of the causal variant in the simulated UK Biobank genotypes dataset, α0 was set to −0.25, and c and αcoding were chosen to produce four different genetic architectures (see Supplementary Table 4). We note that this generative model is different and more complex than the additive inference model implemented in S-LDSC, but may be more realistic as the effect size of coding variants depends now directly on their allele-frequency (and not or their low-frequency/common status). We also performed simulations under an enhancer-enriched architecture by considering the baseline ChromHMM/Segway weak-enhancer62 annotation, which has similar properties as the coding annotation (2.28% of reference low-frequency variants versus 1.83% for coding, and elements with a mean length size of 249bp versus 315bp for coding). To investigate the impact of the LD-dependent architecture created by the enrichment of these two annotations (coding and weak-enhancer variants tend to have low levels of LD23), we randomly created 100 shifted coding (resp. weak-enhancer) annotations, and selected the annotation with an average level of LD (i.e. the shifted annotation with the 50th smallest level of LD computed on low-frequency variants; see ref.23 for a definition of level of LD). Third, we used version 2.3 of BOLT-LMM software26,63 (see URLs) to compute association statistics on UK Biobank dosage data to mimic the fact that we computed summary statistics on imputed data. Finally, we used S-LDSC with our baseline-LF model (except that the 6 new functional annotations were not included in the simulation analyses) to estimate , , and coding/enhancer CVE and LFVE. S-LDSC was run by restricting regression variants to accurately imputed variants (i.e. INFO score33 ≥ 0.99), as we suggested previously5, or to all variants (irrespective of INFO score). We also report results when using an INFO score threshold of 0.5 or 0.9, which did not improve the results (see Supplementary Table 4). We also considered including INFO score explicitly in the regression to down-weight poorly imputed variants (i.e. replacing equation (2) by , where Ij is the INFO score of variant j and ; this approximation assumes that genotype uncertainty decreases the association test statistics), but this did not improve the results, consistent with the fact that summary statistics computed from dosage data already down-weight poorly imputed variants (Supplementary Table 4). We performed 1,000 simulations for each simulation scenario. In each case, we removed 0–3 outlier simulations in which the estimate of was below 0.0001; we did not observe any such outlier results in analyses of real traits (minimum =0.006; Supplementary Table 5).
S-LDSC analyses of UK Biobank data.
We applied S-LDSC with the baseline-LF model to 40 UK Biobank traits, estimated , , and the ratio using the 15 MAF bin annotations, and computed their standard errors using a jackknife procedure. We meta-analyzed the ratio, and multiplied it by the ratio of the number of low-frequency and common variants in the LD reference sample (i.e. 3,398,397/5,353,593) to convert it into a per-variant heritability ratio. To match these ratios to a model in which the variance of per-normalized genotype effect sizes is proportional to , we used low-frequency and common variants of our LD reference panel and computed the ratio using different values of α.
The CVE and LFVE of each functional annotation were compared using a two-sided z-test; these values are independent as they are computed using non-overlapping sets of variants. The regression slope of LFVE on CVE was computed with no intercept. As most of the 33 annotations are correlated, we did not attempt to assess the statistical significance of the regression slope, or of the corresponding correlation between CVE and LFVE. We note that after removing the 9 annotations with significantly different LFVE and CVE in Figure 3, LFVE remained highly correlated to CVE (r=0.83) and only slightly larger than CVE on average (regression slope=1.10).
For CTS analyses, we analyzed the 396 Roadmap6 annotations constructed in Finucane et al.8 from narrow peaks in six chromatin marks (DNase hypersensitivity, H3K27ac, H3K4me3, H3K4me1, H3K9ac, and H3K36me3) in a subset of a set of 88 primary cell types/tissues. We selected CTS annotations for which common variants are disease relevant following Finucane et al.8 guidelines. First, we analyzed each CTS annotation in turn using default S-LDSC (i.e. not our extension to low-frequency variants) by conditioning on all the non-CTS annotations of the baseline-LD model v1.1, the union of annotations for each of the six chromatin marks, and the average of annotations for each mark (as performed in ref.8). We note that our choice to switch from the baseline model5, as performed in ref.8, to the baseline-LD model (which includes MAF bins and LD-related annotations in addition to new functional annotations) was motived by our observation that the baseline model can slightly overestimate functional enrichment due to unmodeled annotations23. We also decided to consider only non-CTS annotations and to remove the four enhancers annotations derived from Vahedi et al.64 (absent from the baseline model and added in the baseline-LD model) as they are T-cell specific and may impact the detection of relevant cell types for traits for which T-cells are a relevant cell type (such as asthma and eczema; see Supplementary Figure 17). We retained all the CTS annotations with a coefficient statistically larger than 0 (using P<0.05/396), selecting a total of 637 trait-annotation pairs with at least one CTS annotation for 36 of 40 traits (all traits except high light scatter reticulocyte count, high cholesterol, sunburn occasion, and age at menopause), including 25 of 27 independent traits (Supplementary Table 9). Finally, we re-analyzed these 637 trait-annotation pairs using our extended S-LDSC with the baseline-LF model, the union of the six chromatin marks, and the average of annotations for each mark. In Figure 4, we report all 637 pairs for completeness, demonstrating the consistency between CVE and LFVE for CTS annotations (Supplementary Table 10). However, as the 1–53 CTS annotations selected for each trait are often highly correlated with each other, we selected for each of the 25 independent traits the “most critical” CTS annotation, defined in the main text and Figure 4 as the CTS annotation with the most statistically significant CVE. For these 25 annotations, we regressed their LFVE on their CVE with no intercept. We also considered 5 alternative definitions of the “most critical” CTS annotation for each trait; for each of these definitions, LFVE were similar to CVE (Supplementary Figure 9). Finally, when testing if a CTS annotation has a significantly larger LFVE than CVE, we used a trait-specific Bonferonni threshold (i.e. 0.05 divided by the number of CTS annotations retained for the trait).
For gene set analyses based on the shet metric31, we divided variants into 5 bins containing the same number of genes (3,073; 3,072 for the last bin). For S-LDSC analyses, we added to the baseline-LF model two annotations for variants inside a protein coding gene (for low-frequency and common variants, respectively; we used the 17,484 protein-genes from ref.65), 10 annotations for variants inside the 5 gene sets, and 10 annotations for non-synonymous variants inside the 5 gene sets (22 annotations in total).
Forward simulations.
To investigate the connection between LFVE, CVE and the distribution of fitness effects (DFE), we performed forward simulations under a Wright-Fisher model with selection using SLiM2 software40 (see URLs). We simulated 1Mb regions of genetic length 1cM with a uniform recombination rate and a uniform mutation rate (2.36×10−8, as recommended in SLiM manual). De novo mutations had probability πdel to be deleterious with a dominance coefficient of 0.5 and a selection coefficient s drawn from a gamma distribution with mean and shape , and had probability 1 - πdel to be neutral (i.e. s=0). We outputted a sample of 5,000 European genomes using the out-of-Africa demographic model of Gravel et al.66 implemented in SLiM. Then, we used Eyre-Walker model12 to compute the per-allele effect size , where c is a constant, Ne is the effective population size, sj the selection coefficient of variant j, is the coupling coefficient between selection and phenotypic effect, and ε is a normally distributed noise. Here, c was set to have a trait heritability h2=0.5 (i.e., where pj is the allele frequency of variant j),Ne was set as the expected coalescent time67 of the European population of the Gravel et al. model (6,524), and ε was set to 0 for simplicity. We note that we focused here on per-variant heritability (i.e. ) and not directional effects, thus our conclusions are independent of the direction of the selection coefficient on the trait and are valid for traits that are either under direct or stabilizing selection.
Unlike our previous forward simulation framework23, we designed these simulations to have a realistic DFE for annotations mimicking both non-synonymous and noncoding variants. Briefly, we created 50 non-synonymous elements with a realistic length 200bp (10kb in total, 1% of the 1Mb simulated genome) separated by non-coding elements of size 14.9kb (99% of the simulated genome; Supplementary Figure 11a). To mimic non-synonymous elements, we used πdel = 80%, = −3.16 × 10−3 and = 0.32, as previously estimated13. Then, we estimated that fixing πdel=40%, =−1.00×10−4, =0.32 for noncoding variants and =0.75 provide a good fit of our UK Biobank heritability and non-synonymous enrichment results (see Supplementary Note).
In most subsequent simulations, we fixed the probability of a deleterious variant to be causal (πdel:causal) at 10%, so that the proportion of de novo non-synonymous variants that are causal (π, defined as π=πdel·πdel:causal) is 8% (resp. 4% for noncoding variants). This allows non-synonymous variants to have LFVE and CVE on the same order of magnitude as the LFVE and CVE observed for the non-synonymous variants inside genes predicted to be under strong negative selection31 (102.0× and 41.4×, respectively; Figure 5). We note that we replicated our main results when using πdel:causal=5% (Supplementary Figure 18).
Next, we investigated the impact of and π on a “functional noncoding” annotation. To do so, we alternately considered 200kb functional elements as non-synonymous elements (1% of the simulated genome) or as functional noncoding elements (1% of the simulated genome), separated by “ordinary noncoding” elements of size 9.8kb (98% of the simulated genome; Supplementary Figure 11b). For each functional noncoding element, we fixed πdel=60% and =0.32 (equal to the value of for non-synonymous and overall noncoding elements). We chose a value πdel in between the value for overall noncoding (πdel=40%) and non-synonymous (πdel=80%) annotations, as we hypothesized that enriched functional noncoding annotations in the human genome have a larger proportion of deleterious variants than the overall noncoding genome. However, we note that we obtained similar results when choosing πdel=40% for the functional noncoding annotation (Supplementary Figure 19). We varied and πdel:causal (and thus π) of the functional noncoding annotation, while retaining πdel:causal=10% for the variants in the non-synonymous and ordinary noncoding elements. (We varied on the logarithmic scale, and report truncated values in the manuscript for simplicity; for example,=−0.003 stands for −3.1623×10−3; see Supplementary Table 12 for exact values). For each scenario, we simulated 1,000 regions of 1Mb for each scenario, merged the outputted variants, and considered 100 randomly chosen sets of causal variants.
When drawing inferences about rare variant (MAF<0.5%) architectures of noncoding functional annotations, we focused on simulations with π=48% for the functional noncoding annotation, because the CVE and LFVE/CVE ratios for the CTS annotations in Figure 4a (between 5 and 20, and between 1 and 2, respectively) roughly correspond to π=48% and between 0.0002 and 0.0006 (Figure 6a-b).
Supplementary Material
Acknowledgments
We thank A. Gusev, C. Marquez-Luna, M. Hujoel, Y. Reshef, F. Hormozdiari, O. Weissbrod, B. Neale, A. Siepel and S.M. Gazal for helpful discussions. This research has been conducted using the UK Biobank Resource (application number 16549). This research was funded by NIH grants U01 HG009379, R01 MH101244, R01 MH107649, R01 MH109978 and U01 HG009088. P.-R.L. was supported by a Burroughs Wellcome Fund Career Award at the Scientific Interfaces and the Next Generation Fund at the Broad Institute of MIT and Harvard.
Footnotes
Competing Financial Interests Statement
The authors declare no conflict of interest.
URLs
ldsc software, http://www.github.com/bulik/ldsc.
baseline-LF annotations: https://data.broadinstitute.org/alkesgroup/LDSCORE/baselineLF.tar.gz.
BOLT-LMM association statistics computed in this study are available at https://data.broadinstitute.org/alkesgroup/UKBB/UKBB_409K.
phastCons elements, http://hgdownload.cse.ucsc.edu/goldenPath/hg19/database/phastConsElements46way*.txt.gz;
Flanking bivalent TSS/enhancers, http://egg2.wustl.edu/roadmap/data/byFileType/chromhmmSegmentations/ChmmModels/coreMarks/jointModel/final/*_15_coreMarks_segments.bed.
BOLT-LMM software, https://data.broadinstitute.org/alkesgroup/BOLT-LMM.
SLiM2 software, https://messerlab.org/slim/.
Code availability
ldsc software is available at http://www.github.com/bulik/ldsc. A tutorial for running our extension of stratified LD score regression is available in https://data.broadinstitute.org/alkesgroup/LDSCORE/baselineLF.tar.gz.
References
- 1.Maurano MT et al. Systematic Localization of Common Disease-Associated Variation in Regulatory DNA. Science 337, 1190–1195 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Trynka G et al. Chromatin marks identify critical cell types for fine mapping complex trait variants. Nat. Genet. 45, 124–130 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Gusev A et al. Partitioning heritability of regulatory and cell-type-specific variants across 11 common diseases. Am. J. Hum. Genet. 95, 535–552 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Pickrell JK Joint analysis of functional genomic data and genome-wide association studies of 18 human traits. Am. J. Hum. Genet. 94, 559–573 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Finucane HK et al. Partitioning heritability by functional annotation using genome-wide association summary statistics. Nat. Genet. 47, 1228–1235 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Kundaje A et al. Integrative analysis of 111 reference human epigenomes. Nature 518, 317–330 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Boyle EA, Li YI & Pritchard JK An Expanded View of Complex Traits: From Polygenic to Omnigenic. Cell 169, 1177–1186 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Finucane HK et al. Heritability enrichment of specifically expressed genes identifies disease-relevant tissues and cell types. Nat. Genet. 50, 621–629 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Yang J et al. Genetic variance estimation with imputed variants finds negligible missing heritability for human height and body mass index. Nat. Genet. 47, 1114–1120 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Zeng J et al. Signatures of negative selection in the genetic architecture of human complex traits. Nat. Genet. 50, 746–753 (2018). [DOI] [PubMed] [Google Scholar]
- 11.Schoech A et al. Quantification of frequency-dependent genetic architectures and action of negative selection in 25 UK Biobank traits. bioRxiv 188086 (2017). doi:10.1101/188086 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Eyre-Walker A Genetic architecture of a complex trait and its implications for fitness and genome-wide association studies. Proc. Natl. Acad. Sci. 107, 1752–1756 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Agarwala V, Flannick J, Sunyaev S, GoT2D Consortium & Altshuler, D. Evaluating empirical bounds on complex disease genetic architecture. Nat. Genet. 45, 1418–1427 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Zuk O et al. Searching for missing heritability: Designing rare variant association studies. Proc. Natl. Acad. Sci. 111, E455–E464 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Mancuso N et al. The contribution of rare variation to prostate cancer heritability. Nat. Genet. 48, 30–35 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Fuchsberger C et al. The genetic architecture of type 2 diabetes. Nature 536, 41–47 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Simons YB, Bullaughey K, Hudson RR & Sella G A population genetic interpretation of GWAS findings for human quantitative traits. PLOS Biol. 16, e2002985 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.The UK10K Consortium. The UK10K project identifies rare variants in health and disease. Nature 526, 82–90 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Astle WJ et al. The Allelic Landscape of Human Blood Cell Trait Variation and Links to Common Complex Disease. Cell 167, 1415–1429.e19 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Sveinbjornsson G et al. Weighting sequence variants based on their annotation increases power of whole-genome association studies. Nat. Genet. 48, 314–317 (2016). [DOI] [PubMed] [Google Scholar]
- 21.Marouli E et al. Rare and low-frequency coding variants alter human adult height. Nature 542, 186–190 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lee S, Abecasis GR, Boehnke M & Lin X Rare-variant association analysis: study designs and statistical tests. Am. J. Hum. Genet. 95, 5–23 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Gazal S et al. Linkage disequilibrium-dependent architecture of human complex traits shows action of negative selection. Nat. Genet. 49, 1421–1427 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Sudlow C et al. UK Biobank: An Open Access Resource for Identifying the Causes of a Wide Range of Complex Diseases of Middle and Old Age. PLOS Med. 12, e1001779 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Bycroft C et al. Genome-wide genetic data on ~500,000 UK Biobank participants. bioRxiv 166298 (2017). doi:10.1101/166298 [Google Scholar]
- 26.Loh P-R, Kichaev G, Gazal S, Schoech AP & Price AL Mixed-model association for biobank-scale datasets. Nat. Genet. 50, 906–908 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Siepel A et al. Evolutionarily conserved elements in vertebrate, insect, worm, and yeast genomes. Genome Res. 15, 1034–1050 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Davydov EV et al. Identifying a high fraction of the human genome to be under selective constraint using GERP++. PLoS Comput. Biol. 6, e1001025 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Adzhubei IA et al. A method and server for predicting damaging missense mutations. Nat. Methods 7, 248 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lindblad-Toh K et al. A high-resolution map of human evolutionary constraint using 29 mammals. Nature 478, 476–482 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Cassa CA et al. Estimating the selective effects of heterozygous protein-truncating variants from human exome data. Nat. Genet. 49, 806–810 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Gazal S, Finucane HK & Price AL Reconciling S-LDSC and LDAK functional enrichment estimates. bioRxiv 256412 (2018). doi:10.1101/256412 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Marchini J & Howie B Genotype imputation for genome-wide association studies. Nat. Rev. Genet. 11, 499–511 (2010). [DOI] [PubMed] [Google Scholar]
- 34.Speed D, Hemani G, Johnson MR & Balding DJ Improved Heritability Estimation from Genome-wide SNPs. Am. J. Hum. Genet. 91, 1011–1021 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Lee SH et al. Estimation of SNP heritability from dense genotype data. Am. J. Hum. Genet. 93, 1151–1155 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Li Y et al. Resequencing of 200 human exomes identifies an excess of low-frequency non-synonymous coding variants. Nat. Genet. 42, 969 (2010). [DOI] [PubMed] [Google Scholar]
- 37.Tennessen JA et al. Evolution and Functional Impact of Rare Coding Variation from Deep Sequencing of Human Exomes. Science 337, 64–69 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Shlyueva D, Stampfel G & Stark A Transcriptional enhancers: from properties to genome-wide predictions. Nat. Rev. Genet. 15, 272–286 (2014). [DOI] [PubMed] [Google Scholar]
- 39.Ganna A et al. Quantifying the Impact of Rare and Ultra-rare Coding Variation across the Phenotypic Spectrum. Am. J. Hum. Genet. 102, 1204–1211 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Haller BC & Messer PW SLiM 2: Flexible, Interactive Forward Genetic Simulations. Mol. Biol. Evol. 34, 230–240 (2017). [DOI] [PubMed] [Google Scholar]
- 41.Kryukov GV, Pennacchio LA & Sunyaev SR Most Rare Missense Alleles Are Deleterious in Humans: Implications for Complex Disease and Association Studies. Am. J. Hum. Genet. 80, 727–739 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Won H et al. Chromosome conformation elucidates regulatory relationships in developing human brain. Nature 538, 523–527 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Short PJ et al. De novo mutations in regulatory elements in neurodevelopmental disorders. Nature 555, 611–616 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Claussnitzer M et al. FTO Obesity Variant Circuitry and Adipocyte Browning in Humans. N. Engl. J. Med. 373, 895–907 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Kichaev G et al. Leveraging polygenic functional enrichment to improve GWAS power. bioRxiv 222265 (2017). doi:10.1101/222265 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Ritchie GRS, Dunham I, Zeggini E & Flicek P Functional annotation of non-coding sequence variants. Nat. Methods 11, 294–296 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Kircher M et al. A general framework for estimating the relative pathogenicity of human genetic variants. Nat. Genet. 46, 310–315 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Ionita-Laza I, McCallum K, Xu B & Buxbaum JD A spectral approach integrating functional genomic annotations for coding and noncoding variants. Nat. Genet. 48, 214–220 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Huang Y-F, Gulko B & Siepel A Fast, scalable prediction of deleterious noncoding variants from functional and population genomic data. Nat. Genet. 49, 618–624 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.di Iulio J et al. The human noncoding genome defined by genetic diversity. Nat. Genet. 50, 333–337 (2018). [DOI] [PubMed] [Google Scholar]
- 51.Bulik-Sullivan BK et al. LD Score regression distinguishes confounding from polygenicity in genome-wide association studies. Nat. Genet. 47, 291–295 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Yang J et al. Common SNPs explain a large proportion of the heritability for human height. Nat. Genet. 42, 565–569 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Lee SH et al. Estimating the proportion of variation in susceptibility to schizophrenia captured by common SNPs. Nat. Genet. 44, 247–250 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Loh P-R et al. Contrasting genetic architectures of schizophrenia and other complex diseases using fast variance-components analysis. Nat. Genet. 47, 1385–1392 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Moore CB et al. Low Frequency Variants, Collapsed Based on Biological Knowledge, Uncover Complexity of Population Stratification in 1000 Genomes Project Data. PLOS Genet. 9, e1003959 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Leslie S et al. The fine-scale genetic structure of the British population. Nature 519, 309–314 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Liu X et al. Functional Architectures of Local and Distal Regulation of Gene Expression in Multiple Human Tissues. Am. J. Hum. Genet. 100, 605–616 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Hormozdiari F et al. Leveraging molecular quantitative trait loci to understand the genetic architecture of diseases and complex traits. Nat. Genet. 50, 1041–1047 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Wang K, Li M & Hakonarson H ANNOVAR: functional annotation of genetic variants from high-throughput sequencing data. Nucleic Acids Res. 38, e164 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Rasmussen MD, Hubisz MJ, Gronau I & Siepel A Genome-wide inference of ancestral recombination graphs. PLoS Genet 10, e1004342 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Auton A et al. A global reference for human genetic variation. Nature 526, 68–74 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Hoffman MM et al. Integrative annotation of chromatin elements from ENCODE data. Nucleic Acids Res. 41, 827–841 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Loh P-R et al. Efficient Bayesian mixed-model analysis increases association power in large cohorts. Nat. Genet. 47, 284–290 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Vahedi G et al. Super-enhancers delineate disease-associated regulatory nodes in T cells. Nature 520, 558–562 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Lek M et al. Analysis of protein-coding genetic variation in 60,706 humans. Nature 536, 285–291 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Gravel S et al. Demographic history and rare allele sharing among human populations. Proc. Natl. Acad. Sci. 108, 11983–11988 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Nordborg M & Krone SM Separation of time scales and convergence to the coalescent in structured populations in Modern Developments in Theoretical Population Genetics Oxford (University Press, 2002). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


