Two determinations of the Ge-68 half-life

Abstract

In nuclear medicine, ⁶⁸Ge is used to generate ⁶⁸Ga for imaging by positron emission tomography (PET) and sealed sources containing ⁶⁸Ge/⁶⁸Ga in equilibrium have been adopted as long-lived calibration surrogates for the more common PET nuclide, ¹⁸F. We prepared several ⁶⁸Ge sources for measurement on a NaI(Tl) well counter and a pressurized ionization chamber, following their decay for 110 weeks (≈ 2.8 half-lives). We determined values for the ⁶⁸Ge half-life of T_1/2 = 271.14(15) d and T_1/2 = 271.07(12) d from the NaI(Tl) well counter and ionization chamber measurements, respectively. These are in accord with the current Decay Data Evaluation Project (DDEP) recommended value of T_1/2 = 270.95(26) d and we discuss the expected impact of our measurements on this value.

1. Introduction

Germanium-68 decays by 100 % electron capture to form ⁶⁸Ga, a short-lived positron emitter (Bé et al., 2013). As such, ⁶⁸Ge has been used for some time to make generators of ⁶⁸Ga for use in positron emission tomography (PET) studies. More recently, ⁶⁸Ge has been finding increasing use as a calibration surrogate for devices used to make industrial and clinical measurements of short-lived positron emitters (Lockhart et al., 2011; Doot et al., 2014; Zimmerman and Cessna, 2010; Zimmerman et al., 2015). A long-lived calibration source must have a well-known activity at the time of measurement. As the period of service goes on for any given source, the decay correction and its associated uncertainty grows. For any technologically important radionuclide, a good half-life with well-characterized uncertainty is crucial. In this work, we add data to a sparse set in order to increase confidence in the ⁶⁸Ge half-life and its uncertainty.

We report here on two determinations of the ⁶⁸Ge half-life by pressurized ionization chamber measurements and by NaI(Tl) well counter measurements. We carried out measurements over a period of 110 weeks (≈ 2.8 half-lives). The data were acquired and analyzed in a manner consistent with other recent half-life determinations at the National Institute of Standards and Technology (NIST; Bergeron and Fitzgerald, 2015; Pibida et al., 2017), looking beyond fit uncertainties to realize conservative but realistic final uncertainties. Finally, we consider our determinations in the context of earlier work, reporting a new evaluation of the ⁶⁸Ge half-life, T_1/2 = 271.05(8) d.¹

2. Materials and methods

2.1. Ge-68 sources

All ⁶⁸Ge sources were prepared in standard NIST borosilicate flame-sealed ampoules, with nominally 5 mL total volume. The carrier solution contained approximately 65 μg each of Ge⁴⁺ and Ga³⁺ in 0.5 mol L⁻¹ HCl. Germanium-68 sources prepared with this carrier solution have been shown to be stable against precipitation and transfer losses for more than 7 a, or nearly 10 half-lives (Zimmerman et al., 2016). Two ampoules with initial ⁶⁸Ge activities of approximately 1.0 kBq (referred to as ampoules 1 and 2) and one with approximately 0.5 kBq (referred to as ampoule 3) were prepared for half-life measurements on the Wizard 2480 NaI(Tl) well counter referred to herein as “GWC” (PerkinElmer, Waltham, MA).² One ampoule with initial ⁶⁸Ge activity of approximately 3.14 MBq was devoted to half-life measurements on a pressurized ionization chamber designated “ICB” (Fitzgerald, 2010). The response from both techniques is mostly from the decay of the short-lived ⁶⁸Ga daughter, but all half-life measurements were performed long after parent/daughter equilibrium was established. Under these conditions, the combined parent-daughter decay curve takes the shape of a single exponential of which the slope is determined by the decay constant of the parent nuclide. Analysis by high-purity germanium spectroscopy revealed no photon-emitting impurities.

2.2. NaI(Tl) well counter measurements

The three ampoules were counted weekly on the NaI(Tl) well counter (GWC) for 75 min each, initially acquiring approximately 3 million counts in an open window (nominally 18 keV to 2000 keV) for the 1 kBq ampoules. The ampoules were centered by custom-built nylon sleeves in the typical scintillation vial sample cassettes. Between ampoules 1 and 2, an ampoule containing cold carrier solution was inserted and between ampoules 2 and 3, an empty sleeve. The average count rate for the cold carrier (4.3(1) s⁻¹) was systematically higher than for the empty sleeve (4.1(1) s⁻¹), possibly due more to rack positioning than to any actual contributions from the carrier. The cold carrier was positioned between the two 1.0 kBq sources, whereas the empty sleeve was between a 1 kBq and a 0.5 kBq source. For the half-life calculations, in each measurement cycle, the average of the cold carrier and empty sleeve count rates was used to calculate the background-subtracted count rate for all samples.

The sample activities were selected to fall in a range of GWC response linearity previously established by measuring a decaying ¹⁸F source. As discussed below, response non-linearity over this range was evaluated conservatively and used to estimate an uncertainty component. Over this range, the GWC software handles deadtime corrections very well; the linearity uncertainty component includes any uncorrected deadtime effects.

No weeks were missed over the course of the experiment, but occasionally, the acquisition day varied by up to 2 d. On three occasions, elevated backgrounds in the laboratory due to parallel activities required the rejection of a count. Further, the sources were measured several times in the first three days, so that ultimately, n = 116, 115, and 114 counts were used for ampoules 1, 2, and 3, respectively.

The long-term stability of the GWC response was monitored by counting an ¹²⁹I (T_1/2 = 16.1(7) × 10⁶ a; Bé et al., 2004) source in each measurement cycle. Over the course of this half-life determination, the relative standard deviation on the decay-corrected count rate for the ¹²⁹I check source was 0.06 %. As described below, this variance was propagated to estimate the singlemeasurement uncertainty in a manner consistent with our previous reports (Bergeron and Fitzgerald, 2015). Some of the variance in the ¹²⁹I response can be attributed to seasonal fluctuations in the ambient conditions in the laboratory. The room housing the GWC typically has higher temperature and relative humidity in the summer than in the winter. As discussed below, seasonal variances were carefully considered in the half-life evaluation and in the uncertainty estimate.

The sensitivity of NaI(Tl) detector responses to ambient conditions is well-understood (see, e.g., Knoll, 2000; Ianakiev et al., 2009). As has been shown clearly and repeatedly, seasonal variations in ambient laboratory conditions should not be interpreted as evidence of new physics (see, e.g., Kossert and Nähle, 2014; Kossert and Nähle, 2015; Schrader, 2016; Pommé et al., 2016).

2.3. Pressurized ionization chamber measurements

One ⁶⁸Ge ampoule was measured approximately weekly on ICB for over two years with some occasional missed weeks. The acquisition software ended counts either when a set standard deviation of the mean (0.02 %) or a set maximum time was reached. The maximum count times were set to 300 seconds initially and increased to 1000 s approximately halfway through the measurements. The shortest count time was 58 s. Each measurement of the ⁶⁸Ge ampoule was followed by measurements of a ²²⁶Ra reference source (RRS50) and of the background. The maximum count times for the radium reference source were set to 300 s, allowing the 0.02 % statistical limit to be consistently achieved. Background current measurements were collected for 1000 s. For the earliest and latest measurements, the ⁶⁸Ge and RRS50 measurements were repeated for 3 to 5 insertions. Due to change in personnel, for a period in the middle of the experiment (from day 364 to day 647), there were no repeat measurements. In principle, using the net ratio of the currents produced by the ⁶⁸Ge ampoule to RRS50 compensates for any environmental effects on the chamber response; in practice, agreement between the half-life determined from the ratio matched very well with the value determined with net currents (vide infra). Over the course of this half-life determination, the relative standard deviation on the decay-corrected (T_1/2 = 1600(7) a; Bé et al., 2008) current was 0.06 %.

3. Results and discussion

3.1. NaI(Tl) well counter

Open window counting data were analyzed as described previously (Bergeron and Fitzgerald, 2015). The half-life was determined from the net count rate data using a weighted least squares fit to a single exponential function. The uncertainty used for weighting was estimated by combining components for the counting statistics (σ_s = N^−0.5 where N is the total net counts), the background uncertainty (σ_b, based on the standard deviation on the average of the count rates for the cold carrier and empty sleeve), and an additional uncertainty component to account for unobserved effects (σ_x, added as necessary to achieve χ²/v ≤ 1). Table 1 gives the details of these components. The “cross-talk correction” applied in some of our experiments was not necessary in this case. The fit uncertainty, u_fit calculated from the fit residuals (Figure 1a) for each source is also given in Table 1.

Table 1.

Uncertainty components for weighting GWC data and uncertainty on the weighted least squares fit for each source.

	σs / %			σb / %			σx / %	ufit / %
ampoule 1	0.06	to	0.13	0.01	to	0.07	0.057	0.008
ampoule 2	0.06	to	0.13	0.01	to	0.07	0	0.007
ampoule 3	0.08	to	0.17	0.03	to	0.14	0.070	0.011

Figure 1.

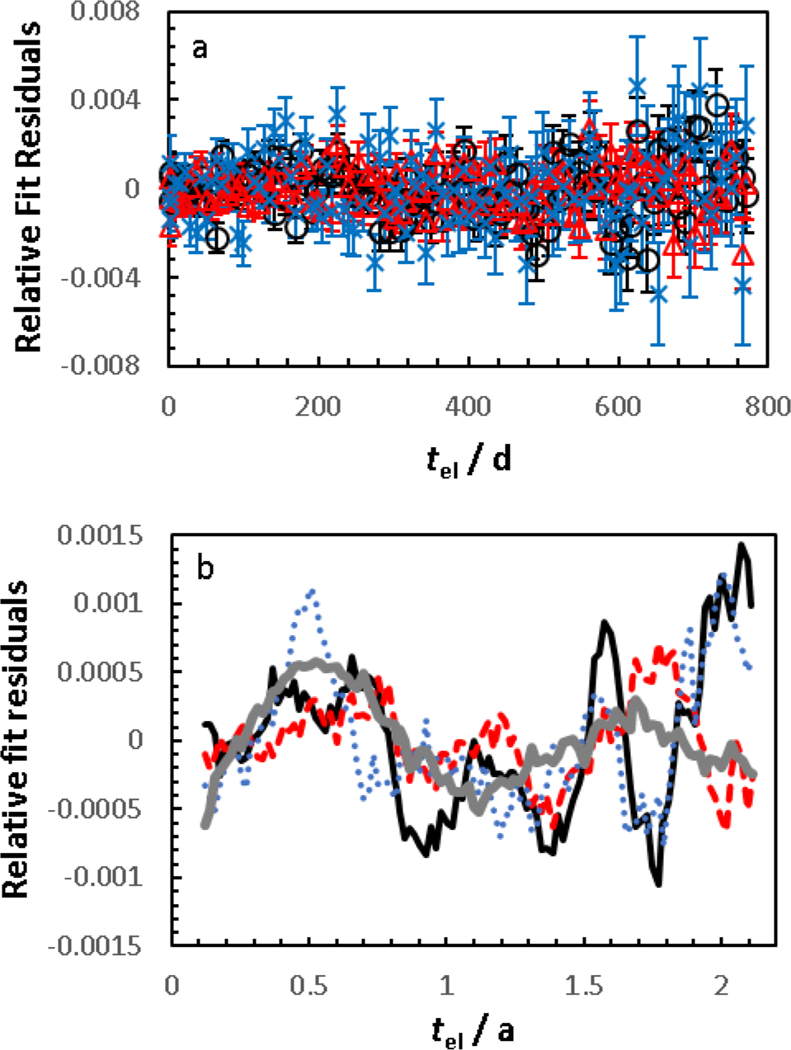
(a) Fit residuals for ampoules 1 (black open circles), 2 (red open triangles), and 3 (blue X’s). The uncertainty bars are calculated by combining the weighting components summarized in Table 1. (b) Fit residuals smoothed with a 10-point running average for ampoules 1 (black solid line), 2 (red dashed line), and 3 (blue dotted line). The smoothed residuals for the ¹²⁹I check source are shown in the bold gray line. Taking the ratio of the ⁶⁸Ge/¹²⁹I count rates helps to correct for the effect of seasonal variations of the ambient laboratory conditions on the NaI(Tl) response.

The fit residuals in Figure 1a hint at a variance component with annual periodicity, especially when smoothed by a 10 point moving average (Figure 1b). The periodicity is more pronounced for the stronger ¹²⁹I check source than for the ⁶⁸Ge sources, and indeed autocorrelation plots for the three ⁶⁸Ge ampoules do not reveal any clear trend. From the amplitude of the oscillation in the ¹²⁹I data and Equation 1 (Pommé et al., 2008)

$$\frac{\sigma T_{1/2}}{T_{1/2}}\approx \left\{\frac{2}{\lambda T}\sqrt{\frac{2}{n+1}}\right\}\frac{\sigma (R)}{R},$$ (1)

the uncertainty on the half-life due to the seasonal oscillation was estimated, u_an = 0.034 % (Table 2). In Equation 1, λ is the decay constant, T the duration of the experiment, n the number of periods of oscillation, and R the measured count rate. The uncertainty due to possible drift of the GWC response, u_drft, is similarly estimated.

Table 2.

Uncertainty budget for the GWC ⁶⁸Ge half-life determination. The italicized components are included for reference, but not used in the evaluation. The final combined uncertainty (u_c = 0.06 % or 0.15 d; k = 1) is calculated from the components shown in bold. The individual components are described in detail in the text.

	T1/2 / d	ufit	urpt	uan	udrft	uratio	ulin	Combined
ampoule 1	271.217	0.008	0.008	0.019	3E-06	0.007	0.011	0.024
ampoule 2	270.995	0.007	0.008	0.013	3E-06	0.007	0.011	0.020
ampoule 3	271.220	0.011	0.008	0.035	3E-06	0.015	0.006	0.038
avg	271.14	0.009	0.008	0.022	3E-06	0.010	0.009	0.028
sd	0.13
sd / %	0.05
uc / %	0.06
uc / d	0.15

Included in Table 2 is an additional uncertainty component (u_ratio) corresponding to the standard deviation on the half-life determined from a fit of the net count rate data and the half-life determined from a fit of the ratio of the ⁶⁸Ge count rate to the ¹²⁹I count rate in each cycle. In principle, normalizing against the check source should provide a correction for the changing environmental conditions that affect the GWC response. On average, the half-lives recovered from the ratios were very slightly longer than those calculated with the net count rate data: T_1/2(ratio)/T_1/2(net) = 1.0001. As one might assume from Figure 1b, the fit uncertainties for the ratios were larger than for the net count rates: u_fit = 0.010 %, 0.007 %, and 0.013 % for ampoules 1, 2, and 3, respectively (compare to u_fit values in Table 1). The u_ratio component is included for reference only, and is not included in the final combined uncertainty. In terms of components of variance, u_ratio should be fully embodied in other terms shown in Table 2.

Table 2 also shows uncertainty contributions from the measurement repeatability, u_rpt, and the GWC linearity, u_lin. The value for u_rpt is estimated from the standard deviation on the ¹²⁹I check source measurements using Equation 1. Note that u_rpt would also be expected to contribute to u_ratio. In addition, u_lin is taken from a conservative estimate of the maximum non-linearity based on measurements of an ¹⁸F source as described previously (Bergeron and Fitzgerald, 2015). Because the measurements were performed at the same time of day (± 2 h) each week, there is no diurnal uncertainty.

By far, the largest component in the total combined uncertainty on half-life, u_c, is the source-to- source variability, calculated as the standard deviation on the half-lives determined for the three ⁶⁸Ge ampoules. The uncertainties estimated for the two 1 kBq ampoules were predictably smaller than for the 0.5 kBq ampoule. However, both an unweighted mean and a weighted mean give the same value for T_1/2 to within the significant digits. From the GWC data, we report T_1/2 = 271.14(15) d.

3.2. Pressurized ionization chamber

Data were analyzed as described previously (Bergeron and Fitzgerald, 2015) as a ratio of the background-corrected current of the ⁶⁸Ge source to the background-corrected current from RRS50. The current from the ²²⁶Ra reference source, RRS50, includes a decay correction to t = 0 of between 1 and 1.00085. The half-life value was determined by a weighted least squares fit of the ratio versus elapsed time. The weighting consisted of a combination of the standard deviation of the mean for the current values for the ⁶⁸Ge, ²²⁶Ra, and background.

The standard deviation of the mean, u_Ge or u_Ra, on any individual ⁶⁸Ge or RRS50 current measurement ranged from 0.02 % to 0.03 %. The equivalent for the background ranged from 1.54 % to 6.10 %, giving an uncertainty, u_bkg, on the ratio of 0.001 % to 0.009 %. On days including repeat measurements, the ratio was averaged and a midpoint of all ⁶⁸Ge measurements was assigned. The components u_Ge or u_Ra used for the weighting on repeat measurements were taken as the averages of those components on the individual measurements. An additional component, u_btw, of 0.036 % was added to all points and corresponds to the average between-insertion standard deviation of the mean, on an individual measurement day, where available. The combination of these components gave a fit weighting that ranged from 0.04 % to 0.05 %.

The current measurements for the ⁶⁸Ge source spanned two electrometer ranges, changing at day 724. An examination of the residuals from a fit of all data revealed a shift associated with this range change. The data collection program for ICB incorporates a correction for the range change that seems inadequate for half-life determinations. Removing the later data from the fit, but calculating the residuals from an extrapolation yields a ratio that is low by an average factor of 0.9995 relative to the value predicted by the extrapolation. Therefore, the data after day 717 were not considered in the reported half-life.

A conservative estimate of the linearity within the electrometer range was made based on prior data collected with a ^99mTc source. The resulting small slope versus current seen in residuals of the ^99mTc data after correcting for decay was applied to the ⁶⁸Ge data. This resulted in a 0.035 % change in the calculated half-life, but no appreciable change in the goodness of fit or χ²/v. This value was incorporated as an uncertainty for linearity, u_lin.

There were a total of 78 points considered in the least-squares fit. The residuals are shown in Figure 2. The black solid circles were used in the half-life determination. The gray open circles are the excluded data. The uncertainty due to the least-squares fit is 0.07 d.

Figure 2.

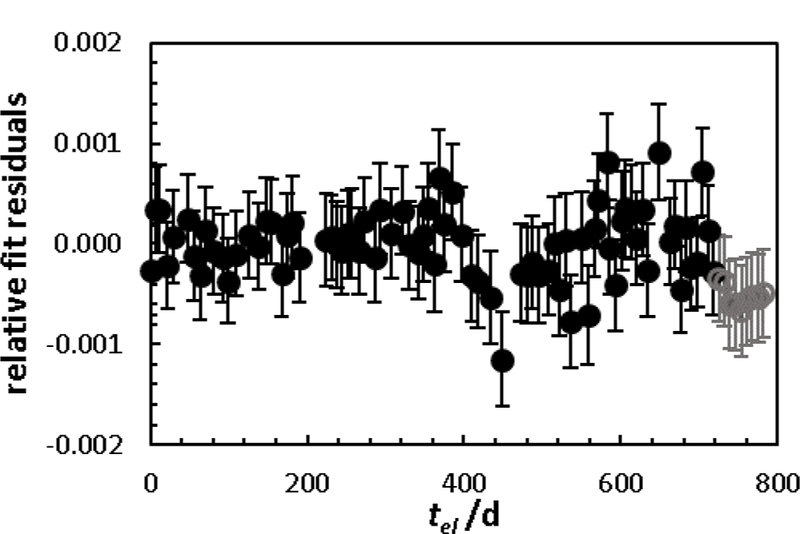
Fit residuals for ICB. Solid black circles are used in the reported value. Open gray circles demonstrate the shift associated with an electrometer range change in the ⁶⁸Ge current measurements. The uncertainty bars are the standard uncertainties on each point, see text.

After accounting for missing weeks, the residuals were examined for autocorrelation using the AUTOCORRELATE PLOT function of the DATAPLOT program (Heckert 2017). No statistically significant (i.e., outside the 99 % confidence limits) non-randomness was identified in the autocorrelation coefficients. However, the coefficients appear to show a trend from positive autocorrelation at a lag of 5 weeks to negative autocorrelation at a lag of 22 weeks. The fit residuals were examined by averaging over groups of 30 d, 49 d, and 98 d. No repeating oscillations were observed. The slight autocorrelation is presumed to arise from the apparent dip in residuals around day 449. The dip is observed only in the data for which a single insertion was performed. The uncertainties used for weighting this portion of the data are slightly larger, slightly deemphasizing those data. Therefore, no additional medium-term uncertainty components were included.

Because the count time was not constant during the entire campaign, the effect of decay during counting was examined. No effect was seen within the significant figures of the reported value.The individual components of uncertainty are summarized in Table 3. The components are combined in quadrature to yield a combined uncertainty of 0.043 %. From the ionization chamber data, we report T_1/2 = 271.07(12) d.

Table 3.

Uncertainty budget for the ICB half-life determination.

Component	Description	ui (%)	ui (d)
ufit	Uncertainty on the half-life resulting from a weighted least-squares fit with 2 parameters	0.026	0.07
uGe	Standard deviation of the mean for a single measurement of current, 0.02% to 0.03%, fully embodied in ufit
uRa	Standard deviation of the mean for a single measurement of current, 0.02% to 0.03%, fully embodied in ufit
ubkg	Uncertainty on the ratio of the 68Ge current to the RRS50 current from the standard deviation of the mean for a single measurement of current, 0.001% to 0.009%, fully embodied in ufit
ubtw	Uncertainty on the ratio of the 68Ge current to the RRS50 current due to 3 to 5 repeated measurements, 0.036%, fully embodied in ufit
ulin	Estimated uncertainty on half-life due to non-linearity of electrometer	0.035	0.09
uimp	No impurities observed by HPGe	--	--
uc	Combined uncertainty	0.043	0.12

3.3. Evaluation of present and earlier determinations

The current Decay Data Evaluation Project (DDEP) evaluation of the ⁶⁸Ge half-life was performed in 1996 (Bé et al., 2013). Four determinations were considered (Crasemann et al., 1956; Rudstam, 1956; Waters et al., 1981; Schönfeld et al., 1994), but the two most precise values, from Waters et al. and Schönfeld et al., dominate the weighted mean of 270.95(26) d.

The measurements by Crasemann et al. (1956) were made over the course of 300 d using a Geiger tube by following a source of ⁶⁸Ge prepared 30 days previously by alpha particle bombardment on a zinc target. The measurements were normalized to measurements made on a ⁶⁰Co source and the resultant half-life is therefore correlated with the published half-life of ⁶⁰Co at that time. Their reported half-life value was 275(20) d.

The details of the measurements of Rudstam (1956) are published only in thesis form and are currently unavailable, but the reported half-life value was 288(6) d.

Twenty-five years later, Waters et al. (1981), working at the National Physical Laboratory (NPL), UK, reported a significant deviation from Rudstam’s value, which was still in use at the time. This prompted a dedicated half-life experiment at NPL in which an ampoule with an initial activity of 2.2 MBq was measured (40 sets of 10 measurements; n = 400) in a pressurized ionization chamber for 130 d (≈ 0.5 half-lives). An uncertainty budget was given for the systematic uncertainty, and the authors describe their analysis of the fit as showing no sign of impurities and as being consistent upon splitting the data into two sets. Their reported half-life was 270.82(27) d.

In the Schönfeld et al. (1994) determination, an ampoule with an initial activity of ≈ 12 MBq was measured in an ionization chamber at the Physikalisch-Technische Bundesanstalt (PTB), Germany, against a radium reference source for “about 1.3 half-lives” (n = 1500). The data were fit by two methods giving the same result to within 0.03 %. The standard deviation of the fits was stated to be on the order of 0.01 % and the “systematic” uncertainty due to instrumental instabilities was said to be < 0.05 %. No fit residuals or detailed uncertainty budget were given, but reference was made to earlier work (Schötzig et al., 1991; Walz et al., 1983) describing the procedures for estimating half-life uncertainties at PTB. These procedures involve a detailed analysis of fit residuals by sub-groups of data to look for instabilities on different timescales, and should be expected to result in a conservative estimate for the total uncertainty on the half-life (Walz et al., 1983). Their reported half-life was 270.99(19) d.

Examining our values in the context of previous measurements (Table 4), we see that both of our results are in agreement within uncertainties with the more recent determinations made by Waters et al. and Schönfeld et al. (see Figure 3) and that the determinations made in 1981 and later are in agreement with Crasemann, et al. only by virtue of the very large uncertainty on the latter value. The Rudstam half-life value now clearly stands out as being inconsistent with the extant data set.

Table 4.

Summary of determined and evaluated half-lives. Uncertainties are given for k = 1.

Reference	T1/2 / d
Rudstam, 1956	288(6)
Crasemann et al., 1956	275(20)
Waters et al., 1981	270.82(27)
Schönfeld et al., 1994	270.99(19)
This work, GWC	271.14(15)
This work, ICB	271.07(12)
Be et al., 2013	270.95(26)
Reevaluation	271.05(8)

Figure 3.

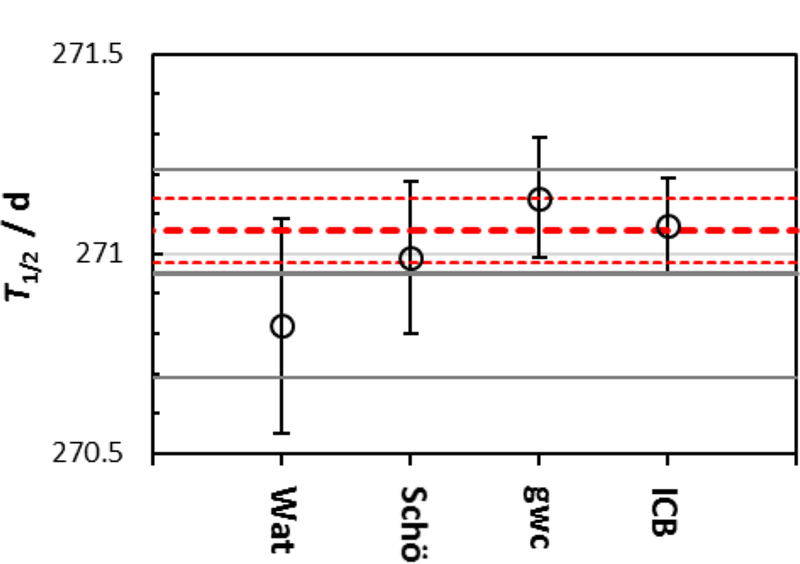
Half-lives with combined standard uncertainties determined by Waters et al. (1981), Schönfeld et al. (1994), GWC, and ICB. The gray solid lines represent the current DDEP evaluated half-life and uncertainty (Bé et al., 2013) while the red dashed lines show our reevaluation including the ICB value. The Crasemann et al. (1956) and Rudstam (1956) half-lives are off the scale shown here.

Applying the procedures adopted for DDEP evaluations of the half-lives using the Limitation of Relative Statistical Weight method (Kellet and Bersillon, 2017) and including both of our new determinations as independent determinations, we find that both of the earlier half-life measurements are excluded as outliers by the Chauvenet criterion (Coleman et al., 1999). The evaluated half-life using this data set would be 271.05(8) d, shown by the red dashed lines on Figure 3, compared to the DDEP value shown by gray solid lines.

It should be noted that with a recent international comparison of ⁶⁸Ge being completed, it is likely that several new half-life measurements will be reported.

4. Conclusions

We determined the half-life of ⁶⁸Ge by NaI(Tl) well counter and pressurized ionization chamber. Our measurements were carried out over about 2.8 half-lives. We carefully considered possible sources of variance to make a conservative but realistic estimate of uncertainty. Our new half-life values, T_1/2 = 271.14(15) d and T_1/2 = 271.07(12) d for the NaI(Tl) well counter and ionization chamber, respectively, agree with the current DDEP recommended value of 270.95(26) d (Bé et al., 2013). A reevaluation of the ⁶⁸Ge half-life results in a slight increase in the half-life, a significant reduction in the uncertainty, and the rejection of the two earliest determinations (Rudstam, 1956; Crasemann et al., 1956) as outliers. As ⁶⁸Ge/⁶⁸Ga sources are increasingly used as a long-lived calibration surrogate for positron emitting radionuclides, the importance of precise decay corrections grows.

Highlights:

• The half-life of Ge-68 is determined by two methods.

• Ionization chamber measurements give a value of 271.07(12) d.

• NaI(Tl) well counter measurements give a value of 271.14(15) d.

• Both values are consistent with the DDEP recommended value and other recent determinations.

• Our value would change the DDEP recommended half-life from 270.95(26) d to 271.05(8) d.