Abstract
Gait modifications in acetabular dysplasia patients may influence cartilage contact stress patterns within the hip joint, with serious implications for clinical outcomes and the risk of developing osteoarthritis. The objective of this study was to understand how the gait pattern used to load computational models of dysplastic hips influences computed joint mechanics. Three-dimensional pre- and post-operative hip models of thirty patients previously treated for hip dysplasia with periacetabular osteotomy (PAO) were developed for performing discrete element analysis (DEA). Using DEA, contact stress patterns were calculated for each pre- and post-operative hip model when loaded with an instrumented total hip, a dysplastic, a matched control, and a normal gait pattern. DEA models loaded with the dysplastic and matched control gait patterns had significantly higher (p=0.012 and p<0.001) average pre-operative maximum contact stress than models loaded with the normal gait. Models loaded with the dysplastic and matched control gait patterns had nearly significantly higher (p=0.051) and significantly higher (p=0.008) average pre-operative contact stress, respectively, than models loaded with the instrumented hip gait. Following PAO, the average maximum contact stress for DEA models loaded with the dysplastic and matched control patterns decreased, which was significantly different (p<0.001) from observed increases in maximum contact stress calculated when utilizing the instrumented hip and normal gait patterns. The correlation between change in DEA-computed maximum contact stress and the change in radiographic measurements of lateral center-edge angle were greatest (R2 = 0.330) when utilizing the dysplastic gait pattern. These results indicate that utilizing a dysplastic gait pattern to load DEA models may be a crucial element to capturing contact stress patterns most representative of this patient population.
Keywords: Discrete Element Analysis, Acetabular Dysplasia, Periacetabular Osteotomy, Contact Stress, Gait
INTRODUCTION
Acetabular dysplasia is a common cause of hip pain and degeneration in the young adult population (Hadley et al., 1990). This deformity is characterized by a shallow acetabulum that inadequately covers the femoral head, which alters force transfer through the hip joint (Noguchi et al., 1999) and elevates cartilage contact stresses, which may in turn accelerate osteoarth (OA) onset and progression (Chegini et al., 2009; Mavcic et al., 2008).
Computational modeling techniques such as finite element analysis (FEA) (Anderson et al., 2010; Harris et al., 2012; Henak et al., 2014; Henak et al., 2011; Knight et al., 2017; Zou et al., 2013) and discrete element analysis (DEA) (Abraham et al., 2013; Armiger et al., 2009; Townsend et al., 2018) have been utilized to predict hip cartilage contact stresses. The majority of these studies have investigated cartilage contact stresses when loading their computational models with walking gait data obtained directly from instrumented total hip implants (Bergmann et al., 2001a). This extensive set of kinematics and kinetics is used so frequently in studies of hip joint mechanics (Abraham et al., 2017; Anderson et al., 2008; Henak et al., 2014; Phillips et al., 2007; Yoshida et al., 2006) because it is considered the most comprehensive due to the direct measurement of hip joint forces. However, the age range of the subjects (51–76 years) from which those data were measured is much older than typical dysplasia patients, and those subjects received instrumented total hip replacements as treatment for OA, meaning that they presumably would have altered their gait to alleviate OA pain (Mont et al., 2007; Perron et al., 2000). Consequently, it is probable that a gait pattern modeled after instrumented total hip data may not be particularly representative of gait in dysplasia patients.
In this study, we investigated the influence of gait parameters used to load dysplastic hip models on the DEA-computed joint mechanics. Pre- and post-operative DEA models of patients previously treated for hip dysplasia with a periacetabular osteotomy (PAO) were subjected to four gait patterns: (1) the frequently utilized instrumented total hip data set (Bergmann et al., 2001a), (2) a gait pattern derived from motion capture in hip dysplasia patients (Skalshoi et al., 2015), (3) a gait pattern derived for matched control patients using identical methodolog to the dysplasia group (Skalshoi et al., 2015), and (4) a gait pattern derived from a separate population of young, healthy individuals by a different research group (Anderson and Pandy, 2001a; Correa et al., 2010). Differences in the DEA-computed contact measures and their relationship to radiographic measurements of dysplastic deformity were evaluated.
METHODS
Under Institutional Review Board approval, pre- and post-operative pelvis CT scans (0.7 mm isotropic voxel size) were selected for thirty consecutive hip dysplasia patients treated with PAO by the same orthopaedic surgeon at our institution between 2007 and 2009. For each patient, an experienced hip surgeon that did not perform the operations measured lateral center edge angle (LCEA) (Clohisy et al., 2008; Novais et al., 2017; Wiberg, 1953), Tönnis angle (Tönnis and Heinecke, 1999), extrusion index (Murphy et al., 1995), anterior center edge angle (ACEA) (Lequesne and de Seze, 1961), and posterior wall sign (Reynolds et al., 1999) on pre- and post-operative radiographs to quantify severity of hip dysplasia and improvement following PAO (Table 1). Patients averaged 29.2±11.5 years of age and weighed 65±26.4 kg at the time of operation.
Table 1.
Patient information for individuals modeled in this work. Illustration of the radiographic measurements can be found in Supplemental Figures S-1 and S-2. Cases of borderline dysplasia are indicated in italics and primarily anteverting PAO cases are shown in gray. All other patients were diagnosed with classic dysplasia. Lateral center edge angle (LCEA), Tonnis angle, and anterior center edge angle (ACEA) are shown in degrees, extrusion index is unitless, and the presence of a posterior wall sign is shown by a +. Blank values of ACEA indicate insufficient quality radiographs from which to make this measurement, and blank values of the posterior wall sign indicate this finding was absent on radiographs.
| Patient Number | Age (yrs) | Weight (kg) | Operative Side | LCEA | Tonnis Angle | Extrusion Index | ACEA | Post Wall Sign | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| pre | post | pre | post | pre | post | pre | post | pre | post | ||||
| 1 | 14 | 83.7 | Right | 7 | 23 | 19 | 7 | 0.35 | 0.20 | 10 | 20 | + | |
| 2 | 14 | 71.6 | Left | 20 | 35 | 7 | −2 | 0.30 | 0.10 | 26 | 40 | + | |
| 3 | 15 | 46.3 | Left | 17 | 29 | 12 | 6 | 0.26 | 0.12 | 32 | 34 | + | |
| 4 | 16 | 67.0 | Left | 6 | 27 | 33 | 10 | 0.40 | 0.17 | 6 | 17 | ||
| 5 | 17 | 81.6 | Right | 20 | 33 | 14 | −1 | 0.29 | 0.09 | 15 | 34 | ||
| 6 | 17 | 75.7 | Left | 20 | 28 | 9 | 4 | 0.25 | 0.14 | 21 | 38 | + | |
| 7 | 18 | 86.0 | Left | 17 | 26 | 13 | 4 | 0.25 | 0.17 | −12 | 25 | ||
| 8 | 19 | 96.9 | Right | 25 | 34 | 8 | 3 | 0.19 | 0.15 | 18 | 31 | + | |
| 9 | 19 | 72.9 | Right | 8 | 28 | 23 | 5 | 0.35 | 0.17 | 30 | + | ||
| 10 | 21 | 50.8 | Left | 20 | 31 | 5 | −1 | 0.20 | 0.09 | 17 | 35 | ||
| 11 | 24 | 88.0 | Right | 31 | 29 | 4 | 5 | 0.17 | 0.18 | 34 | + | ||
| 12 | 25 | 70.0 | Left | 18 | 37 | 13 | 0 | 0.23 | 0.06 | 19 | 17 | + | |
| 13 | 26 | 86.5 | Left | 20 | 26 | 4 | 1 | 0.22 | 0.10 | 28 | 28 | + | |
| 14 | 26 | 76.3 | Right | 24 | 45 | 11 | −3 | 0.16 | 0.05 | 48 | |||
| 15 | 28 | 88.1 | Right | 8 | 36 | 23 | 8 | 0.41 | 0.07 | 31 | 24 | ||
| 16 | 29 | 59.8 | Left | 50 | 41 | −6 | −5 | 0.07 | 0.12 | 59 | + | ||
| 17 | 31 | 107.4 | Right | 21 | 31 | 8 | 2 | 0.30 | 0.16 | 19 | 31 | ||
| 18 | 33 | 93.3 | Left | 28 | 41 | 4 | −3 | 0.16 | 0.01 | 24 | 23 | + | |
| 19 | 33 | 93.3 | Right | 26 | 35 | 12 | 2 | 0.25 | 0.16 | 31 | + | ||
| 20 | 34 | 102.9 | Right | 3 | 22 | 29 | 10 | 0.37 | 0.25 | 7 | 21 | + | + |
| 21 | 36 | 71.0 | Right | −10 | 19 | 35 | 15 | 0.61 | 0.29 | 23 | + | ||
| 22 | 38 | 100.6 | Right | 12 | 34 | 19 | 1 | 0.36 | 0.12 | 7 | 26 | + | |
| 23 | 38 | 93.5 | Right | 18 | 29 | 12 | 11 | 0.33 | 0.18 | 22 | 27 | + | |
| 24 | 38 | 61.0 | Right | 20 | 41 | 24 | 13 | 0.23 | 0.11 | 26 | 28 | + | |
| 25 | 42 | 102.8 | Right | 6 | 29 | 17 | 6 | 0.46 | 0.20 | 7 | 13 | + | |
| 26 | 45 | 65.0 | Right | 12 | 22 | 27 | 16 | 0.34 | 0.21 | 20 | 25 | ||
| 27 | 45 | 83.0 | Right | 12 | 25 | 22 | 10 | 0.37 | 0.14 | 19 | 21 | + | |
| 28 | 47 | 72.4 | Left | 11 | 32 | 22 | 2 | 0.29 | 0.07 | 13 | 44 | + | |
| 29 | 50 | 61.0 | Right | 7 | 29 | 28 | 7 | 0.33 | 0.27 | 0 | |||
| 30 | 54 | 64.4 | Right | 15 | 41 | 19 | 0 | 0.20 | 0.06 | 29 | 4 | + | |
DEA Model Generation
A semi-automated watershed-based algorithm (Thomas et al., 2011) was used to segment femoral, pelvic, and spinal bony geometry from pre-operative and post-operative patient CT scans. Any failures of automated surface identification in subluxed joint surfaces were manually corrected (www.itksnap.org), and the resulting triangulated surface models were smoothed to reduce stair-step artifact (Geomagic Design X 3D; Systems, Inc., Rock Hill SC). Articular cartilage surfaces were approximated by first projecting the femoral and acetabular subchondral bone surfaces a uniform distance of 1 mm, and then smoothing those projected surfaces toward sphericity using a custom iterative smoothing algorithm. (Shivanna et al., 2007; Townsend et al., 2018). The resulting non-uniform cartilage surfaces have been previously shown to yield valid contact stress calculations (Townsend et al., 2018). Patient-specific anatomic landmarks were identified on the bone surface models and used to align the models to the hip joint coordinate system defined by Bergmann et al. (2001a).
Gait Loading Parameters
Four different patterns of the stance phase of walking gait were utilized to load each DEA model. The first was a “gold standard” gait data set with forces and rotations measured from patients with instrumented total hip replacements for OA (“post-THA”) (Bergmann et al., 2001a). The second was a “dysplastic” gait data set with hip forces and rotations obtained from 32 hip dysplasia patients using a combination of 3D motion capture, inverse kinematics, and static optimization (Skalshoi et al., 2015). The third gait pattern modeled was that of the “matched control” group that was age-, weight-, and height-matched to the dysplasia cohort in that same study (Skalshoi et al., 2015). Finally, because muscle modeling techniques often result in higher estimations of joint contact stress than direct measurement (Heller et al., 2001), and because specific modeling assumptions and techniques can lead to different results, a second “normal” gait pattern reported by an alternate research group using similar (3D motion capture), but not identical (dynamic muscle optimization) techniques (Anderson and Pandy, 2001a; Correa et al., 2010) was implemented to account for the effects data collection/modeling technique on calculated joint loading. When necessary, rigid transformations were applied to ensure the forces and rotations could be applied to hip models aligned to the Bergmann-defined hip coordinate system (Bergmann et al., 2001a). All forces and rotations were discretized into 13 evenly-distributed steps spanning the stance phase of gait (Figure 1) to facilitate direct comparison of the resulting contact stress distributions.
Figure 1.
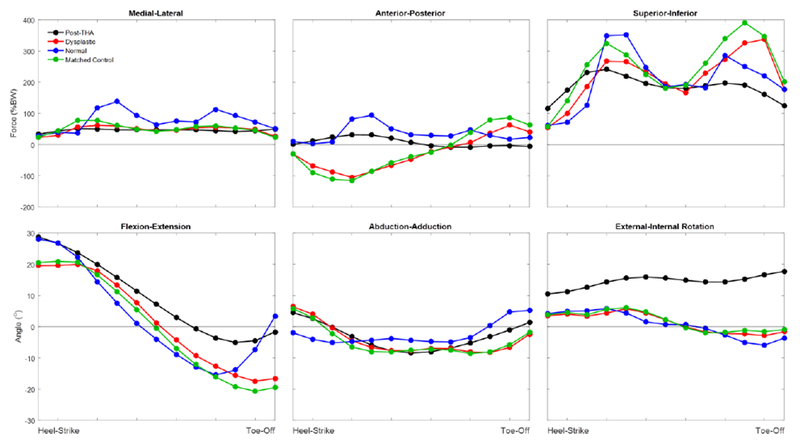
Plots of applied joint reaction forces and hip rotation angles in all three planes of motion. The Bergmann (Post-THA) data were provided as a percentage bodyweight and with associated hip rotation angles (Bergmann et al., 2001a). The Dysplastic and Matched Control data were provided as N/BM2/3 (Skalshoi et al., 2015), which was converted to percentage bodyweight by taking the study’s average patient body mass of 66 kg and multiplying the force data by (66 kg)2/3 to obtain the force in Newtons. The force in Newtons was the divided by (66 kg*9.81 m/s2) and multiplied by 100% to obtain percentage bodyweight for application to the models. The Normal gait pattern that was implemented in the DEA models was taken from a research group that published their joint reaction force data (Anderson and Pandy, 2001a) and their joint angular data (Correa et al., 2010) in two different locations.
Contact Stress Computations
For DEA calculation, the force associated with each gait pattern was scaled to patient body weight and applied along the axis of the femur, which was held fixed. The rotation of the pelvis relative to the femur was governed by the specific gait pattern applied, and the pelvis was free to move in translation to achieve a seated congruent joint position. Cartilage was assigned isotropic linear-elastic material properties (E = 8 MPa, ν = 0.42). Contact stress computations were completed using a custom Newton’s method solver previously developed in MATLAB (Kern and Anderson, 2015) and validated in cadaveric hips (Townsend et al., 2018) to iteratively match spring forces with the applied walking gait forces.
Statistical Analysis
Paired t-tests with a Holm-Bonferroni correction for multiple comparisons were made at each time point in the stance phase of gait to identify statistically significant differences in contact stresses calculated using different input gait patterns. This was done for overall joint values as well as for regional analysis of six regions spanning the acetabular surface. To determine potential relationships between radiographic correction of dysplastic deformity and calculated contact stresses, Pearson’s correlation coefficients were calculated between DEA-calculated contact stresses and radiographic measures.
RESULTS
DEA models loaded with the dysplastic gait had a whole-gait cycle average pre-operative maximum contact stress of 10.5±0.5 MPa, which was significantly greater (p=0.012) than the average pre-operative maximum contact stress of 9.2±0.4 MPa calculated when loading models with normal gait, and nearly significantly greater than those calculated with post-THA gait (7.4±0.4 MPa, p=0.051), but significantly less than the matched control group (12.2±0.5 MPa, p=0.003) (Figure 2). Maximum contact stress for pre-operative models loaded with the dysplastic gait was higher than that calculated in 25/30 (83%) of the pre-operative models loaded with the normal gait, contributing to the significant p-value despite a modest reduction in average maximum contact stress. In contrast, maximum contact stress for pre-operative models loaded with the dysplastic gait was only higher than that calculated in 19/30 (63%) of the pre-operative models loaded with the post-THA gait, explaining the lack of significance despite an overall larger decrease in average maximum contact stress. Maximum pre-operative contact stress was greater with the matched control gait pattern than all other patterns. Maximum contact stress occurred shortly after heel-strike in models loaded with the post-THA and normal gait patterns and toward toe-off when implementing dysplastic and the matched control loading patterns, which corresponds with the increased superior loading near toe-off with those two gait patterns (Figure 1). Following PAO, DEA models loaded with the dysplastic gait pattern had an average decrease in maximum contact stress of 0.7±0.4 MPa, which was significantly (p<0.001) different from increases of 0.5±0.6 MPa and 1.3±0.6 MPa when utilizing the post-THA gait and normal gait, respectively (Figure 2). As expected due to the similarity of the applied gait patterns, the reduction in peak contact stress with the matched control gait pattern (0.8±0.5 MPa) was not significantly different (p=0.222) than for that found with the dysplastic gait cycle. Contact stresses after PAO were reduced laterally and increased medially with all applied gait cycles (Figure 3).
Figure 2.
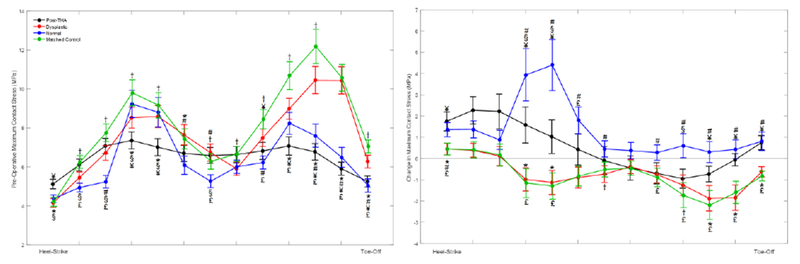
(Left) Force and rotation differences between the applied gait patterns alter the maximum contact stress magnitude and the time at which it occurs during stance phase of gait. DEA models loaded with the dysplastic and matched control gait patterns developed pre-operative maximum contact stress near toe-off, whereas the models loaded with normal or post-THA gait patterns developed maximum contact stress shortly after heel-strike. (Right) DEA models loaded with the dysplastic and matched control gait patterns had average decreases in maximum contact stress after PAO, which were significantly (p<0.001) different from the increases in maximum contact stress for models loaded with arthritic and normal gait patterns. Statistical significance is indicated with the following symbols: *dysplastic vs. post-THA. #dysplastic vs. normal, †dysplastic vs. matched control. §post-THA vs. normal. ¥post-THA vs. matched control. £normal vs. matched control.
Figure 3.
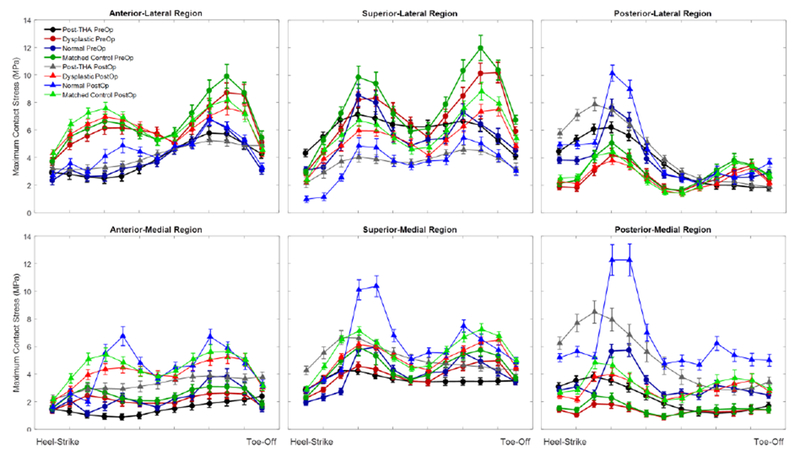
Maximum contact stress over the gait cycle for a regional analysis of contact stress. Use of a dysplastic gait cycle resulted in elevated contact stresses in the anterior-lateral portion of the acetabulum. PAO surgery increased contact stresses medially regardless of applied gait cycle, however the degree of offloading of the lateral compartment varied with the applied loading scheme. Significance of the differences are found in Table 2.
The change in maximum contact stress calculated by DEA models loaded with dysplasti gait had an improved correlation with change in LCEA (R2 = 0.330) compared to models loaded with post-THA, normal, or matched control gait (R2 = 0.071, R2 = 0.008, R2 = 0.310, respectively). Similar findings were evident for comparisons with Tonnis angle and the change in extrusion index (Figure 4), which would indicate that depending on the specific loading input to the model, very different conclusions could be drawn about the relationship between radiographic correction achieved by a PAO and changes in contact stress.
Figure 4.
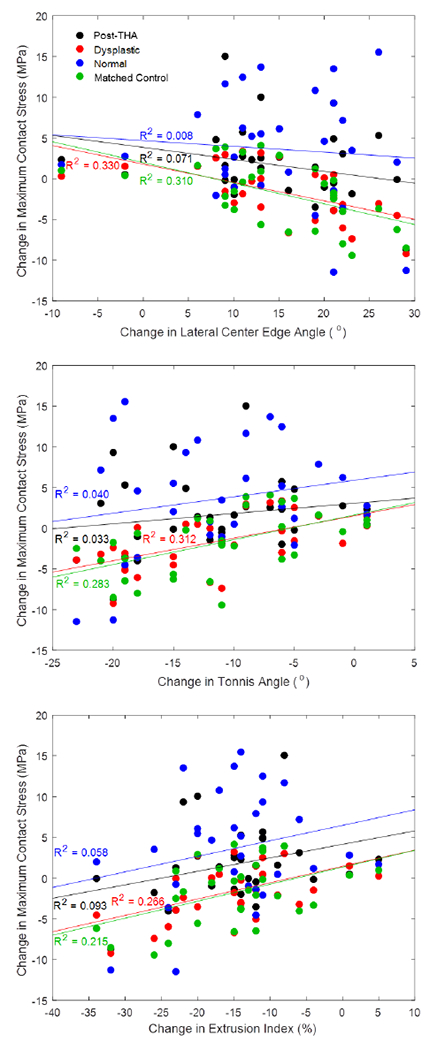
Correlations between the change in DEA-calculated maximum contact stress and the change in lateral center edge angle (top), change in Tonnis angle (middle), and change in extrusion index (bottom) all improve when loading DEA models with dysplastic gait.
DISCUSSION
The objective of this study was to assess how DEA-computed contact stress distributions are affected by the gait parameters used to load the models (Figure 5). Use of a dysplastic gait pattern in pre-operative DEA models resulted in calculation of increased cartilage contact stress, particularly near toe-off (Figure 2). DEA models of post-PAO hips that were loaded with a dysplastic gait pattern had an average decrease in maximum contact stress relative to the preoperative values, which coincides with the clinical assumption that acetabular reorientation improves the biomechanics of the joint. Regional analysis showed that use of a dysplastic gait cycle resulted in calculation of greater contact stress in the anterior-lateral region of the acetabulum, which corresponds to where cartilage damage often presents in dysplasia patients (McCarthy and Lee, 2002). Application of dysplastic gait also improved the correlation of contact stress with the radiographic measures frequently utilized for clinical assessment of acetabular dysplasia. Calculated contact areas (Supplemental Data) paralleled stress data. Interestingly, the data available for the dysplastic hips was extremely similar to that for the matched control group in that study (Skalshoi et al., 2015), and moderately different from the frequently utilized Bergmann data (Bergmann et al., 2001b) and an alternative normal gait cycle (Anderson and Pandy, 2001a; Correa et al., 2010), indicating different relationships between hip deformity and contact stress may be identified depending on the specific loading inputs applied to the contact stress models.
Figure 5.
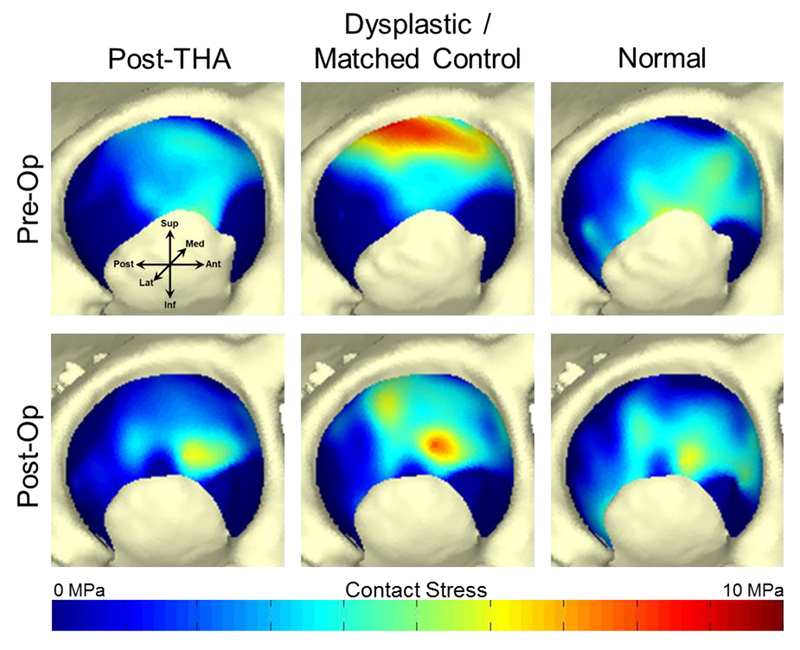
Pre- and post-operative contact stress distributions calculated using all four gait patterns in a single dysplastic patient. Dark blue color indicates no contact between the acetabular and femoral cartilage surfaces at that location. Loading this patient’s DEA models with the dysplastic and matched control gait patterns resulted in decreased and medialized maximum contact stress after PAO, indicating improved joint mechanics that were not appreciated in models loaded with the post-THA or normal gait patterns.
Maximum contact stress values calculated using our DEA methodology were similar in magnitude to those previously reported in DEA and FEA studies of PAO patients (Abraham et al., 2017; Armiger et al., 2009; Henak et al., 2014; Zou et al., 2013), verifying that our methods produce realistic representations of hip joint contact mechanics. However, the majority of those prior studies have evaluated contact mechanics when loading their models only with the instrumented total hip-measured data (Bergmann et al., 2001a), which may call into question the accuracy of those values for dysplasia patients. To our knowledge, this is the first study to assess how motion capture-derived alterations in joint loading by dysplasia patients (Harris et al., 2017; Skalshoi et al., 2015) influence the computed contact mechanics in dysplastic hip joints.
This work has several limitations related to the modeling process. First, we utilized a quasi-static discrete element analysis methodology to perform contact stress calculations. While offering many computational advantages such as numerical stability and rapid execution time, DEA omits the inclusion of shear and continuum mechanics, and the treatment of the material properties of cartilage were limited to simple, linearly elastic behavior. The lack of a use of a contrast agent in this historical set of CT scans precluded modeling of patient-specific cartilage or the labrum. It has been found that DEA can over-predict contact stresses (Abraham et al., 2013), particularly when the cartilage in the models is approximated (Anderson et al., 2010). The cartilage generation methodology used in this work yields cartilage surfaces that are on the lower end of the thickness range (0.7 ± 0.2 mm for the femoral head and 1.2 ± 0.2 mm for the acetabulum) reported for the hip (Adam et al., 1998; Athanasiou et al., 1994; Shepherd a Seedhom, 1999), but which have been shown to yield realistic calculations of contact stress in the hip (Townsend et al., 2018). The available imaging and the use of DEA also prevented inclusion of labral soft tissues in our model, with potential implications for overall accuracy of the computed contact stresses. While previous studies have included extremely detailed patient-specific labrum and cartilage anatomy (Henak et al., 2014), the boundary and loading conditions in that work were based on the Bergmann dataset, which our data suggest may not be realistic for modeling dysplasia.
There are also several limitations related to the modeled gait patterns that warrant discussion. First, we utilized a consecutive patient population with varying deformities of lateral coverage, version abnormalities, and femoral deformities. An individual patient’s deformity would likely influence their specific gait pattern, making inclusion of patient-specific gait pattern loading information highly desirable in addition to patient-specific anatomy in computational models of dysplastic hips. However, given that gait data were not prospectively collected for the thirty subjects modeled in this study, the best available option for loading the models was to use gait patterns that were averages from multiple subjects that encompassed individual variation in movement. We limited the activity modeled to walking gait due to the repeated loading of the joint and availability of input data, although other activities of daily living may be equally or more important to producing damaging contact stress. Improved joint stability after PAO permits the individual to walk in a more normal manner; however, not all gait characteristics normalize following PAO (Gahramanov et al., 2017; Jacobsen et al., 2014; Pedersen et al., 2006; Sucato et al., 2010). Without knowledge of how the patient cohort modeled in this work modified their gait, we were limited to use of the same gait pattern in the post-operative DEA models tha was applied to the corresponding pre-operative models.
We implemented two different “normal” gait patterns, both of which were taken from healthy individuals with similar ages and weights; however, there were notable differences in the reported forces and rotations between these two patterns with the “matched control” pattern being extremely similar to the “dysplastic” pattern and relatively different than the “normal” pattern described for healthy individuals of a similar age. One explanation may be subtle differences in walking speed between the two cohorts, as the walking speed of the “matched control” group that was matched to the dysplasia patients was not specified (Skalshoi et al., 2015), whereas data defining the “normal” gait pattern was metronome controlled (Anderson and Pandy, 2001a). However, it is more likely that the differences in reported gait patterns between those studies was a result of the different modeling approach used in each study. While both research groups utilized musculoskeletal models to obtain their joint forces, the gait information for the “matched control” group was generated using a static optimization technique with a greater number of muscles modeled (Skalshoi et al., 2015), whereas the “normal” gait pattern applied was generated using dynamic optimization techniques that incorporated EMG readings of muscles as both input information and validation checks of calculated forces (Anderson and Pandy, 2001a; Correa et al., 2010). Previous studies have shown wide variability in the agreement between static and dynamic optimization solutions (Anderson and Pandy, 2001b; Morrow et al., 2014), indicating that the optimization method and associated modeling assumptions may have greatly influenced calculated joint forces in those previous studies, and therefore affected the joint contact stresses reported here. The striking similarity between the dysplastic and matched control gait patterns was likely a result of several modeling decisions by Skalshoi, et al. and may indicate that dysplastic gait is only subtly different than normal (Skalshoi et al., 2015). Yet recent work by Harris, et al. has also found differences in joir reaction forces in dysplastic hips (Harris et al., 2017), making it clear that additional studies of dysplastic gait before and after PAO that have associated musculoskeletal modeling approaches to facilitate calculations of joint reaction forces will be important to provide good data upon which to model walking in hip dysplasia patients.
In conclusion, our findings suggest that any modifications in gait by dysplasia patients to stabilize their hip joint may produce elevated cartilage contact stresses that could accelerate OA progression. However, until a strong association between DEA-computed contact stress and clinical outcomes has been established, it remains unclear if the differences in magnitude of maximum contact stress found in this work are sufficient to indicate future joint pathology. Based on the differences in computed contact stresses associated with different applied gait patterns, we believe that utilizing a gait pattern accurate to hip dysplasia patients to load computational models will be critical to capturing cartilage contact stress patterns representative of this particular patient population.
Supplementary Material
Table 2.
P-values are shown for each comparison of the regional maximum contact stresses shown in Figure 3 with statistical significance indicated by bolded values.
| Step of Gait Cycle | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | ||
| Pre-Operative Maximum Contact Stress | Anterior Lateral | Dysplastic vs. Post-THA | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | 0.145 | <0.001 | <0.001 | <0.001 | <0.001 | 0.007 |
| Dysplastic vs. Normal | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | 0.020 | <0.001 | 0.022 | <0.001 | <0.001 | <0.001 | ||
| Dysplastic vs. Matched Control | 0.878 | <0.001 | <0.001 | <0.001 | 0.012 | 0.257 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | 0.007 | <0.001 | ||
| Post-THA vs. Normal | <0.001 | 0.064 | 0.651 | 0.322 | 0.053 | 0.390 | 0.547 | 0.940 | 0.549 | 0.002 | 0.091 | 0.953 | <0.001 | ||
| Post-THA vs. Matched Control | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | ||
| Normal vs. Matched Control | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | ||
| Anterior Medial | Dysplastic vs. Post-THA | 0.590 | 0.010 | <0.001 | <0.001 | <0.001 | 0.004 | 0.095 | 0.253 | 0.061 | 0.065 | 0.233 | 0.569 | 0.041 | |
| Dysplastic vs. Normal | 0.950 | 0.465 | <0.001 | 0.018 | 0.117 | 0.736 | 0.108 | 0.017 | 0.487 | <0.001 | 0.042 | 0.483 | 0.783 | ||
| Dysplastic vs. Matched Control | 0.009 | <0.001 | <0.001 | 0.063 | 0.317 | 0.328 | 0.279 | 0.008 | 0.003 | 0.011 | 0.021 | 0.034 | 0.115 | ||
| Post-THA vs. Normal | 0.424 | <0.001 | 0.502 | 0.001 | <0.001 | 0.002 | 0.369 | 0.038 | 0.032 | <0.001 | 0.005 | 0.194 | 0.010 | ||
| Post-THA vs. Matched Control | 0.994 | <0.001 | <0.001 | <0.001 | <0.001 | 0.002 | 0.045 | 0.028 | 0.003 | 0.007 | 0.050 | 0.168 | 0.107 | ||
| Normal vs. Matched Control | 0.622 | 0.146 | <0.001 | 0.003 | 0.577 | 0.859 | 0.065 | 0.801 | 0.142 | 0.063 | 0.228 | 0.968 | 0.434 | ||
| Superior Lateral | Dysplastic vs. Post-THA | <0.001 | <0.001 | 0.009 | <0.001 | <0.001 | <0.001 | 0.417 | 0.004 | 0.009 | <0.001 | <0.001 | <0.001 | <0.001 | |
| Dysplastic vs. Normal | 0.523 | <0.001 | <0.001 | 0.652 | 0.649 | 0.002 | <0.001 | 0.690 | <0.001 | 0.040 | <0.001 | <0.001 | <0.001 | ||
| Dysplastic vs. Matched Control | 0.051 | <0.001 | <0.001 | <0.001 | 0.034 | 0.045 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | 0.224 | <0.001 | ||
| Post-THA vs. Normal | <0.001 | <0.001 | <0.001 | 0.013 | 0.130 | 0.073 | <0.001 | 0.038 | 0.025 | 0.266 | 0.880 | 0.411 | 0.081 | ||
| Post-THA vs. Matched Control | <0.001 | 0.495 | 0.097 | <0.001 | <0.001 | 0.007 | 0.255 | 0.804 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | ||
| Normal vs. Matched Control | 0.776 | <0.001 | <0.001 | 0.142 | 0.189 | 0.009 | 0.006 | 0.030 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | ||
| Superior Medial | Dysplastic vs. Post-THA | <0.001 | <0.001 | 0.081 | 0.088 | 0.045 | 0.320 | 0.862 | 0.590 | 0.002 | <0.001 | <0.001 | <0.001 | 0.639 | |
| Dysplastic vs. Normal | 0.265 | 0.037 | <0.001 | 0.002 | <0.001 | 0.244 | 0.784 | 0.003 | 0.990 | 0.010 | 0.789 | 0.035 | 0.787 | ||
| Dysplastic vs. Matched Control | 0.116 | <0.001 | <0.001 | 0.030 | 0.160 | 0.789 | 0.812 | <0.001 | <0.001 | <0.001 | <0.001 | 0.047 | 0.010 | ||
| Post-THA vs. Normal | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | 0.060 | 0.910 | 0.039 | 0.023 | <0.001 | <0.001 | 0.051 | 0.330 | ||
| Post-THA vs. Matched Control | 0.016 | 0.882 | 0.006 | 0.009 | 0.052 | 0.280 | 0.958 | 0.075 | <0.001 | <0.001 | <0.001 | <0.001 | 0.698 | ||
| Normal vs. Matched Control | 0.072 | <0.001 | <0.001 | 0.867 | 0.392 | 0.344 | 0.877 | 0.394 | 0.068 | 0.637 | 0.108 | 0.012 | 0.302 | ||
| Posterior Lateral | Dysplastic vs. Post-THA | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | 0.704 | 0.107 | 0.002 | <0.001 | 0.049 | |
| Dysplastic vs. Normal | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | 0.267 | 0.021 | 0.099 | 0.031 | 0.095 | ||
| Dysplastic vs. Matched Control | <0.001 | <0.001 | <0.001 | <0.001 | 0.008 | 0.116 | 0.360 | 0.110 | 0.047 | <0.001 | <0.001 | 0.755 | <0.001 | ||
| Post-THA vs. Normal | <0.001 | <0.001 | <0.001 | <0.001 | 0.018 | 0.031 | 0.004 | 0.536 | 0.671 | <0.001 | 0.021 | 0.003 | <0.001 | ||
| Post-THA vs. Matched Control | <0.001 | <0.001 | <0.001 | 0.002 | <0.001 | <0.001 | <0.001 | <0.001 | 0.782 | <0.001 | <0.001 | <0.001 | 0.003 | ||
| Normal vs. Matched Control | <0.001 | <0.001 | 0.679 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | 0.891 | 0.475 | 0.004 | 0.036 | 0.676 | ||
| Posterior Medial | Dysplastic vs. Post-THA | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | 0.230 | 0.564 | 0.398 | 0.496 | 0.674 | 0.259 | |
| Dysplastic vs. Normal | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | 0.001 | <0.001 | ||
| Dysplastic vs. Matched Control | <0.001 | <0.001 | <0.001 | <0.001 | 0.474 | 0.929 | 0.213 | 0.334 | 0.840 | 0.070 | 0.021 | 0.878 | 0.653 | ||
| Post-THA vs. Normal | 0.090 | 0.031 | <0.001 | <0.001 | <0.001 | <0.001 | 0.037 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | 0.009 | ||
| Post-THA vs. Matched Control | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | 0.145 | 0.529 | 0.175 | 0.245 | 0.646 | 0.301 | ||
| Normal vs. Matched Control | <0.001 | <0.001 | 0.425 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | 0.001 | <0.001 | ||
| Change in Maximum Contact Stress | Anterior Lateral | Post-THA vs. Post-THA | 0.568 | 0.471 | 0.209 | 0.073 | 0.060 | 0.119 | 0.274 | 0.963 | 0.371 | 0.161 | 0.177 | 0.729 | 0.067 |
| Dysplastic vs. Dysplastic | 0.051 | 0.042 | 0.039 | 0.073 | 0.158 | 0.558 | 0.689 | 0.995 | 0.315 | 0.110 | 0.026 | 0.009 | 0.023 | ||
| Normal vs. Normal | 0.367 | 0.253 | 0.384 | 0.010 | 0.002 | 0.004 | 0.326 | 0.474 | 0.637 | 0.916 | 0.937 | 0.417 | 0.420 | ||
| Matched Control vs. Matched Control | 0.047 | 0.019 | 0.011 | 0.063 | 0.321 | 0.635 | 0.919 | 0.807 | 0.237 | 0.036 | 0.006 | 0.004 | 0.017 | ||
| Anterior Medial | Post-THA vs. Post-THA | 0.020 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | |
| Dysplastic vs. Dysplastic | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | ||
| Normal vs. Normal | 0.349 | 0.120 | 0.002 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | ||
| Matched Control vs. Matched Control | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | ||
| Superior Lateral | Post-THA vs. Post-THA | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | 0.022 | |
| Dysplastic vs. Dysplastic | 0.068 | 0.068 | 0.004 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | ||
| Normal vs. Normal | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | ||
| Matched Control vs. Matched Control | 0.053 | 0.044 | 0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | ||
| Superior Medial | Post-THA vs. Post-THA | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | 0.001 | 0.003 | 0.006 | 0.017 | 0.018 | |
| Dysplastic vs. Dysplastic | 0.005 | 0.002 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | 0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | ||
| Normal vs. Normal | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | ||
| Matched Control vs. Matched Control | 0.009 | 0.002 | <0.001 | 0.093 | 0.212 | <0.001 | 0.002 | 0.004 | 0.002 | <0.001 | <0.001 | <0.001 | <0.001 | ||
| Posterior Lateral | Post-THA vs. Post-THA | 0.002 | <0.001 | 0.003 | 0.031 | 0.113 | 0.204 | 0.341 | 0.363 | 0.305 | 0.358 | 0.403 | 0.557 | 0.845 | |
| Dysplastic vs. Dysplastic | 0.173 | 0.332 | 0.496 | 0.373 | 0.237 | 0.295 | 0.408 | 0.462 | 0.357 | 0.361 | 0.611 | 0.665 | 0.539 | ||
| Normal vs. Normal | 0.003 | 0.004 | 0.034 | 0.003 | 0.003 | 0.063 | 0.714 | 0.924 | 0.557 | 0.961 | 0.931 | 0.266 | 0.005 | ||
| Matched Control vs. Matched Control | 0.200 | 0.517 | 0.933 | 0.187 | 0.153 | 0.191 | 0.287 | 0.320 | 0.286 | 0.471 | 0.798 | 0.801 | 0.699 | ||
| Posterior Medial | Post-THA vs. Post-THA | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | |
| Dysplastic vs. Dysplastic | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | ||
| Normal vs. Normal | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | ||
| Matched Control vs. Matched Control | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | ||
ACKNOWLEDGEMENTS
The authors would like to thank Todd McKinley, MD for providing the patient cohort for this study. This work was funded by NIH grant AR055533 and an OREF Career Development Grant. Neither the NIH nor OREF had a role in study design or in the collection, analysis, interpretation, or presentation of the data.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
CONFLICT OF INTEREST
No author has a conflict of interest with this work resulting from commercial relationships.
REFERENCES
- Abraham CL, Knight SJ, Peters CL, Weiss JA, Anderson AE, 2017. Patient-specific chondrolabral contact mechanics in patients with acetabular dysplasia following treatment with peri-acetabular osteotomy. Osteoarthritis Cartilage 25, 676–684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abraham CL, Maas SA, Weiss JA, Ellis BJ, Peters CL, Anderson AE, 2013. A new discrete element analysis method for predicting hip joint contact stresses. Journal of biomechanics 46, 1121–1127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adam C, Eckstein F, Milz S, Putz R, 1998. The distribution of cartilage thickness within the joints of the lower limb of elderly individuals. Journal of anatomy 193 ( Pt 2), 203–214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson AE, Ellis BJ, Maas SA, Peters CL, Weiss JA, 2008. Validation of finite element predictions of cartilage contact pressure in the human hip joint. Journal of biomechanical engineering 130, 051008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson AE, Ellis BJ, Maas SA, Weiss JA, 2010. Effects of idealized joint geometry on finite element predictions of cartilage contact stresses in the hip. Journal of biomechanics 43, 1351–1357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson FC, Pandy MG, 2001a. Dynamic optimization of human walking. Journal of biomechanical engineering 123, 381–390. [DOI] [PubMed] [Google Scholar]
- Anderson FC, Pandy MG, 2001b. Static and dynamic optimization solutions for gait are practically equivalent. J Biomech 34, 153–161. [DOI] [PubMed] [Google Scholar]
- Armiger RS, Armand M, Tallroth K, Lepisto J, Mears SC, 2009. Three-dimensional mechanical evaluation of joint contact pressure in 12 periacetabular osteotomy patients with 10-year follow-up. Acta orthopaedica 80, 155–161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Athanasiou KA, Agarwal A, Dzida FJ, 1994. Comparative study of the intrinsic mechanical properties of the human acetabular and femoral head cartilage. Journal of orthopaedic research : official publication of the Orthopaedic Research Society 12, 340–349. [DOI] [PubMed] [Google Scholar]
- Bergmann G, Deuretzbacher G, Heller M, Graichen F, Rohlmann A, Strauss J, Duda G, 2001a. Hip contact forces and gait patterns from routine activities. Journal of biomechanics 34,859–871. [DOI] [PubMed] [Google Scholar]
- Bergmann G, Deuretzbacher G, Heller M, Graichen F, Rohlmann A, Strauss J, Duda GN, 2001b. Hip contact forces and gait patterns from routine activities. Journal of biomechanics 34, 859–871. [DOI] [PubMed] [Google Scholar]
- Chegini S, Beck M, Ferguson SJ, 2009. The effects of impingement and dysplasia on stress distributions in the hip joint during sitting and walking: a finite element analysis. Journal of orthopaedic research : official publication of the Orthopaedic Research Society 27, 195–201. [DOI] [PubMed] [Google Scholar]
- Clohisy JC, Carlisle JC, Beaule PE, Kim YJ, Trousdale RT, Sierra RJ, Leunig M, Schoenecker PL, Millis MB, 2008. A systematic approach to the plain radiographic evaluation of the young adult hip. The Journal of bone and joint surgery. American volume 90 Suppl 4, 47–66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Correa TA, Crossley KM, Kim HJ, Pandy MG, 2010. Contributions of individual muscles to hip joint contact force in normal walking. Journal of biomechanics 43, 1618–1622. [DOI] [PubMed] [Google Scholar]
- Gahramanov A, Inanici F, Caglar O, Aksoy C, Tokgozoglu AM, Guner S, Baki A, Atilla B, 2017. Functional results in periacetabular osteotomy: is it possible to obtain a normal gait after the surgery? Hip international : the journal of clinical and experimental research on hip pathology and therapy 27, 449–454. [DOI] [PubMed] [Google Scholar]
- Hadley NA, Brown TD, Weinstein SL, 1990. The effects of contact pressure elevations and aseptic necrosis on the long-term outcome of congenital hip dislocation. Journal of orthopaedic research : official publication of the Orthopaedic Research Society 8, 504–513. [DOI] [PubMed] [Google Scholar]
- Harris MD, Anderson AE, Henak CR, Ellis BJ, Peters CL, Weiss JA, 2012. Finite element prediction of cartilage contact stresses in normal human hips. Journal of orthopaedic research : official publication of the Orthopaedic Research Society 30, 1133–1139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris MD, MacWilliams BA, Bo Foreman K, Peters CL, Weiss JA, Anderson AE, 2017. Higher medially-directed joint reaction forces are a characteristic of dysplastic hips: A comparative study using subject-specific musculoskeletal models. Journal of biomechanics 54, 80–87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heller MO, Bergmann G, Deuretzbacher G, Durselen L, Pohl M, Claes L, Haas NP, Duda GN, 2001. Musculo-skeletal loading conditions at the hip during walking and stair climbing. Journal of biomechanics 34, 883–893. [DOI] [PubMed] [Google Scholar]
- Henak CR, Abraham CL, Anderson AE, Maas SA, Ellis BJ, Peters CL, Weiss JA, 2014. Patient-specific analysis of cartilage and labrum mechanics in human hips with acetabular dysplasia. Osteoarthritis Cartilage 22, 210–217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henak CR, Ellis BJ, Harris MD, Anderson AE, Peters CL, Weiss JA, 2011. Role of the acetabular labrum in load support across the hip joint. Journal of biomechanics 44, 2201–2206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacobsen JS, Nielsen DB, Sorensen H, Soballe K, Mechlenburg I, 2014. Joint kinematics and kinetics during walking and running in 32 patients with hip dysplasia 1 year after periacetabular osteotomy. Acta orthopaedica 85, 592–599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kern AM, Anderson DD, 2015. Expedited patient-specific assessment of contact stress exposure in the ankle joint following definitive articular fracture reduction. Journal of biomechanics 48, 3427–3432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knight SJ, Abraham CL, Peters CL, Weiss JA, Anderson AE, 2017. Changes in chondrolabral mechanics, coverage, and congruency following peri-acetabular osteotomy for treatment of acetabular retroversion: A patient-specific finite element study. Journal of orthopaedic research : official publication of the Orthopaedic Research Society 35, 2567–2576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lequesne M, de Seze S, 1961. Le faux profil du bassin: nouvelle incidence radiographique pour l’étude de la hanche. Son utilitè dans les dysplasies et les differentes coxopathies. . Rev Rhum Mal Osteoartic 28, 643–652.14464207 [Google Scholar]
- Mavcic B, Iglic A, Kralj-Iglic V, Brand RA, Vengust R, 2008. Cumulative hip contact stress predicts osteoarthritis in DDH. Clinical orthopaedics and related research 466, 884–891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCarthy JC, Lee J, 2002. Acetabular dysplasia: a paradigm of arthroscopic examination of chondral injuries. Clin Orthop Relat Res 405, 122–128. [DOI] [PubMed] [Google Scholar]
- Mont MA, Seyler TM, Ragland PS, Starr R, Erhart J, Bhave A, 2007. Gait analysis of patients with resurfacing hip arthroplasty compared with hip osteoarthritis and standard total hip arthroplasty. The Journal of arthroplasty 22, 100–108. [DOI] [PubMed] [Google Scholar]
- Morrow MM, Rankin JW, Neptune RR, Kaufman KR, 2014. A comparison of static and dynamic optimization muscle force predictions during wheelchair propulsion. J Biomech 47, 3459–3465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy SB, Ganz R, Müller ME, 1995. The prognosis in untreated dysplasia of the hip. A study of radiographic factors that predict the outcome. The Journal of bone and joint surgery. American volume 77, 985–989. [DOI] [PubMed] [Google Scholar]
- Noguchi Y, Miura H, Takasugi S, Iwamoto Y, 1999. Cartilage and labrum degeneration in the dysplastic hip generally originates in the anterosuperior weight-bearing area: an arthroscopic observation. Arthroscopy 15, 496–506. [DOI] [PubMed] [Google Scholar]
- Novais EN, Duncan S, Nepple J, Pashos G, Schoenecker PL, Clohisy JC, 2017. Do radiographic parameters of dysplasia improve to normal ranges after Bernese periacetabular osteotomy? Clinical orthopaedics and related research 475, 1120–1127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pedersen EN, Alkjaer T, Soballe K, Simonsen EB, 2006. Walking pattern in 9 women with hip dysplasia 18 months after periacetabular osteotomy. Acta orthopaedica 77, 203–208. [DOI] [PubMed] [Google Scholar]
- Perron M, Malouin F, Moffet H, McFadyen BJ, 2000. Three-dimensional gait analysis in women with a total hip arthroplasty. Clin Biomech 15, 504–515. [DOI] [PubMed] [Google Scholar]
- Phillips AT, Pankaj P, Howie CR, Usmani AS, Simpson AH, 2007. Finite element modelling of the pelvis: inclusion of muscular and ligamentous boundary conditions. Medical engineering & physics 29, 739–748. [DOI] [PubMed] [Google Scholar]
- Reynolds D, Lucas J, Klaue K, 1999. Retroversion of the acetabulum: a cause of hip pain. The Journal of bone and joint surgery. British volume 81, 281–288. [DOI] [PubMed] [Google Scholar]
- Shepherd DE, Seedhom BB, 1999. Thickness of human articular cartilage in joints of the lower limb. Annals of the rheumatic diseases 58, 27–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shivanna KH, Grosland NM, Russell ME, Pedersen DR, 2007. Diarthrodial joint contact models: finite element model development of the human hip. Engineering with Computers 24, 155–163. [Google Scholar]
- Skalshoi O, Iversen CH, Nielsen DB, Jacobsen J, Mechlenburg I, Soballe K, Sorensen H, 2015. Walking patterns and hip contact forces in patients with hip dysplasia. Gait & posture 42, 529–533. [DOI] [PubMed] [Google Scholar]
- Sucato DJ, Tulchin K, Shrader MW, DeLaRocha A, Gist T, Sheu G, 2010. Gait, hip strength, and functional outcomes after a Ganz periacetabular osteotomy for adolescent hip dysplasia. J Pediatr Orthop 30, 344–350. [DOI] [PubMed] [Google Scholar]
- Thomas TP, Anderson DD, Willis AR, Liu P, Marsh JL, Brown TD, 2011. ASB Clinical Biomechanics Award Paper 2010 Virtual pre-operative reconstruction planning for comminuted articular fractures. Clin Biomech (Bristol, Avon) 26, 109–115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tönnis D, Heinecke A, 1999. Acetabular and femoral anteversion: relationship with osteoarthritis of the hip. The Journal of bone and joint surgery. American volume 81, 1747–1770. [DOI] [PubMed] [Google Scholar]
- Townsend KC, Thomas-Aitken HD, Rudert MJ, Kern AM, Willey MC, Anderson DD, Goetz JE, 2018. Discrete element analysis is a valid method for computing joint contact stress in the hip before and after acetabular fracture. Journal of biomechanics 67, 9–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiberg G, 1953. Shelf operation in congenital dysplasia of the acetabulum and in subluxation and dislocation of the hip. The Journal of bone and joint surgery. American volume 35, 65–80. [PubMed] [Google Scholar]
- Yoshida H, Faust A, Wilckens J, Kitagawa M, Fetto J, Chao EY, 2006. Three-dimensional dynamic hip contact area and pressure distribution during activities of daily living. Journal of biomechanics 39, 1996–2004. [DOI] [PubMed] [Google Scholar]
- Zou Z, Chavez-Arreola A, Mandal P, Board TN, Alonso-Rasgado T, 2013. Optimization of the position of the acetabulum in a ganz periacetabular osteotomy by finite element analysis. Journal of orthopaedic research : official publication of the Orthopaedic Research Society 31, 472–479. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


