Algorithm Variability in the Estimation of Lung Nodule Volume From Phantom CT Scans: Results of the QIBA 3A Public Challenge

Abstract

Rationale and Objectives:

Quantifying changes in lung tumor volume is important for diagnosis, therapy planning, and evaluation of response to therapy. The aim of this study was to assess the performance of multiple algorithms on a reference data set. The study was organized by the Quantitative Imaging Biomarker Alliance (QIBA).

Materials and Methods:

The study was organized as a public challenge. Computed tomography scans of synthetic lung tumors in an anthropomorphic phantom were acquired by the Food and Drug Administration. Tumors varied in size, shape, and radiodensity. Participants applied their own semi-automated volume estimation algorithms that either did not allow or allowed post-segmentation correction (type 1 or 2, respectively). Statistical analysis of accuracy (percent bias) and precision (repeatability and reproducibility) was conducted across algorithms, as well as across nodule characteristics, slice thickness, and algorithm type.

Results:

Eighty-four percent of volume measurements of QIBA-compliant tumors were within 15% of the true volume, ranging from 66% to 93% across algorithms, compared to 61% of volume measurements for all tumors (ranging from 37% to 84%). Algorithm type did not affect bias substantially; however, it was an important factor in measurement precision. Algorithm precision was notably better as tumor size increased, worse for irregularly shaped tumors, and on the average better for type 1 algorithms. Over all nodules meeting the QIBA Profile, precision, as measured by the repeatability coefficient, was 9.0% compared to 18.4% overall.

Conclusion:

The results achieved in this study, using a heterogeneous set of measurement algorithms, support QIBA quantitative performance claims in terms of volume measurement repeatability for nodules meeting the QIBA Profile criteria.

INTRODUCTION

Because of the aggressive nature of lung cancer, the response of a patient to a particular treatment must be evaluated quickly and efficiently to get therapy started. X-ray computed tomography (CT) is an effective imaging technique for diagnosing lung tumors, planning therapy, and assessing therapy response. In clinical practice, qualitative impressions based on nothing more than visual inspection of the images are frequently sufficient for making patient management decisions. Quantification becomes helpful when tumor masses change slowly over the course of illness. Standards for measurement of objects within images are therefore a necessity to be able to help lung cancer patients. The Quantitative Imaging Biomarker Alliance (QIBA) has led this role, supported by the Radiological Society of North America (RSNA), as “an initiative by researchers, healthcare professionals, and industry to advance quantitative imaging and the use of imaging biomarkers in clinical trials and clinical practice.”¹ The goal of the QIBA is to establish protocols and profiles (standards documents) that will lead to acceptance of quantitative imaging biomarkers by the imaging community, clinical trial industry, regulatory agencies, and clinicians, as reliable evidence of biology and pathophysiology. A QIBA Profile is a document that describes a specific performance claim and how it can be achieved. It is expected to provide specifications that may be adopted by users and equipment vendors to meet targeted levels of performance. The QIBA Profile for CT Tumor Volume Change can be found at http://www.rsna.org/QIBA_Protocols_and_Profiles.aspx.

Determining an appropriate biomarker to measure change in lung tumor size is currently an issue under discussion. Clinicians currently utilize the longest in-plane diameter of each tumor as a measure of tumor size. Growth is measured using the Response Evaluation Criteria In Solid Tumors (RECIST), a well-known response criteria based on measurements of maximum axial diameter as a proxy for volume (1,2). Limitations of RECIST include the assumption that a change in size volume is reflected in the maximum diameter of the tumor, which is often not the case (3).

Many investigators have suggested that quantifying whole tumor volumes could solve many of the limitations of RECIST and would have a major impact on patient management (3–8). Along with magnetic resonance (MR) imaging, functional MR imaging, shear-wave ultrasound imaging, and positron emissions tomography/CT, CT volumetry was chosen by the QIBA as a biomarker to quantify the effects of novel therapeutic candidates for cancer. The QIBA CT technical committee has constructed a systematic “process map” for qualifying volumetry as a biomarker for response to treatment for a variety of medical conditions, including lung disease (9).

The performance of volume estimation algorithms is one of the several factors that can affect bias and variance of CT volumetry (10), in turn affecting whether such measurements can stay within the QIBA Profile guidelines. Currently available algorithms include a wide range of methods, requiring different amounts of user input and different types of software or radiological expertise.

Computer algorithms can assist radiologists in areas such as diagnosis, prognosis, and therapy planning, and contribute to the quality and efficacy of treatment. A number of commercial applications are already available in scanners from multiple vendors in clinical practice. One approach to encourage innovation in the development of such algorithms is through the administration of a public “challenge,” whereby a problem statement is given and solutions are solicited from interested parties that “compete” at addressing the problem statement. Such challenges in the past included the VOLCANO challenge (11,12) and the BIOCHANGE challenge (National Institute of Standards and Technology [NIST]).²

The aim of this study is to characterize the performance of a variety of algorithms with different levels of automation for the task of lung tumor volume estimation with CT in a phantom study, and to determine whether that performance operates within the 15% uncertainty level specified by the QIBA Profile. Phantom studies provide a framework where ground truth is known and can be independently verified. The study supports the development of the QIBA CT Volumetry Profile and is complementary to additional QIBA efforts that examined inter-reader, inter-scanner, and inter-site variability for this task (13), as well as comparisons between different size metrics (14). The study also provides a context in which multiple parties have incentives to participate and cooperate while avoiding direct competition.

MATERIALS AND METHODS

Participant Procedure

The following outlines the procedure taken by participants in our QIBA 3A challenge study:

• Participants submitted an e-mail to the designated registrar (a noncompeting organization, in this case the RSNA) with the signed Participation Agreement and received an anonymous ID back for identification of results.

• Participants downloaded and read the 3A Challenge Protocol on the 3A Wiki.³

• Participants downloaded the 3A challenge data from QI-Bench⁴ as described in the Protocol. QI-Bench provided resources that enabled better use of available data by providing data access methods and an analytical framework for evaluation and optimization.

• Participants took part in two different phases of this study: an initial pilot phase using a subset of the data, followed by the pivotal, or test set, utilizing the rest of the data. The pilot training sets included partially annotated data to set initial parameters for the volume estimation algorithms. The main reason for conducting a pilot study was to collect enough data to make a good estimate of sample size for the main pivotal study (15,16).

• Participants determined tumor volumes for the initial pilot set. Then the fully annotated pilot data set was made available as a training set and for optimization for the followon pivotal study. The full truth data were not shared for the pivotal set. Data for each lesion used in the study included CT scans containing that lesion and one location point for the lesion within those scans. Location points were defined by a nonparticipant.

• Participants used the training data to tune the parameters in their individual algorithms. They were then required to use that set of parameters without modification for analysis of the test data set. (Note: individual participant integrity was relied on to enforce this policy.)

• Participants reported their results in the required formats, signed by the team leader, to the 3A registrar (RSNA). Additionally the participants reported the degree of algorithm automation, either type 2 (allowed post-segmentation correction) or type 1 (no post-segmentation correction). No participant used manual segmentation. Note that the term fully automated algorithm is not used as all algorithms required at least the manual placement of the segmentation starting point (seed) (11). A summary of the degree of automation of algorithms of the participants is given in Table 1.

• Study participants represented academic, nonprofit, and commercial organizations, among others MEDIAN Technologies, Columbia University Medical Center, Fraunhofer MEVIS Institute for Medical Image Computing, MScGE Healthcare, ICON Medical Imaging, INTIO Inc., NYU Langone Medical Center, Perceptive Informatics, Siemens AG, Toshiba Corporation, Vital Images, Inc., and Elucid Bioimaging, Inc. All participating institutions are represented in the coauthors’ list.

Table 1.

Number of Participants with Each Class by the Degree of Automation (Automation Class)

Automation Class	Pilot (n= 12)	Pivotal (n= 10)
Semi-automatic type 1	6 (50%)	4 (40%)
Semi-automatic type 2: limited parameter adjustment (on less than 15% of the cases)	1 (8.3%)	1 (10%)
Semi-automatic type 2: moderate parameter adjustment (on less than 50% of the cases)	1 (8.3%)	0
Semi-automatic type 2: extensive parameter adjustment (more than 50% of the cases)	0	1 (10%)
Semi-automatic type 2: limited image/boundary modification (on less than 15% of the cases)	0	0
Semi-automatic type 2: moderate image/boundary modification (on less than 50% of the cases)	1 (8.3%)	1 (10%)
Semi-automatic type 2: extensive image/boundary modification (more than 50% of the cases)	0	1 (10%)
Unspecified	3 (25%)	2 (20%)

DATA DESCRIPTION

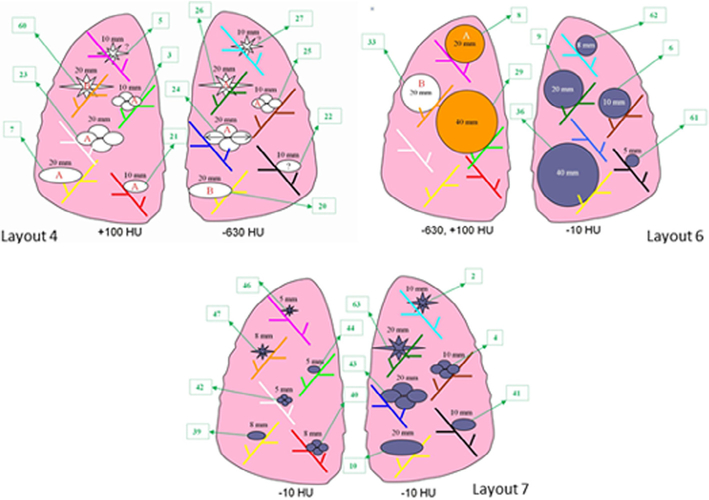
The studies utilized phantom CT scans previously acquired by the Food and Drug Administration (17). The CT data were acquired by attaching synthetic lung tumors in a vasculature insert within an anthropomorphic phantom (N1, Kyoto Kagaku, Kyoto, Japan). Various tumor positions and locations were utilized according to different layouts, shown in Figure 1. The synthetic tumors varied in size (5, 8, 10, 12, 20, and 40 mm), shape (spherical, elliptical, lobulated, and spiculated), and density (−630 HU, −300 HU, −10 HU, +20 HU, and +100 HU). Fifteen high-resolution computed tomography scans containing 97 tumors were used for the pilot phase of the study and 40 high-resolution computed tomography scans containing 408 tumors were used for the pivotal phase. Acquisitions were made using a 16-detector helical CT scanner (Philips Mx800 IDT-16, Amsterdam, The Netherlands) using an exposure of 100 mAs, 120 kVp (peak kilovoltage across the x-ray tube), pitch values of 0.9 and 1.2, two slice collimations (16 × 0.75 mm and 16 × 1.5 mm), and a 50% reconstruction overlap. Two different slice thicknesses, 0.8 mm (using 16 × 0.75 mm collimation) and 5 mm (using 16 × 1.5 mm slice collimation), were considered for image reconstruction, along with a detail (B40f) reconstruction kernel. Table 2 summarizes the characteristics of the data set, including which nodules are consistent with the QIBA Profile. Note that only a fraction of the nodules were 12 or 40 mm in size, or had density of −300 HU or 20 HU. Those nodules were included for completeness in the pivotal study only to stress the system with nodules not seen in the training set.

Figure 1.

Tumor layouts used for the pilot study. Not all of the tumors were used for computed tomography (CT) series of a given layout (courtesy of Food and Drug Administration) (17).

Table 2.

Description of Data Used in the Study: Breakdown of Nodule Characteristics (Shape, Density, Size) and Slice Thickness

			Slice Thickness (mm)
QIBA Type*	Lesion Type		0.8 mm QIBA Type = Yes	5.0 mm QIBA Type = No
No	Spherical	5 mm, −10 HU	6	6
		5 mm, 100 HU	2	2
		8 mm, −10 HU	6	6
		8 mm, 100 HU	2	2
		20 mm, −630 HU	6	6
	Elliptical	5 mm, −10 HU	6	6
		8 mm, −10 HU	6	6
		10 mm, −630 HU	6	6
		20 mm, −630 HU	6	6
	Lobulated	5 mm, −10 HU	6	6
		8 mm, −10 HU	6	6
		10 mm, −630 HU	6	6
		20 mm, −630 HU	6	6
	Spiculated	5 mm, −10 HU	6	6
		8 mm, −10 HU	6	6
		10 mm, −630 HU	6	6
		20 mm, −630 HU	6	6
	Irregular	8 mm, −300 HU	2	2
Yes	Spherical	10 mm, −10 HU	6	6
		10 mm, 100 HU	2	2
		20 mm, −10 HU	6	6
		20 mm, 100 HU	6	6
		40 mm, −10 HU	6	6
		40 mm, 100 HU	6	6
	Elliptical	10 mm, −10 HU	6	6
		10 mm, 100 HU	6	6
		20 mm, −10HU	6	6
		20 mm, 100 HU	6	6
	Lobulated	10 mm, −10 HU	6	6
		10 mm, 100 HU	6	6
		20 mm, −10 HU	6	6
		20 mm, 100 HU	6	6
	Spiculated	10 mm, −10 HU	6	6
		10 mm, 100 HU	6	6
		20 mm, −10 HU	6	6
		20 mm, 100 HU	6	6
	Irregular	10 mm, 100 HU	2	2
		12 mm, 20 HU	2	2
Total			204	204

QIBA, Quantitative Imaging Biomarker Alliance.

Notes: 8 mm of irregular lesion with −300 HU has only four scans of lesions, and 12 mm of irregular lesion with 20 HU has only four scans of lesions.

^*QIBA type include lesions that are equal or greater than 10 mm with non-ground glass nodules (here we set as nodules >−630 HU). Out of 408 scanned lesions, 300 lesions (74%) do not meet the QIBA Profile and 108 lesions (26%) meet the QIBA Profile.

DATA PREPARATION

For each CT series used in the study, the number of nodules chosen varied from 2 to 10. Location points and bounding boxes were given for each nodule. The location points were determined manually by examining the CT series using Digital Imaging and Communication in Medicine (DICOM)capable viewing software (ImageJ, ClearCanvas, and 3DDoctor) and knowledge of the nodule placement during acquisition. The bounding boxes were sized to provide an upper constraint for the volumetric software without revealing the tumor size. The size varied across the set. The data set consisted of the selected CT series along with a study description document in Microsoft (Redmond, USA, US5949181045) Excel format containing the tumor location information (location points and bounding boxes). For the pilot set, tumor volume ground truth values were provided for algorithm tuning. This spreadsheet also served to record the participants’ volumetric results.

STATISTICAL DATA ANALYSIS

The goals of the statistical analyses were to estimate the technical performance in measuring phantom tumor volumes and to identify tumor and imaging characteristics that affect performance. Tumor and imaging characteristics that were evaluated included six tumor sizes, five shapes, five densities, two reconstructed slice thicknesses, and algorithm automation (see Table 2). Four technical performance metrics were considered: percent bias (%bias) was used as a measure of accuracy, within-tumor coefficient of variation (wCV) and between-algorithm reproducibility coefficient (RDC) were used as measures of precision, and total deviation index (TDI) was used as an aggregate measure of both accuracy and precision. For measuring TDI and %bias, we assumed that any imprecision in determining the true volume of the synthetic tumors, which was calculated by dividing weight by material density, was negligible (17).

Let Y_ijkl denote the measured tumor volume for synthetic tumor i by the j-th algorithm (j = 1, 2, . . . J) and k-th slice thickness (k = 1, 2, . . .K), on the l-th imaging occasion (l = 1, 2, . . .L). Let X_i denote the true volume for the i-th synthetic tumor (i = 1, 2, . . .n). The percent bias (%bias) for the j-th algorithm and k-th slice thickness was defined as:

$$\%{\text{Bias}}_{\text{jk}}=\left\{{\sum }_{i=1}^N{\sum }_{l=1}^L\left[\frac{\left(Y_{ijkl}-X_i\right)}{X_i}\right]/(N\times L)\right\}\times 100.$$

The wCV for the j-th algorithm and k-th slice thickness was defined as $wC{V}_{jk}={\sum }_{i=1}^N\left(wC{V}_{ijk}\right)/N$, where $wC{V}_{ijk}=\left(\frac{\sqrt{Va{r}_{ijk}}}{{\overline{Y}}_{ijk}}\right)\times 100,Va{r}_{ijk}={\sum }_{=1}^L{\left(Y_{ijkl}-{\overline{Y}}_{ijk}\right)}^2/(L-1)$, and ${\overline{Y}}_{ijk}$ is the mean of the measured volumes of lesion i using algorithm j at the k-th slice thickness. The repeatability coefficient (RC) (15) is a related measure of precision; it provides the range for 95% of the differences between repeated measurements of a tumor’s volume to lie. It is defined as 2.77 . wCV.

The TDI at 95% coverage (TDI_95%) is an aggregate performance metric that includes both bias and precision (15,16). It was estimated as the 95th percentile of the distribution of the percent differences from the true nodule volume, d_ijk’s, over all n tumors, where d_ijk = |Y_ijkl−X_i|/X_i.

For each nodule characteristic, 95% confidence intervals (CI) for the %bias, wCV, and TDI_95% were constructed with bootstrap resampling (14) because there were multiple lesions from a single image; thus, the lesions are not independent. Additionally, analyses were conducted for the entire set of nodules and for the subset of nodules meeting the QIBA Profile (thin slice ≤ 2.5 mm, size ≥ 10 mm, and solid tumor with excluding density of −630 HU). In the pilot phase, 32 of the 97 met these criteria specified by the QIBA Profile, whereas in the pivotal phase 108 of 408 tumors met these criteria.

Finally, three generalized linear models were built to test the effects of all nodule characteristics and CT slice thicknesses on the performance of the algorithms. The first model was fit to evaluate the significance of all characteristics in predicting %bias, and to test the difference between automated and semi-automated algorithms, adjusting for effects of shapes, densities, sizes, and slice thickness. Second, a model was fit to evaluate the significance of these characteristics in predicting wCV. Similarly, a third model was fit to estimate the reproducibility of the tumor volume when measured by different algorithms. The RDC is a precision metric describing 95% of the differences between volume measurements taken by different algorithms (15). A mixed effect model was used with restricted maximum likelihood estimates for the cases meeting the QIBA Profile. Box-Cox transformations were applied, as needed. For the multiple comparisons within the five shapes and six sizes, P values were adjusted by the Bonferroni method (18,19). Analyses were performed using R (version 2.15.1) (cran.r-project.org) and STATA (v. 12.0, College Station, TX) and freely available scripts (www.qibench.org).

RESULTS

%Bias

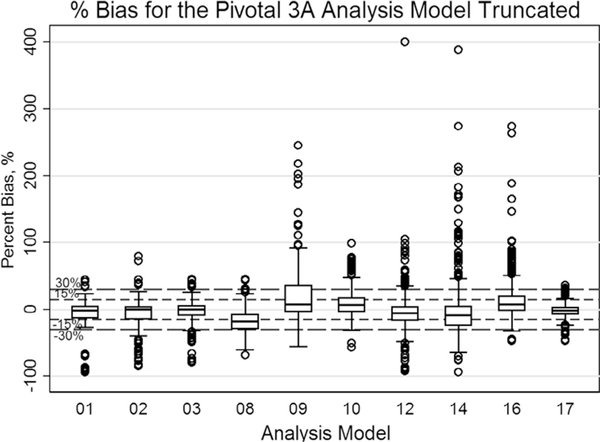
Figure 2 summarizes the estimated %bias over all algorithms used and all nodules, regardless of whether they are compatible with the QIBA Profile or not. There was wide variation in %bias among the algorithms, with %bias ranging from −94% to 674%. For all algorithms, the mean %bias was 1.04%, with 95% CI of [−0.06, 2.13]. For QIBA-compliant nodules (not shown in Figure 2), %bias ranged from −92% to 188%.

Figure 2.

Pivotal: A box-and-whisker plot representing the distribution of percent bias (%bias) in volume measurements (truncated at % error of 400 [five points beyond 400% error were made to be 400% with the maximum value of 674%]). The mid-bold line indicates the median. The upper and lower lines of the box represent the 25% and 75% tile in percent bias, respectively. The thicker dashed lines represent ±15%, and the smaller dotted lines show the location of ±30%. The majority of the percent bias estimates from the 10 participants were within ± 30%. Note that 61% (ranging from 37% to 84%) of nodule measurements met the <15% criterion and 84% (ranging from 72% to 98%) of nodule measurements met the <30% criterion.

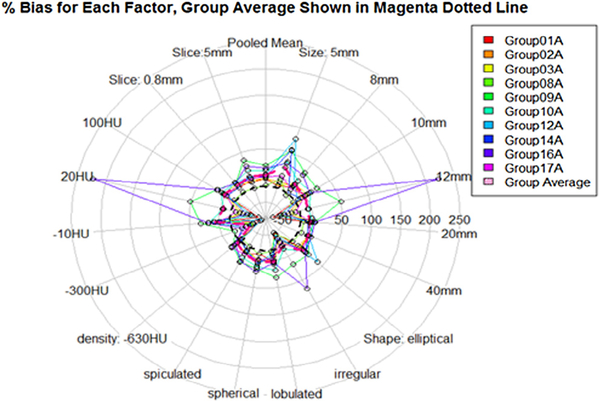
The estimated %bias for individual imaging parameters and nodule characteristics is given in Table 3, and illustrated in radial plots in Figures 3 and 4. The semi-automated type 1 algorithms, which allowed post-segmentation correction, tended to overestimate tumor volume, particularly for lobulated tumors and smaller tumors. Algorithms of type 1 and those of type 2 tended to underestimate spiculated and irregularly shaped nodules and low-density nodules. Across nodule sizes, %bias was highest for the 5-mm nodules, which was expected considering that measurements included those derived from 5-mm thick scans, and the cross-effect between nodule size and slice thickness has been shown to be an important contributing factor in the literature (10). Table 4 summarizes the %bias estimates for nodules meeting the QIBA claim criteria. Irregularly shaped nodule of 12 mm in size with density of 20 HU had a relatively large bias compared to the same-shaped nodule of 10 mm with 100 HU. For this nodule, the combination of shape and density could have played a key role, However, the lack of scan data for this lesion (only two scans were acquired) makes it difficult to draw any real conclusions about the contributing factors. Elliptical and lobulated nodules tended to be overestimated and spiculated, and irregularly shaped nodules tended to be underestimated. Note, however, that there were only three nodules of irregular shape: 8 mm with density −300 HU, 10 mm with density 100 HU, and 12 mm with density of 20 HU (Table 2). These nodules represent a small fraction of the sample size (2% combined) and their number likely contributed to the wider confidence intervals compared to the other shapes. Moreover, the irregular nodules were not represented in the training set. As such, the algorithms could have been inadequately trained to segment these lesions. Excluding these nodules from the analysis, %bias was largest for the low-density nodules (−630 HU). Most commercial algorithms are not designed for such low-density nodules, possibly explaining this result. The %bias was also larger for the smaller nodules (5 mm), which agrees with other findings summarized by Gavrielides et al (10). Table 3 also shows that the %bias was reduced for the thin slice series across algorithms with no post-segmentation editing. It is difficult to make such observations for the algorithms that allowed post-segmentation editing because of the possibility of observer variability, which we did not attempt to measure.

Table 3.

Mean of %Bias and 95% CI of the Mean of %Bias as a Function of Nodule Characteristics and Reconstructed Slice Thickness

Parameter	Value	Semi-Automatic Type 1 Algorithm (%)	Semi-Automatic Type 2 Algorithm (%)	All (%)
Shape	Spherical	4.12	0.86	2.49
		[2.77, 5.47]	[−1.38, 3.17]	[1.13, 3.83]
	Elliptical	5.28	9.54	7.41
		[3.14, 7.33]	[2.86, 16.28]	[4.09, 10.71]
	Lobulated	10.78	−6.89	1.95
		[8.05, 13.3]	[−9.37, −4.37]	[0.02, 3.83]
	Spiculated	−2.29	−7.99	−5.14
		[−4.28, −0.28]	[−10.66, −5.39]	[−6.72, −3.43]
	Irregular	−18.79	−22.70	−20.74
		[−28.95, −8.86]	[−39.96, −5.5]	[−30.96, −10.27]
Density (HU)	−630*	−8.37	−19.44	−13.9
		[−9.58, −7.12]	[−20.79, −18.06]	[−14.88, −12.93]
	−300	−47.88	−57.24	−52.56
		[−58.04, −37.58]	[−63.42, −50.83]	[−59.32, −45.81]
	−10	8.84	5.11	6.97
		[7.14, 10.53]	[1.7, 8.53]	[5.07, 8.78]
	20	−11.02	−0.24	−5.63
		[−33.31, 11.95]	[−49.73, 50.53]	[−32.48, 21.3]
	100	6.05	1.15	3.60
		[4.71, 7.35]	[−1.11, 3.3]	[2.23, 4.91]
Slice thickness (mm)	5*	6.65	0.64	3.65
		[4.71, 8.57]	[−1.65, 2.93]	[2.18, 5.16]
	0.8	0.91	−4.04	−1.57
		[−0.01, 1.83]	[−7.26, −0.8]	[−3.2, 0.1]
Size (mm)	5*	13.77	28.67	21.22
		[8.31, 19.14]	[16.37, 40.98]	[14.24, 28.09]
	8*	4.91	−5.18	−0.14
		[1.63, 8.18]	[−8.79, −1.45]	[−2.71, 2.44]
	10	6.51	−7.92	−0.71
		[4.74, 8.26]	[−9.86, −5.92]	[−2.13, 0.65]
	12	−11.02	−0.24	−5.63
		[−33.15, 1.28]	[−49.88, 50.49]	[−32.25, 20.54]
	20	−1.76	−5.58	−3.67
		[−2.45, −1.11]	[−7.2, −3.97]	[−4.58, −2.81]
	40	0.67	−3.11	−1.22
		[0.18, 1.18]	[−4.58, −1.62]	[−2.05, −0.36]
All		3.78	−1.70	1.04
		[2.68, 4.88]	[−3.67, 0.28]	[−0.06, 2.13]

Note: Results are tabulated across semi-automated type 1 and semi-automated type 2 algorithms.

^*Criteria that do not meet the QIBA Profile; 12 mm of irregular lesion with 20 HU has only four scans.

Figure 3.

Pivotal: %bias by nodule and imaging characteristics: size (5 mm, 8 mm, 10 mm, and 12 mm), shape (ell: ellipsoid, irr: irregular, lob: lobulated, sph: sphere, and spi: speculated), density (−630 HU, −300 HU, −10 HU, 20 HU, and 100 HU), and slice thickness (0.8 mm and 5 mm). For each stratum, the mean %bias for all 10 participants is shown with dotted polygons. The mean of all groups is shown by the magenta dotted lined polygon.

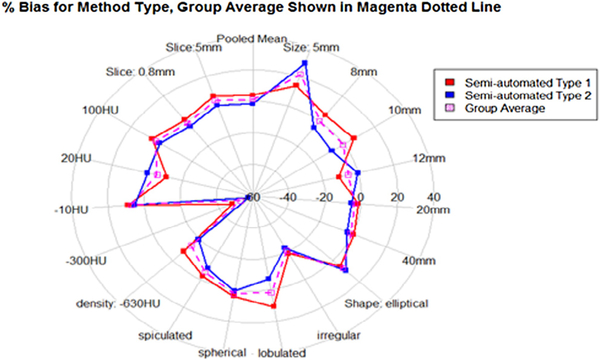
Figure 4.

Pivotal: For semi-automated type 1 (no post-segmentation correction allowed) and semi-automated type 2 (post-segmentation correction allowed) algorithms, the %bias is shown with solid-lined polygons for various nodule and imaging characteristics. The mean %bias of all groups by nodule characteristic is shown by the magenta dotted polygon.

Table 4.

Using Only the Nodules That Meet the QIBA CT Profile, the Mean of %Bias Estimates as a Function of Nodule Characteristics, and Reconstructed Slice Thickness

Shape Parameter	Size, HU Parameters	Semi-Automatic Type 1 Algorithm (%)	Semi-Automatic Type 2 Algorithm (%)	All (%)
Spherical	10 mm, −10 HU	3.07	3.72	3.39
		[−0.08, 6.21]	[0.56, 6.88]	[1.15, 5.63]
	10 mm, 100 HU*	1.36	−4.57	−1.60
		[−2.74, 5.46]	[−12.34, 3.21]	[−6.21, 3.01]
	20 mm, −10 HU	2.35	−2.95	−0.30
		[1.20, 3.49]	[−4.96, −0.94]	[−1.71, 1.11]
	20 mm, 100 HU	3.73	−2.11	0.81
		[2.51, 4.95]	[−3.65, −0.56]	[−0.37, 1.99]
	40 mm, −10 HU	0.19	−3.26	−1.54
		[−0.43, 0.81]	[−4.21, −2.31]	[−2.28, −0.79]
	40 mm, 100 HU	1.56	−0.28	0.64
		[−0.88, 2.24]	[−1.65, 1.09]	[−0.16, 1.45]
Elliptical	10 mm, −10 HU	9.34	−1.62	3.86
		[7.14, 11.54]	[−5.62, 2.38]	[1.24, 6.49]
	10 mm, 100 HU	11.36	4.86	8.11
		[3.81, 18.91]	[−2.82, 12.53]	[2.63, 13.8]
	20 mm, −10 HU	.73	−5.54	−1.41
		[1.68, 3.78]	[−8.10, −2.99]	[−3.14, 0.33]
	20 mm, 100 HU	6.66	20.03	13.34
		[5.56, 7.76]	[6.99, 33.08]	[6.65, 20.04]
Lobulated	10 mm, 10 HU	8.60	−25.10	−8.25
		[5.34, 11.86]	[−37.87, −12.33]	[−15.90, −0.60]
	10 mm, 100 HU	4.73	0.0008	2.36
		[2.25, 7.21]	[−4.03, 4.03]	[−0.08, 4.81]
	20 mm, −10 HU	0.47	−2.13	−0.83
		[−4.22, 5.17]	[−4.30, 0.03]	[−3.39, 1.73]
	20 mm, 100 HU	3.53	−3.06	0.23
		[2.22, 4.84]	[−4.83, −1.29]	[−1.14, 1.61]
Spiculated	10 mm, −10 HU	−5.15	−10.42	−7.78
		[−6.86, −3.43]	[−16.16, −4.68]	[−10.84, −4.73]
	10 mm, 100 HU	−2.00	−8.67	−5.34
		[−4.12, 0.11]	[−11.86, −5.49]	[−7.45, −3.23]
	20 mm, −10 HU	−1.76	−5.58	−4.94
		[−2.45, −1.11]	[−7.2, −3.97]	[−6.85,−3.03]
	20 mm, 100 HU	−2.90	−6.95	−4.92
		[−4.36, −1.44]	[−11.82, −2.07]	[−7.57, −2.28]
Irregular	10 mm, 100 HU	−2.10	−9.11	−5.60
		[−5.21, 1.01]	[−14.44, −3.77]	[−8.96, −2.25]
	12 mm, 20 HU*	−28.90	−11.50	−20.20
		[−36.94, −20.85]	[−72.52, 49.52]	[−49.63, 9.24]
All		1.89	−3.19	−0.65
		[1.05, 2.72]	[−5.04, −1.33]	[−1.66, 0.36]

CT, computed tomography; QIBA, Quantitative Imaging Biomarker Alliance.

Note: Results are tabulated across five semi-automated type 1and 5 semi-automated type 2 algorithms.

^*12 mm of irregular lesion with 20 HU and 10 mm of spherical lesion with 100 HU has only two lesions scans.

In the statistical model, the %bias was significantly affected by nodule shape, density, and size after adjusting for effects due to different participants (all P < 0.001). Estimates of %bias were the largest for irregularly shaped, 12 mm/20 HU nodule, the −300 HU density nodules, and the 5-mm nodules (Fig 3).

wCV

Table 5 summarizes the estimated wCV by individual imaging parameters and nodule characteristics. The wCV is considerably larger for small tumors (less precision) than for larger tumors. The mean wCV over all characteristics was 5.76, with 95% CI of [4.93, 6.59].

Table 5.

Estimated Coefficient of Variation (wCV) as a Function of Nodule Characteristics and Reconstructed Slice Thickness

Parameter	Value	Slice Thickness 0.8 mm (%)	Slice Thickness 5 mm* (%)	All (%)
Shape	Spherical	3.69	4.54	4.11
		[2.60, 4.77]	[3.20, 5.87]	[3.28, 4.94]
	Elliptical	5.19	7.82	6.50
		[2.09, 8.28]	[3.72, 11.91]	[3.94, 9.07]
	Lobulated	7.89	6.28	7.08
		[1.49, 14.29]	[2.54, 10.01]	[4.94, 10.96]
	Spiculated	4.77	7.35	6.06
		[1.99, 7.54]	[2.45, 12.26]	[3.23, 8.89]
	Irregular	6.47	4.48	5.48
		[3.08, 9.85]	[0.61, 8.35]	[2.90, 8.05]
Density (HU)	−630*	3.83	4.16	4.00
		[2.89, 4.77]	[3.07, 5.25]	[3.24, 4.76]
	−300	8.80	3.75	6.27
		[4.16, 13.44]	[0.70, 7.43]	[3.01, 9.54]
	−10	6.81	7.64	7.23
		[3.07, 10.55]	[4.60, 10.68]	[4.66, 9.79]
	20	6.11	6.00	6.06
		[1.91, 10.32]	[−0.68, 12.69]	[2/17, 9.94]
	100	3.76	5.51	4.64
		[1.49, 6.03]	[1.99, 9.04]	[2.37, 6.91]
Size (mm)	5*	13.10	12.35	12.73
		[4.46, 21.74]	[ 8.34, 16.36]	[7.89, 17.55]
	8*	7.56	7.41	7.49
		[3.87, 11.25]	[4.08, 10.74]	[4.89, 10.08]
	10	4.70	6.47	5.59
		[3.14, 6.27]	[4.03, 8.92]	[4.12, 7.05]
	12	6.11	6.00	6.06
		[2.46, 9.77]	[−0.27, 12.29]	[2.63, 9.48]
	20	2.30	3.53	2.91
		[0.95, 3.65]	[0.71, 6.34]	[1.40, 4.43]
	40	0.82	1.34	1.08
		[0.32, 1.32]	[0.63, 2.04]	[0.65, 1.51]
All		5.33	6.18	5.76
		[4.08, 6.59]	[5.15, 7.21]	[4.93, 6.59]

^*Criteria that do not meet the Quantitative Imaging Biomarker Alliance (QIBA) Profile.

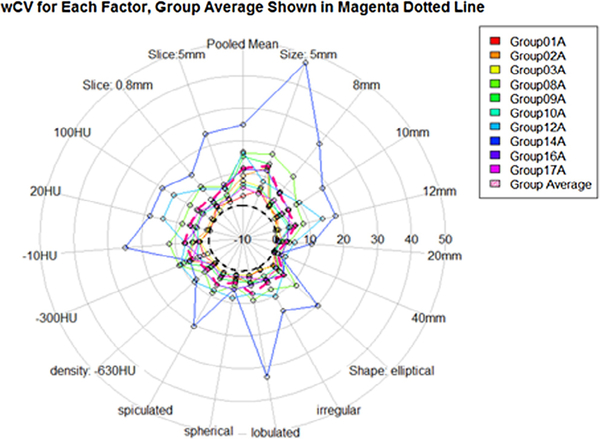
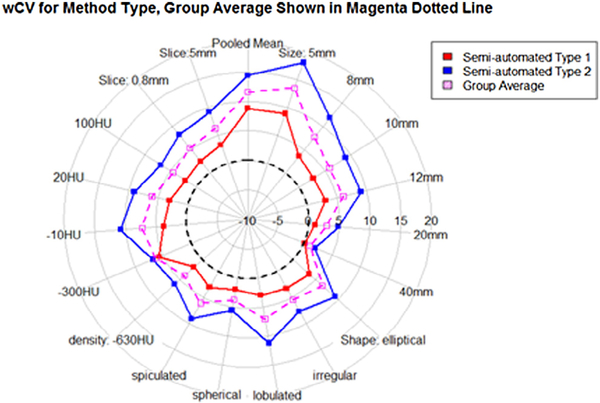
In the statistical model, wCV was significantly affected by nodule shape, size, and the degree of post-segmentation editing after adjusting for the effect from the different participants (all P < 0.001). Figure 5 pictorially shows wCV as a function of the characteristics of nodules: size (5 mm, 8 mm, 10 mm, and 12 mm), shape (ell: ellipsoid, irr: irregular, lob: lobulated, sph: sphere, and spi: speculated), density (−630 HU, −300 HU, −10 HU, 20 HU, and 100 HU), and slice thickness (0.8 mm and 5 mm). This figure shows by each stratum the mean value for all 10 participants and the mean of all groups. Figure 6 shows the wCV for each algorithm type, and there is a consistent and large difference between type 1 and type 2 automation results. The corresponding values for wCV are consistently under (type 1) and over (type 2) the mean wCV of all groups for nearly all of the nodule characteristics. Estimates of wCV were the largest for lobulated nodules, 10 HU nodules, and the smallest sized nodules. As opposed to the %bias measurements, the lobulated and spiculated nodules had a higher overall wCV than the irregularly shaped nodules. We also see differences in size and density wCV rankings between %bias and wCV measurements. It is interesting that the repeatability patterns in terms of size, shape, and density do not exactly follow the accuracy patterns of the measurements. It can be seen that size plays a consistent role, with smaller nodules averaging higher values. Shape does not have as defined a trend across a range of increasingly complicated surfaces. wCV measurements vary over the density groups, although multiple other factors contribute to those group measurements, and the variation is not as large as the %bias variation across the density groups.

Figure 5.

Pivotal: Within-tumor coefficient of variation (wCV) as a function of the characteristics of nodules: size (5 mm, 8 mm, 10 mm, and 12 mm), shape (ell: ellipsoid, irr: irregular, lob: lobulated, sph: sphere, and spi: speculated), density (−630 HU, −300 HU, −10 HU, 20 HU, and 100 HU), and slice thickness (0.8 mm and 5 mm). By each strata, the mean value for all 10 participants is shown with dotted polygons. The mean of all groups is shown by the magenta dotted lined polygon.

Figure 6.

Pivotal: For semi-automated type 1 and semi-automated type 2 algorithms, the within-tumor coefficient of variation (wCV) is shown with solid-lined polygons for various nodule and imaging characteristics. The mean wCV of all groups by nodule characteristic is shown by the magenta dotted lined polygon.

TDI95%

The mean TDI at 95% coverage is 61.22%, with 95% CI of [57.13, 65.30]. The interpretation is that 95% of differences between the measured tumor volume and the true tumor volume are less than 61.2% of the true volume. Table 6 provides the estimated TDI by lesion and imaging characteristics. The TDI tends to be larger for slice thickness of 5 mm compared to 0.8 mm. It is higher for irregularly shaped tumors and varies dramatically by size.

Table 6.

TDI_95% by Nodule and Imaging Characteristics

Parameter	Value	Slice Thickness 0.8 mm (%)	Slice Thickness 5 mm* (%)	All (%)
Shape	Spherical	23.83	70.02	54.26
		[18.87, 28.80]	[61.50, 78.54]	[44.78, 63.74]
	Elliptical	43.27	70.84	44.92
		[16.70, 69.83]	[51.91, 89.76]	[66.49, 66.06]
	Lobulated	49.05	64.86	62.75
		[19.30, 78.79]	[39.87, 89.84]	[37.76, 87.74]
	Spiculated	33.08	62.13	51.91
		[22.07, 44.08]	[43.29, 80.97]	[31.26, 72.55]
	Irregular	83.11	127.43	84.95
		[3.62, 162.61]	[−16.87, 271.73]	[−2.69, 172.58]
Density (HU)	−630*	31.80	42.59	40.57
		[30.28, 33.32]	[41.18, 44.00]	[25.95, 55.19]
	−300	83.11	72.33	78.97
		[75.45, 90.77]	[65.06, 79.60]	[61.86, 96.08]
	−10	48.76	75.91	72.47
		[33.42, 64.09]	[69.77, 82.04]	[57.58, 87.36]
	20	165.12	263.19	188.14
		[65.23, 265.01]	[136.56, 389.83]	[73.68, 302.60]
	100	26.25	53.27	43.63
		[21.74, 30.76]	[44.32, 62.23]	[36.6, 50.62]
Size (mm)	5*	93.79	125.55	113.75
		[23.92, 163.67]	[84.13, 166.98]	[69.68, 157.81]
	8*	64.39	68.64	68.08
		[48.63, 51.24]	[59.25, 78.03]	[46.90, 89.24]
	10	31.74	63.75	51.91
		[28.34, 35.14]	[52.00, 75.49]	[30.09, 73.72]
	12	165.12	263.19	188.14
		[66.89, 263.35]	[134.65, 391.73]	[68.72, 307.56]
	20	21.51	32.30	27.50
		[17.74, 25.28]	[24.21, 40.40]	[6.67, 48.33]
	40	6.07	23.41	15.30
		[4.77, 7.38]	[19.92, 26.89]	[4.98, 25.61]
All		43.27	68.83	61.22
		[36.37, 49.97]	[64.97, 72.68]	[57.13, 65.30]

^*Criteria that do not meet the Quantitative Imaging Biomarker Alliance (QIBA) Profile.

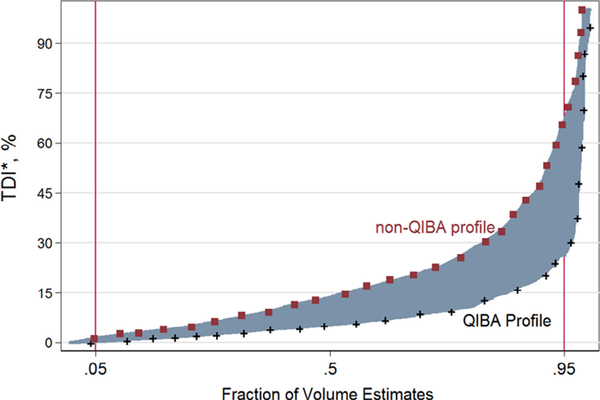
Figure 7 shows the cumulative distribution of the percent differences from the true nodule volume. The TDI_95% is 26.24% (95% CI [18.62%, 33.86%]) when the nodules are part of the QIBA Profile, whereas the TDI_95% is 66.61% (95% CI [63.09%, 70.13%]) for nodules not part of the QIBA Profile. Table 7 shows the TDI_95% by shape, density, and size for those nodules meeting the requirements of the Profile.

Figure 7.

Aggregated performance metrics of total deviation index (truncated at 100%) are shown by the Quantitative Imaging Biomarker Alliance (QIBA) Profile, shape, density, and reconstruction slice thickness.

Table 7.

Mean of %Bias, wCV, and TDI_95% [95% CI] in Volume Estimates Nodule Characteristics within QIBA Profile Criteria and Overall Non-QIBA Profile

QIBA Type*	Parameter	Value	Mean of %Bias	wCV (%)	TDI95% (%)	RDC (mm3), % of Average Volume
Yes	Shape	Spherical	2.49	1.79	13.75%	1721.82
			[1.10, 3.88]	[1.19, 2.40]	[10.10%, 17.40%]	11.91%
		Elliptical	7.41	4.14	30.59%	1622.42
			[2.18, 12.64]	[1.68, 6.60]	[11.32%, 49.86%]	64.39%
		Lobulated	1.95	3.77	20.63%	720.44
			[−1.79, 5.69]	[1.17, 6.37]	[−6.47%, 47.74%]	30.07%
		Spiculated	−3.72	3.00	24.53%	747.44
			[−6.51, −0.93]	[1.24, 4.76]	[16.04%, 33.01%]	32.13%
		Irregular	−10.87	5.30	66.86%	341.53
			[−27.13, 5.38]	[2.03, 8.57]	[−43.2%5, 176.98%]	80.55%
	Density (HU)	−10	−1.98	2.92	20.76%	1065.48
			[−4.97, 1.02]	[0.73, 5.11]	(12.34%, 29.17%)	18.15%
		20	−20.20	6.11	139.44%	NA
			[−53.06, 12.66]	[2.04, 10.18]	[64.08%, 266.15%]	NA
		100	1.48	3.26	25.67%	1536.82
			[0.19, 2.77]	[2.38, 4.14]	(22.87%, 28.48%)	24.91%
	Size (mm)	10–12	−1.60	4.52	36.35%	236.19
			[−4.22, 1.03]	[2.86, 6.18]	(25.44%, 47.27%)	46.50%
		20	0.25	2.27	16.68%	1381.87
			[−1.61, 2.11]	[0.74, 3.79]	[12.51%, 20.86%]	32.09%
		40	−0.45	0.82	6.07%	2726.62
			[−1.01, 0.12]	[0.32, 1.13]	(4.77%, 7.38%)	8.04%
	All (Meeting QIBA Profile)		−0.65	3.250	26.24%	1307.39
			[−1.66, 0. 36]	[2.60, 3.90]	[18.62%, 33.86%]	22.12%
No	Non-QIBA Profile		1.65	6.65	66.61%	1915.34
			[0.18, 3.12]	[5.57, 7.74]	[63.18%, 70.04%]	65.32%

CI, confidence interval; NA, the number of lesions is too little to estimate the reproducibility parameters; QIBA, Quantitative Imaging Biomarker Alliance; TDI, total deviation index; TDI_95%, TDI at 95% coverage; wCV, within-tumor coefficient of variation; RC, repeatability coefficient: 2.77xwCV.

^*QIBA type include lesions that are equal or greater than 10 mm with non-ground glass nodules (here we set as nodules >−630 HU). Out of 408 scanned lesions, 300 lesions (74%) do not meet the QIBA Profile and 108 lesions (26%) meet the QIBA Profile.

Comparison of Metric Results for QIBA-compliant Nodules

Table 7 shows the results of all three metrics—%bias, wCV, TDI_95%—and RDC for nodules that are QIBA-compliant. The QIBA Profile describes the repeatability in making nodule measurements as 15% (ie, RC = 2.77 · wCV). From Table 7, the estimated RC is <15% for all nodules except the one with density of 20 HU (the 12 mm/20 HU irregular nodule). Over all nodules meeting the QIBA Profile, the RC is 9%. This describes the precision of two measurements of a tumor’s volume when the same algorithm is used. When different algorithms were used to measure a tumor’s volume, the variability increased to 22.1%.

Table 8 summarizes the fraction of nodules for each individual participant where the measured and true volumes differ by <15% and by <30% for nodules with characteristics meeting the QIBA claim criteria (n = 108). Eighty-four percent of volume measurements of QIBA-compliant tumors were within 15% of the true volume, ranging from 66% to 93% across algorithms. Ninety-six percent of volume measurements were within the 30% criterion, ranging from 87% to 100% of nodule measurements. Note that for all nodules (i.e. QIBA-compliant and non-compliant nodules), the corresponding numbers were 61% (ranging from 37% to 84%) of nodule measurements met the <15% criterion and 84% (ranging from 72% to 98%) of nodule measurements met the <30% criterion (Fig 2).

Table 8.

Number and Percent of Volume Measurements within 15% and 30% of the True Value for Nodules with Characteristics Meeting the Criteria of the QIBA claim (n= 108)

	grp01	grp02*	grp03*	grp08	grp09*	grp10*	grp12	grp14	grp16	grp17*	All Mean
≤± 15%	96 (89%)	99 (92%)	100 (93%)	71 (66%)	92 (85%)	90 (83%)	79 (73%)	86 (80%)	96 (89%)	96 (89%)	905 (84%)
≤± 30%	106 (98%)	103 (95%)	106 (98%)	100 (93%)	107 (99%)	107 (99%)	94 (87%)	104 (96%)	103 (95%)	108 (100%)	1038 (96%)

Notes: Results are shown for each of the 10 algorithm participants (grp0grp01, grp02^*, grp03^*, grp08, grp09^*, grp10, grp12, grp14, grp16, and grp17). Asterisks are used to indicate semi-automated type 1 algorithms.

^*Semi-automated type 1 algorithm.

DISCUSSION

Ten participants with different volumetric algorithms each used their software to measure the volumes of a variety of lung tumor nodule phantoms from CT scans. The nodule phantoms ranged in various sizes from 5 mm to 40 mm, various geometrical shapes with spherical, elliptical, lobulated, spiculated, and irregular lesions, and density of −630 HU, −300 HU, −10 HU, 20 HU, and 100 HU. The CT reconstructions varied in slice thickness with 0.8 mm and 5 mm. The algorithms, including both allowing or not allowing post-segmentation editing, were applied to CT scans of synthetic lung tumors in anthropomorphic phantoms to characterize their performance individually, and to estimate inter-algorithm variability collectively. The results do not show significant differences between algorithm type (allowing or not allowing post-segmentation editing) for the calculation of the %bias (Fig 4). For the calculation of the wCV, semi-automated type 1 and semi-automated type 2 algorithms delivered very different results (Fig 6). A subgroup of the CT scans of these nodules met the QIBA Profile. Algorithm measurement bias and variability were calculated using the Food and Drug Administration-supplied physical measurement values as ground truth. Our primary goal was to look at the variation in volume measurements over the collection of algorithms and determine if the variability of the measurements was within a 15% uncertainty level set in the QIBA CT Volume Profile for this subgroup of nodules (solid nodules larger than 10 mm, reconstruction slice thickness ≤2.5 mm, and densities >−630 HU). Secondary goals included a wider study of nodules not in this subgroup. Even within the smaller study containing only nodules included in the profile, we see differences in algorithm %bias versus wCV across the groups of nodules separated by size, shape, and density. The consistency of each algorithm is a different measure from how well the algorithm works. Results showed that despite the significant variation in bias across algorithms, 84% of volume measurements of QIBA-compliant tumors were within 15% of the true volume, ranging from 66% to 93% across algorithms. However, it was also shown that when different algorithms were used to measure a tumor’s volume, repeatability increased to 22.1% (overall RDC) compared to 9% (overall RC) when the same algorithm was used (Table 7). This result might support the use of the same volume estimation algorithm for the measurement of volume in temporal scans. Algorithms tended to overestimate the volume of elliptical tumors and underestimate the volume of irregular tumors and tumors with low density. Examination of particular groups of nodules separated by size, shape, density, and slice thickness demonstrated bias similarly across all nodules, whether or not they met the QIBA Profile. Algorithm precision was more uniform for different nodule characteristics; however, precision was notably better as tumor size increased and worse for irregularly shaped tumors. Variability was drastically reduced for the subset of QIBA Profile nodules (RC: 9.0% for the QIBA Profile nodules vs 16.0% for all nodules). For the subgroup of nodules meeting the QIBA Profile, TDI₉₅ was found to be 26% (95% CI [18.6%, 33.9%]). For the entire collection of nodules, including smaller nodules, nodules with densities of −630 HU, and CT data with slice thickness >2.5 mm, we estimated TDI₉₅ to be 61.2% (95% CI [57.1%, 65.3%]. The results are in accordance with several previous studies (20–22).

Our study has several limitations. First, we assumed that the nodules were identical, regardless of their location in the thorax. The same phantom can be placed in various locations near the main bronchial tree or anthropomorphic vessel or the chest wall. Considering possible different artifacts of nodules based on the location in the thorax, our estimates of precision may tend to be higher than if the location had been controlled. Second, we were not able to study the effect of readers using the various algorithms; the effect of readers has been measured in other studies (13,14,23,24). Lastly and most importantly, although our phantom study attempted to consider the full range of tumor sizes, shapes, and densities seen in a clinical population, our study likely underestimated the precision when algorithms are applied to a clinical population.

CONCLUSIONS

Measurement algorithms were performed within a 15% RC for a wide range of tumor sizes, shapes, and densities. Eighty-four percent of volume measurements of QIBA-compliant tumors were within 15% of the true volume, ranging from 66% to 93% across algorithms. These results support the QIBA technical performance claims, as well as the primary hypothesis that quantitative performance claims for tumor volume may be met with a variety of heterogeneous measurement algorithms ranging from methods that allow post-segmentation editing to those that do not.