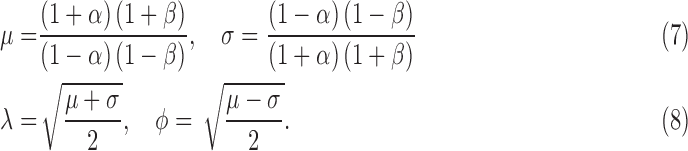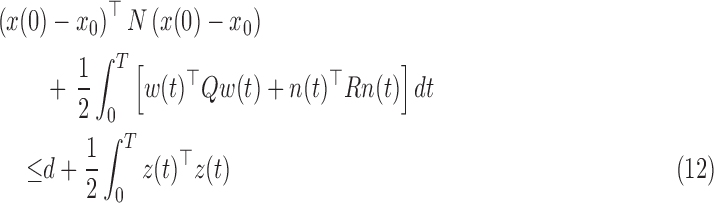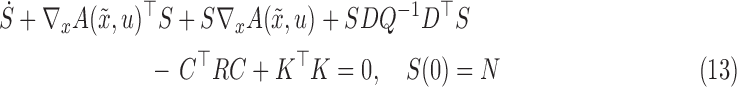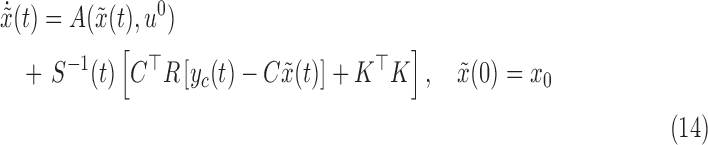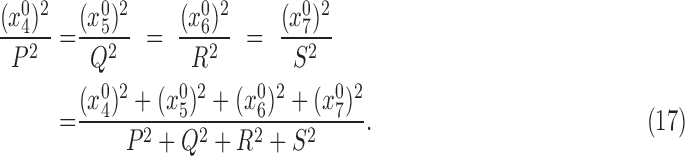Abstract
Wearable inertial measurement units (IMU) measuring acceleration, earth magnetic field, and gyroscopic measurements can be considered for capturing human skeletal postures in real time. Number of movement disorders require accurate and robust estimation of the human joint pose. Though these movements are inherently slow, the accuracy of estimation is vital as many subtle moment patterns, such as tremor are useful to capture under many assessments scenarios. Also, as the end user is a patient with movement disabilities, the practical wearability aspects impose stringent requirements such as the use of minimal number of sensors as well as positioning them in conformable areas of the human body; particularly for longer term monitoring. Estimating skeletal and limb orientations to describe human posture dynamically via model-based approaches poses numerous challenges. In this paper, we convey that the use of measurement conversion ideas-a representation signifying a linear characterization of an inherently non linear estimation problem, pragmatically improves the overall estimation of the limb orientation. A quaternion, as opposed to the Euler angle-based approach is adopted to avoid Gimbal lock scenarios. We also lay a systematic basis for quaternion normalization, typically performed in the pre-filtering stage, by introducing an optimization-based mathematical justification. A robust version of the extended Kalman filter is configured to amalgamate the underlying ideas in enhancing the overall system performance while providing a structured and a comprehensive approach to IMU-based real time human pose estimation problem, particularly in a movement disability capture context.
Keywords: Kalman filter, inertial sensor orientation
This paper presents a new approach to capturing human poses in real time using wearable sensors. The use of measurement conversion ideas, a representation signifying a linear characterization of an inherently non linear estimation problem, pragmatically improves the overall estimation of limb orientations.

I. Introduction
Capturing human pose in real time using wearable sensors is destined to have far-reaching consequences in many practical applications. These applications range from rehabilitation and long-term monitoring in the health care sector [1]–[3], performance evaluation and activity monitoring in sports, to motion capture in movie and gaming industries. Readily available IMU (Inertial Measurement Unit) sensors in an integrated and miniaturised form are considered to be strong candidates for the use in wearable sensors. Indeed, the problem of capturing human movement amounts to estimating the relative attitude of sensory (IMU) devices strategically positioned in different parts of the human body.
Remote health condition monitoring applications are becoming a part of everyday life due to the rapid increase in the aged population, rehabilitation programs for disabilities due to various neurological conditions extending to non-clinical and natural setting such as retirement villages. Stroke and Parkinson’s diseases are common neurological conditions that necessitate remote moment monitoring to provide quality medical care with an affordable cost [4] which is a major concern worldwide. The treatment of Stroke and the Parkinson’s patients require careful supervision of their recovering process through rehabilitation or physiological therapies. The common, yet expensive objective assessment method is measuring specific movements in special laboratories which are equipped with state of the art motion capture infrastructure requiring dedicated staff for operation. This indeed increases the cost of healthcare as well as patient travel to major centres for treatment. The lack of affordable and effective remote motion capture systems [4] enhanced the focus of inertial sensors as an reliable and robust form of Mo-Cap (Motion-Capturing) particularly in the wearable form due to their affordability and usability for long term monitoring. Mo-Cap systems wearing minimal number of sensors in comfortable places is a crucial aspect in any wearable system often not emphasised sufficiently by the designers. This indeed is to ensure uptake and facilitate the use of sensors in rehabilitation programs with meaningful and quantifiable outcomes. Such programs require easily wearable sensors by the disabled user. These aspects (disability and wearability) forms the basis of wearable sensor applications in disability managements and destined to play a major role in providing quality healthcare at an affordable cost for the average user. This inevitably presents a major challenge for the systems designer as the positioning of sensors as well as the number of sensors are crucial factors in enhancing the accuracy and the robustness of the measurement system. Therefore, the more sophisticated signal processing and feature extractions techniques needed to be considered to ensure the necessary estimation accuracies are achieved under these stringent requirements. When the orientation of the limb uniquely defines the attitude of the remaining joint positions, then a single sensor in the particular body part can be used to uniquely estimate the underlying posture of the limb and the adjoining limb under consideration. Consider the shoulder joint with three degrees of freedom and the elbow joint with one degree of freedom. The orientation of the elbow can uniquely determine the orientation of the shoulder. A single IMU sensor positioned on the elbow can therefore determine the attitude of the shoulder joint. This is indeed the case with the hipbone (three degrees of freedom) and the knee joint so that a IMU sensor positioned in the lower leg can determine the orientation of the upper leg. Indeed the clinical protocol surrounding the use of the underlying approach is based on the application. Accurate and robust estimation of joint pose can be vital in numerous applications and for certain joints. Here we concentrate on the crucial ideas of improving the accuracy and robustness using a single sensor and use the human shoulder joint as an example to convey the underlying approach.
Attitude determination of a moving platform with respect to a primary platform using common observation vectors in each coordinate system has a multitude of applications, particularly in the aerospace industry. These independent measurements can conventionally be unidirectional vectors to the stars, sun or the earth’s magnetic field. The attitude (rotation matrix) of a secondary coordinate frame is sought with respect to a primary coordinate frame using vector observations such as magnetometer and accelerometer readings captured in each frame. It is well-known that two measurements are sufficient to estimate the attitude [5] in this context. Almost all algorithms for estimating attitude from vector measurements are mathematically constructed as minimising a loss function that was proposed by Grace Wahba in 1965. Furthermore, non-linear relationships between observed directional cosine vectors are used to estimate the quaternion. The historical problem of identifying attitude using observed directional cosine vectors known as Wahba’s problem can be stated as optimizing a cost function in the following form:
 |
where  are measurements made in the moving frame,
are measurements made in the moving frame,  are the corresponding measurements made in the reference frame,
are the corresponding measurements made in the reference frame, 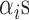 are the non negative weights and
are the non negative weights and 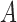 is a
is a 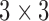 matrix which represents the rotation. The solutions to Wahba’s problem was originally introduced by Harold Black [6] and Paul Davenport in the form of the TRIAD method [7] and Davenport’s q method [5], [8] respectively. Unlike the TRIAD method, Davenport’s q method accounts for noise and for the first time, a quaternion representation was used as opposed to the traditional Euler angles. The QUEST algorithm and Singular Value Decomposition (SVD) method in [5] and [9] are mostly considered to be solutions to this problem. They are employed in a number applications, primarily due to computational efficiency of QUEST as a result of the quaternion representation. Additionally, SVD uses Euler angles to directly produce the rotation matrix, although the gimbal lock can be an impediment. Subsequently, the Estimator of the Optimal Quaternion (ESOQ) method is derived from the QUEST algorithm with improved computational cost.
matrix which represents the rotation. The solutions to Wahba’s problem was originally introduced by Harold Black [6] and Paul Davenport in the form of the TRIAD method [7] and Davenport’s q method [5], [8] respectively. Unlike the TRIAD method, Davenport’s q method accounts for noise and for the first time, a quaternion representation was used as opposed to the traditional Euler angles. The QUEST algorithm and Singular Value Decomposition (SVD) method in [5] and [9] are mostly considered to be solutions to this problem. They are employed in a number applications, primarily due to computational efficiency of QUEST as a result of the quaternion representation. Additionally, SVD uses Euler angles to directly produce the rotation matrix, although the gimbal lock can be an impediment. Subsequently, the Estimator of the Optimal Quaternion (ESOQ) method is derived from the QUEST algorithm with improved computational cost.
Magnetic Angular Rates and Gravity (MARG) sensor array based systems [10] generally uses quaternion based representation when minimising the gyroscopic drift via an analytically derived and optimized gradient descent algorithm on accelerometer and magnetometer data. Indeed, the availability and affordability of MARG sensors with integrated wireless communication capabilities have triggered plethora of research and development activities aimed at number of wearable applications in the recent times.
With 278 joints and 308 bones, capturing the highly flexible human pose is a challenge. Naturally ignoring inflexible fibrous joints, relatively flexible cartilaginous joints and highly flexible synovial joints allow complex movements in the human body. Usually, human motion is identified through carefully analysing spatial reconstruction, trajectory tracking, joint angle determination and derivative computation [11], [12]. Deviation from ideal sensor behaviour due to external interferences and noise reduces the accuracy of the determination of human kinematic components [13], [14].
In general, the orientation of the sensor attached to the human limb is calculated with respect to the reference frame. As the earth’s magnetic field measurements are adversely affected by surrounding magnetic disturbances (power lines and other electrical equipment), filters and model based estimators, such as Kalman filter [5], [15], Complementary filters [16] are considered in many applications to address this issue. The extended Kalman Filter with the QUEST algorithm based approach was used for real time monitoring of human arm movements [17]. The complementary filter minimises the effect of gyroscopic drift with the use of acceleration or magnetic orientation, even though the integration of angular rates in a longer time frame may cause a significant drift where the complementary filter is not able to overcome. Robust Extended Kalman Filter (REKF) [18], [19] is preferred for accounting for large uncertainties involved in system inputs. REKF characteristically assumes a relatively generic uncertainty description and evidently caters for larger variations, particularly when the initialization uncertainties are significant [15], [20]. However, filter parameter tuning is required to achieve estimator convergence with realtime movement tracking [21]. With certain mathematical models, converted measurement approach [20], [22] has been used to obtain a stronger linear formulations. But, this has not been the case for IMU based modelling and even in [17], the non-linear measurement equation is linearized with a first order approximation similar to Extended Kalman filtering in the estimation process. This form of linearizations, particularly in systems with large uncertainties, are known for accumulation of errors and in certain instances the state estimation can potentially diverge. Therefore, in this paper we use a linear formulation for inherently non- linear IMU measurements exploiting the strength in linear systems theory.
Furthermore, as normalization is required for recursive quaternion use [21], [23], an optimization phase is required to further enhance the robustness of the overall approach. The main contributions of this paper are as follows:
-
1)
A converted measurement based approach [20], [22] for addressing an inherently non-linear problem in a linear context to improve the accuracy and reduce the estimator divergence in human movement capturing context.
-
2)
A theoretical justification for normalization of quaternions necessary for recursive model based estimators such as Kalman filtering.
II. Dynamic Model
Superior performance in dynamic model based estimators provides a natural choice for human pose estimation. Dynamic model which facilitates parameter estimation in a rotating and translating frame is crucial while the model can gradually be made sophisticated incorporating full body human bio-kinematic modelling. In this work we use a standard kinematic model to highlight the key contributions of this work. In the proposed algorithm, a quaternion based approach is preferred as it eliminates the need for using trigonometric functions [24] avoiding singularities and gimble lock associated complexities inherent to Euler angle based representations.
Denoting the orientation quaternion in the reference coordinate frame as 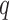 , angular velocity
, angular velocity 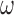 , we state the following equation [17],
, we state the following equation [17],
 |
where, 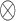 denotes the quaternion multiplication with
denotes the quaternion multiplication with 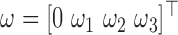 used as a pure quaternion. The gyro drift occurs due to accumulating the white noises of gyroscope readings [10]. Defining the state vector as
used as a pure quaternion. The gyro drift occurs due to accumulating the white noises of gyroscope readings [10]. Defining the state vector as 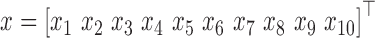 where the
where the  ,
, 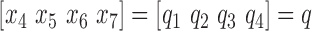 and
and 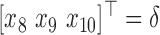 where,
where, 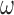 ,
,  and
and  are angular rates, quaternions and gyro drift respectively, we can state the dynamic model as,
are angular rates, quaternions and gyro drift respectively, we can state the dynamic model as,
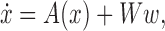 |
where
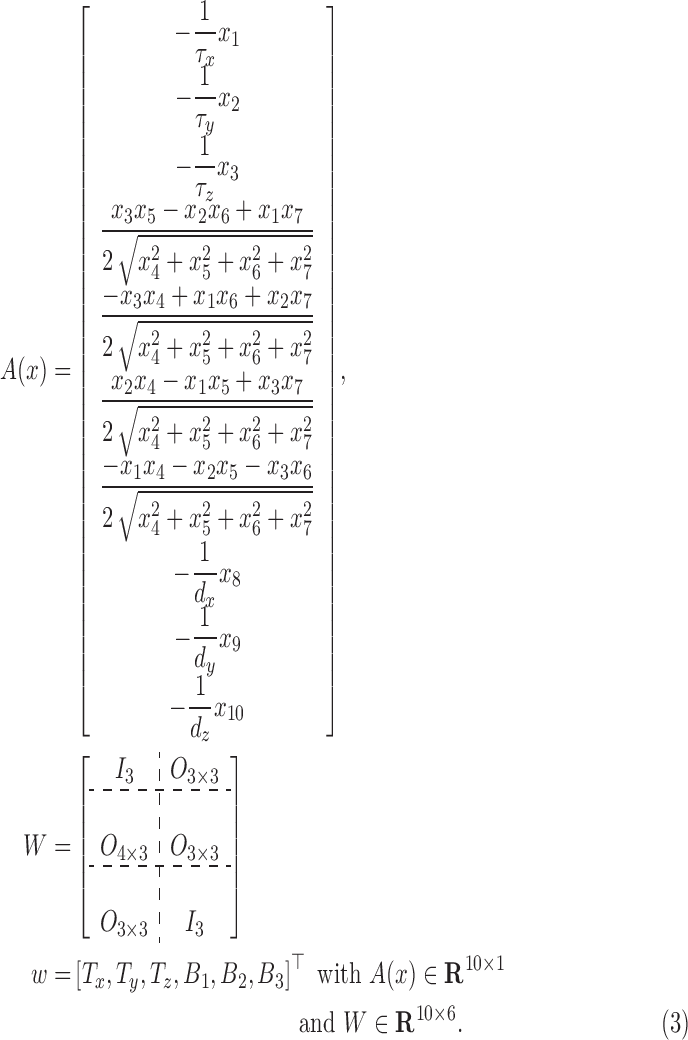 |
Here, 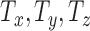 indicate the torque due to uncertain human movements and
indicate the torque due to uncertain human movements and  indicate the uncertainty in the bias responsible for the Gyroscopic drift.
indicate the uncertainty in the bias responsible for the Gyroscopic drift. 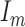 and
and  denotes identity and zero matrix of appropriate dimensions. The measurement model can be stated as follows:
denotes identity and zero matrix of appropriate dimensions. The measurement model can be stated as follows:
 |
where 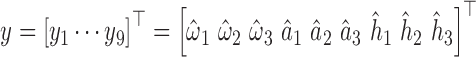 , is the IMU measurement vector with angular rate from gyroscopes, acceleration from accelerometers and orientation of the earth magnetic field from magnetometers. Here,
, is the IMU measurement vector with angular rate from gyroscopes, acceleration from accelerometers and orientation of the earth magnetic field from magnetometers. Here, 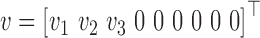 is the measurement noise. Further, the time constant for the motion and variance of continuous white noise is denoted respectively by
is the measurement noise. Further, the time constant for the motion and variance of continuous white noise is denoted respectively by  and
and  [25]. Here
[25]. Here
 |
Let the measurement in the reference frame have 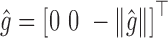 and
and  acceleration and magnetometer readings respectively.
acceleration and magnetometer readings respectively.
Remark 1:
Without the loss of generality we have aligned the
axis of the stationary reference co-ordinate frame in a perpendicular direction to the magnetic direction to simplify the resulting expressions.
The dynamic model and and the associated measurement model given by equation 3 and 4 respectively provides a complete non-linear dynamic description for the sensor motion and the associated measurements.
Now we are in the position to employ the converted measurement approach [20], [22] to the underlying measurement model to obtain a converted linear formulation. Therefore referring to equation 4, we have a unique solution(computed quaternion) given by,
 |
where
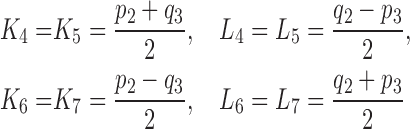 |
with
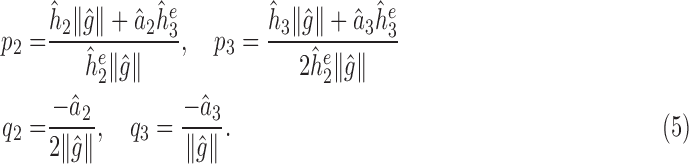 |
Considering the measurement uncertainty, let the measurement model for the converted measurements with respect to magnetometer and accelerometer measurements be:
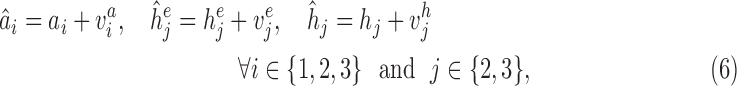 |
where, 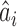 ,
, 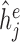 and
and  indicates the accelerometer readings subjected to measurement noise (
indicates the accelerometer readings subjected to measurement noise (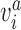 ) and magnetometer measurement subjected to measurement noise (
) and magnetometer measurement subjected to measurement noise (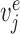 and
and 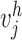 ) in the reference frame and the mobile frame respectively. The error bounds are described in the following form:
) in the reference frame and the mobile frame respectively. The error bounds are described in the following form:
Assumption 1:
The following holds 1 For given constants
and
, let
,
and
and
. In the case of converted measurements, let’s define the following:
Now we can state the converted measurement as,
where
Denoting
the converted measurement model corresponding to the non-linear measurement model in equation 4 can be stated in the linear form of
, where
,
.
III. Robust Non Linear Filtering
Consider nonlinear uncertain systems of the form,
 |
defined on 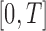 with
with 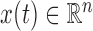 denoting the state of the system and
denoting the state of the system and 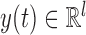 the measurements vector. Further,
the measurements vector. Further,  denote the uncertainty output and the uncertainty inputs respectively.
denote the uncertainty output and the uncertainty inputs respectively.
Assumption 2:
Introduce the following Riccati Differential Equation(RDE)
Then the state propagation is given by,
The reference frame is oriented with the following assumptions.
Remark 2:
Notice here that there is a significant component of the earth’s magnetic field in the
direction in Australia and this cannot be neglected unlike in the case of locations close to the equator.
A. Robustness of the Estimation
The approximate solution for the set of estimated states for the robust set valued state estimation is:
 |
where
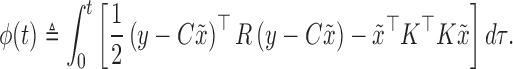 |
Therefore, the centroid of the ellipsoidal set is taken as the estimated state. Let  and
and 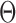 denote the diagonalising and the resulting diagonal matrix respectively while
denote the diagonalising and the resulting diagonal matrix respectively while  and
and 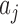 denote the spectral densities of
denote the spectral densities of  and
and 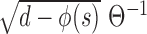 respectively. Taking,
respectively. Taking,  and
and  and noticing
and noticing 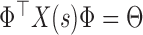 ,
,  and
and  indicate the major axis and the minor axis of the set values state estimation. This provides a measure of the estimation bounds.
indicate the major axis and the minor axis of the set values state estimation. This provides a measure of the estimation bounds.
IV. Robust Optimization Based Approach for Orientation Estimation
The  and
and 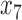 of the state vector denotes the orientation quaternion. The computed quaternions via measurement conversion do not necessarily results in satisfying the quaternion norm requirements due measurement noise and uncertainties. Therefore, we consider a constraint based optimizations approach to ensure the quaternion meet the norm conditions, robust and optimal in a quadratic context. We consider the computed quaternions
of the state vector denotes the orientation quaternion. The computed quaternions via measurement conversion do not necessarily results in satisfying the quaternion norm requirements due measurement noise and uncertainties. Therefore, we consider a constraint based optimizations approach to ensure the quaternion meet the norm conditions, robust and optimal in a quadratic context. We consider the computed quaternions  as
as 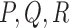 , and
, and  respectively for the following derivation. With
respectively for the following derivation. With 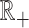 denoting the set of non-negative real numbers, define,
denoting the set of non-negative real numbers, define,
 |
Now we can state the following lemma
Lemma 1:
The solution to the following problem of,
can be stated as follows:
- 1
If
then
is the optimal solution.
- 2
if
then optimal value of
is:
- 3
if
then optimal value of
is:
- 4
Else the optimal value of
is:
.
Proof:
From lemma 3 and 4, we see that if
is an optimal point of problem
, then it also is an optimal point of problem
. Therefore, to solve problem
, we only need to find an optimal point
for problem
. For
, we denote the
-level set for linear functional
as,
. Clearly,
are parallel hyperplanes. Therefore, if
is a supporting hyperplane of the convex set
at
then
is an optimal point and
is the optimal value of problem
. Similar to the proof of lemma 3, if
belongs to one of five sets
then one of four points
,
,
,
is an optimal point of problem
. On the other hand,
is a supporting hyperplane of the convex set
at
if
(for case
.) In this case, (16) implies that
If
then by using the definition of
, we have an unique solution that belongs to
of (16) is
. This indeed is predominantly applicable to the context of our application and hence the optimal value for the quaternion almost always results in
. If
then by using by using the definition of
we have a unique solution that belong to
of (16) is
. Note that if
or
or
or
then we conclude
,
,
,
, respectively. Otherwise (16) has no solution belonging to
.
V. Implementation of the Orientation Estimation
The process of pre filtering is to ensure the frequency bounded noise is filtered out via simple low pass filtering. Using the empirical knowledge, we set the bandwidth of the low pass filters. We use the converted measurement as raw estimates for the linear robust Kalman filter while standard extended Kalman filtering and also the Robust Extended Kalman filtering use the raw measurements when evaluating the performance of the estimators. Indeed, all these use the optimization framework we mathematically justified, to ensure that the standard quarternion constraints are met. As depicted in Figure 2, in the first step, the converted measurement approach is used to compute the quaternion using the magnetometer (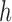 ) and the accelerometer readings (
) and the accelerometer readings (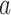 ). The magnetometer readings suffers scaling errors and offset biases. The errors are indeed device specific and hence the normalized readings were used to calculate the quaternions.
). The magnetometer readings suffers scaling errors and offset biases. The errors are indeed device specific and hence the normalized readings were used to calculate the quaternions.
FIGURE 1.

Wahba’s problem.
FIGURE 2.
Block diagram of the algorithm.
A. Extended Kalman Filter Based Approach
The non-linear dynamic and measurement model described in equations 3 and 4 respectively are used in the standard extended Kalman filter implementation.
 |
Numerical values of  and
and  are evaluated as given in [17].
are evaluated as given in [17].
B. Robust Extended Kalman Filter Implementation
The non-linear dynamic and measurement model described in equations 3 and 11 respectively are used under the norm bounded uncertainty assumption given in inequality 12.
C. Robust Extended Kalman Filter With Linear Measurements
The non-linear dynamic and measurement model described in equations 3 and 11 respectively are used under the norm bounded uncertainty assumption given in inequality 12. The non-linear measurement model given in equation 4 is converted to the underlying linear form with the measurement assumptions in 6 resulting in 11. The quaternions obtained in equation 5 as converted measurements are in fact considered as time wise observation in the linear measurement model in equation 11. Hence the measurement vector can be updated as  with the angular rates from gyroscopes, accelerations from accelerometers, orientation of the earth’s magnetic field from magnetometers and the measurement converted quaternions from equation 5. Furthermore, the time constants for the motion and variance of continuous white noise are denoted by
with the angular rates from gyroscopes, accelerations from accelerometers, orientation of the earth’s magnetic field from magnetometers and the measurement converted quaternions from equation 5. Furthermore, the time constants for the motion and variance of continuous white noise are denoted by  and
and 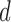 respectively.
respectively.
VI. Computer Simulations
Two hypothetical scenarios were considered to validate the underlying assertions by employing torque 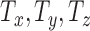 , and time constants
, and time constants  in the respective cartesian axes to emulate the relevant kinematics of the human arm. The torque gradually increases while the arm is being lifted then is kept constant prior to reducing to the resting state which corresponds to the upright position. Gyroscope, accelerometer and magnetometer readings were captured as the simulated kinematics using equation 3, 4 and 5. The resulting measurements were used with different estimators; Extended Kalman Filter (EKF), Robust Extended Kalman Filter (REKF) and Robust Extended Kalman Filter with Linear Measurements (REKFLM) for real time estimation of the arm orientation. The Figure 4 shows the actual angle variation with time and the estimated angle variation from each of the algorithms simultaneously for this hypothetical scenario. Notably, the shoulder pitch, yaw and roll angles deduced from the estimated state is the same for each algorithm compared to the simulated actual angles when the uncertainty is low. However when the gyroscopic bias uncertainty (
in the respective cartesian axes to emulate the relevant kinematics of the human arm. The torque gradually increases while the arm is being lifted then is kept constant prior to reducing to the resting state which corresponds to the upright position. Gyroscope, accelerometer and magnetometer readings were captured as the simulated kinematics using equation 3, 4 and 5. The resulting measurements were used with different estimators; Extended Kalman Filter (EKF), Robust Extended Kalman Filter (REKF) and Robust Extended Kalman Filter with Linear Measurements (REKFLM) for real time estimation of the arm orientation. The Figure 4 shows the actual angle variation with time and the estimated angle variation from each of the algorithms simultaneously for this hypothetical scenario. Notably, the shoulder pitch, yaw and roll angles deduced from the estimated state is the same for each algorithm compared to the simulated actual angles when the uncertainty is low. However when the gyroscopic bias uncertainty (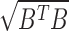 ) where
) where  and
and  and
and 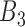 are taken as identical with at 0.00005 increments from 0.00001. The estimation error is increased significantly as depicted in Figure 3. Further, Gaussian noise was introduced to the generated measurements to validate the robustness of each algorithm under measurement noise uncertainty. The signal to noise ratio between 60 dB to 20 dB was introduced to the simulated accelerometer, magnetometer and gyroscope readings with the kinematic model parameters of
are taken as identical with at 0.00005 increments from 0.00001. The estimation error is increased significantly as depicted in Figure 3. Further, Gaussian noise was introduced to the generated measurements to validate the robustness of each algorithm under measurement noise uncertainty. The signal to noise ratio between 60 dB to 20 dB was introduced to the simulated accelerometer, magnetometer and gyroscope readings with the kinematic model parameters of 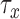 ,
,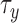 and
and 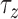 set to
set to 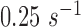 and
and 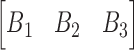 set to
set to 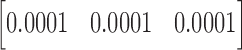 . The second simulation is designed to investigate the optimization algorithm discussed in section IV. Unlike the previous case, the estimated quaternion (
. The second simulation is designed to investigate the optimization algorithm discussed in section IV. Unlike the previous case, the estimated quaternion ( ), prior to using as input to the estimator, is optimized using the proposed algorithm. Indeed it is the standard practice to normalize the quaternion and here we establish a mathematical justification to this process. The model parameters such as time constant and uncertainty constant are the same as they were for the first simulation. Gaussian noise (60 dB - 20 dB Signal-to-noise ratios) was introduced to gyroscope, magnetometer and accelerometer readings in the first simulation.
), prior to using as input to the estimator, is optimized using the proposed algorithm. Indeed it is the standard practice to normalize the quaternion and here we establish a mathematical justification to this process. The model parameters such as time constant and uncertainty constant are the same as they were for the first simulation. Gaussian noise (60 dB - 20 dB Signal-to-noise ratios) was introduced to gyroscope, magnetometer and accelerometer readings in the first simulation.
FIGURE 4.
RMSE of the estimated angle.
FIGURE 3.
The error in estimated angle with against the uncertainty bias (BTB).
VII. Experimental Setup
An inertial measurement sensor in an integrated system with wireless communication was positioned on the wrist of the subject in order to capture the movement of the shoulder joint. The experiments were conducted at Deakin University, Australia under the ethics approval, STEC-07-2015-MADDUMAGE, Human Ethics Advisory Group at Deakin University Australia. Only one wearable sensor was used for the experiment to highlight the crucial requirement of engaging the smallest number of sensors. People with disabilities are usually reluctant to wear number of sensors because it is inconvenient to engage in their day-to-day activities wearing several medical accessories [29]. Hence, we maintained the minimal sensor usage to ensure the comfort and facilitate the uptake.
The scapular movements for identifying normal and abnormal movements based on 3-dimensional measurements are described in [30], [31]. Rotational motion of the scapula with respect to the thorax was described on the basis of a Euler angle sequence of external/ internal rotation (ZS axis), upward/downward rotation (YS axis), and posterior/anterior tilting (XS axis). In our experiment, we have recorded and investigated shoulder movements in under these three common movement scenarios present in multitude of shoulder movement related disabilities: upward/downward rotation (YS axis) in sagittal plane, and posterior/anterior tilting (XS axis) in coronal plane and horizontal rotation in transverse plane (ZS axis). These exercises essentially represent flexion-extension, abduction-adduction and internal-external rotation which commonly used in the examination of shoulder and arm motor functionality using inertial sensors [17], [32]. Typically they are conducted in the bio-kinematic laboratories or under clinical scenarios to assess motor functionality of the shoulder as a subjective assessment for performing day-to-day activities such as lifting a bottle of water or placing a book on a shelf [33], [34] etc.
The validation of the underlying algorithms was conducted through data captured from ten healthy subjects (eight males and two females) using VICON optical system and four healthy subjects (two males and two females) using a Kinect©optical system without any history of joint or muscle impairments. We used VICON system as the benchmark in ascertaining the accuracy of our method. Furthermore, our system was compared with the Kinect© system as a low cost alternative in electro-optical sensing. Each subject was asked to do three simple exercises:
-
1)
Lifting the arm in front of the body by
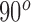 (Forward Flexion-Extension as sub-figures 7-(A) and 7-(B))
(Forward Flexion-Extension as sub-figures 7-(A) and 7-(B)) -
2)
Lifting the arm along the side of the body (Abduction-Adduction as sub-figures 7-(A) and 7-(C)) and
-
3)
Lifting the arm to the back of the body (Backward Flexion-Extension as sub-figures 7-(A) and 7-(D)).
FIGURE 7.
Experiment Setup and Procedure: sensor and marker worn on the wrist, images taken with consent.
Each exercise was repeated three times over approximately 10 minutes with the inertial sensor worn on the distal left arm. The experiment setup is shown in Figure 7. The exercise routines were recorded using VICON optical motion capture system (VICON T40S System) and a Microsoft Kinect© system separately.
Despite of these exercises, the five subjects were employed to conduct horizontal flexion and extension in front of VICON optical motion capture system. These subjects were asked to swing the whole arm by the shoulder. These exercises were repeated three times over approximately 10 minutes with the inertial sensor worn on the distal left arm. The subject is in the orthostatic position with the sensor frames and reference frames are approximately aligned initially. In the underlying formulation, the torques are considered to be uncertainty inputs and the time constants are determined inline with the prior computer simulations discussed in VI.
VIII. Results and Discussion
A. Computer Simulations
The Root Mean Squared Error (RMSE) was plotted in Figure 5 for the three estimators considered; EKF, REKF and REKFLM with the subjected (60dB - 20dB) noise levels. Irrespective of engaging optimized quaternion (section IV), the RMSE was less for REKFLM. This is particularly observable when the uncertainties are significant. Indeed the filter accuracy in estimating the rotation angle improved when the noise level reduced from 20dB to 60dB. The error in EKF increased markedly and the error in REKF was exaggerated compared to the REKFLM. In all the estimation algorithms considered, quaternion optimization had a positive yet reduced impact on lower noise levels (50dB – 60dB) on the angle estimation accuracy unlike for larger noise levels (20dB – 30dB). Indeed the superior estimation accuracy in the Robust Extended Kalman filter with Linear Measurements (REKFLM) is further enhanced with the use of quaternion optimization as depicted in Figure 5. As shown in Figure 6, quaternion optimization resulted in an approximately 30% RMSE improvement in the EKF implementation when the SNR is 20 dB, in addition to a more prominent improvement when the SNR was between 28 dB to 20 dB. In contrast, RMSE improvement in the REKF implantation was 42% when the SNR is 20 dB with noticeable improvements in the 20–30 dB noise range. The RMSE improvement in REKFLM due to quaternion optimization was relatively less in comparison to the other two algorithms; approximately 9% improvement when the SNR is 20 dB. REKFLM outperforms the other estimators albeit all approaches proclaim the benefit of quaternion optimization to varying degrees.
FIGURE 5.
The RMSE subjected to introduced noise.
FIGURE 6.
Percentage improvement due to quaternion optimization.
B. Experiment
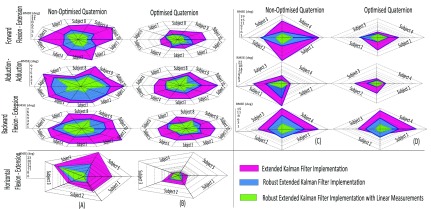
Figure 4 shows the RMSE in the estimated shoulder movement angles for the simple exercise of forward extension, when the movement replicated the execution in a simulated environment. Here the physical movement were carried out as close as possible to the simulated movement and the IMU measurements were then used to estimate the actual angle turned. The arm motion was along a planar trajectory in order to ensure minimal system complexity. This allowed the primary focus to be the assessment of the underlying filtering algorithms. This indeed avoided more complex torques necessary to generate arbitrary trajectories generally experienced in reality. Figure 8 shows the estimated angle (roll angle) difference compared to VICON optical system for the same exercise. Here, Figure (a) and (b) show the RMSE in the corresponding angle differences optimized and non-optimized quaternions respectively. Angles derived from REKFLM were similar to the angles measured from the VICON system irrespective of the engagement of quaternion optimizations (see Figure 8). Quaternion optimization markedly improved each estimation algorithm, reducing the angle estimation error significantly. Table 1 lists the average RMSE for three exercises (Forward Flexion-Extension, Abduction-Adduction and Backward Flexion-Extension) when IMU measurements were compared to both Kinect© and VICON systems. The graph in Figure 9 shows the performance, in terms of RMSE, of each algorithm. Figure (A) and (B) show the RMSE over ten healthy subjects with respect to VICON measurements. Figure (C) and (D) show the RMSE over four healthy subject with respect to Kinect© optical system. Similar to computer simulations, the EKF and REKFLM were the least and most accurate algorithms respectively. Figures (B) and (D) in Figure 9 depict improvement, in terms of RMSE and with respect to VICON and Kinect measurements, due to the engagement of quaternion optimization for each filter and subject respectively. As depicted in table 1, the averaged RMSE with respect to Kinect© when using EKF was reduced by 43%, 34% and 10% for the three exercises respectively due to quaternion optimization while the averaged RMSE in EKF algorithm was reduced by 36%, 21%, and 19% with respect to VICON optical system. For the case of REKF accuracy improved by 47%,49% and 14% with respect to Kinect© system and 30%, 38% and 24% with respect to VICON optical system across the aforementioned exercises. This result implies that the accuracy in EKF and REKF methods improved significantly due to quaternion optimization yet the accuracy of REKFLM algorithm improved by about 14%, 23% and 21% respectively for the above exercises with the Kinect© system. Accuracy of the REKFLM approach was improved by 20%, 21% and 7% for forward Flexion âĂŞ Extension exercise, Abduction âĂŞ Adduction exercise and Backward Flexion-Extension exercise respectively compared to VICON optical system when engaged with quaternion optimization. Further, the accuracies in EKF, REKF and REKFLM were improved by 60%, 56% and 43% for Horizontal Flexion - Extension due to quaternion optimization. We notice that, generally, REKFLM algorithm outperforms EKF and REKF. Furthermore, quaternion optimization significantly improves the state estimation irrespective of the estimator. Further, our proposed estimator was compared with two commonly using approaches: Extended Kalman filter proposed by Bachman et al. and the Madgwick algorithm [11]. The maximum error with respect to an optical system expressed by the EKF during an extension-flexion arm exercise was 9° as described in [17] while the Madgwick algorithm expressed 7° [10]. The error of our proposed robust extended Kalman filter with liner measurements (REKFLM) was less than 3° outperforming the Madgwick algorithm and extended Kalman filter (Table 1).
FIGURE 8.
RMSE in angle estimation for forward extension exercise in comparison to vicon optical system.
TABLE 1. Averaged RMSE Error in Angle Estimation for Arm Exercises in Comparison to Kinect© and VICON System Based Measurements.
| Averaged RMSE of Non- Optimization Quaternion | Averaged RMSE of Optimized Quaternion | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Compared to Kinect© Optical System | Compared to VICON Optical System | Compared to Kinect© Optical System | Compared to VICON Optical System | |||||||||
| EKF | REKF | REKFLM | EKF | REKF | REKFLM | EKF | REKF | REKFLM | EKF | REKF | REKFLM | |
| Forward Flexion-Extension | 14.76° | 9.35° | 4.08° | 8.42° | 4.77° | 2.81° | 8.46° | 5.00° | 3.51° | 5.22° | 3.29° | 2.25° |
| Abduction-Adduction | 11.80° | 7.12° | 3.99° | 6.77° | 5.35° | 3.04° | 7.75° | 3.61° | 3.08° | 5.29° | 3.26° | 2.38° |
| Backward Flexion- Extension | 9.29° | 6.70° | 3.02° | 5.18° | 3.32 | 2.15° | 8.45° | 5.75° | 2.39° | 4.14° | 2.51° | 2.01° |
| Horizontal Flexion- Extension | — | — | — | 15.32° | 8.32° | 5.48° | — | — | — | 6.08° | 3.67° | 3.13° |
FIGURE 9.
Filter performance comparison: angle estimation error (RMS) for the upper arm exercises. (A) and (B) - with respect to VICON optical system, (C) and (D) - with respect to Kinect© optical System.
IX. Conclusion
It has been demonstrated that adopting a linear formulation in the measurement scheme provides improved results for real time human kinematic movement estimation as opposed to the standard approach involving extended Kalman filtering or even robust version of extended Kalman filtering. The measurement conversion based linear approach does, in fact, result in improved estimation accuracy. Indeed, the Quaternion normalization improved the estimation accuracy of all estimators in general and the mathematical verification of the process completes the justification of the current practice in place. Although there is relatively less improvement due to quaternion estimation for the converted measurement Kalman filtering, the proposed approach still outperforms traditional approaches. These assertions have been verified by computer simulations as well as hardware experimentation.
Supplementary Material
IMU Sensor Dataset for human joint pose analysis
38KB
Windows
This paper presents a new approach to capturing human poses in real time using wearable sensors. The use of measurement conversion ideas, a representation signifying a linear characterization of an inherently non linear estimation problem, pragmatically improves the overall estimation of limb orientations.

Appendix
Consider the following optimization problems:
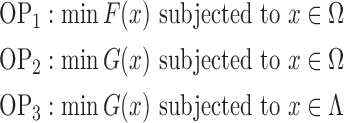 |
Lemma 2:
Consider the problem OP3. Assuming that
is an optimal point of the problem and two points
. If there exists a real number
such that
then
and
are also optimal points.
Proof:
Since
is an optimal point of problem and
, we have
and
. If
is not an optimal point of problem
then
. By linearity of functional
, we have
This is a contradiction. Thus,
is an optimal point. Similarly, we also prove that
is an optimal point.
Lemma 3:
Problem OP3 has at least an optimal point which belong to
.
Proof:
From lemma 2, we can imply that problem
has a optimal point
which belongs to boundary of
. It means that
. Note that
,
and
Therefore, if
then there is an index
such that
. Without loss of generality, we assume that
. By using lemma 2, we can implies that one of three points
,
and
must be an optimal point. It means that problem
has at least an optimal point belonging to
. Now let’s recall the definition of equivalence of optimization problems as given in [35] as follows:
Definition:
Two optimization problems are equivalent if from a solution of one, a solution of the other is readily found and vice versa.
Lemma 4:
The problems are equivalent
Proof:
By expanding functional
and using the constraint
, we can see that
. This implies that if
is an optimal point of problem
then it is also an optimal point of problem
and vice versa. Therefore, problem
is equivalent to problem
. On the other hand, it is easy to see that if
is an optimal point of problem
then it also is an an optimal point of problem
. Note that in the case
then we can using lemma 3 to find another optimal point
. Certainly, this point
is an optimal point of problem
. The rest of the proof is to prove the converse. It means that if
is an optimal point of problem
then we must prove that it also is an optimal point of problem
. If we assume that
is not an optimal point of problem
then there is another point
such that
. By lemma 3, there exist
such that
. This implies that
. This contradicts with that
is an optimal point of problem
. Therefore,
must be an optimal point of problem
. The proof of lemma 4 is completed.
References
- [1].Dowling A. V., Barzilay O., Lombrozo Y., and Wolf A., “An adaptive home-use robotic rehabilitation system for the upper body,” IEEE J. Transl. Eng. Health Med., vol. 2, 2014, Art. no. 2100310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Lee H., Rouse E. J., and Krebs H. I., “Summary of human ankle mechanical impedance during walking,” IEEE J. Transl. Eng. Health Med., vol. 4, 2016, Art. no. 2100407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Nambiar S., Nikolaev A., Greene M., Cavuoto L., and Bisantz A., “Low-cost sensor system design for in-home physical activity tracking,” IEEE J. Transl. Eng. Health Med., vol. 4, 2016, Art. no. 2800806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Bakhai A., “The burden of coronary, cerebrovascular and peripheral arterial disease,” J. Pharmacoeconomics, vol. 22, no. 4, pp. 11–18, 2004. [DOI] [PubMed] [Google Scholar]
- [5].Markley F. L. and Mortari D., “Quaternion attitude estimation using vector observations,” J. Astron. Sci., vol. 48, no. 2, pp. 359–380, 2000. [Google Scholar]
- [6].Black H. D., “A passive system for determining the attitude of a satellite,” AIAA J., vol. 2, no. 7, pp. 1350–1351, 1964. [Google Scholar]
- [7].Black H. D., “Early development of transit, the navy navigation satellite system,” J. Guid., Control, Dyn., vol. 13, no. 4, pp. 577–585, 1990. [Google Scholar]
- [8].Shuster M. D., “A survey of attitude representations,” Navigation, vol. 8, no. 9, pp. 439–517, 1993. [Google Scholar]
- [9].Shuster M. D., “Approximate algorithms for fast optimal attitude computation,” in Proc. AIAA Guid. Control Conf., New York, NY, USA, 1978, pp. 88–95. [Google Scholar]
- [10].Madgwick S. O. H., Harrison A. J. L., and Vaidyanathan R., “Estimation of IMU and MARG orientation using a gradient descent algorithm,” in Proc. IEEE Int. Conf. Rehabil. Robot. (ICORR), Jun./Jul. 2011, pp. 1–7. [DOI] [PubMed] [Google Scholar]
- [11].Rajagopal A., Dembia C. L., DeMers M. S., Delp D. D., Hicks J. L., and Delp S. L., “Full-body musculoskeletal model for muscle-driven simulation of human gait,” IEEE Trans. Biomed. Eng., vol. 63, no. 10, pp. 2068–2079, Oct. 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Pani D.et al. , “A device for local or remote monitoring of hand rehabilitation sessions for rheumatic patients,” IEEE J. Transl. Eng. Health Med., vol. 2, 2014, Art. no. 2100111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Ligorio G. and Sabatini A. M., “A novel Kalman filter for human motion tracking with an inertial-based dynamic inclinometer,” IEEE Trans. Biomed. Eng., vol. 62, no. 8, pp. 2033–2043, Aug. 2015. [DOI] [PubMed] [Google Scholar]
- [14].Sabatini A. M., “Quaternion-based extended Kalman filter for determining orientation by inertial and magnetic sensing,” IEEE Trans. Biomed. Eng., vol. 53, no. 7, pp. 1346–1356, Jul. 2006. [DOI] [PubMed] [Google Scholar]
- [15].Lefferts E. J., Markley F. L., and Shuster M. D., “Kalman filtering for spacecraft attitude estimation,” J. Guid., Control, Dyn., vol. 5, no. 5, pp. 417–429, 1982. [Google Scholar]
- [16].Calusdian J., Yun X., and Bachmann E., “Adaptive-gain complementary filter of inertial and magnetic data for orientation estimation,” in Proc. IEEE Int. Conf. Robot. Autom. (ICRA), May 2011, pp. 1916–1922. [Google Scholar]
- [17].Yun X. and Bachmann E. R., “Design, implementation, and experimental results of a quaternion-based Kalman filter for human body motion tracking,” IEEE Trans. Robot., vol. 22, no. 6, pp. 1216–1227, Dec. 2006. [Google Scholar]
- [18].Petersen I. R. and Savkin A. V., Robust Kalman Filtering for Signals and Systems With Large Uncertainties. Springer, 1999. [Google Scholar]
- [19].Savkin A. V. and Petersen I. R., “Robust state estimation and model validation for discrete-time uncertain systems with a deterministic description of noise and uncertainty,” Automatica, vol. 34, no. 2, pp. 271–274, 1998. [Google Scholar]
- [20].Pathirana P. N., Li S., Trinh H. M., and Seneviratne A., “Robust real-time bio-kinematic movement tracking using multiple kinects for tele-rehabilitation,” IEEE Trans. Ind. Electron., vol. 63, no. 3, pp. 1822–1833, Mar. 2016. [Google Scholar]
- [21].Bar-Itzhack I. Y. and Oshman Y., “Attitude determination from vector observations: Quaternion estimation,” IEEE Trans. Aerosp. Electron. Syst., vol. AES-21, no. 1, pp. 128–136, Jan. 1985. [Google Scholar]
- [22].Pathirana P. N., Herath S. C. K., and Savkin A. V., “Multitarget tracking via space transformations using a single frequency continuous wave radar,” IEEE Trans. Signal Process., vol. 60, no. 10, pp. 5217–5229, Oct. 2012. [Google Scholar]
- [23].Bar-itzhack I. Y., “Optimum normalization of a computed quaternion of rotation,” IEEE Trans. Aerosp. Electron. Syst., vol. AES-7, no. 2, pp. 401–402, Mar. 1971. [Google Scholar]
- [24].Shuster M. D. and Oh S. D., “Three-axis attitude determination from vector observations,” J. Guid. Control, Dyn., vol. 4, no. 1, pp. 70–77, 1981, doi: 10.2514/3.19717. [DOI] [Google Scholar]
- [25].Kim A. and Golnaraghi M. F., “A quaternion-based orientation estimation algorithm using an inertial measurement unit,” in Proc. Position Location Navigat. Symp. (PLANS), Apr. 2004, pp. 268–272. [Google Scholar]
- [26].Nagasaki H., “Asymmetric velocity and acceleration profiles of human arm movements,” Experim. Brain Res., vol. 74, no. 2, pp. 319–326, 1989. [DOI] [PubMed] [Google Scholar]
- [27].Zollo L., Rossini L., Bravi M., Magrone G., Sterzi S., and Guglielmelli E., “Quantitative evaluation of upper-limb motor control in robot-aided rehabilitation,” Med. Biol. Eng. Comput., vol. 49, no. 10, pp. 1131–1144, 2011. [DOI] [PubMed] [Google Scholar]
- [28].Trombly C. A. and Wu C.-Y., “Effect of rehabilitation tasks on organization of movement after stroke,” Amer. J. Occupational Therapy, vol. 53, no. 4, pp. 333–344, 1999. [DOI] [PubMed] [Google Scholar]
- [29].Mannini A., Intille S. S., Rosenberger M., Sabatini A. M., and Haskell W., “Activity recognition using a single accelerometer placed at the wrist or ankle,” Med. Sci. Sports Exerc., vol. 45, no. 11, pp. 2193–2203, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].McClure P. W., Michener L. A., Sennett B. J., and Karduna A. R., “Direct 3-dimensional measurement of scapular kinematics during dynamic movements in vivo,” J. Shoulder Elbow Surg., vol. 10, no. 3, pp. 269–277, 2001. [DOI] [PubMed] [Google Scholar]
- [31].van der Helm F. C. T., “A standardized protocol for motion recordings of the shoulder,” in Proc. 1st Conf. Int. Shoulder Group. Maastricht, The Netherlands: Shaker Publishing, 1997, pp. 27–28. [Google Scholar]
- [32].Picerno P., Viero V., Donati M., Triossi T., Tancredi V., and Melchiorri G., “Ambulatory assessment of shoulder abduction strength curve using a single wearable inertial sensor,” J. Rehabil. Res. Develop., vol. 52, no. 2, pp. 171–180, 2015. [DOI] [PubMed] [Google Scholar]
- [33].Kusoffsky A., Apel I., and Hirschfeld H., “Reaching-lifting-placing task during standing after stroke: Coordination among ground forces, ankle muscle activity, and hand movement,” Arch. Phys. Med. Rehabil., vol. 82, no. 5, pp. 650–660, 2001. [DOI] [PubMed] [Google Scholar]
- [34].Van de Winckel A.et al. , “Can quality of movement be measured? Rasch analysis and inter-rater reliability of the motor evaluation scale for upper extremity in stroke patients (MESUPES),” Clin. Rehabil., vol. 20, no. 10, pp. 871–884, 2006. [DOI] [PubMed] [Google Scholar]
- [35].Boyd S. and Vandenberghe L., Convex Optimization. New York, NY, USA: Cambridge Univ. Press, 2004. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
IMU Sensor Dataset for human joint pose analysis
38KB
Windows
This paper presents a new approach to capturing human poses in real time using wearable sensors. The use of measurement conversion ideas, a representation signifying a linear characterization of an inherently non linear estimation problem, pragmatically improves the overall estimation of limb orientations.