Multi-omic and multi-view clustering algorithms: review and cancer benchmark

Abstract

Recent high throughput experimental methods have been used to collect large biomedical omics datasets. Clustering of single omic datasets has proven invaluable for biological and medical research. The decreasing cost and development of additional high throughput methods now enable measurement of multi-omic data. Clustering multi-omic data has the potential to reveal further systems-level insights, but raises computational and biological challenges. Here, we review algorithms for multi-omics clustering, and discuss key issues in applying these algorithms. Our review covers methods developed specifically for omic data as well as generic multi-view methods developed in the machine learning community for joint clustering of multiple data types. In addition, using cancer data from TCGA, we perform an extensive benchmark spanning ten different cancer types, providing the first systematic comparison of leading multi-omics and multi-view clustering algorithms. The results highlight key issues regarding the use of single- versus multi-omics, the choice of clustering strategy, the power of generic multi-view methods and the use of approximated p-values for gauging solution quality. Due to the growing use of multi-omics data, we expect these issues to be important for future progress in the field.

INTRODUCTION

Deep sequencing and other high throughput methods measure a large number of molecular parameters in a single experiment. The measured parameters include DNA genome sequence (1), RNA expression (2,3), DNA methylation (4) etc. Each such kind of data is termed ‘omic’ (genomics, transcriptomics, methylomics, respectively). As costs decrease and technologies mature, larger and more diverse omic datasets are available.

Computational methods are imperative for analyzing such data. One fundamental analysis is clustering - finding coherent groups of samples in the data, such that samples within a group are similar, and samples in different groups are dissimilar (5). This analysis is often the first step done in data exploration. Clustering has many applications for biomedical research, such as discovering modules of co-regulated genes and finding subtypes of diseases in the context of precision medicine (6). Clustering is a highly researched computational problem, investigated by multiple scientific communities, and a myriad algorithms exist for this task.

While clustering each omic separately reveals patterns in the data, integrative clustering using several omics for the same set of samples has the potential to expose more fine-tuned structures that are not revealed by examining only a single data type. For example, cancer subtypes can be defined based on both gene expression and DNA methylation together. There are several reasons why a clustering based on multiple omics is desirable. First, Multi-omics clustering can reduce the effect of experimental and biological noise in the data. Second, different omics can reveal different cellular aspects, such as effects manifest at the genomic and epigenomic levels. Third, even within the same molecular aspect, each omic can contain data that are not present in other omics (e.g. mutation and copy number). Fourth, omics can represent data from different organismal levels, such as gene expression together with microbiome composition.

A problem akin to multi-omics clustering was investigated independently by the machine learning community, and is termed ‘multi-view clustering’ (see (7) and ‘A Survey on Multi-View Clustering’). Multi-view clustering algorithms can be used to perform clustering of multi-omic data. In the past, methods developed within the machine learning community have proven useful in the analysis of biomedical datasets. However, by and large, multi-view clustering have not penetrated bioinformatics yet.

In this paper, we review methods for multi-omics clustering, and benchmark them on real cancer data. The data source is TCGA (The Cancer Genome Atlas) (8)—a large multi-omic repository of data on thousands of cancer patients. We survey both multi-omics and multi-view methods, with the goal of exposing computational biologists to these algorithms. Throughout this review, we use the terms view and multi-view instead of omic and multi-omics in the context of Machine Learning algorithms.

Several recent reviews discussed multi-omics integration. (9–11) review methods for multi-omics integration, and (12) review multi-omics clustering for cancer application. These reviews do not include a benchmark, and do not focus on multi-view clustering. (13) reviews only dimension reduction multi-omics methods. To the best of our knowledge, (14) is the only benchmark performed for multi-omics clustering, but it does not include machine learning methods. Furthermore, we believe the methods tested in the benchmark do not represent the current state of the art for multi omics clustering. Finally, (7) is a thorough review of multi-view methods, directed to the Machine Learning community. It does not discuss algorithms developed by the bioinformatics community, and does not cover biological applications.

REVIEW OF MULTI-OMICS CLUSTERING METHODS

We divide the methods into several categories based on their algorithmic approach. Early integration is the most simple approach. It concatenates omic matrices to form a single matrix with features from multiple omics, and applies single-omic clustering algorithms on that matrix. In late integration, each omic is clustered separately and the clustering solutions are integrated to obtain a single clustering solution. Other approaches try to build a model that incorporates all omics, and are collectively termed intermediate integration. Those include: (i) methods that integrate sample similarities, (ii) methods that use joint dimension reduction for the different omics datasets and (iii) methods that use statistical modeling of the data.

The categories we present here are not clear-cut, and some of the algorithms presented fit into more than one category. For example, iCluster (15) is an early integration approach that also uses probabilistic modeling to project the data to a lower dimension. The algorithms are described in the categories where we consider them to fit most.

Multi-omics clustering algorithms can also be distinguishable by the set of omics that they support. General algorithms support any kind of omics data, and are therefore easily extendible to novel future omics. Omic specific algorithms are tailored to a specific combination of data types, and can therefore utilize known biological relationships (e.g. the correlation between copy number and expression). A mixture of these two approaches is to perform feature learning in an omic specific way, but then cluster those features using general algorithms. For example, one can replace a gene expression omic with an omic that scores expression in cellular pathways, and thus take advantage of existing biological knowledge.

Throughout this review, we use the following notation: a multi-omic dataset contains M omics. n is the number of samples (or patients for medical datasets), p_m is the number of features in the m’th omics, and X^m is the n x p_m matrix with measurements from the m’th omic. 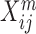is therefore the value of the j’th feature for the i’th patient in the m’th omic. 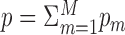is the total number of features, and X is the n × p matrix formed by the concatenation of all X^m matrices. Throughout the paper, for a matrix A, we use A^t to designate its transpose, and consistently with the X^m notation, we use A^m for matrix indexing (and not for matrix powering). Additional notation is chosen to follow the original publications and common conventions.

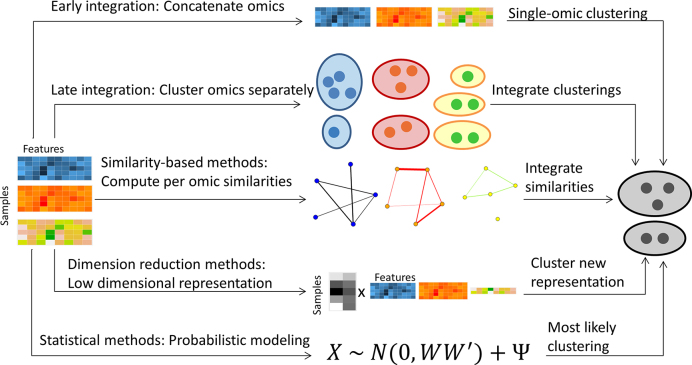
Figure 1 summarizes pictorially the different approaches to multi-omics clustering. A summary table of the methods reviewed here is given in Table 1.

Figure 1.

Overview of multi-omics clustering approaches.

Table 1.

Multi-omic clustering methods

Method	Description	Refs.	Implementation
Early integration
LRAcluster•	Data originate from low rank matrix, omic data distributions modeled based on it	(16)	R
Structured sparsity	Linear transformation projects data into a cluster membership orthogonal matrix	(17)	Matlab
Alternate optimization
MV k-means, MV EM	Alternating k-means and EM. Each iteration is done w.r.t. a different view	(18)	NA
Late integration
COCA	Per omic clustering solutions integrated with hierarchical clustering	(19)	NA
Late fusion using latent models	Per omic clustering solutions integrated with PLSA	(20)	NA
PINS•	Integration of co-clustering patterns in different omics. The clusterings are based on perturbations to the data	(21)	R
Similarity-based methods
Spectral clustering generalizations	Generalizations of similarity based spectral clustering to multi-omics data	(22–25)	Matlab
Spectral clustering with random walks	Generalizations of spectral clustering by random walks across similarity graphs	(26,27)	NA
SNF•	Integration of similarity networks by message passing	(28,29)	R, Matlab
rMKL-LPP•	DR using multiple kernel learning; similarities maintained in lower dimension	(30)	**
Dimension reduction
General DR framework	General framework for integration with DR	(31)	NA
JIVE	Variation in data partitioned into joint and omic-specific	(32)	Matlab,R (33)
CCA•	DR to axes of max correlation between datasets. Generalizations: Bayesian, kernels, >2 omics, sparse solutions, deep learning, count data	(34–43), CCA for count data	R, two omics (44), R, multiple omics
PLS	DR to axes of max covariance between datasets. Generalizations: kernels, >2 omics, sparse solutions, partition into omic-specific and joint variation	(45–52)	R, two omics, Matlab, multiple omics
MCIA	DR to axes of max covariance between multi-omic datasets	(53)	R
NMF generalizations•	DR using generalizations of NMF to multi-omic data	(54–57), EquiNMF, (58,59)	MultiNMF (Matlab)
Matrix tri- factorization	DR. Each omic describes the relationship between two entities	(60)	NA
Convex methods	DR with convex objective functions, allowing unique optimum and efficient computation	(16,61,62)	Matlab
Low-rank tensor MV clustering	Factorization based on low-rank tensors	(63)	Matlab
Statistical methods
iCluster/Plus/Bayes•	Data originate from low dimensional representation, which determines the distribution of the observed data	(15,64,65)	R
PARADIGM	Probabilistic model of cellular pathways using factor graphs	(66)	REST API
Disagreement between clusters	Methods based mainly on hierarchical Dirichlet processes; clustering in different omics need not agree	(67–71)	BCC (R)
Survival-based	Probabilistic model; patient survival data used in the clustering process	(72,73)	SBC (R)
Deep learning
Deep learning methods	Neural networks used for integration. A variant of CCA, early integration and middle integration approaches	(37,74,75)	DeepCCA (Python)

DR: dimension reduction; EM: expectation maximization; MV: multi-view; PLSA: Probabilistic Latent Semantic Analysis; CCA: Canonical Correlation Analysis; PLS: Partial Least Squares; NMF: non-negative matrix factorization. ^•Methods included in the benchmark. Single-omic k-means and spectral clustering were also included in the benchmark. ** Available from the authors upon request.

Early integration

Early integration is an approach that first concatenates all omic matrices, and then applies single-omic clustering algorithms on that concatenated matrix. It therefore enables the use of existing clustering algorithms. However, this approach has several drawbacks. First, without proper normalization, it may give more weight to omics with more features. Second, it does not consider the different distribution of data in the different omics. Finally, it increases the data dimension (the number of features), which is a challenge even in some single-omic datasets. When applying early integration algorithms designed specifically for multi-omics data, or when running single-omic methods on a concatenated matrix, these drawbacks must be addressed. Normalization of the features in different omics can assist in handling the different distributions, and feature selection can be used to decrease the dimension and to give different omics an equal prior opportunity to affect the results.

An additional way to handle the high dimension of the data is by using regularization, i.e. adding additional constraints to a problem to avoid overfitting (76). Specifically, LASSO (Least Absolute Shrinkage and Selection Operator) regularization creates models where the number of features with non-zero effect on the model is low (77), and regularization of the nuclear norm is often used to induce data sparsity. Indeed, LASSO regularization is used by iCluster (15) (reviewed in a later section), and LRACluster uses nuclear norm regularization (reviewed in this section). While any clustering algorithm can be applied using early integration, we highlight here algorithms that were specifically developed for this task.

LRACluster (16) uses a probabilistic model, where numeric, count and binary features have distributions determined by a latent representation of the samples Θ. For example, 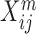is distributed 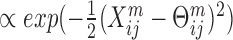, where Θ^m is of the same dimensions as X^m. The latent representation matrix is encouraged to be of low rank, by adding a regularization on its nuclear norm. The objective function for the algorithm is −log (model'slikelihood) + μ · |Θ|_* where Θ is the concatenation of all Θ^m matrices, and | · |_* is the nuclear norm. This objective is convex and provides a global optimal solution, which is found using a fast gradient-ascent algorithm. Θ is subsequently clustered using k-means. This method was used to analyze pan-cancer TCGA data from eleven cancer types using four different omics, and to further find subtypes within these cancer types.

In (17), all omics are concatenated to a matrix X and the algorithm minimizes the following objective: 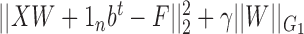. W is a p x k projection matrix, F is an n x k cluster indicator matrix such that F^tF = I_k, 1_n is a column vector of length n of 1’s, b is an intercept column vector of dimension k and γ is a scalar. The algorithm therefore seeks a linear transformation such the projected data are as close to a cluster indicator matrix as possible. That indicator matrix is subsequently used for clustering. The regularization term uses the G₁ norm, which is the l₂ norm for W entries associated with a specific cluster and view, summed over all views and clusters. Therefore, features that do not contribute to the structure of a cluster will be assigned with low coefficients in W.

Alternate optimization

Early research for integration of two views was performed in (78). This work improved classification accuracy for semi-supervised data with two views using an approach termed co-training, and inspired others to analyze multi-view data. One of the first attempts to perform multi-view clustering was (18). In this work, EM (expectation maximization) and k-means, which are widely used single-omic clustering algorithms, were adapted for multi-view clustering. Both EM and k-means are iterative algorithms, where each iteration improves the objective function value. The suggested multi-view versions perform optimization in each iteration with respect to a different omic in an alternating manner. This approach loses theoretical guarantees for convergence, but was found to outperform algorithms that use each view separately, and also naive early integration methods that cluster the concatenated matrix of the two views. Interestingly, (18) report improved results using the multi-view clustering algorithms on single-view datasets that were randomly split to simulate multi-view data. This was the first evidence for improved clustering using multiple views, and for the utility of a multi-view algorithm in clustering single-view data. While this work was very influential, other preliminary multi-view clustering methods (e.g. (22,31)) were since shown to achieve better results on datasets where the gold standard is known.

Late integration

Late integration is an approach that allows to use existing single-omic clustering algorithms on single-omic data. First, each omic is clustered separately using a single-omic algorithm. Different algorithms can be used for each omic. Then, the different clusterings are integrated. The strength of late integration lies in that any clustering algorithm can be used for each omic. Algorithms that are known to work well on a particular omic can therefore be used, without having to create a model that unifies all of these algorithms. However, by utilizing only clustering solutions in the integration phase we can lose signals that are weak in each omic separately.

COCA (19) was applied to pan-cancer TCGA data, to investigate how tumors from different tissues cluster, and whether the obtained clusters match the tissue of origin. The algorithm first clusters each omic separately, such that the m’th omic has c_m clusters. The clustering of sample i for omic m is encoded in a binary vector v_im of length c_m, where v_im(j) = 1 if i belongs to cluster j and 0 otherwise. The concatenation of the v_im vectors across all omics results in a binary cluster indicator vector for sample i. The n × c binary matrix B of these indicator vectors, where 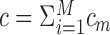, is used as input to consensus clustering (79) to obtain the final clustering of the samples. Alternatively, in (20) a model based on Probabilistic Latent Semantic Analysis (80) was proposed for clustering B. These two methods allow any clustering algorithm to be used on each single omic, and therefore have an advantage when a method is known to perform well for a particular omic. Additionally, they can be used given the clustering solution only when the raw omic data are unavailable.

PINS (21) integrates clusters by examining their connectivity matrices for the different omics. Each such matrix S^m is a binary n x n matrix, where 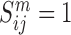if patients i and j are clustered together in omic m, and 0 otherwise. These S^m matrices are averaged to obtain a single connectivity matrix, which is then clustered using different methods based on whether the different S^m matrices highly agree with each other or not. The obtained clusters are tested if they can be further split into smaller clusters. To determine the number of clusters for each omic and for the integrated clustering, perturbations are performed on the data by adding Gaussian noise to it, and the number of clusters is chosen such that the resulting clustering is robust to the perturbations. Unlike the previously presented late integration methods, PINS requires the original data and not only the clustering of each omic, since it performs perturbations to the data.

Several methods for ensemble clustering were developed over the years, and are reviewed in (81). While these were not originally developed for this purpose, they can be used for late multi-omics clustering as well.

Similarity-based methods

Similarity-based methods use similarities or distances between samples in order to cluster data. These methods compute the similarities between samples in each omic separately, and vary in the way these similarities are integrated. The integration step uses only similarity values. Since in current multi-omic datasets, the number of samples is much smaller than the number of features, these algorithms are usually faster than methods that consider all features while performing integration. However, in such methods it may be more difficult to interpret the output in terms of the original features. An additional advantage of similarity-based methods is that they can easily support diverse omic types, including categorical and ordinal data. Each omic only requires a definition of a similarity measure.

Spectral clustering generalizations

Spectral clustering (82) is a widely used similarity-based method for clustering single-view data. The objective function for single-view spectral clustering is max_Utrace(U^tLU) s.t. U^tU = I, where L is the Laplacian (83) of the similarity matrix of dimension n × n, and U is of dimension n × k, where k is the number of clusters in the data. Intuitively, it means that samples that are similar to one another have similar row vectors in U. This problem is solved by taking the k first eigenvectors of L (details vary between versions that use the normalized and the unnormalized graph Laplacian), and clustering them with a simple algorithm such as k-means. The spectral clustering objective was shown to be a relaxation of the discrete normalized cut in a graph, providing an intuitive explanation for the clustering. Several multi-view clustering algorithms are generalizations of spectral clustering.

An early extension to two views performs clustering by computing a new similarity matrix, using the two views’ similarities (22). Denote by W₁ and W₂ the similarity matrices for the two views. Then the integrated similarity, W, is defined as W₁W₂. Spectral clustering is performed on the block matrix

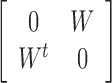Note that each eigenvector for this matrix is of length 2n. Either half of the vector or an average of the two halves are used instead of the whole eigenvectors for clustering using k-means. Note that this method is limited in that it only supports two views.

(23) generalizes spectral clustering for more than two views. Instead of finding a global U matrix, a matrix U^m is defined for each omic. The optimization problem is:

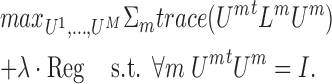L^m is the graph Laplacian for omic m and Reg is a regularization term equal to either 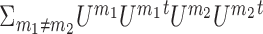or Σ_mU^mU^mtU*U*^t with the additional constraint that U* is an n x k matrix such that U*^tU* = I.

Chikhi (24) uses a different formulation, which does not require a different U^m for each omic, but instead uses the same U for all matrices. The following objective function is used:

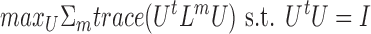This is equivalent to performing spectral clustering on the Laplacian Σ_mL^m. The obtained clusters are then further improved in a greedy manner, by changing the assignment of samples to clusters, while looking directly at the discrete normalized cut objective, rather than the continuous spectral clustering objective.

Li (25) suggests a runtime improvement over (23). Instead of looking at the similarity matrix for all the samples, a small set of ‘representative’ vectors, termed salient points, are calculated by running k-means on the concatenation of all omics and selecting the cluster centers. A similarity matrix is then computed between all these samples in the data and their s nearest salient points. Denote this similarity matrix for the m’th omic by W^m, and let Z^m be its normalization such that rows sum to 1. These matrices are of dimension n × the number of salient points. Next, the matrices

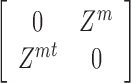are given as input to an algorithm with the same objective as (24). This way, similarities are not computed between all pairs of samples.

The methods above differ in several ways. (23) allows each omic to have a different low dimensional representation, and has a parameter that controls the trade-off between how similar these representations are, and how similarities in the original data are maintained in U^m. Therefore, it allows to express cases where the omics are not assumed to have the same similarity structure (e.g., two samples can be similar in one omic but different in another). On the other hand, Chikhi (24) assumes the same similarity structure, and its greedy optimization step can result in an improved solution in such cases. (25) can be used when the number of samples is exceptionally large.

Zhou and Burges (26) views similarity matrices as networks, and examines random walks on these networks. Random walks define a stationary distribution on each network, which captures its similarity patterns (84). Since that stationary distribution is less noisy than the original similarity measures, Zhou and Burges (26) uses them instead to integrate the networks. Xia (27) also examines random walks on the networks, but argues that the stationary distribution in each network can still be noisy. Instead, the authors compute a consensus transition matrix, that has minimum total distance to the per-omic transition matrices and is of minimal rank. Random walks are highly related to spectral clustering; using a normalized variant of the graph’s Laplacian in spectral clustering results in a solution in which random walks seldom cross between clusters (82). These random walk-based methods are currently competitive with other spectral clustering methods.

Similarity Network Fusion

SNF (Similarity Network Fusion) first constructs a similarity network for every omic separately (28,29). In each such network, the nodes are samples, and the edge weights measure the sample similarity. The networks are then fused together using an iterative procedure based on message passing (85). The similarity between samples is propagated between each node and its k nearest neighbors.

More formally, denote by W^(m) the similarity matrix for the m’th omic. Initially a transition probability matrix between all samples is defined by:

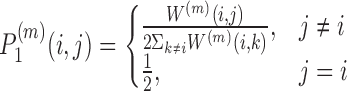and a transition porbability matrix between nearest neighbors is defined by:

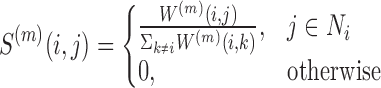where N_i are i’s k nearest neighbors in the input X^m matrices. The P matrices are updated iteratively using message passing between the nearest neighbors: 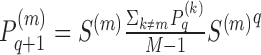where 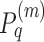is the matrix for omic m at iteration q. This process converges to a single similarity network, summarizing the similarity between samples across all omics. This network is partitioned using spectral clustering.

In (29), SNF is used on gene expression, methylation and miRNA expression data for several cancer subtypes from TCGA. In addition to partitioning the graph to obtain cancer sutbypes, the authors show that the fused network can be used for other computational tasks. For example, they show how to fit Cox proportional hazards (86), a model that predicts prognosis of patients, with a constraint such that similar patients in the integrated network will have similar predicted prognosis.

rMKL-LPP

Kernel functions implicitly map samples to a high (possibly infinite) dimension, and can efficiently measure similarity between the samples in that dimension. Multiple kernel learning uses several kernels (similarity measures), usually by linearly combining them, and is often used in supervised analysis. (30) developed rMKL-LPP (regularized Multiple Kernel Learning with Locality Preserving Projections), which uses multiple kernel learning in unsupervised settings. The algorithm performs dimension reduction on the input omics such that similarities (defined using multiple kernels) between each sample and its nearest neighbors are maintained in low dimension. This representation is subsequently clustered with k-means. rMKL-LPP allows the use of diverse kernel functions, and even multiple kernels per omic. A regularization term is added to the optimization problem to avoid overfitting. The authors run the algorithm on five cancer types from TCGA, and show that using multiple kernels per omic improves the prognostic value of the clustering, and that regularization improves robustness.

Dimension reduction-based methods

Dimension reduction-based methods assume the data have an intrinsic low dimensional representation, with that low dimension often corresponding to the number of clusters. The views that we observe are all transformations of that low dimensional data to a higher dimension, and the parameters for the transformation differ between views. This general formulation was proposed by (31), which suggest to minimize 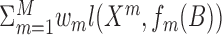, where B is a matrix of dimension n × p, f_m are the parametrized transformations, and w_m are weights for the different views, and l is a loss function. The work further provides an optimization algorithm when the f_m transformations are given by matrix multiplication. That is, f_m(B) = BP^m, and l is the squared Frobenius norm applied to X^m − BP^m. Once B is calculated, single-omic clustering algorithm can be applied to it. This general framework is widely used. Since the transformation is often assumed to be linear, many of the dimension reduction methods are based on matrix factorization. Dimension reduction methods work with real-valued data. Applying these methods to discrete binary or count data is technically possible but often inappropriate.

An advantage of linear dimension reduction methods is that they provide some interpretation for the dominant features in each cluster. For example, in the general framework just presented, each entry in the P^m matrix can be considered as the weight of a feature in a cluster. Such interpretation is missing from similarity-based methods, which ignore the original features once the similarities between samples were calculated. Therefore, dimension reduction methods may be useful when an association between clusters and features is needed.

JIVE

(32) assumes that the variation in each omic can be partitioned to a variation that is joint between all omics, and an omic-specific variation: X^mt = J^m + A^m + E^m where E^m are error terms. Let J and A be the concatenated J^m and A^m matrices, respectively. The model assumes that JA^t = 0, that is, the joint and omic specific variations are uncorrelated, and that rank(J) = r and rank(A_i) = r_i for each omic, so that the structure of each omic and the total joint variation are of low rank. In order for the weight of the different omics to be equal, the input omic matrices are normalized to have equal Frobenius norm. A penalty term is added to encourage variable sparsity. This method was applied to gene expression and miRNA data of Glioblastoma Multiforme brain tumors, and identified the joint variation between these omics.

Correlation and covariance-based

Two of the most widely used dimension reduction methods are Canonical Correlation Analysis (CCA) (34) and Partial Least Squares (PLS) (45). Given two omics X¹ and X², in CCA the goal is to find two projection vectors u¹ and u² of dimensions p₁ and p₂, such that the projected data has maximum correlation:

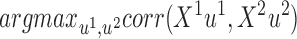These projections are called the first canonical variates, and are the axis with maximal correlation between the omics. The k’th pair of canonical variates, 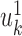and 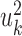are found such that correlation between 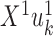and 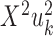is maximal, given that the new pair is uncorrelated (that is, orthogonal) to the previous canonical variates. Chaudhuri et al. (87) proved and showed empirically that if the data originate from normal or log concave distributions, the canonical variates can be used to cluster the data. CCA was formulated in a probabilistic framework such that the optimization solutions are maximum likelihood estimates (88), and further extended to a Bayesian framework (35). An additional expansion to perform CCA in high dimension is Kernel CCA (36). A deep-learning based CCA method, DeepCCA, was recently developed (37). Rather than maximize the correlation between linear projections of the data, the projections are taken to be functions of the data calculated using neural networks, and the optimization process optimizes the parameters for these networks.

Solving CCA requires inversion of the covariance matrix for the two omics. Omics data usually have a higher number of features than samples, and these matrices are therefore not invertible. To apply CCA to omics data, and to increase the interpretability of CCA’s results, sparsity regularization was added (38,39).

CCA supports only two views. Several works extend it to more than two views, including MCCA (39) which maximizes the sum of pairwise correlations between projections and CCA-RLS (40). Luo et al. (41) generalize CCA to tensors in order to support more than two views.

Another line of work on CCA, with high relevance for omics data, investigated relationships between the features while performing the dimension reduction. ssCCA (structure constrained sparse CCA) allows to incorporate into the model known relationships between features in one of the input omics, and force entries in the uⁱ vector for that view to be close for similar features. This model has been developed by (42) and utilized microbiome’s phylogenies as the feature structure. Another model that considers relationship between features was developed in (43). In this work, rather than defining similarities between features, they are partitioned into groups. Regularization is performed such that both irrelevant groups and irrelevant features within relevant groups are removed from the model. Finally, Podosinnikova et al., in ‘Beyond CCA: Moment matching for multi-view models’, extended CCA to support count data, which are common in biological datasets.

PLS also follows a linear dimension reduction model, but maximizes the covariance between the projections, rather than the correlation. More formally, given two omics X¹ and X², PLS computes a sequence of vectors 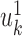and 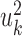for k = 1, 2, … such that 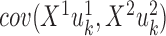is maximal, given that 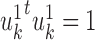, , 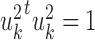and 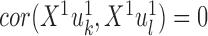for l < k. That is, new projections are not correlated with previous ones. PLS can be applied to data with more features than samples even without sparsity constraints. A sparse solution is nonetheless desirable, and one was developed (46,47). O2-PLS increases the interpretability of PLS by partitioning the variation in the datasets into joint variation between them, and variations that are specific for each dataset and that are not correlated with one another (48). While PLS and O2-PLS were originally developed for chemometrics, they were recently used for omics data as well (89,90). PLS was also extended to use the kernel framework (49), and a combined version of kernel PLS and O2 PLS was developed (50).

Like CCA, PLS was developed for two omics. MBPLS (Multi Block PLS) extends the model to more than two omics (91), and sMBPLS adds sparsity constraints. sMBPLS was developed specifically for omics data (51). It looks for a linear combination of projections of non-gene-expression omics that has maximal correlation with a projection of gene expression omic. An extension of O2PLS also exists for multi-view datasets (52).

Both CCA and PLS can be used in cases where high interpretability is wanted. The different 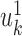and 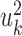vector pairs are those along which the correlation (or covariance) between patients is maximal. They can therefore be used to associate between features from the different views.

An additional method that is based on maximizing covariance in low dimension is MCIA (53), an extension of co-inertia analysis to more than two omics (92). It aims to find projections for all the omics such that the sum of squared covariances with a global variation axis is maximal: 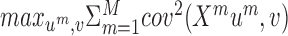. The projections of different omics can be used to evaluate the agreement between the different omics (the distance between projections reflects the level of disagreement between omics). Each of the projections can be used as a representation for clustering.

Non-negative Matrix Factorization

Non-negative Matrix Factorization (NMF) assumes that the data have an intrinsic low dimensional non-negative representation, and that a nonnegative matrix projects it to the observed omic (93). It is therefore only suitable for non-negative data. For a single omic, denote by k the low dimension. The formulation is X ≈ WH, where X is the n × p observed omic matrix, W is n × k and H is k × p. The objective function is 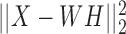, and it is minimized by updating W and H in an alternating manner, using multiplicative update rules, such that solutions remain non negative after each update (94). The low dimension representation W can be clustered using a simple single-omic algorithm. Like other dimension reduction methods, the W and H matrices can be used to better understand the weight of each feature in each cluster. The non-negativity constraint makes this weight more interpretable.

Several methods generalize this model to multi-omic data. MultiNMF (54) uses the following generalization: Each omic X^m is factorized into W^mH^m. This model is equivalent to performing NMF on each omic separately. Integration between the omics is done by adding a constraint that the W^m matrices are close to a ‘consensus’ matrix W*. The objective function is therefore: 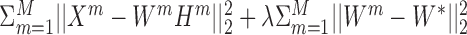. Kalayeh et al. (55) generalizes this method to support weights for features’ and samples’ similarity. (56) extend MultiNMF by further requiring that the low dimensional representation W* maintains similarities between samples (samples that are close in the original dimension must be close in W*). This approach combines factorization and similarity-based methods.

Joint NMF (57) uses a different formulation, where a sample has the same low dimensional representation for all omics: X^m ≈ WH^m. Note that by writing X = WH where X and H are obtained by matrix concatenation, this model is equivalent to early integration. Joint NMF is not directly used for clustering. Rather, the data are reduced to a large dimension (k = 200) and high values in W and H^m are used to associate samples and features with modules that are termed ‘md-modules’. The authors applied Joint NMF on miRNA, gene expression and methylation data from ovarian cancer patients, and showed that functional enrichment among features that are associated with md-modules that is more significant than the enrichment obtained in single-omic modules. In addition, patients in certain modules have significantly different prognosis compared to the rest of the patients. Much like (56) extends multiNMF, EquiNMF extends Joint NMF such that similarities in the original omics are maintained in lower dimension. (58) extends NMF to the case where different views can contain different samples, but constrains certain samples from different views to belong to the same cluster based on prior knowledge. Finally, PVC (59) performs partial multi-view clustering. In this setting, not all samples necessarily have measurements for all views.

The difference between MultiNMf and Joint NMF resembles the difference described previously between similarity-based methods. MultiNMF allows for different omics to have different representations, where the similarity between them is controlled by a parameter. It can therefore be used in cases where the different omics are not expected to have the same low dimensional representation.

Matrix tri-factorization

An alternative factorization approach presented in (60) is tri-matrix factorization. In this framework, each input omic is viewed as describing a relationship between two entities, which are its rows and columns. For example, in a dataset with two omics, gene expression and DNA methylation of patients, there are three entities which are the patients, the genes and the CpG loci. The gene expression matrix describes a relationship between patients and genes, while the methylation matrix describes a relationship between patients and CpG loci.

Each omic matrix R_ij of dimension n_i × n_j that describes the relationship between entities i and j is factorized as 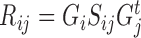, where G_i and G_j provide a low dimensional representation for entities i and j respectively and are of dimensions n_i × k_i and n_j × k_j, and S_ij is an omic-specific matrix of dimension k_i × k_j. As in NMF, the G_i matrices are non-negative. The same G_i matrix is used in all omics with entity i, and in this way data integration is achieved. In the above example, both the gene expression and DNA methylation omics will use the same G matrix to represent patients, but different matrices to represent genes and CpG loci. In this model, an additional matrix describing the relationship between genes and CpGs could optionally be used. This is a major advantage of matrix tri-factorization, as it allows to incorporate prior known relations between different entities, without changing the input omic matrices. (60) adds constraints to the formulation that can encourage entities to have similar representations. This framework was applied to diverse problems in bioinformatics, including in supervised settings: It was used to perform gene function prediction (60), and for patient survival regression (95).

Convex formulations

A drawback of most factorization-based methods is that their objective functions are not convex, and therefore optimization procedures do not necessarily reach a global optimum, and highly depend on initialization. One solution to this issue is by formulating dimension reduction as a convex problem. White et al. (61) relaxes CCA’s conditions and defines a convex variant of it. Performance was assessed on reducing noise in images, but the method can also be used for clustering. However, like CCA, the method only supports two views. Guo (62) presents a different convex formulation for dimension reduction, for the general factorization framework presented earlier, which minimizes 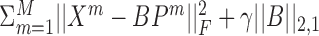. || · ||_{2, 1} is the l_{2, 1} norm, namely the sum of the Euclidean norms of the matrix rows. This relaxation therefore supports multiple views. LRAcluster (16) also uses matrix factorization and has a convex objective function.

Tensor-based methods

A natural extension of factorization methods for multi-omic data is to use tensors, which are higher order matrices. One such method is developed in (63). This method writes each omic matrix as X^m = Z^mX^m + E^m, diag(Z^m) = 0, where Z^m is an n x n matrix and E^m are error matrices. The idea is that each sample in each omic can be represented as a linear combination of other samples (hence the diag(Z^m) = 0 constraint), and that its representation in that base (Z^m) can then be used for clustering. To integrate the different views, the different Z^m matrices are merged to a third-order tensor, Z. The objective function encourages Z to be sparse, and the E^m error matrices to have a small norm.

Statistical methods

Statistical methods model the probabilistic distribution of the data. Some of these methods view samples as originating from different clusters, where each cluster defines a distribution for the data, while other methods do not explicitly use the cluster structure in the model. An advantage of the statistical approach is that it allows to include biological knowledge as part of the model when determining the distribution functions. This can be done either using Bayesian priors or by choosing probabilistic functions, e.g. using normal distribution for gene expression data. An additional advantage of statistical frameworks is their ability to make ‘soft’, probabilistic decisions. For example, a statistical method can not only assign a sample to a cluster, but can also determine the probability that the sample belongs to the cluster. For most formulations, parameter estimation is computationally hard, and different heuristics are used. Several models under the Bayesian framework allow for samples to belong to different clusters in different omics.

iCluster and iCluster+

iCluster (15) assumes that the data originate from a low dimension representation, which determines the cluster membership for each sample: X^mt = W^mZ + ε^m, where Z is a k x n matrix, W^m is an omic specific p_m x k matrix, k is the number of clusters and ε^m is a normally distributed noise matrix. This model resembles other dimension reduction models, but here the distribution of noise is made explicit. Under this model iCluster maximizes the likelihood of the observed data with an additional regularization for sparse W^m matrices. Optimization is performed using an EM-like algorithm, and subsequently k-means is run on the lower dimension representation of the data Z to get the final clustering assignments. iCluster was applied to breast and lung cancer, using gene expression and copy number variations. iCluster was also recently used to cluster more than ten thousand tumors from 33 cancers in a pan-cancer analysis (96). Note that by concatenating all W^m matrices to a single W matrix, and rewriting the model as X^t = WZ + ε, iCluster can be viewed as an early integration approach.

iCluster’s runtime grows fast with the number of features, and therefore feature selection is essential before using it, as was shown in (29). Shen et al. (15) only use genes located on one or two chromosomes in their analysis.

Since iCluster’s model uses matrix multiplication, it requires real-values features. An extension called iCluster+ (64) includes different models for numeric, categorical and count data, but maintains the idea that data originate from a low dimension matrix Z. For categorical data, iCluster+ assumes the following model:

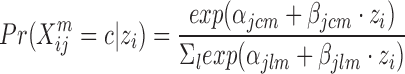while for numeric data the model remains linear with normal error:

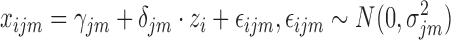A regularization term encouraging sparse solution is added to the likelihood, and a Monte-Carlo Newton–Raphson algorithm is used to estimate parameters. The Z matrix is used as in iCluster for the clustering. The latest extension of iCluster, which builds on iCluster+, is iClusterBayes (65). This method replaces the regularization in iCluster+ with full Bayesian regularization. This replacement results in faster execution, since the algorithm no longer needs to fine tune parameters for iCluster+’s regularization.

PARADIGM

PARADIGM (66) is the most explicit approach to modeling cellular processes and the relations among different omics. For each sample and each cellular pathway, a factor graph that represents the state of different entities within that pathway is created. As a degenerate example, a pathway may include nodes representing the mRNA levels of each gene in that pathway, and nodes representing those genes’ copy number. Each node in the factor graph can be either activated, nominal or deactivated, and the factor graph structure defines a distribution over these activation levels. For example, if a gene has high copy number it is more likely that it will be highly expressed. However, if a repressor for that gene is highly expressed, that gene is more likely to be deactivated. PARADIGM infers the activity of non-measured cellular entities to maximize the likelihood of the factor graph, and outputs an activity score for each entity per patient. These scores are used to cluster cancer patients from several tissues.

PARADIGM’s model can be used for more than clustering. For example, PARADIGM-shift (97) predicts loss-of-function and gain-of-function mutations, by finding genes whose expression value as predicted based on upstream entities in the factor graph is different from their predicted expression value using downstream entities. However, PARADIGM relies heavily on known interactions, and requires specific modeling for each omic. It is also quite limited to the cellular level; For example, it is not clear how to incorporate into the model an omic describing the microbiome composition of each patient.

Combining omic-specific and global clustering

All the methods discussed so far assume that there exists a consistent clustering structure across the different omics, and that analyzing the clusters in an integrative way will reveal this structure more accurately than analyzing each omic separately. However, this is not necessarily the case for biomedical datasets. For example, it is not clear that the methylation and expression profiles of cancer tumors really represent the same underlying cluster structure. Rather, it is possible that each omic represents a somewhat different cluster structure. Several methods take this view point using Bayesian statistics.

Savage et al. (67) define a hierarchical Dirichlet process model, which supports clustering on two omics. Each sample can be either fused or unfused. Fused samples belong to the same cluster in both omics, while unfused samples can belong to different clusters in different omics. Patterns of fused and unfused samples reveal the concordance between the two datasets. This model is extended in PSDF (68) to include feature selection. Savage et al. (67) apply the model to cluster genes using gene expression and ChIP-chip data, while (68) clusters cancer patients using expression and copy number data.

In MDI (69) each sample can have different cluster assignments in different omics. However, a prior is given such that the stronger an association between two omics is, the more likely a sample will belong to the same cluster in these two omics. This association strength adjusts the prior clustering agreement between two omics. In addition to these priors, MDI’s model uses Dirichlet mixture model, and explicitly represents the distribution of the data within each cluster and omic. Since samples can belong to different clusters in different omics, no global clustering solution is returned by the algorithm. Instead, the algorithm outputs sets of samples that tend to belong to the same cluster.

A different Bayesian formulation is given by BCC (70). Like MDI, BCC assumes a Dirichlet mixture model, where the data originate from a mixture of distributions. However, BCC does assume a global clustering solution, where each sample maps to a single cluster. Given that a sample belongs to a global cluster, its probability to belong to that cluster in each omic is high, but it can also belong to a different cluster in that omic. Parameters are estimated using Gibbs sampling (98). BCC was used on gene expression, DNA methylation, miRNA expression and RPPA data for breast cancer from TCGA.

Like MDI and BCC, Clusternomics (71) uses a Dirichlet mixture model. Clusternomics suggests two different formulations. In the first, each omic has a different clustering solution, and the global clusters are represented as the Cartesian product of clusters from each omic. This approach does not perform integration of the multi-omic datasets. In the second formulation, global clusters are explicitly mapped to omic-specific clusters. That way, not all possible combinations of clusters from different omics are considered as global clusters.

Survival-based clustering

One of the areas multi-omics clustering is widely used for is discovering disease subtypes. In this context, we may expect different disease subtypes to have a different prognosis, and this criterion is often used to assess clustering solutions. Ahmad and Fröhlich (72) develop a Bayesian model for multi-omics clustering that considers patient prognosis while clustering the data. Patients within a cluster have both similar feature distribution and similar prognosis. This approach is not entirely unsupervised, as it considers patient survival data, which are also used to assess the solutions. Coretto et al. (73) also develop a probabilistic clustering method that considers survival, and that supports a large number of features compared to (72), which only uses a few dozen features. As the survival data are used as input to the model, it is not surprising that this approach gives clusters with more significantly different survival than other approaches. This was demonstrated on Glioblastoma Multiforme data by (72) and for data from several cancer types by (73), both from TCGA.

Deep multi-view methods

A recent development in machine learning is the advent of deep learning algorithms (99). These algorithms use multi-layered neural networks to perform diverse computational tasks, and were found to improve performance in several fields such as image recognition (100) and text translation (101). Neural networks and deep learning have also proven useful for multi-view applications (102), including unsupervised feature learning (37), (103). Learned features can be used for clustering, as described earlier for DeepCCA. Deep learning is already used extensively for biomedical data analysis (104).

Recent deep learning uses for multi-omics data include (74) and (75). Chaudhary et al. (74) use an autoencoder, which is a deep learning method for dimension reduction. The authors ran it on RNA-seq, methylation and miRNA-seq data in order to cluster Hapatocellular Carcinoma patients. The architecture implements an early integration approach, concatenating the features from the different omics. The autoencoder outputs a representation for each patient. Features from this representation are tested for association with survival, and significantly associated features are used to cluster the patients. The clusters obtained have significantly different survival. This result is compared to a similar analysis using the original features, and features learned with PCA (Principal Component Analysis) rather than autoencoders. However, the analysis in this work is not unsupervised, since the feature selection is based on patient survival.

Liang et al. (75) use a different approach. They analyze expression, methylation and miRNA ovarian cancer data using Deep Belief Networks (105) which explicitly consider the multi-omic structure of the data. The architecture contains separate hidden layers, each having inputs from one omic, followed by layers that receive input from all the single-omic hidden layers, thus integrating the different omics. A 3D representation over {0, 1} is learned for each patient, partitioning the patients into 2³ = 8 clusters. The clustering results are compared to k-means clustering on the concatenation of all omics, but not to other multi-omics clustering methods.

Deep learning algorithms usually require many samples and few features. They use a large number of parameters, which makes them prone to overfitting. Current multi-omic datasets have the opposite characteristics—they have many features and at least one order of magnitude less samples. The works presented here use only a few layers in their architectures to overcome this limitation, in comparison to the dozens of layers used by state-of-the-art architectures for imaging datasets. As the number of biomedical samples increases, deep multi-view learning algorithms might prove more beneficial for biomedical datasets.

BENCHMARK

In order to test the performance of multi-omics clustering methods, we compared nine algorithms on ten cancer types available from TCGA. We also compared the performance of the algorithms on each one of the single-omic datasets that make up the multi-omic datasets, for algorithms that are applicable to single-omic data. The nine algorithms were chosen to represent diverse approaches to multi-omics clustering. Within each approach, we chose methods with available software and clear usage guidelines (e.g. we chose PINS over COCA as a late integration method since COCA does not explicitly state how each single omic should be clustered), and that are widely used, so that a comparison of these methods will be most informative to the community. Three algorithms are early integration methods: LRAcluster, and k-means and spectral clustering on the omics concatenated into a single matrix. For similarity-based algorithms we used SNF and rMKL-LPP. For dimension reduction we used MCCA (39) and MultiNMF. We chose iClusterBayes as a statistical method, and PINS as a late integration approach.

The ten datasets contain cancer tumor multi-omics data, where each dataset is a different cancer type. All datasets contain three omics: gene expression, DNA methylation and miRNA expression. The number of patients range from 170 for AML to 621 for BIC. Full details on the datasets and cancer type acronyms appear in Supplementary File 2.

To assess the performance of a clustering solution, we used three metrics. First, we measured differential survival between the obtained clusters using the logrank test (106). Using this test as a metric assumes that if clusters of patients have significantly different survival, they are different in a biologically meaningful way. Second, we tested for the enrichment of clinical labels in the clusters. We chose six clinical labels for which we tested enrichment: gender, age at diagnosis, pathologic T, pathologic M, pathologic N and pathologic stage. The four latter parameters are discrete pathological parameters, measuring the progression of the tumor (T), metastases (M) and cancer in lymph nodes (N), and the total progression (pathologic stage). Enrichment for discrete parameters was calculated using the χ² test for independence, and for numeric parameters using Kruskal-Wallis test. Not all clinical parameters were available for all cancer types, so a total of 41 clinical parameters were available for testing. Finally, we recorded the runtime of each method. We did not consider in the assessment computational measures for clustering quality, such as heterogeneity, homogeneity or the silhouette score (107), since the different methods perform different normalization on the features (and some even perform feature selection). Full details about the survival and phenotype data appear in Supplementary File 2.

To derive a p-value for the logrank test, the χ² test for independence, and the Kruskal-Wallis test, the statistic for these three tests is assumed to have χ² distribution. However, for the logrank test and χ² test this approximation is not accurate for small sample sizes and unbalanced cluster sizes, especially for large values of the test statistic (this was shown for example in (108) for the logrank test in the case of two clusters). The p-values we report here are therefore estimated using permutation tests (i.e., we permuted the cluster labels between samples and used the test statistic to obtain an empirical p-value). We indeed observed large differences between the p-values based on permutation testing and based on the approximation, for both the logrank test and enrichment of clinical parameters. More details on the permutation tests appear in Supplementary File 1. After permutation testing, the p-values for the clinical labels were corrected for multiple hypotheses (since several labels were tested) using Bonferroni correction for each cancer type and method at significance level 0.05. Results for the statistical analyses are in Supplementary File 3.

We applied all nine methods to the ten multi-omics datasets, and to the thirty single-omic matrices comprising them. The only exceptions were MCCA, which we could not apply to single-omic data, and PINS, which crashed consistently on all BIC datasets*. All methods were run on a Windows machine, except for iCluster which was run on a Linux cluster utilizing up to 15 nodes in parallel. In general, we chose parameters for the methods as suggested by the authors. In case the authors suggested a parameter search, such search was performed, and the best solution was chosen as suggested by the authors, without considering the survival and clinical parameters that are used for assessment. The runtime we report for the methods includes the parameter search. The rationale is that the benchmark aims to record how a user would run the methods in terms of both results quality and total runtime. Details on hardware, data preprocessing and application of the methods appear in Supplementary File 1. Full clustering results appear in Supplementary File 4. All the processed raw data are available at http://acgt.cs.tau.ac.il/multi_omic_benchmark/download.html, and all software scripts used are available at https://github.com/Shamir-Lab/Multi-Omics-Cancer-Benchmark/.

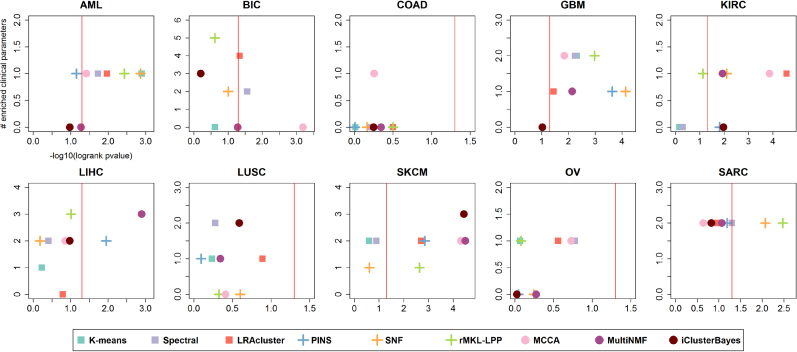
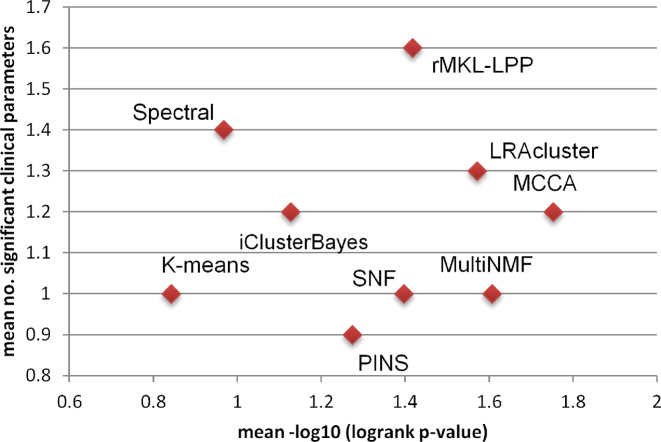
Figure 2 depicts the performance of the benchmarked methods on the different cancer datasets, and Figures 3 and 4 summarize the performance for multi-omics data and for each single-omic separately across all cancer types. No algorithm consistently outperformed all others in either differential survival or enriched clinical parameters. With respect to survival, MCCA had the total best prognostic value (sum of -log10 p-values = 17.53), while MultiNMF was second (16.07) and LRACluster third (15.72). The sum of p-values can be biased due to outliers, so we also counted the number of datasets for which a method’s solution obtains significantly different survival. These results are reported in Table 2. Here, with the exception of iClusterBayes, all methods that were developed for multi-omics or multi-view data had at least four cancer types with significantly different survival. MCCA and LRACluster had five. These cancer types are not identical for all the algorithms.

Figure 2.

Performance of the algorithms on ten multi-omics cancer datasets. For each plot, the x-axis measures the differential survival between clusters (–log₁₀ of logrank’s test P-value), and the y-axis is the number of clinical parameters enriched in the clusters. Red vertical lines indicate the threshold for significantly different survival (P-value ≤ 0.05)

Figure 3.

Mean performance of the algorithms on ten multi-omics cancer datasets. The x-axis measures the differential survival between clusters (mean –log₁₀ of logrank’s test P-value), and the y-axis is the mean number of clinical parameters enriched in the clusters.

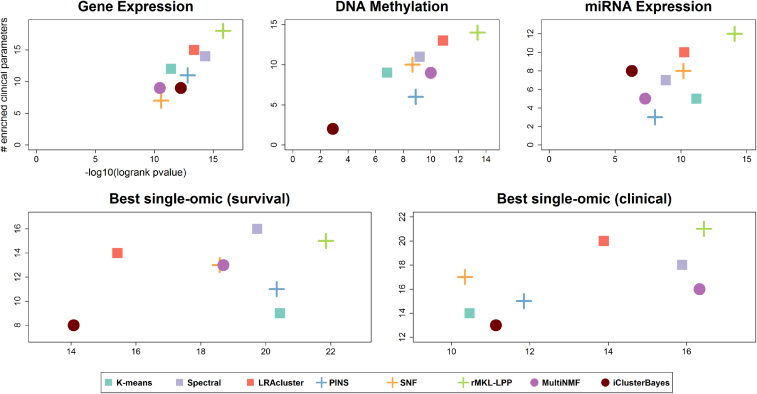
Figure 4.

Summarized performance of the algorithms across ten cancer datasets. For each plot, the x-axis measures the total differential prognosis between clusters (sum across all datasets of –log₁₀ of logrank’s test P-value), and the y-axis is the total number of clinical parameters enriched in the clusters across all cancer types. (A–C) Results for single-omic datasets. (D) Results when each method uses the single omic that achieves the highest significance in survival. (E) Same with respect to enrichment of clinical labels.

Table 2.

Cancer types with significant results per algorithm

	k-means	Spectral	LRAcluster	PINS	SNF	rMKL-LPP	MCCA	MultiNMF	iClusterBayes
Significantly different survival	2	3	5	4	4	4	5	4	2
Significant clinical enrichment	7	8	8	6	7	8	8	6	5

For each benchmarked algorithm, the number of cancer subtypes for which its clustering had significantly different prognosis (first row) and had at least one enriched clinical label (second row) are shown.

rMKL-LPP achieved the highest total number of significant clinical parameters, with 16 parameters. Spectral clustering came second with 14 and LRAcluster had 13. MCCA and MultiNMF, which had good results with respect to survival, had only 12 and 10 enriched parameters, respectively. rMKL-LPP did not outperform all other methods for all cancer types. For example, it had one enriched parameter for SKCM, while several other methods had two or three. We also considered the number of cancer types for which an algorithm had at least one enriched clinical label (Table 2). rMKL-LPP, spectral clustering, LRACluster and MCCA had enrichment in 8 cancer types, despite MCCA having a total of only 12 enriched parameters. Overall, rMKL-LPP outperformed all methods except MCCA, LRACluster and multiNMF with respect to both survival and clinical enrichment. MCCA, LRACluster and multiNMF had better prognostic value, but found less enriched clinical labels.

Each method determines the number of clusters for each dataset. These numbers are presented in Table 3. The numbers vary drastically among methods, from 2 or 3 (iCluster and MultiNMF) to more than 10 on average (MCCA). MCCA, LRACluster and rMKL-LPP partitioned the data into a relatively high number of clusters (average of 10.6, 9.4 and 6.7 respectively), and had good performance, which may indicate that clustering cancer patients into more clusters improves prognostic value and clinical significance. The higher number of clusters is controlled in the logrank and clinical enrichment tests by having more degrees of freedom for its χ² statistic.

Table 3.

Number of clusters chosen by the benchmarked algorithms on ten multi-omics cancer datasets

	AML	BIC	COAD	GBM	KIRC	LIHC	LUSC	SKCM	OV	SARC	Means
K-means	5	2	2	5	2	2	2	2	2	2	2.6
Spectral	9	3	2	5	2	2	2	2	4	2	3.3
LRAcluster	7	7	5	11	3	12	12	15	9	13	9.4
PINS	4	NA	4	2	2	5	4	15	2	3	4.6
SNF	4	2	3	2	4	2	2	3	3	3	2.8
rMKL-LPP	6	7	6	6	11	6	6	7	6	6	6.7
MCCA	11	14	2	11	15	15	12	2	9	15	10.6
MultiNMF	2	2	2	3	2	3	2	2	2	2	2.2
iClusterBayes	2	3	2	2	2	3	2	2	2	2	2.2

The right column is the average number of clusters across all cancer types.

The runtime of the different methods is reported in Table 4. Note that as mentioned earlier, iClusterBayes was run on a cluster, while the other methods were run on a desktop computer. All methods except for LRAcluster and iCluster took less than ten minutes per dataset on average. LRAcluster and iClusterBayes took about 56 and 72 minutes per dataset, respectively.

Table 4.

Runtime in seconds of the algorithms on ten multi-omics cancer datasets

	AML	BIC	COAD	GBM	KIRC	LIHC	LUSC	SKCM	OV	SARC	Means
K-means	96	1306	153	212	102	407	444	723	303	191	394
Spectral	3	8	3	3	3	5	5	6	4	4	4
LRAcluster	957	11655	1405	1370	991	3959	3353	5892	2299	2004	3388
PINS	41	NA	112	115	59	125	228	317	214	113	147
SNF	5	42	7	7	6	14	13	21	9	8	13
rMKL-LPP	222	192	205	221	191	255	213	333	263	238	233
MCCA	12	43	12	13	13	26	25	25	19	16	20
MultiNMF	19	51	25	19	17	35	27	45	21	23	28
iClusterBayes*	2628	7832	3213	2569	2756	5195	4682	6077	4057	3969	4298

The right column is the average runtime across all cancer types. *For iClusterBayes numbers are elapsed time on a multi-core platform.

Figure 4 also shows the performance of the benchmarked methods for single-omic data. While several methods had worse performance on single-omic datasets, some achieved better performance. For example, the highest number of enriched clinical parameters for both single and multi-omic datasets (18) was achieved by rMKL-LPP on gene expression. The gene expression solution also had better prognostic value than the multi-omic solution.

To further test how analysis of single-omic datasets compares to multi-omic datasets, we chose for each dataset and method the single omic that gave the best results for survival and clinical enrichment. In this analysis, rMKL-LPP had both the highest total number of enriched clinical parameters (21), and the highest total survival significance (21.86). The runtime, number of clusters, and survival and clinical enrichment analysis for single-omic datasets appear in Supplementary Files 1 and 3. These results suggest that analysis of multi-omics data does not consistently provide better prognostic value and clinical significance compared to analysis of single-omic data alone, especially when different single-omics are used for each cancer types.

DISCUSSION

We have reviewed methods for multi-omics and multi-view clustering. In our tests on 10 cancer datasets, overall, rMKL-LPP performed best in terms of clinical enrichment, and outperformed all methods except MCCA and MultiNMF with respect to survival. The high performance of MCCA and MultiNMF is remarkable, as these are multi-view methods that were not specifically developed for omics data (though MCCA was applied to it).

Throughout this review we provided guidelines about the advantages and disadvantages of different approaches and algorithms. In the benchmark, no single method consistently outperformed all others on any of the assessment criteria. While some methods were shown to do well, we cannot conclude from this that they should be always preferred. We also could not identify one ‘best’ integration approach, but it is interesting to note that the top two performers with respect to survival were dimension reduction methods.

Careful consideration should be given when applying multi-view clustering methods to multi-omic data, since these data have characteristics that multi-view methods do not necessarily consider. The most prominent of these characteristics is the large number of features relative to the number of samples. For example, CCA inverts the covariance matrix of each omic. This matrix is not invertible when there are more features than samples, and sparsity regularization is necessary. Another feature of multi-omic data is the dependencies between features in different omics, but several multi-view algorithms assume conditional independence of the omics given the clustering structure. This dependency is rarely considered, since it greatly increases the complexity of models. An additional characteristic of current omic data types is that due to cellular regulation, they have an intrinsic lower dimensional representation. The characteristic is utilized by many methods.

In our benchmark, single-omic data alone sometimes gave better results than multi-omics data. This was intensified when for each algorithm the ‘best’ single-omic for each cancer type was chosen. These results question the current assumptions underlying multi-omics analysis in general and multi-omics clustering in particular.

Several approaches may lead to improved results for multi-omics analysis. First, methods that suggest different clusterings in different omics were developed and reviewed here, but were not included in the benchmark, since it is not clear how to compare algorithms that do not output a global clustering solution to those that do. These methods may be more sensitive to strong signals appearing in only some of the omics. Second, future algorithms can perform omic selection in the same manner that algorithms today perform feature selection. In the benchmark, we let each method choose a single-omic for each cancer type given the results of the analysis, which are usually not available for real data. Methods that filter omics with contradicting signals might obtain a clearer clustering. Finally, while some methods for multi-omics clustering incorporate prior biological knowledge, few of them incorporate knowledge regarding the relationship between omics, or between features in different omics. Several statistical methods include some form of biological modeling by describing the distribution of the omics, and MDI tunes the similarity of clustering solutions in different omics based on the omics similarity. However, these methods do not model the biological relationships between omics. A notable exception is PARADIGM, which formulates the relationships between different omics. However, it also requires accurate prior knowledge about biochemical consequences of interactions, which is often unavailable. Methods that model relations between omics might benefit from additional biological knowledge, even without modeling whole pathways. For example, one can incorporate in a model the fact that promoter methylation is anti-correlated with gene expression. As far as we know, such methods were only developed for copy-number variation and gene expression data (e.g. (109)), and not in the context of clustering.

We detected large differences between the p-values derived from the χ² approximation compared to the P-values derived from the permutation tests in the statistical tests we used. The differences were especially large due to the small sample size, small cluster sizes (in solutions with a high number of clusters) and due to a low number of events (high survival) for the logrank test. These p-values are used by single and multi-omic methods to assess their performance, and the logrank p-value is often the main argument for an algorithm’s merit. The large differences between the P-values question the validity of analyses that are based on the χ² approximation, at least for TCGA data. Future work must use exact or permutation-based calculations of the P-value in datasets with similar characteristics to those used here for the benchmark.

The benchmark we performed is not without limitations. Gauging performance using patient survival is somewhat biased to known cancer subtypes, which may have been used in treatment decisions. Additionally, cancer subtypes that are biologically different may have similar survival. This is also true for enrichment of clinical parameters, although we attempted to choose parameters that would not lead to this bias. However, these measures are widely used for clustering assessment, including in the papers describing some of the benchmarked methods. Another limitation of the benchmark is that it only examines clustering, while some of the methods have additional goals and output. For example, in dimension reduction algorithms, the low dimensional data can be used to analyze features, and not only patients, e.g. by calculating axes of variation common to several omics. With respect to feature analysis, multi-omic algorithms can have an advantage over single-omic algorithms that we did not test. Finally, though we selected the parameters of each benchmarked method according to the guidelines given by the authors, judicious fine-tuning of the parameters may improve results.

DATA AVAILABILITY

All the processed raw data are available at http://acgt.cs.tau.ac.il/multi_omic_benchmark/download.html.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

United States–Israel Binational Science Foundation (BSF), Jerusalem, Israel and the United States National Science Foundation (NSF); Bella Walter Memorial Fund of the Israel Cancer Association (in part); Edmond J. Safra Center for Bioinformatics at Tel-Aviv University (to N.R.) (in part). Funding for open access charge: BSF–NSF and ICA grant listed under Funders (in part).

Conflict of interest statement. None declared.