Integrated Optomechanical Arrays of Two High Reflectivity SiN Membranes

Abstract

Multielement cavity optomechanics constitutes a direction to observe novel effects with mechanical resonators. Several exciting ideas include superradiance, increased optomechanical coupling, and quantum effects between distinct mechanical modes among others. Realizing these experiments has so far been difficult, because of the need for extremely precise positioning of the elements relative to one another due to the high-reflectivity required for each element. Here we overcome this challenge and present the fabrication of monolithic arrays of two highly reflective mechanical resonators in a single chip. We characterize the optical spectra and losses of these 200 μm long Fabry-Pérot interferometers, measuring finesse values of up to 220. In addition, we observe an enhancement of the coupling rate between the cavity field and the mechanical center-of-mass mode compared to the single membrane case. Further enhancements in coupling with these devices are predicted, potentially reaching the single-photon strong coupling regime, giving these integrated structures an exciting prospect for future multimode quantum experiments.

Cavity optomechanics explores light-matter interactions by using the established control techniques of optical resonators to manipulate highly sensitive mechanical oscillators.¹ A particularly successful direction is to dispersively couple suspended silicon nitride (SiN) membranes to a rigid optical cavity.² These so-called membrane-in-the-middle (MIM) systems combine independent optical and mechanical oscillators, allowing the use of high finesse cavities to study a variety of mechanical devices. Although recent years have seen tremendous progress in quantum optomechanics and in particular with experiments observing quantum behavior of the mechanical mode,³⁻⁵ most have focused on single mechanical or noninteracting modes. Studying the behavior of multiple directly coupled modes could however allow probing new and exciting regimes of optomechanics,⁶ like superradiance, phonon lasing,^7,8 synchronization,⁹ the study of exceptional points,¹⁰ quantum information processing,¹¹ as well as the direct entanglement of mechanical resonators.¹² It has also been suggested that the collective interaction of several mechanical oscillators can allow the reaching of the single-photon strong coupling regime.¹³ This effect is based on reducing the effective optical mode volume through an array of closely spaced mechanical systems and it becomes stronger as the reflectivity of the individual systems R_m is increased.

Tethered SiN membranes patterned with photonic crystals (PhC) constitute ideal candidates for this type of experiments, as they have excellent mechanical properties, low mass, and high reflectivity due to the PhC which can be engineered to operate at a large range of wavelengths.^14,15 To date, experimental efforts have focused on using independent mechanical membranes to create a mechanical array,^16,17 relying on the intrinsic reflectivity of the bare SiN with one recent attempt to fabricate a membrane on each side of the same chip.¹⁸

In the present work, we monolithically combine two tethered SiN membranes on a single chip and control their reflectivity using PhC patterns. This allows us to avoid having to manually align the mechanical elements to each other, which to date has been a major challenge with such high-reflectivity resonators. To compare the properties of devices with different reflectivity R_m, we fabricate pairs of single and double-membranes for three different PhC parameter sets, spanning R_m from 33% to 99.8% at an operating wavelength of 1550 nm. The optical spectrum of the arrays exhibits Fabry-Pérot interference, which allows us to study the optical loss mechanisms present in the system. The optomechanical coupling rate of the center-of-mass (COM) mode of single and double-membranes to an optical cavity are compared. By changing the incident laser wavelength, we can operate the double-membrane stacks in their reflective or transmissive regimes, corresponding to enhanced or null COM optomechanical couplings, respectively.

Device Design and Fabrication

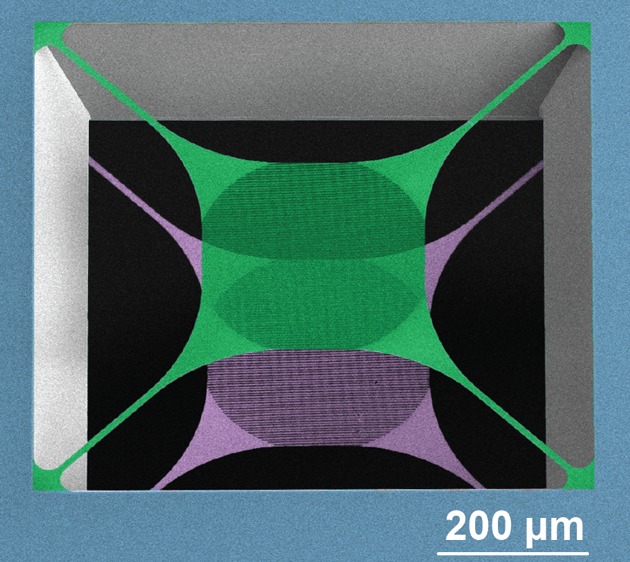
We fabricate our optomechanical devices on 200 nm of low-pressure chemical-vapor deposition (LPCVD) SiN deposited on both sides of a 200 μm thick silicon (Si) substrate. A trampoline membrane is patterned on each side of the chip using electron-beam lithography and then etched into the SiN using a CHF₃/O₂ plasma etch. Finally, the Si inbetween the trampolines is removed with KOH etching. Figure 1 shows a cross-sectional schematic of a final double membrane stack, as well as a false-colored SEM of one of our released devices.

Figure 1.

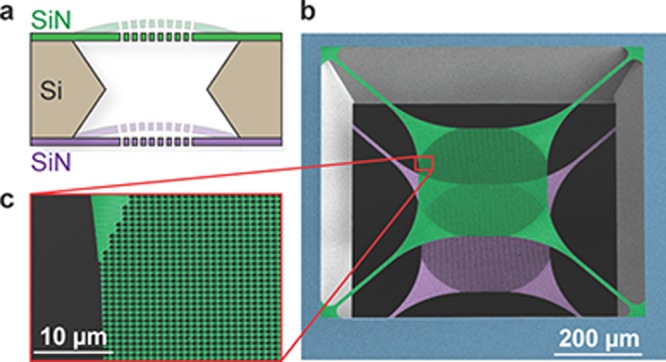
(a) Cross-sectional schematic of a released double membrane stack. (b) False-colored SEM image from the top under an angle of 37° showing a stack of two membranes as depicted in (a). The top (green) and bottom (purple) SiN trampolines form a Fabry-Pérot cavity. (c) Zoom-in of the PhC patterned central pad area of the upper membrane.

At the heart of our devices is a central mirror pad on the tethered membranes. It is patterned with a two-dimensional PhC consisting of a periodic array of holes etched into the SiN device layer. Such a periodic change in the refractive index creates a band gap that can be tailored to a specific wavelength, resulting in reflectivities >99.9%.^14,19 Using S⁴, a Rigorous Coupled-Wave Analysis software, we simulate the spectrum of a given PhC pattern.²⁰ During fabrication, we can accurately tune the PhC resonance to our desired wavelength by adjusting the lattice constant a and hole radius r (see Figure S2 in the Supporting Information for more details). We design three PhC patterns in order to obtain different R_m at our operating wavelength of 1550 nm. We refer to these patterns as Low, Mid, and High R and their geometries and measured R_m at 1550 nm are specified in Table 1. The optical beam we use to probe the PhC has a waist size of about 50 μm. To avoid clipping losses, the diameter of the PhC pattern is 300 μm, while the tether length and width are 318 and 10 μm, respectively.

Table 1.

^a

	a [nm]	r [nm]	Rm at 1550 nm
Low R	1240	475	33%
Mid R	1310	500	56%
High R	1372	525	99.8%

^aLattice constant a and hole radius r of the PhC patterns used in this work as well as their measured reflectivity R_m at our operating wavelength of 1550 nm.

Results and Discussion

For each PhC pattern (cf. Table 1), we fabricate a single- and a double-membrane, which allows us to test all designs on a single chip, greatly facilitating the measurements. In the following subsections, we characterize their optical, mechanical, and optomechanical properties.

Optical Characterization

Single Membranes

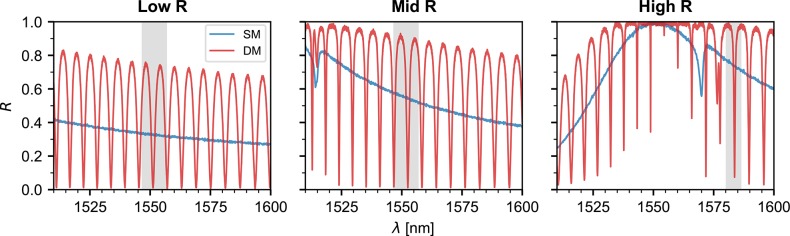
We first obtain the optical spectra of the single devices by scanning a tunable laser from 1510 to 1600 nm and measure the reflected and transmitted signals from the PhC trampolines, which are shown in Figure 2. At 1550 nm, we measure reflectivities of 33%, 56%, and 99.8% for the Low, Mid, and High R samples, respectively. Because this measurement procedure has an uncertainty of 0.5%, we determine the dispersive effect of a device similar to the High R sample on an optical cavity to obtain a lower bound on its transmission at resonance.^19,21 We measure a transmission of 2.5 × 10^–5, comparable to the best reported results in the literature.¹⁹ Finally, we simulate a PhC membrane with an imaginary component of the refractive index of 1.9 × 10^–5,²¹ and estimate that a fraction of of the light is lost when interacting with the devices, due to either absorption or scattering from fabrication imperfections (see Supporting Information for more details).

Figure 2.

Reflection spectra of the devices. The photonic crystal pattern of each device is indicated at the top of each figure, according to the parameters in Table 1. The blue traces correspond to devices composed of a single-membrane (SM), whereas the red traces are from double-membrane stacks (DM). The gray-shaded regions correspond to the wavelength ranges where the center-of-mass optomechanical coupling was measured (see Figures 3 and 4).

Double-Membrane Arrays

The double-membrane arrays have the same PhC design as the individual membranes and we determine their optical response in a similar way, shown in Figure 2. These structures can be modeled as plane-parallel etalons (Figure 1) and the characteristic features of Fabry-Pérot interferometers can be clearly observed in their spectra. The free spectral range FSR_DM of 750 GHz, or 6 nm at a wavelength of 1550 nm, is, as expected, defined by the 200 μm thickness of the Si substrate that separates the two membranes. The line width of the resonances becomes smaller as the reflectivity of the individual membranes increases. This is particularly prominent on the High R sample, where the full width at half-maximum line width changes from 176 GHz at 1521 nm to 8.7 GHz at 1554 nm, corresponding to a change in finesse F from 4.3 to 86. Our best performing samples exhibit line widths as low as 3.3 GHz (F = 220), suggesting a total loss per round-trip of approximately 2π/F = 2.9 × 10^–2.

Several sources contribute to this loss. First, using the measurements presented in the previous section we estimate a lower bound for the round-trip transmission of 5 × 10^–5. However, in general the highest finesse etalon peak is not exactly at the resonance of the PhC, being at most FSR_DM/2 = 3 nm away from it. At this point, the round-trip transmission becomes 2.6 × 10^–2. Second, we expect a round-trip absorption and scattering loss of 6.8 × 10^–4. Finally, some light will be lost due to the finite aperture size of the etalon. Plane-parallel Fabry-Pérot cavities are particularly susceptible to this effect,^22,23 and we estimate it to result in a round-trip loss of 2 × 10^–3. Combining these effects we arrive at estimated total round-trip losses between 2.8 × 10^–3 and 2.9 × 10^–2 (see Supporting Information for more details).

Although the maximum finesse measured in our devices fits well to this range, the fact that we generally measure lower values suggests that they are underestimated. Scattering, which has consistently been identified as one of the main loss mechanisms in other PhC membranes,^19,21 could be higher than expected. In addition, these estimates assume that both membranes have the same reflectivity. In both the Low and Mid R samples the reflection drops to zero at the etalon resonances, indicating that the PhC resonances on the front and back membranes are sufficiently well matched in these regimes. However, with increasing reflectivities, mismatches due to fabrication imperfections and small systematic shifts between the individual PhC mirrors become more apparent and lead to smaller dip depths (cf. the High R device in Figure 2). In fact, as the reflectivity of the individual membranes increases, the dip depth becomes significantly more sensitive to differences between the two mirrors (see Figure S1 in the Supporting Information). This also results in higher round-trip transmission values that can explain the discrepancy between our finesse estimates and measurements.

Mechanical Characterization

We determine the mechanical quality factor of the fundamental modes of both single and double membrane devices by performing interferometric ring-down measurements. The mode frequencies are approximately 150 kHz and the difference in frequency between the front and back membranes is typically around 170 Hz. The small difference of around 0.1% in resonance frequency can be attributed to an irreproducibility in the fabrication process. All devices show unclamped quality factors between 1.2 × 10⁶ and 5.6 × 10⁶. These values are in good agreement with measurements on a similar geometry, which showed quality factors of 4 × 10⁶,¹⁴ indicating that the PhC patterning does not negatively effect their mechanical properties.

Optomechanical Characterization

In order to obtain the optomechanical characteristics of the devices, we place them inside an optical cavity. The optical modes of this larger cavity strongly depend on the position of the membranes inside. By measuring the changes in cavity mode frequency ω_c as a function of the device displacement x, we are able to determine the linear optomechanical coupling between the cavity and the device’s center-of-mass mechanical modes, which we define as G ≡ max{|∂ω_c/∂x|}. The cavity has a free spectral range FSR_c = 3.13 GHz and an empty cavity half width at half-maximum of κ/2π = 550 kHz. We align our tunable laser to the cavity and measure the transmitted light. The laser frequency is then scanned as a function of the device position, which allows us to directly obtain ω_c(x) and calculate the optomechanical coupling.

Let us first consider the case of a single-membrane, where the cavity modes are affected by the membrane position and reflectivity R_m, according to 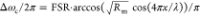.² The so-called linear coupling regime occurs when a membrane is placed close to x = λ/8 + nλ/4, n ∈ . Around these points, the cavity frequency changes linearly with the membrane position and the optomechanical coupling is given by

1

The first column of Figure 3 shows the cavity transmission as a function of laser frequency shift and displacement of the single-membrane samples. The wavelength at which the measurements were taken is indicated above each plot. The points of high transmission correspond to cavity modes. Because of alignment imperfections between the laser, the cavity, and the membranes, in addition to the fundamental cavity mode, we also observe higher order modes, which can be coupled to each other.²⁴ The fundamental optical mode frequency depends on the membrane position with a periodicity of x/λ = π/2 and the amplitude of the frequency oscillations increases with the membrane reflectivity, as indicated by eq 1. Using these data, we obtain G by numerically calculating |∂ω_c/∂x| and taking its maximum value, which occurs at the positions of linear coupling. The blue data points in Figure 4 show the single membranes’ coupling around a narrow wavelength window. In addition we plot the coupling as calculated by the reflectivity measured in Figure 2 and eq 1. Within this wavelength range, the reflectivity of each device varies little and therefore G is practically constant. The average measured couplings G/2π for the Low, Mid, and High R samples are 3.8(6), 5.7(9), and 7.7(12) MHz/nm, whereas the expected values using eq 1 and 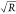are 4.5, 5.8, and 6.8 MHz/nm. Despite the large uncertainty, mainly due to the displacement calibration, the results are in good agreement with eq 1.

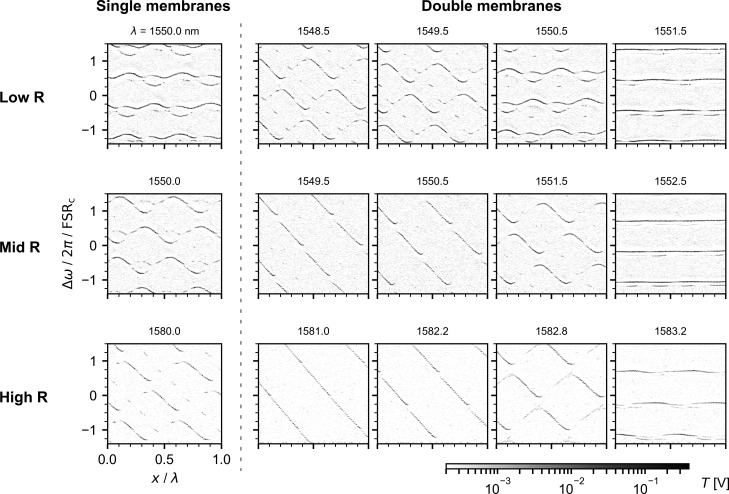
Figure 3.

Optical cavity transmission T as a function of the frequency shift Δω of the incident laser and of the displacement x of several mechanical devices placed in the middle of the cavity. Δω is normalized by the cavity free spectral range FSR_c = 3.13 GHz and x by the laser wavelength λ which is indicated on top of each plot. We measured multiple devices in the middle of the cavity: on the left of the dashed line we study single-membranes and on the right double-membranes. The type of photonic crystal used in each sample is indicated on the left of the figure. Note that in order to work in a regime with a slow reflectivity change and large dip depth, the High R samples were studied at a wavelength for which R_m = 0.76.

Figure 4.

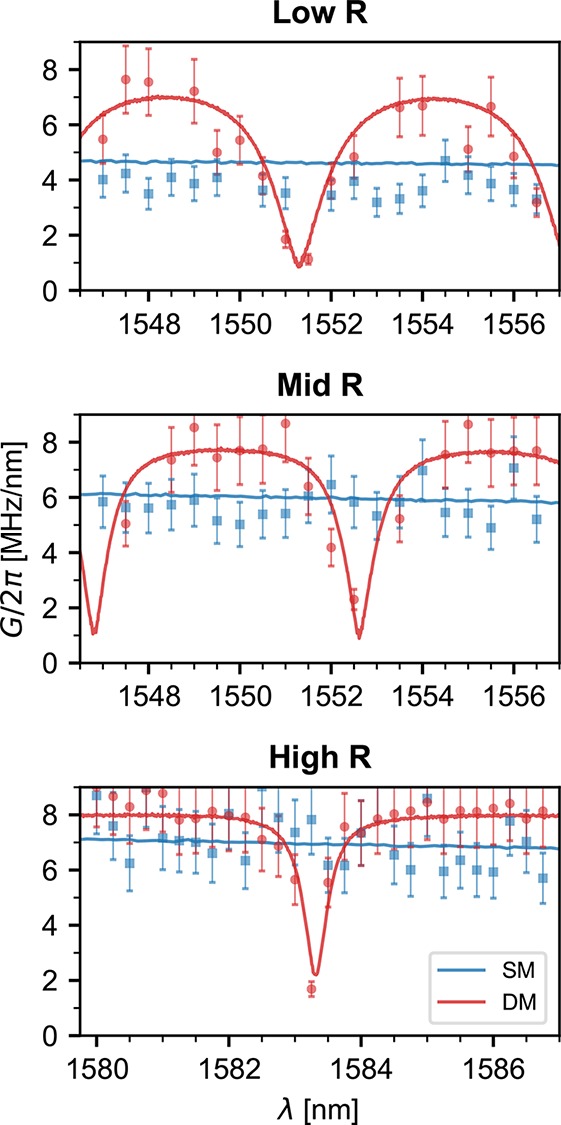
Center-of-mass optomechanical coupling G/2π as a function of wavelength λ obtained through the derivative of the cavity dispersion max{|∂ω_c/∂x|} (points) and through the membrane-in-the-middle model 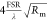(lines). The blue data are taken from single- (SM) and the red from double-membrane (DM) devices. The corresponding PhC patterns are indicated on top of each figure with the wavelength range studied here marked in gray in Figure 2.

Finally, we follow the same approach to obtain the coupling rate between the cavity and the COM displacement of the double-membrane chips, schematically represented in Figure 1. The crucial difference between single and double-membranes is that the latter’s spectra vary more strongly with wavelength. In particular, over one FSR_DM, the device reflectivity can quickly change from zero to one (see Figure 2). When the reflectivity is low, the COM mode of the device will interact weakly with the external cavity. Correspondingly, at a reflection maximum the coupling will be higher than that of a device composed of only one membrane. In columns 2 to 5 of Figure 3, the measured cavity dispersion for the three double-membranes studied is shown. We perform these measurements at several wavelengths spanning half a FSR_DM, between which the reflectivity varies between its maximum and minimum values. Note that for the High R sample we choose to study a resonance for which R_m ∼ 0.76 (λ close to 1580 nm) since for higher R_m the laser fine scanning range becomes similar to the resonance line width, and the dip depth decreases, making the coupling oscillations less visible. Column 2 corresponds to the reflectivity maxima. When comparing it with column 1, it becomes clear that the cavity frequency varies more strongly than in the single-membrane case. The data in column 5 are taken close to a transmission maximum where, as discussed, the COM motion has little influence on the cavity frequency. Columns 3 and 4 show wavelengths in between the maximum reflection and transmission of the double-membrane stacks. The extracted COM coupling is plotted in red in Figure 4. As discussed, the coupling oscillates between almost zero and values larger than those of the individual membranes. The oscillation follows the device’s spectral response, indicating that the COM coupling of a double-membrane is well described by eq 1, a model derived from the single-membrane case.

In conclusion, we have fabricated and characterized stacks of optomechanical devices that operate in various low to high reflectivity regimes. The devices presented here are patterned onto a single chip without the need for additional bonding steps or micropositioners. Our devices form a flexible platform in which the finesse can be freely tuned. Placing these devices inside an optical cavity allows the direct comparison of membrane-in-the-middle systems in multiple reflectivity regimes, such as proposed in ref (25). We see an enhancement of the optomechanical coupling rate between the COM motion of the two membranes and the cavity field as a function of reflectivity, when compared to a single membrane system.

More importantly, we can tune the system such that the COM coupling is practically zero. The theory of the collective motion of optomechanical arrays predicts that at these points the cavity field becomes resonant with the inner cavity and thus couples strongly to the relative motion of the membranes. This is the regime where single-photon strong coupling in an optomechanical system could be achievable.¹³ We are currently working on improving the stability of our setup in order to probe these relative motional modes. For devices with large R_m, like the ones presented here, the coupling enhancement of the differential mechanical motion is limited by the ratio L/2d between the length of the optical cavity L and the separation between the membranes d.²⁶ Given our experimental parameters, this should allow us to observe an enhancement of up to 120. Increasing this value further could be done by replacing the Si substrate by a thin sacrificial layer as the spacer between mirrors, considerably decreasing d to values similar to¹⁶ but keeping the advantages of monolithic fabrication presented here.

Even more interestingly, the single-photon cooperativity scales quadratically with the single-photon coupling strength, which in our case could boost this important figure of merit by 4 orders of magnitude, assuming the mechanical and optical dissipation rates stay the same. For many experiments, coherent control in the strong single-photon coupling regime is not necessary but reaching cooperativities greater than one is sufficient for performing several quantum protocols.^1,27 Other interesting experiments could include synchronization of mechanical modes,⁹ studying exceptional points in optomechanics with independent mechanical systems, as well as superradiance^7,8 and state transfer between mechanical systems.¹⁸ In addition, our arrays could serve as rigid, stable free-space optical filters with adjustable finesse. The arrays also constitute an optomechanical system by themselves, whose mirrors are both movable and with engineerable optical and mechanical properties. As both mirrors and mechanical resonators are monolithically combined, the system is inherently stable, greatly relaxing the setup complexity of typical free-space optomechanical setups, and making it an ideal platform for simple studies of radiation-pressure effects.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.8b03240.

• Detailed fabrication, challenges, and solutions, setups, estimation of optical losses, mode profile analysis, additional figures (PDF)

Author Contributions

C.G. and J.P.M. contributed equally to this work.

The authors declare no competing financial interest.