IVF success corrected for drop-out: use of inverse probability weighting

Abstract

STUDY QUESTION

Does inverse probability weighting (IPW) provide a more valid estimate of the cumulative incidence of live birth after multiple cycles of IVF?

SUMMARY ANSWER

IPW can provide a more accurate estimate of treatment success for counseling and decision-making regarding IVF.

WHAT IS KNOWN ALREADY

Different approaches have been used to define and calculate IVF success; however, many of these approaches have limitations and potentially violate statistical assumptions. IPW can address potential selection bias that arises when people do not continue IVF treatment after a failed cycle.

STUDY DESIGN, SIZE, DURATION

Data were derived from a cohort study of women undergoing their first fresh embryo transfer IVF cycle at our institution between 1 January 1995 and 31 December 2014. All autologous cycles (fresh and frozen) were included, up to six total cycles.

PARTICIPANTS/MATERIALS, SETTING, METHODS

We identified 20 015 women who underwent 47 079 IVF cycles and had 10 031 live births during the study period. The cumulative incidence of live birth was calculated using three approaches. First, we used a standard Kaplan–Meier approach, ‘the optimistic approach’, censoring women when they dropped out of treatment. Second, we used a ‘conservative’ Kaplan–Meier approach that assumed women who dropped out of treatment did not achieve a live birth. Finally, we used IPW to calculate the probability of remaining in treatment, while accounting for differences in treatment drop out. IPW up-weights the data of those remaining under observation who resembled the women who dropped out of treatment, thereby decreasing the potential selection bias resulting from loss to follow-up. The IPW was incorporated into a Kaplan–Meier approach.

MAIN RESULTS AND THE ROLE OF CHANCE

The cumulative incidence of live birth was 72.1% (95% CI: 71.0–73.1%) for the optimistic approach, 50.1% (49.4–50.8%) for the conservative approach and 66.8% (65.5–68.1%) for the IPW approach. Among women < 38 years of age, the cumulative incidence of live birth calculated by the IPW was slightly higher than that calculated by the optimistic approach. For women 41–42 years of age, the IPW cumulative incidence of live birth was slightly lower. The IPW was similar to the optimistic approach for the other age groups. The conservative estimate was lowest for all age groups.

LIMITATIONS, REASONS FOR CAUTION

Only clinical data recorded by the providers during an IVF cycle were used to generate weights for IPW. Covariates included: age, gravidity and year at the start of the cycle; primary infertility diagnosis; procedure type (i.e. whether a fresh or frozen embryo was transferred); number of mature oocytes retrieved; number of embryos transferred; cycle cancellation; pregnancy loss in the cycle; and insurance status. We were unable to determine exact reasons for treatment drop out (e.g. cessation of IVF treatment, transfer to another institution or spontaneous pregnancy). Our IPW model was moderately predictive based on the c-statistic from the calculation of the denominator of the weight; however, residual selection bias may remain due to the limited range of covariate data.

WIDER IMPLICATIONS OF THE FINDINGS

IPW can be used in a variety of settings to address selection bias introduced by differential loss to follow up or treatment drop out.

STUDY FUNDING/COMPETING INTEREST(S)

AMM was supported by National Institutes of Health (NIH) T32 HD052458—Boston University Reproductive, Perinatal and Pediatric Epidemiology Training Program. The authors report no conflicts of interest.

TRIAL REGISTRATION NUMBER

N/A.

Introduction

Accurate estimation of IVF success rates is critical for patients, who want to understand and compare their treatment options, for clinicians, who need to counsel patients and evaluate their practices, and for other stakeholders, such as regulators and insurers, who need to ensure the safety of IVF (Daya, 2005; Maheshwari et al., 2015). Given that many women undergo multiple IVF cycles to achieve a live birth and some women do not return for treatment after a failed cycle (Daya, 2005), valid estimation of IVF success rates is a challenge. The psychological burden related to IVF is one of the most common reasons why couples discontinue treatment (Bensdorp et al., 2016; Rich and Domar, 2016; Pedro et al., 2017; Domar et al., 2018), particularly couples with insurance that defrays some or all of the costs (Rich and Domar, 2016; Domar et al., 2010, 2018). Additional reasons include out-of-pocket costs, loss of insurance coverage, concerns about facing treatment, other cost and scheduling implications, or a spontaneous pregnancy (Malizia et al., 2009; Rich and Domar, 2016; Domar et al., 2018).

Different approaches have been used to measure IVF success, each with limitations. Primarily, many methods do not consider that it may take more than one oocyte retrieval or a combination of both fresh and frozen embryo transfer cycles to achieve a live birth (Daya, 2005; Malizia et al., 2009; Missmer et al., 2011; Rank and Moral, 2015). Considering the psychological burden of a failed IVF cycle (Rich and Domar, 2016), this information is important to patients. Survival analysis has been used to calculate the cumulative incidence of live birth, while accounting for multiple cycles. Survival analysis methods assume that censoring is uninformative, meaning that the probability of success for those who are lost to follow up or discontinue treatment is the same as the average probability of success for those who remain in treatment. Several studies, however, have found that women who do not return for treatment have a lower probability of live birth than women who remain in treatment (Daya, 2005; Malizia et al., 2009; Maheshwari et al., 2015; Pedro et al., 2017). By censoring women who do not return for treatment, the uninformative censoring assumption may be violated. The resulting selection bias potentially leads to an overestimate of the cumulative incidence of live birth (Daya, 2005; Hogan and Scharfstein, 2006; Howe et al., 2016).

In a prior study, Malizia et al. (2009) used two different approaches to evaluate the impact of censoring. First, the authors estimated an ‘optimistic’ scenario using standard survival analysis, censoring women who dropped out of treatment. Then, in the same cohort, they estimated a ‘conservative’ scenario by including all women who were censored for the full length of follow-up (six cycles) and assuming they did not have a live birth during that time period. The cumulative incidence of live birth was 72% using the optimistic approach and 51% using the conservative approach.

These findings demonstrate the potential magnitude of bias in estimates of live birth incidence among IVF patients when treatment continuation is related to ‘risk’ of live birth itself. One potential method to account for this risk-dependent loss to follow-up is inverse probability weighted (IPW) estimation (Cole and Hernán, 2004; Hernán et al., 2004). IPW, when applied to censoring, assigns weights to each observation that stays in the model. An observation will have a larger weight if its characteristics are more like those who drop out, based on the characteristics that are available in the data for each observation. A new pseudo-population is created in which the observations that remain better reflect the characteristics of the entire cohort, including those who drop out. In this pseudo-population, the effect of selection bias due to loss to follow up is minimized or even eliminated, since loss to follow up is no longer an issue (Hernán et al., 2004). The ability of IPW to minimize selection bias depends on adequate information about the characteristics of the population. The IPW estimate is the cumulative incidence of live birth if a woman achieves a live birth or completes up to six IVF cycles.

In the present report, we use IPW methods to estimate the cumulative incidence of live birth while accounting for the lower probability of IVF success among those who drop out of treatment. In addition, we compare unweighted estimates with the estimates obtained using IPW methods.

Materials and Methods

Study population

For each woman who had at least one IVF cycle at Boston IVF, we identified the first fresh autologous embryo transfer cycle from 1 January 1995 through 31 December 2014. We included all subsequent autologous cycles, fresh and frozen, for each woman until the first live birth or up to six completed cycles, whichever came first. An autologous cycle refers to a cycle performed with the woman’s own oocyte, regardless of whether the sperm was from the partner or a donor. In contrast, a donor cycle refers to a cycle using a donated oocyte, regardless of whether the sperm was from the partner or donor. Our institutional review board approved this study.

Outcome

We measured the cumulative incidence of live birth across multiple IVF cycles. Each fresh-embryo and frozen-embryo transfer cycle was included as a distinct treatment cycle.

Covariates

Covariate information was abstracted from the electronic medical record. Age, gravidity, procedure type (i.e. whether a fresh or frozen embryo was transferred), donor or autologous cycle, year of the cycle and primary infertility diagnosis were recorded at the start of each cycle by the clinician. Cycle characteristics and outcomes, including number of mature oocytes retrieved, number of embryos transferred, whether the cycle was canceled or whether there was a pregnancy loss in the cycle, were also recorded by the clinicians during or at the end of each cycle.

Statistical analysis

We used several analytic techniques to calculate the cumulative incidence of live birth. First, we reported the incidence of live birth at each IVF cycle and the cumulative incidence of live birth with all cycles in the denominator, the ‘per-cycle’ incidence of live birth. Second, we used a traditional Kaplan–Meier survival analysis, an ‘optimistic’ approach, where women were censored if they did not have a live birth and did not return for a subsequent IVF cycle or at the end of six IVF cycles. The analysis encompasses up to six cycles, similar to the Malizia et al. (2009) analysis and because it is common for insurance coverage in Massachusetts. Third, to mirror Malizia et al. (2009), we generated a ‘conservative’ estimate by assuming that women who dropped out of treatment had zero probability of live birth and therefore not censoring them before the end of six IVF cycles.

Finally, we implemented IPW, with censoring defined as for a traditional Kaplan–Meier approach. The dataset contained one observation for each IVF cycle with a variable to indicate whether the woman continued to the next treatment cycle. Next, we calculated the denominator of the weight. We used pooled logistic regression to determine the probability of continuing to the next cycle by using continuation as the dependent variable and all time varying and time-invariant covariates as the independent variables. The time-varying covariates chosen for the weights were as follows: age, gravidity and year at the start of the cycle; procedure type (i.e. whether a fresh or frozen embryo was transferred); number of mature oocytes retrieved; number of embryos transferred; cycle cancellation; pregnancy loss in the cycle; and insurance status. The time-invariant covariates available were parity and primary infertility diagnosis. For the primary infertility diagnosis, if the diagnosis recorded at the first cycle was ‘unknown’, we used the first known recorded diagnosis at a subsequent cycle, unless the diagnosis was never changed. C-statistics were used to determine the predictability of the pooled logistic model for the denominator. The probability was calculated for each treatment cycle and then multiplied across each individual to create the denominator of the final weight, known as the unstabilized IPW. Unstabilized weights may have extreme observations due to individuals with a rare combination of covariates (and thus a large weight) that can influence the results (Hernán et al., 2000; Cole and Hernán, 2008). Therefore, a numerator is added to the weights that contains time-invariant covariates only, creating a stabilized weight (Hernán et al., 2000; Cole and Hernán, 2008; Cain et al., 2016). The process for building the numerator was identical to building the denominator, except that only time-invariant covariates were used and multiplied across each individual for the final numerator weight. Stabilized IPWs should have a mean of one (Cole and Hernán, 2008). Finally, to further ensure that one individual with a rare combination of covariates did not influence the final result due to potential violations of positivity, the final weights were truncated at the 99th percentile (Cole and Hernán, 2004). The IPW was used in the final Kaplan–Meier approach (Xie and Liu, 2005).

For the optimistic, conservative and IPW approaches, we calculated the cumulative incidence of live birth by subtracting the survival probability from 1, and we plotted Kaplan–Meier curves. We stratified each analysis by age, a strong predictor of IVF success. We used the age at the start of the first cycle for all approaches. Age categories were based on the Society for Assisted Reproductive Technology standards (<30, 30 to <35, 35 to <38, 38 to <41, 41–42, >42 years), with a category added for those aged <30 years (Rank and Moral, 2015).

Results

We included 20 015 women who contributed 47 079 IVF cycles and 10 031 live births. The median time between the start of the first and last IVF cycle was 2.5 months (interquartile range: 0.0–7.8 months). The median time between each cycle was 0.61 months (interquartile range: 0.0–1.2 months). Demographic characteristics for participants at the start of their first cycle are presented in Table I. On average, women were 35.7 ± 4.6 years of age, and the majority were nulliparous (61.4%). Close to one-third (32.0%) had an unknown cause for infertility, and most (86.9%) had private insurance. At the end of the first cycle, 19.3% of women eligible for the next cycle did not return for cycle 2. This proportion increased with each cycle, with 37.7% of those eligible to return for cycle 6 not returning. The proportion of eligible women returning for subsequent cycles decreased with increasing age (Table II).

Table I.

Baseline characteristics of IVF cohort at the beginning of cycle 1, n = 20 015.

Characteristics	N = 20 015
Age (years)	35.7 ± 4.6
Gravidity
0	9568 (47.8)
1	4885 (24.4)
2	2589 (12.9)
3+	2453 (12.3)
Unknown	520 (2.6)
Parity
0	12 289 (61.4)
1	3983 (19.9)
2+	1090 (5.4)
Unknown	2653 (13.3)
Primary infertility diagnosis
Female factor infertility
Ovarian dysfunction	1583 (7.9)
Diminished ovarian reserve	1092 (5.5)
Endometriosis	1366 (6.8)
Polycystic ovarian syndrome	354 (1.8)
Tubal factor infertility	2966 (14.8)
Uterine factor infertility	475 (2.4)
Other	839 (4.2)
Male factor infertility	4668 (23.3)
Unknown	6395 (32.0)
Pre-implantation genetic screening	277 (1.4)
Insurance status
Insured	17 385 (86.9)
Self-pay	1550 (7.7)
Unknown	1080 (5.4)

Data presented as mean ± standard deviation or n (%).

Table II.

Cycle-specific IVF success and cycle distribution, stratified by age (in years) at the start of cycle 1.

Cycle number	Number in cohort	Live birth, N (%)	Eligible to return for next cycle	Number (%) not returning for next cycle
1	20 015	4744 (23.7)	15 271	2951 (19.3)
2	12 320	2545 (20.7)	9775	2472 (25.3)
3	7303	1466 (20.1)	5837	1755 (30.1)
4	4082	723 (17.7)	3359	1145 (34.1)
5	2214	375 (16.9)	1839	694 (37.7)
6	1145	178 (15.5)	–
Total cycles	47 079	10 031 (21.3)	–
Age <30
1	2281	710 (31.1)	1571	315 (20.1)
2	1256	354 (28.2)	902	165 (18.3)
3	737	222 (30.1)	515	123 (23.9)
4	392	94 (24.0)	298	90 (30.2)
5	208	60 (28.8)	148	57 (38.5)
6	91	20 (22.0)	–
Total cycles	4965	1460 (29.4)	–
Age 30 to <35
1	6570	2018 (30.7)	4552	671 (14.7)
2	3880	1005 (25.9)	2875	562 (19.5)
3	2313	567 (24.5)	1746	458 (26.2)
4	1288	281 (21.8)	1007	307 (30.5)
5	700	151 (21.6)	549	184 (33.5)
6	365	77 (21.1)	–
Total cycles	15 116	4099 (27.1)	–
Age 35 to <38
1	4411	1113 (25.2)	3298	530 (16.1)
2	2768	637 (23.0)	2131	502 (23.6)
3	1629	319 (19.6)	1310	367 (28.0)
4	943	170 (18.0)	773	237 (30.7)
5	536	83 (15.5)	453	151 (33.3)
6	302	41 (13.6)	–
Total cycles	10 589	2363 (22.3)	–
Age 38 to <41
1	3990	713 (17.9)	3277	661 (20.2)
2	2616	406 (15.5)	2210	623 (28.2)
3	1587	273 (17.2)	1314	418 (31.8)
4	896	127 (14.2)	769	268 (34.9)
5	501	56 (11.2)	445	174 (39.1)
6	271	29 (10.7)	–
Total cycles	9861	1604 (16.3)	–
Age 41–42
1	1862	160 (8.6)	1702	455 (26.7)
2	1247	121 (9.7)	1126	385 (34.2)
3	741	71 (9.6)	670	261 (39.0)
4	409	43 (10.5)	366	164 (44.8)
5	202	21 (10.4)	181	91 (50.3)
6	90	9 (10.0)	–
Total cycles	4551	425 (9.3)	–
Age >42
1	901	30 (3.3)	871	318 (36.5)
2	553	22 (4.0)	531	235 (44.3)
3	296	14 (4.7)	282	128 (45.4)
4	154	8 (5.2)	146	79 (55.1)
5	67	4 (6.0)	63	37 (58.7)
6	26	2 (7.7)	–
Total cycles	1997	80 (4.0)	–

The per-cycle success of IVF decreased with each cycle, from 23.7% for cycle 1 to 15.5% for cycle 6, and was 21.3% on average (Table II). Among women < 30 years old at the start of their first cycle, the per-cycle success was higher, at 31.1% in cycle 1 and 22.0% in cycle 6, and 29.4% on average. In contrast, among women over 42 years of age, the per-cycle success was lower, at 3.3% in cycle 1 and 7.7% in cycle 6, with an average of 4.0%.

All available covariates were used in building the IPW model. We included: age at the start of the IVF cycle, gravidity and year at the start of the cycle; procedure type (i.e. whether a fresh or frozen embryo was transferred); number of mature oocytes retrieved; number of embryos transferred; cycle cancellation; pregnancy loss in the cycle; and insurance status, as the time-varying covariates in the denominator of the model, as well as parity and primary infertility diagnosis. The overall c-statistic for the denominator of the IPW was 0.68 (Supplementary Table S1). Parity and primary infertility diagnosis were also included as the time-invariant covariates in the numerator. After truncating the weights at the 99th percentile, the mean of the stabilized weights was 0.98.

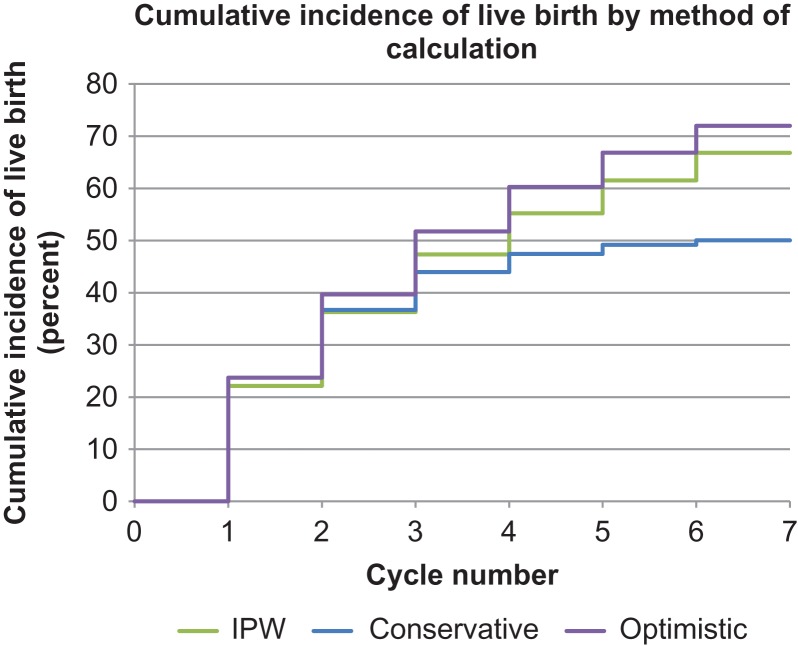
The cumulative incidence of live birth for up to six IVF cycles was 72.1% (95% CI: 71.0–73.1%) using the optimistic approach (Table III and Fig. 1). Using the conservative approach, the cumulative incidence of live birth was 50.1% (95% CI: 49.4–50.8%) after six cycles. Using the IPW approach, the cumulative incidence of live birth after six IVF cycles was 66.8% (95% CI: 65.5–68.1%). There was a difference in the cumulative incidence of live birth by age. Women <30 years of age had a cumulative incidence of live birth for the optimistic estimate (85.4%), conservative estimate (66.1%) and IPW estimate (90.8%). Women who were over 42 years of age at their first cycle had a cumulative incidence of live birth of 27.2% (optimistic), 10.8% (conservative) and 27.6% (IPW).

Table III.

Comparison of cumulative incidence of live birth by statistical approach, stratified by woman’s age (years) at the start of cycle 1.

	Kaplan–Meier ‘Optimistic’ approacha	Kaplan–Meier ‘Conservative’ approachb	IPW approachc
Whole cohort	72.1% (71.0–73.1)	50.1% (49.4–50.8)	66.8% (65.5–68.1)
Age <30	85.4% (82.9–87.7)	66.1% (64.0–68.2)	90.8% (88.4–92.8)
Age 30 to <35	81.3% (79.7–82.7)	64.4% (63.2–65.6)	85.1% (83.5–86.6)
Age 35 to <38	72.3% (70.2–74.3)	55.6% (54.1–57.1)	74.6% (72.3–76.8)
Age 38 to <41	60.9% (58.3–63.5)	41.2% (39.7–42.7)	59.6% (56.8–62.5)
Age 41–42	46.1% (41.2–51.4)	24.1% (22.4–26.0)	41.5% (37.1–46.1)
Age>42	27.2% (18.7–38.6)	10.8% (9.2–12.6)	27.6% (22.2–34.0)

Data presented as cumulative incidence (95% confidence interval).

^aTraditional Kaplan–Meier estimate where women were censored if they did not have a live birth and did not return for a subsequent IVF cycle.

^bKaplan–Meier estimate assuming no censoring and no live birth for women who did not return for treatment.

^cKaplan–Meier approach incorporating the inverse probability weight (IPW) using the probability of returning for a subsequent cycle based on the woman’s characteristics.

Figure 1.

Comparison of Kaplan–Meier (‘Optimistic’ approach), no censoring (‘Conservative’ approach) and inverse probability weighting (IPW) approaches to calculate cumulative incidence of live birth.

The age-stratified cumulative incidence of live birth was similar for the IPW and optimistic approaches. Among women <38 years of age, the cumulative incidence of live birth calculated by the IPW was slightly higher than the optimistic approach. For women 41–42 years of age, the IPW cumulative incidence of live birth was slightly lower. The IPW was similar to the optimistic approach for the other age groups. The conservative estimate was lowest for all age groups.

Discussion

While several approaches to quantifying IVF success have been implemented in previous studies, many of them have methodological limitations (Daya, 2005; Malizia et al., 2009; Missmer et al., 2011; Rank and Moral, 2015). Within one cohort of patients, we calculated the cumulative incidence of live birth using three different analytic techniques: the optimistic (traditional Kaplan–Meier), conservative (Kaplan–Meier assuming no censoring) and IPW (Kaplan–Meier incorporating weighting) approaches. Our results from the optimistic and conservative approaches were very similar to Malizia et al. (2009) who used the same clinic data based on a shorter time period (2000–2005). The IPW-estimated cumulative incidence of live birth for the whole cohort fell between the conservative and optimistic approaches, as expected, although was very similar to the optimistic approach. In age-stratified analyses, the optimistic Kaplan–Meier and IPW approach remained similar, but the IPW did not fall between the conservative and optimistic approaches for all age groups. In the younger age groups (<38 years of age), the IPW estimated a higher cumulative incidence of live birth than the optimistic approach. This may be due to differences in the reason for treatment drop out. For example, younger women may be more likely to not continue treatment due to a spontaneous pregnancy (Domar et al., 2018). In the IPW approach, the younger women who drop out may have similar characteristics to those women with higher fertility potential; the weight for the women with higher fertility potential that remain in treatment would be higher to account for this. In a Kaplan–Meier approach, the assumption would be that women who drop out have the same probability of a live birth as the average probability of women who remain in treatment (including older women and women with lower fertility potential); thus, for younger women, the Kaplan–Meier approach may be an underestimate. In contrast, the cumulative incidence of live birth in the ≥38 age groups was similar between the IPW and optimistic approaches. There are several potential explanations for this. The first is that the IPW approach was unable to account for some of the potential selection bias due to limited covariate information. In the older age groups, the proportion of women achieving a live birth does not decrease with each subsequent cycle, as would be expected. This may be related to insurance mandates for autologous IVF coverage. Some insurance companies require more strict criteria in older women in order to cover the cost of autologous IVF. Often, these women must undergo additional testing related to their fertility potential, which is not required in younger women. It is therefore possible that the women who return for subsequent autologous IVF cycles are more likely to have a live birth than those who discontinue treatment or move on to donor IVF. Unfortunately, we were not able to include all of this testing information in our IPW weight, due to limitations in the electronic data. The second explanation is small sample sizes in those older age categories. The third explanation is that the uninformative censoring assumption is not violated in these age groups and there is no selection bias. In other words, the women in these age strata are more uniform with respect to their IPW predictors and had similar weights. In prior work from the same IVF clinic, many in the older age groups reported reasons for treatment discontinuation related to stress and financial burden (Domar et al., 2018), which may be unrelated to the probability of live birth. In order for selection bias to be present and for the IPW to be different, the reasons for treatment discontinuation need to be related to the probability of live birth.

The IPW method has several limitations. First, although we were able to minimize selection bias due to informative censoring based on the covariates we had available, residual bias may remain, as mentioned above. We were unable to account for important factors such as body mass index, smoking, employment status, stress, medical comorbidities, other potential predictors of fertility and treatment decision making, and spontaneous pregnancies. We were also unable to confirm that the first fresh autologous embryo transfer cycle in our medical records was the woman’s first cycle, since we did not have data from other clinics. We did not have data at Boston IVF prior to 1995, and were also unable to determine whether any of the women in our cohort had IVF cycles prior to 1995. Inclusion in the model of these additional covariates may have improved predictability of the estimates. In addition, although we used all available covariates in our IPW model, the c-statistic generated by the pooled logistic regression for the denominator of the IPW was 0.68, indicating that our model was not strongly predictive of remaining uncensored. Truncating the weights also may lead to residual confounding because we are artificially lowering the weights for those with a unique combination of characteristics. Finally, we were unable to determine the ‘true’ probability of a live birth for those who discontinue treatment. Although there is a strong theoretical framework for the use of IPW to address selection bias due to loss to follow-up, further work is needed to understand how the IPW approach compares to the true probability of live birth, perhaps in datasets or clinics with complete follow-up information.

IPW has several strengths, notably the ability to decrease bias due to loss of follow-up which is related to live birth, although this is limited to the information we have available to build the weights. Although our clinic is in Massachusetts, which has insurance mandates to cover infertility treatment, such as IVF, loss of insurance and out-of-pocket expenses are a significant issue in this population (Domar et al., 2018). The pattern of drop out may be different in populations without the mandate or in populations that differ from this study population. Additionally, insurance status may be a proxy for other socioeconomic or demographic factors that could affect the probability of live birth. The IPW approach allows the flexibility to include this information for a more accurate population-specific estimate. Models that are more predictive would better address potential bias. In addition, this approach can be tailored to different study questions beyond cumulative incidence of live birth and used in marginal structural models to mitigate selection bias in estimating exposure-outcome associations.

Currently, there is limited information about why couples discontinue IVF treatment and further research in this area is needed. Understanding the reasons for treatment discontinuation and loss of follow up is important and this information may be included in future IPW models for better prediction and more accurate estimates. Nevertheless, using IPW can provide clinicians, patients and stakeholders with a more accurate estimate of treatment success for counseling and decision-making regarding IVF.

Funding

National Institutes of Health (NIH) T32 HD052458—Boston University Reproductive, Perinatal and Pediatric Epidemiology Training Program to A.M.M.

Conflict of interest

The authors report no conflicts of interest.

Authors’ contributions

A.M.M.: conceived the study design completed the data analysis, and wrote the article. L.A.W.: significantly contributed to conception of the study design and interpretation of the data, critically revised the article, and approved the final version. M.P.F.: significantly contributed to conception of the study design and interpretation of the data, critically revised the article, and approved the final version. J.W.: significantly contributed to analysis and interpretation of the data, critically revised the article, and approved the final version. A.P.: significantly contributed to interpretation of the data, critically revised the article, and approved the final version. M.R.H.: significantly contributed to conception of the study design as well as analysis and interpretation of the data, critically revised article, and approved final version.