Importance evaluation of spectral lines in Laser-induced breakdown spectroscopy for classification of pathogenic bacteria

Abstract

The correct classification of pathogenic bacteria is significant for clinical diagnosis and treatment. Compared with the use of whole spectral data, using feature lines as the inputs of the classification model can improve the correct classification rate (CCR) and reduce the analyzing time. In order to select feature lines, we need to investigate the contribution to the CCR of each spectral line. In this paper, two algorithms, important weights based on principal component analysis (IW-PCA) and random forests (RF), were proposed to evaluate the importance of spectra lines. The laser-induced plasma spectra (LIBS) of six common clinical pathogenic bacteria species were measured and a support vector machine (SVM) classifier was used to classify the LIBS of bacteria species. In the proposed IW-PCA algorithm, the product of the loading of each line and the variance of the corresponding principal component were calculated. The maximum product of each line calculated from the first three PCs was used to represent the line’s importance weight. In the RF algorithm, the Gini index reduction value of each line was considered as the line’s importance weight. The experimental results demonstrated that the lines with high importance were more suitable for classification and can be chosen as feature lines. The optimal number of feature lines used in the SVM classifier can be determined by comparing the CCRs with a different number of feature lines. Importance weights evaluated by RF are more suitable for extracting feature lines using LIBS combined with an SVM classification mechanism than those evaluated by IW-PCA. Furthermore, the two methods mutually verified the importance of selected lines and the lines evaluated important by both IW-PCA and RF contributed more to the CCR.

1. Introduction

In clinical field, the diagnosis of many diseases and the determination of their development stages depend on the detection of the corresponding bacteria and microorganisms [1]. Bacterial resistance has shown the increasing prevalence due to the inability to identify specific pathogens in time and use specific corresponding antibiotics [2–4]. Meantime, rapid and reliable analysis of pathogen specimens in hospital settings can also help prevent cross-infection in patients [5,6]. Therefore, the rapid and accurate classification and identification of bacteria is significant to choose corresponding preventive measures and the targeted medicine opportunely.

The traditional existing identification methods have some limitations. For instance, the morphological identification method takes a lot time and labor with an unstable phenotype and low sensitivity [7]. Immunodiagnostic technology and DNA-based detection methods cannot identify the pathogen without the corresponding antibody or molecular chain. Meanwhile, cross-reactions with unrelated species are common and identification based on sequencing is laborious, time-consuming and costly [8,9]. Some new techniques such as matrix-assisted laser desorption ionization–time of flight mass spectrometry (MALDI-TOF MS) [10], rapid antimicrobial susceptibility testing (AST) [11], multiplex Polymerase Chain Reaction (multiplex PCR) [12] and fluorescent indicator technology [13] have also been used in clinical occasions to determinate the type of bacteria and other microbial pathogens rapidly. However, due to the expensive price of these instruments, the number of qualified hospitals is limited so that these techniques are not available for many patients. Meanwhile, through these non-in situ testing methods, the results may be generated faster, but still need time to be brought from laboratory to patients and doctors. So, it is a challenge to develop a cost-effective, accurate, rapid and easy-to-use method for bacterial discrimination.

As a new elemental analysis technology, LIBS has been used to identify medical and biological samples [14,15]. Combined with chemometrics algorithms, it can reach a high accuracy in classification of clinical samples [16]. LIBS is a rapid, real-time, in situ, multi elements simultaneous detection technique without the need of sample preparation [17]. In LIBS analysis, a laser pulse is locally coupled into the sample material and a plasma is generated within material evaporating. In the cooling process of plasma, element-specific radiation was emitted and detected by a spectrometer [18]. The wavelength and intensity of these spectral lines represent the type and concentration of the corresponding elements [19–21].

In particular bacteria identification field, R. A. Multari et al concluded that LIBS, in combination with appropriately constructed chemometric models, could be used to classify Escherichia coli and Staphylococcus aureus [22]. D. Marcos-Martinez et al used LIBS combined with neural networks (NNs) to identify Pseudomonas aeroginosa, Escherichia coli and Salmonella typhimurium and reached a certainty of over 95% [23]. Recently, D. Prochazka et al combined laser-induced breakdown spectroscopy and Raman spectroscopy for multivariate classification of bacteria [24]. Although all the six kinds of bacteria can be classified correctly with merged data, with only LIBS data, just three kinds can be classified.

In above experiments, whole spectral range or a broad spectral range was selected in order to cover all spectral characteristics of the samples. However, though the spectral information contained in the whole spectrum is the most abundant, a lot of information is irrelevant for classification [25,26]. Meanwhile, the complexity of data processing is closely related to the amount of spectral data [27]. Therefore, it is necessary to extract the feature lines from the whole spectrum.

Usually people select spectral ranges or lines of interest manually based on prior knowledge and theoretical composition of sample [28,29]. Using the intensity of 13 emission lines from 5 different elements (P, C, Mg, Ca, and Na), S. J. Rehse et al characterized a mixture of two bacteria. The mixed sample with a mixing ratio higher than 80:20 can be identified accurately based on discriminant function analysis (DFA) [30]. But manual selection requires operators with a wealth of relevant knowledge and experience. And we cannot make sure whether lines corresponding to the theoretical composition can reflect the differences among samples.

Recently machine learning methods were proposed to extract spectral features from both LIBS and other spectra objectively and efficiently [31–33]. W. Li and J. Du used decision tree algorithm to choose features from hyperspectral data as candidate attributes for vegetable classification [34]. Evelyn Vor et al used PCA algorithm for LIBS feature extraction in the identification of alloys [35]. But using their proposed extracting methods, only the feature lines can be selected, but whether these feature lines are appropriate for classification cannot be evaluated.

In this paper, we defined an importance weight of each line to evaluate the contribution of this line to the classification result and proposed two methods, importance weights based on Principal Components Analysis (IW-PCA) and Random Forests (RF), to evaluate the importance weights of lines. We selected the lines with high importance weights as feature lines. Furthermore, the effect of different number of feature lines to classification result was analyzed. Six kinds of common pathogenic bacteria were chosen as samples. The LIBS spectra of these samples were measured and divided into training set and testing set. According to the evaluated importance weights, different number of lines were extracted from training set as features. Using these features as input variables and labels of bacteria type as output variables established an SVM classifier to describe the mapping between them. And then the classifier was used to classify the testing set spectra. We investigated which evaluating method performed better and how many feature lines is suitable in LIBS-SVM by comparing their influences on the final classification accuracies, respectively. The results demonstrated that evaluating importance weights of lines is of practical importance for extracting features in LIBS-SVM classifier.

2. Materials and methods

2.1. LIBS experimental measuring setup

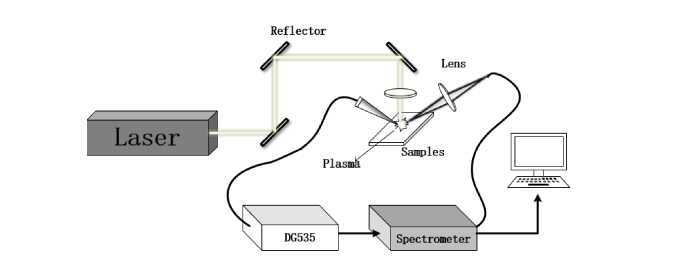
A schematic of the experimental LIBS setup is illustrated in Fig. 1. A flash-pumped Q-switched Nd: YAG laser (λ = 1064 nm, repetition frequency 1 Hz, pulse duration 5 ns, beam diameter ∅6 mm, energy 64 mJ/pulse) was used to excite the sample’s surface. The laser propagation direction was changed through three plane mirrors and finally focused on the sample surface by a convex lens with a focal length of 100 mm. The plasma radiation was focused into a fiber (∅ 600 μm) through a lens with a focal length of 36 mm. The outlet of optical fiber was connected to a two-channel spectrometer (AvaSpec 2048-2-USB2, Avantes). Spectral data collected by the spectrometer covered a range of 190 nm to 1100 nm with a resolution of 0.2~0.3 nm. External trigger used in the system included a photodetector and a digital delayer (SRS-DG535, Stanford Research System). When the photodetector detected the plasma radiation signal, the spectrometer was triggered by DG535 after a preset delay time. The spectral acquisition delay time was set to 1.28μs to reduce Bremsstrahlung radiation. The integration time of CCD was 2 ms.

Fig. 1.

Schematics of the LIBS experimental setup.

2.2. Bacteria sample preparation

In this work, six kinds of common pathogenic bacteria were chosen as samples, including two kinds of Staphylococcus (Staphylococcus aureus 26068, Staphylococcus aureus 26003), three kinds of Escherichia coli (Escherichia coli TG1, Escherichia coli JM109, Escherichia coli 44113), and a kind of Bacillus (Bacillus cereus 63301) (Provided by Research Institute of Chemical Defense, 102205, Beijing, China.). The cultured bacteria samples were smeared on the slides evenly, formed 20 × 40 mm² thin layers with 20 μm thickness. Three-dimensional motorized stage was used to adjust the focus position of the laser on the samples. And for every bacterial sample, 400 spectra were collected, each on a fresh position.

3. Results and discussion

3.1. Spectral data preprocessing

400 spectra collected for each type of sample were divided into training part and test part, which had 300 and 100 spectra, respectively. Due to the fluctuation of laser energy and flatness and uniformity of the samples’ surfaces, the collected spectral data also fluctuated. Therefore, data from two parts were respectively averaged. In each part, every spectrum was considered as a vector in multidimensional space, and then the cosine values of the inner angle between each spectrum and the average spectrum were calculated. The larger the cosine value was, the more similar it was to the average spectrum. According to the cosine values from high to low we extracted the most similar 75% spectra with the average in each part, which means 225 in training part and 75 in testing part. By this way, outliers can be removed from the data. Then every three spectra got an average in each part to reduce the data fluctuation furtherly. Finally, for each type of sample, the training set has 75 spectra and the testing set has 25 spectra.

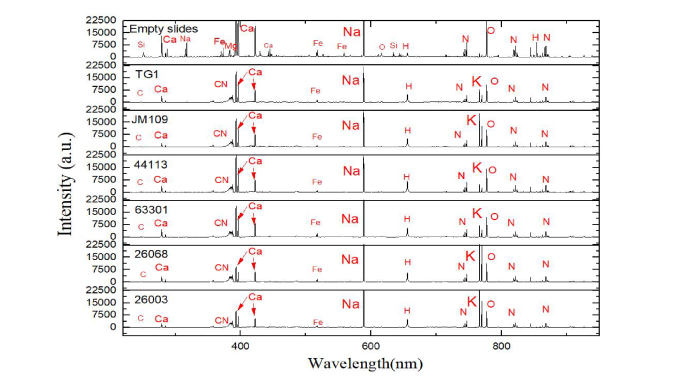
The spectra got from an empty slide and six samples are shown in Fig. 2. In the spectrum of empty slides, many lines related to 8 elements (Si, Ca, Na, Fe, Mg, O, H, N) can be seen. For the six samples, several obvious spectral lines related to CN band and 8 elements (C, Ca, Fe, Na, H, N, K, and O) can be found. Comparing with the spectrum of empty slide, these spectra of samples were obviously different. Among these samples slides, the spectra of Staphylococcus aureus 26068 and 26003 look very similar. However, although the TG1, JM109 and 44113 both belong to Escherichia coli, their spectra are different at some lines such as potassium and calcium lines.

Fig. 2.

LIBS spectra of 6 kinds of bacteria after preprocessing and the empty slides.

Although there are some differences among the intensities of specific lines, these spectra were too similar to recognize by eye. All the obvious lines (85 lines in this case) were selected and their areas were calculated for representing line intensities, as listed in Table 1. Then we extracted feature lines from training set using IW-PCA and Random Forests and established SVM classification models, respectively. Finally, the correct classification rate (CCR, the ratio of the correct classification number and the total number) of the models was tested using testing set.

Table 1. The 85 selected lines and corresponding elements.

Line Wavelength(nm)	Element	Line Wavelength(nm)	Element	Line Wavelength(nm)	Element	Line Wavelength(nm)	Element
247.8	C	423.4	Ca	616.1	Na	833.4	H
279.5	Ca	430.3	Ca	643.9	Na	844.6	O
279.8	Ca	431.9	Ca	645.8	N	854.5	H
284.8	Fe	436.8	Fe	649.1	N	856.8	N
315.4	Fe	437.8	Fe	656.3	H	859.4	N
317.5	Fe	442.7	Fe	714.8	Ca	862.9	N
358.2	Fe	443.1	Ca	715.7	O	865.6	N
373.7	Ca	445.5	Ca	742.4	N	866.5	H
382.9	CN	485.9	Fe	744.6	N	868.3	N
383.4	CN	486.4	Fe	746.6	N	870.3	N
384.6	CN	487.8	Fe	766.5	K	871.2	N
385.7	CN	516.7	Fe	769.9	K	871.9	N
386.5	CN	517.7	Fe	777.4	O	904.6	N
388.0	CN	526.3	Fe	794.8	O	906.2	C
393.4	Ca	558.7	Fe	818.5	N	907.8	C
396.8	Ca	559.5	Fe	819.6	C	909.5	C
414.8	Fe	568.3	Na	820.0	N	911.2	C
416.1	Fe	589.0	Na	821.6	N	926.3	O
417.6	Fe	589.6	Na	822.2	O	938.7	N
419.1	Fe	612.1	Na	822.8	O	939.3	N
420.7	Ca	615.4	Na	823.5	O	940.6	C
422.7	Ca

3.2. Importance evaluation using importance weights based on principal component analysis (IW-PCA)

Principal component analysis (PCA) is an unsupervised learning method. By projecting down into a less dimensional subspace through the linear transformation, it can transform the raw data into a set of linearly independent representations of each dimension [36,37] and be commonly used to reduce dimensionality in high dimension data [32,35]. In PCA, the variance of each principal component represents the proportion of original information they retain. The first principal component expressed the spatial direction with the largest variance [37]. Every spectral line has a corresponding loading in each principal component.

PCA has been used in selecting LIBS feature lines [35]. In each chosen PC, they selected lines with high loadings as features. We proposed PCA can also be used to evaluate the importance of spectral lines. We think the line with high loading is more important. Normally, only the first PC cannot reflect the enough spectral information. So other PCs were selected sequentially to increase cumulative variance. We selected loadings from the first several PCs with cumulative variance over 95% to evaluate the importance of lines. However, because the describe variance of each PC is different and loadings of the same line in different PCs are also different, only using loadings is not enough for evaluating importance weights of lines. Therefore, variances of principal components and loadings of lines should be combined to evaluate the importance of each line.

In the proposed evaluating method IW-PCA, the first several PCs whose cumulative variance was more than 95% were used in analysis after projecting down spectral data. In each PC, every line had a loading representing the importance in this PC. The higher loading value represented more important. Considering the variance representing the importance of a PC, for each line, the product of its loading and the variance of the corresponding PC was calculated. And the maximum product calculated from the first several PCs was defined as the importance weight of this line.

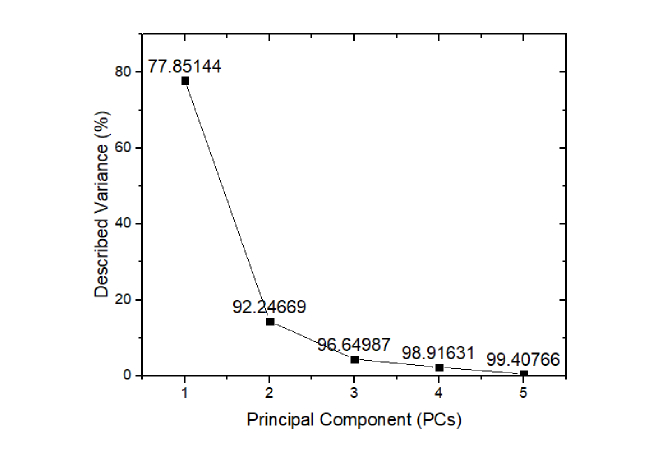
The training set data was used to build the PCA model. The variances of first five PCs were shown in Fig. 3. For each PCs, the cumulative variances were labeled above the points. The cumulative variance of first three PCs (PC1-77.85144%, PC2-14.39525%, PC3-4.40318%) was more than 95%, so we used the first three PCs in the succeeding analysis.

Fig. 3.

The variance described by each principal component.

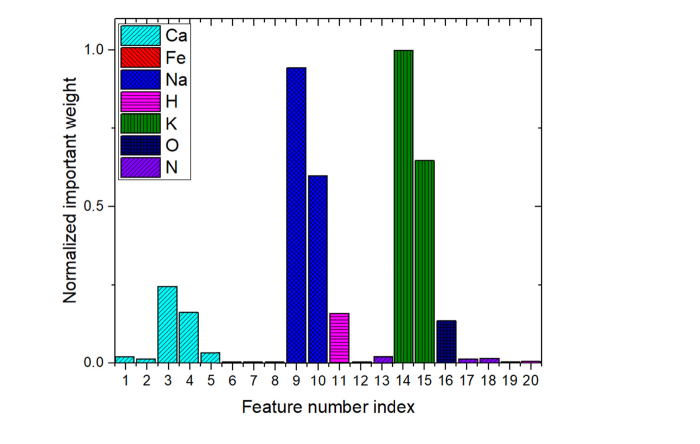
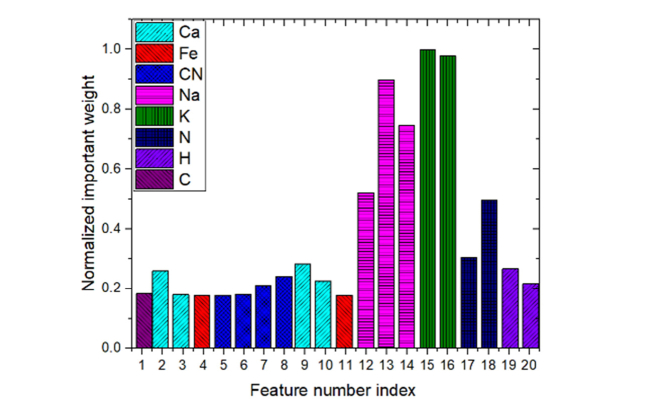
The most important 20 spectral lines evaluated by IW-PCA and their normalized importance weights were listed in Table 2 and shown in Fig. 4 in the wavelength order. As illustrated in Fig. 4, bars with different colors show that the 20 lines extracted by IW-PCA are related to 7 elements (Ca, Fe, Na, H, K, O, and N).

Table 2. The most important 20 feature lines evaluated by IW-PCA.

Feature number index	Line Wavelength (/nm)	Corresponding element	Normalized importance weight	Feature number index	Line Wavelength (/nm)	Corresponding element	Normalized importance weight
1	279.5	Ca	0.022	11	656.3	H	0.159
2	279.8	Ca	0.015	12	744.6	N	0.006
3	393.4	Ca	0.246	13	746.6	N	0.021
4	396.8	Ca	0.162	14	766.5	K	1.000
5	422.7	Ca	0.033	15	769.9	K	0.647
6	430.3	Ca	0.005	16	777.4	O	0.135
7	445.5	Ca	0.005	17	818.5	N	0.015
8	517.7	Fe	0.004	18	821.6	N	0.017
9	589.0	Na	0.945	19	844.6	O	0.006
10	589.6	Na	0.599	20	854.5	H	0.006

Fig. 4.

Importance weights and related elements of the most important 20 lines evaluated by IW-PCA.

3.3 Importance evaluation using random forests

Random Forests (RF) is an integrated classifier composed of a set of decision tree classifiers. It is based on the Classification and Regression Trees (CART) model and belongs to Ensemble Learning, a branch of machine learning [38]. With a given argument, each decision tree classifier votes to determine the final classification result. As a classification model based on the Decision Tree, the node is divided by the difference between each sample at a certain spectral line in the process of generating each tree [39,40]. If the two bacterial samples have a large difference in intensity at a certain line, or maybe one of the bacteria does not have this feature line, then the two bacteria can be directly distinguished at this node.

The spectra number of training set (described as N) was 75 for each sample, 450 for all. Each time a spectrum was chosen from each sample randomly, 450 spectra were chosen and built a new data set after 75 times repeatedly through putting back method. Based on this new set, a CART binary decision tree model was established. This process was called self-boosting [41] and used to reduce the training set relevance of each decision tree. All the built trees were established through this way, and each tree classifier utilized a unique training set constructed by the self-boosting method. Each tree was grown to the maximum size until no further splits are possible. When N is large enough, through self-boosting, a result can be derived from Eq. (1) that about a third of the initial spectra were not chosen even once. This part of the spectral data was called out-of-bag data and could be used as an unknown set to test the model. In practice, spectral data is not large enough, the size of out-of-bag data remains uncertain. However, the possibility of over-fitting could also be reduced by self-boosting.

$$\underset{N\to \infty }{\lim }{(1-\frac{1}{N})}^N=\frac{1}{e}\approx 0.368$$ (1)

In the classification problem, assuming there are K classes, the probability of the sample points belonging to the k class is p_k. Then the probability distribution of the Gini index is defined as

$$\text{Gini}(D)={\displaystyle \sum _{k=1}^K{p}_k(1-p_k)=1-{\displaystyle \sum _{k=1}^K{p}_k^2}}$$ (2)

where D was the whole collection of six kinds of spectral data in this case, and K was six. For a given sample set, the Gini index is calculated by

$$\text{Gini}(D)=1-{{\displaystyle \sum _{k=1}^K\left(\frac{\left|C_k\right|}{\left|D\right|}\right)}}^2$$ (3)

where C_k is a subset of samples belonging to the k class of D. |D| and |C_k| are the sizes of collection D and C_k respectively. If the sample collection D can be divided into two parts according to whether the classification basis A is equal in two parts, then under condition of classification basis A, the Gini index can be defined as

$$\mathrm{Gini}(D,A)=\frac{\left|D_1\right|}{\left|D\right|}\mathrm{Gini}(D_1)\text{+}\frac{\left|D_2\right|}{\left|D\right|}\mathrm{Gini}(D_2)$$ (4)

where Gini(D) describes the uncertainty of set D, and Gini(D, A) describes the uncertainty after divided by the classification basis A. For each tree, when the classification basis A was used to divide the whole set, the degree of Gini index reduction was calculated as

$${\Delta }_j=\text{Gini}(D)-\text{Gini}(D,A)$$ (5)

where j represents results calculated from different splits at the same basis. The corresponding classification basis with large Gini index reduction value expresses the large decreasing of the sample set’s uncertainty and can be considered as important basis. In this case, each spectra line can be regarded as a classification basis A. Therefore, the random forests classification model has derived an important function: the importance of each spectra line can be measured by the decreasing of their Gini index. For each spectra line, listed the 450 numbers from high to low. When chose the split between every two number, a Gini(D, A) can be calculated. And in order to get the largest ${\Delta }_j$, the smallest one was chosen as Gini(D, A). Then the average of $\Delta$ $,\overline{\Delta },$ calculated for each line was defined as its importance weight. In the built random forests model, there were 85 chosen spectra lines in all, and for every CART decision tree, 9 specific lines were chosen randomly to build the tree model. Each decision tree grew completely without pruning.

According to the value of the importance of lines measured using RF algorithm, the appropriate lines were extracted as features for bacterial classification. In the Python language, RF algorithm has integrated function package named sklearn package. Call the RandomForestClassifier function in the sklearn package, and set the parameters as follows:

• (1) The size of the random forests was 10,000 in order to ensure the stability of the importance measurement results.
• (2) The parallel thread parameter was −1, meaning that the number of parallel thread was equal to the number of CPU cores.
• (3) The default minimum number of spectra used to divide node in the function was 2.
• (4) The minimum number of spectra contained in the leaf node was 1.

The most important 20 spectral lines and their normalized importance weights were listed in Table 3 and shown in Fig. 5 in the wavelength order. As illustrated in Fig. 5, bars of different colors show that the 20 lines extracted by RF are related to 7 elements (C, Ca, Fe, Na, K, N, and H) and one molecular band (CN band).

Table 3. The most important 20 feature lines evaluated by Random Forests.

Feature number index	Line Wavelength (/nm)		Corresponding element	Normalized importance weight	Feature number index	Line Wavelength (/nm)	Corresponding element	Normalized importance weight
1		247.8	C	0.182	11	417.6	Fe	0.177
2		279.5	Ca	0.258	12	568.3	Na	0.520
3		279.8	Ca	0.178	13	589.0	Na	0.898
4		317.5	Fe	0.177	14	589.6	Na	0.745
5		384.6	CN	0.176	15	766.5	K	1.000
6		385.7	CN	0.178	16	769.9	K	0.978
7		386.5	CN	0.212	17	818.5	N	0.304
8		388.0	CN	0.240	18	820.0	N	0.500
9		393.4	Ca	0.283	19	854.5	H	0.266
10		396.8	Ca	0.225	20	866.5	H	0.216

Fig. 5.

Importance weights and related elements of the most important 20 lines evaluated by Random Forests.

As shown in Fig. 4 and Fig. 5, the two evaluating methods gave different importance of lines and based on this the importance order of lines was different. It can be concluded that the top 5 feature lines all belong to the main emission lines corresponding to Na and K. For Na, the empty slide also had clear lines, but the intensities were different with bacteria samples. And for K, there was significant difference between slides and samples. These reflected that the lines of Na and K represented pathogenic bacteria and were considered more effective for bacterial classification than other elements. This coincides with the biologically prior knowledge that Na⁺ and K⁺ are the two important cations in living cell and play an important role in controlling intracellular and extracellular balance. Although the bacteria contained a large amount of C, H, O, and N elements, the environment also contained a large amount of these elements when the LIBS experiment was carried out in a standard atmospheric air environment. When laser interacted with samples, the surrounding air particles were also excited, therefore, the contribution of C, H, O, and N to the classification was less than the metal elements.

Considering the most important 20 lines evaluated by IW-PCA and RF, which were listed in Table 4, 10 lines were selected both in the two algorithms (related to Ca, Na, K, N, and H). Besides, lines related to CN were only selected by RF and Oxygen lines were only selected by IW-PCA. The two methods both gave high importance weights to Potassium lines, and both of them selected two Potassium lines at 766.5nm and 769.9nm. Still some elements like Fe, Ca, Na, N and H were related to the extracting lines in both two methods, but the lines related to each element were not exactly same. In general, the RF selected less lines related to elements both in the samples and ambient environment gas.

Table 4. Comparing of differences between the most important 20 lines evaluated by IW-PCA and Random Forests.

FEATURE LINES(NM)	247.8	279.5	279.8	317.5	384.6	385.7	386.5	388.0	393.4	396.8
ELEMENT	C	Ca	Ca	Fe	CN	CN	CN	CN	Ca	Ca
IW-PCA		√	√						√	√
RF	√	√	√	√	√	√	√	√	√	√
FEATURE LINES(NM)	417.6	422.7	430.3	445.5	517.7	568.3	589.0	589.6	656.3	744.6
ELEMENT	Fe	Ca	Ca	Ca	Fe	Na	Na	Na	H	N
IW-PCA		√	√	√	√		√	√	√	√
RF	√					√	√	√
FEATURE LINES(NM)	746.6	766.5	769.9	777.4	818.5	820.0	821.6	844.6	854.5	866.5
ELEMENT	N	K	K	O	N	N	N	O	H	H
IW-PCA	√	√	√	√	√		√	√	√
RF		√	√		√	√			√	√

3.4 Classification results based on an SVM classifier

An SVM classifier was chosen to classify the spectral data in this paper. As a supervised learning model used in data classification and regression, it can be used to classify linearly separable data directly [42,43]. Moreover, using kernel function to map the non-linearly separable data from low-dimensional space to high-dimensional feature space, SVM can classify non-linearly separable data without increasing the calculating complexity [44,45]. With such advantage, SVM has been widely used to classify LIBS spectral data [42,44–47]. Commonly used kernel functions include Polynomial Kernel Function, Gaussian Kernel Function, String Kernel Function and so on. Gaussian Kernel Function was used in our analysis process.

Generally, when data are linearly separable, two parallel hyperplanes can be chosen to separate two types of data correctly. Linear separable SVM maximize the interval between two hyperplanes to determine the maximum-margin hyperplane which lies halfway between them. The maximum-margin hyperplane can be defined by

$$wx+b=0$$ (6)

where w is the normal vector and b is the intercept.

The value of the function margin y_i(wx_i + b) represents whether the classification is correct or not and the level of confidence. However, when w and b both change with multiples, the function margin has changed but the hyperplane remains the same one. Therefore, the normalized geometric margin in Eq. (7) is used to represent the confidence of the classification and the magnitude of the error more reliably.

$$\gamma \text{=}\frac{y_{\text{i}}(w{x}_i+b)}{\Vert w\Vert }$$ (7)

The SVM classifier was built based on MATLAB version 2016a (MathWorks, Natick, Mass.). Based on the order of importance weights, the first j (j = 1, ..., 20) important lines listed in Table 2 and Table 3 were used as inputs of the SVM classifier, respectively. With Gaussian Kernel Function, the best punishment parameter c = 65.0333, and the best kernel parameter g = 0.1000 were automatically determined based on Particle Swarm Optimization algorithm.

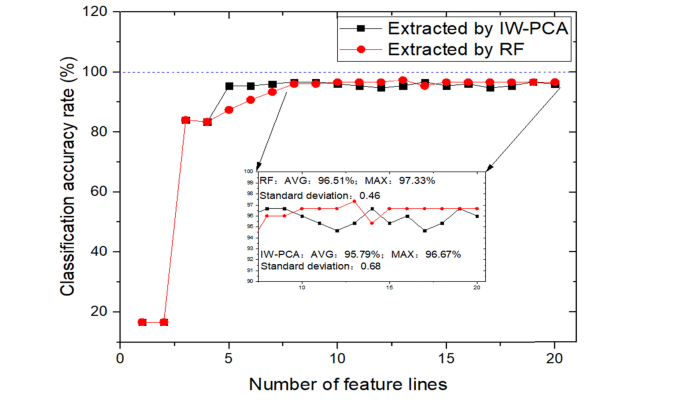
When using whole 85 lines to build the model, the classification accuracy reached 95.33% and it cost about 143.71 s for analyzing. The feature lines were selected by importance order evaluated by IW-PCA and RF algorithms. When using different number of feature lines extracted by these two algorithms to build the model, the CCRs of the testing set were shown in Fig. 6 and the analyzing time was around 21.86 s to 71.83 s. The number of feature lines from 1 to 20 showed in Fig. 6 were chosen according to the order of importance.

Fig. 6.

CCR according to the number of feature lines (Extracted by IW-PCA and RF, respectively) used in SVM model.

Due to the high degree of similarity between the spectra of bacterial samples, especially for the same type of bacteria, it is difficult to classify all bacterial samples by one or two lines. As shown in Fig. 6, when using only one or two feature lines as inputs of the classifier, no matter they were extracted by IW-PCA or RF, the CCR was only 16.67%. When the third line was added to the classifier, the CCR became higher than 80%. For IW-PCA and RF, the CCRs of models built using less than 4 feature lines were same. For the RF extracting method, using more than 8 feature lines to build the classifier, the classification results tend to be stable. The CCR remained 96.67% with 10 to 20 feature lines except two points (95.33% and 97.33%). For the IW-PCA extracting method, using more than 5 lines to build the model, the classification accuracy of the test set fluctuated from 94.67% to 96.67%. Using 8 to 20 lines extracted by RF and IW-PCA as inputs of the SVM classifier, the results were listed in Table 5.

Table 5. CCRs of SVM using feature lines extracted by IW-PCA and RF.

	Average CCR	Highest CCR	Standard deviation
IW-PCA	95.79%	96.67%	0.68
RF	96.51%	97.33%	0.46

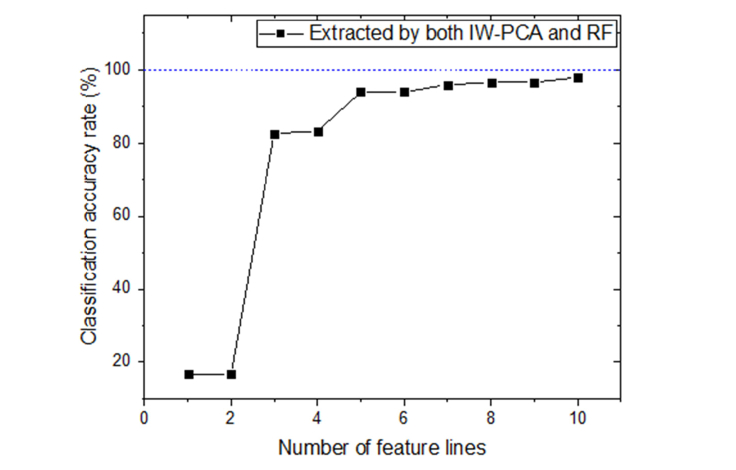
For RF algorithm, average CCR was 96.51%, standard deviation was 0.46, and the highest classification rate reached 97.33%. And for IW-PCA, the highest classification rate reached 96.67%, the average CCR was 95.79% with a standard deviation of 0.68. From this perspective, extracting the feature lines based on importance evaluated by IW-PCA or RF can improve the CCR effectively. Considering the results mentioned in Table 4, using feature lines extracted both by IW-PCA and RF may improve the CCR further. According to the importance order evaluated by RF, using different number of feature lines selected by both two algorithms as inputs of SVM classifier, the results were illustrated in Fig. 7.

Fig. 7.

CCR according to the number of feature lines (Extracted by both IW-PCA and RF) used in SVM model.

As shown in Fig. 7, when using all 10 feature lines selected by both two algorithms, the CCR was improved further and reached 98% finally and the process cost 26.39s, which illustrated that the effectiveness of the two algorithms was mutually validated, and the lines evaluated important both by IW-PCA and RF contributed more to the classification accuracy.

Comparing with the CCR of whole spectra (95.33% in this case), the listed results verified the extracted feature lines based on evaluated importance weights were meaningful to classification. It can be summarized that evaluating importance weights of lines is helpful to extract optimal feature lines. Feature lines extracted by importance evaluated with RF were more suitable for the classification application of LIBS combined with SVM. This may be because that the PCA algorithm commonly extracts the lines with high peak intensities, and cannot make sure these lines are the most dominant feature lines in the classification. Furthermore, the two methods can confirm each other and the lines evaluated important both by IW-PCA and RF contributed more to the CCR.

4. Conclusion

The complexities and tardiness in identification of pathogenic bacteria make it one of the most urgent problems in clinical hospital setting. In view of this, LIBS combined with SVM were utilized to identify and classify 6 kinds of typical pathogens in this paper. To improve the technique performance, IW-PCA and RF were proposed to evaluate the importance of spectral lines and extract optimal lines as classifier inputs. It can be considered that the importance weights of each line can be evaluated and appropriate feature lines can be extracted by using these two algorithms. Using the whole 85 lines to build the model, it can reach an accuracy of 95.33% in an average time about 143.71 s. Using lines extracted by IW-PCA and RF, the average accuracy reached 95.79% and 96.51% respectively, and analyzing time reduced to around 21.86 s to 71.83 s. Considering the CCR performed better than using all lines in the classifier, the importance of feature lines was verified. Using lines extracted by RF as inputs, the average and highest CCRs were both higher than using lines selected by IW-PCA. Therefore, RF algorithm is more suitable for evaluating the importance of spectral lines than IW-PCA using in LIBS-SVM classification mechanism. Furthermore, the two methods mutually verified the importance of selected lines and the lines evaluated important both by IW-PCA and RF contributed more to the CCR. Using the feature lines selected both by two algorithms, the highest classification accuracy is 98%, which demonstrated LIBS is a potential feasible technique in identifying pathogenic bacteria.

Funding

National Natural Science Foundation of China (NSFC) (61775017).

Disclosures

The authors declare that there are no conflicts of interest related to this article.