Automatic segmentation of OCT retinal boundaries using recurrent neural networks and graph search

Abstract

The manual segmentation of individual retinal layers within optical coherence tomography (OCT) images is a time-consuming task and is prone to errors. The investigation into automatic segmentation methods that are both efficient and accurate has seen a variety of methods proposed. In particular, recent machine learning approaches have focused on the use of convolutional neural networks (CNNs). Traditionally applied to sequential data, recurrent neural networks (RNNs) have recently demonstrated success in the area of image analysis, primarily due to their usefulness to extract temporal features from sequences of images or volumetric data. However, their potential use in OCT retinal layer segmentation has not previously been reported, and their direct application for extracting spatial features from individual 2D images has been limited. This paper proposes the use of a recurrent neural network trained as a patch-based image classifier (retinal boundary classifier) with a graph search (RNN-GS) to segment seven retinal layer boundaries in OCT images from healthy children and three retinal layer boundaries in OCT images from patients with age-related macular degeneration (AMD). The optimal architecture configuration to maximize classification performance is explored. The results demonstrate that a RNN is a viable alternative to a CNN for image classification tasks in the case where the images exhibit a clear sequential structure. Compared to a CNN, the RNN showed a slightly superior average generalization classification accuracy. Secondly, in terms of segmentation, the RNN-GS performed competitively against a previously proposed CNN based method (CNN-GS) with respect to both accuracy and consistency. These findings apply to both normal and AMD data. Overall, the RNN-GS method yielded superior mean absolute errors in terms of the boundary position with an average error of 0.53 pixels (normal) and 1.17 pixels (AMD). The methodology and results described in this paper may assist the future investigation of techniques within the area of OCT retinal segmentation and highlight the potential of RNN methods for OCT image analysis.

1. Introduction

Optical coherence tomography (OCT) is a non-invasive imaging technique that allows high-resolution cross-sectional imaging of ocular tissues such as the retina [1–3]. Retinal OCT imaging has been used extensively for characterizing the normal retina and its individual layers and in the detection and monitoring of ocular diseases such as age-related macular degeneration (AMD) [4–6], glaucoma [7], and diabetic retinopathy [8] which present changes in the normal retinal layer topology. However, the manual analysis of OCT images to extract the boundary position and subsequent structural characteristics of the retinal layers is time consuming, subjective, and prone to error, hence the need for efficient and automatic segmentation techniques.

There has been extensive previous work in the area of automatic OCT image analysis, and the segmentation of retinal layers has been a significant focus, with a range of approaches presented including: Markov boundary models [9], sparse higher order potentials [10], diffusion filtering [11], diffusion maps [12], gradient maps [13], Chan-Vese (C-V) models [14], kernel regression (KR)-based classification [15], and graph-based methods [13,16,17]. The drawback with a number of these methods is their reliance on specific “ad-hoc” rules, resulting in poor performance in the presence of noise and/or artifacts. Recent work has attempted to address these issues by utilizing machine learning techniques for OCT image segmentation. These recent studies have used a number of approaches including support vector machines [18], neural networks [19–30] and random forests [31]. Fang et al [20] utilized a patch-based convolutional neural network and graph search based approach (CNN-GS) to segment nine retinal layers in OCT images of patients with non-exudative age-related macular degeneration. Extending upon this, Hamwood et al [21], investigated the effect of patch size and network complexity on the overall performance and proposed an improved CNN architecture for analysis of OCT images of healthy eyes. Loo et al [22], used a novel deep learning approach (DOCTAD) that combined convolutional neural networks and transfer learning to perform the segmentation of photoreceptor ellipsoid zone defects in OCT images. ReLayNet, proposed by Roy et al [23], utilized a fully-convolutional neural network architecture to perform semantic segmentation of retinal layers and intraretinal fluid in macular OCT images. Fully-convolutional networks were also utilized by Xu et al [24], in a dual-stage deep learning framework for retinal pigment epithelium detachment segmentation.

The recurrent neural network (RNN) has been used for a variety of problems, particularly where sequential data is present. Some examples include language modelling [32], machine translation [33], handwriting recognition/generation [34], sequence generation [35], and speech recognition [36,37]. The effectiveness of RNNs when applied to image-based tasks has also been investigated. Visin et al. [38] compared the image classification ability of an RNN to that of a CNN and presented a novel architecture (ReNet) specifically designed to handle 2D images as the input. One layer of the ReNet architecture contained four RNNs, each of which was designed to sweep over the image in a different direction. Performance of the ReNet architecture for evaluating the MNIST (28x28 grayscale), CIFAR-10 (32x32 RGB), and SVHN (32x32 RGB) image data sets was reported to be similar to some CNNs. However, their architecture did not outperform state-of-the-art CNNs on any of the data sets. In a more recent paper [39], the ReNet architecture was explored further and coupled with a CNN for use in end-to-end image segmentation, reporting state-of-the-art performance on the Weizmann Horse (variable sized grayscale and RGB), Oxford Flowers 17 (variable sized RGB), and CamVid (960x720 RGB) data sets. In particular, the authors cited the usefulness of RNNs to capture global dependencies. Earlier work by Graves et al [40], also explored the application of RNNs to images, presenting a multi-dimensional RNN (MD-RNN) in which they replaced the single recurrent connection with one for every dimension in the input. Likewise, another variant of the RNN, the convolutional LSTM (C-LSTM), was introduced by Shi et al [41], in their work with short-term precipitation forecasting.

Recently, several papers have examined the use of RNNs for medical image analysis. Chen et al [42], combined a fully-convolutional network (FCN) approach with a recurrent neural network for 3D biomedical image segmentation in which the images were comprised of a sequence of 2D slices. The FCN was used to extract intra-slice contexts into feature maps, which were then passed to the RNN to extract the inter-slice contexts. In their work on automatic fetal ultrasound standard plane detection, Chen et al [43], used a knowledge transferred network that first extracted spatial features using a CNN which were then explored temporally using a RNN. A similar methodology was employed by Kong et al [44], using a temporal regression network (TempReg-Net) for end-systole and end-diastole frame identification in MRI cardiac sequences. Stollenga et al [45], introduced their PyraMid-LSTM and both highlighted the effectiveness of RNNs for spatiotemporal tasks and reported state-of-the-art performance on a data set for brain MRI segmentation. Investigating dynamic cardiac MRI reconstruction, Qin et al [46], used a novel convolutional recurrent neural network which outperformed existing techniques in terms of both speed and accuracy and also required fewer hyper parameters. In another paper, Xie et al [47], attempted to use a clockwork recurrent neural network (CW-RNN) [48] based architecture to accurately segment muscle perimysium.

While a RNN approach has proven successful in the analysis of a range of medical images, to the best of our knowledge, there is no previous work utilizing RNNs as an approach to segment retinal boundaries in OCT images. There is also little evidence of RNNs being applied directly to individual medical images to extract spatial features. Instead, they have been used predominantly to extract temporal features from sequences of feature maps, with convolutional neural networks (CNNs) preferred to operate spatially on each image as a prior step. In this work, a novel recurrent neural network combined with a graph search approach (RNN-GS) is presented. This combines patch-based boundary classification using RNNs with a subsequent graph search to delineate retinal layer boundaries. This approach is partly inspired by the work of Fang et al [20], but in the methodology presented here the CNN is replaced with a RNN. A detailed selection of the RNN architecture and configuration as well as the evaluation of the optimal RNN model is presented.

The paper is structured as follows. In Section 2, the RNN-GS methodology and approach is outlined, including details about the data sets used as well as the RNN model and architecture selection. Section 3 presents experimental classification results for a range of RNN architectures which were used to inform the empirical selection of a suitable RNN design. Section 4 presents the segmentation results for the selected RNN design with performance evaluated against other CNN based methods. Discussion of the method and results are provided in Section 5. Concluding remarks are included in Section 6.

2. Method

2.1 Data set 1 (normal OCT images)

The first data set (data set 1) used in this work consists of a range of OCT retinal images from a longitudinal study that has been described in detail in a number of previous publications [21,49–51], The data comprises OCT retinal scans for 101 children taken at four different visits over an 18-month period. All subjects had normal vision in both eyes and no history of ocular pathology. The images were acquired using the Heidelberg Spectralis (Heidelberg Engineering, Heidelberg, Germany) SD-OCT instrument. At each visit, each subject had two sets of six foveal centered radial retinal scans taken. The instrument’s Enhanced Depth Imaging mode was used and automatic real time tracking was also utilized to improve the signal to noise ratio by averaging 30 frames for each image. The acquired images each measure 1536x496 pixels (width x height). With a vertical scale of 3.9 µm per pixel and a horizontal scale of 5.7 µm per pixel, this corresponds to an approximate physical area of size 8.8x1.9 mm (width x height). These images were exported and analyzed using custom software where an automated graph based method [13,52], was used to segment seven retinal layer boundaries for each image. This segmented data was then assessed by an expert human observer who manually corrected any segmentation errors. Throughout this paper, “B-scan” refers to an individual full-size (1536x496) image while “A-scan” corresponds to a single column of a B-scan.

The seven layer boundaries within the labelled data include the outer boundary of the retinal pigment epithelium (RPE), the inner boundary of the inner segment ellipsoid zone (ISe), the inner boundary of the external limiting membrane (ELM), the boundary between the outer plexiform layer and inner nuclear layer (OPL/INL), the boundary between the inner nuclear layer and the inner plexiform layer (INL/IPL), the boundary between the ganglion cell layer and the nerve fiber layer (GCL/NFL) and the inner boundary of the inner limiting membrane (ILM).

For computational reasons, only a portion of all the described data was used throughout this work. Two subsets of data are defined here. For neural network training and validation, a set of images (labelled data A) was selected. For training, 842 B-scans were used consisting of all available scans from both sets from 39 randomly selected participants’ first two visits. For validation, 223 B-scans were used consisting of all available scans from both sets from 20 different randomly selected participants’ third visit. A second set of images (labelled data B) was selected for evaluation of the method. This set consisted of 115 images comprised of all available scans from one set from 20 randomly selected participants’ fourth visit. There was no overlap of participants or visits between the training, validation and evaluation sets with the intention of obtaining an accurate representation of the network generalizability to unseen data.

2.2 Data set 2 (AMD OCT images)

The second data set (data set 2) [53] consists of a range of OCT retinal images from individuals with and without age-related macular degeneration (AMD). Within this, 100 B-scans each from 269 AMD participants and 115 healthy participants are provided. For each B-scan, segmentation of three retinal layer boundaries are provided (from an automated graph-search method that was manually corrected by expert image graders). The three layer boundaries within the labelled data include the inner aspect of the inner limiting membrane (ILM), the inner aspect of the retinal pigment epithelium drusen complex (RPEDC) and the outer aspect of Bruch’s membrane (BM).

Like data set 1, not all available data was used in this work due to computational reasons. Two subsets of data are again defined here with ‘labelled data A’ for network training/validation and ‘labelled data B’ for evaluation. Only images from the AMD individuals were used from this data set. Labelled data A comprised of 15 B-scans (scans 40-54) each from 160 participants (participants 1-160) (2,400 B-scans total). From this, the first 120 participants (participants 1-120) were used for training (1,800 B-scans) and the final 40 participants (participants 121-160) were used for validation (600 B-scans). Labelled data B consisted of 15 scans (scans 40-54) each from the next 20 participants not used in labelled data A (participants 161-180) (300 B-scans total). There was no overlap between data used in labelled data A and B or between the training and validation sets.

2.3 Overview

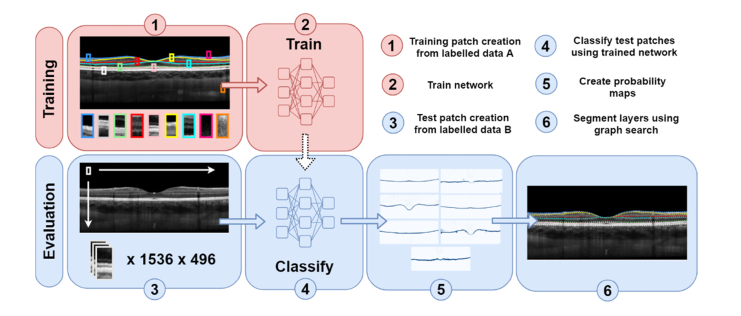
An overview of the recurrent neural network and graph search method (RNN-GS) utilized in this paper is presented in Fig. 1. This method is similar to that used by Fang et al [20] but here a RNN is used in place of the CNN.

Fig. 1.

Overview of the RNN-GS method for segmentation of retinal layers, where red boxes represent training steps and blue are evaluation steps. For training (labelled data A) and evaluation (labelled data B) there was no overlap between participants.

Further details of the recurrent neural network model are provided in Section 2.4. For the method, there are two main phases: training and evaluation. In the training phase, the labelled OCT data (labelled data A), is used to construct a dictionary of image patches for each class. The patches are centered upon the layer boundaries of interest. These patches are then used to train the RNN as a classifier as detailed in Section 2.5. In the second phase, evaluation of new data (labelled data B) is performed. The OCT images are split into patches for every single pixel of the image. The trained neural network is then used to predict the class of each patch and generate per class probability maps for the entire image. The layer boundaries are then delineated by performing a shortest-path graph search as outlined in Section 2.6. The methods and models used for comparison are described in Section 2.7. Finally, the overall evaluation of the method is described in Section 2.8.

2.4 Recurrent neural network model

Recurrent neural networks (RNNs) differ from other network configurations, such as CNNs, with the addition of feedback from the output to the input. This enables the network to utilize a past sequence of inputs to inform future outputs, which ultimately gives the network memory. RNNs may be trained using an extension of the backpropagation algorithm called backpropagation-through-time (BPTT) [54–56]. In their basic form, RNNs are comprised of recurrent units which pass a concatenation of the previous output and current input through an activation function. However, these simple recurrent units have issues in practice. Most notably are the problems of vanishing and exploding gradients [57–59]. More complex recurrent units have been designed and proposed to deal with this, namely the long-short term memory (LSTM) [57], and gated recurrent unit (GRU) [60].

The layers within the ReNet architecture [38], use a set of four RNNs operating in different directions to perform the task of image classification. Each RNN layer can operate either horizontally or vertically over sequences of image pixels and this can be done with one pass (unidirectional), or two passes (bidirectional). A number of parameters are also associated with each layer including the receptive field size (width x height in pixels), number of filters, and type of recurrent unit. Each additional filter can give the network an opportunity to learn a different pattern. In terms of the recurrent unit types, both the LSTM and GRU are considered as options within each layer. The receptive field corresponds to the volume that is processed by the RNN at each step in each sequence. For each RNN, the spatial dimensions (width and height) of the output volume are equal to the respective sequence lengths in each direction. These sequence lengths are equal to the spatial dimensions of the input volume divided by the corresponding receptive field dimensions. Meanwhile, the depth (number of channels) of the output volume is simply equal to the number of filters.

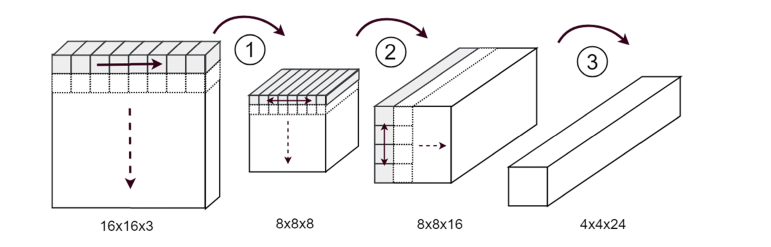
For example: an 8 filter horizontal unidirectional RNN operating with an input volume size of 16x16x3 (width x height x channels) and a receptive field size of 2x2, would mean that a volume of size 2x2x3 is processed by the RNN for each of 8 steps (horizontally), for each of 8 sequences (vertically), with an overall output volume size of 8x8x8. A visualization of this example is illustrated in step 1 of Fig. 2. For bidirectional layers, the output volumes of each pass are concatenated together along the depth dimension as depicted in steps 2 and 3.

Fig. 2.

Example of a model with three stacked RNN layers showing how the activation volume is manipulated as it passes through the network. Each grey volume corresponds to the volume (receptive field width x receptive field height x channels) processed at a particular step within the first sequence operated on by the RNN. The direction of this operation is indicated by the solid arrows. The dotted outline volumes belong to each step of the following sequence and the dashed arrows indicate the order the sequences are processed in. 1) Horizontal unidirectional RNN with a 2x2 receptive field and 8 filters. 2) Horizontal bidirectional RNN with a 1x1 receptive field and 16 filters (8 / pass). 3) Vertical bidirectional RNN with a 2x2 receptive field and 24 filters (12 / pass).

To avoid overfitting to the training data, the dropout regularization technique was utilized [61]. Here, each layer is equipped with a level of dropout which corresponds to the percentage of units in that layer which are randomly turned off (dropped) in each epoch. Batch normalization [62], at the input to each layer was also used. This ensures that the mean and variance of each mini-batch is scaled to 0 and 1 respectively, which can help to improve the performance and stability of the network during training.

2.5 Training and patch classification

The RNN model is trained as a classifier. This is done by constructing small overlapping patches from the OCT images and assigning each to a class based on the layer boundary that they are centered upon. These constitute the “positive” training examples. For patches not centered upon a layer boundary, Fang et al [20], utilized a single class for “negative” training examples, also called the “background” class. In this study, two background classes were used with the intention to better capture the different background features of the OCT image, particularly some of the features and image artefacts in the retina, vitreous (anterior to the retina) and in the choroid and scleral region (posterior to the retina). The first background class consists of patches centered within the retina (between the ILM and RPE for data set 1 and between the ILM and BM for data set 2) as well as in a small region of both the vitreous and choroid directly above and below the retina respectively. The height of these smaller regions is set to be equal to the patch height. All patches within the described area that are not centered on any boundary are considered part of this class. The second background class consists of patches centered in a region bounded between the bottom of the first background class region and the bottom of the image. Zero-padding is added to any patches at the edge of images where required.

Using the ‘labelled data A’ images as described in Section 2.1 and 2.2, patches were created for both training and validation (for both data set 1 and data set 2). Patches were created for each class with background examples randomly selected within their corresponding ranges. To reduce computational burden, the total number of patches was restricted with patches only created for every eighth column of each image. For data set 1, the training set was comprised of ~1,450,000 patches with an additional ~380,000 for validation. This was a nine-class classification problem with equally weighted classes. Similarly, for data set 2, the training set was comprised of ~980,000 patches with an additional ~320,000 for validation. This was a five-class classification problem with equally weighted classes. In an effort to maximize training performance, all patches were normalized (0-1) before they were input to the network. However, unlike previous studies [13,20,21], intensity normalization and other image pre-processing steps were not used in this work for any of the data sets.

The Adam algorithm [63], a stochastic gradient-based optimizer, was used to train the network by minimizing log loss (cross-entropy) [64]. Empirically, Adam performs well in practice with little to no parameter adjustment and compares favorably to other stochastic optimization methods [63]. Due to Adam’s relatively quick convergence to good solutions in a small number of epochs, no early stopping was used for training. In addition, given the adaptive per-parameter learning rates that this optimizer possesses, no learning rate scheme was deemed to be necessary. The network was trained for 50 epochs with a batch size of 1024 and the model that yielded minimum validation loss was selected. This is similar to approaches described and used elsewhere [65,66]. The number of epochs and the batch size were chosen empirically, while the algorithm parameters were left at their recommended default values. The Keras API [67], with Tensorflow [68], backend in Python was the programming environment of choice.

2.6 Probability maps and graph search

For a single OCT test image, patches are generated for every pixel and passed to the trained neural network to be classified. From this, per class probability maps can be constructed and a graph search performed to delineate the layer boundaries. The idea was proposed by Chiu et al [13], for the segmentation of OCT images which has been adapted in a number of CNN studies [20,21]. However, in contrast to previous work, in this study the search path was not limited between the top and bottom layer boundaries. Each probability map can be used to construct a directed graph where the pixels in the map correspond to vertices in the graph. Each vertex is connected to its three rightmost neighbors (diagonally above, horizontally, diagonally below). The weights of these connections are given by the equation:

$$w_{sd}=2-(P_s+P_d)+\text{}{w}_{\min },$$ (1)

where P_s and P_d are the probabilities (0-1) of the source and destination vertices respectively, and w_min = 1x10⁻⁵ is a small positive number added for system stability.

To automate the start and end point initialization, a column of maximum intensity pixels is appended to both the left and right of the image. As well as being connected to their rightmost neighbors, vertices in these columns are also connected vertically from top to bottom. This allows for a graph search algorithm, like Dijkstra’s shortest-path algorithm [69], as used here, to start at the top-left corner and traverse the graph through to the bottom-right corner without any manual interaction. In this way, a graph cut is performed and this shortest path is used as the predicted location of the layer boundary.

2.7 Comparison of methods

A comparison between the RNN-based method and a patch-based CNN method is presented. The CNN method used is identical except that the RNN is replaced by a CNN. The CNN used here is the so-called “complex CNN” proposed by Hamwood et al [21]. This is trained identically to the RNN as described in Section 2.5.

In addition, a comparison between the patch-based method and a full image-based method is also provided. The method for comparison is a fully-convolutional network and graph search method (FCN-GS). For this, the patch-based classifier network is replaced with a U-Net [70], style architecture similar to that used by Venhuizen et al [26]. The FCN used here consists of four down sampling blocks each with two 3x3 convolutional layers. The network was trained for 50 epochs with a batch size of three using Adam with default parameters in a similar way to the patch-based networks in Section 2.5. Cross-entropy loss is used here to classify each pixel of the image into one of eight area classes. These eight areas are constructed between adjacent layer boundaries and the top and bottom of the image as required to create an overall area mask. For A-scans where at least one layer boundary is not defined, the image is zeroed with the corresponding columns in the area mask set to be defined as the top-most region. The overall method is similar to that used by Ben-Cohen et al [25], where the FCN is used for semantic segmentation on whole OCT images. Instead of classifying patches to generate probability maps, the Sobel filter is applied to the area probability maps output from the FCN to extract the boundary probability maps. A shortest-path graph search is then performed using these boundary probability maps in the same way as the patch-based method.

2.8 Evaluation

As described in Section 2.1 for data set 1 and Section 2.2 for data set 2, the images contained in labelled data B were used to evaluate the whole method. By comparing the predicted boundary positions to the truth (the segmentation from the expert human observer), the mean error and mean absolute error with their associated standard deviations were calculated for each layer across the whole test set. For data set 1, the full-width image was used for both patch creation and performing the graph search. However, due to the lack of consistency of the layers around the left and right extremities of the image (e.g. presence of optic nerve head and shadows), the first and last 100 pixels of each side were excluded from the final error calculations and comparisons. For data set 2, the full-width image was used as input to the network with a full-width probability map used for the graph search. However, as the true layer boundaries were not defined in every column, only those columns with all true boundary locations present were used for error calculations and comparisons.

3. RNN design

In order to design a suitable RNN architecture for patch classification, the impact of various network parameters on performance was examined. This section presents the results for a range of experiments including; the impact of patch size and direction of operation (Section 3.1), receptive field size (Section 3.2), number of filters (Section 3.3), stacking and ordering of layers (Section 3.4), and fully-connected layers (Section 3.5).

Visin et al. [38], used dropout after each layer in their network while Srivastava et al. [61], show that 50% dropout is a sensible choice for a variety of tasks. As such, 50% dropout is added after each fully-connected layer in Section 3.5. However, due to the relatively small number of parameters in the RNN layers used here, this level of dropout was deemed to be unnecessary and a potential hindrance to performance. Instead, 25% dropout is used after each RNN layer to ensure sufficient network capacity.

All networks were trained identically as described in Section 2.5. The experiments are performed only utilising data set 1 to allow for a fair comparison with Hamwood et al. [21], and their CNN which was also tested and optimized using normal OCT images. The generalizability of each network is assessed by measuring the classification accuracy on the validation set (described as part of labelled data A in Section 2.1). This is computed by dividing the number of correctly classified patches by the total number of patches. Due to randomness associated with both the network weight initialization and batch ordering leading to possibly different solutions, each experiment was performed three times and the results were averaged. These experiments were used to inform the careful selection of the most suitable final RNN architecture that was employed, which is described in Section 3.6.

3.1 Patch size and direction

For the design of the RNN, it is of interest to investigate the effect of the patch size (height x width pixels) on the network performance. In their CNN-GS approach, Fang et al [20], used a 33x33 patch size centered on the layer boundaries, while Hamwood et al [21], showed that increasing the size can improve network performance. With this in mind, 32x32, 64x32, 32x64 and 64x64 patches are compared on a range of RNN architectures. Even-sized dimensions are chosen to facilitate the network model and to avoid additional zero padding. Because of the even-size, the patch cannot be truly centered, and therefore each is consistently placed with the layer boundary positioned on the pixel above and to the left of the central point.

Table 1 outlines the results of the experiments undertaken. A small but significant improvement in classification accuracy was observed when using a vertically oriented 64x32 patch (longer along the A-scan direction) compared to a 32x32 (about 1.1% mean improvement). However, this level of improvement is much less pronounced when comparing the 32x32 with the horizontally oriented 32x64 patch size (about 0.4% mean improvement). Despite possessing twice as many pixels, the 64x64 patch does not exhibit a clear performance benefit compared to the 64x32 patch (below 0.1% mean improvement). Thus, the 64x32 patch size appears to yield the best trade-off between accuracy and complexity for the tested sizes. It should be noted that other patch sizes were not tested for computational reasons.

Table 1. Effect of patch size and direction on validation classification accuracy (%). The mean (standard deviation) of the accuracy for three training runs (GRU, 32 filters / pass, 2x2 receptive field, 25% dropout).

	Patch Size (height x width pixels)
Architecture	32x32	64x32	32x64	64x64	Mean
Vertical Unidirectional	95.17 (0.05)	96.28 (0.02)	95.44 (0.06)	96.26 (0.07)	95.78
Horizontal Unidirectional	94.48 (0.03)	95.77 (0.04)	95.13 (0.06)	96.10 (0.02)	95.37
Vertical Bidirectional	95.33 (0.06)	96.18 (0.05)	95.51 (0.02)	96.01 (0.12)	95.75
Horizontal Bidirectional	94.55 (0.08)	95.71 (0.09)	95.19 (0.06)	95.95 (0.15)	95.35
Mean	94.88	95.98	95.31	96.08

Within the ReNet layers [38], RNNs were used separately to process the input horizontally or vertically. To better understand the impact that the direction of operation has on network performance, these different options were considered. As shown in Table 1, the direction of operation appears to have a small impact on the classification accuracy, although it is worth noting that RNNs operating in the vertical direction outperform their horizontal counterparts by a small percentage. However, operating bi-directionally does not appear to yield improved performance.

3.2 Receptive field size

The effect of the receptive field size on the network performance was also investigated. Visin et al [38], used a receptive field size of 2x2 between each of their ReNet layers. Here, a variety of square and rectangular receptive field sizes were compared on a single-layer vertical unidirectional RNN with the results outlined in Table 2. Similar to the effect of patch size described in Section 3.1, the vertical rectangular receptive fields provide a marginal improvement in performance compared to the equivalent horizontal variants, attributable to the vertical nature of the layer structure in the image. Overall, most of the tested sizes give similar performance indicating that the size of the receptive field does not have a significant impact on the accuracy for the tested data set.

Table 2. Effect of receptive field size on validation classification accuracy (%). The mean (standard deviation) of the accuracy for three training runs are reported. (GRU, 32 filters, 64x32 patch size, single-layer vertical unidirectional RNN, 25% dropout).

Square		Rectangular
Size	Acc. (%)	Size	Acc. (%)	Size	Acc. (%)
1x1	96.12 (0.05)	1x4	96.10 (0.12)	8x1	96.37 (0.03)
2x2	96.28 (0.02)	4x1	96.28 (0.01)	2x8	96.08 (0.08)
4x4	96.29 (0.06)	2x4	96.24 (0.05)	8x2	96.44 (0.02)
8x8	96.13 (0.10)	4x2	96.35 (0.03)	4x8	96.13 (0.08)
16x16	95.82 (0.06)	1x8	96.09 (0.05)	8x4	96.38 (0.03)

3.3 Number of filters

Increasing the number of filters gives the neural network more parameters and hence more opportunity to learn. The change in classification accuracy, as the number of filters in a single layer vertical unidirectional RNN is varied, was investigated to better estimate the optimal number of filters and the impact on performance. Table 3 shows that adding more filters yields a small increase in classification accuracy, albeit with diminishing returns. For this single layer network, choosing 32 filters gives a good trade-off between accuracy and complexity.

Table 3. Effect of number of filters on validation classification accuracy (%). The mean (standard deviation) of the accuracy for three training runs are reported. (GRU, 2x2 receptive field, 64x32 patch size, single-layer vertical unidirectional RNN, 25% dropout).

Filters	Network parameters	Acc. (%)
8	37,273	95.62 (0.08)
16	74,857	96.05 (0.04)
32	151,177	96.28 (0.02)
64	308,425	96.32 (0.02)

3.4 Stacked layers and order

The ReNet architecture [38], uses several layers of RNNs, each of which first operate on the input vertically before horizontally. Here, the effect of adding additional layers to the network as well as the order that these are stacked together was evaluated. The results presented in Table 4 indicate that stacking layers improves the classification accuracy. Further, stacking both horizontal and vertical RNN layers yields greater performance than solely using vertical ones. There is no noticeable performance difference when changing the stacking order. This is also the case when using bi-directional RNNs, reinforcing the results presented in Section 3.1.

Table 4. Effect of stacked layers and order on validation classification accuracy (%). The mean (standard deviation) of the accuracy for three training runs are reported. (GRU, 2x2 receptive field, 32 filters / pass, 64x32 patch size, 25% dropout each layer).

Architecture	Acc. (%)	Architecture	Acc. (%)
Vertical Unidirectional	96.28 (0.02)	Horizontal Unidirectional + Vertical Unidirectional	96.69 (0.02)
2 x Vertical Unidirectional	96.59 (0.02)	Vertical Unidirectional + Horizontal Unidirectional	96.69 (0.02)
3 x Vertical Unidirectional	96.67 (0.01)	Horizontal Bidirectional + Vertical Bidirectional	96.70 (0.01)
		Vertical Bidirectional + Horizontal Bidirectional	96.73 (0.02)

3.5 Fully-connected layers

Visin et al. [38], used one or more fully-connected (FC) output layers of size 4096 in their ReNet architecture. The effect of including a fully-connected layer in our network design was also evaluated. The results presented in Table 5 show that adding a fully-connected layer has little benefit given the corresponding drastic increase in network parameters.

Table 5. Effect of fully-connected output layer size on validation classification accuracy (%). The mean (standard deviation) of the accuracy for three training runs are reported. (GRU, 2x2 receptive field, 32 filters, 64x32 patch size, single-layer vertical unidirectional RNN, 25% dropout for RNN layer, 50% dropout for fully-connected layer).

FC layer size	Network parameters	Acc. (%)
0	151,177	96.28 (0.02)
32	528,329	96.37 (0.04)
64	1,052,937	96.39 (0.04)
128	2,102,153	96.32 (0.03)

3.6 RNN architecture selection

Based on the experimental findings presented in Sections 3.1-3.5, a RNN architecture was selected. An overview of this architecture is provided in Table 6. As discussed in Section 3.5, no fully-connected layers are used due to their seemingly negligible performance benefit. Two sets of vertical and horizontal bi-directional layers are used, each with a size of 32 filters (16 per direction) and 25% dropout. Because the classification is based on pixel level accuracy, the first two layers are equipped with a 1x1 receptive field to enable the network to initially process the full-sized image on a pixel by pixel basis. The subsequent layers utilize a 2x2 receptive field with the intention of allowing the network to learn context at different levels. As described in Sections 3.1-3.5, the network operates with gated recurrent units (GRUs) which were found to perform comparably to LSTMs for this problem.

Table 6. The selected RNN architecture. 4 bidirectional layers are utilized with two operating vertically and two horizontally. Each layer contains 16 filters per pass for a total of 32 filters each.

Layer Architecture	Receptive Field	Filters (/ pass)
Vertical Bidirectional	1x1	16
Horizontal Bidirectional	1x1	16
Vertical Bidirectional	2x2	16
Horizontal Bidirectional	2x2	16

4. Results

4.1 Normal OCT data (data set 1)

Using normal OCT images (data set 1) as described in Section 2.1, the RNN-GS method was evaluated as described in Section 2 using the RNN architecture selected and trained as outlined in Section 3. Utilizing a 64x32 patch size, the network yielded a validation classification accuracy of 96.84% (0.05) taken as the average over three training runs. The mean accuracy of the seven boundary classes (excluding the background) was 98.25% (0.06) with the individual per-class accuracies ranging between 96.52% (0.08) (the IPL) and 99.24% (0.08) (the ILM). With the chosen patch size, the RNN architecture consisted of ~70,000 total parameters. Using an Nvidia GeForce GTX 1080Ti + Intel Xeon W-2125 the average evaluation time per B-scan was ~145 seconds. Here, the time to generate the probability maps was ~105 seconds on average with an average of ~40 seconds to perform the graph search for all seven boundaries.

The segmentation results for each layer boundary are presented below in terms of the mean error and the mean absolute error as well as their standard deviations. The patch-based approach was also evaluated using the Complex CNN architecture as described in Section 2.7 using the same set of 64x32 patches. To support the patch dimensionality, a 13x5 fully-connected output layer was used. Averaged over three training runs, the CNN provided a validation classification accuracy of 96.36% (0.04), 0.48% lower than the RNN. The per-class accuracies ranged between 95.65% (0.85) (the IPL) and 99.17% (0.11) (the ILM) with a mean accuracy for the seven boundary classes of 97.94% (0.08), 0.58% lower than the RNN. This CNN architecture consisted of ~1,200,000 total parameters, approximately 17 times as many as the RNN. Using the same hardware, the average evaluation time per B-scan was approximately 65 seconds, about 2.2 times faster than the RNN. Given the same time for the graph search (~40 seconds), this corresponds to ~25 seconds on average to generate the probability maps which is about 4.2 times faster than the RNN.

The segmentation errors in terms of boundary positions (in pixels) are presented in Table 7. The mean errors (and mean absolute errors) between methods are of similar magnitude, which suggests that the two networks give a similar level of performance with the RNN based approach performing marginally better on each boundary with a 0.02 to 0.05 pixels mean absolute error improvement with the exception of the GCL/NFL (0.12 pixels improvement in mean absolute error). This corresponds to an average improvement of 0.05 pixels (mean absolute error) with the RNN-GS yielding an average of 0.53 pixels mean absolute error on each boundary compared to the CNN-GS with 0.58. Both RNN-GS and CNN-GS performed the best on the ISe boundary with 0.33 and 0.35 pixels mean absolute error respectively, whereas both performed the poorest on the GCL/NFL with respective mean absolute errors of 0.84 and 0.96 pixels. The standard deviations of the errors are also consistently smaller for the RNN-GS method for each of the considered layers, indicating a greater level of consistency in the segmentation compared to the CNN-GS approach.

Table 7. Data set 1 (normal OCT images) position error (in pixels) of each layer boundary for each of the tested methods. The results are reported in mean values and (per A-scan standard deviation). The best results (smallest error) for each boundary are highlighted in bold text.

	RNN-GS		CNN-GS		FCN-GS
Layer Boundary	Mean error	Mean abs. error	Mean error	Mean abs. error	Mean error	Mean abs. error
ILM	0.01 (0.97)	0.46 (0.85)	−0.02 (1.01)	0.48 (0.89)	−0.16 (0.87)	0.53 (0.71)
GCL/NFL	0.11 (2.22)	0.84 (2.06)	-0.06 (2.90)	0.96 (2.74)	−0.10 (1.54)	0.79 (1.33)
INL/IPL	-0.13 (1.10)	0.56 (0.95)	−0.16 (1.17)	0.60 (1.02)	−0.26 (1.07)	0.61 (0.92)
OPL/INL	-0.10 (1.31)	0.69 (1.12)	−0.11 (1.41)	0.73 (1.21)	−0.16 (0.96)	0.63 (0.75)
ELM	0.02 (0.75)	0.35 (0.67)	0.09 (0.91)	0.38 (0.83)	−0.20 (0.88)	0.42 (0.80)
ISe	0.02 (1.02)	0.33 (0.96)	0.06 (1.03)	0.35 (0.98)	−0.05 (0.78)	0.38 (0.68)
RPE	−0.13 (1.10)	0.48 (1.00)	−0.16 (1.15)	0.53 (1.03)	-0.12 (0.90)	0.47 (0.78)

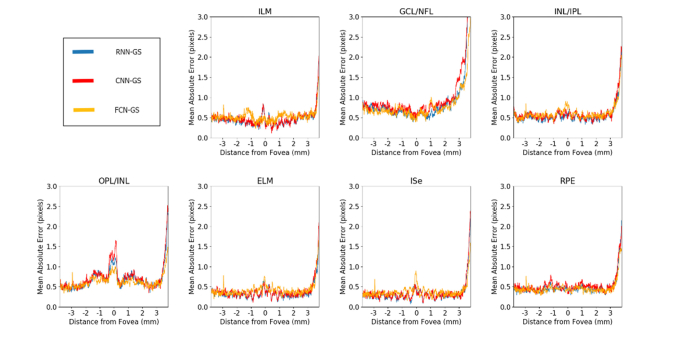
The error profiles in Fig. 3 also demonstrate consistently small errors across the central 6 mm of the B-scan for each layer, and also shows a high level of similarity between the two considered methods, with the exception of the GCL/NFL where RNN-GS performed noticeably better across the entire boundary. Observing these profiles also shows that both networks exhibit a noticeable central error spike for the OPL/INL boundary attributable to the merging of the layer boundaries at the fovea. Also, all the layer boundaries showed a spike in error on the far right side of the profile, which corresponds to the location of the optic nerve head for a number of scans, where retinal boundaries disappear in this region. Some example segmentation plots for data set 1 using the RNN-GS method are displayed in Fig. 4.

Fig. 3.

Data set 1 (normal OCT images) mean absolute error profiles of each boundary for each of the tested methods.

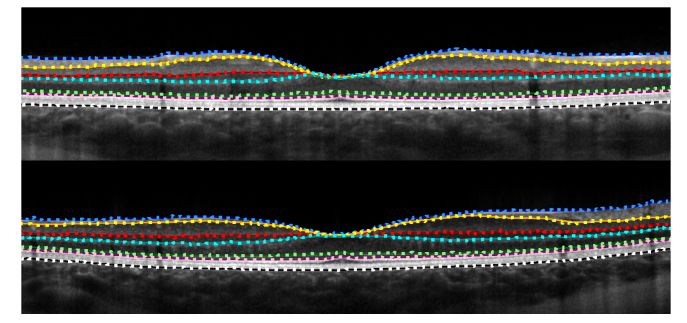
Fig. 4.

Example RNN-GS segmentation plots of two different participants from data set 1 (normal OCT images) with the locations of the true (solid lines) and predicted (dotted lines) boundaries marked showing the close level of agreement between them.

The patch-based method employed here is also compared with a fully-convolutional based approach (FCN-GS) as described in Section 2.7. In terms of the boundary position error (Table 7), the FCN-GS method is comparable in accuracy to RNN-GS and CNN-GS with an average mean absolute error of 0.55 pixels compared to 0.53 and 0.58 for RNN-GS and CNN-GS respectively. However, FCN-GS shows a greater level of consistency for the segmentations with smaller standard deviations on all boundaries with the exception of the ELM. Similar to the two patch-based methods, FCN-GS showed the lowest error on the ISe and highest error on the GCL/NFL. In addition, Fig. 3 shows the error profiles of FCN-GS to be somewhat similar to the two patch-based methods. The FCN contained ~490,000 parameters, approximately 7 times more than the RNN. However, the FCN was much faster in general with a per-image probability map creation requiring about one second, approximately 100 times faster than the RNN. For per-image evaluation overall, FCN-GS was ~3.5 times faster than RNN-GS when taking the graph search into consideration.

4.2 AMD OCT data (data set 2)

Given the importance of applying automatic image segmentation to pathological data, the RNN-GS, CNN-GS and FCN-GS methods were also evaluated using only AMD OCT images (data set 2), as described in Section 2.2. Again, 64x32 size patches are employed for the patch-based methods. Table 8 lists the results for the boundary position errors for the three layer boundaries present in this data. For RNN-GS, the ILM was relatively simple to segment with a mean absolute error of 0.38 pixels and standard deviation of 0.92 pixels showing a similar level of performance to that for the normal OCT images in data set 1 (Table 7). However, CNN-GS and FCN-GS performed significantly worse than RNN-GS on this boundary in terms of both accuracy and consistency, attributable to a small number of major failure cases not evident for RNN-GS. For the RPEDC boundary, the three methods performed comparably in terms of both accuracy and consistency, while FCN-GS clearly provided the best overall performance on the BM boundary. Overall, the RNN-GS and FCN-GS performed comparably overall in terms of mean absolute error with an average of 1.17 and 1.07 pixels respectively while CNN-GS was lower with an average of 1.53 pixels. Figure 5 shows some example segmentation plots from data set 2 using the RNN-GS method.

Table 8. Data set 2 (AMD OCT images) position error (in pixels) of each layer boundary for each of the tested methods. The results are reported in mean values and (per A-scan standard deviation). The best results (smallest error) for each boundary are highlighted in bold text.

	RNN-GS		CNN-GS		FCN-GS
Layer Boundary	Mean error	Mean abs. error	Mean error	Mean abs. error	Mean error	Mean abs. error
ILM	-0.03 (0.99)	0.38 (0.92)	-0.68 (7.26)	1.10 (7.21)	0.14 (4.29)	0.65 (4.24)
RPEDC	−0.52 (3.05)	1.05 (2.91)	−0.64 (3.30)	1.17 (3.15)	-0.43 (3.12)	1.03 (2.97)
BM	0.91 (4.69)	2.07 (4.31)	1.19 (5.01)	2.31 (4.60)	0.46 (3.79)	1.53 (3.50)

Fig. 5.

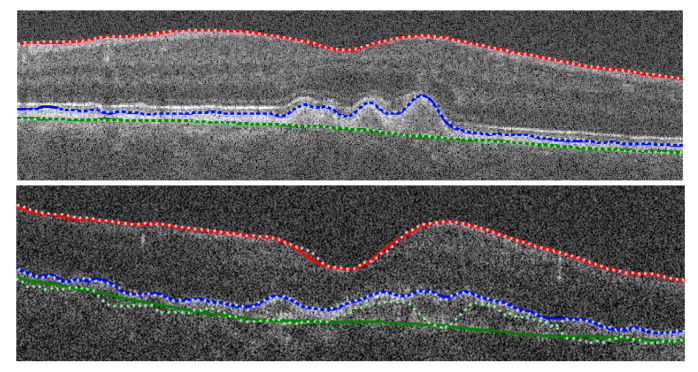
Example RNN-GS segmentation plots of two different participants from data set 2 (AMD OCT images) with the locations of the true (solid lines) and predicted (dotted lines) boundaries marked. The top image shows close agreement between the predictions and truths while the bottom image shows an example of a failure case for the BM boundary with a relatively high level of disagreement between the true and predicted boundaries.

5. Discussion

This study has proposed the novel use of recurrent neural networks to segment the retinal layers in macular OCT images of healthy and pathological data sets. The RNN-GS approach presented combines a recurrent neural network operating as a patch-based classifier with a subsequent graph search over the corresponding probability maps. This work was partly inspired by the previously proposed CNN-GS method for retinal image segmentation [20], as well as the RNN-based ReNet architecture [38], proposed as an alternative to CNNs for image classification. Despite the extensive work in the area of OCT retinal layer segmentation, to the best of our knowledge, RNNs have not previously been applied to OCT image analysis.

The careful selection of the final RNN architecture was informed using insights gained from a range of experiments. Of the tested patch sizes, the vertically oriented 64x32 rectangular patch (longer along the A-scan) yielded the best trade-off between accuracy and complexity. In particular, its superior performance compared to the horizontally oriented 32x64 variant, which is consistent with the vertical gradient change observed along the transition between adjacent layers. A similar result was obtained when observing the effect of the RNN operating direction, with vertical RNNs outperforming horizontal ones. On the other hand, varying the size of the receptive field had negligible effects on performance. For a single layer RNN, diminishing returns were observed with respect to the number of filters. This informed an appropriate trade-off between accuracy and complexity of 32 filters which was used for each layer in the final RNN architecture. With regards to the operating direction, stacking both horizontal and vertical layers outperformed unidirectional stacked layers. This informed the decision to utilize layers of both directions within the final network. Fully-connected output layers did not provide a sufficient accuracy/complexity trade-off and were therefore not included in the chosen RNN design. Like Visin et al [38], there was no observed performance difference between the LSTM and GRU recurrent units.

Using a data set comprising normal OCT images (data set 1), the segmentation results showed the RNN based approach performed competitively in comparison to a CNN approach using the same patch-size. RNN-GS showed marginally smaller mean absolute errors for all seven layer boundaries and a greater consistency (i.e. smaller standard deviations) in the segmentation than CNN-GS. Overall, mean absolute errors of less than one pixel for all seven layer boundaries were observed, with less than half a pixel for four of those boundaries, indicating close agreement to the truth. Despite possessing 17 times fewer parameters, the evaluation time of RNN-GS was longer than that of CNN-GS. This can be attributed to the relatively high number of operations required to process an image sequentially as is the case with the RNN.

To gauge the performance on pathological data, RNN-GS and CNN-GS were also evaluated using a data set comprising OCT images from patients exhibiting age-related macular degeneration (data set 2). The RNN showed competitive performance with smaller mean absolute errors for all three layer boundaries corresponding to a mean improvement of 0.36 pixels. In particular, CNN-GS exhibited a small number of major failure cases for the ILM boundary. These failure cases were the result of the relatively high level of noise within some B-scans where the ILM was less well defined. These failures were not evident for RNN-GS possibly indicating a greater robustness of the method in the presence of noise. Segmentation of the RPEDC and BM boundaries proved more challenging in the presence of pathological features. However, for both of these boundaries, RNN-GS exhibited marginally superior mean absolute errors and standard deviations compared to CNN-GS continuing the trend evident within the results from the normal OCT images.

It should be noted that this work did not focus on the performance of the method with regards to different ocular pathologies with only one type of pathological data (AMD) investigated here. In addition, the RNN network architecture here was optimized using data from normal OCT images. Future work should attempt to further explore the application of this method to pathological data by extending the types of pathologies present within the data as well as investigating an optimal network architecture for such.

In the past, RNNs have proven useful for tasks involving sequential data whereas CNNs have had considerable success when applied to image data. Consequently, RNNs have received less attention for image classification problems. Here, the ability of an RNN to perform competitively against a CNN on such a task was investigated. RNNs are suited to sequential data, so the good performance relative to the CNN may be attributed to the sequential nature of the retinal layer structure and features. In all, RNNs provide a viable alternative to CNNs for this particular problem even with retinal pathology and poor image quality conditions (AMD data).

It should be noted that the 64x32 patch size used here is not necessarily the most optimal, with a number of alternative patch sizes not tested for computational reasons. Nonetheless, these are promising results and the performance here is encouraging. Future work may investigate other patch sizes and, in particular, larger vertically-oriented rectangular patches as these appear to give the best tradeoff between performance and speed.

The patch-based approach presented here (RNN-GS) was compared to a full image-based approach utilizing a fully-convolutional network (FCN-GS). For normal OCT images (data set 1), the accuracy was comparable with RNN-GS. However, FCN-GS was more consistent in the segmentation with lower standard deviations for most boundaries. FCN-GS was also much faster in terms of evaluation highlighting this as a possible drawback of the patch-based method especially when time is critical (e.g. for many clinical applications where rapid segmentation performance is required). However, it should be noted that optimizing the speed of the RNN was not a focus here and should be investigated in future work.

For AMD OCT images (data set 2), the overall accuracy between RNN-GS and FCN-GS was again comparable. Like CNN-GS, FCN-GS exhibited a number of major failure cases, which were responsible for the relatively high mean absolute error and standard deviation on the ILM. On the other hand, FCN-GS was more accurate and consistent on the BM boundary. It is possible that the superior performance is a result of the greater amount of context available to the FCN while processing the whole image at once. Future work in the area may further investigate the relative performance of the patch-based method compared to full-image based methods.

6. Conclusions

In this paper, the RNN-GS method exhibited promising results for the segmentation of retinal layers in healthy individuals and AMD patients. In addition, RNNs have been identified as a sensible alternative to CNNs for tasks with images involving a sequence as is the case with the layer structure observed in the OCT retinal images used in this work. The results and the RNN-GS methodology presented here may assist future work in the domain of OCT retinal segmentation and highlight the potential of RNN-based methods for OCT image analysis.

Funding

Rebecca L. Cooper 2018 Project Grant (DAC); Telethon – Perth Children’s Hospital Research Fund (DAC).

Disclosures

The authors declare that there are no conflicts of interest related to this article.